Kinematic network of joint motion provides insight on gait coordination: An observational study on Parkinson's disease

Abstract

The analysis of gait kinematics requires to encode and collapse multidimensional information from multiple anatomical elements. In this study, we address this issue by analyzing the joints' coordination during gait, borrowing from the framework of network theory. We recruited twenty-three patients with Parkinson's disease and twenty-three matched controls that were recorded during linear gait using a stereophotogrammetric motion analysis system. The three-dimensional angular velocity of the joints was used to build a kinematic network for each participant, and both global (average whole-body synchronization) and nodal (individual joint synchronization, i.e., nodal strength) were extracted. By comparing the two groups, the results showed lower coordination in patients, both at global and nodal levels (neck, shoulders, elbows, and hips). Furthermore, the nodal strength of the left elbow and right hip in the patients, as well as the average joints' nodal strength were significantly correlated with the clinical motor condition and were predictive of it. Our study highlights the importance of integrating whole-body information in kinematic analyses and the advantages of using network theory. Finally, the identification of altered network properties of specific joints, and their relationship with the motor impairment in the patients, suggests a potential clinical relevance for our approach.

Highlights

• •Network theory allows to manage multiple degrees of freedom to assess coordination.
• •The aim was to demonstrate how Parkinson's disease impacts joint coordination during walking
• •Our approach aims to examine global and nodal (joint-specific) features of the kinematic networks
• •Results highlight the clinical relevance of a network-based approach to analyze gait coordination

1. Introduction

The investigation of voluntary movement bestows considerable attention on the analysis of joint excursions due to its significance in understanding both the kinematics and the biomechanics of human body [1]. To this regard, the articular range of motion (RoM) defined as the extent of a joint movement, provides crucial information about joints functioning, body posture, and, above all, kinematic coordination [[2], [3], [4], [5]]. Traditionally, the study of RoMs has primarily focused on individual joints, providing valuable information about the capacity of each individual joint to move through its anatomical range. However, human movement involves the coordination of multiple joints, which operate in a coordinated fashion under the control of both the musculoskeletal and the nervous systems, yielding smooth, purposeful, and efficient movements [5]. Understanding the complex physiological kinematics of the joints [3,[6], [7], [8]] is crucial for a comprehensive analysis of motor function.

To date, only a few studies explicitly focused on the way the joints coordinate to produce the expected movement. Günther et al. evaluated the contribution of the leg joints to quiet human stance, estimating the coupling among ankle, knee, and hip joints [9]. The authors described the synergistic kinematic dynamics of these joints and stressed the individual contribution of each to quiet stance. Further investigations widened this framework, evaluating synchronization of leg joints (i.e., ankle, knee, and hip) at different frequencies [10]. The authors, by filtering the kinematic time series of each joint, highlighted the presence of frequency-specific coupling between different joints, emphasizing the importance of synchronization mechanism in the kinematics of human movement. Nevertheless, those studies were conducted in quiet standing and only considered a few joints. Another study from Roemmich et al., investigated ipsilateral and contralateral interlimb coordination of hips and shoulders during gait, finding reduced coupling in patients with Parkinson's disease (PD) with respect to healthy older adults [11].

However, for a comprehensive investigation, the information to consider to assess coordination requires to handle the spatio-temporal high-order synergistic interactions among several musculoskeletal segments, which requires to consider a high number of degrees of freedom (DOF) in a three-dimensional space. Based on Bernstein's considerations [4] about coordination and the problem of mastering the many DOF implicated in each movement, Turvey proposed a series of assumptions that may underlie the overall principles governing the physiological mechanisms regulating motor coordination [5]. A fundamental theory lies in the idea that a reduction of the dimensionality of the information is required (and realized) by the neural control in order to cope with the highly demanding task of coordination [3,5]. One of the approaches used to reduce data dimensionality while extracting relevant information on the kinematics, is represented by principal component analysis (PCA) [12]. PCA allows to explain the variance in the data and individuate the patterns that characterize a movement. For instance, Alexandrov et al. employed PCA to measure the coupling between lower leg joints (i.e., hip, knee, and ankle) during trunk bending in patients with PD and healthy controls. The author found that patients with PD displayed increased coupling variability and disproportioned ratios between joints. Nonetheless, even though PCA allows us to determine the contribution of individual joints to the principal components, the kinematic synergies between the joints and their specific assessment remain ambiguous. To this regard, a holistic approach such as the one provided by network theory [13] may represent an adequate method to manage the dimensionality of the information involved in motor tasks and convey the multidimensional information represented by kinematic interactions occurring among several joints. Network theory is a branch of mathematics that provides a framework for analyzing the relationships among elements of complex systems [13]. By its means, it is possible to analyze how individual elements interact and influence each other. Within this framework, the single elements are represented as nodes, and the relationships between them are represented as edges (i.e., links). By examining the structure and properties of the network, it is possible to investigate the functional organization, the patterns of connectivity, and the dynamics of the system as a whole. Furthermore, it is possible to investigate the role and the weight of each single node with respect to the whole network or extract global information about the whole system. In a previous paper [14] we conceived a kinematic network considering bones' landmarks as nodes, and the coordination among these elements as edges. We named the resulting network human kinectome. In such a way, we were able to extract relevant and subject-specific information, representative of human movement. Furthermore, we found that the kinectome of patients with Parkinson's disease was different (as there was a trunk hyper-synchronization) as compared to healthy subjects. Parkinson's disease (PD) is a neurodegenerative disorder which compromises primarily (but not exclusively) the motor function. PD can serve as a valuable model to study the kinematic relations between anatomical segments and how the nervous system controls these dynamic interactions. There is a general agreement on the finding that joints' RoM are reduced in PD patients, and this feature, that includes all lower limbs joints, is consistent across studies with patients at different stages of the disease [[15], [16], [17], [18]]. Consequently, the study of joints' RoMs kinematics is of particular interest in evaluating disabling motor symptoms in PD patients, including rigidity and impaired posture.

In this paper, we aimed to demonstrate that joints coordination can be evaluated in the framework of network theory, and that such an approach allows to represent physiological kinematic patterns and to assess their alterations. Furthermore, we hypothesize that kinematic alterations occur not only in the range of motion of individual joints but also in the synergies between joints. Hence, the joint excursions of PD individuals (in the off medication condition) and healthy matched controls were recorded using a stereophotogrammetric system with reflective markers. Velocity of joints' excursion was considered as representative of movement control [19], hence, the standardized covariance between joints' angular velocities was measured to build a coordination matrix (i.e., kinematic networks) for each participant. We hypothesized that joint coordination is lower in patients as compared to healthy controls. The kinematic networks were compared between groups at both the global (averaged synchronization among joints) and the nodal (individual joint synchronization with the whole network) level. Furthermore, we hypothesized that the subject-specific network features of the patients were related to the clinical motor impairment, as assessed by the part III of the Unified Parkinson's Disease Rating Scale (UPDRS-III) [20]., which specifically assesses the motor impairment. To evaluate this hypothesis, we used linear correlation and multilinear regression analyses, to test whether a correlation exists and whether the network features could predict the UPDRS-III score, respectively.

2. Materials and methods

2.1. Participants

Twenty-three patients affected by PD (according to the United Kingdom Parkinson's Disease Brain Bank criteria) [21], and twenty-three healthy controls (HC) were enrolled (Table 1). We aimed to match the controls as closely as possible for sex, age, education level, body mass index (BMI), and walking speed [[22], [23], [24]], ensuring that there were no statistically significant differences. Furthermore, both the patients and the controls reported not participating in structured physical activity or sports. Inclusion criteria for patients were: 1) minimum age of 45 years; 2) Hoehn & Yahr (H&Y) score <3 while off-medicament; 3) disease duration <15 years. Exclusion criteria for both groups included: 1) Mini-Mental State Examination (MMSE) score <24 [25]; 2) Frontal Assessment Battery (FAB) score <12 [26]; 3) Beck Depression Inventory II (BDI-II) > 13 [27]; 4) further neurological or psychiatric disorders; 5) use of additional psychoactive drugs; 6) any further physical or medical conditions causing walking impairment (besides Parkinson's disease for the patients' group). The sample size was based on previous literature on the same research topic. A written informed consent was obtained from all participants, in accordance with Helsinki declaration. The study was approved by the AORN “A. Cardarelli” Ethic Committee (protocol number: 00019628) on July 21, 2020.

Table 1.

Participants' characteristics, including the statistical comparison between the healthy control group (HC) and the patients with Parkinson's disease (PD), for demographic, anthropometric, neuropsychological parameters. Abbreviations: Body mass index (BMI), mini mental state examination (MMSE), frontal assessment battery (FAB), Beck's depression inventory (BDI), unified Parkinson's disease rating scale part III (UPDRS-III). Value expressed as mean (± standard deviation).

	HC	PD	p-value
Demographic
Age (years)	65.39 (±11.8)	65.3 (±11.59)	0.991
Education (years)	12.22 (±5.81)	10.74 (±3.84)	0.251
Gender (f/m ratio)	7/16	6/17	0.743
Anthropometric
BMI	24.28 (±5.81)	26.15 (±2.96)	0.183
Neuropsychological
MMSE	27.59 (±1.69)	28.14 (±2.13)	0.334
FAB	16.12 (±1.74)	16.7 (±2.81)	0.416
BDI	6.91 (±3.8)	6.26 (±4.62)	0.635
Clinical
UPDRS-III	-	29.2 (± 16)	-
Disease Duration (months)	-	89.19 (± 50.4)	-

2.2. Intervention and data collection

The protocol consisted of stereophotogrammetric recording of both PD and HC individuals during gait (Fig. 1A). Specifically, the patients were recorded while in off state (participants did not assume levodopa in the last 14–16 h before the recordings). Before the acquisition, the UPDRS-III score of each patient was acquired. All the subjects were instructed to walk forth and back through a measured space 10 m long, and were recorded while walking in the central part of the path. We avoided recording participants during direction changes, as this study focused on linear gait. The best trials were considered, (i.e., when all the markers were highly visible), obtaining eight gait cycles for each participant.

Fig. 1.

From data recording to network building. The figure displays a concise description of the pipeline. A. Participants are recorded while walking through a stereophotogrammetric system. Red circles represent the joints of interest for our analysis. B. Time series related to the velocity of joints' excursion during gait cycle are computed. C. Pearson Correlation Coefficient between pairs of joints was computed as a proxy for coordination. D. Coefficients of correlation are stored in a matrix that presents the joints on rows and columns, and the coordination values between couples on the specific edges. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Data collection was performed in the Motion Analysis Laboratory of the University of Naples Parthenope. We used a recording camera system composed of eight infrared stereophotogrammetric cameras (ProReflex Unit—Qualisys Inc., Gothenburg, Sweden) and 55 reflective markers. The markers were positioned on each subject in specific anatomical landmarks, according to the modified Davis protocol [28], like in Minino et al. [29]. Data were filtered using a lowpass 4th order Butterworth filter with 0.16Hz cutoff frequency. For each participant we obtained the three-dimensional time series of the position of the 55 passive markers during gait. This information was used to calculate the excursion angle (in 3D space), in each frame, of the following joints: neck, shoulders, elbows, pelvis, hips, knees, ankles. Specifically, based on the bone segments built in the Visual 3D software, we computed the three-dimensional angle between couple of segments, according to the following formula [1]:

$${\theta }_{3D}=\frac{\left(AB\bullet BC\right)}{\left(\Vert AB\Vert \bullet \Vert BC\Vert \right)}$$ [1]

where ϴ_3D is the angle, B is 3D point of the joint of interest, A and C are the point of the proximal and distal ends, respectively.

Hence, we obtained a time series for each joint angle. Then, we calculated the first derivative of the angles with respect to time to obtain the angular velocity (Fig. 1B).

2.3. Network implementation

We used the network approach to build a kinematic network based on joints’ angular velocity [13,14]. Within this framework, our points of interest were the joints, which correspond to the nodes of the network. The edges, on the other hand, which are the elements connecting the nodes, were set to be the kinematic relationships between the time series of each pair of nodes. These kinematic relationships were calculated as standardized covariance, hence measured using the Pearson correlation coefficient between each couple of joints, as an expression of coordination (Fig. 1C). Correlating all the time series among them we obtained a matrix for each participant, whose rows and columns represented the joints (nodes of the network), and each entry (i.e., the edges) represented the correlation coefficient between couples of joints [30] (Fig. 1D). Nodes on the diagonal, that represents the correlation between the same time series are set from 1 to 0 since they are of no interest. Please note that, we employed a fully connected network where each joint is related with all the others, based on the assumption that coordination between joints occurs even if the considered joints are not directly anatomically connected (e.g., typical antiphase swing between leg and contralateral arm) [31].

2.4. Community detection

We performed a community detection analysis, to investigate the modular organization of the kinematic coordination of the two groups. The analysis was performed based on the assumption that there are highly differentiated subnetworks of joints, i.e., kinematic synergies [32], that may represent functional groups performing specific tasks during gait. Modularity is a measure that assesses the presence of separate clusters in a network. To determine the community structure within each group (both healthy individuals and patients), we utilized the Louvain method, by applying consensus clustering across 100 iterations [33,34]. The Louvain method is a community detection algorithm used in network analysis to identify and reveal the underlying modular structure of a network. It is an iterative algorithm that optimizes the modularity of the network by iteratively moving nodes between communities. The goal is to maximize the density of edges within communities while minimizing the density of edges between communities. With this method, the joints that work synergically were grouped in the same cluster, as a result of a data-driven algorithm.

2.5. Network analysis

From each matrix we extracted global and nodal strength, as network metrics for further analyses [35]. Nodal strength is obtained by summing all the edges incident upon a given node; specifically, since negative correlation coefficients represent correlations as well, nodal strength is calculated by summing the absolute value of the edges. Similarly, global strength is obtained by averaging the absolute values of the edges. At nodal level, the nodal strength represents the total correlation of a specific joint with all the other joints across the network, while at global level it represents the average correlation across all joints. Both metrics were compared between HC and PD groups.

2.6. Comparison with different measures

To provide an overview of the behavior of a different metric within the same dataset, we set out to compute a parameter that can be related to motor control. In particular, we took into consideration the smoothness of movement, measured through the spectral arc length (SPARC) metric [36]. SPARC quantifies the arc length of the Fourier magnitude spectrum over an adaptive frequency range. It effectively captures movement intermittencies while remaining unaffected by amplitude or duration, demonstrating that smoothness not only reflects fluidity but also the precision in controlling movement. Both metrics were calculated for each joint and then compared between HC and PD groups.

2.7. Statistics

Statistical analyses were performed in MATLAB 2022a. Network nodal strength values were compared between groups through permutation testing. The subjects’ labels were randomly shuffled 10,000 times, and at each iteration the absolute value of the difference between the surrogates group means was computed, obtaining a random distribution of the differences [37]. We compared the observed difference to the random distribution to obtain the statistical significance. Correlation analysis between nodal strength values and motor scores was performed through the Pearson correlation test. Multilinear regression model with k-fold cross validation (k = 5) [38] was employed to assess the UPDRS-III prediction based on network nodal strength values (variance inflation factor was used to assess multicollinearity among predictors [39]). P-values were corrected by false discovery rate and only corrected p-values <0.05 were considered as significant.

3. Results

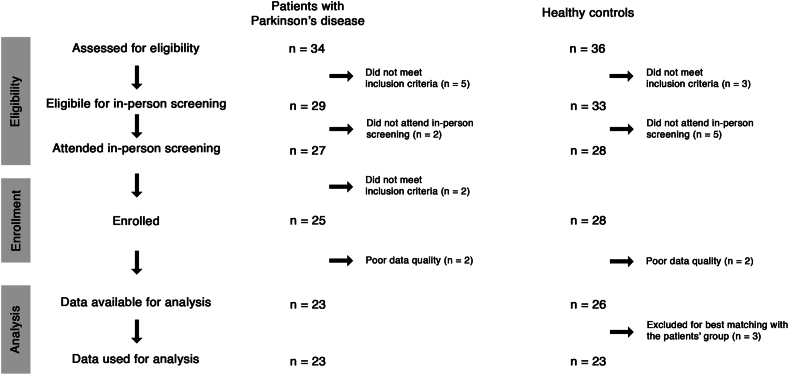
For this study, thirty-four patients affected by PD and twenty-six healthy controls (HC) were assessed for eligibility, as shown in the enrollment flow chart in Fig. 2. Five patients and three HC did not meet the inclusion criteria. At the in-person screening, twenty-eight HC and twenty-seven patients attended, of which two did not meet the inclusion criteria. Thus, twenty-eight HC and twenty-five patients were enrolled from July 22, 2020 to August 10, 2020. Upon reviewing the recorded data, 2 patients and 2 HC showed low-quality data and were therefore excluded from further analysis. The final analyses were conducted on twenty-three patients and twenty-three HC selecting the best matching between the two groups.

Fig. 2.

Enrollment flow chart. The figure shows the flowchart describing the enrollment of study participants, from eligibility to analysis. The sample size at each step is reported separately for patients and healthy controls.

First, we built the covariance matrices based on the joints’ angular velocity, to assess the coordination among all joints during gait, for each participant. We analyzed the modular organization of the kinematic network of the two groups, and compared network metrics (i.e., joint-specific nodal strength and average nodal strength) in HC and PD patients. Finally, we investigated the relationship between network metrics and clinical motor impairment in PD.

3.1. Modularity analysis

The modularity analysis highlighted the groups of joints that are functionally coordinated during walking (Fig. 3). HC and PD patients exhibited similar clustering, although some differences were present. The two main clusters, which included the ipsilateral shoulder and elbow and the contralateral hip, were preserved in patients (although, as shown in the subsequent analysis, the level of coordination of these joints was lower in patients as compared to controls). The main difference was in the lower limbs. There, HC showed a cluster for each leg, highlighting strong coordination between ipsilateral knee and ankle during walking. In PD patients, the right ankle and knee did not belong to the same coordination cluster. Finally, the neck and pelvis also appeared in separate clusters in both groups and did not show coordination with any other body element.

Fig. 3.

Visual representation of the kinematic network built on the joints' angular velocity. The networks of healthy controls (HC) and patients with Parkinson's disease (PD) are represented both in the shape of a matrix and as schematic visualization. In the matrix version, node labels are colored to reflect their cluster membership, as determined by community analysis. Please note that values on the diagonal, representing the correlation between the same time series, have been set to 0, as they are of no interest. Similarly, in the skeleton-based schematic visualization, the nodes (representative of the joints) are colored according to their cluster, representing kinematic synergies. The size of the nodes depends on the values of nodal strength (the larger the size of the node, the greater its value). The connections between nodes are displayed as black lines, and, similarly, the thickness of the lines depends on the value of the corresponding edge. For visualization purposes, only the top 25 % of edges with the highest values are shown.

3.2. Networks features

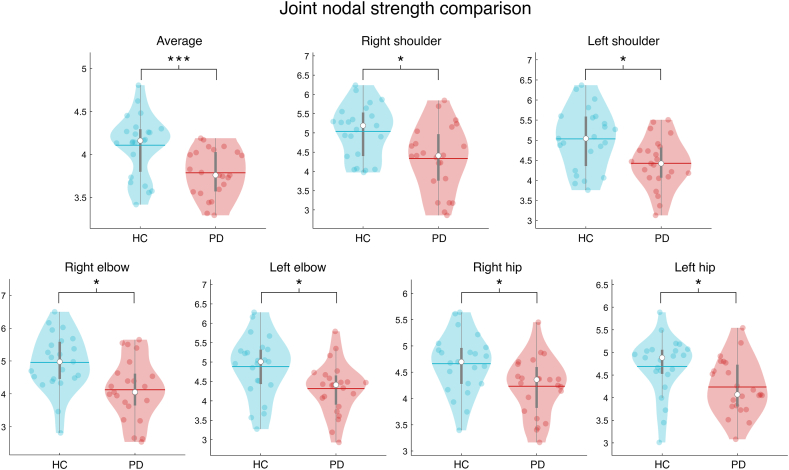
Afterwards, we moved to compare the joint-specific and global characteristics of HC and PD networks. Healthy subject showed significantly higher average nodal strength as compared to the patients (p < 0.001) (Fig. 4). Furthermore, nodal comparison showed significant differences in six joints. Compared to the HC, the PD group displayed lower nodal strength values of the following joints: right shoulder (p = 0.004; pFDR = 0.021), left shoulder (p = 0.005; pFDR = 0.021), right elbow (p = 0.002; pFDR = 0.021), left elbow (p = 0.013; pFDR = 0.03), right hip (p = 0.01; pFDR = 0.029), left hip (p = 0.018; pFDR = 0.035) (Fig. 4).

Fig. 4.

Comparison of joint networks features. Violin plot of the comparison between joint nodal strength values of healthy controls (HC) and individuals with Parkinson's Disease (PD). Each violin displays the distribution of data; dots within each violin represent the observations; horizontal lines represent the average value of the group; each violin contains a box plot with a white circle representing the median value. Please note that healthy subjects display higher values (i.e., higher coordination) at both global (i.e., Average), and nodal level. * pFDR-value <0.05, ** pFDR-value <0.01, *** pFDR-value <0.001.

3.3. Clinical correlations

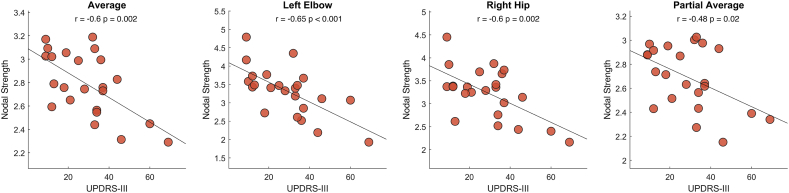
Thereafter, we looked for relationships between the clinical condition and the joint network's characteristics. Fig. 5 displays the statistically significant correlation between the average nodal strength and the UPDRS-III (r = −0.62, p = 0.0017). Furthermore, we investigated whether the nodal features would also relate to the clinical condition. Indeed, UPDRS-III were significantly correlated with both left elbow (r = −0.65, p = 0.0007, pFDR = 0.0088) and right hip (r = −0.6, p = 0.0024, pFDR = 0.0143) nodal strength (Fig. 5). Finally, we asked ourselves if the correlation between UPDRS-III and average nodal strength was mainly driven by the contribution of the left elbow and the right hip. Hence, we calculated the average nodal strength again, but this time excluding both left elbow and right hip. We found that even in this case the (partial) average nodal strength was significantly correlated with the clinical condition (r = −0.48, p = 0.02).

Fig. 5.

Correlation with clinical motor impairment. Correlation analysis (performed using Pearson's correlation coefficient) between joints' nodal strength values and clinical motor impairment evaluated through the part III of the Unified Parkinson's Disease Rating Scale (UPDRS-III). Correlation coefficient (r) and p-values (p) are reported for each analysis. All significant correlations display a negative coefficient, which means the higher the impairment evaluated with the clinical scale, the lower the coordination. Furthermore, average nodal strength was recalculated (partial average) without considering left elbow and right hip, excluding the possibility that the correlation between clinical condition and average nodal strength was driven by the nodal components.

3.4. Prediction of the clinical impairment through a multilinear model

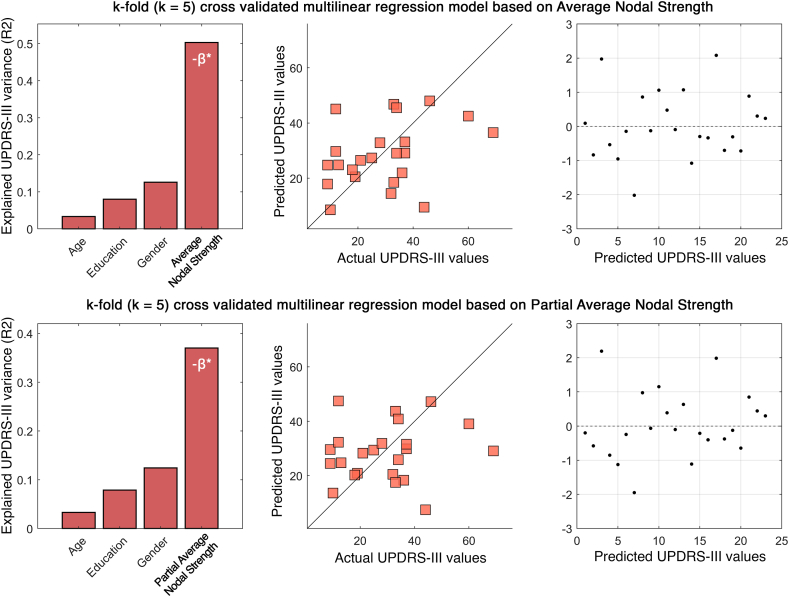
Finally, keeping into consideration the features that were correlated with the UPDRS-III (i.e., average nodal strength, left elbow nodal strength, right hip nodal strength, partial average nodal strength), we set out to test their predictive power towards the UPDRS-III using a multilinear model including age, education and gender as nuance variables, validated with a k-fold cross validation scheme. Surprisingly, all the nodal strength values (including the partial average nodal strength, i.e., the average nodal strength without the right hip and left elbow contribution) significantly contributed to the prediction. In particular, multilinear models based on average nodal strength (p = 0.002, β = −0.639) and partial average nodal strength (p = 0.018, β = −0.519) predicted 47 % and 33 % of UPDRS-III variance, respectively (Fig. 6).

Fig. 6.

Clinical impairment prediction based on global network features. First row, consisting of the three top panels, shows the results of the predictive model based on average nodal strength; the second row, consisting of the three bottom panels, shows the results based on the partial average nodal strength (average nodal strength without contribution of the joints that are significantly correlated with the UPDRS-III). First panels (panels on the left side of the figure) display the R2 values while adding predictors; significant predictors are in bold and report the negative beta coefficient (-β*); second panels (the two panels in the middle) compare actual vs predicted clinical motor scores; third panels (on the right side of the figure) show the distribution of the residuals. Predicted values are obtained performing k-fold cross validation with k = 5. UPDRS-III: part III of the Unified Parkinson's Disease Rating Scale.

Concerning the nodal strength values, multilinear regression models based on left elbow (p < 0.001, β = −0.717) and right hip (p = 0.001, β = −0.773) predicted 54 % and 43 % of the UPDRS-III variance, respectively (Fig. 7).

Fig. 7.

Clinical impairment prediction based on joint-specific network features. The first row, consisting of the three top panels, shows the results of the predictive model based on left elbow nodal strength; the second row, consisting of the three bottom panels, shows the results based on the right hip nodal strength. First panels (panels on the left side of the figure) display the R2 values while adding predictors; significant predictors are in bold and report the negative beta coefficient (β*); second panels (the two panels in the middle) compare actual vs predicted clinical motor scores; third panels (on the right side of the figure) show the distribution of the residuals. Predicted values are obtained performing k-fold cross validation with k = 5. UPDRS-III: part III of the Unified Parkinson's Disease Rating Scale.

3.5. Comparison with different metrics

With regard to the comparison of joint-specific smoothness, we only found significant results before FDR correction. Specifically, patients with PD (compared to HC) showed lower SPARC values (i.e., lower smoothness) in right shoulder (mean PD = −6.81, mean HC = −5.43, p = 0.022, pFDR = 0.152) and right elbow (mean PD = −6.47, mean HC = −5.55, p = 0.028, pFDR = 0.152), and these values were not correlated with the UPDRS-III.

4. Discussion

In this study, we evaluated the joints' coordination in healthy individuals and people with PD utilizing the framework of network theory. The underlying idea of this approach assumes that a thorough evaluation of the motor function must include the mutual relationship among all body segments. Despite the informative nature of the individual characteristics of limbs and joints, we believe it is useful to integrate this information by also focusing on the relationships between the different parts of the body involved in movement. Indeed, humans realize their movement accurately coordinating multiple body segments, and only through the adequate tuning of the whole system it is possible to accomplish motor tasks [4]. Studying motor behavior in known physiopathological conditions like Parkinson's Disease may allows us to gain further insights into the nervous system's regulation of movement. Therefore, we utilized a network approach to assess joint coordination by quantifying the interdependence of angular velocities among the joints during gait. This way, each node (i.e., joint) of the network captures the influence of all other nodes, thereby allowing to analyze movement into a holistic framework.

Coordination is a mechanism that allows to tune the coupling among different body parts in order to perform a measured and (globally) smooth movement [5]. In our analysis, patients with PD displayed lower global coordination compared to healthy individuals. This result can be interpreted as a reduction in the ability to synchronize the movement of different musculoskeletal segments during gait. In PD, the loss of dopamine can also affect the timing and sequencing of muscle contractions required for complex movements like walking [[40], [41], [42]]. As a result, individuals with Parkinson's disease may experience difficulties in maintaining a steady and coordinated gait, leading to more fragmented and less fluid walking pattern. To this regard, please note that patients and controls walking speeds were kept as similar as possible, since it is widely reported that walking speed affects the gait pattern [43]. Additionally, the impairment of global kinematic coordination may also be influenced by secondary factors such as muscle stiffness, postural instability, and reduced proprioception [44,45]. These factors further contribute to the overall motor dysfunction observed in Parkinson's disease, impacting the smoothness and precision of movements.

Then, moving to the nodal characteristics of the network, we obtained detailed information with respect to specific joints. The results revealed that the patients presented altered coordination that included joints throughout the whole body. In particular, shoulders, elbows, and hips nodal strength values were the lowest in the patients' group. This result highlights the reduced capability of individuals with PD to appropriately couple the movement of several body segments, mostly within the upper part of the body [[46], [47], [48]]. Surprisingly, the lower part of the body (ankle and knee) seems not to display any significant result, whereas ankle and knee impairments are commonly reported in studies on PD [[49], [50], [51], [52]]. To this regard, Shiba et al. [53], analyzing the biomechanics of lower limbs in patients with Parkinson's disease (considering various conditions such as on/off medication and with/without freezing of gait), highlighted significant differences compared to the control group also in knees and ankles kinematics. Specifically, considering patients in the off condition and without freezing of gait (i.e., those most similar to our sample), they showed several alterations in the flexion-extension movements of both the ankle and the knee (as well as the hip) compared to healthy controls. It should be emphasized that our analysis is different in nature and focuses on coordination (i.e., the interaction between different parts). The network approach does not aim to replace current knowledge but to integrate it to offer a broader perspective. In this case, our hypothesis is that although alterations (e.g., reduction in peak range of motion) are present, the coordination between joints is sufficiently preserved, as the patient is indeed able to walk and thus execute the necessary kinematic synergies. Further investigations and specific experimental designs conducted on larger samples will be able to focus on this aspect to verify whether coordination alterations also exist in the kinematics of the knee and ankle. It should be noted that even the smoothness measure did not highlight differences in knee and ankle joints. One possibility is that our sample, consisting of patients with a low staging grade, does not show significant alterations in movement control and coordination, even though their range of movement may be limited. However, it should also be noted that as evidenced by the community detection algorithm, the ankle and the knee of the right side failed to work synergistically in PD, with respect to the healthy controls. This aspect may be related to the asymmetries, a common feature of parkinsonian gait [54,55].

The coordination among articular excursions was explored in previous studies on PD, by investigating the coupling between selected pairs of joints. Roemmich et al., evaluated the ipsilateral and contralateral interlimb coordination between hip and shoulder [11], analyzing the cross-covariance of the joint angle vectors, thereby exploiting a technique similar to the one that we utilized to build the matrices of joint kinematics. The authors found reduced coordination in patients with respect to healthy controls. Kellaher et al., performed a similar study, this time with the participants walking backwards, which yielded similar results [56]. However, these analyses were limited to a few selected pairs of joints and did not take into consideration all the possible combinations among multiple pairs of joints. Our framework lends itself as a coherent development of these analyses, based on the robust and updated framework of network theory and allowing to effectively convey high-dimensional patterns within a single mathematical object (i.e., a matrix). Information that is comparable to the ones calculated by Roemmich et al. is indeed available as the individual edges of these kinematic matrices and represent the coordination between couple of joints. As shown in Fig. 3, the ipsilateral coordination between hips and shoulders is not present among the mostly coordinated edges, while the contralateral coordination, despite being represented, is clearly lower (narrower lines in the PD representation). Furthermore, patients displayed lower general coordination of hips and shoulders in node-specific analysis.

As a further step, we investigated the relationship between our network-extracted features and the motor impairment evaluated through UPDRS-III. We found out that global and nodal features related to the kinematic network, were correlated to the clinical motor condition. In particular, the average nodal strength of the network, a metric conveying information about the whole body, negatively correlated with the clinical score. The interpretation of this result is straightforward and tells us that the lower the average nodal strength (i.e., the overall joints' coordination), the higher the clinical impairment. Moreover, nodal correlation between specific joints’ nodal strength and the UPDRS-III score also showed the same trend, involving the right hip and the left elbow joints. First, it should be noted that right hip may be seen as a key point as it represents the connection between the upper and the lower body. Hence, in this case the right hip joint correlation may refer to the inability to coordinate such pivotal point to the remaining joints. Our hypothesis is that this feature is related to the unilateral stiffness that commonly affects PD patients at the early stage [[57], [58], [59]]. Then, since bipedal locomotion occur with contralateral movement of the upper and the lower body, it does not come as a surprise that at the upper level the left side of the body (i.e., left elbow joint) presents a similar correlation with the clinical motor impairment, likely as a form of biomechanical compensation. Finally, it should be noted that the correlation between the average nodal strength and the UPDRS-III is also confirmed even when we exclude the right hip and the left elbow nodal strength from the computation. This confirms that the correlation with the average coordination ability was not exclusively driven by the contribution of those joints (i.e., the left elbow and the right hip), thereby a global coordination impairment correlated the clinical motor scores occurs in PD.

The relationship between clinical scores and joint coordination was found also in the study performed by Roemmich et al. [11]. Indeed, the authors found that the upper-lower extremities (i.e., shoulder and hip, respectively) coordination was related to the motor impairment (evaluated with UPDRS-III). Similarly, our study showed that the higher the coordination, the lower the UPDRS-III score. Furthermore, the multilinear regression analysis confirmed the predictive power of the nodal strength over the UPDRS-III. This result strengthens the clinical relevance of the network approach to movement analysis. Furthermore, setting the analysis in a k-fold cross validation framework increases the possible reproducibility and the generalization capacity of our findings [60].

Our results are in line with existing theories that dysfunction of motor circuits and neural synchronization are key factors in the pathophysiology of Parkinson's disease [61]. The reduced motor coordination observed in our patients supports the hypothesis of a breakdown in communication and synchronization between the brain areas responsible for motor control [62]. However, our results also suggest that motor dysfunction in Parkinson's may not be uniform, but rather localized or more pronounced in certain areas of the body (that may vary at different disease staging), suggesting the possible alteration of physiological kinematic synergies. To this regard, low beta oscillation, known to be involved in the regulation of motor control and neural synchronization, may play a relevant role [63,64]. In Parkinson's patients, a significant reduction in corticomuscular coherence associated with these oscillations may explain the reduced motor coordination and the altered kinematic synergies. Future studies could explore how these techniques can be integrated into existing theoretical models of Parkinson's (i.e., integrating corticomuscular and/or synergies with kinematic synergies) and contribute to a more detailed understanding of motor and neural interactions.

Our work presents limitations that need to be discussed. First, it should be emphasized that the sample size is small. Further studies with larger sample sizes are necessary to confirm our results. Moreover, the sample of patients examined refers to an early stage of the disease. While this is beneficial for the homogeneity of the sample, it does not allow us to generalize our findings to other stages of the disease. Further studies on diverse populations are necessary to confirm the applicability of our results to the entire population of individuals with Parkinson's. Furthermore, concerning possible confounding factors, when matching the two groups with regard to the physical activity, we only collected self-reported information that none of the participants was practicing structured physical activity. A more extensive quantitative data collection to assess the level of activity/inactivity would be advised.

5. Conclusion

In conclusion, we showed that valuable insight about the overall movement patterns and coordination can be gained by measuring the joints' kinematic network. This methodological approach offers the possibility to characterize the coordination, allowing the assessment of each part of the body in a holistic view that always keep into consideration the whole-body movement. Furthermore, network features of this analysis are predictive of the clinical motor impairment, suggesting that such an approach may be useful to monitor the development of the disease, focusing both on specific body parts, or on the average coordination during gait. In particular, our approach suggests that during the rehabilitation and functional recovery of the patient, great attention should be paid not only to improving mobility but also to the ability to properly coordinate joint movements. The network approach could, in the future, serve as a resource for health specialists for the proper assessment of the patient's coordination abilities, compared to possible reference values gathered from appropriate populations. Furthermore, it should be noted that, while the primary focus is about the measurement and analysis of joint movements, it inherently entails information about muscle coordination as well. The joint angles and velocities utilized to build the network are a direct result of the underlying muscle activations orchestrated by the brain. Hence, studying the coordination patterns and the relationships between joint movements, may allow to investigate higher functions in pathophysiological conditions affecting the motor behavior, such as PD. Specifically, it may be possible to indirectly obtain information on the coordination mechanisms in place at higher levels of control, such as the synergistic muscular activation operated by the central nervous system. However, while interesting, further studies are needed to verify to which extent it is possible to find a direct link between the kinematic network and higher cognitive functions.

Ethical approval statement

The study was approved by the AORN “A. Cardarelli” Ethic Committee (protocol number: 00019628).

Funding

Governo Italiano Ministero per lo sviluppo Economico, ACCORDI PER INNOVAZIONE. Approccio User-friendly integrato per Diagnosi, Assistenza e Cura Efficaci - AUDACE. CUP: B69J23006050007. European Union “NextGenerationEU”, (Investimento 3.1.M4. C2), project IR0000011, EBRAINS-Italy of PNRR.

Data availability

Data will be available on https://www.ebrains-italy.eu/.

CRediT authorship contribution statement

Emahnuel Troisi Lopez: Writing – original draft, Visualization, Methodology, Investigation, Formal analysis, Conceptualization. Marianna Liparoti: Writing – review & editing, Resources, Investigation, Data curation. Roberta Minino: Writing – review & editing, Resources, Investigation, Data curation. Antonella Romano: Writing – review & editing, Visualization, Methodology, Data curation. Arianna Polverino: Writing – review & editing, Methodology, Investigation, Data curation. Anna Carotenuto: Writing – review & editing, Resources, Data curation. Domenico Tafuri: Writing – review & editing, Resources, Data curation. Giuseppe Sorrentino: Writing – original draft, Project administration, Investigation, Funding acquisition, Conceptualization. Pierpaolo Sorrentino: Writing – review & editing, Project administration, Investigation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.