Abstract representations emerge in human hippocampal neurons during inference

Abstract

Humans have the remarkable cognitive capacity to rapidly adapt to changing environments. Central to this capacity is the ability to form high-level, abstract representations that take advantage of regularities in the world to support generalization¹. However, little is known about how these representations are encoded in populations of neurons, how they emerge through learning and how they relate to behaviour^2,3. Here we characterized the representational geometry of populations of neurons (single units) recorded in the hippocampus, amygdala, medial frontal cortex and ventral temporal cortex of neurosurgical patients performing an inferential reasoning task. We found that only the neural representations formed in the hippocampus simultaneously encode several task variables in an abstract, or disentangled, format. This representational geometry is uniquely observed after patients learn to perform inference, and consists of disentangled directly observable and discovered latent task variables. Learning to perform inference by trial and error or through verbal instructions led to the formation of hippocampal representations with similar geometric properties. The observed relation between representational format and inference behaviour suggests that abstract and disentangled representational geometries are important for complex cognition.

A task in which participants learned to perform inference led to the formation of hippocampal representations whose geometric properties reflected the latent structure of the task, indicating that abstract or disentangled neural representations are important for complex cognition.

Main

Humans have a remarkable capacity to make inferences about hidden states that describe their environment^3–5 and use this information to adjust their behaviour. One core cognitive function that enables us to perform inference is the construction of abstract representations of the environment^5–7. Abstraction is a process through which relevant shared structure in the environment is compressed and summarized, while superfluous details are discarded or represented so that they do not interfere with the relevant ones^8,9. This process often leads to the discovery of latent variables that parsimoniously describe the environment. By performing inference on the value of these variables, frequently from partial information, the appropriate actions for a given context can rapidly be deployed^5,10, thereby generalizing from past experience to new situations.

What would be the signature of an abstract neural representation that enables this kind of adaptive behaviour? The simplest form of abstraction is one in which all the irrelevant information is discarded—for example, when the representations of pedestrian crossings in left-driving (UK) and right-driving (USA) nations are two unique and distinct patterns of neural activity that do not depend on sensory details (such as whether the crossing is in the city or countryside) (Fig. 1a). Looking left or right before crossing (two actions separated by a plane in the activity space that represents a linear readout) would readily generalize to the countryside after visiting a city. However, this kind of invariance is rarely observed in the brain. A more general geometric definition of an abstract representation has been proposed¹¹; consider the non-trivial geometrical arrangement in Fig. 1b, in which the geographical area (city or countryside) and the nation of a crossing are represented along two orthogonal directions (the two variables are disentangled). The activity projected along one of these directions is invariant with respect to the value of the other variable. This type of invariance has important computational properties: it allows a simple linear readout to generalize to new situations. We therefore use this property as the defining characteristic of an abstract representation: a representation of a particular variable is abstract if a linear decoder trained to report the value of that variable can generalize to new conditions. The novel conditions are defined by the values of other variables. Representations with these properties have been observed in monkeys^11–13, in rodents^14,15 and in artificial neural networks^11,16,17. Are these abstract representations also observed in the human brain? How are they formed as a function of learning, and do they matter for behaviour? The hippocampus is thought to be critical for the implementation of abstraction and inference-related computations^{10,11,16–23}, but it remains unknown whether abstract representations can emerge in the hippocampus in the timescales needed for rapid learning.

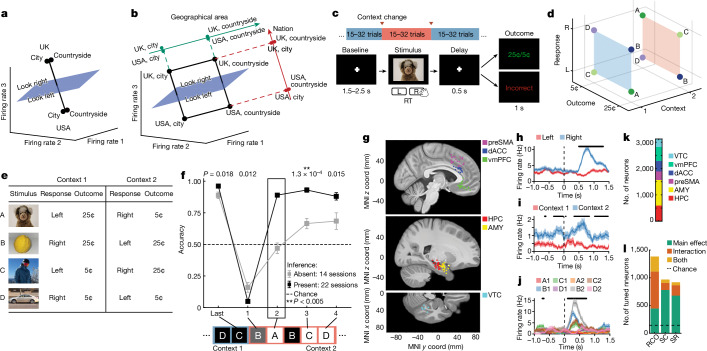
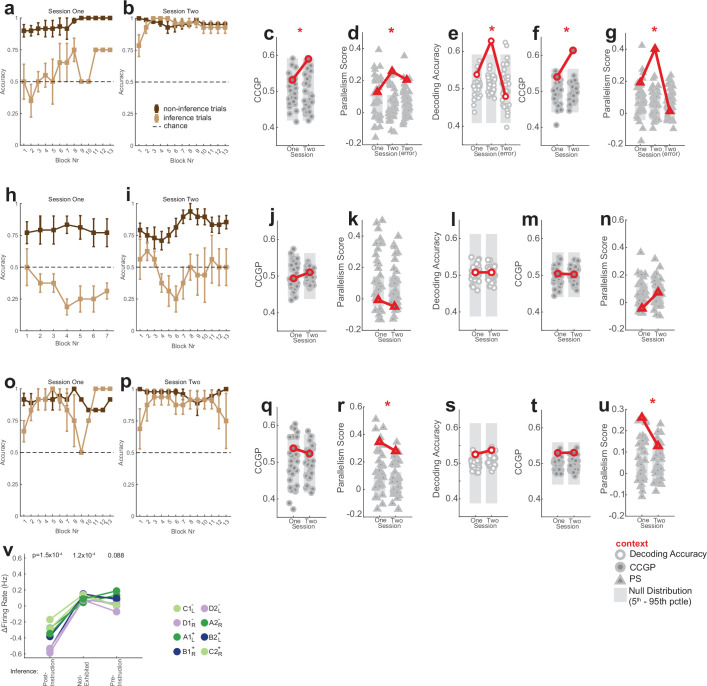
Fig. 1. Task, behaviour and single-neuron tuning.

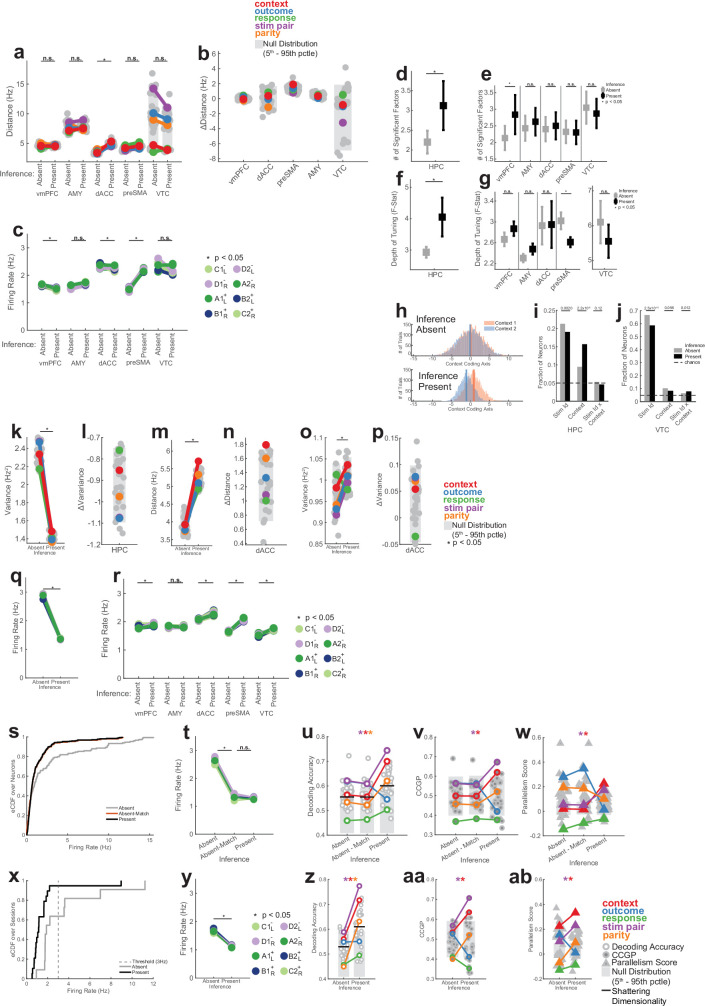
a,b, Possible definitions of abstraction as clustering (a) or generalization (b). In the latter, the two variables are orthogonal to each other and preserved, whereas one of the variables (geographic area) is discarded in the former. c, Task and example trial. Blocks of trials alternated between the two contexts. In each trial, the stimulus remained on the screen until participants pressed a button, followed by the outcome. d,e, Task structure. d, Each stimulus (A–D) is associated with a single correct response and results in either a high or low reward if the correct response is given. e, Stimulus–response relationships are inverted between contexts 1 and 2. f, Behaviour. Accuracy is shown separately for inference present (n = 22) and absent (n = 14) sessions for the last trial before the context switch, the first trial after the context switch and for the remaining three inference trials averaged over all trials in each session (mean ± s.e.m. across sessions). The dashed line marks chance. The black box indicates inference trial 1. **P < 0.005 for rank-sum inference sbsent versus present over sessions. g, Electrode locations. Each dot denotes a microwire bundle. Locations are shown on the same hemisphere (right) for visualization purposes only. h–j, Example neurons that encode response (h), context (i) and mixtures of stimulus ID (indicated by A–D) and context (indicated by 1 or 2) (j). Error bars are ± s.e.m. across trials. t = 0 is stimulus onset. Black points indicate P < 0.05 of one-way ANOVA of plotted variables. k, Number of units recorded in each brain area. l, Number of single units across all brain areas showing significant main or interaction effects to at least one variable (n-way ANOVA, P < 0.05, Methods). Variables tested: response (R), context (C), outcome (O), and stimulus ID (S). Brain areas assessed: amygdala (AMY), dorsal anterior cingulate cortex (dACC), hippocampu (HPC), presupplementary motor area (preSMA), and ventromedial prefrontal cortex (vmPFC).

Task and behaviour

We recorded the activity of populations of neurons in the brains of patients with epilepsy while they learned to perform a reversal learning task (17 patients, 42 sessions; Supplementary Table 1). Patients viewed a sequence of images and indicated for each whether they thought that the associated action was a ‘left’ or ‘right’ response (Fig. 1c). Participants discovered from the feedback provided after each response what the correct response was for a given image. There were two fixed mappings (stimulus–response maps) between each of the four stimuli: the associated correct response and reward given for a correct response (Fig. 1e). Which of the two fixed mappings was active changed at random times (Fig. 1c), requiring participants to infer when a context switch occurred from the feedback received. The two stimulus–response maps were systematically related: all stimulus–response pairings were inverted between the two contexts (Fig. 1e). Therefore, the participants who had learned the stimulus–response maps could make a mistake immediately after the switch but then, following one instance of negative feedback, they could infer that the context had changed and update their stimulus–response associations according to the other map. Therefore, if participants were performing inference, they could respond accurately to stimuli that they had not yet experienced in the new context. We refer to the trials in which a given stimulus was encountered for the first time following a context switch as inference trials (excluding the first trial that resulted in the negative feedback) and to the remaining trials as non-inference trials. Patients performed with high accuracy in non-inference trials in 36 of the recorded sessions (Extended Data Fig. 1a,b and Methods state exclusion criteria). Each of the 36 included sessions was classified as either an ‘inference present’ or ‘inference absent’ session depending on the accuracy by which patients responded to the first inference trial (Fig. 1f (timepoint 2) and Methods).

Extended Data Fig. 1. Task behavior and single-neuron responses across all recorded regions.

(a) Task performance of n = 49 control subjects. Accuracy is reported as an average for each subject over all non-inference trials (left) and all inference trials (right; included are 3 the three trials after every switch in which an image was seen the first time after the switch, i.e. timepoints 2–4 in Fig. 1f). Chance is 50%. This task variant is equivalent to the first session of the task encountered by patients (before explicit instructions of latent task structure). 46/49 subjects performing above chance on non-inference trials. (b) Performance of patients in non-inference trials. Each dot is a single session. Only sessions where patients exhibited above-chance accuracy on non-inference trials are shown (36/42 sessions, p < 0.05, one-sided Binomial Test on all non-inference trials vs. 0.5). (c) Non-inference performance for context 1 and 2 for the n = 36 sessions included in the analysis. Error bars are SEM over blocks. The reported p-value is a paired two-sided t-test between the mean accuracies for Context 1 and Context 2 across all sessions. (d) Same as (c), but with reaction time (RT), computed as time from stimulus onset to button press for every trial. Mean RT’s are also computed by block. n = 36 sessions. (e-f) Performance as a function of time in the task for the (e) inference absence and (f) inference present groups. Shown is the accuracy for the last non-inference trial before a switch and the first inference trial after a switch. Accuracy is shown block-by-block averaged over a 3-block window (mean ± s.e.m. across sessions). (g-i) Behavioral performance for the subjects in the post-instruction, not-exhibited, and pre-instruction groups, respectively. See Fig. 1f for notation. Plot shows performance on the last trial before the context switch, the first trial after the context switch, and for the first inference trial (Trial 2) averaged over all trials in each session (mean ± s.e.m. across sessions). Dashed line marks chance. The first inference trial performance (block box) was used to classify patients the patients, so significance is not reported for this trial. P-values are a one-way binomial test vs. 0.5. (j) Example hippocampal neuron that encodes stimulus identity. Raster trials are reordered based on stimulus identity, and sorted by reaction time therein (black curves). Stimulus onset occurs at time 0. Black points above PSTH indicate times where 1-way ANOVA over the plotted task variables was significant (p < 0.05). Errorbars are ±s.e.m. across trials. (k-p) Normalized activity for all neurons recorded from the hippocampus (k), amygdala (l), VTC (m), dACC (n), preSMA (o), and vmPFC (p). Each is plotted as a heat map of trial-averaged responses to each unique condition (8 total, specified by unique Response-Context-Outcome combinations). Z-scored firing rates are computed from 0.2 s to 1.2 s after stimulus onset for every trial. Each row of the heat map corresponds to the activity of a single neuron, and columns correspond to each of the 8 conditions. Neurons are ordered such that adjacent rows (neurons) are maximally correlated in 8-dimensional condition response space. This approach would allow for modular tuning to visibly emerge in the heat map if groups of neurons were clustered in their response profiles. (q) Percentage of neurons across all areas that exhibit tuning. Tuning was assessed by fitting a 2 × 2 × 2 (Response-Context-Outcome) ANOVA for every individual neuron’s firing rate during a 1 s window during the stimulus presentation period. Significant neurons were counted as p < 0.05 for main effects or interaction effects involving the stated variables. Significanctly different proportions of tuned neurons between inference present and absent sessions is determined via a two-sided z-test, where “*” indicates p < 0.05, “***” indicates p < 0.005, and “n.s.” indicates “not significant”. (r) Same analysis as (q), but for a 4 × 2 ANOVA for stimulus identity and context. (s) Same analysis as (q), but for a 4 × 2 ANOVA for stimulus identity and response. (t) Percentages of tuned neurons shown separately for each region (compare to Fig. 1j). Single-neuron tuning is identified using a 3-Way ANOVA (Response × Context × Outcome), corresponding to column 1 (RCO) of Fig. 1j. (u) Same as (t), but single-neuron tuning identified here using 2-Way ANOVA (Stimulus ID × Context), corresponding to column 2 (SC) of Fig. 1j.

Single-neuron recordings

Neural data recorded in the 36 included sessions yielded 2,694 (of 3,124) well-isolated single units, henceforth neurons, distributed across the hippocampus (494 neurons), amygdala (889 neurons), presupplementary motor area (269 neurons), dorsal anterior cingulate cortex (310 neurons), ventromedial prefrontal cortex (463 neurons) and ventral temporal cortex (VTC, 269 neurons) (Fig. 1g,k). Action potentials discharged by neurons were counted during two 1 s long trial epochs: during the baseline period (base, −1s to 0 s before stimulus onset), and during the stimulus period (stim, 0.2 to 1.2 s after stimulus onset).

Single-neuron responses during the two analysis periods were heterogeneous. During the stimulus period, some neurons showed selectivity to one or several of the four variables stimulus identity, response, (predicted) outcome and context (Fig. 1h–j and Extended Data Fig. 1j show example neurons tuned to response and context). Other neurons were modulated by combinations of these variables (Fig. 1j, example neuron tuned to conjunction of stimulus and context). Across all brain areas, 54% of units (1,447 out of 2,694) were tuned to one or several task variables, with 26% of units (706 out of 2,694) showing only interaction effects, 17% (449 out of 2,694) showing only main effects and 11% (292 out of 2,694) showing both when fitting a three-way analysis of variance (ANOVA) for response, context and outcome (Fig. 1l, RCO column, chance was 135 out of 2,694 units, factor significance at P < 0.05 and Extended Data Fig. 1t shows each brain area separately). These findings indicate diverse tuning to many task variables simultaneously across all brain regions (Extended Data Fig. 1k–p,t–u).

Geometric analysis approach

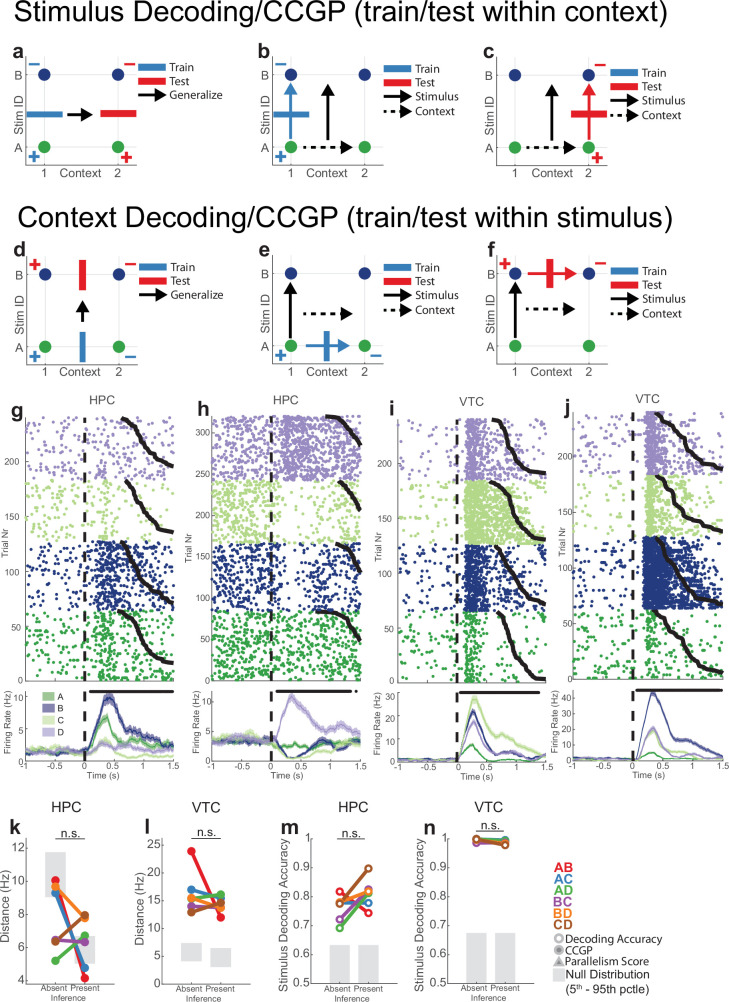
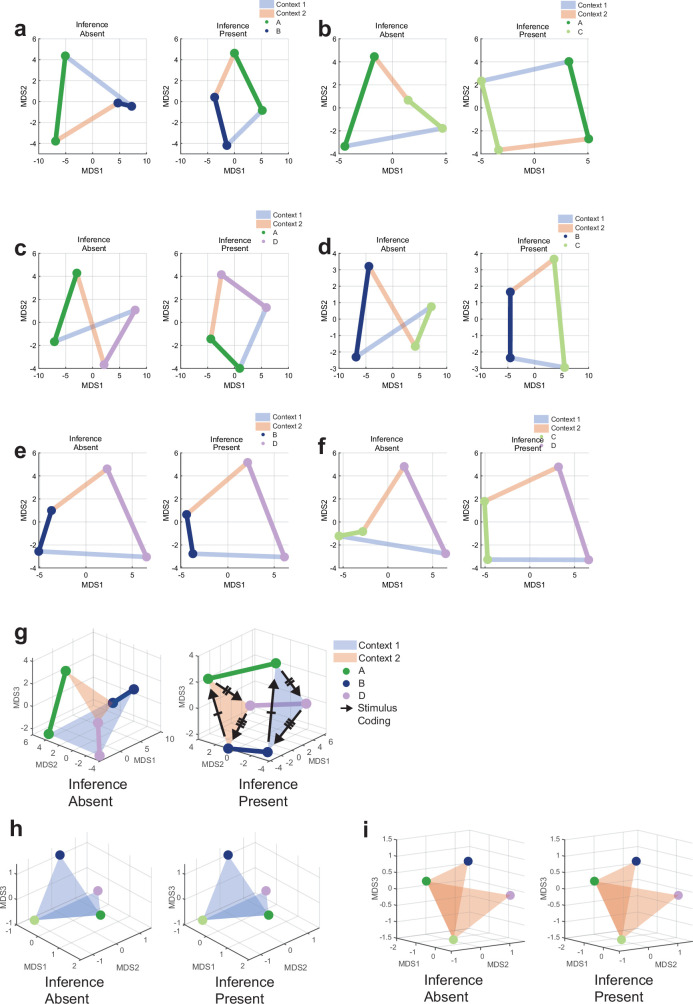
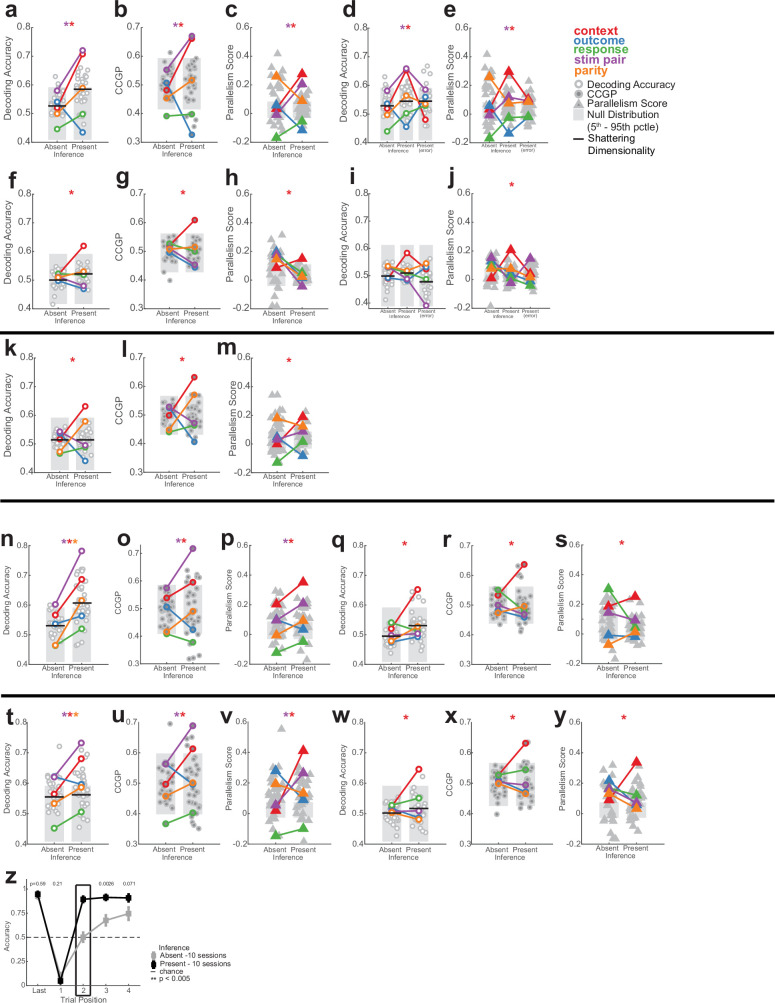
We analysed neural pseudo-populations constructed by pooling all recorded neurons across patients (Methods). In our task, the geometry of a representation was defined by the arrangement in the activity space of the eight points that represented the population responses in different experimental conditions (Fig. 2d). Low-dimensional disentangled geometries would be abstract because they confer on a linear readout the ability to cross-generalize. Consider a simplified situation with three neurons (the axes) and two stimuli in two contexts (Fig. 2a–c). Imagine that the four points (two per context) are arranged on a relatively low-dimensional square (the maximal dimensionality for four points is three), with the context encoded along one side and stimulus along the two orthogonal sides (Fig. 2a). Then, a linear decoder for stimulus (A versus B), trained only on context 1 conditions, can readily generalize to context 2 (Fig. 2b) and the stimulus is said to be abstract. This ability to generalize is due to the parallelism of the stimulus coding directions in the two contexts (Fig. 2c). Moreover, context and stimulus are represented in orthogonal subspaces, and hence, they are called disentangled variables^24,25. This means that context is also abstract.

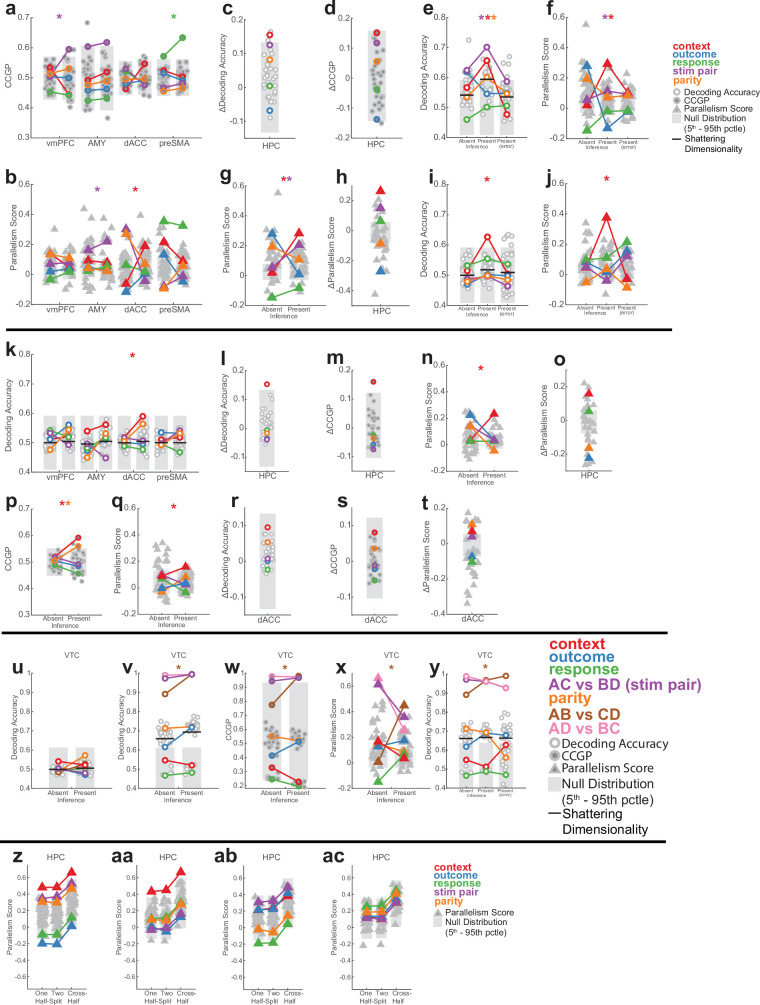
Fig. 2. Multiple abstract variables emerge with inference in hippocampus.

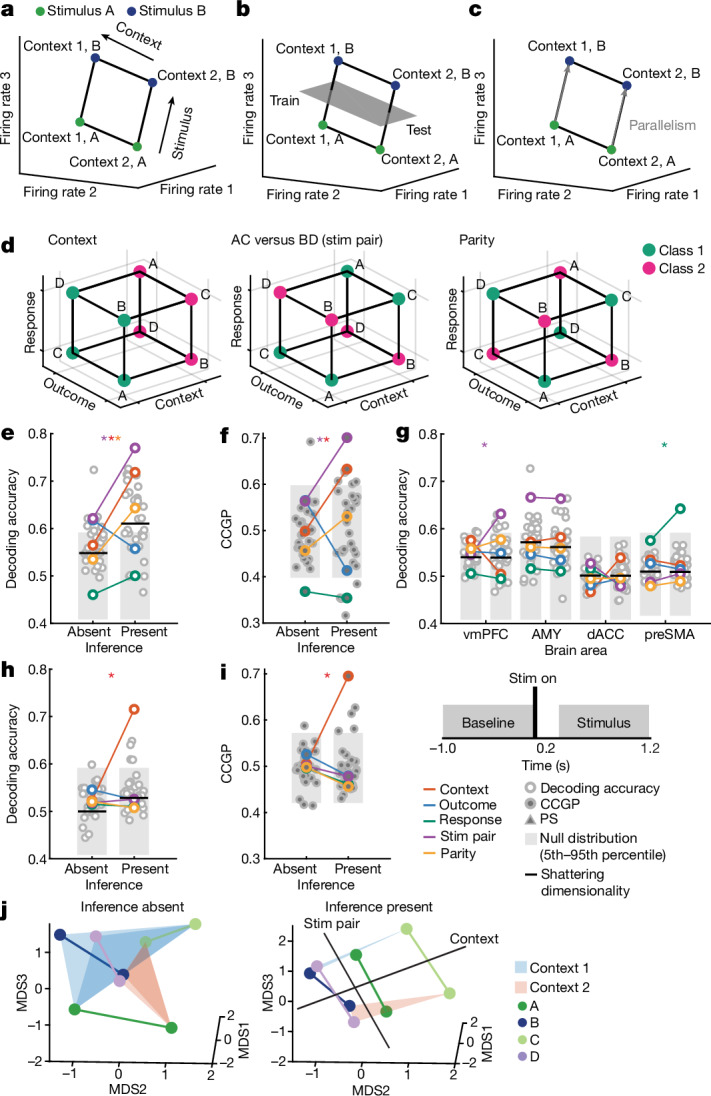
a, Example neural state space formed by three neurons. Points represent the response patterns in various task conditions. Black arrows mark coding vectors. b, CCGP. A decoder is trained to differentiate between stimulus A and B in context 1 and evaluated in context 2. If context is represented in an abstract format, then the decoder generalizes, yielding high CCGP for context. c, PS. In disentangled representations, the coding vectors (arrows) are parallel. d, Illustration of the dichotomies (variables) context, stim pair and parity with class labels indicated. See Extended Data Fig. 2 for all dichotomies. e,f, Neural representation during stimulus period in hippocampus. Context and stim pair are decodable in inference present sessions (e) and are encoded in an abstract format (f). Each dot shows one of the 35 dichotomies. The horizontal black line shows shattering dimensionality. Grey bars denote the 5th–95th percentile of the null distribution. Stars denote named dichotomies that are above chance in inference present sessions and are significantly different from their corresponding inference absent value (P_RS < 0.05/35, two-sided rank-sum test, Bonferroni corrected for multiple comparisons across all dichotomies). g, Decodability of all dichotomies for the other brain areas. AMY, amygdala. See e for notation. h,i, Neural representation during baseline period in hippocampus is decodable in inference present (h) and encoded in an abstract format (i). Trials are labelled according to the previous trial. See e,f for notation. Context differed significantly between present and absent (P = 1.1 × 10⁻³³ and P = 2.4 × 10⁻³⁴, respectively). j, Hippocampal population response during the stimulus period in inference absent and present sessions shown using MDS (Methods). Points correspond to stimuli and context combinations, black lines show hypothetical hyperplanes for context and stimulus pair decoders. In all panels, neuron counts are balanced between inference absent and inference present sessions for every brain area to make values comparable. *P < 0.05.

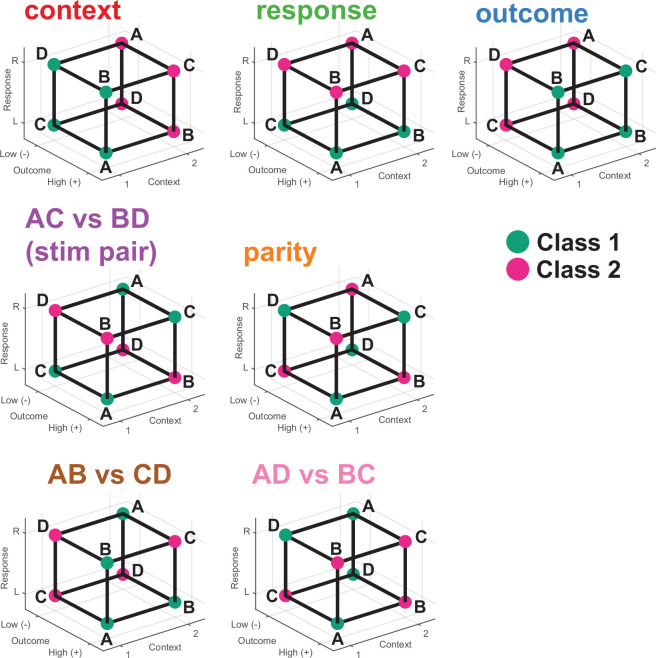
We use two metrics to assess whether information was represented in this way in the neural data: cross-condition generalization performance (CCGP), which assesses the ability of a linear decoder to generalize across conditions, and the parallelism score (PS), which measures the cosine similarity of different coding vectors. High CCGP and PS are defining characteristics of an abstract representation of a variable. We considered the representational geometry of all 35 possible variables. Each variable corresponds to one possible balanced split (dichotomy) of the eight task conditions into two groups of four conditions each (Fig. 1b,d and Extended Data Fig. 2). We highlight in Fig. 2d the interpretable variables that turned out to be important in the analysis: context, behaviourally relevant stimulus grouping (stim pair) and parity (which measures the degree of nonlinear interactions of variables in the neural population). Last, we refer to the average decodability across all possible variables as shattering dimensionality^11,26, a metric that assesses the dimensionality of the representation.

Extended Data Fig. 2. Visual representation of all named balanced dichotomies.

Illustration of the named balanced dichotomies that correspond to condition splits that have clearly interpretable meaning with respect to the construction of the task. For example, the context dichotomy (top left), arises from assigning all conditions for context = 1 to one class and all conditions for which context = 2 to the other class. The specific assignment of class labels 1 and 2 is arbitrary, and inverting the labels still corresponds to the same meaning for the dichotomy. All named dichotomies shown here are color coded to reflect their value in all Shattering Dimensionality, CCGP, and Parallelism Score plots, and this color code remains consistent throughout the paper whenever balanced dichotomies are considered.

Context is abstract in hippocampus

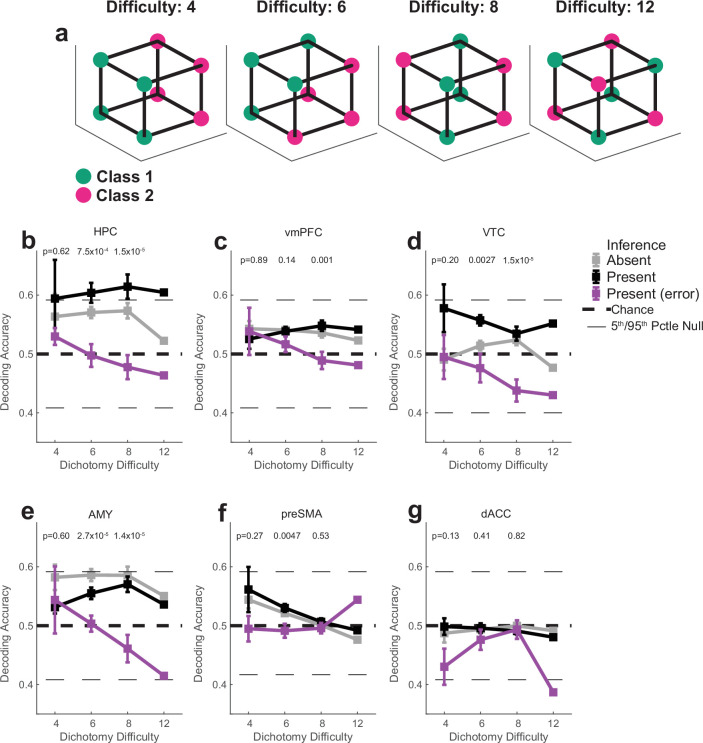
We first compared the decodability of variables between inference present and absent sessions in the hippocampus. Following stimulus onset, shattering dimensionality was larger in inference present sessions (Fig. 2e, inference absent versus present, 0.57 versus 0.62, P_RS = 2.7 × 10⁻³, rank-sum over dichotomies). The two variables that increased the most in decodability were latent context (Fig. 2e, red, inference absent versus present, P_RS = 2.9 × 10⁻²⁷, P_Absent = 0.12, P_Present = 5.1 × 10⁻⁵; P_Absent and P_Present are non-parametric significance tests versus chance based on the empirically estimated null distribution and P_RS is a pair-wise comparison using a two-tailed rank-sum test) and stim pair (Fig. 2e, purple, inference absent versus present, P_RS = 5.0 × 10⁻²⁷, P_Absent = 0.015, P_Present = 7.9 × 10⁻⁷, t). A third dichotomy also became more decodable: parity (Fig. 2d,e, orange; P_RS = 1.5 × 10⁻²¹, P_Absent = 0.27, P_Present = 0.0055). The parity dichotomy is an indicator of the expressiveness of a neural representation because it probes for nonlinear interactions. Generalizing this finding, dividing different dichotomies into increasing levels of ‘difficulty’ reveals that average decoding accuracy is highest for the most difficult dichotomies in the hippocampus (Extended Data Fig. 5).

Extended Data Fig. 5. Effect of inference and errors on shattering dimensionality as a function of dichotomy difficulty.

“Dichotomy difficulty” quantifies the amount of non-linear interaction of task variables needed in a population of neurons to decode a given dichotomy (see methods). (a) Example dichotomies of increasing difficulty. The difficulty 4 dichotomy corresponds to context and difficulty 12 dichotomy corresponds to parity (Extended Data Fig. 2). (b-g) Decoding accuracy as a function of dichotomy difficulty for different brain regions. Reported values (mean +/− SEM) are computed over dichotomy decoding accuracies, where the average decoding accuracy for each dichotomy is computed with 1000 repetitions of re-sampled estimation (see methods). Black dashed lines indicate chance level (50% for binary decoding), horizontal black lines indicate the 5^th and 95^th pctle of the null distribution. P-values are computed by conducting a one-way ANOVA over dichotomies independently for every dichotomy difficulty (Bonferroni multipe comparison corrected). This value is not meaningfully computable for difficulty 12, which contains a single dichotomy (the parity dichotomy), and is therefore not reported. Decoding accuracy from the hippocampus (b) is higher in inference present compared to inference present sessions. In error trials, decoding is at chance. n = 1000 random resamples.

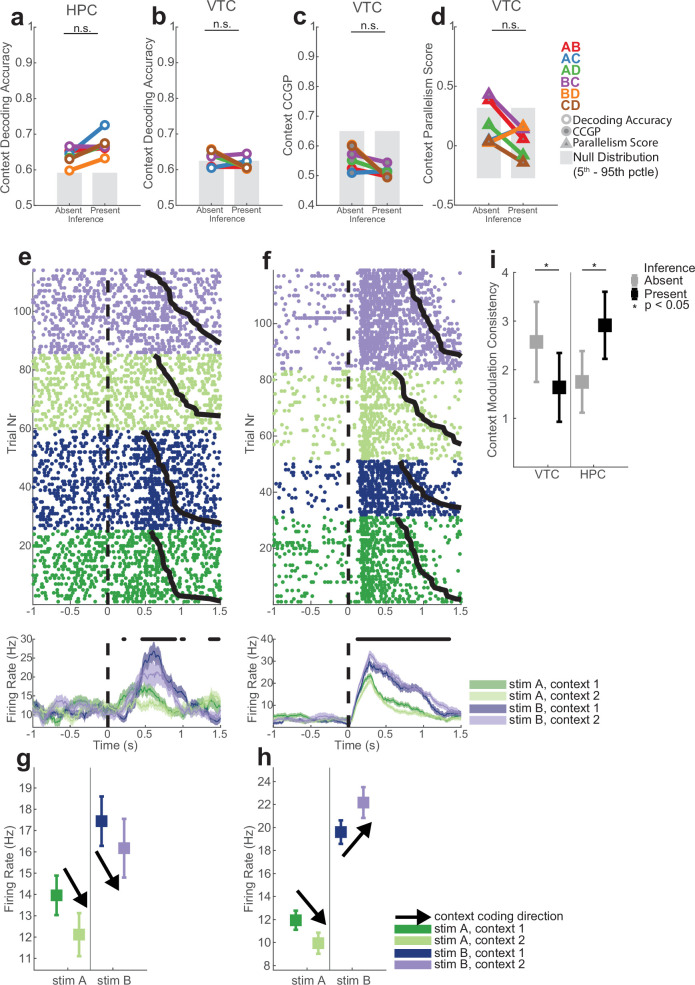
We next examined the format of the dichotomies context, stim pair and parity in the hippocampus. During the stim period, CCGP (Fig. 2f and Extended Data Fig. 3d) was significantly elevated for both the context (Fig. 2f, red, inference absent versus present, P_RS = 2.0 × 10⁻²⁸, P_Absent = 0.51, P_Present = 0.02) and stim pair (Fig. 2f, purple, inference absent versus present, P_RS = 2.0 × 10⁻²⁸, P_Absent = 0.17, P_Present = 0.0011) variables in inference present but not in inference absent sessions. Similarly, during the prestimulus baseline period, context alone was encoded in an abstract format only in sessions in which participants could perform inference (Fig. 2h,i and Supplementary Note 1).

Extended Data Fig. 3. Additional geometric analysis during stimulus processing and baseline periods.

(a) CCGP for other brain regions during stimulus period. See Fig. 2 for notation. Significant named dichotomies are marked when the dichotomies are above the 95^th percentile of the null distribution in inference present sessions and significantly different between inference absent and present (RankSum p < 0.01/35, Bonferroni corrected for balanced dichotomies). Significant increases were observed in vmPFC for stim pair (purple, p_Absent = 0.45, p_Present = 0.014) and preSMA for response (green, p_Absent = 0.045, p_Present = 0.0010) Stim pair CCGP in AMY was above chance for both inference absent and present sessions (purple, p_Absent = 0.050, p_Present = 0.039). (b) Same as (a), but for PS. PS increased significantly for stim pair in amygdala (purple, p_Absent = 1.3 × 10⁻⁴, p_Present = 9.0 × 10⁻⁸) and context in the dACC (red, p_Absent = 0.99, p_Present = 3.9 × 10⁻¹²). (c) Change in decoding accuracy. (d) Same as (c), but for CCGP. (e-f) Error trial analysis for neural response following stimulus onset in the hippocampus. Context (red) is not decodable and not in an abstract format in incorrect trials during inference present sessions. Only correct trials are used in inference absent sessions. Horizontal black bars indicate shattering dimensionality. Stars denote named dichotomies that are above chance in the inference present trials and are significantly different from their corresponding inference absent value (p < 0.05/35, Bonferroni corrected). p_Present = 0.0028, p_Present = 2.0 × 10⁻³, and p_Present = 0.037 for context, stim pair and parity, respectively in panel (e) and p_Present = 1.1 × 10⁻¹⁶ and p_Present = 0.0030 for context and stim pair in panel (f). (g) PS for hippocampus. Context PS was significantly larger (red, p_Absent = 0.55, p_Present = 1.4 × 10⁻¹⁵), as was stim pair (purple, p_Absent = 0.17, p_Present = 1.7 × 10⁻⁸). (h) Same as (c), but for PS. (i,j) Error trial analysis for the baseline period in the hippocampus. See (e-f) for notation. p_Present = 0.012 and p_Present = 0 for context in (i) and (j), respectively. (k-o) Analysis of baseline period for other brain regions (k) and the hippocampus (l-o). Compare to Fig. 2h. (k) Significant increases were observed in dACC for context (red, p_Absent = 0.37, p_Present = 0.049). SD was not different from chance (p_RS>0.05 or all areas). (l-m) Change in decoding accuracy and CCGP. (n) PS. Context is the only named dichotomy for which the PS is significantly different from chance in nference present sessions (red, p_Absent = 0.37, p_Present = 1.2 × 10⁻¹⁰). (o) Change is PS shown in (n). (p-t) Analysis of baseline period for the dACC. (p) Context (red, p_Absent = 0.26, p_Present = 0.018) is in an abstract format. (q) Context PS (red, p_Absent = 0.18, p_Present = 0.013) is significant in inference present sessions. (r-s) Change in decoding accuracy (r), CCGP (s), and PS (t). Parity and context PS increase significantly (p = 0.0016 and p = 0.026, respectively). (u-y) Analysis of responses in VTC. (u) Decoding during pre-stimulus baseline. None of the dichotomies are decodable during inference absent or present (p > 0.05 for all dichotomies) and SD does not significantly differ (0.50 vs 0.51, p_RS = 0.34). (v-y) Analysis of stimulus period. (v) Decodability. The stimulus dichotomies are decodable both during inference absent and inference present sessions. SD increased significantly (inference absent vs present, 0.66 vs 0.70, p_RS = 0.0056). Dichotomies: purple, p_Absent = 6.8 × 10⁻¹³, p_Present = 6.6 × 10⁻¹⁴, brown, p_Absent = 2.2 × 10⁻⁹, p_Present = 6.0 × 10⁻¹⁴, pink, p_Absent = 1.1 × 10⁻¹³, p_Present = 6.7 × 10⁻¹⁴. Context is not significantly decodable (red, p_Absent = 0.24, p_Present = 0.38). (w) CCGP. Two stimulus dichotomies are in an abstract format in inference absent and all three are in an abstract format in inference present (purple, p_Absent = 0.0054, p_Present = 0.0036, brown, p_Absent = 0.057, p_Present = 0.0029, pink, p_Absent = 0.0030, p_Present = 0.0032). (x) PS. PS for two of the stimulus dichotomies is above chance in inference absent sessions, and all three are above chance in inference present sessions (purple, p_Absent = 0, p_Present = 4.3 × 10⁻¹³, brown, p_Absent = 0.73, p_Present = 0, pink, p_Absent = 0, p_Present = 5.9 × 10⁻⁷). (y) Error trial analysis. Decoders are trained on correct trials and evaluated on error trials in inference present sessions. All stimulus identity-related dichotomies are decodable during error trials (purple, p_{Present(error)} = 7.8 × 10⁻¹¹, brown, p_{Present(error)} = 1.1 × 10⁻¹³, pink, p_{Present(error)} = 8.7 × 10⁻¹¹) and SD does not decrease (black bar, inference present vs present (error), 0.67 vs. 0.66, p_RS = 0.65). (z-ac) Cross-session generalization. (z) PS for context during the stimulus period for random half-splits of the inference present sessions (Left, Middle column, 11 sessions in each half). Cross-half context PS is also computed through cross-session neural geometry alignment (Right Column, see Methods). Baseline context PS is significantly above chance within each half and across halves (p_{Half-Split One} = 0.0081, p_{Half-Split Two} = 0.0098, p_Cross-Half = 0.033). (aa) Same as (z), but for the baseline period. Context PS is significantly above chance within each half and across halves (p_{Half-Split One} = 0.0029, p_{Half-Split Two} = 0.0022, p_Cross-Half = 0.010). (ab) Same as (z), but for the inference absent sessions (7 sessions in each half) during the stimulus period. (ac) Same as (ab), but for the baseline period. In all panels, the gray shaded bar indicates 5^th-95^th percentile of the null distribution and horizontal black lines indicate SD. All p_Absent, p_Present, p_Half-split, and p_Cross-Half values stated are estimated empirically based on the null distribution shown. All p_RS values stated are a two-way ranksum test.

This difference in representation between inference absent and inference present sessions was unique to the hippocampus. No other recorded region showed a significant change in shattering dimensionality (Fig. 2g, black line, all P > 0.05) or decodability of the variable context or parity (Fig. 2g, red and orange). Although other task variables were also represented in an abstract format in other brain regions, only the hippocampus simultaneously represented the two variables context and stim pair in an abstract format (Extended Data Fig. 3a,b and Supplementary Results). These two variables are thus represented in roughly orthogonal subspaces (Fig. 2j shows a summary of this roughly disentangled neural geometry).

Context is absent in error trials

We next examined error trials to test whether the presence of context as an abstract variable in the hippocampus was associated with trial-level performance. Contrasting correct with error trials in inference present sessions revealed that decodability and format of the relevant dichotomies in error trials was similar to that in inference absent sessions both during the stimulus period (Extended Data Fig. 3e,f) and during the baseline period (Extended Data Fig. 3i,j). This includes, in particular, the context and parity dichotomy (Extended Data Fig. 3e,f, see legends for statistics). These findings demonstrate that both the content and format of the hippocampal neural representation are correlated with behaviour on a trial-by-trial basis.

Stimulus and context are abstract

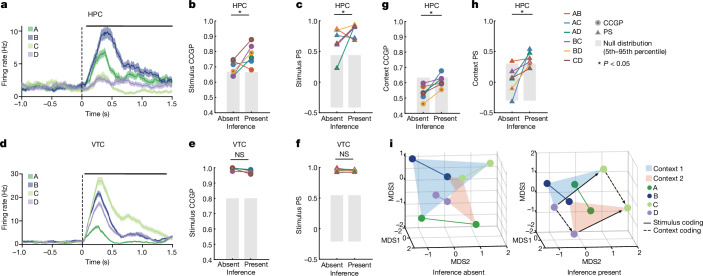
Many individual hippocampal neurons in humans encode the identity of visual stimuli^27,28. In our data, 109 out of 494 (22%) of neurons in the hippocampus were tuned to stimulus identity (Fig. 3a and Extended Data Fig. 6g,h show examples). We therefore next asked how the variable context interacted with stimulus identity and how this interaction changed with the ability to perform inference. As the four visual stimuli do not share any apparent structure, we do not expect to observe any structured geometry within each context. For this reason, we studied the geometry of pairs of stimuli (for example, stimulus A versus B) in the two contexts. To contrast with the hippocampal results, we examined the responses in the VTC, in which 195 out of 269 (73%) of neurons (Fig. 3d and Extended Data Fig. 6i,j show examples) were modulated by stimulus identity. At the population level, VTC neurons encoded stimulus identity-related balanced dichotomies in an abstract format (Extended Data Fig. 3u–y, purple, brown, pink, P_{Absent/Present} < 10⁻¹⁰). The dichotomy context, however, was not decodable in the VTC in both inference present and absent sessions (baseline period, Extended Data Fig. 3u, red; compare with Fig. 2h and stimulus period, Extended Data Fig. 3v, red, compare with Fig. 2e). Furthermore, error trial analysis showed that stimulus-related dichotomies were still decodable during errors in VTC (Extended Data Fig. 3y, purple, brown, pink, P_{Present(Error)} < 10⁻¹⁰) but not the hippocampus (Extended Data Fig. 3e, stim pair dichotomy). Context was therefore encoded as an abstract variable in the hippocampus but not in the VTC in correct trials. In error trials, VTC but not hippocampus represented stimulus identity. This contrast provides us with an opportunity to examine what changes in the hippocampus specifically when the behaviourally relevant variable context was represented in an abstract format.

Fig. 3. Stimulus representations become structured around context with inference in hippocampus but not VTC.

a–f, Encoding of stimulus identity across contexts. a–c, Responses in hippocampus (HPC) following stimulus onset carry information about stimulus identity. a, Example hippocampal neuron encoding stimulus identity. b,c, Representational geometry of stimulus identity across contexts. Analysis is conducted over pairs of stimuli in each context (legend). Significance of differences is tested using a two-sided rank-sum test comparing inference absent and present over all stimulus pairs (*P < 0.05, NS otherwise). All other conventions identical to those in Fig. 2. b,c, CCGP (P_RS = 0.041) (b) and PS (P_RS = 0.040) (c) for stimulus coding across contexts significantly increased in inference present compared to inference absent sessions. d–f, Responses in VTC following stimulus onset carry information about stimulus identity. d, Example VTC neuron encoding stimulus identity. e,f, CCGP (P_RS = 0.15) (e) and PS (P_RS = 0.39) (f) for stimulus coding across contexts does not differ significantly between inference absent and inference present sessions. g,h, Same analysis as in a–f, but for encoding of context across stimulus pairs for hippocampus (see b,c for plotting conventions). CCGP (P_RS = 0.012) (g) and PS for context coding vectors between pairs of stimuli (P_RS = 0.015) (h) both significantly increase from inference absent to inference present sessions. i, Summary of changes in neural geometry in hippocampus. Shown is the MDS of condition-averaged responses of all recorded neurons shown for inference absent and present sessions. Points are average population vector responses to combinations of stimuli and context. Lines connect the same stimuli across context. Abstract coding of stimulus across contexts (solid arrows) and context across stimuli (dashed arrows) are highlighted for one pair of stimuli (C and D). The data in this plot are identical to those of Fig. 2j. Error bars in a,d are ±s.e.m. across trials. All P_RS values are from a two-sided rank-sum test.

Extended Data Fig. 6. Cross-condition generalization performance for stimulus identity and context defined over stimulus pairs.

(a-f) Illustration of analysis over pairs of stimuli. When considering a pair of stimuli (e.g. A and B) across two contexts (e.g. 1 and 2), there are four possible task conditions (A1, B1, A2, B2). On these points, stimulus (A1A2 vs B1B2) and context (A1B1 vs A2B2) can be decoded in a straightforward manner, but is not informative about the format in which stimulus and context are encoded. Rather, the CCGP for stimulus across contexts (a-c) and for context across stimuli (d-f) provide information about the structure of the two variables and how they interact. (a-c) Illustration of CCGP for assessing whether stimuli are abstract with respect to context. (a) A linear decoder (blue bar) is trained to distinguish between stimuli A and B in context 1 (blue + and – correspond to class labels for training). The decoder is then tested (generalized) on context 2, where stimulus identity is decoded (red bar, + and – for class labels). (b) The training step. (c) The testing step. Arrows show the stimulus and context coding vectors. (d-f) Illustration of CCGP for assessing whether context is abstract with respect to stimulus identity. See (a-c) for notation. (g-j) Example neurons from hippocampus (g,h) and VTC (i,j) with tuning for stimulus identity. Plotting conventions identical to those used in Extended Data Fig. 1j. (k-l) Distances between pairs of stimulus representations in hippocampus (k) and VTPC (l). Color code indicates stimulus pair. Distance is the Euclidean distance between the stimulus centroids, each of which is an N (# of neurons) dimensional vector of average firing rates during stimulus presentation. Neuron counts are balanced between inference absent and inference present sessions. Null distributions are geometric nulls. Significance of the difference is tested by two-sided ranksum test computed over stimulus pairs, and n.s. indicates p > 0.01. p_RS = 0.39, p_RS = 0.40, p_RS = 0.13, and p_RS = 0.026 for panels (k-l), respectively. (m-n) Decodability of stimulus identity for hippocampus (m) and VTC (n). Each datapoint is a binary decoder between the two stimulus identities in a given pair. Significance of the difference between inference absent and inference present decodability is also established by Ranksum test over average decoding accuracies and n.s. indicates p > 0.05.

We next conducted a geometric stimulus-pair analysis to study the interaction of stimulus identity and context coding in the same neural population. The stimulus-pair analysis was designed to detect the presence of simultaneous abstract coding of stimulus identity across contexts and abstract coding of context across stimuli (see Extended Data Fig. 6a–f for an illustration).

The average stimulus decoding accuracy across all individual stimulus pairs in the hippocampus did not differ significantly between inference absent and inference present sessions (0.73 versus 0.76; Extended Data Fig. 6m, P_RS = 0.13, rank-sum over stimulus pairs). By contrast, the geometry of the stimulus representation changed: it became disentangled from context as indicated by significant increases in stimulus CCGP (Fig. 3b, P_RS = 0.041) and stimulus PS (Fig. 3c, P_RS = 0.040) in the inference present sessions. This finding suggests that the representation of stimulus identity was reorganized with respect to the emerging context variable. Note that context was not decodable in inference absent sessions as a balanced dichotomy (Fig. 2e, red). Nevertheless, stimulus decoders did not generalize well across the two contexts in inference absent sessions. This result indicates that context did modulate stimulus representations in the hippocampus, but in a way that was entangled with stimulus identity. This effect was specific to the hippocampus: in VTC, the neural population geometry was unchanged, as indicated by no significant differences in stimulus decodability (Extended Data Fig. 6n, P_RS = 0.15), stimulus CCGP (Fig. 3e, P_RS = 0.15), stimulus CCGP (Fig. 3e, P_RS = 0.15) and stimulus PS (Fig. 3f, P_RS = 0.39).

The presence of abstract coding for one variable (stimulus identity) does not necessarily imply that the other variable (context) is also present in an abstract format. Therefore, we next examined the variable context separately for each pair of stimuli. In the hippocampus, context was decodable for individual pairs of stimuli both during inference absent and inference present sessions, without a significant difference between the two (Extended Data Fig. 7a; 0.63 versus 0.67; P_RS = 0.065). However, in inference present sessions, the format of the variable context changed so that it was abstract across stimulus pairs as indicated by increases in context CCGP (Fig. 3g, P_RS = 0.012) and context PS (Fig. 3h, P_RS = 0.015) relative to the inference absent group. By contrast, in the VTC, whereas context was decodable from some stimulus pairs (Extended Data Fig. 7b, see legend for statistics), the format of the representation did not change in the way that would be expected for the formation of an abstract variable. Rather, there was a significant decrease in context CCGP (Extended Data Fig. 7c, P_RS = 0.026) and no significant difference in context PS (Extended Data Fig. 7d, P_RS = 0.39).

Extended Data Fig. 7. Additional context CCGP analysis over stimulus pairs for hippocampus and ventral temporal cortex (stimulus period).

(a-b) Context decoding accuracy for individual stimulus pairs in hippocampus (a) and VTC (b). (c-d) Context CCGP and Context PS for individual stimulus pairs for VTC (compare to Fig. 3g,h for hippocampus). n.s. is p > 0.01 of two-tailed ranksum test comparing absent vs. present. p_RS = 0.026 for (c). (e-h) Example neurons from hippocampus (e-g) and VTC (f-h) that are modulated by both stimulus identity and context. Error bars in PSTH (bottom) are ± s.e.m. across trials. (g,h) Mean ± s.e.m. firing rates during the stimulus period. Black arrows indicate the direction in which the firing rate for a stimulus is modulated by context. n = 120 trials. (i) Change in the consistency of context-modulation for stimuli averaged over stimulus-tuned neurons in VTC (n = 104) and HPC (n = 63). Context modulation consistency is the tendency for a neuron’s firing rate to shift consistently (increase or decrease) to encode context across stimuli (see methods). There was a significant interaction between brain area (HPC/VTC) and session type (inference absent/present); 2 × 2 ANOVA, p_Area = 0.36, p_Inference = 0.64, p_x = 4.5 × 10⁻⁵), indicating that modulation consistency increased in HPC in inference present sessions, whereas the opposite was the case in VTC.

These findings indicate that the emergence of context as an abstract variable in the hippocampus when patients can perform inference is coupled with the reorganization of stimulus representations so they are also more disentangled, thereby forming a jointly abstracted code for stimuli and context. This transformation of the representation is visible directly in a reduced dimensionality visualization of the data (Fig. 3i, Extended Data Fig. 8 and Supplementary Video 1). By contrast, we found no systematic reorganization of stimulus representations in VTC.

Extended Data Fig. 8. Hippocampal MDS plots summarizing changes in stimulus and context geometry.

(a-f) 2D MDS plots for individual stimulus pairs. See Fig. 2j for notation. MDS was conducted independently for inference absent and inference present sessions, making individual MDS axes not directly comparable. But note that relative distances are comparable because we matched the number of neurons. Only correct trials are shown. Disentangling of context and stimulus identity is present across most stimulus pairs, with the notable exception of the B/D stimulus pair (e), which is correlated with outcome and therefore cannot be dissociated from outcome using CCGP. The emergence of quadrilaterals with approximately parallel sides for all other stimulus pairs (a-d, f) is a signature of disentangling of stimulus identity and context. (g) Changes in neural geometry. MDS of condition-averaged responses of all recorded HPC neurons shown for inference absent (left) and inference present (right) sessions. All plotting conventions are identical to those in (a-f), except MDS was applied with N_dim = 3, and three stimuli (A,B,D) are plotted simultaneously. Black arrows on the inference present plot highlight parallel coding of stimuli across the two context planes. (h,i) MDS plots of HPC condition-averaged responses shown for context 1 (h) and context 2 (i) separately. Axes are directly comparable here between inference absent and present due to alignment via CCA prior to plotting. Note that the stimulus geometry in each context is a tetrahedral (maximal dimensionality, unstructured) regardless of the presence or absence of inference behavior.

Explaining the geometrical changes

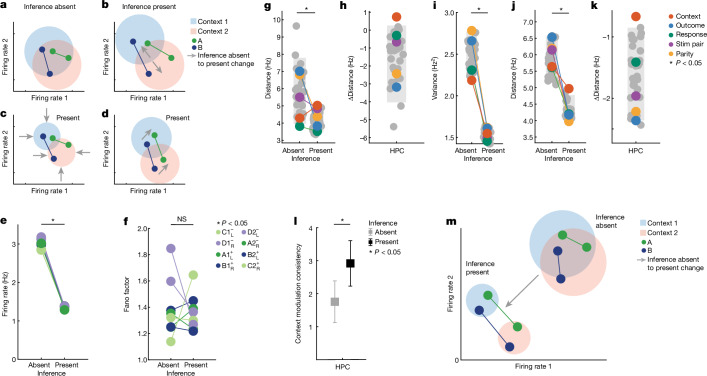
We next examined what aspects of neuronal activity changed in the hippocampus to give rise to abstract variables. We considered the following non-mutually exclusive possibilities: (1) increase in distances between conditions (Fig. 4a,b), (2) decrease in variance of the population response along the coding direction (Fig. 4c) and (3) increase in parallelism of coding directions (Fig. 4d).

Fig. 4. Firing-rate properties underlying the emergence of abstract variables in the hippocampus.

a–d, Changes that could give rise to abstract variables. Shaded circles represent variability, and grey arrows signify changes between inference absent and present. a, Original, when variable is not abstract. b, Increase in distance. c, Decrease in variance. d, Increase in parallelism. e, Firing rates of hippocampal neurons during stimulus period decreased (P_RS = 8.3 × 10⁻⁵, two-sided rank-sum over conditions). Colour indicates task state, with coding indicating identity (for example, task condition C1⁻_L describes stimulus C, context 1, outcome $-$, response L). f, Fano factor was not significantly different between inference present and absent sessions (two-sided rank-sum test, P_RS = 0.99). g, Population distance between centroids for all 35 balanced dichotomies. Average distances decrease from inference absent to present (P_RS = 2.9 × 10⁻⁸, rank-sum over dichotomies). Grey bars indicate the 5th–95th percentile of the geometric null distribution. h, Context alone is the only dichotomy whose distance significantly increases from inference absent to present (red, P_ΔDist = 0.040, against geometric null of difference). HPC, hippocampus. i, Average trial-by-trial variance projected along the coding direction decreased on average between inference absent and inference present sessions (P_RS = 6.5 × 10⁻¹³, rank-sum test). j,k, Same as g,h, but for spike counts during the baseline period. Trials are grouped by identify the previous trial. Distance was significantly reduced across all dichotomies (j, P_RS = 6.4 × 10⁻¹³, rank-sum over dichotomies) and context alone shows a distance reduction that is smaller than would be expected by chance (k, red, P_ΔDist = 0.027, against geometric null of difference). l, Stimulus-tuned neurons in the hippocampus were modulated by context more consistently in inference present sessions (P_RS = 0.0039) during the stimulus period (n = 63, error bars are ±s.e.m. across neurons). m, Illustration of changes in neural state space. Context dichotomy distance increased, variance decreased and consistency of stimulus modulation across contexts increased. In all panels, P_RS values are from a two-sided rank-sum test and grey bars indicate the 5th–95th percentile of the geometric null distribution.

We first examined whether mean firing rates across all recorded neurons differed between inference absent and inference present sessions. The firing rate across conditions decreased from 3.37 ± 0.13 to 1.36 ± 0.03 Hz (±s.e.m.): a 60% reduction on average during the stimulus period (Fig. 4e, P_RS = 8.3 × 10⁻⁵). Firing rates were also reduced during the baseline period (3.29 ± 0.09 to 1.38 ± 0.02 Hz, 58% reduction, Extended Data Fig. 9q). This firing-rate reduction was unique to the hippocampus (Extended Data Fig. 9c,r). The firing-rate reduction led to a decrease in the average distance between class centroids across all dichotomies in inference present sessions except one (5.77 ± 0.22 to 4.17 ± 0.07 Hz, P_RS = 2.9 × 10⁻⁸, Fig. 4g). The lone exception was the context dichotomy, for which distance increased (4.3 versus 5.0 Hz, P_Absent = 0.87, P_Present = 0.076, P_ΔDist = 0.040, Fig. 4g,h and Extended Data Fig. 9h). Indeed, context was the dichotomy with the largest change in distance in firing-rate space when comparing the inference present and inference absent conditions (Fig. 4h). This isolated significant rise in context separability was not seen in any of the other recorded brain areas during the stimulus period (Extended Data Fig. 9a,b). Similarly, during the baseline period, the distance between context centroids decreased the least in the hippocampus (5.6 versus 5.0 Hz, P_Absent = 0.68, P_Present = 0.0007, P_ΔDist = 0.027, Fig. 4j,k) despite the significant decrease in distance over all dichotomies that was also observed here due to the firing-rate reduction (5.85 ± 0.08 to 4.25 ± 0.04 Hz, P_RS = 6.5 × 10⁻¹³, Fig. 4j).

Extended Data Fig. 9. Additional analysis for firing rate property changes that are underlying geometric changes.

(a-j) Stimulus period analysis. (a) Distance between centroids for other brain regions. Plotting conventions are identical to Fig. 4g. Neuron counts were only balanced for each region. Significant change in average dichotomy separation determined by a two-tailed ranksum test, Bonferroni corrected for 5 multiple comparions. (b) Changes in inter-centroid distance for balanced dichotomies. No distances for named dichotomies changed more than would be expected by chance. (c) Mean firing rates for individual task conditions for all regions other than HPC. See Fig. 4e for notation. Significant change in average dichotomy separation determined by a two-tailed ranksum test, Bonferroni corrected for 5 multiple comparions. (d-g) Changes in single-neuron tuning quantified by a 3-way ANOVA (Response, Context, Outcome) with interactions. Significant factors (p < 0.05) were identified for every neuron and averages of both the number of factors per neuron (d,e) and the depth of tuning of those factors quantified by the F-Statistic (e,g) are reported (mean ± s.e.m. across neurons). Significance of difference between inference absent and present sessions was assessed by two-tailed ranksum test over significant neurons between the two groups. n = 58,47,24,22,96,118 for HPC, vmPFC, AMY, dACC, preSMA, and VTC, respectively. (h) Assessment of single trial variability of context coding. For each trial, the population response was projected onto the coding axis for context. Vertical lines indicating the mean. (i-j) Fraction of hippocampal (i) and VTC (j) neurons that exhibit selectivity for a given variable. For every neuron, selectivity is determined with a 4 × 2 ANOVA (Stimulus Identity, Context), with a per-factor significance threshold of p < 0.05. Significant differences in tuned fractions between inference absent and inference present assessed with two-tailed z-test. (k-r) Baseline period analysis for hippocampus (k-l) and dACC (m-p). (k) Average trial-by-trial variance of individual trials projected onto the coding direction for every dichotomy. See Fig. 4i for notation. Average variance along coding directions decreased significantly between inference absent and inference present sessions (p_RS = 6.5 × 10⁻¹³, ranksum over dichotomies). (l) Change in variance for all dichotomies shown in (k). No named dichotomies fell outside the null distribution. (m-n) Same as (a,b) but for the dACC at baseline. See Fig. 4g for plotting conventions. Average distance between dichotomy centroids increased (p_RS = 2.9 × 10⁻⁸, ranksum over dichotomies). Context was significantly separated (p_Absent = 0.48, p_Present = 0.0065). (n) Changes in distance between inference present and inference absent sessions for all dichotomies shown in (m). Context alone (red, p_Δ = 0.047) exhibited a greater increase in distance than expected by chance. (o-p) Same as (k-l), but for he dACC. Average variance along coding directions increased significantly (p_RS = 6.0 × 10⁻³, ranksum over dichotomies). (q) Mean baseline firing rates in hippocampus (p_RS = 1.6 × 10⁻⁴, ranksum over conditions). See Fig. 4e for plotting conventions. Ranksum test over conditions. (r) Same as (q) but for the other brain areas. Ranksum test over conditions. Note that all brain regions other than AMY exhibit slight but significant increases (p_RS  = 0.050, 0.23, 1.6 × 10⁻⁴, 1.6 × 10⁻⁴, and 1.6 × 10⁻⁴ for vmPFC, AMY, dACC, preSMA, and VTC, respectively). (s-w) Control analysis for stimulus period after distribution-matching for firing rate. (s) Distribution of mean stimulus firing rates over all hippocampal neurons in the inference absent (gray) and inference present (black) sessions, as well as randomly thinned inference absent firing rates that distribution-match the inference present firing rates (orange). (t) Mean firing rates before and after distribution matching. Ranksum test over conditions. p_RS = 1.6 × 10⁻⁴ for absent vs. absent-match. (u-w) Replication of key results for the set of neurons that are distribution matched. Plotting conventions are those shown in Fig. 2. No meaningful differences are present between inference absent and distribution-matched inference absent for any dichotomy/metric. (u) p_Present = 1.8 × 10⁻⁶, p_Present = 6.4 × 10⁻⁶, and p_Present = 0.016 for context, stim pair, and parity respectively. (v) p_Present = 0.035 and p_Present = 0.0047 for context and stim pair. (w) p_Present = 7.2 × 10⁻¹⁰ and p_Present = 3.6 × 10⁻⁶ for context and stim pair. (x-ab) Control analysis for stimulus period after excluding high-hippocampal-firing-rate sessions. (x) Distribution of mean hippocampal firing rate over inference absent (gray) and inference present (black) sessions. Each point in the distribution corresponds to the mean hippocampal firing rate over all neurons in a single session. Vertical dashed line indicates 3 Hz threshold. Hippocampal neurons from all inference absent and inference present sessions above this threshold were excluded from analysis shown in (y-ab). 131/169 inference absent neurons (10/14 sessions) and 318/325 inference present neurons (21/22 sessions) are retained. (y) Same as (t), but computed using all sessions with mean hippocampal firing rate <3 Hz (p_RS = 1.6 × 10⁻⁴). (z-ab) Neural geometry measures re-computed excluding hippocampal neurons from high-firing-rate sessions. No meaningful differences are apparent except the above-chance context PS in inference absent sessions (red, p_Absent = 2.2 × 10⁻⁸). In all panels, * indicates p < 0.05 and ns indicates not significant. All p_Absent, and p_Present values stated are estimated empirically based on the null distribution shown. All p_RS values stated are a two-sided ranksum test.

Next, we assessed changes in the variability of the population response along the coding direction of each dichotomy. The variance along the coding direction of neuronal responses in the hippocampus decreased for all dichotomies in inference present when compared to inference absent sessions during both the stimulus period (2.51 ± 0.16 versus 1.53 ± 0.06, P_RS = 6.5 × 10⁻¹³, Fig. 4i) and the baseline period (2.49 ± 0.09 versus 1.58 ± 0.02, P_RS = 6.5 × 10⁻¹³, Extended Data Fig. 9k,l). However, this decrease could be a consequence of the reduction in firing rates under the assumption of Poisson statistics. We conducted a condition-wise fano-factor analysis to assess whether the variance reduction was beyond that expected for the reduction in firing rates. This analysis revealed no significant differences in fano factors between inference absent and inference present sessions during the stimulus period (1.39 ± 0.22 versus 1.36 ± 0.14, P_RS = 0.99, Fig. 4f) and the baseline period (1.61 ± 0.26 versus 1.45 ± 0.11, P_RS = 0.19). Together, these two findings suggest that the decrease in variance along dichotomy coding directions is explained by the decreases in firing rate.

Did changes in tuning of individual neurons give rise to the increases in parallelism for context across stimuli (see Extended Data Fig. 7e–h for examples)? A stimulus-tuned neuron also modulated by context could do so consistently across all stimuli (for example, firing rate increased for all stimuli), or inconsistently (for example, firing rate increased for some stimuli and decreased for others). We quantified the consistency of context modulation across stimuli for each individual neuron (Methods). The consistency of context modulation in the hippocampus increased significantly in inference present sessions (Fig. 4l and Extended Data Fig. 7i, 1.8 ± 0.2 versus 2.9 ± 0.3, P_RS = 0.0049). This effect was specific to hippocampus: in VTC, the same metric decreased significantly (Extended Data Fig. 7i, 2.6 ± 0.3 versus 1.6 ± 0.2, P_RS = 0.0039).

These data indicate that the geometric changes seen in the hippocampus were due to the following (Fig. 4m): (1) an increase in separation between condition average representations of the two contexts despite relaxing towards the origin (decrease in firing rate), (2) decreases in variance along the coding direction, and (3) neurons becoming increasingly consistent (parallel coding directions) in their modulation across stimulus and context dimensions.

Effect of verbal instructions

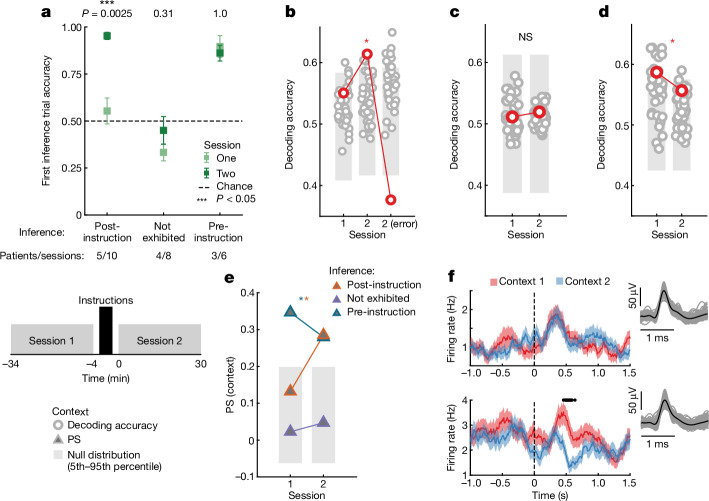
Did the format of the representation differ between participants who discovered the underlying latent variable context by themselves and those who only did so after receiving verbal instructions? We provided all patients with verbal instructions detailing the latent task structure after session 1 (Fig. 5, inset), allowing us to examine this question. We divided patients into three types on the basis of their behaviour: those who showed inference behaviour in the first session (pre-instruction inference, three patients, six sessions; Extended Data Fig. 1i); those who showed inference behavior after being given verbal instructions (post-instruction inference, five patients, ten sessions; Extended Data Fig. 1g); and those who did not perform inference even after being provided with verbal instructions (inference ‘not exhibited’, four patients, eight sessions; Extended Data Fig. 1h). Only patients who performed accurately in non-inference trials in both sessions one and two were included in one of these three groups (Extended Data Fig. 1g–i, ‘last’; five patients excluded, Supplementary Table 1). The principal difference between the post-instruction (Fig. 5a and Extended Data Fig. 10a,b) and inference not exhibited (Fig. 5a and Extended Data Fig. 10h,i) groups is their ability to perform inference following the verbal instructions, with both groups performing the task accurately otherwise. The pre-instruction inference group, on the other hand, showed above-chance inference performance during both sessions (Fig. 5a and Extended Data Fig. 10o,p).

Fig. 5. Abstract hippocampal representation of context is present following successful verbal instructions.

a, Top, behavioural performance on the first inference trial for patients that performed inference after instructions (n = 10 sessions, post-instruction), those that did not perform inference even after instructions (n = 8 sessions, not exhibited) and those that performed inference already before instructions (n = 6 sessions, pre-instruction). Error bars are ±s.e.m. across sessions and P values are rank-sum session 1 versus 2. Bottom, schematic of the experiment. Session before and after high-level instructions are referred to as sessions 1 and 2, respectively. b–d, Encoding of context during the stimulus period in different groups of patients. The first trial following a switch is excluded from this analysis. *P < 0.05 against null in any column of a given geometric measure plot estimated empirically from the null distribution. b, Post-instruction group. Context was significantly decodable in session 2 correct but not error trials and also not in session 1 (P₁ = 0.17, P_1(correct) = 0.016, P_RS = 3.1 × 10⁻¹⁹, P_2(error) = 0.99). c, Not exhibited group. Context was not significantly decodable (P₁ = 0.44, P₂ = 0.42). d, Pre-instruction group. Context was decodable in session 1 (P₁ = 0.014, P_Two = 0.17). e, Summary of changes due in instructions based on the PS for context. Neuron counts are equalized across groups by subsampling. Context PS increases significantly from session 1 to 2 in the post-instruction group (P_{Postinstruction,i} = 0.20, P_{Postinstruction,2} = 0.0028). Context PS is not significantly different from chance for the not exhibited group (P_{Not exhibited,1/2} < 0.5) and is different from chance in both sessions for the pre-instruction inference (P_{Pre-instruction,1/2} < 0.005) group. All P values are versus chance and are empirically estimated from the null distribution. f, Example hippocampal neuron with univariate context encoding in the session after (bottom) but not before (top) instructions (one-way ANOVA, P_One = 0.40, P_Two = 0.010). Error bars are ±s.e.m. across trials.

Extended Data Fig. 10. Additional analysis of the effect of instructions on hippocampal neural geometry.

(a-g) Post-instruction inference group. (a-b) Behavior. Identical to Extended Data Fig. 1e,f, except now the session recorded immediately preceding and immediately following verbal instructions are shown. Average performance is computed as a moving average with a 3-block window on the last three trials before a context switch (non-inference) and on the first inference trial after a switch (inference). Error bars are standard errors computed over subjects. Chance performance is 0.5. (c-d) Geometric measures during the stimulus period. Only context is shown as a named dichotomy for visual clarity. (c) CCGP (context, red, p_One = 0.27, p_Two = 0.046, p_RS = 1.4 × 10⁻³¹) and (d) PS (context, red, p_One = 0.029, p_Two = 3.5 × 10⁻⁶, p_Two(error) = 0.0028). (e-g) Geometric measures during the baseline period. (e) Decoding accuracy (context, red, p_One = 0.35, p_Two = 0.0014, p_Two(error) = 0.55, p_RS = 1.4 × 10⁻²⁰). (f) CCGP (context, red, p_One = 0.33, p_Two = 0.0037, p_RS = 3.0 × 10⁻³⁴). (g) PS (context, red, p_One = 0.017, p_Two = 7.5 × 10⁻⁸, p_Two(error) = 0.40). (h-n) Same as (a-g), but for inference not-exhibited group. (j-k) Geometric measures during the stimulus period. (j) CCGP (context, red, p_One = 0.56, p_Two = 0.39, p_RS = 0.004). (k) PS (context, red, p_One = 0.81, p_Two = 0.95). (l-n) Geometric measures during the baseline period. (l) Decoding accuracy (context, red, p_One = 0.45, p_Two = 0.45, p_RS = 0.68). (m) CCGP (context, red, p_One = 0.45, p_Two = 0.47, p_RS = 0.15). (n) PS (context, red, p_One = 0.93, p_Two = 0.30) for the. (o-u) Same as (a-g), but for the pre-instruction inference group. (q-r) Geometric measures during the stimulus period. (q) CCGP (context, red, p_One = 0.23, p_Two = 0.19, p_RS = 0.0045). (r) Parallelism Score (context, red, p_One = 6.3 × 10⁻⁸, p_Two = 4.5 × 10⁻⁷). (s-u) Geometric measures during the baseline period. (s) Decoding accuracy (context, red, p_One = 0.37, p_Two = 0.47, p_RS = 0.036), (t) CCGP (context, red, p_One = 0.30, p_Two = 0.50, p_RS = 5.9 × 10⁻⁷), and (u) PS (context, red, p_One = 1.7 × 10⁻⁵, p_Two = 0.029). (v) Changes in hippocampal firing rates for the 3 different sub-groups of session pairs. Firing rate changes are computed during the stimulus presentation period (0.2 s to 1.2 s after stim onset) from consecutive sessions. Points are average changes in condition-averaged firing rates (8 unique conditions). Changes in firing rate that significantly differed from zero (two-sided t-test, p < 0.05/3, boneferroni corrected) are indicated with a “*” (p = 1.5 × 10⁻⁴, 1.2 × 10⁻⁴, and 0.088). Post-instruction inference group alone exhibited significant decrease in firing rate. Inference not-exhibited group exhibited an increase in firing rate. In all panels stated p-values denoted as p_One and p_Two are estimated empirically based on the null distribution shown. All p_RS values stated are a two-way ranksum test.

In the post-instruction inference group, context was decodable in the hippocampus during the stimulus period on correct trials in the session following the verbal instructions (Fig. 5b, P_One = 0.17, P_Two = 0.016, P_RS = 3.1 × 10⁻¹⁹).This representation of context was in an abstract format, as indicated by significant increases in both CCGP (Extended Data Fig. 10c; P_One = 0.28, P_Two = 0.047, P_RS = 8.4 × 10⁻¹⁶ and PS (Extended Data Fig. 10d; P_One = 0.023, P_Two = 1.2 × 10⁻⁶). Successful performance in the task was associated with context being represented abstractly in the hippocampus, as both the decodability (Fig. 5b, P_Two(error) = 0.99, session 2 correct versus error, P_RS = 4.3 × 10⁻²⁰) and PS (Extended Data Fig. 10d, P_Two(error) = 1.1 × 10⁻⁴) of context decreased significantly on error trials in session 2. Context was also encoded in an abstract format during the baseline period in the same performance dependent manner as context in the stimulus period (Extended Data Fig. 10e–g). By contrast, in patients in the inference not exhibited group, context was not encoded by hippocampal neurons during the stimulus (Fig. 5c and Extended Data Fig. 10j,k, all P_One/Two > 0.05) nor the baseline (Extended Data Fig. 10l,n all P_One/Two > 0.05) periods in session 2. Thus, the ability of post-instruction group patients to perform inference following instructions was associated with the rapid emergence of an abstract context variable in their hippocampus.

This effect could also be appreciated at the single-neuron level in the hippocampus. In the instruction successful group, the proportion of neurons that are linearly tuned to context (P < 0.05, one-way ANOVA for context) during both the stimulus (8% (6 out of 75 neurons) versus 18% (17 out of 93 neurons), P = 0.027) and baseline (7% (5 out of 75 neurons) versus 16% (15 out of 93 neurons), P = 0.029) periods increased in session 2 versus session 1 (Fig. 5f shows an example). By contrast, in the not exhibited group, there was no significant change in tuning to context at the single-neuron level both during the stimulus period (6% session 1 versus 6% session 2, P = 0.41) and the baseline period (8% session 1 versus 5% session 2, P = 0.27).

For the pre-instruction inference patient group, context was already decodable during session 1 (Fig. 5d, P_One = 0.014) and the PS was significant and near the top of the dichotomy rank order in sessions 1 and 2 (Extended Data Fig. 10r, P_One = 1.5 × 10⁻⁹, P_Two = 1.7 × 10⁻⁶). A similar trend was observed with the baseline context representation for these patients (Extended Data Fig. 10s–u). This finding suggests that the context variable these patients learned experientially during session 1 was in an abstract format.

Last, we compared the geometry of the context representations formed by each of the three patient groups (balancing number of neurons, Methods). Context PS increased significantly in the post-instruction inference group, from levels not different from chance during session 1 (P_{One,Post-inst} = 0.20, Fig. 5e) to a level comparable to the pre-instruction inference group during session 2 (P_{Two,Post-inst} = 0.0028, P_Two,Pre-inst = 0.0035, Fig. 5e). The PS in the pre-instruction inference group, on the other hand, did not change significantly and was already above chance in session 1 (Fig. 5e, see legend for statistics). These findings suggest that hippocampal neurons in the pre-instruction inference group carried an abstract representation of context before receiving verbal instructions, and retained that geometry after receiving instructions. Furthermore, neurons of participants in the post-instruction inference group encode a task representation whose geometry resembled that of the pre-instruction group, indicating that a similar representational geometry can be constructed through either experience or within minutes through instruction to support inference in a new task.

Discussion

How can a neural or biological network efficiently encode many variables simultaneously^11,29? One solution is to encode variables in an abstract format so they can be re-used in new situations to facilitate generalization and compositionality^24,30–34. Here we show that such an abstract representation emerged in the human hippocampus as a function of learning to perform inference. The format by which latent context and stimulus identity were represented was predictive of the ability to perform behavioural generalizations that rely on contextual inference. Patients performed well on non-inference trials in all sessions included in the analysis, indicating that they understood the task. Therefore, the difference between the inference present and absent sessions was only in whether they performed inference following the covert context switch (Fig. 1f). For those sessions in which patients did not perform inference, there was no systematic relationship between context coding vectors across stimuli. For sessions in which patients performed inference, there was alignment of the context coding direction across stimuli (making them parallel), indicating that the context variable had been disentangled from the stimulus identity variable in the hippocampi of these patients (Figs. 2j and 3i). As a result, the two variables became disentangled, thereby allowing generalization. This representation was implemented by the hippocampus using a broadly distributed code as evidenced by the high context PS (Extended Data Fig. 3f,g,j,n) and the lack of reliance on univariately tuned context neurons to generate the abstract context representation (Extended Data Fig. 4a–j and Supplementary Note 2). Thus, the geometry we study here did not trivially arise from classically tuned neurons.

Extended Data Fig. 4. Additional control analyses for Hippocampal representational geometry after excluding univariantly tuned neurons.

Identical analysis to the main geometric analysis shown in Fig. 2, except that neurons are excluded from the analysis with the following criteria: in (a-j), neurons with significant linear tuning for Context, Response, or Outcome (2 × 2 × 2 ANOVA, Any Main Effect p < 0.01), and in (k-m), neurons with significant linear tuning for Stimulus Identity or Context (4x2 ANOVA, Any Main Effect p < 0.01). 455/494 neurons were retained for the stimulus period analysis (a-e) and 458/494 neurons were retained for the baseline period analysis (f-j). All primary results for changes in hippocampal geometry were recapitulated apart from decodability of the parity dichotomy during the stimulus period (a). (a-e) Stimulus period analysis. (a) Decodability. Context (red, p_Absent = 0.36, p_Present = 0.0001, p_RS = 1.6 × 10⁻³¹) and stim pair (purple, p_Absent = 0.078, p_Present = 4.2 × 10⁻⁵, p_RS = 6.6 × 10⁻³¹) was decodable and SD (0.54 vs. 0.58, p_RS = 0.0013) increased. (b) CCGP. Context (red, p_Absent = 0.63, p_Present = 0.0016, p_RS = 5.2 × 10⁻³⁴) and stim pair (purple, p_Absent = 0.17, p_Present = 0.00095, p_RS = 5.3 × 10⁻³⁴) increased. (c) PS. Context (red, p_Absent = 0.40, p_Present = 3.7 × 10⁻¹³) and stim pair (purple, p_Absent = 0.83, p_Present = 1.2 × 10⁻⁷) increased. (d-e) Error trial analysis. (d) Decodability. Context (red, p_Absent = 0.36, p_Present = 0.0029, p_{Present(error)} = 0.64, p_RS = 1.5 × 10⁻²⁰) and stim pair (purple, p_Absent = 0.071, p_Present = 0.0021, p_{Present(error)} = 0.062, p_RS = 2.0 × 10⁻⁵) were decodable only in error trials. SD was not significantly different (inference present vs present (error), 0.56 vs. 0.55, p_RS = 0.62) during the stimulus presentation. (e) PS. Context (red, p_Absent = 0.40, p_Present = 4.6 × 10⁻¹⁵, p_{Present(error)} = 0.012) was largerest in correct trials. (f-j) Baseline analysis. (f) Context decodability (red, p_Absent = 0.37, p_Present = 0.013, p_RS = 2.2 × 10⁻²⁶) and SD (black, 0.50 vs. 0.52, p_RS = 0.036). (g) CCGP. Context (red, p_Absent = 0.31, p_Present = 0.0044, p_RS = 1.9 × 10⁻³³) differed significantly. (h) PS. Context differed significantly (red, p_Absent = 0.12, p_Present = 0.0055). (i-j) Error trial analysis during the baseline. (i) Decodability. Context was elevated but not significantly during correct trials (red, p_Absent = 0.55, p_Present = 0.12, p_{Present(error)} = 0.37). SD increased significantly (black, inference present vs present (error), 0.51 vs. 0.49, p_RS = 0.030). (j) PS. Context increased significantly in correct trials (red, p_Absent = 0.66, p_Present = 8.5 × 10⁻⁹, p_{Present(error)} = 0.30). (k-m) Same as (a-c), but after removing neurons tuned to stimulus identity using the 2-Way ANOVA during the stimulus period. 412/494 neurons were retained. Context remains in an abstract format. (k) Context decodability (red, p_Absent = 0.38, p_Present = 0.0088, p_RS = 4.1 × 10⁻²⁸). SD was not significantly different (black, 0.53 vs. 0.53, p_RS = 0.69). (l) CCGP. Context (red, p_Absent = 0.51, p_Present = 6.0 × 10⁻⁴, p_RS = 2.5 × 10⁻³⁴) increased significantly. (m) PS. Context (red, p_Absent = 0.77, p_Present = 2.3 × 10⁻⁶) increased significantly. (n-s) Seizure onset zone exclusion analysis. Analysis shown is identical to Fig. 2, except that hippocampal neurons recorded in seizure onset zones were removed. 410/494 neurons were retained for analysis. Results were effectively identical to that reported in Fig. 2, with every significant named dichotomy increase during stimulus (n-p) and baseline (q-s) periods being recapitulated in the absence of SOZ hippocampal neurons. (t-z) Non-inference performance control analysis. Identical analysis to the main geometric analysis shown in Fig. 2, except that inference absent and inference present sessions were distribution-matched for non-inference trial performance. Pairs of inference absent and inference present sessions with at most 7.5% difference in non-inference trial performance were selected, prioritizing sessions with more hippocampal neurons. This matching process yielded 10 inference absent sessions (152 neurons) and 10 inference present sessions (187 neurons) whose average non-inference performances did not statistically significantly differ (92.8% v.s. 94.7%, p_RS = 0.58, ranksum over sessions). All main geometric findings were recapitulated for the stimulus (t-v) and baseline (w-y) periods. (z) Distribution-matched behavior. P-values are one-way binominal test vs. 0.5. n = 10 sessions in each group. Error bars are ±s.e.m. across sessions. In all panels, the gray shaded bar indicates 5^th–95^th percentile of the null distribution and horizontal black lines indicate SD. All p_Absent, and p_Present values stated are estimated empirically based on the null distribution shown. All p_RS values stated are a two-way ranksum test.

Inferential reasoning is thought to rely on cognitive maps, which have been observed in the hippocampus and other parts of the brain^19,35–39. Cognitive maps are thought to underlie inferential reasoning in various complex cognitive and spatial domains^{3,10,35,36,40,41}. However, little is known about how maps for cognitive spaces emerge at the cellular level in the human brain as a function of learning. Here we show that a cognitive map that organizes stimulus identity and latent context in an ordered manner emerges in the hippocampus. The cognitive map emerges because task states in one context, indexed by stimulus identity, become systematically related to the corresponding task states in the other context through a dedicated context coding direction that is disentangled from stimulus identity (Fig. 3b,c,g–i). Furthermore, the relational codes between task states (stimuli) in each context are preserved across contexts.

Hippocampal cognitive maps observed in other studies are often different from those that we observed because the encoded variables are observed to nonlinearly interact, a signature of high-dimensional representations. These representations are believed to be the result of a decorrelation of the neural representations (recoding) that is aimed at maximizing memory capacity^42–44. This form of preprocessing leads to widely observed response properties, such as those of place cells⁴⁵. However, there is some evidence of hippocampal neurons that encode one task variable independently of others^{15,21,46–51}. In these studies, no correspondence was shown between different representational geometries in the hippocampus and differences in behaviour. Here the task representations generated when patients cannot perform inference (but can still perform the task) are systematically different from the abstract hippocampal representations of context and stimulus identity that correlate with inference behaviour¹¹. Finally, it is important to stress that we also observed an increase in the shattering dimensionality, which has been in shown in other studies to be compatible with the low dimensionality of disentangled representations^11,15.

We found stimulus identity codes in brain regions other than the hippocampus, but these mostly lacked reorganization as a function of learning to perform inference. This code stability is particularly salient in the VTC, a region analogous to macaque IT cortex, in which neurons construct a high-level representation of visual stimuli^52–54. Some studies conducting unit recordings in this general region in humans show that neurons show strong tuning to stimulus identity⁵⁵. We similarly find that VTC neurons encode visual stimulus identity (Fig. 3d–f and Extended Data Fig. 6n). However, these responses were not modulated by latent context in a systematic manner. As a result, despite being decodable for some individual stimulus pairs, context was not represented in an abstract format. Rather, in VTC, context was only weakly decodable for a subset of the stimuli, context decodability did not change between inference absent and inference present sessions (Extended Data Fig. 7b,c), and stimulus identity geometry was not reorganized relative to context in inference present sessions (Fig. 3e,f). Our study therefore shows that disentangled context-stimulus representations emerged in the hippocampus, but not in the upstream visually responsive region VTC.

In our study, verbal instructions resulted in changes in hippocampal task representations that correlated with behavioural changes. The emergence of this representation in the session immediately following the instructions in the post-instruction inference group is correlated with their newfound ability to perform inference and suggests that hippocampal representations can be modified on the timescale of minutes through verbal instructions (Fig. 5). This change in representation is qualitatively different from the standard approach of studying the emergence of a ‘learning set’, wherein a low-dimensional representation of abstract task structure emerges slowly over days through trial-and-error learning^47,56,57. Our finding of similar representational structure in the hippocampus in participants who learned spontaneously and those who only learned after receiving verbal instructions suggests that both ways of learning can potentially lead to the same solution in terms of neural representations. In complex, high-dimensional environments, learning abstract representations through trial and error becomes exponentially costly (the curse of dimensionality), and instructions can be used to steer attention towards previously undiscovered latent structure that can be explicitly represented and used for behaviour. Our findings suggest that when high-level instructions successfully alter behaviour, underlying neural representations can be rapidly modified to resemble one learned through experience.

Methods

Participants

The study participants were 17 adult patients who were implanted with depth electrodes for seizure monitoring as part of an evaluation for treatment for drug-resistant epilepsy (Supplementary Table 1). No statistical methods were used to predetermine the sample size but this number of patients is large relative to other similar studies. All patients provided informed consent and volunteered to participate in this study. Research protocols were approved by the institutional review boards of Cedars-Sinai Medical Center, Toronto Western Hospital and the California Institute of Technology.

Psychophysical task and behaviour

Participants performed a serial reversal learning task. There were two possible static stimulus–response–outcome (SRO) maps, each of which was active in one of the two possible contexts. Context was latent and switches between context were uncued. Each recording session consisted of 280–320 trials grouped into 10–16 blocks of variable size (15–32 trials per block) with block transitions corresponding to a change in the latent context.

Patients completed 42 sessions of the task, typically in pairs of two back-to-back sessions on the same recording day (mean, 2.4 sessions per day, minimum two, maximum four; Supplementary Table 1). New stimuli were used in every session, thus requiring patients to re-learn the SRO maps through trial and error at the start of every session.

Each trial consisted of a blank baseline screen, stimulus presentation, speeded response from the participant, followed by feedback after a brief delay (Fig. 1a). Responses were either left or right in every trial. In each session, stimuli were four unique images, each chosen from a different semantic category (human, macaque, fruit, car). If a patient performed several sessions, new images not seen before by the patient were chosen for each session. The task was implemented in MATLAB (Mathworks) using PsychToolbox v.3.0 (ref. ⁵⁸). Images were presented on a laptop positioned in front of the patient and subtended roughly 10° of visual arc (300 px², 1,024 × 768 screen resolution, 15.6 inch (40 cm) monitor, 50 cm viewing distance). Patients provided responses using a binary response box (RB-844, Cedrus).

Receipt of reward in a given trial was contingent on the accuracy of the response provided. In each trial, either a high or low reward (25 cents (¢) or 5¢) was given if the response was correct, and no reward (0¢) if incorrect. Whether a given trial resulted in high or low reward if the response was correct was determined by the fixed SRO map (Fig. 1c). Stimulus–response associations were constructed such that two out of four images (randomly selected) were assigned one response and the other two images were assigned the other (for example, human and fruit, left; macaque and car, right). Thus, in each context, each stimulus was uniquely specified by a combination of its correct response (left or right) and reward value (high or low). Crucially, the SRO maps of the two possible contexts were constructed so that they were the opposite of each other from the point of view of the associated response (Fig. 1c). To fully orthogonalize also associated reward, half of the reward values stayed the same and the others switched. This structured relationship of stimuli across contexts led to the full orthogonalization of the response, context and reward variables (Fig. 1b,c). Crucially, the stimulus–response map inversion across contexts provided the opportunity for patients to perform inferential reasoning about the current state of the SRO map, and therefore the latent context.

As rewards were provided deterministically, participants could infer that a context switch had occurred on receiving a single error to the first stimulus they encounter in the new context, and immediately respond correctly to the rest of the stimuli the first time they encounter them in the new context. The behavioural signature of inferential reasoning was thus the accuracy on the trials that occurred immediately after the first error trial. Specifically, we took a participant’s performance on the first instance of the other stimuli encountered in the new context as a measure of that participant’s inference capabilities (Extended Data Fig. 1a; note that although there are three inference trials after every context switch, each corresponding to a different stimulus, only the first inference trial was used to determine whether a session was in the inference present or absent group: below).

Patients completed several sessions of the task, in each of which new stimuli were chosen. After completion of the first session, the experimenter provided a standardized description of the latent contexts and SRO reversal to the patient (Supplementary Methods). These instructions were given regardless of how well the patient performed in the immediately preceding session. Each session took roughly 30 min (mean 1,154 s, range 898–1,900 s), and the inter-session break during which instructions were provided lasted roughly 4 min (Fig. 5a, bottom; mean duration 241 s, range 102–524 s). After this brief interlude, the participants completed the task again with a new set of four stimuli.

Behavioural control

We administered a control version of the task identical to the ‘first session’ described above to n = 49 participants recruited on Amazon Mechanical Turk (MTurk), who provided informed consent under a protocol approved by the institutional review board of Cedars-Sinai Medical Center (exempt study). No statistical methods were used to predetermine the sample size. We then used this data to calibrate the difficulty of the task. Most (roughly 75%) of the control participants demonstrated proper inference performance, and the remaining 25% demonstrating slow updating of SROs after a context switch, consistent with a behavioural strategy in which each stimulus is updated independently (Extended Data Fig. 1a).

Analysis of behaviour

Six of the 42 sessions were excluded due to at-chance performance in non-inference trials (binomial test, P > 0.05). A session was classified as ‘inference present’ if performance on the first of the three possible inference trials that occurred after the context switches was significantly above chance (timepoint 2 in Fig. 1f, binomial test on inference trial 1, P < 0.05) and as ‘inference absent’ (n = 14 sessions, P > 0.05, binomial test on inference trial 1) otherwise.

Electrophysiology

Extracellular electrophysiological recordings were conducted using microwires embedded within hybrid depth electrodes (AdTech Medical). The patients we recruited for this study had electrodes implanted in at least the hippocampus, as well as in addition subsets of amygdala, dorsal anterior cingulate cortex, upplementary motor area, ventromedial prefrontal cortex and VTC as determined by clinical needs (Supplementary Table 1). Implant locations were often bilateral, but some patients only had unilateral implants as indicated by clinical needs. Broadband potentials (0.1 Hz–9 kHz) were recorded continuously from every microwire at a sampling rate of 32 kHz (ATLAS system, Neuralynx). All patients included in the study had well-isolated single neuron(s) in at least one of the brain areas of interest.

Electrode localization was conducted using a combination of pre-operative magnetic resonance imaging and postoperative computed tomography using standard alignment procedures as previously described (using freesurfer v.5.3.0 and v.7.4.1)^59,60. Electrode locations were coregistered to the to the MNI152-aligned CIT168 probabilistic atlas⁶¹ for standardized location reporting and visualization using Advanced Normalization Tools v.2.1 (refs. ^59,60). Placement of electrodes in grey matter was confirmed through visual inspection of participant-specific computed tomography and magnetic resonance imaging alignment, and not through visualization on the atlas.

Spike detection and sorting

Raw electric potentials were filtered with a zero-phase lag filter with a 300 Hz–3 kHz passband. Spikes were detected and sorted using the OSort software package v.4.1 (ref. ⁶²). All spike sorting outcomes were manually inspected and putative single units were isolated and used in all subsequent analyses. We evaluated the quality of isolated neurons quantitatively using our standard set of metrics^63–65, including the proportion of inter-spike interval violations shorter than 3 ms, signal-to-noise ratio of the waveform, projection distance between pairs of isolated clusters and isolation distance of each cluster relative to all other detected spikes. Only well-isolated neurons as assessed by these spike sorting quality metrics were included.

Selection of neurons, trials and analysis periods

Activity of neurons was considered during two epochs throughout each trial: the baseline period (base), defined as −1 to 0 s preceding stimulus onset on each trial and the stimulus period (stim), defined as 0.2 to 1.2 s following stimulus onset on each trial. Spikes were counted for every neuron on every trial during each of these two analysis periods. The resulting firing-rate vectors were used for all encoding and decoding analyses. For the stimulus period, because patients would sometimes respond before 1.2 s (reaction time 1.08 ± 0.04 s over sessions), we determined that 75.15% of all spikes occurred before a response was provided across all recorded neurons, indicating that analyses performed with these spike counts predominantly, but not exclusively, reflect predecision processing. Tests of single-neuron selectivity were conducted using N-way ANOVAs with significance at P < 0.05, where N was either 2 for models of stim ID (A, B, C, D) and context (1, 2), or 3 for models that included outcome (high, low), response (left, right) and context (1, 2). All variables were categorical, and all models were fit with all available interaction terms included. In Fig. 1l, a unit is marked as linearly tuned if it has at least one significant main effect, and nonlinearly tuned if it has at least one significant interaction term in the ANOVA model.

Population decoding analysis

Single-trial population decoding analysis was performed on pseudo-populations of neurons assembled across all neurons recorded across all patients. We pooled across sessions within each anatomically specified recording area as described previously^59,66. We aggregated neurons across participants into a pseudo-population that consists of all neurons recorded in a given brain area, which allows us to examine populations of several hundred neurons in humans despite inability to record this many neurons simultaneously. This analysis approach is possible because all participants performed the same task, so that conditions could be matched across all relevant variables for a given trial in the pseudo-population (for example, trial 1 might be context 1, correct response, stimulus A, response right, outcome high). The justification for using this approach is threefold. First, independent population codes, in which the information that each neuron provides can be characterized by its own tuning curve, can be understood by recording one neuron at a time and aggregating them for analysis⁶⁷. This is the type of code we are examining. Second, we seek to establish the content and structure of information that is reliably present in a given brain area across participants. This can only be achieved by recording in many participants. Third, in most instances, decoding from pseudo-populations yields the same results from simultaneously recorded neurons^68,69. Results between the two approaches can differ when noise correlations are considered, which can have complex effects on the geometry of the underlying representation⁶⁷. Here noise correlations are not the topic of interest. Noise correlations are present for the subgroups of neurons in the pseudo-population that were recorded simultaneously. To avoid potential effects of these remaining noise correlations, we removed them by randomly scrambling the order of trials for every neuron included in the pseudo-population (as we have described before^59,66).

Decoding was conducted using support vector machines with a linear kernel and L2 regularization as implemented in MATLAB’s fitcsvm function. No hyperparameter optimization was performed. All decoding accuracies are reported for decoding accuracy for individual trials. Decoding accuracy is estimated out of sample using fivefold cross-validation unless otherwise specified (for example, cross-condition generalization). Many of the decoding analyses in this work consist of grouping sets of distinct task conditions into classes, then training a support vector machine to discriminate between those two groups of conditions. Neurons included in the analysis were required to have at least K correct trials of every unique condition to be included in the analysis (K = 15 trials unless otherwise stated). To construct the pseudo-population, we then randomly sampled K trials from every unique condition and divided those trials into the groups required for the current decoding analysis for every neuron independently. Randomly sampling correct trials in this way allowed us to destroy noise correlations that might create locally correlated subspaces from neurons recorded in the same area and session⁵⁹.

To account for the variance in decoding performance that arose from this random subsampling procedure, all reported decoding accuracies are the average resulting from 1,000 iterations of subsampling and decoder evaluation. A similar trial balancing and subsampling procedure was conducted for all analyses that report decoding accuracy on incorrect trials, but with K = 1 trial or condition required as incorrect for the neuron to be included in analysis. Various other analyses conducted throughout this work, including representation geometry measures, centroid distances and coding direction variances, all rely on this procedure of balanced correct and incorrect trial subsampling, and averaging across 1,000 iterations of the computed metric to study the relationships between task conditions in an unbiased manner. All reported values have been computed with this approach unless otherwise stated.

Balanced dichotomies

Our task has eight possible states (Fig. 1b). We characterized how neurons represented this task space by assessing how a decoder could differentiate between all possible ‘balanced dichotomies’ of these eight task conditions (Fig. 1b).

The set of all possible balanced dichotomies is defined by all possible ways by which the eight unique conditions can be split into two groups containing four of the conditions each (for example, four points in context 1 versus 4 points in context 2 is the context dichotomy). There are 35 possible balanced dichotomies (nchoosek(8,4)/2). We considered all 35 possible dichotomies to perform our analysis in an unbiased manner (Supplementary Table 2 shows all dichotomies). Some of the possible balanced dichotomies are easily interpretable because they correspond to variables that were manipulated in the task. We refer to these balanced dichotomies as the ‘named dichotomies’, which are: context, response, outcome, stimulus pair (stim pair) and parity. These dichotomies are shown individually in Extended Data Fig. 2. The stim pair dichotomy corresponds to the grouping of stimuli for which the response is the same in either context (A and C versus D and B; Fig. 2d). The parity dichotomy is the balanced dichotomy with the maximal nonlinear interaction between the task variables (Extended Data Fig. 2).

For decoding balanced dichotomies during the prestimulus baseline, the task states are defined by the values of the previous trial (not the upcoming, the identity of which is unknown to the participant). The reason for doing so is to examine persistent representations of the previous trial.

Defining decoding difficulty of dichotomies

We quantify the relative degree of nonlinear variable interactions needed by a neural population to classify a given dichotomy using a difficulty metric that rates dichotomies that require proximal task conditions to be placed on opposite sides of the decision boundary as more difficult. Note that proximity of task conditions in task space here is defined with respect to the variables that were manipulated to construct the task space. The conditions corresponding to (response L, outcome low, context 1) and (response L, outcome low, context 2) are proximal because their task specifications differ by a single variable (hamming distance 1) whereas (response L, outcome low, context 1) and (response R, outcome high, context 2) are distal as their task specifications differ by all three variables (Hamming distance 3). With this perspective, we can systematically grade the degree of nonlinearity required to decode a given dichotomy with high accuracy as a function of the number of adjacent task conditions that are on opposite sides of the classification boundary for that dichotomy. For a set of eight conditions specified by three binary variables, this corresponds to the number of adjacent vertices on the cube defined by the variables that are in opposing classes (Extended Data Fig. 5a). We define this number as the difficulty for a given dichotomy, and can compute it directly for every one of the 35 balanced dichotomies. The smallest realizable dichotomy difficulty is 4, and corresponds only to named dichotomies that align with the axis of one of the three binary variables used to specify the task space. The largest realizable dichotomy is 12, and this corresponds to the parity dichotomy because the dichotomy difficulty (number of adjacent conditions with opposing class membership) is maximized in this dichotomy by definition. All remaining dichotomies lie between these two extremes in difficulty, and computing average decoding accuracy over dichotomies of increasing difficulty gives a sensitive readout of the degree of nonlinear task variable interaction present in a neural population.

Geometric analysis of balanced dichotomies

We used three measures to quantify the geometric structure of the neural representation¹¹: shattering dimensionality, CCGP and PS. A high CCGP and PS for a variable indicates that the variable is represented in an abstract format.

Shattering dimensionality is defined as the average decoding accuracy across all balanced dichotomies. It is an index of the expressiveness of a representation, as representations with higher shattering dimensionality allow more dichotomies to be decoded. The content of a representation is assessed by considering which balanced dichotomies are individually decodable better than expected by chance.

CCGP assesses the extent to which training a decoder on one set of conditions generalized to decoding a separate set of conditions. High CCGP for a given variable indicates that the representation of that variable is disentangled from other variables. CCGP is reported in a cross-validated manner by training and testing decoders on single trials. Note that to compute CCGP, all trials from a set of conditions are held out from the training data, which is different from the typical ‘leave-one-out’ type decoding. The remaining held-in conditions are used to train the decoder, and performance is then evaluated on the held-out conditions (trial-by-trial performance). The CCGP for a given balanced dichotomy is the average over all possible 16 combinations of held-out conditions on either side of the dichotomy boundary. One of the four conditions on each side of the dichotomy are used for testing, whereas the remaining three on each side of the dichotomy are used for training. For each of the 16 possible train and test splits, the decoder is trained on all correct trials from the remaining six conditions, and performance is evaluated on the two held-out conditions.

PS assesses how coding directions for one variable are related to each other across values of other variables in a decoder agnostic manner. The PS is defined for every balanced dichotomy as the cosine of the angle between two coding vectors pointing from conditions in one class to conditions in the other for a given dichotomy. The coding directions are estimated using the average activity for each condition. Note that the PS is a direct geometrical measure that focuses on the structure of the representation, whereas the CCGP also depends on the noise and its shape because it is based on single trials. Coding vectors are computed by selecting four conditions (two on either side of the dichotomy), computing the normalized vector difference between the mean population response for each of the two pairs, then computing the cosine between said coding vectors. This procedure is repeated for all possible pairs of coding vectors, and the average over all cosines is reported. As the correct way of pairing conditions on either side of the dichotomy is not known a priori, we compute the cosine average for all possible configurations of pairing conditions on either side of the dichotomy, then report the PS as the maximum average cosine value over configurations.

Null distribution for geometric measures

We used two approaches to construct null distributions for significance testing of the geometric measures shattering dimensionality, CCGP and PS.

For the shattering dimensionality and decoding accuracy of individual dichotomies, the null distribution was constructed by shuffling trial labels between the two classes on either side of each dichotomy before training and testing the decoder. After shuffling the order of the trial labels, the identical procedures for training and testing were used. This way of constructing the null distribution destroys the information content of the neural population while preserving single-neuron properties such as mean firing rate and variance.

For the CCGP and PA, we used a geometric null distribution¹¹. Before training, we randomly swapped the responses of pairs of neurons within a given condition. For example, for one task condition, all of neuron 1’s responses are assigned to neuron 2 and all of neuron 2’s responses are assigned to neuron 1; for another task condition, all of neuron 1’s responses are assigned to neuron 3, and so on). This way of randomly shuffling entire condition responses leads to the situation in which neural population responses by condition are held constant, but the systematic cross-condition relationships that exist for a given neuron are destroyed. This way of shuffling creates a maximally high-dimensional representation, thereby establishing a conservative null distribution for the geometric measures CCGP and PS.

All null distributions are constructed from 1,000 iterations of shuffled trial-resampling using either trial-label shuffling (shuffle null) or random rotations designed to destroy low-dimensional structure (geometric null).

Neural geometry alignment analysis

To answer the question of whether the geometry of a variable was common across different groups of sessions, we aligned representations between two neural state spaces. Each state space is formed by non-overlapping sets of neurons, and the two spaces are aligned using subsets of task conditions. A cross-session-group PS was then computed by applying the same alignment to a pair of held-out conditions, one on either side of the current dichotomy boundary. Alignment and cross-group comparisons were performed in a space derived using dimensionality reduction (six dimensions). For a given dichotomy, two groups of sessions with N and M neurons were aligned by applying singular value decomposition to the firing-rate normalized condition averages of all but two of the eight task conditions, one on either side of the dichotomy boundary. The top six singular vectors corresponding to the non-zero singular values from each session group were then used as projection matrices to embed the condition averages from each session group in a six-dimensional space. Alignment between the two groups of sessions, in the six-dimensional space, was then performed by computing the average coding vector crossing the dichotomy boundary for each session group, with the vector difference between these two coding vectors defining the ‘transformation’ between the two embedding spaces. To compare whether coding directions generalize between the two groups of sessions, we then used the data from the two remaining held-out conditions (in both session groups). We first projected these data points into the same six-dimensional embedding spaces and computed the coding vectors between the two in each embedding space. We then applied the transformation vector to the coding vector in the first embedding space, thereby transforming it into the coordinate system of the second session groups. Within the second session group embedding space, we then computed the cosine similarity between the transformed coding vector from the first session group and the coding vector from the second session group to examine whether the two were parallel (if so, the coding vectors generalize). We repeated this procedure for each of the other three pairs of conditions being the held-out pair, thereby estimating the vector transformation of each pair of conditions independently. The average cosine similarity was then computed over the held-out pairs. All possible configurations of conditions aligned on either side of the dichotomy boundary are considered (24 in this case), and the maximum cosine similarity over configurations is returned as the PS for that dichotomy (plotted as ‘cross-half’ in Extended Data Fig. 3z). As a control, we also computed the PS for held-out conditions within the same embedding space without performing cross-session alignment (plotted as ‘half-split’ in Extended Data Fig. 3z). Note that the differences in both the average PS and the null distribution when comparing within-session and across-session parallelism are expected behaviours and arise from the increased expressive power of the cross-session approach due to fitting transformation vectors in a relatively low-dimensional (six) space. This step is not performed for the within-session control because there is no need to align neural activity to its own embedding space.

MDS

Low-dimensional visualization of neural state spaces was achieved using multi-dimensional scaling (MDS) performed on matrices of condition-averaged neural responses. Pair-wise distances between condition averages were initially computed in N-dimensional neural state space, where N is the number of neurons used to construct the space. Pair-wise distances were then used to compute either a two- or three-dimensional representation of the condition averages using the ‘mdscale’ method in MATLAB. In figures in which two different MDS plots are shown side-by-side, canonical correlation analysis was used to align the axes of the two-dimensionally reduced neural state spaces. This approach was necessary because, in general, neural state spaces constructed with different sets of neurons were being compared. We note that we use MDS only to summarize and visualizing high-dimensional neural representations. All conclusions drawn are based on geometric measures computed in the original full neural state space.

Analysis of incorrect trials

For determining decoding accuracy for trials in which participants provided an incorrect response (‘error trials’), decoders were trained and evaluated out of sample on all correct trials in inference absent and inference present sessions (denoted as inference absent and inference present trials, respectively). The accuracy of the decoder was then evaluated on the left out error trials in the inference present sessions (denoted as ‘inference present (error)’ trials) that were balanced by task condition. Neurons from sessions without at least one incorrect trial for each of the eight conditions were excluded. We did not estimate CCGP separately for correct and incorrect trials. The PS was estimated using only correct trials for inference present and inference absent. For inference present (error), parallelism was computed using one coding vector (difference between two conditions) from correct trials and one coding vector from incorrect trials. All other aspects of the PS calculation remained as described earlier. The very first trial after a context switch was excluded from analysis (it was incorrect but by design, as the participant cannot know when a context switch occurred).

Stimulus identity geometry analysis

We repeated the geometric analysis described above for subsets of trials to examine specifically how the two variables context and stimulus interact with each other. To do so, we considered each possible pair of stimuli (AB, AC, AD, BC, BD, CD) separately. For each stimulus pair, we then examine the ability to decode and the structure of the underlying representation for two variables: stimulus identity (Supplementary Table 3) and context (Supplementary Table 4) (Fig. 3).

For stimulus identity, what is decoded is whether the stimulus identity is the first or second possible identity in each pair (that is, ‘A versus B’ for the AB pair). Stimulus CCGP (Fig. 3b,e) is calculated by training a decoder to decide A versus B in context 1 and testing the decoder in context 2 and vice versa (the CCGP is the average between these two decoders). Stimulus PS (Fig. 3c,f) is the angle between the two coding vectors A versus B in context 1 and 2.

For context, decoding accuracy is estimated by training two decoders to decide context 1 versus context 2 for each of the two stimuli in a stimulus pair. The reported decoding accuracy is the average between these two decoders (Extended Data Fig. 7a,b). For example, for the stimulus pair AB, one such decoder each is trained for all A trials and all B trials. Context CCGP (Fig. 3g and Extended Data Fig. 7c) is calculated by training a decoder to differentiate between contexts 1 and 2 based on the trials in the first identity of the pair and tested in the second pair, and vice versa. The reported context CCGP value for a given stimulus pair is the average between the two. Similarly, context PS (Fig. 3h and Extended Data Fig. 7d) is the angle between the two coding vectors context 1 versus context 2 estimated separately for the first and second stimulus in a pair.

Distance and variance analysis

We computed a series of metrics to quantify aspects of the population response that changed between inference absent and inference present sessions. We used (1) the firing rate, (2) distance in neural state space between classes for balanced dichotomies and stimulus dichotomies (dichotomy distance), (3) variance of neural spiking projected along the coding directions for those dichotomies (coding direction variance) and (4) the condition-wise fano factor (Fig. 4).

Firing rate (Fig. 4e) was the mean firing rate averaged across all neurons during the stimulus period, reported separately for correct trials of every unique task condition. Values reported during the baseline (Extended Data Fig. 9q,r) are computed with an identical procedure using firing rates from before 1 s before stimulus onset.

Dichotomy distance (Fig. 4g,h,j,k) was defined as the Euclidean distance in neural state space between the centroids of the two classes on either side of the decision boundary for that dichotomy. Centroids were computed by constructing the average response vector for each class using a balanced number of correct trials from every condition included in each class through a resampling procedure (described below). Null distributions reported for dichotomy distances are geometric null distributions.

Coding direction variance (Fig. 4i) was computed for a given balanced dichotomy by projecting individual held-out trials onto the coding vector of the decoder trained to differentiate between the two groups of the balanced dichotomy being evaluated. The coding direction was estimated by training a linear decoder on all trials except eight (one from each condition either side of the dichotomy). The vector of weights estimated by the decoder (one for each neuron) was normalized to unit magnitude to estimate the coding vector. The projection of the left out trial onto this coding vector was then calculated using the dot product. This process was repeated 1,000 times, generating a distribution of single-trial projections onto the coding vector for each dichotomy. The variance of the distribution of 1,000 projected data points was then computed and reported as the variance for a given balanced dichotomy (Fig. 4i).

The condition-wise fano factor (Fig. 4f) was computed separately for each neuron. We used all correct trials for a given balanced dichotomy to estimate the mean firing rate and standard deviation and then took the ratio between the two to calculate the fano factor for each neuron. Reported fano factors are the average of all fano factors across all neurons from that area and/or behavioural condition. Fano factors are computed by condition because grouping trials across conditions could lead to task variable coding (signal) contaminating the fano-factor measurement, which should ideally only reflect trial-by-trial variation around the mean for roughly Poisson-distributed firing rates.

The context-modulation consistency (Fig. 4l) was also computed separately for each neuron. Context-modulation consistency is the tendency for a neuron’s firing rate to shift consistently (increase or decrease) to encode context across stimuli. For each neuron, it was computed by determining the sign of the difference (±) between the mean firing rate for a given stimulus between the two contexts, and summing the number of stimuli that show the same modulation (either increase or decrease) across the two contexts. This consistency can take on values between 0 (increase in firing rate to encode context for half of the stimuli, decrease in firing rate for the other half) and 4 (either increase or decrease in firing rate for all four stimuli).

Bootstrap resampled estimation of measures and null distributions

All the measures described in the preceding sections were estimated using a trial and neuron-based resampling method. This resampling strategy was used to assure that every measure reported was comparable between a set of conditions by assuring that the same number of neurons and data points were used to train and test classifiers. Metrics were recomputed 1,000 times with resampling and all null distributions were computed with 1,000 iterations of shuffling and recomputing. Plotted boundaries of null distributions correspond to the fifth and 95th percentiles as estimated from the 1,000 repetitions.

A single iteration of the resampling estimation procedure proceeds as follows. For all analyses that involved a comparison of a metric between two behavioural conditions (inference absent versus inference present or session 1 versus session 2), the same number of neurons was included in both conditions by on a region-by-region basis. For a neuron to be included, at least 15 correct trials for each of the eight unique task conditions had to exist (120 correct trials total). Across patients, the number of correct trials per condition varied: minimum 10.9 ± 1.3 trials per condition, mean 25.0 ± 0.6 trials per condition, maximum 39.6 ± 1.2 trials per condition (mean ± s.e.m.). After identifying the neurons that met this inclusion criteria, an equal number were randomly sampled from both behavioural conditions. The number of considered neurons was set to the number of neurons available in the smallest group.

When constructing feature matrices for decoding, 15 trials were randomly selected from each unique condition that was included in the given analysis. Trial order was shuffled independently for every neuron within a condition to destroy potential noise correlations between neurons that were simultaneously recorded. For decoding and shattering dimensionality, out-of-sample accuracy was estimated with fivefold cross-validation. For generalization analyses (CCGP), all trials were used in training as performance was evaluated on entirely held-out conditions. For vector-based measures (dichotomy distance, variance, PS), all trials in relevant conditions were used to compute condition centroids. In the case of variance estimation, all trials except one on either side of the dichotomy boundary were used to learn the coding axis, then the held-out trials were projected onto the coding axis. As previously stated, these procedures were repeated 1,000 times with independent random seeds to ensure independent random sampling of neurons and trials across iterations.

Statistics

All significance values (P values) in the paper are estimated as following unless stated otherwise. P values of decodability, CCGP or PS versus chance for the absent and present group are labelled as P_Absent or P_Present, respectively, and are estimated using a one-sided non-parametric bootstrap test based on the empirically estimated null distribution as described above. The P value of the non-parametric boostrap test is equal to the number of iterations in the null distribution that are larger or equal than the observed value (one-sided), divided by the number of iterations. P values for comparing decodability, CCGP or PS between the inference absent and present conditions are performed using a two-sided Wilcoxon rank-sum test and labelled as P_RS. Differences between decodability, CCGP or PS between two conditions are tested using the empirically estimated empirically based on the null distribution estimated as described above and labelled as P_ΔVariable.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-024-07799-x.

Author contributions

Conceptualization was by J.M., U.R., C.D.S. and S.F. Tasks were designed by J.M. and D.L.K. Data were collected by J.M., H.S.C. and A.R.C. Data were analysed by H.S.C. and J.M. H.S.C., U.R. and S.F. wrote the paper. U.R. and S.F. provided supervision. C.M.R. provided clinical care and facilitated experiments. Surgeries were carried out by A.N.M. and T.A.V.

Peer review

Peer review information

Nature thanks Timothy Behrens, Yunzhe Liu and Ila Fiete for their contribution to the peer review of this work. Peer reviewer reports are available.

Data availability

Data used in this study are publicly available at OSF (10.17605/OSF.IO/QPT8F)⁷⁰.

Code availability

Example code to reproduce the results is available as part of the data release (see ‘Data availability’).

Competing interests

The authors declare no competing interests.

Extended data

is available for this paper at 10.1038/s41586-024-07799-x.

Supplementary information

The online version contains supplementary material available at 10.1038/s41586-024-07799-x.