Abstract
Protein complexes are fundamental to all cellular processes, so understanding their evolutionary history and assembly processes is important. Gene duplication followed by divergence is considered a primary mechanism for diversifying protein complexes. Nonetheless, to what extent assembly of present-day paralogous complexes has been constrained by their long evolutionary pathways and how cross-complex interference is avoided remain unanswered questions. Subunits of protein complexes are often stabilized upon complex formation, whereas unincorporated subunits are degraded. How such cooperative stability influences protein complex assembly also remains unclear. Here, we demonstrate that subcomplexes determined by cooperative stabilization interactions serve as building blocks for protein complex assembly. We further develop a protein stability-guided method to compare the assembly processes of paralogous complexes in cellulo. Our findings support that oligomeric state and the structural organization of paralogous complexes can be maintained even if their assembly processes are rearranged. Our results indicate that divergent assembly processes by paralogous complexes not only enable the complexes to evolve new functions, but also reinforce their segregation by establishing incompatibility against deleterious hybrid assemblies.
Subject terms: Molecular evolution, Proteolysis
Understanding assembly processes of protein complexes is crucial. The authors have developed a method to deduce protein complex assembly paths in living cells, revealing that the altered assembly pathways of paralogous complexes enable neo-functionalization and mitigate cross-complex interference.
Introduction
Most proteins do not act as isolated entities. Instead, they associate with other proteins to form stable protein complexes to fulfill their functions. Many eukaryotic heteromeric protein complexes are composed of paralogous proteins or exhibit striking one-to-one homology to subunits of other complexes, indicating that gene duplication followed by divergence is a common mechanism by which protein complexes diversify and evolve new roles1,2.
Evolutionarily related homologous protein complexes may arise upon partial or complete duplication of components in the ancestral complexes. Partial duplication results in concurrent complexes that share both identical components and homologous components arising from gene duplication. Duplication of all subunits in a complex, followed by independent evolution, gives rise to parallel complexes with similar but no shared components3,4. After a gene duplication event, one copy may acquire a different function (neo-functionalization), or the two paralogs partition the ancestral function among them (subfunctionalization)5. Extensive step-wise partial duplications within and across complexes and subsequent sequence divergence over a long evolutionary history can result in paralogous protein complexes displaying sub- or neo-functionalities. Examples of such paralogous protein families include the farnesyltransferase and geranylgeranyltransferase complexes, the clathrin adapter protein complexes, the SWI/SNF complexes, the PCI complexes, and the snRNP LSm/Sm complexes.
Adopting this duplication-diversification mechanism has considerable advantages over de novo protein complex formation. For instance, the evolutionary diversification of LSm/Sm heteromeric complexes in eukaryotes showcases a general increase in RNA-processing complexity among eukaryotes6,7. The inherent similarity among paralogous complexes also provides stronger connectivity among their cellular functions that may facilitate their coordinated regulation. Nevertheless, such pronounced similarity among complex subunits also imposes a challenge for the specificity/fidelity of their assembly processes and increases the tendency of cross-complex interactions. To what extent such paralogous interference impacts the assembly of similar protein complexes and whether mechanisms exist to prevent potential harmful crosstalk have not been intensively investigated. Moreover, it remains unexplored if the inter-subunit interactions and assembly processes of duplicated complexes are preserved or remodeled to adapt to new functions.
Understanding how protein complexes are formed in cellulo is fundamental, yet our current knowledge has mostly been obtained from in vitro studies8–10. Multiple cellular factors are involved in safeguarding protein complex formation, such as molecular chaperones and proteolysis systems, as well as the varied locations within cells where assembly occurs11–13. Consequently, assembly paths of complexes in vitro may not adequately reflect conditions in cellulo. Rather than being a random process of subunit coalescence, protein complex assembly is considered analogous to protein folding, and thus proceeds via energetically optimal intermediate assemblies14,15. A widespread phenomenon is that subunits of protein complexes are stabilized upon complex formation, whereas unincorporated subunits are degraded by proteolysis13,16,17. Such cooperative stabilization, i.e., protein stabilization upon associating with relevant partners, is likely to profoundly influence how protein complex assembly proceeds, but a systematic characterization of cooperative stabilization networks within multimeric protein complexes and their relationships with complex assembly processes is lacking.
Here, we demonstrate that cooperative stability plays a crucial role in protein complex formation and that the modularity of protein complex assembly can be inferred by defining cooperative stabilization interactions among complex subunits. Moreover, we have developed a technology based on protein stability-guided connectivity to deduce the assembly processes of the PCI and LSm/Sm paralogous complex families, which includes both parallel and concurrent protein complexes. Our findings reveal limited conservation of ancestral cooperative stabilization interactions and support that structurally alike paralogous complexes do not necessarily adopt the same assembly strategy. The divergent assembly processes of paralogous complexes not only enable their sub- or neo-functionalization but also mitigate cross-complex interference.
Results
Cooperative stabilization drives the assembly of protein complexes
We applied GPS (Global Protein Stability) assay18 to investigate the impact of cooperative stability on protein complex assembly. The GPS approach relies on the translation of two fluorescent proteins from one mRNA transcript by means of an expression cassette containing a single promoter and an internal ribosome entry site (IRES) (Fig. 1A). The green fluorescent protein (GFP) is fused either at the N- or C-terminus of the protein of interest, whereas the red fluorescent protein (RFP) serves as an internal control for protein synthesis. Since RFP and the GFP-fusion protein are translated from a bicistronic transcript, and RFP is a stable protein not processed by known cellular protein degradation machineries, the fluorescence intensities of RFP, GFP, and the GFP/RFP ratio detected by FACS (fluorescence-activated cell sorting) serve as proxies for measuring protein synthesis rate, protein abundance, and protein lifespan/stability, respectively, of the target protein of interest (Supplementary Fig. 1A).
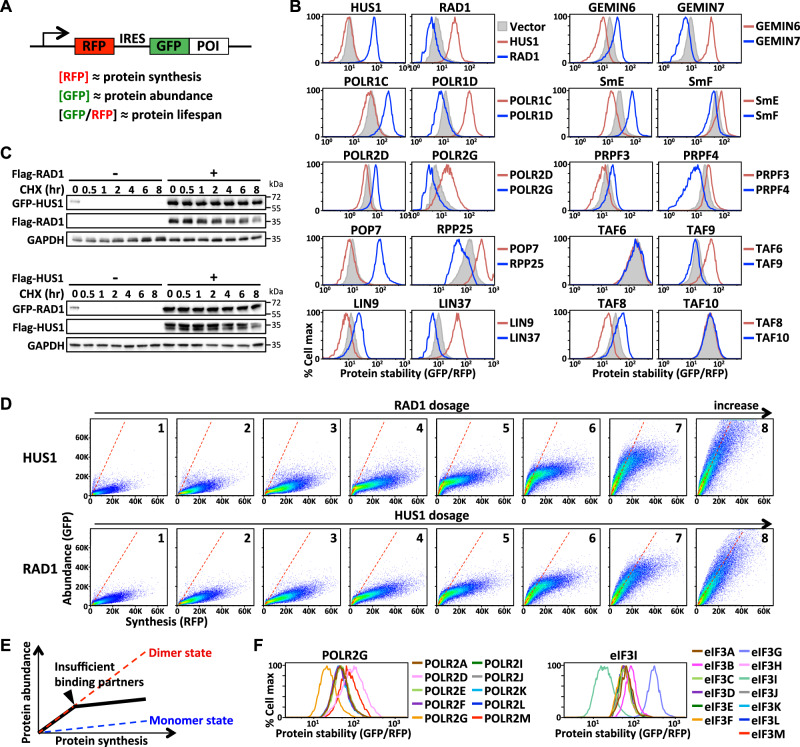
Fig. 1. Cooperative stabilization interactions are prevalent among proteins that form a stable complex.
A A schematic depiction of the GPS reporter system. The fluorescent signal intensities of RFP, GFP, and the GFP/RFP ratio represent proxies for measuring the protein synthesis, abundance, and stability, respectively, of the protein of interest (POI). B GPS analysis of the proteins labeled above the plots co-expressing the proteins labeled at right. C Cycloheximide (CHX)-chase analysis of HUS1 (top panel) or RAD1 (bottom panel) with/without RAD1 or HUS1 co-expression, respectively. GAPDH serves as a loading control. Blots are representative of three independent experiments. D The synthesis-abundance relationships of HUS1 (top panel) and RAD1 (bottom panel) in response to increasing dosages of RAD1 and HUS1 co-expression (plot 1 to plot 8), respectively, as measured by FACS. Each dot represents data from a single cell. Red dashed lines indicate the expected synthesis-abundance relationship when RAD1 and HUS1 form a heterodimer. E A schematic diagram illustrating the nonlinear synthesis-abundance correlation of a subunit due to an inadequate supply of stabilizing partners. The biphasic profile (black line) represents the differential stability of assembled and free subunits. F GPS analysis of POLR2G and eIF3I with co-expression of indicated RNA polymerase II and eIF3 subunits, respectively. Source data are provided as a source data file.
A stable protein complex exhibits a fixed stoichiometry of its individual subunits. To verify if surplus unassembled complex subunits are eliminated by proteolysis, we compared the protein lifespans of individual complex subunits when expressed at different levels using the GPS reporter driven by the UBC, EF1α and CMV promoters, whose relative strengths are approximately 1:3:10 in HEK293T cells (Supplementary Fig. 1B). Our study is focused on subunits of stable and obligate protein complexes that perform general housekeeping functions. Indeed, we observed a negative correlation between protein synthesis level and protein lifespan for protein complex subunits, but not for destabilized GFP controls (Supplementary Fig. 1C). Treating cells with proteasome inhibitors restored the consistent protein lifespan of protein complex subunits under conditions of protein synthesis variation, indicating that this dosage compensation is proteasome-dependent (Supplementary Fig. 1D). To determine if elevated proteolysis was attributable to a failure to find appropriate binding partners, we co-expressed known interacting components in the same complex and measured their protein lifespans by GPS assays or cycloheximide-chase analysis (Fig. 1B, C). Our results indicate that reciprocal cooperative stabilization interactions are common in diverse obligate protein complexes. We identified HUS1-RAD1, POLR1C-POLR1D, POLR2D-POLR2G, POP7-RPP25, LIN9-LIN37, GEMIN6-GEMIN7, SmE-SmF and PRPF3-PRPF4 as mutual stabilization pairs in the 9-1-1, RNA polymerase I, RNA polymerase II, ribonuclease P, DREAM/LINC, SMN, Sm and U4/U6-U5 tri-snRNP complexes, respectively. This stabilization interaction is occasionally unilateral, as seen for both the TAF6/TAF9 and TAF8/TAF10 pairs in the TFIID complex (Fig. 1B).
We selected the HUS1-RAD1 complex as a proof of concept to quantitatively characterize the degree to which protein half-life is changed when free subunits (i.e. monomeric HUS1 and RAD1) assemble to form heterodimeric complexes. Providing an excess of wild-type RAD1, but not its mutant defective in HUS1 binding, stabilized HUS1 protein, and vice versa, suggesting that physical binding is crucial for HUS1-RAD1 co-stabilization (Supplementary Fig. 1E, F). To examine HUS1-RAD1 interactions quantitatively, we introduced heterogeneous amounts of wild-type RAD1 using a 2A-BFP (blue fluorescent protein) construct into the HUS1 GPS dosage library cells that expressed varying amounts of GFP-HUS1 fusion proteins (Supplementary Fig. 1G). In this system, millions of single cells, each possessing a unique combination of HUS1 and RAD1 expression levels, were analyzed together as a single sample by means of three-color FACS. The fluorescence signal intensities of BFP, RFP, and GFP, as well as the GFP/RFP ratio of each cell, reflect the RAD1 synthesis level, HUS1 synthesis level, HUS1 protein abundance, and HUS1 protein stability in that cell, respectively. We separated cells into eight fractions based on their RAD1 expression levels (i.e., as represented by BFP fluorescence intensities) and illustrated the HUS1 synthesis-abundance correlation of each cell fraction as serial plots (Supplementary Fig. 1H; Fig. 1D top panel, plots 1–8). Our results reveal RAD1 dosage-dependent transformation of the HUS1 state, i.e., from unstable monomer (RAD1 deficient, plot 1) to stable RAD1-bound dimer (RAD1 surplus, plot 8). By examining each individual plot (for which amounts of RAD1 supplementation are fixed), we noted that the HUS1 synthesis-abundance relationship was clearly biphasic. This nonlinear profile reflects bound and unbound HUS1 being degraded at different rates. The inflection point between these two-phase states reflects the amount of synthesized HUS1 beginning to outstrip the amounts of available RAD1 (Fig. 1E). We performed a reciprocal experiment and detected similar RAD1/HUS1 synthesis level-dependent RAD1 state transitions (Fig. 1D bottom panel). We built a mathematical model for protein heterodimer formation and applied our experimental data to estimate the relative protein degradation rate constants of the RAD1 and HUS1 monomers, as well as for the RAD1-HUS1 dimer (see “Methods” section). Our results predicted that the protein lifespans of HUS1 and RAD1 increase 7.94- and 5.04-fold, respectively, when they form a heterodimeric complex relative to those of their monomeric states. This profound partner-dependent protein stabilization likely critically influences how protein complex assembly proceeds, but it has not yet been characterized systematically.
We wondered if cooperative stabilization is a default scenario between any subunits or if it only arises between particular components within a multimeric protein complex. We found that co-stabilization interactions are highly specific (Fig. 1F). For instance, POLR2G was stabilized only by POLR2D and POLR2M, but not by other interacting partners in the RNA polymerase II complex. Similarly, eIF3I was only stabilized by eIF3B and eIF3G. According to the protein folding theory drawn from Levinthal’s paradox, a protein must fold through a series of metastable intermediate states14. Analogously, protein complex assembly is likely to proceed via energetically favorable intermediate subcomplexes. We hypothesized that subunits displaying stronger cooperative stabilization tend to form an intermediate subcomplex prior to further assembling into a larger complex because their respective monomeric states are labile (Supplementary Fig. 1I). It has been shown previously that large heteromeric protein complexes are composed of both non-exponentially degraded (NED) and exponentially degraded (ED) elements19. The two-state degradation profile of NED subunits reflects the cooperative stabilization interactions characterized herein. Consistent with our hypothesis, NED proteins were shown previously to possess a larger interaction interface and to assemble earlier than their ED counterparts19.
Deducing eIF3 complex assembly processes based on protein stability-guided modularity
To examine the role of cooperative stabilization interactions in protein complex assembly, we characterized the eIF3 (eukaryotic initiation factor 3) complex, the physical binding pattern and subunit organization of which have already been established (Fig. 2A, B)8,9,20,21. The eIF3 complex is the largest translation complex and it belongs to a member of the paralogous PCI (Proteasome, CSN, eIF3) complex family21. Human eIF3 consists of 13 non-identical protein subunits, denoted eIF3A to eIF3M. Tandem mass spectrometry and solution disruption experiments have revealed that the eIF3 complex is composed of three tightly associated structural modules, denoted I [eIF3A/B/I/G], II [eIF3F/M/H], and III [eIF3K/L/E/D/C], respectively, together with a labile subunit eIF3J that is attached to the complex via eIF3B (Fig. 2A)22. eIF3J is substoichiometric and may represent an eIF3-associated factor rather than being a truly integral eIF3 subunit8,20. Our results indicate that apart from eIF3J, all other eIF3 subunits exhibit proteolysis-mediated dosage compensation, with their protein synthesis and abundance levels being decoupled through proteasome-mediated degradation (Supplementary Fig. 2A).
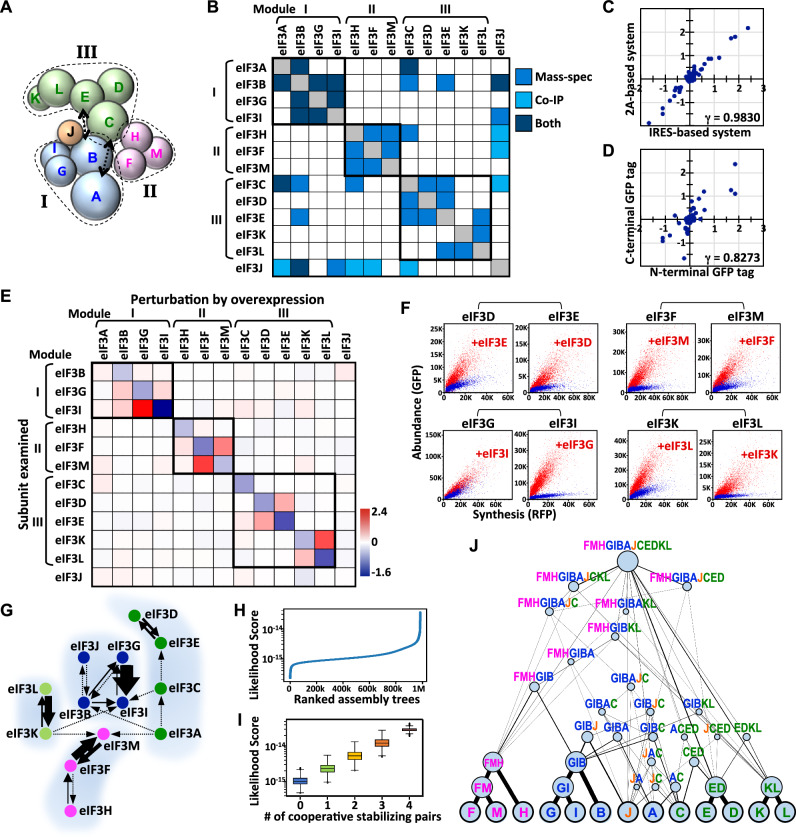
Fig. 2. Inferring the eIF3 assembly process based on cooperative stabilization interactions.
A Model of eIF3 subunit architecture based on dissociation and mass spectrometry analyses. Subunits of modules I, II, and III are colored blue, magenta, and green, respectively. Black arrows denote physical interactions not readily presented in this model. B The eIF3 physical interaction map according to the available literature. Different detection methods (shown at right) are colored differently. C, D Correlation analyses for results generated from IRES- versus 2A-based GPS systems, and N- versus C-terminal GFP-tagged eIF3 subunits. Data points represent fold-changes in protein stability (GFP/RFP ratio). E The eIF3 subunit stability connectivity map, as measured by the IRES-based GPS system. The matrix heatmap represents a log2-fold-change in the value of protein stability (GFP/RFP ratio) for the eIF3 subunit indicated on the left in response to overexpressing the eIF3 subunit indicated on top. F The synthesis-abundance correlation of the eIF3 subunit indicated on top with (red) or without (blue) providing the eIF3 subunit indicated on the plot. G Louvain network modularity analysis of data shown in (E). Arrows represent stabilization interactions. X→Y indicates that X stabilizes Y, whereas X↔Y denotes that X and Y mutually stabilize each other. The thickness of the arrows is proportional to the intensity of protein stabilization. Subunits in the same network cluster are shown in the same color and surrounded by a light gray shadow. H The score distribution for all possible binary eIF3 assembly trees. I Correlation analysis between likelihood scores and the presence of intermediate subcomplexes formed by cooperative stabilization partners (eIF3D-E, G-I, F-M, K-L). The box plots illustrate the 25th and 75th percentiles, and the whiskers extend to 1.5 times of the interquartile range (IQR). Horizontal lines within the box plots represent medians. Outliers are plotted as individual points. The number of points for each box plot from left to right, are 357,194,157,953, 66,973,726,080, 5,272,663,680, 211,003,200, and 3,752,640, respectively. J DAG presentation of the top 1000 ranked binary eIF3 assembly trees. The thickness of lines and the size of circles are proportional to the likelihood. Source data are provided as a source data file.
To capture all possible pairwise co-stabilization interactions within the eIF3 complex, we built GPS reporter cell lines for each eIF3 subunit by integrating their GPS construct as a single copy into the genome of HEK293T cells. Then, we systematically perturbed the protein stability network in these reporter cells by individually overproducing unlabeled eIF3 subunits by means of viral-mediated transduction (multiplicity of infection (MOI) ≈ 5) and assessed any resulting changes in the lifespan of the examined GFP-tagged eIF3 proteins by GPS assays. We were unable to examine the eIF3A subunit because the eIF3A GPS reporter cells were not viable. Human eIF3 has been shown to interact with IRES and it mediates 5′cap-independent translation23. To verify the fidelity of the results deduced from our IRES-based GPS assay, we performed the same experiments using a 2A peptide-based GPS reporter (Supplementary Fig. 2B). Since the GFP tag may interfere with protein interactions, we placed GFP at either the N- or C-terminus of the inspected eIF3 subunits and examined both variants.
Our results revealed a strong correlation between independent experimental replicates (Supplementary Fig. 2C, γ = 0.9957), as well as between the IRES- versus 2A-based GPS systems (Fig. 2C, γ = 0.9830), supporting the appropriateness of our analytical approach and data quality. We observed overall agreement between results from N- and C-terminally GFP-tagged eIF3 proteins, with few exceptions (Fig. 2D; Supplementary Fig. 2C). Specifically, placing GFP at the N-terminus of eIF3D and eIF3G abolished their interaction with eIF3E and eIF3I, respectively. We reason that GFP fusion is more likely to abolish/inhibit an interaction, rather than create/enhance it, and it is improper to fix the positions of the GFP tags in all eIF3 subunits since each eIF3 component adopts its own unique three-dimensional structure. Therefore, we extracted the strongest interactions (positive and negative) from either the N- or C-terminal GFP tag datasets and merged these to generate a complete eIF3 protein stability connectivity map (Fig. 2E; Supplementary Fig. 2B).
Our data reveal four conspicuous mutually stabilizing pairings: eIF3D-E, eIF3G-I, eIF3F-M, and eIF3K-L (Fig. 2F). The subunits composed of each pair are adjacent within the eIF3 architecture and physically associate with each other, suggesting that their interaction is direct (Fig. 2A, B). Unlike eIF3’s physical interactions that are both intra- and intermodular, all co-stabilization interactions solely occur within the same structural module (Fig. 2B, E). Thus, our findings highlight the specificity of mutual stabilizing interactions and indicate that protein association does not always enhance protein lifespan. We applied two community detection algorithms, i.e., Louvain and Infomap, to illustrate the eIF3 modular interactions and uncovered consistent clustering patterns. These analyses reveal four separate eIF3 protein stability-based network clusters comprising [B/G/I/J], [H/F/M], [K/L] and [A/C/E/D], with each of these clusters harboring an apparent mutually stabilizing subunit pair: eIF3G-I, eIF3F-M, eIF3K-L, and eIF3D-E, respectively (Fig. 2G). Notably, these stability-based network clusters and the structural modules defined by physical associations are not identical. Specifically, eIF3K/L and eIF3C/D/E belong to discrete stability-guided network clusters, despite being physically located in the same structural module (module III) (Fig. 2A, G).
Subcomplexes driven by cooperative stabilization interactions are likely to serve as building blocks for further higher-order assembly of entire protein complexes. Consistent with this hypothesis, the eIF3D-E, eIF3K-L, and eIF3F-M dimers have previously been demonstrated to serve as intermediates for assembling the eIF3 complex10,24. Next, we applied stability-guided modularity deduced by GPS assays to infer how the eIF3 complex forms in cellulo. We made a few assumptions in our model. First, protein complex formation is an ordered multi-step reaction and each step involves binary interactions between a pair of subunits/subcomplexes given that the probability of more than two species colliding instantaneously is negligible. Hence, the assembly process can be represented as a binary tree analogous to hierarchical clustering procedures. Second, a protein complex can form through multiple potential assembly paths because each assembly step is a molecular collision event and therefore stochastic in nature. Third, certain assembly paths are more probable than others due to differential binding affinities and co-stabilization interactions between subunits/subcomplexes. The cooperative protein stability score measured by GPS assays reports a combined effect from both such factors.
We developed an algorithm to enumerate all possible binary eIF3 assembly processes (∼3.16 × 1011) and assessed their likelihood scores based on the degree of inter-subunit co-stabilization within the eIF3 complex (Supplementary Fig. 3A; Fig. 2H) (see “Methods” section). The likelihood score we calculated for assembly trees positively correlates with the number of intermediate dimeric subcomplexes formed by mutually stabilizing partners (Fig. 2I). To illustrate our results more conveniently, we compressed the top 1000 ranked eIF3 assembly trees into a single Directed Acyclic Graph (DAG), in which nodes and edges denote subunits/subcomplexes and interactions, respectively (Fig. 2J; Supplementary Fig. 3B). The nodes and edges were weighted according to the frequencies at which they occurred within the top-ranking assembly trees. Our data reveal that eIF3 complex assembly occurs in a highly modular manner. More specifically, it begins predominantly with the formation of the eIF3F-M, G-I, D-E, and K-L dimers. Then, the F-M and G-I dimers are further expanded to form H-F-M and B-G-I trimeric complexes. The resulting dimers and trimers serve as building blocks for further assembly into the whole eIF3 complex. Our model is consistent with the eIF3 assembly process inferred using other approaches24. This consistency supports the feasibility of using protein stability-guided modularity to infer protein complex assembly processes in cellulo.
Divergence of the cooperative stabilization interactions within PCI complexes
Paralogous complexes are commonly found in eukaryotic genomes. However, it remains unclear if they are assembled via a conserved pathway. To address this question, we compared the protein stability-guided modularity of paralogous PCI complexes, which includes the regulatory lid of the 26S proteasome (P), the COP9 signalosome (CSN, C), and the eIF3 complex (I)25. Both the proteasome lid and CSN comprise nine distinct protein subunits and they are more closely related to each other than either is to eIF3 that contains 13 subunits. PCI complexes share a conserved PCI/MPN octameric core consisting of six PCI-domain-containing proteins plus two MPN-domain-containing proteins21. The one-to-one subunit correspondence in their octameric core supports that PCI complexes originated from a common evolutionary ancestor (Supplementary Fig. 4A)26–28. Despite their genetic and structural homology, each PCI complex performs a discrete cellular function. The eIF3 complex plays a central role in protein synthesis, whereas the CSN and proteasome lid are components of the ubiquitin-proteasome pathway21,29.
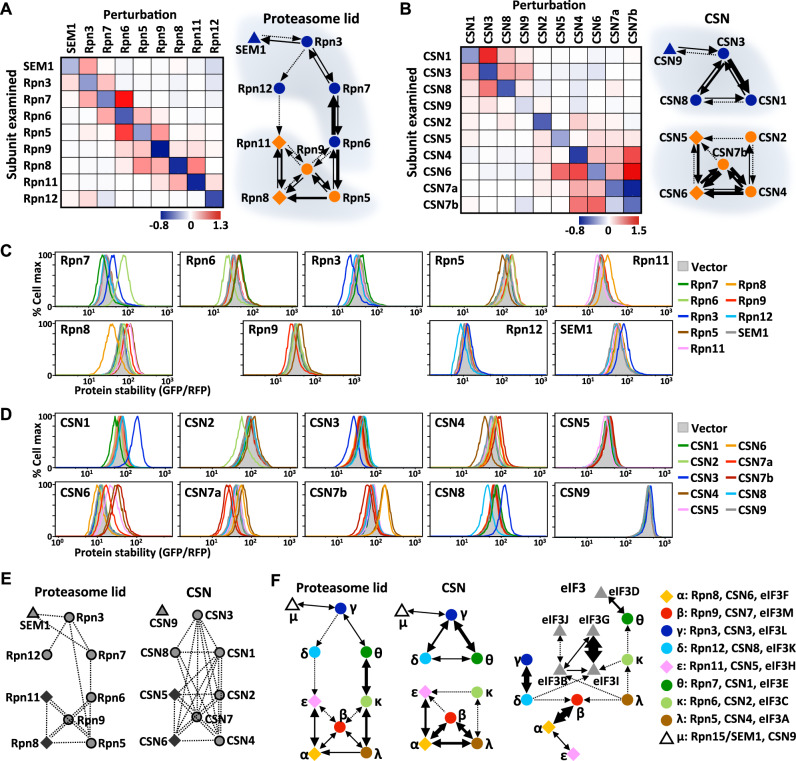
We applied the same approach described above for eIF3 complex assembly to characterize the assembly processes of the proteasome lid and CSN (Supplementary Fig. 4B). Interestingly, the network topologies of the cooperative stabilization interactions in the PCI complexes were dissimilar. Our data reveal four disjoined mutually stabilizing pairs in the eIF3 complex (Fig. 2E, F). In the proteasome lid, co-stabilizing interactions result in a connected chain topology comprising modules [Rpn3/6/7/12/SEM1] and [Rpn5/8/9/11], with the Rpn12 subunit only being loosely associated with the interaction network (Fig. 3A, C). In contrast, the mutual stabilizing interactions in the CSN give rise to two unconnected modules, i.e., [CSN1/3/8/9] and [CSN2/4/5/6/7] (Fig. 3B, D). CSN2, CSN5, and CSN9 are likely peripheral subunits because they presented weak interactions with other CSN components. The human CSN7 subunit is encoded by two genes (CSN7a and CSN7b) created by a recent gene duplication event30. In addition to the module topology, our data reveal that CSN7b has a competitive advantage over CSN7a in being incorporated into the CSN complex (Fig. 3D). Similar to eIF3, strong mutually stabilizing protein pairs in the proteasome lid and CSN have been demonstrated as displaying physical binding interactions (Fig. 3E)31–37. However, physical binding does not always affect protein lifespan and only certain subunits within a complex are subject to partner-mediated stabilization.
Fig. 3. Cooperative stabilization network rewiring in PCI complexes.
A, B The protein stability-based interaction map of the proteasome lid (A) and CSN (B) complexes. Louvain network modularity analysis of the data is shown on the right. Proteins with PCI or MPN domains or without these domains are denoted as circles, diamonds, or triangles, respectively. C, D Protein stability analysis of the subunit indicated on the plot upon supplying the subunit indicated at right. E A schematic to summarize the inter-subunit physical associations in the proteasome lid and CSN complexes identified by previous mass spectrometry analyses and co-immunoprecipitation experiments. F Cooperative stabilizing network topologies for the three PCI complexes. Paralogous subunits are represented in the same color and denoted according to the Latin alphabet indicated at left. Arrows denote directional cooperative stabilization interactions, with line thickness proportionally reflecting the intensity of protein stabilization. Source data are provided as a source data file.
To aid our comparison by adopting an evolutionary perspective, we examined stability-based interactions of the three PCI complexes in concert. For clarity, we have color-coded paralogous proteins and labeled them using the unified Latin alphabet (Fig. 3F right). Our results reveal that even though the overall network structures are partially conserved, many interactions have been altered or maintained but with different intensities (Fig. 3F). Consistent with their evolutionary relationships, the proteasome lid and CSN complexes share more similar structures than they do with the elF3 complex. The eIF3 complex harbors five exclusive subunits (eIF3B, D, G, I, J) that lack paralogs in the CSN or proteasome lid. Our analysis indicates that [eIF3B/G/I/J] and eIF3D join eIF3 separately; [eIF3B/G/I/J] represents an independent module linked to the eIF3 interaction network via λ/eIF3A, κ/eIF3C and δ/eIF3K, with eIF3D being individually associated with other eIF3 components via θ/eIF3E (Fig. 3F bottom). Moreover, both κ and δ have already changed their interaction partners in the proteasome lid and CSN. These results suggest that altered cooperative stabilization interactions may permit new interactions, which could facilitate the evolution of new functions.
We noticed that the most prominent difference between the proteasome lid and CSN is the interaction between the subunits we denote θ and κ; θ/Rpn7 and κ/Rpn6 of the proteasome lid are strong reciprocal stabilizers, but θ/CSN1 and κ/CSN2 of the CSN are not co-stabilizing (Fig. 3C, D, F). We wondered what might be the molecular mechanism underlying the rewiring of this co-stabilization network. Interestingly, despite the θ-κ interacting interfaces in the proteasome lid and CSN complexes being highly divergent at the primary sequence level, they look remarkably analogous from the viewpoint of protein structure (Fig. 4A). Another apparent reconfiguration among the paralogous PCI complexes occurred between θ and γ; θ-γ co-stabilization only exists in the proteasome lid and CSN, but not in eIF3 (Fig. 3F). As for the θ-κ interactions, the θ-γ interface in the three PCI complexes looks structurally similar, yet the residues involved in binding differ (Supplementary Fig. 4C). Therefore, structural information cannot be used to infer co-stabilization interactions.
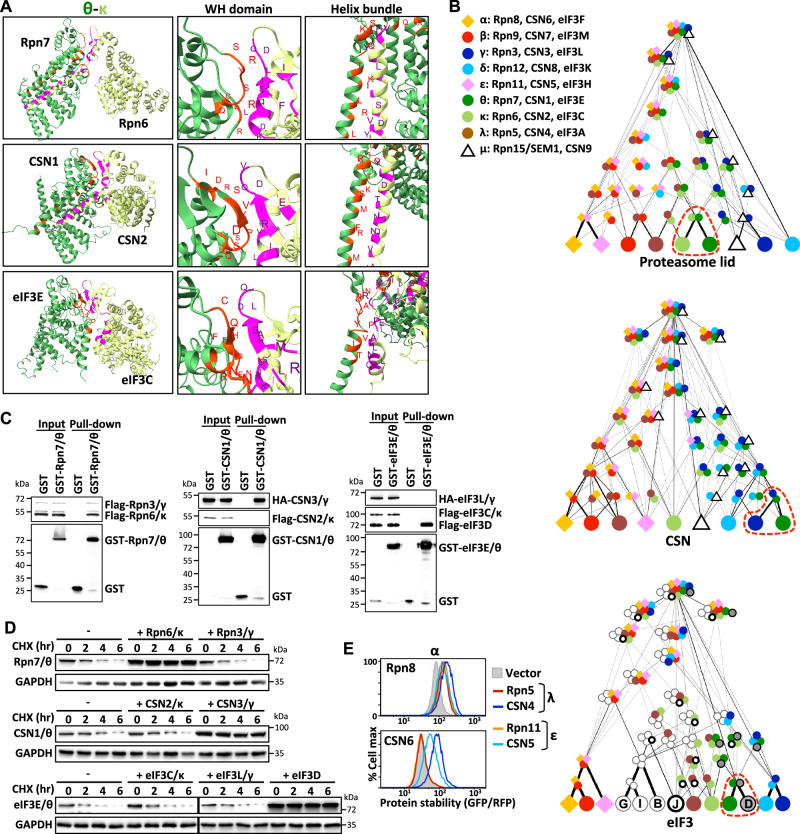
Fig. 4. Divergent assembly strategies adopted by PCI complexes.
A The binding interface between the θ and κ subunits of PCI complexes (PDB: 5L4K, 4D10, 6YBD). Residues of the θ and κ subunits involved in the binding interface are labeled red and magenta, respectively. B Comparison of the assembly process of PCI complexes based on their cooperative stabilization interactions. The assembly process of each complex is presented as a DAG, in which nodes are subunits/subcomplexes and edges are interactions between two partners. The edges have been weighted according to the frequencies at which they occurred within the top-ranking assembly trees. Red dashed circles mark the preferred assembly partner of the θ subunit at the initial assembly step. C GST pull-down analysis of the θ (Rpn7/CSN1/eIF3E) subunit of the proteasome lid, CSN and eIF3 complexes. Blots are representative of three independent experiments. D CHX-chase analysis of the θ (Rpn7/CSN1/eIF3E) subunits with/without κ (Rpn6/CSN2/eIF3C), γ (Rpn5/CSN4/eIF3A) or eIF3D co-expression. GAPDH serves as a loading control. Blots are representative of three independent experiments. E Cross-complex interactions between α and λ or ε paralogs. Source data are provided as a source data file.
We applied deduced stability-guided modularity to compare the likely assembly mechanism of the three PCI complexes. Strikingly, our models suggest that the assembly scheme of the three PCI complexes differ overall both in terms of individual protein assembly steps and overall modular organization (Fig. 4B). On close inspection, these deviations appear to arise at the initial step of protein coalescence, i.e., the types of dominant dimeric intermediates over the course of complex assembly are not the same. For example, the θ subunit (Rpn7/CSN1/eIF3E) preferentially interacts with the κ/Rpn6 subunit in the proteasome lid, but it predominantly assembles with the γ/CSN3 subunit and eIF3D in the CSN and eIF3 complexes, respectively (as revealed by the red dashed circles in Fig. 4B). We performed pull-down and cycloheximide-chase analysis to verify that assembly and the stabilizing partner of the θ subunit of the proteasome lid, CSN or eIF3 complex, respectively, differ (Fig. 4C, D). The modest binding observed between Rpn7/θ and Rpn3/γ may be bridged by Rpn6/κ. In addition, the global assembly topologies of the three PCI complexes also differ. We observed no clear modularity in the course of the proteasome lid assembly. Consistent with previous findings38, δ/Rpn12 is the last component incorporated into the proteasome lid. In contrast, the DAG of CSN reveals two clearly distinct modules (adjusted p-value = 0.0081; see “Methods” section). Our assembly model supports that in the course of CSN formation, interactions within each module are generated first before interactions form between these two modules. Assembly of eIF3 also occurs in a modular manner. It begins with the formation of four small independent subcomplexes—[α/β/ε], [γ/δ], [θ-eIF3D] and [eIF3B/G/I]—before further assembling into the entire eIF3 complex.
Given the partial preservation of ancestral cooperative stabilizations among the three PCI complexes, we wondered if cross-complex co-stabilization interactions also exist. Our results indicate that each subunit only interacts with its corresponding partners from the same complex, implying minimal cross-complex interactions among PCI complexes (Supplementary Fig. 4D). This finding suggests ancestral cooperative stabilization interactions are maintained through protein co-evolution. Exceptions to this phenomenon are the α-λ and α-ε interactions. We observed cross-complex interaction between α and λ or ε paralogs from the proteasome lid and CSN complexes (Fig. 4E). α/Rpn8 was stabilized by both of its authentic partners, i.e., λ/Rpn5 and ε/Rpn11, but also by its CSN-associated paralogs, i.e., λ/CSN4 and ε/CSN5, respectively. The crosstalk effect is unidirectional, probably due to the CSN complex having stronger α-λ and α-ε interactions. Collectively, these results support that cooperative stabilization interactions and assembly processes in paralogous PCI protein complexes have been rewired. Moreover, reconfigured assembly processes can reduce the likelihood of deleterious cross-complex mixed assemblies.
Reconfiguration of the co-stabilization network in paralogous LSm and Sm complexes
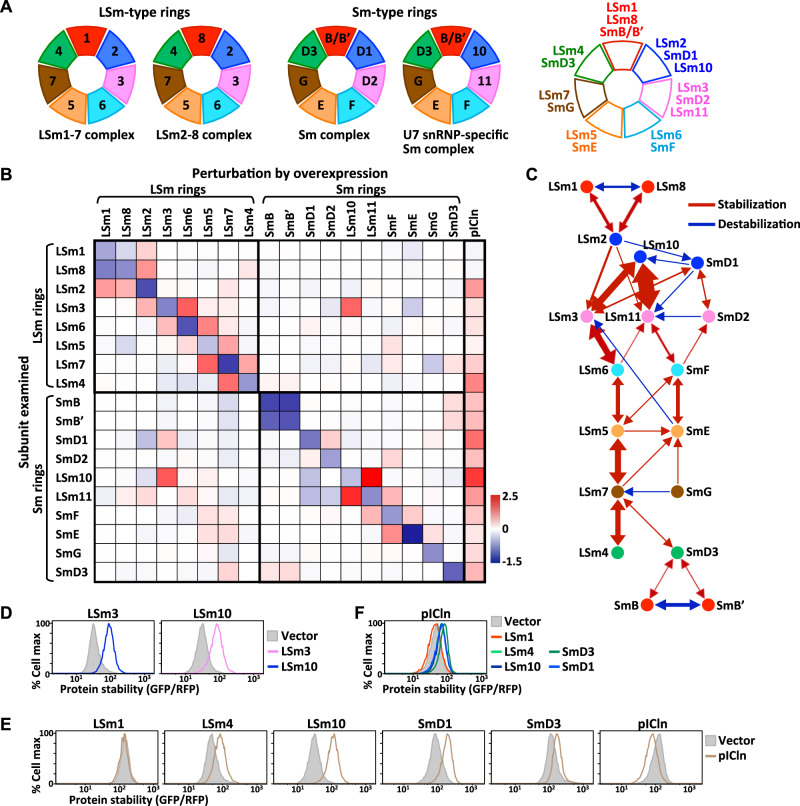
We extended our analysis to the Sm and LSm (like Sm) paralogous complexes. Sm and LSm proteins share a conserved structural fold, termed the Sm fold, and they typically assemble into a homomeric or heteromeric torus to regulate RNA metabolism39. Eubacteria and Archaea only carry one or two LSm/Sm proteins forming homomeric complexes. In contrast, eukaryotic genomes host more than 20 LSm/Sm proteins that assemble into various heteroheptameric complexes, including two LSm-type rings (the LSm1-7 complex and LSm2-8 complex) and two Sm-type rings (the Sm complex and U7 snRNP-specific Sm complex) (Fig. 5A)6,7. Each of these complexes regulates different steps of RNA processing, including splicing, editing, and degradation39. Phylogenetic analysis has indicated that the expansion of the eukaryotic LSm/Sm gene family proceeded through two waves of repeated partial duplications and divergence (Supplementary Fig. 5A)40. The first wave created multiple paralogous LSm genes from a single ancestral gene. Each paralogous ancestral LSm gene then duplicated again, resulting in seven further Sm genes. Consequently, each of the seven Sm proteins displays higher sequence homology to their corresponding LSm proteins than to other Sm proteins. The paralogous relationships between LSm and Sm proteins are summarized in Fig. 5A.
Fig. 5. Protein stability connectivity map of LSm and Sm proteins.
A Schematic depiction of the subunit arrangement of the LSm- and Sm-type complexes. Paralogous proteins are represented by the same colors. The paralogous relationships between LSm and Sm proteins are indicated at right. B The protein stability-based interaction map of LSm/Sm proteins. The matrix heatmap represents log2-fold-change in protein stability of the protein indicated at left upon overproducing the protein indicated on top. LSm/Sm subunits are ordered according to the complex they are associated with and the subunit arrangement in the corresponding complex shown in (A). C A network diagram depicting the entire LSm/Sm protein stability-based interaction network, in which nodes are subunits and edges are interactions between two partners. Paralogous proteins are shown in the same colors. Positive/stabilization or negative/destabilization interactions are indicated as red or blue arrows, respectively. X→Y indicates that supplying X stabilizes/degrades Y, whereas X↔Y denotes that X and Y are mutually stabilizing/degrading. The thickness of the arrow lines is weighted according to the degree of interaction. D Protein stability analysis of LSm3 and LSm10 by GPS assays. E Protein stability analysis of proteins indicated on top with or without providing pICln. F Protein stability analysis of pICln with or without co-expressing the LSm/Sm proteins indicated at right. Source data are provided as a source data file.
To deduce the assembly process of human LSm/Sm complexes and their potential crosstalk, we mapped stability-based connectivity among ten LSm proteins (LSm1-8, LSm10, LSm11), eight Sm proteins (SmB/B′, D1, D2, D3, E, F, G, where B′ is a splicing variant of B), as well as pICln that functions as an assembly chaperone for Sm complexes (Fig. 5B). Our results revealed a strong correlation between independent experimental replicates (Supplementary Fig. 5B, γ = 0.9708), as well as overall agreement between results from the N- and C-terminal GFP-tagged LSm/Sm proteins (Supplementary Fig. 5C, γ = 0.8742). Consistent with the notion that surplus unassembled LSm/Sm subunits are cleared by proteolysis, elevating the expression level of each individual LSm/Sm protein resulted in a reduction of its own lifespan (as revealed by the diagonal pattern of blue boxes from upper left to lower right in Fig. 5B). In some cases, enhanced expression of a given LSm/Sm protein also reduced the lifespan of other complex components, in particular its corresponding paralogs or isoforms, implying competition for identical binding partners exists between specific LSm/Sm pairs, such as LSm1-LSm8 and SmB-SmB′ (Fig. 5B). To display protein stability-based interactions among LSm/Sm proteins more intuitively, we have depicted our results as a network diagram in which nodes of the same color denote paralogous proteins, and the red and blue arrows of different thickness represent the weighted positive/stabilization and negative/destabilization interactions, respectively (Fig. 5C). Similar to PCI complexes, cooperative stabilization interactions only exist between particular LSm/Sm proteins. Despite the existence of minor cross-complex interactions, strong mutual stabilizing interactions arose primarily within LSm or Sm complexes, with the LSm3-LSm10 interaction being an apparent exception (Fig. 5B, D). Indeed, the physical association between LSm3 and LSm10 has been reported previously41,42. Together, our data imply a general discrepancy between components forming LSm- and Sm-type complexes in vivo. Notably, despite LSm1, LSm8 and SmB/B′ being paralogous proteins, our analysis reveals a definite distinction between [LSm1/LSm8] and SmB/B′ in terms of their stability profiles, in accordance with the notion that LSm1 and LSm8 are more phylogenetically related to each other than either is to SmB/B′ (Fig. 5B; Supplementary Fig. 5A). Although pICln has only been reported as a chaperone assisting Sm ring assembly, we found that pICln stabilized practically all Sm and LSm proteins, apart from LSm1, LSm5 and LSm8 (Fig. 5B, E), revealing that pICln may also be involved in LSm assembly. Interestingly, excessive expression of pICln facilitated its own degradation, and expressing LSm/Sm proteins also reciprocally stabilized pICln (Fig. 5E, F).
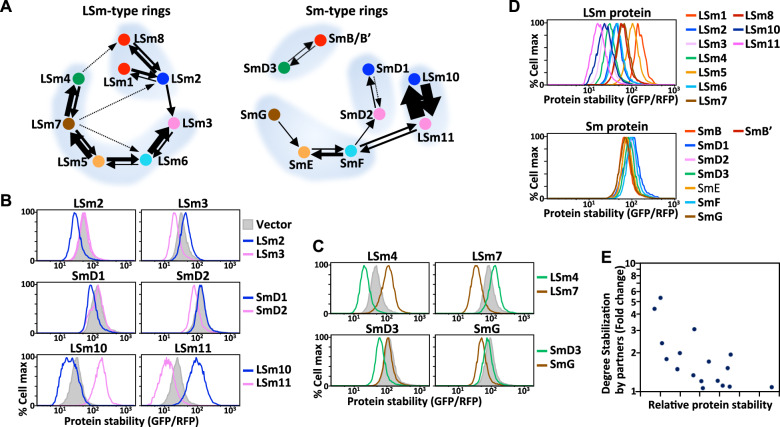
Next, we compared cooperative stabilization interactions between LSm- and Sm-type complexes. As for the different PCI complexes described above, the groupings of reciprocal stabilizers in the LSm and Sm rings varied considerably (Fig. 6A), indicating that their assembly paths differ in cellulo. For instance, LSm1/8 interacts with LSm2 in LSm-type rings, whereas SmB/B′ (an LSm1/8 paralog) assembles with SmD3 (an LSm4 paralog) in Sm-type rings. Upon comparing paralogous protein pairs, we observed that the LSm10-LSm11 pair displayed marked reciprocal stabilization, but it was much more moderate for the paralogous LSm2-LSm3 and SmD1-DmD2 pairs (Fig. 6B). Similarly, the LSm4-LSm7 pair proved to be mutually stabilizing, but the paralogous SmD3-SmG pair was not (Fig. 6C). Apart from these different groupings, we also noted that the cooperative stabilization interactions within LSm-type rings were stronger overall and more integrated than those of Sm-type rings (Fig. 6A). The stability interactions of LSm-type rings resolved as being chain-like and comprising two network clusters [LSm1/8-2] and [LSm3-6-5-7-4] (Fig. 6A left). Remarkably, the layout of stability-based LSm protein interactions exactly mirrors the arrangement of subunits in the LSm complex determined by crystal structure analysis, i.e., LSm1-2-3-6-5-7-4 (Supplementary Fig. 5D, E). In contrast, the stability-based connections in Sm-type complexes were mostly weak but revealed four network clusters, i.e., [SmD3-B/B′], [SmD1-D2], [LSm10-11] and [SmF-E-G] (Fig. 6A right). Importantly, these mutually stabilizing Sm dimers/trimers exactly match Sm assembly intermediates revealed by in vitro assembly experiments43. This consistency reinforces the reliability of using protein stability-guided modularity to infer protein complex assembly processes.
Fig. 6. Divergence of protein stability-guided modularity in LSm- and Sm-type complexes.
A Louvain two-nearest-neighbor analysis of LSm- and Sm-type complexes based on data shown in Fig. 5B. Nodes of the same color denote paralogous proteins, and black arrows represent directional cooperative stabilization interactions. The thickness of the arrow lines proportionally reflects the degree of protein stabilization. Subunits forming the same network cluster are surrounded by a light gray shadow. B, C Comparison of paralogous interactions within LSm and Sm complexes in terms of cooperative stabilization. Protein stability analysis by GPS assay of proteins indicated on top with or without co-expressing the proteins indicated at right. D Comparison of protein stability among various LSm and Sm proteins upon their low-level expression (from a single copy of the GPS reporter). GFP was tagged at the C-termini of LSm/Sm proteins. E Correlation analysis between the stability of unassembled LSm/Sm proteins and their degrees of stabilization by corresponding partners.
To investigate cooperative stabilization interactions further, we analyzed the lifespan of unassembled LSm/Sm proteins by expressing them alone (at either low or high levels) and comparing the outcome with the degree of partner-dependent stabilization for each individual LSm/Sm protein. Unexpectedly, the lifespan of unassembled LSm proteins proved to be surprisingly divergent, whereas Sm proteins were generally more stable (Fig. 6D; Supplementary Fig. 5F). Association with stabilizing partners by co-expression reduced the differences in protein stability among paralogous LSm/Sm proteins (Supplementary Fig. 5G). The lifespan of unassembled LSm/Sm proteins was negatively correlated with their degree of partner-mediated stabilization (t-test for correlation = −0.6779; p-value = 0.00199) (Fig. 6E). For example, orphaned LSm10 and LSm11 were the least stable among LSm/Sm proteins, yet they displayed the strongest partner-dependent stabilization (Fig. 6B, D). These findings highlight an underappreciated impact of protein interaction networks on protein lifespan and emphasize the critical importance of investigating how protein stability is regulated in native cellulo contexts. In summary, our results reveal that the assembly process of paralogous PCI and LSm/Sm complexes has been evolutionarily rearranged.
Discussion
We have performed an unprecedentedly comprehensive comparison among paralogous protein complexes from the viewpoint of protein stability-based modularity. Our results show a strong divergence of cooperative stabilization networks in the PCI and LSm/Sm paralogous protein complex families, revealing a unique and previously unappreciated characteristic of paralogous protein complexes. Although their structural organizations are maintained, paralogous protein complexes do not necessarily adopt the same assembly strategy as their ancestral complex but instead can evolve one anew. Altering assembly processes allows paralogous complexes to recruit new subunits, facilitating neo-functionalization. The divergence in assembly strategies also helps to insulate their functional modules from perturbation by building incompatibilities against higher-order mixed assemblies and precluding the formation of toxic nonfunctional chimeric complexes.
Although significant advances have been made in identifying protein complexes, their formation processes have remained difficult to characterize44,45. At present, determining the assembly path of protein complexes mainly relies on in vitro reconstruction of protein complexes using recombinant proteins, or, alternatively, structural information is gathered to establish the physical interactions between subunits. Our data suggest that structural information is insufficient to deduce the assembly processes of protein complexes in cellulo. Electrospray mass spectrometry has also been widely deployed, but it relies on the assumption that protein complex assembly pathways in vivo are the reverse of disassociation processes defined in vitro8,31,32. That assumption is questionable and it remains unclear if, in fact, assembly processes in vitro reflect the crowded cellular environment. For instance, molecular chaperones and cellular proteolysis systems are typically missing from in vitro models. Interestingly, nearly half of the subunit pairs found to cooperatively stabilize each other in our study were previously identified as assembling co-translationally46,47, highlighting the importance of characterizing protein complex assembly processes in cellulo. A major advantage of our protein stability-based approach is that we analyzed protein complexes in living cells in which all cellular factors remain intact. Our method can be adapted to analyze protein complexes for which structural information is lacking or that are difficult to purify. It also efficiently captures assembly intermediates that may not be sufficiently stable to survive biochemical purification procedures. This technology is adaptable to systematic high-throughput platforms and is also applicable to different cell types and cell states, in which different complex subunits may be involved.
Nevertheless, there are potential issues to be considered when deploying this method. For instance, the GFP tag may influence complex assembly. To resolve this issue, we generated two datasets in which GFP had been fused at either the N- or C-terminus of the examined protein, resulting in highly consistent outcomes. It is also possible to apply the same approach without utilizing an epitope tag by using Western blotting or quantitative mass spectrometry instead. In addition, our approach relies on protein overproduction, with the caveat that ectopic overexpression might lead to nonphysiological complex formation. Nevertheless, it has been shown previously that NED subunits are in fact produced naturally in super-stoichiometric quantities in normal disomic cells19. Furthermore, in accordance with our finding that eIF3K-L, eIF3D-E, and eIF3G-I are co-stabilizing pairs, previous individual knockdown experiments in HeLa cells also indicated that protein levels of the eIF3K and L, eIF3D and E, and eIF3G and I pairs are strictly dependent on each other24. Lastly, our study focuses on stable and obligate protein complexes. Whether cooperative stability applies to subunits forming transitory protein complexes or multitasking subunits (i.e., shared between different complexes or involved in additional activities independent of the complex itself) remains to be examined48,49.
The clear reconfiguration of the co-stabilizing network in paralogous LSm/Sm and PCI complexes strongly suggests that these paralogous complexes do not assemble via identical pathways. Numerous independent lines of evidence echo our conclusions. The assembly models of the eIF3 complex derived from genetic knockdown and biochemical approaches are consistent with our conclusions10,24. Previous analysis of the CSN and proteasome lid assembly mechanisms also supports that subunits of these two complexes coalesce in different orders, with Rpn12/δ or CSN5/ε being the last-assembled subunits for the proteasome lid and CSN, respectively50. Functionally, incorporation of Rpn12 couples completion of proteasome lid assembly to its attachment to form a complete 19S proteasomal regulatory particle38. CSN5 acts as the catalytic center for the CSN complex, yet it does not exert any activity until the holoenzyme has been assembled51. Likewise, the assembly modes and RNA recognition properties of the LSm- and Sm-type complexes have also proven quite different. LSm-type rings assemble spontaneously and are stable without RNA. The LSm2-8 complex interacts with RNA substrates via end recognition, with the uridine nucleotide at the 3′ end of the RNA molecule being anchored by LSm3 and the preceding three nucleotides being recognized by LSm2/8/452. In contrast, Sm-type rings only assemble in the presence of RNA upon the preformed [SmD1-D2], [SmD3-B] and [SmE-F-G] subcomplexes having coalesced43. The Sm complexes form passive scaffolds around RNA via internal RNA recognition, whereby seven consecutive nucleotides, each of which is recognized by a distinct Sm protein, are bound within the central aperture of the Sm complex52. Together, these findings indicate that the assembly processes follow a hidden logic according to the function of the complex. Possessing a unique assembly process can ensure that a complex executes its specific function more efficiently. Moreover, refiguring an assembly process can reduce cross-complex interactions among paralogous subunits, further enhancing complex specificity.
Our finding of evident rewiring of co-stabilizing networks in the PCI and LSm/Sm complex families is intriguing considering their genetic and structural homology and the central role of cooperative stabilization interactions in driving protein complex formation. The stable integrity of large protein complexes is maintained via multiple inter-subunit interactions. It is possible that this multivalent molecular interaction microenvironment provides an ideal scenario for protein complex diversification due to its greater tolerability to changes in interactions among individual subunits or even interaction partners without eliciting loss of protein complex integrity, thereby endowing flexibility to develop new network properties53. Although the initial changes may be due to genetic drift, assembly reconfiguration is likely driven by selection once the functions of paralogous complexes start to diversify.
The molecular mechanism driving cooperative stabilization network rewiring in duplicated complexes may be attributable to the gain or loss of degrons (degradation signals) in unassembled subunit species. Proteasome-mediated proteolysis requires highly specific interactions between ubiquitin ligases and their corresponding degrons in substrate proteins13,16,17. For instance, the UBE2O, HUWE1, and CRL4DCAF12 ubiquitin ligases recognize exposed juxtaposed basic and hydrophobic patches, a short stretch of positively-charged residues, and C-terminal double glutamate residues as the degrons of uncomplexed RPL24, RPL26, and CCT5 proteins, respectively, to trigger their degradation54–56. Those degron motifs are buried within the structure upon complex formation and thus assembled proteins can evade degradation. It is possible that coordinated substitutions of amino acids occurring as pairs of duplicated binding subunits co-evolve coincide with unanticipated gain or loss of degron sequences and, consequently, reconfiguration of cooperative stabilization networks. In line with this speculation, despite being structurally similar, we observed near-complete sequence divergence at the θ-κ and θ-γ interacting surface of the three PCI complexes. Rather than concerted duplication of all components at once, step-wise partial duplication is considered a prevalent evolutionary route for duplication of protein complexes57. It is tempting to explore if the reconfiguration of co-stabilization interactions correlates with the relative duplication ages of different subunits of paralogous protein complexes.
Our results provide additional conceptual advances regarding protein complex formation processes and how protein lifespan is regulated in cells. Our findings support the notion that complex assembly is both ordered and modular15,58. This modular design is advantageous because it reduces the complexity of the assembly process and, consequently, minimizes the likelihood of erroneous aggregates. It also allows rapid regulation at complex levels and enables modules to be interchanged to form distinct protein complexes. Interestingly, cooperative stabilization interactions can either be reciprocal (symmetrical dependency) or unilateral (asymmetrical dependency) and only certain subunits within a complex are subjected to partner-mediated cooperative stabilization. Considering the unilateral interaction between TAF6/TAF9 for instance (TAF9 is stabilized by TAF6, but the reverse is not true), our data suggests that, unlike unassembled TAF9 that is labile, unassembled monomeric TAF6 is stable in the cell. Therefore, the loss or gain of distinct individual subunits could have diverse impacts on the integrity of corresponding protein complexes. Importantly, stabilization depends on the ability of each protein to homodimerize or heterodimerize. Unlike proteins that form heteromeric complexes, proteins that form homopolymers can “self-stabilize” (rather than being stabilized by their binding partners). Consequently, the lifespan of this latter group of proteins “increases” when their own protein synthesis level is elevated. Finally, our findings illustrate the importance of analyzing protein lifespan in the context of native protein-protein interaction networks. Identical proteins (i.e., having the same amino acid sequence and covalent modifications) in a uniform proteolytic environment can display distinct lifespans, depending on their individual interaction networks within cells. We anticipate that further investigations of protein lifespan-directed interactomes will prove highly valuable in gaining deeper insights into proteome organization, regulation, and evolution.
Methods
Cell culture and manipulations
HEK293T (ATCC® CRL-3216) cells were cultured in Dulbecco’s Modified Eagle’s Medium supplemented with 10% fetal bovine serum (Hyclone), 100 μg/ml of streptomycin and 100 U/ml of penicillin (Gibco) at 37 °C in a 6% CO2 atmosphere. To block proteasome-dependent protein degradation, cells were treated with 1 μM bortezomib (BioVision) or 10 μM MG132 (Merck Millipore) for 8 h. For the cycloheximide-chase assay, cells were treated with 100 μg/mL cycloheximide (Calbiochem), followed by sample collection at multiple time-points. Cell transfection was performed using TransIT-293 transfection reagent (Mirus Bio) according to the manufacturer’s instructions. To produce lentiviruses, HEK293T cells were co-transfected with pRev, pTat, pHIV gag/pol, pVSVG, and the lentiviral construct of interest. Viral particle-containing supernatants were collected 48 h post-transfection. Transduction was conducted in a medium containing 8 μg/mL polybrene (Sigma-Aldrich) for 24 h.
GST pull-down assay
HEK293T cells stably expressing GST‐tagged and Flag-tagged or HA-tagged PCI subunits were harvested and lysed in ice-cold IP‐lysis buffer (20 mM Tris pH 7.6, 150 mM NaCl and 0.5% IGEPAL CA‐630) supplemented with protease inhibitors (Roche). The clarified lysates were incubated with Glutathione‐conjugated beads (GE Healthcare Life Sciences) for 4 h at 4 °C. The beads were washed three times in IP‐lysis buffer and then boiled in 2× Laemmli sample buffer. The eluted proteins were subjected to immunoblotting. Primary antibodies used for immunoblotting were purchased from the following venders: GST (GE Healthcare, 27457701 at 1:1000), Flag (Sigma‐Aldrich, M2 at 1:1000), HA (Abcam, ab130275 at 1:1000), GFP (Takara Bio Clontech, JL‐8, 632381 at 1:1000) and GAPDH (GeneTex, 100118 at 1:1000). Source data are provided as a source data file.
Characterization of protein stability-based interactions by GPS assays
To generate GPS reporter constructs, the genes of interest were cloned into pLenti-GPS vectors (N and C-GFP tag versions) by means of Gateway recombination (Invitrogen). To circumvent the GFP tag potentially interfering with protein binding, we prepared both N- and C-terminally GFP-tagged GPS reporter constructs for each subunit for comparison. The GPS reporter was driven by the EF1α promoter unless otherwise indicated. To generate GPS reporter cell lines, HEK293T cells were infected with lentiviruses carrying GPS constructs at a low MOI of ∼0.2 and then selected by 1 μg/ml puromycin (Clontech) for 10 days. Since the GPS reporter was integrated into each cellular genome as a single copy, and the expression level of the gene downstream of the IRES site, i.e., the GFP-fusion protein, is only ∼30% that of the gene upstream of IRES, i.e., RFP, the expression level of the GFP-fusion protein lies within physiological ranges and is not highly overexpressed.
To map stability-based interactions between subunits within a protein complex, we separately overexpressed subunits forming the same complex using lentiviruses prepared from a 2A-BFP construct at a MOI of ∼5 and analyzed the treated GPS reporter cells by FACS 40 h post-infection. Subunits from unrelated protein complexes were included as negative controls. The BFP signal indicates the synthesis rate of the overexpressed subunit.
FACS analysis was performed by using a BD LSR Fortessa system (BD Biosciences) operated by BD FACSDivaTM software. The 405-nm, 488-nm, and 561-nm lasers were used to stimulate BFP, GFP, and RFP, respectively. No background correction or compensation was applied. Cells were gated by doublet discrimination and RFP signals. The RFP-positive cells were further gated by BFP signals to discriminate GPS reporter cells overexpressing the given subunit. A total of 20,000 RFP-positive single cells were recorded for each reporter cell line. To ensure data consistency, all GPS experiments were independently performed in duplicate or triplicate. Histograms and scatter diagrams were plotted in FlowJo software.
Quantitative characterization of the HUS1-RAD1 cooperative stabilization interaction
Data collection
To generate HUS1 and RAD1 GPS dosage cell libraries, HEK293T cells were separately infected with different amounts of lentiviruses expressing HUS1 and RAD1 GPS reporters (MOI ranged from 1∼5) and mixed together. To express HUS1 and RAD1 at different dosages, library cells were separately infected with different amounts of 2A-BFP viruses expressing HUS1 or RAD1 (MOI ranged from 1∼10) and then mixed together. In this system, millions of single cells, each possessing a unique combination of HUS1 and RAD1 expression levels, were analyzed together as a single sample by means of three-color FACS. We analyzed 1,000,000 RFP-positive cells by FACS for HUS1 and RAD1 GFP dosage cell libraries expressing different amounts of RAD1 and HUS1, respectively.
Data processing
We exported the RAD1 (examined subunit)-HUS1 (overexpressed subunit) and the HUS1 (examined)-RAD1 (overexpressed) FACS data as plain text files containing the BFP, RFP, and GFP intensities of individual cells determined by FlowJo software. We subdivided the BFP signals into multiple intervals and split the data points of (BFP, RFP, GFP) triplets into subsets accordingly. For each split dataset, we used a linear model (Y = RX) to fit the GFP(Y) and RFP(X) signals, where R is the GFP/RFP ratio. R increases with BFP when BFP is below a threshold (K), but it starts to decrease when BFP surpasses K. We identified K to be 16561 and 22248 for the RAD1-HUS1 and HUS1-RAD1 datasets, respectively. By setting these two values as the upper limits of BFP signals, we obtained 887,002 (89.99% of the RAD1-HUS1 dataset) and 926,278 (94.37% of the HUS1-RAD1 dataset) data points for subsequent analysis. All data processing and model fitting were performed in Python 3.7 with the NumPy 1.19.5 and SciPy 1.4.1 Python packages.
Mathematical modeling of heterodimer formation
To quantify the cooperative stabilization interaction between HUS1 and RAD1, we built a mathematical model of the heterodimeric protein complex formation system. This model can capture the nonlinearity of the FACS data and estimate explainable parameters (e.g. cooperative stability) by fitting to experimental data. There are three components in the heterodimer formation system, i.e., protein 1 (), protein 2 (), and the - heterodimer (). Since all the proteins we examined in the experiments were driven by constitutive promoters, we set the synthesis rates of and as constants ( and respectively). All protein species (, , and ) have their own degradation rates (, , and , respectively). Dimerization was assumed to be much faster than synthesis and degradation, so equilibrium is reached instantaneously, and Eq. 1 always holds:
| 1 |
where is the association constant.
Thus, we described the system by Eqs. 2−5:
| 2 |
| 3 |
| 4 |
| 5 |
where and are the total concentrations of and , respectively. Equations 2 and 3 state that the total concentration of a protein species is the sum of its concentrations in the monomeric and dimeric forms. Equations 4 and 5 describe that the net rate of change for a protein species is its synthesis rate minus the degradation rates of these two forms. By solving these equations at steady-state where , we obtained solutions for , , and in terms of the model parameters:
| 6 |
| 7 |
| 8 |
is obtained by adding Eqs. (6) and (8):
| 9 |
where
The cooperative stability strength is defined as the ratio of the degradation rate constants of the monomer and dimer:
| 10 |
where .
Model fitting to estimate cooperative stability
We used the curve fitting function in the SciPy python package to find the parameter values (i.e., degradation rate constants) that best fit the experimental data. The GFP intensities of the GPS data represent the total concentration of protein 1 (). The RFP and BFP intensities represent the synthesis rate () and synthesis rate (), respectively. Since the units of RFP and BFP intensities are not equivalent for representing the protein synthesis rates, we introduced a factor (n) into the model to correct for the difference between RFP and BFP signals:
| 11 |
Thus, our model has five undetermined parameters (, , , , ). We set three possible initial values (0.1, 1, and 10) for each parameter and generated all possible combinations (35 = 243) of initial value sets for the five parameters.
| 12 |
An initial parameter set specifies the relationship between GFP (), RFP (), and BFP () as a function of and according to Eq. (9):
| 13 |
The loss function quantifies the square distance between the measured GFP and predicted according to the model :
| 14 |
Optimization of was undertaken by setting initial values of to each one of the 243 possible combinations and iteratively applying gradient descent until convergence. We separately fitted the RAD1-HUS1 and HUS1-RAD1 datasets by setting the lower bound of each parameter as zero. The fitting result for and is robust to different sets of initial values, with only a few outliers. Therefore, we used the median of the 243 results and Eq. (10) to estimate the cooperative stability of RAD1 and HUS1, respectively.
Generation of phylogenetic trees for LSm and Sm proteins
The evolutionary history was inferred using a Maximum Likelihood method based on the JTT matrix-based model59. The tree with the highest log likelihood (−3787.65) is shown. The percentage of trees in which the associated taxa clustered together is shown next to the branches. Initial tree(s) for the heuristic search were obtained automatically by applying Neighbor-Joining and BioNJ algorithms to a matrix of pairwise distances estimated using a JTT model and then selecting the topology with superior log likelihood value. The analysis involved 18 amino acid sequences. There were a total of 128 positions in the final dataset. Evolutionary analyses were conducted in MEGA760.
Network modularity analysis
To identify modules in a protein complex, we applied two community detection algorithms, Louvain and Infomap, by using the R package igraph. The input graphs were the undirected connections filtered according to cooperative stabilization strengths between each pair of complex subunits (>1.2). The function, cluster_louvain, implements the multi-level modularity optimization algorithm to find clusters displaying strong modularity in large networks based on the modularity measure and a hierarchical approach. The weights of the connections between each node were defined as the cooperative stabilization strengths between each pair of complex subunits. The modularity algorithm measures the density of connections within clusters compared to the density of connections between clusters. The other function, cluster_infomap, exploits the map equation to find cluster structures in networks by minimizing the description length of the motion of a random walk. The cooperative stabilization strength between each pair of complex subunits was set as the edge weight, which represents the likelihood of the random walker using that connection to reach the next object.
Algorithm to score the likelihood of complex assembly trees
Concept and overview of the algorithm
A multi-component protein complex is formed by incrementally agglomerating smaller subunits. An assembly history denotes a series of these assembly events. For instance, a trimer ABC can be formed by first joining A and B and then appending C to the AB dimer (A, B, C AB, C ABC). We postulated that the assembly processes of protein complexes exhibit the following properties according to the basic principles of chemical reactions and our empirical data. First, two subunits are joined at each step of the assembly process since the probability of more than two subunits colliding instantaneously is negligible. Hence, an assembly history can be represented as a binary tree analogous to the hierarchical clustering process. Second, protein complexes can form through multiple possible assembly histories since each assembly step is a molecular collision event and hence stochastic in nature. Third, despite their stochasticity, certain assembly histories are much more likely to occur due to the differential stabilities of subcomplexes. Subcomplexes possessing stronger levels of cooperative stability tend to form earlier in the assembly process since they are more stable than the constituent subunits. Based on these assumptions, we proposed algorithms to enumerate all possible assembly histories of a relatively small protein complex, to assess the likelihood of each assembly history from its cooperative stability data, and to represent the likely assembly histories concisely as a DAG (Directed Acyclic Graph). The algorithms are illustrated by a schematic diagram in Fig. S3A and are described further below.
Input:
-
Matrix () of the pairwise cooperative stability data for complex subunits
Output:
An ensemble of all possible binary assembly trees with likelihood scores
DAG representation of the top-ranking assembly trees
Procedure:
Generate all possible assembly trees for a given protein complex
Calculate their likelihood scores based on cooperative stability data
Integrate the top-ranking assembly trees into a DAG
Generation of all possible assembly trees
We developed a two-phase tree generation procedure. In the first phase, we generated all possible structures of binary trees with distinct leaves (subunits). In the second phase, we enumerated all possible assignments of leaf node identities for each tree structure.
Phase 1: Enumerating binary tree structures with a fixed number of leaf nodes.
We represent a binary tree with a regular expression defined below. We denote as a string surrounded by parentheses on both sides: , where is either an integer or two substrings . The former and latter expressions represent a subtree of a single node and a subtree with two branches, respectively. For instance, (((1),(1)),(1)) represents a binary tree with three leaf nodes that are compatible with the assembly history (A, B, C AB, C ABC). The integer denotes the number of descendant leaf nodes of the subtree. We further define as a set of all binary splits of an integer where the first number is not smaller than the second number:
| 15 |
The algorithm recursively duplicates and unfolds the strings until all subtrees at the bottom level comprise single leaf nodes. Initially, we assigned the singleton tree collapsing all leaf nodes to the tree set: The process was repeated for the following steps until no tree in contains numbers greater than 1:
Select a tree which contains numbers greater than 1.
Find the first number in greater than 1 and denote it as .
For each binary split , duplicate and replace the substring with . Denote the modified tree as . .
Remove from .
The output of phase 1 is the collection of all binary tree structures . It is time-consuming for small complexes and intractable for non-small complexes since the number of binary tree structures scales exponentially with the number of leaf nodes ( where is the number of nodes). For instance, for 10, 20, and 50 nodes, there are , binary trees, respectively.
Phase 2: Enumerating all leaf node assignments of each binary tree structure.
A naïve approach to generate all leaf node assignments of a binary tree structure is to exhaustively permute integers and assign each permuted integer to a leaf node in the order of the regular expression (from left to right). This approach yields multiple permutations corresponding to the same equivalent assignment. If the left and right branches of a subtree have identical structures, then two distinct permutations are equivalent by swapping the leaf nodes under the two branches. An accurate algorithm should avoid this type of over-counting and report a list of distinct assembly histories respecting a binary tree structure. A is the regular expression of a binary tree structure. We denote an ordered partition of distinct integers , , where is the number of components, and each component consists of distinct integers from . Initially, construct and a list . concentrates all the integers in the root node. The following procedures were repeated until all elements in has components:
Select a with .
Find the first component in consisting of more than one integer. Denote it as .
Identify the node in corresponding to component . By definition is an internal node and has two children.
Identify the subtrees and of the left and right branches under . Denote the numbers of leaf nodes in and to be and respectively, where .
- Enumerate all combinations of split integers into two groups with and members, respectively.
-
51.If subtrees and have different structures, then each split in step 5 induces a unique refined partition of component . Duplicate and replace component with two components and respecting the split. The resulting partition has components: .
-
52.If subtrees and have identical structures, then only half of the splits are unique since the splits are equivalent by swapping the left and right branches of the tree. Thus, repeat 5.1 only on half of the unique splits.
-
51.
Remove from .
The output is a list of -component partitions respecting the tree structure . According to these procedures, each internal node induces unique partitions if the left and right branches have different structures and unique partitions otherwise. The total number of leaf node assignments of a tree is the product of these terms over all internal nodes and becomes , where is the number of the internal nodes in with identical structures of the left and right branches. For instance, a tree with two-leaf nodes has unique assignment, and a symmetric binary tree with eight leaf nodes has seven internal nodes with identical left and right branches, and the number of unique assignments is . The number of leaf node assignments also grows exponentially with the number of leaf nodes. As an example, for the eIF3 complex with 13 distinct subunits, there are 983 binary tree structures and a total of 316,234,143,225 (∼3.16 × 1011) possible assembly trees.
Calculation of likelihood scores for all possible assembly trees
For each assembly history (a binary tree with a leaf node assignment), we proposed an algorithm to evaluate its likelihood score in terms of the matrix of pairwise cooperative stability scores. In brief, we parsed the tree into a unique sequence of binary assembly events. The probability of each assembly event is positively related to the scores of member pairs between the two subcomplexes, and the likelihood score is the product of probabilities over these assembly events. Moreover, the probability of merging large subcomplexes at later stages of the assembly sequence should be considerably higher since the number of possible choices is more limited. For instance, in the last stage, the remaining two subcomplexes have only one choice of merging into the full complex with probability 1 (we ignore the possibility of no change). Therefore, each term denotes the conditional probability of an assembly event among all possible assembly events compatible with the current subcomplex configurations.
Input:
Assembly binary tree () and leaf node assignment ().
Cooperative stability matrix ()
Output:
Likelihood score
Procedures:
Set the initial subcomplex configuration {} of distinct monomers.
Parse into a sequence of triads following a topological order from left to right. A triad () consists of a parent node and two children nodes .
Set .
- For repeat the following procedures:
-
41.Obtain all subcomplexes according to and the current configuration .
-
42.Identify the triad () at step , and the monomers belonging to and . If the iteration step is not specified, we dispense with the subscript and denote the triad ().
-
43.Calculate the assembly tendency as the geometric mean of all pairwise cooperative stability strengths between monomers belonging to and :
16 -
44.Construct as the set of all subcomplex pairs in . Each member represents a possible assembly event compatible with the current configuration. Calculate the assembly tendency of each .
-
45.Update the subcomplex configuration of the next step by merging monomers in and : .
-
46.Evaluate the conditional probability of transitioning the subcomplex configuration from to by normalizing the sum of the assembly tendencies over all possible assembly events:
17 -
47.Update
-
41.
The likelihood score is
We conducted an exhaustive search by calculating the likelihood scores of all possible assembly trees of the eIF3, proteasome lid, and CSN complexes. We wrote a custom Python script with Cython for acceleration and with Multiprocessing for parallel computing and ran the script on a high-performance computer (Intel® XEON® E7-4870, 2.30 GHz, 32 cores were used).
DAG representation of top-ranking assembly trees
Multiple complex assembly histories are likely to occur according to the cooperative stability data. To aggregate the information from multiple assembly histories, we consolidated the top 1000 assembly trees (in terms of the likelihood scores) by overlaying them in one single DAG. For simplicity, we set a cutoff (>30) to filter out low-frequency edges. After filtering, some nodes might lose connections to other nodes. We removed these nodes by checking if they have path(s) to/from the final complex/monomer using the shortest path length function in the Networkx python package. We then drew the DAG and used the edge weight (thickness) and node size to represent their frequency among the 1,000 top-ranking trees.
Quantification of the two-branch feature in the DAG of CSN assembly trees
Overview
The CSN assembly DAG manifests as two big components with sparse connections between them. To test if this two-branch feature is statistically significant, we developed a quantitative analysis of leaf nodes in a DAG for statistical tests. We first calculated the distances between the nine CSN subunits in the DAG. By aggregating subunits into two groups, the distances were classified into two types (intra-group distances or inter-group distances). We then performed a statistical test for differences between these two distance distributions and calculated the p-value from 10,000 bootstrap samples.
Input:
DAG representation of the assembly trees
Two groups of leaf nodes in the DAG
Output:
p-value of the null hypothesis that there is no difference between these two groups
Procedure:
Quantify distances between leaf nodes in the DAG
-
Calculate the pairwise distances and obtain the inter-group and intra-
group distance distributions
Perform the Kolmogorov–Smirnov test on these two distributions
Bootstrapping to estimate the p-value
Distance quantification for subunits in a DAG
Intuitively, the distance between two subunits in one assembly history (binary tree) is the number of steps needed to coalesce into one subcomplex, which is half of the distance of the shortest path connecting them. Since multiple assembly histories may occur for any coalescent event, we approximated coalescence by a Markov process defined in the DAG. Suppose a node in the DAG is adjacent to higher-order nodes with edge weights , respectively. We define the probability of transitioning from to as the normalized weight of . The probability of traversing along a specific path is the product of the normalized weights of its edges: .
We then considered two-leaf nodes and in the DAG. We defined a most recent common ancestor (MRCA) of and as node where the paths from to and the paths from to share no nodes other than . represents a subcomplex where and coalesce together. denotes the collection of all MRCAs of and . For each , suppose there are paths connecting to and paths connecting to . By averaging the probabilities of all possible paths from A to and from B to , we obtained probabilities for these two subunits to reach the subcomplex :
| 18 |
Thus, the probability for A and B to coalesce () can be calculated as the average of the product of probabilities for A and B coalescing to each :
| 19 |
We then defined the distance between A and B () as the reciprocal of :
| 20 |
Calculation of distances between all pairs of subunits in the DAG
According to our description in the previous section, we calculated = 36 distances for all possible pairs of all nine CSN subunits in the DAG of the top-2000 assembly trees. We divided the nine CSN subunits into two groups (6, 7, 5, 4, 2 and 9, 8, 3, 1) based on the two modules identified by modularity analysis. Thus, the 36 distances could be classified into intra-group distances (n = 16) or inter-group distances (n = 20).
Statistical testing and bootstrap p-values
We tested if the two types of distances are drawn from the same distribution by means of a two-sample Kolmogorov–Smirnov test (KS test):
H0: The distributions of intra- and inter-group distances in the CSN DAG are from the same population of random DAGs.
H1: The distributions of intra- and inter-group distances in the CSN DAG are from different populations.
We calculated the KS test statistic t and then performed 10,000 bootstraps by randomizing the order of the nine CSN subunits in the DAG and re-calculated the pairwise distances and statistic t*. Then we estimated the p-value as:
| 21 |
where I (condition) = 1 when the condition is true and 0 otherwise.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Source data
Acknowledgements
We thank C.Y. Chu, S.Y. Hsu, L.T. Lee, H.C. Lin, K.H. Lin, and J. O’Brien for suggestions and assistance. This work was supported by Investigator Award AS-IA-108-L02 from Academia Sinica and NSTC grants 111-2326-B-001-008, 112-2326-B-001-005, and 111-2311-B-001-014_MY3 awarded to H.C.Y.; the Data Science Statistical Cooperation Center of Academia Sinica and NSTC grants 110-2118-M-001-007-MY2 and 110-2118-M-001-003-MY2 awarded to C.H.Y.; and Investigator Award AS-IA-110-L01 from Academia Sinica and NSTC grant 111-2326-B-001-015 awarded to J.Y.L.
Author contributions
C.W. Yeh, S.T. Lin, L.C. Wang and S.C. Chen performed GPS assays and mapped protein stability-based interactions in PCI and LSm/Sm complexes; K.L. Hsu carried out mathematical modeling and built the algorithm to score protein complex assembly trees; K.H. Yeh and C.H. Yu performed network modularity analysis; T.T. Li examined physical binding between eIF3 subunits; W.C. Huang performed protein structural analysis and cloned mutant HUS1 and RAD1 genes; C.F.J. Liu performed phylogenetic analysis; J.Y. Leu wrote the paper; C.H. Yeang supervised mathematical modeling and the algorithm to score protein complex assembly trees; H.C.Y. characterized HUS1-RAD1 interaction, designed experiments, analyzed data, supervised the project and wrote the paper.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Data availability
The atomic coordinates used in this study are available in the Protein Data Bank (PDB) under accession codes 5L4K, 4D10, and 6YBD. All data generated in this study are provided in the Supplementary Information and Source Data files. Source data are provided with this paper.
Code availability
The source codes for qualifying cooperative stabilization by mathematical modeling and reconstruction of protein complex assembly processes have been deposited in Zenodo61,62.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51286-w.
References
- 1.Pereira-Leal, J. B., Levy, E. D., Kamp, C. & Teichmann, S. A. Evolution of protein complexes by duplication of homomeric interactions. Genome Biol.8, R51 (2007). 10.1186/gb-2007-8-4-r51 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mallik, S., Tawfik, D. S. & Levy, E. D. How gene duplication diversifies the landscape of protein oligomeric state and function. Curr. Opin. Genet. Dev.76, 101966 (2022). 10.1016/j.gde.2022.101966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Szklarczyk, R., Huynen, M. A. & Snel, B. Complex fate of paralogs. BMC Evol. Biol.8, 337 (2008). 10.1186/1471-2148-8-337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mallik, S. & Tawfik, D. S. Determining the interaction status and evolutionary fate of duplicated homomeric proteins. PLoS Comput. Biol.16, e1008145 (2020). 10.1371/journal.pcbi.1008145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kuzmin, E., Taylor, J. S. & Boone, C. Retention of duplicated genes in evolution. Trends Genet.38, 59–72 (2022). 10.1016/j.tig.2021.06.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mura, C., Randolph, P. S., Patterson, J. & Cozen, A. E. Archaeal and eukaryotic homologs of Hfq: A structural and evolutionary perspective on Sm function. RNA Biol.10, 636–651 (2013). 10.4161/rna.24538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Scofield, D. G. & Lynch, M. Evolutionary diversification of the Sm family of RNA-associated proteins. Mol. Biol. Evol.25, 2255–2267 (2008). 10.1093/molbev/msn175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhou, M. et al. Mass spectrometry reveals modularity and a complete subunit interaction map of the eukaryotic translation factor eIF3. Proc. Natl Acad. Sci. USA105, 18139–18144 (2008). 10.1073/pnas.0801313105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sun, C. et al. Functional reconstitution of human eukaryotic translation initiation factor 3 (eIF3). Proc. Natl Acad. Sci. USA108, 20473–20478 (2011). 10.1073/pnas.1116821108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Smith, M. D. et al. Assembly of eIF3 mediated by mutually dependent subunit insertion. Structure24, 886–896 (2016). 10.1016/j.str.2016.02.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Le Tallec, B. et al. 20S proteasome assembly is orchestrated by two distinct pairs of chaperones in yeast and in mammals. Mol. Cell27, 660–674 (2007). 10.1016/j.molcel.2007.06.025 [DOI] [PubMed] [Google Scholar]
- 12.Makhnevych, T. & Houry, W. A. The role of Hsp90 in protein complex assembly. Biochim. Biophys. Acta1823, 674–682 (2012). 10.1016/j.bbamcr.2011.09.001 [DOI] [PubMed] [Google Scholar]
- 13.Juszkiewicz, S. & Hegde, R. S. Quality control of orphaned proteins. Mol. Cell71, 443–457 (2018). 10.1016/j.molcel.2018.07.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dill, K. A. & Chan, H. S. From Levinthal to pathways to funnels. Nat. Struct. Biol.4, 10–19 (1997). 10.1038/nsb0197-10 [DOI] [PubMed] [Google Scholar]
- 15.Marsh, J. A. et al. Protein complexes are under evolutionary selection to assemble via ordered pathways. Cell153, 461–470 (2013). 10.1016/j.cell.2013.02.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Padovani, C., Jevtic, P. & Rape, M. Quality control of protein complex composition. Mol. Cell82, 1439–1450 (2022). 10.1016/j.molcel.2022.02.029 [DOI] [PubMed] [Google Scholar]
- 17.Pla-Prats, C. & Thomä, N. H. Quality control of protein complex assembly by the ubiquitin-proteasome system. Trends Cell Biol.32, 696–706 (2022). 10.1016/j.tcb.2022.02.005 [DOI] [PubMed] [Google Scholar]
- 18.Yen, H. C., Xu, Q., Chou, D. M., Zhao, Z. & Elledge, S. J. Global protein stability profiling in mammalian cells. Science322, 918–923 (2008). 10.1126/science.1160489 [DOI] [PubMed] [Google Scholar]
- 19.McShane, E. et al. Kinetic analysis of protein stability reveals age-dependent degradation. Cell167, 803–815.e21 (2016). 10.1016/j.cell.2016.09.015 [DOI] [PubMed] [Google Scholar]
- 20.Fraser, C. S. et al. The j-subunit of human translation initiation factor eIF3 is required for the stable binding of eIF3 and its subcomplexes to 40 S ribosomal subunits in vitro. J. Biol. Chem.279, 8946–8956 (2004). 10.1074/jbc.M312745200 [DOI] [PubMed] [Google Scholar]
- 21.Pick, E., Hofmann, K. & Glickman, M. H. PCI complexes: beyond the proteasome, CSN, and eIF3 Troika. Mol. Cell35, 260–264 (2009). 10.1016/j.molcel.2009.07.009 [DOI] [PubMed] [Google Scholar]
- 22.ElAntak, L., Tzakos, A. G., Locker, N. & Lukavsky, P. J. Structure of eIF3b RNA recognition motif and its interaction with eIF3j: structural insights into the recruitment of eIF3b to the 40 S ribosomal subunit. J. Biol. Chem.282, 8165–8174 (2007). 10.1074/jbc.M610860200 [DOI] [PubMed] [Google Scholar]
- 23.Siridechadilok, B., Fraser, C. S., Hall, R. J., Doudna, J. A. & Nogales, E. Structural roles for human translation factor eIF3 in initiation of protein synthesis. Science310, 1513–1515 (2005). 10.1126/science.1118977 [DOI] [PubMed] [Google Scholar]
- 24.Wagner, S., Herrmannová, A., Šikrová, D. & Valášek, L. S. Human eIF3b and eIF3a serve as the nucleation core for the assembly of eIF3 into two interconnected modules: the yeast-like core and the octamer. Nucleic Acids Res.44, 10772–10788 (2016). 10.1093/nar/gkw972 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hofmann, K. & Bucher, P. The PCI domain: a common theme in three multiprotein complexes. Trends Biochem. Sci.23, 204–205 (1998). 10.1016/S0968-0004(98)01217-1 [DOI] [PubMed] [Google Scholar]
- 26.Enchev, R. I., Schreiber, A., Beuron, F. & Morris, E. P. Structural insights into the COP9 signalosome and its common architecture with the 26S proteasome lid and eIF3. Structure18, 518–527 (2010). 10.1016/j.str.2010.02.008 [DOI] [PubMed] [Google Scholar]
- 27.Rezende, A. M. et al. The translation initiation complex eIF3 in trypanosomatids and other pathogenic excavates-identification of conserved and divergent features based on orthologue analysis. BMC Genom.15, 1175 (2014). 10.1186/1471-2164-15-1175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rozen, S. et al. CSNAP is a stoichiometric subunit of the COP9 signalosome. Cell Rep.13, 585–598 (2015). 10.1016/j.celrep.2015.09.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kim, T., Hofmann, K., von Arnim, A. G. & Chamovitz, D. A. PCI complexes: pretty complex interactions in diverse signaling pathways. Trends Plant Sci.6, 379–386 (2001). 10.1016/S1360-1385(01)02015-5 [DOI] [PubMed] [Google Scholar]
- 30.Dubiel, D., Rockel, B., Naumann, M. & Dubiel, W. Diversity of COP9 signalosome structures and functional consequences. FEBS Lett.589, 2507–2513 (2015). 10.1016/j.febslet.2015.06.007 [DOI] [PubMed] [Google Scholar]
- 31.Sharon, M. et al. Symmetrical modularity of the COP9 signalosome complex suggests its multifunctionality. Structure17, 31–40 (2009). 10.1016/j.str.2008.10.012 [DOI] [PubMed] [Google Scholar]
- 32.Sharon, M., Taverner, T., Ambroggio, X. I., Deshaies, R. J. & Robinson, C. V. Structural organization of the 19S proteasome lid: insights from MS of intact complexes. PLoS Biol.4, e267 (2006). 10.1371/journal.pbio.0040267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bai, M. et al. In-depth analysis of the lid subunits assembly mechanism in mammals. Biomolecules9, 213 (2019). [DOI] [PMC free article] [PubMed]
- 34.Kapelari, B. et al. Electron microscopy and subunit-subunit interaction studies reveal a first architecture of COP9 signalosome. J. Mol. Biol.300, 1169–1178 (2000). 10.1006/jmbi.2000.3912 [DOI] [PubMed] [Google Scholar]
- 35.Tsuge, T., Matsui, M. & Wei, N. The subunit 1 of the COP9 signalosome suppresses gene expression through its N-terminal domain and incorporates into the complex through the PCI domain. J. Mol. Biol.305, 1–9 (2001). 10.1006/jmbi.2000.4288 [DOI] [PubMed] [Google Scholar]
- 36.Kotiguda, G. G. et al. The organization of a CSN5-containing subcomplex of the COP9 signalosome. J. Biol. Chem.287, 42031–42041 (2012). 10.1074/jbc.M112.387977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Serino, G. et al. Characterization of the last subunit of the arabidopsis COP9 signalosome: implications for the overall structure and origin of the complex. Plant cell15, 719–731 (2003). 10.1105/tpc.009092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tomko, R. J. Jr. & Hochstrasser, M. Incorporation of the Rpn12 subunit couples completion of proteasome regulatory particle lid assembly to lid-base joining. Mol. Cell44, 907–917 (2011). 10.1016/j.molcel.2011.11.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.He, W. & Parker, R. Functions of Lsm proteins in mRNA degradation and splicing. Curr. Opin. Cell Biol.12, 346–350 (2000). 10.1016/S0955-0674(00)00098-3 [DOI] [PubMed] [Google Scholar]
- 40.Veretnik, S., Wills, C., Youkharibache, P., Valas, R. E. & Bourne, P. E. Sm/Lsm genes provide a glimpse into the early evolution of the spliceosome. PLoS Comput. Biol.5, e1000315 (2009). 10.1371/journal.pcbi.1000315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lehner, B. & Sanderson, C. M. A protein interaction framework for human mRNA degradation. Genome Res.14, 1315–1323 (2004). 10.1101/gr.2122004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rual, J. F. et al. Towards a proteome-scale map of the human protein-protein interaction network. Nature437, 1173–1178 (2005). 10.1038/nature04209 [DOI] [PubMed] [Google Scholar]
- 43.Raker, V. A., Plessel, G. & Luhrmann, R. The snRNP core assembly pathway: identification of stable core protein heteromeric complexes and an snRNP subcore particle in vitro. EMBO J.15, 2256–2269 (1996). 10.1002/j.1460-2075.1996.tb00579.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Onischenko, E. et al. Maturation kinetics of a multiprotein complex revealed by metabolic labeling. Cell183, 1785–1800.e26 (2020). 10.1016/j.cell.2020.11.001 [DOI] [PubMed] [Google Scholar]
- 45.Mashtalir, N. et al. Modular organization and assembly of SWI/SNF family chromatin remodeling complexes. Cell175, 1272–1288.e20 (2018). 10.1016/j.cell.2018.09.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kamenova, I. et al. Co-translational assembly of mammalian nuclear multisubunit complexes. Nat. Commun.10, 1740 (2019). 10.1038/s41467-019-09749-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Panasenko, O. O. et al. Co-translational assembly of proteasome subunits in NOT1-containing assemblysomes. Nat. Struct. Mol. Biol.26, 110–120 (2019). 10.1038/s41594-018-0179-5 [DOI] [PubMed] [Google Scholar]
- 48.Mintseris, J. & Weng, Z. Structure, function, and evolution of transient and obligate protein-protein interactions. Proc. Natl Acad. Sci. USA102, 10930–10935 (2005). 10.1073/pnas.0502667102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Matalon, O., Horovitz, A. & Levy, E. D. Different subunits belonging to the same protein complex often exhibit discordant expression levels and evolutionary properties. Curr. Opin. Struct. Biol.26, 113–120 (2014). 10.1016/j.sbi.2014.06.001 [DOI] [PubMed] [Google Scholar]
- 50.Meister, C., Gulko, M. K., Köhler, A. M. & Braus, G. H. The devil is in the details: comparison between COP9 signalosome (CSN) and the LID of the 26S proteasome. Curr. Genet.62, 129–136 (2016). 10.1007/s00294-015-0525-7 [DOI] [PubMed] [Google Scholar]
- 51.Echalier, A. et al. Insights into the regulation of the human COP9 signalosome catalytic subunit, CSN5/Jab1. Proc. Natl Acad. Sci. USA110, 1273–1278 (2013). 10.1073/pnas.1209345110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhou, L. et al. Crystal structures of the Lsm complex bound to the 3’ end sequence of U6 small nuclear RNA. Nature506, 116–120 (2014). 10.1038/nature12803 [DOI] [PubMed] [Google Scholar]
- 53.Lai, H. Y., Yu, Y. H., Jhou, Y. T., Liao, C. W. & Leu, J. Y. Multiple intermolecular interactions facilitate rapid evolution of essential genes. Nat. Ecol. Evol.7, 745–755 (2023). 10.1038/s41559-023-02029-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Yanagitani, K., Juszkiewicz, S. & Hegde, R. S. UBE2O is a quality control factor for orphans of multiprotein complexes. Science357, 472–475 (2017). 10.1126/science.aan0178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sung, M. K. et al. A conserved quality-control pathway that mediates degradation of unassembled ribosomal proteins. eLife5, e19105 (2016). [DOI] [PMC free article] [PubMed]
- 56.Pla-Prats, C., Cavadini, S., Kempf, G. & Thomä, N. H. Recognition of the CCT5 di-Glu degron by CRL4(DCAF12) is dependent on TRiC assembly. EMBO J.42, e112253 (2023). 10.15252/embj.2022112253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Pereira-Leal, J. B. & Teichmann, S. A. Novel specificities emerge by stepwise duplication of functional modules. Genome Res.15, 552–559 (2005). 10.1101/gr.3102105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Marsh, J. A. & Teichmann, S. A. Structure, dynamics, assembly, and evolution of protein complexes. Annu. Rev. Biochem.84, 551–575 (2015). 10.1146/annurev-biochem-060614-034142 [DOI] [PubMed] [Google Scholar]
- 59.Jones, D. T., Taylor, W. R. & Thornton, J. M. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci.8, 275–282 (1992). [DOI] [PubMed] [Google Scholar]
- 60.Kumar, S., Stecher, G. & Tamura, K. MEGA7: molecular evolutionary genetics analysis version 7.0 for bigger datasets. Mol. Biol. Evol.33, 1870–1874 (2016). 10.1093/molbev/msw054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hsu, K.-L. & Yeang, C.-H. QCS (Quantifying Cooperative Stability): quantification of cooperative stabilization by model fitting to GPS data (v1.0.0). Zenodo10.5281/zenodo.11395487 (2024). [Google Scholar]
- 62.Hsu, K.-L. & Yeang, C.-H. RPCA: reconstruction of Protein Complex Assembly from Cooperative Stabilization Matrix (v1.0.0). Zenodo10.5281/zenodo.11396252 (2024). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The atomic coordinates used in this study are available in the Protein Data Bank (PDB) under accession codes 5L4K, 4D10, and 6YBD. All data generated in this study are provided in the Supplementary Information and Source Data files. Source data are provided with this paper.
The source codes for qualifying cooperative stabilization by mathematical modeling and reconstruction of protein complex assembly processes have been deposited in Zenodo61,62.