Dual sensitivity of sarcoplasmic/endoplasmic Ca²⁺-ATPase to cytosolic and endoplasmic reticulum Ca²⁺ as a mechanism of modulating cytosolic Ca²⁺ oscillations

Abstract

The effects of ER (endoplasmic reticulum) Ca²⁺ on cytosolic Ca²⁺ oscillations in pancreatic acinar cells were investigated using mathematical models of the Ca²⁺ oscillations. We first examined the mathematical model of SERCA (sarcoplasmic/endoplasmic reticulum Ca²⁺-ATPase) to reproduce the highly co-operative inhibitory effect of Ca²⁺ in the ER lumen on ER Ca²⁺ uptake in the acinar cells. The model predicts that luminal Ca²⁺ would most probably inhibit the conversion of the conformation state with luminal Ca²⁺-binding sites (E₂) into the conformation state with cytoplasmic Ca²⁺-binding sites (E₁). The SERCA model derived from this prediction showed dose–response relationships to cytosolic and luminal Ca²⁺ concentrations that were consistent with the experimental data from the acinar cells. According to a mathematical model of cytosolic Ca²⁺ oscillations based on the modified SERCA model, a small decrease in the concentration of endoplasmic reticulum Ca²⁺ (approx. 20% of the total) was sufficient to abolish the oscillations. When a single type of IP₃R (IP₃ receptor) was included in the model, store depletion decreased the spike frequency. However, the frequency became less sensitive to store depletion when we added another type of IP₃R with higher sensitivity to the concentration of free Ca²⁺ in the cytosol. Bifurcation analysis of the mathematical model showed that the loss of Ca²⁺ from the ER lumen decreased the sensitivity of cytosolic Ca²⁺ oscillations to IP₃ [Ins(1,4,5)P₃]. The addition of a high-affinity IP₃R did not alter this property, but significantly decreased the sensitivity of the spike frequency to IP₃. Our mathematical model demonstrates how luminal Ca²⁺, through its effect on Ca²⁺ uptake, can control cytosolic Ca²⁺ oscillations.

INTRODUCTION

Cytosolic Ca²⁺ oscillation is a widespread phenomenon, found in a variety of excitable and non-excitable cells. In excitable cells, periodic changes of the plasma membrane potential can drive cytosolic Ca²⁺ oscillations by stimulating voltage-dependent Ca²⁺ channels. On the other hand, oscillations in non-excitable cells are based on periodic release of Ca²⁺ from the intracellular Ca²⁺ store and Ca²⁺ uptake into the store. The release of Ca²⁺ from the internal stores, which are mainly in the ER (endoplasmic reticulum), is mediated by Ca²⁺ channels, such as IP₃Rs {IP₃ [Ins-(1,4,5)P₃] receptors} and RyRs (ryanodine receptors), in the ER membrane. Opening of the channels is regulated by cytosolic second messengers [e.g. IP₃, cADPR (cADP-ribose) and NAADP (nicotinic acid–adenine dinucleotide phosphate)]. The uptake of cytosolic Ca²⁺ into the ER, which restores [Ca²⁺]_c (concentration of free Ca²⁺ in the cytosol) to the resting level, is mediated by Ca²⁺-ATPases located in the ER membrane [SERCAs (sarcoplasmic/endoplasmic reticulum Ca²⁺-ATPases)].

Ca²⁺-transport mechanisms in pancreatic acinar cells have been well characterized, and the kinetics of both cytosolic and ER Ca²⁺ have been investigated in detail by the combined use of ER-trapped fluorescent calcium indicators [1] and measurement of Ca²⁺-dependent Cl⁻ current [2]. We have demonstrated previously that an incubation of acinar cells in a Ca²⁺-free medium during Ca²⁺ oscillations caused a continuous decrease in [Ca²⁺]_ER (concentration of free Ca²⁺ in the ER), accompanied by a reduction of the amplitude of Ca²⁺ oscillations [3]. Ca²⁺ lost from the ER to the cytosol is excluded by PMCA (plasma membrane Ca²⁺-ATPase), since there is rapid activation of this pump during each cytosolic Ca²⁺ spike, as demonstrated for this cell type [4]. In the acinar cells, a decrease of spike amplitude was seen as soon as store depletion became detectable. A relatively small decrease in [Ca²⁺]_ER [compared with the store depletion evoked by supramaximal doses of ACh (acetylcholine)] was sufficient to abolish cytosolic Ca²⁺ oscillations completely. Such phenomena imply a robust effect of Ca²⁺ in the ER lumen on cytosolic Ca²⁺ oscillations.

One of the possible mechanisms by which [Ca²⁺]_ER affects cytosolic Ca²⁺ oscillations is inhibition of Ca²⁺ uptake by ER Ca²⁺. We have demonstrated previously that in intact acinar cells, an increase in [Ca²⁺]_ER suppressed ER Ca²⁺ uptake [2]. The inhibition by high [Ca²⁺]_ER was highly co-operative (Hill coefficient >4) and the uptake rate was halved when [Ca²⁺]_ER was increased by approx. 50 μM. Such high co-operativity has also been shown in HL-60 cells [5] and dorsal root ganglia neurons [6]. High sensitivity of Ca²⁺ uptake to [Ca²⁺]_ER would allow modulation of Ca²⁺ oscillations by a relatively small decrease of [Ca²⁺] in the store. The major subtype of SERCA in both pancreatic acinar cells and HL-60 cells is SERCA2b [7,8]. The activity of SERCA2b is known to be regulated by direct interaction with ER resident chaperones, including calreticulin [9,10], calnexin [11] and ERp57 [12]. The interaction between SERCA2b and the ER chaperones is sensitive to the condition of the Ca²⁺ store, suggesting that SERCA2b may respond to a change of the luminal [Ca²⁺] by using ER chaperones as ER Ca²⁺ sensors. These data indicate that the luminal sensitivity of Ca²⁺ uptake in the acinar cells and HL-60 cells reflects the property of SERCA2b.

A variety of mathematical models are available to analyse qualitative and quantitative properties of Ca²⁺ oscillations [13]. Although the stimulatory effect of cytosolic Ca²⁺ on Ca²⁺ uptake was included in most of these models, the inhibitory effect of luminal Ca²⁺ has rarely been taken into account. On the other hand, mathematical models have been developed to study the activity of SERCAs in isolated microsomes [14,15], and could reproduce the effect of luminal Ca²⁺ on the turnover rate of the pump, although the effects of luminal Ca²⁺ in these models were quantitatively different from what has been observed in pancreatic acinar cells. However, it should be possible to modify these models using experimental data from the acinar cells to obtain a mathematical model of ER Ca²⁺ uptake that can be used in Ca²⁺ oscillation models for pancreatic acinar cells.

In the present study, we first developed a mathematical model of SERCA2b to reproduce the effect of luminal Ca²⁺ on ER Ca²⁺ uptake that was seen in the pancreatic acinar cell. Then the SERCA2b model was incorporated into a computational model of cytosolic Ca²⁺ oscillations in the acinar cells. An attempt was made to reproduce the observed effect of luminal Ca²⁺ on the cytosolic Ca²⁺ oscillations by comparing the kinetics of both [Ca²⁺]_c and [Ca²⁺]_ER with the experimental data from the acinar cells. Thereafter bifurcation analysis was utilized to analyse the effects of luminal Ca²⁺ on the properties of cytosolic Ca²⁺ oscillations.

METHODS

Mathematical models were designed using Maple (Maplesoft, Ontario, Canada) and implemented in SIMULINK (The Mathworks, Natick, MA, U.S.A.). The flux control coefficients in the kinetic model of SERCA were calculated using GEPASI [16]. All the bifurcation analyses were carried out using XPPAUT [17].

RESULTS

Kinetic models of SERCAs

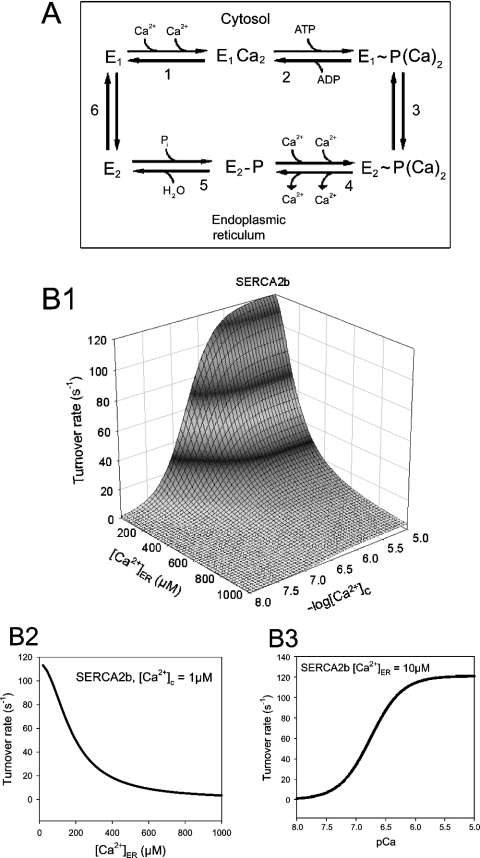
The kinetic models for the reaction cycle of SERCAs were based on the model developed by Dode et al. [14]. In this model, the reversible catalytic cycle was composed of the following reactions (see Figure 1A): (1) binding of two Ca²⁺ to the SERCA pump from the cytoplasmic side of the ER membrane, (2) phosphorylation of the pump by ATP, (3) conversion from the E₁ (cytoplasmic high-affinity Ca²⁺-binding sites) into the E₂ (luminal low-affinity Ca²⁺-binding sites) conformation state and translocation of Ca²⁺ from the cytoplasmic side to the luminal side of the ER membrane, (4) release of Ca²⁺ into the ER lumen, (5) dephosphorylation of the pump and (6) conversion from the E₂ into the E₁ conformation state. All the reactions are described as first-order reactions (except for the binding of Ca²⁺).

Figure 1. Reaction cycle and dose–response of turnover rate to cytosolic and luminal Ca²⁺ in SERCA2b model.

(A) Reaction cycle of SERCA. Clockwise direction of a reaction in the cycle is defined as a ‘forward’ reaction. The numbers shown with the reactions are used in the text in order to refer to individual reactions. (B1) Estimated dose–response of the turnover rate of SERCA2b against [Ca²⁺]_c and [Ca²⁺]_ER. Note that [Ca²⁺]_c is expressed on a logarithmic scale and [Ca²⁺]_ER is on a linear scale (this representation is chosen for visual convenience). (B2) Turnover rate at different [Ca²⁺]_ER when [Ca²⁺]_c=1 μM. (B3) Turnover rate at different [Ca²⁺]_c when [Ca²⁺]_ER=10 μM.

Since the model of Dode et al. [14] was based on experimental data relating to SERCA1a, we needed to adjust the parameters to reproduce the property of SERCA2b in pancreatic acinar cells. It has been shown that SERCA2b sensitivity to cytosolic Ca²⁺ is higher than for SERCA1a {K_a,0.5 (half maximum activation by cytosolic Ca²⁺)=0.27 μM and 0.44 μM respectively, when expressed in COS cells [18]}. Therefore we increased the affinity for cytosolic Ca²⁺ in reaction 1 from 1.79 μM to 1.1 μM. The data from HL-60 and pancreatic acinar cells suggest that luminal Ca²⁺ can inhibit ER Ca²⁺ uptake, both at high and low cytosolic Ca²⁺ concentrations [2,5]. On the other hand, the data from Dode et al. [14] indicate that the effect of luminal Ca²⁺ on SERCA1a is much more predominant at high [Ca²⁺]_c. This difference in the relationship between cytoplasmic Ca²⁺ and luminal Ca²⁺ indicates that SERCA2b responds to luminal Ca²⁺ using a mechanism that is distinct from that employed by SERCA1a.

We hypothesized that there is another reaction in the cycle that is affected by luminal Ca²⁺. The reaction should affect the turnover rate to a similar degree at both low and high [Ca²⁺]_c in order to be consistent with the above observation in the acinar cell. The strength of the effect resulting from a change of the rate constant of a local reaction v_i (e.g. an individual reaction in the catalytic cycle of SERCA) on the global flux J (e.g. the turnover rate of the pump) can be quantified as

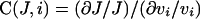where (∂J/J) is the fractional change of the global flux, (∂v_i/v_i) is the fractional change of the rate constant of the local reaction and C(J,i) is the ratio of the fractional changes, called flux control coefficient [19]. By calculating the control coefficients of the individual steps in the catalytic cycle of SERCA, we can determine which step has the greatest potential to influence the overall turnover rate. It has been shown that, when a parameter (such as [Ca²⁺]_ER) acts on the global flux through its direct influence on a local reaction, the strength of the response of the global flux to the parameter (or response coefficient) is determined by the control coefficient of the local reaction multiplied by the strength of the response of the local reaction to the parameter (or elasticity) [19]. Therefore a sufficient response of the global flux to the parameter can be achieved only at a reaction step that has a sufficiently large flux control coefficient.

We assumed that the luminal Ca²⁺ could only affect the E₂ conformation and, therefore, only the control coefficients for the reactions that involve E₂ were calculated (Table 1). In the majority of cases, forward reactions had larger control coefficients than backward reactions, which would be expected if the forward reactions were dominant at the steady state. A cytosolic Ca²⁺ rise from 100 nM to 10 μM increased the control coefficients (except for reaction 6) approx. 10-fold, which may explain why luminal Ca²⁺ has a larger effect at higher concentrations of cytosolic Ca²⁺. The forward direction of reaction 6 (E₂→E₁ conversion) had the highest control coefficient at a cytosolic Ca²⁺ concentration of 100 nM among the reactions in the catalytic cycle, which was relatively insensitive to cytosolic Ca²⁺ changes. This suggests that the E₂→E₁ conversion is most likely to be responsible for the sensitivity of ER Ca²⁺ uptake to luminal Ca²⁺ in HL-60 and pancreatic acinar cells.

Table 1. Flux control coefficients of turnover rate of SERCA1a model.

[Ca²⁺]_ER was fixed at 100 μM.

	Flux control coefficients (forward/backward)
Reaction	[Ca2+]c=100 nM	[Ca2+]c=10 μM
3	3.15×10−2/−1.67×10−3	2.11×10−1/−1.11×10−2
4	2.14×10−2/−2.23×10−3	1.43×10−1/−1.46×10−2
5	3.86×10−2/−9.73×10−4	2.53×10−1/−4.75×10−4
6	4.59×10−1/−4.30×10−1	2.24×10−1/−2.56×10−2

For estimation of the parameters, we assumed that SERCA1a and SERCA2b would show the same property (except for the sensitivity to cytosolic Ca²⁺) when the store was empty. On the other hand, an increase in [Ca²⁺]_ER would inhibit the E₂→E₁ conversion with a Hill coefficient of 2. The dose-dependency of the turnover rate against [Ca²⁺]_ER at [Ca²⁺]_c=100 nM was fitted to the data from [2] to obtain the apparent affinity of the pump to luminal Ca²⁺. This gave us the SERCA2b kinetic model, whose estimated dose–response curves against [Ca²⁺]_c and [Ca²⁺]_ER are shown in Figure 1(B1). The rate constants of the reactions are shown in Table 2.

Table 2. Rate constants for the kinetic model of SERCA2b.

Reaction numbers refer to Figure 1. c, [Ca²⁺]_c; e, [Ca²⁺]_ER.

	Rate constants (s−1)
Reaction	Forward	Backward
1	5000×c1.65/(c1.65+1.11.65)	10
2	700	5
3	600	50
4	1000	13580×e2/(e2+15502)
5	500	1
6	4.64×106/(e2+87.42)	600

Figure 1(B1) shows that the turnover rate of SERCA2b was inhibited strongly by luminal Ca²⁺ both at low and high cytosolic [Ca²⁺], which is in agreement with the experiments performed in pancreatic acinar and HL-60 cells. With [Ca²⁺]_c=1 μM, the turnover rate was 114.3 s⁻¹ at [Ca²⁺]_ER=10 μM and 3.28 s⁻¹ at [Ca²⁺]_ER=1 mM, and K_i,0.5 (half maximum inhibition by luminal Ca²⁺)=176 μM (Figure 1B2). The estimated K_i,0.5 was close to the resting [Ca²⁺]_ER in the pancreatic acinar cell (approx. 150 μM [20]). The K_a,0.5 was 0.18 μM (Figure 1B3, [Ca²⁺]_ER=10 μM).

Effect of [Ca²⁺]_ER and SERCA activity on cytosolic Ca²⁺ oscillations in the whole-cell model

We constructed a ‘whole-cell model’ for Ca²⁺ oscillations in pancreatic acinar cells. This whole-cell model was composed of two compartments: the cytoplasm and the ER. The model included the following transport mechanisms: (i) Ca²⁺ release from the store via IP₃Rs, (ii) Ca²⁺ leak from the store, (iii) Ca²⁺ extrusion by PMCA, (iv) Ca²⁺ uptake by SERCA2b. The details of the transport mechanisms are given in the Appendix.

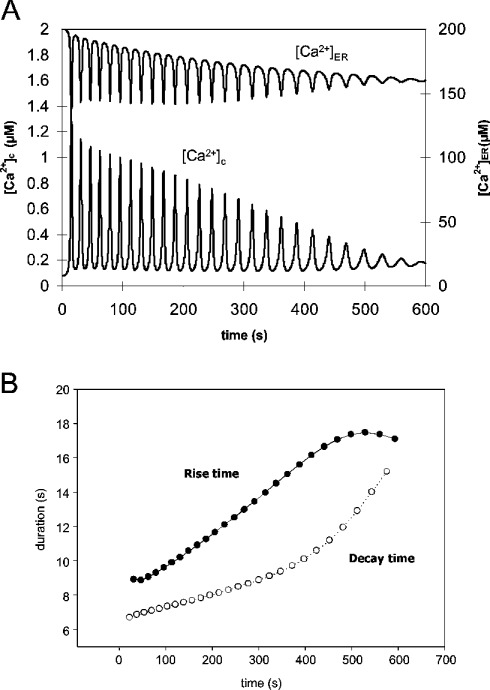
Figure 2(A) shows Ca²⁺ spike changes during continuous Ca²⁺ extrusion without compensation by Ca²⁺ influx through the plasma membrane. This would correspond to the experimental observation of cytosolic Ca²⁺ oscillations with no external Ca²⁺. Ca²⁺ oscillations were initiated by an increase of [IP₃] from 0 to 0.254 μM at t=0. In the model, the amplitudes of the cytosolic Ca²⁺ responses decreased as [Ca²⁺]_ER decreased, and oscillations eventually disappeared at [Ca²⁺]_ER=160 μM. The periods between the spikes gradually increased as the store depletion progressed. We could see an increase in both rise time (time from the base to the peak of the next spike, 8.9 s in the first spike and 17.1 s in the last spike), and decay time (the spike period minus the rise time, 6.7 s in the first spike and 15.2 s in the last) (Figure 2B).

Figure 2. Simulation of cytosolic Ca²⁺ oscillations in a pancreatic acinar cell during gradual store depletion.

The gradual depletion of the Ca²⁺ store in the model was achieved by the extrusion of cytosolic Ca²⁺ by PMCA and the lack of compensating Ca²⁺ influx through the plasma membrane. (A) [Ca²⁺]_c (lower trace) and [Ca²⁺]_ER (upper trace) during the simulation. At the resting condition [Ca²⁺]_c=0.08 μM and [Ca²⁺]_ER=200 μM. The cell was stimulated by increasing [IP₃] from 0 to 0.254 μM. (B) The rise time (•) and the decay time (○) of cytosolic Ca²⁺ spikes during the simulation.

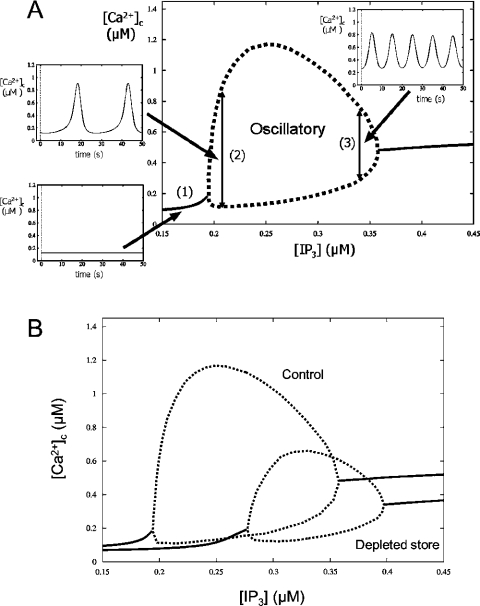
In order to learn more about the mechanism of spike modulation by luminal Ca²⁺, we carried out bifurcation analysis. Figure 3(A) shows a typical shape of a bifurcation curve for IP₃-induced Ca²⁺ oscillations. The diagram displays [Ca²⁺]_c at different [IP₃]. At low and high [IP₃], [Ca²⁺]_c does not oscillate, and the diagram shows the steady state [Ca²⁺]_c (solid lines). At an intermediate [IP₃], [Ca²⁺]_c oscillates and the diagram shows the maximum (peak) and the minimum (baseline) [Ca²⁺]_c (broken lines). Therefore this diagram is showing the range of [IP₃] which gives oscillations as well as the range of [Ca²⁺]_c when it is oscillatory.

Figure 3. Bifurcation analysis of the modifications of Ca²⁺ oscillations by store depletion.

(A) A typical bifurcation diagram of [Ca²⁺]_c against [IP₃] in IP₃-induced Ca²⁺ oscillations is presented. Steady-state solutions (solid line) and the maxima and the minima of [Ca²⁺]_c during Ca²⁺ oscillations (broken line) are shown. [Ca²⁺]_c will be stationary when [IP₃] is outside the ‘oscillatory’ area (1). [Ca²⁺]_c oscillates when [IP₃] is in the ‘oscillatory’ area, which is encompassed by the broken line (2 and 3). Oscillation frequency is faster at higher [IP₃] (3) than lower [IP₃] (2). (B) Bifurcation diagrams of [Ca²⁺]_c against [IP₃] in the whole-cell model. Steady-state solutions (solid line), the maxima and the minima of [Ca²⁺]_c during Ca²⁺ oscillations (broken line) are shown. S=200 μM in control and S=160 μM in depleted store.

Figure 3(B) shows the bifurcation diagram of cytosolic Ca²⁺ in the whole-cell model with [IP₃] as a bifurcation parameter. A decrease of S (resting [Ca²⁺]_ER at [Ca²⁺]_c=0.08 μM) from 200 μM to 160 μM decreased the maximum oscillation amplitude of the oscillations by 0.515 μM (from 1.05 μM to 0.535 μM), but did not abolish the oscillations. It also raised both the minimum and maximum [IP₃] for Ca²⁺ oscillations from [IP₃]_min=0.196 μM, [IP₃]_max=0.358 μM (S=200 μM) to [IP₃]_min=0.278 μM, [IP₃]_max=0.397 μM (S=160 μM). This shift of the bifurcation curve towards higher [IP₃] can be interpreted as ‘desensitization’ of Ca²⁺ response to IP₃, because a higher [IP₃] will be required to obtain Ca²⁺ oscillations when the store is depleted.

Multiple subtypes of IP₃R may decrease the sensitivity of spike frequency to store depletion

Although store depletion has normally been observed to decrease both spike frequency and amplitudes, there are some cases with little frequency change, even when the spike amplitude was reduced strongly due to store depletion [3,4,21]. Since minor parameter modifications in our whole-cell model failed to reproduce such stability of spike frequency, we decided to incorporate an extra mechanism in the model: an additional subtype of the IP₃R. It has been shown that there are at least three distinct subtypes (types 1, 2 and 3) of IP₃R in mammalian cells, including pancreatic acinar cells [22,23]. The proportion of the IP₃R subtypes varies between cell types [23], and it has been suggested that changes in this proportion can affect cytosolic Ca²⁺ signals [24,25]. The properties of the IP₃R subtypes differ in many ways, including the sensitivity to activation by cytosolic Ca²⁺ [26,27] and IP₃ [25,28], inhibition by cytosolic Ca²⁺ [29,30], and susceptibility to phosphorylation by protein kinase A [31].

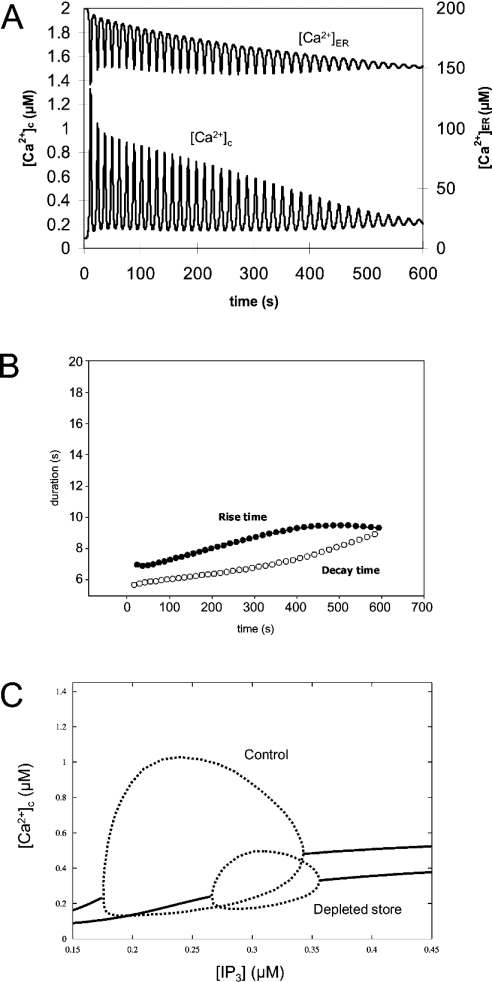
We included in our whole-cell model the sensitivity difference between the IP₃R subtypes to activation by cytosolic Ca²⁺ and that was sufficient to reproduce the behaviour of spike frequency when the store was depleted. It has been suggested that the type-3 IP₃R plays the major role in the generation of agonist-induced cytosolic Ca²⁺ oscillations in pancreatic acinar cells [31,32]. However, the type-2 IP₃R, which has a higher affinity for cytosolic Ca²⁺ than the type-3 IP₃R [25,27,29], could also contribute to Ca²⁺ oscillations. Significant levels of expression of the type-2 IP₃R subtype were observed in the pancreas [23,33], whereas the level of the type-1 IP₃R is reported to be low [23] and unlikely to contribute to the Ca²⁺ signalling in this cell type. In order to model the heterogeneous expressions of IP₃R subtypes qualitatively, we incorporated an IP₃R with higher affinity for cytosolic Ca²⁺ in the whole-cell model, in addition to the IP₃R used in the previous model. Figure 4(A) shows Ca²⁺ spike changes during continuous Ca²⁺ extrusion without Ca²⁺ influx through the plasma membrane. As before, store depletion decreased the spike amplitude and abolished spiking at [Ca²⁺]_ER of approx. 150 μM, which was slightly lower than in the whole-cell model with a single type of IP₃R. Rise time (from 6.5 s to 10.7 s) and decay time (from 5.7 s to 9.0 s) (Figure 4B) also increased, but the magnitude of the changes was smaller than in the simulation based on a single IP₃R. This effect of a high-affinity IP₃R on the stability of spike frequency was seen only when its contribution to Ca²⁺ release was relatively small (20% of total release in the example shown in Figure 4A) and having a larger proportion of high-affinity IP₃R inhibited Ca²⁺ oscillations (results not shown).

Figure 4. Simulation of cytosolic Ca²⁺ oscillations in a pancreatic acinar cell during gradual store depletion when two subtypes of IP₃R are present.

The store was depleted gradually in the same way as in Figure 2. (A) [Ca²⁺]_c (lower trace) and [Ca²⁺]_ER (upper trace) in the whole-cell model with two subtypes of IP₃R. In this simulation, it was assumed that the ‘high-affinity’ IP₃R subtype had three times higher affinity to cytosolic Ca²⁺ than the subtype used for the simulation in Figure 2. (B) The rise time (•) and the decay time (○) of Ca²⁺ spikes during the simulation. (C) Bifurcation diagrams of [Ca²⁺]_c against [IP₃] in the whole-cell model. Steady-state solutions (solid line), the maxima and the minima of periodic orbits (broken line) are shown. S=200 μM in control and S=160 μM in depleted store.

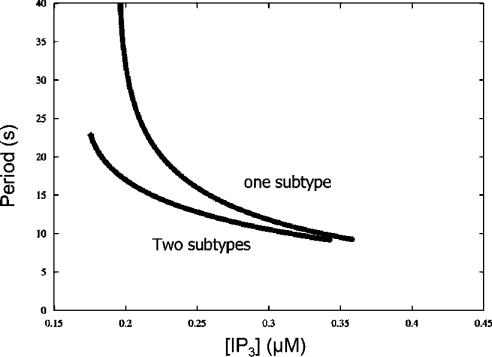
Figure 4(C) shows the bifurcation diagram of cytosolic Ca²⁺. The decrease of S (resting [Ca²⁺]_ER at [Ca²⁺]_c=0.08 μM) from 200 μM to 160 μM decreased the maximum amplitudes of the oscillations by 0.571 μM (from 0.897 to 0.326 μM) and shifted the curve to higher [IP₃] ([IP₃]_min=0.176 μM, [IP₃]_max=0.342 μM with S=200 μM; [IP₃]_min=0.266 μM, [IP₃]_max=0.356 μM with S=160 μM). The extent of the amplitude changes of the oscillations and the curve shift were comparable with that of the whole-cell model with a single IP₃R subtype. This suggests that the co-expression of two IP₃R subtypes did not significantly alter the basic property of the inhibition of Ca²⁺ oscillations by store depletion. However, co-expression seems to affect the sensitivity of the Ca²⁺ spike frequency to [IP₃]. Figure 5 shows the spike period at different [IP₃]. When only a single IP₃R was expressed, a decrease in [IP₃] increased the spike period rapidly and went beyond 40 s at the lowest possible [IP₃] for sustainable Ca²⁺ oscillations. The spike period in the model with two IP₃R subtypes was similar compared with the single IP₃R system when [IP₃] was high, but was much smaller when [IP₃] was low.

Figure 5. Relationship between [IP₃] and oscillation periods when one or two IP₃R subtypes were present.

The traces compare the relationship between the period of cytosolic Ca²⁺ oscillations and [IP₃] in the mathematical models with one and two subtypes of IP₃R.

DISCUSSION

In the present study, we have developed a mathematical model for SERCA2b, and analysed the effect of the ER luminal Ca²⁺ on cytosolic Ca²⁺ oscillations. Using data for the relationship between [Ca²⁺]_ER and ER Ca²⁺ uptake rate in intact pancreatic acinar cells [2], as well as kinetic data from isolated ER vesicles [14,18], we have produced a portrait of the dual dependence of SERCA2b activity on cytosolic and ER Ca²⁺ as a three-dimensional plot. Our SERCA2b model is based on prediction from the flux control coefficients of the mathematical model for SERCA1a, indicating that there should be an additional effect of luminal Ca²⁺ on SERCA2b that inhibits ER Ca²⁺ uptake at low [Ca²⁺]_c. Our mathematical model of SERCA is more complete than previously published models [14,15], because it reproduces accurately not only the sensitivity of ER Ca²⁺ uptake to luminal Ca²⁺ in the acinar cells, but also modulation of this sensitivity by cytosolic Ca²⁺, which was not addressed by previous models. Khan et al. [34] showed that a [Ca²⁺]_ER rise increased the phosphorylation level of SERCAs by P_i. As a high concentration of P_i alone was not sufficient for maximum phosphorylation, they suggested that there must be binding sites for luminal Ca²⁺ in an unphosphorylated form. Therefore the effect of luminal Ca²⁺ would be shifting the equilibrium from E₁ to E₂ that was subsequently phosphorylated by P_i in their experiments. This is consistent with our hypothesis that the conversion from E₂ into E₁ is sensitive to luminal Ca²⁺.

In the computational models, store depletion decreased both the amplitude and frequency of cytosolic Ca²⁺ oscillations. In bifurcation diagrams, store depletion raised both the lower and higher thresholds of [IP₃] and ‘desensitized’ Ca²⁺ oscillations to [IP₃]. It has been shown experimentally that the spike frequency and amplitude are positively correlated to [IP₃] in pancreatic acinar cells [35] and, therefore, this shift of the bifurcation curve would decrease both amplitude and frequency of Ca²⁺ oscillations. It may appear to be counter-intuitive that an increase of ER Ca²⁺ uptake stimulated by store depletion prolonged the decay time, as these two events are often considered to be negatively correlated [36,37]. This puzzling relationship between ER Ca²⁺ uptake rate and decay time is associated with the decrease of spike amplitude caused by store depletion. When the amplitude is smaller, the feedback inhibition of Ca²⁺ release by cytosolic Ca²⁺ and the stimulation of Ca²⁺ uptake by store depletion will be weaker. In this situation, both rise and decay times will become longer. The pattern of change in spike shapes during gradual store depletion in our model is consistent with the change during ACh-induced slow Ca²⁺ spikes (period >100 s) in the pancreatic acinar cell with decreased external Ca²⁺ [4].

Spike amplitudes decrease with constant spike frequency during gradual store Ca²⁺ depletion. This was observed both with regard to ACh-induced fast oscillations [3] and CCK (cholecystokinin)-induced slow oscillations in pancreatic acinar cells [4,38]. In the mathematical model, it is possible to enhance the stability of spike frequency by co-expressing two subtypes of IP₃R. Therefore ACh and CCK may also be utilizing more than one release mechanism to generate Ca²⁺ oscillations. Pancreatic acinar cells have all three subtypes of IP₃R [23], as well as cADPR- [39] and NAADP- [40] mediated release mechanisms, which are strongly linked to the RyR [41].The interaction between these Ca²⁺-release mechanisms is crucial for the generation of the spatial and temporal patterns of Ca²⁺ oscillations [42]. Changes in CCK concentration have much smaller effects on the frequency of Ca²⁺ oscillations than on the amplitude [43], which supports our model in which the spike frequency is stable when Ca²⁺ oscillations are governed by multiple Ca²⁺-release mechanisms. However, if the frequency is controlled by oscillations in the concentration of the Ca²⁺-releasing second messenger, store depletion would also decrease amplitude without affecting its frequency [44]. Such a mechanism has not been demonstrated in pancreatic acinar cells, where application of second messengers through a patch pipette is sufficient to cause Ca²⁺ oscillations [42]. However, oscillations of the messenger concentration cannot be ruled out in some types of agonist-induced Ca²⁺ oscillations.

Since the rate of Ca²⁺ release from the ER should depend on the concentration gradient of Ca²⁺ across the ER membrane, [Ca²⁺]_ER can also affect Ca²⁺ release. Caroppo et al. [45] reported recently that the extent of IP₃-induced Ca²⁺ release, assessed by changes in the fluorescence of ER-trapped Mag-fura-2, was dependent on the luminal Ca²⁺ concentration. Falcke et al. [46] also showed that the overexpression of SERCA2b in Xenopus oocytes elevated [Ca²⁺]_ER and increased the amplitude of Ca²⁺ oscillations. By comparing the experimental results with mathematical models, Falcke et al. [46] suggested that the enhancement of Ca²⁺ release caused by the elevation of [Ca²⁺]_ER could offset the inhibitory effect of the increased Ca²⁺ uptake. Since only the IP₃R was sensitive to the luminal Ca²⁺ in their mathematical model, their results indicate that [Ca²⁺]_ER can modulate cytosolic Ca²⁺ oscillations in Xenopus oocytes through its effect on the IP₃R when the Ca²⁺ uptake is insensitive to luminal Ca²⁺. If the rate of Ca²⁺ release is proportional to the Ca²⁺ concentration gradient between the ER and the cytosol, [Ca²⁺]_ER would affect Ca²⁺ release much less than Ca²⁺ uptake, since [Ca²⁺]_ER can inhibit Ca²⁺ uptake with high co-operativity. Instead, luminal Ca²⁺ may alter the open probability of Ca²⁺-release channels in a non-linear fashion by direct or indirect interactions with the channels.

Recently, Sneyd et al. [47] examined the relationship between cytosolic Ca²⁺ oscillations and plasma membrane Ca²⁺ influx both theoretically and experimentally. They argued, using mathematical models, that the total cellular Ca²⁺ during steady state Ca²⁺ oscillations can be lower than in the resting condition and just above the threshold level to maintain cytosolic Ca²⁺ oscillations. In this condition, the loss of cellular Ca²⁺ during a Ca²⁺ spike due to Ca²⁺ extrusion by PMCA would need to be recovered by Ca²⁺ entry from the plasma membrane in the inter-spike period before the next Ca²⁺ rise. Therefore blockage of Ca²⁺ influx during steady-state Ca²⁺ oscillations will keep the total Ca²⁺ below the threshold and thereby acutely abolish the oscillations. They supported this concept by showing experimentally that blockade of Ca²⁺ influx and efflux by La³⁺ during carbachol-induced Ca²⁺ oscillations could acutely block cytosolic Ca²⁺ oscillations in HEK-293 cells. The difference between their model and ours, in which the removal of external Ca²⁺ reduced Ca²⁺ spike amplitudes only gradually, can be explained by the difference in the kinetics of the Ca²⁺ oscillations observed. While we modelled relatively fast Ca²⁺ oscillations (period of approx. 10 s), Sneyd et al. [47] examined slow Ca²⁺ oscillations (period of approx. 100 s) in which each Ca²⁺ spike will be accompanied by significant Ca²⁺ extrusion. Park et al. [3] observed small, but detectable, decreases of [Ca²⁺]_ER (approx. 20 μM) during each slow Ca²⁺ oscillation spike. In this case, the recovery of [Ca²⁺]_ER would depend on Ca²⁺ influx. No such changes in [Ca²⁺]_ER were observed during fast Ca²⁺ oscillation spikes. This suggests that, during the fast oscillations, the decrease in Ca²⁺ influx from the plasma membrane will not have an immediate effect on [Ca²⁺]_ER. Therefore the effect of blocking Ca²⁺ influx observed by Sneyd et al. [47] is not directly applicable to our model. Nevertheless, it is remarkable that a small decrease in [Ca²⁺]_ER, during an inter-spike period, can be sufficient to abolish Ca²⁺ oscillations, and this suggests that SERCA2b, known to be present in HEK-293 cells [48], may have a strong luminal sensitivity in this cell type, exactly as in the acinar cell.

Using computational models, we analysed the effect of changes in [Ca²⁺]_ER on Ca²⁺ oscillations in pancreatic acinar cells. Our SERCA2b model successfully reproduced the highly non-linear inhibition of ER Ca²⁺ uptake by luminal Ca²⁺ in this cell type and demonstrated the dual dependence of Ca²⁺ uptake on [Ca²⁺]_c and [Ca²⁺]_ER. In the whole-cell model, we observed a high sensitivity of the amplitude of cytosolic Ca²⁺ oscillations to changes in [Ca²⁺]_ER that was consistent with the experimental finding [3]. A whole-cell model with a single IP₃R type did not reproduce the ability of Ca²⁺ oscillations to retain the spike frequency when the amplitude was being reduced by store depletion. However, we have found that the inclusion of an additional subtype of IP₃R with higher affinity to cytosolic Ca²⁺ enhanced the stability of spike frequency during store depletion, suggesting a co-operative effect between the IP₃R subtypes. We expect that our mathematical models will advance understanding of the regulation of Ca²⁺ oscillations by cytosolic and luminal Ca²⁺.

APPENDIX

The structure of the whole-cell model

The differential equations for [Ca²⁺] in the cytosol (c) and the endoplasmic reticulum (e) were:

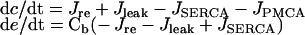where C_b is the ratio of the Ca²⁺-buffering capacities of the cytosol and the ER, J_re is the Ca²⁺-release rate from the IP₃R, J_leak is the Ca²⁺-leak rate from the ER, J_SERCA is the Ca²⁺-uptake rate by SERCA and J_PMCA is the Ca²⁺-extrusion rate by PMCA.

Ca²⁺ uptake by SERCA

Turnover rates were calculated from the kinetic models of SERCA2b and converted into uptake rate by multiplying them by conversion factors (V_p).

Ca²⁺ release from IP₃R

We used the mathematical model of Ca²⁺ waves in pancreatic acinar cells of Sneyd et al. [49] for the IP₃R model. This model assumed three states of the receptor (shut, open or inactive) where [IP₃] and [Ca²⁺]_c regulate the transit of the states. The differential equations for the probability of three states (x for shut, y for open and z for inactive state) were:

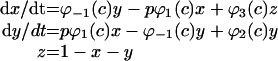where φ₁(c)=(k₁R₁+r₂c)/(R₁+c), φ₋₁(c)=(k₋₁+r₋₂)R₃/(c+R₃), φ₂(c)=(k₂R₃+r₄c)/(R₃+c), φ₃(c)=(k₃R₅+r₆c)/(R₅+c) and P(c)=y⁴.

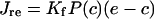where p is [IP₃], P(c) is open probability and K_f is the maximum Ca²⁺ release rate from the IP₃R.

Ca²⁺ extrusion by PMCA

The rate of Ca²⁺ extrusion from the cytosol by the plasma membrane in a pancreatic acinar cell was measured as described by Camello et al. [50] using the droplet technique. We derived an empirical relationship between cytosolic Ca²⁺ and the extrusion rate from the measurements:

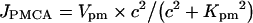where V_pm is the maximum extrusion rate and K_pm is the apparent affinity of PMCA to cytosolic Ca²⁺.

Ca²⁺ leak from the ER

It has been shown that the leak rate does not change significantly when [Ca²⁺]_ER is above 100 μM [2]. Therefore J_leak was set to be constant in the whole-cell model.

All the parameter values for the whole-cell model are summarized in Table A1. These values were used in all the simulations unless otherwise stated.

Table A1. Parameters for the whole-cell model of Ca²⁺ oscillations in pancreatic acinar cells.

Parameter	Value (unit)	Parameter	Value (unit)
Kf	54 (μM·s−1)	r6	0
k1	0	R1	6 (μM)
k−1	0.88 (s−1)	R3	50 (μM)
k2	0.53 (s−1)	R5	1.6 (μM)
k3	1 (s−1)	Jleak	0.2 (μM·s−1)
r2	100 (s−1)	Vp	0.0257 (μM)
r−2	0	Vpm	0.0028 (μM·s−1)
r4	20 (s−1)	Kpm	0.23 (μM)