Assessing structural uncertainty of biochemical regulatory networks in metabolic pathways under varying data quality

Abstract

Ordinary differential equation (ODE) models are powerful tools for studying the dynamics of metabolic pathways. However, key challenges lie in constructing ODE models for metabolic pathways, specifically in our limited knowledge about which metabolite levels control which reaction rates. Identification of these regulatory networks is further complicated by the limited availability of relevant data. Here, we assess the conditions under which it is feasible to accurately identify regulatory networks in metabolic pathways by computationally fitting candidate network models with biochemical systems theory (BST) kinetics to data of varying quality. We use network motifs commonly found in metabolic pathways as a simplified testbed. Key features correlated with the level of difficulty in identifying the correct regulatory network were identified, highlighting the impact of sampling rate, data noise, and data incompleteness on structural uncertainty. We found that for a simple branched network motif with an equal number of metabolites and fluxes, identification of the correct regulatory network can be largely achieved and is robust to missing one of the metabolite profiles. However, with a bi-substrate bi-product reaction or more fluxes than metabolites in the network motif, the identification becomes more challenging. Stronger regulatory interactions and higher metabolite concentrations were found to be correlated with less structural uncertainty. These results could aid efforts to predict whether the true metabolic regulatory network can be computationally identified for a given stoichiometric network topology and dataset quality, thus helping to identify optimal measures to mitigate such identifiability issues in kinetic model development.

Introduction

As the biomanufacturing industry has rapidly grown, there has been an increasing demand for mechanistic modeling of metabolism at the cellular scale for strain engineering¹. These models empower data-driven investigation of biological systems and thus inform experimental design and accelerate the engineering cycle². While steady-state models such as flux balance analysis have been used to predict the performance of engineered cells³, these analyses fail to capture the dynamic nature of cellular metabolism⁴. The dynamics of metabolic pathways are often studied using ordinary differential equation (ODE) models⁵ that facilitate the identification of kinetic bottleneck reactions and of ways to improve productivity⁶.

A challenge in constructing ODE models for metabolic pathways is uncertainty about the networks of direct (allosteric) interactions between metabolites and enzymes that often control reaction rates⁷. While large swaths of the chemical reaction network are highly conserved across organisms, metabolite-level regulatory interactions can vary significantly across organisms or even across experimental conditions for the same organism. As a result, despite significant advances in the identification of protein-metabolite interactions in vitro^8,9 and the development of computational approaches to identify allosteric sites^10,11, large-scale organism-specific and condition-specific experimental identification of these interactions remains elusive¹². If these regulatory interactions are not known and thus not incorporated into models, the predictability of those models can be significantly compromised as observed flux changes cannot be explained^13–16.

Computational kinetic modeling approaches have helped to address this challenge. Link et al.¹⁷ fitted models with putative allosteric regulation to experimental data and identified the key interactions that govern the switch between gluconeogenesis and glycolysis. Hackett et al. developed an approach to systematically add regulatory interactions to a model and assess whether there is an improved fit, which led to the discovery of novel regulatory interactions¹⁸. Many previously unknown metabolite-level regulatory interactions in various organisms were uncovered using related approaches^19,20. However, these often require a large amount of experimental data or several iterations of experimentation and modeling, which is not always feasible. Moreover, correct identification of regulatory interactions can be severely hampered by a lack of high-quality data: noisy and low-frequency metabolite measurements can allow ODE models to assume incorrect regulatory networks to fit as well as the correct regulatory network (i.e., overfit), leaving uncertainty as to the true structure.

Two diverse strategies are commonly used to develop computational kinetic models in the face of this challenge. In one strategy, unknown regulatory interactions are identified with model discrimination. For example, ModelMaGe²¹ and TopoFilter²² automatically generate and manage alternative model structures given heuristics for model reduction to make the computations tractable, while Guillen-Gosalbez et al.²³ identified the model structure and performed parameter estimation simultaneously to handle the trade-off between model complexity and fitting accuracy. A second strategy assumes that identifying correct regulatory interactions is not possible and uses ensembles of models to deal with structural uncertainty. For example, ensemble models for signaling network structures have been developed using logic-based models to account for structural uncertainty²⁴. The choice between these two strategies depends on the availability and quality of experimental data, and significant computational or experimental efforts can potentially be saved with the choice of the correct strategy upfront. Further, whether the correct strategy is chosen will affect the downstream model interpretation and utility. If it is possible to identify the correct regulatory network confidently but an ensemble modeling strategy was taken, mechanistic understanding of the biological system would be lost, and thus, the model would underperform its potential. On the other hand, if an ensemble modeling strategy should have been used when one chooses to identify a single regulatory network structure, model predictability could be compromised. It is also worth noting that the approaches described above were designed for gene regulatory networks and signaling networks, not metabolic pathways where partial network structure can be assumed to be known and the strength of regulatory interactions plays a larger role in model accuracy.

The structural uncertainty issue is under-characterized, mainly due to the nested nature of structure uncertainty and parameter identifiability²⁵. Parameter identifiability is quite well-studied, with approaches developed to quantify and mitigate the issue^26–34. For structural parameter identifiability, which is the potential for multiple sets of parameters to reproduce the same characteristic behavior independent of any data, approaches like reparameterization can mitigate the issue^28,30. For practical parameter identifiability, which is where a single set of parameters cannot be distinguished from the rest due to limitations of data quality, the uncertainty of parameters can be quantified by confidence intervals or posterior probability densities^33,35, and ensemble modeling approaches can be used to account for uncertainties in parameter values^36–38. However, parameter identifiability analyses can only be performed given a single well-defined model structure, as minor structural changes can significantly alter dependencies³⁹. This means that structural uncertainty both confounds and is confounded by parameter identifiability issues for regulatory networks in metabolic pathways.

This stresses the significance of elucidating whether, given limited experimental data availability and quality, it is feasible to identify the correct model structure from data. Are some regulatory interactions inherently more difficult to identify than others? If so, what are the characteristics that make them hard to identify? With regards to data, what characteristics of the data impact the difficulty of identifying the metabolite-level regulatory network? And under what combination of data quality and structure complexity can we confidently identify one correct regulatory network?

Here, we begin to explore these questions via the analysis of four common topological motifs in metabolic pathways. We assessed the difficulty of identifying the structure of metabolic regulatory networks by fitting alternative network models to data of varying qualities. A variety of factors were found to jointly impact the identification of true regulatory networks, including the noise and sampling frequency of the data, missing metabolite profiles, topological location of metabolites with missing profiles, and the strength and relative position of the underlying regulatory network topology. These insights could be used to aid future efforts to mitigate, or at least predict, limitations on regulatory structure identification in metabolic models.

Results

To assess the impact of data quality and network topologies on regulatory network structural uncertainty in metabolic pathways, we studied common stoichiometric and regulatory network motifs under different conditions of synthetic, noise-added data generated with biochemical systems theory (BST) kinetics. We used four reaction network topologies (Fig. 1) with three to six regulatory network topologies (Supplementary Fig. 1), each with 20 parameterizations that yield diverse kinetic profiles. We generated three noisy replicates of data for each topology pair’s parameterizations, with four different sampling rates and three different noise levels, as well as the removal of data for specific metabolites (reflecting analytical instrument limitations) from some datasets. Each of these datasets was then used to fit a comprehensive set of regulatory network models (subject to the constraints described in Methods). Parameter estimation was performed on the regulatory kinetic parameters only, assuming that kinetic parameters for stoichiometric interactions were known. The candidate network models were then ranked based on Bayesian Information Criterion (BIC) scores, and the rank of the true regulatory network model was recorded as a proxy for structural uncertainty. This yielded a total of 41,040 cases (with each case defined as the ranking for one noisy replicate of a given stoichiometric and regulatory topology with a given parameterization, sampling rate, noise level, and metabolite removal status), including 12,960 cases for the determined, underdetermined, and multi-substrate motifs each and 2160 cases for the cycle motif. The impact of metabolites with missing data was only examined in the more computationally tractable determined, underdetermined, and multi-substrate motifs. The distribution of true model ranks was then analyzed to assess the impact of noise levels, metabolite missingness, and underlying network topologies. A common enzyme kinetics rate law, Michaelis–Menten, was also used to assess structural uncertainty for a subset of cases, and the uncertainty was significantly worse (Supplementary Fig. 2).

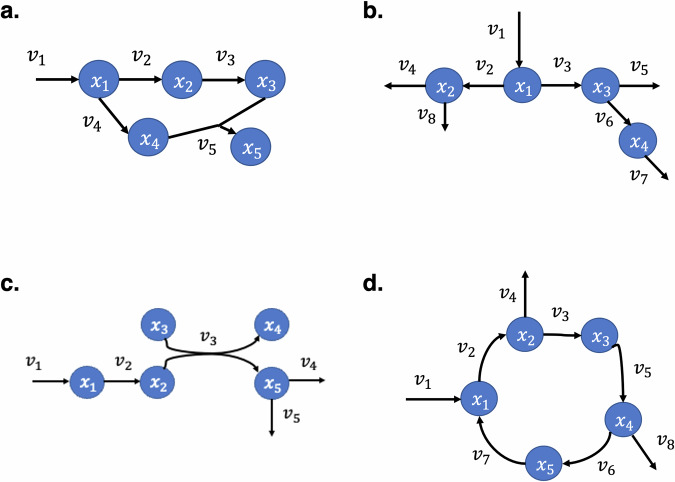
Fig. 1. Network motifs studied.

a Determined motif with stoichiometric merge; b underdetermined motif due to multiple stoichiometric branch points; c multi-substrate; d cycle. Metabolites are represented by blue circles containing metabolite labels x_i in white, while reactions are represented by black arrows with adjacent v_i labels in black.

True network rank is correlated with the noise and sampling rate of the data

Across 4 sampling rates ranging from 100 to 1000 time points per metabolite and 3 noise levels ranging from CoV = 0.05–0.25, we found a direct relationship between the quality of the data and the ability to identify the true regulatory network. The true network rank distribution for each of the 12 {sampling rate, noise level} pairs for the determined motif is shown in Fig. 2a. The frequency of the top-ranked network, being the true network generally decreases with increasing noise and decreasing sampling rate, which is to be expected. The rank distribution for the underdetermined, multi-substrate, and cycle motifs shown in Supplementary Fig. 3 follows the same trend. Lower sampling rates from 10 to 50-time points per metabolite were studied for the determined motif in Supplementary Figs. 4 and 5, showing the continuation of the same trends. With fewer data points and more noise in the experimental data, incorrect regulatory network models can better overfit the data, yielding fits similar to or better than that of the true regulatory network model. We used a Spearman correlation to quantitatively characterize the relationship between the rank and sampling rate or noise. For the determined motif, we found a Spearman coefficient of −0.207 between the true network rank and sampling rate, and a Spearman coefficient of 0.248 between the true network rank and CoV (Fig. 2b). It is worth noting that other factors, such as the 20 different parameterizations, are major contributors of variability to the relatively low Spearman correlation coefficient; an example of the variability among different parameterizations is shown in Supplementary Fig. 6. While there is variability across individual parameterizations, the general trends in the aggregate average behavior are consistent across stoichiometric topologies (Fig. 2b).

Fig. 2. Impact of noise and sampling rate.

a Distribution of the rank of the true regulatory network model among all possible regulatory network models in the determined motif across all underlying true regulatory network structures, parameterizations, and replicates for 12 different noise conditions. Slices of the pie charts represent the percentage of cases where the true regulatory network is ranked in the corresponding category. The percentage of high ranks decreases as the sampling rate decreases or the noise increases. b Spearman correlation coefficients across all cases for the relationship between the true regulatory network model rank and sampling frequency or CoV in the determined, underdetermined, multi-substrate, and cycle motifs.

The impact of missing metabolite profiles varies with network topology and the position of the missing metabolite

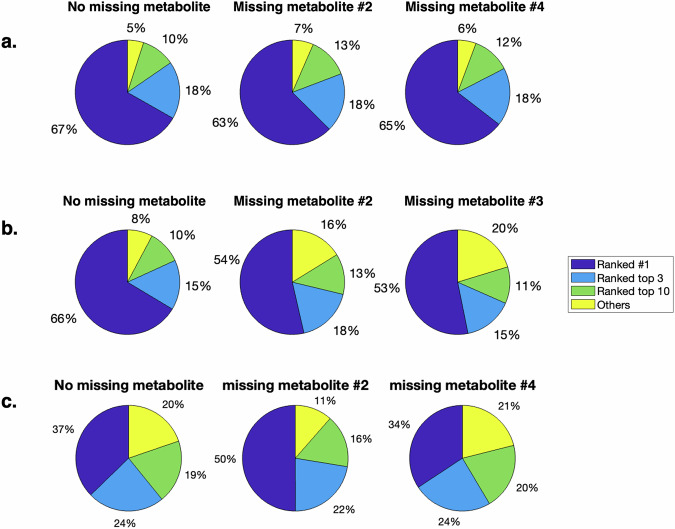
Individual metabolites having completely missing measurement profiles is a common occurrence in metabolomics data due to challenges including metabolite annotation/identification and limits of detection⁴⁰. To assess the impact of this phenomenon, two metabolites were arbitrarily selected from the determined, underdetermined, and multi-substrate motifs to be withheld from training datasets for all parameterizations, data noise levels, and sampling frequencies. While the unavailability of metabolite profiles for metabolites #2 and #4 in the determined motif did not change the true network rank distributions (two-sample Kolmogorov–Smirnov test, α = 0.05) and thus the structural uncertainty, removal of data for metabolites #2 and #3 in the underdetermined motif changed the rank distributions (two-sample Kolmogorov–Smirnov test, α = 0.05), indicating worsened structural uncertainty for that motif (Fig. 3). In the multi-substrate motif, removal of metabolite #2, surprisingly, benefits the structural uncertainty. This could be due to the high concentrations of metabolite #2 and the associated large signal-dependent noise. The large noise may outweigh the fitting error of the other metabolites and cause overfitting to noise. Removal of metabolite #4 did not change the true network rank distribution.

Fig. 3. Impact of missing data.

Distribution of the rank of the true regulatory network model given different missing metabolites in the a determined motif, b underdetermined motif, and c multi-substrate motif. Slices of the pie charts represent the percentage of cases where the true regulatory network is ranked in the corresponding category across all underlying true regulatory networks, parameterizations, replicates, noise levels, and sampling frequencies. A two-sample Kolmogorov–Smirnov test was used to compare the rank distribution between datasets with and without a missing metabolite profile (α = 0.05); in the determined motif the differences were not significant, whereas in the underdetermined and multi-substrate motifs they were significant.

We assessed the impact of all other possible missing metabolite profiles at a subset of noise conditions (nT = 100 and CoV = 0.25; nT = 100 and CoV = 0.05; Supplementary Figs. 7 and 8). We used only a subset of noise conditions to make the problem more computationally tractable, because in both stoichiometric topologies tested above, any single noise condition was found to be reasonably representative of the trend observed in 3 (Supplementary Figs. 9 and 10). We found that at low noise (CoV = 0.05), structural uncertainty in the determined motif is robust to the removal of any single metabolite profile, while in the underdetermined motif, it is robust to only missing metabolites #1 and #4, one at a branch point and one in a linear pathway. On the other hand, at higher noise (CoV = 0.25), the structural uncertainty in the determined motif is robust to the removal of most metabolite profiles except for #1, whereas the removal of any metabolite profile has a detrimental impact on the structural uncertainty in the underdetermined motif (Supplementary Figs. 7 and 8). These results indicate that determined systems may be more robust to missing metabolite profiles than underdetermined systems and that the position of the missing metabolite in the underdetermined systems has varying impacts on uncertainty.

Some types of regulatory networks are easier to identify than others

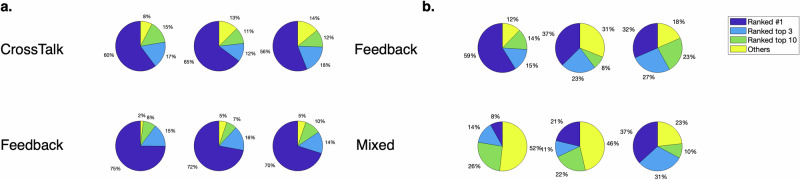
To assess the extent to which structure uncertainty can be attributed to the topology and other characteristics of the true regulatory network, we analyzed the true network rank distribution across each of the six regulatory network topologies in the determined, underdetermined, and multi-substrate motifs. In the determined and underdetermined motifs, the six regulatory network topologies can be split into two categories: one with regulatory interactions spanning across branches (Crosstalk), and the other with feedback regulatory interactions only (Feedback). In the multi-substrate motif, the six regulatory network topologies can be split into one with feedback only (Feedback) and one with mixed feedback and feedforward regulatory interactions (Mixed). For the determined motif, two regulatory network topologies yielded different true network rank distributions from the rest: one with crosstalk and one with feedback only (Supplementary Fig. 11). Both involve regulatory control exerted by metabolite #5, which is a merge point for two network branches, while other regulatory network topologies do not involve metabolite #5. For the underdetermined motif, the regulatory network topologies with crosstalk were found to have different true network rank distributions than those with feedback only (two-sample Kolmogorov–Smirnov test, α = 0.05) (Fig. 4a). For the multi-substrate motif, identification of correct regulatory interactions for the regulatory network topologies involving feedforward regulatory interactions was found to be more difficult than for those involving feedback regulatory interactions only (Fig. 4b). To further explore potential factors at play in identification, regulatory networks with a single interaction were studied (Supplementary Figs. 12–14), revealing that the challenge of identifying correct regulatory interactions seems to be related to individual regulatory interactions. In the underdetermined motif, regulatory interactions involving a metabolite on a linear pathway are easier to identify than others, while regulatory interactions involving fluxes downstream of the 2nd branch points are harder to identify. In the multi-substrate motif, regulatory networks involving feedforward interaction or a multi-substrate reaction are harder to identify. Taken together, these results suggest that the topological position of the regulator metabolite and the complexity or topological proximity of the regulator to the regulated reaction can have a substantial impact on the difficulty of identifying the true regulatory network.

Fig. 4. Impact of regulatory interaction characteristics.

Distribution of the rank of the true regulatory network model for different regulatory network topologies in the a underdetermined b multi-substrate motif. Slices of the pie charts represent the percentage of cases where the true regulatory network is ranked in the corresponding category across all parameterizations, noise levels, sampling frequencies, and replicates. a rank distributions for the three crosstalk regulatory network topologies are significantly different than the three feedback ones. b rank distributions for the three mixed regulatory network topologies are significantly different than the three feedback-only ones. A two-sample Kolmogorov–Smirnov test was used to compare rank distributions (α = 0.05).

Furthermore, the strength of individual regulatory interactions seems to often play a role in structural uncertainty. All regulatory parameters whose magnitudes had a non-zero correlation (α = 0.05) with the rank of the true regulatory network model had negative correlation coefficients (Supplementary Fig. 15), suggesting that a larger regulatory kinetic parameter—which indicates a stronger regulatory interaction, whether positive or negative—is correlated with less structural uncertainty.

Characteristic features of time-course data are correlated with the rank

We next sought to identify whether there might be any characteristics of the measured time-course metabolite datasets that are correlated with structural uncertainty. We calculated 30 time-course data-derived features (Supplementary Table 1) for each metabolite profile and then found their respective correlations with the true regulatory network rank across all regulatory topologies, parameterizations, noise conditions, and sampling rates for each network motif using a Spearman correlation coefficient. Since we found many time-course-derived features to be highly correlated with the sampling rate (Supplementary Fig. 16), the correlation analysis was performed for each sampling rate separately. 52, 34, 14, and 14 features were found to have significant Spearman correlation coefficients (α = 0.05) with at least one sampling rate for the determined, underdetermined, multi-substrate, and cycle motifs, respectively (Supplementary Data 1). The five features that are most significantly correlated with true regulatory network model rank for each stoichiometric network topology are shown in Fig. 5.

Fig. 5. Impact of time-course data.

Spearman correlation coefficients for the top five time-course-derived features in each stoichiometric network topology at each sampling rate. Correlation coefficients for each feature are calculated across all parameterizations, noise levels, replicates, and regulatory network structures.

A more detailed analysis of these correlated time-course-derived features revealed a few interesting trends (Fig. 5). First, in the determined motif, the top five significantly correlated time-course-derived features all have positive correlation coefficients with rank and thus are positively correlated with structural uncertainty. These time-course-derived features are mostly related to the derivatives or the slope of the dynamic profile. This indicates that larger changes in metabolite accompanied by lower sampling rates are associated with structural uncertainty. In the underdetermined, multi-substrate, and cycle motifs, features in Fig. 5 are mostly related to the absolute value of one certain metabolite, and larger minimum and mean concentrations are associated with increased structural identification, suggesting that larger metabolite concentrations are often associated with improved uncertainty. In addition, the correlation coefficients at higher sampling rates are generally (though not always) smaller in magnitude than those at lower sampling rates, suggesting that the change in numerical values in these features, as the sampling rate decreases, plays a key role in the increased challenge of identifying the correct regulatory network topology as the sampling decreases.

Discussion

We have found that specific data quality and network topology features are linked to the challenges of identifying the correct regulatory network topology in a metabolic network from metabolite profiling data. High noise and low sampling rates in the data pose heightened obstacles in discerning the network structure, as would be expected. Additionally, the impact of metabolites with missing profiles is more detrimental to chemical reaction networks with more fluxes than metabolites but can vary based on the topological position of the metabolite with respect to both the regulatory and stoichiometric topologies. In terms of the characteristics of regulatory networks and of the time-course data, weaker regulatory interactions, lower metabolite concentrations, and faster concentration changes accompanied by lower sampling frequency were associated with increased difficulty in identifying correct regulatory network structures. In addition, the topological proximity of the regulator to the regulated reaction greatly impacts the uncertainty in the underdetermined network motif, and feedforward regulatory interactions are harder to identify than feedback interactions in the multi-substrate motif. Additional studies are warranted for multi-substrate reaction motifs that also include mass conservation (e.g., cofactor recycling), which may face different challenges in structural uncertainty. Though this study was limited to four common network motifs using BST kinetics, characteristics of the data and topology were found to collectively influence the identification of regulatory network models in metabolic systems. These observations help us understand the unexploited boundary of topology complexity and data quality at which the true regulatory network can be inferred and motivate structural uncertainty analysis on more network motifs. For example, identifying the correct regulatory interaction in a determined network motif is feasible in a high noise condition and when metabolite profiles are missing, while the identification in a slightly more complicated multi-substrate network motif is challenging even at a low noise condition. Taken together, the insights and trends identified in this work support the importance of broader efforts to identify the right strategy to address structural uncertainty challenges effectively, which would lead to better models of cellular metabolism to support biomanufacturing efforts.

Methods

Test models

Four common stoichiometric topological motifs present in metabolic pathways (Fig. 1) were chosen for study as an initial testbed for exploration. These motifs were selected as they can be readily identified as parts of common biochemical networks, and thus represent a kind of building block whose study would be valuable. For example, the determined motif can be found in the glycolysis and steroid hormone biosynthesis pathway, the underdetermined motif can be found in highly branched pathways such as pyruvate metabolism, and the cycle motif is inspired by pathways such as the TCA cycle, urea cycle, and Krebs cycle. For the determined motif, 12 different regulatory networks were used for the study: three with two regulatory interactions spanning across branches (Crosstalk), three with only two feedback regulatory interactions (Feedback), and six with single feedback or crosstalk regulatory interaction. For the underdetermined motif, 13 total were studied, including three two-interaction networks involving crosstalk, three two-interaction networks involving only feedback, and seven single feedback or crosstalk regulatory interactions. Seven networks with single feedback or feedforward interaction, three two-interaction networks involving feedback only, and three two-interaction networks involving a mix of feedback and feedforward were studied for the multi-substrate motif. Three different regulatory networks were used for the cycle motif. The regulatory networks for each stoichiometric topology are included in Supplementary Fig. 1. For each combination of topology and regulatory network, 20 different parameterizations were tested.

Generating synthetic data

Synthetic data were used in this study to decouple the impacts of experimental noise from inherent structural uncertainty issues. To generate these data, ODE models assuming power-law kinetics were used. Example equations for these models are provided in Supplementary Fig. 17. Kinetic BST parameters for stoichiometric reactions were sampled from a uniform distribution [0,2], while those for regulatory interactions were sampled from [−2,2]. For regulatory networks with a single interaction, all kinetic parameters were modified from parameterizations in two-interaction regulatory networks. Time-course metabolite data were generated by solving the ODE system in MATLAB using ode15s. To model experimental measurements, the original noiseless data were modified to be at various levels of data quality. Down-sampling of the metabolite data was accomplished by evenly sampling nT time points over the time interval. Measurement noise was added by replacing concentrations with a random value drawn from the normal distribution $N_{i,k}~\left(y_i\left(t_k\right),CoV\cdot y_i\left(t_k\right)\right)$ where $y_i\left(t_k\right)$ is the value of metabolite i at time point k, and CoV is a coefficient of variance. The addition of signal-independent noise does not significantly impact uncertainty (Supplementary Fig. 18). To model the issue of metabolites that cannot be measured or annotated via metabolomics approaches, the time course for some metabolites was removed from some datasets.

Assessing structure uncertainty

Structural uncertainty was assessed by defining regulatory networks for a given stoichiometric topology, calculating metabolite profiles for each regulatory network, and then using the resulting simulated metabolite profiles to fit different candidate regulatory network models. Due to the combinatorial nature of the regulatory networks, to keep the computational time manageable we assumed that one metabolite cannot regulate more than one flux and one flux cannot be regulated by more than one metabolite. In all, 227 putative regulatory networks were generated for the determined and multi-substrate motif, 823 for the underdetermined motif, and 4079 for the cycle motif. Parameter estimation was then performed on the regulatory kinetic parameters only, assuming that kinetic parameters for stoichiometric interactions were known. Eight initial points were sampled from the range [−10,10] for each candidate regulatory network, and the fmincon function in MATLAB (which uses an interior-point method) was used to find parameter values locally, minimizing the sum of square residuals with respect to the generated noisy synthetic data. The mean and standard deviation of the objective value is then calculated, and if the standard error is larger than 0.1, 16 more optimization runs with initial points are run to increase the likelihood of finding a minimum closer to the global minimum. We acknowledge that global optima may not be guaranteed in these optimization runs, which is a challenge for all regulatory interaction models. The candidate regulatory network models were then ranked by their BIC scores. BIC was chosen to be the metric among the seven metrics tested as it consistently outperformed other metrics in discerning the true network structure model in initial testing (Supplementary Fig. 19). Since there is no established or widely-used metric for the degree of uncertainty in regulatory network structures, uncertainty was assessed using the rank of the correct regulatory network as a proxy: the correct network ranking first was interpreted as minimal structural uncertainty, while higher rankings indicated more structural uncertainty since overfitted incorrect models could outperform the correct model.

Feature generation

To explore whether there are characteristics of the data quality or of the data characteristics that make the correct regulatory network in a given case unidentifiable, multiple features were analyzed. Categories of features studied include noise-indicating factors such as a number of datapoints and CoV, time-course derived features, and the strength of regulatory interactions as indicated by magnitudes of true regulatory kinetic parameters. Time-course-derived features were generated with tsfel in temporal and statistical domains⁴¹.

Correlation between the rank of the true regulatory network and features

The Spearman correlation coefficient was used to assess the correlation between the rank of the true regulatory network and each feature. The analyses were performed on all datapoints as well as on subsets of the data to minimize the impact of confounding factors (i.e., covariance of different features). For example, it was found that some time-course features are highly correlated with the sampling rate, so the correlation between true regulatory network rank and the time-course features (4320 datapoints) was also performed for each individual sampling rate (1080 datapoints). In all cases, a Bonferroni correction was applied to adjust for multiple hypothesis testing.

Author contributions

YH: conceptualization, formal analysis, investigation, software, visualization, writing—original draft, writing—review and editing; M.P.S.: conceptualization, funding acquisition, supervision, writing—review and editing. All authors read and approved the final manuscript.

Data availability

The data generated and analyzed during the current study are available in the GitHub repository: https://github.com/gtStyLab/Uncertainty.git.

Code availability

The underlying code for this study is available in the Uncertainty GitHub repository and can be accessed via this link: https://github.com/gtStyLab/Uncertainty.git.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41540-024-00412-x.