Walking symmetry is speed and index dependent

Abstract

Gait symmetry is one of the most informative aspects describing the quality of gait. Many indices have been proposed to quantify gait symmetry. Among them, indices focusing on the comparison of the two body sides (e.g., Symmetry Angle, SA) and indices based on the analysis of the locomotor act as a whole, dealing with the body center of mass (e.g., Symmetry Index, SI_BCoM) or lower trunk accelerometry (e.g., improved Harmonic Ratio, iHR) have been proposed. Remarkably, the relationship between these indices has received little attention so far, as well as the influence of gait speed on their values. The aim of this study is to investigate this relationship by comparing the SA, SI_BCoM, and iHR, and to explore the effect of walking speed on these indices. Ten healthy adults walked for 60 s on a treadmill at seven different speeds (from 0.28 to 1.95 m s⁻¹) and simulate an asymmetric gait (ASYM) at 0.83 m s⁻¹. Marker-based trajectories were recorded, and the body center of mass 3D trajectory was obtained. Simultaneously, lower trunk 3D linear accelerations were collected using a triaxial accelerometer. SI_BCoM, iHR, and SA were calculated for each stride, each anatomical direction, and each condition. Perfect symmetry was never displayed in any axes and any indices. Significant differences existed between SI_BCoM, and iHR in all anatomical directions (p < 0.0001). The walking speed significantly affected SI_BCoM and iHR values in anteroposterior and craniocaudal directions, but not in mediolateral. Conversely, no walking speed effect was found for SA (p = 0.28). All three indices significantly discriminated between ASYM and the corresponding walking condition (p < 0.05). Gait symmetry may differ significantly according to the data source, mathematical approach, and walking speed. Healthy individuals display an asymmetrical gait and acknowledging this aspect is crucial when establishing rehabilitation objectives and assessing the quality of gait in the clinical setting.

Introduction

Locomotion is accomplished through complex and timely interactions among the nervous, muscular, and skeletal systems. The quantitative assessment and description of these functions is the objective of gait analysis¹. Effectively answering the question “how a given individual walks” is one of the primary goals of gait analysis¹.

The quality of gait can be assessed considering different aspects. Among them, gait symmetry has been widely acknowledged as one of the most informative, along with the maintenance of balance, mechanical loads on tissues, and energy expenditure^1,2. In general, gait symmetry refers to a perfect agreement between the actions of the left and right sides of the body, with specific reference to the lower limbs action^3,4. From a functional point of view, asymmetry in gait has been associated with an increased metabolic cost during locomotion⁵, with reduced bone density and osteoporosis in the affected limb, as well as an increased joint load and a consequent higher risk of osteoarthritis in the opposite limb⁶. For these reasons, quantifying gait symmetry provides crucial information to identify underlying deficits, guide clinical decisions, and monitor rehabilitation outcomes^4,7.

A vast number of indices have been proposed in the literature to quantify gait symmetry, based on different data sources and approaches⁴. Discrete approaches based on equations to calculate symmetry from discrete values of gait features, e.g. spatiotemporal parameters (like the Symmetry Ratio ⁸, the Symmetry Index⁹, or the Symmetry Angle¹⁰) are widely adopted. On the other hand, non-linear or statistical approaches based on the comparison of series of data describing the behaviour/mechanics of the two sides of the body over a complete gait cycle (like ground reaction forces, joint kinematics, or kinetics [for a detailed description please refer to Viteckova et al.⁴]) have been proposed. Ultimately, a third approach is used based on the analysis of the body centre of mass (BCoM), being the point that better represents the whole-body movement. This approach diverges from the preceding ones as it does not compare the behaviour of the right and left sides of the body, but rather focuses on the assessment of the locomotor act in its entirety and aims at providing a global metric describing the symmetry of gait. In this context, an index based on the trajectory of the BCoM have been proposed (SI_BCoM)¹¹ and applied^12–15. With a similar intent and leveraging the widespread use of wearable accelerometers located on the lower trunk, near the BCoM, other symmetry indices based on the signal frequency content have been devised. Among them, the Harmonic Ratio (HR)¹⁶, and its modified version, i.e., the improved Harmonic Ratio (iHR)¹⁷, have gained extensive popularity in recent years^17–20.

Remarkably, the relationship between indices comparing the behavior of the two body sides Vs those focusing on the BCoM (or a point closed to the BCoM) has received very little attention so far. Only one study compared the SI_BCoM with the Symmetry Angle¹⁰ and found no significant correlation between them¹³. Furthermore, highly controversial results have been reported about the influence of gait speed on these different indices, thus raising questions on their interpretation in pathological and healthy cohorts characterized by extremely different walking speeds^21–25.

The aim of the present study is thus twofold: (1) to investigate the relationship among different approaches to quantify gait symmetry by comparing three different indices, i.e., the SI_BCoM, iHR, and Symmetry Angle, obtained respectively from the BCoM trajectory, the lower trunk acceleration, and a temporal parameter of gait; (2) to investigate the effect of walking speed on these three indices. Comparative evaluation was conducted in healthy adults walking on a treadmill at seven different walking speeds.

Material and methods

Participants and experimental protocol design

Ten healthy adults (4 women, 1.71 ± 0.08 m height, 68.2 ± 10.2 kg body mass, 34.5 ± 8.5 years old (mean ± standard deviation)) participated in the study approved by the University of Rome “Foro Italico” Ethics Committee (CAR 101/2021). This sample size complied with the minimum number of participants recommended by an a priori power analysis purposely performed (α = 0.05; power (1 − β) = 0.95, effect size f: 0.3) for a two-way repeated measure ANOVA (within and between interaction)²⁶. Participants signed informed consent in accordance with the Declaration of Helsinki. They walked for 60 s on a treadmill at seven different speeds: 0.28, 0.56, 0.83, 1.11, 1.39, 1.67, and 1.95 m s⁻¹ (namely from 1 to 7 km h⁻¹ with steps of 1 km h⁻¹), whose order was randomized. Each participant was also asked to simulate an asymmetric gait at 0.83 m s⁻¹, and a 60-s walk was also registered for this condition (ASYM). No indication was provided about the kind of asymmetry to be simulated or the affected side. A 6-min treadmill acclimatization protocol was performed by each participant before data acquisition²⁷. Participants were first asked to stay still for 5 s and then start walking at the speed selected by the operator. Measurements started when the treadmill was at a constant speed. The accuracy of the treadmill was verified before the experiments to ensure it maintained the required belt speed which was monitored during the steady speed using one of the markers placed on the participants' shoes.

Data acquisition

The 3D trajectories of 18 reflective markers located on the main joint centres according to Pavei et al.^28–30 were recorded using a 6-camera stereophotogrammetric system (Vicon Vero, Oxford Metrics, UK, 200 Hz). Simultaneously, lower trunk 3D proper linear accelerations were collected using a triaxial accelerometer (Inertial Measurement Unit - IMU) (APDM Opal, Portland, OR, USA, 200 Hz, 25 g, ± 16 g) located at the L1–L2 level. The two systems were electronically synchronized through a trigger box. Marker and accelerometer positioning was performed by the same expert operator. Markers were attached to the participants’ skin using double-sided tape, whereas the accelerometer was firmly fixed using an elastic belt. The accelerometer axes were carefully aligned with the anteroposterior (AP), mediolateral (ML), and craniocaudal (CC) anatomical axes.

Data analysis

Marker positions were filtered through a zero-lag 2nd-order Butterworth low-pass filter with a cut-off frequency identified by a residual analysis on each marker coordinate³¹. The time course of the BCoM 3D position was estimated as the weighted mean of an 11‐segment model based on Dempster's inertial parameters of body segments^28,29. Left and right foot strike events were identified from markers positions according to the method proposed by O’Connor et al.³². These events were considered to segment stride and step cycles and to calculate all symmetry indices listed below. For each considered stride, the BCoM trajectory was represented by a closed 3D loop (Lissajous contours), describing its displacement with respect to its average position¹¹.

The following gait symmetry indices were then computed.

Symmetry Index (SI_BCoM)

SI_BCoM was calculated for each stride from the marker-based BCoM trajectory based on its harmonic content, as proposed by¹¹ (detailed procedures are reported in the Supplementary Material of Minetti et al.¹¹). Briefly, the 3D trajectory of the BCoM is mathematically defined by 10-harmonic Fourier series, whose coefficients are used to calculate the Symmetry Index (SI_BCoM) for each anatomical axis¹¹. A perfectly symmetrical gait would yield only even harmonics along the AP and CC axes, and only odd harmonics in the ML direction^11,33. These harmonics are considered intrinsic to the phenomenon, whereas the harmonics which lead to deviations from the ideal gait are named extrinsic. The terms intrinsic and extrinsic refer to the interpretation proposed by Cappozzo³⁴ where the locomotor act is seen as composed of an intrinsic pure form of movement pattern, eventually deformed by extrinsic causes. Based on this terminology, SI_BCoM was defined as follows:

$${\mathit{SI}}_{BCoM\_k}=\frac{{\sum }_{j=1}^k{c}_I^j}{{\sum }_{j=1}^k\left(c_I^j,+,c_E^j\right)}·100$$ 1

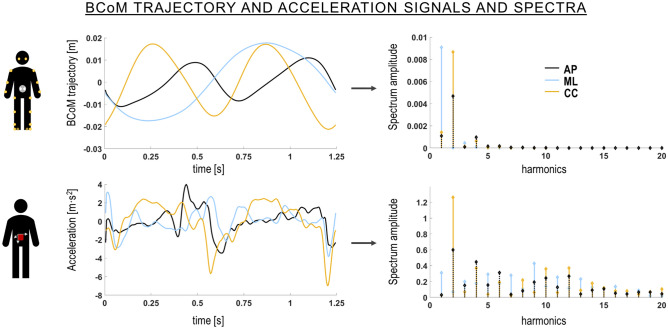
where c_I^j and c_E^j are, respectively, the amplitude of the jth intrinsic and extrinsic harmonics for each BCoM trajectory component k¹¹ (Fig. 1). SI_BCoM was expressed in percentage so that it ranged from 0% (total asymmetry) to 100% (perfect symmetry).

Figure 1.

Body centre of mass (BCoM) trajectory and acceleration signals with the relevant amplitude spectra in the anteroposterior (AP), mediolateral (ML) and craniocaudal (CC) directions over one randomly chosen stride of a participant walking at 1.39 m s⁻¹.

Improved Harmonic Ratio (iHR)

The 3D proper acceleration measured by the trunk mounted IMU was considered. To guarantee identical starting conditions for all participants, the accelerometer was verticalized through a rigid transformation computed in the static phase at the beginning of each trial which corrected for both the pitch and roll angles³⁵. This transformation was applied to the measured acceleration in each sampled instant of time. The resulting local axes were considered to approximate anatomical axes (AP, ML, CC). After removing the mean value from each acceleration component, the iHR was obtained for each stride as follows¹⁷:

$${\mathit{iHR}}_k=\frac{{\sum }_{j=1}^k{P}_I^j}{{\sum }_{j=1}^k\left(P_I^j,+,P_E^j\right)}·100$$ 2

where P_I^j and P_E^j are, respectively, the power (amplitude squared) of the jth intrinsic and extrinsic harmonics for each acceleration component k (Fig. 1). The first 20 harmonics were considered. The iHR relies on the same concept and harmonic analysis as the SI_BCoM, with the difference that acceleration signals and the power of each harmonic are considered. Exactly like SI_BCoM, iHR ranges from 0% (total asymmetry) to 100% (perfect symmetry).

Symmetry Angle (SA)

Finally, from foot strike events, left and right step durations (d_L and d_R) were calculated and the Symmetry Angle (SA)¹⁰ was computed for each stride as follow:

$$SA=\frac{[{45}^{\circ }-\text{arctan}(\frac{d_L}{d_R})]}{{90}^{\circ }}·100$$ 3

If d_L > d_R, the ratio between the step durations was inverted so that each deviation from perfect symmetry had the same direction, regardless the “affected” body side. An SA value of 0% indicates perfect symmetry, whereas ± 100% indicates that the two values are equal and opposite in magnitude. This index was selected among many others based on discrete approaches because it has been demonstrated that it overcomes most limitations of the latter (normalization to reference values, artificial inflation)^4,10.

For each participant and each condition, SI_BCoM, iHR, and SA were obtained for each stride performed at a steady state. Data were analysed with purposely written LabVIEW (v13, National Instrument, USA) and Matlab® (R2016a, The MathWorks Inc., USA) scripts.

Statistics

For each index value, a preliminary outlier analysis was performed based on a threshold of ± 3 on the z-score to remove outliers from the data set. For each participant and each condition, the mean (μ) and standard deviation (σ) values of SI_BCoM, iHR, and SA over the analysed strides were calculated for each walking speed after checking for normality and were considered for further analysis. The normal distribution of μ and σ was then verified using the Shapiro–Wilk test of normality. To investigate whether significant differences existed between SI_BCoM and iHR and to assess the effect of walking speed on both parameters, a two-way repeated measure ANOVA was performed both on μ and σ. When a significant “index” or “speed” effect was found, pairwise comparisons were analysed through post hoc tests using the Bonferroni correction. Similarly, to investigate the effect of walking speed on SA values and its variability, a one-way repeated measure ANOVA was performed both on μ and σ followed by post hoc comparison with the Bonferroni correction. Finally, the presence of significant differences between the ASYM condition and walking at the same speed (0.83 m s⁻¹) was investigated in SI_BCoM, iHR, and SA using a paired t-test. Statistical analysis was performed using the GraphPad software (version 8.4.2, California, USA, α = 0.05).

Results

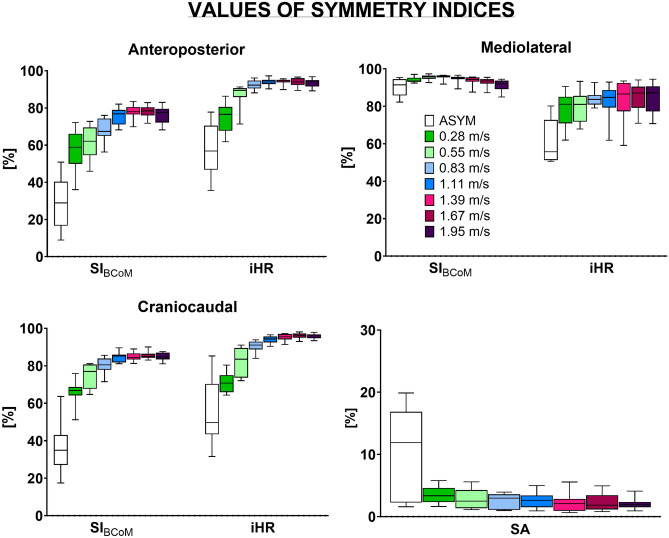
A total number of 3383 strides was analysed, with a minimum and a maximum of 208 and 627 strides for the slowest (0.28 m s⁻¹) and the fastest (1.95 m s⁻¹) walking conditions, respectively. Excluding the ASYM condition, SI_BCoM values ranged from 36.0% (at 0.28 m s⁻¹) to 83.5% (at 1.39 m s⁻¹), from 84.9% (at 1.95 m s⁻¹) to 97.3% (at 0.55 m s⁻¹), and from 51.2% (at 0.28 m s⁻¹) to 90.0% (at 1.67 m s⁻¹), in the AP, ML, and CC directions, respectively (Fig. 2); whereas iHR values ranged from 61.8% (at 0.28 m s⁻¹) to 97.2% (at 1.11 m s⁻¹), 59.1% (at 1.39 m s⁻¹) to 94.4% (at 1.95 m s⁻¹), and 64.4% (at 0.28 m s⁻¹) to 98.1% (at 1.67 m s⁻¹), in the AP, ML, and CC directions, respectively (Fig. 2). SA values ranged from 0.6% (at 1.39 m s⁻¹) to 5.7% (at 0.28 m s⁻¹) (Fig. 2).

Figure 2.

Box plots of the mean (μ) values over strides of Symmetry Index (SI_BCoM), the improved Harmonic Ratio (iHR), and the Symmetry Angle (SA) in the anteroposterior (AP), mediolateral (ML) and craniocaudal (CC) directions over each considered walking speed as well as when simulating asymmetrical walking (ASYM condition). The box height and whiskers represent the variability of the symmetry indices over participants.

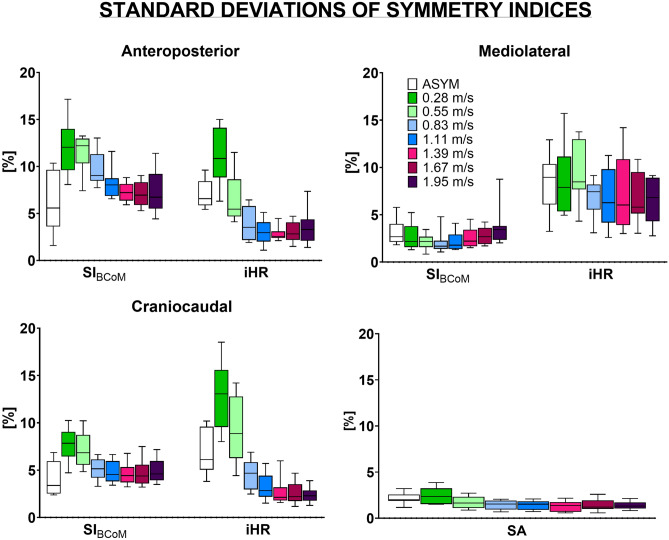
The variability of the symmetry indices ranged from 0.8 to 17.2% for SI_BCoM, from 1.1 to 18.5% for iHR, and from 0.6 to 3.9% for SA (Fig. 3). The highest variation in standard deviation was observed when walking at slower speeds (0.28 and 0.55 m s⁻¹) for all indices. Furthermore, the SI_BCoM exhibited its greatest variability in the AP direction, while the iHR in the CC direction. Notably, the iHR index displayed substantial between-subject variability in the ML component, irrespective of walking speed (Fig. 3).

Figure 3.

Box plots of the standard deviation (σ) values over strides of Symmetry Index (SI_BCoM), the improved Harmonic Ratio (iHR), and the Symmetry Angle (SA) in the anteroposterior (AP), mediolateral (ML) and craniocaudal (CC) directions over each considered walking speed as well as when simulating asymmetrical walking (ASYM condition). The box height and whiskers represent how the standard deviation of each index over strides changes among participants.

Effect of index and walking speed on gait symmetry

The two-way repeated measure ANOVA showed a significant effect of the “index” factor in all three directions (Table 1). The walking speed was found to significantly affect SI_BCoM and iHR values in AP and CC directions, but not in ML, whereas a significant “index × speed” interaction was obtained for all components (Table 1).

Table 1.

ANOVA results for the mean values of SI_BCoM and iHR symmetry indices.

	SS	DF	MS	F (DFn, DFd)	p value
AP
Index	13,139	1	13,139	F (1, 18) = 114.0	< 0.0001
Speed	6756	6	1126	F (2.31, 41.6) = 66.2	< 0.0001
Index × speed	470	6	78.4	F (6, 108) = 4.6	< 0.001
ML
Index	4513	1	4513	F (1, 18) = 30.7	< 0.0001
Speed	154	6	25.6	F (1.55, 27.8) = 1.1	0.326
Index × speed	393	6	65.5	F (6, 108) = 2.9	< 0.05
CC
Index	2919	1	2919	F (1, 18) = 56.3	< 0.0001
Speed	8397	6	1400	F (1.99, 35.8) = 143.0	< 0.0001
Index × speed	155	6	25.8	F (6, 108) = 2.6	< 0.05

Results of the two-way repeated measure ANOVA results for the mean values of the symmetry indices.

SS sum of squares, DF degrees of freedom, MS mean squares, F F-ratio, DFn degree of freedom for the numerator of the F-ratio, DFd degree of freedom for the denominator of the F-ratio.

Significant values are in bold.

Post hoc analyses for the “index” factor indicated that SI_BCoM and iHR mean values significantly differed in all walking speeds in the AP direction (p < 0.01). In ML and CC directions, significant differences were found, respectively, at low and high walking speeds. Specifically, SI_BCoM and iHR were significantly different from 0.28 to 1.11 m s⁻¹ for the ML component (p < 0.05), whereas, in the CC direction, they differed significantly from 0.83 to 1.95 m s⁻¹ (p < 0.001).

As for the influence of walking speed on gait symmetry values, several significant differences were displayed by the post hoc analyses for both SI_BCoM and iHR, particularly in AP and CC directions (detailed results are reported in the Supplementary Material). Overall, both SI_BCoM and iHR values increased with speed until they reach a plateau in AP and CC directions, whereas in the ML direction, they displayed a rather constant trend with only SI_BCoM values significantly decreasing from 0.83 to 1.67 m s⁻¹ (p < 0.05).

When considering the effect of walking speed on gait symmetry as assessed using SA, the one-way ANOVA analysis showed no significant speed effect (F(6, 62) = 1.26, p = 0.28).

For what concerns the effect of index and walking speed on the variability of SI_BCoM and iHR, stride-to-stride symmetry variability significantly changed according to the index in all directions except CC, and according to the walking speed in all directions except ML (Table 2). Similarly, a significant speed effect was found for the SA variability (F(6, 62) = 4.22, p < 0.01). Detailed results about post hoc analyses are reported in the Supplementary Material.

Table 2.

ANOVA results for the standard deviations of the SI_BCoM and iHR symmetry indices.

	SS	DF	MS	F (DFn, DFd)	p value
AP
Index	597	1	597	F (1, 18) = 57.2	< 0.0001
Speed	743	6	124	F (3.41, 61.50) = 54.1	< 0.0001
Index × speed	78	6	13	F (6, 108) = 5.7	< 0.0001
ML
Index	819	1	819	F (1, 18) = 60.1	< 0.0001
Speed	36	6	6	F (1.76, 31.64) = 1.6	0.209
Index × speed	67	6	11	F (6, 108) = 3.0	< 0.01
CC
Index	2	1	2	F (1, 18) = 0.2	0.642
Speed	856	6	143	F (2.86, 51.47) = 60.6	< 0.0001
Index × speed	236	6	39	F (6, 108) = 16.7	< 0.0001

Results of the two-way repeated measure ANOVA results for the standard deviations of the symmetry indices.

SS sum of squares, DF degrees of freedom, MS mean squares, F F-ratio, DFn degree of freedom for the numerator of the F-ratio, DFd degree of freedom for the denominator of the F-ratio.

Significant values are in bold.

Comparison with the ASYM condition

Both SI_BCoM and iHR significantly discriminated between ASYM and the corresponding walking condition (0.83 m s⁻¹) in all three directions (SI_BCoM: t = 9.51, df = 9, p < 0.0001; t = 3.58, df = 9, p < 0.01; t = 9.71, df = 9, p < 0.0001 for AP, ML, and CC directions respectively; iHR: t = 8.28, df = 9, p < 0.0001; t = 7.38, df = 9, p < 0.0001; t = 6.85, df = 9, p < 0.0001 for AP, ML, and CC respectively). Similarly, a significant difference existed between ASYM and walking at 0.83 m s⁻¹ for SA (t = 2.96, df = 9, p = 0.016).

In terms of stride-to-stride symmetry variability, significant differences were found between ASYM and walking at 0.83 m s⁻¹ for both SI_BCoM and iHR in AP (SI: t = 3.23, df = 9, p < 0.05; iHR: t = 5.02, df = 9, p < 0.001), as well as for SA (t = 2.97, df = 9, p < 0.05). Conversely, no difference was found for the ML and CC direction for both SI_BCoM and iHR.

Discussion

The present study focuses on the quantification of gait symmetry and on the influence of walking speed on this aspect. Specifically, three different symmetry indices were extracted from the trajectory of the body center of mass, the acceleration measured at the lower trunk, and step duration during walking on a treadmill at seven different speeds.

Gait symmetry values in terms of SI_BCoM, iHR, and SA are in agreement with the existing literature for the walking speeds already investigated, either on treadmill^11,13 or overground^14,17,36. Participants exhibited peak values of gait symmetry for both SI_BCoM and iHR across the entire spectrum of walking speeds they covered. This supports the idea that individuals may not achieve their maximum symmetry when they walk at their self-selected pace. Furthermore, the speed at which gait symmetry was maximum varied depending on the specific anatomical axis and index being considered. A similar pattern was observed for SA, where peak values were achieved within a range of walking speeds spanning from 0.28 to 1.95 m s⁻¹. Interestingly, perfect symmetry was not displayed in any axes and any indices. This aligns with previous studies reporting that a certain degree of asymmetry is present even in healthy people, reflecting natural functional differences between the two body sides^3,11,37–40. This degree of asymmetry changes according to the considered index and anatomical axis and should be taken into account when comparing healthy and pathological populations. Similarly, variability in stride-to-stride gait symmetry changes based on the chosen index, direction, and speed, spanning from 1 to 18% (Fig. 3). Specifically, a greater standard deviation was found for low walking speeds for all three indices (especially in the AP and CC directions for SI_BCoM and iHR). The iHR index displayed a significant greater variability with respect to SI_BCoM in the ML direction. This agrees with previous research, which observed that the variability of the iHR was twice as pronounced in the ML direction compared to the other two directions, in young and elderly people as well as in amputees walking at self-selected speed¹⁷. These varying degrees of variability need to be taken into account when determining the required sample size in future studies.

When comparing gait symmetry obtained from the BCoM trajectory and from accelerometric signals, the results revealed significant differences in all three anatomical directions (Fig. 2). Essentially, SI_BCoM and iHR can provide distinct information about the symmetry of gait. This may be due to several factors: first the considered data source, both in terms of location and type of signal. The BCoM trajectory is derived using a weighted segmental approach, while acceleration is measured at the lower trunk, approximately at L1–L2 level. The fact that these two “points” do provide different information has been widely demonstrated^28,30. Furthermore, a prior study conducted by Navvab Motlagh and Arshi¹³ used SI_BCoM to quantify gait symmetry from both the BCoM and a single marker on the sacrum: their findings indicated discrepancies between the two approaches, especially in the AP direction. This is consistent with the results of the present study, which further expand this difference to the other directions. Second, SI_BCoM relies on the amplitude of the harmonics, whereas iHR considers the power of these harmonics. This distinction might account for the higher values observed with iHR in the AP and CC directions compared to SI_BCoM (Fig. 4). However, it does not explain the opposite trend observed in the ML direction, where SI_BCoM consistently demonstrated average values exceeding 90% across all walking speeds, including the ASYM condition. These findings suggest that when analyzing the BCoM trajectory, the ML component is less affected by asymmetrical characteristics when compared to the AP and CC components¹¹. This is not the case when considering the acceleration measured at lower trunk level and might be explained by the different frequency content of the two signals: whereas the ML component of the BCoM trajectory is essentially characterized by a “pure” sinusoidal wave (first harmonic), the Fourier spectrum of the ML acceleration measured at the lower trunk displays peaks across nearly all odd harmonics (Fig. 1). Interestingly, this applies to the ASYM condition as well.

Figure 4.

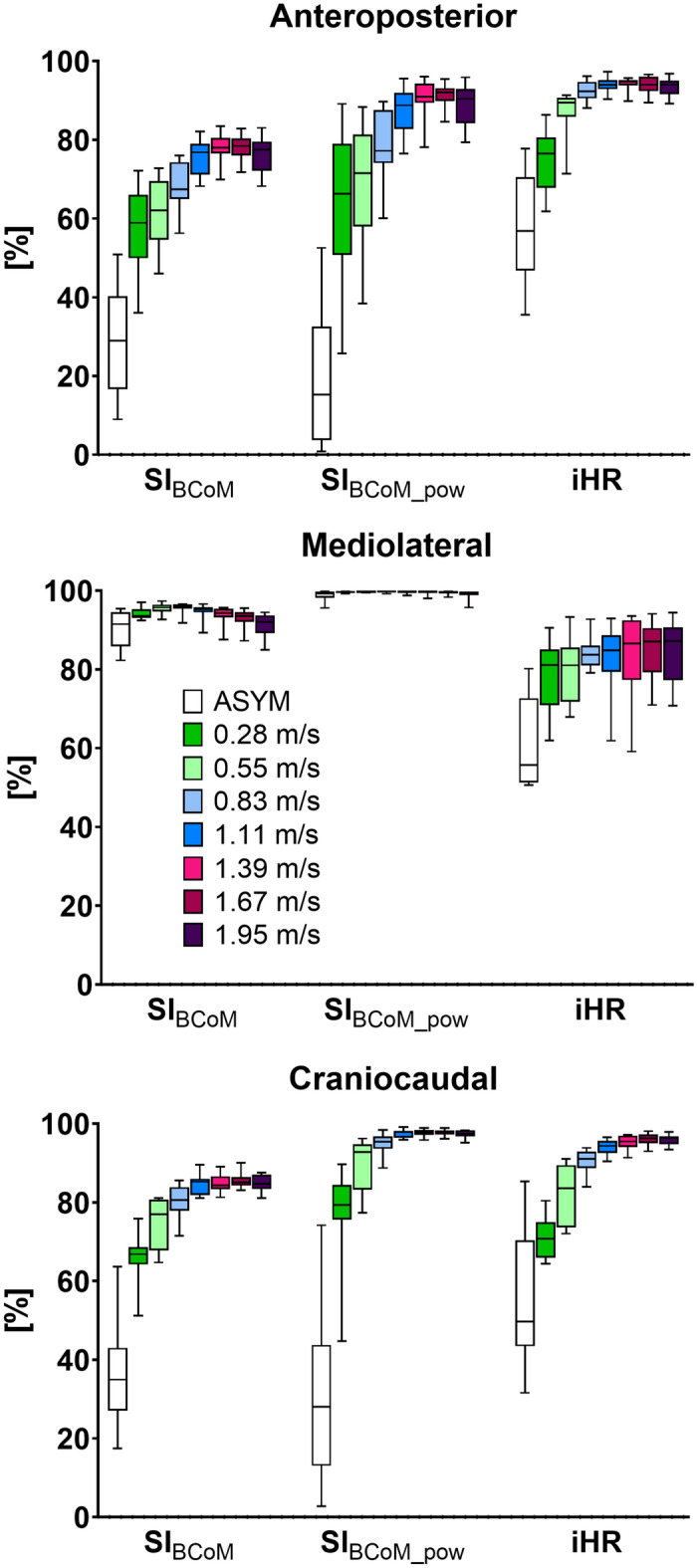
Box plots of the mean values over strides of Symmetry Index (SI_BCoM), the SI obtained using the power of each harmonic instead of the amplitude (SI_{BCoM_pow}), and the improved Harmonic Ratio (iHR) in the anteroposterior (AP), mediolateral (ML) and craniocaudal (CC) directions over each considered walking speed as well as when simulating asymmetrical walking (ASYM condition).

The effect of walking speed on gait symmetry has been investigated in previous studies, with no unanimous consensus emerging on this matter. The outcomes vary depending on the data source, the mathematical approach used to quantify symmetry and the range of walking speed considered²⁴. In the present study, SA does not exhibit any speed-related effect, whereas both SI_BCoM and iHR do show a speed-dependent effect, displaying significantly smaller values at low walking speed. These values reach their maximum and remain relatively constant between 1.11 and 1.39 m s⁻¹. This trend aligns with findings from previous studies, even though they might not necessarily employ the same data sources or mathematical approaches as the present study^{11,13,15,23,33,41}. The different behavior of SA, when compared to the other indices, suggests that a spatiotemporal parameter like step duration may not adequately capture the complex dynamic of the whole body. It is worth noting that this study is the first to investigate seven different walking speeds, ranging from 0.28 to 1.95 m s⁻¹. This comprehensive analysis allows for a thorough characterization of a wide range of speeds commonly encountered in various contexts of human walking, including those involving pathological populations. Consequently, our findings underscore the importance of considering the effect of walking speed when assessing gait symmetry in clinical settings where pathological and control populations may walk at significantly different speeds^22,41,42.

All three indices effectively discriminate simulated asymmetrical gait from typical gait at the same speed. While there was considerable variability among individuals in all indices for the ASYM condition, it is noteworthy that the stride-to-stride variability in this condition was actually less than that observed across all walking speeds, especially for SI_BCoM in the AP and CC directions. This indicates a high level of within-subject consistency in replicating an asymmetrical gait pattern (Fig. 3).

The present study considers exclusively young, healthy participants. Future research should encompass a wider range of age groups and diverse anthropometric profiles as well as individuals with pathological conditions characterized by asymmetrical gait.

Conclusions

This study demonstrates that gait symmetry, as assessed from the body centre of mass trajectory, can differ significantly compared to symmetry obtained from lower trunk acceleration or temporal parameters of gait. It is crucial to be meticulous about the specific aspect under consideration when quantifying gait symmetry, as the interpretation of the results can significantly hinge on the data source and mathematical approach employed. Importantly, current findings support the idea that gait is asymmetrical in the healthy population. Acknowledging this aspect is crucial when establishing rehabilitation objectives and assessing the quality of gait in patients with pronounced walking asymmetry. Additionally, it is important to note that frequency-based symmetry metrics can be influenced by gait speed. This highlights the need for caution when comparing individuals walking at different speeds.

Author contributions

E. B. contributed to the conception and design of the work, to the acquisition, analysis, and interpretation of data. E.B. wrote the main manuscript text and prepared figures and tables. A.C. contributed to the design of the work. G.P. contributed to the conception and design of the work, to the acquisition, analysis, and interpretation of data. All authors substantively revise the manuscript and approved the submitted version of the manuscript.

Funding

This study was funded by the Eurepean Union - NextGenerationEU - M4, C2, 1.1, under the project PRIN 2022 (DD MUR n.104 del 02.02.2022) entitled “CARAMELLA - Contactless And ReliAble MovEment anaLysis with miLlimeter-waves rAdars” – CUP H53D23000550006, Project Code: BERG_E_24_RN_PRIN_CARAMELLA_01 (2022TLSWHM).

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-69461-w.