Multiclass Segmentation of Suspicious Findings in Simulated Breast Tomosynthesis Images Using a U-Net

Abstract

Our lab has built a next-generation tomosynthesis (NGT) system utilizing scanning motions with more degrees of freedom than clinical digital breast tomosynthesis systems. We are working toward designing scanning motions that are customized around the locations of suspicious findings. The first step in this direction is to demonstrate that these findings can be detected with a single projection image, which can guide the remainder of the scan. This paper develops an automated method to identify findings that are prone to be masked. Perlin-noise phantoms and synthetic lesions were used to simulate masked cancers. NGT projections of phantoms were simulated using ray-tracing software. The risk of masking cancers was mapped using the ground-truth labels of phantoms. The phantom labels were used to denote regions of low and high risk of masking suspicious findings. A U-Net model was trained for multiclass segmentation of phantom images. Model performance was quantified with a receiver operating characteristic (ROC) curve using area under the curve (AUC). The ROC operating point was defined to be the point closest to the upper left corner of ROC space. The output predictions showed an accurate segmentation of tissue predominantly adipose (mean AUC of 0.93). The predictions also indicate regions of suspicious findings; for the highest risk class, mean AUC was 0.89, with a true positive rate of 0.80 and a true negative rate of 0.83 at the operating point. In summary, this paper demonstrates with virtual phantoms that a single projection can indeed be used to identify suspicious findings.

1. INTRODUCTION

Women with radiographically dense parenchyma are usually associated with having an increased risk of cancer.^1,2 Breast density can limit the sensitivity of screening exams and potentially result in missed detections (known as masked cancers) or mischaracterizations of lesions.³ Personalized screening programs recommend additional or supplemental imaging for women with dense or complex mammary parenchyma to detect more cancers at early stages.^3–8 However, for those who receive supplemental imaging, the current imaging methods lack specificity.^9–12 Currently, no direct quantitative criterion exists to identify women for supplemental or triaged imaging, resulting in a greater number of false-positive (FP) findings.

A prototype next-generation tomosynthesis (NGT) system was built at the University of Pennsylvania (Penn) to improve the detection and characterization of breast lesions and the discrimination of glandular (dense) from adipose tissue.¹³ The NGT design incorporates in the x-ray source scanning an additional component of motion in the posteroanterior direction, reducing out-of-focus structures when compared with conventional imaging systems.^13,14 Our ultimate goal is to integrate fast and intelligent methods into the NGT engine (and future designs) to identify suspicious areas and to improve the image quality in regions that are prone to mask cancers. In this paper, we investigate how a single 2D projection image can be used to identify regions that are prone to masking. Our long-term goal is to design more complex scanning motions that are directed specifically around these regions. This paper represents the first step in that direction by demonstrating the feasibility of real-time image analysis using a single 2D projection image, which could be used to guide the choice of x-ray source locations in the remainder of the scan.

Virtual clinical trial (VCT) methods have been used to evaluate, optimize, and validate the acquisitions of the NGT design.^15–17 VCTs are usually targeted toward specific clinical tasks, requiring computational simulations of human anatomy (anthropomorphic phantoms).¹⁵ To simulate clinical tasks that require a risk assessment of masked cancers or characterization of breast lesions, anthropomorphic phantoms should realistically simulate the anatomic noise seen in images of the mammary parenchyma.¹⁸ Just a few studies have been reported in the literature about VCT methods for assessing and estimating the risk of masking cancers.^19,20 Mainprize et al. developed a masking index that locally assesses the signal-to-noise ratio of synthetic images using noise spectrum, modulation transfer function, and a task function that represents the psycho-visual model for lesion detectability.¹⁹ However, nonlinear imaging modalities, such as digital breast tomosynthesis (DBT), complicate the use of these traditional metrics of image quality.²¹ In addition, the simulation of complex mammary parenchyma is required to validate the use of objective metrics proposed for estimating the risk of masking cancers.¹⁸

Computer simulations of Perlin noise can improve substantially the realism of mammary parenchyma of virtual breast phantoms.¹⁸ Perlin noise²² uses gradient values that are smoothly connected by an interpolation function that is used to generate complex textures and patterns in medical imaging.^18,23 Dustler et al. have proposed the use of a variation of Perlin noise called fractal noise (or fractional Brownian motion) to simulate realistic small-scale breast structures that improve the complexity of simulated mammary parenchyma of phantoms.^24,25

In this study, we used a Graphics Processing Unit (GPU) based library to accelerate simulations of Perlin-noise phantoms.¹⁸ We developed an automated method to identify suspicious regions that are prone to mask cancers in Perlin- noise phantoms. These suspicious regions are considered “hotspots” for masking cancers. A U-Net architecture²⁶ was trained for multiclass segmentation of hotspot areas in breast images simulated using the NGT acquisition geometry. The central aim of this study is to demonstrate that hotspots can be detected in a single projection image, as this is motivated by our long-term goal of designing scanning motions that are customized around the locations of these findings.

2. MATERIALS & METHODS

2.1. Data Simulation

2.1.1. Breast Outline and Mammary Parenchyma

Breast outlines were simulated using software that models breasts under mammography compression using the principal component analysis (PCA) method.^27,28 The PCA software characterizes and models realistically the compressed breast curvature between the support table and the compression paddle. In total, 20 outlines of 0.2 mm³ voxel size were modeled under craniocaudal (CC) compression (Figure 1A). The outlines were created using 30, 40, and 50 mm of compressed breast thickness (CBT). The chest-wall to nipple distance (CND) varied from 50 to 110 mm.

Figure 1.

(A) Example of PCA-based breast outline, (B) simulation of coarse tissue, (C) parenchyma simulation, and (D) volume view resulting from Perlin noise-based breast phantom (CC compression).

Recursive partitioning software²⁹ was used to simulate coarse tissue within the binary outline (adipose, glandular, and Cooper’s ligaments shown in Figure 1B). The coarse phantoms were simulated using 25–45% overall volumetric breast density. Note that only dense phantoms were simulated to represent breast anatomies with an increased likelihood of masked lesions. An erosion morphology operation was applied to the binary volumes to simulate the breast skin. The skin thickness was varied randomly in a [0.2, 2.4] mm interval using ball structuring elements.^30,31

Finally, 3D fractal noise (also known as Perlin noise)²² was simulated within the internal region of each outline to represent the anatomy of breast parenchyma (Figure 1C).^18,32 The fractal noise parameters known as lacunarity, persistence, and octaves were varied using the values {2, 3}, {0.75, 1.00}, and 6, respectively. These parameters were previously reported by Dustler et al.^24,25 The noise frequencies were normalized between [0.0001, 1] interval, and the log_e was applied to the voxel distribution, resulting in frequencies that are proportional to the linear x-ray attenuation of the materials in the log scale.³³ The voxel values were normalized within a 6-bit (unsigned) resolution (where materials 0 and 63 represent air and skin, respectively). The output of this normalization is known as the “Perlin phantom” (Figure 1D).^18,32 The Perlin phantoms were simulated using the open-source Perlin-CuPy methods (developed in-site).^18,32

2.1.2. Lesions

Soft-tissue lesions (ellipsoidal and spiculated) were simulated and embedded in the Perlin-noise phantoms (Figure 2). Two lesions were embedded in each phantom using a random position in the posteroanterior (x) and chest-wall (y) direction but always in the center of the phantom in the craniocaudal direction (z). The spiculated models were segmented and scaled from contrast-enhanced magnetic resonance images in three orthogonal views (sagittal, coronal, and transverse).³⁴ A voxel additive method³⁵ was used to insert the lesion models in the phantoms. The attenuation of lesions is controlled by varying a weighting factor³⁵ (w_l) of the partial volume of voxels. In this study, w_l was set to 0.20 and 0.35 for lesions simulated using the ellipsoidal and spiculated models, respectively. The lesion dimensions were 7×7×7 mm³ for both models.

Figure 2.

Volume view of breast lesion models: (A) ellipsoidal, and (B-D) spiculated masses.³⁵

2.1.3. X-ray Images and Risk Maps

Each voxel from the simulated breasts represents a composite material that consists of a complementary mixture of adipose and glandular tissue (partial volume).¹⁸ For the 61 materials used to simulate Perlin noise (breast tissue and lesions), the composition of the partial volume of voxels decreases linearly from 99% to 1% of adipose tissue and increases linearly from 1% to 99% of glandular tissue.¹⁸ These composite materials vary the x-ray attenuation of the images.¹⁸

The OpenVCT framework³⁶ was used to simulate DBT projections of the breast phantoms. The projection algorithm uses a fast GPU implementation of the Siddon method for ray-tracing.³⁷ The DBT projections were simulated assuming the conventional acquisition geometry of the NGT system, following a left-to-right scanning motion along the chest wall (Table 1). For the purpose of this study, only the central projection image was used to train the U-Net model (more details in the next section). We want to demonstrate the feasibility of modifying the subsequent x-ray source locations from the NGT default scan. The acquisition exposure settings were simulated using the automatic exposure control data.¹⁴ The attenuation coefficient data of the materials used to simulate phantoms come from the International Commission on Radiation Units & Measurements (ICRU) Report 44.³⁸

Table 1.

Summary of DBT acquisition parameters.

X-Ray Imaging
Number of Projections	15
Medio-lateral (ML) Distance of Projections (max, mm)	180
Posterior-anterior (PA) Distance of Projections (max, mm)	0
Anode and Filter Materials	Tungsten and Aluminum
Filter Thickness (mm)	0.7
Angular Range ML (°)	±7.5
Tube Motion	Step-and-Shoot
Detector
X-Ray Converter Material	Amorphous Selenium (a-Se)
Detector Element Size (width × height, mm)	0.085 × 0.085
Number of Elements (width × height, #)	3584 × 2816
Detector Size (width × height, mm)	304.64 × 239.36
Source-to-Image Distance in central projection (mm)	722.0

The maximum intensity projection (MIP) of the coarse phantoms (Figure 1B) was used to create “risk maps” (Figure 3A). MIP projects the coarse voxels from the phantoms with the maximum intensity (i.e., maximum risk) that falls in the way of parallel rays traced from the source to the plane projected at the x-ray detector. The maps were categorized into different classes: background+skin (risk 0), breast tissue predominantly adipose (risk 1), predominantly dense (risk 2), and lesion (risk 3). The maps were used to train a U-Net model along with the corresponding central DBT projection (Figure 3B). The purpose of training the U-Net model in this manner is to demonstrate the feasibility of using a single projection image to identify hotspots, as this could ultimately be applied to designing a system capable of real-time image analysis for task- directed scanning motions.

Figure 3.

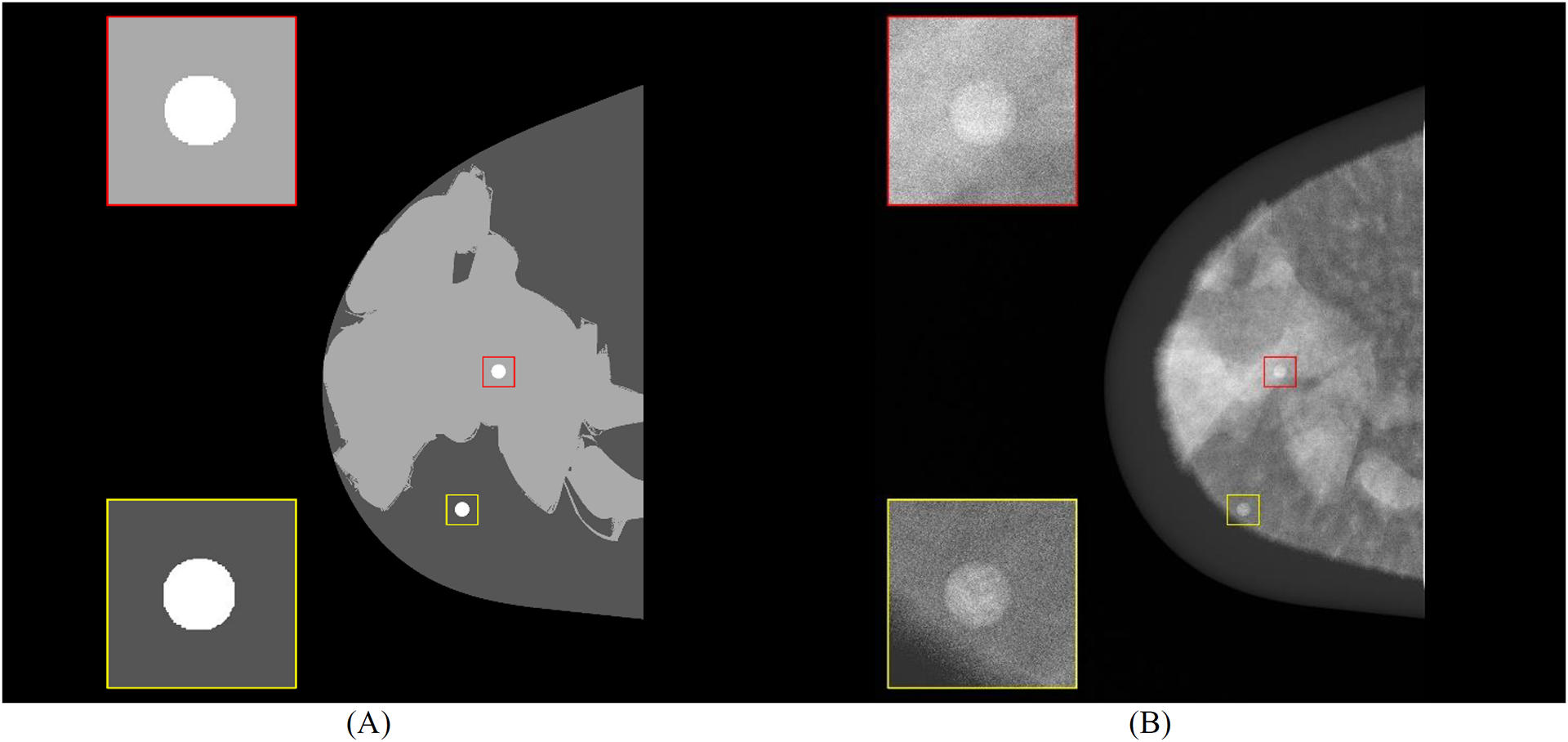
Central slice (craniocaudal) of (A) mask using 4-class masks (background, predominantly adipose, predominantly dense, and diseased tissue) and (B) central DBT projection (for processing - contrast levels modified with window level settings) with highlighted breast curvature (dark gray). Spherical masses embedded in simulated tissue predominantly dense (red) and predominantly adipose (yellow) are shown.

2.2. Multiclass Segmentation

The U-Net architecture²⁶ was used to predict risk maps from DBT projections ([0,1] normalization). The images were cropped to reduce the excessive background and the burden of processing. The cropped region corresponds to the max of CND size of the thickest phantom. The U-Net consists of 4-encoder layers that down-sample the reconstructed images and 4-decoder layers that up-sample the segmented regions of the risk maps (Figure 4). Two convolutions (3×3 kernel) and one max-pooling (2×2 kernel) with leaky rectified linear unit (ReLU) activation are performed in each encoder layer. Padded kernels were used to maintain the aspect ratio of the input images. Batch normalization (BN) was used after each convolution. The final convolution (conv 1×1) maps a feature vector (feature maps) to the number of classes.

Figure 4.

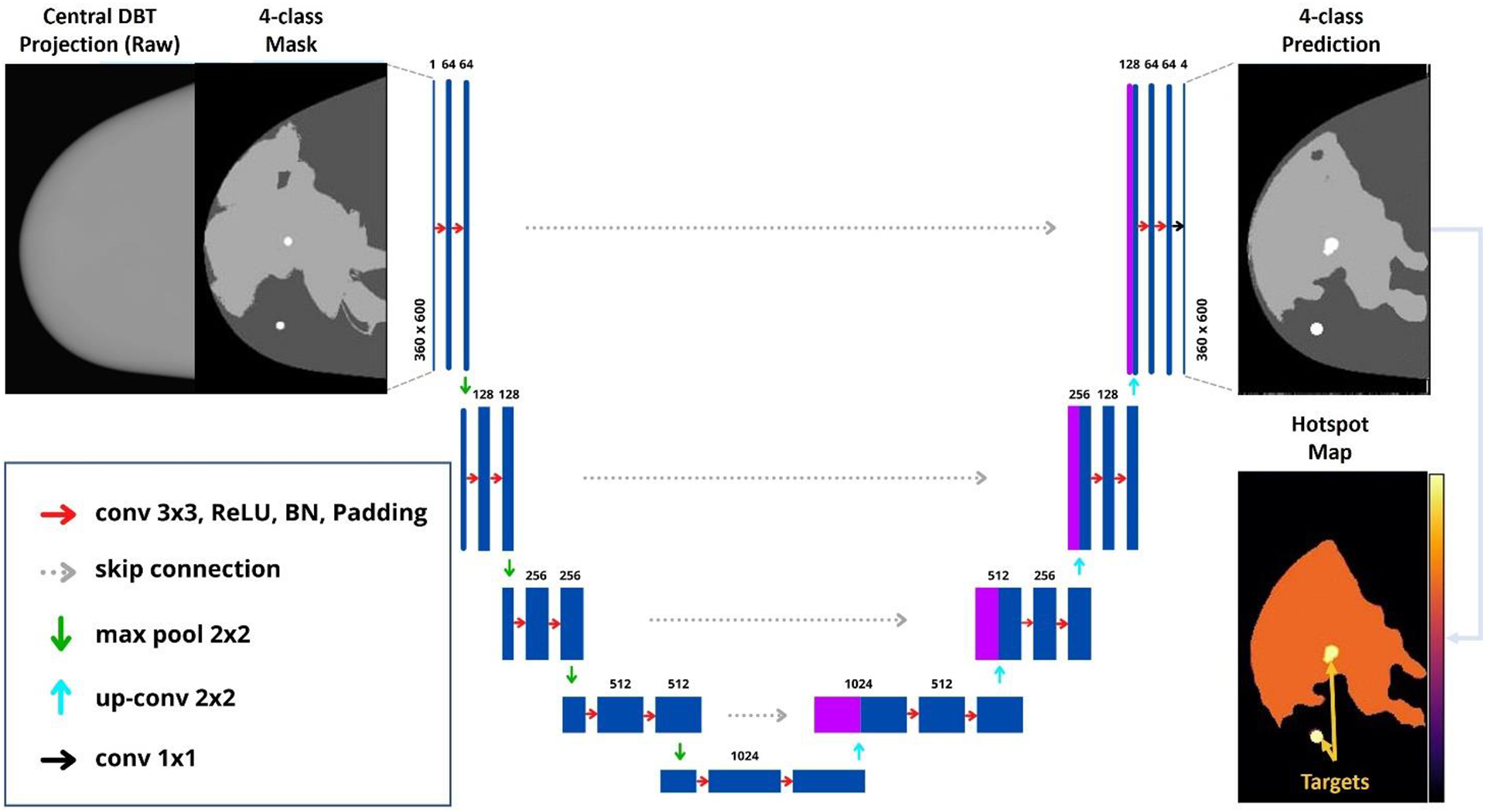
U-Net architecture implemented for multiclass segmentation of risk maps.

A U-Net model was trained for multi-class segmentation using four classes (Figure 3). The model was trained on two NVIDIA Quadro P5000 GPUs with 32 GB of RAM. We used a batch size of 22, 12 workers (sub-processes used for loading images), learning rate of 1×10⁻⁵, and Adam optimizer. Early stopping was used to optimize the number of epochs of each training model (max of 250 epochs) and to avoid poor generalization performance. Weighted cross-entropy was used as the loss function (weights 1, 1, 2, 2). The hyperparameters multiplicator (weights) and learning rate were optimized using weights and bias sweeps (wandb, version 0.12). The model was built using PyTorch 1.10 and Python 3.9.9.

In total, 168, 48, and 24 input images (360×600 pixels) were used for training, validation, and testing, respectively (ratio 70:20:10%, respectively). For each set, the input images were randomly selected but equally distributed by volumetric breast density, lesion type, Perlin parameters, and breast thickness to avoid bias in the training models. The predictions of the test set were obtained, and the predictions for each class (softmax) were used to create hotspot maps (Figure 4).

The performance of the models was evaluated using the area under the pooled receiver operating characteristic (ROC) curve (AUC). The R libraries “pROC” (version 1.17) and “auctestr” (version 1.0) were used to collect the ROC statistics. The operating point of the ROC curve was defined to be the point that minimizes Euclidean distance relative to the upper left corner of ROC space; at this operating point, we calculated the true positive rate (TPR), true negative rate (TNR), positive predictive value (PPV), and negative predictive value (NPV). Finally, the segmentation metrics Jaccard (Jac) and Dice coefficients were calculated using the 4-class predictions.

3. RESULTS

Our preliminary results have shown that the developed software is capable of precisely segmenting regions with the lowest risk of lesions (risk class 0, Figure 5B) in the central projection (Figure 5A). The software predictions (Figure 5C) indicate efficient differentiation between tissue predominantly adipose (risk class 1) and predominantly dense (risk class 2). In addition, regions with lesions are segmented by the U-Net models and classified with the highest risk (risk class 3). Note that the “hottest spots” (i.e., peaks of confidence) show the highest peaks of regions with lesions in the confidence images (Figure 5D). For future work, we will use the hotspot images to reduce the number of false positives from the predictions.

Figure 5.

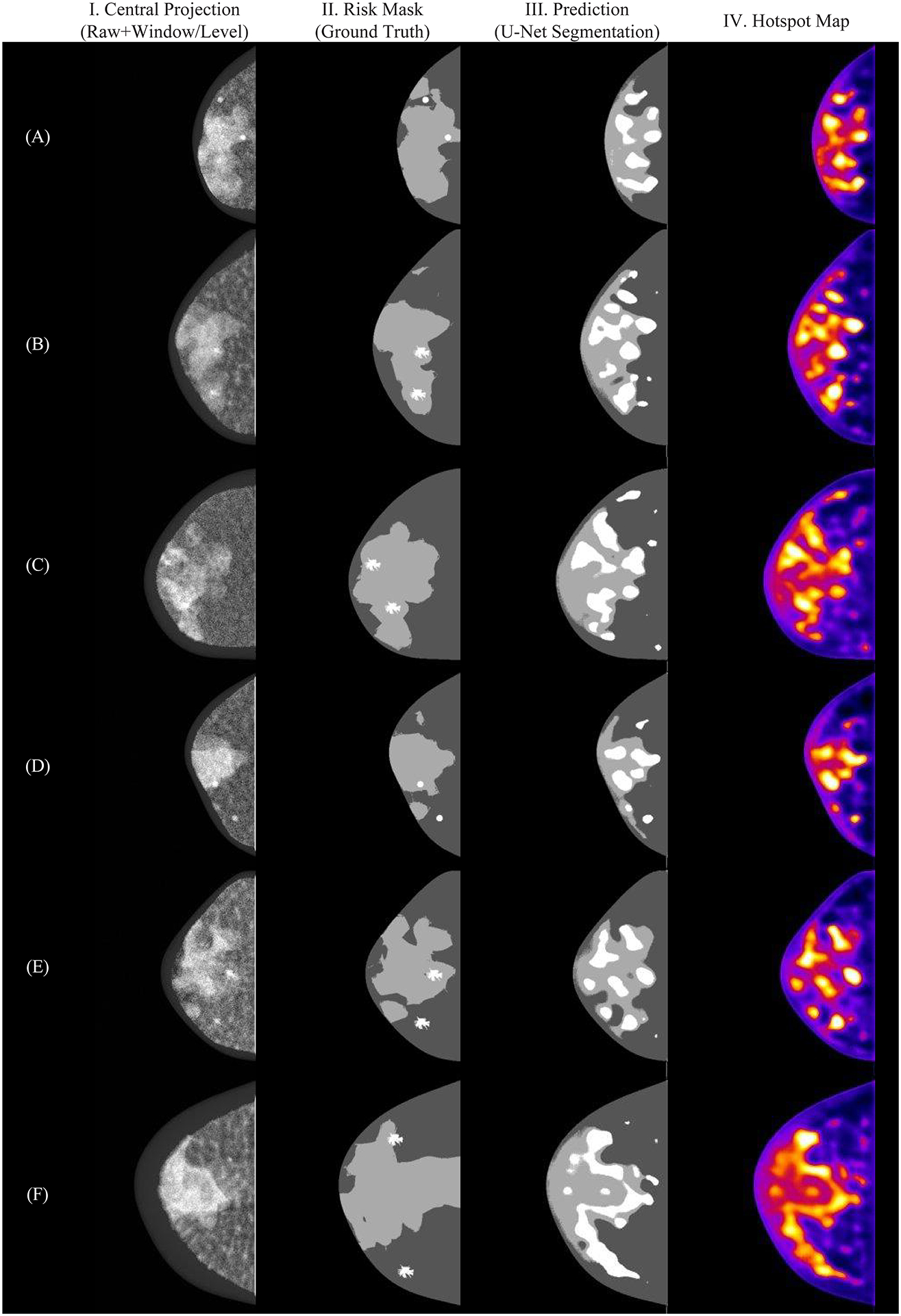
Examples of multi-class segmentation using U-Net model: (I) central projection, (II) risk masks, (III) predictions and (IV) hotspot map.

The multiclass model shows an ideal segmentation for risk class 0 (Figure 6B). Thus, the classification metrics were calculated without considering the predicted values for this class. For risk class 1, the ROC (Figure 6A) resulted in an AUC value of 0.93, demonstrating an effective segmentation of predominantly adipose tissue. Risk class 3 resulted in the lowest values of Dice (0.11) and Jaccard (0.06) due to a large number of false positives. However, this class shows a high TPR (0.80), which is comparable to risk class 2 (0.81). This result is consistent with the hotspots (i.e., peaks of confidence) found in the confidence images (Figure 5B).

Figure 6.

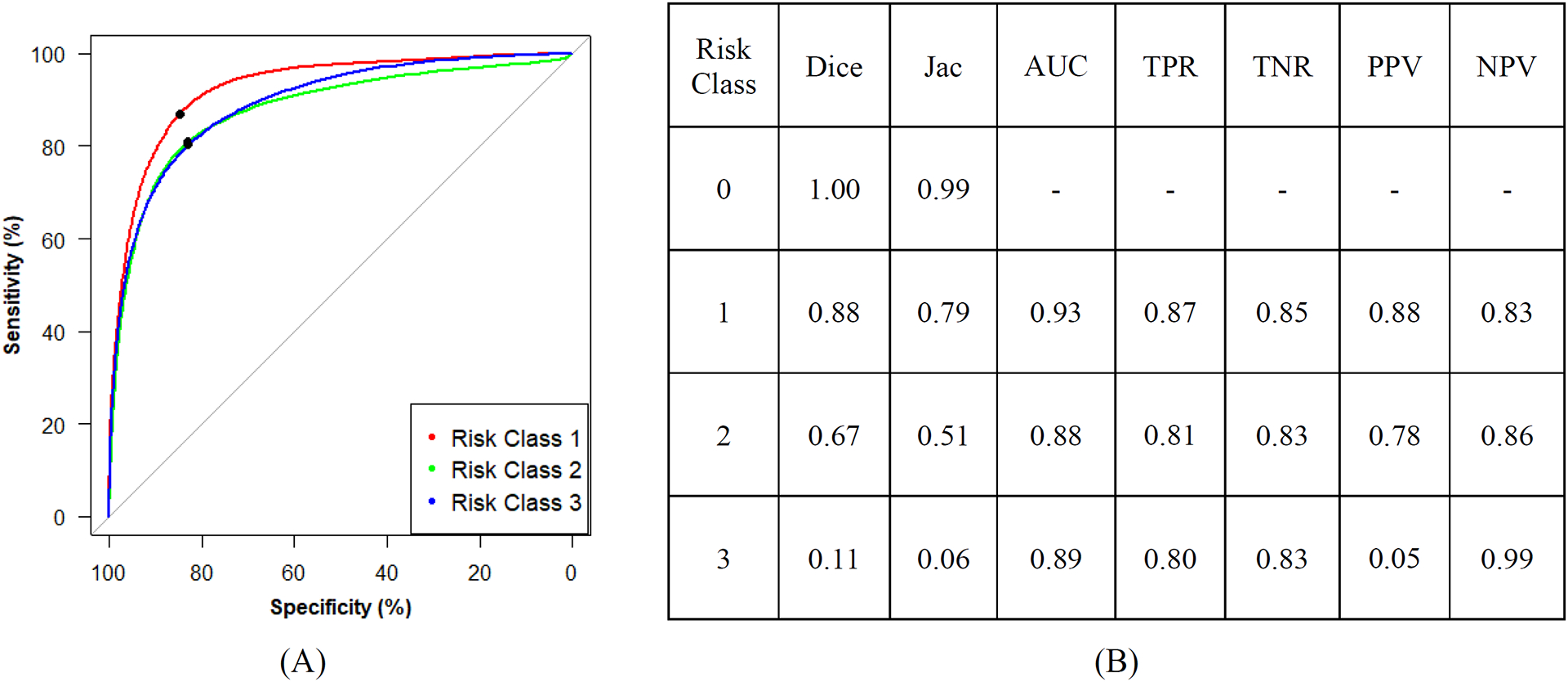
(A) Receiver operating characteristic curves (operating point in black) and (B) summary of segmentation and classification metrics.

The weighted cross-entropy loss maximizes the accuracy of the learning model, avoiding overfitting due to imbalanced data between the four classes. Based on these results, the sweeping of hyperparameters penalizes the segmentation of predominantly dense tissue to improve the segmentation of lesions, improving the accuracy of locating hotspot regions.

4. DISCUSSION AND CONCLUSION

The sensitivity of cancer detection by screening mammography is reduced in women with dense breasts, resulting in masked cancers and mischaracterizations of lesions. In this work, we have developed an automated method to identify suspicious areas in breast phantoms with a single 2D projection image. Our future work will apply this method to designing a DBT system capable of identifying suspicious areas in real time and dynamically calculating the scanning motion that optimizes visualization of these areas, potentially improving the sensitivity of cancer detection and the characterization of suspicious findings. It is important to mention that the ultimate goal of the software is not to be used as a computer-aided diagnosis (CAD) system. Instead, the software should be used to indicate regions with a higher likelihood of cancer.

This study has some limitations. Spiculated lesions have sharp ramifications on the tumor that can vary greatly in density and length, from a few millimeters to several centimeters (Figure 2). These ramifications complicate the segmentation, reducing the performance of the model shown in the segmentation metrics (Figure 5B). In addition, the linear attenuation coefficient of the lesions composed of soft tissue is very close to the dense tissue, which compromises the differentiation between risk class 2 and 3. However, the ultimate goal of this study is not the perfect segmentation of lesions (or dense tissue). Instead, we will use this software to indicate the locations of suspicious findings to improve the NGT acquisitions.

Another limitation of this study is that the U-Net model for identifying hotspots was developed with virtual breast phantoms as opposed to clinical images. Future work will explore alternate strategies for training the U-Net model using clinical images with known findings. In addition, we will increase the number of images for the test and validation set, use cross-validation during the training process, and investigate the use of alternative focal loss functions to improve the segmentation of the U-Net.