Abstract
Exoskeletons have enormous potential to improve human locomotive performance1–3. However, their development and broad dissemination are limited by the requirement for lengthy human tests and handcrafted control laws2. Here we show an experiment-free method to learn a versatile control policy in simulation. Our learning-in-simulation framework leverages dynamics-aware musculoskeletal and exoskeleton models and data-driven reinforcement learning to bridge the gap between simulation and reality without human experiments. The learned controller is deployed on a custom hip exoskeleton that automatically generates assistance across different activities with reduced metabolic rates by 24.3%, 13.1% and 15.4% for walking, running and stair climbing, respectively. Our framework may offer a generalizable and scalable strategy for the rapid development and widespread adoption of a variety of assistive robots for both able-bodied and mobility-impaired individuals.
Humans possess efficient and versatile mobility that stems from evolution, growth and learning4. Precise control of musculoskeletal systems produces natural transitions among various locomotion activities. Exoskeletons demonstrated the capability to improve human performance during walking for able-bodied individuals1,2 and to restore mobility for people with disabilities3. However, their control strategies typically use either a predefined assistance profile or hours-long human tests for each participant, even when only developing strategies for walking1 (Fig. 1a). Consequently, there is a formidable cost when the controller is applied to another participant or another activity. Moreover, handcrafted control laws for each activity are often required for several activities. This further complicates the controller design as the number of activities increases, making it impractical for the widespread adoption of wearable robots2.
Fig. 1 |. Experiment-free optimization of exoskeleton assistance through learning in simulation.
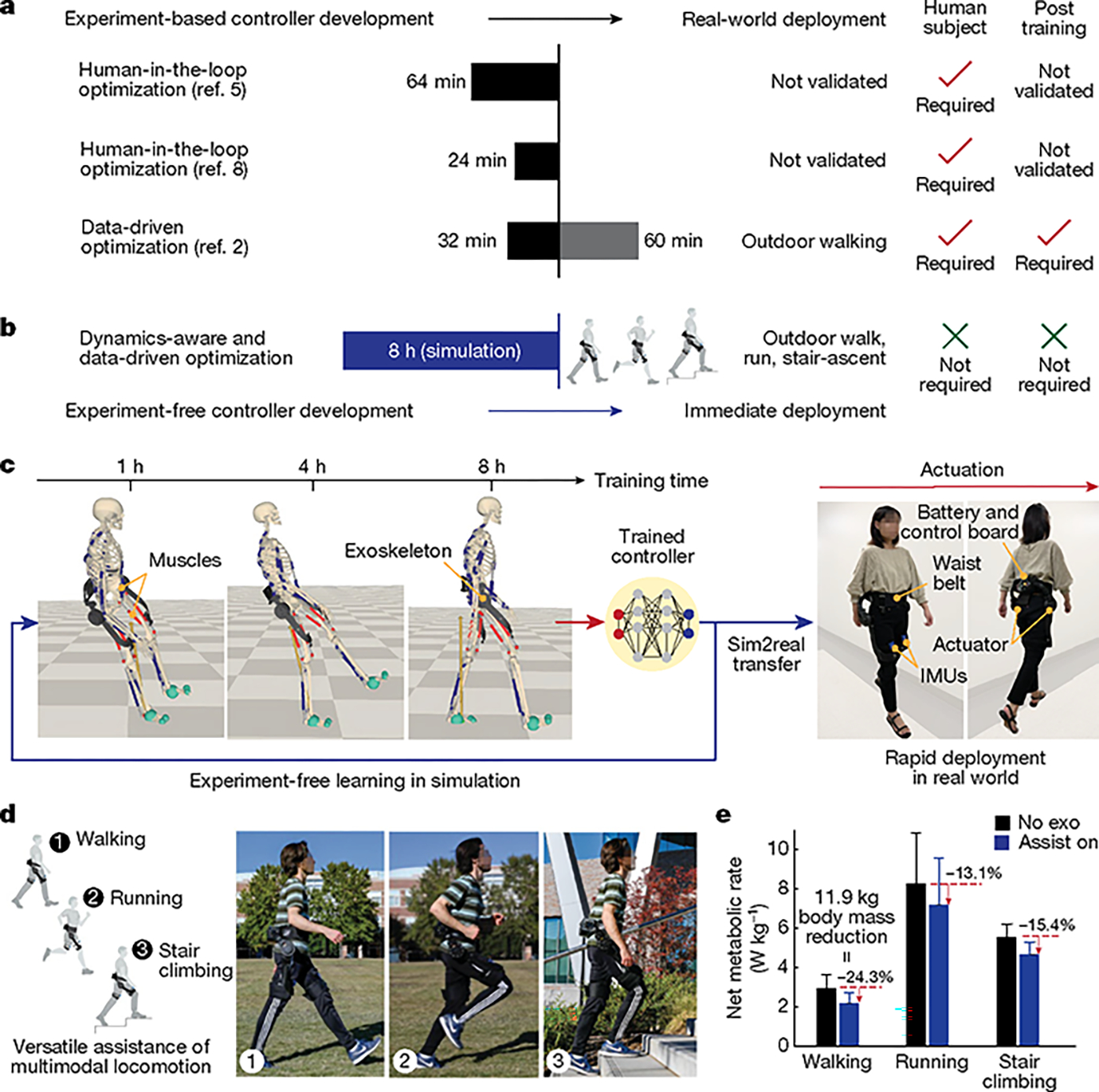
a, Existing experiment-based strategies for the controller development and real-world deployment of exoskeletons. The post-training column indicates the tuning time needed for the controller to be deployed in the real-world application. b, The proposed experiment-free method is called learning in simulation. c, The controller training based on neural networks in simulation for 8 h (left) and the immediate real-world deployment of an autonomous learned controller on an untethered exoskeleton without further training (right). d, Assistance of walking, running and stair climbing by the learned controller. e, Reduced metabolic cost for three activities (walking, running and stair climbing) by the adaptive learned controller. Values in e are mean and s.d. (the experiments in e were repeated independently; n = 8 for walking, n = 8 for running, n = 8 for stair climbing).
One challenge which impedes controller development is the substantial labour and time required for human subjects. Laboratory-based testbeds5–7 were developed to apply a wide range of assistance profiles to characterize the human response to robotic assistance. Human-in-the-loop optimization8 and myoelectric control9 optimized assistive torque to minimize metabolic rate, a key metric of human performance. However, this process may require more than 30 min per participant during walking8,9. A data-driven method2 enabled optimization for outdoor walking in 30 min for each participant. Although these methods have shown remarkable reductions in energy expenditure, they still require substantial human tests. One recent control method10 took less than 10 min to tune control parameters for tracking a predefined hip joint position trajectory, without reductions of metabolic rate. Simulation-based learning is a potential solution; however, no simulation has demonstrated their benefits in experiments with a physical robot because they either do not incorporate controller design11,12 or do not consider human–robot interaction13,14 in the simulation. How to develop a controller to enhance human performance purely from simulation remains an open question.
A second challenge of controller development pertains to accommodating the distinct biomechanics of multigait human locomotion. State-of-the-art algorithms use two levels of discrete control which first classify different locomotion activities and then discretize the gait cycle into several phases. Different control laws are applied for each segmented gait phase15,16 and each control law requires manual tuning of control parameters. Several control methods were proposed which directly generate the assistance profile for the full gait cycle using the estimated joint moment14,17 or a predefined trajectory18. However, these methods are tailored for discrete locomotion activities and require human training data for each activity. In addition, assistive torque produced by these methods can be uncomfortable because they are unable to handle transitions among locomotion activities. Reinforcement learning enables smooth control owing to its adaptability to environments and situations. However, it is primarily studied for robot control19–21 and does not involve humans, which poses unique challenges for controller design. A previous study to control a human–prosthesis system with reinforcement learning was limited to position tracking of a predefined gait kinematics trajectory22. Our previous work imposed predefined kinematic trajectories to drive the steady-state walking of a human in simulation23,24, in which the virtual human model simulated a person with quadriplegia and had no volitional interaction with the robot. Therefore, a compelling need arises for a method capable of learning a versatile controller to assist multimodal locomotion without relying on human tests or handcrafted rules.
Experiment-free learning-in-simulation framework
Here, we present an experiment-free learning-in-simulation framework which is data-driven and dynamics-aware, using reinforcement learning to expedite the development of exoskeleton controllers for multimodal locomotion assistance (Fig. 1b). First, to enable experiment-free learning, the data-driven components of our approach consist of three interconnected multilayer perceptron neural networks for motion imitation, muscle coordination and exoskeleton control (Fig. 2). Our control framework learns from human kinematic trajectory data for walking, running and stair climbing, obtained from a motion capture dataset25 (10 s reference data for each activity from one representative subject). Subsequently, the neural-network-based exoskeleton controller evolved through millions of epochs of musculoskeletal simulation to improve human performance by maximizing rewards (that is, the reduction of muscle activations). The training of the control policy runs once for 8 h on a graphics processing unit (GPU) (RTX3090, NVIDIA) for the controller to learn effective assistance for all three activities (Fig. 1c). Second, to improve simulation fidelity and training data-efficiency, the dynamics-aware components of our approach incorporate a 50 d.f. full-body musculoskeletal model with 208 skeletal muscles of lower and upper limbs (Fig. 2a) and the mechanical model of a custom hip exoskeleton used in this study (Fig. 2b). Reinforcement learning is notoriously data hungry26 and is thus computationally expensive. By incorporating physics models into the learning process, we are able to guide the learning process and improve efficiency. Third, we use a linear elastic model27 to simulate realistic human–robot contact to facilitate controller design. The musculoskeletal model and exoskeleton controller are trained simultaneously to produce high-fidelity biomechanical reactions with exoskeleton assistance, ultimately obtaining a unified controller across three activities and their transitions purely in simulation (Fig. 2c).
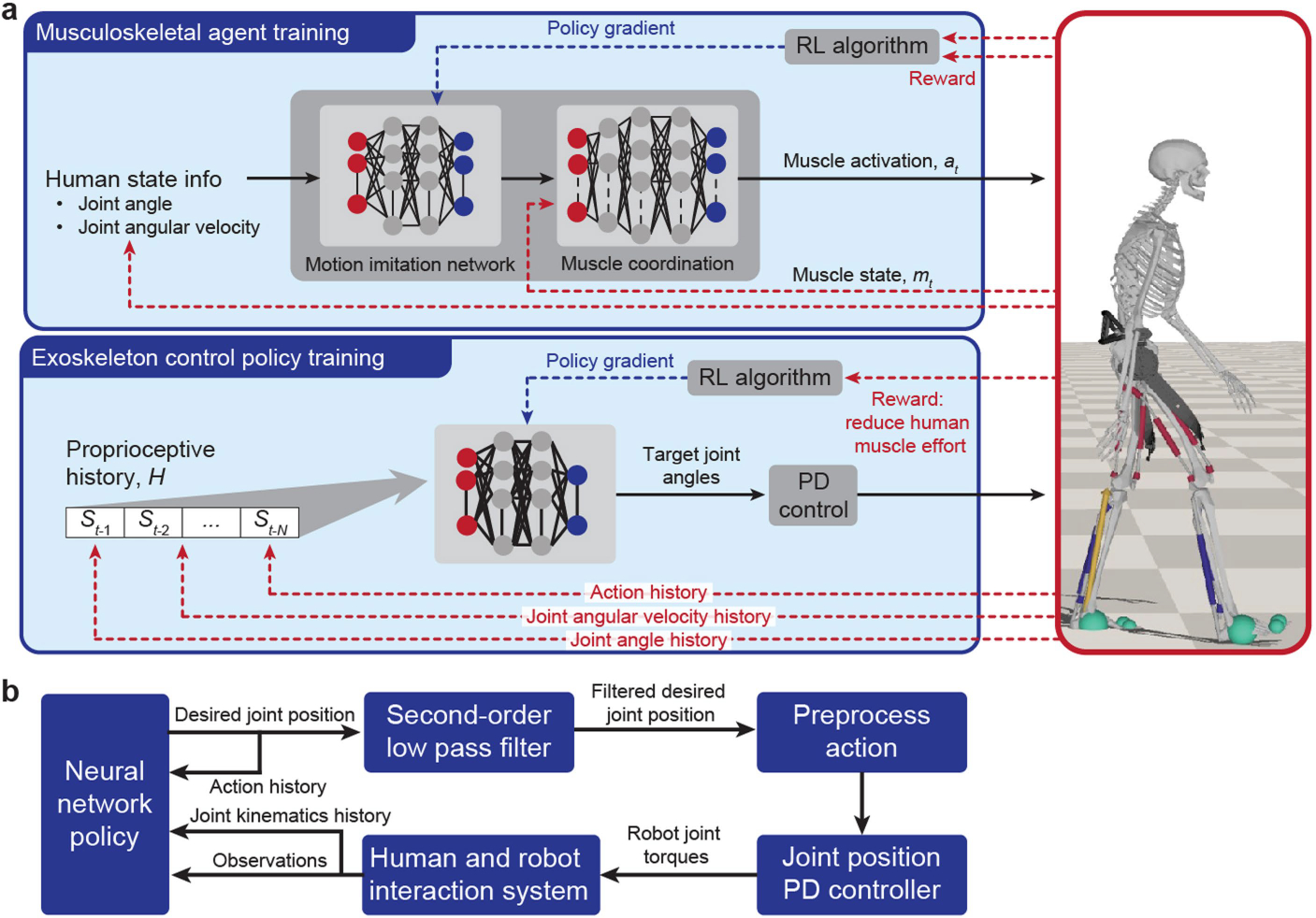
Fig. 2 |. Learning-in-simulation framework.

a, Full-body musculoskeletal human model consisting of 208 muscles. b, Physics-based exoskeleton model. c, Reinforcement learning in a data-driven and dynamics-aware human–exoskeleton simulation consisting of a motion-imitation neural network for versatile activities, a muscle coordination neural network for replication of human muscular responses and an exoskeleton control neural network for automatic generation of continuous assistance torque profiles. d, Deployment of the learned controller in the physical system.
Our learning-in-simulation framework enables end-to-end control as it maps the sensor inputs of a robot to assistive torque without any intermediate steps. The learned controller is computationally efficient and consists of a three-layer fully connected network and thus it can be implemented on a microcontroller. Compared to human-in-the-loop methods which require expensive equipment and extensive human tests to tune of the device, our controller requires kinematic measurements which are easy to obtain from portable wearable sensors, that is, one nine-axis inertial measurement unit (IMU) sensor (LPMS-B2, LP-Research) on each thigh, and accommodates three activities and transitions automatically without handcrafted control (Figs. 1d and 2d). The generated assistive torque profile is adaptive to different kinematic patterns (thigh angle and thigh angular velocities) of each user in each activity (Fig. 3b). This controller is computationally efficient and effective because the control policy was trained and optimized in simulation, which closely resembles the dynamics and biomechanics of the physical world. The primary contribution of this work is our control approach and its experiment-free efficiency and versatility for three locomotion activities obtained by means of learning in simulation. The controller also significantly reduced metabolic expenditures in three activities compared to state-of-the-art portable exoskeletons (Figs. 1e and 5c). These results highlight the feasibility of our reinforcement learning method despite large biomechanics variability among different individuals.
Fig. 3 |. Generalizable and adaptive assistive torque by the learned controller.

a, Schematic illustration for the experimental setup. b, Assistive torque profiles (normalized by body weight) for walking at 0.75, 1. 25 and 1.75 m s−1 and running at 2 m s−1 as a function of gait phases. Each line represents the assistance profile of one of the eight participants averaged across around 30 strides. c, Maximum assistive torque for each activity. In box plots, centre lines represent the median, box limits delineate the 25th and 75th percentiles and whiskers reflect maximum and minimum values (n = 8; individual participants). The experiments in b and c were repeated independently for each speed. Results for maximum flexion time, maximum extension torque and gait duration are available in Supplementary Fig. 1.
Fig. 5 |. Reduction in metabolic rate during walking, running and stair climbing.

a, Average net metabolic rate for level walking at 1.25 m s−1, running at 2.0 m s−1, stair climbing at 65 steps min−1 under three conditions (assist on, assist off and no exoskeleton). b,c, Metabolic rate reduction compared with the state-of-of-the-art portable hip exoskeletons13,15,28,30–36 (b) and portable knee41,44 and portable ankle2,45 exoskeletons (c) for walking (1.25 m s−1), running (2.5 m s−1) and stair climbing. A full list of comparisons is available in Supplementary Tables 4 and 5. In box plot of a, centre lines represent the median, box limits delineate the 25th and 75th percentiles and whiskers reflect maximum and minimum values (n = 8 for walking; n = 8 for running; n = 8 for stair climbing; individual participants). The experiments in a were repeated independently for each activity. Statistical significance and P values are determined by one-sided paired t-test; *P ≤ 0.05; **P ≤ 0.01.
Activity-adaptive versatile control
To demonstrate the controller’s ability to adapt to different locomotion activities, we conducted a treadmill experiment (Extended Data Table 1 listed the participants’ information) for walking and running at three different speeds. The weights and biases in the controller network are taken directly from the simulation and the inputs are thigh angles and angular velocities measured from one IMU sensor mounted on each thigh. These wearable sensor inputs are used to decode human intention and generate the desired assistive torque of the exoskeleton (Fig. 3a). The controller consists of a three-layer neural network and is implemented on a desktop computer running Simulink Real-time. Our method does not require intermediate activity detection or gait cycle detection. The assistance torque is generated in real-time at each time step (100 Hz, namely, 0.01 s) using the current thigh angle and thigh angular velocity plus the history data from the past 0.03 s (corresponding to three time steps). Through training in the simulation, our controller learned to treat human movement as a continuous process and produces appropriate real-time assistance torque which is synergistic to the user movement during not only steady-state movements but also the transition phases. To facilitate comparison with the literature8,13,15,28–36, we conducted treadmill experiments for walking at 0.75, 1.25 and 1.75 m s−1 and running at 2 m s−1. We chose to test across gait speeds to demonstrate the generalizability of the control policy. The assistive torque generated by the controller learned in the simulation is adaptive to walking and running at different speeds. The torque profiles of each participant (n = 8) were slightly different in shape for each activity because our controller was adaptive to different kinematic locomotion patterns (thigh angle and angular velocity) of each participant (Fig. 3b). The magnitude of the torque profile between walking and running also increases with locomotion speeds, demonstrating its ability to provide synergistic assistance for activities with different intensities (Fig. 3c).
Continuous assistive torque profile
To demonstrate the controller’s ability to generate smooth and synergistic assistance for three activities and their transitions, we conducted an activity-varying experiment in the real world for one participant. The participant started from slow walking at approximately 0.8 m s−1, accelerated to running at approximately 2 m s−1, then decelerated and finally began stair climbing (seven stairs) in a smooth manner (Fig. 4a). The same neural network controller used in the treadmill experiment was implemented on a hierarchical mechatronics architecture with a high-level microcontroller (Raspberry Pi 4) which sent torque commands to a low-level microcontroller (Teensy, PJRC) located in a waist-mounted control box. The torque profile during walking, running and stair climbing exhibited a distinct change in the profile shape as well as the magnitude of the assistance (Fig. 4b). Mechanical power of the exoskeleton also varied with the locomotion intensity (Fig. 4c), demonstrating the ability of the controller to provide synergistic assistance to the user. Several minor negative power peaks are present because readings of the IMU sensors do not precisely reflect the actual movement of the thighs because of soft wearable straps. Yet, these negative peaks are small (corresponding to an average of 3.47% of total delivered mechanical work for each gait cycle) and durations are brief (approximately 0.04–0.08 s, corresponding to 6–8% gait cycle), which has a negligible effect on the overall benefit of the exoskeleton assistance.
Fig. 4 |. Representative assistive torque during various activities and locomotion transitions.

a, Snapshots of a representative participant during continuously transitioned activities in one trial. b,c, Continuous assistive torque (b) and mechanical power (c) profiles autonomously generated by the learned controller during locomotion transitions between walking (about 0.8 m s−1), running (about 2 m s−1) and stair climbing.
Versatile assistive control with metabolic rate reduction
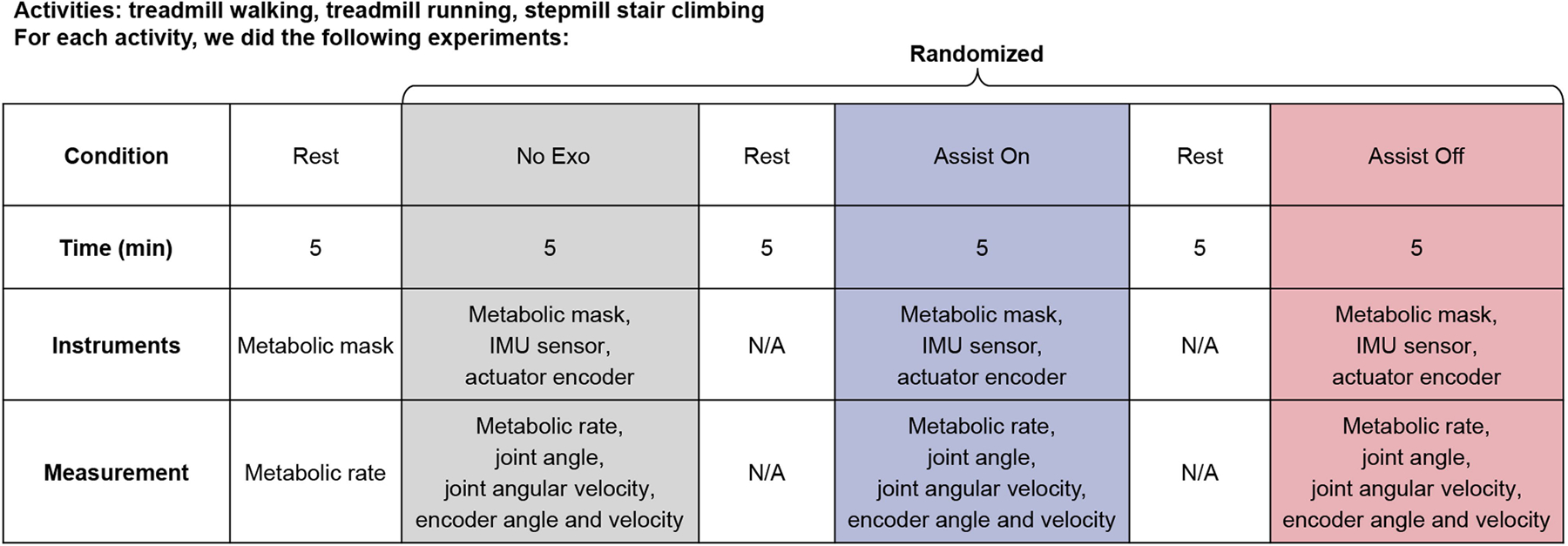
Metabolic rate is one key metric used to evaluate human performance during exoskeleton-assisted locomotion37. The robotic assistance substantially improved the energy economy of several participants during walking (n = 8), running (n = 8) and stair climbing (n = 8) for all participants, demonstrating the effectiveness of the controller (Fig. 5a, Extended Data Fig. 6 and Extended Data Table 2). For each activity, we tested three different conditions, namely, assist on, assist off and no exoskeleton (no exo). Two nine-axis IMU sensors mounted on both thighs were used to measure the joint angles and angular velocities. During level walking at 1.25 m s−1 on a treadmill for 5 min, the net metabolic rate (last 2 min) for the no exo condition of 2.91 ± 0.26 W kg−1 was reduced to 2.19 ± 0.19 W kg−1 for the assist on condition (mean ± s.e.m.). The metabolic rate reduction of the assist on conditions compared with the no exo conditions ranges from 19.9% to 30.8%, with an average of 24.3% (Fig. 5a). During level running at 2.0 m s−1 on the treadmill for 5 min, the net metabolic rate (collected for the last 2 min) for the no exo condition of 8.25 ± 0.92 W kg−1 was reduced to 7.19 ± 0.85 W kg−1 for the assist on condition (mean ± s.e.m.). The metabolic rate reduction of the assist on conditions compared with the no exo conditions ranges from 7.6% to 20.8%, with an average of 13.1%. During stair climbing at 65 steps min−1 on a step mill for 5 min, the net metabolic rate (collected for the last 2 min) for the no exo condition of 5.54 ± 0.24 W kg−1 was reduced to 4.66 ± 0.22 W kg−1 for the assist on condition. The metabolic rate reduction of the assist on conditions compared with the no exo conditions ranges from 8.7% to 25.7%, with an average of 15.4% (Fig. 5a). Collectively and to the best of our knowledge, these are the highest metabolic rate reductions among the previous literature with portable hip exoskeletons for walking, running and stair climbing (Fig. 5b,c).
Discussion
The key challenge in the development of simulation-to-reality (sim-2real) methods for wearable robots stems from the challenge of considering the interaction of both the human and robot, as well as the formidable sim2real gap which exists when a trained controller is deployed on physical robots27,38. We address these challenges with three aspects of our learning-in-simulation framework. First, our control neural network is designed to decouple the measurable states (that is, wearable sensor inputs) and unmeasurable states (for example, human joint moments and muscle activations) (Extended Data Fig. 1) so that the neural network controller only relies on measurable states to directly generate an assistive torque profile. Second, the three neural networks in our framework are trained simultaneously in the simulation such that the learning process concludes only when the exoskeleton controller reduces human effort and the virtual human model performs the desired locomotion while keeping balance. Third, we use domain randomization on the kinematic properties of the physical models in the simulation so that the learned controller is generalizable to different human subjects, thus promoting adaptive assistance.
Our data-driven and dynamics-aware reinforcement learning method with musculoskeletal simulation provides a foundation for turnkey solutions in controller development for wearable robots. Our simulation-trained end-to-end controller can generate continuous assistive profiles for walking, running, stair climbing and their transitions without any experimental tuning or handcrafted control laws. The controller produces immediate human energy reduction when directly deployed on physical hardware. This learning-in-simulation method is an important advancement in wearable robotics and potentially offers a scalable solution for exoskeletons, overcoming the need for time-consuming equipment for rapid deployment in the real world. As a generalized and efficient learning framework, this learning-in-simulation control method is applicable for a wide variety of exoskeletons including both portable2,32,34,36,39–42 and tethered8,31,40,42,43 versions, hip exoskeletons28,31,33,35,36,40, knee exoskeletons41,42,44 and ankle exoskeletons2,43,45. With a similar torque density as the state-of-the-art portable exoskeleton46, the increased human performance achieved in this work mainly stems from our experiment-free and versatile controller with our robot. In addition, our robot produces substantial output torque (18 N m) which is beneficial to assist several activities such as running and stair climbing which require more assistance than walking.
In this work, our neural-network-based controller generates adaptive assistance torque profiles which are specific to the kinematic locomotion patterns of each user (Fig. 3). The controller requires simple and easy-to-measure thigh kinematics (angle and angular velocity) as inputs through wearable IMU sensors (Figs. 2d and 3a). This level of individualization is achieved purely through computer simulation without any online tuning process or human subject training with the device. Thus, it facilitates the generalization of our method to other activities. The controller in this work was trained for able-bodied individuals and is not directly applicable to people with gait impairments or amputation because of the substantial biomechanical differences. Because this generalized method can simulate both robotic devices and human biomechanics, we can create digital twins of the human and robot in the simulation. For human simulation, our method can model humans with various gait impairments, making it potentially suitable to assist people with disabilities (for example, stroke, osteoarthritis and cerebral palsy) with a reformulation of reward functions to account for different gait characteristics such as joint loading or range of motion and minor individualized data to address their specific needs. For device simulation, our method can be extended to a wide variety of robotic assistive devices (for example, exoskeletons and prostheses39,47), aiding both able-bodied individuals with intact limbs as well as those with amputation. Our proposed training framework has the potential to adapt the human musculoskeletal model in simulations to account for specific impairments or muscle weakness. The effectiveness of such customized controllers for patients, compared to their performance with able-bodied individuals, will need to be studied in future work.
This study shows that we can bridge the sim2real gap in wearable robotics by means of learning-in-simulation of an end-to-end controller to immediately assist multimodal locomotion. Previous studies are limited by intensive human tests, handcrafted rules and the inability to adapt to different activities. We demonstrate through steady-state walking and running experiments (Fig. 3) and the activity transition experiment (Fig. 4) that our controller can generate synergistic assistance to the user’s versatile movements. Although the primary contribution of this work is the experiment-free and versatile assistance, the experimental results also show that we have achieved the greatest metabolic cost reduction for walking, running and stair climbing among state-of-the-art portable exoskeletons (Supplementary Table 4). Training such a controller using reinforcement learning in the simulation is challenging, especially properly defining the reward function. We found that it is crucial to incorporate both dynamics-aware physical equations and data-driven learning of three networks into the training process as the physical models facilitated the controller to learn an effective policy through millions of epochs of simulation. We also found that a reward function which includes tracking of kinematic reference joint trajectory, centre-of-pressure-based balance performance and reduction of muscle activations produces a controller that was ultimately successful. Previous research demonstrated that muscle activation provides a good prediction of metabolic rate48–51 when compared with other biological metrics, such as centre-of-mass work and total joint work and optimizing leg muscle activations during gait can significantly reduce metabolic costs52. Although it might be tempting to directly incorporate the metabolic rate terms into the reward function, the metabolic energy simulation involves muscle parameter calibration on hundreds of muscles, which poses potential reliability issues for computation. In addition, the complex computation of metabolic energy will further elicit non-smooth changes in the reward function over time steps, a situation difficult for reinforcement learning applications. Thus, further study is warranted because of its notably more complex mechanisms compared to muscle activation.
We believe the success of our controller can be attributed to the following factors. First, our end-to-end method directly maps human kinematic input to robot assistance output without the need for discrete activity classification or gait phase segmentation. Second, our framework incorporates the robot controller in the simulation in concert with musculoskeletal modelling, closing the loop in simulation for the training process, whereas open-loop control is used in state-of-the-art study18. Third, our method only requires low-dimensional sensor input (one IMU per leg) to infer high-dimensional human kinetics in 50 joint d.f. in the latent space which are not measurable. However, our controller also has limitations. When gaits which dramatically deviate from walking, running or stair climbing (that is, the training data used here from a public dataset25) occur, the controller may not be able to provide as effective assistance as in the normal case (Supplementary Fig. 5). If the gait patterns deviate too much off the limit (that is, the actual hip joint range of motion is more than 50% away from that of the reference kinematic trajectory used in the simulation), the controller will set the assistance to zero and let the user take full control. Future work may involve an investigation into active intervention from the controller to assist the user in recovering from such conditions.
Online content
Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41586-024-07382-4.
Methods
Dynamics-aware modelling of human muscle mechanics
In the muscle coordination neural network, we replicated human muscle mechanics to simulate authentic musculoskeletal responses. This approach enables realistic simulations of human movements, given that such movements are predominantly driven by muscle activations. As the human musculoskeletal model is composed of rigid skeletal segments connected by geometrically stretchable muscles, the contraction and relaxation of these muscles lead to the rotation of joints and therefore the motion of the whole body. Muscle activations that are regulated by the nervous system determine the change of the muscle fibre length and further, the change of muscle force. The musculoskeletal model (Fig. 2a and Extended Data Fig. 3) was parametrized to be 170 cm in height, 72 kg in weight consisting of 50 joint d.f. and 208 musculotendon units for the complete upper and lower body. The modelled d.f. included eight revolute joints (tibia, foot and forearm) and 14 ball-and-socket joints (femur, talus, spine, torso, neck, head, shoulder, arm and hand, each with 3 d.f.). Each musculotendon unit was represented as a polyline which began at the origin of the muscle, passed through a sequence of waypoints and ended at the insertion point53. An active muscle force was generated by each musculotendon unit through contraction which was applied between the two bones at its origin and insertion. When the musculotendon unit was fully relaxed (without active contraction), only passive force was produced as a result ot its background elasticity. Muscle tension was generated by the contraction of muscle fibres using a Hill-type model54:
| (1) |
where is the muscle length, is the muscle activation, and are force–length and force–velocity functions and is the passive force developed by a muscle. The actual muscle force was given by:
| (2) |
where is the maximum isometric force that the muscle cangenerate. The force-length relationship was specified by an exponential function.
| (3) |
where is a shape factor, is the passive muscle strain.
Dynamics-aware modelling of human dynamics of motion-imitation network
We modelled the human dynamic response to evaluate the influence of muscle forces and exoskeleton assistance on human movements. We used Euler–Lagrangian equations in generalized coordinates:
| (4) |
where is the vector of joint angles, is the vector of joint angular accelerations, superscript is the matrix transpose, is the vector of external forces and is the vector of muscle forces, which is a function of muscle activations for all muscles. denotes the generalized mass matrix and comprises of Coriolis and gravitational forces. and are the Jacobian matrices that map the muscle and external forces to the joint space, respectively.
Dynamics-aware modelling of human–robot interaction of exoskeleton control network
We modelled human–robot interaction to evaluate the influence of the exoskeleton assistance on human movements. As an exoskeleton was not perfectly fixed to the wearer’s body because of soft wearables, the actual torque experienced by a wearer was not equal to the generated tor que from the actuators. To simulate the interaction forces and moments at all wearable strap locations (Fig. 2c), we imported the three-dimensional CAD model of the exoskeleton to the simulation environment and connected it to the musculoskeletal model by means of linear bushing elements. A linear bushing element represented a bushing (B) connecting a Cartesian coordinate frame55 fixed on the exoskeleton to a Cartesian coordinate frame fixed on the human wearer with linear translational and torsional springs and dampers. During motion, the deviation of the two frames in the translational and torsional directions amidst the human and exoskeleton gave rise to bushing forces and moments which were given by:
| (5) |
where is the vector of translational distances along the , and axes between the origins of the two frames and is the vector of body-fixed Euler angles between the two frames. and represent the translational stiffness and translational damping along the , and directions, respectively. and represent the rotational stiffness and rotational damping around the , and axes, respectively. We modelled different resistance strengths of straps along different directions. Specific values for each of these parameters are available in Supplementary Table 1 and were chosen on the basis of empirical testing.
Data-driven learning of motion-imitation neural network
The motion-imitation neural network (three layers, 256 × 256 × 50 in size) (Extended Data Fig. 2) was designed for the human musculoskeletal model to learn walking, running and stair climbing motions in the simulation. The network took in the human full-body human kinematic states (hip joint angle and angular velocity) as the input and produces target human joint angle profiles for each activity. The objective of the motion-imitation neural network was to learn an imitation policy for the human agent that maximizes the following discounted sum of reward:
| (6) |
where is the expectation of the reward, is the number of time steps in each epoch, and is the time index. We designed the reward function as the weighted sum of several subrewards to encourage the human musculoskeletal model to imitate a target motion (walking, running and stair climbing) while satisfying a few constraints. Parameters , and represent the subrewards corresponding to joint position error, pelvis position error and centre of pressure (COP) of the musculoskeletal model (for detecting balance), respectively. Parameter denotes the corresponding weight for each subreward. The imitation reward was designed to encourage the human agent to minimize the position difference between the actual and reference motion from datasets in terms of the joint position and pelvis position . We used 10 s(120 Hz×1,200frames) of reference data from one representative subject in walking, running and stair climbing from the public motion capture database25:
| (7) |
| (8) |
where is the index of joints, () are the reference positions of the joints and root from the dataset. Parameters and are the actual human joint angles.
The term describes how well the controller maintains balance with the exoskeleton assistance in terms of movement of the whole system’s CoP. A higher reward was generated when the CoP is in a region S around the centre of the foot support (Supplementary Fig. 7):
| (9) |
where is the weight, is the Euclidean distance between the CoP and the centre of . The output of this neural network is the desired joint angles at the 50 joint d.f. of the human musculoskeletal model to produce the desired locomotion. Following that, we used proportional-derivative control to specify the desired joint angles, which directly correspo nd to the desired human joint torques :
| (10) |
where and are proportional and derivative gains used to compute the desired joint acceleration respectively. The weights , and are hyperparameters of the neural networks. Grid search is used to find the optimal values for hyperparameters. It involves performing an exhaustive search on a specific hyperparameter configuration. For example, is chosen from [0.25, 0.5,0.75,1] and is chosen from [0.1,0.2,0.3,…,0.9,1]. We assessed the overall reward equations (7)–(9) using all weight combinations and identified the set of weights that yielded the best overall performance during testing: , and .
Data-driven learning of muscle coordination
The muscle coordination neural network (four layers, 512 × 256 × 256 × 208 in size; Extended Data Fig. 3) was constructed to actuate the human musculoskeletal model through modulation of muscle activations. The network took desired human joint torques from the motion-imitation neural network as input and output activation values for each of the 208 muscles. The lower limb muscles (n = 108) are included in the calculation of the reward function equation (11) because we assume the assistance to the hip does not affect the upper body muscles. During the optimization process using equation (11), all these 108 muscles were treated as a whole to minimize the overall muscle activity. The muscle activations were applied to the musculotendon units over the entire body which in turn move the skeletal segments that elicit human movements. The objective of this network was to adjust the activations of each muscle to best reproduce the target joint torques.
To train the neural network, we formulated it into a supervised learning-based regression problem to learn collaboratively with the motion-imitation neural network. A deterministic policy was used to minimize the differences between the actuated joint accelerations and the desired human joint acceleration based on the output of the motion-imitation network, which led to the following design of the loss function:
| (11) |
where are the weighting factors regularizing the muscle activation effort.
Data-driven learning of exoskeleton control
The neural network of exoskeleton controller (three layers, 128 × 64 × 2 in size) (Extended Data Fig. 4) produces high-level real-time assistance torque commands to assist the current activity. The network takes proprioceptive history (joint angles and angular velocities from three consecutive previous time steps, 16 × 1 vector) from the IMU sensor on each leg as input and consequently outputs joint target positions for the exoskeleton motors. Our method only takes low-dimensional sensor input to infer high-dimensional human kinetics in 50 joint d.f. in the latent space which are not measurable. This is because human movement (kinematics data) can encode information about the underlying human physiological processes such as metabolic energy2. The objective was to learn a continuous control policy for the exoskeleton which maximizes the following discounted sum of rewards to improve human performance:
| (12) |
| (13) |
The instantaneous reward comprises five subrewards: is the muscle work, is the action smoothness, is the exoskeleton energy consumption, is the corresponding weight for each subreward. The subreward was used to prevent a human model from falling down. Parameters and correspond to the same subrewards used in the motion-imitation neural network. This ensures that the reward of the exoskeleton control neural network achieves its maximum only if the human model is able to follow the desired trajectory, thus facilitating sim2real transfer by incorporating human response. The reward encourages the controller to generate a smooth assistance profile to improve the subject comfort. We penalized the second-order finite difference derivatives of the actions (target joint angle):
| (14) |
In our experiment, , and . To ensure smooth motion, the output from the trained controller neural network was first filtered by a second-order low-pass filter before being applied to the exoskeleton. Subsequently, to further obtain responsive corrections on the joint torques, a proportional-derivative control loop was used for which preprocessed actions are specified as proportional-derivative setpoints. The final proportional-derivative-based torques applied to the hip joint are determined from:
| (15) |
where and are proportional and derivative gains, respectively.
Closed-loop simultaneous training of three neural networks
We developed a decoupled training scheme (Supplementary Tables 1 and 2) using PyTorch in which the exoskeleton neural network controller only requires measurable inputs from wearable sensors in the physical world (for example, human joint angles and angular velocities), whereas the musculoskeletal model had access to more intricate information from the model which generally is not available in reality (for example, the activation level of each muscle, real-time CoP and so on). However, to ensure a causal relationship between the musculoskeletal model and the exoskeleton controller, we incorporated subrewards related to muscle work and joint/pelvis position tracking error in the reward function equations (12) and (13) of the exoskeleton control neural network so that it achieves high reward only if both trainings are successful. Such training setup ensures that the exoskeleton control policy incorporates human response during its training process to facilitate real-world deployment.
It is a well-known challenge to transfer a trained controller from simulation to real-world settings while ensuring accuracy and behaviour similar to that in the physical environment (for example, individual human properties and robot properties)56–58. Typically, such attempts usually result in undesirable performance27,38 (for example, ill-timed robotic assistance or unsafe action from the robot) which can in part be attributed to the discrepancy in the exoskeleton dynamics between the real world and the simulation. To tackle this challenge and bridge the sim2real gap, our solution incorporated domain randomization, a machine learning technique that was first proposed by Tobin et al. to facilitate bridging the sim2real gap for object localization59. First, we perturbed robot dynamics parameters and musculoskeletal dynamics parameters to enhance the robustness of the trained policy to this discrepancy. We randomly sampled the dynamics properties of the exoskeleton (for example, mass, inertia, centre of mass, friction coefficient and observation latency; Supplementary Table 3) from a uniform distribution in each episode to account for the modelling error. Second, for musculoskeletal dynamics parameters, the maximum isometric force in the Hill-type model equations (1)–(3) of all lower limb muscles was randomized within a prescribed range to account for muscle strength variability among each individual. Combining these two approaches, the optimization objective in equation (12) was then modified to maximize the expected reward across a distribution of dynamics characteristics :
| (16) |
where represents the perturbed dynamics parameter values in the simulation. This intentionally introduced variability in the simulation, enabling the trained controller to be more robust against heterogeneous real-world conditions.
We ran the simulation on a computer equipped with an NVIDIA RTX3090 GPU. The simulation was terminated when the reward value of the exoskeleton control network converged and stopped increasing at around iteration no. 3,500. With one iteration taking around 8 s, the entire simulation took slightly less than 8 h.
Deployment of the learned controller
We evaluated the efficiency and versatility of the trained controller on our portable hip exoskeleton60 with quasi-direct drive actuation61 in both indoor and outdoor settings. The hip exoskeleton has a total weight of 3.2 kg and can produce a peak torque of 18 N m. For fixed-speed experiments on the treadmill, the exoskeleton was connected to a target personal computer with Simulink Real-time system (MathWorks) (Supplementary Fig. 2) to log both robot and human data (for example, human kinematics, robot states, output of each neural network and metabolic rate data). The Simulink system ran both a high-level exoskeleton control neural network and a low-level motor control module. The deployed exoskeleton control network in the Simulink model imported the network parameters directly from the simulation. For outdoor experiments with three activities, we implemented the same controller on portable electronics using a microcontroller (Raspberry Pi 4) running high-level control in Python which sends the generated torque commands to a mid-level microcontroller (Teensy, PJRC) which finally regulates the low-level motor control (Extended Data Fig. 5 and Supplementary Fig. 3).
Extended Data
Extended Data Fig. 1 |. Overview of the learning-in-simulation control framework.
a,b, Schematic illustrations for the learning-in-simulation architecture (a) and the control structure for online deployment (b).
Extended Data Fig. 2 |. Motion imitation neural network for versatile activities.

Schematic illustrations for the autonomous learning framework of the reference motions (walking, running, stair climbing) from datasets based on human kinematics input and joint torque command output.
Extended Data Fig. 3 |. Muscle coordination neural network.

Schematic illustrations for the muscle coordination neural network based on human joint torque input and human muscle actuation output.
Extended Data Fig. 4 |. Exoskeleton control neural network.

Schematic illustrations for the exoskeleton control neural network based on exoskeleton state history input and joint torque command output.
Extended Data Fig. 5 |. Exoskeleton design.

a–c, Overall view of the whole system (a), actuator (b) and electronics (c).
Extended Data Fig. 6 |. Experiment protocol for metabolic rate and kinematic data collection during walking, running and stair climbing (also available on Protocol Exchange at: https://doi.org/10.21203/rs.3.pex-2632/v1).
Extended Data Table 1 |.
Participant information
| Participant | Sex | Body mass (Kg) | Height (cm) | Age (year) | Activity | Exoskeleton experience |
|---|---|---|---|---|---|---|
| Participant 1 | M | 62 | 179 | 22 | Walking, running, stair climbing | YES |
| Participant 2 | M | 70 | 174 | 26 | Walking, running, stair climbing | YES |
| Participant 3 | M | 70 | 178 | 32 | Walking, running, stair climbing | NO |
| Participant 4 | M | 85 | 181 | 27 | Walking, running, stair climbing | YES |
| Participant 5 | M | 109 | 180 | 27 | Walking, running, stair climbing | YES |
| Participant 6 | F | 50 | 165 | 26 | Walking | YES |
| Participant 7 | F | 56 | 160 | 30 | Walking | YES |
| Participant 8 | F | 45 | 158 | 29 | Walking | NO |
| Participant 9 | M | 80 | 180 | 29 | Running, stair climbing | YES |
| Participant 10 | M | 70 | 176 | 34 | Running, stair climbing | YES |
| Participant 11 | M | 66 | 170 | 30 | Running, stair climbing | YES |
| Mean ± SD | 69.4 ± 17.7 | 172.8 ± 8.4 | 28.4 ± 3.3 |
Extended Data Table 2 |.
Summary of experiments
| Activity | Participant | Scenario | Measurement | Metric | Control variables | Results |
|---|---|---|---|---|---|---|
| Walking (1.25 ms−1) | n = 8 | Laboratory controlled condition | Net metabolic rate | Metabolic reduction (%) | Fixed time to 5 mins, averaged last 2 mins data | 24.3% metabolic reduction |
| Running (2.0 m s−1) | n = 8 | Laboratory controlled condition | Net metabolic rate | Metabolic reduction (%) | Fixed time to 5 mins, averaged last 2 mins data | 13.1% metabolic reduction |
| Stair ascent (65 steps min1) | n = 8 | Laboratory controlled condition | Net metabolic rate | Metabolic reduction (%) | Fixed time to 5 mins, averaged last 2 mins data | 15.4% metabolic reduction |
| Transition from walking to running (0.8 to 2 m s−1) and to stair-climbing | One representative participant | Outdoor | Thigh joint angle, angular velocity, and torque profile | Torque, power and exoskeleton-delivered mechanical work | Changed speed about every 7 steps | Smooth transition of torque and power, gradually increased delivered work |
Supplementary Material
Acknowledgements
We thank Y. K. Chen at the Massachusetts Institute of Technology for constructive feedback and discussion of this work. This work was supported in part by the National Science Foundation (NSF) CAREER award CMMI 1944655, National Institute on Disability, Independent Living and Rehabilitation Research (NIDILRR) DRRP 90DPGE0019, Switzer Research Distinguished Fellow (SFGE22000372), NSF Future of Work 2231419 and National Institute of Health (NIH) 1R01EB035404.
Footnotes
Competing interests S.L. and H.S. are co-inventors on intellectual property related to the controller discussed in this work. H.S. is a co-founder of and has a financial interest in Picasso Intelligence, LLC. The terms of this arrangement have been reviewed and approved by NC State University in accordance with its policy on objectivity in research. The remaining authors declare no competing interests.
Code availability
Pseudocode for the learning-in-simulation algorithm and training process can be found in the GitHub repository https://github.com/IntelligentRobotLearning/pseudocode_learning_in_simulation.
Additional information
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41586-024-07382-4.
Peer review information Nature thanks Joonho Lee and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Reprints and permissions information is available at http://www.nature.com/reprints.
Data availability
All data supporting the findings of this study are available in the Article and its Supplementary Information. Source data are provided with this paper.
References
- 1.Siviy C et al. Opportunities and challenges in the development of exoskeletons for locomotor assistance. Nat. Biomed. Eng. 7, 456–472 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Slade P, Kochenderfer MJ, Delp SL & Collins SH Personalizing exoskeleton assistance while walking in the real world. Nature 610, 277–282 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Awad LN et al. A soft robotic exosuit improves walking in patients after stroke. Sci. Transl. Med. 9, eaai9084 (2017). [DOI] [PubMed] [Google Scholar]
- 4.Geyer H, Seyfarth A & Blickhan R Compliant leg behaviour explains basic dynamics of walking and running. Proc. R. Soc. B 273, 2861–2867 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang J et al. Human-in-the-loop optimization of exoskeleton assistance during walking. Science 356, 1280–1284 (2017). [DOI] [PubMed] [Google Scholar]
- 6.Ferris D, Sawicki G & Domingo A Powered lower limb orthoses for gait rehabilitation. Top. Spinal Cord Inj. Rehabil. 11, 34–49 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Veneman JF et al. Design and evaluation of the LOPES exoskeleton robot for interactive gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 15, 379–386 (2007). [DOI] [PubMed] [Google Scholar]
- 8.Ding Y, Kim M, Kuindersma S & Walsh CJ Human-in-the-loop optimization of hip assistance with a soft exosuit during walking. Sci. Robot. 3, eaar5438 (2018). [DOI] [PubMed] [Google Scholar]
- 9.Koller JR, Jacobs DA, Ferris DP & Remy CD Learning to walk with an adaptive gain proportional myoelectric controller for a robotic ankle exoskeleton. J. Neuroeng. Rehabil. 12, 97 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang Q et al. Imposing healthy hip motion pattern and range by exoskeleton control for individualized assistance. IEEE Robot. Autom. Lett. 7, 11126–11133 (2022). [Google Scholar]
- 11.Dembia CL, Bianco NA, Falisse A, Hicks JL & Delp SL Opensim moco: musculoskeletal optimal control. PLoS Comput. Biol. 16, e1008493 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Song S et al. Deep reinforcement learning for modeling human locomotion control in neuromechanical simulation. J. Neuroeng. Rehabil. 18, 126 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gordon DF, McGreavy C, Christou A & Vijayakumar S Human-in-the-loop optimization of exoskeleton assistance via online simulation of metabolic cost. IEEE Trans. Robot. 38, 1410–1429 (2022). [Google Scholar]
- 14.Durandau G, Rampeltshammer WF, van der Kooij H & Sartori M Neuromechanical model-based adaptive control of bilateral ankle exoskeletons: biological joint torque and electromyogram reduction across walking conditions. IEEE Trans. Robot. 38, 1380–1394 (2022). [Google Scholar]
- 15.Lim B et al. Delayed output feedback control for gait assistance with a robotic hip exoskeleton. IEEE Trans. Robot. 35, 1055–1062 (2019). [Google Scholar]
- 16.Meuleman J, Van Asseldonk E, Van Oort G, Rietman H & Van Der Kooij H LOPES II—design and evaluation of an admittance controlled gait training robot with shadow-leg approach. IEEE Trans. Neural Syst. Rehabil. Eng. 24, 352–363 (2015). [DOI] [PubMed] [Google Scholar]
- 17.Molinaro DD, Kang I, Camargo J, Gombolay MC & Young AJ Subject-independent, biological hip moment estimation during multimodal overground ambulation using deep learning. IEEE Trans. Med. Robot. Bionics 4, 219–229 (2022). [Google Scholar]
- 18.Shepherd MK, Molinaro DD, Sawicki GS & Young AJ Deep learning enables exoboot control to augment variable-speed walking. IEEE Robot. Autom. Lett. 7, 3571–3577 (2022). [Google Scholar]
- 19.Bellegarda G & Ijspeert A CPG-RL: learning central pattern generators for quadruped locomotion. IEEE Robot. Autom. Lett. 7, 12547–12554 (2022). [Google Scholar]
- 20.Li Z et al. Reinforcement learning for robust parameterized locomotion control of bipedal robots. In 2021 IEEE International Conference on Robotics and Automation (eds Meng Q-H & Sun Y) 2811–2817 (IEEE, 2021). [Google Scholar]
- 21.Siekmann J, Godse Y, Fern A & Hurst J Sim-to-real learning of all common bipedal gaits via periodic reward composition. In IEEE International Conference on Robotics and Automation (eds Meng Q-H & Sun Y) 7309–7315 (IEEE, 2021). [Google Scholar]
- 22.Wen Y, Si J, Brandt A, Gao X & Huang HH Online reinforcement learning control for the personalization of a robotic knee prosthesis. IEEE Trans. Cybernet. 50, 2346–2356 (2019). [DOI] [PubMed] [Google Scholar]
- 23.Luo S et al. Reinforcement learning and control of a lower extremity exoskeleton for squat assistance. Front. Robot. AI 8, 702845 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Luo S et al. Robust walking control of a lower limb rehabilitation exoskeleton coupled with a musculoskeletal model via deep reinforcement learning. J. Neuroeng. Rehabil. 20, 34 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.CMU Graphics Lab Motion Capture Database. http://mocap.cs.cmu.edu/ (Carnegie Mellon University; accessed 10 November 2021). [Google Scholar]
- 26.Adadi A A survey on data-efficient algorithms in big data era. J. Big Data 8, 24 (2021). [Google Scholar]
- 27.Salvato E, Fenu G, Medvet E & Pellegrino FA Crossing the reality gap: a survey on sim-to-real transferability of robot controllers in reinforcement learning. IEEE Access 9, 153171–153187 (2021). [Google Scholar]
- 28.Kim J et al. Autonomous and portable soft exosuit for hip extension assistance with online walking and running detection algorithm. In 2018 IEEE International Conference on Robotics and Automation (eds Zelinksy A & Park F) 5473–5480 (IEEE, 2018). [Google Scholar]
- 29.Zhang X et al. Enhancing gait assistance control robustness of a hip exosuit by means of machine learning. IEEE Robot. Autom. Lett. 7, 7566–7573 (2022). [Google Scholar]
- 30.Cao W, Chen C, Hu H, Fang K & Wu X Effect of hip assistance modes on metabolic cost of walking with a soft exoskeleton. IEEE Trans. Autom. Sci. Eng. 18, 426–436 (2020). [Google Scholar]
- 31.Kim J et al. Reducing the energy cost of walking with low assistance levels through optimized hip flexion assistance from a soft exosuit. Sci. Rep. 12, 11004 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Seo K, Lee J & Park YJ Autonomous hip exoskeleton saves metabolic cost of walking uphill. In International Conference on Rehabilitation Robotics (ed. Masia L) 246–251 (IEEE, 2017). [DOI] [PubMed] [Google Scholar]
- 33.Nasiri R, Ahmadi A & Ahmadabadi MN Reducing the energy cost of human running using an unpowered exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 26, 2026–2032 (2018). [DOI] [PubMed] [Google Scholar]
- 34.Ning C, Li Y, Feng K, Gong Z & Zhang T Soochow Exo: a lightweight hip exoskeleton driven by series elastic actuator with active-type continuously variable transmission. In IEEE International Conference on Mechatronics and Automation (eds Hirata H, Xu W & Guo J) 1432–1437 (IEEE, 2022). [Google Scholar]
- 35.Kim DS et al. A wearable hip-assist robot reduces the cardiopulmonary metabolic energy expenditure during stair ascent in elderly adults: a pilot cross-sectional study. BMC Geriatr. 18, 230 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kim J et al. Reducing the metabolic rate of walking and running with a versatile, portable exosuit. Science 365, 668–672 (2019). [DOI] [PubMed] [Google Scholar]
- 37.Sawicki GS, Beck ON, Kang I & Young AJ The exoskeleton expansion: improving walking and running economy. J. Neuroeng. Rehabil. 17, 25 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Koos S, Mouret J-B & Doncieux S The transferability approach: crossing the reality gap in evolutionary robotics. IEEE Trans. Evol. Comput. 17, 122–145 (2012). [Google Scholar]
- 39.Halilaj E et al. Machine learning in human movement biomechanics: best practices, common pitfalls and new opportunities. J. Biomech. 81, 1–11 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lee G et al. Reducing the metabolic cost of running with a tethered soft exosuit. Sci. Robot. 2, eaan6708 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Lee D, Kwak EC, McLain BJ, Kang I & Young AJ Effects of assistance during early stance phase using a robotic knee orthosis on energetics, muscle activity and joint mechanics during incline and decline walking. IEEE Trans. Neural Syst. Rehabil. Eng. 28, 914–923 (2020). [DOI] [PubMed] [Google Scholar]
- 42.Franks PW et al. Comparing optimized exoskeleton assistance of the hip, knee and ankle in single and multi-joint configurations. Wearable Technol. 2, e16 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nuckols RW et al. Individualization of exosuit assistance based on measured muscle dynamics during versatile walking. Sci. Robot. 6, eabj1362 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shepertycky M, Burton S, Dickson A, Liu Y-F & Li Q Removing energy with an exoskeleton reduces the metabolic cost of walking. Science 372, 957–960 (2021). [DOI] [PubMed] [Google Scholar]
- 45.Mooney LM & Herr HM Biomechanical walking mechanisms underlying the metabolic reduction caused by an autonomous exoskeleton. J. Neuroeng. Rehabil. 13, 4 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Seo K, Lee J, Lee Y, Ha T & Shim Y Fully autonomous hip exoskeleton saves metabolic cost of walking. In 2016 IEEE International Conference on Robotics and Automation (eds Kragic D, Bicchi A & De Luca A) 4628–4635 (IEEE, 2016). [Google Scholar]
- 47.Seth A et al. OpenSim: simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput. Biol. 14, e1006223 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Blake OM & Wakeling JM Estimating changes in metabolic power from EMG. Springerplus 2, 229 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bruns RE, Vos P & Wedge RD Electromyography as a surrogate for estimating metabolic energy expenditure during locomotion. Med. Eng. Phys. 109, 103899 (2022). [DOI] [PubMed] [Google Scholar]
- 50.Silder A, Besier T & Delp SL Predicting the metabolic cost of incline walking from muscle activity and walking mechanics. J. Biomech. 45, 1842–1849 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Jackson RW & Collins SH An experimental comparison of the relative benefits of work and torque assistance in ankle exoskeletons. J. Appl. Physiol. 119, 541–557 (2015). [DOI] [PubMed] [Google Scholar]
- 52.Hortobágyi T, Finch A, Solnik S, Rider P & DeVita P Association between muscle activation and metabolic cost of walking in young and old adults. J. Gerontol. A 66, 541–547 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lee S, Park M, Lee K & Lee J Scalable muscle-actuated human simulation and control. ACM Trans. Graph. 38, 73 (2019). [Google Scholar]
- 54.Thelen DG Adjustment of muscle mechanics model parameters to simulate dynamic contractions in older adults. J. Biomech. Eng. 125, 70–77 (2003). [DOI] [PubMed] [Google Scholar]
- 55.Zhou X & Zheng L Model-based comparison of passive and active assistance designs in an occupational upper limb exoskeleton for overhead lifting. IISE Trans. Occup. Ergon. Hum. Factors 9, 167–185 (2021). [PMC free article] [PubMed] [Google Scholar]
- 56.Hwangbo J et al. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 4, eaau5872 (2019). [DOI] [PubMed] [Google Scholar]
- 57.Lee J, Hwangbo J, Wellhausen L, Koltun V & Hutter M Learning quadrupedal locomotion over challenging terrain. Sci. Robot. 5, eabc5986 (2020). [DOI] [PubMed] [Google Scholar]
- 58.Tan J et al. Sim-to-real: learning agile locomotion for quadruped robots. Preprint at 10.48550/arXiv.1804.10332 (2018). [DOI] [Google Scholar]
- 59.Tobin J et al. Domain randomization for transferring deep neural networks from simulation to the real world. In 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (eds Zhang H & Vaughan R) 23–30 (IEEE, 2017). [Google Scholar]
- 60.Yu S et al. Quasi-direct drive actuation for a lightweight hip exoskeleton with high backdrivability and high bandwidth. IEEE ASME Trans. Mechatron. 25, 1794–1802 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Huang T-H et al. Modeling and stiffness-based continuous torque control of lightweight quasi-direct-drive knee exoskeletons for versatile walking assistance. IEEE Trans. Robot. 38, 1442–1459 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data supporting the findings of this study are available in the Article and its Supplementary Information. Source data are provided with this paper.


