Abstract
We focused on solitonic phenomena in wave propagation which was extracted from a generalized breaking soliton system in (3 + 1)-dimensions. The model describes the interaction phenomena between Riemann wave and long wave via two space variable in nonlinear media. Abundant double-periodic soliton, breather wave and the multiple rogue wave solutions to a generalized breaking soliton system by the Hirota bilinear form and a mixture of exponentials and trigonometric functions are presented. Periodic-soliton, breather wave and periodic are studied with the usage of symbolic computation. In addition, the symbolic computation and the applied methods for governing model are investigated. Through three-dimensional graph, density graph, and two-dimensional design using Maple, the physical features of double-periodic soliton and breather wave solutions are explained all right. The findings demonstrate the investigated model’s broad variety of explicit solutions. All outcomes in this work are necessary to understand the physical meaning and behavior of the explored results and shed light on the significance of the investigation of several nonlinear wave phenomena in sciences and engineering.
Keywords: Generalized breaking soliton system, Double-periodic soliton, Breather wave, Hirota operator, Travelling wave
Subject terms: Mathematics and computing, Optics and photonics
Introduction
Currently, the nonlinear partial differential equations are widely utilized to determine the exact soliton solution of a variety of natural phenomena1–5. Nonlinear phenomena use in various scientific fields such as, plasma physics, solid state physics, fluid dynamics, chemical kinetics and mathematical biology6–10. The applications of nonlinear models cover physics11,12, network13, computer science14, and many other fields15. Exact solutions can be evaluated without the effect of nonlinear resistances in propagation using Hirota derivatives. In the literature16, there are various viewpoints on the fractional derivative operator. However, numerous scholars and scientists have been investigating the potential of nonlinear operator for the past three decades such as Galerkin finite element technique17, Paul–Painlevé approach18, the Exp-function scheme19, the extended trial equation scheme20, the -expansion scheme21, etc. Based on the above methods, plenty of the exact solutions including different schemes have been worked, for example, the generalized exponential rational function method22, Gaussian traveling wave solution23, seismic attenuation for geotechnical24, the generalized trial equation scheme25, a wavelet approach26. Since the 1950s, the concept of soliton has been put forward in the study of nonlinear phenomena, which makes the study of nonlinear partial differential equations (NLPDEs) solution become a hot spot in nonlinear science including orthogonal frequency division multiplexing27, Fluid inverse volumetric modeling28, network governance step by step method29 and the neural network method30. However, due to the complexity of NLPDEs, the results of mathematical research have not provided a universally effective method to find the exact solution at present. With the emergence of a variety of solution methods, not only the past difficult to solve the equation has been solved, but also new, has important physical meaning of the solution has been discovered and applied in practice. Nonlinear differential equations have been widely employed to describe a wide range of physical processes, not just in mathematics but also in physics, biology, and engineering, for example: the conservation of mass, electrochemical analysis, groundwater flow problem, viscoelastic damping models, fractional quantum mechanics, classical mechanics, and propagation of acoustical waves31–35. Several effective techniques have been established to find the clear and specific solutions of nonlinear models for instance such as machine learning methods36, He’s variational direct technique37, the discrete mean-field stochastic systems38, bistable origami flexible gripper39, the breather wave solutions40. The nonlinear problems are characterized by dispersive and dissipative effects, advection, convection, and diffusion process such as N-lump solutions41, seismic wave attenuation42, the development of deep geothermal energy43, hyperbolic shear polaritons44, the modified Schrödinger’s equation via innovative approaches45. A wide class of analytical techniques other schemes have been applied to solve nonlinear problems such as the parabolic dish solar collector46, the renewable energy sources47, a hybrid convolutional neural network48, a hybrid robust-stochastic approach49, a optimal chiller loading50. Furthermore, many mathematical models have been constructed based on more theory and applied assumptions. Many researchers have constructed on these problems including the distributed series reactor51, an intelligent algorithm52, the deep learning method53, the trigonometric quadrature rules54, nonlinearities of SiGe bipolar phototransistor55. Several researchers have studied the modified and optimization technique such as the robust optimization technique56, random variables with Copula theory57, and power systems58. Jiand and co-workers studied the asymptotic properties for the drift parameter estimators in the fractional Ornstein-Uhlenbeck process with periodic mean function and long range dependence59. Authors investigated the distinct types of the exact soliton solutions to an important model called the beta-time fractional (1 + 1)-dimensional nonlinear Van der Waals equation60. The versatility of electrofabrication for the customized manufacturing of functional gradient soft matter was studied in61. The multiple soliton solutions for the generalized Bogoyavlensky–Konopelchenko equation along with solutions contain first-order, second-order, and third-order wave solutions were analyzed62.
A precise balance between the nonlinear and dispersion elements in the evolution system gives rise to the solitons, a typical nonlinear phenomenon. The soliton theory has a wide range of useful applications. For instance, optical soliton has unquestionably produced the basis for optical fibre communication and the current Internet era. Two and more solitons coexist and interact often in an evolution system. With the exception of phase, solitons interact and clash most frequently in an elastic manner, preserving their propagation speed, amplitude, and direction. Solitons may collide inelastically in some settings. Even in extremely uncommon situations, soliton fusion and fission can occur63–65.
The primary goal of this research is to offer generalized breaking soliton system in (3 + 1)-dimensions arising in wave propagation a significant number of trustworthy analytical closed-form solutions. Additionally, wave designs from distinctive soliton solutions’ nonlinear behavior in 3D, 2D, and stage plane examination has been appeared. The express methods’ versatile profile structures are very unmistakable and supportive for basic forms. Only a very small number of findings from previous research have been released, and the resulting periodic and single soliton compositions are entirely original. Furthermore, this research could be seen as a complement to previous relevant articles.
For reasons known to all, the researchers of shallow water wave in various field is critical for further study in physical systems when we turn to mathematical physics, nonlinear optics, optical fibres and communication engineering in which the nonlinear evolution equation was recently developed. Feng et al.66 obtained the exact analytical solutions and novel interaction solutions by Hirota bilinear method and symbolic computation. Ma et al.67 obtained the localized interaction solutions based on a Hirota bilinear transformation. The multi-component Sasa-Satsuma integrable hierarchies was studied via an arbitrary-order matrix spectral problem, based on the zero curvature formulation68. Analytical one-, two-, three- and four-soliton solutions of the (2 + 1)-dimensional variable-coefficient Sawada-Kotera equation were constructed based on its Hirota bilinear form69. A fourth-order time-fractional partial differential equation with Riemann–Liouville definition was studied using the general method of separation of variables70.
Although solitons theoretically possess unique properties that allow them to maintain their propagation shape, speed, and amplitude, in practical application scenarios, the propagation of solitons is often influenced by various complex factors such as common damping, initial or boundary perturbations, evolving dissipation, and variable nonlinearity71. These factors directly affect the soliton dynamics, leading to energy loss, amplitude attenuation, deformation, and deceleration during propagation. To address these issues, it is necessary to introduce certain physical factors mentioned above in nonlinear evolution systems, such as the multimodal vision-language learning paradigm method72, a complete language-vision interaction network73, the multimodal hybrid parallel network method74, a multi-scale channel-spatial attention75, Fourier decomposition method76.
In this paper, we will discuss the following generalized breaking soliton system in (3 + 1)-dimensions77
| 1 |
with and and are free parameters. System (1) is derived from the generalization of the following (2 + 1)-dimensional generalized breaking soliton system
| 2 |
where and and are the nonzero parameters. System (2) is investigated by different methods in Refs.78–80. Using and the following relation
| 3 |
then, the bilinear form B(T) of Eq. (1) will be arisen as
| 4 |
with the bilinear operator D
| 5 |
in which and . Hence, we get
| 6 |
The (2 + 1)-dimensional Zoomeron model extensively was utilized the extended Jacobian elliptic function and the modified extended tanh techniques to derive the analytical solutions87. The improved Kudryashov, the novel Kudryashov, and the unified methods were used to demonstrate new wave behaviors of the Fokas–Lenells nonlinear waveform arising in birefringent fibers88. The linear stability technique and bifurcation analysis were employed to assess the stability of the fractional 3D Wazwaz–Benjamin–Bona–Mahony model89. The novel waveforms and bifurcation analysis for the fractional Klein–Fock–Gordon structure were investigated in90. N-solitons and interaction solution for the (3 + 1)-D negative-order KdV first structure that arises in shallow-water waves were studied91. The Hirota bilinear formation was used to analyze novel collision solutions between the lump and kinky waves of the (3 + 1)-D Jimbo–Miwa-like model92.
In essence, the generalized breaking soliton system characterizes the propagation of nonlinear dispersive waves within (3 + 1)-dimensions, embodying a balance between nonlinear convection effects and dispersive tendencies originating from the medium.
The structure of this paper is given as under:
The double-periodic soliton method is presented in the second section by plenty of the solutions. Application of breather wave is discussed in the third section. The result and discussion are investigated in fourth section. Fifth section points to the multiple rogue wave and its application on mentioned system. Finally, we approach some kind of results and conclusion in sixth section.
Double-periodic soliton solutions
Recently, “three-wave method” was revised for obtaining the double-periodic soliton solutions to NLPDEs81, such as the (2 + 1)- and (3 + 1)-dimensional BLMP equation82, the (2 + 1)-dimensional breaking soliton equation83, the new (2 + 1)-dimensional KdV equation84. Following the steps of this method, T(x, y, t) has a solution of the following form
| 7 |
where and are constants to be determined later. The assumptions used in the “three-wave method” are special cases of Eq. (7). Substituting Eq. (7) into Eq. (3), a set of algebraic equations about and are obtained. With the aid of Mathematica software, we have the following results:
Case (1):
| 8 |
Case (2):
| 9 |
Case (3):
| 10 |
Case (4):
| 11 |
Case (5):
| 12 |
Case (6):
| 13 |
Case (7):
| 14 |
Case (8):
| 15 |
Case (9):
| 16 |
Case (10):
| 17 |
Case (11):
| 18 |
Case (12):
| 19 |
Case (13):
| 20 |
Case (14):
| 21 |
Case (15):
| 22 |
Case (16):
| 23 |
Case (17):
| 24 |
Case (18):
| 25 |
Case (19):
| 26 |
Interpretation of results for double-periodic soliton
In this section, we discuss the dynamic properties by setting some special values for the free parameters in these solutions. For example, substituting
| 27 |
into Eq. (14), we can obtain the following double-periodic soliton solution
| 28 |
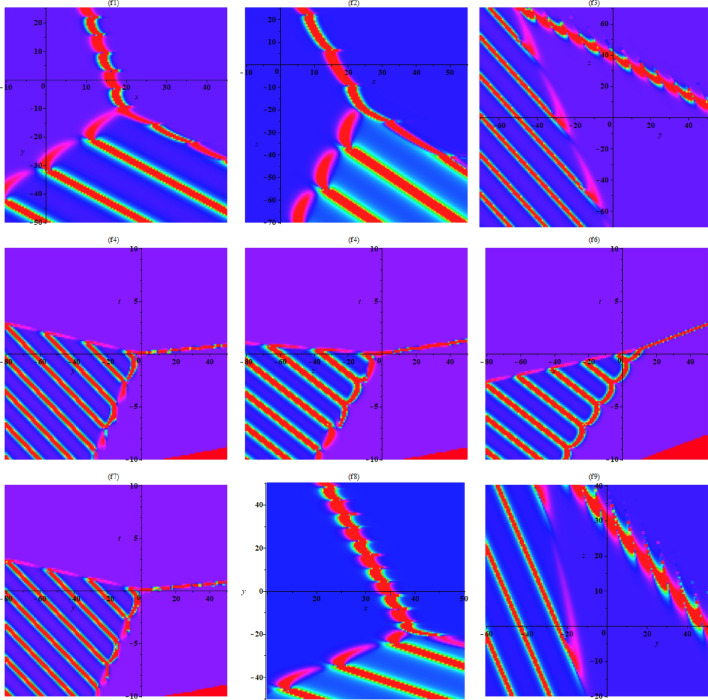
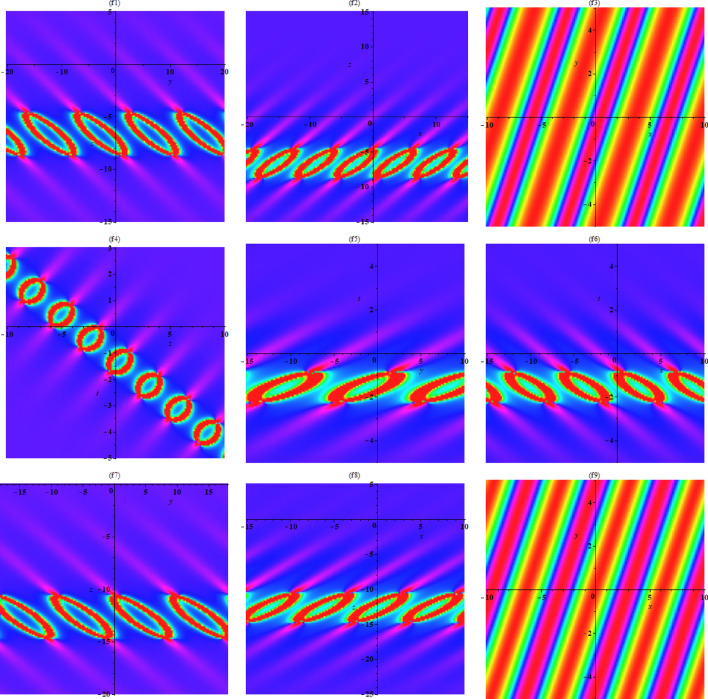
The dynamic properties to Eq. (28) are described in Figs. 1. Figure 1 shows the interaction between two periodic soliton solutions for specified values of , respectively.
Fig. 1.
Double-periodic soliton (28) with different parameters of Case (7) , respectively.
By substituting below
| 29 |
into Eq. (18), we can obtain the following double-periodic soliton solution
| 30 |
The dynamic properties to Eq. (30) are described in Fig. 2. Figure 2 shows the interaction between two periodic soliton solutions for specified values of , respectively.
Fig. 2.
Double-periodic soliton (30) with different parameters of Case (7) , respectively.
By putting below
| 31 |
into Eq. (26), we can obtain the following double-periodic soliton solution
| 32 |
The dynamic properties to Eq. (32) are described in Figs. 3, 4 and 5. Figures 3, 4 and 5 show the interaction between two periodic soliton solutions for specified values of parameters including Fig. 3 the first row , the second row and the third row and including Fig. 4 the first row , the second row and the third row and also Fig. 5 the first row , the second row and the third row .
Fig. 3.
Double-periodic soliton (30) with different parameters of (The first row): Case (19) , (The second row): Case (19) and (The third row): Case (19) .
Fig. 4.
Double-periodic soliton (30) with different parameters of (The first row): Case (19) , (The second row): Case (19) and (The third row): Case (19) .
Fig. 5.
Double-periodic soliton (30) with different parameters of (The first row): Case (19) , (The second row): Case (19) and (The third row): Case (19) .
Breather wave solutions
According to Three-wave method is used for obtaining the Breather wave solutions by following the steps of this method, T(x, y, z, t) has a solution of the following form
| 33 |
where and are constants to be determined later. The assumptions used in the “Three-wave method” are special cases of Eq. (33). Substituting Eq. (33) into Eq. (3), a set of algebraic equations about and are obtained. With the aid of Mathematica software, we have the following results:
Case (1):
| 34 |
Case (2):
| 35 |
Case (3):
| 36 |
Case (4):
| 37 |
Case (5):
| 38 |
Case (6):
| 39 |
Case (7):
| 40 |
Case (8):
| 41 |
Case (9):
| 42 |
Case (10):
| 43 |
Case (11):
| 44 |
Case (12):
| 45 |
Case (13):
| 46 |
Case (14):
| 47 |
Case (15):
| 48 |
Case (16):
| 49 |
Case (17):
| 50 |
Case (18):
| 51 |
Interpretation of results for breather wave
In this section, we discuss the dynamic properties by setting some special values for the free parameters in these solutions. For example, substituting
| 52 |
into Eq. (48), we can obtain the following breather wave soliton solution
| 53 |
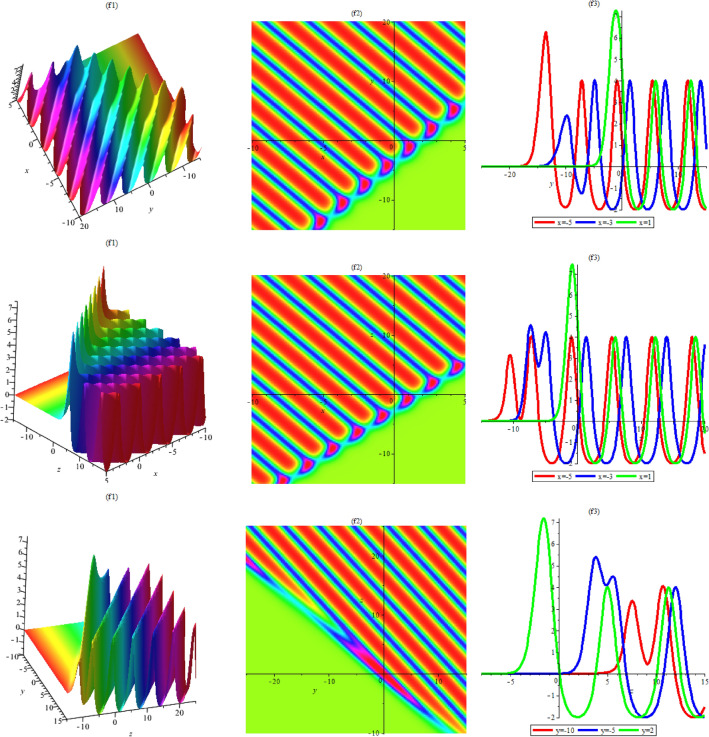
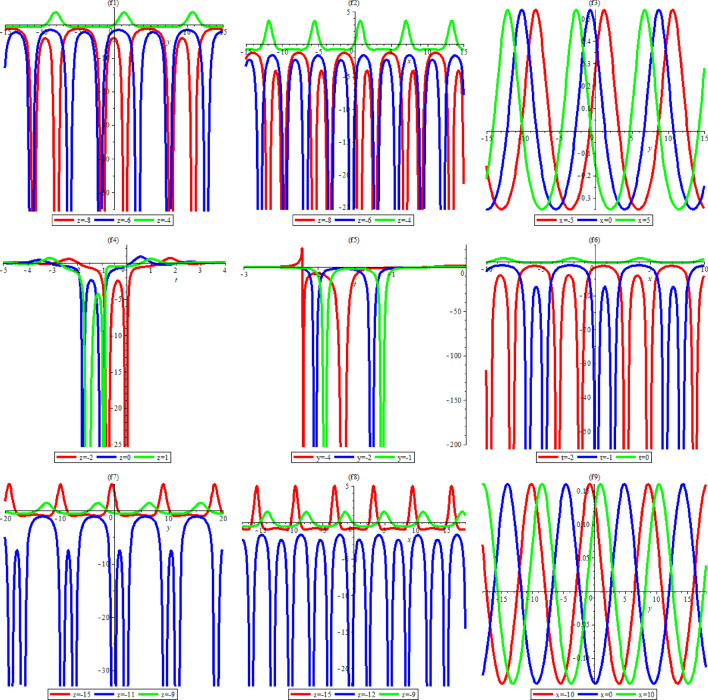
The dynamic properties to Eq. (53) are described in Figs. 6 and 7. Figures 6 and 7 show the interaction breather wave soliton solutions for specified values of , respectively. Figure 6 includes density solutions and Fig. 7 presents two dimensional behaviours.
Fig. 6.
Breather wave soliton (53) with different parameters of Case (15) , respectively.
Fig. 7.
2D plot of Breather wave soliton (53) with different parameters of Case (15) , respectively.
By substituting below
| 54 |
into Eq. (50), we can obtain the following breather wave soliton solution
| 55 |
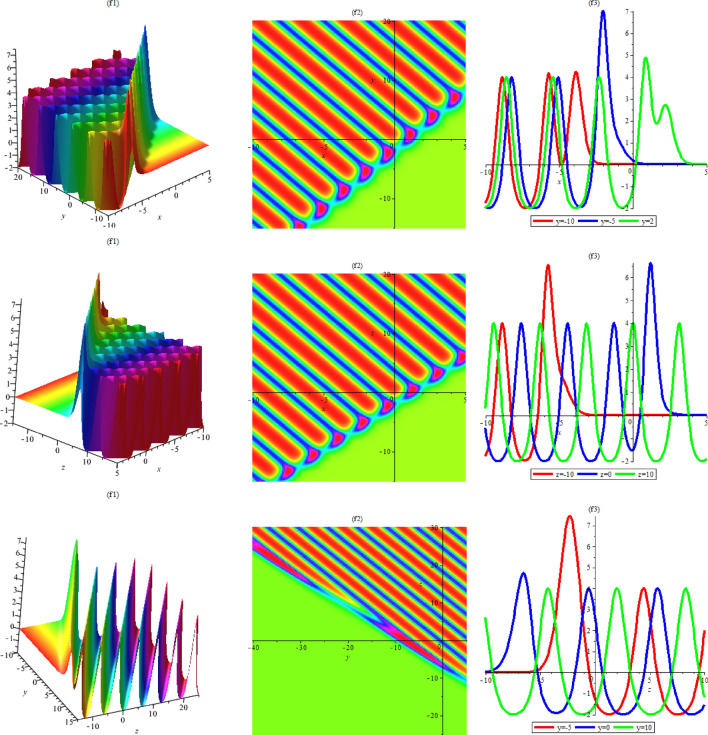
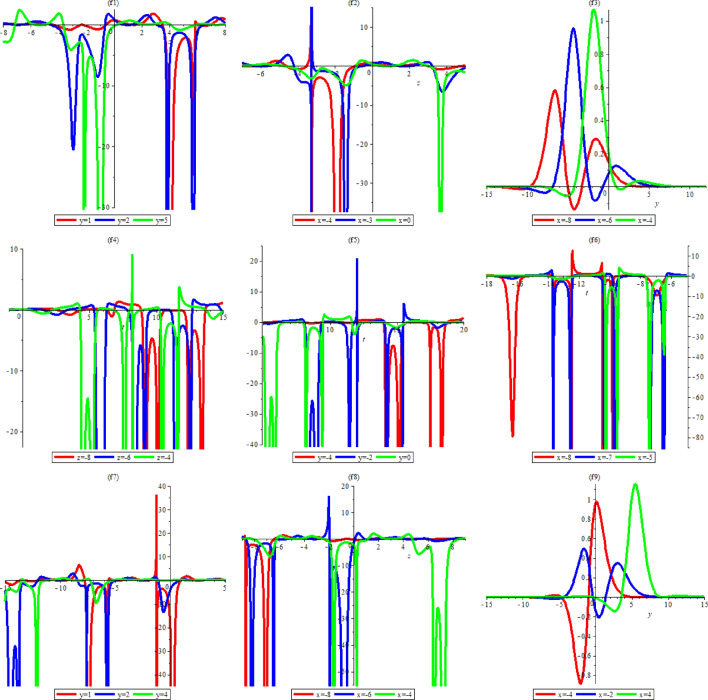
The dynamic properties to Eq. (55) are described in Fig. 8. Figure 8 show the interaction breather wave soliton solutions for specified values of , respectively. Figure 8 includes density solutions.
Fig. 8.
Breather wave soliton (55) with different parameters of Case (15) , respectively.
By substituting below
| 56 |
into Eq. (51), we can obtain the following breather wave soliton solution
| 57 |
The dynamic properties to Eq. (57) are described in Figs. 9 and 10. Figures 9 and 10 show the interaction breather wave soliton solutions for specified values of , respectively. Figure 9 includes density solutions and Fig. 10 presents two dimensional behaviours.
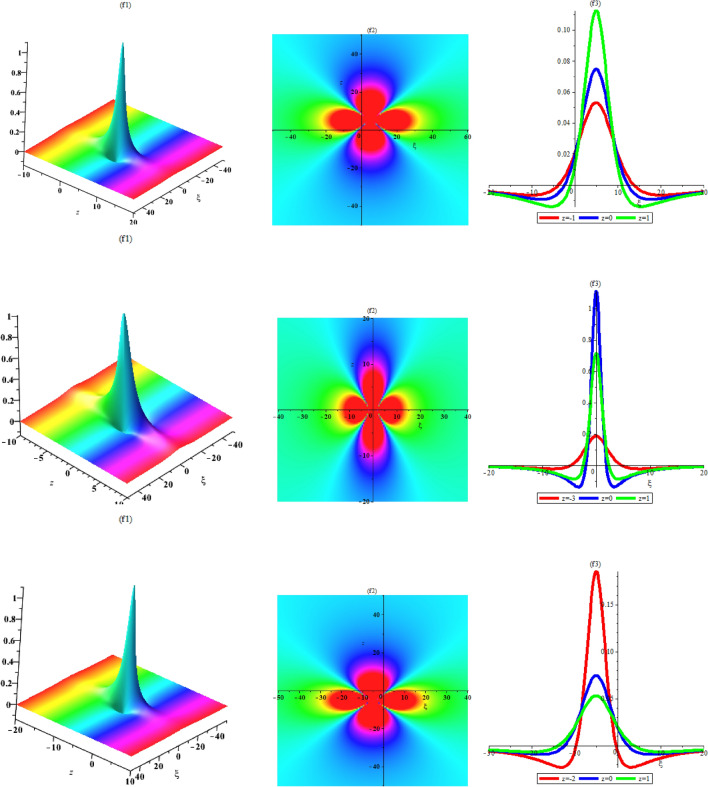
Fig. 9.
Density plots of Breather wave soliton (57) with different parameters of Case (15) , respectively.
Fig. 10.
2D plots of Breather wave soliton (57) with different parameters of Case (15) , respectively.
Multiple Rogue wave
This part explains a efficient clarification of different Exp-function strategy85,86 so that it can be encourage connected to the nonlinear PDEs as bellow:
Step 1: Consider NLPDE
| 58 |
A Painlevé analysis is introduced
| 59 |
according to the dependant variable function T. Step 2: By utilizing the relation (59), the nonlinear equation (58) is given as the following Hirota’s bilinear form
| 60 |
where and b, d are the real values. Moreover, the D-operator is shown as
| 61 |
where the vectors , and are arbitrary nonnegative integers. Step 3: Let86
| 62 |
with
| 63 |
, where and p, q are real values. The coefficients can be found, and special values p, q are utilized to control the wave center. The rest steps were presented in85. Based on , Eq. (6) is transformed as bellow form
| 64 |
in which b, d are unfound parameters and Eq. (64) is used using the below bilinear transformation
| 65 |
With considering at (62), then (62) will be as
| 66 |
without loss of generality, we can choose . Inserting (66) into (65) and setting all the coefficients of the different powers of to zero, the nonlinear algebraic equations are reached as
| 67 |
Solving Eq. (67), we get
| 68 |
Therefore, the solution of Eq. (66) is
| 69 |
by supposing , then the first-order rogue wave solutions of Eq. (1) is given
| 70 |
The above rogue wave has the following features
| 71 |
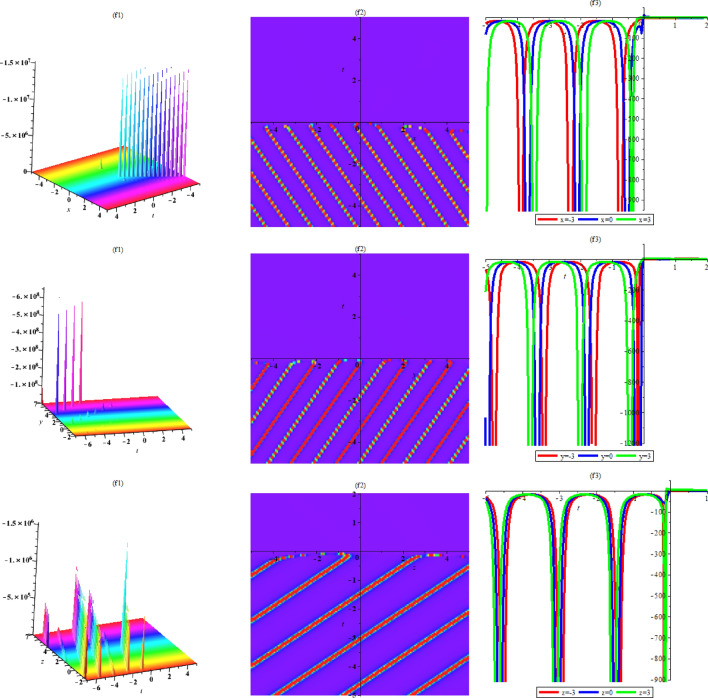
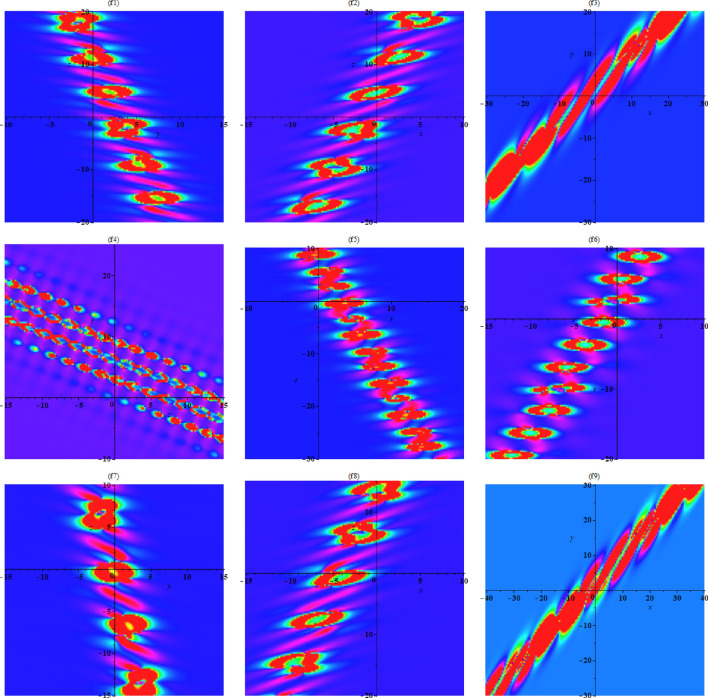
By selecting suitable values of parameters, the graphical representation of periodic wave solution is presented in Fig. 11 including 3D plot, contour plot, and 2D plot when three spaces arise at spaces , , and . In Fig. 11 (the first row) the rogue wave has one center (5, 5), (the second row) the rogue wave has one center (0, 0), while in Fig. 11 (the third row) the rogue wave has one center . Because of using a simple computation, the lump has two critical points, but we investigate only one point . At the point , the second order derivative and Hessian matrix can be determined in below
| 72 |
If , then the solution is the lump solution is the only local maximum point of function , while if , then the local minimum point of function does not occurs. Based on above analysis, the point is a maximum value point with value in which is . Figure 11 (the first row) is presented for first rogue solution with values . Figure 11 (the second row) is shown for first rogue solution with values . Moreover, Fig. 11 (the third row) is presented for first rogue solution with values .
Fig. 11.
The one-order rogue wave (70) at the first row , the second row and the third row .
For finding second rogue wave, take at (62), then (62) will be as
| 73 |
for simplifying we choose . Inserting (73) into (65) we can get the following results:
| 74 |
in which and are arbitrary values. Thus, the second-order rogue wave solutions of Eq. (1) is given as
| 75 |
where is given in Eq. (73). We analysis of second order rogue wave solution plots related to (73) with parameters available in (74). Figure 12 (the first row) is presented for second rogue solution with values . Figure 12 (the second row) is shown for second rogue solution with values . Moreover, Fig. 12 (the third row) is presented for second rogue solution with values .
Fig. 12.
The second form rogue wave (75) at (the first row), (the second row) and (the third row).
Sets of solutions are listed as:
| 76 |
Result and discussion
This portion compares the arrangements to a generalized breaking soliton system in (3 + 1)-dimensions arising in wave propagation inferred from the expository wave arrangements in this article and those found within the writing. Numerous analysts have examined to analyze a generalized breaking soliton system arising with diverse procedures. Alternately, the nonlinear differential administrator has been utilized to produce numerous wave arrangements for the specified equation as shown in the related section.
Furthermore, an analysis based on the Hirota bilinear approach is made on arrangements advertised in this original copy as well as we found by wrinkle soliton arrangements. In spite of employing a assortment of strategies, four cases have been effectively completed including periodic form solutions to a generalized breaking soliton system. Among them, cosines function forms also investigated the exact soliton solutions. Also, numerous soliton arrangements for the given demonstrate are found utilizing the hirota bilinear method.
Conclusion
This paper included two methods including the Hirota bilinear technique to resolve the (3 + 1)-dimensional a generalized breaking soliton system. As a resultant, numerous double-periodic solitons and breather waves were created, counting singular wave arrangement, periodic wave solution, asymptotic case of periodic wave solution, and soliton solutions. In addition, the multiple rogue wave solutions were obtained. The affect of wave speed and other free variables on the wave profile was additionally examined. This approach was proven to be effective and applicable to a variety of NLEEs in mathematical physics. The display comes about can be extended indeed encourage when different other sorts of nonlinearities are examined. This can be formidable research in the future.
In the field of nonlinear engineering, the soliton structures found in the literature may be of interest to researchers. It was realized that this strategy is brief, worthwhile, and productive and that considerable number of solutions can be obtained in comparison to previous ways. The accuracy of the results was tested using Maple software by substituting the obtained results into the original equation.
Acknowledgements
The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-51).
Author contributions
The authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Funding
This research was funded by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-51).
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Hui, Z. et al. Switchable single- to multiwavelength conventional soliton and bound-state soliton generated from a NbTe2 saturable absorber-based passive mode-locked erbium-doped fiber laser. ACS Appl. Mater. Interfaces16(17), 22344–22360 (2024). 10.1021/acsami.3c19323 [DOI] [PubMed] [Google Scholar]
- 2.Han, D. et al. LMCA: A lightweight anomaly network trafc detection model integrating adjusted mobilenet and coordinate attention mechanism for IoT. Telecommun. Syst.84, 549–564 (2023). 10.1007/s11235-023-01059-5 [DOI] [Google Scholar]
- 3.Dou, J. et al. Surface activity, wetting, and aggregation of a per-fuoropolyether quaternary ammonium salt surfactant with a hydroxyethyl group. Molecules28(20), 7151 (2023). 10.3390/molecules28207151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fei, R., Guo, Y., Li, J., Hu, B. & Yang, L. An improved BPNN method based on probability density for indoor location. IEICE Trans. Inf. Syst.106(5), 773–785 (2023). 10.1587/transinf.2022DLP0073 [DOI] [Google Scholar]
- 5.Li, X. et al. Electric-feld-driven printed 3D highly ordered microstructure with cell feature size promotes the maturation of engineered cardiac tissues. Adv. Sci.10(11), 2206264 (2023). 10.1002/advs.202206264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hong, J., Gui, L. & Cao, J. Analysis and experimental verification of the tangential force effect on electromagnetic vibration of pm motor. IEEE Trans. Energy Convers.38(3), 1893–1902 (2023). 10.1109/TEC.2023.3241082 [DOI] [Google Scholar]
- 7.He, X. et al. Excellent microwave absorption performance of LaFeO3/Fe3O4/C perovskite composites with optimized structure and impedance matching. Carbon213, 118200 (2023). 10.1016/j.carbon.2023.118200 [DOI] [Google Scholar]
- 8.Zhao, Y. et al. Intelligent control of multilegged robot smooth motion: A review. IEEE Access11, 86645–86685 (2023). 10.1109/ACCESS.2023.3304992 [DOI] [Google Scholar]
- 9.Meng, S., Meng, F., Chi, H., Chen, H. & Pang, A. A robust observer based on the nonlinear descriptor systems application to estimate the state of charge of lithium-ion batteries. J. Franklin Inst.360(16), 11397–11413 (2023). 10.1016/j.jfranklin.2023.08.037 [DOI] [Google Scholar]
- 10.Chen, D. L., Zhao, J. W. & Qin, S. R. SVM strategy and analysis of a three-phase quasi-Z-source inverter with high voltage transmission ratio. Sci. China Tech. Sci.66, 2996–3010 (2023). 10.1007/s11431-022-2394-4 [DOI] [Google Scholar]
- 11.Chen, D., Zhao, T., Han, L. & Feng, Z. Single-stage multi-input buck type high-frequency link’s inverters with series and simultaneous power supply. IEEE Trans. Power Electron.37(6), 7411–7421 (2022). 10.1109/TPEL.2021.3139646 [DOI] [Google Scholar]
- 12.Chen, D., Zhao, T. & Xu, S. Single-stage multi-input buck type high-frequency link’s inverters with multiwinding and time-sharing power supply. IEEE Trans. Power Electron.37(10), 12763–12773 (2022). 10.1109/TPEL.2022.3176377 [DOI] [Google Scholar]
- 13.Wang, T., Zhang, S., Yang, Q. & Liew, S. C. Account service network: A unified decentralized web 3.0 portal with credible anonymity. IEEE Netw.37(6), 101–108 (2023). 10.1109/MNET.2023.3321090 [DOI] [Google Scholar]
- 14.Li, J., Tang, H., Li, X., Dou, H. & Li, R. LEF-YOLO: A lightweight method for intelligent detection of four extreme wildfires based on the YOLO framework. Int. J. Wildland Fire33, WF23044 (2023). 10.1071/WF23044 [DOI] [Google Scholar]
- 15.Zhao, Y. et al. Release pattern of light aromatic hydrocarbons during the biomass roasting process. Molecules29(6), 1188 (2024). 10.3390/molecules29061188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang, M., Xie, X., Manafian, J., Ilhan, O. A. & Singh, G. Characteristics of the new multiple rogue wave solutions to the fractional generalized CBS-BK equation. J. Adv. Res.38(38), 131–42 (2022). 10.1016/j.jare.2021.09.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wu, W. et al. Numerical and analytical results of the 1D BBM equation and 2D coupled BBM-system by finite element method. Int. J. Mod. Phys. B36(28), 2250201 (2022). 10.1142/S0217979222502010 [DOI] [Google Scholar]
- 18.Liu, M. et al. Wave profile, Paul–Painlevé approaches and phase plane analysis to the generalized (3+1)-dimensional shallow water wave model. Qual. Theor. Dyn. Syst.23, 41 (2024). 10.1007/s12346-023-00896-8 [DOI] [Google Scholar]
- 19.Manafian, J. On the complex structures of the Biswas–Milovic equation for power, parabolic and dual parabolic law nonlinearities. Eur. Phys. J. Plus130, 255 (2015). 10.1140/epjp/i2015-15255-5 [DOI] [Google Scholar]
- 20.Manafian, J., Foroutan, M. R. & Guzali, A. Applications of the ETEM for obtaining optical soliton solutions for the Lakshmanan–Porsezian–Daniel model. Eur. Phys. J. Plus132, 494 (2017). 10.1140/epjp/i2017-11762-7 [DOI] [Google Scholar]
-
21.Manafian, J. Optical soliton solutions for Schrödinger type nonlinear evolution equations by the
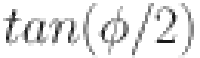 -expansion method. Optik127, 4222–4245 (2016). 10.1016/j.ijleo.2016.01.078 [DOI] [Google Scholar]
-expansion method. Optik127, 4222–4245 (2016). 10.1016/j.ijleo.2016.01.078 [DOI] [Google Scholar] - 22.Zhu, C., Al-Dossari, M., Rezapour, S. & Gunay, B. On the exact soliton solutions and different wave structures to the (2+1) dimensional Chaffee–Infante equation. Results Phys.57, 107431 (2024). 10.1016/j.rinp.2024.107431 [DOI] [Google Scholar]
- 23.Kai, Y. & Yin, Z. On the Gaussian traveling wave solution to a special kind of Schrödinger equation with logarithmic nonlinearity. Mod. Phys. Lett. B36(02), 2150543 (2021). 10.1142/S0217984921505436 [DOI] [Google Scholar]
- 24.Bouchaala, F., Matsushima, J. & Ali, M. Potential of seismic attenuation for geotechnical investigation of carbonate subsurface. In NSG2023 29th European Meeting of Environmental and Engineering Geophysics, vol. 2023, No. 1, 1–5 (European Association of Geoscientists Engineers, 2023).
- 25.Li, R. et al. Different forms of optical soliton solutions to the Kudryashov’s quintuple self-phase modulation with dual-form of generalized nonlocal nonlinearity. Results Phys.46, 106293 (2023). 10.1016/j.rinp.2023.106293 [DOI] [Google Scholar]
- 26.Surugiu, M. R., Vasile, V., Mazilescu, R., Surugiu, C. & Vasile, R. An analysis of the government revenue-expenditure nexus: A wavelet approach for the Romanian case. Econ. Finance Lett.10(1), 78–93 (2023). 10.18488/29.v10i1.3299 [DOI] [Google Scholar]
- 27.Kapse, Y. D. & Mohani, S. P. Performance analysis of OFDM with variations in cyclic prefix and FFT lengths. Rev. Comput. Eng. Res.10(4), 182–198 (2023). 10.18488/76.v10i4.3551 [DOI] [Google Scholar]
- 28.Xie, X. et al. Fluid inverse volumetric modeling and applications from surface motion. IEEE Trans. Visualiz. Comput. Graphics. 10.1109/TVCG.2024.3370551 (2024). [DOI] [PubMed]
- 29.Aghazadeh, M. R., Asgari, T., Shahi, A. & Farahm, A. Designing strategy formulation processing model of governmental organizations based on network governance. Quart. J. Public Organ. Manag.4(1), 29–52 (2016). [Google Scholar]
- 30.Gholamiangonabadi D, Nakhodchi S, Jalalimanesh A, & Shahi A. Customer churn prediction using a meta-classifier approach; A case study of Iranian banking industry. In Proc Int Conf Indust Eng Operat Manag 364–375 (2019).
- 31.Nisar, K. S. et al. Novel multiple soliton solutions for some nonlinear PDEs via multiple Exp-function method. Results Phys.21, 103769 (2021). 10.1016/j.rinp.2020.103769 [DOI] [Google Scholar]
- 32.Zhang, H., Manafian, J., Singh, S., Ilhan, O. A. & Zekiy, A. O. Novel multiple soliton solutions for some nonlinear PDEs via multiple Exp-function method. Results Phys.25, 104168 (2021). 10.1016/j.rinp.2021.104168 [DOI] [Google Scholar]
- 33.Xie, G. et al. A gradient-enhanced physics-informed neural networks method for the wave equation. Eng. Anal. Bound. Elem.166, 105802 (2024). 10.1016/j.enganabound.2024.105802 [DOI] [Google Scholar]
- 34.Zhu, L. et al. A novel hybrid excitation magnetic lead screw and its transient sub-domain analytical model for wave energy conversion. IEEE Trans. Energy Convers.10.1109/TEC.2024.3354512 (2024). 10.1109/TEC.2024.3354512 [DOI] [Google Scholar]
- 35.Zhang, K. et al. Eatn: An efficient adaptive transfer network for aspect-level sentiment analysis. IEEE Trans. Knowl. Data Eng.35(1), 377–389 (2021). [Google Scholar]
- 36.Zhao, G., Bouchaala, F. & Jouini, M.S. Anisotropy estimation by using machine learning methods. In Seventh International Conference on Engineering Geophysics, Al Ain, UAE, vol. 16–19, 217–221 (Society of Exploration Geophysicists, 2024).
- 37.Chen, W. et al. Cutting-edge analytical and numerical approaches to the gilson-pickering equation with plenty of soliton solutions. Mathematics11, 3454 (2023). 10.3390/math11163454 [DOI] [Google Scholar]
- 38.Zhang, T., Deng, F. & Shi, P. Nonfragile finite-time stabilization for discrete mean-field stochastic systems. IEEE Trans. Autom. Control68(10), 6423–6430 (2023). 10.1109/TAC.2023.3238849 [DOI] [Google Scholar]
- 39.Liu, W., Bai, X., Yang, H., Bao, R. & Liu, J. Tendon driven bistable origami flexible gripper for high-speed adaptive grasping. IEEE Robot. Autom. Lett.9(6), 5417–5424 (2024). 10.1109/LRA.2024.3389413 [DOI] [Google Scholar]
- 40.Dawod, L. A., Lakestani, M. & Manafian, J. Breather wave solutions for the (3+1)-D generalized shallow water wave equation with variable coefficients. Qual. Theor. Dyn. Syst.22, 127 (2023). 10.1007/s12346-023-00826-8 [DOI] [Google Scholar]
- 41.Pan, Y. et al. N-lump solutions to a (3+1)-dimensional variable-coefficient generalized nonlinear wave equation in a liquid with gas bubbles. Qual. Theor. Dyn. Syst.21, 127 (2022). 10.1007/s12346-022-00658-y [DOI] [Google Scholar]
- 42.Bouchaala, F., Ali, M.Y., Matsushima, J., Jouini, M.S., Mohamed, A.A.I. & Nizamudin, S. Experimental study of seismic wave attenuation in carbonate rocks. SPE J. 1–15 (2024).
- 43.Wang, K. et al. Experimental study of mechanical properties of hot dry granite under thermal-mechanical couplings. Geothermics119, 102974 (2024). 10.1016/j.geothermics.2024.102974 [DOI] [Google Scholar]
- 44.Jia, G. et al. Valley quantum interference modulated by hyperbolic shear polaritons. Phys. Rev. B109, 155417 (2024). 10.1103/PhysRevB.109.155417 [DOI] [Google Scholar]
- 45.Zhu, C., Al-Dossari, M., El-Gawaad, N. S. A., Alsallami, S. A. M. & Shateyi, S. Uncovering diverse soliton solutions in the modified Schrödinger’s equation via innovative approaches. Results Phys.54, 107100 (2023). 10.1016/j.rinp.2023.107100 [DOI] [Google Scholar]
- 46.Mehrpooya, M., Ghadimi, N., Marefati, M. & Ghorbanian, S. A. Numerical investigation of a new combined energy system includes parabolic dish solar collector, stirling engine and thermoelectric device. Int. J. Energy Res.45(11), 16436–16455 (2021). 10.1002/er.6891 [DOI] [Google Scholar]
- 47.Jiang, W., Wang, X., Huang, H., Zhang, D. & Ghadimi, N. Optimal economic scheduling of microgrids considering renewable energy sources based on energy hub model using demand response and improved water wave optimization algorithm. J. Energy Storage55(1), 105311 (2022). 10.1016/j.est.2022.105311 [DOI] [Google Scholar]
- 48.Erfeng, H. & Ghadimi, N. Model identification of proton-exchange membrane fuel cells based on a hybrid convolutional neural network and extreme learning machine optimized by improved honey badger algorithm. Sustain. Energy Tech. Asses.52, 102005 (2022). [Google Scholar]
- 49.Cai, W. et al. Optimal bidding and offering strategies of compressed air energy storage: A hybrid robust-stochastic approach. Renew. Energy143, 1–8 (2019). 10.1016/j.renene.2019.05.008 [DOI] [Google Scholar]
- 50.Saeedi, M., Moradi, M., Hosseini, M., Emamifar, A. & Ghadimi, N. Robust optimization based optimal chiller loading under cooling demand uncertainty. Appl. Therm. Eng.148, 1081–1091 (2019). 10.1016/j.applthermaleng.2018.11.122 [DOI] [Google Scholar]
- 51.Yuan, Z., Wang, W., Wang, H. & Ghadimi, N. Probabilistic decomposition-based security constrained transmission expansion planning incorporating distributed series reactor. IET Gener. Trans. Distrib.14(17), 3478–3487 (2020). 10.1049/iet-gtd.2019.1625 [DOI] [Google Scholar]
- 52.Mir, M., Shafieezadeh, M., Heidari, M. A. & Ghadimi, N. Application of hybrid forecast engine based intelligent algorithm and feature selection for wind signal prediction. Evol. Syst.11(4), 559–573 (2020). 10.1007/s12530-019-09271-y [DOI] [Google Scholar]
- 53.Zhang, J., Khayatnezhad, M. & Ghadimi, N. Optimal model evaluation of the proton exchange membrane fuel cells based on deep learning and modified African vulture optimization algorithm. Energy Sources A44, 287–305 (2022). 10.1080/15567036.2022.2043956 [DOI] [Google Scholar]
- 54.Ali, T. A. A., Xiao, Z., Jiang, H. & Li, B. A class of digital integrators based on trigonometric quadrature rules. IEEE Trans. Ind. Electron.71(6), 6128–6138 (2024). 10.1109/TIE.2023.3290247 [DOI] [Google Scholar]
- 55.Diop, A. M. et al. Design electrical model noise and perform nonlinearities of SiGe bipolar phototransistor. Int. J. Innov. Res. Sci. Stud.6(4), 731–740 (2023). [Google Scholar]
- 56.Yu, D. et al. Energy management of wind-PV-storage-grid based large electricity consumer using robust optimization technique. J. Energy Storage27, 101054 (2020). 10.1016/j.est.2019.101054 [DOI] [Google Scholar]
- 57.Dongmin, Y. & Ghadimi, N. Reliability constraint stochastic UC by considering the correlation of random variables with Copula theory. IET Renew. Power Gener.13(14), 2587–93 (2019). 10.1049/iet-rpg.2019.0485 [DOI] [Google Scholar]
- 58.Chen, L. et al. Optimal modeling of combined cooling, heating, and power systems using developed African vulture optimization: A case study in watersport complex. Energy Sources A44, 4296–4317 (2022). 10.1080/15567036.2022.2074174 [DOI] [Google Scholar]
- 59.Jiang, H., Li, S. M. & Wang, W. G. Moderate deviations for parameter estimation in the fractional Ornstein–Uhlenbeck processes with periodic mean. Acta Math. Sin. English Ser.40, 1308–1324 (2024). 10.1007/s10114-023-2157-z [DOI] [Google Scholar]
- 60.Qawaqneh, H., Manafian, J., Alharthi, M. & Alrashedi, Y. Stability analysis, modulation instability, and beta-time fractional exact soliton solutions to the Van der Waals equation. Mathematics12, 2257 (2024). 10.3390/math12142257 [DOI] [Google Scholar]
- 61.Lei, M. et al. Electro-sorting create heterogeneity: Constructing a multifunctional janus film with integrated compositional and microstructural gradients for guided bone regeneration. Adv. Sci.11, 2307606 (2024). 10.1002/advs.202307606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Manafian, J., Ilhan, O. A., Alizadeh, A. & Mohammed, S. A. Multiple rogue wave and solitary solutions for the generalized BK equation via Hirota bilinear and SIVP schemes arising in fluid mechanics. Commun. Theor. Phys.72, 075002 (2020). 10.1088/1572-9494/ab8a13 [DOI] [Google Scholar]
- 63.Manafian, J. et al. Dynamical behaviors of lumpoff and rogue wave solutions for nonlocal Gardner equation. Math. Prob. Eng.2022, 100324 (2022). 10.1155/2022/9360263 [DOI] [Google Scholar]
- 64.Chen, W. et al. Cutting-edge analytical and numerical approaches to the Gilson-Pickering equation with plenty of soliton solutions. Math.11(16), 3454 (2023). 10.3390/math11163454 [DOI] [Google Scholar]
- 65.Qian, Y. et al. Nonparaxial solitons and the dynamics of solitary waves for the coupled nonlinear Helmholtz systems. Opt. Quant. Electron.55, 1022 (2023). 10.1007/s11082-023-05232-7 [DOI] [Google Scholar]
- 66.Feng, Y., Bilige, S. & Wang, X. Diverse exact analytical solutions and novel interaction solutions for the (2+1)-dimensional Ito equation. Phys. Scr.95, 095201 (2020). 10.1088/1402-4896/aba71b [DOI] [Google Scholar]
- 67.Ma, H. C., Wu, H. F., Ma, W. X. & Deng, A. P. Localized interaction solutions of the (2+1)-dimensional Ito equation. Opt. Quant. Electron.53, 303 (2021). 10.1007/s11082-021-02909-9 [DOI] [Google Scholar]
- 68.Liu, Y., Zhang, W. X. & Ma, W. X. Riemann–Hilbert problems and soliton solutions for a generalized coupled Sasa–Satsuma equation. Commun. Nonlinear Sci. Num. Simul.118, 107052 (2023). 10.1016/j.cnsns.2022.107052 [DOI] [Google Scholar]
- 69.Zeng, S., Liu, Y., Chen, X. & Zhang, W. X. Various breathers, lumps, line solitons and their interaction solutions for the (2+1)-dimensional variable-coefficient Sawada–Kotera equation. Results Phys.42, 105992 (2022). 10.1016/j.rinp.2022.105992 [DOI] [Google Scholar]
- 70.Kai, Y., Chen, S., Zhang, K. & Yin, Z. Exact solutions and dynamic properties of a nonlinear fourth-order time-fractional partial differential equation. Waves Random Complex Media10.1080/17455030.2022.2044541 (2022). 10.1007/s11071-022-07322-9 [DOI] [Google Scholar]
- 71.Liao, L. et al. Color image recovery using generalized matrix completion over higher-order finite dimensional algebra. Axioms12(10), 954 (2023). 10.3390/axioms12100954 [DOI] [Google Scholar]
- 72.Chen, C., Han, D. & Chang, C. C. MPCCT: Multimodal vision-language learning paradigm with context-based compact transformer. Pattern Recogn.147, 110084 (2024). 10.1016/j.patcog.2023.110084 [DOI] [Google Scholar]
- 73.Chen, C., Han, D. & Shen, X. CLVIN: Complete language-vision interaction network for visual question answering. Knowl.-Based Syst.275, 110706 (2023). 10.1016/j.knosys.2023.110706 [DOI] [Google Scholar]
- 74.Shi, S., Han, D. & Cui, M. A multimodal hybrid parallel network intrusion detection model. Connect. Sci.35, 2227780 (2023). 10.1080/09540091.2023.2227780 [DOI] [Google Scholar]
- 75.Wanh, H., Han, D., Cui, M. & Chen, C. NAS-YOLOX: A SAR ship detection using neural architecture search and multi-scale attention. Connect. Sci.35, 1–32 (2023). 10.1080/09540091.2023.2257399 [DOI] [Google Scholar]
- 76.Chen, X., Yang, P., Wang, M., Hu, F. & Xu, J. Output voltage drop and input current ripple suppression for the pulse load power supply using virtual multiple quasi-notch-filters impedance. IEEE Trans. Power Electron.38(8), 9552–9565 (2023). 10.1109/TPEL.2023.3275304 [DOI] [Google Scholar]
- 77.Gai, L., Wu, W., Ding, T. & Qian, Y. Lump wave solutions, lump-stripe soliton inelastic collision phenomena and rogue-type wave solutions for a generalized breaking soliton system in (3+1)-dimensions. Wave Motion124, 103243 (2024). 10.1016/j.wavemoti.2023.103243 [DOI] [Google Scholar]
- 78.Ma, Y. L. & Li, B. Q. Interactions between soliton and rogue wave for a (2+1)-dimensional generalized breaking soliton system: Hidden rogue wave and hidden soliton. Comput. Math. Appl.78, 827–839 (2019). 10.1016/j.camwa.2019.03.002 [DOI] [Google Scholar]
- 79.Osman, M. S. On multi-soliton solutions for the (2+1)-dimensional breaking soliton equation with variable coefficients in a graded-index waveguide. Comput. Math. Appl.75, 1–6 (2018). 10.1016/j.camwa.2017.08.033 [DOI] [Google Scholar]
- 80.Ilhan, O. A. & Manafian, J. Periodic type and periodic cross-kink wave solutions to the (2+1)-dimensional breaking soliton equation arising in fluid dynamics. Mod. Phys. Lett. B33, 1950277 (2019). 10.1142/S0217984919502774 [DOI] [Google Scholar]
- 81.Long, W. Multiple periodic-soliton solutions to Kadomtsev–Petviashvili equation. Appl. Math. Comput.218, 368–75 (2011). 10.1016/j.amc.2011.05.072 [DOI] [Google Scholar]
- 82.Liu, J. G., Zhu, W. H., He, Y. & Seadawy, A. R. Complexiton solutions and periodic-soliton solutions for the (2+1)-dimensional BLMP equation. AIMS Math.5(1), 421–439 (2020). 10.3934/math.2020029 [DOI] [Google Scholar]
- 83.Liu, J. G. & Tian, Y. New double-periodic soliton solutions for the (2+1)-dimensional breaking soliton equation. Commun. Theor. Phys.69, 585–97 (2018). 10.1088/0253-6102/69/5/585 [DOI] [Google Scholar]
- 84.Liu, J. G., Zhu, W. H., Lei, Z. Q. & Ai, G. P. Double-periodic soliton solutions for the new (2+1)-dimensional KdV equation in fluid flows and plasma physics. Anal. Math. Phys.10, 41 (2020). 10.1007/s13324-020-00387-y [DOI] [PubMed] [Google Scholar]
- 85.Ren, J., Ilhan, O. A., Bulut, H. & Manafian, J. Multiple rogue wave, dark, bright, and solitary wave solutions to the KP-BBM equation. J. Geom. Phys.164, 104159 (2021). 10.1016/j.geomphys.2021.104159 [DOI] [Google Scholar]
- 86.Manafian, J. Multiple rogue wave solutions and the linear superposition principle for a (3+1)-dimensional Kadomtsev–Petviashvili–Boussinesq-like equation arising in energy distributions. Math. Method Appl. Sci.44, 14079–93 (2021). 10.1002/mma.7676 [DOI] [Google Scholar]
- 87.Ullah, M. S., Roshid, H. O. & Ali, M. Z. New wave behaviors and stability analysis for the (2+1)-dimensional Zoomeron model. Opt. Quant. Electron.56, 240 (2024). 10.1007/s11082-023-05804-7 [DOI] [Google Scholar]
- 88.Ullah, M. S., Roshid, H. O. & Ali, M. Z. New wave behaviors of the Fokas–Lenells model using three integration techniques. PLoS One18(9), e0291071 (2023). 10.1371/journal.pone.0291071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Ullah, M. S., Ali, M. Z. & Roshid, H. O. Bifurcation analysis and new waveforms to the first fractional WBBM equation. Sci. Rep.14, 11907 (2024). 10.1038/s41598-024-62754-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Ullah, M. S., Ali, M. Z. & Roshid, H. O. Bifurcation analysis and new waveforms to the fractional KFG equation. Partial Differ. Equ. Appl. Math.10, 100716 (2024). 10.1016/j.padiff.2024.100716 [DOI] [Google Scholar]
- 91.Ullah, M. S. Interaction solution to the (3+1)-D negative-order KdV first structure. Partial Differ. Equ. Appl. Math.8, 100566 (2023). 10.1016/j.padiff.2023.100566 [DOI] [Google Scholar]
- 92.Ullah, M. S., Ahmed, O. & Mahbub, Md. A. Collision phenomena between lump and kink wave solutions to a (3+1)-dimensional Jimbo–Miwa-like model. Partial Differ. Equ. Appl. Math.5, 100324 (2022). 10.1016/j.padiff.2022.100324 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.