A Single Model for the Thermodynamics and Kinetics of Metal Exsolution from Perovskite Oxides

Abstract

Exsolution has emerged as an outstanding route for producing oxide-supported metal nanoparticles. For ABO₃-perovskite oxides, various late transition-metal cations can be substituted into the lattice under oxidizing conditions and exsolved as metal nanoparticles after reduction. A consistent and comprehensive description of the point-defect thermodynamics and kinetics of this phenomenon is lacking, however. Herein, supported by hybrid density-functional-theory calculations, we propose a single model that explains diverse experimental observations, such as why substituent transition-metal cations (but not host cations) exsolve from perovskite oxides upon reduction; why different substituent transition-metal cations exsolve under different conditions; why the metal nanoparticles are embedded in the surface; why exsolution occurs surprisingly rapidly at relatively low temperatures; and why the reincorporation of exsolved species involves far longer times and much higher temperatures. Our model’s foundation is that the substituent transition-metal cations are reduced to neutral species within the perovskite lattice as the Fermi level is shifted upward within the bandgap upon sample reduction. The calculations also indicate unconventional influences of oxygen vacancies and A-site vacancies. Our model thus provides a fundamental basis for improving existing, and creating new, exsolution-generated catalysts.

Introduction

Nanoparticles of transition metals, finely distributed on oxide supports, constitute established catalytic systems. In recent years, exsolution has become a key method for producing such metal nanoparticles anchored at the surfaces of ABO₃ perovskite-oxide hosts.^1,2 These systems provide a range of benefits over those produced by conventional methods—enhanced catalytic activity, high resistance to agglomeration, homogeneous size distribution, high tunability, and efficient use of precious metals. An enormous variety of host ABO₃ perovskite compositions has been studied,³⁻¹¹ with the exsolving metal residing initially on the perovskite’s B-site and with a high concentration of A-site vacancies.¹² One representative composition^1,2,13 is thus Sr_1–3x/2La_xTi_1–yNi_yO_3–y, with Sr as the host A-site cation, La as the donor species that compensates the A-site deficiency, Ti as the host B-site cation and Ni as the B-site substituent (that will exsolve). Treating such systems at elevated, but not very high, temperatures in moderately reducing conditions results in the exsolution of the B-site substituent as stable, embedded, well-distributed metal nanoparticles.

Although, or perhaps even because, exsolution has been observed for such an enormous variety of ABO₃ perovskite systems,³⁻¹¹ the thermodynamic origin of exsolution is unclear. It has been proposed that the combination of A-site deficiency from the starting composition and oxygen deficiency introduced by reduction is responsible for B-site exsolution. This combination produces a surfeit of B-site cations, and to ameliorate the situation, the perovskite lattice expels these B-site cations.^1,4,13,14 This proposal is inconsistent, however, with the general observation that only the substituent B-site cations exsolve and not the host B-site cations. The proposed instability of the perovskite lattice cannot explain, therefore, the exsolution of B-site substituent cations. An alternative proposal considers exsolution to occur when the Gibbs energy of reduction of the transition-metal oxide becomes negative.^1,15,16 Support for this proposal comes from the good agreement found between those transition-metal cations that have been observed experimentally to exsolve from perovskites thus far (and also those that have not) and their respective Gibbs energies of reduction. Nonetheless, this approach is incomplete: the exsolution process is implicitly separated into two (physically reasonable) steps, the transition-metal oxide’s removal from the perovskite-oxide host and its subsequent reduction, but the first step is ignored. This first step, furthermore, has to be unfavorable (because its reverse is highly favorable), and its Gibbs energy may be larger in magnitude than the Gibbs energy of reduction. This approach, by being not only incomplete but also empirical, does not provide a fundamental explanation of exsolution. A third proposal involves the segregation energy of the substituent B-site cations to the surface. According to density-functional-theory (DFT) calculations,^17,18 the energy for the cosegregation of the B-site substituent and an oxygen vacancy is predicted to be much higher than the segregation energy of the B-site substituent alone, and hence, a substantial increase in oxygen-vacancy concentration leads to exsolution. The first problem with this proposal is that segregation to the surface is not exsolution. If a Ni cation has segregated to a surface, it occupies a site in the first atomic layer(s) of the solid and hence it is still within the host lattice. It has not yet been exsolved as a second phase. A second problem with the segregation proposal is that it requires the oxygen-vacancy concentration to be very low in the oxidized state (which is not the case, for instance, for our representative composition Sr_1–3x/2La_xTi_1–yNi_yO_3–y) and to increase strongly when the system is reduced. Indeed, almost all exsolving perovskites contain abundant amounts of oxygen vacancies to compensate the net concentration of acceptor species. The larger problem with this proposal is that the segregation energy of Ni²⁺ alone is already negative, meaning that reducing conditions are not necessary: already under oxidizing conditions, Ni²⁺ should segregate to the surface. And last, as a fourth problem of this proposal, metal nanoparticles submerged in the bulk are also formed,¹⁹ which demonstrates that the presence of a surface (and by extension, a thermodynamic driving force for segregation to the surface) is not a necessary condition for exsolution to occur. Thus, cosegregation of B-site substituents and oxygen vacancies to the surface is also evidently unable to explain exsolution.

In addition to the thermodynamic origin of exsolution being unclear, the reasons for the relatively fast kinetics are unknown. Exsolution has been found to take place, for instance, at temperatures of T = 1173 K within hundreds of seconds²⁰ (although much longer times are generally used to produce catalytic systems). The characteristic temperature–time window for cation transport processes in titanate perovskites,²¹⁻²³ however, is substantially different, as evidenced by the typical synthesis conditions for the starting solid solutions, of T > 1400 K for tens of hours^{1,2,12,20,24,25} (see Figure 1). Curiously, the kinetics of reincorporation of the exsolved component under oxidizing conditions²⁶ are consistent with the standard (high) temperature–(long) time window. It is the discrepancy between exsolution conditions, on the one hand, and synthesis and reincorporation conditions, on the other, that is as yet unexplained.

Figure 1.

Schematic illustration of the preparation and exsolution processes. A transition-metal oxide is incorporated into a perovskite host lattice at high temperatures under oxidizing conditions. Subsequently, upon reduction at much lower temperatures, the transition metal is exsolved as metal nanoparticles.

Lastly, it is remarkable that perovskite oxides constitute the vast majority of host materials that undergo exsolution.²⁷ We suspect that many other oxide systems have been examined experimentally, but the comparatively poor performance of such systems has resulted in these negative results remaining unpublished. If one could understand what combination of factors makes the perovskites such excellent exsolution systems, one could exploit this knowledge to facilitate property optimization and to accelerate the development of new systems.

In this way we arrive at the three critical questions to be addressed in this study: Why does the transition-metal substituent exsolve but not the host B-site cation? How can exsolution take place at such low temperatures in such short times? And why does the ABO₃ perovskite structure constitute such a good host material? Herein, we propose a single model that provides answers to these three main questions, and to some secondary questions as well. The core of the model is that the transition-metal substituents change their valence within the perovskite matrix, as the Fermi level shifts upward past the relevant charge-transition levels within the bandgap upon oxide reduction, Ni²⁺ in SrTiO₃, for example, becoming Ni⁺ and then Ni⁰. In comparison with Ni²⁺, the neutral species are energetically unfavored in the perovskite lattice, and are thus expelled; and being neutral, they can migrate far more easily within the ABO₃ perovskite lattice. Our model thus stands in contrast to the standard model, in which substituent cations are reduced only once they have reached the surface, after they have left the lattice. To elucidate our model, we examine, by means of hybrid DFT calculations, point-defect behavior in the model system of A-site deficient SrTiO₃ with Ni as the late transition-metal substituent (Ni being the most intensively studied exsolution substituent).¹⁰

Although the term exsolution has been applied to a variety of phenomena,^7,28 in this study we favor a narrower definition: Transition-metal species coming out of a lattice upon reduction, leaving the host composition otherwise unchanged and the host lattice otherwise intact (Figure 1). Consequently, cases that involve host cations or that involve lattice decomposition do not fall under our definition. Furthermore, in such cases, alternative explanations are available. Here it will suffice to mention three examples. The first is the appearance of SrO on the surface of SrTiO₃ after a high-temperature anneal.²⁹ In this case, the host Sr cations come out of the lattice because of the active SrO partial-Schottky equilibrium that produces strontium and oxygen vacancies in the bulk.³⁰ The second example is A-cation or B-cation based phases appearing on the surface of thin films produced, for example, by pulsed laser deposition. Such thin-film samples will generally contain concentrations of A-site and B-site cation vacancies that are far above their equilibrium values and in general not equal.^22,31,32 High-temperature treatments allow such systems to reach equilibrium by expelling excess B-site or excess A-site cations (respectively) as part of a second phase at the surface. The third example is the appearance of native B-site species from a nonsubstituted perovskite lattice, such as LaNiO₃.³³ In this case, the perovskite lattice undergoes phase decomposition to a binary oxide and a metal.

In this study, hybrid DFT calculations were carried out with the HSE06³⁴⁻³⁶ functional in VASP.³⁷⁻⁴⁰ Defect formation energies, corrected for artificial interactions between periodic images as necessary,⁴¹ were used to obtain the charge-transition levels of Ni and defect reaction energies; the energy of the oxygen molecule was corrected for overbinding.^42,43 Activation barriers of defect migration were obtained by climbing image nudged elastic band (CI-NEB) calculations.^44,45 Further details are given as Supporting Information.

Throughout the manuscript, we employ a modified version of Kröger–Vink^46,47 notation to describe point defects, using absolute (real) charges instead of relative charges.^48,49 Given the variety of Ni charge states and possible sites (A site, B site, interstitial site), the use of absolute charge is less confusing. For example, divalent Ni cations sitting on a Ti site and in an interstice are thus Ni²⁺_Ti and Ni²⁺_i, respectively (rather than Ni^″_Ti and Ni^••_i); and an oxygen site from which O^2– has been removed is thus v_O.

Results and Discussion

Transition-metal cations in perovskite SrTiO₃ and BaTiO₃ have long been known to change their formal charge states upon changes in oxygen partial pressure. Particularly well-studied species include Fe⁵⁺, Fe⁴⁺ and Fe³⁺.⁵⁰⁻⁵⁷ Ni has not been examined experimentally to the same extent, but the charge states Ni⁴⁺, Ni³⁺, and Ni²⁺ have been reported.⁵⁸⁻⁶⁴ Other transition-metal cations have received scant attention. The possibility of neutral species has been ignored. Nevertheless, trends concerning the charge-transition levels of first-row transition-metal cations in BaTiO₃ have been recently extracted by Klein et al.(65) Assuming systematic trends and extrapolating [see Figure 14a of ref (65)], we tentatively predict for SrTiO₃ (we are aware that charge-transition levels in BaTiO₃ and SrTiO₃ are not necessarily identical⁶⁶) a Ni²⁺/Ni⁺ transition at 1 eV below the conduction-band (CB) edge and a Ni⁺/Ni⁰ transition just below the CB edge [or equivalently 2.2 and 3.2 eV above the valence-band (VB) edge].

In our DFT calculations we determined for cubic SrTiO₃ charge-transition levels not only for Ni^z+_Ti but also for the defect associate with an oxygen vacancy, (Ni^z+_Tiv_O); for substitutional species on the A site, Ni^z+_Srv_O; and for five species with Ni as an interstitial, Ni^z+_Ti, (Ni^z+_iv_O), (Ni^z+_iv_Ov_Sr), (Ni^z+_iv_O2v_Sr), and (Ni^z+_iv_Ov_Ti). The Ni_i associates with v_Sr are examined, not only because of the material’s A-site deficiency, but also because of the results of a previous DFT study;⁶⁷ those with v_Ti, because the formation of Ni_i from Ni_Ti results in the formation of v_Ti. Our results are summarized in Figure 2 for levels between VB and CB edges and around them. The value of the bandgap used in Figure 2, of 3.34 eV, is taken from our hybrid DFT calculations; it compares well with the experimental value of 3.25 eV.⁶⁸⁻⁷⁰

Figure 2.

Thermodynamic charge-transition levels of different Ni-containing defects in SrTiO₃ obtained from hybrid DFT calculations. The six defects are divided into three groups that refer to B-site, A-site, and interstice occupation, respectively. The blue region indicates the valence band; the orange region, the conduction band. ^†The (Ni²⁺_iv_Ov_Sr) associate refers to a different configuration, in which the Ni²⁺ ion is displaced from the octahedral interstice toward the A-site vacancy.

The results of Figure 2 confirm the existence of various transition levels for Ni-containing defects within the band gap of SrTiO₃ but show a more complicated picture than our tentative predictions. According to our hybrid DFT calculations, not all examined Ni defects display all charge states from 4+ to 0. In particular, we found that, for Ni residing on the B-site, the charge states Ni⁴⁺_Ti, Ni³⁺_Ti and Ni²⁺_Ti are stable, in line with the results of an earlier DFT study.⁷¹ As part of an associate with an oxygen vacancy,⁵⁸ Ni^z+_Ti can assume 3+ and 2+ charge states, with the 2+/1+ level being just above the CB edge. On the A site—or to be precise: relaxed from a slightly off-center A-site symmetry position—Ni is also present as either 3+ or 2+. In other words, as a substitutional species Ni⁰ is not accessible on either cation site because the relevant charge-transition levels are well above the CB minimum. Residing in an octahedral interstice as an isolated species, only Ni²⁺_i is stable, as found in a previous DFT study of Ni²⁺_i in perovskite BaZrO₃.⁶⁷ With an adjacent oxygen vacancy, however, Ni_i can take 2+, 1+ and 0 charge states; and adding one or two A-site vacancies to this associate shifts both transition levels, but they remain essentially accessible. The main results of Figure 2, therefore, are that a Ni cation can be reduced within the perovskite lattice to Ni⁺ and even to Ni⁰, but only if present as an interstitial and as part of an associate with an oxygen vacancy (or with oxygen and cation vacancies); and that the reduction of a Ni cation to Ni⁺ or Ni⁰ occurs at different Fermi levels, depending on the nature of the Ni_i-containing associate.

It is worth emphasizing that the equilibrium concentration of a particular Ni species in a particular charge state on a particular site will depend on the position of the Fermi level and thus on the oxygen partial pressure and temperature. Let us consider, for example, Ni^z+_Ti species in Figure 2. At low Fermi levels, corresponding to oxidizing conditions, Ni⁴⁺_Ti will be the dominant charge state, with Ni³⁺_Ti and Ni²⁺_Ti present at nonzero, though perhaps negligible, concentrations; if the sample is now reduced sufficiently, such that the Fermi level crosses the Ni⁴⁺_Ti/Ni²⁺_Ti charge-transition level, the dominant charge state will be Ni²⁺_Ti, with Ni³⁺_Ti and Ni⁴⁺_Ti present at nonzero, though perhaps negligible, concentrations. In this way, one recognizes that the absence of charge transitions involving Ni³⁺_Ti in Figure 2 does not mean that this charge state is not stable. It just means that it is not the dominant one: a nonzero concentration of Ni³⁺_Ti will be present at all finite temperatures.^72,73 (The case of Fe³⁺_Ti/Fe⁴⁺_Ti concentrations in SrTiO₃ is considered quantitatively, for example, in Figures 2 and 3 of ref (74)) Since neither the defect chemistry of exsolution systems is known quantitatively nor has the Fermi level been determined in situ, we have no information as to the position of the Fermi level in the bandgap, neither before nor after reduction. We note, therefore, that at T = 1000 K, a change in oxygen partial pressure from 1 bar to 10^–20 bar corresponds to the Fermi level shifting upward by ΔE_F = 1 eV.⁷⁵

Based on these results and on the trends identified by Klein et al.,⁶⁵ we assert, first, that other transition-metal substituents will have different charge-transition levels within the bandgap and hence will require more or less reducing conditions, corresponding to different Fermi-level shifts, for exsolution; and second, that the (easily reducible) late transition-metal cations, such as Ni, Cu, Pd and Rh, will have accessible neutral levels. For early transition-metal cations, the charge-transition levels will tend to be well above the CB edge.

There is good qualitative agreement between these results for substitutional species on the B site and those obtained in two experimental studies^58,63 of SrTiO₃ under oxidizing conditions (i.e., Fermi levels relatively close to the VB edge). In one study,⁶³ Ni⁴⁺_Ti species were found through a combination of X-ray techniques; and in a different study,⁵⁸ (Ni³⁺_Tiv_O) associates were detected by means of electron paramagnetic resonance. However, a third study⁶² reported charge-transition levels in SrTiO₃ for Ni⁴⁺_Ti/Ni³⁺_Ti (of 0.15 eV above the VB edge) and for Ni³⁺_Ti/Ni²⁺_Ti (of 1.2 eV above the VB edge), values that are inconsistent with the results shown in Figure 2. These experimental values were not obtained directly, however, but by fitting a defect-chemical model to electrical conductivity data as a function of temperature. In addition, the possibility of defect associates such as (Ni^z+_Tiv_O) being present and having different charge-transition levels was not taken into account. Consequently, the values of ref (62) must be considered effective values, and a direct comparison with our data is, therefore, not possible.

We turn now to the thermodynamics of the exsolution reaction, assuming for simplicity that the point defects constitute a dilute solution. Below we propose an overall exsolution reaction that is a combination of several point-defect reactions: (in no particular order) reduction of the oxide; full Schottky disorder, or rather its reverse; Ni species forming defect associates; Ni species changing their valence; Ni species being displaced from substitutional to interstitial sites; and expulsion of Ni⁰ from the lattice. We briefly examine the first two reactions (oxide reduction and Schottky disorder), since there are data against which our calculated energies can be validated. In addition, we examine the expulsion of Ni⁰ from the lattice, since this defect reaction is a key part of our model. Thereafter we propose directly the overall exsolution reaction. By taking this shortcut, we avoid having to specify which defect associates in which charge states are involved (see Figure 2) and in which order defect association, two valence changes and site displacement occur. In any case, all defect associates containing Ni are intermediate species and are thus eliminated in the overall reaction.

For the reduction of SrTiO₃ according to

1

we obtained from the hybrid DFT calculations a value of Δ_redE = 5.7 eV, in excellent agreement with experimental values⁷⁶⁻⁷⁹ of (5.2 to 6.2) eV. For the full Schottky reaction

2

our calculations yield Δ_SchE of 2.20 eV per defect, in reasonable agreement with values of 1.64 and 2.61 eV reported in previous DFT studies,^80,81 and values of (1.6 to 2.4) eV reported in pair-potential studies.⁸²⁻⁸⁴ The good agreement for both these defect reaction energies gives us some confidence in the overall predicted reaction energy.

The expulsion of Ni⁰ from an Ni_i-containing associate in the perovskite lattice according to, for example

3

or

4

is predicted to occur with a reaction energy of Δ_expsE = −3.00 eV without v_Sr and Δ_expsE = −1.12 eV with v_Sr. These negative values highlight the thermodynamic reason for exsolution: the perovskite lattice permits Ni²⁺ to be reduced to Ni⁰ (see Figure 2), but it does not like having Ni⁰ present.

Our overall reaction for exsolution, starting with one Ni acceptor cation and its compensating oxygen vacancy (representing y in Sr_1–3x/2La_xTi_1–yNi_yO_3–y), reads

5

We computed the energy of this reaction, Δ_exsolnE, from our calculated energies of defect formation, ignoring contributions arising from interface-specific energies (see later). Calculated in this way, Δ_exsolnE refers to standard conditions (1 bar O₂), and hence, it has to be corrected for exsolution occurring under reducing conditions. This correction, corresponding to a decrease in the chemical potential of oxygen, Δμ_O2, is given by

6

From thermodynamic tables,⁸⁵ we obtain 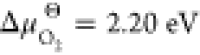at 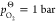for a typical exsolution temperature of T = 1000 K. For a pressure of p_O2 = 10^–20 bar, we then obtain a correction of Δμ_O2 = −6.17 eV. In this way we come to a—thermodynamically favorable—overall reaction energy of Δ_exsolnE = −2.33 eV.

One benefit of including the reverse full Schottky reaction in eq 5 is that it makes Δ_exsolnE strongly favorable (see below). Another benefit is that it yields the morphological changes in the sample that are needed to explain the embedding of the metal nanoparticles in the surface (socketing) and in the oxide bulk. The reverse of the full Schottky reaction corresponds to the annihilation of a full unit cell of the perovskite lattice at the surface (or an internal surface), that is, the filling of one v_Sr, one v_Ti and three v_O in the bulk with the appropriate host ions from a surface. Lastly, we note that including the reverse Schottky reaction provides an additional contribution (see below) to why the surface orientation (and termination) of the perovskite grains plays a role in exsolution:² Schottky disorder corresponds to the removal of host ions from the bulk and their attachment at a surface, and thus its energy depends on the surface orientation.

In order to emphasize the first thermodynamic benefit (the inclusion of the reverse Schottky reaction), we consider as an alternative the exsolution of Ni²⁺ from the B site to the surface as a second phase, without including the reverse Schottky reaction

7

combined with the subsequent reduction of NiO under exsolution conditions

8

Equation 7 is highly unfavorable, with an energy of ΔΕ = 7.53 eV. In addition to emphasizing the importance of the reverse Schottky reaction, this is a satisfying result, since the reverse reaction of eq 7 is evidently highly favored, i.e., the incorporation of Ni²⁺ into the perovskite lattice. (One should note that segregation from the perovskite lattice to the surface does not change this energy of 7.53 eV, since the Ni²⁺ cation has to leave the perovskite lattice.) The second reaction is favorable, with an energy of −1.54 eV, giving a reaction energy for

9

of 9.08 eV at 0 K and 6.00 eV under our assumed exsolution conditions (T = 1000 K, p_O2 = 10^–20 bar). [Trying to explain exsolution only with eq 8—this is the second explanation discussed in the Introduction(1,15,16)—is clearly incomplete, since eq 7 also needs to be included.]

Returning to our overall exsolution reaction of eq 5, we calculated the Δμ_O2 correction for a wide range of temperatures and oxygen partial pressures, and in this way we map out the conditions under which exsolution is thermodynamically favorable, i.e., the conditions under which Δ_exsolnE(T,pO₂) becomes negative. The results are plotted in Figure 3. As noted above, interface-specific energetic contributions are not included in these calculations. These are (i) the increased surface energy arising from morphological changes of the oxide host, (ii) the surface energy of the nanosized Ni particles, (iii) the interfacial energy of the perovskite|metal interface, and (iv) the variation in Δ_SchE with surface orientation. Since the first two are positive, the third is negative, and the fourth could be either, the boundary in Figure 3 will be shifted in some nontrivial manner. The dominant contribution to the overall reaction energy, however, will be Δ_exsolnE(T,pO₂) of eq 5, since it determines if the transition-metal substituent is expelled from the host lattice, whereas the interface-specific terms will affect the shape, size and distribution of the metal nanoparticles on the surface. There will also be a shift in the line that comes from moving from the dilute-solution thermodynamics of our DFT calculations to the concentrated solid-solutions of experiment with >1% defects. Nevertheless, we do find in Figure 3 that sintering at T = 1423 K in air, for example,²⁴ allows nickel to be incorporated into the perovskite lattice, and that exsolution at T = 1000 K under typical exsolution conditions is possible. Importantly, the results also indicate that a critical p_O2 is necessary at a given temperature; this may explain the observation that a critical amount of oxygen vacancies is required for exsolution.²

Figure 3.

Thermodynamic prediction of conditions necessary for the exsolution of Ni from SrTiO₃ based on the reaction energy for the overall exsolution reaction, eq 5. The dotted line refers to Δ_exsolnE = 0; the area above and to the right corresponds to a negative reaction energy and thus to conditions under which exsolution can take place (in the absence of kinetic hindrance). Interface-specific energies are not included (see text); dilute-solution thermodynamics are assumed.

While the results also predict that the lower the exsolution temperature, the more strongly reducing the conditions have to be, the reaction kinetics may become too slow at lower temperatures to allow the reaction to proceed on a reasonable time scale. Indeed, successful exsolution from titanate-based perovskites at temperatures below ca. 800 K has not been reported,^86,87 which is consistent with, but does not confirm, a kinetic limitation at these lower temperatures. This brings us, then, to the second critical question: Why is exsolution possible at relatively low temperatures in relatively short times?

Let us consider the initial kinetics of the exsolution process. Having been exposed to reducing conditions, a perovskite exsolution system will lose oxygen through ambipolar diffusion of oxygen vacancies and electronic species (electrons or holes). As a consequence, the slower of these two species will determine the overall rate of oxygen out-diffusion, and in our representative exsolution system with high electronic conductivity, this will be oxygen vacancies (and in systems with dominant ionic conductivity, this will be electronic species). As the reduction front advances into the sample, the local Fermi level shifts upward within the bandgap, leading to changes in the populations of Ni in its various charge states and on its various lattice sites. Since perovskite-type oxides are generally excellent oxide-ion conductors but extremely poor cation conductors, we focus our attention on cation migration processes. For the exsolution of Ni in perovskite SrTiO₃, there are, then, two processes for which the migration of Ni species is important: the individual jump of a Ni cation from a substitutional site to an interstitial site, and the long-range out-migration of Ni⁰_i, comprising multiple individual jumps. Ni also substitutes under oxidizing conditions for Ti, and therefore we also consider this possibility.

We examined first the migration of Sr²⁺ on the A-site of SrTiO₃ by a vacancy mechanism because it is a standard case against which our results can be validated. The CI-NEB calculations indicated a linear ⟨100⟩ path and an almost cosinusoidal energy profile, with an activation barrier of 4.13 eV. This value agrees well with results from experimental^21,22,88 and computational⁸⁹⁻⁹¹ studies, in which activation energies of (3.5 to 4.0) eV are reported. Interestingly, and of relevance below, we find that the presence of a neighboring v_Ti lowers the barrier for the migration of Sr²⁺ to only 1.48 eV.

Next, we examined the migration of B-site cations on the B-site sublattice by a vacancy mechanism. We note that the migration of B-site cations along ⟨110⟩ in perovskites is energetically unfavorable because of the strong electrostatic repulsion between the migrating cation and the two A-site cations in the saddle-point configuration.⁹² As a consequence, migration along ⟨100⟩ will be preferred (only one A-site cation in the saddle-point configuration), and it will be further assisted by an A-site vacancy (no A-site cations in the saddle-point configuration). Indeed, CI-NEB calculations yielded an activation barrier for the migration of Ti⁴⁺ by a vacancy mechanism along ⟨100⟩ of 6.54 eV, a barrier that is lowered substantially to 3.40 eV when an adjacent v_Sr is present. For the Ni species that are stable substituting for Ti⁴⁺, i.e., Ni⁴⁺, Ni³⁺ and Ni²⁺, the calculated barriers for a v_Sr-assisted jump to a neighboring v_Ti (see Table 1) are smaller in comparison. Consequently, for the long-range diffusion of the entire Ni^z+_Tiv_Tiv_Sr associate in an A-site-deficient composition with very few v_Ti present, there are three steps in series, and the rate-determining step according to our calculations will be that for v_Ti migration (i.e., the jump of Ti⁴⁺), since the activation energies for the migration steps of Ni^z+_Ti (with a neighboring v_Sr) and v_Sr (with a neighboring v_Ti, see above) are much lower. It will therefore be the activation energy of 3.40 eV that constitutes the effective barrier for long-range diffusion of Ni^z+_Ti species. This activation energy is similar to those found for cation diffusion in the standard temperature–time window,^21,22 and hence it does not seem to explain the discrepancy mentioned in the Introduction.

Table 1. Activation Energies of Migration for B-Site Cations in SrTiO₃ along ⟨100⟩, in the Presence of v_Sr^a.

species	Ti4+	Ni4+	Ni3+	Ni2+	Ni1+
ΔmigE [eV]	3.40	3.02	2.84	2.09	n.a.

^aThese barriers refer to the individual jumps for Ni^z+_Ti jumping to a neighbouring v_Ti, but they do not correspond to the effective barrier for long-range diffusion.

Coming now to the migration jump of Ni²⁺ or Ni⁺ from a Ti site to a neighboring interstitial site, we kept the model simple by having a neighboring oxygen vacancy and a neighboring strontium vacancy. CI-NEB calculations indicated no barrier for the jump, that is, the system’s energy increased continuously as the Ni ion moved from the Ti site to the interstitial site. Under equilibrium conditions, the energy difference between initial and final states, of ca. 2.5 eV for both species, will determine the populations of the two configurations according to p(Ni^z+_i)/p(Ni^z+_Ti) = e^–ΔE/k_BT. During exsolution, however, the interstitial Ni cations will be quickly reduced in the subsequent step(s) to Ni⁰_i, thus forcing further Ni cations from Ti sites into interstitial sites in order to re-establish the quasi-equilibrium. Two points should be noted here. First, only after Ni_i has migrated away from v_Ti can it be reduced to Ni⁰_i (see Figure 2). Second, without v_Sr, the energies are ca. 1.5 eV higher, indicating that A-site vacancies, by lowering the energy of the interstitial ions, will accelerate the kinetics of Ni jumping from the B sites to interstitial sites.

The migration of Ni⁰_i out of the lattice depends, of course, on the defect associate that dominates. Instead of covering all possible defect associates, we probe only the simplest case, the migration of Ni⁰_i as part of the Ni⁰_iv_O associate. The migration energy for Ni⁰ is found to be only 1.44 eV. We attribute this surprisingly low value to the migrating species being neutral. This low value also generates the question as to the activation barrier for v_O migration as part of the Ni⁰_iv_O associate. Such a barrier is found to be 1.45 eV (which is much higher than the activation energy for the migration of a free oxygen vacancy, of ca. 0.6 eV⁹³⁻⁹⁷). The long-range diffusion of the Ni⁰_iv_O associate will thus be characterized by an effective activation energy of ca. 1.45 eV.

Our migration analysis thus indicates that Ni⁰_i species can be produced and that they are mobile in the lattice as part of the Ni⁰_iv_O associate. It is tempting to conclude that the diffusion of the Ni⁰_iv_O associate determines the overall rate of exsolution, but we refrain from doing so because we have not examined all possibilities and because we have only activation energies (and an energy difference) and not pre-exponential terms. Conceivably, the transfer of Ni cations from substitutional sites to interstices could determine the overall rate. It is also conceivable that oxygen-vacancy diffusion in lattices containing A-site vacancies and Ni species^98,99 is slower than the out-diffusion of the Ni⁰_i species. Lastly, it is also conceivable that the rate-determining step may change during the course of an exsolution run.

It is worth stressing that Ni⁰_i diffusion as part of the Ni⁰_iv_O associate does not involve cation vacancies. In perovskite systems it can occur, therefore, much faster than the vacancy-mediated migration of the host cations. This has consequences for the kinetics of socket formation, in the form of the reverse Schottky reaction, relative to that of Ni expulsion from the perovskite. Specifically, we suppose that sockets will initially form at those places at the surface (and in the bulk) where sufficient v_Sr, v_O and Ni_Ti species are present, such that the concomitant formation of Ni_i species (and thus v_Ti) and of two further v_O supplies all the species necessary for the reverse Schottky reaction to occur, without the need for long-range migration of host cations. At those places where not all defects for the reverse Schottky reaction are present, Ni may be expelled from the solid to form on the surface Ni_ad species, which through surface diffusion may join the growing Ni nanoparticle. At longer time scales, cation-vacancy migration to the nascent socket can occur, but Ni⁰_i may diffuse to the growing Ni nanoparticle from much further away, since the migration of cation vacancies is not necessary for the migration of Ni⁰_i. If v_Sr do diffuse out of a region, however, the kinetics of Ni_i forming from Ni_Ti will slow down drastically, because the energy difference for Ni between Ti and interstitial sites rises substantially (see above).

These results also provide an explanation for why the reincorporation of Ni into the perovskite is sluggish:²⁶ nanoparticles of Ni metal quickly become nanoparticles of NiO upon oxidation, but Ni²⁺, which is soluble in the perovskite, diffuses in as a Ni²⁺_Tiv_Tiv_Sr associate, and thus with an activation energy of 3.40 eV, or without v_Sr mediation, as Ni²⁺_Tiv_Ti (i.e., from B-site to B-site), and thus with an activation energy of 6.54 eV.

Lastly, we come to the third major question: What makes perovskites such superior exsolution systems? The vast majority of reports concern this class of host oxides; very few examine fluorites, spinels and simple binary oxides, and even fewer examine other oxides.²⁷ We are aware that, without knowing exactly why other materials failed as exsolution systems, it is difficult to identify the key characteristics of perovskites. Nevertheless, we hypothesize that some or all of the following features are important: facile chemical diffusion of oxygen out of the lattice, as this allows for quick reduction; the ability to accommodate oxygen nonstoichiometry; the ability to accommodate high cation-vacancy concentrations on the nonsubstituent cation sublattice, as this allows in a structure with two cation sublattices reverse Schottky disorder and thus socketing; an electronic-band structure that provides both charged and neutral charge-transition levels within an accessible range; the possibility to accommodate transition-metal interstitials in various charge states, and the ease of migration of such transition-metal species, as this allows fast cation transport while maintaining stability of the host. But we may also turn the question round: Why are other oxides comparatively bad exsolution host materials? Fluorite oxides, for example, are good oxygen-ion conductors, but the exsolution kinetics will be slow, if fast cation-interstitial transport does not take place. Charge-transition levels for neutral species may be too high for reduction in Ar/H₂ mixtures. Spinels do exhibit fast cation transport, but there are no additional interstitial positions available since the cations already reside in the octahedral and tetrahedral sites of the fcc anion lattice. Oxygen diffusion in spinels is also relatively slow. Systematic studies on these possibly unpromising systems are, therefore, required, in order to draw strong conclusions.

Conclusions

In the standard picture of the exsolution process, transition-metal cations are first removed from a perovskite lattice upon exposure to reducing conditions, after which they are reduced to the metal at the surface. Our model, supported by the results of hybrid DFT calculations shown in Figures 2 and 3 for Ni in SrTiO₃, confirms the opposite description: Ni cations can be reduced within the perovskite lattice to Ni⁰, and it is these energetically unfavored species that are expelled from the lattice to form metal nanoparticles. Specifically, our model indicates that upon reduction, which shifts the Fermi level upward within the bandgap, certain transition-metal substituents can be reduced within the oxide host if they have suitable charge-transition levels within the bandgap. In this way, we account naturally for a variety of experimental observations concerning not only the thermodynamics but also the kinetics of the exsolution process. Indeed, our model also provides an alternative definition of metal-nanoparticle exsolution from oxide hosts: the expulsion of a substituent upon valence change as charge-transition levels within the band gap are crossed.

This model is applicable to all materials that possess a bandgap, within which transition-metal substituents exhibit charge transition levels. The material does not need to be a good electronic conductor: an upward shift in Fermi level occurs in all oxides as chemical diffusion of oxygen out of the material occurs. The model is possibly applicable to thin-film systems, if other origins of nanoparticle appearance on the surface (e.g., a lattice containing high, nonequilibrium concentrations of v_A or v_B reaching equilibrium) can be ruled out.

We are aware that the model is incomplete, since, for example, the rate-determining step in the exsolution process is unclear. In addition, we make several predictions that are consistent with experimental data (e.g., a critical concentration of oxygen vacancies, only late transition-metal cations having accessible neutral levels) but they need to be investigated systematically and quantitatively in experiments. Further progress, we contend, will require a strong interplay between experiment and computation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.4c03412.

• Details of the hybrid DFT calculations, energy profiles from CI-NEB calculations (PDF)

Author Contributions

All authors have given approval to the final version of the manuscript.

This project has received funding: from the European Union’s Horizon 2020 research and innovation program under grant agreement no 101017709 (EPISTORE); from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—463184206 (SFB 1548, FLAIR: Fermi Level Engineering Applied to Oxide Electroceramics); and from EPSRC under grant EP/R023603/1.

The authors declare no competing financial interest.