Abstract
Defining the loss function is an important part of neural network design and critically determines the success of deep learning modeling. A significant shortcoming of the conventional loss functions is that they weight all regions in the input image volume equally, despite the fact that the system is known to be heterogeneous (i.e., some regions can achieve high prediction performance more easily than others). Here, we introduce a region-specific loss to lift the implicit assumption of homogeneous weighting for better learning. We divide the entire volume into multiple sub-regions, each with an individualized loss constructed for optimal local performance. Effectively, this scheme imposes higher weightings on the sub-regions that are more difficult to segment, and vice versa. Furthermore, the regional false positive and false negative errors are computed for each input image during a training step and the regional penalty is adjusted accordingly to enhance the overall accuracy of the prediction. Using different public and in-house medical image datasets, we demonstrate that the proposed regionally adaptive loss paradigm outperforms conventional methods in the multi-organ segmentations, without any modification to the neural network architecture or additional data preparation.
Keywords: Deep learning, loss function, medical image, neural network, segmentation
1. Introduction
ORGAN contouring on a medical image is a crucial step in many clinical procedures and is typically done manually in clinical practice [1], [2]. However, manual delineation of the involved organs is a labor-intensive and time-consuming task, and the results may be operator-dependent [3], [4]. Taking the head-and-neck cancer case as an example, a dosimetrist or physician might spend several hours in contouring tens of organs for radiation therapy planning, largely limiting the quality and efficiency of patient care. Therefore, auto-contouring tools are urgently needed in the clinic [5], [6].
Recently, deep learning methods have achieved great success in auto-segmentation. Indeed, convolutional neural network (CNN)-based algorithms [7], [8], [9], [10], [11], [12], [13], [14], [15], [16] and emerging transformer network-based methods [17], [18], [19], [20] are increasingly adopted for both tumor and normal tissue auto-segmentation in computed tomography (CT), magnetic resonance, ultrasound, and other medical imaging modalities
In deep learning, a loss function is generally used to measure the discrepancy between the network prediction and the ground truth and to guide the optimization of the network parameters [21], [22], [23], [24], [25], [26], [27]. Dice loss and cross-entropy loss are the two most representative loss functions for the task [28], [29], [30]. Briefly, the former calculates the overlap between the predicted segmentation volume and the ground truth, and the latter measures the pixel-wise difference between the two. However, both loss functions treat all pixels equally without taking into account the heterogeneity of the system [31], [32], [33]. Some pixels, such as those near an organ boundary with low tissue contrast, are usually more difficult to delineate. These “difficult” pixels are generally the ones that limit the performance of current deep learning networks. Therefore, paying more attention to these pixels may improve the learning efficiency and auto-segmentation performance.
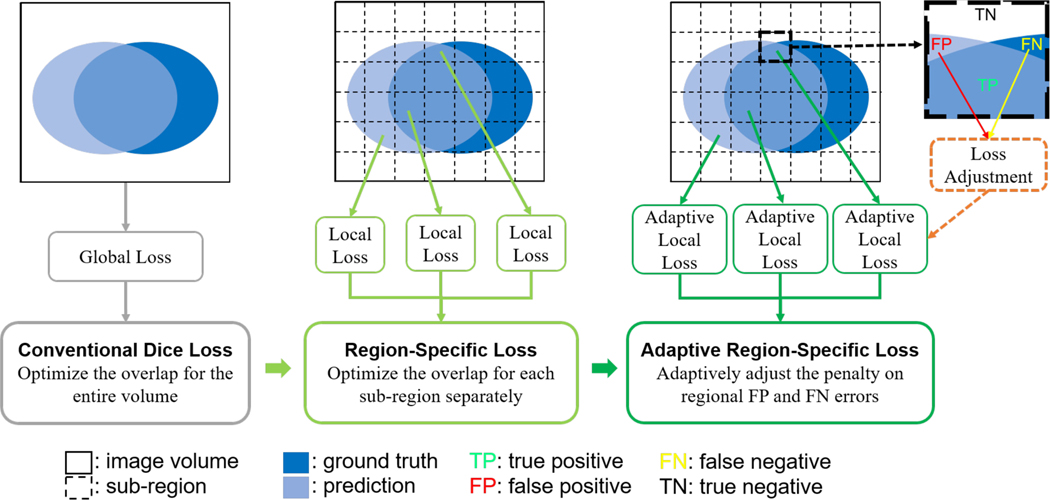
In this study, we propose a region-specific loss scheme to improve the decision-making of deep learning. As shown in Fig. 1, different from conventional Dice loss in which the overlap between the prediction and ground-truth is computed for the entire image volume, we divide the volume into sub-regions and optimize the network prediction for each sub-region separately. This region-specific loss allows to automatically adjust the weight of each sub-region in such a way that more emphases are placed on those sub-regions that are difficult to achieve high prediction accuracy.
Fig. 1.
Illustration of the conventional Dice loss (left) and the proposed loss designs, including the region-specific loss (middle) and adaptive region-specific loss (right).
Generally, the network prediction accuracy varies with the training step as the two types of segmentation errors, false positive (FP) and false negative (FN) errors change during the learning process [34]. In other words, using a pre-defined loss function does not always yield an optimal learned network. In Dice loss, for example, the FP and FN errors are equally emphasized, which corresponds to the harmonic mean of precision and recall. In some scenarios, there might be a severe imbalance of the two types of errors in medical image auto-segmentation. The network is generally more prone to FN errors than FP errors when the segmentation target is much smaller than the background. The Dice loss was extended to Tversky loss [35] to enable a flexible trade-off between the two types of errors. However, the performance of this loss function is sensitive to the hyperparameters controlling the trade-off between the two types of errors. Seo et al. [34] further extended the Tversky loss into a generalized loss function, in which a strategy was designed for stepwise adjustment of the loss parameters during training to achieve better performance. For optimal performance, a similar strategy is applied to the region-specific loss such that the trade-off between the FP and FN errors is adjusted adaptively during the network training process based on the local prediction result.
The main contributions of this study are as follows:
We propose a novel concept of region-specific loss to improve the performance of deep learning prediction.
We develop an algorithm to optimize the region-specific loss function with adaptive adjustment of hyperparameters during the training process to optimally balance the local FP and FN errors.
We carry out experiments on different CT segmentation datasets and demonstrate the effectiveness of the proposed method.
The resultant adaptive region-specific loss function is quite broad and can be applied to most segmentation learning frameworks without any modification of the network architecture or change of the data pre-processing procedure. The region-specific framework can also be generalized to many other deep learning tasks. In the following, we first discuss the related works in Section 2 and elaborate on the details of our methods in Section 3. The experiment conditions and results are described in Section 4. We then discuss key points about our methods and results in Section 5 and draw our conclusions in Section 6.
2. Related Work
2.1. Medical Image Auto-Segmentation
In recent years, deep learning techniques have been widely adopted for various medical image processing tasks, particularly image segmentation [7], [8], [9], [10], [11], [12], [13], [14], [15], [16]. While deep learning networks have demonstrated comparable performance to manual delineation in some cases, accurately segmenting certain regions of interest remains a common challenge, such as dealing with organ boundaries that have low contrast in imaging [26], [30], [32], [36], [37]. To tackle this challenge, various strategies have been proposed. One such strategy involves incorporating attention mechanisms into the network architecture, enabling it to concentrate more accurately on critical features in medical images [38], [39], [40]. By emphasizing relevant regions and suppressing irrelevant information, attention mechanisms help improve segmentation accuracy. Another approach involves leveraging non-local mechanisms to enhance local predictions based on global feature information [18], [19], [20], [41]. These mechanisms consider the relationship between different regions of the image, allowing the network to capture contextual information and make more informed segmentation decisions. Furthermore, integration of prior anatomical knowledge into networks has proven beneficial [42], [43]. Ensemble networks, which combine the strengths of individual networks, have also contributed to advancements in medical image segmentation and improved overall segmentation accuracy [44], [45]. In this study, we propose to enhance auto-segmentation by focusing on the loss function. This approach offers a generalizable solution that can be applied to different auto-segmentation tasks without the need to modify the deep learning network itself.
2.2. Auto-Segmentation Loss Functions
The choice of the loss function plays a crucial role in training auto-segmentation networks. While the cross-entropy loss [29] and Dice loss [28] are commonly used in medical image auto-segmentation due to their effectiveness and simplicity, they have certain limitations [20], [30], [31] that need to be addressed, such as poor performance with highly imbalanced data. Recently, researchers have proposed more sophisticated loss functions. The Tversky loss [35] extends the Dice loss by incorporating a weight parameter that controls the balance between false positives and false negatives, resulting in improved performance for datasets with high data imbalance. The Focal Tversky loss [46] goes further by focusing more on challenging examples that are difficult to predict accurately. The Generalized Dice loss [47], another variant of the Dice loss, assigns distinct weights to different segmentation classes based on their ground truth volumes, ensuring that all classes are adequately learned by the network. Furthermore, the Sensitivity-Specificity loss [48] optimizes the balance between sensitivity and specificity during training. In this study, we propose a novel loss function based on the Dice loss and Tversky loss, which achieves region-specific enhancement for different sub-regions and adapts false prediction penalties in each sub-region. This approach aims to improve the performance of deep learning-based auto-segmentation algorithms.
3. The Proposed Method
3.1. Conventional Dice Loss
For image segmentation, the network prediction consists of the probability that each pixel belongs to the target organ versus the background. The Dice similarity coefficient (DSC) [49] is commonly used to measure the spatial overlap between the network-predicted volume and the ground truth. It is defined as:
| (1) |
where and denote the predicted and ground truth volumes, respectively. Based on the DSC, the Dice loss function was proposed for deep learning-based segmentation, which is approximately equal to 1-DSC and defined as [28]:
| (2) |
where denotes the network-predicted probability of pixel belonging to the target organ, and denotes the corresponding binary ground truth value. denotes the whole image volume, and a constant is used here to avoid division-by-zero singularities. Therefore, the optimization objective of Dice loss is to fully overlap the prediction and ground truth volumes. The Dice loss equation can be differentiated with respect to the -th pixel of the prediction, yielding the gradient:
| (3) |
During the auto-segmentation learning, some parts of the target organ, such as the inner area or some landmarks with distinct contrast, are usually predictable easily with high accuracy. On the other hand, for some other parts such as the organ boundary regions with low imaging contrast, it may be challenging for the network to accurately classify the pixels, leading to inferior results of segmentation [26], [30], [36]. Unfortunately, the conventional Dice loss only optimizes with regard to the whole volume overlap, and thus each pixel within the target or background region is treated equally without considering the various segmentation difficulties that may arise in different sub-regions, which might yield sub-optimal networks.
3.2. Region-Specific Loss
To overcome the limitations of the Dice loss described above, we propose a novel approach with region-specific enhancement. To address the differential need of emphasis on different parts of the image volume, we divide the prediction volume into different sub-volumes and carry out Dice loss calculation for each of them separately. In this way, each local or regional Dice loss only focuses on prediction optimization for one specific sub-region, independent of optimization in other sub-regions. The final region-specific loss is a sum of the regional Dice losses of all the sub-regions:
| (4) |
According to Eq. (3), the gradient of the region-specific loss is only influenced by the prediction and label distributions in the sub-region, rather than the distributions in the entire image volume as in the global Dice loss. Since the prediction and label distributions vary with the sub-region, the contribution of a pixel’s prediction to the network optimization depends on its location. If a sub-region can be easily predictable by the network, the prediction values in this sub-region would be very close to the corresponding ground truth values. This results in the final gradient value in this sub-region being close to zero, and less weight is assigned to the prediction optimization in this sub-region. Therefore, the proposed region-specific loss can implicitly and automatically improve the deep learning efficiency by lowering the importance of well-predicted sub-regions, enabling region-specific weighting during the training process. In this study, the prediction volume for each case is divided into a 16×16×16 sub-region grid for region-specific loss calculation.
3.3. Adaptive Region-Specific Loss
In pixel-wise segmentation learning, the network attempts to maximize the true positive (TP) prediction and minimize the FP and FN errors. DSC can be regarded as the harmonic mean of precision and recall [30], and thus the FP and FN are weighted equally in the Dice loss function. For medical image segmentation, the volumes of some target organs are usually much smaller than the background volume, which may lead to a severe data imbalance problem that biases the network prediction toward the background, and FN errors tend to be more dominant than FP errors during the network training. To achieve a better trade-off between the precision and recall performances, Tversky loss function [35] as defined in Eq. (5) is developed, which introduces functional parameters and to control the magnitude of penalty for FP and FN, respectively.
| (5) |
Note that the Tversky loss is more general than Dice loss and degenerates to 1-DSC when . When is greater than , the Tversky loss places more emphasis on FN errors to improve recall.
The and parameters in the original Tversky loss are pre-defined before training. Since the choice of these parameters heavily influences the final learning performance, their values are typically fine-tuned via manual trial-and-error to achieve an optimal prediction, which is a computationally expensive process. Moreover, the recall and precision performances of the network change during the training process, and thus use of pre-selected hyperparameters may result in sub-optimal performance [34]. Here, we further introduce an adaptive error penalty for each sub-region based on the proposed region-specific loss. Considering that Tversky loss is more general than Dice loss enabling control of the trade-off between FP and FN errors, it is adopted as the foundation for the adaptive region-specific loss calculation in this study:
| (6) |
where the parameters and are fine-tuned during the training process to emphasize different types of regional errors and optimize the network learning. According to the Tversky loss (Eq. (5)), and penalize FP and FN errors, respectively. In a specific sub-region, if the FP error is greater than the FN error, the value of should be increased to increase the penalty on the FP error and boost precision. Likewise, value would be increased to penalize the FN error and boost recall [35]. Specifically, the following algorithms are designed to adjust the and parameters based on the fraction of FP and FN errors in a given sub-region :
| (7) |
| (8) |
According to Eqs. (7) and (8), both and values vary in the range [A, A+B] and increase linearly with the fraction of FP and FN errors, respectively. Thereby, the emphasis of the loss function on the FP and FN errors is adaptively fine-tuned according to the network prediction result in the sub-region during training. We empirically set the constant coefficients A and B at 0.3 and 0.4 in this study, and further explore the impact of the hyperparameter adjustment range in the ablation study. Note that in the case of FP = FN in a sub-region, , which means that the loss function places the same importance on the two prediction errors and approches Eq. (4).
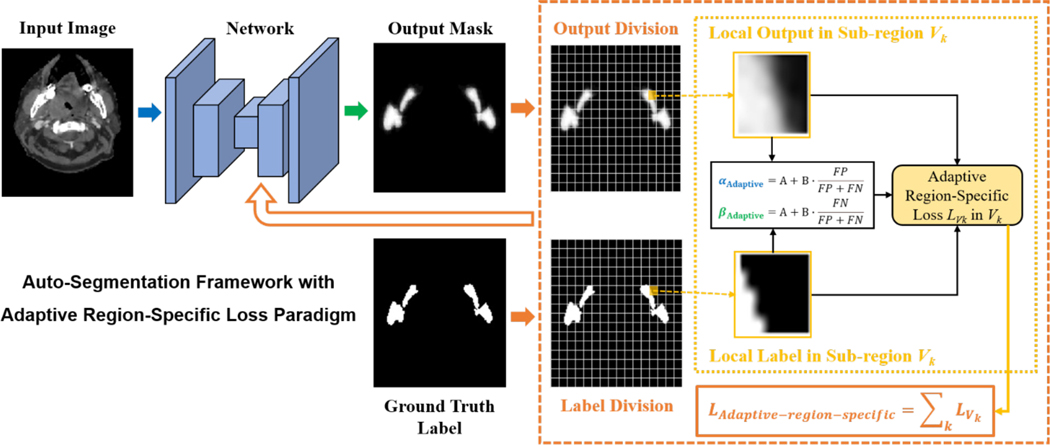
The deep learning framework with the proposed adaptive region-specific loss (Eq. (6–8)) is shown in Fig. 2. The proposed loss scheme not only provides an effective way to achieve region-specific enhancement for different sub-regions by placing more importance on difficult-to-predict sub-regions, but also realizes adaptive error penalty in each sub-region with auto-adjusted function parameters during the training process, which is promising to enable more effective auto-segmentation learning.
Fig. 2.
Framework of the deep learning-based auto-segmentation with the proposed loss design paradigm.
3.4. Network and Training Details
A V-Net [28] architecture with batch normalization [50] and dropout [51] is implemented for 3D multi-organ auto-segmentation in medical images. The input to the network is the whole image volume, and the output are the corresponding pixel-wise probability maps for the desired target organs and background based on Softmax activation. A combination of conventional Dice loss and cross-entropy loss is used as the baseline loss function in our experiments, which have been widely used in multi-organ segmentation studies [52], [53], [54]:
| (9) |
where is the total number of target organs plus one (the background) and is the trade-off between the Dice loss and cross-entropy loss . The adaptive moment (Adam) algorithm [55] is applied to optimize the weights of the network. On-the-fly data augmentation is also applied by using various image transformations, including random flipping, translation, and scaling, to increase the variability of different data representations. The framework is implemented in PyTorch, and the computations are performed on the NVIDIA GeForce RTX 2080 Ti GPU with 11 GB memory.
4. Experiments
4.1. Datasets and Preprocessing
Two separate medical image datasets for auto-segmenattion of head and neck organs are used to analyze the effectiveness of our methods, and two additional abdominal and liver datasets are used in the ablation study for further validation.
PDDCA Dataset:
The first public dataset is the Public Domain Database for Computational Anatomy (PDDCA) from the MICCAI Head and Neck Auto-Segmentation Challenge 2015 [56]. The dataset consists of head-and-neck CT images from 48 patient cases, and the contours for nine organs are annotated for each case: brainstem, chiasm, mandible, left and right optic nerves, left and right parotid glands, and left and right submandibular glands. The binary mask of each organ is generated from the corresponding contour data and serves as the label for network training. The mask of the background is also generated based on the organ masks. Each CT image has an in-plane pixel spacing ranging from 0.76 to 1.27 mm, and the interslice thickness from 1.25 to 3.0 mm. The image and label volumes are cropped to fit the patient contour, then resized to a fixed resolution of 1.5mm×1.5mm×1.5mm. A HU window of [–200, 400] is adopted to threshold the image pixel intensities, then the intensities are rescaled to [–1, 1] to remove irrelevant details. Overall, 32 cases are selected for network training, 6 cases for validation, and 10 cases for testing.
In-house Dataset:
The second in-house dataset contains 67 clinical head-and-neck CT scans collected from the Stanford University Medical Center in accordance with institutional review board (IRB) guidelines. For each patient scan, 14 organs are manually contoured by physicians and used as the ground truth, including the brainstem, left and right brachial plexus, esophagus, larynx, lips, mandible, oral cavity, left and right parotid glands, pharynx, spinal cord, left and right submandibular glands. The original image volume is cropped and resampled to 128×144×256 size. Image intensities are truncated to the range [−160, 240], then normalized to [–1, 1]. Overall, 49 cases are randomly selected for training, 8 cases for validation, and 10 cases for testing.
Abdominal Dataset:
To further validate the effectiveness of the proposed approach in different body sites, the dataset released in the MICCAI 2015 Multi-Atlas Abdomen Labeling Challenge [57] is utilized as an ablation study. The dataset contains 30 3D abdominal CT scans from patients with contrast enhancement in portal venous phase. The image volume is cropped and resampled to 144×96×112 size. Image intensities are truncated to the range [−500, 800], and then normalized to [–1, 1]. We report the DSC on eight abdominal organs (aorta, gallbladder, left kidney, right kidney, liver, pancreas, spleen, stomach). A three-fold cross-validation is employed, with 20 cases for training and 10 cases for validation.
LiST Dataset:
Another public liver dataset is sourced from the 2017 Liver Tumor Segmentation (LiTS) Challenge [58], [59]. This dataset includes 131 patient cases with contrast-enhanced 3D CT scans, where the contours of the liver and liver tumor are annotated for each case. The original image volume is cropped and resampled to 192×144×80 size. Image intensities are truncated to the range [−250, 250], then normalized to [−1, 1]. For the training process, a random selection of 86 cases is used, while 15 cases are allocated for validation, and the remaining 30 cases are reserved for testing purposes.
4.2. Performance Evaluation
To evaluate the performance of our proposed region-specific enhancement and adaptive error penalty methods on the segmentation task, for each dataset, we conduct multi-organ segmentation learning with the same network and training conditions, using three different combinations of loss functions: 1) using only the baseline loss (Eq. (9)) for network optimization (Baseline), to obtain a baseline result; 2) combining the baseline loss and region-specific loss (Eq. (4)) for optimization (Baseline+Region-Specific) to evaluate the enhancement of region-specific loss in which each sub-region is treated separately and differently; and 3) combining the baseline loss and adaptive region-specific loss (Eq. (6)) during training (Baseline+Adaptive Region-Specific) to further show the effect of adaptive fine-tuning of hyperparameters in the region-specific loss, demonstrating the performance of the final proposed loss scheme. Besides, cross-entropy loss [29] and Dice loss [28] are also used individually during network training for comparison.
In the evaluation study, DSC is used as the main performance metric, which measures the spatial overlap between the auto-segmentation result and the ground truth [36]. Moreover, the recall and precision [60], 95th percentile Hausdorff distance (HD95) [61], and average surface distance (ASD) [62], are also calculated for a more comprehensive evaluation. The four metrics are defined as:
| (10) |
| (11) |
| (12) |
| (13) |
where denotes the Euclidean distance between pixel and pixel .
4.3. Experimental Results
4.3.1. Quantitative Results
The performance of the proposed region-specific loss and adaptive region-specific loss on auto-segmentation learning is studied using the two head and neck datasets. The evaluation DSC results for each target organ are summarized in Tables 1 and 2 for the public PDDCA and the in-house datasets, respectively. On average, the baseline loss and the two proposed methods all show better DSC results than the regular cross-entropy loss and Dice loss for the two datasets. Since the baseline loss expressed as a combination of Dice loss and cross-entropy loss outperforms any of the two loss functions alone, it is utilized as a benchmark for the analysis. By employing the region-specific loss in addition to the baseline loss, the average DSCs are increased from 0.751 and 0.657 to 0.764 and 0.669 for the two datasets respectively, demonstrating the effectiveness of region-specific optimization of the network. The average DSCs are further enhanced to 0.772 and 0.685 when the hyperparameters of region-specific loss that control the trade-off between the FP and FN errors are adjusted adaptively during the training process.
TABLE 1.
DSCs for each target organ in the PDDCA dataset.
| Organ | C | D | B | B+RS (Proposed) | B+ARS (Proposed) |
|---|---|---|---|---|---|
| Brainstem | 0.824±0.005 | 0.823±0.016 | 0.830±0.020 | 0.849±0.008 | 0.856±0.009 |
| Chiasm | 0.264±0.100 | 0.489±0.037 | 0.488±0.010 | 0.462±0.023 | 0.494±0.028 |
| Mandible | 0.883±0.059 | 0.904±0.020 | 0.905±0.012 | 0.935±0.002 | 0.938±0.002 |
| Optic Nerve Left | 0.131±0.187 | 0.700±0.012 | 0.660±0.011 | 0.703±0.009 | 0.679±0.013 |
| Optic Nerve Right | 0.261±0.204 | 0.669±0.008 | 0.672±0.015 | 0.693±0.016 | 0.682±0.013 |
| Parotid Left | 0.811±0.013 | 0.842±0.016 | 0.829±0.035 | 0.849±0.010 | 0.863±0.005 |
| Parotid Right | 0.776±0.019 | 0.802±0.013 | 0.831±0.006 | 0.829±0.015 | 0.829±0.005 |
| Submandibular Left | 0.702±0.037 | 0.755±0.021 | 0.768±0.017 | 0.771±0.009 | 0.789±0.006 |
| Submandibular Right | 0.728±0.056 | 0.759±0.001 | 0.779±0.027 | 0.789±0.018 | 0.815±0.010 |
| Average | 0.598±0.011 | 0.749±0.008 | 0.751±0.008 | 0.764±0.002 | 0.772±0.003 |
C, D, B, B+RS, B+ARS stand for the cross-entropy loss, Dice loss, baseline loss, a combination of the baseline loss and region-specific loss, and a combination of the baseline loss and adaptive region-specific loss, respectively. The best results are highlighted in bold.
TABLE 2.
DSCs for each target organ in the in-house dataset.
| Organ | C | D | B | B+RS (Proposed) | B+ARS (Proposed) |
|---|---|---|---|---|---|
| Brainstem | 0.757±0.032 | 0.788±0.005 | 0.765±0.014 | 0.785±0.017 | 0.800±0.007 |
| Brachial Plexus Left | 0.329±0.031 | 0.283±0.245 | 0.421±0.016 | 0.429±0.026 | 0.451±0.015 |
| Brachial Plexus Right | 0.340±0.046 | 0.293±0.253 | 0.461±0.012 | 0.442±0.026 | 0.474±0.005 |
| Esophagus | 0.522±0.021 | 0.578±0.028 | 0.464±0.055 | 0.537±0.066 | 0.574±0.020 |
| Larynx | 0.691±0.021 | 0.745±0.025 | 0.750±0.029 | 0.743±0.010 | 0.765±0.003 |
| Lips | 0.360±0.003 | 0.493±0.034 | 0.500±0.005 | 0.471±0.027 | 0.490±0.015 |
| Mandible | 0.790±0.021 | 0.827±0.016 | 0.814±0.016 | 0.840±0.020 | 0.863±0.014 |
| Oral Cavity | 0.654±0.007 | 0.723±0.010 | 0.716±0.034 | 0.692±0.008 | 0.689±0.006 |
| Parotid Left | 0.763±0.010 | 0.803±0.003 | 0.797±0.010 | 0.803±0.010 | 0.806±0.010 |
| Parotid Right | 0.741±0.008 | 0.766±0.019 | 0.757±0.011 | 0.777±0.014 | 0.776±0.004 |
| Pharynx | 0.530±0.040 | 0.654±0.017 | 0.654±0.009 | 0.671±0.013 | 0.674±0.007 |
| Spinal Cord | 0.686±0.012 | 0.707±0.016 | 0.704±0.011 | 0.752±0.022 | 0.765±0.002 |
| Submandibular Left | 0.581±0.041 | 0.673±0.030 | 0.665±0.004 | 0.689±0.018 | 0.717±0.004 |
| Submandibular Right | 0.672±0.033 | 0.733±0.030 | 0.722±0.023 | 0.737±0.036 | 0.742±0.013 |
| Average | 0.601±0.005 | 0.647±0.011 | 0.657±0.005 | 0.669±0.012 | 0.685±0.001 |
Compared with the baseline loss, the DSC results of 8 out of 9 organs in the PDDCA dataset and 12 out of 14 organs in the in-house dataset show improvement when region-specific enhancement or adaptive error penalty are introduced during training. Taking the mandible as an example, employing the two proposed loss functions improves the DSC by 0.030 and 0.033, respectively, for the PDDCA dataset, and 0.026 and 0.049, respectively, for the in-house dataset.
Tables 3 and 4 show the organ-averaged results evaluated by using the four metrics. In addition to average DSC, average recall, precision, HD95 and ASD are almost improved with the region-specific loss for both datasets, providing more evidence for its effectiveness. Moreover, the introduction of adaptive error penalty further improves the average DSC, HD95 and ASD values. We noticed that its impact on recall and precision is different for the two datasets. For the PDDCA dataset, the average recall is increased by 0.023 (0.778 to 0.801), whereas the precision is decreased by 0.012 (0.778 to 0.766), indicating that the precision is sacrificed slightly to improve the recall. For the in-house dataset, recall is increased only by 0.006, and the precision is increased by 0.016.
TABLE 3.
Organ-averaged DSC, recall, precision, HD95, and ASD evaluation results for the PDDCA dataset obtained with the three different loss functions.
| Loss | DSC | Recall | Precision | HD95 (mm) | ASD (mm) |
|---|---|---|---|---|---|
| Baseline | 0.751±0.008 | 0.763±0.017 | 0.770±0.015 | 4.522±0.635 | 1.087±0.083 |
| Baseline+ Region-Specific |
0.764±0.002 | 0.778±0.016 | 0.778±0.011 | 4.046±0.205 | 1.032±0.058 |
| Baseline+Adaptive Region-Specific | 0.772±0.003 | 0.801±0.021 | 0.766±0.012 | 3.836±0.281 | 1.026±0.021 |
C, D, B, B+R, B+AR stand for the cross-entropy loss, Dice loss, baseline loss, a combination of the baseline loss and region-specific loss, and a combination of the baseline loss and adaptive region-specific loss, respectively. The best results are highlighted in bold.
TABLE 4.
Organ-averaged DSC, recall, precision, HD95, and ASD evaluation results for the in-house dataset obtained with the three different loss functions.
| Loss | DSC | Recall | Precision | HD95 (mm) | ASD (mm) |
|---|---|---|---|---|---|
| Baseline | 0.657±0.005 | 0.729±0.011 | 0.632±0.005 | 13.441±0.614 | 12.786±0.537 |
| Baseline+Region-Specific | 0.669±0.012 | 0.754±0.016 | 0.636±0.008 | 14.133±0.918 | 12.604±1.515 |
| Baseline+Adaptive Region-Specific | 0.685±0.001 | 0.760±0.015 | 0.652±0.014 | 13.013±0.565 | 11.283±0.322 |
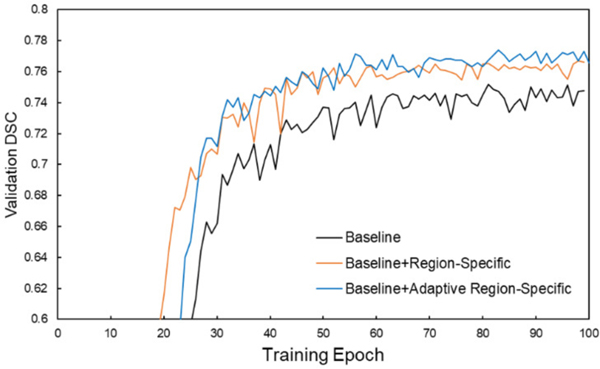
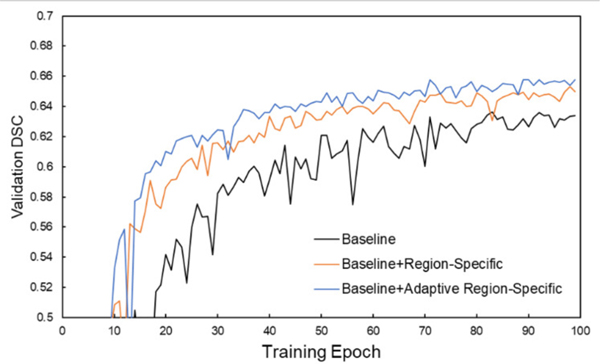
DSC performances on the validation dataset during network training for the three different loss functions are shown in Figs. 3 and 4 for the PDDCA and in-house datasets. It is observed that the validation performance gradually increases through the learning process and gradually saturates after approximately 80 epochs. The learning curves using the adaptive region-specific loss outperform the curves using the region-specific loss, and both outperform the curves using only the baseline loss by a visually obvious margin, showing the benefits of the proposed methods.
Fig. 3.
Evolution of DSC performance on the validation set of the PDDCA dataset during training with the three different loss functions.
Fig. 4.
Evolution of DSC performance on the validation set of the in-house dataset during training with the three different loss functions.
4.3.2. Qualitative Results
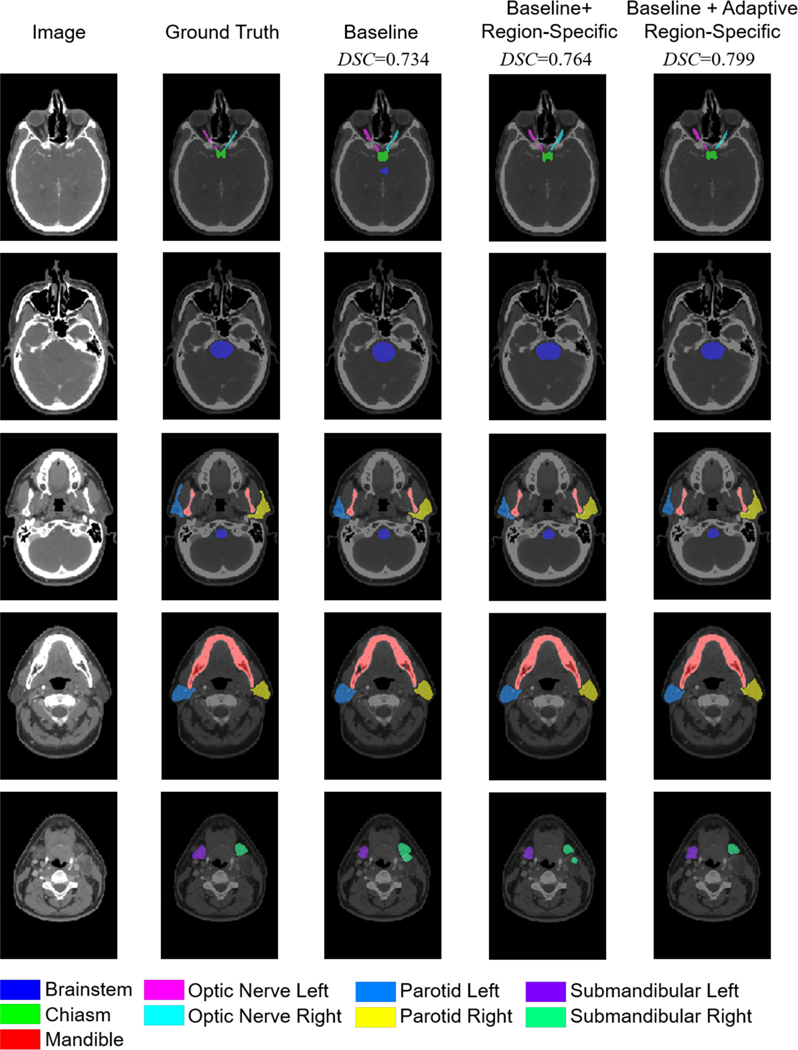
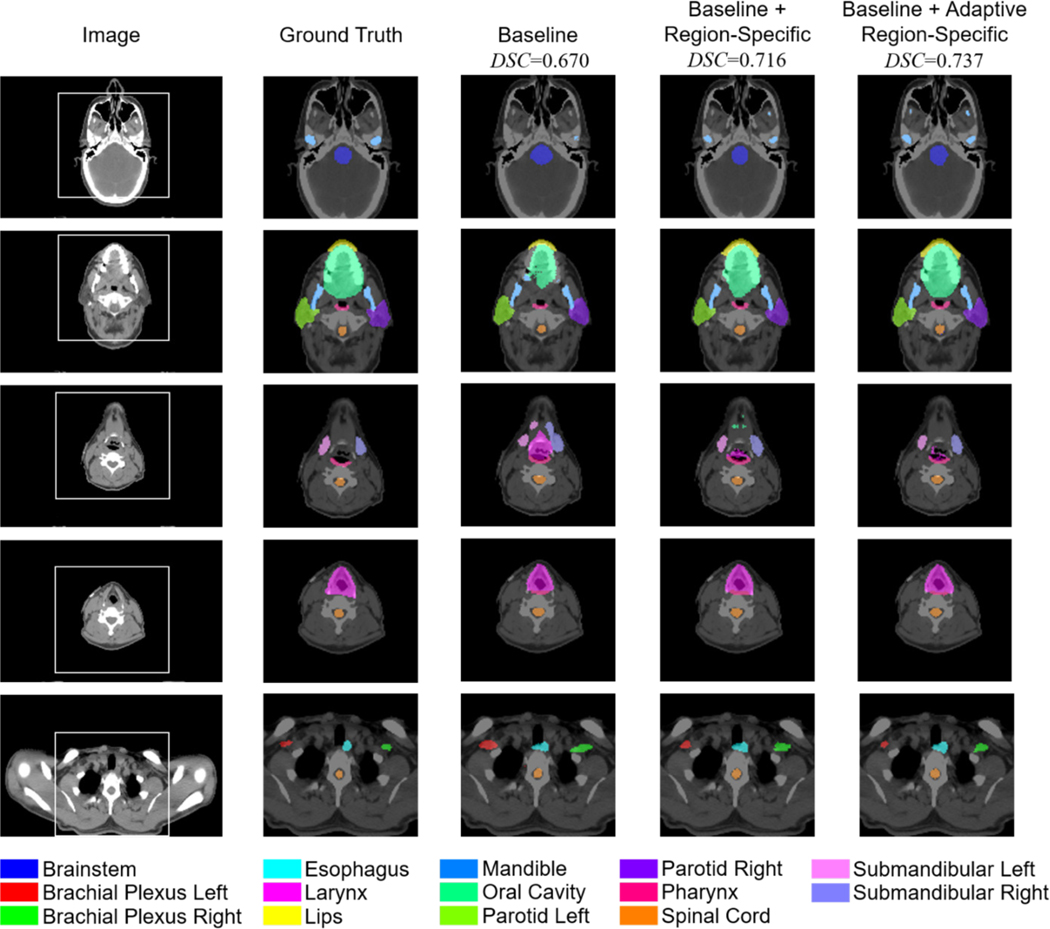
In Figs. 5 and 6, qualitative analyses of the auto-segmentation results are presented. By using the region-specific loss and adaptive region-specific loss, the predicted organ masks are improved and closer to the ground truth labels, clearly outperforming the baseline results. Taking the right submandibular organ as an example, as shown in the last row of Fig. 5 and the third row of Fig. 6, the baseline network tends to predict masks that are much larger than the ground truth labels. This is corrected by the proposed loss functions. Visual inspection of the prediction masks shows that our methods are promising for use in clinical auto-segmentation.
Fig. 5.
Qualitative comparison of the auto-segmentation results for a typical case in the PDDCA dataset using the three different loss functions, as well as the ground truth labels. The five rows are five representative axial slices from the image volume. Average DSC results of the nine organs are listed.
Fig. 6.
Qualitative comparison of auto-segmentation results for a typical case in the in-house dataset using the three different loss functions, as well as the ground truth labels. The five rows are five representative axial slices from the image volume. The first column is the original CT image, and the second to fifth columns are enlarged versions of the white square box on the original CT image for presentation clarity. Average DSC results of the 14 organs are listed.
4.3.3. Ablation Study
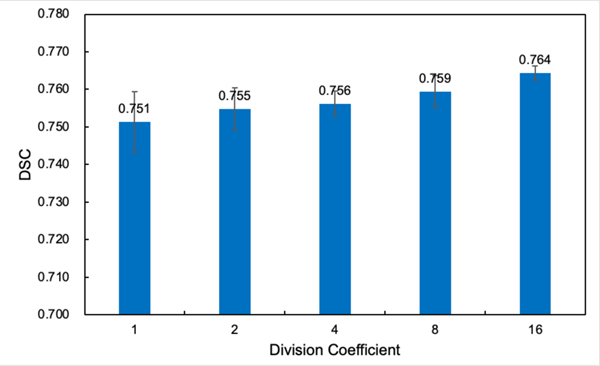
To further validate the effectiveness of the proposed region-specific loss and adaptive region-specific loss, we conduct some ablation studies, mainly on the PDDCA dataset. First, we investigate the impact of the sub-region division on the performance of the region-specific loss. By using different division coefficients (DCs) ranging from 1~16, which means the whole image volume is evenly divided into DC×DC×DC sub-regions, the DSC performance of the region-specific loss on the public PDDCA dataset is shown in Fig. 7. It is noteworthy that DC=1 corresponds to the conventional global Dice loss. The results show that as the number of divided sub-regions increases and the volume of each sub-region decreases, the performance of the region-specific loss improves progressively.
Fig. 7.
DSC performance of the region-specific loss on the PDDCA dataset with different image volume division coefficients (DCs).
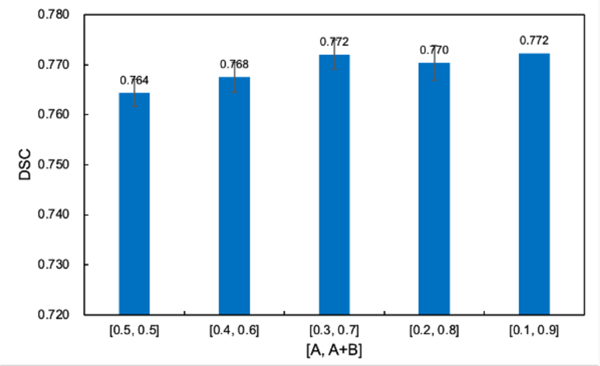
We further study the impact of adjustment range of hyperparameters in the adaptive region-specific loss, i.e., A and B values in Eqs. (7) and (8), on its performance. As shown in Fig. 8, with the increase of the adjustment range of and , which is defined as [A, A+B], the DSC performance of the adaptive region-specific loss gradually increases and then saturates. Therefore, a larger dynamic adjustment range of the loss function might promise to enable a more flexible trade-off between the two types of errors and achieve a more accurate overall prediction.
Fig. 8.
DSC performance of the adaptive region-specific loss on the PDDCA dataset with different adjustment ranges [A, A+B] of and .
The performaces of the proposed region-specific loss and adaptive region-specific loss are also compared with other region-based segmentation loss, i.e., focal Tversky loss [46], Generalized Dice loss [47], and Sensitivity-Specificity loss [48]. The Dice results of these loss functions on the PDDCA dataset are shown in Table 5. It shows that both the region-specific loss and adaptive region-specific loss outperform the other three region-based segmentation loss functions.
TABLE 5.
DSCs for each target organ in the PDDCA dataset with different loss functions.
| Organ | FT | GD | SS | RS | ARS |
|---|---|---|---|---|---|
| Brainstem | 0.853±0.009 | 0.839±0.004 | 0.846±0.006 | 0.849±0.008 | 0.856±0.009 |
| Chiasm | 0.515±0.017 | 0.493±0.020 | 0.506±0.011 | 0.462±0.023 | 0.494±0.028 |
| Mandible | 0.918±0.007 | 0.918±0.005 | 0.922±0.008 | 0.935±0.002 | 0.938±0.002 |
| Optic Nerve Left | 0.703±0.006 | 0.695±0.003 | 0.695±0.008 | 0.703±0.009 | 0.679±0.013 |
| Optic Nerve Right | 0.687±0.020 | 0.668±0.018 | 0.673±0.001 | 0.693±0.016 | 0.682±0.013 |
| Parotid Left | 0.817±0.057 | 0.849±0.006 | 0.838±0.002 | 0.849±0.010 | 0.863±0.005 |
| Parotid Right | 0.812±0.006 | 0.805±0.016 | 0.808±0.022 | 0.829±0.015 | 0.829±0.005 |
| Submandibular Left | 0.771±0.004 | 0.769±0.008 | 0.762±0.040 | 0.771±0.009 | 0.789±0.006 |
| Submandibular Right | 0.757±0.028 | 0.794±0.008 | 0.785±0.015 | 0.789±0.018 | 0.815±0.010 |
| Average | 0.759±0.010 | 0.759±0.001 | 0.760±0.004 | 0.764±0.002 | 0.772±0.003 |
FT, GD, SS, RS, ARS stand for the focal Tversky loss, Generalized Dice loss, Sensitivity-Specificity loss, region-specific loss, and adaptive region-specific loss, respectively. The best results are highlighted in bold.
To further validate the generalizability of our proposed loss paradigm, we apply it to another public abdominal dataset. The results, as presented in Table 6, indicate that both the proposed region-specific loss and adaptive region-specific loss could improve the auto-segmentation performance on this abdominal dataset, with the organ-averaged DSC increased from 0.687 to 0.710 and 0.725, respectively. Moreover, our approach results in improved DSC values for all the eight organs. Therefore, our loss paradigm promises to enhance the auto-segmentation performance in different body sites.
TABLE 6.
DSCs for each target organ in the abdominal dataset with different loss functions.
| Organ | Baseline | Baseline+RS | Baseline+ARS |
|---|---|---|---|
| Aorta | 0.792±0.031 | 0.791±0.054 | 0.819±0.052 |
| Gallbladder | 0.467±0.033 | 0.475±0.074 | 0.461±0.087 |
| Kidney Left | 0.730±0.097 | 0.782±0.070 | 0.788±0.049 |
| Kidney Right | 0.742±0.113 | 0.754±0.131 | 0.774±0.102 |
| Liver | 0.870±0.046 | 0.908±0.021 | 0.915±0.025 |
| Pancreas | 0.449±0.077 | 0.453±0.158 | 0.495±0.167 |
| Spleen | 0.807±0.110 | 0.849±0.072 | 0.847±0.058 |
| Stomach | 0.639±0.104 | 0.665±0.159 | 0.698±0.106 |
| Average | 0.687±0.062 | 0.710±0.086 | 0.725±0.077 |
RS and ARS stand for the region-specific loss and adaptive region-specific loss, respectively. The best results are highlighted in bold.
The Dice performances of our methods on the public LiST dataset are presented in Table 7. The application of the proposed region-specific loss and adaptive region-specific loss has led to improved auto-segmentation results for both the liver and liver tumor. Specifically, the DSC increased from 0.942 to 0.950 and 0.959 for the liver, and from 0.339 to 0.360 and 0.386 for the liver tumor, respectively. These improvements further validate the effectiveness of our proposed loss paradigm.
TABLE 7.
DSCs for liver and liver tumor in the LIST dataset.
| Organ | Baseline | Baseline+RS | Baseline+ARS |
|---|---|---|---|
| Liver | 0.942±0.003 | 0.950±0.005 | 0.959±0.001 |
| Liver Tumor | 0.339±0.008 | 0.360±0.009 | 0.386±0.012 |
| Average | 0.641±0.003 | 0.655±0.002 | 0.673±0.006 |
RS and ARS stand for the region-specific loss and adaptive region-specific loss, respectively. The best results are highlighted in bold.
5. Discussion
Image auto-segmentation is a critical task in clinical practice. Much work has been devoted to using deep learning to automate the segmentation process. In this study, we introduce, for the first time, a region-specific loss for improved deep learning-based segmentation by optimizing network prediction results locally and separately. In contrast to conventional Dice loss, which implicitly treats all pixels within the image volume equally, our region-specific loss optimizes the network with consideration of individualized abilities of different sub-regions in achieving accurate segmentation. During network training, the gradient of conventional Dice loss at a pixel depends on the network prediction and the ground truth values of the entire image volume. Therefore, even for the pixels with accurately predicted results, the Dice loss will still yield non-zero gradient values at these pixels if the overall prediction is not completely accurate (Eq. (3)). That is, these pixels may still contribute to the network optimization during the training. In contrast, the proposed region-specific loss alleviates this problem by dividing the whole volume into multiple sub-regions. In this way, the regional loss gradient only depends on the local prediction and the ground truth values, with the gradient value approaching zero in the sub-region where the predictions are accurate. Thus, compared to the conventional loss scheme, our approach allows the algorithm to focus more on a subset of sub-regions with low prediction accuracy. Our experimental results clearly demonstrate the superiority of region-specific loss over the conventional loss function.
Based on the region-specific loss, we further develop an adaptive region-specific loss with adaptive error penalty during the network training. In contrast to the conventional loss function that is pre-defined before training, the proposed loss function adjusts the relative emphasis on FP and FN errors adaptively by fine-tuning the penalty parameters based on the regional prediction results. Since the adaptive region-specific loss is applied to each sub-region separately, the exact adjustments of the optimization emphasis and the resulted loss calculations differ across different sub-regions. The final loss calculation enables region-specific enhancement with adaptive error penalty for improved deep learning. Noteworthy, the key insight here is adaptively adjusting the emphasis of the loss function according to the regional prediction result during the learning process. While the Tversky loss is used as an example in our adaptive region-specific optimization, it should be emphasized that the approach is quite general, and other loss functions, such as sensitivity-specificity loss [48], could also be adopted in our method.
There are some studies to direct attention toward specific regions of the target volume. For example, the boundary-based loss is proposed to focus on improving the prediction results near organ boundaries [26], [30], [32]. However, since it is difficult to directly differentiate the distance measurement metric during the optimization process, a distance map must be pre-calculated before applying the loss function. What’s more, some sophisticated network strictures, such as FocusNet [63], Ua-Net [5], and SOARS [45] are also developed for accurate auto-segmentation, which first detect the region of interest (ROI) of a specific organ and then conduct the fine auto-segmentation within the ROI. In this study, the proposed region-specific loss can be directly applied to most auto-segmentation studies without additional data preparation or modification of the neural network architecture. The basic element of our loss design paradigm is Dice loss or Tversky loss, which can be used as an effective addition to the global Dice loss or global Tversky loss in the same cases. Region-based loss [21], [30] (such as Dice loss) is an important type of loss function in deep learning fields. In theory, our region-specific loss can be generalized to other tasks where the region-based loss is applicable, such as weakly-supervised image registration [64], [65], to improve the existing prediction results. In passing, we mention that region-specific penalty has also been proposed as a general technique for radiation therapy planning and dose optimization [66].
In an extreme scenario where a sub-region has no groud-truth foreground, but the prediction contains foreground, then gradients of the region-specific loss for the predicted values are always zero according to Eq. (3), which makes it difficult (if not impossible) to optimize the prediction errors. Computationally, this adverse effect can be alleviated or minimized. On one hand, in a sub-region, if there is no foreground pixel for a specific segmentation target, it means these pixels belong to other targets or the background class. By optimizing the FN error prediction for other targets or the background class, the proposed region-specific loss could indirectly improve the FP optimization for the specific segmentation target in this extreme scenario. On the other hand, since the ground truth in a sub-region is already known during the network training, we will not apply the region-specific loss for the class that does not exist in the sub-regions. In other words, we will only apply our loss to the class that exists in the sub-region to improve the computational efficiency (note that this will not impact the gradient computation).
The main purpose of this study is to introduce the region-specific and adaptive error penalty concepts for loss calculation to show the promise of this scheme for auto-segmentation learning, but each section in this study uses a simple designment that can be improved with future research. For example, in our calculation, the prediction volume is divided empirically into a 16×16×16 grid to generate each sub-region without considering the potential difference in the characteristics of the different target organs. A future direction would be to examine methods of dividing the sub-regions more intelligently to accommodate the size of the target organ. Non-cubic shape could also be assigned to each sub-region according to the target organ shape, which could further explore the potential of our region-specific loss scheme. Finally, this study uses a linear relation to fine-tune the penalty parameters based on the fraction of FP and FN errors. An algorithm better relating the error penalty with the regional prediction result may further improve network learning.
6. Conclusion
This study introduces a novel concept of local loss for deep learning-based auto-segmentation. Our method could achieve region-specific enhancement of different sub-regions and adaptive error penalty in each sub-region during the training process, leading to more effective network learning. Experimental results on different medical image datasets demonstrate that our method significantly improves the auto-segmentation performance without modifying the network architecture or requiring additional data preparation. The proposed adaptive region-specific loss thus promises to provide a useful approach for improved deep learning decision-making.
Acknowledgments
The authors acknowledge the funding supports from the National Cancer Institute (1R01CA227713, 1R01CA256890, and 1R01CA160986), Varian Medical Systems, Viewray Inc., Human-Centered Artificial Intelligence, and Clinical Innovation Fund from Stanford Cancer Institute. (Corresponding authors: Bin Han and Lei Xing).
Biographies

Yizheng Chen received both the B.Eng. degree and Ph.D. degree from the Department of Engineering Physics, Tsinghua University, Beijing, China, in 2014 and 2019, respectively. He is currently a postdoctoral scholar at the Laboratory of Artificial Intelligence in Medicine and Biomedical Physics in the Department of Radiation Oncology, Stanford University. His research interests include medical image auto-segmentation and registration, deep learning, and radiotherapy.

Lequan Yu (Member, IEEE) received the B.Eng. degree from the Department of Computer Science and Technology, Zhejiang University, Hangzhou, China, in 2015, and the Ph.D. degree from the Department of Computer Science and Engineering, The Chinese University of Hong Kong, Hong Kong, in 2019. He is currently an assistant professor at the Department of Statistics and Actuarial Science, The University of Hong Kong. His research lies at medical image analysis, computer vision, machine learning and AI in healthcare.

Jen-Yeu Wang is currently a research data analyst at the Laboratory of Artificial Intelligence in Medicine and Biomedical Physics in the Department of Radiation Oncology, Stanford University. His research interests include medical image auto-segmentation, genomic analysis, and deep learning.

Neil Panjwani received the B.S. degree in Biomedical Engineering and Economics from Duke University, in 2010, and the M.D. degree from the University of California, San Diego, in 2017. He is currently an assistant professor at the Department of Radiation Oncology, University of Washington. His research interests include artificial intelligence, medical imaging, digital health, and health systems.

Jean-Pierre Obeid received the M.D. degree from the University of Miami Leonard M Miller School of Medicine, in 2017. He is currently a radiation oncology specialist in the Department of Radiation Oncology, Cleveland Clinic Florida. His research interests include internal medicine, radiation oncology, and machine learning.

Wu Liu received the B.S. degree from Nanjing University, Nanjing, China. He obtained his M.S. degree in Computer Science, and Ph.D. degree in Medical Physics from the University of Wisconsin-Madison, Madison, in 2007. He is currently an associate professor at the Department of Radiation Oncology, Stanford University. His research interests include artificial intelligence in image and biological guided radiotherapy, and medical image analysis.

Lianli Liu received the Ph.D. degree from the Department of Electrical Engineering and Computer Science at the University of Michigan, Ann Arbor, in 2018. She is currently a clinical assistant professor at the Department of Radiation Oncology, Stanford University. Her current research interests include medical image reconstruction, image analysis, and optimizing MRI for radiotherapy.

Nataliya Kovalchuk received the B.S. degree from the Drohobych State University, Ukraine, in 2002, and Ph.D. degree from the University of South Florida, in 2008. She is currently a clinical associate professor at the Department of Radiation Oncology, Stanford University. Her research interests include medical image auto-segmentation, deep learning, and radiotherapy.

Michael Francis Gensheimer received the M.D. degree from the Vanderbilt University School of Medicine, Tennessee, in 2010. He is currently an associate professor at the Department of Radiation Oncology, Stanford University. His research interests include head and neck cancer, radiation oncology, medical prognosis analysis, and application of machine learning to cancer research.

Lucas Kas Vitzthum received the M.D. degree from the University of Minnesota School of Medicine, Minnesota, in 2015. He is currently an assistant Professor at the Department of Radiation Oncology, Stanford University. His research interests include radiotherapy development, predictive modeling to personalize patient treatment, and research that can address unmet clinical needs.

Beth M. Beadle received the B.A. degree from Northwestern University College of Arts and Sciences, Illinois, in 1996, and the M.D. degree from Northwestern University Feinberg School of Medicine, in 2004. She is currently a professor at the Department of Radiation Oncology, Stanford University. Her research interests include head and neck cancer, and radiation oncology.

Daniel T. Chang received the M.D. degree from Wayne State University, Michigan, in 2002. He was previously the Sue and Bob McCollum Professor of the Department of Radiation Oncology, Stanford University, and is currently the Isadore Lampe Professor and Chair of the Department of Radiation Oncology, University of Michigan. His research interests include advanced radiotherapy techniques, developing novel modalities and technologies for delivering radiotherapy, and using machine learning and other approaches to optimize care.

Quynh-Thu Le received the M.D. degree from the University of California, San Francisco, in 1993. She then joined the Stanford faculty in 1997. She became the Chair of the Stanford Radiation Oncology Department in September 2011. She also holds the Katharine Dexter McCormick & Stanley Memorial Professorship at Stanford University. She is the Chair of the NRG Oncology Group. Her research focuses on the identification of biomarkers for prognosis, and translating laboratory findings to the clinic and vice versa in head and neck cancer.

Bin Han received both the B.Eng. degree and M.Eng. degree from the Department of Engineering Physics, Tsinghua University, Beijing, China, in 2003 and 2006, respectively, and the Ph.D. degree from the Rensselaer Polytechnic Institute in 2011. He is currently a clinical associate professor at the Department of Radiation Oncology, Stanford University. His current research interests include medical image analysis, artificial intelligence in medicine, brachytherapy, and image-guided radiotherapy.

Lei Xing received the Ph.D. degree from Johns Hopkins University, in 1992. He is currently the Jacob Haimson Sarah S. Donaldson Professor of medical physics and the Director of the Medical Physics Division, Department of Radiation Oncology, Stanford University. He also holds affiliate faculty positions at the Department of Electrical Engineering, Bio-X and Molecular Imaging Program, Stanford University. His current research interests include medical imaging, artificial intelligence in medicine, treatment planning, image-guided interventions, nanomedicine, and applications of molecular imaging in radiation oncology.
Contributor Information
Yizheng Chen, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Lequan Yu, Department of Statistics and Actuarial Science, The University of Hong Kong, Hong Kong, China..
Jen-Yeu Wang, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Neil Panjwani, Department of Radiation Oncology, University of Washington, WA 98133 USA..
Jean-Pierre Obeid, Department of Radiation Oncology, Cleveland Clinic Florida, FL 32960 USA..
Wu Liu, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Lianli Liu, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Nataliya Kovalchuk, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Michael Francis Gensheimer, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Lucas Kas Vitzthum, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Beth M. Beadle, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA.
Daniel T. Chang, Department of Radiation Oncology, University of Michigan, MI 48109 USA.
Quynh-Thu Le, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Bin Han, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
Lei Xing, Department of Radiation Oncology, Stanford University, Stanford, CA 94305 USA..
REFERENCES
- [1].Zhang T, Chi Y, Meldolesi E, and Yan D, “Automatic delineation of on-line head-and-neck computed tomography images: toward on-line adaptive radiotherapy,” International Journal of Radiation Oncology* Biology* Physics, vol. 68, no. 2, pp. 522–530, Jun. 2007. [DOI] [PubMed] [Google Scholar]
- [2].Wang S. et al. , “CT male pelvic organ segmentation via hybrid loss network with incomplete annotation,” IEEE transactions on medical imaging, vol. 39, no. 6, pp. 2151–2162, Jan. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Lei Y. et al. , “CT prostate segmentation based on synthetic MRI-aided deep attention fully convolution network,” Medical physics, vol. 47, no. 2, pp. 530–540, Feb. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wang S. et al. , “CT male pelvic organ segmentation using fully convolutional networks with boundary sensitive representation,” Medical image analysis, vol. 54, pp. 168–178, May 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Tang H. et al. , “Clinically applicable deep learning framework for organs at risk delineation in CT images,” Nature Machine Intelligence, vol. 1, no. 10, pp. 480–491, Oct. 2019. [Google Scholar]
- [6].Yang Z. et al. , “A web-based brain metastases segmentation and labeling platform for stereotactic radiosurgery,” Medical physics, vol. 47, no. 8, pp. 3263–3276, Aug. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Xu M, Guo H, Zhang J, Yan K, and Lu L, “A New Probabilistic V-Net Model with Hierarchical Spatial Feature Transform for Efficient Abdominal Multi-Organ Segmentation,” 2022, arXiv: 2208.01382.
- [8].Jin D. et al. , “DeepTarget: Gross tumor and clinical target volume segmentation in esophageal cancer radiotherapy,” Medical Image Analysis, vol. 68, Feb. 2021, Art. no. 101909. [DOI] [PubMed] [Google Scholar]
- [9].Seo H, Huang C, Bassenne M, Xiao R, and Xing L, “Modified U-Net (mU-Net) with incorporation of object-dependent high level features for improved liver and liver-tumor segmentation in CT images,” IEEE transactions on medical imaging, vol. 39, no. 5, pp. 1316–1325, Oct. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lei Y. et al. , “Ultrasound prostate segmentation based on multidirectional deeply supervised V-Net,” Medical physics, vol. 46, no. 7, pp. 3194–3206, Jul. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wang S. et al. , “CT male pelvic organ segmentation via hybrid loss network with incomplete annotation,” IEEE transactions on medical imaging, vol. 39, no. 6, pp. 2151–2162, Jan. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Qin D. et al. , “Efficient medical image segmentation based on knowledge distillation,” IEEE Transactions on Medical Imaging, vol. 40, no. 12, pp. 3820–3831, Jul. 2021. [DOI] [PubMed] [Google Scholar]
- [13].Xing G. et al. , “Multi-scale pathological fluid segmentation in OCT with a novel curvature loss in convolutional neural network,” IEEE Transactions on Medical Imaging, early access, Jan. 11, 2022. [DOI] [PubMed]
- [14].Shi G, Xiao L, Chen Y, and Zhou SK, “Marginal loss and exclusion loss for partially supervised multi-organ segmentation,” Medical Image Analysis, vol. 70, May 2021, Art. no. 101979. [DOI] [PubMed] [Google Scholar]
- [15].Vu MH, Norman G, Nyholm T, and Löfstedt T, “A Data-Adaptive Loss Function for Incomplete Data and Incremental Learning in Semantic Image Segmentation,” IEEE Transactions on Medical Imaging, vol. 41, no. 6, pp. 1320–1330, Dec. 2021. [DOI] [PubMed] [Google Scholar]
- [16].Ibragimov B. and Xing L, “Segmentation of organs-at-risks in head and neck CT images using convolutional neural networks,” Medical physics, vol. 44, no. 2, pp. 547–557, Feb. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Liu Z. et al. , “Swin transformer: Hierarchical vision transformer using shifted windows,” In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 10012–10022. [Google Scholar]
- [18].Chen J. et al. , “Transunet: Transformers make strong encoders for medical image segmentation,” 2021, arXiv:2102.04306.
- [19].Valanarasu JMJ, Oza P, Hacihaliloglu I, and Patel VM, “Medical transformer: Gated axial-attention for medical image segmentation,” In International Conference on Medical Image Computing and Computer-Assisted Intervention. Cham, Switzerland: Springer, Sep. 2021, pp. 36–46. [Google Scholar]
- [20].Petit O, Thome N, Rambour C, Themyr L, Collins T, and Soler L, “U-net transformer: Self and cross attention for medical image segmentation,” In International Workshop on Machine Learning in Medical Imaging. Cham, Switzerland: Springer, Sep. 2021, pp. 267–276. [Google Scholar]
- [21].Jadon S, “A survey of loss functions for semantic segmentation,” In 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Oct. 2020, pp. 1–7. [Google Scholar]
- [22].Zotti C, Luo Z, Humbert O, Lalande A, and Jodoin P-M, “GridNet with automatic shape prior registration for automatic MRI cardiac segmentation,” In International workshop on statistical atlases and computational models of the heart. Cham, Switzerland: Springer, Sep. 2017, pp. 73–81. [Google Scholar]
- [23].Qu H, Yan Z, Riedlinger GM, De S, and Metaxas DN, “Improving nuclei/gland instance segmentation in histopathology images by full resolution neural network and spatial constrained loss,” In International conference on medical image computing and computer-assisted intervention. Cham, Switzerland: Springer, Oct. 2019, pp. 378–386. [Google Scholar]
- [24].Hayder Z, He X, and Salzmann M, “Boundary-aware instance segmentation,” In Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 5696–5704. [Google Scholar]
- [25].Al Arif SM, Knapp K, and Slabaugh G, “Shape-aware deep convolutional neural network for vertebrae segmentation,” In International Workshop on Computational Methods and Clinical Applications in Musculoskeletal Imaging. Cham, Switzerland: Springer, Sep. 2017, pp. 12–24. [Google Scholar]
- [26].Karimi D, and Salcudean SE, “Reducing the Hausdorff distance in medical image segmentation with convolutional neural networks,” IEEE Transactions on medical imaging, vol. 39, no. 2, pp. 499–513, July. 2019. [DOI] [PubMed] [Google Scholar]
- [27].Zhao S, Wu B, Chu W, Hu Y, and Cai D, “Correlation maximized structural similarity loss for semantic segmentation,” 2019, arXiv:1910.08711.
- [28].Milletari F, Navab N, and Ahmadi S-A, “V-net: Fully convolutional neural networks for volumetric medical image segmentation,” In 2016 fourth international conference on 3D vision (3DV), Oct. 2016, pp. 565–571. [Google Scholar]
- [29].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” In International Conference on Medical image computing and computer-assisted intervention. Cham, Switzerland: Springer, Oct. 2015, pp. 234–241. [Google Scholar]
- [30].Ma J. et al. , “Loss odyssey in medical image segmentation,” Medical Image Analysis, vol. 71, Jul. 2021, Art. no. 102035. [DOI] [PubMed] [Google Scholar]
- [31].El Jurdi R, Petitjean C, Honeine P, Cheplygina V, and Abdallah F, “High-level prior-based loss functions for medical image segmentation: A survey,” Computer Vision and Image Understanding, vol. 210, Sep. 2021, Art. no. 103248. [Google Scholar]
- [32].Kervadec H, Bouchtiba J, Desrosiers C, Granger E, Dolz J, and Ayed IB, “Boundary loss for highly unbalanced segmentation,” In International conference on medical imaging with deep learning, May 2019, pp. 285–296. [Google Scholar]
- [33].Wang L, Wang C, Sun Z, and Chen S, “An improved dice loss for pneumothorax segmentation by mining the information of negative areas,” IEEE Access, vol. 8, pp.167939–167949, Aug. 2020. [Google Scholar]
- [34].Seo H, Bassenne M, and Xing L, “Closing the gap between deep neural network modeling and biomedical decision-making metrics in segmentation via adaptive loss functions,” IEEE transactions on medical imaging, vol. 40, no. 2, pp. 585–593, Oct. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Salehi SSM, Erdogmus D, and Gholipour A, “Tversky loss function for image segmentation using 3D fully convolutional deep networks,” In International workshop on machine learning in medical imaging. Cham, Switzerland: Springer, Sep. 2017, pp. 379–387. [Google Scholar]
- [36].Xie Y, Zhang J, Lu H, Shen C, and Xia Y, “SESV: Accurate medical image segmentation by predicting and correcting errors,” IEEE Transactions on Medical Imaging, vol. 40, no. 1, pp. 286–296, Sep. 2020. [DOI] [PubMed] [Google Scholar]
- [37].Yang D, Roth H, Wang X, Xu Z, Myronenko A, and Xu D, “Enhancing Foreground Boundaries for Medical Image Segmentation,” May. 2020, arXiv:2005.14355.
- [38].Schlemper J, et al. , “Attention gated networks: Learning to leverage salient regions in medical images,” Medical image analysis, vol. 53, pp. 197–207, Apr. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Cheng J, et al. , “ResGANet: Residual group attention network for medical image classification and segmentation,” Medical Image Analysis, vol. 76, 102313, Feb. 2022. [DOI] [PubMed] [Google Scholar]
- [40].Jin Q, Meng Z, Sun C, Cui H, and Su R, “RA-UNet: A hybrid deep attention-aware network to extract liver and tumor in CT scans,” Frontiers in Bioengineering and Biotechnology, vol. 8, 1471, Dec. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Wang Z, Zou N, Shen D, and Ji S, “Non-local U-Nets for biomedical image segmentation,” In Proceedings of the AAAI conference on artificial intelligence, vol. 34, no. 04, pp. 6315–6322, Apr. 2020. [Google Scholar]
- [42].Li P, et al. , “Semantic Graph Attention With Explicit Anatomical Association Modeling for Tooth Segmentation From CBCT Images,” IEEE Transactions on Medical Imaging, vol. 41, no. 11, pp. 3116–3127, May 2022. [DOI] [PubMed] [Google Scholar]
- [43].Huang H, et al. , “Medical image segmentation with deep atlas prior,” IEEE Transactions on Medical Imaging, vol. 40, no. 12, pp. 3519–3530, Jun. 2021. [DOI] [PubMed] [Google Scholar]
- [44].Shi F, et al. , “Deep learning empowered volume delineation of whole-body organs-at-risk for accelerated radiotherapy,” Nature Communications, vol. 13, no. 1, pp. 6566, Nov. 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Ye X, et al. , “Comprehensive and clinically accurate head and neck cancer organs-at-risk delineation on a multi-institutional study,” Nature Communications, vol. 13, no. 1, pp. 6137, Oct. 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Abraham N, and Khan NM, “A novel focal tversky loss function with improved attention u-net for lesion segmentation,” In 2019 IEEE 16th international symposium on biomedical imaging (ISBI 2019), Apr 2019, pp. 683–687. [Google Scholar]
- [47].Sudre CH, Li W, Vercauteren T, Ourselin S, and Cardoso MJ, “Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations,” In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: Third International Workshop, DLMIA 2017, and 7th International Workshop, ML-CDS 2017, Sep. 2017, pp. 240–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Brosch T, and Tam R, “Deep 3D convolutional encoder networks with shortcuts for multiscale feature integration applied to multiple sclerosis lesion segmentation,” IEEE transactions on medical imaging, vol. 35, no. 5, pp. 1229–1239, Feb. 2016. [DOI] [PubMed] [Google Scholar]
- [49].[36]Crum WR, Camara O, and LG D. Hill, “Generalized overlap measures for evaluation and validation in medical image analysis,” IEEE transactions on medical imaging, vol. 25, no. 11, pp. 1451–1461, Oct. 2006. [DOI] [PubMed] [Google Scholar]
- [50].Ioffe S, and Szegedy C, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” In International conference on machine learning, Jun. 2015, pp. 448–456. [Google Scholar]
- [51].Srivastava N, Hinton G, Krizhevsky A, Sutskever I, and Salakhutdinov R, “Dropout: a simple way to prevent neural networks from overfitting,” The journal of machine learning research, vol. 15, no. 1, pp. 1929–1958, Jan. 2014. [Google Scholar]
- [52].Li Z, Li Z, Liu R, Luo Z, and Fan X, “Coupling Deep Deformable Registration with Contextual Refinement for Semi-Supervised Medical Image Segmentation,” In 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI), Mar. 2022, pp. 1–5. [Google Scholar]
- [53].Taghanaki SA et al. , “Combo loss: Handling input and output imbalance in multi-organ segmentation,” Computerized Medical Imaging and Graphics, vol. 75, pp. 24–33, Jul. 2019. [DOI] [PubMed] [Google Scholar]
- [54].Isensee F, Jaeger PF, AA Kohl S, Petersen J, and MaierHein KH, “nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation,” Nature methods, vol. 18, no. 2, pp. 203–211, Feb. 2021. [DOI] [PubMed] [Google Scholar]
- [55].Kingma DP and Ba J, “Adam: A method for stochastic optimization,” Dec. 2014, arXiv:1412.6980.
- [56].Raudaschl PF et al. , “Evaluation of segmentation methods on head and neck CT: auto-segmentation challenge 2015,” Medical physics, vol. 44, no. 5, pp. 2020–2036, May 2017. [DOI] [PubMed] [Google Scholar]
- [57].Landman B, Xu Z, Igelsias JE, Styner M, Langerak TR, and Klein A, “2015 MICCAI multi-atlas labeling beyond the cranial vault workshop and challenge,” In Proc., 2015.
- [58].Bilic P, et al. , “The liver tumor segmentation benchmark (LiST),” Medical Image Analysis, vol. 84, pp. 102680, Feb. 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Antonelli M, et al. , “The medical segmentation decathlon,” Nature communications, vol. 13, no. 1, pp. 4128, July 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Sajid S, Hussain S, and Sarwar A, “Brain tumor detection and segmentation in MR images using deep learning,” Arabian Journal for Science and Engineering, vol. 44, no. 11, pp. 9249–9261, Nov. 2019. [Google Scholar]
- [61].Zhong T, Huang X, Tang F, Liang S, Deng X, and Zhang Y. “Boosting‐based cascaded convolutional neural networks for the segmentation of CT organs-at-risk in nasopharyngeal carcinoma,” Medical physics, vol. 46, no. 12, pp. 5602–5611, Dec. 2019. [DOI] [PubMed] [Google Scholar]
- [62].Wang S. et al. , “A multi-view deep convolutional neural networks for lung nodule segmentation,” In 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jul 2017, pp. 1752–1755. [DOI] [PubMed] [Google Scholar]
- [63].Kaul C, Manandhar S, and Pears N, “Focusnet: An attention-based fully convolutional network for medical image segmentation.” In 2019 IEEE 16th international symposium on biomedical imaging (ISBI 2019), Apr. 2019, pp. 455–458. [Google Scholar]
- [64].Hu Y. et al. , “Weakly-supervised convolutional neural networks for multimodal image registration,” Medical image analysis, vol. 49, pp. 1–13, Oct. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Chen Y. et al. , “MR to ultrasound image registration with segmentation-based learning for HDR prostate brachytherapy,” Medical Physics, vol. 48, no. 6, pp. 3074–3083, Jun. 2021. [DOI] [PubMed] [Google Scholar]
- [66].Yang Y, and Xing L, “Inverse treatment planning with adaptively evolving voxel-dependent penalty scheme: Adaptive voxel-dependent penalty scheme for inverse planning,” Medical physics, vol. 31, no. 10, pp. 2839–2844, Oct. 2004. [DOI] [PubMed] [Google Scholar]