Protein interaction quantified in vivo by spectrally resolved fluorescence resonance energy transfer

Abstract

We describe a fluorescence resonance energy transfer (FRET)-based method for finding in living cells the fraction of a protein population (α_T) forming complexes, and the average number (n) of those protein molecules in each complex. The method relies both on sensitized acceptor emission and on donor de-quenching (by photobleaching of the acceptor molecules), coupled with full spectral analysis of the differential fluorescence signature, in order to quantify the donor/acceptor energy transfer. The approach and sensitivity limits are well suited for in vivo microscopic investigations. This is demonstrated using a scanning laser confocal microscope to study complex formation of the sterile 2 α-factor receptor protein (Ste2p), labelled with green, cyan, and yellow fluorescent proteins (GFP, CFP, and YFP respectively), in budding yeast Saccharomyces cerevisiae. A theoretical model is presented that relates the efficiency of energy transfer in protein populations (the apparent FRET efficiency, E_app) to the energy transferred in a single donor/acceptor pair (E, the true FRET efficiency). We determined E by using a new method that relies on E_app measurements for two donor/acceptor pairs, Ste2p–CFP/Ste2p–YFP and Ste2p–GFP/Ste2p–YFP. From E_app and E we determined α_T≈1 and n≈2 for Ste2 proteins. Since the Ste2p complexes are formed in the absence of the ligand in our experiments, we conclude that the α-factor pheromone is not necessary for dimerization.

INTRODUCTION

Förster resonance energy transfer, also known as fluorescence resonance energy transfer (FRET), is a process through which the excitation of a fluorescent molecule is transferred non-radiatively (i.e. without exchange of a photon) to a nearby molecule [1]. FRET is used increasingly for the study of molecular interactions in living cells or single bimolecular complexes [2–6]. Renewed interest in FRET is due in large part to characterization of the green fluorescent protein (GFP) [7] and the creation of its blue (BFP), cyan (CFP) and yellow (YFP) variants [8,9]. Proteins of interest may be labelled with these naturally fluorescent markers for FRET studies in almost any living cell.

An important parameter to be obtained from FRET studies is the energy-transfer efficiency, which can be determined either from a reduction in the donor fluorescence in the presence of acceptor [2–4,10] or from an enhancement of acceptor emission due to energy transfer from the donor [11–14]. Determination of the FRET signal in the background of other fluorescence signals by current methods requires a low donor emission at those wavelengths at which the acceptor emits, and low direct excitation of the acceptor at the excitation wavelengths of the donor; in other words, donor and acceptor should present low ‘spectral cross-talk.’ These conditions can be satisfied partially for some pairs of GFP variants [5,9], although this is at the expense of reducing the signal of interest, i.e. the FRET efficiency. In addition, with current methods, combinations of excitation wavelengths and detection filters must be used for the extraction of useful information from the fluorescence spectra, and these may all complicate the experimental protocols.

Recent publications have demonstrated the feasibility of spectrally resolved fluorescence microscopy [15]. The fluorescence intensity from more than one fluorophore is measured at several wavelengths so that composite fluorescence spectra are recorded. From this, acceptor and donor spectra are subsequently deconvoluted for further analysis. Spectrally resolved fluorescence has also proved useful in FRET studies involving stoichiometric (1:1) amounts of donor and acceptor molecules [16]. However, the possibility of applying this technique to fully quantitative FRET studies on systems with arbitrary (and unknown) proportions of donor and acceptor molecules has yet to be explored.

We have developed a method for quantitative FRET studies in single living cells, which relies on acquisition of fluorescence spectra using a wavelength-tunable confocal laser-scanning microscope followed by separation of the spectra into donor and acceptor components. With this, the average efficiency of energy transfer in a donor/acceptor pair and the fraction of interacting proteins can be determined. The latter information, hitherto unavailable to molecular and cell biologists, is of great significance for understanding the dynamics of protein–protein interactions in living cells.

We used our method to study the oligomerization of the α-factor receptor protein Ste2 (Ste2p), which is involved in the signalling pathway for mating in yeast (Saccharomyces cerevisiae) [17]. Substitution on its cytoplasmic tail with fluorescent tags (GFP variants) results in FRET when a donor-carrying Ste2 protein encounters an acceptor-tagged Ste2p [18,19]. In the present study we examined single cells (budding yeast) expressing: (a) single populations of Ste2 proteins tagged with GFP, CFP, or YFP, that were used in identification of the emission spectra of the tagged proteins in vivo, and (b) combinations of populations of either Ste2p–CFP or Ste2p–GFP (donor molecules), and Ste2p–YFP (acceptor) that can form Ste2p–CFP/Ste2p–YFP or Ste2p–GFP/Ste2p–YFP complexes respectively.

Measurement of donor fluorescence in the presence and absence of acceptor was first achieved by employing the standard method of acceptor photobleaching in a confocal microscope [3,20,21]. From this, an ‘apparent FRET efficiency’ (E_app) was obtained, which represents the overall efficiency of energy transfer in protein populations including non-interacting molecules. We introduce a simple mathematical procedure that relies on the ratio of E_app between cell populations comprising Ste2p–CFP/Ste2p–YFP and Ste2p–GFP/Ste2p–YFP protein complexes to provide the average fraction of energy transferred in a single donor/acceptor pair, or the ‘true FRET efficiency’ (E). So far this important parameter in FRET studies could be determined only from fluorescence lifetime measurement (FLM) [22–25]; our method makes it available also to those research laboratories that rely for FRET studies on spectrally resolved confocal microscopes, spectrofluorometers or flow cytometers.

Acceptor photobleaching, although very convenient to use in FRET studies due to its simplicity, poses a number of technical and conceptual difficulties, which we address below.

First, it is generally recognized that the bleaching process may be too slow to be practical in studies of biological systems which are inherently dynamic. Although the use of the confocal laser-scanning microscope substantially reduces the time necessary to achieve acceptor photobleaching [20], we observed that complete photobleaching of all acceptor molecules was not always possible within a reasonable time (see below). In some cases, especially in studies of dynamic systems, complete photobleaching is not even desirable, as it would leave no useable reporter molecules after the first set of measurements. In response to this difficulty we developed a simple mathematical model, which suggests that only partial stepwise bleaching of the acceptor is necessary for reliable FRET efficiency computations. When applied to Ste2p–GFP/Ste2p–YFP protein complexes, partial photobleaching produced a value for the FRET efficiency similar to that obtained with ‘complete’ bleaching, but requiring considerably shorter exposure time.

Secondly, during the process of acceptor photobleaching, an undesirable, significant bleaching of the donor is also induced; if unaccounted for, this may lead to underestimation of the FRET efficiency. This effect has also been observed by Karpova et al. [20]. In this paper we deal with this problem by introducing methods to correct for donor bleaching, both for the ‘complete’ and for the gradual acceptor bleaching cases mentioned above.

By applying a gradual-photobleaching method, we were able to determine E_app for cells containing Ste2p–GFP and Ste2p–YFP in oligomeric and/or monomeric forms. From this, and by using an E value obtained as explained above, the fraction of donors that form oligomers with acceptors (α_D) was determined. We also obtained a value of E_app from sensitized emission (i.e. from the increase in acceptor fluorescence due to energy transfer [1]) and, subsequently, the fraction of interacting acceptor molecules (α_A). α_A and α_D, together with the knowledge of the ratio of concentrations of acceptor to donor proteins present in a cell or a cellular region of interest, provide a complete set of data for determining the amount of interacting proteins. Thus, we were able to obtain from intensity-based FRET measurements in living cells the fraction of interacting Ste2 proteins and the average number of monomers constituting a Ste2p homo-oligomer. In addition, knowledge of E makes possible, at least in principle, the determination of the inter-molecular distance in a protein complex in vivo, with some limitations that have to be properly taken into account (see below). The biological relevance of our results is discussed in light of recent findings pertaining to Ste2p and other members of the family of G protein-coupled receptors (GPCRs) [26–28]. We believe that this general method of FRET-based stoichiometry will be of considerable interest to those who wish to quantify, in living cells, the fraction of a protein population that forms either homo- or hetero-oligomers.

EXPERIMENTAL

Biological material

Variants of the GFP used in this study are called, for convenience, GFP, CFP and YFP. They contain the following amino acid substutions (given in single amino-acid code) of the GFP cloned from Aequorea victoria: GFP, S65T Q80R; CFP, F64L S65T Y66W N146I M153T V163A N212K; YFP, S65G S72A T203Y. Note that the Q80R substitution has been reported previously as an innocuous amino-acid change likely introduced by a PCR mutation during the original cloning of GFP [7]. Ste2p–CFP, Ste2p–GFP and Ste2p–YFP, singly or in combination, were expressed from low-copy (CEN/ARS) plasmids in a strain of S. cerevisiae lacking a functional copy of STE2 in the chromosome (KBY58; MATa leu2-3,112 ura3-52 his3-Δ1 trp1 sst1-Δ5 ste2Δ). Plasmids MO105 (STE2-CFP TRP1 CEN/ARS) and MO149 (STE2-YFP URA3 CEN/ARS) and strain KBY58 were gifts of K. J. Blumer [18,29]. Ste2 was fused to CFP or YFP at position 304 in the amino acid sequence, eliminating all but 8 amino acids of the cytoplasmic tail of Ste2p [18]. This was done in order to decrease the distance, and hence increase FRET efficiency, between GFP variants in a receptor oligomer. The plasmid called pYF1969 (STE2–GFP TRP1 CEN/ARS) was constructed by replacing the CFP sequence of pMO105 with GFP (S65T Q80R) DNA.

Yeast strains were grown on synthetic-complete solid medium lacking those nutrients that were required to select for the plasmid(s) of interest. Yeast colonies were resuspended in water, and deposited on solid medium as a drop that was then allowed to form a streak by tilting the plate. These plates were incubated overnight at 30 °C. Approx. 2 μl of 0.2 M KCl were taken up in a sterile pipette tip, which was then used to collect cells from a freshly growing streak by gentle scraping. The liquid and cells formed a suspension on a glass slide, which was then covered with a 22× 22 mm glass coverslip. The KCl solution and residual glucose from the growing medium helped maintain high pH (>7) in the cell interior [30,31]. This created optimum conditions for a high constant quantum yield of the fluorescent proteins [32] throughout the process of acquisition of fluorescence data. A decay in fluorescence, indicative of an acidification of the cytoplasmic medium due to complete consumption of external glucose, was only observed in our study after keeping the cells for more than 10 min on the microscope slide. This well exceeded the time necessary to acquire complete sets of fluorescence data.

Image acquisition and analysis

Yeast cells were observed using a Leica DM IRBE™ (Leica Microsystems, IL, U.S.A.) confocal laser scanning microscope with a 100× power objective and immersion oil, and the images were collected and stored at a 256×256 pixel density. The temperature was maintained at a constant 19±0.5 °C.

For FRET analysis under conditions of complete bleaching, an initial differential interference contrast (DIC) image was acquired to focus the objective and stored for future reference of cell boundaries. Cells were excited by using the 458 nm line of an Argon-ion laser, and 16 images were collected of fluorescence emissions over 5-nm-wide windows separated by 1-nm gaps, and beginning either at 460 nm (for cells bearing Ste2p–CFP) or at 472 nm (for Ste2p–GFP) (see Figure 1A). An image was taken at 520–525 nm of cells excited by using 514-nm laser radiation. This wavelength is appropriate for generating the maximum emission of acceptor (Ste2p–YFP) fluorescence, and insignificant donor fluorescence. Repeated scans (a total of ∼60) using 514-nm light (∼3 mW of power at the specimen level) were applied for 30 s as a means of photobleaching the acceptor proteins. This was followed by acquisition of another image at the emission peak (520–525 nm) of cells excited by 514-nm laser radiation to probe acceptor photobleaching. A second series of 16 images was collected using 458-nm light for excitation followed by acquisition of a final DIC image.

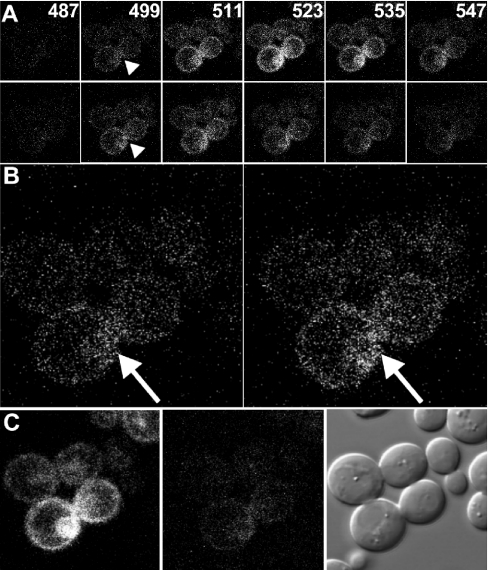
Figure 1. FRET in cells expressing Ste2p–GFP and Ste2p–YFP.

(A) Cells that co-express Ste2p–GFP and Ste2p–YFP were excited by the 458-nm line of an Argon-ion laser. Emission images (6 out of the 16 sampled) at the indicated wavelengths (in nm) were obtained before (top panels) and after (bottom panels) bleaching by 60 scans (lasting about 30 s) using a 514-nm laser. Arrowheads indicate an area with more pronounced GFP fluorescence after bleaching of YFP. (B) Enlarged emission images at 499 nm from (A) before (left-hand panel) and after (right-hand panel) bleaching of the yellow fluorescent protein. (C) Images showing the fluorescent emission of Ste2p–YFP at 523 nm upon excitation at 514 nm before (left-hand panel) and after (centre panel) bleaching, and the cells in DIC (right-hand panel) after photobleaching to show the cells are intact.

The method for collecting images for gradual-bleaching analysis was similar to the complete bleaching method. Instead of a 60-scan bleach, cells were scanned five times using the 514-nm laser, which always included the collection of an image at the beginning and the end of the bleaching interval. Each interval was followed by the collection of 16 images covering progressive 5-nm windows of emission of cells excited by 458-nm laser radiation. A total of six partial bleachings and spectral scans were performed.

Using Leica TCS™ image quantification software, image pixels were ascribed values ranging from 0 (black) to 255 (white) on a 256-values gray scale, and the fluorescence intensity of whole cells was obtained as an average gray value over all pixels contained in the area of interest (i.e. the cell). Intensities in the emission windows were plotted against the median wavelength value for each 5-nm window to form emission fluorescence spectra (see below). Means of at least 20 separate spectra for Ste2p–CFP, Ste2p–GFP, and Ste2p–YFP were then normalized to their peak intensity values (see Figure 2); we refer to these as ‘normalized’ spectra. These were used subsequently for analysis of the composite spectra of cells bearing either Ste2p–CFP/Ste2p–YFP or Ste2p–GFP/Ste2p–YFP (see below).

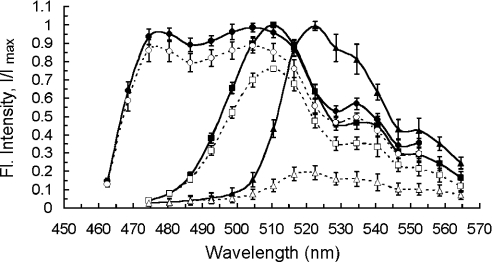
Figure 2. Excitation and emission spectra of GFP variants used in this study.

Normalized fluorescence emission spectra of CFP- (circles), GFP- (squares) and YFP-tagged (triangles) Ste2 proteins in yeast cells measured by a confocal microscope (see Experimental section) before (filled symbols, solid lines) and after (open symbols, dashed lines) 60 scans (approx. 30 s) by 514-nm light (photobleaching). Data are means±S.D. over n=21 (for CFP), n=23 (GFP) and n=52 (YFP) cells. Lines serve as guides to the eyes only.

No correction for background fluorescence was necessary, as this contribution to the total spectra was kept to a minimum (less than 5%, and typically 2–3%) by selecting for analysis those cells that showed both donor and acceptor fluorescence intensities higher than 15 units (within the above-described range of 256 gray scale values). Spectra with peak intensities larger than approx. 200 units were excluded from our analysis, in order to avoid any nonlinear effects introduced by saturation of the intensity images. The upper limit could be elevated by increasing the pixel density of the image, but this increased the size of the computer files and decreased the acquisition speed. Conceivably, this selection slightly narrowed the distribution of GFP- (or CFP-) and YFP-tagged Ste2p among cell populations, without affecting significantly its shape.

Decomposition of fluorescence spectra

The individual contributions of donor and acceptor signals to an experimentally obtained composite spectrum need to be separated for subsequent calculation of the apparent FRET efficiency (see below). These spectra are determined by fitting the measured spectrum to the function:

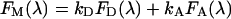(1a)

where F_M(λ) is the simulated composite spectrum, and F_D(λ) and F_A(λ) are the normalized spectra of donor (either GFP or CFP) and acceptor (YFP) chromophores, as defined above. k_D and k_A are scaling factors for donor and acceptor spectra respectively, and represent the individual amounts of fluorescence emitted. Mathematically, spectral decomposition amounts to using appropriate mathematical expressions for the computation of values for k_D and k_A that are necessary to simulate an experimental spectrum. These expressions are obtained [33] from least-squares calculation as (explicit dependence on λ, is omitted, for brevity):

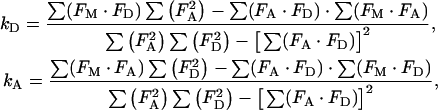(1b)

where the Σ (F_x·F_y) represents the sum over the intensity values corresponding to all wavelengths of the F_X and F_Y spectra in the parenthesis, with X and Y standing for the measured (M), donor (D), and acceptor (A) spectra.

Theory of the method

FRET efficiency in intensity-based micro-fluorometry can be determined both from diminished donor [2–4,10] and enhanced acceptor fluorescence (i.e. sensitized emission) following energy transfer [11–14]. These will be dealt with separately below.

Quantifying FRET from donor photobleaching

An apparent FRET efficiency E_app can be defined in the case of quenched donor fluorescence as the fractional decrease in donor emission due to the transfer of energy to the acceptor [1], namely:

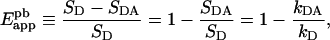(2)

where S_D≡k_D×w_D is the integrated donor fluorescence spectrum, or the spectral integral, in the absence of acceptor; S_DA is the (similarly defined) donor spectral integral in the presence of acceptor; w_D is the area of the normalized spectrum of the donor (see Table 1); and k_DA and k_D represent the scaling factors defined in the Experimental section. The term ‘apparent’ signifies that the efficiency determined from Equation 2 is a global measure of the efficiency of the energy transfer in populations of proteins containing large numbers of donors and acceptors, only a fraction of which are paired. In contrast, the true FRET efficiency, E, refers to the transfer of energy between an acceptor and a donor molecule in a single pair. To be precise, in this study the ‘true FRET efficiency’ refers to an average of E over a large number of protein complexes contained by a cell, excluding those proteins that do not form complexes at all.

Table 1. Spectral characteristics of the three fluorescent probes presented in Figure 2.

Probe type	Bleaching coefficient, β*	Area of normalized spectra, w (a.u.)†	Maximum extinction coefficient, εM(M−1·cm−1)	Quantum yield, Q	Overlap integral with YFP, J (nm4)‡
CFP	0.90	69	29250±4600§	0.40§	2.21×1010
GFP	0.76	43	53500±2100∥	0.64∥	3.47×1010
YFP	0.19	39	82600±1900¶	0.61¶	−

* Obtained in this work after 60 scans at 514 nm in the confocal microscope.

† Corresponding to the normalized spectra in Figure 2.

‡ See Appendix B for details of the calculation.

§ From [37,38].

∥ From [32,37].

¶ From [37,38,50].

Determination of the scaling factor for the donor spectrum in the absence of acceptor (k_D) can be done by photobleaching the acceptor and measuring the donor fluorescence spectrum [1,2]. During acceptor photobleaching at acceptor maximum excitation wavelength λ_A^M, the donor can also be bleached significantly, since in most cases λ_A^M lies also in the excitation spectrum of the donor. Thus k_D can be underestimated and a correction is required: k_D in Equation 2 is replaced by k_D^pb/β_D, where k_D^pd is the donor fluorescence after photobleaching, and β_D (≤ 1, see Table 1) is the donor-bleaching coefficient or the fraction of donors remaining after irradiation (β_D=0 for complete bleaching). Equation 2 then becomes:

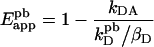(3)

With a few exceptions (see e.g. [20]), donor photobleaching has been ignored in acceptor-photobleaching experiments, and it is apparent from Figure 2 that photobleaching can not be neglected.

In general only a fraction α_D of total donor molecules form complexes with acceptor molecules that lead to resonant energy transfer [1], while 1−α_D molecules do not form productive complexes. Thus, one can derive from Equation 3 the true FRET efficiency by subtracting from k_DA the signal from donors not coupled to acceptors, i.e. (1−α_D) k_D^pd/β_D, and replacing k_D with α_Dk_D^pd/β_D, so as to consider only the donors that were previously (i.e. before bleaching) involved in resonant energy transfer with acceptors:

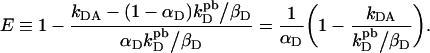(4a)

This equation can be rearranged, using Equation 3 again, as:

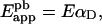(4b)

Equation 4(b) states that the apparent FRET efficiency is given by the product between E and the fraction of donor molecules that interact with A molecules (α_D).

If acceptor bleaching is incomplete, only those D/A pairs in which A has been inactivated by photobleaching will lead to a fluorescence increase of D. This effect reduces the fraction of D that participate in the E calculation from α_D to α_D (1−β_A); β_A is the acceptor photobleaching coefficient (β_A=0 for the ideal case of complete acceptor bleaching). Then:

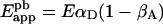(5)

which gives the necessary link between true and apparent FRET efficiencies in partial acceptor photobleaching experiments. If E is known for a given D/A pair then, based on the method of decomposition of fluorescence spectra presented here, one can determine from E_app^pb the fraction of donor-tagged molecules that form complexes with acceptor-tagged proteins (α_D=[D]_A/[D]_T with [D]_T being the total concentration of D, and [D]_A the concentration of D in complexes with A).

Sensitized emission

As mentioned above, sensitized emission is defined as an increase in the acceptor fluorescence, compared with what would be observed from direct acceptor excitation alone, due to non-radiative transfer of energy from an excited nearby donor. It is relatively straightforward to derive the equation for E_app in the case of sensitized emission (denoted below as E_app^se) by assuming conservation of excitation energy in a complex formed of acceptor and donor molecules. In our notation for acceptor fluorescence in the presence (k_AD) and absence (k_A) of the donor, the equation reads [1]:

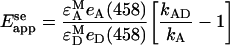(6)

where ε_A^M and ε_D^M are extinction coefficients of the acceptor and donor molecules at their respective maximum excitation wavelengths, and e_A(458) and e_D (458) are the normalized (to maximum values) absorptions of A and D at the wavelength (458 nm) used in this work for D excitation. Emission from acceptors in the ‘absence’ of donors (k_A) can be determined by using a wavelength for A excitation that produces no significant excitation of D, such as the 514-nm line used in this study (see above). In this way, k_A in Equation 1 can be determined by rescaling k_A obtained upon excitation at 514 nm (i.e. k_A⁵¹⁴) with a coefficient, which we denote by η. This coefficient includes fluorescent-molecule related properties as well as instrumental parameters (see Equation A2 in Appendix A), and is defined as the ratio of fluorescence intensities (detected at 520–525 nm) obtained from excitation at 458 nm and 514 nm respectively, of cells expressing only Ste2p–YFP proteins. Equation (6) reads in this case:

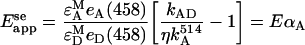(7)

Similar to the bleaching method, if E is known for an average D/A pair, then one can determine from E_app^se the fraction of acceptor-tagged molecules that form complexes with donor-tagged proteins, α_A=[A]_D/[A]_T (with [A]_T, being the total concentration of A, and [A]_D the concentration of A in complexes with D). It is important to note that for a cell containing different total concentrations of acceptor, [A]_T, and donor, [D]_T, the apparent efficiency determined from sensitized emission (Equation 7) may be different from that obtained from donor photobleaching (cf. Equation 5), since α_A and α_D could be different.

It should be remarked that up to this point in the theory no assumption has been made with regard to the size of the oligomer. The only requirement would be that, for oligomers containing more than two monomers, the acceptors are symmetrically distributed around donors, on average. This is often a reasonable assumption, but, as a precaution, its merits should be assessed separately for each protein system investigated, akin to the problem of evaluation of the uncertainties in the dipole orientation factor (see our discussion at the end of ‘Determination of the true FRET efficiency’ section; also [34]). Therefore, the whole theory above holds exactly for the case of dimers and is a good approximation for the case of higher order oligomers (trimers and tetramers, etc.).

Determination of E by using two fluorescent protein pairs

The true FRET efficiency for Förster-type energy transfer is related to the inter-chromophore distance, r, through the conventional formula:

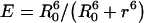(8)

where R₀ is the Förster distance, characteristic of a given donor-acceptor chromophore pair. Let us now consider two different D/A pairs, such as the Ste2p–CFP/Ste2p–YFP and Ste2p–GFP/Ste2p–YFP pairs used in this work. If the α_D is the same for Ste2p–GFP/Ste2p–YFP and Ste2p–CFP/Ste2p–YFP pairs, the ratio of the apparent FRET efficiency of Ste2p–GFP/Ste2p–YFP (denoted by E_app^GY) to that of Ste2p–CFP/Ste2p–YFP (E_app^CY) reduces, according to Equation 5, to the ratio of the true FRET efficiencies E, namely E_app^GY/E_app^CY=E^GY/E^CY, which we denote by φ (note that we omit hereafter the superscript ‘pb’ of E_app, for simplicity). Although this assumption may not necessarily be valid in some cases, we will show in the next section that it is valid for GFP and CFP used in this study. This simple equality between the ratios of the true and apparent FRET efficiencies is valid for any degree of acceptor photobleaching (cf. Equation 5). This is because the acceptor is bleached to the same extent (on average) in both cases, so that when the apparent FRET efficiencies are expressed as a ratio, the average of the factor 1−β_A in Equation 5 corresponding to the population of cells containing Ste2p–GFP/Ste2p–YFP cancels out the 1−β_A factor for the cells containing Ste2p–CFP/Ste2p–YFP. This cancellation is, of course, valid if the same number of bleaching scans is used to bleach the acceptor (Ste2p–YFP) in the presence of the Ste2p–CFP and the Ste2p–GFP donors, as in our study.

Furthermore, on noting that CFP and GFP have very similar structures [35], we assume that the average distance r between the donor and acceptor chromophores is the same for the two combinations of donor and acceptor. Using Equation 8 and the efficiencies ratio φ, the following equation can be derived:

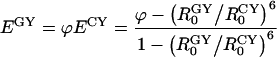(9)

Rewriting Equation 9 with the use of the definition of Förster distance (Equation B1 in Appendix B), we obtain:

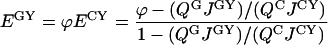(10)

where Q^G and Q^C are the quantum yields of the donor molecules (GFP and CFP respectively), and J^GY and J^CY are the spectral overlap integrals for each D/A pair, as defined in Appendix B. From this equation, the true FRET efficiencies can be calculated, which will be used below in estimating the fraction of interacting Ste2 proteins. According to this equation, by using two D/A pairs for which r is the same, E can be determined independently of the orientation factor κ², the index of refraction n, and the acceptor extinction coefficient ε_A^M all of which enter the formula for R₀ (see Appendix B). Determination of E independently of these three physical parameters eliminates significant uncertainties, particularly those originating from the orientation factor κ² [34].

Calculation of the fraction of interacting proteins and oligomer size

Having determined E, one could attempt to determine the fraction of interacting proteins and the average number of monomers forming an oligomer. For proteins that form only hetero-oligomers (i.e. that only interact with proteins not of their own type), the donor tag would be normally attached to one protein type and the acceptor would be attached to the other protein type, and thus a donor-tagged protein would only couple to an acceptor-tagged protein. In this case α_D=[D]_A/[D]_T, which defines the fraction of proteins labelled with the donor fluorophore that are interacting with acceptor-labelled proteins, can be calculated using Equation 5. The fraction of the second protein involved in the interaction may be obtained by either switching the fluorophores of the two proteins and then obtaining α_D for the second protein, or by calculating the value of α_A=[A]_D/[A]_T, which defines the fraction of proteins labelled with A that are interacting with D-labelled proteins, using Equation 7. To summarize, for hetero-oligomeric systems, knowledge of E, E_app^pb, E_app^se, and the extent of acceptor photobleaching, β_A, permits the calculation of α_D, which completely characterizes the binding stoichiometry of D, and α_A, which completely characterizes the binding of A.

However, if the proteins form homo-oligomers (i.e. interact with proteins of their own type), then the fluorescent tags can form DD and AA complexes in addition to AD complexes, which are directly detectable by FRET. Note that to avoid confusion, we reserve the term hetero-oligomer for those interactions involving binding domains of different proteins. We call homodimers or homo-oligomers those complexes formed by the same protein (e.g. Ste2p), not those complexes in which all proteins are tagged only with A or only with D fluorophores. For homo-oligomeric systems a little more modelling effort is therefore necessary in order to determine the stoichiometry of the system. For such cases, a relevant parameter would be the total fraction of interacting proteins in homo-oligomeric complexes, defined as α_T={[A]_b+ [D]_b}/{[A]_T+[D]_T}, with [A]_b and [D]_b being the concentration of acceptors and donors, respectively, bound in complexes of all types (i.e. AA, DD, and AD). We will show below how α_T can be determined from the experimentally accessible parameters α_A and α_D. In addition, we will derive an equation that will permit determination of the average size of the oligomer, in terms of the number of monomers forming the complex.

Adair and Engelman [36] have proposed a model, for the case with no free monomers, that relates the FRET efficiency determined from photobleaching to the fraction of donor-tagged proteins, P_D=[D]_T/{[A]_T+[D]_T}, and the size of the oligomer, n (n=2 for dimer, 3 for trimers, etc). In our own notations, Adair and Engelman (AE) theory gives α_D=(1−P_Dⁿ⁻¹). Those authors successfully applied the model to show dimerization of glycophorin A, a membrane protein of red blood cells, which has a single transmembrane domain. When free monomers are also present, one has to correct the AE formula by multiplying it with the fraction of total bound donors, α_Db=[D]_b/[D]_T and replace P_D with P_Db=[D]_b/{[A]_b+[D]_b}. Thus,

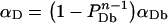(11a)

Analogously, one can write an equation for α_A as:

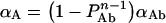(11b)

where P_Ab=[A]_b/{[A]_b+[D]_b} represents the fraction of acceptor-tagged proteins in complexes, and α_Ab=[A]_b/[A]_T is the fraction of total bound acceptors. Equations 11(a) and 11(b) can be rigorously proved by generalizing AE treatment based on the binomial distribution to the case of free monomers. Although we actually followed that path in our original derivation, we only present here this intuitive procedure for writing Equations 11(a) and 11(b), to avoid unnecessary lengthening of this subsection of the paper. From the above definitions of P_Ab, P_Db, α_Db, α_Ab and α_T one can readily obtain the following relations:

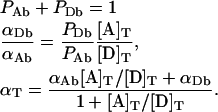(12)

The ratio of Equations 11(a) and 11(b) together with Equation 12(b) leads to:

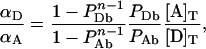(13)

while combination of Equations 11(a) and 11(b) with Equation 12(c) provides:

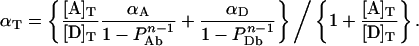(14)

We note that for the case of self-associating proteins such as Ste2p there is no difference, as regards the binding properties, between A-tagged proteins and D-tagged proteins. Therefore, for a large number of cells, the average number of acceptors, 〈[A]_T〉, equals the average number of donors, 〈[D]_T〉, or 〈[A]_T〉/〈[D]_T〉=1 (where 〈〉 stands for ‘average’). For the same reason, and by using Equation 12(a), 〈P_Ab〉=〈P_Db〉=1/2. Thus, Equation 14 reduces to:

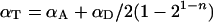(15)

which can be used for determination of α_T if the average number (n) of monomers in a complex is known. If not known by other means, n can be evaluated from Equation 13, provided that the number of proteins in complexes is much larger than the number of free monomers. In such a case, P_Ab and P_Db can be approximated by P_A and P_D, respectively, and Equation 13 simplifies as:

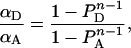(16)

with 1−P_A=P_D=1/{1+[A]_T/[D]_T}. This equation can be used for the evaluation of n, since the ratio [A]_T/[D]_T is accessible experimentally.

RESULTS

Spectral characteristics of GFP variants

Selection of the appropriate excitation wavelengths for FRET measurements with the laser-scanning microscope, and subsequent quantitative analysis of the FRET data (see below), requires examination of the emission and excitation spectra, as well as the quantum yields and extinction coefficients of Ste2p–CFP, Ste2p–GFP, and Ste2p–YFP. These properties collectively can be termed the ‘spectral properties’ of the fluorescent molecules. Extensive work has been done for the characterization of the spectral properties of most widely used GFP variants [7,32,37–39]. For the mutant GFP proteins used in this paper, we used the excitation spectra as described previously [38]. Accordingly, the 458-nm line minimally excites the acceptor molecules (Ste2p-YFP), while providing sufficient excitation for both donors (Ste2p-CFP and Ste2p-GFP). On the other hand, the 514-nm line almost exclusively excites Ste2p–YFP, whose fluorescence can be thus detected essentially in the absence of the donor in our FRET study presented below.

The emission spectra of the fluorescent probes excited with a 458-nm laser were determined by measuring emission spectra of individual cells containing Ste2p–GFP (n=23 cells), Ste2p–CFP (n=21 cells) and Ste2p–YFP (n=52 cells). Normalized emission spectra of intact as well as bleached fluorophores were then obtained (Figure 2) as explained in the Experimental section. Owing to our experimental protocols (see Experimental), the cell internal pH>7 was optimal for obtaining maximum quantum yields for all three GFP variants used herein [32,37,38], over a period of time long enough to permit acquisition of all the necessary data for each cell under investigation. Therefore, it is likely that the literature excitation spectra, quantum yield, and extinction coefficients (Table 1), as well as our emission spectra are obtained under similar conditions of pH. We will use these normalized emission spectra for the separation of composite fluorescence spectra into donor and acceptor components, as discussed in the next subsection.

Integration of the normalized emission spectra in Figure 2 provided the normalized spectral integrals for the three fluorescent proteins (Table 1). The spectral integrals will be used to evaluate the concentration ratios for CFP-, and GFP-, and YFP-tagged Ste2p (see next subsection and Appendix A). The concentrations ratio for the first two proteins (the FRET donors) is particularly important for verifying one of the assumptions underlying the theory for determination of the true FRET efficiency, E.

The bleaching sensitivities of different chromophores were quantified through a photobleaching coefficient, β, defined as the average ratio between the fluorescence intensities after and before bleaching. As seen in Figure 2, the three GFP variants used in this work showed different photobleaching sensitivities (Table 1). The most sensitive was YFP (due to better matching of the 514-excitation wavelength with the YFP excitation maximum, and also because of its higher photobleaching sensitivity [5,38]). Hence, the fluorescence intensity of YFP after photobleaching was reduced to less than 20% of the intact chromophore. This important property of YFP can be used to advantage in FRET studies in vivo (see below).

The overlap integrals for the D/A pairs, calculated as explained in Appendix B, are also included in Table 1, as they are used in evaluation of the Förster distances (R₀) for the two protein pairs.

Determination of the true FRET efficiency

Computation of the E_app for cells that express both donor and acceptor molecules, requires the decomposition of fluorescence spectra into donor and acceptor components, in terms of the parameters k_D and k_A, which represent the scaling factors of donor and acceptor spectra (see Experimental). k_A is a composite parameter that incorporates the contribution to the spectrum of directly excited acceptor (at 458 nm in our experimental setup) plus the emission of the acceptor excited through resonant energy transfer. However, k_D represents a single type of signal: the directly excited donor fluorescence. Therefore, the calculation of E_app from acceptor photobleaching (i.e. by using Equation 3) is more robust than that based on sensitized emission, which uses a number of additional parameters that have to be known with precision (i.e. Equation 7). We employ quasicomplete bleaching of the acceptor (YFP) to detect the increase in donor fluorescence due to absence of energy transfer, and thereby E. However, as we will show later on, the sensitized emission method is also important, since, together with the acceptor photobleaching method, it provides complete information regarding the amount of interacting proteins for proteins that form homo-oligomeric complexes, as in the case presented in this study.

The images in Figures 1(A) and 1(B) demonstrate clearly the increase in donor fluorescence after bleaching the acceptor (Figure 1C) with 514-nm laser radiation in live yeast cells. However, quantification of this increase is complicated by the presence of YFP fluorescence signal before the bleaching of the cells. Spectral deconvolution addresses this problem by separating the composite spectrum into its components of donor and acceptor spectra.

Two typical examples of composite fluorescence spectra are presented in Figures 3 and 4 for two cells, each containing two populations of Ste2 proteins tagged with either CFP and YFP (Figure 3) or GFP and YFP (Figure 4). The best-fit parameters obtained from the analysis using Equation 1 are summarized in Table 2 for both figures. The simulated curves [represented by solid and dashed lines in Figures 3 and 4, (top panels)] reproduced very well the measured spectra (● and ▲) for the two fluorescent pairs, both for bleached and unbleached cases. Spectral decomposition of the fluorescent signals revealed an increase in the donor fluorescence spectra following acceptor photobleaching, from which values of E_app (also included in Table 2) have been computed by using Equation 3, with the donor bleaching coefficient, β_D, taken from Table 1.

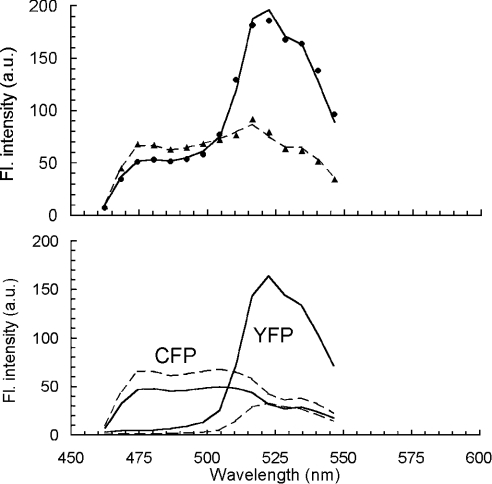
Figure 3. Spectral deconvolution of composite fluorescence spectra of cells expressing Ste2p–CFP and Ste2p–YFP.

Fluorescence spectra of a typical yeast cell containing two distinct populations of Ste2p–CFP and Ste2p–YFP (top panel). The data were acquired by a confocal laser scanning microscope under excitation at 458 nm before (●) and after (▲) bleaching of YFP (by ∼60 scans with 514 nm laser radiation) under the same microscope. The solid and dashed lines, are spectra simulated by Equation 1, before and after photobleaching respectively. Simulated spectra (top panel) decomposed into cyan and yellow components by plotting the first and second term of Equation 1 individually (bottom panel). Solid lines, spectra before bleaching; dashed lines, spectra after bleaching. Note an increase in the spectral area for CFP following YFP bleaching, as a result of the FRET interaction in the system.

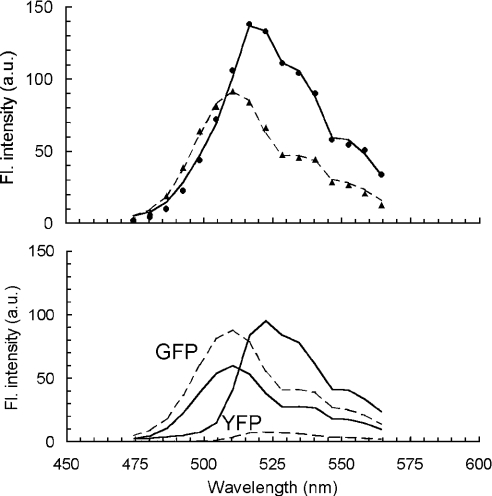
Figure 4. Spectral deconvolution of composite fluorescence spectra of cells expressing Ste2p–GFP and Ste2p–YFP.

The details are as in Figure 3 legend, but with GFP replacing CFP.

Table 2. Best-fit parameters obtained from simulations of the experimental spectra in Figures 3 and 4 with Equation 1.

Apparent FRET efficiency, E_app, was computed from Equation 3. β_D, taken from Table 1. See text for definition of all symbols.

Donor	YFP state	kDA	kpbD/βD	kA	Epbapp
CFP (Figure 3)	Intact	50.4	−	165.0	0.34
	Bleached	−	76.4	33.0*
GFP (Figure 4)	Intact	60.7	−	95.4	0.48
	Bleached	−	116.7	6.8*

* Note that complete bleaching was not achieved.

We applied the analytical method presented above to five digital images each containing several cells (typically three) expressing both Ste2p–CFP and Ste2p–YFP, and obtained an average E_app and a standard deviation for each digital image. The weighted average and the standard error (S.E.M.) were then obtained from these (E_app=0.23±0.02). Similarly, for six images of cells expressing Ste2p–GFP and Ste2p–YFP, E_app±S.E.M. was 0.38±0.03. It should be noted that standard errors associated with these averages are due mostly to the wide distribution of protein concentrations among individual cells. This is because, according to Equation 4, E_app represents the product between E and the fraction of donor-tagged Ste2 proteins in complexes (α_D). The latter depends on the relative amounts of D and A molecules, which vary from cell to cell due to variation in the number of plasmids encoding the fluorescently tagged proteins. (Details of the determination of α_D are addressed in the next sub-section.)

From our data above, the ratio E_app^GY/E_app^CY=φ for the two fluorescent protein pairs is found to be 1.62±0.18, which agrees with the value of approx. 1.6 that can be inferred from a recently published study involving GFP variants [16]. From this ratio, and by using Equation 10, one can determine the average true FRET efficiency, or the efficiency of energy transfer within protein complexes containing donor and acceptor fluorophores and excluding the signal from noninteracting proteins. It should be recalled that Equation 10 was derived on the assumption that the average α_D is the same for both D/A pairs, which would be true if the concentrations of fluorescently active GFP and CFP molecules inside the cells are nearly equal. This implies that the time necessary for maturation of a fluorescent protein is shorter than the time elapsed between the creation and destruction of a Ste2 molecule (or the protein turnover). In general, therefore, either Equation 10 should be corrected to accommodate possible differences in α_D of the two different donors, or the donors should be so chosen that their corresponding α_D are nearly equal. For the CFP and GFP variants used in our work, the latter situation applies. Indeed, by using Equation A(3) in Appendix A and the relevant parameters from Table 1, the ratio of the average concentrations of Ste2p–GFP and Ste2p–CFP inside cells expressing these donor molecules separately in the presence of acceptor molecules (Ste2p–YFP) is obtained (0.86±0.20); therefore, within the error margin, the concentrations of Ste2p–CFP and Ste2p–GFP are equal, and thus, Equation 10 is valid. From this equation, the values of E were calculated to be 36±10% for Ste2p–CFP/Ste2p–YFP and 59±12% for Ste2p–GFP/Ste2p–YFP. The errors represent systematic errors in the physical parameters in Equation 10 and statistical errors (i.e. those due to variation in protein expression) determined above, added in quadrature. The latter E value will be used below in estimating the fraction of interacting Ste2 proteins.

An additional benefit of combining the data from two D/A pairs to determine E would be the extraction of the absolute inter-chromophore separation r from Equation (8), without recourse to external calibration. Determination of r requires knowledge of R₀ and thereby of the orientation factor, κ², between donor and acceptor transition moments (see Appendix B). This problem has been investigated in details by a number of authors (see for example Dale et al. [40,41]), and reviewed by Clegg [34]. In essence, the range of κ² values either can be determined experimentally from measurements of fluorescence polarization, or estimated theoretically by making some reasonable assumptions about the rotational degree of freedom of the fluorescent tags. Precise determination of r could be done in future studies; we only remark here the theoretical possibility for determination of this parameter.

Estimation of the fraction of interacting proteins

Complete photobleaching of the acceptor was seldom possible in our experiments (see Figures 3 and 4 and Table 2). On average, residual YFP fluorescence was about 10%, even after the acceptor was exposed to 514 nm laser radiation for relatively long periods of time (several minutes, or more than 150 sample scans). This might be due to diffusion of the fluorescent protein-tagged Ste2p from the out-of-the-focal-plane regions of the cell that are less affected by bleaching, or to the recovery from the dark state of the fluorescence of a small fraction of photobleached YFP [7,21,42]. To test whether the above two effects (or others not considered here) could indeed be the cause for the incomplete acceptor photobleaching, and not just the continuous production and maturation of YFP tags, we conducted a simple experiment in which we monitored YFP fluorescence recovery after photobleaching with 30 scans of 514-nm intense laser light. The result was that, after photobleaching, the fluorescence decreased on average (n=8 cells) to 14±1% of the initial intensity and then increased with time to reach a plateau at 24±2% of the initial level in about 90 s. This plateau persisted over the whole duration of our experiment (t=210 s), suggesting that continuous production and maturation of YFP molecules could not be the main cause for incomplete bleaching, because, if it were, the fluorescence intensity would have continued to increase indefinitely with time. By contrast, the fact that we observed a plateau suggests the diffusion of the fluorophores into the focal plane from other parts of the cell as a most likely explanation; the recovery was not complete, though, because out-of-the-focal plane fluorophores were also bleached to an appreciable extent by the 514-nm light. In any case, our observed incomplete acceptor photobleaching constitutes, regardless of its exact cause, an additional source of error in determination of the fraction of interacting proteins from FRET studies relying on the complete bleaching method. (Here again, the reader should be reminded that this error does not affect our determination of E using Equation 10, as we discussed in the Theory of the Method section.)

Fortunately, Equation 5 suggests that partial, stepwise bleaching of the acceptor (equivalent to a stepwise decrease in β_A) offers an alternative to ‘complete’ bleaching. Equation 5 allows calculation of the fraction of D in D/A complexes independent of the degree of fluorescence recovery due to diffusion and other processes, because the actual concentrations of donors and acceptors at the time of measurements are probed through their fluorescent intensities. Conversely, Equation 5 can be tested using the gradual bleaching method.

Data acquisition using the gradual acceptor-bleaching method in cells that contain distinct α-factor receptor populations of Ste2p–GFP and Ste2p–YFP was done as described in the Experimental section. A bleaching coefficient, β_A [the ratio between the acceptor fluorescence intensities at 520–525 nm (the peak of the YFP emission spectrum) after and before bleaching, upon excitation at 514 nm], was calculated for each bleaching step. Then we determined, for each degree of acceptor bleaching, the GFP fluorescence, k_D, that contributes to the total spectra obtained by excitation at 458 nm (as explained in the Experimental section).

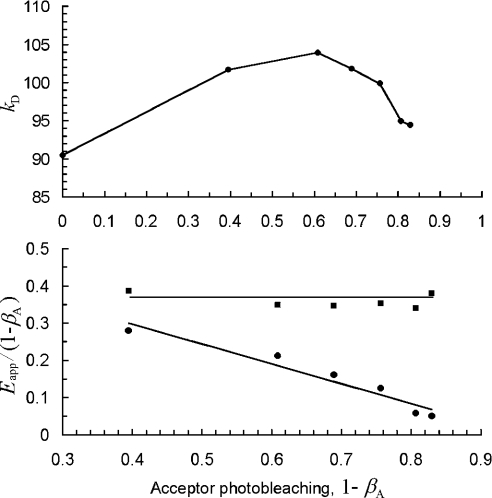
A typical plot of k_D as a function of the acceptor bleaching degree 1−β_A is presented in Figure 5 (top panel). The intensity of donor fluorescence increased significantly as acceptor photobleaching progressed, due to the decrease in donor energy loss through energy transfer, until a maximum value was reached at 1−β_A≈0.62. Beyond that point, no further significant bleaching of the acceptor was observed, and the concurrent donor bleaching became evident as a decrease in the donor fluorescence intensity. The marked difference between the bleaching sensitivities of acceptor (YFP) and donor (GFP) makes it possible to distinguish between the opposing effects of acceptor and donor bleaching on donor fluorescence intensity.

Figure 5. Correction for donor photobleaching effects when using the gradual photobleaching method.

Effect of acceptor photobleaching by 514-nm light on the donor fluorescence intensity (top panel), expressed as scaling factor of the GFP spectrum (i.e. k_D in Equation 1). The apparent FRET efficiency (bottom panel) uncorrected for donor photobleaching (●) appears to decrease with acceptor bleaching degree. The FRET efficiency corrected for donor bleaching (■) as described in the text does not change with the acceptor bleaching degree. Lines serve as guide to the eyes only.

From the data in Figure 5 (top panel), one can determine E_app for each 1−β_A value. We first approximate E_app according to Equation 2, with k_DA corresponding to k_D in Figure 5 (top panel) for 1−β_A=0 (i.e. no bleaching). Next, E_app values are divided by the corresponding degree of acceptor photobleaching 1−β_A, and the results are plotted again against 1−β_A, as in Figure 5 (bottom panel). According to Equation 5, the quantity E_app/(1−β_A) should yield a horizontal line, Eα_D, when plotted against 1−β_A, since E is constant and the fraction of donor molecules present in D/A pairs (α_D) does not vary with bleaching. However, our data [Figure 5, bottom panel (•)] show a negative slope, indicating the necessity for donor-photobleaching correction. This was performed [Figure 5, bottom panel (▪)] as described in Appendix C.

By repeating the analysis presented in this sub-section for digital images typically containing three cells that express Ste2p–GFP and Ste2p–YFP, we obtained an average and S.D. for Eα_D for each image. The weighted mean and S.E.M. for twelve images were then calculated to be Eα_D=0.37±0.02. This value is in agreement with that determined from (quasi)complete acceptor photobleaching (0.38±0.03, see above). From Eα_D=0.37±0.02 obtained through gradual bleaching, and using the above value for E of 0.59±0.12, α_D was estimated to be 0.63±0.13 (statistical and systematic errors are added in quadrature). It is worth noting that in order to prove the validity of the model and the effectiveness of the correction for donor photobleaching we performed several bleaching steps. However, two bleaching steps would be sufficient for extraction of the apparent efficiency; this shortens substantially the time necessary for performing photobleaching experiments to just a few seconds.

As discussed above, α_D defines the fraction of Ste2 proteins labelled with the donor fluorophore that are interacting with acceptor-labelled Ste2p. We also estimated the fraction of interacting acceptors, α_A, by determining E_app^se=Eα_A from sensitized emission for each cell in the twelve images used above for gradual photobleaching. Eα_A was calculated by using Equation 7 with k_AD (the YFP fluorescence in the presence of GFP) determined from decomposition of fluorescence spectra obtained by excitation at 458 nm (as explained in the Experimental section) and k_A⁵¹⁴, determined by detection at 520–525 nm of the fluorescence excited by the 514-nm laser line. The correction factors in Equation 7 are taken from Table 1 and [38], while η (=0.30) was determined by measuring, in separate experiments, the emission of Ste2–YFP upon excitation at 458 and 514 nm. From the Eα_A values obtained for each cell, mean and S.D. values were obtained for each digital image. The weighted mean and S.E.M. for twelve images were then calculated to be Eα_A=0.37±0.01, from which α_A was estimated as 0.63±0.13.

As mentioned in the last subsection of the Theory of the Method section, for a large number of cells the average concentrations of acceptors, [A]_T, and donors, [D]_T, in the cells are equal, and so are the average P_Ab and P_Db. For such a case, Equation 13 predicts that α_D/α_A equals unity, which is consistent with the value of 1.00±0.19 that is obtained from our data above (errors added in quadrature).

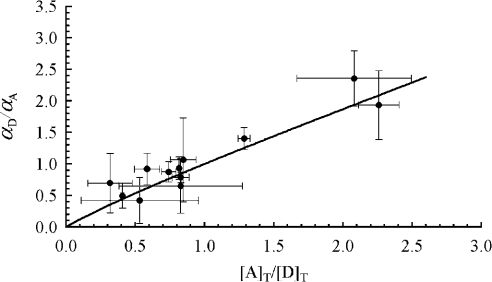
For proteins that would form only hetero-oligomers, α_D completely characterizes the binding stoichiometry of D and α_A completely characterizes the binding of A. However, in this paper, by choosing a protein (Ste2p) that forms homo-oligomers, we took the study to a higher level of complexity, for which the interacting proteins can form DD (i.e. Ste2p–GFP/Ste2p–GFP) and AA (i.e. Ste2p–YFP/Ste2p–YFP) complexes, in addition to AD or DA (i.e. Ste2p–GFP/Ste2p–YFP) that are the only complexes detectable by FRET. For this case, a more meaningful parameter is the fraction of Ste2 proteins present in all types of complexes, α_T={[A]_b+[D]_b}/{[A]_T +[D]_T}. To determine α_T, we first need to determine the average number of monomers in a complex, n. This can be done by plotting α_D/α_A for each digital image against [A]_T/[D]_T and finding the n value that best fits Equation 16 to the data. It is important to note that in our present work, as well as in most FRET experiments conducted in vivo, one has limited control on the [A]_T/[D]_T values. This is because of the poor control one can exert on the number of plasmids inserted into the cell and on their level of expression in individual cells, and also because of the inhomogeneous distribution within the cell of the gene products (i.e. the proteins), even if the level of expression could be controlled. Therefore, instead of attempting to vary controllably the molar fraction of A and D, we simply performed a relatively large number of measurements (over 39 cells, grouped in 12 sets), and calculated [A]_T/[D]_T for each cell by using Equation A(4) in Appendix A with the correction factors taken from [38] and Table 1, and η=0.30 as above. Means±S.D. of α_D/α_A for each image (or set of cells) were plotted against their corresponding mean±S.D. of [A]_T/[D]_T and n (=2.27±0.43) was determined by fitting Equation 16 to the plot (see Figure 6). Using the determined n value, we were then able to evaluate α_T by using Equation 15. The result was that (0.63+0.63)/(2−2^2−2.27)=1.08 or about 100% of the Ste2p were in dimeric complexes, on average.

Figure 6. Determination of the number of oligomers in a complex.

Means (●) and S.D. (bars) of α_D/α_A for each image (containing typically three cells) were plotted against their corresponding means±S.D. of [A]_T/[D]_T (see text for details). The solid line is obtained from simulations with Equation 16 and the n value (2.27±0.43) that minimizes the χ² of the fit divided by the number of degrees of freedom (0.5).

DISCUSSION

We have demonstrated that a spectral-decomposition method can be used conveniently, even in the presence of high overlap between acceptor and donor spectra, as in the case of GFP/YFP fluorescent proteins. Used in conjunction with two different pairs of donors and acceptors, and a gradual bleaching method, our method permits a detailed verification of our theory for FRET-based stoichiometry. This method offers the possibility for full quantification of protein–protein interactions in living cells, including the true FRET efficiency, the fraction of proteins in complexes and the distance separating them. Depending on the distribution of the target protein within the cell, the method can be applied to the study of an entire cell or only of certain regions of interest within the cell, such as cell organelles, or on the cell membrane. In order to facilitate application of our method in laboratories with access to a laser scanning confocal microscope, we append a summary of the method as Appendix D.

Our main result was to show quantitatively that a majority of Ste2p in living cells forms dimeric complexes in the absence of Ste2p ligand, or the α-factor. Interactions were detected on the cell membrane and in internal membranes, where we also saw fluorescence (see Figure 1). Our demonstration of oligomer formation is also consistent with a report demonstrating the co-immunoprecipitation of differentially tagged Ste2p [43]. In addition, oligomer formation of Ste2p was demonstrated in cultures [18,19] as well as in fractionated membranes from the cell surface and endoplasmic reticulum [44].

It is important to note that the analysis presented in this paper remains valid no matter which factor is responsible for the complex formation – the Ste2p/Ste2p interaction or the weak tendency of some GFP variants to dimerize [45]. However, several published results suggest that the interaction between Ste2p–CFP and Ste2p–YFP, which can be detected by FRET, is mediated by domains of Ste2p and not by the physical interaction of CFP and YFP. FRET between Ste2p–CFP and Ste2p–YFP can be reduced below the level of detection by over-expressing a wild-type untagged Ste2p protein [18]. A similar experiment was reported to reduce FRET by more than 60% [44]. The co-expression of transmembrane domains 2 through 7 of Ste2p (that is, lacking the N-terminal extracellular domain and transmembrane domain 1) fused separately to CFP and YFP results in an 80% decrease in FRET [44]. Co-expression of YFP-tagged transmembrane domains 6 and 7 with CFP-tagged wild-type receptor resulted in less than 15% of the FRET detected between wild-type forms [44]. Finally, specific single amino-acid substitutions in the first transmembrane domain of Ste2p resulted in a greater than 70% reduction in FRET [46]. These findings support strongly the argument that oligomerization is mediated through contact between domains of Ste2p, in particular, transmembrane domain 1, rather than through the interaction of CFP and YFP, which replace the C-terminal cytoplasmic domain of Ste2p.

The α-factor receptor protein of S. cerevisiae belongs to a family of membrane proteins called GPCRs [28]. Recent studies have shown that members of this family are capable of forming homodimers and/or heterodimers (reviewed in [26] and [27]). Although Ste2p oligomerization does not increase in response to binding of its ligand [18] some GPCRs do show an increase in FRET upon agonist stimulation [47]. In this study, we have used haploid yeast cells that are of mating type a (KBY58 [29]). Although haploid yeast in the wild are capable of switching from type a to α, laboratory strains carry a mutation (ho) which prevents a strains from being mixed with α strains [48]. As a result, our strains are free of the Ste2p ligand, α-factor, which is produced only by α cells [17]. Our results indicate that ∼100% of the Ste2p molecules are in dimeric complexes in the absence of this ligand. This is true also of receptors in internal membranes, confirming the demonstration of FRET between Ste2p subunits in endoplasmic reticulum that was purified from yeast cells [44]. We conclude that in the case of Ste2p, dimerization in itself is not promoted by the ligand in signal propagation. Nevertheless, dimerization is important for signal propagation since amino acid substitutions of Ste2p that impair complex formation, without affecting binding of the ligand, cause defects in signalling [46].

APPENDIX A

Fluorescence intensity and determination of fluorescent protein concentration ratios

For low concentrations of the fluorescent molecules, the total fluorescence intensity (or the spectral integral – see main text for details) upon excitation at λ can be related to spectral and to instrumental parameters by the following formula (adapted from [49]):

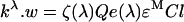(A1)

where k^λ is a scaling factor defined in the main text, and w is the integral of elementary fluorescence spectrum over all emission wavelengths, ζ(λ) is an instrumental factor that incorporates the intensity of the excitation light, transmission efficiency of the excitation light, fluorescence collection efficiency, photodetector sensitivity, etc., Q is the fluorescent molecule quantum yield, e(λ) is its optical absorption relative to the maximum value, ε^M is the extinction coefficient determined at the wavelength corresponding to the excitation maximum, C is the fluorophore concentration, and l is the sample optical path. If k is known for an excitation wavelength λ₁, equation A1 can be used to determine the fluorescence intensity upon excitation at λ₂,

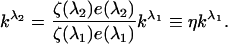(A2)

In our experiments, λ₁=514 nm, and λ₂=458 nm, and η=0.30 was determined experimentally by measuring the emission of Ste2-YFP upon excitation at 458 and 514 nm.

We also used equation A1 to determine the ratio of average concentration of Ste2p–CFP in cells expressing Ste2p–CFP and Ste2p–YFP to the average concentration of Ste2p–GFP in cells expressing Ste2p–GFP and Ste2p–YFP (see Experimental),

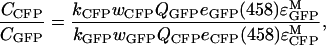(A3)

and the ratio of the concentration of Ste2p–YFP to the average concentration of Ste2p–GFP in cells expressing Ste2p–GFP and Ste2p–YFP,

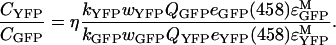(A4)

The unknown parameters in Equation A3 and Equation A4 were experimentally determined either by us or by other authors (as cited in Table 1).

APPENDIX B

Definition of the Förster radius

An important parameter characterizing the energy transfer in a donor/acceptor pair is the Förster radius R₀, which represents the distance between the two chromophores at which FRET efficiency E decays to half of its maximum value. This is defined by a well-known equation [1],

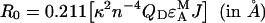(B1)

where κ² is the dipole orientation factor, n is the index of refraction of the external medium (=1.4), Q_D is the quantum yield of the donor molecule (CFP or GFP), and ε_A^M is the acceptor maximum extinction coefficient (i.e. determined at the wavelength corresponding to the excitation maximum). κ² was evaluated as described below, while the last two parameters are taken from Table 1. J is the overlap integral given by:

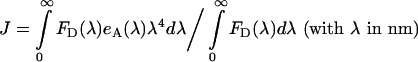(B2)

where e_A (λ) is the acceptor (YFP) normalized excitation spectrum. Excitation spectrum of YFP and emission spectra of CFP and GFP were as published in the literature [38]. We used literature emission spectra for CFP and GFP instead of our own spectra plotted in Figure 2, because of the higher resolution of the spectra acquired by a spectrofluorometer over those obtained with the confocal microscope. The pH values at which these spectra were acquired are similar to the internal pH of the yeast cells used in our experiments, which was controlled as explained in Experimental and according to the literature on yeast [30,31]. Due to our method that employs two fluorophore pairs, Förster radii are not required for our data analysis, only the quantum yields of the donor fluorophores and the overlap integrals, J. However, as a check of the correctness of our evaluation of J (see Table 1), we determined also R₀ (by using the same κ²=2/3 as Patterson et al. [51] and the spectral parameters from Table 1), which were 47 Å for Ste2p–CFP/Ste2p–YFP pair and 55 Å for Ste2p–GFP/Ste2p–YFP. These values agree with published values [51,52].

APPENDIX C

Characterization of donor photobleaching

β_D is not available experimentally for cells that simultaneously express D and A. Therefore, we conducted additional experiments on cells that separately express Ste2p–GFP and Ste2p–YFP to obtain information about the bleaching dynamics of the donor and the acceptor respectively. In these experiments, cells were bleached using 514-nm laser light by following the same protocol used for gradual bleaching of cells that contain both fluorescent proteins. We observed an exponential decay in the fluorescence intensity of YFP (results not shown), for which the 514-nm radiation was highly effective in bleaching (Figure 2).

In contrast to YFP, the fluorescence intensity of GFP decreased linearly with the number of bleaching scans (results not shown), with slopes p ranging from −1.5 scan⁻¹ to −0.1 scan⁻¹. This is because the exposure time used in this work is short compared with that necessary for an efficient bleaching of GFP. Based on this observation of a linear decrease of donor fluorescence intensity as a function of the number of bleaching scans, N_scans, an expression can be obtained for the donor bleaching coefficient:

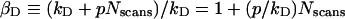(C1)

This expression was used for calculating E_app corrected for donor bleaching (i.e. by using Equation 3). To this end, we set k_D to a value that was slightly higher than the maximum k_D measured [∼105 for the data in Figure 5 (top panel)], and adjusted p until E_app/(1−β_A) traced a horizontal line against 1−β_A [p=−1 for the data in Figure 5 (bottom panel)], as it should (see above). In mathematical terms, this procedure amounted to minimizing the standard deviation [S.D.=0.02 for Figure 5 (bottom panel)] of all E_app/(1−β_A) values from the mean (0.36 for corrected donor bleaching). According to Equation 5, this value (0.36±0.02 for data in Figure 5) represents the Eα_D corrected for donor-bleaching effects. Knowledge of the exact value of k_D is unnecessary for the precise determination of Eα_D, because it is only the ratio p/k_D that enters the Eα_D computation. An implicit advantage of this fitting-based method of correction for donor photobleaching is the fact that it allows for the possibility that donors not involved in FRET show higher photobleaching sensitivity from those involved in FRET (which spend less time in the excited state).

APPENDIX D

Summary of the method for determination of the true FRET efficiency

(1) Generate strains expressing each candidate interacting protein as fusions to GFP(S65T), CFP, and YFP. Ideally, a gene expressing a fluorescently tagged protein will replace the wild-type gene at the chromosomal locus. Strains that do not express non-fluorescent forms of either protein are a minimum requirement.

(2) Excite cells with a 458-nm laser and measure the fluorescence intensity of whole cells or regions of interest. Fluorescent signals must be obtained from a number of discrete windows spanning the entire emission spectrum of the fluorophore. We have used 16 windows, each 5 nm wide and separated by a 1 nm gap. For example, in the case of collecting spectra for proteins tagged with CFP, the first three windows of emission collection were: 460 nm to 465 nm, 466 nm to 471 nm and 472 nm to 477 nm.

(3) Plot intensity, normalized to the peak value of fluorescence, as a function of the median wavelength of each emission window. Adjust laser power, photomultiplier tube voltages and mirrors in order to generate curves, which match the shape of the emission spectra of GFP, CFP and YFP (see Figure 2). Avoid collecting images with intensities exceeding linear limits of the detection device as this will lead to a spectrum with a flat peak.

(4) Use a 514-nm laser to excite cells expressing proteins fused to YFP. Measure the fluorescence intensity at the peak of the emission spectra (520 nm to 525 nm).

(5) Construct strains matching all combinations of donor and acceptor proteins, i.e. for each interaction, make strains expressing CFP/YFP and GFP/YFP fusion protein pairs.

(6) Use the 458-nm laser to excite cells containing donor and acceptor proteins, generating images as described in step 2 for subsequent quantitation of intensities.

(7) Excite the same cells using a 514-nm laser as described in step 4, generating an image for measuring the intensity of YFP fluorescence. Bleach the cells so that the YFP fluorescence (upon excitation at 514 nm) decreases detectably.

(8) Repeat steps 6 and 7 and again step 6.

(9) Deconvolute the spectra to generate k_DA (donor fluorescence before acceptor bleaching), and k_D1 and k_D2 (donor fluorescence after bleaching intervals 1 and 2). The authors will send a computer file (in MS Excel™) upon request to facilitate spectral deconvolution and the calculation of E_app from the data collected in the preceding steps.

(10) Determine φ, the ratio of the values of E_app from GFP/YFP and CFP/YFP labelled protein partners. Use Equation 9, φ and the values for R₀ from Appendix B to calculate E.

The fraction of interacting proteins in hetero-oligomeric complexes

(11) Use gradual acceptor bleaching method to determine E_app for cells containing GFP- and YFP-tagged proteins; calculate the fraction of donor-labelled proteins participating in an interaction, α_D=E_app/E, by using E value determined at step 10. In the case of a hetero-oligomeric complex, α_D defines the amount of proteins labelled with D that forms complexes. The fraction of the second protein participating in the complex may be found by switching the fluorophores, thereby making the second protein the donor, or by continuing with step 12 below.

The fraction of interacting proteins in homo-oligomeric complexes

For homo-oligomeric systems, the fraction of interacting proteins is defined by α_T and can be estimated if the fraction of interacting donors, α_D, and acceptors, α_A, as well as the number of monomers in an oligomer are known. Estimation of these parameters is done as in the following steps.

(12) Estimate α_A by using Equation 7 with k_AD (the YFP fluorescence in the presence of GFP) determined from decomposition of fluorescence spectra obtained by excitation at 458 nm and k_A⁵¹⁴ determined by detection at 520–525 nm of the fluorescence excited by the 514-nm laser line. The correction factors in Equation 7 are taken from [38] and Table 1, while η is determined by measuring, in separate experiments, the emission of Ste2–YFP upon excitation at 458 and 514 nm.

(13) Calculate α_D/α_A.

(14) Estimate [A]_T/[D]_T by using Equation A4 in Appendix A and the correction factors determined as in step 12.

(15) Plot the α_D/α_A data obtained from step 13 versus [A]_T/[D]_T obtained at step 14, and fit Equation 16 to the plot to obtain n, the number of monomers in an oligomer.

(16) Use Equation 15 and n from step 15 to determine the fraction of proteins present in complexes α_T.