Quantification of the time-varying epidemic growth rate and of the delays between symptom onset and presenting to healthcare for the mpox epidemic in the UK in 2022

Abstract

The mpox epidemic in the UK began in May 2022, with rates of new cases unexpectedly and rapidly declining during August 2022. Interpreting trends in infection requires disentangling the underlying growth rate of cases from the delay from symptom onset to presenting to healthcare. We developed a nowcasting Bayesian method which incorporates time-varying delays (EpiLine) to quantify the changes in the delay from symptom onset to healthcare presentation and the underlying mpox growth rate over the period May-August 2022 in the UK. We show that the mean delay between symptom onset and healthcare presentation for mpox in the UK decreased from 22 days in early May 2022 to 10 days by early June and 8 days in August 2022. When we account for these dynamic delays, the time-varying growth rate declined gradually and continuously in the UK during the May-August 2022 period. Not accounting for varying time delays would have incorrectly characterised the growth rate by a sharp increase followed by a rapid decline in mpox cases. Our results highlight the importance of correctly quantifying the delay between symptom onset to healthcare presentation when characterising the epidemic growth of mpox in the UK. The gradual reduction in the rate of epidemic spread, which pre-dated the vaccine roll-out, is consistent with gradual risk reduction or acquired immunity amongst the highest risk individuals. Our study highlights the need for public health agencies to record the delays from symptom onset to healthcare presentation early in an outbreak.

Introduction

Mpox (monkeypox) is a zoonotic infection caused by a virus that belongs to the family of Orthopoxvirus. Since the first human reported case of mpox in the Democratic Republic of Congo in 1970, sporadic human cases have been identified both inside and outside of Africa¹. On May 7, 2022, mpox was detected in a traveller returning to the United Kingdom from Nigeria, with the rate of reported cases in the UK then increasing until mid-July before declining (Fig. 1a)².

Figure 1.

Estimated reporting delay and epidemic growth rate $r\left(t\right)$ using UKHSA data. (a) Number of daily reported cases and daily symptoms onset (only reported by 40–80% cases) along with the fitted posterior density of the symptoms onset (for all reported cases). For the vast majority of reported cases in May the symptoms onset date is known, thus the posterior distribution and the reported data fit well to mid-May. For cases reported from June onwards, the proportion for which the date of symptoms onset was known declined, thus the reported symptoms onset is less than the posterior distribution. (b) Distribution of the reported delays (the time between onset of symptoms and reporting to healthcare providers) for those developing symptoms at the start of May and June 2022. (c) Epidemic growth rate $r\left(t\right)$ of mpox in the UK when accounting for dynamic reporting delays, showing a gradual decline over the reporting period. The right-axis converts $r\left(t\right)$ to a doubling or halving time. (d) Estimates (median and 25,75 percentiles) of the reported delay indexed by the date of symptoms onset. In all graphs the solid lines are the median estimates and the shaded area being the 5%-95% confidence interval.

Mpox virus is an infectious pathogen which can be transmitted through close physical contact and fomites. Since the onset of the mpox epidemic in the UK in early May 2022, and over the epidemic period May–September 2022, the UK Health Security Agency (UKHSA) has been monitoring and responding to the outbreak in the UK⁸. As part of the response, our group had access to mpox data and tracked the epidemic potential giving informed advice to aid public health policy.

During the 2022 outbreak, mpox cases were predominantly amongst gay and bisexual men who have sex with men (GBMSM) with clusters of cases linked with venues where individuals were exposed to the virus through close, often sexual, contact³. Pre-symptomatic transmission was found to be a significant component of this outbreak, with approximately 53% of transmission prior to symptom onset⁴. Initial symptoms for mpox can be influenza-like (e.g. fever or sore throat) with reported incubation periods of 3–20 days⁵ and mean incubation period of 7–9 days^5,6. This is followed by smallpox-like rashes, which sequentially progress to macules, papules and vesicles before crusting over after 2–4 weeks ⁷. Within the UK mpox epidemic, healthcare professionals obtained details of symptoms and their time of onset for a fraction of the confirmed cases. There was a variation in the uncertainty around the date-dependant confirmed cases from 77/97 confirmed cases (~ 80%) in the first two weeks of the outbreak in May 2022 to 163/495 confirmed cases (~ 40%) during August 2022⁸. Initially, the delay between the onset of symptoms and presenting to healthcare providers was up to a month (based on data within UKHSA mpox response group). As the awareness of the disease increases, due to public health information or other interventions, the delays in presenting to healthcare providers may decrease with people reporting infection earlier.

When models are fit to epidemics, one would ideally have data on the number of people infected each day. However, the data typically available is the number of symptomatic cases who present to healthcare providers each day (i.e. reported cases). Therefore, models are normally fit to the reported cases, with the delay between infection and reporting being modelled as a static distribution. This delay distribution consists of the incubation period (infection to symptoms) and the delay from symptom onset to accessing healthcare, and is typically estimated from detailed studies on a subset of early cases in the epidemic. Whilst the incubation period is not expected to change over time, the delay between symptom onset and accessing healthcare is likely to decrease as public awareness of the epidemic increases. If this delay from symptom onset to healthcare presentation decreases rapidly, it would lead to a surge in reported cases due to the effect of people at different stages of disease presenting to healthcare providers at the same time. Hence it is important to quantify how the time between symptom onset and healthcare presentation changes in the course of an epidemic.

The general approach in modelling mpox 2022 epidemic was either using Bayesian models such as²⁰ or a more mechanistic SEIR model¹¹ that allow for processes such as vaccination to be more readily modelled. The former model used Bayesian doubly interval censored model adjusted for right truncation to calculate the time from infection to hospital admission, infection to a first positive test, and the length of hospital stay whilst keeping the distribution of infection to symptom onset uniform. The latter model had constant time from symptom onset to presenting to healthcare and focused on evaluating the impact of vaccination on the trajectory of the mpox epidemic.

The two aims of our study were to quantify time-varying delays between symptom onset and healthcare presentation, and also the time-varying epidemic growth rate of the mpox epidemic in the UK in 2022. This is non-trivial since both together contribute to observed data, and so require statistical deconvolution (disentangling). The two datasets we used were the total number of reported cases, and the self-reported symptoms onset time which was provided by a subset of cases. At the time of analysis, we did not find required statistical tools within existing ‘nowcasting’ software, and so to perform this analysis, we developed a Bayesian model (“EpiLine”) which simultaneously estimated the time-varying delay between symptom onset and healthcare presentation and the epidemic growth rate over the period May–August 2022 in the UK.

Methods

In this study, we illustrate the development and application of a custom nowcasting Bayesian method which incorporates time-varying delays (EpiLine) to simulate the growth rate of symptomatic cases, from both actual mpox data in the UK as well as simulated data, aiming to quantify the time between mpox symptom onset to healthcare presentation and the growth rate over the mpox epidemic in the UK in 2022.

EpiLine model

To jointly quantify the changes in delays in the distribution of time $\tau$ from symptom onset to healthcare presentation at time $t$, denoted $f\left(\tau ,t-\tau \right)$ and its effect on estimating the epidemic growth rate, denoted $r\left(t\right)$. We developed a Bayesian model incorporating both a dynamic growth rate and dynamic delays called EpiLine (https://github.com/BDI-pathogens/EpiLine). The model was implemented in R software (https://www.r-project.org), version 4.1.3.

The model was built to understand the interaction between the symptom-healthcare presentation time distribution and the underlying dynamics of the infection rate, therefore we use a very simple model for the number of people developing the symptoms each day. The model contains a generative model which calculates the expected number of reported cases on a particular day, and an observation model for the observed data (same approach as Epidemia uses for estimating daily deaths¹⁹). We model the daily growth rate $r\left(t\right)$ with a simple Gaussian process, the daily number of people of developing symptoms $S\left(t\right)$ is given by

$$r\left(t\right)\sim N\left(r,\left(t,-,1\right),,,{\sigma }_{r_{\mathit{GP}}}^2\right)$$

$$S\left(t\right)=S\left(t,-,1\right)e^{r(t)}$$

where ${\sigma }_{\mathit{rGP}}^2$ is the daily variance of the Gaussian process. Gaussian processes were used because of their flexibility to model time varying processes and provide confidence intervals even when the underlying mechanisms for time variation are unknown. Note that by making $r\left(t\right)$ a Gaussian process instead of $S\left(t\right)$ implies the prior is that the change in $S\left(t\right)$ is the same as the previous day. Next we define $f\left(\tau ,t\right)$ as the probability of someone presenting to healthcare with an infection on day $(t+\tau$), if they developed symptoms on day $t$. Note that $\tau$ can be negative if a case is found prior to symptoms developing (e.g. if contact-traced and tested positive). On day $t$ the expected number of cases presenting to healthcare is $\mu \left(t\right)$ and given by

$$\mu \left(t\right)=\sum _{\tau =-{\tau }_{\mathit{post}}}^{{\tau }_{\mathit{pre}}}f\left(\tau ,,,t,-,\tau \right)S(t-\tau )$$

where ${\tau }_{\mathit{pre}}$ is the maximum number of days pre-reporting the case develops symptoms and ${\tau }_{\mathit{post}}$ the maximum number of days post-reporting the case develops symptoms. The number of observed cases presenting to healthcare $C\left(t\right)$ is modelled as a negative binomial variable

$$C\left(t\right)\sim NB\left(\mu ,\left(t\right),,,{\varphi }_{\mathit{OD}}\right),$$

where ${\varphi }_{\mathit{OD}}$ is the over-dispersion parameter. The symptom-healthcare presentation time distribution must support both positive and negative values. In addition, empirically it is observed that this distribution can be highly skewed with heavy tails, therefore we model it using the Johnson SU distribution which contains four parameters $(\xi ,\lambda ,\gamma ,\delta$, so can fit mean, variance, skew and kurtosis). To account for the changes in the distribution over time, we model these four parameters using simple Gaussian processes

$$\xi \left(t\right)\sim N(\xi \left(t,-,1\right),{\sigma }_{{\xi }_{\mathit{GP}}}^2),$$

$$\lambda \left(t\right)\sim N(\lambda \left(t,-,1\right),{\sigma }_{{\lambda }_{\mathit{GP}}}^2),$$

$$\gamma \left(t\right)\sim N\left(\gamma ,\left(t,-,1\right),,,{\sigma }_{{\gamma }_{\mathit{GP}}}^2\right),$$

$$\delta \left(t\right)\sim N\left(\delta ,\left(t,-,1\right),,,{\sigma }_{{\delta }_{\mathit{GP}}}^2\right).$$

At the end of the reporting period, there may not be many cases presenting to healthcare for each symptoms date (since the data is right censored), therefore there is the option to make the distribution static after a particular time $t_{\mathit{static}}$ (i.e. when then $t>t_{\mathit{static}}$ $\xi \left(t\right)=\xi \left(t_{\mathit{static}}\right)).$ These parameters are estimated using line list data of individual cases where the symptoms date and healthcare presentation date are known. Note, cases where only the healthcare presentation date is known are included in the daily report totals $C\left(t\right)$, but not in the symptom-healthcare presentation line list. The incompleteness of case data including the symptom date as well as the healthcare presentation date is the reason why cases based on symptoms date cannot be modelled directly.

From the line-list, let $N_S\left(t\right)$ be the number of people who reported symptoms onset as of day $t$, and let $n_{\mathit{SR}}\left(t,\tau \right)$ be the number of people who reported symptoms onset as of day $t$ and presented to healthcare authorities on day $t+\tau$. For day $t$, we model $\left\{n_{\mathit{SR}}\left(t,-{\tau }_{\mathit{post}}\right),\dots ,n_{\mathit{SR}}\left(t,{\tau }_{\mathit{pre}}\right)\right\}$ using a multinomial distribution with parameters $\left\{x\left(t,-{\tau }_{\mathit{post}}\right),\dots ,x\left(t,{\tau }_{\mathit{pre}}\right)\right\}$. The multinomial parameters are set as the expected number given the total number of cases which reported symptoms onset on that date and the symptoms-healthcare presentation delay distribution for that day.

$$x\left(t,,,\tau \right)=\frac{N_S\left(t\right)\tilde{f}(t,\tau )}{F(t,\tau )},$$

$$F\left(t,,,\tau \right)=\sum _{\tau =-{\tau }_{\mathit{post}}}^{{\tau }_{\mathit{pre}}}\tilde{f}\left(\tau ,,,t,-,\tau \right),$$

$$\tilde{f}\left(t,,,\tau \right)=\left\{\begin{array}{c}f\left(t,,,\tau \right),ift+\tau inreportingperiod\\ 0,otherwise\end{array}\right)$$

where the factor $F\left(t,\tau \right)$ is adjusting for the fact that the line-list is date-censored given that it only includes dates from the reporting period. The distributions for $\left\{n_{\mathit{SR}}\left(t,-{\tau }_{\mathit{post}}\right),...,n_{\mathit{SR}}\left(t,{\tau }_{\mathit{pre}}\right)\right\}$ on different days are assumed to be independent and also independent of the total number of cases observed on each day.

To initiate the model, range prior distributions are put on the initial values of all the parameters as well as the variances of the Gaussian processes. The posterior distribution of all parameters were sampled by Markov Chain Monte Carlo (MCMC) using the software Stan in the R package rstan¹⁰. This allowed for the model to be simultaneously fit to both the daily cases presenting to healthcare and the line-list of cases for which the onset of symptoms was known, thus providing an estimate of $r\left(t\right)$ corrected for changes in the symptom-healthcare presentation delays.

Epidemiological data

Mpox data was collected by the UK Health Security Agency (UKHSA) health protection teams from targeted testing of infected individuals (with specimens processed by UKHSA affiliated laboratories and NHS laboratories), and questionnaires (collected by UKHSA health protection teams). The definition of a case included both confirmed cases and highly probable individuals with a positive polymerase chain reaction (PCR) test. All mpox cases were combined in a linelist which was used for analysis. Data were extracted as of August 31, 2022, at which time 2746 people had been identified with mpox in the UK. We identified the dates of symptom onset and the date of being reported to HPZone (where UKHSA teams store the data collected during an incident) by matching pseudo identifier numbers to the line list. We used the time when the case was reported to HPZone to be a proxy for the time when the case was presented to healthcare providers.

Data analysis with EpiLine

We applied EpiLine to the data from May 07, 2022 to August 31, 2022 sampling the posterior distribution of the model parameters i.e. both the growth rate and the distribution from symptom onset to healthcare presentation. To explore the importance of allowing a dynamic distribution from symptom onset to healthcare presentation, we alternatively used a static distribution with the parameters from the dynamic fit on May 07, 2022. This date was chosen as an estimate of the distribution in the early phase of the epidemic. This static distribution had a mean of 15 days, which was then used to re-estimate the growth rate over the whole period. Finally, we investigated the effect of date-censoring on the growth rate projections by re-sampling the model parameters using different date cut-off times.

Application of EpiLine on simulated data

To check the robustness of EpiLine, we applied the model to simulated data. A simulated line-list was generated by drawing the delay for each symptomatic individual from the symptom-presentation distribution for that day and then down-sampling (by 20%) to mimic the incompleteness of this data in the real data sets. Additionally, to mimic the real data, we seeded the epidemic at the start of April 2022 and allowed it to grow with a constant growth rate until the end of May 2022 (Figure S1a). From the start of June 2022 the growth rate declined linearly, turning negative in mid-July 2022 (Figure S1c, red line). The distribution from symptom onset to healthcare presentation was modelled to be similar to that estimated from the actual data. Similar to the analysis on the real data, we re-estimated $r\left(t\right)$ using the same static distribution from symptom onset to healthcare presentation. Finally, we repeated the date-censoring analysis.

Results

The time from symptom onset to healthcare presentation with mpox substantially declined over the epidemic

Applying EpiLine to the mpox data, we estimated that the time from symptom onset to healthcare presentation declined from about 21.9 days (CrI 16.7–30.8 days) for people who developed symptoms in early May 2022, to around 9.6 days (CrI 8.6–10.8 days) for people who developed symptoms in early June and 7.8 days (CrI 7.0–8.9 days) for people who developed symptoms in August 2022 (Fig. 1b,d). Hence the time from symptom onset to healthcare presentation declined substantially over the course of the UK epidemic.

Growth rates declined slowly with dynamic time from symptom onset to healthcare presentation

Allowing for a dynamic time from symptom onset to healthcare presentation, we estimated the epidemic growth rate had a doubling time of 10.3 days (CrI 6.6–23.9 days) in early May 2022. Subsequently the estimated growth rate gradually decreased in May and June turning negative in early July (Fig. 1c and Fig. 2a, blue curve). We note that a positive growth rate $r\left(t\right)$ corresponds to an effective reproduction number $R_e\left(t\right)$ greater than 1, and a negative $r\left(t\right)$ corresponds to a $R_e\left(t\right)$ less than 1. Note that since $r\left(t\right)$ is the growth rate of new symptomatic cases, it will lag the growth rate of new infections by the incubation period (7–9 days^5,6); suggesting that the new infections would have started to decline in late June 2022.

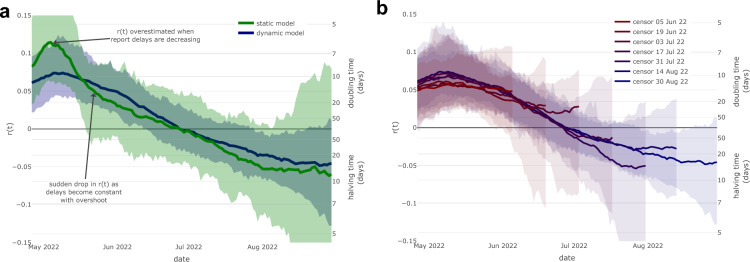
Figure 2.

Epidemic growth rate $r\left(t\right)$ using static reporting delays and censored data. (a) Epidemic growth rate $r\left(t\right)$ estimated using a static symptom-report delay as of May 7th 2022 (green) and using dynamic delays (blue). Note the static delay model estimates a higher peak $r\left(t\right)$ (doubling time of 6 days vs 10 days) and a larger decline of $r\left(t\right)$ in May 2022 (to a doubling time of 22 days vs 14 days), compared to the model adjusting for dynamic delays. (b) Estimated epidemic growth rate $r\left(t\right)$ using date-censored mpox line-list data. In both graphs the solid lines are the median estimates with the shaded area being the 5–95% confidence interval.

Using a misspecified model with a static distribution of delay from onset to report would have misled observers to infer that growth rates had increased and declined sharply over the epidemic period

A naive approach might have used a static distribution from symptoms onset to healthcare presentation for the sake of making inference simpler. To compare this approach to the dynamic distribution, we estimated that this incorrect approach would have led to the inference that the growth rate had a doubling time of 6 days in the first two weeks of May 2022 compared with 10 days with dynamic delays (Fig. 2a; green curve). Subsequently, the estimated growth rate declined more rapidly throughout May 2022, leading to a slowing of the doubling time to 22 days at the end of May compared to the estimate of 14 days with dynamic delays.

As noted previously, this is likely due to the effect of more people presenting to healthcare providers in late May even if they had first developed symptoms much earlier. As measured by a change in $r\left(t\right)$, the decrease throughout May 2022 was 0.073 (CrI 0.002–0.186) with static delays versus 0.015 (CrI − 0.048 vs 0.076) with dynamic delays. While the difference is not statistically significant, this is primarily due to the poor precision of the static model during May resulting in wide confidence intervals in the drop of $r\left(t\right)$ in the static model. This poor fit of this model to the data reflects the deficiency of a static model during a time in which the delays are dynamic.

The results are robust to date-censoring

Our final analysis showed that the estimates of $r\left(t\right)$ were consistent at times at least 10 days prior to each censor date, however, flattened in the 10 days immediately prior to the censor date. This is because newly symptomatic cases in the final 10 days are unlikely to have presented to healthcare by the censor date, therefore the estimate of $r\left(t\right)$ here will be dominated by its prior (i.e. Gaussian process without drift). Flattening the estimates of $r\left(t\right)$ is desirable when interpreting right censored data and corresponds to projecting the impact of no change in policy.

Testing the reliability of the method with simulated data

Because the inferential method for joint estimation of $f\left(\tau ,t\right)$ and $r\left(t\right)$ is deceptively complex, requiring assumptions on the Gaussian process that maintain identifiability during the deconvolution process, we verified the power and accuracy of the method on simulated epidemic curves. With simulated data for a similar epidemic, the inference method (Epiline) was able to capture the dynamic time-varying delays and slowly declining epidemic growth rate (Figure S1). In contrast, when re-estimating the growth rate using the misspecified model with the static symptom-presentation distribution, we found, similar to the actual data (Fig. 2a), the incorrect inference of first over estimating the growth rate increase and then estimating a rapid decline (Figure S2a). Finally, the re-estimated value of $r\left(t\right)$ from simulated data was consistent up to about 10 days before the censor date, with $r\left(t\right)$ flattening in the final few days and reverting to its prior distribution (compare Fig. 2b and Figure S2b). The posterior confidence intervals were narrower in the simulated data because the simulated epidemic size was about 7 times larger than the actual epidemic.

Discussion

In this paper we developed a Bayesian model (EpiLine) that captures dynamic changes in the time from symptom onset to healthcare presentation and applied it to the UK mpox epidemic in 2022. Our results show that the time from symptom onset to healthcare presentation was dynamic and declined from an average of 22 days in early May 2022 to 10 days by early June and 8 days in August 2022, documenting one of the factors that will have contributed to controlling the epidemic. When we account for these dynamic delays in healthcare presentation, we found that the time-varying growth rate declined gradually over the epidemic. However, using a misspecified model with static delays in healthcare presentation (i.e. using a median value during the initial phase) incorrectly over estimated the initial growth rate and then implied a rapid decline. For example, a modelling study which was fit to weekly reported UK mpox cases, required a substantial rapid change in sexual behaviour in the GBMSM and wider community in May and June 2022 to fit the apparent surge and then flattening of reported cases¹¹. However, as noted by the authors, they did not model delays in healthcare presentation, such as those we discuss here, and which we suggest were the cause of the apparent sharp drop in the growth rate around the end of May 2022. Their results may have been different if they had accounted for this, especially when considering the large parameter space sampled during the calibration process.

Our results demonstrate the importance of accounting for dynamic changes in the time from symptom onset to healthcare presentation. Most previous studies have modelled the delays between symptom onset (or infection) and healthcare presentation to be static e.g.^15,16. However, a couple of nowcasting models have accounted for dynamic delays in the context of the STEC O104:H4 outbreak in Germany¹⁷ and measles in the Netherlands¹⁸. Consistent with our findings, both studies reported that accounting for dynamic delays improved nowcasts. Our work adds to this literature by highlighting the qualitative effect dynamic delays have on the epidemic curve in the context of a small but rapidly growing epidemic i.e. the 2022 mpox epidemic in England.

Following the UK Joint Committee on Vaccination and Immunisation (JCVI)’s recommendation, vaccination against mpox in the UK was offered to GBMSM at highest risk from June 21, 2022 ¹² with the vaccination campaign speeding up from July 22, 2022¹³. However, our analysis suggests that the number of new symptomatic cases was already falling by early July 2022, thus vaccinations were not the cause of this initial decline in growth rate. We hypothesise that if the declines are not caused by vaccination, then the most likely causes are a combination of immunity and behaviour change. Hence, our results of a gradual drop in growth rate can be interpreted to be consistent with the core GBMSM transmission group possibly gaining immunity due to high prevalence, alongside more rapid diagnosis and more gradual reductions in high risk behaviour due to public health campaigns.

This study had some limitations. Firstly, the focus of this study was the impact of changes in the delays from symptom onset to healthcare presentation on estimates of growth rate. However, a second aspect of reporting to consider is changes in the overall case ascertainment rate. In the context of this analysis it would be the proportion of people who develop symptoms on a particular day who ever present to healthcare services. Unfortunately, without independent survey data it is extremely difficult to estimate the case ascertainment rate or changes in it and thus we assume that it is constant over time in our analysis. In periods where the case ascertainment rate increases/decreases, estimates of growth rate based on reported cases will be overestimated/underestimated. In the first phase of this mpox epidemic in the UK, it is possible that the case ascertainment rate increased with public awareness, thus initial estimates of growth rate were too high even after correcting for the shortening in the symptom onset to healthcare presentation delay. The subsequent fall in growth rate (calculated from reported cases) could be partly explained by a reduction in case ascertainment rate as public concern about mpox reduced due to no fatalities, however, as yet there is no evidence to support or refute this hypothesis.

Furthermore, EpiLine is designed to estimate the epidemic growth rate in the presence of unknown and dynamic delays in healthcare presentation. Whilst health authorities typically collate statistics on the total number of confirmed positive cases by day, detailed follow-ups such as the date when symptoms first developed or estimates of the date of transmission are only collected for a subset of individuals. For this study we had statistics on the date of symptoms onset for 40%-80% of cases but not estimates of the transmission dates. Additionally, we did not have data to estimate the generation time distribution, which itself could be time-varying, so therefore modelling new infections directly was not possible. Therefore we chose to model the number of symptomatic cases directly, assuming that the delays between infection and symptoms onset are approximately constant. We think that this is a sensible choice here, although a possible alternative would be to take this to be uniformly distributed between 5 and 21 days, the suggested time it takes for mpox symptoms to occur.

While our study was focused on modelling the dynamic delays and growth rate of mpox in one setting, our findings have policy implications for general outbreaks across settings. Specifically, we show the importance of modelling reduced delays to presenting to healthcare in order to correctly interpret the status of the epidemic. Shorter delays can prevent onward transmission, and allows prompt use of antivirals post infection. Hence, our study highlights the importance and need for public health agencies to focus on reducing time delays early in an outbreak and when tailoring the optimal policy response.

In summary, we developed EpiLine which simultaneously models dynamic delays between symptom onset and healthcare presentation, and the epidemic growth rate. Applying it to the 2022 UK mpox outbreak, we demonstrated that in the initial phases, the delays changed rapidly, and also that it was essential to account for the dynamic delay to correctly estimate the epidemic growth rate.

Author contributions

RH, JPG and CF conceived the study. RH and JPG developed and undertook the modelling with input from CF and in conversations within UK Health Security Agency (UKHSA). RH and JPG wrote the manuscript, with input from CF, TW, AC and NW. All authors approved the final version. RH and JPG are the manuscript’s guarantors.

Data availability

The data used in this study is not publicly available. UKHSA operates a robust governance process for applying to access protected data that considers: the benefits and risks of how the data will be used; compliance with policy, regulatory and ethical obligations; data minimisation; how the confidentiality, integrity, and availability will be maintained; retention, archival, and disposal requirements; best practice for protecting data, including the application of ‘privacy by design and by default’, emerging privacy conserving technologies and contractual controls. Access to protected data is always strictly controlled using legally binding data sharing contracts. UKHSA welcomes data applications from organisations looking to use protected data for public health purposes. To request an application pack or discuss a request for UKHSA data you would like to submit, contact DataAccess@ukhsa.gov.uk.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-68154-8.