Universal cold RNA phase transitions

Significance

Life exists even in the extreme cold, yet we know little about how RNA functions at low temperatures. We have recently found unexpected RNA properties at near-to-zero temperatures, specifically a phase transition to a cold RNA phase that implies a hidden, altered RNA biochemistry. We have investigated cold RNA biochemistry using single-RNA force spectroscopy. At low temperatures, we find that sequence-independent contributions of RNA–water interactions outweigh sequence-dependent base pairing, leading to misfolding of fully complementary hairpins. RNA in the cold may have profound implications for understanding the cold adaptation of RNA biochemistry in present-day psychrophilic biota and may have shaped the evolution of a primordial RNA world.

Abstract

RNA’s diversity of structures and functions impacts all life forms since primordia. We use calorimetric force spectroscopy to investigate RNA folding landscapes in previously unexplored low-temperature conditions. We find that Watson–Crick RNA hairpins, the most basic secondary structure elements, undergo a glass-like transition below $T_G\sim 20°$C where the heat capacity abruptly changes and the RNA folds into a diversity of misfolded structures. We hypothesize that an altered RNA biochemistry, determined by sequence-independent ribose–water interactions, outweighs sequence-dependent base pairing. The ubiquitous ribose–water interactions lead to universal RNA phase transitions below T_G, such as maximum stability at $T_S\sim 5°$C where water density is maximum, and cold denaturation at $T_C\sim -50°$C. RNA cold biochemistry may have a profound impact on RNA function and evolution.

Of similar chemical structure to DNA, the deoxyribose-ribose and thymine-to-uracil differences endow RNA with a rich phenomenology (1–3). RNA structures are stabilized by multiple interactions among nucleotides and water, often with the critical involvement of magnesium ions (4–6). Such interactions compete in RNA folding, producing a rugged folding energy landscape (FEL) with many local minima (7, 8). To be functional, RNAs fold into a native structure via intermediates and kinetic traps that slow down folding (9, 10). The roughness of RNA energy landscapes has been observed in ribozymes that exhibit conformational heterogeneity with functional interconverting structures (11–13) and misfolding (14–17). Single-molecule methods have revealed a powerful approach to investigate these questions by monitoring the behavior of individual RNAs one at a time, using fluorescence probes (18, 19) and mechanical forces (20, 21). Previous studies have underlined the crucial role of RNA–water interactions at subzero temperatures in liquid environments (22–24) raising the question of the role of water in a cold RNA biochemistry. Here, we carry out RNA pulling experiments at low temperatures, showing that fully complementary RNA hairpins unexpectedly misfold below a characteristic glass-like transition temperature $T_G\sim 20°$C, adopting a diversity of compact folded structures. This phenomenon is observed in both monovalent and divalent salt conditions, indicating that magnesium–RNA binding is not essential for this to happen. Moreover, misfolding is not observed in DNA down to $5°$C. These facts suggest that the folded RNA arrangements are stabilized by sequence-independent $2^{\prime }$-hydroxyl–water interactions that outweigh sequence-dependent base pairing. Cold RNA misfolding implies that the FEL is rugged with several minima that kinetically trap the RNA upon cooling, a characteristic feature of glassy matter (25). RNA folding in rugged energy landscapes is accompanied by a reduction of RNA’s configurational entropy. A quantitative descriptor of this reduction is the folding heat capacity change at constant pressure, $\mathrm{\Delta }{C}_p$, directly related to the change in the number of degrees of freedom available to the RNA molecule. Despite its importance, $\mathrm{\Delta }{C}_p$ measurements in nucleic acids remain challenging (26–28). We carry out RNA pulling experiments at low temperatures and show that $\mathrm{\Delta }{C}_p$ abruptly changes at $T_G\sim 20°$C, a manifestation that the ubiquitous nonspecific ribose–water interactions overtake the specific Watson–Crick base pairing at sufficiently low temperatures.

RNA Misfolds at Low Temperatures

We used a temperature-jump optical trap (SI Appendix, section A, Methods) to unzip fully complementary Watson–Crick RNA hairpins featuring two 20 bp stem sequences (H1 and H2) and loops of different sizes ($L=4,8,10,12$ nucleotides) and compositions (poly-A or poly-U) (SI Appendix, section B, Methods). Pulling experiments were carried out in the temperature range 7 to 42 ^°C at 4 mM MgCl₂ and 1 M NaCl in a 100 mM Tris-HCl buffer (pH 8.1). Fig. 1A shows the temperature dependence of the force-distance curves (FDCs) for the dodeca-A (12 nt) loop hairpin sequence H1L12A at 4 mM magnesium. At and above room temperature ($T\ge 25°$C), H1L12A unfolds at ∼20 to 25 pN (blue force rips in dashed gray ellipse), and the rupture force distribution is unimodal (Fig. 1B, LeftmostTop panel at $25°$C), indicating a single folded native state (N). At $T\le 17°$C, new unfolding events appear at higher forces (∼30 to 40 pN, dashed black ellipse). The bimodal rupture force distribution (Fig. 1B, Right Top panels) shows the formation of an alternative misfolded structure (M) that remains kinetically stable over the experimental timescales. Below $T=10°$C, the misfolded population shows >50% occupancy. Analogous results were obtained with sodium ions (SI Appendix, Fig. S2). The formation of stable nonnative structures for H1L12A is not predicted by algorithms such as Mfold (29), Vienna package (30), McGenus (31), pKiss (32), and Sfold (33). Furthermore, misfolding is not observed for the equivalent DNA hairpin sequence with deoxy-nucleotides (34). We refer to this phenomenon as cold RNA misfolding.

Fig. 1.

Cold RNA misfolding. (A) Unfolding (blue) and refolding (red) FDCs from H1L12A unzipping experiments (Top-Left) at temperatures 7 to 42 ^°C and 4 mM MgCl₂. The gray-dashed ellipse indicates native (N) unfolding events. Unexpected unfolding events from a misfolded (M) structure appear below $25°$C (black-dashed ellipse) that become more frequent upon lowering T from $17°$C to $7°$C. (B) Classification of N (blue dots) and M (red dots) rupture events at $T\le 25°$C and Worm-like chain (WLC) fits for each state (dashed lines). The Top panels show rupture force distributions at each T. The Inset of the Leftmost panel shows the parameters of rupture force events (see text).

Misfolding can be characterized by the size of the force rips at the unfolding events, which imply a change in the RNA molecular extension, $\mathrm{\Delta }x$. The value of $\mathrm{\Delta }x$ is obtained as the ratio between the force drop $\mathrm{\Delta }f$ and the slope $k_{\text{s}}$ of the FDC measured at the rupture force f_r, $\mathrm{\Delta }x=\mathrm{\Delta }f/k_{\text{s}}$ (Inset of Left panel in Fig. 1B). Fig. 1B shows $\mathrm{\Delta }x$ versus f_r for all rupture force events in H1L12A at four selected temperatures. Two clouds of points are visible below $25°$C, evidencing two distinct folded states, the native (N, blue) and the misfolded (M, red). A Bayesian network model (SI Appendix, section C, Methods) has been implemented to assign a probability to each data point to belong to N or M (color-graded bar in Fig. 1B). At a given force, the released number of nucleotides for N and M (n_N, n_M) is directly proportional to $\mathrm{\Delta }x$ (SI Appendix, section S2). To derive the values of n_N and n_M, a model of the elastic response of the single-stranded RNA (ssRNA) is required. We have fitted the datasets ($\mathrm{\Delta }x,f_r$) for N and M to the worm-like chain (WLC) elastic model (SI Appendix, section D, Methods) using the Bayesian network model, finding $n_N=52(1)$ (blue dashed line) and $n_M=46(1)$ (red dashed line) for the number of released nucleotides upon unfolding the N and M structures. Notice that n_N matches the total number of nucleotides in H1L12A (40 in the stem plus 12 in the loop), while M features 6 nt less than n_N. These can be interpreted as remaining unpaired nt in M or that the $5^{\prime }-3^{\prime }$ end-to-end distance in M has increased by ∼3 nm, roughly corresponding to 6 nt.

RNA Flexibility at Low-T Promotes Misfolding

To characterize the ssRNA elasticity, we show the force-extension curves versus the normalized ssRNA extension per base in Fig. 2A for H1L12A at different temperatures. Upon decreasing T, the range of forces and extensions becomes wider due to the higher unfolding and lower refolding forces. Moreover, a shoulder in the force-extension curve is visible below $32°$C (SI Appendix, Fig. S3), indicating the formation of nonspecific secondary structures. A similar phenomenon has been observed in ssDNA (37). The force-extension curves (triangles and circles in Fig. 2A) at each temperature were fitted to the WLC model, with persistence length l_p and interphosphate distance d_b as fitting parameters (Fig. 2B and SI Appendix, (1) in section D, Methods). Only data above the shoulder have been used to fit the WLC (SI Appendix, section S1). The values l_p and d_b show a linear T dependence (red symbols in Fig. 2C) that has been used for a simultaneous fit of the ssRNA elasticity at all temperatures (blue lines in Fig. 2A). Over the studied temperature range, l_p (Fig. 2C, Left panel) increases with T by a factor of ∼2.5, whereas d_b (Fig. 2C, Right panel) decreases by only ∼20%. The increase of l_p with T is an electrostatic effect (34) that facilitates the bending of ssRNA at the lowest temperatures, promoting base contacts and misfolding.

Fig. 2.

Temperature-dependent ssRNA elasticity. (A) Force versus the ssRNA extension per base at different temperatures. Two methods have been used to extract the ssRNA molecular extension: the force-jump (magenta triangles up—unfolding—and down—refolding) and the two-branches method (black circles) (35, 36). Blue lines are the fits to the WLC in the high-force regime (see text). (B) Representation of the ssRNA elastic response according to the WLC model. The persistence length (l_p) measures the polymer flexibility, and the interphosphate distance (d_b) is the distance between contiguous bases. The computation of the total hairpin extension accounts for the contribution of the molecular diameter (d). (C) T dependencies of l_p (Left) and d_b (Right). Linear fits (solid lines) with error limits (dashed lines) are also shown and give slopes equal to $0.17(2)$ Å/K for l_p and $-0.04(1)$ Å/K for d_b.

Cold RNA Misfolding Is a Universal Sequence-Independent Phenomenon

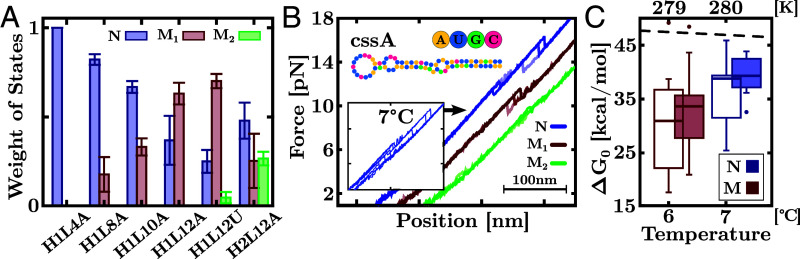
The ubiquity of cold misfolding is due to the flexibility of the ssRNA rather than structural features such as stem sequence, loop size, and composition. To demonstrate this, we show results for another five hairpin sequences in Fig. 3A with different stem sequences and loop sizes. To assess the effect of loop size, three hairpins have the same stem as H1L12A but tetra-A, octa-A, and deca-A loops (H1L4A, H1L8A, and H1L10A respectively). A fourth hairpin features a dodeca-U loop (H1L12U) to avoid base stacking in the dodeca-A loop of H1L12A. The fifth hairpin, H2L12A, has the same loop as H1L12A but features a different stem. Except for H1L4A, all hairpins misfold below $T=25°$C, as shown by the emergence of unfolding events at forces above 30 pN (blue rips in the black dashed ellipses in Fig. 3A) compared to the lower forces of the unfolding native events ∼20 (gray dashed ellipses). Fig. 3B shows the Bayesian-clustering classification of the different unfolding trajectories at $7°$C and $25°$C, in line with the results for H1L12A shown in Fig. 1B. The hairpin composition impacts misfolding, while H1L8A, H1L10A, and H1L12A show a single M at $7°$C, H1L12U and H2L12A feature two distinct misfolded states at high (M₁) and low (M₂) forces (black dashed ellipses for H1L12U and H2L12A in Fig. 3A).

Fig. 3.

Universality of cold RNA misfolding. (A) Unfolding (blue) and refolding (red) FDCs of hairpins H1L4A, H1L8A, H1L10A, H1L12U, and H2L12A at $25°$C and $7°$C. Gray-dashed ellipses indicate native (N) unfolding events. Except for H1L4A, all RNAs show unfolding events from misfolded (M) structures at $7°$C (black-dashed ellipses). Hairpins H1L12U and H2L12A (featuring a dodeca-U loop and a different stem sequence) show a second misfolded structure at low forces (zoomed Insets). Hairpin sequences are shown in each panel. (B) Bayesian classification of the unfolding events for the hairpins in panel (A) at $T=7°$C. The dashed lines are the fits to the WLC for the different states. The Top panels show the rupture force distributions.

The effect of the loop is to modulate the probability of formation of the native stem relative to other stable conformations. Indeed, H1L4A with a tetraloop has the largest stability among the studied RNAs (38), preventing misfolding down to $7°$C (Fig. 3B). Misfolding prevalence increases with loop size due to the higher number of configurations and low entropic cost of bending the loop upon folding. The ssRNA elastic responses in H1L12A, H1L12U, and H2L12A show a systematic decrease of l_p upon lowering T (SI Appendix, Fig. S5) and therefore an enhancement of misfolding due to the large flexibility of the ssRNA. Fig. 4A shows the fraction of unfolding events at $7°$C for all hairpin sequences for N (blue), M₁ (red), and M₂ (green). Starting from H1L4A, misfolding frequency increases with loop size, with the second misfolded state (M₂) being observed for H1L12U and H2L12A within the limits of our analysis. Compared to the poly-A loop hairpins (SI Appendix, Fig. S6), the unstacked bases of the poly-U loop in H1L12U confer a larger d_b and extension to the ssRNA (red dots in SI Appendix, Fig. S5). Elastic parameters for the family of dodecaloop hairpins are reported in SI Appendix, Table S2. The fact that hairpins containing poly-A and poly-U dodecaloops misfold at low temperatures demonstrates that stacking effects in the loop are nonessential to misfolding.

Fig. 4.

Features of cold RNA misfolding. (A) Frequency of N, M₁, and M₂ unfolding events for the different RNA hairpins at $7°$C. (B) Unfolding FDCs of cssA RNA at $7°$C and 4 mM MgCl2 (Inset) classified into native (N) and misfolded (M₁ and M₂) states. (C) $\mathrm{\Delta }{G}_0$ values at $7°$C in 4 mM MgCl₂ (empty boxes) and 400 mM Nacl (solid boxes). Temperature axis in ^°C (Bottom label) and K (Top label). Box-and-whisker plots show the median (horizontal thick line), first and third quartiles (box), 10th and 90th percentiles (whiskers), and outliers (dots). The black dashed line is the Mfold prediction.

To further demonstrate the universality of cold RNA misfolding, we have pulled the mRNA of bacterial virulence protein CssA from Neisseria meningitidis, an RNA thermometer that changes conformation above 37 ^°C (39). Fig. 4B shows several FDCs measured at $7°$C and 4 mM MgCl2 (Inset), evidencing that the mRNA misfolds into two structures (M₁, red; M₂, green).

RNA Misfolds into Stable and Compact Structures at Low Temperatures

The Bayesian analysis of the force rips has permitted us to classify the unfolding and refolding trajectories into two sets, $N\rightleftharpoons U$ and $M\rightleftharpoons U$ (Figs. 1B and 3B). We have applied the fluctuation theorem (40, 41) to each set of trajectories of H1L12A to determine the free energies of formation of N and M from the irreversible work (W) measurements at $7°$C (SI Appendix, section E, Methods and section S4). In Fig. 4C, we show $\mathrm{\Delta }{G}_0$ estimates for N (blue) and M (red), finding $\mathrm{\Delta }{G}_0^N=38(9)$ kcal/mol and $\mathrm{\Delta }{G}_0^M=30(10)$ kcal/mol in 4 mM MgCl2 (empty boxes). We have also measured $\mathrm{\Delta }{G}_0$ at 1 M NaCl and extrapolated it to 400 mM NaCl, the equivalent concentration to 4 mM MgCl2 according to the 100:1 salt rule (41). We obtain $\mathrm{\Delta }{G}_0^N=37(3)$ kcal/mol and $\mathrm{\Delta }{G}_0^M=31(8)$ kcal/mol (filled boxes), in agreement with the magnesium data. Within the experimental uncertainties, $\mathrm{\Delta }{G}_0$ for N is higher by ∼5 kcal/mol than for M, reflecting the higher stability of Watson–Crick base pairs in N. Notice that the Mfold prediction for N ($\mathrm{\Delta }{G}_0^N=47$ kcal/mol, black dashed line) overestimates $\mathrm{\Delta }{G}_0$ by 10 kcal/mol.

We have also examined the distance between the folded and the transition state $x^{‡}$ in H1L12A to quantify the compactness of the folded structure. We have determined $x^{‡}$ from the rupture force variance ${\sigma }^2$ using the Bell-Evans model, through the relation ${\sigma }^2=0.61{(k_{\text{B}}T/x^{‡})}^2$ (SI Appendix, section S5). We find that average rupture forces for N and M decrease linearly with T, whereas ${\sigma }^2$ values are T-independent and considerably larger for M, ${\sigma }_M^2\sim 50{\sigma }_N^2$, giving $x_M^{‡}=0.7(4)$ nm and $x_N^{‡}=4.8(6)$ nm (SI Appendix, Fig. S10). Therefore, $x_M^{‡}\ll x_N^{‡}$ with M featuring a shorter $x^{‡}$ and a more compact structure than N.

The RNA Glassy Transition

The ubiquity of the cold RNA misfolding phenomenon suggests that RNA experiences a glass transition below a characteristic temperature T_G where the FEL develops multiple local minima. Fig. 5A and SI Appendix, Fig. S11 illustrate the effect of cooling on the FEL (42, 43). Above $25°$C, the FEL has a unique minimum for the native structure N (red-colored landscape). The projection of the FEL along the molecular extension coordinate shows that N is separated from U by a transition state (TS) (Top Inset, red line). Upon cooling, the FEL becomes rougher with deeper valleys, promoting misfolding (green and blue colored landscapes). The distance from M to TS is shorter than from N to TS, reflecting that M is a compact structure (Bottom Inset, green and blue lines).

Fig. 5.

Cold RNA misfolding and phase transitions. (A) Illustration of a multicolored folding energy landscape (FEL) at different temperatures (SI Appendix, Fig. S11). The temperature arrow indicates the tendency to explore low-lying energy states with the FEL becoming rougher upon cooling: from high (red) to intermediate (green) and low (blue) temperatures. Transition state (TS) distances are typically shorter for M than N, denoting disordered and compact misfolded structures. The encircled schematic folds are for illustration purposes. (B) Temperature-dependent entropy (black) and enthalpy (gray) of N for H1L12A (empty symbols) and H1L4A (full symbols). The results are reported in SI Appendix, Tables S5 and S6. Fits to the entropy values in the hot (red) and cold (blue) regimes for H1L12A (solid lines) and H1L4A (dashed lines) are also shown. The transition between the two regimes occurs at $T_G\sim 293 \text{K}\sim 20°$C (dashed gray band) with a sudden change in $\mathrm{\Delta }{C}_p$. Inset Stability curves of H1L12A (empty black circles) and H1L4A (solid gray squares). Maximum stability is found at $T_S\sim 278 \text{K}\sim 5°$C (vertical black line) with melting temperatures at $T_H\sim 370 \text{K}\sim 100°$C (red lines). Extrapolations of $\mathrm{\Delta }{G}_0(T)$ in the cold regime predict cold denaturation at $T_C\sim 220 \text{K}\sim -50°$C for both hairpins (blue lines).

The glassy transition is accompanied by the sudden increase in the heat capacity change ($\mathrm{\Delta }{C}_p$) between N and U below $T_G\sim 20°$C for H1L12A and H1L4A. $\mathrm{\Delta }{C}_p$ equals the temperature derivative of the folding enthalpy and entropy, $\mathrm{\Delta }{C}_p=\partial \mathrm{\Delta }H/\partial T=T\partial \mathrm{\Delta }S/\partial T$ and can be determined from the slopes of $\mathrm{\Delta }H(T)$ and $\mathrm{\Delta }S(T)$ (SI Appendix, section F, Methods and section S8). We observe two distinct regimes: above T_G (hot, H) and below T_G (cold, C). While $\mathrm{\Delta }{C}_p^{\text{H}}\sim 1.5·{10}^3$ cal mol⁻¹K⁻¹ is similar for both H1L12A and H1L4A (parallel red lines in Fig. 5B), $\mathrm{\Delta }{C}_p^{\text{C}}$ differs: $\mathrm{\Delta }{C}_p^{\text{C}}=8(1)·{10}^3$ cal mol⁻¹K⁻¹ for H1L12A versus $\mathrm{\Delta }{C}_p^{\text{C}}=5.8(4)·{10}^3$ cal mol⁻¹K⁻¹ for H1L4A (unparallel blue lines in Fig. 5B) showing the dependence of $\mathrm{\Delta }{C}_p^{\text{C}}$ on loop size at low-T. Despite the different $\mathrm{\Delta }{C}_p^{\text{C}}$ values, $\mathrm{\Delta }{S}_0=0$ and stability ($\mathrm{\Delta }{G}_0$) is maximum at $T_S=5(2)°$C (Fig. 5B, Inset) for both H1L4A and H1L12A (vertical black lines in Fig. 5B, main and Inset). Finally, the $\mathrm{\Delta }{C}_p^{\text{C}}$ values predict cold denaturation at the same $T_C\sim -50°$C for both sequences. The agreement between the values of T_G, T_S, and T_C suggests that cold RNA phase transitions are sequence independent, occurring in narrow and well-defined temperature ranges for all RNAs.

Cold denaturation is also observed in proteins with large $\mathrm{\Delta }{C}_p$ values. In proteins, the balance of hydrophobic and hydrophilic interactions with water plays a critical role in their stability and folding (44, 45). However, proteins show a disparity of cold denaturation temperatures, e.g. frataxin shows cold denaturation around $10°$C (46), whereas other proteins denature at much lower temperatures. In contrast, RNA stability is influenced by the interplay between hydrogen bonding, base stacking, and electrostatic interactions. In particular, the electrostriction effects by water molecules around phosphate groups and the interactions of the RNA with cations hydration shells (due to the salt ions) might contribute to the $\mathrm{\Delta }{C}_p$ increase upon lowering T. This could be tested in experiments with other ion types such as potassium and lithium.

Discussion

Calorimetric force spectroscopy measurements on hairpin sequences of varying loop size, composition, and stem sequence show RNA misfolding at low-T in monovalent and divalent salt conditions. The phenomenon’s ubiquity leads us to hypothesize that nonspecific ribose–water bridges overtake the preferential Watson–Crick base pairing of the native hairpin, forming compact structures at low temperatures. Cold misfolding is intrinsic to RNA, as it is not observed for the equivalent DNA hairpin sequences. In addition, magnesium ions are not crucial for it to happen, indicating the ancillary role of magnesium-mediated base-pairing interactions. Upon cooling, the diversity of RNA–water interactions promoted by the ribose increases the ruggedness of the FEL. Previous unzipping experiments of long (2 kb) RNA hairpins at $25°$C already identified stem-loops of ∼20 nucleotides as the misfoldons for RNA hybridization (41). The short RNA persistence length at low T (∼4 Å at $10°$C, Fig. 2C) facilitates nonnative contacts between distant bases and the exploration of different configurations. Indeed, the higher flexibility of the U-loop in H1L12U enhances bending fluctuations and misfolding compared to the stacked A-loop in H1L12A (Fig. 4A). Cold RNA misfolding has also been reported in Nuclear Magnetic Resonance studies of the mRNA thermosensor that regulates the translation of the cold-shock protein CspA (47), aligning with the CssA results of Fig. 4B. Cold RNA misfolding should not be specific to force-pulling but also present in temperature-quenching experiments where the initial high-entropy random coil state further facilitates nonnative contacts (48). We foresee that cold RNA misfolding might help to identify misfoldon motifs, contributing to developing rules for tertiary structure prediction (49, 50).

Most remarkable is the large $\mathrm{\Delta }{C}_p^{\text{C}}$ values for H1L12A and H1L4A below $T_G\sim 20°$C (293 K), which are roughly 4 to 5 times the high-T value above T_G, implying a large configurational entropy loss and a rougher FEL at low temperatures. The increase in $\mathrm{\Delta }{C}_p$ below T_G (dashed gray band in Fig. 5B) is reminiscent of the glass transition predicted by statistical models of RNA with quenched disorder (51, 52). As $\mathrm{\Delta }{C}_p=C_p^U-C_p^N$, we attribute this change to the sudden reduction in $C_p^N$ and the configurational entropy loss upon forming N (25). Both hairpins show maximum stability $\mathrm{\Delta }{G}_0$ at $T_S\sim 5°$C (278 K) where $\mathrm{\Delta }{S}_0$ vanishes (Fig. 5B). The value of T_S is close to the temperature where water density is maximum ($4°$C), with low-T extrapolations predicting cold denaturation at $T_C\sim -50°$C (220 K) for both sequences. This result agrees with neutron scattering measurements of the temperature at which the RNA vibrational motion arrests, ∼ 220 K (6, 24). We hypothesize that $T_S\sim 5°$C and $T_C\sim -50°$C mark the onset of universal phase transitions determined by the primary role of ribose–water interactions that are weakly modulated by RNA sequence, a result with implications for RNA condensates (53, 54) and RNA catalysis (55). The nonspecificity of ribose–water interactions should lead to a much richer ensemble of RNA structures and conformational states and more error-prone RNA replication. The multiplicity of RNA conformations could be characterized in hopping experiments, where long-time data series at low T are recorded by keeping the force constant using a feedback loop as has been shown for the R3 domain of protein talin (56). Cold RNA could be relevant for extremophilic organisms, such as psychrophiles, which thrive in subzero temperatures (57). Finally, misfolding into compact and kinetically stable structures might help preserve RNAs in confined liquid environments such as porous rocks and interstitial brines in the permafrost of the arctic soil and celestial bodies as well as niches exposed to freeze-thaw cycles (58, 59). This fact might have conferred an evolutionary advantage to RNA viruses for surviving during long periods (60) with implications on ecosystems due to the ongoing climate change (61). The ubiquitous sequence-independent ribose–water interactions at low temperatures frame a new paradigm for RNA self-assembly and catalysis in the cold. It is expected to impact RNA function profoundly, having potentially accelerated the evolution of a primordial RNA world (62, 63).

Materials and Methods

Temperature-Jump Optical Trap.

We used a temperature-jump optical trap to perform unzipping experiments at different temperatures (64). Our setup adds to a MiniTweezers device (65) a heating laser of wavelength $\lambda =1,435$ nm to change the temperature inside the microfluidics chamber. The latter is designed to damp convection effects caused by the laser nonuniform temperature, which may produce a hydrodynamics flow between medium regions (water) at different T. The heating laser allows for increasing the temperature by discrete amounts of $\mathrm{\Delta }T\sim +2.5°$C up to a maximum of $\sim +30°$C with respect to the environment temperature, T₀. Operating the instrument in an icebox cooled down at a constant $T_0\sim 5°$C, and outside the box at ambient temperature (25 ^°C), we carried out experiments in the T range $[7,42]°$C. Despite not involving direct measurement of heat, we refer to this method as calorimetric force spectroscopy as it allows for the derivation of the temperature-dependent nucleic acids thermodynamics from mechanical work measurements.

In a pulling experiment, the molecule is tethered between two polystyrene beads through specific interactions with the molecular ends (66). One end is labeled with a digoxigenin (DIG) tail and binds with an anti-DIG coated bead (AD) of radius 3 μm. The other end is labeled with biotin and binds with a streptavidin-coated bead (SA) of radius 2 μm. The SA bead is immobilized by air suction at the tip of a glass micropipette, while the AD bead is optically trapped. The unfolding process is carried out by moving the optical trap between two fixed positions: the molecule starts in the folded state, and the trap-pipette distance (λ) is increased until the hairpin switches to the unfolded conformation. Then, the refolding protocol starts, and λ is decreased until the molecule switches back to the folded state.

The unzipping experiments were performed at two different salt conditions: 4 mM MgCl₂ (divalent salt) and 1 M NaCl (monovalent salt). Both buffers have been prepared by adding the salt (divalent or monovalent) to a background of 100 mM Tris-HCl (pH $8.1$) and 0.01% NaN₃. The NaCl buffer also contains 1 mM ethylenediaminetetraacetic acid. The pulling protocols have been carried out at a constant pulling speed, $v=100$ nm/s. We sampled 5 to 6 different molecules for each hairpin and at each temperature, collecting at least ∼200 unfolding-folding trajectories per molecule.

RNA Synthesis.

We synthesized six different RNA molecules made of a 20 bp fully complementary Watson–Crick stem, ending with loops of different lengths ($L=4,8,10,12$ nucleotides) and compositions (poly-A or poly-U). The hairpins are flanked by long hybrid DNA/RNA handles (∼500 bp). Further details about the sequences are given SI Appendix, Fig. S1 and Table S1.

The RNA hairpins have been synthesized using the steps in ref. 67. First, the DNA template (Merck) of the RNA is inserted into plasmid pBR322 (New England Biolabs) between the HindIII and EcoRI restriction sites and cloned into the Escherichia coli ultracompetent cells XL10-GOLD (Quickchange II XL site-directed mutagenesis kit). Second, the DNA template is amplified by Polymerase Chain Reaction (KOD polymerase, Merck) using T7 promoters. The RNA is obtained by in vitro RNA transcription (T7 megascript, Merck) of the DNA containing the RNA sequence flanked by an extra 527 and 599 bases at the 3^′-end and 5^′-end, respectively, for the hybrid DNA-RNA handles. Finally, labeled biotin (5^′-end) and digoxigenin (3^′-end) DNA handles, complementary to the RNA handles, are hybridized to get the final construct.

Bayesian Clustering.

We use a mixture hierarchical Bayesian model (probabilistic graph network) to classify unfolding events as either emanating from a native or a misfolded initial folded state. The model is a soft classifier, giving each trace a probability (score) to belong to a given state. The model is described in SI Appendix, section S3.

ssRNA Elastic Model.

The ssRNA elastic response has been modeled according to the worm-like chain (WLC), which reads

$$f(x)=\frac{k_{\text{B}}T}{4l_p}\left[{\left(1-\frac{x}{n{d}_b}\right)}^{-2}-1+4\frac{x}{n{d}_b}\right],$$ [1]

where l_p is the persistence length, d_b is the interphosphate distance and n is the number of bases of the ssRNA. More details on the WLC model and the fitting method used to derive its parameters can be found in SI Appendix, section S1.

Free Energy Determination.

Given a molecular state, $\mathrm{\Delta }{G}_0(N)$ is the hybridization free energy of the N base pairs of the folded structure when no external force is applied ($f=0$). $\mathrm{\Delta }{G}_0(N)$ is obtained from the free energy difference, $\mathrm{\Delta }{G}_{\lambda }$, between a minimum (${\lambda }_{\text{min}}$) and a maximum (${\lambda }_{\text{max}}$) optical-trap positions where the molecule is folded and unfolded, respectively. Thus, one can write

$$\mathrm{\Delta }G(\lambda )=\mathrm{\Delta }{G}_0(N)+\mathrm{\Delta }{G}_{\text{el}}(\lambda ),$$ [2]

where $\mathrm{\Delta }{G}_{\text{el}}(\lambda )$ is the elastic energy upon stretching the ssRNA between ${\lambda }_{\text{min}}$ and ${\lambda }_{\text{max}}$. The latter term can be computed by integrating the WLC (Eq. 1). As unzipping experiments are performed by controlling the optical-trap position (not the force), this requires inverting Eq. 1 (SI Appendix, section S1).

We used the fluctuation theorem (68) (FT) to extract $\mathrm{\Delta }G(\lambda )$ from irreversible work (W) measurements. This is computed by integrating the FDC between ${\lambda }_{\text{min}}$ and ${\lambda }_{\text{max}}$, $W={\int }_{{\lambda }_{\text{min}}}^{{\lambda }_{\text{max}}}fd\lambda$ (Inset in SI Appendix, Fig. S8). Given the forward ($P_{\text{F}}(W)$) and reverse ($P_{\text{R}}(W)$) work distributions, the FT reads

$$\frac{P_{\text{F}}(W)}{P_{\text{R}}(-W)}=exp\left(\frac{W-\mathrm{\Delta }G(\lambda )}{k_{\text{B}}T}\right),$$ [3]

where the minus sign of $P_{\text{R}}(-W)$ is due to the fact that $W<0$ in the reverse process. When the work distributions cross, i.e. $P_{\text{F}}(W)=P_{\text{R}}(-W)$, Eq. 3 gives $W=\mathrm{\Delta }G(\lambda )$. Let us notice that the FT can only be applied to obtain free-energy differences between states sampled under equilibrium conditions. However, pulling experiments at low T are carried out under partial equilibrium conditions, with misfolding being a kinetic state. It is possible to extend the FT to our case by adding to $\mathrm{\Delta }G(\lambda )$ from Eq. 3 the correction term $k_{\mathrm{B}}log({\varphi }_{\text{F}}^i/{\varphi }_{\text{R}}^i)$, where ${\varphi }_{\text{U(R)}}$ is the fraction of forward (reverse) trajectories of state $i=\text{N},\text{M}$ (40). Given $\mathrm{\Delta }G(\lambda )$, the free energy at zero force, $\mathrm{\Delta }{G}_0(N)$, is computed from Eq. 2 by subtracting the energy contributions of stretching the ssRNA, the hybrid DNA/RNA handles, and the bead in the trap. The first two terms are obtained by integrating the WLC in Eq. 1, while the latter is modeled as a Hookean spring of energy $\mathrm{\Delta }{G}_b(x)=1/2k_{\text{b}}{x}^2$, where $k_{\text{b}}$ is the stiffness of the optical trap.

Derivation of the Heat Capacity Change.

To derive $\mathrm{\Delta }{C}_p$, we have measured the enthalpy $\mathrm{\Delta }{H}_0$ and entropy $\mathrm{\Delta }{S}_0$ of N at different T’s for H1L12A and H1L4A. $\mathrm{\Delta }{S}_0$ is obtained from the extended form of the Clausius–Clapeyron equation in a force (65), while $\mathrm{\Delta }{H}_0=\mathrm{\Delta }{G}_0+T\mathrm{\Delta }{S}_0$. Both $\mathrm{\Delta }{H}_0$ and $\mathrm{\Delta }{S}_0$ are temperature dependent, with a finite $\mathrm{\Delta }{C}_p$ (SI Appendix, section S8). This has been obtained by fitting the T-dependent entropies to the thermodynamic relation $\mathrm{\Delta }{S}_0(T)=\mathrm{\Delta }{S}_m+\mathrm{\Delta }{C}_{p}log(T/T_m)$, where T_m is the reference temperature and $\mathrm{\Delta }{S}_m$ is the entropy at $T=T_m$.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.