Numerical quantification of the vibronic broadening of the ${\text{SrTiO}}_3$ Ti L-edge spectrum

Abstract

The 2p⁵3d¹ excited state of the ${\text{Ti}}^{4+}$ ion in ${\text{SrTiO}}_3$ couples to ${\text{e}}_{\text{g}}$ distortions of the local oxygen cage, leading to a Jahn–Teller vibronic broadening of the excited states. We quantify this contribution to the broadening of the spectral features of the Ti L edge of ${\text{SrTiO}}_3$ by solving a model Hamiltonian, taking parameters for the Hamiltonian from previous first-principles calculations. Evaluation of the model Hamiltonian indicates that vibronic coupling accounts for the majority of the broadening observed for the L₃ edge, but only a minority of the L₂-edge spectral width. The calculations reveal that, with increasing temperature, the spectral features become increasingly asymmetric and the amount of vibronic broadening grows approximately linearly.

1. Introduction

Spectroscopic numerical methods, whether based on the manybody $GW$ approximation to the Bethe–Salpeter equation or time-dependent density-functional theory, have advanced considerably [1]. Accurate photon absorption spectra may be obtained for many systems of interest. Absorption peaks have three readily apparent features: energy position, relative intensity, and energy width. Until recently, calculations have typically focused on obtaining the positions and intensities of the excited-state peaks, while simply adding broadening ad hoc to match experimental results. However, spectral widths hold valuable information on the environmental coupling to the notional excited states, which may consist of atomiclike electronic excitations in ionic crystals. Broadening mechanisms can be separated into intrinsic and extrinsic effects. Extrinsic broadening arises when the species under investigation experiences a multitude of local environments. For example, the ${\text{Ti}}^{4+}$ ions in ${\text{SrTiO}}_3$ may feel different crystal fields due to imperfections and strain. This situation results in small shifts in peak position from site to site. Intrinsic broadening occurs because the conceptual atomic electronic excitations (e.g. the 2p⁵3d¹ state of ${\text{Ti}}^{4+}$) are not true eigenstates, but couple to more complicated electronic states, e.g. via Auger decay, or to other modes of the The spectral broadening due to this environmental coupling can be interpreted alternatively as stemming from either finite lifetimes for the atomic excitations or an increased number of final states beyond just these simple excitations. Understanding and developing the ability to control the environmental coupling of systems in the electronic excited state is a problem of great interest from both fundamental and applied science perspectives where electronic decay processes are responsible for limiting efficiencies in, for example, photovoltaic and solid-state lighting applications.

The Ti L edge of ${\text{SrTiO}}_3$ is a convenient system to study because the ${\text{d}}^0$ ground state of ${\text{Ti}}^{4+}$ produces a simple spectrum that has been extensively investigated both experimentally [2, 3] and numerically [4–7]. Furthermore, titanates, several of which are ferroelectric [8], are technologically relevant materials. The ${\text{d}}^0$ ground state of ${\text{Ti}}^{4+}$ is excited to the 2p⁵3d¹ configuration in which a hole is present in one of the six 2p states while an electron occupies one of the ten 3d states. This allows for 60 finals states, which may be designated by $|{\underset{\_}{m}}_{\ell }^{(2\text{p})},{\underset{\_}{m}}_s^{(2\text{p})};m_{\ell }^{(3\text{d})},m_s^{(3\text{d})}\rangle$. All of these final states are accessible by optical dipole selection rules due to spin–orbit coupling. Calculation of this L-edge spectrum can be accomplished by solving the multiplet Hamiltonian

$$H_{\text{mult}}=\left[H_{\text{av}}+L\cdot S(\text{p})+g(i,j)\right]+H_{\text{xf}}.$$ (1)

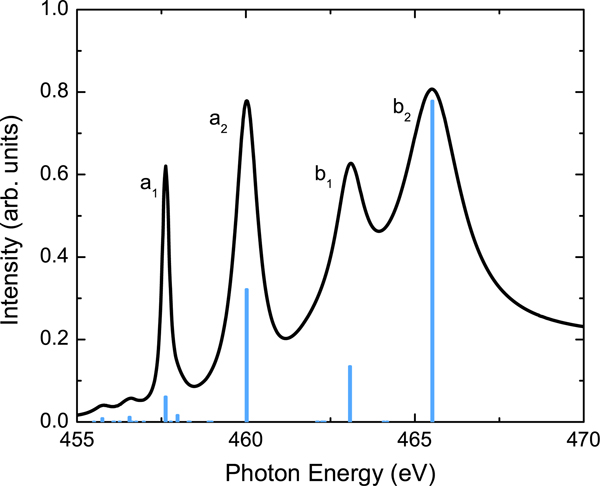
The terms in the bracket constitute the atomic multiplet Hamiltonian while $H_{\text{xf}}$ introduces crystal field effects. $H_{\text{av}}$ is a constant that gives a single peak at the average value of the 60 2p → 3d transitions. The second term is the spin–orbit interaction for the 2p hole. We neglect the spin–orbit interaction for the 3d electron as this effect is smaller by a factor of 100 than that of the 2p hole [9]. The spin–orbit interaction for the 2p hole splits the six-fold degeneracy of the 2p level into the two-fold degenerate 2p_1/2 states and the four-fold degenerate 2p_3/2 states, which, when adjoined with a tenfold degenerate 3d level form a 20-fold degenerate L₃ and 40-fold degenerate L₂ peak, with intensity ratio of 1:2. $H_{\text{xf}}$ gives the interaction of the atomic states with the crystal field, which for ${\text{Ti}}^{4+}$ in cubic ${\text{SrTiO}}_3$ consists of the octahedral field of the oxygen atoms. The octahedral crystal field splits the 3d states into the six-fold degenerate T_2g and four-fold degenerate ${\text{E}}_{\text{g}}$ levels, breaking both the L₂- and L₃ edges into two peaks with degeneracy and intensity ratios of 3:2. The direct and exchange Coulomb interactions between the excited electron and hole, in states $i$ and $j$, are included in $g(i,j)$. Untreated manybody effects may be accounted for by scaling the Hartree–Fock values of $g(i,j)$ to 80% [10]. The Coulomb interactions further break the degeneracy of the 60 transitions, causing low intensity peaks to split off the L₃ edge and appear at lower energy. Both edges are shifted in energy and their intensity ratios are strongly affected; the final calculated spectrum (lines in figure 1) has four primary peaks and three lesser features.

Figure 1.

Ti L-edge absorption spectra for ${\text{SrTiO}}_3$. Blue (gray) lines give the unbroadened 2p⁶3d⁰ to 2p⁵3d¹ multiplet spectrum while the solid curve gives the spectrum broadened to resemble experiment.

The multiplet Hamiltonian may be evaluated semi-empirically [4, 5] or by the Bethe–Salpeter method [6, 7]. We follow the semi-empirical approach, using a spin–orbit parameter of 3.78 eV and a crystal field splitting of 2.0 eV. Figure 1 contains the seven multiplet peaks for ${\text{Ti}}^{4+}$, both unbroadened, as obtained from the solution of equation (1), and broadened to match experimental results [11]. Good agreement with the experimental spectrum is obtained by using broadenings of 0.1 eV, 0.4 eV, 0.6 eV, and 1.0 eV for the $a_1$, $a_2$, $b_1$, and $b_2$ peaks, respectively. The minor pre-edge features were broadened 0.3 eV and an additional Gaussian broadening of 0.05 eV was applied to the entire spectrum to simulate experimental resolution. (A step edge was also added for comparison to the experimental spectrum.) The widths of these peaks have been attributed [4, 5] to varying combinations of broadening due to Coster–Kronig decay, solid-state broadening, and charge transfer. However, to fully understand spectra one needs to be able to obtain the spectral widths by parameter-free calculations. Toward this aim, we quantify the primary intrinsic spectral broadening of the Ti L edge of ${\text{SrTiO}}_3$ due to interactions between the excited electronic state and the nuclear motion.

The solid-state vibrational broadening occurs, in part, through the interaction of the excited 3d electron with the crystal field. Since the 3d electron of the ${\text{d}}^1$ excited state of ${\text{Ti}}^{4+}$ occupies an antibonding orbital, the local ${\text{TiO}}_6$ octahedron experiences a Jahn–Teller instability that couples the ${\text{E}}_{\text{g}}$ electron states with the ${\text{e}}_{\text{g}}$ cage distortions. For a long-lived excited electronic state, an E-e Jahn–Teller polaron would occupy the lattice site in the ${\text{d}}^1$ state, similarly to the observation of small and intermediate ${\text{T}}_2\text{-e}$ polarons at ${\text{Ti}}^{3+}$ sites in ${\text{BaTiO}}_3$ [12, 13]. While such ground-state polarons have well defined energies, the generation of a transient excited-state polaron in the present case allows for involvement of a varying number of vibrational quanta, and hence, a multitude of final-state energies. The absorption peaks are modified and broadened due to the expanded set of final states, and because the 3d orbitals become mixed in the presence of the altered crystal field. In section 2 we present the formalism used to quantify the spectral broadening due to the dynamic generation of an E-e Jahn–Teller polaron, and the results and discussion are given in section 3. We find that these vibronic effects account for a majority of the observed broadening of the L₃ peaks, but a smaller fraction of the spectral widths for the L₂ edge. Possible sources for the remaining broadening are discussed.

2. Computational methods

Vibrational broadening of the Ti L-edge spectrum of ${\text{SrTiO}}_3$ occurs because distortions of the crystal field alter the energies of the electronic states and mix those states. The energy spectrum of the coupled electron–lattice system may be found be solving the model Schrödinger equation

$$\left[H_{\text{mult}}^{(0)}+H_{\text{vib}}+W\right]{\chi }_K=E_K{\chi }_K$$ (2)

for the eigenvalues $E_K$. The wavefunctions ${\chi }_K$ exist in the combined state space of the 2p hole, the 3d excited electron, and the relevant vibrational modes. $H_{\text{mult}}^{(0)}$ is the multiplet Hamiltonian of equation (1), discussed in section 1, evaluated for the undistorted lattice. The vibrational Hamiltonian $H_{\text{vib}}={\sum }_{\lambda }ħ{\omega }_{\lambda }\left(n_{\lambda }+1/2\right)$ is assumed to be harmonic, including modes $\lambda$ with energy $ħ{\omega }_{\lambda }$ and occupancy $n_{\lambda }$. The electron–lattice interaction term W is discussed further below.

Vibronic broadening for this system is due primarily to an E-e Jahn–Teller distortion in the ${\text{d}}^1$ excited state that produces a transient polaron. The general solution of the E-e Jahn–Teller problem has been discussed in detail previously [14]. In the present case, the electronic excitation is localized to a single Ti site and a polaron forms about that site, but relaxes as the electronic excitation decays. Therefore, the vibrational modes that we include in equation (2) are not extended phonon modes, but vibrations localized at the excited site. While the physical lattice distortion may extend over several unit cells, we make the approximation of considering only ${\text{e}}_{\text{g}}$ symmetry distortions of the single oxygen cage surrounding the Ti site. The computational approach we utilize is a generalization of that reported for the calculation of the vibronic broadening of the Ti K-edge spectrum of ${\text{SrTiO}}_3$ [15]. We summarize the essential steps for clarity.

The local vibrational modes that have the greatest effect on the Ti ${\text{d}}^1$ excitation spectrum of cubic ${\text{SrTiO}}_3$ were previously determined [15] by mapping the electronic ground- and excited-state Born–Oppenheimer surfaces along the generalized coordinates of several phonon modes. This investigation determined that the ${\text{e}}_{\text{g},3z^2-r^2}$ and ${\text{e}}_{\text{g},x^2-y^2}$ modes most strongly impact the energies of the $d^1$ excited states. Therefore, only broadening due to the ${\text{e}}_{\text{g}}$ modes will be considered when computing the vibronic effects. Furthermore, only the ${\text{E}}_{\text{g}}$ electronic states are strongly affected by these lattice distortions [15]. The force constants for the interaction between the ${\text{E}}_{\text{g}}$ excited electronic system and the ${\text{e}}_{\text{g}}$ vibrational modes was estimated from the derivatives of the excited-state energy with respect to the mode amplitudes. A value of $F=-2.3\text{eV}{\text{Å}}^{-1}$ was obtained for both ${\text{e}}_{\text{g}}$ modes. Ground-state calculations were performed using a plane-wave pseudopotential code within the local-density approximation of density-functional theory and the excited-state energies were obtained by solving the Bethe–Salpeter equation in the GW approximation. Details of the calculations are given in [6, 7, 15].

Since it is unrealistic to model a polaron with a fully periodic phonon mode, the validity of the force constant determined in this manner is not obvious. We performed a simple calculation to check the accuracy of this result. Treating the ions as point charges where oxygen has a charge of $2e$ and titanium has a charge of $-4e(e<0$ is the electron charge), the force acting on the central titanium ion was calculated for two cases. In the first case, all oxygen atoms were displaced according to the ${\text{e}}_{\text{g}}$ phonon modes, while in the second case only the oxygen atoms of the central cage were displaced from their equilibrium positions. Within this model calculation, we found only a 5% difference in the force constants for the two cases, indicating that the previously determined value of $F$ is reasonable. This also suggests that broadening results will not depend significantly on whether the polaron is modeled as a distortion of only the local oxygen cage, as is done in this work, or as a more extended distortion.

The energies of the local ${\text{e}}_{\text{g}}$ cage distortion modes have been estimated [15] from the short-range O–O interatomic force constants. (The interatomic force constants for ${\text{SrTiO}}_3$ were estimated based on those reported for ${\text{BaTiO}}_3$ and ${\text{PbTiO}}_3$ [16].) The two local modes were found to be degenerate with energy $ħ\omega =0.0335$ eV.

Since the ${\text{e}}_{\text{g}}$ vibration modes have even parity, the 3d electron states with odd azimuthal quantum number are not affected. The electron–phonon interaction term of equation (2) is

$$\begin{gathered} W=F\frac{Q_{\theta }}{2}\sum _{\sigma }\left[2a_{0\sigma }^{†}{a}_{0\sigma }-a_{2\sigma }^{†}{a}_{2\sigma }-a_{-2\sigma }^{†}{a}_{-2\sigma }\right] \\ -F\frac{Q_{\theta }}{2}\sum _{\sigma }\left[a_{2\sigma }^{†}{a}_{-2\sigma }+a_{-2\sigma }^{†}{a}_{2\sigma }\right] \\ -F\frac{Q_{ϵ}}{\sqrt{2}}\sum _{\sigma }\left[a_{0\sigma }^{†}{a}_{2\sigma }+a_{2\sigma }^{†}{a}_{0\sigma }+a_{0\sigma }^{†}{a}_{-2\sigma }+a_{-2\sigma }^{†}{a}_{0\sigma }\right], \end{gathered}$$ (3)

where $a_{m\sigma }^{†}\left(a_{m\sigma }\right)$ is the 3d excited electron creation (annihilation) operator with $m$ the azimuthal quantum number and σ the spin. Since we make the simplification of evaluating the multiplet Hamiltonian at the equilibrium lattice configuration of the electronic ground state, the electron creation and annihilation operators are also constructed for this lattice configuration. The ${\text{e}}_{\text{g}}$ local mode coordinate operators are $Q_{\lambda }=\sqrt{ħ/(2\mu \omega )}\left(b_{\lambda }^{†}+b_{\lambda }\right)$; $\mu$ is the oxygen ion mass. The index $\lambda =\theta$ corresponds to the ${\text{e}}_{\text{g},3z^2-r^2}$ mode, while $\lambda =ϵ$ indicates the ${\text{e}}_{\text{g},x^2-y^2}$ mode. $b_{\lambda }^{†}\left(b_{\lambda }\right)$ is the creation (annihilation) operator for mode $\lambda$. $F$ is the electron–lattice force constant reported above.

The electron–lattice interactions in equation (3) affect the energy of the 3d states and mix these states. The first set of terms gives the change in energy of the 3d states due to coupling to the ${\text{e}}_{\text{g},3z^2-r^2}$ mode (the ${\text{e}}_{\text{g},x^2-y^2}$ mode does not alter the energies of the states). The terms in the second bracket give scattering between the $m_{\ell }=\pm 2$ states caused by the ${\text{e}}_{\text{g},3z^2-r^2}$ mode, and the last set of terms are scattering between the $m_{\ell }=0,2$ states and between the $m_{\ell }=0,-2$ states caused by the ${\text{e}}_{\text{g},x^2-y^2}$ mode.

3. Results and discussion

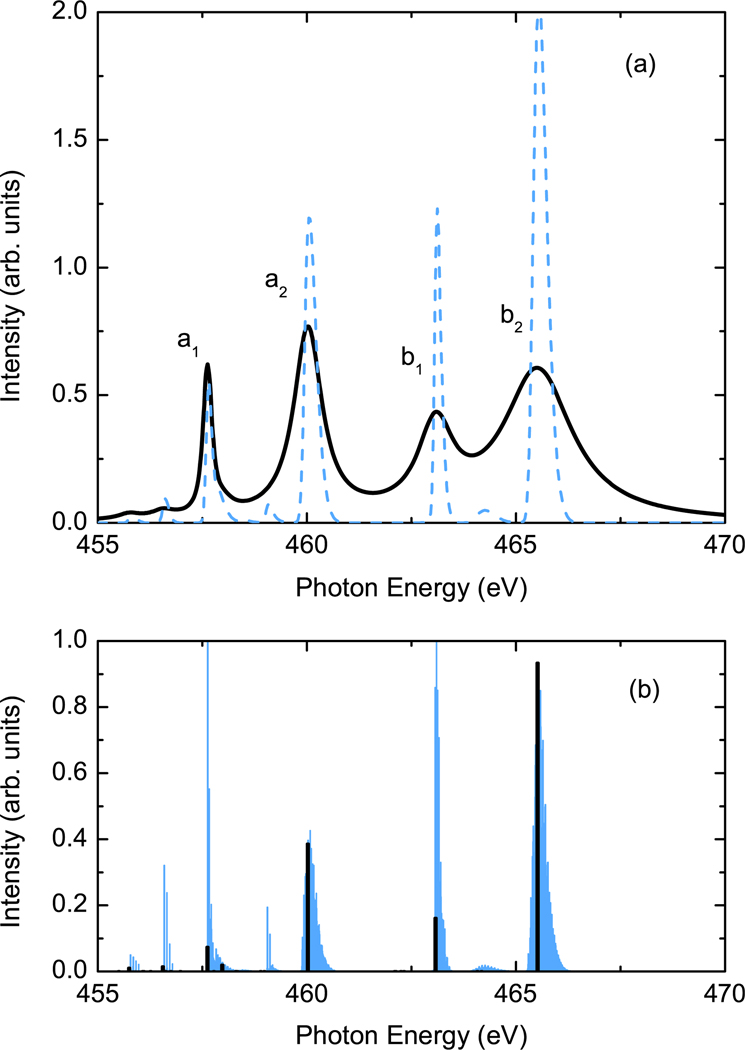
We quantify the degree of vibronic broadening of the Ti L edge of ${\text{SrTiO}}_3$ by first adjoining the space of the ${\text{e}}_{\text{g}}$ local modes $\left(|n_{\theta },n_{ϵ}\rangle \right)$ to the multiplet Hilbert space $\left(|{\underset{\_}{m}}_{\ell }^{(2\text{p})},{\underset{\_}{m}}_s^{(2\text{p})};m_{\ell }^{(3\text{d})},m_s^{(3\text{d})}\rangle \right)$ to form the 6 × 10 × N × N dimensional effective vibronic state space $|{\underset{\_}{m}}_{\ell }^{(2\text{p})},{\underset{\_}{m}}_s^{(2\text{p})};m_{\ell }^{(3\text{d})},m_s^{(3\text{d})};n_{\theta },n_{ϵ}\rangle$. We solve equation (2) with the Haydock recursion method [17] using the electronic wavefunctions for the undistorted lattice. Convergence of the results requires $N=200$ oscillator levels. Figure 2(b) compares the solution of equation (2) for the vibrationally coupled multiplet spectrum to the uncoupled multiplet spectrum obtained from equation (1) and presented previously in figure 1. This comparison indicates that the vibronic coupling has the largest absolute effect on the $a_2$ and $b_2$ peaks, as previously suggested [4]. However, the $a_1$ and $b_1$ peaks are also affected. Close inspection of the vibronic and multiplet spectra in figure 2(b) reveals that two new minor features appear with vibronic coupling. These new peaks are well isolated between the $a_1$ and $a_2$ peaks and between the $b_1$ and $b_2$ peaks, respectively, and likely result from admixture of electronic states of various symmetries in electro-vibrational states when the vibrational coupling is incorporated. For instance, a purely electronic state that has no dipole-allowed transition to the electronic ground state might be admixed with states that do have dipole-allowed transitions. However, these new peaks have little spectral intensity and would likely be difficult to resolve experimentally.

Figure 2.

Effect of vibronic coupling on the Ti L-edge absorption spectra of ${\text{SrTiO}}_3$. (a) The solid black curve gives the absorption spectrum with all broadening effects while the blue (gray) dashed curve gives the absorption spectrum including only vibronic coupling. (b) The vibronically coupled multiplet spectrum (blue or gray lines) is compared to the unbroadened multiplet spectrum of figure 1 (black lines).

In order to quantify the spectral broadening due to vibronic coupling both the unbroadened atomic multiplet spectrum of figure 1 and the vibronic spectrum of figure 2(b) are smoothed by convolving with a Gaussian of 0.05 eV width. The full-width-half-maxima values of the peaks of the smoothed atomic multiplet spectrum (not shown) are subtracted from the full-width-half-maxima values of the peaks of the smoothed vibronic spectrum (shown in figure 2(a)). This procedure reveals a vibronic broadening of 0.07 eV, 0.24 eV, 0.09 eV, and 0.29 eV for the $a_1$, $a_2$, $b_1$, and $b_2$ peaks, respectively. The present results differ moderately from the broadening allocation inferred previously by de Groot et al [4], who estimated minimal solid-state broadening (vibrational and dispersional) for the $a_1$ and $b_1$ peaks and 0.5 eV of solid-state broadening for the $a_2$ and $b_2$ peaks. We find that vibronic coupling accounts for the majority of the broadening of the $a_1$ and $a_2$ peaks, but a lesser fraction of the widths of the $b_1$ and $b_2$ peaks. The numerical results for the spectral widths are summarized in table 1 and the smoothed vibronic spectrum is compared to the fully broadened spectrum in figure 2(a), giving an visual indication of the importance of vibronic coupling. Contrary to the Ti K-edge case [15], the Ti L edge is significantly impacted by vibronic coupling.

Table 1.

Broadening of the four main spectral features. The total and vibronic full-width-half-maximum values of the four primary spectral features of figure 1 are given in eV.

	$a_1$	$a_2$	$b_1$	$b_2$
Total	0.1	0.4	0.6	1.0
Vib.	0.07	0.24	0.09	0.29

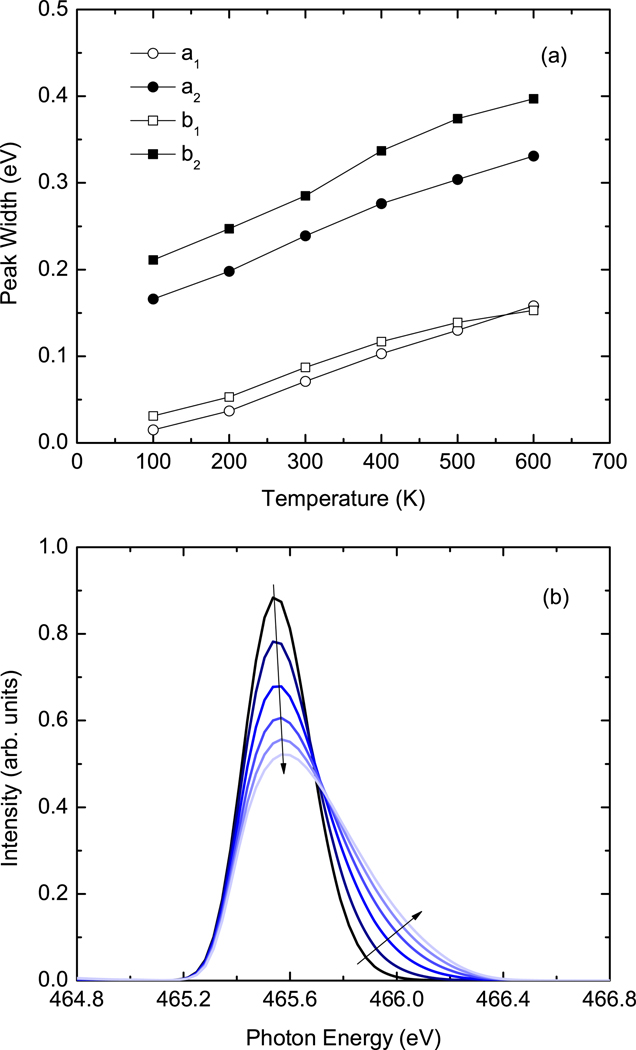
The degree of vibronic broadening depends on the initial lattice configuration, prior to photoexcitation. In many cases this lattice configuration will depend on a thermal population of phonons. Therefore, the vibronic broadening should be temperature-dependent. The oxygen cage distortions introduced by phonons can be decomposed into normal modes. As it is overwhelmingly the ${\text{e}}_{\text{g}}$ modes that couple to the 3d electrons, we approximate the temperature dependence of the initial-state lattice distortion with a thermal population of the local ${\text{e}}_{\text{g}}$ modes, which have an energy equivalent to $ħ\omega /k_{\text{B}}=389\text{K}$ ($k_{\text{B}}$ is Boltzmann’s constant). To determine the temperature dependence of the broadening, we solve equation (2) for several initial-state occupancies of the ${\text{e}}_{\text{g}}$ modes and form a thermal average of the results. The peak widths are found to increase approximately linearly with temperature, about 0.3 meV K⁻¹, as shown in figure 3(a). (The broadened spectra of figure 2, the widths reported in table 1, and the broadening quoted previously pertain to the 300 K result.) Inspection of the temperature dependence of the peaks further reveals that the lineshape becomes increasingly asymmetric with temperature. The temperature dependence of the $b_2$ peak lineshape is presented in figure 3(b). Coupling to the ${\text{e}}_{\text{g}}$ local modes splits each electronic multiplet level into several peaks (as shown in figure 2(b)), and spectral weight is shifted to the high energy side of the distribution as the initial-state ${\text{e}}_{\text{g}}$ phonon population increases.

Figure 3.

Temperature dependence of the vibronic broadening. The top panel shows the full-width-half-maximum of the $a_1$, $a_2$, $b_1$, and $b_2$ peaks as a function of temperature. The bottom panel presents the temperature dependence of the $b_2$ peak. The included curves have temperatures that increase from 100 to 600 K in increments of 100 K in the order indicated by the arrows.

In these calculations we have assumed that the vibrational Hamiltonian is harmonic and that the lattice constant, vibrational frequency, and electron–lattice force constant are independent of temperature. In reality, lattice vibrations contain anharmonic terms that cause thermal expansion, which gives a temperature dependence to each of these quantities. While inclusion of these effects would constitute a more thorough calculation we expect that this would make only a small quantitative change to the results. The broadening we find is of the expected size and, over the temperature range that we consider, the lattice constant changes by less than 1% [18] while the bulk modulus [19] and phonon frequencies [20] both change by approximately 10%.

Several additional sources exist for the difference between the observed total spectral broadening and the vibronic broadening presently calculated. We have reported multiplet calculations assuming ${\text{Ti}}^{4+}$ and O²⁻ charge states, but these values can vary in real samples through charge transfer both between the metal ions and the ligands, and between two metal ions. The broadening effect on the spectrum of ${\text{SrTiO}}_3$ of such charge transfer was recently investigatedboth semi-empirically and from first principles [5]. Coster–Kronig decay is also expected to further broaden the $b_1$ and $b_2$ peaks.

4. Conclusions

By solving a model Hamiltonian containing parameters previously determined from first-principles calculations, we have evaluated the vibronic broadening of the Ti L-edge absorption spectrum of ${\text{SrTiO}}_3$. The largest absolute broadening occurs for the $a_2$ and $b_2$ peaks, 0.24 eV and 0.29 eV, respectively. However, vibronic broadening accounts for a larger fraction, 70% and 60%, of the total broadening for the $a_1$ and $a_2$ peaks, respectively. These results were obtained using an initial-state ${\text{e}}_{\text{g}}$ cage distortion consistent with a room temperature thermal phonon population. The broadening was found to increase with temperature at a rate of 0.3 meV K⁻¹. Two new minor features appeared in the spectrum, having become optically allowed by the electron–lattice coupling.