Abstract
Numerous hydrological applications, such as soil erosion estimation, water resource management, and rain driven damage assessment, demand accurate and reliable rainfall erosivity data. However, the scarcity of gauge rainfall records and the inherent uncertainty in satellite and reanalysis-based rainfall datasets limit rainfall erosivity assessment globally. Here, we present a new global rainfall erosivity dataset (0.1° × 0.1° spatial resolution) integrating satellite (CMORPH and IMERG) and reanalysis (ERA5-Land) derived rainfall erosivity estimates with gauge rainfall erosivity observations collected from approximately 6,200 locations across the globe. We used a machine learning-based Gaussian Process Regression (GPR) model to assimilate multi-source rainfall erosivity estimates alongside geoclimatic covariates to prepare a unified high-resolution mean annual rainfall erosivity product. It has been shown that the proposed rainfall erosivity product performs well during cross-validation with gauge records and inter-comparison with the existing global rainfall erosivity datasets. Furthermore, this dataset offers a new global rainfall erosivity perspective, addressing the limitations of existing datasets and facilitating large-scale hydrological modelling and soil erosion assessments.
Subject terms: Hydrology, Natural hazards, Environmental impact
Background & Summary
Land degradation is a growing global threat to ecosystem goods and services1. It is a human-induced phenomenon that reduces the capacity of soil to support life. As the world population continues to increase, the pressure on soil resources increases, and food security declines2. Soil erosion is a leading process of land degradation due to the detachment of fertile topsoil layers, which plays a vital role in global food security, water security, ecosystem services, and climate change abatement3,4,5. It was estimated that human actions may be responsible for nearly 60% of soil erosion6. Water and wind erosion detach 75 billion metric tons of soil annually, with agricultural land accounting for most of these losses7. The most important type of water erosion is topsoil erosion (splash and sheet processes), which is estimated to occur on 920 M ha of global land, while rill and gully erosion occur on 175 M ha of global land8. According to the report of United Nations9, erosion is one of the significant threats to the soil and impedes progress towards achieving the Sustainable Development Goals (SDGs) related to SGD15 (Life on land) and SGD2 (Zero hunger).
Rainfall erosivity (R-factor) is one of the critical drivers of the soil erosion processes with the greatest spatiotemporal variability10,11. Rainfall erosivity is generally estimated from empirical relations using storm kinetic energy and maximum 30-min rainfall intensity utilising pluviographs of more than 20 years12. In the early 21st century, Yang et al.6 estimated global-scale rainfall erosivity and soil erosion change due to climate and land use changes using the Revised Universal Soil Loss Equation (RUSLE). Further, the Global Land Degradation Information System (GLADIS)13 database was also prepared to provide insight into the global land degradation status and trends. A lack of relatively high temporal-resolution (1–60 min) global rainfall datasets forced these pioneering studies to use medium-resolution (monthly and annual) rainfall datasets for rainfall erosivity estimation. In recent periods, Naipal et al.14 improved the global rainfall erosivity estimation using the rainfall intensity equation for different climatic regions based on the rainfall erosivity datasets from the United States and Europe.
Further, Panagos et al.11 developed the Global Rainfall Erosivity Database (GloREDa) using relatively high temporal-resolution rainfall erosivity data (1–60 min) from 63 countries. Liu et al.15 used a daily erosivity model from limited station sites at a global scale to understand the changes in rainfall erosivity across the globe between 1980 and 2017. More recently, Panagos et al.16 estimated monthly global rainfall erosivity using more than 45,000 monthly erosivity records from 65 countries. Moreover, in recent decades, efforts6,10,11,13–16 have been made to refine the understanding of the global erosivity estimation and reduction in modelling uncertainties. However, the utilization of high-resolution rainfall datasets for estimating rainfall erosivity in global studies has remained limited.
In recent times, noteworthy efforts have been made to update previously developed rainfall erosivity datasets or iso-erodent maps at continental or national levels17–22. These initiatives have been complemented by the recent availability of high-resolution rainfall datasets for many countries, providing valuable new insights into spatiotemporal rainfall erosivity patterns23. The existing global dataset has been used widely as a primary dataset for comparison and benchmarking in numerous regional24,25 and global studies10,26. However, the existing global datasets11,14 showed regional uncertainty due to the limited availability of gauge stations18,19,21,27. Moreover, the existing global rainfall erosivity datasets showed limitations in capturing spatial variation for regions receiving intense rainfall27. Furthermore, rainfall erosivity estimated from low-temporal resolution datasets is prone to incorrect estimation of erosivity values28. The availability of a high-quality rainfall erosivity dataset is a prerequisite for soil erosion estimation and water resource allocations. Given the limited availability of alternative datasets, the scientific community is compelled to rely on pioneering research based on existing datasets, notwithstanding their acknowledged limitations. Nonetheless, the limitations of existing datasets have become evident, showing the scope of the improvements.
The recent availability of global and regional satellite and reanalysis datasets at the sub-hourly and hourly temporal scales provide an opportunity to estimate rainfall erosivity over a large spatial extent. Many recent studies have been conducted to understand the possible role of rainfall erosivity estimation from the satellite and reanalysis rainfall datasets10,25,27,29–35. It is essential to acknowledge that the satellite and reanalysis datasets have inherent uncertainties, which imparts uncertainty in rainfall erosivity estimates10,24,27,29,34.
The inherent uncertainty in satellite and reanalysis data-based rainfall erosivity estimates and the uncertainty in the existing global rainfall erosivity datasets limits the reliable use of these products in soil erosion modelling and policy-making. Improving knowledge and reducing uncertainty in global rainfall erosivity datasets with newer high-resolution global datasets is essential for decision-makers and earth-system modellers. For instance, Panagos et al.36 combined the measured erosivity datasets with General Circulation Models (GCMs), simulating future projections of rainfall erosivity for 2050 and 2070. At the global scale, there is a limited number of rainfall erosivity datasets available, and earth system modellers are seeking new datasets with a fresh perspective. While multisource-based datasets have proven reliable for many hydrological applications37, they have been limitedly used in rainfall erosivity estimation. For example, using a non-parametric quantile regression forest, Bhuiyan et al.38 showed that a multi-source precipitation dataset significantly improved the streamflow simulations. Similarly, Pham et al.39 illustrated the effectiveness of Artificial Intelligence (AI) models incorporating meteorological parameters in predicting daily rainfall in Vietnam. Additionally, prior studies have explored various merging techniques, including geostatistical interpolation40,41 and machine learning-based merging using Support Vector Machine42,43, Random Forest44 and XGBoost45, and Neural Network46 to integrate global precipitation products with limited gauge observations. These approaches have effectively addressed the limitations associated with individual satellite and reanalysis datasets. Moreover, the notable success achieved by machine learning models motivates us to extend their application to rainfall erosivity estimation, leveraging multi-source datasets. We employed a Gaussian Process Regression-based machine learning model, which shows promise in enhancing the accuracy and robustness of rainfall erosivity estimation.
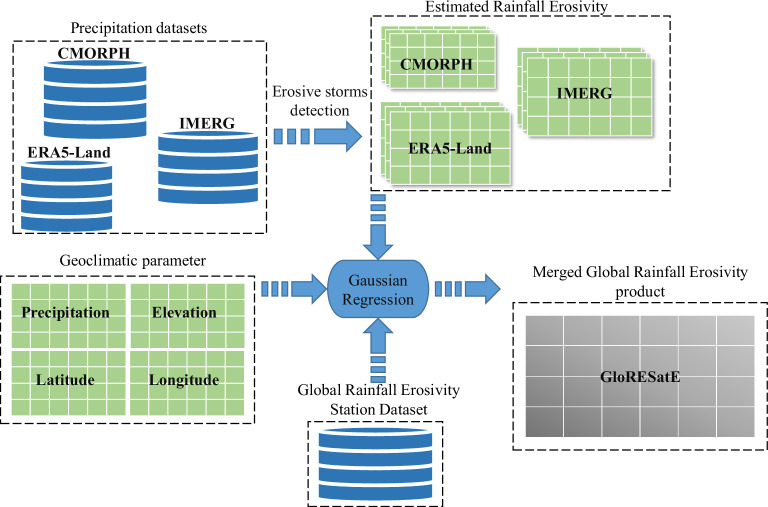
Therefore, this study aims to present a new global rainfall erosivity dataset generated using a machine learning-based fusion of erosivity estimated from multiple datasets. First, we estimated annual rainfall erosivity from two high-resolution gridded global satellites and one reanalysis precipitation dataset covering the most recent available periods. This process included the estimation of annual rainfall erosivity from satellite-based datasets such as IMERG-Final Run and CMORPH, as well as the reanalysis dataset ERA5-Land. These erosivity estimates and geoclimatic parameters, specifically elevation, latitude, longitude, and mean annual precipitation from the IMERG-Final Run dataset were used to construct a robust regression framework. Within this framework, we integrated a collection of gauge rainfall erosivity data from 6,170 stations across the globe. This amalgamation enabled us to generate a unified global rainfall erosivity dataset, seamlessly merging information from satellite, reanalysis, and gauge records. The workflow of this study is shown in Fig. 1.
Fig. 1.
A framework for generating a new global rainfall erosivity dataset.
Methods
Rainfall datasets
The present study utilises two high-resolution gridded global satellites and one reanalysis precipitation dataset for rainfall erosivity estimation. The satellite precipitation datasets used in this study are (a) Climate Prediction Center Morphing Technique (CMORPH) (Version 1) (10.25921/w9va-q159) and (b) Integrated Multi-satellitE Retrievals for GPM (IMERG) (Version 6) (https://disc.gsfc.nasa.gov/datasets) Final Run. The reanalysis dataset used in this study is the Fifth generation of European ReAnalysis (ERA5)- Land (https://cds.climate.copernicus.eu/cdsapp). More detailed information about the datasets can be found in the Supplementary Information. An overview of the datasets used is available in Table 1.
Table 1.
Overview of satellite and reanalysis precipitation datasets used in this study.
| Datasets | Spatial resolution (Approx.) | Spatial coverage | Temporal resolution | Period covered | References |
|---|---|---|---|---|---|
| CMORPH (Version 1) | 0.07° × 0.07° | 60° N-S | 30 min | 1998–2021 | Xie et al.116,117 |
| IMERG Final Run (Version 6) | 0.1° × 0.1° | 90° N-S | 30 min | 2001–2020 | Huffman et al.118 |
| ERA5-Land | 0.1° × 0.1° | 90° N-S | 60 min | 2001–2021 | Muñoz-Sabater et al.119 |
Global rainfall erosivity station dataset
The rainfall erosivity station dataset was collected by conducting a thorough literature survey of the already published studies. Through an extensive literature survey and survey of regional datasets around the globe, a large number of high-resolution rainfall erosivity station datasets were collected and compiled as a representative database covering different climatic and geographical regions worldwide. This global rainfall erosivity station dataset includes the following datasets:
A collection of rainfall erosivity datasets of 12 counties across the globe estimated using high-resolution long-term rainfall data. The collection includes rainfall erosivity data from the United States19,47, Micronesia19,47, China18, and Iran22. The dataset also consists of the rainfall erosivity literature survey dataset used for rainfall erosivity study over South America20 including Argentina48, Brazil49–51, Chile52, Colombia53,54, Paraguay55, Peru56, Uruguay57, and Venezuela58.
The rainfall erosivity data collected through the literature survey from 27 countries across the globe. This includes the data of Australia59–61, Bangladesh62, Brazil63,64, Canada65,66, Honduras67, India68,69, Malaysia70,71, Mauritius72, South Korea73, Japan74,75, and New Zealand76 and the rainfall erosivity literature survey data from 16 countries in Africa used in continental study29,77, including Cape Verde78 and Canary Islands79.
Data from the recently launched Global Rainfall Erosivity Dataset (GloREDa)16,80. From the GloREDa, we used the rainfall erosivity dataset of European countries and other countries’ rainfall erosivity data, including Israel, Japan, Kuwait, Palestine, the Russian Federation, Turkiye, and Yemen. This encompasses rainfall erosivity data from a total of 36 counties.
Detailed information about most of the high-resolution (1–60 min) rainfall erosivity datasets collected and used in this study has been given in Table 2. A high-resolution hourly rainfall dataset from the India Meteorological Department (IMD) (https://dsp.imdpune.gov.in/index.php) was incorporated with temporal coverage from 1969 to 2021. The estimated rainfall erosivity from these 249 stations was further amalgamated into the global rainfall erosivity station dataset, resulting in a comprehensive representation of 296 stations in India.
Table 2.
Overview of high-resolution long-term mean annual rainfall erosivity dataset used in the study collected from different sources.
| Continent | Country/Island | Number of Stations | Temporal Resolution | Start and end year (Approx.) | Author |
|---|---|---|---|---|---|
| Africa | Mauritius | 4 | 6 min | 2005–2008 | Anderson72 |
| Australia - Oceania | Australia | 159 | 6 min | 1961–2000 | Yu, B et al.60,61 |
| Australia - Oceania | New Zealand | 32 | 10 min | 1997–2012 | Klik et al.76 |
| Australia - Oceania | Micronesia, Guam, Hawai | 75 | 15 min | 1970–2013 | McGehee et al.19, NCDC47 |
| Asia | India | 296 | 1 min, 15 min, 60 min | 1994–2015, 1969–2021 | Dash et al.68; Babu et al.69; This study |
| Asia | Kuwait, Russian Federation, Israel, Palestinian Territory, Turkiye, Yemen | 367 | 1–60 min | 1961–2016 | Panagos et al.16,80 |
| Asia | South Korea | 41 | 5 min | 1961–2015 | Lee et al.120; Shin et al.73 |
| Asia | Malaysia | 34 | 10 min | 1999–2008 | Leow et al.71 |
| Asia | Japan | 82 | 10 min, 60 min | 1995–2015, 1990–2009 | Laceby et al.75; Santosa et al.74. Panagos et al.16,80 |
| Asia | China | 173 | 10 min, 1 min | 1998–2002, 1951–2018 | Ma et al.121; Yue et al.18 |
| Europe | Austria | 76 | 5 min | 1995–2015 | Johannsen et al.21 |
| Europe | Czechia | 85 | 10 min | 1989–2003 | Hanel et al.122 |
| Europe | Austria, Belgium, Bulgaria, Croatia, Cyprus, Czechia, Denmark, Estonia, France, Germany, Greece, Hungary, Ireland, Italy, Latvia, Liechtenstein, Lithuania, Luxembourg, Netherlands, Poland, Portugal, Romania, Russian Federation, Slovakia, Slovenia, Spain, Sweden, Switzerland, United Kingdom | 1804 | 1–60 min | 1980–2022 | Panagos et al.16,80,123; Borrelli et al.111 |
| North America | United States | 2351 | 15 min | 1970–2013 | McGehee et al.19, NCDC47 |
| North America | Puerto Rico | 22 | 15 min | 1970–2013 | McGehee et al.19, NCDC47 |
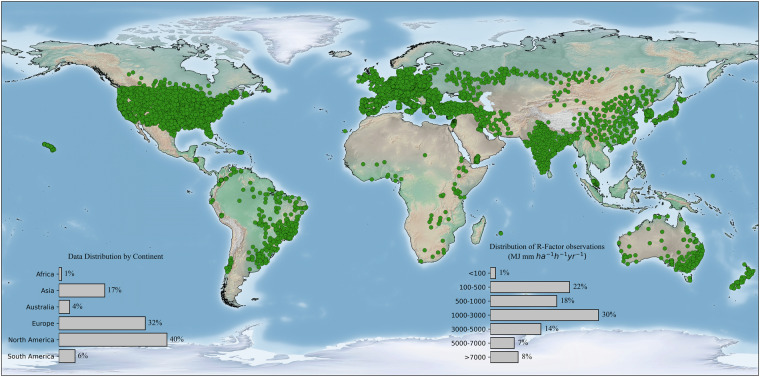
Moreover, the global station dataset used in this study contains representative annual rainfall erosivity values of 6,170 stations covering 72 counties worldwide. The global rainfall erosivity station dataset (Fig. 2) contains ~91% of the stations that use high-resolution rainfall data (≤60 min), and the rest uses the regional rainfall erosivity equation for rainfall erosivity estimation. The number of representative rainfall erosivity stations varies among the continents. North America has the highest number of representative rainfall erosivity stations, with 2,441 stations (~40%), and Africa has the lowest number of rainfall erosivity stations, with 52 stations (~1%). Europe has 1,965 (~32%) stations, the second-highest contributor to the dataset. We have collected 1069 (~17%) and 266 (~4%) stations over Asia and Australia-Oceania, well represented to the erosivity classes. Over South America, 377 (~6%) station data was collected, including data from high erosivity countries Brazil, Colombia, and Venezuela.
Fig. 2.
Locations of global rainfall erosivity station (n = 6,170) dataset used in this study.
The dataset exhibits a comprehensive representation across various climate zones and therefore rainfall erosivity conditions. Approximately 8% of the stations demonstrate very high rainfall erosivity values exceeding 7,000 MJ.mm.ha−1.h−1.year−1, around 7% of total stations have rainfall erosivity values within the 5,000 to 7000 MJ.mm.ha−1.h−1.year−1. Nearly 30% of the stations have rainfall erosivity values ranging between 1,000 to 3,000 MJ.mm.ha−1.h−1.year−1, and approximately 23% register rainfall erosivity values below 500 MJ.mm.ha−1.h−1.year−1.
Harmonization of different time resolutions in original data
In addressing the variability in the range of available time resolution of data, calibration of erosivity values at different time resolutions becomes necessary. According to GloRESatE statistics, approximately 69.1% of stations provided rainfall data at very high resolution (≤15 min), around 13.3% at intermediate resolution (30 min), and the remaining around 8.8% at a resolution of 60 min. Given this heterogeneity, a calibration process is crucial.
A 30-min time resolution was chosen as an acceptable compromise between the coarse resolution of 60 min and the higher ones (≤15 min). All the rainfall erosivity values obtained from the various temporal resolutions were converted to 30-min rainfall erosivity values using a conversion factor derived from high-resolution rainfall erosivity data from Europe81. Numerous studies worldwide have employed similar conversion factors to harmonize different rainfall erosivity datasets16,82.
It is worth mentioning that the final version of the global rainfall erosivity station dataset consists of a collection of 30-min rainfall erosivity values harmonized from various temporal resolutions. These calibration factors, developed in the European study, align with range values provided in the literature from studies conducted in China83, Italy84, India82, and the USA85–87.
Rainfall erosivity estimation
The rainfall erosivity was estimated from gridded satellite and reanalysis datasets at temporal resolutions of 30 and 60 min, following the procedure outlined in recent studies10,27,87. The rainfall events with a cumulative rainfall of more than 12.7 mm were considered erosive events, and rainfall less than 1.27 mm of more than 6 h was considered dry period87. The total kinetic energy of the erosive storm was computed using the rainfall kinetic energy and intensity equation (Eq. 1), a modified version of Brown-Foster relationship88. The same equation has been popularly used in recent studies18,19 and Revised Soil Loss Equation Version 2 (RUSLE2)89. The total kinetic energy (Eq. 2) was estimated, summing the kinetic energy of each time interval. Finally, average annual rainfall erosivity (Eq. 3) was estimated, averaging the total rainfall erosivity of years.
| 1 |
where e is a rainfall kinetic energy per unit depth (MJ.ha−1.mm−1) for a particular period, and i is the rainfall intensity in mm.h−1.
The total kinetic energy (E) of an erosive event was calculated by summing the multiplication of the rainfall kinetic energy per unit depth (e) (MJ.ha−1.mm−1) and rainfall depth (θ) (mm) over the entire period of the erosive storm.
| 2 |
where D is the total duration of the erosive storm, and dt is the time increment of the erosive storm.
The rainfall erosivity was calculated by multiplying the total kinetic energy (E) (MJ.ha−1) with the maximum 30-minute intensity (I30) (mm.h−1) of the storm. The mean annual rainfall erosivity (R) was calculated by summing all storm erosivity values over the years and dividing by the total number of year records.
| 3 |
where R is the mean annual rainfall erosivity in MJ.mm.ha−1.h−1.year−1, n is the number of years, and m is the total number of erosive events.
Merging multi-source datasets
The proposed merged long-term mean annual rainfall erosivity product, Global Rainfall Erosivity from Reanalysis and Satellite Estimates (GloRESatE) is prepared to address uncertainty in satellite and reanalysis erosivity estimates and the limited availability of observed rainfall erosivity dataset globally. We used a machine learning-based regression approach to merge multiple satellite and reanalysis datasets with the station datasets to improve the accuracy of global rainfall estimation. This integration is accomplished by considering geoclimatic covariates. Essentially, this approach aims to identify a relation between the estimated rainfall erosivity from satellite and reanalysis sources, alongside geoclimatic variables, and the global rainfall erosivity station dataset. The covariates used in this study involve
Estimated rainfall erosivity: Derived long-term (2001–2020) mean of annual rainfall erosivity estimates from the satellite (IMERG-Final Run and CMORPH) and reanalysis (ERA5-Land) datasets.
Geoclimatic parameter: Latitude, longitude of grids, and elevation data from the ~1 km WorldClim90 dataset (https://www.worldclim.org/).
Climatic parameter: The long-term (2001–2020) mean annual precipitation from the IMERG-Final Run dataset.
Initially, we employed an area conservative regridding technique91 to re-grid all datasets into common grids. While various algorithms exist for regridding datasets into common grids, they may not be optimal for rainfall and rainfall erosivity data due to their high intermittency and localised extremes92. To address this challenge, we utilised an area-conservative regridding scheme, ensuring the preservation of total values during the process. The regridding from finer to coarser resolution was accomplished using the following equation92,93:
| 4 |
where denotes the value of any variable over the designated cell k with an area Ak. pn represents the variable value at the source cell n, while N represents the total number of source cells intersecting within the designated cell. Ank indicates the intersection area between cells n and k.
Then, we used Gaussian Process Regression (GPR)94 to establish a robust regression framework between derived covariates and gauge rainfall erosivity estimates. The known capability of the machine learning models to capture non-linear relationships between input and output variables, suppressing the constraints of traditional statistical models, is expected to improve global rainfall erosivity estimation. The response variable (y) and covariate variable vectors (x), the regression function can be written as
| 5 |
where f(x) represents the deterministic part of the model. It combines feature x with weights w, transformed by the kernel function K. The represents random noise with mean 0 and variance σ2.
The Radial Basis Function (RBF) kernel is most commonly used in machine learning; it can model complex relationships between input and output variables. The GPR model was tested for kernel functions, including ‘rbf’ and ‘Matern’ kernels. Among the tested kernels, a ‘rbf’ showed an excellent performance. The Radial Basis Function used in this study can be written as
| 6 |
where l is the length scale parameter (l > 0) and d(xiyj) is the Euclidian distance between two points xi and yj.
Feature importance of predictor variables
In our study, we utilised a machine learning-based Random Forest model to assess the importance of each feature used in our analysis. Random Forest employs a bootstrapping approach where trees are grown in a decorrelated manner. If B number of trees are identically distributed with positive pairwise correlation ρ and each with variance σ2, the variance of all trees can be expressed as95:
| 7 |
As B increases, the second term diminishes, indicating that the correlation of bagged tree pairs limits the benefits of averaging. Specifically, when trees are grown, a subset of m ≤ p input variables is randomly selected as candidates. After B, such trees are grown, the Random Forest predictor is formulated as:
| 8 |
where θb represents the characteristics of the b-th Random Forest tree in terms of split variables, cutpoints at each node, and terminal node values.
Optimisation of the model
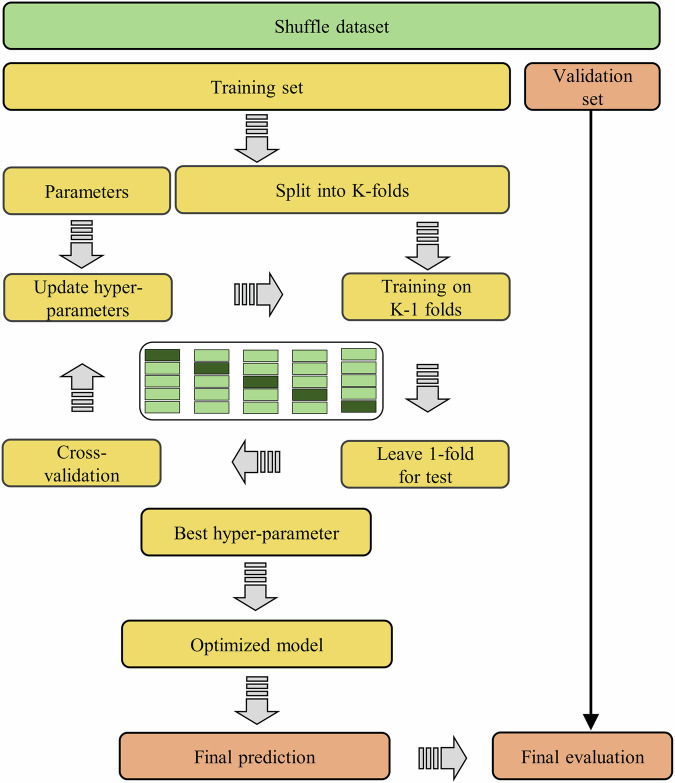
The process unfolds as follows: First, the entire dataset underwent a randomised splitting process to ensure robust model training and evaluation. Initially, 80% of the entire dataset was allocated for training purposes, with the remaining 20% reserved for validation, as illustrated in Fig. 3. Subsequently, the training dataset was partitioned into K-folds, with K set to 5. This involved dividing the dataset into K equal-sized subsets, utilising K-1 folds for training and the remaining fold for testing. This process was iterated K-times, rotating the testing set each time to ensure comprehensive model assessment.
Fig. 3.
Outline of the methodology used for the model testing.
Moreover, the dataset was categorised into three sets: training, testing, and validation. During the cross-validation procedure, varying sets of the ‘length scale’ and regularisation parameter (‘alpha’) of the GPR model were explored to enhance model performance while minimising errors. This process obtained an optimal value of hyperparameters by maximising the cross-validation score. The Bayesian Optimization Algorithm96 (BOA) process effectively optimised the hyperparameters. This algorithm treats the objective function as a black-box function, seeking to maximise the output return value with minimal trials.
Notably, BOA relies on an optimised observation-fitting probability model97. An alternative function is created to find the value that minimises the objective function based on the past evaluation results of the objective function. Compared to other methods, BOA selects the parameters based on past evaluation results, saving search time and optimising efficiency98. The BOA process includes four primary steps99: 1. Defining the hyperparameter search space, 2. Evaluating the test set with a set of hyperparameters, 3. Using the objective function to choose hyperparameter values for the new evaluation, and 4. Reviewing the objective function results, finalizing hyperparameter values, and assessing them on the test set.
Accuracy evaluation
In this study, we evaluated the dataset performances using four statistical indicators. The indicators include Percentage Error (PE), Pearson’s correlation coefficient (r), Nash Sutcliffe Efficiency (NSE), and unbiased Root Mean Square Error (ubRMSE). A more detailed definition of these performance indicators can be found in Supplementary Information and Chicco et al.100, Moriasi et al.101, Press et al.102, Krause et al.103, and Ma, H. et al.104.
| 9 |
| 10 |
| 11 |
| 12 |
where O is the observed values, P is the estimated values, is the mean value of observed values, is the mean of estimated values, and E represents the mean operator.
Data Records
The estimated global annual rainfall erosivity for each satellite and reanalysis dataset, at their original spatial resolution, is available on Zenodo105 (10.5281/zenodo.11078865). The merged global rainfall erosivity product, estimated from satellite and reanalysis data and incorporating the global rainfall erosivity station dataset, has also been uploaded to the same repository. This product has a spatial resolution of 0.1° × 0.1° and is freely available for download. All the raster datasets are provided with a “.tif” extension, and the estimated rainfall erosivity is in units of MJ.mm.ha−1.h−1. The long-term mean annual rainfall erosivity values are in MJ.mm.ha−1. h−1.year−1.The details about every file in the repository are as follows:
“CMORPH.zip”: Contains global rainfall erosivity data estimated from the CMORPH dataset spanning from 1998 to 2021 with a spatial resolution of approx. 0.07° × 0.07°. Each file is named “CMORPH _yyyy.tif”, where “yyyy” represents the year. Each “.tif” file contains 13 bands, with “Band 1” to “Band 12” containing the monthly rainfall erosivity from January to December and “Band 13” containing the annual rainfall erosivity for that year.
“IMERGFinalRun.zip”: Contains global rainfall erosivity data estimated from the IMERG Final Run dataset spanning from 2001 to 2020 with a spatial resolution of 0.1° × 0.1°. Each file is named “IMERGFinalRun_yyyy.tif”, where “yyyy” represents the year. The Band structure of each “.tif” file is similar to “CMORPH_yyyy.tif” files.
“ERA5Land.zip”: Contains global rainfall erosivity data estimated from the ERA5 Land dataset spanning from 2001 to 2021 with a spatial resolution of 0.1° × 0.1°. Each file is named “ERA5Land_yyyy.tif”, where “yyyy” represents the year. The Band structure of each “.tif” file is similar to the “CMORPH_yyyy.tif” file.
“EstimatedMean.zip”: Contains the temporal mean annual rainfall erosivity of all three gridded satellites and the reanalysis dataset. Each file is named “xxxx_mean_yyyy_zzzz.tif”, where “xxxx” is the name of the satellite or reanalysis dataset, “yyyy” is the start year, and “zzzz” is the end year of the mean.
“GloRESatE.zip”: Contains the merged global long-term mean annual rainfall erosivity product with a spatial resolution of 0.1° × 0.1°, the file named “GloRESatE.tif” and associated uncertainty file named “Uncertainty.tif.”
“Rainfall Erosivity Data.csv”: Contains the observed global rainfall erosivity station dataset.
Technical Validation
Performance of merging
The Gaussian Process Regression (GPR) is a powerful and flexible non-parametric regression technique with the added advantage of probabilistic uncertainty estimation. In this study, we used GPR to merge the multi-source datasets. A comprehensive analysis was conducted on all the parameters utilised for model fitting to ensure robustness. A Random Forest model was employed to assess the importance of each parameter, revealing the potential of overfitting attributed to a single parameter (Supplementary Information). The analysis highlighted the CMORPH R-factor as the most crucial one, given the utilisation of the bias-corrected CMORPH dataset.
Additionally, the IMERG R-factor emerged as another crucial factor for consideration, contributing significantly to model accuracy. The geoclimatic parameters also showed significant importance for the modelling. They were included for the accurate representation, especially in high-altitude regions. The optimised GPR model used in this study demonstrated good performance (Table 3) with a training Nash Sutcliffe Efficiency (NSE) of 0.920, a correlation coefficient of 0.957 and an unbiased Root Mean Square Error (ubRMSE) of 873 MJ.mm.ha−1.h−1.year−1. Through optimisation involving adjustments to the length scale and regularisation parameter (alpha), the model achieved a good cross-validation score of 0.879 from 5-fold with the optimised parameters. Furthermore, the GPR model underwent further evaluation against a separate validation set, revealing a good NSE of 0.876 and an ubRMSE of 1015 MJ.mm.ha−1.h−1.year−1. Overall, the optimised GPR model employed in this study exhibited consistent and robust performance across training-testing and validation sets, highlighting its efficiency and suitability for the merging.
Table 3.
Selected model parameters and performance during training and validation.
| Kernel | Search space | Optimised value | Metrics | Training | Validation |
|---|---|---|---|---|---|
| RBF | 10−5 to 105 | Length Scale: 52.47 | PE (%) | +7 ± 42 | +9 ± 51 |
| r | 0.957 | 0.936 | |||
| 10−5 to 105 | Alpha: 0.030 | NSE | 0.920 | 0.876 | |
| ubRMSE (MJ.mm.ha−1.h−1.year−1) | 873 | 1015 |
Comparison of satellite and reanalysis estimates with observed dataset
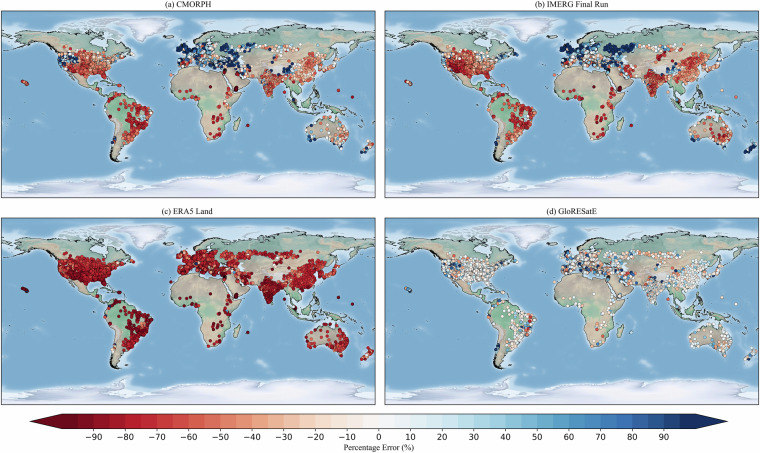
The mean annual rainfall erosivity estimated from satellite and reanalysis datasets from 2001 to 2020 was compared with a global rainfall erosivity station dataset of 6,170 representative stations across 72 countries. Since the ERA5-Land rainfall erosivity was computed from the 60-min precipitation dataset, the extracted rainfall erosivity values were converted to 30-min rainfall erosivity for fair comparison by multiplying the conversion factor106 as used for the global rainfall erosivity station dataset. The percentage error with the global rainfall erosivity station dataset has been shown in Fig. 4a–c. At the global scale, the overall mean (±standard deviation) percentage error varies significantly across different datasets, ranging from −70 (±29) % to +10 (±262) % (Table 4). The detailed definitions used for the performance estimation of the datasets are provided in the Supplementary Information. Among the dataset, IMERG-derived rainfall erosivity exhibited a low mean percentage error (−3%) with a high standard deviation (±99%), while ERA5-Land showed a high mean percentage error (−70%). The IMERG-F (Final Run) derived rainfall erosivity displayed a strong positive correlation (r = 0.777) with the global rainfall erosivity station dataset at the global scale. Notably, the IMERG-F-derived rainfall erosivity showed the lowest ubRMSE of 2151 MJ.mm.ha−1.h−1.year−1 among all the derived rainfall erosivity datasets. The CMORPH dataset has a similar correlation (r = 0.726) with the global rainfall erosivity station dataset. However, the correlation between the reanalysis data-derived rainfall erosivity and the global rainfall erosivity station dataset was low, with a correlation coefficient of less than 0.50. Overall, at the global scale, IMERG-F-derived rainfall erosivity showed better performance than other datasets, exhibiting a stronger correlation, low percentage error, and low unbiased Root Mean Square Error (ubRMSE) compared to the global rainfall erosivity station dataset.
Fig. 4.
Percentage error in the long-term mean annual rainfall erosivity between global rainfall erosivity station dataset and estimated four rainfall erosivity datasets.
Table 4.
Evaluation metrics results for the different climatic regions, comparing long-term mean rainfall erosivity estimated from the three rainfall products with the global rainfall erosivity station dataset.
| Datasets | Metrics | All-inclusive | Tropical | Arid | Temperate | Cold | Polar |
|---|---|---|---|---|---|---|---|
| CMORPH | PE (%) | +10 ± 262 | −47 ± 38 | +37 ± 613 | +13 ± 132 | +6 ± 97 | +92 ± 195 |
| r | 0.726 | 0.553 | 0.570 | 0.602 | 0.775 | — | |
| NSE | 0.352 | −0.584 | 0.195 | 0.167 | 0.470 | — | |
| ubRMSE (MJ.mm.ha−1.h−1.year−1) | 2209 | 4010 | 967 | 2268 | 845 | — | |
| IMERG-Final | PE (%) | −3 ± 99 | −50 ± 30 | −32 ± 116 | +4 ± 111 | +11 ± 78 | +101 ± 259 |
| r | 0.777 | 0.656 | 0.637 | 0.694 | 0.791 | — | |
| NSE | 0.373 | −0.597 | 0.134 | 0.233 | 0.538 | — | |
| ubRMSE (MJ.mm.ha−1.h−1.year−1) | 2151 | 3814 | 927 | 2119 | 811 | — | |
| ERA5-Land | PE (%) | −70 ± 29 | −79 ± 43 | −75 ± 23 | −70 ± 30 | −66 ± 20 | −42 ± 77 |
| r | 0.356 | 0.120 | 0.626 | 0.407 | 0.862 | — | |
| NSE | −0.290 | −2.307 | −0.310 | −0.541 | −0.237 | — | |
| ubRMSE (MJ.mm.ha−1.h−1.year−1) | 2821 | 5637 | 1053 | 2542 | 993 | — |
The evaluation results for different climatic conditions are summarised in Table 4. The global climatic regions were identified using the 1-km Koppen-Geiger107 climate classification map (Supplementary Information). Due to the limited availability of the rainfall erosivity station data in the polar climate region, only the percentage error (PE) has been estimated. Across tropical climatic regions, the rainfall erosivity estimated from satellite precipitation datasets has a substantial underestimation (mean PE ~ −50%) compared to the global rainfall erosivity station dataset. The reanalysis-derived rainfall erosivity shows an even greater underestimation, exceeding the mean PE by −80%. A low mean percentage error has been observed in the temperate climatic region using the CMORPH (+13 ± 132%) and IMERG-F (+4 ± 111%) dataset, with a notably high standard deviation of percentage error. In the cold climatic conditions, ERA5-Land showed significant underestimation. Across the polar climatic regions, all satellite datasets overestimated rainfall erosivity; however, reanalysis-derived data showed underestimation. Among the satellite-derived rainfall erosivity, IMERG-F exhibited a strong positive correlation (r > 0.65) with the global rainfall erosivity station dataset for the tropical climatic regions. Other satellite-derived rainfall erosivity products show a moderate positive correlation with the tropical climatic regions. A similar positive correlation has been observed for almost all the satellite and reanalysis-derived rainfall erosivity products in arid and cold climatic conditions. Furthermore, ERA5-Land-derived rainfall erosivity showed a strong positive correlation of more than 0.80 in cold climatic conditions.
Additionally, we evaluated the performance efficiency of estimated rainfall erosivity from the satellite and reanalysis datasets compared to the global rainfall erosivity station dataset using the Nash-Sutcliffe efficiency (NSE) for different climatic regions. Despite a moderate positive correlation, the results indicated unsatisfactory efficiency (NSE < 0.30) for the tropical climatic regions, suggesting the inefficiency of the satellite-derived rainfall erosivity datasets in accurately estimating rainfall erosivity values for tropical climates. Similar unsatisfactory performances from the satellite and reanalysis-derived rainfall erosivity were observed in temperate and cold climatic conditions.
Furthermore, the ubRMSE for the satellite-derived rainfall erosivity dataset was notably high (~4,000 MJ.mm.ha−1.h−1.year−1) in the tropical climatic regions, with even higher values (~5,500 MJ.mm.ha−1.h−1.year−1) for the reanalysis derived rainfall erosivity. Among the satellite and reanalysis-derived datasets, the IMERG-F-derived rainfall erosivity had the lowest ubRMSE across most climates, showcasing its superior performance. Despite the limitations of satellite and reanalysis datasets at the sub-daily temporal scale, IMERG-F consistently showed more accuracy than other satellite and reanalysis estimates, aligning closely with the outcome of the global review of IMERG dataset108. Moreover, it is worth noting that the satellite-derived rainfall erosivity generally performed better than the reanalysis-derived estimates for most climatic conditions. However, over cold climates, reanalysis-derived estimates showed a higher correlation with the observed dataset, possibly due to the limitations of satellite estimates over cold climates109. Furthermore, it is important to highlight that none of the satellite and reanalysis datasets consistently exhibited very good performances across all climate regions, underscoring the necessity for significant improvements.
Comparison of GloRESatE with the existing global product
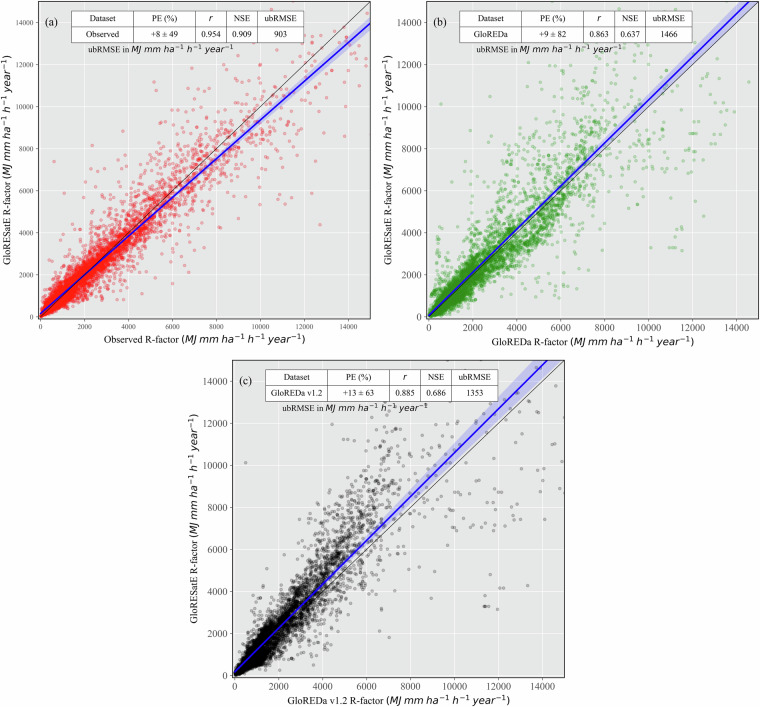
The existing 30 arc-seconds (~1 km) global rainfall erosivity map and Global Rainfall Erosivity Database (GloREDa) prepared by Panagos et al.11,16. showed an incremental improvement over the previous studies. Among the available global datasets, GloREDa has served as a benchmark for many global10 and regional studies24,25,34 in recent decades. Therefore, the newly developed merged GloRESatE105 estimate was compared with the GloREDa versions and global rainfall erosivity station datasets (Fig. 5). The rainfall erosivity values were extracted from the raster datasets (GloREDa and GloRESatE105) for the common locations within the global rainfall erosivity station dataset.
Fig. 5.
Scatter plot of estimated global rainfall erosivity in this study (GloRESatE105) with (a) the global rainfall erosivity station dataset, (b) the existing global estimates GloREDa (Panagos et al.11) and (c) GloREDa v1.2 (Panagos et al.16).
The performance was evaluated using Ordinary Least Squares (OLS) regression (Table 5) and evaluation metrics. For a perfect fit, the best-fit line should match the regression line with the black 1:1 line and have an intercept of zero and a regression coefficient close to one. Notably, the regression line between the modelled GloRESatE105 rainfall erosivity dataset and the global rainfall erosivity station dataset is close to the 1:1 line and showed an excellent coefficient of determination (R2 = 0.910). The regression coefficient is close to one, and the intercept is low. The merged GloRESatE product showed an overall mean percentage error (PE) of only +8 (±49) % and a correlation (r) of 0.954. The Nash-Sutcliffe efficiency (NSE) of GloRESatE105 modelled data is 0.910, which is much higher than the original satellite and reanalysis-derived rainfall erosivity products. The merged dataset showed a very low ubRMSE value of 903 MJ.mm.ha−1.h−1.year−1, the lowest among other datasets.
Table 5.
Ordinary Least Squares (OLS) regression statistics of our estimated global rainfall erosivity (GloRESatE105) compared to the global rainfall erosivity station dataset and existing global rainfall erosivity datasets (GloREDa11,16).
When compared to the existing global rainfall erosivity dataset (GloREDa11), the GloRESatE105 exhibited a coefficient of determination (R2) of 0.745, mean percentage error (PE) of +9 (±82) %, and an ubRMSE of 1466 MJ.mm.ha−1.h−1.year−1. Our estimates also showed a good performance with the newly launched GloREDa v1.2, which has a correlation of 0.885 and NSE of 0.686, with a percentage error of only + 13%. Moreover, our dataset correlates more with the new version of GloREDa than the earlier version. The better performance of the developed GloRESatE105 rainfall erosivity dataset compared to the original satellite and reanalysis estimates underscores the need to utilise multi-source datasets to improve the performance of the global rainfall erosivity dataset. Furthermore, including more gauge station data in the global rainfall erosivity modelling brings an incremental improvement. Our newly developed global rainfall erosivity product shows a lower percentage error, higher correlation, and enhanced efficiency in capturing the variability in the rainfall erosivity compared to the global rainfall erosivity station dataset and existing Global Rainfall Erosivity Database (GloREDa).
Comparison of GloRESatE at the continental-scale
We cross-validated the accuracy of the GloRESatE105 at the continental scale using statistical metrics with respect to the global rainfall erosivity station dataset. The evaluation results are presented in Table 6. Remarkably, the merged rainfall erosivity product GloRESatE105 exhibits good correlations with the global rainfall erosivity station dataset across all six continents. Specifically, over North America, Asia, and Africa, GloRESatE105 showed correlation coefficients of 0.970, 0.945, and 0.971, respectively. Moreover, at the continental scale, the GloRESatE showed an excellent correlation value of more than 0.90 for most continents, with a slightly lower correlation of 0.862 observed over Europe and 0.880 over South America. The GloRESatE105 showed a low percentage error for all continents, staying within ∓ 10% except for Australia-Oceania, which reached +24%. The excellent Nash-Sutcliffe efficiency (NSE) values were observed over the Africa, Australia-Oceania, Asia, and North American continents. The ubRMSE of GloRESatE remained low over Europe and North America (~500 MJ.mm.ha−1.h−1.year−1); however, it is higher over Africa, Australia-Oceania, Asia, and South America (ubRMSE > 1,000 MJ.mm.ha−1.h−1.year−1). It is important to note that Europe and North America exhibit low mean rainfall erosivity, while Africa, Australia-Oceania, Asia, and South America have significantly higher rainfall erosivity values. The higher ubRMSE values over these continents can be attributed to their high rainfall erosivity values.
Table 6.
Evaluation metrics results at the continental scale between the newly developed GloRESatE dataset and the global rainfall erosivity station dataset.
| Continents | PE (%) (mean ± standard deviation) | r | NSE | ubRMSE (MJ.mm.ha−1.h−1.year−1) |
|---|---|---|---|---|
| Africa | +1 (±26) | 0.971 | 0.932 | 1433 |
| Asia | +8 (±46) | 0.945 | 0.891 | 1387 |
| Australia-Oceania | +24 (±50) | 0.913 | 0.822 | 1553 |
| Europe | +9 (±61) | 0.862 | 0.724 | 405 |
| North America | +4 (±30) | 0.970 | 0.936 | 534 |
| South America | +8 (±38) | 0.880 | 0.772 | 1767 |
At the continual scale, earlier assessments over Africa77 reported a similar NSE of 0.90 and correlation (r) of 0.95 using the African Rainfall Erosivity Sub-regional Empirical Downscaling (ARESED) model. Our results over Africa are very close to the ARESED model statistics. Riquetti et al.20 developed a geographical model to estimate rainfall erosivity over South America with a coefficient of determination (R2) of 0.63 and a percentage bias of −1.80%. Our result also showed a similar percentage error over South America with an NSE of 0.772. This also indicates an incremental improvement over South America as this study uses a higher number of stations. The existing rainfall erosivity model for Europe106 had a cross-validation score (R2) of 0.63 and a fitting score (R2) of 0.72 with gauge datasets. Our results also showed a similar performance with an overall score (NSE) of 0.724 over Europe. Using satellite rainfall data and the method proposed by Vrieling et al.29,110, an existing study over Australia30 showed an excellent coefficient of determination (R2) of 0.86 with the gauge data. Our result also showed a similar good performance with an NSE of 0.822 over Australia. Moreover, these results collectively show the excellent performance of the merged rainfall erosivity products, GloRESatE105, across all continents.
Comparison of GloRESatE at the regional scale
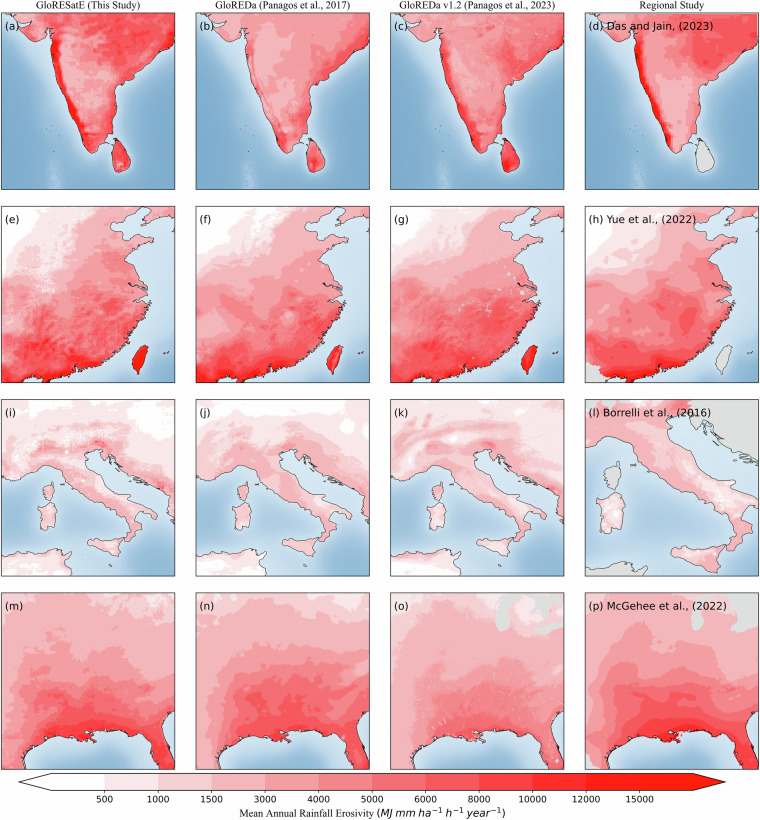
Further, at the regional level, we conducted a comparative analysis between the GloRESatE105 estimates and those from the GloREDa11,16, as well as the regional rainfall erosivity datasets from India82, Italy111, the United States19, and China18 (Fig. 6). The spatial maps from these datasets for four high erosive regions were plotted side by side. The result shows very similar spatial patterns between GloRESatE and the compared datasets. However, our findings indicated that the coastal regions of India exhibit higher rainfall erosivity compared to earlier estimates of GloREDa. The updated version (GloREDa v1.2) aligns well with our observations. GloRESatE105 estimates showed similar spatial patterns over Southern Europe, East Asia and North America when compared to both the versions of GloREDa11 estimates and regional studies18,19. Although our results indicate relatively higher rainfall erosivity values in these regions compared to GloREDa, this observation aligns well with the findings of regional studies.
Fig. 6.
Comparison of spatial maps GloRESatE105 datasets (This Study), from GloREDa estimates (Panagos et al.11,16), and regional datasets for the four different locations (a–d) part of South Asia, (e–h) part of Southern Europe, (i–l) part of East Asia and (m–p) part of North America.
In Table 7, we summarise the evaluation results of GloRESatE105 with the regional and existing global datasets for four different countries. Our finding revealed a moderate correlation (r = 0.608 and 0.688) between the GloREDa estimates and our estimated GloRESatE dataset, but a strong correlation (r = 0.786) with the regional study was found over India. Furthermore, compared to the station rainfall erosivity over India, the GloRESatE105 shows an overall percentage error of only +10 (±39) % and a good NSE of 0.707. Similarly, over China, the GloRESatE has a +10 ( ± 67) % mean error with the observed station rainfall erosivity dataset. Other statistical measures, such as correlation (r = 0.977) and NSE (0.954), also showed excellent GloRESatE performance in China with the observed stations. The GloRESatE dataset showed a PE of +7 (±42) % over the United States with the station erosivity dataset. Over the United States, our estimates revealed an excellent correlation (r) of 0.950 and an NSE of 0.900 with the observed stations. Similarly, across the complex topography of Italy, the GloRESatE dataset exhibited a only +9 (±58) % error with a good correlation with the observed dataset. A strong correlation (r = 0.853) was observed with GloREDa v1.2 over Italy. Furthermore, the developed GloRESatE105 dataset demonstrates a remarkable performance with a significantly lower ubRMSE value. The recent studies in China18, United States19, India27, and Austria21 also showed a certain uncertainty in the existing global rainfall erosivity dataset at the regional scale. However, we believe the newly developed rainfall erosivity dataset from the multi-source dataset will help bridge the knowledge gap in the existing global rainfall erosivity dataset.
Table 7.
Evaluation metrics results at the regional scale between the newly developed GloRESatE dataset and existing datasets.
| Region | Dataset | PE (%) (mean ± standard deviation) | r | NSE | ubRMSE (MJ.mm.ha−1.h−1.year−1) |
|---|---|---|---|---|---|
| India | Global rainfall erosivity station dataset | +10 ± 39 | 0.846 | 0.707 | 2175 |
| GloREDa11 | +43 ± 70 | 0.608 | −2.82 | 3031 | |
| GloREDa v1.216 | +26 ± 42 | 0.688 | −0.40 | 2738 | |
| Das and Jain82 | +20 ± 36 | 0.786 | 0.532 | 2460 | |
| China | Global rainfall erosivity station dataset | +10 ± 67 | 0.977 | 0.954 | 541 |
| GloREDa11 | +2 ± 42 | 0.962 | 0.925 | 675 | |
| GloREDa v1.216 | −1 ± 32 | 0.967 | 0.934 | 639 | |
| Yue et al.18 | +6 ± 49 | 0.989 | 0.967 | 451 | |
| Italy | Global rainfall erosivity station dataset | +9 ± 58 | 0.770 | 0.540 | 671 |
| GloREDa11 | +4 ± 31 | 0.647 | 0.029 | 501 | |
| GloREDa v1.216 | +8 ± 24 | 0.853 | 0.679 | 345 | |
| Borrelli et al.111 | +20 ± 54 | 0.702 | 0.404 | 520 | |
| United States | Global rainfall erosivity station dataset | +7 ± 42 | 0.950 | 0.900 | 687 |
| GloREDa11 | +2 ± 44 | 0.900 | 0.800 | 922 | |
| GloREDa v1.216 | +37 ± 44 | 0.930 | 0.660 | 808 | |
| McGehee et al.19 | +17 ± 451 | 0.989 | 0.967 | 321 |
Summary
Utilising high-resolution precipitation datasets from two satellites (CMORPH and IMERG) and one reanalysis (ERA5-Land), global rainfall erosivity was derived over more than 20 years. Furthermore, a regression-based approach was employed to create a merged long-term mean annual rainfall erosivity product, utilising observed rainfall erosivity data collected from 6,170 stations across 72 countries.
The preliminary analysis revealed significant uncertainty in the long-term mean annual rainfall erosivity estimated from satellite and reanalysis datasets. However, the merged rainfall erosivity product, developed using a machine learning–based Gaussian Process Regression, exhibited significant improvement. Similar merging technique has been used in many studies while merging rainfall datasets from different sources37–39,42,45,112. The GPR-based merging approach used in this study demonstrated successful integration of rainfall erosivity from these diverse sources.
Furthermore, in addition to incorporating rainfall or rainfall erosivity products, integrating environmental variables further enhanced the merging process, particularly for locations lacking observed data and high altitudes. Compared to existing datasets, the prepared dataset added rainfall data points globally, leading to good agreement at the regional scale. These results underscore the potential of the dataset prepared using the blending of multi-source datasets. It represents a promising global and regional soil erosion monitoring and water resource management resource.
Usage Notes
In this study, we present GloRESatE, a global rainfall erosivity dataset that offers mean annual rainfall erosivity data globally, along with estimated modelling uncertainty. The estimated rainfall erosivity from three different gridded satellite and reanalysis datasets for each month and year are also provided for further use in hydrometeorological applications. However, it is imperative to acknowledge and consider the uncertainty associated with satellite and reanalysis datasets for their accurate interpretation and application. Furthermore, these datasets can facilitate the merging of rainfall erosivity derived from satellite and reanalysis estimates at any spatio-temporal scale, thereby reducing the cost of further research and efforts in duplicating work. We recommend using our main product, GloRESatE, instead of estimated rainfall erosivity from satellite and reanalysis datasets for soil erosion, hydrological modelling, water resource management, and climate impact assessment.
Moreover, GloRESatE also holds relevance for policymakers, earth system modellers, and scientists working in fields like agriculture, ecology, and flood management. It presents a harmonised rainfall erosivity product, consolidating data from diverse temporal resolutions into a unified 30-min resolution. While the rainfall erosivity data suits numerous applications directly, users are encouraged to convert it to an alternate resolution if necessary, ensuring compatibility with specific analytical or modeling requirements.
Limitations and future scopes
The development of GloRESatE involved incorporating a vast number of globally observed station datasets, along with multiple satellite and reanalysis datasets, aimed at enhancing the global rainfall erosivity estimation. However, it is essential to acknowledge certain uncertainties that may have been introduced while compiling global rainfall erosivity station datasets from different sources. These uncertainties can be attributed to several factors: (1) The rainfall erosivity estimates obtained from different temporal resolutions and various estimation methods, including the adaptations of the Universal Soil Loss Equation (USLE)113 and its subsequent versions, namely RUSLE87 and RUSLE289. (2) The rainfall erosivity estimated from different temporal resolutions was converted to a 30-min rainfall erosivity value using the conversion factor used in the earlier global study11. However, this may cause uncertainty at the regional scale114,115. (3) The gauge rainfall erosivity dataset estimated from other formulations than USLE113 and RUSLE87 can have slight deviations, potentially affecting the dataset’s accuracy at the regional scale. Moreover, the fixed interval rainfall dataset has been used for rainfall erosivity estimation. Ideally, a breakpoint dataset should be used in this case28; however, due to unavailability, such a dataset was not used. (4) The estimated rainfall erosivity values from breakpoint datasets will be higher than our estimated values88. Our results should be verified before benchmarking in any studies. Furthermore, due to the unavailability of the time-series data of observed rainfall erosivity at the global level, the long-term mean annual rainfall erosivity dataset has been prepared in this study. However, a similar assimilation of the multi-source dataset for each year or month can be applied to prepare long-term time series of rainfall erosivity at the regional and global scales.
Supplementary information
Acknowledgements
The authors acknowledge researchers and scientists across the globe for making their valuable rainfall erosivity dataset available. Special acknowledgements are extended to the following agencies for directly providing open-access datasets. NASA and JAXA for providing GPM (IMERG) datasets, ECMWF for providing ERA5 and ERA5-Land, NOAA for providing bias-corrected CMORPH datasets, European Soil Data Centre (ESDAC) for providing Global Rainfall Erosivity Database (GloREDa), India Meteorological Department (IMD) for providing high-resolution hourly gauge station rainfall datasets of India. We also acknowledge Ju-young Shin (Kookmin University, South Korea), Lisbeth L. Johannsen (Institute for Land and Water Management Research, Austria), and Aniruddha Saha (Indian Institute of Technology Roorkee, India) for their valuable suggestions.
Author contributions
M.K.J. and S.D. conceived and designed the analysis. S.D., S.Y., C.R.M., M.A., P.R. and P.B. were responsible for data collection. S.D. and V.G. conducted the analysis and drafted the initial manuscript, which was subsequently reviewed and revised by all authors.
Code availability
Code used in this study is accessible on GitHub (https://github.com/subhankar17th/R-factor.git).
Competing interest
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41597-024-03756-5.
References
- 1.Borrelli, P. et al. Land use and climate change impacts on global soil erosion by water (2015–2070). Proc. Natl. Acad. Sci. USA117, 21994–22001 (2020). 10.1073/pnas.2001403117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.IPCC. Special Report on climate change, desertification, land degradation, sustainable land management, food security, and greenhouse gas fluxes in terrestrial ecosystems (SR2). Ipcc (Intergovernmental Panel on Climate Change (IPCC), 2019).
- 3.Li, J., He, H., Zeng, Q., Chen, L. & Sun, R. A Chinese soil conservation dataset preventing soil water erosion from 1992 to 2019. Sci. Data10, 319 (2023). 10.1038/s41597-023-02246-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wuepper, D., Borrelli, P. & Finger, R. Countries and the global rate of soil erosion. Nat. Sustain.3, 51–55 (2020). 10.1038/s41893-019-0438-4 [DOI] [Google Scholar]
- 5.Das, S., Jain, M. K. & Gupta, V. An assessment of anticipated future changes in water erosion dynamics under climate and land use change scenarios in South Asia. J. Hydrol.637, 131341, 10.1016/j.jhydrol.2024.131341 (2024).
- 6.Yang, D., Kanae, S., Oki, T., Koike, T. & Musiake, K. Global potential soil erosion with reference to land use and climate changes. Hydrol. Process.17, 2913–2928 (2003). 10.1002/hyp.1441 [DOI] [Google Scholar]
- 7.Pimentel, D. et al. Environmental and economic costs of soil erosion and conservation benefits. Science (80-.).267, 1117–1123 (1995). 10.1126/science.267.5201.1117 [DOI] [PubMed] [Google Scholar]
- 8.Oldeman, L. R. Global extent of soil degradation. in Bi-Annual Report 1991-1992/ISRIC 19–36 (ISRIC, 1992).
- 9.FAO & ITPS. The World’s Soil Resources: Main Report. Report: 607 (2015).
- 10.Bezak, N., Borrelli, P. & Panagos, P. Exploring the possible role of satellite-based rainfall data in estimating inter- and intra-annual global rainfall erosivity. Hydrol. Earth Syst. Sci.26, 1907–1924 (2022). 10.5194/hess-26-1907-2022 [DOI] [Google Scholar]
- 11.Panagos, P. et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep.7, 1–12 (2017). 10.1038/s41598-017-04282-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Renard, K. G. & Freimund, J. R. Using monthly precipitation data to estimate the R-factor in the revised USLE. J. Hydrol.157, 287–306 (1994). 10.1016/0022-1694(94)90110-4 [DOI] [Google Scholar]
- 13.Nachtergaele, F. et al. Global Land Degradation Information System (GLADIS) - An Information database for Land Degradation Assessment at Global Level. Gladis110, 110 (2011). [Google Scholar]
- 14.Naipal, V., Reick, C. & Pongratz, J. & Van Oost, K. Improving the global applicability of the RUSLE model - Adjustment of the topographical and rainfall erosivity factors. Geosci. Model Dev.8, 2893–2913 (2015). 10.5194/gmd-8-2893-2015 [DOI] [Google Scholar]
- 15.Liu, Y., Zhao, W., Liu, Y. & Pereira, P. Global rainfall erosivity changes between 1980 and 2017 based on an erosivity model using daily precipitation data. Catena194, 104768 (2020). 10.1016/j.catena.2020.104768 [DOI] [Google Scholar]
- 16.Panagos, P. et al. Global rainfall erosivity database (GloREDa) and monthly R-factor data at 1 km spatial resolution. Data Br.50, 109482 (2023). 10.1016/j.dib.2023.109482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yin, S. Q., Zhang, W., Xie, Y., Liu, S. & Liu, F. Spatial distribution of rainfall erosivity in China based on high-density station network. Soil Water Conserv.10, 45–51 (2013). [Google Scholar]
- 18.Yue, T., Yin, S., Xie, Y., Yu, B. & Liu, B. Rainfall erosivity mapping over mainland China based on high-density hourly rainfall records. Earth Syst. Sci. Data14, 665–682 (2022). 10.5194/essd-14-665-2022 [DOI] [Google Scholar]
- 19.McGehee, R. P. et al. An updated isoerodent map of the conterminous United States. Int. Soil Water Conserv. Res.10, 1–16 (2022). 10.1016/j.iswcr.2021.06.004 [DOI] [Google Scholar]
- 20.Riquetti, N. B., Mello, C. R., Beskow, S. & Viola, M. R. Rainfall erosivity in South America: Current patterns and future perspectives. Sci. Total Environ.724, 138315 (2020). 10.1016/j.scitotenv.2020.138315 [DOI] [PubMed] [Google Scholar]
- 21.Johannsen, L. L. et al. An update of the spatial and temporal variability of rainfall erosivity (R-factor) for the main agricultural production zones of Austria. Catena215, 106305 (2022). 10.1016/j.catena.2022.106305 [DOI] [Google Scholar]
- 22.Azari, M., Oliaye, A. & Nearing, M. A. Expected climate change impacts on rainfall erosivity over Iran based on CMIP5 climate models. J. Hydrol.593, 125826 (2021). 10.1016/j.jhydrol.2020.125826 [DOI] [Google Scholar]
- 23.Ballabio, C. et al. Mapping monthly rainfall erosivity in Europe. Sci. Total Environ.579, 1298–1315 (2017). 10.1016/j.scitotenv.2016.11.123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kim, J., Han, H., Kim, B., Chen, H. & Lee, J. H. Use of a high-resolution-satellite-based precipitation product in mapping continental-scale rainfall erosivity: A case study of the United States. Catena193, 104602 (2020). 10.1016/j.catena.2020.104602 [DOI] [Google Scholar]
- 25.Raj, R., Saharia, M., Chakma, S. & Rafieinasab, A. Mapping rainfall erosivity over India using multiple precipitation datasets. Catena214, 106256 (2022). 10.1016/j.catena.2022.106256 [DOI] [Google Scholar]
- 26.Borrelli, P., Ballabio, C., Yang, J. E., Robinson, D. A. & Panagos, P. GloSEM: High-resolution global estimates of present and future soil displacement in croplands by water erosion. Sci. Data9, 1–9 (2022). 10.1038/s41597-022-01489-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Das, S., Jain, M. K. & Gupta, V. A step towards mapping rainfall erosivity for India using high-resolution GPM satellite rainfall products. Catena212, 106067 (2022). 10.1016/j.catena.2022.106067 [DOI] [Google Scholar]
- 28.Flanagan, D. C., McGehee, R. P. & Srivastava, A. Evaluation of different precipitation inputs to WEPP. in ASABE 2020 Annual International Meeting1, 10.13031/aim.202000740 (American Society of Agricultural and Biological Engineers, 2020).
- 29.Vrieling, A., Sterk, G. & de Jong, S. M. Satellite-based estimation of rainfall erosivity for Africa. J. Hydrol.395, 235–241 (2010). 10.1016/j.jhydrol.2010.10.035 [DOI] [Google Scholar]
- 30.Teng, H. et al. Assimilating satellite imagery and visible-near infrared spectroscopy to model and map soil loss by water erosion in Australia. Environ. Model. Softw.77, 156–167 (2016). 10.1016/j.envsoft.2015.11.024 [DOI] [Google Scholar]
- 31.Teng, H. et al. Improving rainfall erosivity estimates using merged TRMM and gauge data. Remote Sens.9, 1134 (2017). 10.3390/rs9111134 [DOI] [Google Scholar]
- 32.Chen, Y., Xu, M., Wang, Z., Gao, P. & Lai, C. Applicability of two satellite-based precipitation products for assessing rainfall erosivity in China. Sci. Total Environ.757, 143975 (2021). 10.1016/j.scitotenv.2020.143975 [DOI] [PubMed] [Google Scholar]
- 33.Chen, Y. et al. New gridded dataset of rainfall erosivity (1950–2020) on the Tibetan Plateau. Earth Syst. Sci. Data14, 2681–2695 (2022). 10.5194/essd-14-2681-2022 [DOI] [Google Scholar]
- 34.Delgado, D., Sadaoui, M., Ludwig, W. & Méndez, W. Spatio-temporal assessment of rainfall erosivity in Ecuador based on RUSLE using satellite-based high frequency GPM-IMERG precipitation data. Catena219, 106597 (2022). 10.1016/j.catena.2022.106597 [DOI] [Google Scholar]
- 35.Fenta, A. A. et al. An integrated modeling approach for estimating monthly global rainfall erosivity. Sci. Rep.14, 8167 (2024). 10.1038/s41598-024-59019-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Panagos, P. et al. Global rainfall erosivity projections for 2050 and 2070. J. Hydrol.610, 127865 (2022). 10.1016/j.jhydrol.2022.127865 [DOI] [Google Scholar]
- 37.Bhuiyan, M. A. E., Nikolopoulos, E. I. & Anagnostou, E. N. Machine learning–based blending of satellite and reanalysis precipitation datasets: A multiregional tropical complex terrain evaluation. J. Hydrometeorol.20, 2147–2161 (2019). 10.1175/JHM-D-19-0073.1 [DOI] [Google Scholar]
- 38.Bhuiyan, M. A. E., Nikolopoulos, E. I., Anagnostou, E. N., Quintana-Seguí, P. & Barella-Ortiz, A. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci.22, 1371–1389 (2018). 10.5194/hess-22-1371-2018 [DOI] [Google Scholar]
- 39.Pham, B. T. et al. Development of advanced artificial intelligence models for daily rainfall prediction. Atmos. Res.237, 104845 (2020). 10.1016/j.atmosres.2020.104845 [DOI] [Google Scholar]
- 40.Ly, S., Charles, C. & Degré, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci.15, 2259–2274 (2011). 10.5194/hess-15-2259-2011 [DOI] [Google Scholar]
- 41.Fenta, A. A. et al. Improving satellite-based global rainfall erosivity estimates through merging with gauge data. J. Hydrol.620, 129555 (2023). 10.1016/j.jhydrol.2023.129555 [DOI] [Google Scholar]
- 42.Du, J., Liu, Y., Yu, Y. & Yan, W. A prediction of precipitation data based on Support Vector Machine and Particle Swarm Optimization (PSO-SVM) algorithms. Algorithms10, 57 (2017). 10.3390/a10020057 [DOI] [Google Scholar]
- 43.Samui, P. Application of Least Square Support Vector Machine (LSSVM) for Determination of Evaporation Losses in Reservoirs. Engineering03, 431–434 (2011). 10.4236/eng.2011.34049 [DOI] [Google Scholar]
- 44.Nguyen, G. V. et al. Application of random forest algorithm for merging multiple satellite precipitation products across South Korea. Remote Sens.13, 4033 (2021). 10.3390/rs13204033 [DOI] [Google Scholar]
- 45.Lei, H., Zhao, H. & Ao, T. A two-step merging strategy for incorporating multi-source precipitation products and gauge observations using machine learning classification and regression over China. Hydrol. Earth Syst. Sci.26, 2969–2995 (2022). 10.5194/hess-26-2969-2022 [DOI] [Google Scholar]
- 46.Bhuiyan, M. A. E., Yang, F., Biswas, N. K., Rahat, S. H. & Neelam, T. J. Machine Learning-Based Error Modeling to Improve GPM IMERG Precipitation Product over the Brahmaputra River Basin. Forecasting2, 248–266 (2020). 10.3390/forecast2030014 [DOI] [Google Scholar]
- 47.NCDC, NESDIS, NOAA & U.S. Department of Commerce. U.S. 15 Minute Precipitation Data. Available at: https://www.ncei.noaa.gov/metadata/geoportal/rest/metadata/item/gov.noaa.ncdc:C00505/html#.
- 48.Gaitán, J. et al. Estimación de la pérdida de suelo por erosión hídrica en la República Argentina. INTA-Instituto Nacional de Tecnología Agropecuaria. (Ediciones INTA, 2017).
- 49.De Mello, C. R., Viola, M. R., Owens, P. R., De Mello, J. M. & Beskow, S. Interpolation methods for improving the RUSLE R-factor mapping in Brazil. J. Soil Water Conserv.70, 182–197 (2015). 10.2489/jswc.70.3.182 [DOI] [Google Scholar]
- 50.Waltrick, P. C., Mello Machado, M. A., De Dieckow, J. & de Oliveira, D. Estimativa Da Erosividade De Chuvas No Estado Do Paraná Pelo Método Da Pluviometria: Atualização Com Dados De 1986 A 2008a 2008. Rev. Bras. Cienc. do Solo39, 256–267 (2015). 10.1590/01000683rbcs20150147 [DOI] [Google Scholar]
- 51.Viola, M. R., Avanzi, J. C., de Mello, C. R., de Lima, S. O. & Alves, M. V. G. Distribuição e potencial erosivo das chuvas no Estado do Tocantins. Pesqui. Agropecu. Bras.49, 125–135 (2014). 10.1590/S0100-204X2014000200007 [DOI] [Google Scholar]
- 52.Bonilla, C. A. & Vidal, K. L. Rainfall erosivity in Central Chile. J. Hydrol.410, 126–133 (2011). 10.1016/j.jhydrol.2011.09.022 [DOI] [Google Scholar]
- 53.Moreno-pérez, D. F. Determinación y mapificación de la erosividad de la lluvia en la cuenca del embalse La Copa, Boyacá. Ingenio Magno6, 34–36 (2015). [Google Scholar]
- 54.Echeverri, L., Humberto, F. & Moncayo, O. Rainfall Erosivity in the South Center Zone of the Department of Caldas, Colombia Erosividad De Las Lluvias En La Región Centro-Sur Del Departamento De Caldas, Colombia. Rev. Fac. Nac. Agron. Medellín63, 5307–5318 (2010). [Google Scholar]
- 55.Rodriguez. Erosividad De La Lluvia En El Departamento De Alto Paraná, Paraguay. Angewandte Chemie International Edition, 6(11), 951–952. 5–24 (2012).
- 56.Correa, S. W., Mello, C. R., Chou, S. C., Curi, N. & Norton, L. D. Soil erosion risk associated with climate change at Mantaro River basin, Peruvian Andes. Catena147, 110–124 (2016). 10.1016/j.catena.2016.07.003 [DOI] [Google Scholar]
- 57.Pérez Bidegain, M., Piaggio, J. M., Baethgen, W. & García Préchac, F. Actualización del factor erosividad de la lluvia en Uruguay. Agrociencia21, 91–99 (2017). 10.31285/AGRO.21.2.11 [DOI] [Google Scholar]
- 58.Lujan, D. L. & Gabriels, D. Assessing the rain erosivity and rain distribution in different agro-climatological zones in Venezuela. Soc. Nat.1, 16–29 (2005). 10.14393/SN-v1-2005-9671 [DOI] [Google Scholar]
- 59.Lu, H. et al. Predicting sheetwash and rill erosion over the Australian continent. Aust. J. Soil Res.41, 1037–1062 (2003). 10.1071/SR02157 [DOI] [Google Scholar]
- 60.Yu, B. & Rosewell, C. J. Rainfall erosivity estimation using daily rainfall amounts for South Australia. Aust. J. Soil Res.34, 721–733 (1996). 10.1071/SR9960721 [DOI] [Google Scholar]
- 61.Yu, B. Rainfall erosivity and its estimation for Australia’s tropics. Aust. J. Soil Res.36, 143–165 (1998). 10.1071/S97025 [DOI] [Google Scholar]
- 62.Musabbir, M. et al. Spatiotemporal variability of rainfall erosivity and its teleconnection with atmospheric circulation in monsoon-driven climate region. Catena221, 106762 (2023). 10.1016/j.catena.2022.106762 [DOI] [Google Scholar]
- 63.Cecílio, R. A., de Oliveira, J. P. B., de Teixeira, D. B. S., Pruski, F. F. & Zanetti, S. S. Database of rainfall erosivity factor for 141 locations in Brazil. Lat. Am. Data Sci.1, 95–101 (2021). 10.53805/lads.v1i3.37 [DOI] [Google Scholar]
- 64.Oliveira, P. T. S., Wendland, E. & Nearing, M. A. Rainfall erosivity in Brazil: A review. Catena100, 139–147 (2013). 10.1016/j.catena.2012.08.006 [DOI] [Google Scholar]
- 65.Wall, G. J. et al. RUSLEFAC - Revised Universal Soil Loss Equation for Application in Canada: A Handbook for Estimating Soil Loss from Water Erosion in Canada. Agriculture117, 117 (2002). [Google Scholar]
- 66.Wall, G. J., Dickinson, W. T. & Greuel, J. Rainfall erosion indices for Canada east of the Rocky Mountains. Can. J. Soil Sci.63, 271–280 (1983). 10.4141/cjss83-027 [DOI] [Google Scholar]
- 67.Mikhailova, E. A., Bryant, R. B., Schwager, S. J. & Smith, S. D. Predicting Rainfall Erosivity in Honduras. Soil Sci. Soc. Am. J.61, 273–279 (1997). 10.2136/sssaj1997.03615995006100010039x [DOI] [Google Scholar]
- 68.Dash, C. J., Das, N. K. & Adhikary, P. P. Rainfall erosivity and erosivity density in Eastern Ghats Highland of east India. Nat. Hazards97, 727–746 (2019). 10.1007/s11069-019-03670-9 [DOI] [Google Scholar]
- 69.Babu, R., Tejwani, K. G., Agarwal, M. C. & Bhushan, L. S. Distribution of erosion index and iso-erodent map of India. Indian J. Soil Conserv. (1978).
- 70.Nasidi, N. M., Wayayok, A., Abdullah, A. F. & Kassim, M. S. M. Spatio-temporal dynamics of rainfall erosivity due to climate change in Cameron Highlands, Malaysia. Model. Earth Syst. Environ.7, 1847–1861 (2021). 10.1007/s40808-020-00917-4 [DOI] [Google Scholar]
- 71.Leow, C. S., Engineering, R. & Drainage, U. Development of rainfall erosivity isohyet map for Peninsular Malaysia. in 3rd International Conference on Managing Rivers in the 21st Century: Sustainable Solutions for Global Crisis of Flooding, Pollution and Water Scarcity 748–756 (2011).
- 72.Anderson, R. L. Rainfall Erosivity Attributes on Central and Western Mauritius. (2012).
- 73.Shin, J. Y., Kim, T., Heo, J. H. & Lee, J. H. Spatial and temporal variations in rainfall erosivity and erosivity density in South Korea. Catena176, 125–144 (2019). 10.1016/j.catena.2019.01.005 [DOI] [Google Scholar]
- 74.Santosa, P. B., Mitani, Y. & Ikemi, H. Estimation of RUSLE EI30 based on 10 min interval rainfall data and GIS-based development of rainfall erosivity maps for Hitotsuse basin in Kyushu Japan. in 2010 18th International Conference on Geoinformatics, Geoinformatics 2010 1–6 10.1109/GEOINFORMATICS.2010.5568195 (IEEE, 2010).
- 75.Laceby, J. P. et al. Rainfall erosivity in catchments contaminated with fallout from the Fukushima Daiichi nuclear power plant accident. Hydrol. Earth Syst. Sci.20, 2467–2482 (2016). 10.5194/hess-20-2467-2016 [DOI] [Google Scholar]
- 76.Klik, A., Haas, K., Dvorackova, A. & Fuller, I. C. Spatial and temporal distribution of rainfall erosivity in New Zealand. Soil Res.53, 815–825 (2015). 10.1071/SR14363 [DOI] [Google Scholar]
- 77.Diodato, N., Knight, J. & Bellocchi, G. Reduced complexity model for assessing patterns of rainfall erosivity in Africa. Glob. Planet. Change100, 183–193 (2013). 10.1016/j.gloplacha.2012.10.016 [DOI] [Google Scholar]
- 78.Mannaerts, C. M. & Gabriels, D. Rainfall erosivity in Cape Verde. Soil Tillage Res.55, 207–212 (2000). 10.1016/S0167-1987(00)00104-5 [DOI] [Google Scholar]
- 79.Rodríguez Rodríguez, A. et al. Forms of eroded soil organic carbon in andosols of the Canary Islands (Spain). Geoderma121, 205–219 (2004). 10.1016/j.geoderma.2003.11.009 [DOI] [Google Scholar]
- 80.Global Rainfall Erosivity database (GloREDa). Zenodo10.5281/zenodo.8036998 (2023). 10.5281/zenodo.8036998 [DOI]
- 81.Panagos, P. et al. Monthly rainfall erosivity: Conversion factors for different time resolutions and regional assessments. Water (Switzerland)8, 119 (2016). [Google Scholar]
- 82.Das, S. & Jain, M. K. Unravelling the future changes in rainfall erosivity over India under shared socio-economic pathways. Catena232, 107417 (2023). 10.1016/j.catena.2023.107417 [DOI] [Google Scholar]
- 83.Yin, S., Xie, Y., Nearing, M. A. & Wang, C. Estimation of rainfall erosivity using 5- to 60-minute fixed-interval rainfall data from China. Catena70, 306–312 (2007). 10.1016/j.catena.2006.10.011 [DOI] [Google Scholar]
- 84.Porto, P. Exploring the effect of different time resolutions to calculate the rainfall erosivity factor R in Calabria, southern Italy. Hydrol. Process.30, 1551–1562 (2016). 10.1002/hyp.10737 [DOI] [Google Scholar]
- 85.Istok, J. D., McCool, D. K., King, L. G. & Boersma, L. Effect of Rainfall Measurement Interval on Ei Calculation. Trans. Am. Soc. Agric. Eng.29, 730–734 (1986). 10.13031/2013.30221 [DOI] [Google Scholar]
- 86.Williams, R. G. & Sheridan, J. M. Effect of rainfall measurement time and depth resolution on EI calculation. Trans. Am. Soc. Agric. Eng.34, 402–406 (1991). 10.13031/2013.31675 [DOI] [Google Scholar]
- 87.Renard, K., Foster, G., Weesies, G., McCool, D. & Yoder, D. Predicting soil erosion by water: a guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE). Agric. Handb. No. 703 404 (1997).
- 88.McGehee, R. P., Flanagan, D. C., Srivastava, P. & Nearing, M. A. Rainfall erosivity: Essential historical, conceptual, and practical perspectives for continued application. in Precipitation: Earth Surface Responses and Processes 373–394, 10.1016/B978-0-12-822699-5.00014-8 (Elsevier, 2021).
- 89.Foster, G. R. et al. User’s Guide: Revised Universal Soil Loss Equation Version 2 (RUSLE2). US Dep. Agric. Agric. Res. Serv.2, 1–429 (2008). [Google Scholar]
- 90.Fick, S. E. & Hijmans, R. J. WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol.37, 4302–4315 (2017). 10.1002/joc.5086 [DOI] [Google Scholar]
- 91.Jones, P. W. First- and second-order conservative remapping schemes for grids in spherical coordinates. Mon. Weather Rev.127, 2204–2210 (1999). [DOI] [Google Scholar]
- 92.Chen, C. J., Senarath, S. U. S., Dima-West, I. M. & Marcella, M. P. Evaluation and restructuring of gridded precipitation data over the Greater Mekong Subregion. Int. J. Climatol.37, 180–196 (2017). 10.1002/joc.4696 [DOI] [Google Scholar]
- 93.Kim, H. C. et al. A conservative downscaling of satellite-detected chemical compositions: NO2 column densities of OMI, GOME-2, and CMAQ. Remote Sens.10, 1001 (2018). 10.3390/rs10071001 [DOI] [Google Scholar]
- 94.Rasmussen, C. E. & Williams, C. K. I. Gaussian processes for machine learning. 1 (Springer, 2006).
- 95.Cutler, A., Cutler, D. R. & Stevens, J. R. Random forests. Ensemble Mach. Learn. Methods Appl. 157–175, 10.1007/9781441993267_5 (2012).
- 96.Nogueira, F. Bayesian Optimization: Open source constrained global optimization tool for Python. GitHub. Seehttps://github.com/bayesian-optimization/BayesianOptimization (2014).
- 97.Morita, Y. et al. Applying Bayesian optimization with Gaussian process regression to computational fluid dynamics problems. J. Comput. Phys.449, 110788 (2022). 10.1016/j.jcp.2021.110788 [DOI] [Google Scholar]
- 98.Mangukiya, N. K. & Sharma, A. Alternate pathway for regional flood frequency analysis in data-sparse region. J. Hydrol.629, 130635 (2024). 10.1016/j.jhydrol.2024.130635 [DOI] [Google Scholar]
- 99.Rong, G. et al. Rainfall induced landslide susceptibility mapping based on bayesian optimized random forest and gradient boosting decision tree models—a case study of shuicheng county, china. Water (Switzerland)12, 1–22 (2020). [Google Scholar]
- 100.Chicco, D., Warrens, M. J. & Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci.7, e623 (2021). 10.7717/peerj-cs.623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Moriasi, D. N. et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE50, 885–900 (2007). 10.13031/2013.23153 [DOI] [Google Scholar]
- 102.Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. Numerical recipes 3rd edition: The art of scientific computing. (Cambridge university press, 2007).
- 103.Krause, P., Boyle, D. P. & Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci.5, 89–97 (2005). 10.5194/adgeo-5-89-2005 [DOI] [Google Scholar]
- 104.Ma, H. et al. Satellite surface soil moisture from SMAP, SMOS, AMSR2 and ESA CCI: A comprehensive assessment using global ground-based observations. Remote Sens. Environ.231, 111215 (2019). 10.1016/j.rse.2019.111215 [DOI] [Google Scholar]
- 105.Das, S. et al. GloRESatE - Global Rainfall Erosivity from Reanalysis and Satellite Estimates. Zenodo, 10.5281/zenodo.11078865 (2024). 10.5281/zenodo.11078865 [DOI]
- 106.Panagos, P. et al. Rainfall erosivity in Europe. Sci. Total Environ.511, 801–814 (2015). 10.1016/j.scitotenv.2015.01.008 [DOI] [PubMed] [Google Scholar]
- 107.Beck, H. E. et al. Present and future köppen-geiger climate classification maps at 1-km resolution. Sci. Data5, 1–12 (2018). 10.1038/sdata.2018.214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Pradhan, R. K. et al. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ.268, 112754 (2022). 10.1016/j.rse.2021.112754 [DOI] [Google Scholar]
- 109.Tang, G., Clark, M. P., Papalexiou, S. M., Ma, Z. & Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ.240, 111697 (2020). 10.1016/j.rse.2020.111697 [DOI] [Google Scholar]
- 110.Vrieling, A., Hoedjes, J. C. B. & van der Velde, M. Towards large-scale monitoring of soil erosion in Africa: Accounting for the dynamics of rainfall erosivity. Glob. Planet. Change115, 33–43 (2014). 10.1016/j.gloplacha.2014.01.009 [DOI] [Google Scholar]
- 111.Borrelli, P., Diodato, N. & Panagos, P. Rainfall erosivity in Italy: a national scale spatio-temporal assessment. Int. J. Digit. Earth9, 835–850 (2016). 10.1080/17538947.2016.1148203 [DOI] [Google Scholar]
- 112.Van, L. N. et al. Evaluation of Numerous Kinetic Energy-Rainfall Intensity Equations Using Disdrometer Data. Remote Sens. 15 (2023).
- 113.Wischmeier, W. H. & Smith, D. D. Predicting rainfall erosion losses: a guide to conservation planning. (Department of Agriculture, Science and Education Administration, 1978).
- 114.Yue, T. et al. Effect of time resolution of rainfall measurements on the erosivity factor in the USLE in China. Int. Soil Water Conserv. Res.8, 373–382 (2020). 10.1016/j.iswcr.2020.06.001 [DOI] [Google Scholar]
- 115.Janapati, J., Seela, B. K., Lin, P. L., Wang, P. K. & Kumar, U. An assessment of tropical cyclones rainfall erosivity for Taiwan. Sci. Rep.9, 1–14 (2019). 10.1038/s41598-019-52028-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Xie, P. et al. NOAA Climate Data Record (CDR) of CPC Morphing Technique (CMORPH) High Resolution Global Precipitation Estimates, Version 1. NOAA National Centers for Environmental Information. 10.25921/w9va-q159 (2019).
- 117.Xie, P. et al. Reprocessed, bias-corrected CMORPH global high-resolution precipitation estimates from 1998. J. Hydrometeorol.18, 1617–1641 (2017). 10.1175/JHM-D-16-0168.1 [DOI] [Google Scholar]
- 118.Huffman, G. J., DT, B., EJ, N. & J, T. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation. NASA/GSFC. Nasa/Gsfc Code612, 83 (2020). [Google Scholar]
- 119.Muñoz-Sabater, J. et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data13, 4349–4383 (2021). 10.5194/essd-13-4349-2021 [DOI] [Google Scholar]
- 120.Lee, J. H. & Heo, J. H. Evaluation of estimation methods for rainfall erosivity based on annual precipitation in Korea. J. Hydrol.409, 30–48 (2011). 10.1016/j.jhydrol.2011.07.031 [DOI] [Google Scholar]
- 121.Ma, X., He, Y., Xu, J., Van Noordwijk, M. & Lu, X. Spatial and temporal variation in rainfall erosivity in a Himalayan watershed. Catena121, 248–259 (2014). 10.1016/j.catena.2014.05.017 [DOI] [Google Scholar]
- 122.Hanel, M., Máca, P., Bašta, P., Vlnas, R. & Pech, P. The rainfall erosivity factor in the Czech Republic and its uncertainty. Hydrol. Earth Syst. Sci.20, 4307–4322 (2016). 10.5194/hess-20-4307-2016 [DOI] [Google Scholar]
- 123.Panagos, P., Ballabio, C., Borrelli, P. & Meusburger, K. Spatio-temporal analysis of rainfall erosivity and erosivity density in Greece. Catena10.1016/j.catena.2015.09.015 (2016).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
Supplementary Materials
Data Availability Statement
Code used in this study is accessible on GitHub (https://github.com/subhankar17th/R-factor.git).