Abstract
Within fluid mechanics, the flow of hybrid nanofluids over a stretching surface has been extensively researched due to their influence on the flow and heat transfer properties. Expanding on this concept by introducing porous media, the current study explore the flow and heat and mass transport characteristics of hybrid nanofluid. This investigation includes the effect of magnetohydrodynamic (MHD) with chemical reaction, thermal radiation, and slip effects. The nanoparticles, copper, and alumina are combined with water for the formation of a hybrid nanofluid. Using the self-similar method for the reduction of Partial differential equations (PDEs) to the system of Ordinary differential equations (ODEs). These nonlinear equation systems are solved numerically using the bvp4c (boundary value solver) technique. The effect of the different physical non-dimensional flow parameters on different flow profiles such as velocity, temperature, concentration, skin friction, Nusselt and mass transfer rate are depicted through graphs and tables. The velocity profiles diminish with the effect of magnetic and slip parameters. The temperature and concentration slip parameters reduce the temperature and concentration profile respectively. The higher values of magnetic factor lessened the skin friction coefficient for both slip and no-slip conditions. An elevation in the thermal slip parameter reduced the boundary layer thickness and the heat transfer from the surface to the fluid. The Nusselt number amplified with the climbing values of the radiation parameter. The mass transfer rate depressed with the solutal slip parameter. Comparison is made with the published work in the literature and there is excellent agreement between them.
Keywords: Hybrid nanofluid, Stretching surface, Slip conditions and magnetohydrodynamic (MHD), Bvp4c
Subject terms: Engineering, Mathematics and computing, Physics
Introduction
The exploration of nanofluid has expanded significantly among researchers due to its wide-ranging significance in various fields such as biomedicine, cooling for electronic devices, transportation, heat exchangers, and many more. Diverse nanoparticles such as grapheme, silver, copper, alumina, silica, and carbon nanotube must be incorporated into the base fluid to enhance the thermal conductivity of common fluids like ethylene glycol water, kerosene, and engine oils. The utilization of nanotechnology in industry had become prevalent due to the distinctive physical and chemical properties exhibited by materials at the nanometer scale. Fluids containing nano-scale particles are called nanofluids, a term initially coined by Choi1. In their work, Choi et al.2 demonstrated that incorporating a small quantity of less than 1% by volume of nanoparticles into conventional heat transfer liquids resulted in a notable enhancement of the fluid's thermal conductivity reaching approximately twice its original value. Vedavathi et al.3 examined the Darcy nanofluid over an enlarging surface with thermal radiation and chemical reaction numerically. They concluded that with the heightened values of magnetic and Darcy number, the velocity profile declined while the temperature graphs boosted. The demand to enhance the thermal performance of the fluids in science and technology a new class of fluid called hybrid nanofluids was utilized. The formation of hybrid nanofluid involves more than one nanoparticle in a base fluid. Abas et al.4 studied the Cu and alumina blood-base hybrid nanofluid with thermophoresis and Arrhenius activation energy. They concluded that the concentration graph raised with activation and thermophoresis parameters. Additionally, the rate of heat transport is more pronounced than nanofluid. Propylene glycol hybrid nanofluid two-dimensional Williamson fluid flow over a convectively heated porous surface examined by Ali et al.5. They revealed that the heat transfer rate of hybrid nanofluid is higher, compared to other regular fluids. Moreover, the temperature and entropy profile amplified with radiation factor. Saeed et al.6 examined Darcy Forchheimer hybrid nanofluid flow having carbon nanotubes and iron oxide past an exponentially extending curved surface. They found that the rate of heat transfer increased by 3.1461% more than other fluids. Guedri et al.7 studied the two-dimensional ternary hybrid nanofluid over an extended surface with entropy generation. The higher values of both the electric and magnetic parameters promoted the Bejan number while hindering the generation of entropy. Dawar et al.8 studied the magnetized and non-magnetize non-Newtonian flow over a stretchy cylinder. They marked that the intensified values of the velocity graph escalated, on the other hand velocity lines curtailed. Zangooee et al.9 used the fifth-order RKF method for the solution of hybrid nanofluid across a two directional enlarging surface with non-uniform magnetic field. They concluded that the temperature had direct linked with the enhancement of the shape factor. Rehman et al.10 examined the application of hybrid nanofluids in industries to enhance their thermal performance. They noted that both the magnetic and Eckert number boost the temperature profile. The investigation of the fluid flow over an extended surface was pertinent to several key applications in engineering, particularly within the domains of metallurgy and chemical engineering processes. These uses frequently revolved around the cooling of continuous strips or filaments by drawing them through a quiescent fluid. The research conducted by Crane11 probed into the examination of the steady two-dimensional boundary layer Newtonian fluid flow over a surface undergoing stretching. This exploration contributed valuable insights into the understanding of relevant phenomena in these industrial processes. After Crane the attention of many scientists drawn toward the problem of stretching surface. Homotopic modeling of mixed-mode high-velocity bio-convective flow in a water-based hybrid nanofluid across a thermal convective exponentially expanding structure examined by Shamshuddin et al.12. Das13studied the slip effect on non-linear stretching surface. The finding revealed that the boundary layer thickness and stream-wise velocity enrich with the enhanced value of the stretching factor. Numerically deliberated the MHD steady flow over a stretchy surface by14. Their result was in excellent agreement with the previous work. Also, the heat transfer rate raised with Hartman number and stretching ratio factors. Waqas et al.15 studied the effect of thermal radiation in the presence of a heat source on hybrid nanofluid over an extended surface. The growing values of the thermal radiation declared the higher profile for temperature while diminishing for Deborah number. By imposing innovative bilateral reactions, Shamshuddin et al.16 builted a model of a two-phase nanofluid flowing through a bidirectional stretching sheet. The findings showed that a higher stretching value increased the nanofluid's velocity, whereas a lower Casson parameter decreased the x and y velocities. Bouslimi et al.17 numerically studied the thermally radiated Williamson nanofluid over a permeable stretching surface in the existence of heat generation and absorption using the fourth-order Rung-Kutta method. They found that the Nusselt number decreased with the augmented heat generation and absorption coefficient values. Furthermore, the skin friction declined with magnetic and Darcy numbers. The work was carried out by Lone et al.18 to examined the Casson hybrid nanofluid flow induced by external forces as it passed an exponentially extending surface. Extensive analysis of the data showed that as magnetic, mixed convection, buoyancy ratio, Casson, and porosity parameters escalated, fluid motion deteriorated. The literature19–21 investigated the MHD flow over a permeable and non-permeable stretching surface. Sajid et al.22 investigated numerically micro polar flow over a curved stretching surface by Runge- Kutta method. They found that the drag force is more for flat surfaces as compared to curved surfaces. Additionally, a curved sheet has a thicker boundary layer than a flat sheet.
Magnetohydrodynamics is a field of investigation that examined the dynamics of electrically conductive materials. The term comprises magneto for magnetic effects hydro for water and dynamic for movement. In this phenomena forces arise from magnetic fields induced by currents. Researchers have been significantly drawn his attention to this field in recent decades. MHD played a crucial role in geophysics engineering and astrophysics. Notably, it contributes to the cooling of nuclear reactors using liquid metals and the confinement of plasma. Aerospace vehicles also benefit from the application of MHD. Kumar et al.23 evaluated natural convection within MHD flow where an accelerated plate was taken into account along with the effects of Hall current and Soret-Dufour. The mass transfer rate grows with the Schmidt number. To explored the impact of activation energy Reddy et al.24 examined the radiative MHD nanofluid over a porous wedge. They disclosed that the boundary layer thickness expands with the growing of activation energy. Furthermore, the Nusselt number declined with the Eckert and thermophoresis parameters. Ali et al.25 scrutinized the MHD flow with variable thickness of the extended sheet containing TiO2 and copper nanoparticles. They used the Cattaneo-Christov heat flux model to enhance the thermal performance. They concluded that temperature amplified with nanoparticle volume percentage. The thermally radiative mixed convected hybrid nanofluid flow studied by Vishalaskshi et al.26 past over an extending and shrinking surface with a dual effect of inclined MHD. The velocity was the growing function of Rayleigh number. Naveed et al.27 used curvilinear coordinates to examine the MHD flow over an extended curved surface. They noted that the unsteadiness parameter suppresses both pressure and momentum boundary layer thickness.
The presence of slip boundary conditions is defined by a correlation between the tangential velocity at the surface and the shear stress applied to the wall. Navier introduced the term slip boundary condition after establishing a connection between slip rate and shear stress. Maxwell provided a straightforward explanation for velocity slip, attributing it to a change in velocity parallel to both the creep term and the surface. Thermal slip involves temperature variations along a surface with a specific temperature and concentration slip refers to the alteration in the current concentration due to the introduction of a new solute concentration. Andersson28 conducted earlier studies that considered the slip boundary Newtonian flow over an extended surface. He presented a comprehensive closed-form solution for the Navier–Stokes equations addressing MHD flow over a stretching sheet. Subsequently the Andersson contribution, Wang29 further advanced the field by unveiling a closed-form solution similarity solution for complete Navier–Stokes equations specifically for the flow over a stretching sheet with partial slip. Hayat et al.30 extended the work of previous researchers by introducing thermal slip conditions. They explored the dynamic of unsteady MHD flow and heat transfer over a sponge-extended surface incorporating slip conditions. Sharma et al.31 numerically examined the slip effect on micro polar flow over an extended porous surface. The slip and porous factors cut down the velocity profile. Ali et al.32 explored microorganism Darcy Forchheimer’s nanofluid flow with slip condition over a spinning disk. They used both numerical and analytical method for the computating of the flow model. Raza et al.33 studied the heat and mass transfer characteristic of three-dimensional MHD flow considering the effects of the slip across a rotating channel. The provided references34–37 contain the investigation and findings of the slips’ effects on different flow problems.
This study aims to examine MHD hybrid nanofluid over a bi-directional permeable stretching sheet considering slip flow and heat transport of the hybrid nanofluid () having nanoparticles and are suspended in the base fluid water. It is well-known that these nanoparticles have many engineering applications, including cosmetics, the automobile industry, the home industry, cancer therapy, food packaging, medicines, textiles, paper, plastics, paints, ceramics, food colourants, soaps, and many more. The core of the ongoing proposed model is to analyze the effects of different slips factors on the flow and heat transmission behavior of water base hybrid nanofluid. The proposed model of the nanofluid is still not being study by the researcher with such configured effects based on the cited literature. The governing PDEs are transformed into ODEs and subsequently solved numerically. To validate the numerical approach the results are compared with those of Hayat et al.38 for different values. Additionally, the study explores the influence of a strong magnetic field, thermophoresis, Brownian motion, thermal radiation, and chemical reaction. Furthermore, the effects of different non-dimensional parameters on flow profile and rate of heat and mass transfer are examined.
Mathematical model
Consider a steady MHD hybrid nanofluid three-dimensional flow over a stretching surface. Assume that the sheet is porous and stretched in two directions i.e. and as shown in (Fig. 1). The coordinates of the surface is taken along directions with velocities respectively. The extended surface is placed along and directions with velocities and respectively where are positive constants. The axis is normal to the plane i.e. perpendicular to the flow direction. The surface temperature and concentration of the sheet is denoted by . Whereas the ambient temperature and concentration are . A transversal magnetic field is applied parallel to axis with strength . The thermal radiation and first-order chemical reaction are incorporated in energy and concentration equation. Additionally, the velocity slip, thermal slip, and concentration slip conditions are taken into consideration. The below equations describe the MHD three-dimensional hybrid nanofluid flow over a bi-directional stretching surface under the above-mentioned assumptions39,40:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
Figure 1.

Geometry of flow problem.
The boundary conditions are given below39,41:
| 6 |
The similarity transformations are given as40;
| 7 |
Here are the velocities temperature and concentration slip parameters respectively. is the Roseland approximation for radiative heat flux along direction and defined as below26,42:
| 8 |
Ignored the higher order term, the generalized form of Taylor series for is:
| 9 |
Using Eq. (8 and 9) the Eq. (4) can be written as:
| 10 |
Employing the similarity transformation in Eq. (6) to the equations represented from serial (1 to 5) the nonlinear systems of ODEs are:
| 11 |
| 12 |
| 13 |
| 14 |
The transformed boundary conditions are:
| 15 |
is the Prandtl number, is thermophoresis parameter, is the velocity slip parameter, is Schmidt number, is ratio parameter, is porosity parameter, is Radiation parameter, is the magnetic, is the velocity slip parameter along y direction, is Brownian motion parameter, is thermal slip parameter, is chemical reaction parameter, and solutal Slip factor is . Here ,,, and are constants.
The theoretical model of hybrid nanofluid is given in (Table 1). In which is the dynamic viscosity, the density is denoted by , is the heat capacitance, is the thermal conductivity, and is the electrical conductivity of the fluid. The subscript are used for hybrid, nanofluid, and base fluid respectively. are the nanoparticles volume fraction of and nanoparticles. The thermophysical property of , and base fluid are defined in (Table 2).
Table 1.
The thermophysical properties of hybrid nanofluid45.
| Properties name | Thermophysical characteristic of hybrid nanofluid |
|---|---|
| Density | |
| Heat capacitance | |
| Dynamic viscosity | |
| Thermal conductivity | |
| Electrical conductivity |
Table 2.
The thermophysical property of with 46.
| Name | Base fluid | Nanoparticles | |
|---|---|---|---|
| Density | 997.1 | 8933 | 3970 |
| Specific heat | 4179 | 385 | 765 |
| Thermal conductivity | 0.613 | 401 | 40 |
| Electrical conductivity | 0.05 | 1 | |
| Pr | 6.2 | ||
Quantities of interest
The physical quantities which are important in engineering science and industrial process are42–44:
| 16 |
| 17 |
Using Eqs. (5 and 17) the simplified form of the Eq. (16) is given by:
| 18 |
where represent Nusselt number, are skin friction coefficients and are mass transfer rate.
Numerical procedure
To solve the ODEs the bvp4c solver is used in MATLAB software. To set the problem for bvp4c the given below steps are as follows:
The boundary value problem is defined.
Apply the similarity transformations.
Achieved the nonlinear ODEs, with the boundary constraints.
Write the boundary value problem in first-order ordinary differential equation, so that we can easily compute it in MATLAB.
Find obtained the outcomes graphically and numerically.
Let
| 19 |
Using Eq. (20) we write the equation from (10–13) in the following form:
| 20 |
| 21 |
| 22 |
| 23 |
The new converted boundary circumstances are:
| 24 |
Validation of code
Comparison with previously published paper from the existing literature has been made to verify the precision of the present results. Table 2 demonstrates that the numerical values of the friction drag coefficients and in this paper across various values closely align with the results published by Hayat et al.38. Consequently, we have confidence in the high accuracy of our results for analyzing the flow problem.
Discussion
This section contain the impact of different physical parameters on MHD hybrid nanofluid slip flow over a bi-directional extended surface. These physical parameters are Magnetic parameter , radiation parameter velocity slip parameters , concentration slip , thermal slip parameters , thermophoresis , Brownian motion and chemical reaction . The flow fields are velocity along and directions, temperature and concentration represented by , , and respectively. The skin frictions are , Nusselt number and mass transfer is . Table 2 represents the thermophysical characteristics of the nanoparticles and base fluid. Table 3 shows the comparison of the present work with the already published work. This results shows that the current values are closely aligned with the work of Hayat et al.38. Figures 2, 3 illustrates the effect of on and velocities of the hybrid nanofluids respectively. An enhancement in results in a decrease in the velocity profiles due to an external resistance. Consequently, the velocity gradients slow down leading to a reduction in the thickness of the momentum boundary layer and drop in the flow velocities. Physically the amplified value of generates Lorentzian MHD drag force, which opposing fluid motion across the entire domain. Additionally the combined with the slip effect functions as a hindering force. This retarding force can regulate the fluid velocity proving beneficial in various application such as coating of wire, metal and MHD power generation etc. In Figs. 4, 5 the influence of the velocity slip parameters and on and are elucidate. Elevating and induces a reduction in and . Particularly the augmentation of and is associated with a reduction in the thickness of the momentum boundary layer, leading to a subsequent decrease in the velocity within this layer. Under slip conditions, it is noteworthy that the velocity of the stretching surface differs from that of the flow over the surface. In the given hybrid nanofluid flow over a linearly two directional extending surface both and exhibit identical effects along and directions as depicted in (Figs. 4, 5). Figures 6, 7 explore the impact of on and . An increase in manifests as a dual effect on and . Specifically a higher value of correlates with a reduction in and a simultaneous increase in . The mathematical definition shows that has inverse relation with the extending velocity constant along direction. Conversely a directly relationship is observed with constant stretching velocity along direction. Consequently the rise in leads to a decrease in due to its inverse relation with while concurrently augmenting owing to its direct relation with as a result escalating enhances and reduces of the hybrid nanofluid. Particles' average velocity decrease due to this enhanced rotation, which obstructs their linear translational motion. A more organized and constrained movement of the particles is produced by the interaction of rotational and translational dynamics, which helps to explain the decrease in . The sway of on is display in (Fig. 8). This Figure shows that an elevation in there is a corresponding increase in of hybrid nanofluid. This phenomenon is attributed to the heightened thermal resistance of the fluid driven by the tendency of thermophoretic distribution to elevate the non-dimensional fluid temperature. The catalyst behind this occurrence is the temperature gradient. As the rise fluid particles undergo a movement toward higher energy levels, departing from colder regions. This migration contributes to an elevation in the profile. This is due to the fact that nanoparticles have the ability to carry heat more efficiently, which ultimately results in a more effective transfer of thermal energy throughout the fluid. Additionally, the increased motion of the nanoparticles can have the effect of enhancing the mixing of the nanofluid, which can also contribute to an increase in temperature. This shows a direct link of with . The influence of on is depicts in (Fig. 9). As the values of enhance there is a corresponding growth in .This behavior can be elucidated by the fact that augmenting the values results in heightened random motion among fluid particles. This escalated random motion in turn elevates the mean kinetic energy of fluid particles, leading to an increase in of hybrid nanofluid. Figure 10 display the impacts of the thermal slip parameter on .The augmented values of decline the curve of . Physically even with a modest amount of heat transferred from the sheet to the fluid the values of wall temperature and thermal boundary layer thickness decrease with an increase in parameter. This implies that a higher values induces a more efficient heat transfer mechanism resulting in a reduction of both wall temperature and thermal boundary layer thickness. As a result curves of hybrid nanofluid drops with the growing values of . The impact of on is illustrated in (Fig. 11). The finding shows that the rises with the expansion of values. This relationship is explained by the fact that when enrich the fluid receives more heat leading to an augmentation in both temperature and thermal boundary layer thickness. It is quite probable that the radiation factor denotes the system's radiative heat transfer mechanisms and their strength. The thermal equilibrium and redistribution of heat are affected by the increased interchange of thermal energy by electromagnetic waves, which occurs when the radiation factor increases. The radiative heat process signifies due to the augmentation in thermal distribution has a heightened impact on temperature. The change in with the escalating value of is shown in (Fig. 12). From Fig. 12 it is eminent that decreases when increases. The impact of on is depicts in (Fig. 13). The panel diminishes as parameter enhances. This occurrence is attributed to the heightened participation of particles in the chemical reaction resulting in an over reduction in the concentration profile. Physically when grows, the quantity of solute molecules increases, resulting in a drop in . The thickness of the solutal boundary layer is significantly reduced by destructive chemical reactions. Therefore the enrichment in , decline the of hybrid nanofluid. The impact of on is portraits in (Fig. 14). The impact of on is characterized by a monotonic trend, as the values of grows the concentration boundary layer thickness also upsurges. Furthermore the graph illustrates the magnitude of the concentration gradient on the sheets surface diminishes with higher values of . Additional the Sherwood number which signifies the mass transfer rate at the surface decreases as increases is shown is (Table 6). This decrease more pronounced in hybid nanofluid as compared to nanofluid. Thermophoresis describes the movement of particles driven by temperature gradient. As the thermophoresis factors enhance it exerts a stronger effect on the distribution of thermal energy and particle concentrations. This increase indicates that the system undergoes a more significant separation of particles according to their thermal responses. The enhanced thermophoresis factor impacts the thermal distribution by causing particles to move in the temperature gradient direction, thereby altering temperature. At the same time, it affects the concentration distribution by causing particles to migrate based on their size shape, and thermal properties. The change in in response to varying is shown in (Fig. 15). As upsurge in results in a reduction of the concentration boundary thickness. Additionally the concentration gradient magnitude at the sheets surface rises with the higher values of . Consequently of the hybrid nanofluid at the surface enhances with the hike of shown in (Table 6). The random movement of nanoparticles in this phenomena results in a reduction in their kinetic energy, which in turn results in a reduction in the rate at which heat is transmitted. As the value of Nb grows, the number of collisions between fluid particles also increases, which results in a decrease in the amount of mass that is transferred from the heated sheet to the cool fluid. Figures 16, 17 shows the impacts of on the streams lines and countours plots. From these Figures it is clear that with the higher values of the streams lines expands while the distance between the curves of contours lines suppress . This demonstrates that the streamline pattern has been altered as a result of the increased intensity of the magnetic field. Table 4 illustrates the change in the and concerning with no slip and slip effects. Upon examining the Table 4 it becomes evident that with an increase in there is a corresponding increase in the values of and . Furthermore in the presence of slip effect the skin friction is reduces. The effect of on Nusselt number are shown in (Table 5). The ascending values of parameters diminishes the heat transfer rate whereas the enhancements the Nusselt number. The effect of on Sherwood number are shown in (Table 6). As the growing values of parameters reduce the mass transfer rate whereas the and boosts the Sherwood number.
Table 3.
Comparison of the skin friction with Hayat et al.38 for varying values of .
| Present Results | Hayat et al.38 | |||
|---|---|---|---|---|
| 0.0 | 1.0000 | 0.0000 | 1.0000 | 0.0000 |
| 0.2 | 1.0358 | 0.1479 | 1.0395 | 0.1487 |
| 0.4 | 1.0686 | 0.3490 | 1.0757 | 0.3492 |
| 0.6 | 1.1089 | 0.5908 | 1.1099 | 0.5905 |
| 0.8 | 1.1432 | 0.8666 | 1.1424 | 0.8666 |
| 1.0 | 1.1723 | 1.1723 | 1.1723 | 1.1723 |
Figure 2.
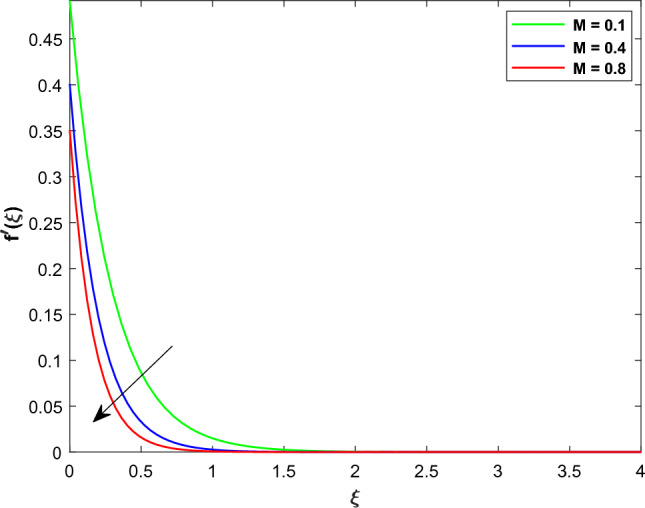
profile for various values of .
Figure 3.

profile for various values of .
Figure 4.
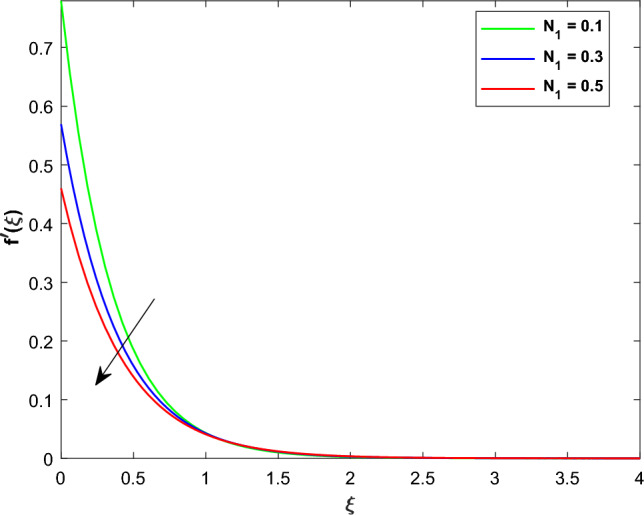
profile for various values of .
Figure 5.

profile for various values of .
Figure 6.

profile for various values of .
Figure 7.
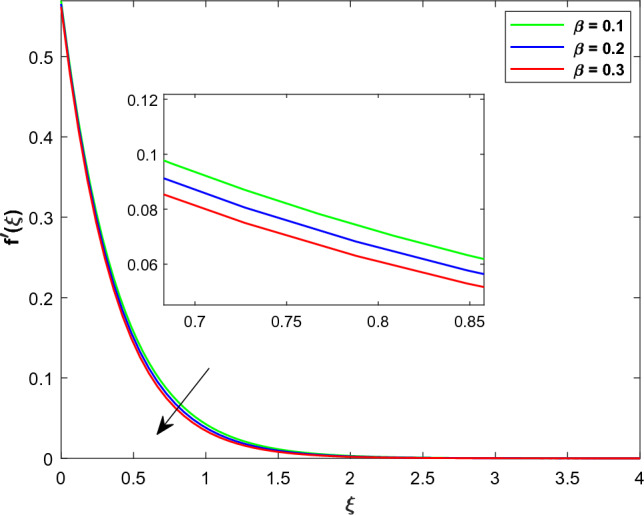
profile for various values of .
Figure 8.
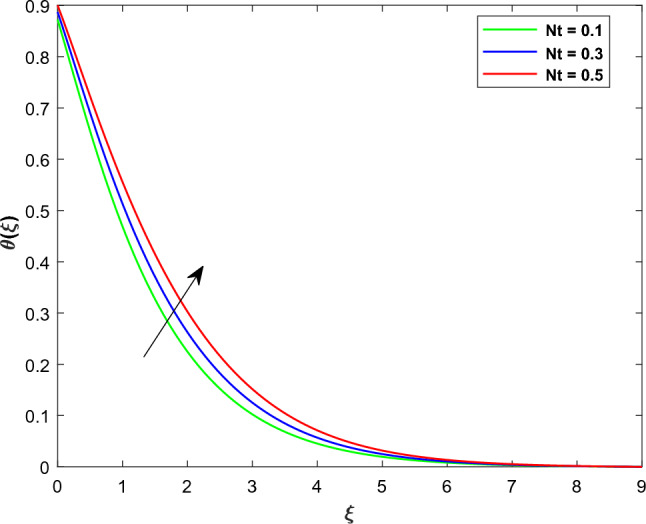
profile for various values of .
Figure 9.

profile for various values of .
Figure 10.

profile for various values of .
Figure 11.

profile for various values of .
Figure 12.

profile for various values of .
Figure 13.
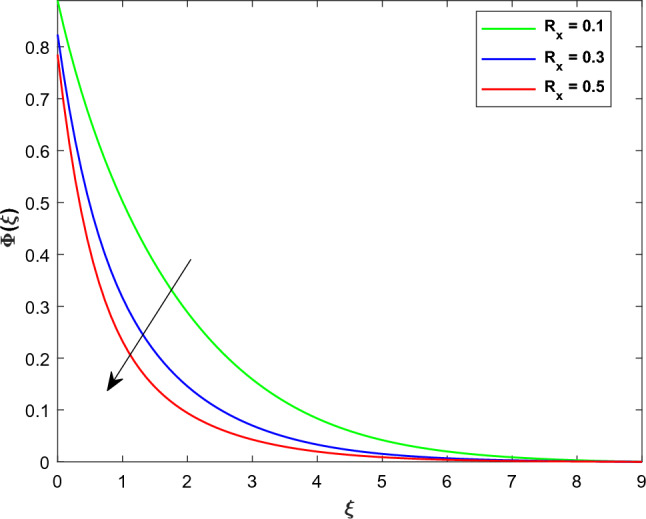
profile for various values of .
Figure 14.

profile for various values of .
Table 6.
The impact of ,, and on .
| Sherwood number | |||||
|---|---|---|---|---|---|
| Hybrid nanofluid | Nanofluid | ||||
| 0.3 | 0.2 | 0.3 | 0.1 | 0.485489 | 0.450611 |
| 0.4 | 0.425439 | 0.407857 | |||
| 0.5 | 0.388775 | 0.389414 | |||
| 0.3 | 0.3 | 0.70877 | 0.654592 | ||
| 0.4 | 0.772827 | 0.715967 | |||
| 0.5 | 0.808423 | 0.749406 | |||
| 0.2 | 0.4 | 1.02502 | 1.00976 | ||
| 0.5 | 1.12553 | 1.11349 | |||
| 0.6 | 1.21366 | 1.20374 | |||
| 0.3 | 0.3 | 0.478887 | 0.441364 | ||
| 0.4 | 0.442345 | 0.409286 | |||
| 0.5 | 0.410962 | 0.381531 | |||
Figure 15.

profile for various values of .
Figure 16.
The stream lines and contours plots for for . (a) For , (b) For , (c) For , (d) For .
Figure 17.
The stream lines and contours plots for .
Table 4.
The impact of on and in the presence of slip and no slip effect.
| 1.0 | 0.7421 | 0.1265 | 0.3900 | 0.0726 |
| 2.0 | 0.8924 | 0.1606 | 0.4408 | 0.0850 |
| 3.0 | 1.0209 | 0.1888 | 0.4774 | 0.0933 |
Table 5.
The impact of ,, and on .
| Nusselt number | |||||
|---|---|---|---|---|---|
| Hybrid nanofluid | Nanofluid | ||||
| 0.1 | 0.2 | 0.3 | 0.2 | 1.03433 | 0.655002 |
| 0.2 | 0.946672 | 0.583784 | |||
| 0.3 | 0.865933 | 0.520006 | |||
| 0.1 | 0.3 | 0.807502 | 0.478815 | ||
| 0.4 | 0.682385 | 0.38813 | |||
| 0.5 | 0.571436 | 0.311103 | |||
| 0.2 | 0.4 | 0.987553 | 0.613366 | ||
| 0.5 | 1.02608 | 0.641111 | |||
| 0.6 | 1.06247 | 0.667248 | |||
| 0.3 | 0.3 | 0.906574 | 0.749216 | ||
| 0.4 | 0.869076 | 0.720873 | |||
| 0.5 | 0.834019 | 0.694137 | |||
Final remarks
There has been a revolution in the field of thermal engineering as a result of the improved potential of hybrid nanofluids, which significantly increases the efficiency of heat exchangers and saves energy. The current declaration intends to inspect a numerical analysis of the heat and mass transfer characteristics of three dimensional MHD hybrid nanofluid flow over a porous bi-directional stretching sheet, considering slip effects. The flow is assumed to be laminar, steady, and incompressible. A hybrid nanofluid has been composed by dispersing of Cu and Al2O3 nanoparticles in water. The governing equations initially formulated as partial differential equations and then transformed into a nonlinear system of ordinary differential equations through appropriate transformations. The bvp4c technique in MATLAB is employed for solving these equations. Several involve parameters impacts on flow distributions have been studied and elucidated through graphs and tables. The slip conditions are also used to examine different distributions of flows. The accuracy of the numerical approach is validated by comparing the results with previously published work demonstrating excellent agreement. The study's findings are summarized as follows:
The fluid velocity along and directions slowed down with the rising values of the magnetic and slip parameters.
The ratio parameter has dual impact on velocity along and directions. The amplified value of beta enhance the velocity along direction and suppress along direction.
The temperature profile grows with radiation and thermophoresis parameters.
An elevation in the thermal slip parameter led to a reduction in both the boundary layer thickness and the heat transfer from the surface to the fluid.
The concentration profiles exhibits increment with thermophoresis parameter while decline with rising chemical reaction, Brownian motion parameters.
Growing values of the concentration slip parameter reduced the mass transfer resulting in a reduction of the concentration profile.
The higher values of magnetic parameter decrease the skin friction coefficient for both slip and no slip. The skin friction is higher for no slip condition.
The heat transfer rate decreasing function of Brownian, thermophoresis while increasing with radiation factor.
The mass transfer rate boosts with Brownian and chemical reaction and declines with thermophoresis parameter.
The stream lines becomes wide with the improved values of magnetic parameter while the contours plots close to each other.
Future direction
In Future work, we can focus on the effect of various factors such as:
Variable chemical reaction of higher order.
Activation energy.
Nonlinear thermal radiation and heat source.
Different types of nanoparticles.
Abbreviations
Porosity parameter
Velocity along axis
Coordinates of axis
- ,
Velocity slip parameter along and directions
Stretching velocities
Thermophoresis parameter
Ratio parameter
Chemical reaction
Radiation parameter
Brownian motion
Thermal slip parameter
Dynamic viscosity
Thermal conductivity
Strength of the magnetic field
- T
Temperature of the fluid
Prandtl number
Brownian diffusion coefficient
Ambient temperature
Concentration slip parameter
Thermophoreis diffusion coefficient
Wall temperature
Ambient concentration
Concentration of the fluid
Skin friction coefficient directions
Local Nusselt number
Positive constants along directions
Specific heat
Sherwood number
Stefan-Boltzmann constant
Schmidt number
Radiative heat flux
Electrical conductivity
Surface concentration
Density
Base fluid
Nanofluid
Hybrid nanofluid
Author contributions
Hakeem Ullah (1), Syed Arshad Abas (2), Mehreen Fiza(3), Ilyas Khan(4), Ariana Abdul Rahimzai(5), Ali Akgul(6) Author’s Contribution authors (1,2,3,4,5,6) Conceptualization, Formal analysis, Resources, Software, Supervision, Writing—original draft authors (1,2,4,5,6) Methodology, Resources, Software, Validation, Writing—original draft authors (4,3,1,6) Resources, Validation, Writing—original draft authors (2,3,4,6) Resources, Visualization, authors (4,2,5,6) Resources, Validation, authors (1,5,3,2,4) Conceptualization, Formal analysis, Supervision, Visualization.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Choi, S.U.S. & Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. (ASME International Mechanical Engineering Congress & Exposition, San Francisco, 1995).
- 2.Choi, S. U. S., Zhang, Z. G., Yu, Wl., Lockwood, F. E. & Grulke, E. A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett.79, 2252–2254 (2001). 10.1063/1.1408272 [DOI] [Google Scholar]
- 3.Vedavathi, N., Dharmaiah, G., Venkatadri, K. & Gaffar, S. A. Numerical study of radiative non-darcy nanofluid flow over a stretching sheet with a convective nield conditions and energy activation. Nonlinear Eng.10, 159–176 (2021). 10.1515/nleng-2021-0012 [DOI] [Google Scholar]
- 4.Abas, S. A., Ullah, H., Islam, S. & Fiza, M. A passive control of magnetohydrodynamic flow of a blood-based Casson hybrid nanofluid over a convectively heated bi-directional stretching surface. Z Angew. Math Mech.104, e202200576 (2023). 10.1002/zamm.202200576 [DOI] [Google Scholar]
- 5.Ali, F., Zaib, A., Reddy, S., Alshehri, M. H. & Shah, N. A. Impact of thermal radiative carreau ternary hybrid nanofluid dynamics in solar aircraft with entropy generation: Significance of energy in solar aircraft. J. Therm. Anal. Calorim.149, 1495–1513 (2024). 10.1007/s10973-023-12734-9 [DOI] [Google Scholar]
- 6.Saeed, A. et al. Darcy-Forchheimer hybrid nanofluid flow over a stretching curved surface with heat and mass transfer. PLoS ONE16, e0249434 (2021). 10.1371/journal.pone.0249434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guedri, K. et al. Thermally dissipative flow and entropy analysis for electromagnetic trihybrid nanofluid flow past a stretching surface. ACS Omega7, 33432–33442 (2022). 10.1021/acsomega.2c04047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dawar, A., Shah, Z., Alshehri, H. M., Islam, S. & Kumam, P. Magnetized and non-magnetized Casson fluid flow with gyrotactic microorganisms over a stratified stretching cylinder. Sci. Rep.11, 16376 (2021). 10.1038/s41598-021-95878-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zangooee, M. R., Hosseinzadeh, K. & Ganj, D. D. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate. Nonlinear Eng.11, 143–155 (2022). 10.1515/nleng-2022-0019 [DOI] [Google Scholar]
- 10.Rehman, A., Khan, D., Mahariq, I., Elkotb, M. A. & Elnaqeeb, T. Viscous dissipation effects on time-dependent MHD Casson nanofluid over stretching surface: A hybrid nanofluid study. J. Mol. Liq.408, 125370 (2024). 10.1016/j.molliq.2024.125370 [DOI] [Google Scholar]
- 11.Crane, L. J. Flow past a stretching plate. Zeitschrift für Angew. Math. Phys. ZAMP21, 645–647 (1970). 10.1007/BF01587695 [DOI] [Google Scholar]
- 12.Shamshuddin, M. D., Saeed, A., Mishra, S. R., Katta, R. & Eid, M. R. Homotopic simulation of MHD bioconvective flow of water-based hybrid nanofluid over a thermal convective exponential stretching surface. Int. J. Numer. Methods Heat Fluid Flow34, 31–53 (2024). 10.1108/HFF-03-2023-0128 [DOI] [Google Scholar]
- 13.Das, K. Nanofluid flow over a non-linear permeable stretching sheet with partial slip. J. Egypt. Math. Soc.23, 451–456 (2015). 10.1016/j.joems.2014.06.014 [DOI] [Google Scholar]
- 14.Alarifi, I. M. et al. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry11, 297 (2019). 10.3390/sym11030297 [DOI] [Google Scholar]
- 15.Waqas, H. et al. Heat transfer analysis of hybrid nanofluid flow with thermal radiation through a stretching sheet: A comparative study. Int. Commun. Heat Mass Transf.138, 106303 (2022). 10.1016/j.icheatmasstransfer.2022.106303 [DOI] [Google Scholar]
- 16.Shamshuddin, M. D., Asogwa, K. K. & Ferdows, M. Thermo-solutal migrating heat producing and radiative Casson nanofluid flow via bidirectional stretching surface in the presence of bilateral reactions. Numer. Heat Transf. Part A Appl.85, 719–738 (2024). 10.1080/10407782.2023.2191873 [DOI] [Google Scholar]
- 17.Bouslimi, J. et al. MHD Williamson nanofluid flow over a stretching sheet through a porous medium under effects of joule heating, nonlinear thermal radiation, heat generation/absorption, and chemical reaction. Adv. Math. Phys.2021, 1–16 (2021). 10.1155/2021/9950993 [DOI] [Google Scholar]
- 18.Lone, S. A. et al. Computational analysis of MHD driven bioconvective flow of hybrid Casson nanofluid past a permeable exponential stretching sheet with thermophoresis and Brownian motion effects. J. Magn. Magn. Mater.580, 170959 (2023). 10.1016/j.jmmm.2023.170959 [DOI] [Google Scholar]
- 19.Khan, U., Waini, I., Ishak, A. & Pop, I. Unsteady hybrid nanofluid flow over a radially permeable shrinking/stretching surface. J. Mol. Liq.331, 115752 (2021). 10.1016/j.molliq.2021.115752 [DOI] [Google Scholar]
- 20.Jamshed, W., Devi, S. U. & Nisar, K. S. Single phase based study of Ag-Cu/EO Williamson hybrid nanofluid flow over a stretching surface with shape factor. Phys. Scr.96, 065202 (2021). 10.1088/1402-4896/abecc0 [DOI] [Google Scholar]
- 21.Abbas, N., Rehman, K. U., Shatanawi, W. & Malik, M. Y. Numerical study of heat transfer in hybrid nanofluid flow over permeable nonlinear stretching curved surface with thermal slip. Int. Commun. Heat Mass Transf.135, 106107 (2022). 10.1016/j.icheatmasstransfer.2022.106107 [DOI] [Google Scholar]
- 22.Sajid, M., Ali, N., Abbas, Z. & Javed, T. Flow of a micropolar fluid over a curved stretching surface. J. Eng. Phys. Thermophys.84, 864–871 (2011). 10.1007/s10891-011-0544-2 [DOI] [Google Scholar]
- 23.Kumar, M. A., Reddy, Y. D., Goud, B. S. & Rao, V. S. Effects of soret, dufour, hall current and rotation on MHD natural convective heat and mass transfer flow past an accelerated vertical plate through a porous medium. Int. J. Thermofluids9, 100061 (2021). 10.1016/j.ijft.2020.100061 [DOI] [Google Scholar]
- 24.Reddy, M. V. et al. Magneto-Williamson nanofluid flow past a wedge with activation energy: Buongiorno model. Adv. Mech. Eng.16, 16878132231223028 (2024). 10.1177/16878132231223027 [DOI] [Google Scholar]
- 25.Ali, A. et al. Hall effects and Cattaneo-Christov heat flux on MHD flow of hybrid nanofluid over a varying thickness stretching surface. Mod. Phys. Lett. B38, 2450130 (2024). 10.1142/S0217984924501306 [DOI] [Google Scholar]
- 26.Vishalakshi, A. B. et al. MHD hybrid nanofluid flow over a stretching/shrinking sheet with skin friction: Effects of radiation and mass transpiration. Magnetochemistry9, 118 (2023). 10.3390/magnetochemistry9050118 [DOI] [Google Scholar]
- 27.Naveed, M., Abbas, Z. & Sajid, M. Hydromagnetic flow over an unsteady curved stretching surface. Eng. Sci. Technol. Int. J.19, 841–845 (2016). [Google Scholar]
- 28.Andersson, H. I. Slip flow past a stretching surface. Acta Mech.158, 121–125 (2002). 10.1007/BF01463174 [DOI] [Google Scholar]
- 29.Wang, C. Y. Flow due to a stretching boundary with partial slip—An exact solution of the Navier-Stokes equations. Chem. Eng. Sci.57, 3745–3747 (2002). 10.1016/S0009-2509(02)00267-1 [DOI] [Google Scholar]
- 30.Hayat, T., Qasim, M. & Mesloub, S. MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int. J. Numer. Methods Fluids66, 963–975 (2011). 10.1002/fld.2294 [DOI] [Google Scholar]
- 31.Sharma, S. et al. MHD micro polar fluid flow over a stretching surface with melting and slip effect. Sci. Rep.13, 10715 (2023). 10.1038/s41598-023-36988-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ali, F. et al. Scrutinization using both numerical and analytical techniques for darcy forchheimer flow in the gyrotactic microorganism of nanofluid over a rotating disk. Numer. Heat Transf. Part B Fundam.10.1080/10407790.2023.2300678 (2024). 10.1080/10407790.2023.2300678 [DOI] [Google Scholar]
- 33.Raza, J., Rohni, A. M., Omar, Z. & Awais, M. Heat and mass transfer analysis of MHD nanofluid flow in a rotating channel with slip effects. J. Mol. Liq.219, 703–708 (2016). 10.1016/j.molliq.2016.04.003 [DOI] [Google Scholar]
- 34.Ramzan, M. et al. Heat transfer analysis of the mixed convective flow of magnetohydrodynamic hybrid nanofluid past a stretching sheet with velocity and thermal slip conditions. PLoS ONE16, e0260854 (2021). 10.1371/journal.pone.0260854 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ali, B. et al. Numerical investigation of heat source induced thermal slip effect on trihybrid nanofluid flow over a stretching surface. Results Eng.20, 101536 (2023). 10.1016/j.rineng.2023.101536 [DOI] [Google Scholar]
- 36.Syahirah Wahid, N. et al. Three-dimensional stretching/shrinking flow of hybrid nanofluid with slips and joule heating. J. Thermophys. Heat Transf.36, 848–857 (2022). 10.2514/1.T6488 [DOI] [Google Scholar]
- 37.Anuar, N. S., Bachok, N. & Pop, I. Numerical computation of dusty hybrid nanofluid flow and heat transfer over a deformable sheet with slip effect. Mathematics9, 643 (2021). 10.3390/math9060643 [DOI] [Google Scholar]
- 38.Hayat, T., Awais, M. & Obaidat, S. Three-dimensional flow of a Jeffery fluid over a linearly stretching sheet. Commun. Nonlinear Sci. Numer. Simul.17, 699–707 (2012). 10.1016/j.cnsns.2011.05.042 [DOI] [Google Scholar]
- 39.Razi, S. M., Soid, S. K., Abd Aziz, A. S., Adli, N. & Ali, Z. M. Williamson nanofluid flow over a stretching sheet with varied wall thickness and slip effects. J. Phys. Conf. Ser.1366, 012007 (2019). 10.1088/1742-6596/1366/1/012007 [DOI] [Google Scholar]
- 40.Khan, I., Rahman, A. U., Dawar, A., Islam, S. & Zaman, A. Second-order slip flow of a magnetohydrodynamic hybrid nanofluid past a bi-directional stretching surface with thermal convective and zero mass flux conditions. Adv. Mech. Eng.15, 1–12 (2023). 10.1177/16878132221149894 [DOI] [Google Scholar]
- 41.Ibrahim, W. & Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids75, 1–10 (2013). 10.1016/j.compfluid.2013.01.014 [DOI] [Google Scholar]
- 42.Zainal, N. A., Nazar, R., Naganthran, K. & Pop, I. The impact of thermal radiation on Maxwell hybrid nanofluids in the stagnation region. Nanomaterials12, 1109 (2022). 10.3390/nano12071109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Teh, Y. Y. & Ashgar, A. Three dimensional MHD hybrid nanofluid flow with rotating stretching/shrinking sheet and Joule heating. CFD Lett.13, 1–19 (2021). 10.37934/cfdl.13.8.119 [DOI] [Google Scholar]
- 44.Arshad, M. et al. Rotating hybrid nanofluid flow with chemical reaction and thermal radiation between parallel plates. Nanomaterials12, 4177 (2022). 10.3390/nano12234177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Aly, E. H. & Pop, I. MHD flow and heat transfer near stagnation point over a stretching/shrinking surface with partial slip and viscous dissipation: Hybrid nanofluid versus nanofluid. Powder Technol.367, 192–205 (2020). 10.1016/j.powtec.2020.03.030 [DOI] [Google Scholar]
- 46.Khan, M., Ali, W. & Ahmed, J. A hybrid approach to study the influence of hall current in radiative nanofluid flow over a rotating disk. Appl. Nanosci.10, 5167–5177 (2020). 10.1007/s13204-020-01415-w [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.




