Deconvoluting XPS Spectra of La-Containing Perovskites from First-Principles

Abstract

Perovskite-based oxides are used in electrochemical CO₂ and H₂O reduction in electrochemical cells due to their compositional versatility, redox properties, and stability. However, limited knowledge exists on the mechanisms driving these processes. Toward this understanding, herein we probe the core level binding energy shifts of water-derived adspecies (H, O, OH, H₂O) as well as the adsorption of CO₂ on LaCoO₃ and LaNiO₃ and correlate the simulated peaks with experimental temperature-programmed X-ray photoelectron spectroscopy (TPXPS) results. We find that the strong adsorption of such chemical species can affect the antiferromagnetic ordering of LaNiO₃. The adsorption of such adspecies is further quantified through Bader and differential charge analyses. We find that the higher O 1s core level binding energy peak for both LaCoO₃ and LaNiO₃ corresponds to adsorption of water-related species and CO₂, while the lower energy peak is due to lattice oxygen. We further correlate these density functional theory-based core level O 1s binding energies with the TPXPS measurements to quantify the decrease of the O 1s contribution due to desorption of adsorbates and the apparent increase of the lattice oxygen (both bulk and surface) with temperature. Finally, we quantify the influence of adsorbates on the La 4d, Co 2p, and the Ni 3p core level binding energy shifts. This work demonstrates how theoretically generated XPS data can be utilized to predict species-specific binding energy shifts to assist in deconvolution of the experimental results.

1. Introduction

Perovskites are used in a broad range of applications including low-temperature electrolysis,¹ solid oxide electrolysis cells (SOECs),² and photocatalytic applications.³ Importantly, perovskite oxides can catalyze the coelectrolysis of H₂O and CO₂ in an SOEC⁴⁻⁷ allowing for the storage of renewable energy in the chemical bonds of CO and H₂ (syngas). When coupled with existing processes such as Fischer–Tropsch, this method provides a solution to reduce emissions and facilitates net-zero carbon energy storage in liquid fuel form.⁶⁻⁸ Considerable research has been focused on improving the activity of perovskite oxides in electrochemical cells to the level of metallic catalysts⁶ but a lack of consistency in the characterization of these cells has led to a limited fundamental understanding of the reduction reaction. One complication to characterizing the clean surface are adspecies present on perovskite surfaces at room temperature as shown by many X-ray photoelectron spectroscopy (XPS) studies on the O 1s spectra.⁹⁻¹² In their theoretical work, Blanck et al. investigated the adsorption of water molecules on the surface of LaFeO₃ (121) and (100).¹³ They found that water is adsorbed through a dissociative mechanism forming surface hydroxide, leading to a change in the perovskite surface structure.¹³ The additional complexity associated with surface hydroxyls convolutes the experimental surface spectra; thus, insights from theory can be used to increase the understanding of perovskite surfaces by deconvoluting the surface sensitive XPS spectra based on first-principles-based calculations.

There are several studies on the effect of water on the XPS features of LaNiO_3–x thin films.^9,10 An XPS study by Mickevičius et al. fitted the lower energy peak of the O 1s spectra of LaNiO₃ with two contributions (528.98 and 529.72 eV) to the different contributions of oxygen species in the oxide structure coordinated with La and Ni, respectively.⁹ The lower energy peak was divided into two different oxide structures due to the different types of chemical bonds occurring in the perovskite lattice. They observed that the Ni–O and the La–O bonds exhibit covalent behavior while Ni–O–Ni bonds exhibit metallic behavior shown by a DOS analysis.⁹ This study concluded that the higher energy peak contributions at 530.97 and 532.96 eV are an indication of the adsorption of OH groups and water, respectively.⁹ Similarly, Bondarenka et al. conducted a dual peak deconvolution showing a broad lower energy peak containing contributions of several different oxygen species on the surface.¹⁰ They assigned the peaks as 528.96 eV for the lattice of O^2–, 531.35 eV for OH groups on the surface, and 533.17 eV as water adsorbed on the surface. As such, there are competing narratives in the literature as to the nature of the contributions on the LaNiO₃ surface with some important adsorbates, such as CO₂, not considered in these studies.

Similar studies that deconvolute the XPS of LaCoO₃ (001) exist.^11,12 Stoerzinger et al. found the LaCoO₃ higher energy peak in the O 1s spectra changes significantly under different relative humidities allowing for the effects of adspecies on the surface to be characterized.¹² The O 1s spectra at room temperature is broken down into a bulk peak at 528.7 eV, a higher energy peak at 531.5 eV attributed to surface species and the adsorption of CO₃^–, a higher energy shoulder appears at 535 eV attributed to gas-phase H₂O, and an intermediate peak at 530.5 eV attributed to OH groups adsorbed on the surface.¹² They concluded the higher binding energy of the surface oxygen as compared to bulk oxygens was due to electronic or structural surface reconstruction because of the polar nature of perovskites and the undercoordination of surface oxygens. This work considered the effects of oxygen containing adspecies on the La 4d and Co 3p spectra finding the increase in relative humidity did little to change the resulting spectra.¹² There are disagreements in the literature about the contributions to the surface peaks as pointed out by the authors of this study.¹² Previous papers attributed the contributions to the peaks to the adsorption of oxidized carbon species, surface hydroxyls, adsorbed water, and undercoordinated oxygen. Although their methods differ from other studies because they model water adsorption specifically, there are still questions about how CO₂ effects the XPS spectra that are unanswered by these authors.

Experimentally, the XPS spectra are typically deconvoluted using values taken from the existing literature studying a comparable compound or by identifying obvious features in the spectra. Additionally, many of the experimental XPS spectra in the literature are produced using thin-film perovskites which would not directly translate to nanoparticle oxide systems that are used for catalysis.⁹⁻¹² The different surface structures of realistic samples from wet chemistry could affect the adsorption of species on the surface and thus their binding energies. As such, we measure the experimental XPS spectra of a realistic perovskite catalyst surface. To gain a deeper understanding of these surfaces, we propose deconvoluting experimental XPS spectra from first-principles-based density functional theory (DFT) calculations to determine how adspecies affect the electronic properties at the perovskite surface. There exists a need for clarifying the assignments of peaks to better understand the contributions to the experimental data.^9,10 We investigate two lanthanum-based LaBO₃ perovskites, where the B-site is varied through different substitutions (Ni and Co), with the presence of adsorbates on the surface (H, O, OH, H₂O, and CO₂) to produce a first-principles-based model of experimental XPS spectra using the core level binding energy shifts of the La, B-site, and O. We correlate the theoretical XPS results of the O 1s spectra with not only experimental room temperature XPS measurements but also with temperature-dependent XPS measurements of the O 1s spectra. These temperature-dependent measurements facilitate the deconvolution of the O 1s signal arising from the bulk structure of the perovskite with the corresponding signal arising from the presence of adsorbates on the surface as a consequence of the dissociative adsorption of water¹¹ and CO₂ adsorption on the oxide surface. The deconvolution of XPS spectra using first-principles-based methods will improve the knowledge surrounding adspecies on perovskite surfaces by providing reproducible binding energies of adspecies.

2. Methods

2.1. Theoretical Methods

We conduct theoretical calculations utilizing the Vienna Ab Initio Software Package (VASP) version 5.4.1¹⁴ with the revised Purdue–Burke–Erzenholf (RPBE) functional, a generalized gradient approximation (GGA) functional.¹⁵ While this functional has proven to underestimate the band gap energy,^16,17 it has also shown to reproduce experimental formation energies of LaBO₃ compounds. Thus, we hypothesize it will be sufficiently accurate to reproduce the XPS data we model using first-principles-based calculations. We use a planewave basis with the projector augmented wave method^18,19 released in 2015²⁰ to describe the wave functions of the surfaces and model the core electrons of atoms within the surface.

In order to model the XPS spectra, we first optimized the lattice constant using bulk structures. Typically, a cubic unit cell is used to model the bulk structure of perovskites since such a structure is more computationally efficient than the corresponding orthorhombic or the rhombohedral structures. The cubic cell is used even if the cubic structure is not the one experimentally observed for LaNiO₃ and LaCoO₃.^21,22 Due to these previous omissions, we model the bulk structure of LaNiO₃ and LaCoO₃ using the rhombohedral structures to make our model consistent with the experimental observations.²³ The Supporting Information outlines the procedure for finding the equilibrium volume. We find an equilibrium volume of approximately 955.12 ų for a 2 × 2 × 2 bulk rhombohedral LaNiO₃ (a = b = c = 10.94 Å, α = β = γ = 61.47°) using a 4 × 4 × 4 Monkhorst–Pack grid. The corresponding optimization of the 1 × 1 × 1 bulk rhombohedral LaCoO₃ unit cell is 115.39 ų (a = b = c = 5.40 Å, α = β = γ = 61.72°) using an 8 × 8 × 8 Monkhorst–Pack grid. The corresponding plots for the total energy as a function of volume for both surfaces are shown in the Supporting Information as Figure S1.

For the LaNiO₃ bulk unit cell, we performed spin-polarized calculations to properly capture the antiferromagnetic (AFM) ordering of the surface. Perovskite structures typically have AFM ordering associated with them below the Néel temperature, which can be understood to occur because of a superexchange interaction, which occurs when the cation is subject to the crystalline field arising from octahedrally or tetrahedrally surrounding anions.²⁴⁻²⁶ Although the presence of AFM ordering has been taken into account to a certain extent in the literature when modeling the bulk properties of perovskite structures,^21,27 literature rarely accounts for the AFM ordering when modeling the surface of perovskites.^8,22,28,29 However, for the LaCoO₃ surface, GGA functionals predict the ground state structure to be a low-spin nonmagnetic (NM) state and other functionals must be used to predict AFM ordering.³⁰ As such, we have performed NM calculations for LaCoO₃.

Once we determined the optimized lattice constant, we performed surface energy calculations using p(2 × 2) 6-layer (LaNiO₃) and 4-layer (LaCoO₃) surfaces to model these systems in the ground state.^17,31 We calculated surface energies using eq 1.

1

A is the area of the surface exposed to the vacuum and N is the number of bulk unit cells used to make the surface unit cell. In this work, we model LaNiO₃ (001) with a NiO-termination, which has been proven to be the most stable surface structure of this perovskite by others³² and ourselves, as shown in Figure S2a. On the other hand, we find the LaCoO₃ (110) facet is the most stable, as shown in Figure S2b. Such a result is consistent with the experimental XRD measurements³³ and theoretical calculations³⁴ results in the literature that have found the (110) facet is the dominant peak. Although the LaO-termination of the LaCoO₃(110) surface is more stable than the CoO-terminated surface by 0.02 eV as calculated by ourselves, the CoO-termination will be used because the B-site cation is more active in the reduction reaction due the transfer of electrons between the B-site and oxygens within the system while the A-site stabilizes the structure.^4,35 For all surface calculations, we sampled the Brillouin zone using a 4 × 4 × 1 k-point Monkhorst–Pack grid. In all surface calculations, we relax the top two layers to model surface–adsorbate interactions and fix the bottom layers to approximate the bulk. A vacuum layer of 10 Å and a dipole correction along the z-direction exist to prevent interactions between the top and bottom surfaces of the slab. A Gaussian smearing with a width of 0.05 eV is used, and the convergence criterion was 10^–5 eV and 0.03 eV/Å for electronic energies and interatomic forces on the relaxed layers, respectively. The LaNiO₃ and LaCoO₃ surfaces are both shown in Figure 1. The LaNiO₃ surface is shown with optimized AFM ordering of the surface. As Figure 1 shows, the number of spin up and spin down atoms on the surface is uneven, but the overall cell exhibits AFM ordering as it has equal spin up and spin down nickel ions and the net magnetic moment is close to zero.

Figure 1.

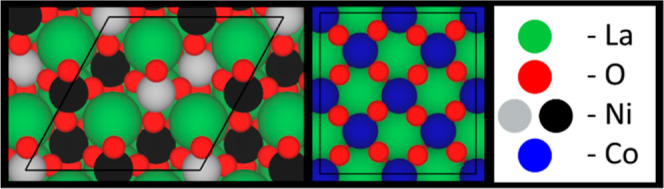
Clean p(2 × 2) 6-layer surfaces of LaNiO₃ (001) with a NiO-termination and LaCoO₃ (110) with a CoO-termination. Spin up and spin down Ni are shown in black and gray, respectively.

We model adspecies present on perovskite surfaces by adsorbing H, O, OH, H₂O, and CO₂. To determine the most favorable adsorption sites, we calculate the adsorption energy of the adsorbate n on the perovskite surfaces, as given in eq 2.

2

E_n+LaBO3 is the total energy of the LaBO₃ surface (B = Ni and Co) with one adsorbed species on the surface n, E_LaBO3 is the total energy of the bare surface, and E_n(g) is the total energy of the corresponding adsorbed species in the gas phase. Equations for each species are listed in the Supporting Information (eqs S1–S5). We performed differential charge transfer calculations to investigate the adsorption of adspecies in their most favorable position to determine the amount of charge transfer upon adsorption using eq 3.

3

Δρ is the overall charge transfer, ρ_AB is the charge of the surface with adsorbed species, ρ_A is the charge of the surface without adsorbed species, and ρ_B is the charge of the adspecies in the gas phase. Additionally, we conducted the corresponding Bader charge analyses.

Once the two most favorable adsorption positions have been determined, we quantify the core level binding energy (CLBE) values of oxygen and carbon contained in adspecies and the atoms surrounding the adsorbed species to simulate the spectra for O 1s, C 1s, Ni 3p, and La 4d for the LaNiO₃ surface and O 1s, C 1s, Co 2p, and La 4d for the LaCoO₃ surface. Although initial and final state approximations in VASP can model the effects of ejecting an electron from a core level orbital and thus model XPS spectra, the final state approximation is far more accurate since the electrons of the atom are allowed to relax after a core electron is excited to a valence shell allowing for the inclusion of screening effects whereas, in an initial state approximation, the potential is fixed, so the valence electrons do not relax.³⁶ The CLBE equation is given in eq 4(36)

4

where E_(n–1) is the energy from the final state approximation when one atom in the surface has a core level electron removed, E_(n) is the ground state energy of the same surface without a core electron removed, E_ref(n–1) is the reference final state approximation energy, and E_ref(n) is the ground state energy of the reference surface. Without E_experimental, the equation solves for the core level binding energy shifts (CLBESs). The addition of E_experimental shifts the theoretical reference peak to the same value as the corresponding peak in the experimental spectra, allowing for direct comparison. More details on the reference species are given in the Supporting Information. We provide a detailed method for determining CLBESs and CLBEs for the surface species and adspecies in the Supporting Information with a fully deconvoluted oxygen O 1s spectrum on the LaNiO₃ surface in Figure S3.

2.2. Experimental Methods

2.2.1. Sample Preparation

LaBO₃ (B = Ni or Co) perovskite oxides were synthesized using a sol–gel method.⁵ Initially, precursors were prepared by dissolving stoichiometric amounts of metal nitrates (i.e., La(NO₃)₃·6H₂O and Ni(NO₃)₂·6H₂O or Co(NO₃)₂·6H₂O) in deionized water at room temperature, followed by stirring. Citric acid was added to the mixture as a complexing agent at a 1.1 to 1 molar ratio with respect to metal ions. This was followed by continuously stirring the mixture at 85 °C until the gelation process was completed by water removal. The resulting gel was heated from room temperature to 400 °C using a heating rate of 3 °C/min under an air flow. The sample was then combusted at 400 °C for 3 h to remove the organics. The resulting powder was crushed prior to calcination at 750 °C for 5 h to achieve the appropriate perovskite crystal structure.

2.2.2. Sample Characterization

The resulting powder samples have been characterized initially using standard methods such as X-ray diffraction (XRD) without further treatment to check their crystal structure.⁵ It should be emphasized that these are powder samples used for catalysis and not epitaxially grown well-defined, thin films as reported in many studies in the literature.⁹⁻¹² Two different methods were used to perform experimental XPS studies. High resolution studies were performed using Thermo Fisher NEXSA with a monochromatic Al K_α source at an energy of 1486.6 eV. The measurements were conducted using a step size of 0.1 eV. Pass energies for the survey scans and the high-resolution analysis (HR-XPS) were 160 and 25 eV, respectively. La 4d and Ni 3p core level regions were chosen for analysis due to the overlap between the La 3d and the Ni 2p spectra. Data were analyzed using CasaXPS software, and a Shirley-type background was used in all analyses. Temperature-dependent and additional C 1s XPS experiments were performed using a Focus HV-CSA300/15 electron energy analyzer (Hünstetten-Kesselbach, Germany). Excitation was supplied by unmonochromated Al and Mg K_α (SPECS XR50, Berlin, Germany). Spectra have been recorded with a pass energy of 100 eV resulting in an overall resolution of about 2 eV. The samples have been pressed as pellets and mounted with Tantalum stripes. Heating steps have been reached by using an e-beam heater. Data analysis has been performed using UNIFIT software.³⁷

3. Results and Discussion

3.1. Theoretical Results

The presence of adsorbates on the perovskite surface impacts the local coordination of surface atoms and changes the surface chemistry. Under electrolysis conditions, water species dissociate and form water fragments on the perovskite surface.¹² These fragments affect the electronic structure and influence the reactivity. Surface contributions to the XPS spectra are frequently reported to be found at core binding energies lower than those of bulk signals. We note that Freund and co-workers reported shifts to higher binding energies for CaO³⁸ and MgO.³⁹ However, in both cases, the shifts were observed only for the metal, not the oxygen. Other calculations in the literature place surface oxygen peaks at low binding energies.⁴⁰ However, studies on the effects of fragments on the electronic structure have not been correlated with first-principles-based models on perovskite surfaces. We systematically tested the possible adsorption sites for isolated water adspecies as well as for water fragments (H, OH, and H₂O) on LaNiO₃ (001) and LaCoO₃ (110). Additionally, as a target adspecies for the coelectrolysis, we adsorb CO₂ on the surface. This is the first step toward understanding the effects of adspecies on the electronic structure and deconvolution of the surface sensitive XPS spectra. For bond lengths, bond angles, and adsorption energies, values in the text are an average when an error bar is present and exact value if an error bar is not present. The errors are calculated using standard deviations of the values used to calculate the average. As a note, species referred to in the text marked with an asterisk (*) are adsorbed species.

3.1.1. Adspecies Studies on LaNiO₃

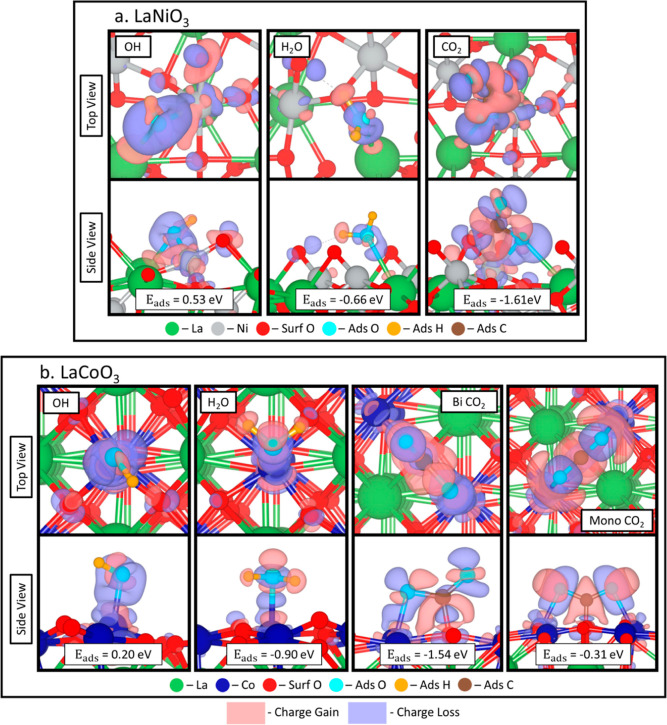
The most stable configurations of H, O, OH, H₂O, and CO₂ adspecies on the AFM LaNiO₃ surface are shown in Figure 2 along with the adsorption energy of each adspecies on the surface. All of the configurations listed in Table 1 are shown in Figures S4–S8. Large differences in adsorption energies between the up and down cases can be attributed to differences in final adsorption positions detailed in Table S1 with the labels shown in Figure S9. In all cases, H adsorbs to a surface of O with the same bond length (H*–O: 0.980 ± 0.003 Å) (Figure S4), however, with more favorable positions (Figures 2a and S4: configurations 3 up, 3 down, 4 up and 4 down), the H shifts away from the surface by 0.560 ± 0.019 Å, pulling the surface O with it forming a surface OH. The most favorable O adsorption positions (Figure 2b: configurations 1 up and 1 down) occur when O closely adsorbs to a La (O*–La: 2.600 ± 0.001 Å) and a surface O (O*–O: 1.320 ± 0.001 Å). In the less favorable configurations, the O coordinates with a La (O*–La: 2.650 ± 0.11 Å) and nickel (O*–Ni: 1.860 ± 0.08 Å) shown in Figure S5, which is close to lattice oxygen bonds (O–La: ∼2.5 Å; and O–Ni: ∼1.9 Å). The oxygen would most likely not be incorporated into the lattice, as it is less favorable than forming an O₂ molecule on the surface. The OH species adsorbs most favorably (Figures 2c and S5: configurations 1 up, 2 up, 2 down and 3 up) when bridging a La (O*–La: 2.450 ± 0.004 Å) and a Ni atom (O*–Ni: 1.900 ± 0.005 Å). Although the adsorption energies for OH are positive, the dissociation of water on the surface has been predicted to be the most favorable adsorption mechanism.¹¹ When calculating the adsorption energy of OH, we choose to approximate the gas phase OH energy as shown in eq S3 of the Supporting Information to account for the O–H bond and the dissociation energy, but the effect of this makes the adsorption energy positive. An alternative gas phase OH energy can be calculated using H₂ and O₂ as a reference, but this results in very strong adsorption energies of −2.42 eV vs 0.53 eV for the LaNiO₃ surface. This reference energy does not account for the O–H bond present in OH and, therefore, is missing key descriptors to calculate the adsorption of OH.

Figure 2.

Optimized adsorption site positions for the most favorable configuration of (a) H, (b) O, (c) OH, (d) H₂O, and (e) CO₂ on NiO-terminated LaNiO₃ (001). The labels for the cases correspond to the values labeled in Table 1 and the adsorption energy (in eV) is labeled within the box. Spin up and spin down Ni are shown in black and gray, respectively.

Table 1. Energetics of the Adsorption Configurations in eV on LaNiO₃^a.

adsorption energy (Eads) for H, O, OH, H2O and CO2 (eV)
	H		O		OH		H2O		CO2
configuration	up	down	up	down	up	down	up	down	up	down
1	–1.58	–1.57	–0.78	–0.78	0.53	1.44	–0.61	–0.45	–1.57	–1.61
2	–1.10	–1.10	–0.27	–0.25	0.53	0.53	–0.48	–0.66
3	–2.02	–2.02	–0.32	–0.07	0.53	0.62	–0.63	–0.62
4	–2.02	–2.02					–0.16	–0.33

^aThe corresponding conformations are shown in Figures S4–S8.

While previous literature reports that H₂O adsorbs on the Ni(111) surface with an adsorption energy of −0.30 eV,⁴¹ the average adsorption energy of H₂O on the LaNiO₃ surface is −0.49 ± 0.16 eV (Figures 2d and S7). In the most favorable configuration (Figure 2d: configuration 2 down), the H₂O adsorbs to La (O*–La: 2.74 Å). The H₂O in the second most favorable position (Figure 2d: configuration 3 up) bridges a La (O*–La: 2.81 Å) and Ni (O*–Ni: 3.21 Å). One case of H₂O adsorption (Figure S6: configuration 5) resulted in the dissociation of H₂O with a high adsorption energy of −0.77 eV, confirming that H₂O dissociation is favorable.¹¹ We have previously studied the adsorption of CO₂ using DRIFTS spectra and found that CO₂ adsorbs in a bidentate configuration as CO₂ forms a carbonate with a surface oxygen.⁵ LaNiO₃ adsorbed CO₂ strongly (Figures 2e and S8) with an adsorption energy of −1.59 ± 0.02 eV, but on Ni(100), CO₂ adsorbs with an adsorption energy −0.27 eV.⁴² The adsorption of CO₂ lengthened the O*–C*–1 bond from the gas phase length 1.18 Å to 1.35 ± 0.001 Å (see Figure S9) and decreased the CO₂ bond angle from the gas phase angle of 180° to 126.96 ± 0.15°. Both changes to the CO₂ structure indicate the activation of CO₂, the first step for CO₂ conversion to CO.

3.1.2. AFM Versus NM Effects on LaNiO₃

Although it is not possible to fully constrain the magnetic moment of the surface using the version of VASP employed in this work, we have attempted to quantify the adsorption of each adspecies near nickel atoms with spin up and spin down magnetic moments and compare similar cases. In the case of larger, closed shell molecules (H₂O and CO₂), it is harder to determine the spin state due to the proximity of the molecules to both spin up and spin down Ni atoms within the surface. For open shell molecules (H, O, and OH), the adsorption position can be more clearly distinguished with respect to being adsorbed within a spin up versus a spin down cell. Typically, we find only slight differences in the final adsorption energies of molecules on the spin up and spin down cells adsorbed in comparable configurations as seen with water adsorption in the 3 down and 3 up positions (Figure S7). As a counter example, the adsorption energy of H₂O differs for cases 4 up and 4 down (Figure S7) but the molecules are in remarkably similar positions. The only identifiable difference between these cases is the AFM ordering of the surface, which could be attributed to the differences in adsorption energy. While differences in the final adsorption positions contribute to the difference in adsorption energies between some configurations, the AFM ordering could cause these differences in the final adsorption position of the atoms on such surfaces.

While open shell adsorbates typically change the magnetic moments of the surface Ni with respect to the bare surface, they do so with a certain pattern. Conversely, the adsorption of closed shell adsorbates creates a vast variety of AFM ordering configurations on the surface as shown in Figure 2. As an example of a closed shell adsorbate, the adsorption energy of CO₂ differs by 0.04 eV between the adsorption on a spin up and a spin down cell as shown in Figure 2e. While not a significant difference, the adsorption of CO₂ onto different cells changes the magnetic ordering as compared to the bare surface as well (bare surface shown in Figure 1 and with surface adspecies shown in Figure 2), which will affect the underlying reaction barriers involving CO₂ activation. The presence of other adspecies affects the magnetic ordering of the surface in an analogous way compared to the bare surface with specific values of the magnetic moments for the exposed Ni atoms shown in Table S2. The change in magnetic moments is not negligible and the adsorption of species on the surface can significantly change the magnetic moments of Ni atoms directly affected by the adsorption of adspecies.

Further, AFM ordering changes the adsorption energy of adspecies on the LaNiO₃ surface as compared to the nonmagnetic (NM) surface as shown in Figure 3 with the corresponding adsorption configurations shown in Figure S10. The NM calculations are performed using a relaxed geometry of the NM LaNiO₃ surface with the corresponding volume versus total energy plots shown in Figure S11. We optimized adsorbates on the NM surface in the same position as the corresponding AFM calculation to make the comparison as clear as possible. Both OH and H₂O adsorb to the NM surface more favorably by 0.03 eV, but charge transfer calculations show that the AFM surface has more charge exchange with the adsorbates (Figure S12a,b). The AFM surface more favorably adsorbs the H, O, and CO₂ by 0.11, 0.12, and 0.53 eV, respectively. The adsorption energy of CO₂ improved with AFM due to increased charge transfer between the AFM surface atoms and the CO₂ molecule (Figure S12c). Due to the qualitative nature of charge transfer images, we also conducted a Bader charge analysis of the adsorption of OH, H₂O, and CO₂ for both the NM surface (Table S3) and the AFM surface (Table S4) to get a quantitative analysis of this adsorption, but the small differences in charges between the NM and AFM do not elucidate any trends. We used the more energetically favorable AFM LaNiO₃ surface for further calculations.

Figure 3.

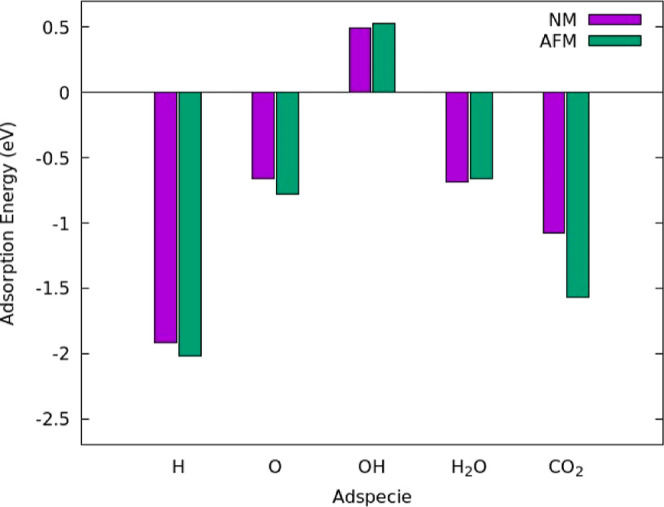
Comparison of the adsorption energies in eV between the AFM and NM surfaces for all adspecies on the surface. Plot shows the adsorption energy for the most favorable adsorption position on the AFM surface and the NM surface is optimized in the same adsorption position. Although both surfaces were optimized using their respective bulk, the clean surface reference for both the NM and AFM case was the AFM clean surface energy since it is more energetically favorable.

3.1.3. Adspecies Studies on LaCoO₃

Similar to the AFM LaNiO₃ surface, we modeled the adsorption of water fragments, water molecules, and carbon dioxide on the surface of a NM LaCoO₃. As explained in Section 2.1, we do not account for AFM ordering in this system. This results in favorable adsorption for H, O, H₂O, and CO₂ with the most favorable positions shown in Figure 4 and the adsorption energies for all tested configurations listed in Table 2. A detailed description of adsorption positions exists in Table S5, with a key shown for the bonds in Figure S18. When hydrogen adsorbs most favorably to a surface oxygen (Figure 4a: configurations 1 and 2), the surface oxygen is centered between the Co atoms on the surface (O–Co: 2.110 ± 0.050 Å). Oxygen preferentially adsorbs to a surface Co (O*–Co: 1.590 ± 0.005 Å) in the most favorable positions (Figure 4b: configuration 1 and 2). We also observe a lifting of the cobalt from the surface (Co Lift: 1.330 ± 0.015 Å), indicating that the addition of oxygen destabilizes the cobalt bonds with the surface oxygen changing the local coordination of the Co atom. For hydroxide adsorption, the hydroxide adsorbs most favorably (Figure 4c: configuration 1 and 2) to a Co atom (O*–Co: 1.760 ± 0.005 Å). Hydroxide configuration 3 is most favorable but has broken up on the surface when adsorbed (Figure S15). On the LaCoO₃ surface, water adsorbs quite favorably with an average adsorption energy of −0.86 ± 0.03 eV and Zhang et al. found the adsorption energy of water on Co(0001) was −0.42 eV⁴³ meaning the perovskite structure highly enhances the adsorption of water over a purely metallic surface. In all cases, water adsorbs favorably (Figure 4d: configuration 1 and 3) on a Co atom (*O–Co: 2.010 ± 0.013 Å) with the hydrogen atoms pointing toward surface oxygen atoms. As we found in our previous work,⁵ CO₂ adsorbs in both a monodentate and a bidentate configuration forming a carbonate with a surface oxygen. When adsorbed in a bidentate configuration (side view shown in Figure 5b: Bi CO₂), the O*–C*–1 bond lengthens to 1.31 Å and the O*–C*–O* bond angle decreases to 130.23° (Figure 4e: configuration 1). In the monodentate configuration (side view shown in Figure 5b: mono CO₂), the O*–C* bonds have an average length of 1.25 ± 0.01 Å and the O*–C*–O* bond angle decreases to 132.56° (Figure 4e: configuration 2). The bidentate configuration is more favorable than the monodentate configuration by 1.23 eV (−1.54 and −0.31 eV). When compared to CO₂ adsorption energies on Co(0001), the perovskite lattice greatly increases the adsorption energy from −0.44 eV signifying the addition of Co to a perovskite lattice increases the interaction between the CO₂ molecule and the surface increasing the activity of the surface.⁴⁴

Figure 4.

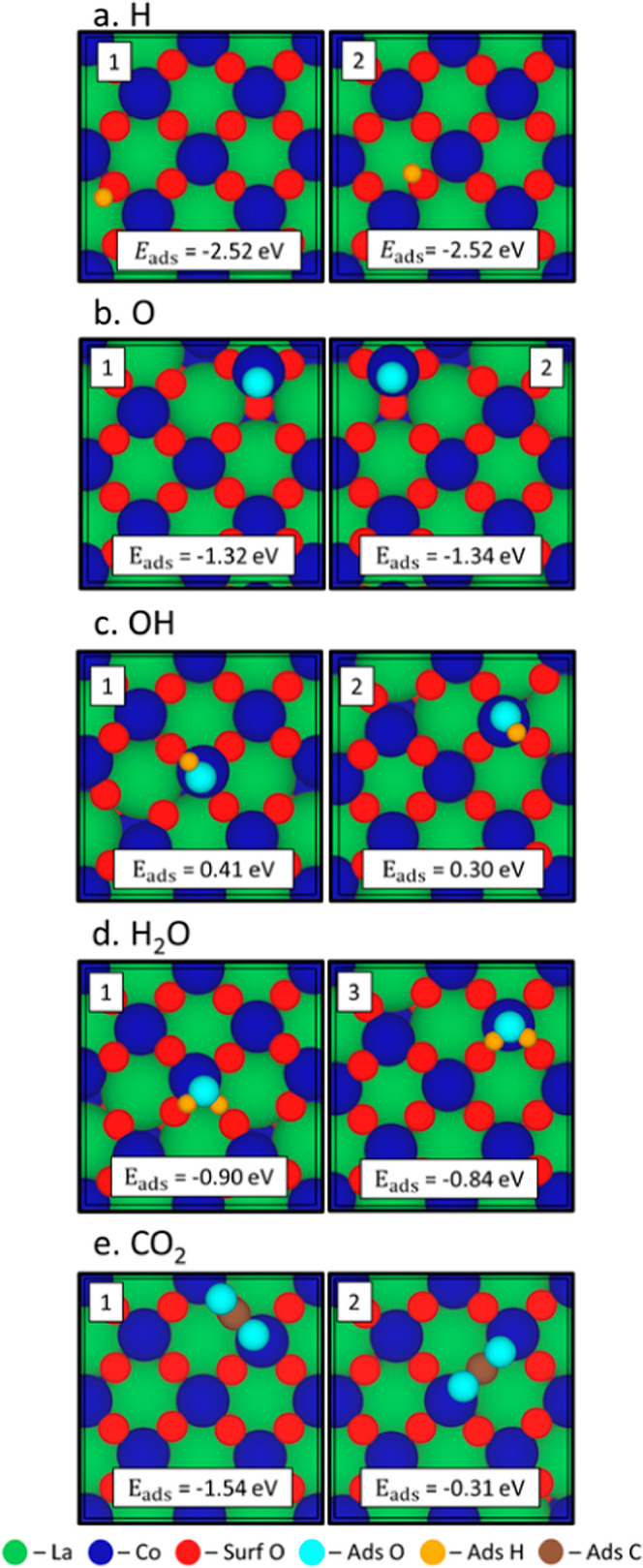
Optimized adsorption site positions of the most favorable configuration of (a) H, (b) O, (c) OH, (d) H₂O, and (e) CO₂ on CoO-terminated LaCoO₃ (110). The labels for the cases correspond to the values labeled in Table 2 and adsorption energy (in eV) is labeled within the box.

Table 2. Energetics of the Adsorption Configurations in eV on LaCoO₃^a.

adsorption energy (Eads) for H, O, OH, H2O and CO2 (eV)
configuration	H	O	OH	H2O	CO2
1	–2.52	–1.32	0.41	–0.90	–1.54
2	–2.52	–1.34	0.30	–0.83	–0.31
3	–1.51	–0.78	0.20	–0.84
4	–1.55	–0.69	1.69	–0.81

^aThe corresponding configurations are shown in Figures S13–S17.

Figure 5.

Charge transfer calculations for the most favorable configurations of OH, H₂O, and bidentate CO₂ on LaNiO₃ (a) and OH, H₂O, bidentate CO₂, and monodentate CO₂ on LaCoO₃ (b). Isosurface used is 0.005 electrons/Bohr.³ Red indicates charge gain, and blue indicates charge loss. AFM ordering is not used in the LaNiO₃ calculations in order to facilitate the comparison with the LaCoO₃ surface, since that surface does not include spin polarization effects. The effect of spin polarization is quantified in Figure S12 and in the text concerning these figures.

3.1.4. Charge Transfer of Adspecies on LaNiO₃ and LaCoO₃

Comparing the LaNiO₃ and LaCoO₃ surfaces, we find the Co perovskite surface adsorbed all water and water fragments stronger than the Ni-based perovskite surface possibly due to the more oxyphilic nature of the Co surface increasing the adsorption energy of the water fragments over the Ni surface.²¹ To understand this further, we performed a differential charge analysis to understand the adsorption patterns shown in Figures 2 and 4, respectively, for both LaNiO₃ (Figure 5a) and LaCoO₃ (Figure 5b) surfaces. For OH adsorbed on the LaNiO₃ surface, the H atom gains charge, whereas the adsorbed O loses charge to the surface. On the LaCoO₃ surface, adsorbed O in OH loses charge, but adsorbed H does not exhibit charge transfer. Even though there are positive adsorption energies, there is definite charge transfer between the surface and the OH molecule indicating it is being adsorbed. Water adsorption on the LaNiO₃ surface results in the surface gaining charge from the adsorbed O atom and H gaining charge from the surface. When H₂O adsorbs to the LaCoO₃ surface, the adsorbed O loses charge to the surrounding H atoms of the water molecule. The adsorption of bidentate CO₂ occurs similarly on LaNiO₃ and LaCoO₃. We find that the C atom gains charge from the bound lattice and adsorbed O within the CO₂. While the O within the CO₂ molecule bonded to the surface loses charge to the surface, the O in the CO₂ molecule that points away from the surface loses charge to the C. For monodentate CO₂ adsorption, the gain and loss of charge is even across the adsorbed CO₂ molecule with the C atom gaining electrons and the adsorbed O atoms within the CO₂ molecule losing charge. The Bader charge analysis is shown in Table S6 (LaNiO₃) and Table S7 (LaCoO₃), but there are few conclusions that can be drawn from this data. One significant charge transfer that occurs is for the oxygen bound to the C on the LaNiO₃ surface when CO₂ adsorbs on the surface indicating that it is highly affected by the adsorption of CO₂. The other significant charge transfer that occurs is for the O contained in the OH molecule when adsorbed to the LaCoO₃ surface.

3.1.5. Theoretical Core Level Binding Energy Shift Studies

For all spectra figures, the experimental spectra along with the theoretical spectra below are depicted. The theoretical spectra are separated into surface, H, O, OH, H₂O, and CO₂ contributions. To make modeling XPS tractable, we excite only atoms in the top two layers of both the LaNiO₃ and LaCoO₃ surface. While this does not allow us to evaluate depth effects, we can gather information about CLBEs as a result of adspecies’ presence on the surface. The pictures inserted to the right of the graph are images of the specific adsorbed and surface species. As a note, they do not represent all configurations used to make the spectra and may not correspond directly to the peak because the peak is made from the Gaussian distribution of all contributions. As stated in the Methods section, we list the detailed steps in the Supporting Information with a sample of the deconvolution of the oxygen O 1s spectra on the LaNiO₃ surface with all contributions marked being shown in Figure S3. Atoms exposed to the vacuum will be referred to as surface atoms, and atoms within the perovskite lattice will be referred to as bulk atoms. We have considered how the presence of adspecies alters the core level binding energy values of the three closest lattice species, which is clearly non-negligible.

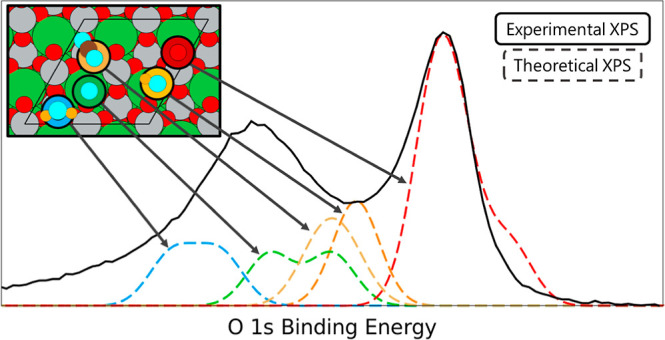
We show our theoretical spectra of the 1s of O of LaNiO₃ in Figure 6 with the values used to calculate the spectra shown in Table S8. The experimental data has two peaks: a lower energy peak at 528.3 eV and a higher energy peak at 531.1 eV. In the theoretical surface spectra shown in Figure 6, we added 527.25 eV to all theoretical CLBESs (both surface and adsorbate spectra) in order to match the CLBEs of the theoretical surface peak’s apex to match the experimental bulk peak’s apex at 528.3 eV. When one applies this uniform shift, we obtain an average CLBE of 528.26 ± 0.18 eV (Figure 6 surface-2) for bulk atoms, which is higher than of the surface atoms that have an average CLBE of 527.27 ± 0.01 eV (Figure 6 surface-1). We note that the surface spectra were modeled under both NM and AFM ordering shown in Figure S19. Although the difference in magnetism affected the range of CLBEs, the overall peak value was not appreciably different and AFM was unnecessary for experimental deconvolution using theoretical contributions. The result of hydrogen adsorption to the surface oxygen increases the CLBE of the surface oxygen by 2.87 ± 0.11 eV to 530.15 ± 0.12 eV (Figure 6 H-1) reflecting the creation of a surface hydroxide. The oxygen adspecies contributes to the higher energy peak as well at a slightly lower energy of 529.96 ± 0.01 eV (Figure 6 O-1), but the closely coordinated surface oxygen’s CLBE (Figure 6 O-3) increased by 3.62 ± 0.01 eV to 530.9 ± 0.02 eV. The hydroxide peak occurs at 529.56 ± 0.01 eV (Figure 6 OH-1) but this does not correlate with the literature value of 530.97 eV.⁹ The higher energy peak at 531.1 eV mostly corresponds with the adsorption of water resulting in a peak at 531.99 ± 0.39 eV. This result is lower than the experimental literature reports that place a “water peak” at 532.96 eV which is thought to be due to the presence of adspecies resulting from the decomposition of water.¹⁰ The CLBE of adsorbed oxygen in monodentate carbon dioxide had an average value of 529.95 ± 0.22 eV (Figure 6 for CO₂-1 and CO₂-3). The large standard deviation is due to the differences in coordination of the oxygens in carbon dioxide with one adsorbed to the surface and the other pointed toward the vacuum. Further details about the CLBEs of surrounding atoms are found in Supporting Information.

Figure 6.

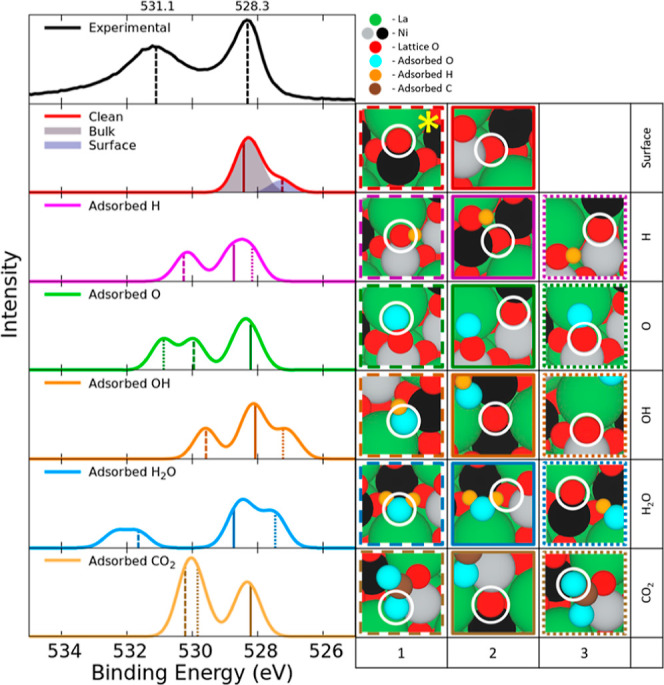
Experimental XPS O 1s for LaNiO₃ surface data plotted with two peaks one at 531.1 eV and one at 528.3 eV. The second graph depicts the spectra of the surface without adsorbed species and the last five graphs show the spectra of the adsorbed species and the effects of the adsorbed species on the nearby surface atoms. The reference oxygen used to calculate CLBESs is marked with a yellow star. The values of the CLBEs are listed in Table S4 and these values are convoluted using Gaussian distributions to simulate the theoretical spectra. On the right: Images of species contributing to each of the peaks in the presence of adsorbed atoms/molecules. The border color and line type correspond to the energies marked on the theoretical XPS graph. Spin up and spin down Ni are shown in black and gray, respectively. The corresponding O species for which the XPS is simulated are circled in white.

For LaNiO₃, we calculated the C 1s spectra of bidentate CO₂ adsorbed on the surface shown in Figure S20 and compared it with our experimental spectra having peaks at 284.8 and 289.0 eV. Previous literature assigns the lower energy peak composed of adventitious carbon at 284.6 eV and the higher energy peak composed of carbonates at 288.6–289.6 eV.⁴⁵ Our simulated spectra gave a C 1s CLBE of CO₂ at 287.6 eV while the adventitious carbon peak occurs at 284.4 eV. The simulated CO₂ peak does not have enough variety in simulated carbon containing adspecies to capture the range of values convoluted in the higher energy peak.

Similar to what we did for LaNiO₃, we also determined the CLBEs of surface atoms and adsorbates on the LaCoO₃ surface with the calculated CLBE values listed in Table S9. The experimental spectrum has two peaks shown in Figure 7: a higher energy peak at 531.4 eV and a lower energy peak at 528.7 eV. The lower energy peak values correspond with previous results putting the lattice oxygen peak at 528.7 eV.¹² We added a 527.92 eV uniform shift to the theoretical CLBESs to match the theoretical bulk peak’s apex to the experimental bulk peak’s apex at 528.7 eV. The exposed surface oxygen’s CLBE splits into two modes: the first mode (Figure 7 surface-1) with a CLBE of 527.92 ± 0.00 eV, which are below the highest surface atoms by 0.52 Å, and the highest surface oxygens that form a second mode at 528.26 ± 0.00 eV. Similar to the LaNiO₃ surface, the bulk lattice oxygen has higher CLBEs of 528.72 ± 0.14 eV (Figure 7 surface-2) than the surface oxygen (Figure 7 surface-1). Hydrogen adsorption on a surface oxygen forms a surface hydroxide shifting the CLBE of the oxygen by 2.69 ± 0.01 eV to 530.95 ± 0.01 eV (Figure 7 H-1). When oxygen adsorbs to a surface cobalt, the adsorbed oxygen has a CLBE of 528.17 ± 0.01 eV (Figure 7 O-1), but surface oxygens still adsorbed to the surface cobalt contribute to the higher energy peak with a CLBE of 529.32 ± 0.00 eV (Figure 7 O-2). The adsorption of OH groups on the surface resulted in a higher energy peak at 529.44 ± 0.02 eV (Figure 7 OH-1). This only roughly correlates with experimental data showing a OH peak at 530.5 eV.¹² When H₂O adsorbs on the surface, the adsorbed O in H₂O has an average CLBE of 532.75 ± 0.22 eV (Figure 7 H₂O-1). Stoerzinger et al. reported the higher energy peak on the LaCoO₃ surface to being due to undercoordinated surface oxygen and the lower energy peak is due to bulk lattice oxygen,¹² but here we find that the higher energy peak is due to water adsorption. We calculated the CLBEs of carbon dioxide in both bidentate and monodentate configurations, leading to slight differences in CLBEs of the respective configurations. In the bidentate configuration (site 1 in Figure 4), the oxygen adsorbed closer to the surface has a higher CLBE of 530.89 eV (the turquoise atom pictured in Figure 7 CO₂-3 but not circled) while the oxygen pointing to the vacuum (Figure 7 CO₂-3) had a lower CLBE of 530.60 eV. As for the monodentate configuration (site 2 in Figure 4) the CO₂ adsorbs with both adsorbed O close to the surface with an average CLBE of 530.17 ± 0.04 eV (both pictured in Figure 7 CO₂-1). For details about the surrounding atoms, please refer to Supporting Information.

Figure 7.

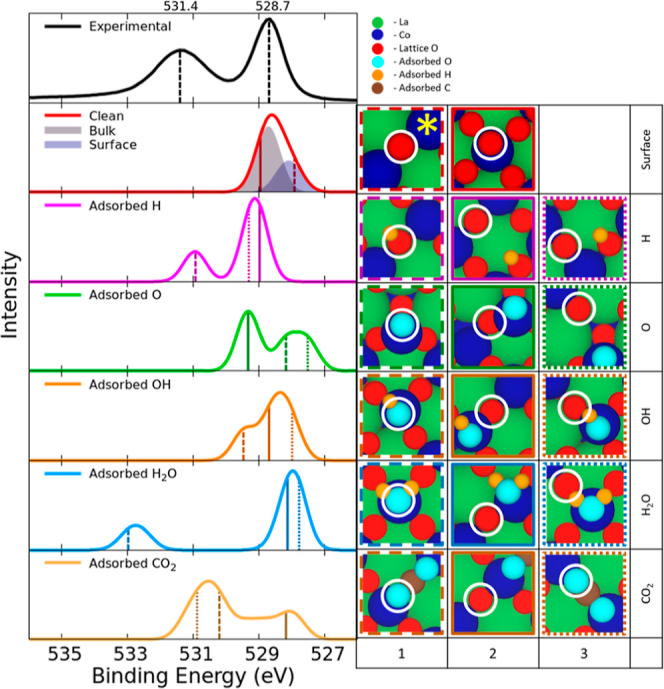
Experimental XPS O 1s for LaCoO₃ surface data plotted with two peaks, one at 531.4 eV and one at 528.7 eV. The second inset from the top depicts the spectra of the surface without adsorbed species, and the last five insets show the spectra of the adsorbed species and the effects of the adsorbed species on the nearby surface atoms. The reference oxygen used to calculate CLBESs is marked with a yellow star. The values of the CLBEs convoluted by using Gaussian distributions are listed in Table S5. On the right: Images of species contributing to each of the peaks in the presence of adsorbed atoms/molecules. The border color corresponds to the energies marked on the theoretical XPS graph.

We also calculated the C 1s CLBEs associated with the adsorption of CO₂ on the surface for LaCoO₃. The experimental spectra have two peaks, a lower energy peak at 285.2 eV and a higher energy peak at 289.0 eV, shown in Figure S21. As shown in our previous work,⁵ CO₂ adsorbs on the surface in bidentate and monodentate configurations and as such we considered both possibilities for the C 1s spectra. The bidentate configuration had a CLBE of 288.8 eV, which is higher than the CLBE of the monodentate configuration at 288.2 eV, with the lower energy peak set to 285.2 eV. The higher CLBE is associated with the decreased stability of the bidentate configuration on the surface. Stoerzinger et al. analyzed the C 1s spectra of LaCoO₃ at varying temperatures and relative humidities finding there are two peaks with one peak composed of adventitious carbon at 284.9 eV and the other attributed to the adsorption of carbonate species at 288.1 eV.¹² This corresponds well with our data, further confirming the presence of carbonates, which could form by the adsorption of carbon dioxide to a surface oxygen at standard conditions.

We have also investigated the spectra of the A-site and B-site for both surfaces, but there is little information that can be gained from the theoretical spectra. The experimental La 4d spectra of the LaNiO₃ surface shown in Figure S22 has two peaks with values of 103.8 and 100.9 eV. We also quantified the La 4d CLBE spectra of LaCoO₃ as shown in Figure S23 with experimental peaks present at 104.0 and 101.0 eV. In both theoretical La 4d spectra, we would expect to see some differences in the spectra when adspecies adsorb due to charge transfer with the adspecies, but we observe relatively narrow spectra at nearly unchanged positions no matter the adsorbate. The largest difference in the theoretical spectra occurs with carbon dioxide on the LaCoO₃ surface due to the bidentate and monodentate adsorption, but the adsorption of hydrogen also increases the CLBEs of La. Experimentally, the doublet present in the La 4d spectra appears because of spin orbital splitting and additional satellite formation that occurs when a core electron is excited resulting in the redistribution of charges of the La 4f orbital.⁴⁶ This can only be modeled when using time-dependent DFT (TDDFT) which is beyond the scope of this work.⁴⁷

We conducted a similar study of the XPS spectra of the B-site metals. For the LaNiO₃ surface, we model the Ni 3p spectra instead of the more commonly used Ni 2p XPS because it overlaps with the La 3d spectra making deconvolution of those spectra difficult.¹⁰ As shown in Figure S24, the experimental Ni 3p spectrum is broad due to spin–orbit interaction and the multiplet state present in the Ni 3p spectra⁴⁸ with a peak at 67.3 eV whereas the theoretically predicted spectra only predict a narrow range of binding energies. Even though we modeled AFM ordering for LaNiO₃, the small changes in the CLBEs are closely tied to the depth in the surface. The addition of adsorbed species only slightly affects the CLBEs with water increasing the CLBEs the most. For LaCoO₃, the experimental Co 2p spectra shown in Figure S25 have spin–orbit split XPS spectra with peaks at 779.8 and 795.1 eV and additional smaller features arising from the interaction between the core hole and un-ionized electrons otherwise known as screening. Bidentate and monodentate CO₂ adsorption widened the Co 2p spectra, but all of the other spectra were narrow. Similarly to the La 4d spectra, the multiplet structure of the B-site spectra cannot be modeled without the addition of TDDFT.⁴⁷

3.1.6. Coverage Effects on Theoretical Core Level Binding Energy Shifts for LaNiO₃

Coverages affect the adsorption energies of adsorbates and, therefore, are important to consider when calculating CLBEs for theoretical spectra. We investigated the coverage effects on the LaNiO₃ surface. For each adsorbate (H, O, OH, H₂O, and CO₂), we adsorb four of each adspecies within the unit cell in equivalent positions on the LaNiO₃ surface based on the most favorable configuration determined by the adsorption of a single adspecies. We define this coverage as a monolayer coverage. The data concerning the adsorption energies is shown in Figure S26. We find that the adsorption energy decreases under higher coverages for all adsorbates with differing strengths. Both H₂O and O adsorption energies are affected the least by higher coverages with adsorption energy differences of 0.07 and 0.08 eV, respectively. H and OH adsorption energies are slightly more affected by higher coverages with differences in the adsorption energy of 0.16 and 0.19 eV, respectively. CO₂ is by far the most affected by the higher coverages, with an energy difference of 0.52 eV.

We investigated coverage effects on the CLBEs of each respective adsorbate. In Figures S27–S31, we show the O 1s experimental spectra and O 1s theoretical spectra for both a single adsorbate within the unit cell (SA) on the surface and a monolayer coverage (ML) of the same adsorbate. The images to the right show atoms in the same position in the SA and the ML case to illustrate the effects of monolayer coverage on the CLBEs of specific atoms. We calculated the CLBEs of seven surrounding oxygen atoms and all adsorbed oxygens. The respective CLBEs of all sampled atoms are in Table S10. We list the CLBEs of the atoms depicted in the spectra figures with the difference in the CLBE of the SA and ML cases in Table S11. From this table, the most significant difference we see is the increase in CLBE of the adsorbed O in H₂O by 0.34 eV shown in position 1 Figure S30. This indicates why our original calculation without coverage effects does not capture the higher CLBEs of water present in our data. The adsorbed OH also increases in CLBE by 0.21 eV, as shown in position 1 Figure S29. Higher coverages affected the other adsorbates slightly differently. Both CLBE of the adsorbed O in the O and the OH decrease by −0.32 and −0.46 eV as shown in Figure S28 position 1 and Figure S29 position 1. For CO₂, the CLBE of the adsorbed oxygen closest to the surface increases by 0.15 eV as shown in Figure S31 position 1 while the CLBE of the oxygen facing the vacuum decreases by −0.35 eV shown as in Figure S31 position 3. By including coverage effects, we can more accurately quantify the contributions due to adspecies.

3.2. Experimental Temperature Dependent Data

The temperature dependence of the experimental features in the O 1s spectra was quantified to verify the assignments made by theory. The resulting O 1s spectra are depicted in Figure 8. It has to be emphasized that the experimental data was obtained on a pressed powder sample obtained by a sol–gel process with subsequent calcination in air and transfer of the sample to the XPS setup. No surface cleaning or other preparation has been performed once in vacuum except for the gradual heating. No special activation procedure (e.g., reduction) and no active gas dosing was employed, thus we observed the samples in their native state.

Figure 8.

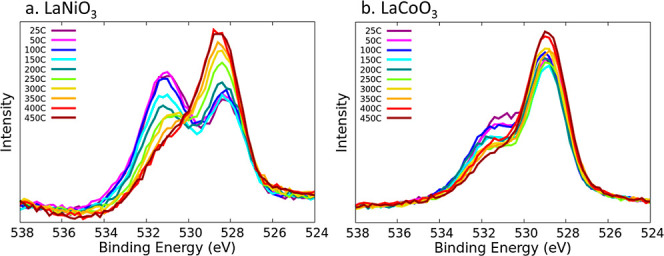
O 1s temperature-dependent spectra of (a) LaNiO₃ and (b) LaCoO₃. The temperatures tested range from 25 to 450 °C.

As mentioned before, the spectra exhibit two main features. It also has to be noted that the O 1s core level natural line width (Lorentzian width describing the core hole lifetime) together with the experimental broadening in general offers a very limited possibility to identify different contributions by respective obvious spectral features due to the rather large full width at half-maximum. The gradual disappearance of the high binding energy core level component with increasing temperature clearly indicates that this peak corresponds to the presence of adspecies on the surface. The temperature dependent data further supports the strong adsorption of water-derived species and CO₂ because of the high temperatures of around 400 °C needed to desorb the adspecies. Further, we speculate that the increase in intensity of the low energy peak is due to the reduced damping of the XPS signal arising from the substrate lattice O species. In the LaNiO₃ temperature dependent plot (Figure 8a), the peak at lower core level energy values shifts slightly to higher values as the temperature increases. This could be attributed to the surface restructuring of the LaNiO₃ at high temperatures.⁵ As an example of the deconvolution of the LaNiO₃ temperature-dependent spectra, Figure S32 shows the result for 25, 100, 200, 300, and 400 °C.

Using the information from the theoretical calculations (from both the low and high coverage regime), an analysis of the experimental LaNiO₃ data is performed in Figure 9. Figure 9 shows the change of the absolute peak areas of O 1s contributions with temperature in XPS temperature programmed desorption (TPD) experiments. For this fit, a total of six contributions at fixed binding energy positions (fixed CLBEs) were used to project the major features of the calculated spectra. Besides a general lattice oxygen contribution (located at a binding energy of about 528.2 eV, shifting slightly with an increase in temperature by about 0.2 eV) that increases slightly with an increase in temperature, a feature to account for the surface species at lower binding energies was assumed. As can be seen (and as expected), this feature does not show a significant intensity under the conditions of the experiment as no clean surface area is present. The feature at about 529.0 eV would summarize OH motifs but does not obtain significant intensity either. Here, the widths of the contributions of more than 2 eV do not allow for a clear distinction of features with small relative CLBEs. A component positioned at 529.7 eV should be representative of adsorbed CO₂. The fact that its contribution increases might signal that CO₂ is not located at the outermost surface. The next contribution at 531.0 eV comprises mainly adsorbed oxygen atoms but also parts of adsorbed water and clearly decreases due to desorption. Finally, a component that could specifically be assigned to larger amounts of adsorbed water at around 532.5 eV shows thermal desorption of water. In interpreting such results, one has to consider that all components have been modeled with a single set of constant widths, whereas in the literature one often finds different spectral shapes. Although both interpretations might have their justification, we want to note that certain contributions like the high binding energy water part might easily be covered by other components with larger widths, as observed by Mickevičius et al.⁹ However, a calculation-based analysis allows different contributions to be distinguished more clearly.

Figure 9.

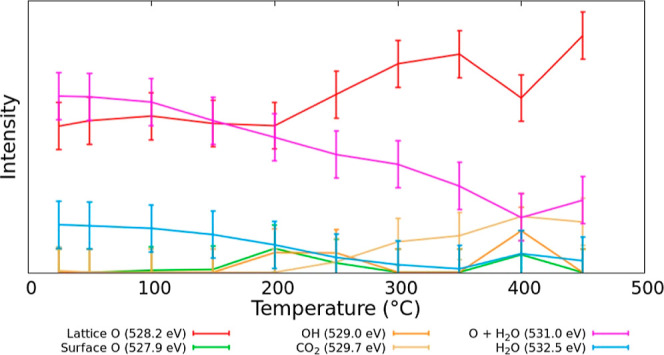
O 1s contributions to the XPS spectra based for LaNiO₃ as a function of temperature in XPS temperature desorption studies.

A similar deconvolution is conducted on the LaCoO₃ surface as shown in Figure S33. This evaluation does not include coverage effects. Interestingly, for LaCoO₃ a fit with only two components would be sufficient to describe the data well with the O 1s contributions of the lattice and adsorbates. Comparing the calculated spectra in Figure 7, this could be due to the simpler structure with less contributions. There is obviously less change in intensity of the high binding energy peak in the experimental temperature-dependent spectra compared to LaNiO₃, which contributes to a lack of significant changes of the XPS spectra as a function of temperature highlighted in Figure S33. The theoretical deconvolution still gives reasonable values for the various adspecies on the surface.

4. Conclusions

We coupled experimental XPS with theoretical modeling to discern the contributions of various surface-bound species on perovskite oxides to realistic XPS experimental spectra. We show that the RPBE functional is sufficient to capture these results. While this method cannot be used to predict multiplets or spin–orbit splitting in the A-site and B-site spectra, it is useful for deconvoluting the O 1s spectra over traditional methods. Interpretation of experimental XPS spectra is limited by instrumental broadening convoluting the various adspecies contributions. Although experimental deconvolution is routinely conducted via software, theoretically calculated CLBEs provide deeper insights into the composition of surface species and our data disproves claims made in the literature about the contributions to the XPS of the surfaces that we studied.^9,11 Each of the adspecies studied in this work (H, O, OH, H₂O, and CO₂) has specific CLBEs associated with their adsorption. The surrounding atoms also experience shifts due to the absorption of species on the surface. We observe differences in CLBEs between the adsorption configurations of molecules on the surface specifically shown by CO₂ on LaCoO₃ in the monodentate and bidentate configurations. We have also conducted coverage tests showing that the coverage effects have a significant effect on the resulting CLBEs of the adspecies and surface species. In the quantitative analysis of the temperature-dependent data such a coverage dependence complicates the analysis even further as with increasing temperature we anticipate the coverages to change. Thus, not a single set of fit components at a fixed energy position is suitable for the description. However, in order not to overinterpret the data, we still use fixed positions but mimic the changing coverage by introducing a peak to include the most prominent coverage-dependent difference. This level of analysis of the contributions to experimental XPS spectra is critical to understanding the complex surface chemistry of perovskite oxides.

AFM ordering is rarely modeled as it has a high computational cost associated with it, but we find the addition of AFM does affect the resulting adsorption energies and provides insights into the electronic properties of the surface. The adsorption of CO₂ is strengthened as compared to the other adspecies modeled in this work due to increased charge transfer between the adspecies and the surface. The adsorption of species also greatly affected the surface AFM ordering, indicating the magnetic ordering of the surface is sensitive to the surrounding environment. For the modeling of these spectra, the inclusion of AFM ordering does not seem to change the peak value for the overall spectra model even if the individual CLBEs change slightly and a NM calculation can be used when modeling these spectra.

Our results show that the adsorption of water is stronger on the perovskite surface than on the respective metallic nickel and cobalt surfaces, showing that the incorporation of the B-site metal into the La-perovskite lattice increases the adsorption energy of the adspecies on the surface. The available electronic states in a perovskite lattice stabilize adspecies over those of a pure metal. Similarly to water, CO₂ adsorbs on the perovskite surface more strongly than the metallic surface. For CO₂ to undergo dissociation to form CO, the CO₂ molecule must be activated and adsorbed stably to the catalyst surface.⁴⁹ The perovskite surface stabilizes the CO₂ molecule on the surface and activates it, as signified by the C–O bond lengthening and bond angle decreasing. However, very strongly adsorbed adspecies can lead to poisoning of the active sites and reduction in the catalytic reactivity, which may be the case in the LaNiO₃ surface more than the LaCoO₃ surface. There is little work on perovskites with respect to the mechanism and this gap in knowledge needs to be addressed to understand how to augment the catalytic activity. Therefore, it is imperative to continue to study these surfaces to elucidate factors such as electric fields or B-site substitutions to stabilize the adsorbates without poisoning active sites.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.4c00440.

• Total energy as function of volume; surface energies of possible surface terminations; example of fully deconvoluted O 1s spectra; adsorption of species on LaNiO₃; comparison between AFM and NM surfaces; total energy as a function of volume; charge transfer calculations; adsorption of species on LaCoO₃; comparison of NM and AFM O 1s spectra for LaNiO₃; C 1s LaNiO₃ theoretical spectra; C 1s LaCoO₃ theoretical spectra; La 4d theoretical spectra for LaNiO₃; La 4d theoretical spectra for LaCoO₃; Ni 3p theoretical spectra for LaNiO₃; Co 2p theoretical spectra for LaCoO₃; single adsorbate versus monolayer coverage adsorption of each adsorbate on LaNiO₃; theoretical O 1s spectra; experimental O 1s spectra deconvoluted using theoretical contributions at different temperatures; O 1s contribution for experimental spectra for LaCoO₃ as a function of temperature (PDF)

• Crystallographic data for a DFT-based structure (CIF)

• Crystallographic data for a DFT-based structure (CIF)

Author Contributions

CRediT: Ariel Whitten formal analysis, software, visualization, writing-original draft; Dezhou Guo data curation, investigation; Elif Tezel data curation, investigation; Eranda Nikolla funding acquisition, project administration, resources, supervision, writing-review & editing; Reinhard Denecke data curation, investigation, writing-review & editing; Jean-Sabin McEwen conceptualization, funding acquisition, supervision, writing-review & editing.

The authors declare no competing financial interest.