Estimating lags in a kraft mill

Abstract

In pulp mills, lags obscure the effect of upstream operations on downstream measurements. Here, we estimate lags in a Canadian pulp mill using autoregressive exogenous (ARX) models. First, we show that ARX models can approximate lags in a process simulation that resembles the liquor storage tanks in pulp mills, a major source of lag in the kraft recovery cycle. Then, we use ARX models to estimate the lagged effect of a change in species pulped on as-fired liquor heating value, viscosity, and boiling point rise. Additionally, we compare the predictions of the ARX models to autoregressive (AR) models and a persistence model. The estimated lags between a change in species and heating value (49 h) and boiling point rise (41 h) agree with a detailed simulation of the mill and are close to estimated hydraulic residence times, suggesting that the liquor tanks exhibit imperfect mixing. A lagged effect of species change on viscosity could not be identified. ARX and AR models produce similar predictions that are slightly better than those of a persistence model. Finally, we show that process measurements upstream of units characterized by large residence times will likely provide little benefit to prediction accuracy.

1. Introduction

Pulp mills comprise storage tanks that delay the impacts of upstream disturbances on downstream operations. This is helpful in preventing issues in one area of a mill from spreading to other mill areas. However, as a result, models relating measurements upstream and downstream of these storage tanks must account for such delays. Here, we define lag as the time before a change upstream begins to significantly affect a downstream measurement. While, in some cases, lags are approximately equal to hydraulic residence times, this need not be the case. Mixing, other transport phenomena, reaction kinetics, and non-idealities can cause the time before significant impact (the lag) and the hydraulic residence time to differ (Ljung 1998). Lags are particularly important when developing machine-learning models or applying statistical techniques as lags affect how data should be pre-processed before model fitting. Ideally, these lags would be identifiable from normal operating data alone (Box et al. 2015).

Black liquor, an aqueous by-product of the pulping process, is concentrated before being burned in a recovery boiler to recover pulping chemicals and energy. The liquor fed into the boiler is as-fired liquor. Specifically, our goal is to estimate the lag between a change in species pulped and as-fired heating value, viscosity, and boiling point rise (BPR). Heating value, typically reported as higher heating value (HHV), is important as the heat of combustion drives the recovery of sodium sulfide and production of steam in the recovery boiler (Adams 1997). Viscosity and BPR affect droplet formation as liquor is sprayed into the recovery boiler which, if poorly controlled, can result in excess carryover, fouling, and depletion of the char bed (Miikkulainen et al. 2005). All three liquor properties are known to vary with wood species (Hart 2022). While lag estimation in mills and other process data has been investigated elsewhere, to our knowledge, in a mill, the lag between a change in species pulped and the as-fired properties has not been explored.

1.1. Objectives

In this study, our objective is to identify the lag between changes in wood species pulped and the corresponding changes in as-fired black liquor HHV, viscosity, and BPR based only on process data. If these lags could be identified, operators could better anticipate when process parameters would be affected by upstream disturbances, allowing them to act preemptively to avert negative impacts. Further, by using a data-driven approach instead of heuristics, lag estimates would be repeatable, systematic, and not rely solely on process experience.

2. Process lag estimation in the literature

Multiple studies in the recent literature investigate process lag estimation. Generally, the approaches can be divided into six categories (Table 1). In many mills and in some studies (Correia et al. 2018), lags are estimated heuristically. While these estimates can be accurate, they rely on process experience which can take years to acquire. In contrast, we focus on data-driven methods that do not require as much process experience. In this section, we discuss data-driven process lag estimation approaches in the recent literature along with their limitations.

Table 1:

Categorization of lag estimation methods in the recent literature.

Lag estimation method	Example
Heuristic	Correia et al. (2018)
Hydraulic residence time (Zenger and Ylinen 1994)	Sayda and Taylor (2003)
Lipschitz index (He and Asada 1993)	Wang and Chen (2006) Sainlez and Heyen (2013) Rebello et al. (2022)
Correlation analysis	Dahlbäck (2020) Graziani and Xibilia (2021) Topalian et al. (2022) Ekbåge et al. (2019)
Feature engineering	Lee et al. (2006) Galicia et al. (2011) Graziani and Xibilia (2019) Graziani and Xibilia (2021) Chen and Zhao (2020) John and Ferbinteanu (2021)
Hyperparameter tuning	Ettaleb et al. (1998) Almeida and Park (2013) Matos et al. (2008) Mechaqrane and Zouak (2004) Chetouani (2008) El-Din and Smith (2002) Galicia et al. (2011)

2.1. Hydraulic residence time

One approach is to assume that hydraulic residence times are equal to process lags. A simple hydraulic residence time can be used:

$$T_d(t)=\frac{V(t)}{Q(t)},$$ (1)

where T _d is residence time, V is tank volume, and Q is the volumetric flowrate through the tank. This approach is the simplest, quickly providing a rough lag estimate. Zenger and Ylinen (1994) expanded on this residence time calculation:

$$V(t)=\underset{t-T_d(t)}{\overset{t}{\int }}Q(\tau )\mathrm{d}\tau .$$ (2)

Unlike Equations (1) and (2) accounts for variations in volumetric flowrate and tank volume as fluid travels through the tank. Sayda and Taylor (2003) used Equation (2) to estimate lags in a mechanical pulp bleaching process. Unfortunately, as mentioned earlier, hydraulic residence times may incorrectly predict lags as a result of ignoring mixing effects, reaction kinetics, and non-idealities.

2.2. Lipschitz index

In order to account for non-idealities, a popular alternative is the method by He and Asada (1993). They define the Lipschitz quotient

$$q_{i,j}=\frac{|y_i-y_j|}{|x_i-x_j|},i\ne j,$$ (3)

where y is the system output, x is the system input. This can be expanded to

$$q_{i,j}^n=\frac{|\delta y|}{\sqrt{{(\delta x_1)}^2+\cdots +{(\delta x_n)}^2}}$$ (4)

and used to calculate the Lipschitz index q of model order n

$$q^n={\left(\prod _{k=1}^p\sqrt{n}{q}^n(k)\right)}^{\frac{1}{p}},$$ (5)

where q ⁿ (k) is the kth largest Lipschitz quotient among all  $q_{i,j}^n$ , and p is a positive number (usually p = 0.01N). Generally, the Lipschitz index q ⁿ decreases as model order n increases. The value of n at which q ⁿ plateaus is the chosen model order. This approach has been used in a number of studies (Rebello et al. 2022; Sainlez and Heyen 2013; Wang and Chen 2006). It is popular because it has been shown to identify lags in non-linear systems. Unfortunately, this method can result in prohibitively large input sizes, and if the lags are large or if the sampling frequency is high, uninformative input data will be retained, bloating the model. The importance of minimizing model size is discussed by Galicia et al. (2011).

2.3. Hyperparameter tuning

Other approaches treat lag estimation as a type of hyperparameter tuning. Souza and Araújo (2011) combined forward-selection with a support vector machine model, treating increasingly lagged values of inputs as possible, additional inputs. Their approach suffers the same drawback as the Lipschitz index: uninformative inputs can be retained. Almeida and Park (2013) used trial-and-error to estimate the necessary time delay for a neural network model of an evaporation plant in a pulp mill. However, this brute force method can become intractable if the model is large and if many possible time delays must be checked.

2.4. Correlation analysis

Sometimes, the cross-correlation between the output and varying lagged values of the input are compared to identify lags. Graziani and Xibilia (2019) estimated lags based on the cross-correlation of engineered features, going as far as to experiment with other types of cross-correlation metrics (Graziani and Xibilia 2021). However, the proposed correlations do not account for autocorrelation in the input (Bisgaard and Kulahci 2011; Box et al. 2015). Since the inputs are usually autocorrelated, their impact on the output is “smeared” over time. By not accounting for the dynamics of the input, spurious correlations emerge, such as positive cross-correlations between input measurements in the future and output measurements in the past.

2.5. Feature engineering

Finally, some studies transform process data into a latent space and estimate the lags in the latent space. For example, Chen and Zhao (2020) used dynamic principal component analysis (diPCA) to transform process data into latent variables and compared the cross-correlations between the latent variables and other variables, where peak cross-correlations indicated lags. Similarly, John and Ferbinteanu (2021) transformed time series data into graphs before performing cross-correlation analysis. Unfortunately, due to the use of engineered features, these methods can be difficult to interpret.

2.6. ARX models

In this study, we model the relationships for a variety of input-output pairs in a simulated two-tank system and in a Canadian kraft pulp mill using autoregressive exogeneous (ARX) models, which account for autocorrelations in both the input and output. In the process of identifying these models, the lags between inputs and outputs are identified. Ettaleb et al. (1998) demonstrated this approach with simulated autoregressive moving-average exogenous (ARMAX) processes, and Matos et al. (2008) used ARX models to model the relationship between digester parameters and the viscosity of bleached pulp. While Galicia et al. (2011) used DPLS regression to approximate kappa number, they considered using ARX models to estimate the necessary amount of historical data and dead times to incorporate into the model. Wasson (2016) used Box-Jenkins transfer function models, which belong to the same family of models as ARX models (Ljung 1998), to estimate the lags of inputs to a hog fuel boiler.

We first validate the use of ARX models using a simple, numerical simulation of two tanks in series with an added artificial delay. Then, we apply the approach to mill data. The estimated lags of the mill are compared to estimated hydraulic residence times and the estimated lags from a detailed simulation of the mill (Rogerson 2022).

3. Methodology

3.1. Two tank simulation

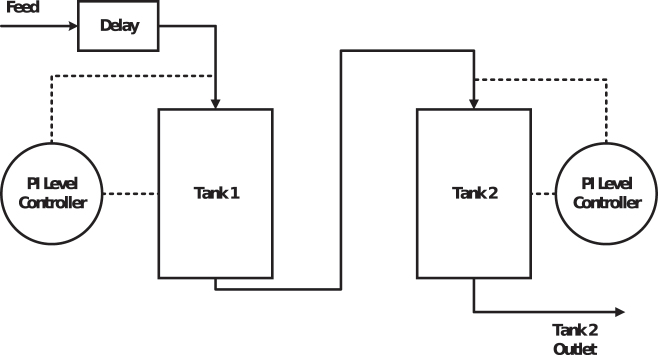
Liquor storage tanks are predicted to create the largest lags in mills. As a result, using CADSIM Plus (Aurel Systems 2019), we developed a simulation of a water-NaCl solution flowing through two tanks in series (Figure 1). In the simulation, tank volumes, flowrates, and feed concentration are manipulated. Proportional-integral level controllers with noisy, oscillating setpoints and large integral terms manipulate flowrates to simulate the oscillating tank level control in a mill: while a mill pulps softwood, the volume of stored black liquor increases; during hardwood operation, the volume of stored liquor decreases. Additionally, all simulation parameters can be injected with noise. The magnitude of this noise varies for each parameter and is indicated in Table 2. Finally, a transport lag (box labelled “delay”) is placed before the first tank to simulate imperfect mixing (i.e., a dead-time). Once the simulation was initiated (Table 2), it was allowed to run for 15,000 time steps (1 time step = 1 min). The first 2000 time steps of data were not analyzed as the simulation was reaching steady-state during this time.

Figure 1:

Schematic of the two-tank simulation.

Table 2:

Two-tank simulation initial conditions.

Parameter	Initial value	Noise primary standard deviation	Noise secondary standard deviation	Oscillation amplitude	Oscillation frequency	Oscillation noise amplitude primary standard deviation	Oscillation noise amplitude secondary standard deviation	Ramp rate
Tank 1 volume	500 m3	None	None	None	None	None	None	None
Tank 2 volume	100 m3	None	None	None	None	None	None	None
Feed water flowrate	30 LPS	None	None	None	None	None	None	None
Feed NaCl flowrate	0.1 kg/s	0.05	0.01	None	None	None	None	None
Tank 1 level SP	50 %	5	1	10	0.01	3	1	1
Tank 2 level SP	50 %	5	1	10	0.001	3	1	1
Tank 2 outlet flowrate	20 kg/s	None	None	5	0.01	None	None	0.1
Transport lag	10 min	None	None	None	None	None	None	None

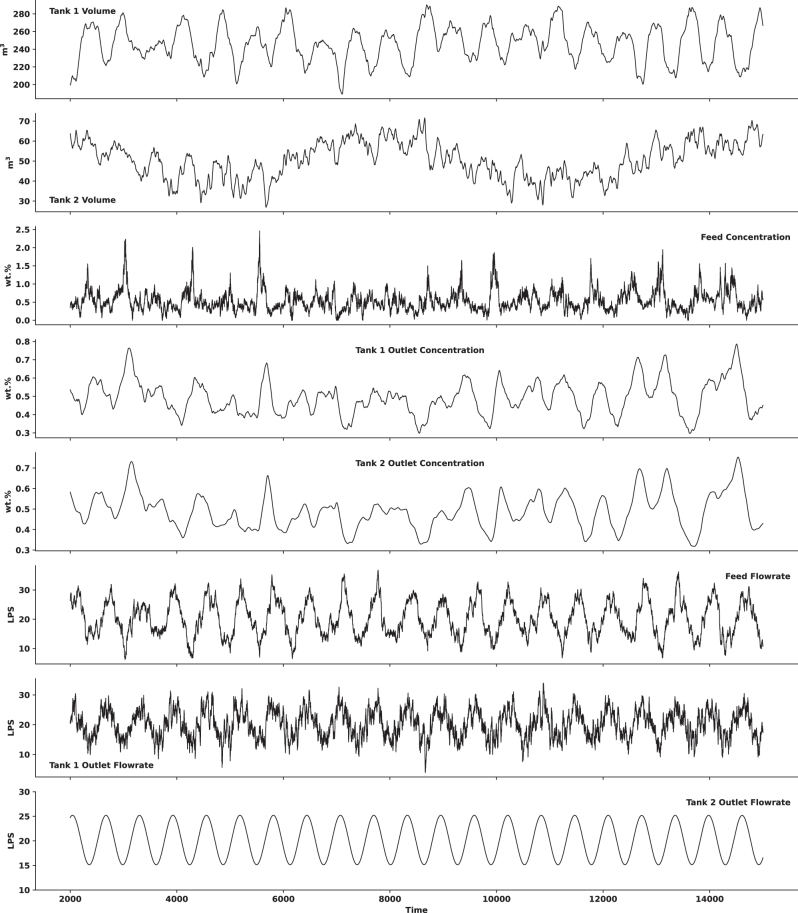
The simulation data is shown in Figure 2. All measurements exhibit noise except for the outlet flowrate from Tank 2, which was oscillated without noise. While the feed concentration is quite noisy, most of that noise is attenuated in Tank 1. This is likely due to the large volume of fluid in Tank 1 (initially 250 m³) relative to its inlet flowrate (30 LPS): the NaCl is diluted in the tank. The marginal amount of noise in the concentration exiting Tank 1 is attenuated in Tank 2. This is expected: the inlet flowrate of Tank 2 is similar to Tank 1, but Tank 2 contains less fluid to dilute its inlet (50 m³ vs. 250 m³).

Figure 2:

Data from two-tank simulation.

3.2. Mill data

Mill data (Figure 3) was obtained from a North American mill that pulps both hardwood and softwood. The dataset spans November 2022 to April 2023, contains 90 measurements from the digester to the recovery boiler, and was sampled at a 10-min frequency. The 90 measurements were chosen based on mill expertise, and the data was filtered for normal operation: digester production rate above 400 ADMTPD and recovery boiler production rate above 1.5 tons per day DS. HHV was calculated as

$$\mathrm{H}\mathrm{H}\mathrm{V}=\frac{\frac{A+20}{\gamma }-g}{0.7}\frac{r}{24},$$ (6)

where A is the total flowrate of air to the boiler, γ is an excess air characterization, g is the flowrate of air consumed by natural gas, and r is the liquor firing rate. The mill verified Equation (6) against laboratory measurements of black liquor heating value. Viscosity was calculated using

$$\mathrm{V}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y}=0.1351L^3-26.8456L^2+1795.92L-40314.5,$$ (7)

where L is the pump motor load. Equation (7) was developed in-house by the mill using an online viscometer which measured a sidestream of the as-fired tank’s re-circulation pump. Finally, BPR was calculated as

$$\mathrm{B}\mathrm{P}\mathrm{R}=T_{\text{Liq}}-T_{\text{Vap}},$$ (8)

where T _Liq is the temperature of liquor exiting the as-fired tank and T _Vap is the temperature of the vapour exiting the as-fired tank. The temperature of the vapour is estimated based on the pressure of the vapour and a steam table, assuming that the vapour exiting the tank is at saturation.

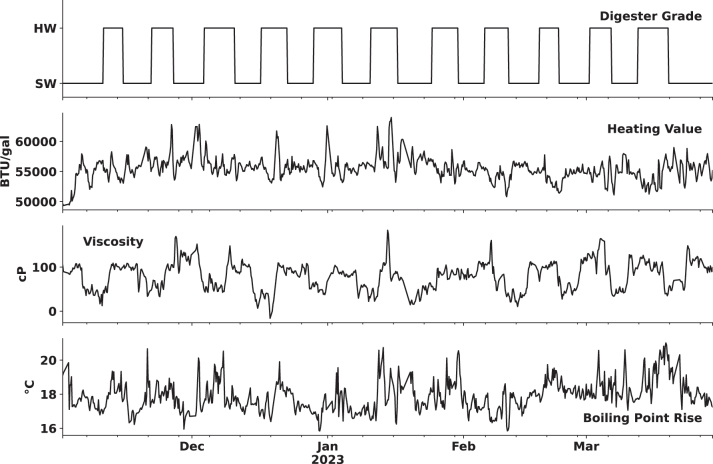
Figure 3:

Species changes and as-fired liquor properties (4 h averaged).

Equations (6) and (7) are empirical correlations while Equation (8) is the definition of BPR. Measurements falling outside of the 0.5 and 99.5 percentiles were dropped to remove spurious measurements, and missing data (roughly 12 % of the data) was imputed using linear interpolation.

3.3. ARX models

ARX models, which belong to the family of polynomial models described by Ljung (1998), represent the output as a linear combination of lagged inputs and outputs:

$$\begin{array}{c}A(q)Y_t=B(q)X_t+{\epsilon }_t,\\ A(q)=1+a_1{q}^{-1}+\cdots +a_{n_a}{q}^{-n_a},\\ B(q)=b_1{q}^{-n_k}+\cdots +b_{n_b}{q}^{-n_k-n_b},\\ Y_t=a_1{Y}_{t-1}+\cdots +a_{n_a}{Y}_{t-n_a}+b_1{X}_{t-n_k}+\cdots +b_{n_b}{X}_{t-n_k-n_b}+{\epsilon }_t,\end{array}$$ (9)

where Y _t is the system output; X _t is the system input; n _a and n _b are the lag orders of the polynomials A(q) and B(q), respectively; q is the shift operator; and $\epsilon \sim \mathcal{N}\left(0,{\sigma }_{\epsilon }\right)$ is a white noise process. Importantly, n _k is the lag between input and output, and its identification is the focus of this work. Equation (9) is analogous to the combination of a filtered input and filtered white noise. This is the preferred representation by Ljung (1998) and Box et al. (2015) as it makes explicit that the system is driven by noise ɛ _t .

3.4. Model fitting procedure

The same fitting procedure was used for both the simulation data and the mill data. Model identification was done using the System Identification Toolbox in MATLAB 2022 (The MathWorks Inc 2022). First, the data was split into training, validation, and testing sets. For the simulation data, the first 4000 rows were used as training data, and the proceding 2000 rows were used as validation data, resulting in a 30/15/55 train/validation/test split. For the mill data, the first 1500 rows were used as training data, and the proceeding 500 rows were used as validation data, resulting in a 28/15/57 train/validation/test split. For fitting linear models, datasets on the order of hundreds of samples are typical. We favoured a smaller training and validation set in order to create as large of a testing set as possible. A larger unseen testing set leads to a more robust assessment of the fitted model and estimated lags. Additionally, smaller training and validation sets demonstrate that, in practice, lags can be estimated sooner: less time is spent waiting for sufficient data.

After partitioning the data, ARX models with n _a = [1:10], n _b = [0:10], and n _k = [0:50] were evaluated. The possible orders of lagged inputs n _b include 0, allowing for the input to be ignored if beneficial. For each input-output pair, the selected model was the one that maximized the explained variance in the validation data. The coefficients of the identified ARX models are shown in Table 3. The performances of the identified ARX models against the testing data were compared to persistence models (no fitting procedure required) and autoregressive (AR) models. AR models were fitted in a similar manner as ARX models, except digester grade was not considered (B(q) = 0). The persistence model is an ARX model, where A(q) = 1 − q ⁻¹ and B(q) = 0.

Table 3:

ARX model coefficients.

HHV	A(q)	1 − 0.6164q −1 − 0.3835q −2
	B(q)	−158.1q −49 − 41.27q −50 − 273.1q −51 + 722.8q −52 − 18.54q −53 − 11.95q −54 − 493.9q −55 + 641.5q −56 − 367.3q −57
Viscositya	A(q)	1 − 0.9917q −1
	B(q)	4.096q −11 − 6.529q −12 + 3.057q −13 − 2.095q −14 + 1.982q −15 − 0.4065q −16 − 2.529q −17 + 4.124z −18 − 4.308z −19 + 3.651z −20
BPR	A(q)	1 − 1.068q −1 + 0.1896q −2 − 0.02325q −3 − 0.09807q −4
	B(q)	−0.1079q −41 + 0.1457q −42 − 0.03551q −43 + 0.1035q −44 − 0.09997q −45 + 0.1846q −46 − 0.2691q −47 − 0.003473q −48 − 0.1942q −49 + 0.2724q −50

^aDoes not outperform AR model: lag likely incorrect.

3.5. Model performance metrics

Model performances were evaluated based on three metrics: coefficient of determination (R ²), mean absolute percentage error (MAPE), and root mean squared error (RMSE). If over n samples, y is the true value, $\widehat{y}$ is the predicted value, and $\overline{y}$ is the average of true values, then R ², MAPE, and RMSE are calculated as

$$R^2=1-\frac{\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2},$$ (10)

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=\frac{1}{n}\sum _{i=1}^n\frac{|y_i-\widehat{y_i}|}{|y_i|},$$ (11)

and

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2},$$ (12)

respectively.

4. Results and discussion

4.1. Two-tank simulation

With the two tank simulation data, the hydraulic residence times calculated using Equation (2) overestimate the true lags whereas the lag estimates of the ARX models are close to the true lags (Table 4). This was expected as Equation (2) assumes a plug flow through vessels while the simulated tanks are perfectly mixed. These results show that ARX models can identify lags that differ from hydraulic residence times.

Table 4:

Lag estimates for two tank simulation.

Input – output	Actual lag (min)	Median hydraulic residence time estimate (min)	ARX model lag estimate (min)
Feed – tank 1 outlet	10	203	10
Feed – tank 2 outlet	10	245	11
Tank 1 outlet – tank 2 outlet	0	42	1

4.2. Mill data

While a lagged effect between digester grade and as-fired viscosity is weak and likely insignificant, the estimated lags of the ARX models relating digester grade to HHV and BPR seem reasonable (Table 5) and improve predictions (Table 7). The estimated lags agree with those proposed by Rogerson (2022) who simulated the same mill with constant tank volumes. Rogerson estimated that, when transitioning from softwood to hardwood, the initial presence of hardwood organics in the as-fired liquor occurs 15 h after species change and that the as-fired liquor is composed of 95 % hard wood organics after 65 h. Similarly, when transitioning from hardwood to softwood, the initial and 95 % changes are seen at 12 h and 41 h, respectively. The ARX models were identified using data that contained both types of transitions, so it is reasonable that the lag that optimizes model performance is slightly longer than that estimated for hardwood to softwood transitions and slightly shorter than that estimated for softwood to hardwood transitions. The lag between digester grade change and BPR is expected to be lower as the BPR is calculated at the final storage tank, which is separated from the as-fired liquor ring header by the volume of the storage tank. We estimated the hydraulic residence time of this tank to be 4–5 h based on Equation (2), and Rogerson (2022) estimates this lag to be roughly 7 h.

Table 5:

Lag estimates for mill data.

Input – output	Median hydraulic residence time estimate (h)	ARX model lag estimate (h)
Digester grade – black liquor HHV	43	49
Digester grade – black liquor viscosity	43	11a
Digester grade – black liquor BPR	38	41

^aLikely insignificant.

Table 7:

Prediction test data metrics on mill data (1 h predictions).

	HHV			Viscosity			BPR
	R 2	MAPE (%)	RMSE	R 2	MAPE (%)	RMSE	R 2	MAPE (%)	RMSE
Persistence	0.70768	1.109	901.60	0.96618	6.092	5.867	0.86661	1.085	0.361
AR	0.72531	1.071	873.98	0.96619	6.081	5.866	0.86837	1.088	0.359
ARX	0.72749	1.066	870.52	0.96544	6.124	5.930	0.86994	1.089	0.357

Additionally, we combined our estimated hydraulic residence times of storage tanks with the residence time estimates of smaller unit operations by Rogerson (2022) to obtain total hydraulic residence time estimates between a change in digester grade and properties of as-fired liquor (Table 5). Except for as-fired viscosity, where the estimated lagged effect is weak and likely incorrect, the estimated hydraulic residence times are close to the ARX model lag estimates.

Unlike the two tank simulation results, with the mill data, the hydraulic residence times and estimated lags are close. This suggests that the liquor storage tanks exhibit imperfect mixing. Again, Equation (2) assumes a plug flow through the vessel. If there were significant mixing in any of the storage tanks throughout the process, the ARX mode lag estimates would be lower than the hydraulic residence time estimates, like in the two-tank simulation. Instead, the lag estimates are close to the hydraulic residence time estimates. Likely, the volume of liquid inside the mill storage tanks are so large relative to the volumetric flowrate passing through that the liquor inside the tank is minimally agitated. As a result, liquor fed to the tanks is poorly mixed and lingers.

4.3. Comparing predictions of ARX and AR models

While a lag may be identified during the fitting of an ARX model (n _k ≠ 0), a final check using simpler models and unseen test data is important to detect spurious estimates. In this study, the ARX models are bivariate: they consider both past output measurements and an exogenous input (species). If, on unseen test data, the ARX model predictions are more accurate than a model that does not consider species, i.e., an AR model, then there is evidence that the estimated effect of species, including its lag, is significant. Similarly, if an AR model fails to outperform a simple persistence model, that suggests the autocorrelation identified by the AR model is insignificant. In this section, we compare the accuracies of the persistence model, the fitted AR models, and the fitted ARX models in both the two-tank simulation and the mill data.

For the two tank simulation, ARX models provide a small improvement in all metrics over AR models, which are more accurate than a persistence model (Table 6). Similarly, for the mill HHV data, both AR and ARX models predict test data more accurately and explain larger amounts of variability in the test data than a persistence model (Table 7). While AR and ARX models for BPR similarly explain more variability in the test data and achieve lower RMSEs, they produce larger MAPEs. For both HHV and BPR, the improvements relative to the baseline persistence models are small. Further, compared to the AR models, the performances of ARX models that consider digester grade are marginally better for as-fired HHV and BPR and slightly worse for as-fired viscosity. That the bivariate forecasts (ARX models) for HHV and BPR are more accurate than univariate forecasts (AR models) suggests that digester grade significantly influences HHV and BPR in this dataset (Tsay 2013).

Table 6:

Prediction test data metrics on two tank simulation data (1 min predictions).

	Feed – tank 1 outlet			Feed – tank 2 outlet			Tank 1 outlet – tank 2 outlet
	R 2	MAPE (%)	RMSE	R 2	MAPE (%)	RMSE	R 2	MAPE (%)	RMSE
Persistence	$>0.99$	0.17	1.05 × 10−3	$>0.99$	0.13	7.97 × 10−4	$>0.99$	0.13	7.97 × 10−4
AR	$>0.99$	0.033	2.04 × 10−4	$>0.99$	0.0049	3.59 × 10−5	$>0.99$	0.0049	3.59 × 10−5
ARX	$>0.99$	0.012	9.00 × 10−5	$>0.99$	0.0046	3.45 × 10−5	$>0.99$	0.0044	3.36 × 10−5

For viscosity, the type of wood pulped likely impacts the viscosity of as-fired liquor, but a significant effect could not be seen in this dataset with our methodology. One reason may be due to viscosity having more “inertia” compared to HHV and BPR. As will be shown later, inertial units such as liquor storage tanks can introduce dynamics that diminish the observable effect of upstream disturbances on downstream measurements. The dynamics of the effect of species on each as-fired liquor property probably differs. For example, below 50 % solids content, removing lignin from black liquor affects viscosity but not BPR (Moosavifar et al. 2006). As a result, the observable effect of species change on viscosity may be more diminished than those of HHV or BPR due to different process dynamics. This could also be exacerbated by the mill’s control system, whose goal is to suppress observable variations. Open-loop testing may provide the necessary data to observe the effect of species change on viscosity. However, it is likely impractical to perform open-loop testing on such a large area of the mill, which includes large, important units such as the digester and evaporators.

Finally, many factors, in addition to species, have been shown to affect black liquor viscosity such as kappa number and ash content (Zaman and Fricke 1996). It is possible that the impacts of other process operations on viscosity such as digester operation and ash recycling compete to be seen against the impact of species. Perhaps, with additional exogenous inputs, an ARX model would be able to identify the impact of species change on viscosity while accounting for the impacts of other potential exogenous inputs.

4.4. Similarity between ARX and AR model performances

Despite marginal improvements in prediction, the ARX models provide process insight: the lag between a change in species of wood pulped and the resulting change in as-fired liquor properties can be estimated. This demonstrates how process prediction and process insight are distinct goals. If a model is only needed for prediction, the trade-off of increased model complexity for marginal improvements in prediction accuracy by the ARX model may be unnecessary. However, if the goal is to understand the relationship between an input and an output, then the ARX model is preferred: the AR model does not describe the relationship between an input and output.

The similar performance between ARX and AR models is likely due to the heavy autocorrelation of process data. As mentioned earlier, ARX models can be thought of as a combination of a filtered input and filtered white noise. However, if the output Y _t is heavily autocorrelated (i.e., the coefficients a _i in Equation (9) are large), X _t will do little to boost prediction accuracy. Both the simulation data and the mill data in this work, like most process data, are highly autocorrelated.

To demonstrate the affect of autocorrelation, consider the two-tank simulation (Figure 1). If C ₀ is the concentration of NaCl in the feed stream; C ₁ is the NaCl concentration in the outlet of tank 1; C ₂ is the concentration of NaCl in the outlet of tank 2; Q is the volumetric flowrate; V ₁ is the volume of fluid tank 1; V ₂ is the volume of fluid in tank 2; and perfect mixing is assumed, then the dynamics of Tanks 1 and 2 are described by the equations

$$V_1\frac{\text{d}{C}_1}{\mathrm{d}t}=Q{C}_0(t)-Q{C}_1(t)$$

and

$$V_2\frac{\text{d}{C}_2}{\mathrm{d}t}=Q{C}_1(t)-Q{C}_2(t).$$

Now, discretize both equations and substitute ${\tau }_i=\frac{V_i}{Q}$ :

$$\frac{{\tau }_1}{\mathrm{\Delta }t}\left(C_{1,t}-C_{1,t-\mathrm{\Delta }t}\right)=C_{0,t}-C_{1,t},$$

$$\frac{{\tau }_2}{\mathrm{\Delta }t}\left(C_{2,t}-C_{2,t-\mathrm{\Delta }t}\right)=C_{1,t}-C_{2,t},$$

which can be rearranged to obtain

$$C_{1,t}=\left(1-\frac{1}{1+\frac{\mathrm{\Delta }t}{{\tau }_1}}\right)C_{0,t}+\frac{1}{1+\frac{\mathrm{\Delta }t}{{\tau }_1}}{C}_{1,t-\mathrm{\Delta }t}$$

and

$$C_{2,t}=\left(1-\frac{1}{1+\frac{\mathrm{\Delta }t}{{\tau }_2}}\right)C_{1,t}+\frac{1}{1+\frac{\mathrm{\Delta }t}{{\tau }_2}}{C}_{2,t-\mathrm{\Delta }t},$$

respectively. Finally, substitute ${\rho }_i=\frac{1}{1+\frac{\mathrm{\Delta }t}{{\tau }_i}}$ :

$$\begin{array}{c}{C}_{1,t}=\left(1-{\rho }_1\right)C_{0,t}+{\rho }_1{C}_{1,t-\mathrm{\Delta }t}\\ C_{2,t}=\left(1-{\rho }_2\right)C_{1,t}+{\rho }_2{C}_{2,t-\mathrm{\Delta }t}\end{array}$$ (13)

The autocorrelations of C _1,t and C _2,t are ρ ₁ and ρ ₂, respectively. Each autocorrelation depends on the hydraulic residence time τ _i and the sampling interval Δt. Large residence times relative to short sampling intervals (τ ≫ Δt) are typical in process data. As a result, mill measurements tend to be highly autocorrelated (ρ _i ≈ 1). In the two tank system (Equation (13)), this causes the correlations between C _2,t and upstream measurements, C _0,t and C _1,t , to be small.

This suggests that, in practice, predictive models will benefit little from measurements upstream of units characterized by large residence times relative to the sampling interval. This does not imply that upstream properties are irrelevant: in the two-tank system, C ₀ determines C ₁ and C ₂. Rather, the observed correlation between downstream measurements and upstream disturbances depends on the magnitude of residence times as compared to the sampling interval.

As a result, the sampling interval is an important consideration when fitting models and identifying lags. If the interval is too large, the effects of autocorrelation would diminish, but relevant signal may go unseen. In contrast, if the interval is too small, the relevant signal may be buried in high-frequency noise. In this study, we used a sampling interval of 1 h, which aligns with suggestions by Box et al. (2015) and Ljung (1998) that sampling intervals for chemical processes should be on the order of hours. When a shorter sampling interval (30 min) or a longer one (4 h) was used, the identified ARX models for HHV and BPR produced unrealistic lags and failed to outperform the AR models. For viscosity, as with the 1 h sampling interval, ARX models underperformed the AR model. This highlights the importance of comparing the bivariate models and the univariate models on unseen test data as a final check. Additionally, a shorter sampling interval should be favoured. Since lags are estimated as a number of timesteps, a shorter sampling interval provides a more precise lag estimate.

5. Conclusions

Simple ARX models seem to capture process lags in the kraft recovery process. Here, we validated the use of ARX models to identify lags in a simulation of two tanks in series. Then, we fit ARX models to data from a North American mill, estimating the lagged effect of a change in species pulped on three as-fired liquor properties: HHV, viscosity, and BPR. The estimated lags for BPR (41 h) and as-fired HHV (49 h) agree with a detailed simulation of the mill and are close to the estimated hydraulic residence times through the same system. The effect of a change in digester grade on as-fired viscosity could not be identified and is suspected to be masked by noise. While the ARX models provide process insight, they provide marginal improvements over AR models and the persistence model for process prediction. This is likely due to the autocorrelation of mill measurements. We derive this result for the case of species concentration throughout two tanks in series. This suggests that, in practice, measurements upstream of units characterized by large residence times provide little benefit to predictive models.