Abstract
The core autocatalytic cycle of the formose reaction may be enhanced or eroded by the presence of simple molecules at life’s origin. Utilizing quantum chemistry, we calculate the thermodynamics and kinetics of reactions both within the core cycle and those that deplete the reactants and intermediates, such as the Cannizzaro reaction. We find that via disproportionation of aldehydes into carboxylic acids and alcohols, the Cannizzaro reaction furnishes simple catalysts for a variety of reactions. We also find that ammonia can catalyze both in-cycle and Cannizzaro reactions while hydrogen sulfide does not; both, however, play a role in sequestering reactants and intermediates in the web of potential reactions.
Keywords: origin of life, thermodynamics, kinetics, prebiotic chemistry, formose reaction, sugars
1. Introduction
It is curious that autocatalytic cycles are ubiquitous in living systems [1] but rare in benchtop chemistry. The oligomerization of formaldehyde (CH2O) into sugars via aldol reactions, known as the formose reaction, is one of the rare exceptions. Its mechanism was first elucidated in 1959 by Breslow [2], with an update in 2014 [3], and has been extensively studied for its potential in food production [4]. While often mentioned in origin-of-life chemistry as a “simple” route to ribose (and other sugars utilized in extant biochemistry), the formose reaction typically forms a complex and intractable mixture under (catalytic) alkaline conditions [5] with acids and alcohols produced via the competing Cannizzaro reaction.
Early prebiotic chemical syntheses focused on finding conditions to increase ribose selectivity; three examples are using phosphates [6], borate [7], or trying to find the best metal catalysts [8]. But more recently, the messiness of the formose reaction is embraced as a feature, not a bug. The Huck group systematically probed how environmental conditions affect the observed product distribution [9,10,11]. Paschek et al. investigated the effect of catalysts that might be present in carbonaceous chondrites [12], Omran considered chemical gardens resembling hydrothermal vents [13], Vinogradoff et al. utilized olivine silicate catalysts [14], and Haas et al. examined mechanochemical effects [15].
The formose reaction also caught the attention of computational modelers as a classic test case to examine chemical reaction networks. Examples include heuristics-aided quantum chemistry [16], graph-theoretical approaches coupled with quantum calculations [17], and utilizing machine learning on reaction-rule networks [18]. These large-scale studies took a bird’s-eye view, showcasing the complexity of the system with its myriad compounds, but do not focus on individual reactions or how molecules in the network may act recursively as catalysts. Our present work complements these approaches by examining in detail one small portion of the formose reaction—its smallest autocatalytic core. At this small yet focused scale, we previously generated a free energy map (thermodynamics and kinetics) of the uncatalyzed formose reaction [19]; our present work extends the earlier work by examining the effect of catalysts and exploring reactions that may sequester reactants and intermediates in the smallest autocatalytic cycle.
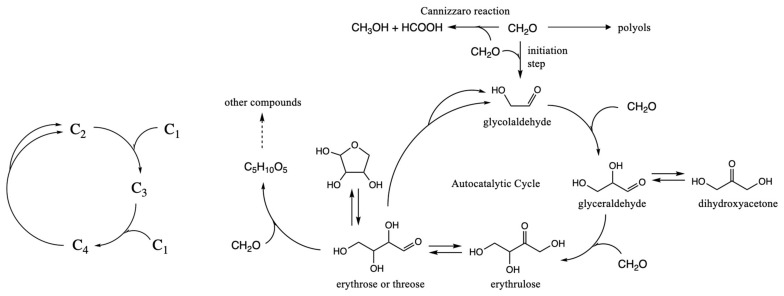
The smallest autocatalytic cycle of the formose reaction is shown in Figure 1. CH2O is the C1 “food” species. The linchpin C2 species is glycolaldehyde. C3 and C4 species can be produced via successive aldol addition of C1 food; larger sugars are also synthesized via this route. The key to autocatalysis is that C4 can undergo a retro-aldol reaction to produce two linchpin C2 species, thereby accelerating the consumption of C1 food with each successive turn of the cycle. In the formose reaction, myriad aldol condensations and retro-aldol reactions take place; for example, you could have C2 + C3 → C5 or C6 → C3 + C3, although a core autocatalytic cycle can be achieved with just C1 through C4 species.
Figure 1.
Core autocatalytic cycle of the formose reaction.
Several features of this core cycle deserve mention, and we will make reference to our earlier work [19] on the free energy map of the thermodynamics and (uncatalyzed) kinetics of these reactions. Forming the C2 linchpin directly from CH2O (the initiation step) is very challenging kinetically because, without an umpolung species, it is difficult to make C–C bonds; our previously calculated barrier is 45.3 kcal/mol. However, once a small amount of the C2 linchpin is formed, the direct dimerization is bypassed. Food is consumed via the much lower barrier C2 + C1 → C3 and C3 + C1 → C4 reactions. The retro-aldol C4 → C2 + C2 reaction regenerates (more) C2 and accelerates the consumption of C1. As the food supply dwindles, a wider variety of sugars in the C5 to C7 range are produced.
Off-cycle reactions can deplete the concentrations of the C1 to C4 species involved in the cycle. The Cannizzaro disproportionation reaction parasitizes the cycle by removing CH2O food, but by producing HCOOH, it may add a catalyst to enhance reaction rates within the cycle. (The C2, C3, and C4 sugars can also undergo Cannizzaro reactions.) All the aldehydes can form polyols by oligomerization reactions forming C–O bonds. This could sequester some of the reacting species, slowing down reactions in the cycle, but also reduce parasitic reactions and provide an equilibrating pool of reactants, thus lengthening the lifetime of autocatalytic cycles. Keto-enol isomerization reactions (e.g., glyceraldehyde to dihydroxyacetone for the C3 species) or ring closures (e.g., erythrose or threose for the C4 species) may play similar sequestering roles.
Our previous free energy map only considered uncatalyzed reactions in aqueous solution under neutral conditions. The present work considers whether other small molecules may act as catalysts to influence the kinetics or act as sequestering agents to influence the thermodynamics of the reactions involved in (or adjacent to) the core cycle. The small molecules being considered in this article are (1) the C1 products of the Cannizzaro reaction CH3OH and HCOOH; (2) small molecular acids that may be found in hydrothermal vent reactions, such as carbonic acid and acetic acid; and (3) small molecules that provide reduced nitrogen and sulfur, NH3 and H2S, that may have been present at life’s origin.
To keep this investigation tractable, there is much we excluded. The rich chemistry of HCN (and formamide) is the subject of a future paper. Cyanide provides an umpolung C1 reactant and combines readily with aldehydes, making C–C bonds, and the plethora of intermediates increases many-fold. HCN is also a “high energy” reactant compared to the carbon and nitrogen sources that are prebiotically plausible: CO2 and NH3. Our calculated free energy change for the reaction CO2 + NH3 + H2 → HCN + 2 H2O is +18 kcal/mol. (Carbon monoxide is also excluded in this study and may be considered a cyanide analog). We have also excluded ions because the results are less than satisfactory with our current computational protocol (see Section 2 below). Finally, we limit ourselves to just the C2 to C4 “sugars” in the smallest autocatalytic cycle, as shown in Figure 1.
This article is organized as follows: After describing our computational protocol and its limitations, the combined Results and Discussion section (Section 3) will go through each of the reactions relevant to Figure 1, starting with C1 and working our way through the C2, C3, and C4 reactions. Finally, we will consider sequestering the sugars by direct reaction with NH3 and H2S.
2. Computational Methods
Since we will be comparing our present calculations to our previous work, we apply the same computational protocol [19]. Here, we provide a brief description of that protocol for the convenience of our readers. Some of the text in this section is reproduced from our recent work on CHO systems published in this journal [20] since we think that description is both clear and succinct. Essentially, we calculate the free energies in an aqueous solution using quantum chemical methods, and our protocol shows suitable agreement with available experimental results for CHO systems [19,20,21,22]. Here are the computational details:
The geometry of each molecule is optimized, and its electronic energy is calculated at the B3LYP [23,24,25,26] in favor of density functional theory with the 6-311G** basis set. To maximize the probability of finding global minima, multiple conformers are generated using molecular mechanics (MMFFs force field [27]). The optimized structures are embedded in a Poisson–Boltzmann continuum to calculate the aqueous solvation contribution to the free energy. While this does not provide a specific concentration, it assumes a dilute solution such that the electrostatic field generated by a neighboring solute molecule is effectively screened by the water solvent. One can consider all solutes to have the same relative concentrations in our calculations. Zero-point energy corrections are included, and we apply the standard temperature-dependent enthalpy correction term (for 298.15 K) from statistical mechanics by assuming translational and rotational corrections are a constant times kT and that low-frequency vibrational modes generally cancel out when calculating enthalpy differences. So far, this is standard fare.
However, entropic corrections in aqueous solution are problematic [28,29,30]. Changes in free energy terms for translation and rotation are poorly defined in solution due to restricted complex motion, particularly as the size of the molecule increases (thus increasing its conformational entropy). Free energy corrections come from two different sources: thermal corrections and implicit solvent. Neither of these parameters is easily separable, nor do they constitute all the required parts of the free energy. We follow the approach of Deubel and Lau [31], assigning the solvation entropy of each species as half its gas-phase entropy (calculated using standard statistical mechanics approximations similar to the enthalpy calculations described above), based on proposals by Wertz [32] and Abraham [33] that upon dissolving in water, molecules lose a constant fraction (~0.5) of their entropy.
To estimate activation energies, transition states were optimized by including several explicit water and/or catalytic molecules to aid in transferring H moieties. All calculated transition states have one significant negative eigenvalue corresponding to the reaction coordinate (eigenvector) involving bond breaking/forming. Several conformers are tested in each case, and we only report the lowest calculated barriers.
When put to the test by first calculating the equilibrium concentrations in a self-oligomerizing solution of 1 M glycolaldehyde at 298 K, our protocol fared very well compared to subsequent NMR measurements [22]. Our relative Gibbs free energies in aqueous solution are typically within 0.5 kcal/mol compared to experimental results. That being said, our protocol did show systematic errors of 2–3 kcal/mol when calculating barriers involving carbonyl chemistry when compared to experimental results. Going to a higher level of theory does not reduce this error [34]. For the few SN2 reactions we considered, having to daisy chain an additional 3–4 water molecules to facilitate proton transfer results in barriers that may be up to 10 kcal/mol too high, consistent with our previous work [19,35]. Using carboxylate anions with diffuse functions to represent weak acids gives poorer results compared to keeping the COOH group neutral [20]. Our previous attempts to incorporate H3O+ (and its larger cousins) as catalysts also gave unrealistic barriers and structures, with transition states quickly falling into local minima [36]. We have also attempted using Group I or Group II metal cations in conjunction with hydroxide as catalysts (unpublished results) that run into similar issues.
Quantum chemistry is about error cancellation, and our protocol (with its foibles, including the simplistic entropy correction) has worked well even with this systematic error for activation barriers. Thus, we do well on thermodynamics and just okay on kinetics (but at least we are in the ballpark for the majority of the carbonyl chemistry and aldol reactions in this work), and we want to be very clear about both the opportunities and the limitations of our protocol in this brief description.
3. Results and Discussion
Throughout this paper, for the thermodynamics of a chemical reaction, the reaction free energy will be designated ΔG. For a transition state, kinetic barriers will be designated ΔG‡ and will typically refer to the forward direction. From the ΔG and ΔG‡ values for the forward reaction, the thermodynamics and kinetics of the reverse reaction can be easily ascertained. All numerical values are in kcal/mol, abbreviated as kcal. In each subsection, we begin with the uncatalyzed reaction (water may facilitate proton transfer) before examining the inclusion of a potential catalyst. The potential catalysts in this study are NH3, H2S, methanediol (the hydrated form of CH2O, which is dominant in aqueous solution), the C1 Cannizzaro products CH3OH and HCOOH, along with three other acids (carbonic, acetic, and glycolic) that are likely to be present in prebiotic systems.
3.1. Formaldehyde Hydration
As the main “food” species, CH2O in aqueous solution is typically hydrated and exists primarily as methanediol, CH2(OH)2. The reaction is as follows:
| CH2O + H2O → CH2(OH)2 ΔG = −4.6 kcal |
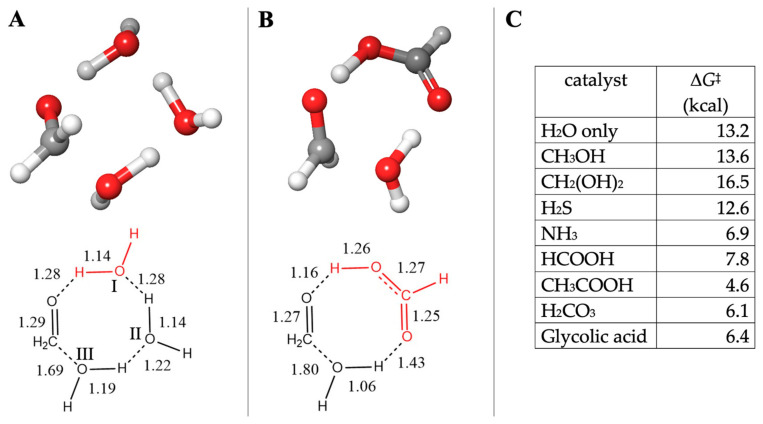
The optimal uncatalyzed transition state includes two additional explicit water molecules forming an eight-center transition state, as shown in Figure 2A; the barrier ΔG‡ is 13.2 kcal. The reactant water molecule is labeled III, and the additional water molecules are labeled I and II. Both our ΔG and ΔG‡ values are in good agreement with experimental results, as discussed in our previous work [19].
Figure 2.
Transition state structures (A,B) and barriers (C) for formaldehyde hydration.
To investigate if prebiotically plausible small molecules potentially present in the solution can catalyze this reaction, we replace the water molecule I with CH3OH, CH2(OH)2, NH3, or H2S. (Replacing the water molecule II is either less or equally favorable.) Or we can replace both water molecules I and II with a carboxylic acid moiety, as shown in Figure 2B with formic acid. This optimal transition state structure is geometrically similar to the eight-center water-only transition state in Figure 2A, but there are some notable differences in the bond distances. The acidic proton of HCOOH is 1.16 Å to the carbonyl-O, while the corresponding distance is 1.28 Å for the uncatalyzed reaction. The hydrating water molecule has a longer C…O distance of 1.80 Å instead of 1.69 Å in the water-only transition state. These are consistent with an acid-catalyzed mechanism where the proton transfer proceeds ahead of the nucleophilic addition of the reactant water to CH2O.
From the table in Figure 2C, we see that CH3OH, CH2(OH)2, and H2S have no catalytic efficacy for formaldehyde hydration. The barriers are either similar to or greater than the uncatalyzed ΔG‡ of 13.2 kcal. As a proton transfer agent, NH3 substantially reduces the barrier. For the four carboxylic acids tested, the barrier is approximately halved. This fits well with NMR studies on the hydration and dehydration of formaldehyde [37], where the observed exchange rate constants (kex = khyd + kdehyd) were ~16 s−1 at pH 7.4 and range from ~4 s−1 in the pH 3–6 range (barriers are not provided in that work, but since ln 16 = 2.77 and ln 4 = 1.39, one might surmise that the barrier is approximately half in the acidic pH range). The order of our calculated ΔG‡ for the acids is likely not significant, given the computational error, and our later results will see some swaps in the order. Thus, we cannot relate the pKa or an acid to its catalytic ability in this reaction. (The NMR results also do not show much distinction in the pH 3–6 range.)
Our results are consistent with experimental observations that under neutral or acidic conditions, in addition to CH2(OH)2, formaldehyde can oligomerize via C–O bond formation to form acetals, hemiacetals, and oxane rings [4] at higher concentrations of CH2O. This begins with the dimerization of formaldehyde to form the hemiacetal.
| CH2O + CH2(OH)2 → HOCH2OCH2OH ΔG = −4.0 kcal |
But since this is slightly less exergonic than formaldehyde hydration, at least under the “dilute” conditions of our computational protocol, the equilibrium will favor monomers, and the dimerization of CH2(OH)2 would be marginally endergonic.
| 2 CH2(OH)2 → HOCH2OCH2OH + H2O ΔG = +1.2 kcal |
The formation of the six-membered trioxane (CH2O)3 and larger oxane rings is also endergonic relative to monomeric aqueous CH2(OH)2, as shown in our previous work [19].
In commercial use, methanol is typically added to aqueous formaldehyde solutions to prevent higher oligomers from forming. From our calculations,
| CH2(OH)2 + CH3OH → CH3OCH2OH + H2O ΔG = −1.4 kcal |
| CH3OCH2OH + CH3OH → CH3OCH2OCH3 + H2O ΔG = −1.4 kcal |
and thus, methanol acts as a capping group by favorably forming acetals. This suggests that the effective concentration of formaldehyde in aqueous solution can be lowered when a sequestering agent such as CH3OH is present. Since CH3OH is produced in the Cannizzaro reaction (see next subsection), we expect it to be present in prebiotic mixtures containing CH2O. We will consider the sequestering of the aldehydes in more detail later in this article.
3.2. The C1 Cannizzaro Reaction
Formaldehyde can disproportionate into methanol and formic acid. The reaction is thermodynamically favorable and catalyzed under alkaline conditions [5].
| CH2O + CH2(OH)2 → HCOOH + CH3OH ΔG = −19.6 kcal |
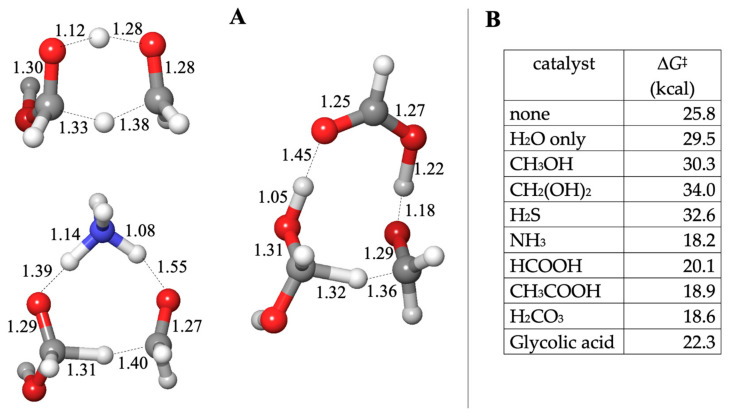
The lowest energy transition state had an uncatalyzed barrier of ΔG‡ = 25.8 kcal and did not require additional explicit water molecules (adding them increased ΔG‡). The hydride is transferred directly between the two carbons as the proton hops between the oxygens, as shown in Figure 3A. A catalyst molecule can be added in two possible positions: between the two carbons to facilitate the hydride transfer or between the carbonyl-O of CH2O and the hydroxyl of CH2(OH)2 to facilitate proton transfer. In all cases, the latter situation was favored.
Figure 3.
Transition state structures (A) and barriers (B) for the C1 Cannizzaro reaction.
Our calculated ΔG‡ values are shown in Figure 3B. Once again, we find that alcohols and H2S do not catalyze the reaction; the barriers are in the 30–34 kcal range (similar to adding one explicit water molecule where ΔG‡ is 29.5 kcal). The carboxylic acids and NH3 lower the barrier by 4–8 kcal, a similar range to what we found in formaldehyde hydration. When NH3 is a catalyst, the bond distances suggest that it abstracts a proton from CH2(OH)2 early in the process (the O…H distance is 1.39 Å while the forming N–H bond has already shortened to 1.14 Å). The hydride is being transferred (C…H distances of 1.31 and 1.40 Å), but no proton transfer is yet observed from NH3 to the carbonyl-O of CH2O. This mimics a base-catalyzed reaction. It also suggests that one way to get around the difficulty of explicitly including hydroxide (in an anionic transition state) is to utilize NH3 as a proxy.
The structure with HCOOH is interesting. The hydride is being transferred (C…H distances of 1.32 and 1.36 Å) in concert with the proton transfer between HCOOH and CH2O (O…H distances of 1.22 and 1.18 Å). The abstraction of the proton from CH2(OH)2 is only barely beginning (the O–H bond has only marginally lengthened to 1.05 Å). Is this an acid-catalyzed reaction? Probably not; it looks mostly like the water-only transition state, except that HCOOH facilitates the process and lowers ΔG‡. This illustrates why we should be cautious in interpreting our transition states and barriers. Molecular HCOOH acts as a proxy catalyst by lowering the barrier, but this does not imply an acid-catalyzed reaction. While Cannizzaro reactions are catalyzed by a strong base, we have not found any reference to acid catalysis, although we find one reference of the uncatalyzed reaction in aqueous solution proceeding at high temperature and high pressure [38].
In a buffered pH of ~7, NH3 exists primarily as ammonium, and HCOOH is in its carboxylate form in solution. Thus, we emphasize that in our calculations, molecular NH3 and HCOOH are acting as proxy catalysts. If there was a microenvironment in which the reactants and our neutral molecular “catalysts” are present, and they collide in the right orientation with sufficient energy, then the barrier might be lower in that instance. But in bulk quantities in an actual experiment at a particular pH, these specific molecules might not be catalytic. Thus, looking at transition state structures is important; only then can we see that HCOOH is acting as a proxy for an acid-catalyst in formaldehyde hydration but not in the Cannizzaro reaction. Conversely, NH3 is acting as a proxy for a base-catalyst in the Cannizzaro reaction but not in formaldehyde hydration. Both molecules lead to lowered ΔG‡ in both reactions. We will revisit this issue in our concluding remarks.
3.3. Glycolaldehyde Reactions: Enolization, Aldol, Hydration, and Cannizzaro Reactions
Glycolaldehyde is the linchpin molecule of the smallest autocatalytic cycle in the formose reaction. Access to larger sugars comes from the feasibility of aldol additions; thus, the simplest aldol addition involves glycolaldehyde reacting with formaldehyde to form the C3 sugar glyceraldehyde. We will only consider the formation of D-glyceraldehyde. Its mirror image would have the same free energy; thus, the thermodynamics do not change (and we expect equal amounts of D and L sugars to be formed in this scenario, as observed experimentally in the formose reaction if no chiral catalysts are added). Transition states for aldol addition to form the enantiomers are also mirror images, so the barriers should also be equal. The aldol addition is feasible because glycolaldehyde is enolizable. Thus, we first examine the enolization reaction.
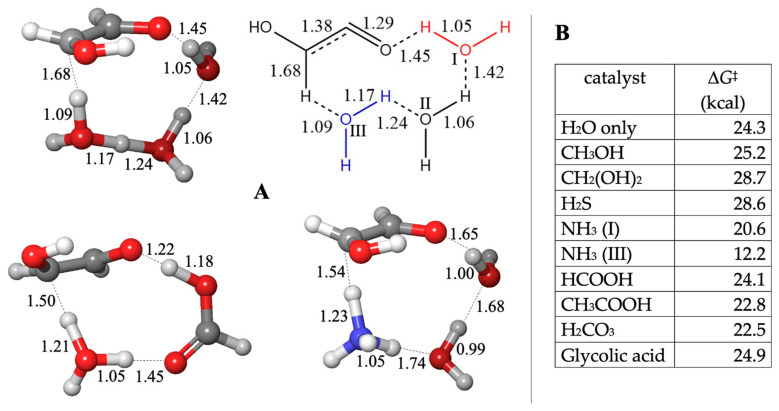
The enolization reaction has ΔG = +6.8 kcal, and the uncatalyzed barrier is 24.3 kcal. As shown in Figure 4A, the optimal 10-center transition state utilizes three water molecules. The C–H bond breaks first (C…H is 1.68 Å), and the waters at positions II and III resemble a H5O2+ moiety. At the other end (involving water at position I), the O…H is just starting to form at 1.45 Å. Placing the alcohols and H2S in position I gives the lowest barriers, but just like before, these have higher ΔG‡, as shown in Figure 4B. The optimal position for carboxylic acids is to replace waters II and III. The C–H bond has not stretched as far (at 1.50 Å), while at the other end, the proton transfer is midway (O…H distances are 1.22 and 1.18 Å). The ΔG‡ values are similar to the water case. If NH3 replaced water in position I, the results are similar (with a marginally lower ΔG‡), but the barrier is significantly lowered (to 12.2 kcal) if NH3 is in position III. The C…H distance is 1.54 Å, and it looks like NH3 has mostly abstracted the hydrogen but not yet relayed it through the hydrogen bond network.
Figure 4.
Transition state structures (A) and barriers (B) for the C1 + C2 → C3 aldol reaction.
In the aldol addition, CH2O adds to the enol of glycolaldehyde, forming a C–C bond. The product formed is glyceraldehyde. Since the enol is a transient species, our ΔG and ΔG‡ values for the reaction are with reference to the aldehydes.
| CH2O + C2H4O2 → C3H6O3 ΔG = −9.4 kcal |
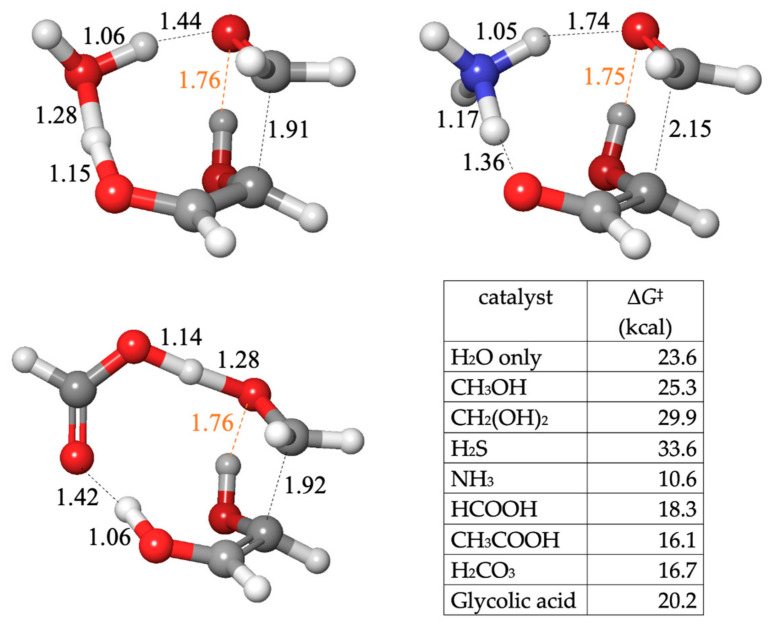
The reaction is exergonic and remains so even if applied to the aldehyde-hydrates. Unlike the thermodynamic reversibility of oligomers forming and breaking C–O bonds, the equilibrium clearly favors C–C bond formation, as analyzed in our previous work [19]. As to the kinetics, our calculations yield ΔG‡ = 23.6 kcal for the uncatalyzed reaction. As shown in Figure 5, the forming C…C distance is 1.91 Å. The proton transfer distances are similar to what we observed in previous reactions. There is a hydrogen bond (dashed orange line) that does not directly participate in bond breaking/forming.
Figure 5.
Transition state structures and barriers for the C1 + C2 → C3 aldol reaction.
Similar to previous cases, the alcohols and H2S have either similar or higher barriers. The carboxylic acids have ΔG‡ values in the 16–20 kcal range. From Figure 5 (HCOOH), the C…C distance is similar, while the O…H distances favor proton transfer from the acid to CH2O over the enol-to-carbonyl proton transfer. The base-catalyzed features are more apparent with NH3 (with a very low barrier of 10.6 kcal): A proton is pulled early from the enol to form the enolate while the C…C forming bond is more distant at 2.15 Å. The NH4+ moiety has not begun to transfer a proton back to CH2O (the H…O distance is 1.74 Å). As we saw in the Cannizzaro reaction, NH3 acts as an effective proxy for base-catalyzed mechanisms.
At this point, we have considered four distinct reaction mechanisms: C–O bond formation (hydration), C–C bond formation (aldol), non-redox H-shifts via enolization, and redox H-shifts in the Cannizzaro disproportionation. Because the remaining reactions in this paper will recapitulate similar transition states, we will focus our attention mainly on NH3 and HCOOH as proxy catalysts and compare these to only having water molecules as a proton shuttle.
Glycolaldehyde hydration is similar to formaldehyde hydration, except the thermodynamics are less favorable. Our calculated ΔG for hydration is +0.5 kcal. This may seem surprising because one might expect hydration to be favored and for the reaction to be exergonic in a dilute solution. Indeed, if we include concentration corrections for a 1 M aqueous solution of glycolaldehyde, equilibrium slightly favors the hydrate. We have extensively analyzed the oligomers of glycolaldehyde in solution, and our computational protocol is in excellent agreement with NMR measurements [22], but in that paper, we also discuss why reporting concentration-corrected ΔG values can be misleading in a messy system where the concentrations of different reactants, intermediates, and products can range over many orders of magnitude. Thus, in this work (and in our previous free energy maps), we report our ΔG values without concentration corrections. Our uncorrected values provide a baseline for subsequent kinetic simulations that are beyond the scope of the present work. In our previous work, the barrier for glycolaldehyde hydration was 16.1 kcal, in good agreement with experimental results [22]. In the present work, HCOOH lowers the barrier to 11.0 kcal, while NH3 lowers it to 10.1 kcal. This is similar to what we found for CH2O hydration discussed earlier.
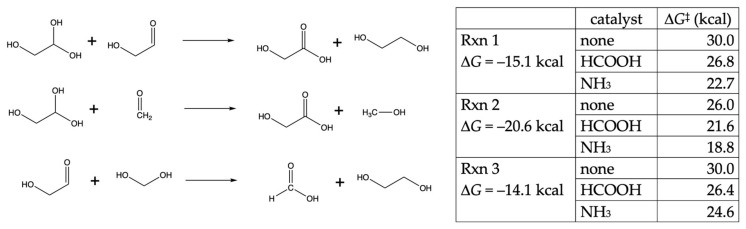
Similar to formaldehyde, glycolaldehyde can also participate in Cannizzaro reactions. These may be self-disproportionation reactions (Rxn 1 in Figure 6), although more likely to be cross-Cannizzaro reactions between a C1 and C2 species (Rxn 2 and Rxn 3 in Figure 6) since formaldehyde (and its hydrate) is likely to be found in higher concentrations in the early stages of the formose reaction. The ΔG and ΔG‡ values of Rxn 2 are similar to the C1 Cannizzaro reaction discussed previously. The ΔG and ΔG‡ values of Rxn 1 and Rxn 3 are similar but ~4–6 kcal higher than Rxn 2.
Figure 6.
Cannizzaro reactions of glycolaldehyde.
These results are not surprising from our thermodynamic map of CHO compounds [20]. Essentially, the reaction exergonicity is driven by the relative stability of CH2O to CH3OH (18 kcal) versus the relative stability of glycolaldehyde to ethylene glycol (13 kcal). Since the transition states are similar, Hammond’s postulate suggests we will see similar differences in the barriers. Our results do imply that once the C1 food runs out, Cannizzaro reactions are less favored in the larger species; similar to the C2 case, the relative stability is ~14 kcal in both the C3 (glycolaldehyde to glycerol) and C4 cases (erythrose to erythritol). Thus, reduction of the C1 species (CH2O to CH3OH) is favored in the cross-Cannizzaro.
3.4. Glyceraldehyde Reactions: Isomerization and Aldol Addition
Glyceraldehyde favorably isomerizes into dihydroxyacetone in aqueous solution. Our calculated ΔG for the reaction is −3.5 kcal, and the uncatalyzed barrier is 24.8 kcal (very similar to the 24.3 kcal enolization barrier for glycolaldehyde). The isomerization is a two-step reaction going through an enol intermediate. Figure 7 shows the ΔG and ΔG‡ values for enol formation. Since dihydroxyacetone is more stable than glyceraldehyde, these values are 3.0–3.5 kcal higher starting from dihydroxyacetone. The enolization barriers of glyceraldehyde with HCOOH and NH3 are very similar to those for glycolaldehyde, as expected, since the transition states are structurally similar. Uncatalyzed, the isomerization is relatively slow, but lower barriers with the proxy catalyst NH3 allow for more rapid interconversion. Dihydroxyacetone could be one way to sequester glyceraldehyde.
Figure 7.
Enolization of glyceraldehyde and dihydroxyacetone. ΔG and ΔG‡ values in kcal.
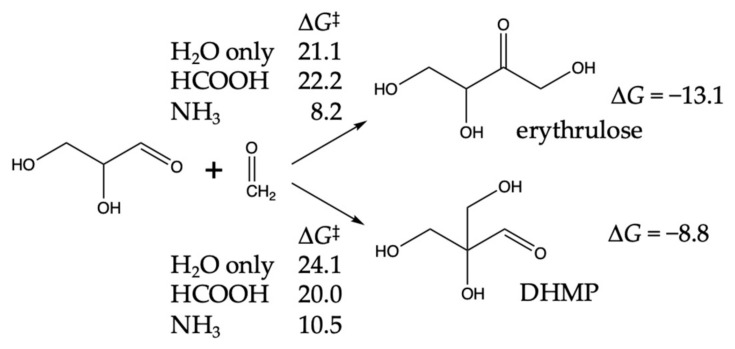
For the C3 + C1 → C4 aldol addition, we had previously determined [19] that the path to forming the ketone erythrulose had lower (uncatalyzed) barriers compared to forming the aldehydes, erythrose, or threose. However, we had not considered the formation of a branched tetrose 2,3-dihydroxy-2-(hydroxymethyl)propanal, which we will refer to as DHMP. Our results are shown in Figure 8.
Figure 8.
C3 + C1 → C4 aldol addition. ΔG and ΔG‡ values in kcal.
For erythrulose formation, ΔG for the reaction is −13.1 kcal. While this is 4 kcal more exergonic than C2 + C1 → glyceraldehyde, it is because erythrulose is more stable than its aldehyde counterparts erythrose and threose by 4.2 and 3.5 kcal, respectively. The water-only barrier is 21.1 kcal, or 3.3 kcal lower than C2 + C1 → glyceraldehyde. While we expected the barrier with the HCOOH proxy catalyst to be lower than 21 kcal, this was not the case even after trying multiple conformations. (We did find a lower barrier with CH3COOH.) The barrier with the NH3 proxy catalyst is lowered by 13 kcal, a similar magnitude compared to C2 + C1 → glyceraldehyde.
DHMP formation is less exergonic. Steric hindrance destabilizes DHMP by ~1 kcal compared to its unbranched counterparts, erythrose and threose. The barriers for water-only, HCOOH, and NH3 closely matched what we found for C2 + C1 → glyceraldehyde.
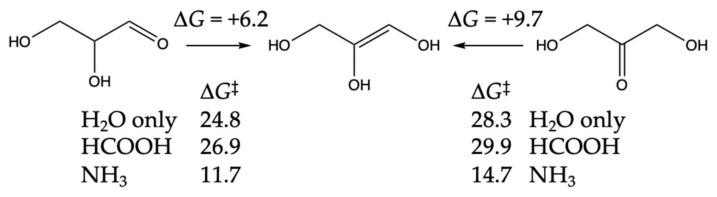
Since glyceraldehyde can either convert into dihydroxyacetone or undergo aldol addition with CH2O to form erythrulose, and in both cases, our transition states go through the C3 enediol intermediate, there is competition between the two reactions. The aldol addition is thermodynamically favored with ΔG = −13.1 kcal compared to the isomerization with ΔG = −3.5 kcal (uphill 6.2 to the enediol, then downhill 9.7 to the ketone). The aldol reaction is also kinetically favored. From the enediol, the water-only aldol addition has ΔG‡ = 21.1 − 6.2 = 14.9 kcal, while the enol-to-keto isomerization has ΔG‡ = 28.3 − 9.7 = 18.6 kcal. Thus, we would expect aldol addition to outcompete enol-to-keto isomerization when CH2O is plentiful. (NH3 lowers the barriers for both reactions by similar amounts; thus, aldol addition is still favored.) This fits with what Appayee and Breslow found in their follow-up experiments [3] prompted by work in Benner’s group [39]; at higher concentrations of CH2O, hardly any dihydroxyacetone is observed, but at lower concentrations, enolization can come into play.
Additionally, Appayee and Breslow [3] proposed a 1,2-hydride shift for the isomerization of glyceraldehyde to dihydroxyacetone based on deuterium labeling experiments. According to their mechanism, this conversion is catalyzed by Ca2+ and hydroxide ions. Because our protocol is limited to neutral species (as discussed in Section 2), we can only investigate this with neutral molecule catalysts. The optimal transition state has one mediating water molecule between the oxygens, as shown in Figure 9. The proton from the 2-hydroxy group has been mostly transferred (H…O is 1.49 Å), while the middle C…H (at 1.24 Å) is only just starting to break. This is somewhat analogous to Appayee and Breslow’s proposed mechanism, where deprotonation takes place before the deuterium transfer. However, our calculated ΔG‡ is 30.0 kcal, which is higher than enolization. Adding HCOOH or NH3 in place of the mediating water molecule does not lower the calculated barrier.
Figure 9.
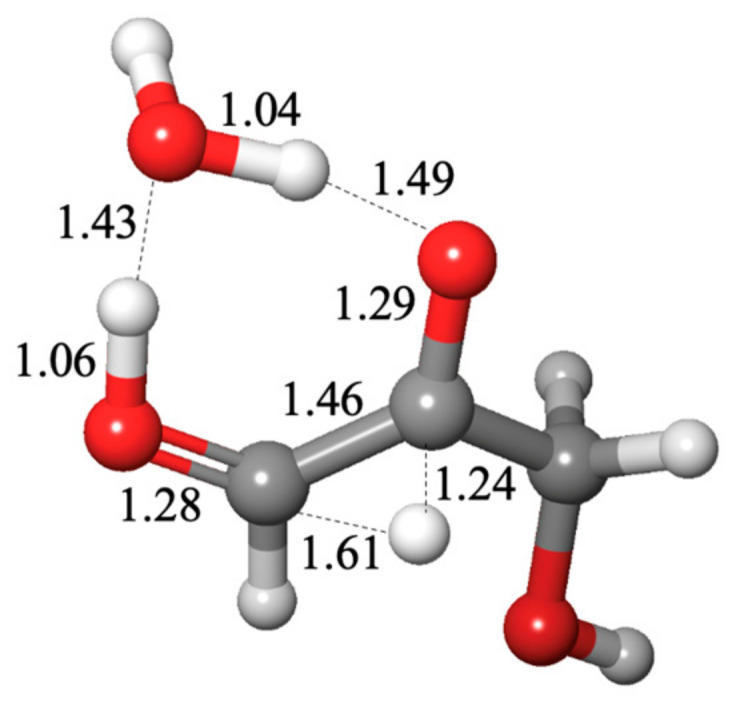
Transition state of 1,2-hydride shift for glyceraldehyde-dihydroxyacetone isomerization.
Because our calculations do not mimic the most productive experimental formose reaction conditions for sugar synthesis (high pH, the presence of divalent metal ions or borate, higher temperatures, and reactant concentrations), they limit the mechanisms we can explore, and we cannot always make direct comparisons to experimental results. However, our consistent protocol allows us to peg the energies of the myriad compounds that may show up in a messy prebiotic mixture. This approach has allowed us to generate a series of intersecting free energy maps under a set of baseline conditions for a wide range of prebiotic systems. And while our protocol has its limitations, we have some confidence that our calculated free energies are reasonable and can be validated, as discussed in Section 2.
3.5. Tetrose Reactions: Isomerization, Ring Closure, and Retro-Aldol Splitting
While erythrulose is the most stable of the tetrose sugars, it does not easily undergo retro-aldol splitting to form glycolaldehyde. The key step of re-forming the C2 linchpin facilitates autocatalysis in the formose reaction. Instead, it is the aldehyde that more favorably undergoes the retro-aldol reaction; thus, erythrulose has to first isomerize into erythrose or threose. For the enolization of erythrulose, we calculate ΔG to be +9.7 kcal, essentially matching the enolization of its C3 counterpart, dihydroxyacetone. The barriers are also similar: ΔG‡ values are 29.4, 28.7, and 13.0 kcal for the water-only, HCOOH, and NH3 proxy catalysts. (See Figure 7 for the counterpart C3 values).
The linear C4 aldehydes can potentially be sequestered by ring closure reactions and thus less susceptible to retro-aldol reactions. We previously calculated the free energy changes for both D-erythrose and D-threose into their α- and β-furanoses [19]; the linear tetroses and their furanoses are 1 kcal or less apart, so we expect both to be present at equilibrium. Since ring closure and opening resemble hydration and dehydration, it is not surprising that the barriers are similar in magnitude.
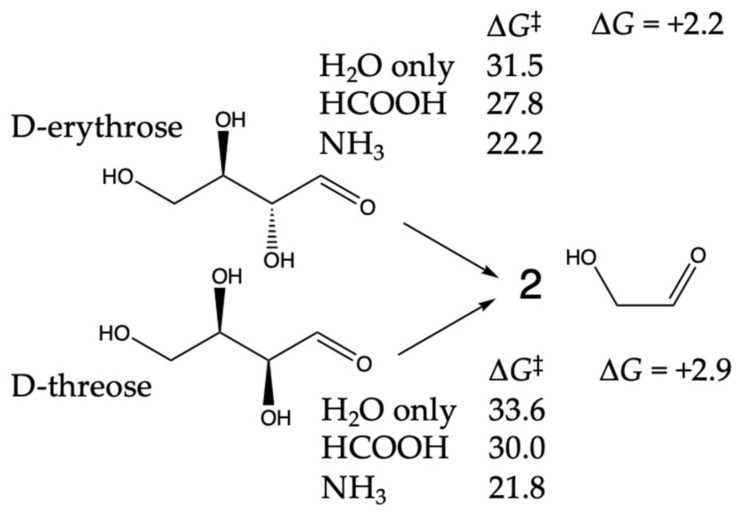
We had not considered the retro-aldol C4 → C2 + C2 in our previous work, so we will examine it more carefully here. Our results are shown in Figure 10. The retro-aldol splitting is marginally endergonic. Since D-threose is more stable than D-erythrose by 0.7 kcal, the retro-aldol of D-threose is 0.7 kcal more endergonic, and its corresponding barriers are also marginally higher. At over 30 kcal/mol for the water-only barriers, the uncatalyzed retro-aldol is expected to be quite slow at room temperature. HCOOH and NH3 proxy catalysts lower ΔG‡, but these values are still over 20 kcal/mol. It is not surprising that the retro-aldol (being endergonic) has higher barriers than the (exergonic) aldol additions.
Figure 10.
C4 → C2 + C2 retro-aldol splitting. ΔG and ΔG‡ values in kcal.
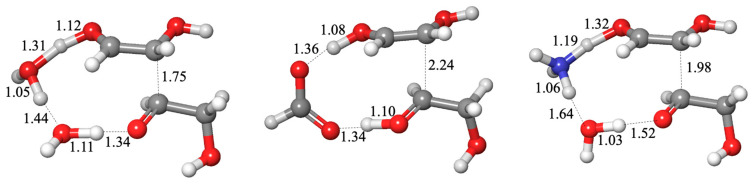
The three retro-aldol transition states for D-erythrose are shown in Figure 11. For water-only, the breaking C–C bond at 1.75 Å has not extended very far, while the O…H distances suggest that the proton hops between water and erythrose have proceeded substantially. For HCOOH, the acid proton has mostly hopped to the aldehyde carbonyl (O–H is 1.08 Å), and the breaking C–C bond is substantially longer at 2.24 Å. For NH3, the aldehyde carbonyl is starting to grab a proton (O…H is 1.32 Å), and that is because NH3 has already grabbed a proton (N–H is 1.06 Å) from the neighboring water, which has also grabbed its proton (O–H is 1.03 Å) from the alcohol group on erythrose.
Figure 11.
Transition state structures for retro-aldol splitting.
3.6. Sequestering and Parasitic Reactions
Earlier, we discussed how CH3OH, produced in the C1 Cannizzaro reaction, could sequester CH2O via acetal formation. In this section, we examine possible reactions that may either sequester or remove “food” or intermediates from the smallest autocatalytic cycle. Most of our analysis will focus on the C1 compounds, and we will discuss extrapolations to the C2, C3, and C4 sugars in the cycle.
We saw earlier that the addition of water to CH2O to form the hydrate CH2(OH)2 was exergonic 4.6 kcal with a barrier of 13.2 kcal. What if instead of acting as proxy catalysts, NH3 or H2S could add to CH2O in a similar way? (The transition states both include two additional water molecules facilitating proton transfer.)
| CH2O + NH3 → CH2(OH)(NH2) ΔG = −4.6 kcal ΔG‡ = 3.9 kcal |
| CH2O + H2S → CH2(OH)(SH) ΔG = −3.9 kcal ΔG‡ = 12.1 kcal |
Both reactions are exergonic. CH2(OH)(NH2) is similar in relative energy to the hydrate, while CH2(OH)(SH) is higher by 0.7 kcal. Since the barrier for NH3 addition is significantly lower in the presence of NH3, we expect NH3 to favorably react with aldehydes if present in the solution. H2S is marginally disfavored and, unless present in high concentration, is less likely to be found added to CH2O. The dominant species in aqueous solution is still CH2(OH)2.
Since CH3OH may be generated from Cannizzaro reactions, NH3 and H2S could potentially act as attacking nucleophiles in an SN2 reaction.
| CH3OH + NH3 → CH3NH2 + H2O ΔG = −2.8 kcal ΔG‡ = 32.2 kcal |
| CH3OH + H2S → CH3SH + H2O ΔG = −8.1 kcal ΔG‡ = 20.6 kcal |
Both reactions are exergonic, but the barriers are higher. Recall from Section 2 that our SN2 transition states require a daisy chain of 3–4 additional water molecules, and in our experience, our calculated barriers are artificially high. (We calculate ΔG‡ = 43.3 kcal for the self-barrier for CH3OH + H2O.) In a dilute aqueous solution, the equilibrium may shift toward hydrolyzing CH3NH2, but the exergonicity of CH3SH formation suggests that it might persist in solution as a potential reactant. The lower ΔG‡ for H2S addition suggests that CH3SH formation might be quite facile in a messy formose system spiked with H2S.
Since HCOOH may also be present from Cannizzaro reactions, nucleophilic addition of NH3, H2S, and CH3OH (with subsequent elimination of water as a leaving group) could respectively lead to amides, thioacids, and esters. (Since this is a two-step reaction, we report ΔG‡ for the rate-determining step.)
| HCOOH + NH3 → HC(O)NH2 + H2O ΔG = –5.4 kcal ΔG‡ = 24.1 kcal |
| HCOOH + H2S → HC(O)SH + H2O ΔG = +10.0 kcal ΔG‡ = 33.1 kcal |
| HCOOH + CH3OH → HCO2CH3 + H2O ΔG = –0.4 kcal ΔG‡ = 26.3 kcal |
Amide formation is exergonic, as expected, and the barrier is moderate. Once amides are formed, their hydrolysis (with a barrier of ~30 kcal) is slower. Formamide, the C1 product of this reaction, is prominent in prebiotic chemistry scenarios [40,41]. We have previously computed the route to formamide via the hydrolysis of HCN, which is more exergonic but has a higher barrier [42]. On the other hand, forming the thioacid is rather endergonic, and this contributes to its higher barrier. From our recent work mapping the free energies of small CHOS compounds [43], we find that thioester formation is less endergonic (6–7 kcal), and thus, coupled with the stability of CH3SH as a reactant, a feasible route to thioesters may be envisioned. With regard to ester formation, our calculated ΔG close to zero suggests that in a relatively dilute aqueous solution, the equilibrium favors hydrolysis.
While C1 food is plentiful, the possible presence of CH2(OH)(NH2) and CH2(OH)(SH) in solution opens up the possibility of additional Cannizzaro reactions from the favorable reduction in CH2O to CH3OH.
| CH2O + CH2(OH)(NH2) → HC(O)NH2 + CH3OH ΔG = –25.0 kcal ΔG‡ = 23.3 kcal |
| CH2O + CH2(OH)(SH) → HC(O)SH + CH3OH ΔG = –10.2 kcal ΔG‡ = 28.9 kcal |
In this third route to formamide, the reaction exergonicity doubly benefits from the stability of the amide and the reduction to CH3OH. The barrier is similar to the self-disproportionation of formaldehyde and its hydrate, which was reported earlier. Unlike the aforementioned route to the thioacid, the Cannizzaro reaction, in this case, is exergonic, although it also has a high barrier. (This suggests a promising route for thioester formation, and we are generating several energy maps utilizing CH3SH as a reactant and expect to present those results in our next publication.)
Looking at this small subset of reactions suggests that the possibilities multiply exponentially as we go beyond C1 compounds. For the C2 compounds, besides glycolaldehyde and its hydrate, we might see glycolic acid and ethylene glycol as first-order Cannizzaro products, but subsequent redox reactions might lead to acetic acid and ethanol. All these compounds can react with each other (and with NH3, H2S, CH3NH2, CH3SH, etc.), leading to a plethora of compounds—a very messy system! We expect to pursue some of the promising reactions in the near future, but since we have been examining the smallest autocatalytic cycle, we close this section by presenting our results on the thermodynamics for adding water, NH3, and H2S to the carbonyl group of the C2, C3, and C4 sugars.
The results in Table 1 suggest that reaction with NH3 can potentially sequester the aldehydes, but the reaction is reversible, and the barriers are likely to be very low (as we saw for NH3 adding to CH2O). H2S is less effective as a sequestering agent. For the ketones, the addition reactions are all endergonic, and we do not expect sequestration to be a factor. If the aldehyde-NH3 adducts subsequently participate in exergonic Cannizzaro reactions, these are unlikely to be reversible and, therefore, parasitic on the cycle. While the barriers are expected to be significant (23 kcal in the case of C1), they are not insurmountable at moderate to higher temperatures.
Table 1.
Thermodynamics of addition reactions to sugar carbonyls.
| Sugar | Added Molecule | ΔG (kcal) |
|---|---|---|
| Glycolaldehyde | H2O | +0.4 |
| NH3 | −0.4 | |
| H2S | +2.6 | |
| Glyceraldehyde | H2O | −0.1 |
| NH3 | 0.0 | |
| H2S | +2.2 | |
| Dihydroxyacetone | H2O | +2.6 |
| NH3 | +3.7 | |
| H2S | +7.2 | |
| Erythrose | H2O | −0.4 |
| NH3 | −0.7 | |
| H2S | +2.8 | |
| Threose | H2O | +1.1 |
| NH3 | +0.1 | |
| H2S | +3.5 | |
| Erythrulose | H2O | +3.8 |
| NH3 | +2.8 | |
| H2S | +6.0 |
4. Overall Free Energy Map and Concluding Remarks
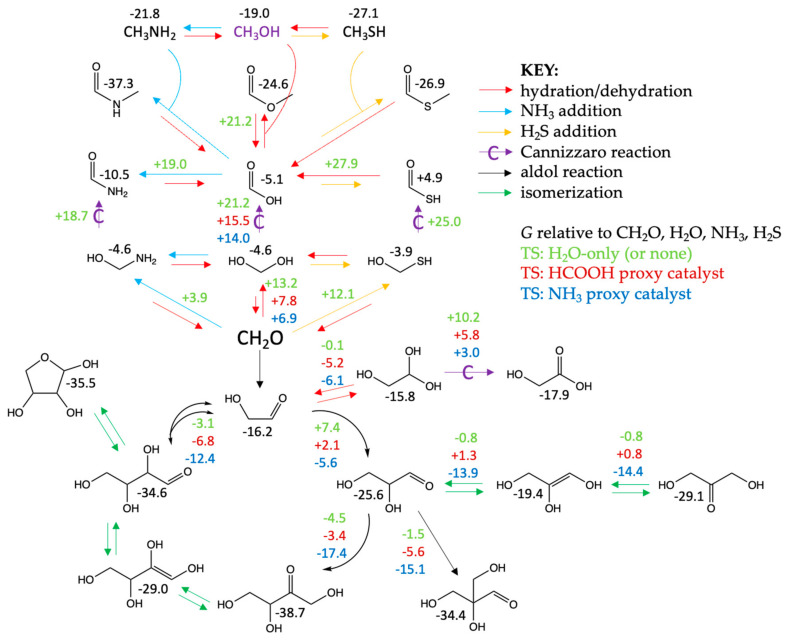
In the previous section, we discussed the reactions of C1, C2, C3, and C4 “sugars” piecemeal with ΔG and ΔG‡ values for each individual reaction. In this section, we will look at the overall free energy map. With multiple pathways, we have found it easier to present our results, not along a particular reaction coordinate but with a bird’s-eye-view schematic, as shown in Figure 12. For this to be effective, we need to choose a set of reference compounds and assign them relative free energies of zero. Our reference compounds will be CH2O, H2O, NH3, and H2S.
Figure 12.
Overall free energy map with G values in kcal relative to CH2O, H2O, NH3, and H2S.
The numbers in black and colored fonts are for stable minima and transition states, respectively. The G value for CH2O in the center of Figure 12 is zero. At a glance, you can see the relative stability of each compound with respect to the reference states. Making new C–C bonds via aldol additions is significantly exergonic. For example, the reaction of glycolaldehyde (G = −16.2) with formaldehyde to form glyceraldehyde (G = −25.6 kcal) has a ΔG of −25.6 − (−16.2 + 0) = −9.4 kcal as shown in Section 3.3. The uncatalyzed (H2O-only) transition state (G = +7.4 in green font) tells us that the forward barrier ΔG‡ is +7.4 − (−16.2) = +23.8 kcal while the reverse barrier would be ΔG‡ = +7.4 − (−25.6) = +33.2 kcal. For the HCOOH catalyzed reaction (transition state G = +2.1 in dark red font), the forward barrier ΔG‡ is +2.1 − (−16.2) = 18.3 kcal (as shown in Figure 5) while the reverse barrier would be ΔG‡ = +2.1 − (−25.6) = +27.7 kcal.
As a second example, consider the reaction of HCOOH (G = −5.1) reacting with H2S (G = 0, a reference compound) to form the thioacid HC(O)SH (G = +4.9). ΔG of this reaction is +4.9 − (−5.1 + 0) = +10.0 kcal. On the other hand, the reaction of HCOOH with CH3SH (G = −27.1) to form the thioester HC(O)SCH3 (G = −26.9) has ΔG = −26.9 − (−5.1 −27.1) = +5.3 kcal. Hence, forming the thioester is less endergonic than forming the thioacid, as discussed in Section 3.6. Except for the exergonic formation of amides, the sequestering reactions (top half of Figure 12) have ΔG close to zero or slightly endergonic.
Figure 12 is only a very small part of what may take place in a messy formose reaction if NH3 and H2S are present. All the reactions in the top half only show reacting C1 species, but because the formose reaction generates C2, C3, and C4 aldehydes, ketones, alcohols, and carboxylic acids (the latter two via Cannizzaro reactions), these can further react with each other and with NH3 and H2S. While we do not have all these calculations completed, what we have presented thus far allows us to make reasonable first approximations of both the thermodynamics and kinetics of these myriad reactions. We expect to set up kinetic simulations to explore potential product distributions in this complex system in a future publication when we have accumulated more data.
Figure 12 also summarizes most of the results we have discussed in the previous section, and we hope this has provided the reader with a free energy “map” to see where the hills and valleys are located, how high the hills are, and how deep or shallow the valleys lie. The takeaway summary: (1) C–C bond-forming aldol reactions are thermodynamically more favorable than C–O, C–S, or C–N bond formation. (2) Kinetically, C–N bond formation has the lowest barriers. (3) Cannizzaro reactions open access to species with other redox states and are thermodynamically driven by forming the reduced (alcohol) product, although the kinetic barriers are relatively high. (4) HCOOH and NH3 can be used as proxy catalysts in computational studies; looking at the transition states gives us a sense of whether a reaction may be acid- or base-catalyzed, but we should be cautious not to over-interpret the results. (5) The exponentially growing set of compounds in the formose reaction includes many opportunities for some intermediates to act as catalysts, sequestering agents, or even parasites of the autocatalytic cycle. Our study only touches a very small part of the initial steps that may occur, but we hope it serves as a guide for future studies.
A big origins-of-life question is how and if an autocatalytic cycle of (sugar) aldehydes evolved into a proto-metabolic cycle of carboxylic acids analogous to the reverse TCA cycle. Kinetically, the main impact of HCOOH is catalyzing the disproportionation of aldehydes to form more acids, parasitizing the formose cycle, while furnishing acids via Cannizzaro reactions toward constructing an analogous cycle of carboxylic acid proto-metabolites. HCOOH has little impact on the enolization and aldol additions required to form larger compounds. On the other hand, NH3 lowers the barriers of all reactions and acts as an indiscriminate catalyst. By doing so, it allows thermodynamics to play a role in favoring the formation of larger molecules (potential biomass) via new C–C bonds in aldol additions. Thermodynamically, amide bonds are also more stable. This may hint at some roles of nitrogen in extant life today; we find them in biocatalytic proteins or in secondary metabolites, but they are not metabolites in the core pathways, such as glycolysis and the TCA cycle. The eventual evolution to a carboxylic acid cycle with higher barriers now requires catalysts to proceed (because aldol reactions are no longer as feasible kinetically), thus leading to selectivity and control in metabolism.
Acknowledgments
This research was supported by the University of San Diego; J.K. acknowledges a University Professor Award from the university for funding. Shared computing facilities were provided by the saber3 computing cluster at the University of San Diego.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/life14080933/s1, Table S1: Energy breakdown of molecules and transition states.
Author Contributions
Conceptualization, J.K.; methodology, J.K.; validation, J.K. and L.P.T.; formal analysis, J.K. and L.P.T.; investigation, J.K. and L.P.T.; data curation, J.K. and L.P.T.; writing—original draft preparation, J.K. and L.P.T.; writing—review and editing, J.K.; visualization, J.K. and L.P.T.; supervision, J.K.; project administration, J.K. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in Supplementary Materials.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding Statement
This research received no external funding.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Xavier J.C., Hordijk W., Kauffman S., Steel M., Martin W.F. Autocatalytic chemical networks at the origin of metabolism. Proc. Biol. Sci. 2020;287:20192377. doi: 10.1098/rspb.2019.2377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Breslow R. On the Mechanism of the Formose Reaction. Tetrahedron Lett. 1959;1:22–26. doi: 10.1016/S0040-4039(01)99487-0. [DOI] [Google Scholar]
- 3.Appayee C., Breslow R. Deuterium studies reveal a new mechanism for the formose reaction involving hydride shifts. J. Am. Chem. Soc. 2014;136:3720–3723. doi: 10.1021/ja410886c. [DOI] [PubMed] [Google Scholar]
- 4.Mizuno T., Weiss A.H. Synthesis and Utilization of Formose Sugars. Adv. Carbohydr. Chem. Biochem. 1974;29:173–227. doi: 10.1016/S0065-2318(08)60250-4. [DOI] [Google Scholar]
- 5.Omran A., Menor-Salvan C., Springsteen G., Pasek M. The Messy Alkaline Formose Reaction and Its Link to Metabolism. Life. 2020;10:125. doi: 10.3390/life10080125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mueller D., Pitsch S., Kittaka A., Wagner E., Wintner C.E., Eschenmoser A. Chemistry of a-aminonitriles. Aldomerization of glycolaldehyde phosphate to rac-hexose 2,4,6-triphosphates and (in presence of formaldehyde) rac-pentose 2,4-diphosphates: Rac-allose 2,4,6-triphosphate and rac-ribose 2,4-diphosphate are the main reaction products. Helv. Chim. Acta. 1990;73:1410–1468. doi: 10.1002/hlca.19900730526. [DOI] [Google Scholar]
- 7.Ricardo A., Carrigan M.A., Olcott A.N., Benner S.A. Borate minerals stabilize ribose. Science. 2004;303:196. doi: 10.1126/science.1092464. [DOI] [PubMed] [Google Scholar]
- 8.Zubay G. Studies on the lead-catalyzed synthesis of aldopentoses. Orig. Life Evol. Biosph. 1998;28:13–26. doi: 10.1023/A:1006551410542. [DOI] [PubMed] [Google Scholar]
- 9.Robinson W.E., Daines E., van Duppen P., de Jong T., Huck W.T.S. Environmental conditions drive self-organization of reaction pathways in a prebiotic reaction network. Nat. Chem. 2022;14:623–631. doi: 10.1038/s41557-022-00956-7. [DOI] [PubMed] [Google Scholar]
- 10.Van Duppen P., Daines E., Robinson W.E., Huck W.T.S. Dynamic Environmental Conditions Affect the Composition of a Model Prebiotic Reaction Network. J. Am. Chem. Soc. 2023;145:7559–7568. doi: 10.1021/jacs.3c00908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bris A., Baltussen M.G., Tripodi G.L., Huck W.T.S., Franceschi P., Roithova J. Direct Analysis of Complex Reaction Mixtures: Formose Reaction. Angew. Chem. Int. Ed. 2024;63:e202316621. doi: 10.1002/anie.202316621. [DOI] [PubMed] [Google Scholar]
- 12.Paschek K., Kohler K., Pearce B.K.D., Lange K., Henning T.K., Trapp O., Pudritz R.E., Semenov D.A. Possible Ribose Synthesis in Carbonaceous Planetesimals. Life. 2022;12:404. doi: 10.3390/life12030404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Omran A. Plausibility of the Formose Reaction in Alkaline Hydrothermal Vent Environments. Orig. Life Evol. Biosph. 2023;53:113–125. doi: 10.1007/s11084-020-09599-5. [DOI] [PubMed] [Google Scholar]
- 14.Vinogradoff V., Leyva V., Mates-Torres E., Pepino R., Danger G., Rimola A., Cazals L., Serra C., Pascal P., Meinert C. Olivine-catalyzed glycolaldehyde and sugar synthesis under aqueous conditions: Application to prebiotic chemistry. Earth Planet Sci. Lett. 2024;626:118558. doi: 10.1016/j.epsl.2023.118558. [DOI] [Google Scholar]
- 15.Haas M., Lamour S., Christ S.B., Trapp O. Mineral-mediated carbohydrate synthesis by mechanical forces in a primordial geochemical setting. Commun. Chem. 2020;3:140. doi: 10.1038/s42004-020-00387-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rappoport D., Galvin C.J., Zubarev D.Y., Aspuru-Guzik A. Complex Chemical Reaction Networks from Heuristics-Aided Quantum Chemistry. J. Chem. Theory Comput. 2014;10:897–907. doi: 10.1021/ct401004r. [DOI] [PubMed] [Google Scholar]
- 17.Simm G.N., Reiher M. Context-Driven Exploration of Complex Chemical Reaction Networks. J. Chem. Theory Comput. 2017;13:6108–6119. doi: 10.1021/acs.jctc.7b00945. [DOI] [PubMed] [Google Scholar]
- 18.Roszak R., Wolos A.B.M., Glen L., Konka J., Jensen P., Burgchardt P., Zadlo-Dobrowolska A., Janiuk P., Szymkuc S., Grzybowski B.A. Emergence of metabolic-like cycles in blockchain-orchestrated reaction networks. Chem. 2024;10:952–970. doi: 10.1016/j.chempr.2023.12.009. [DOI] [Google Scholar]
- 19.Kua J., Avila J.E., Lee C.G., Smith W.D. Mapping the Kinetic and Thermodynamic Landscape of Formaldehyde Oligomerization under Neutral Conditions. J. Phys. Chem. A. 2013;117:12658–12667. doi: 10.1021/jp4098292. [DOI] [PubMed] [Google Scholar]
- 20.Kua J., Hernandez A.L., Velasquez D.N. Thermodynamics of Potential CHO Metabolites in a Reducing Environment. Life. 2021;11:1025. doi: 10.3390/life11101025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kua J., Hanley S.W., De Haan D.O. Thermodynamics and Kinetics of Glyoxal Dimer Formation: A Computational Study. J. Phys. Chem. A. 2008;112:66–72. doi: 10.1021/jp076573g. [DOI] [PubMed] [Google Scholar]
- 22.Kua J., Galloway M.M., Millage K.D., Avila J.E., De Haan D.O. Glycolaldehyde Monomer and Oligomer Equilibria in Aqueous Solution: Comparing Computational Chemistry and NMR Data. J. Phys. Chem. A. 2013;117:2997–3008. doi: 10.1021/jp312202j. [DOI] [PubMed] [Google Scholar]
- 23.Vosko S.H., Wilk L., Nusair M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980;58:1200–1211. doi: 10.1139/p80-159. [DOI] [Google Scholar]
- 24.Becke A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- 25.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- 26.Becke A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
- 27.Halgren T.A. MMFF VII. Characterization of MMFF94, MMFF94s, and other widely available force fields for conformational energies and for intermolecular-interaction energies and geometries. J. Comput. Chem. 1999;20:730–748. doi: 10.1002/(SICI)1096-987X(199905)20:7<730::AID-JCC8>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 28.Warshel A., Florian J. Computer simulations of enzyme catalysis: Finding out what has been optimized by evolution. Proc. Natl. Acad. Sci. USA. 1998;95:5950–5955. doi: 10.1073/pnas.95.11.5950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wiberg K.B., Bailey W.F. Chiral diamines 4: A computational study of the enantioselective deprotonation of Boc-pyrrolidine with an alkyllithium in the presence of a chiral diamine. J. Am. Chem. Soc. 2001;123:8231–8238. doi: 10.1021/ja0107733. [DOI] [PubMed] [Google Scholar]
- 30.Nielsen R.J., Keith J.M., Stoltz B.M., Goddard W.A., 3rd A computational model relating structure and reactivity in enantioselective oxidations of secondary alcohols by (-)-sparteine-Pd(II) complexes. J. Am. Chem. Soc. 2004;126:7967–7974. doi: 10.1021/ja031911m. [DOI] [PubMed] [Google Scholar]
- 31.Deubel D.V., Lau J.K. In silico evolution of substrate selectivity: Comparison of organometallic ruthenium complexes with the anticancer drug cisplatin. Chem. Commun. 2006;23:2451–2453. doi: 10.1039/b601590e. [DOI] [PubMed] [Google Scholar]
- 32.Wertz D.H. Relationship between the gas-phase entropies of molecules and their entropies of solvation in water and 1-octanol. J. Am. Chem. Soc. 1980;102:5316–5322. doi: 10.1021/ja00536a033. [DOI] [Google Scholar]
- 33.Abraham M.H. Relationship between solution entropies and gas phase entropies of nonelectrolytes. J. Am. Chem. Soc. 1981;103:6742–6744. doi: 10.1021/ja00412a036. [DOI] [Google Scholar]
- 34.Krizner H.E., De Haan D.O., Kua J. Thermodynamics and Kinetics of Methylglyoxal Dimer Formation: A Computational Study. J. Phys. Chem. A. 2009;113:6994–7001. doi: 10.1021/jp903213k. [DOI] [PubMed] [Google Scholar]
- 35.Kua J., Paradela T.L. Early Steps of Glycolonitrile Oligomerization: A Free-Energy Map. J. Phys. Chem. A. 2020;124:10019–10028. doi: 10.1021/acs.jpca.0c09922. [DOI] [PubMed] [Google Scholar]
- 36.Kua J., Miller A.S., Wallace C.E., Loli H. Role of Acid in the Co-oligomerization of Formaldehyde and Pyrrole. ACS Omega. 2019;4:22251–22259. doi: 10.1021/acsomega.9b03931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rivlin M., Eliav U., Navon G. NMR studies of the equilibria and reaction rates in aqueous solutions of formaldehyde. J. Phys. Chem. B. 2015;119:4479–4487. doi: 10.1021/jp513020y. [DOI] [PubMed] [Google Scholar]
- 38.Tsujino Y., Wakai C., Matubayashi N., Nakahara M. Noncatalytic Cannizzaro-type reaction of formaldehyde in hot water. Chem. Lett. 1999;28:287–288. doi: 10.1246/cl.1999.287. [DOI] [Google Scholar]
- 39.Kim H.J., Ricardo A., Illangkoon H.I., Kim M.J., Carrigan M.A., Frye F., Benner S.A. Synthesis of Carbohydrates in Mineral-Guided Prebiotic Cycles. J. Am. Chem. Soc. 2011;133:9457–9468. doi: 10.1021/ja201769f. [DOI] [PubMed] [Google Scholar]
- 40.Saladino R., Crestini C., Pino S., Costanzo G., Di Mauro E. Formamide and the origin of life. Phys. Life Rev. 2012;9:84–104. doi: 10.1016/j.plrev.2011.12.002. [DOI] [PubMed] [Google Scholar]
- 41.Bizzarri B.M., Saladino R., Delfino I., Garcia-Ruiz J.M., Di Mauro E. Prebiotic Organic Chemistry of Formamide and the Origin of Life in Planetary Conditions: What We Know and What Is the Future. Int. J. Mol. Sci. 2021;22:917. doi: 10.3390/ijms22020917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kua J., Thrush K.L. HCN, Formamidic Acid, and Formamide in Aqueous Solution: A Free Energy Map. J. Phys. Chem. B. 2016;120:8175–8185. doi: 10.1021/acs.jpcb.6b01690. [DOI] [PubMed] [Google Scholar]
- 43.Kua J., Miller N.A. Preliminary Free Energy Map of Prebiotic Compounds Formed from CO2, H2 and H2S. Life. 2022;12:1763. doi: 10.3390/life12111763. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data presented in this study are available in Supplementary Materials.