Prediction of Two-Dimensional Janus Transition-Metal Chalcogenides: Robust Ferromagnetic Semiconductor with High Curie Temperature

Abstract

Two-dimensional (2D) ferromagnetic semiconductors (FM SCs) provide an ideal platform for the development of quantum information technology in nanoscale devices. However, many developed 2D FM materials present a very low Curie temperature (T_C), greatly limiting their application in spintronic devices. In this work, we predict two stable 2D transition metal chalcogenides, V₃Se₃X₂ (X = S, Te) monolayers, by using first-principles calculations. Our results show that the V₃Se₃Te₂ monolayer is a robust bipolar magnetic SC with a moderate bandgap of 0.53 eV, while V₃Se₃S₂ is a direct band-gap FM SC with a bandgap of 0.59 eV. Interestingly, the ferromagnetisms of both monolayers are robust due to the V–S/Se/Te–V superexchange interaction, and T_Cs are about 406 K and 301 K, respectively. Applying biaxial strains, the FM SC to antiferromagnetic (AFM) SC transition is revealed at 5% and 3% of biaxial tensile strain. In addition, their high mechanical, dynamical, and thermal stabilities are further verified by phonon dispersion calculations and ab initio molecular dynamics (AIMD) calculations. Their outstanding attributes render the V₃Se₃Y₂ (Y = S, Te) monolayers promising candidates as 2D FM SCs for a wide range of applications.

1. Introduction

With the development of device minimization processing, various two-dimensional (2D) semiconductors (SC) with large surface-to-volume ratios and intriguing electronic properties have attracted intensive attention [1,2,3,4,5,6,7,8]. Among them, the emergence of 2D ferromagnetic semiconductors (FM SCs) has drawn particular interest by combining the complementary function of SCs and FM materials, allowing the coupling and dependent control of electron charge and spin [9,10,11]. Compared with conventional electronics based on electron charge degree of freedom [12,13,14], 2D FM SCs show advantages of high energy-efficient performance, faster information operation, non-volatile data storage, etc. Unfortunately, most 2D semiconducting materials are found to be nonmagnetic due to their incompatibility between semi-conductivity and magnetism [15]. In addition, a long-range magnetic ordering in magnetism is difficult to maintain because of thermal agitation, according to the Mermin–Wagner theorem [16]. These challenges largely limit the widespread applications of 2D FM SC-based spintronics devices.

The experimental breakthroughs in 2D FM SCs were the successful preparation of the CrI₃ monolayer and Cr₂Ge₂Te₆ bilayer in 2017 [17,18]. Inspired by these achievements, a number of 2D FM SCs were fabricated and predicted by experimental and theoretical researchers, including transition-metal (TM) halides [17], TM dichalcogenides (TMDs) [19], TM chalcogenide-halide Janus complexes [20], and their various derivatives [21]. Despite the progress, most of these FM SCs possess lower than room temperature T_C. For example, the T_Cs of the CrI₃ monolayer [22] and the Cr₂Ge₂Te₆ bilayer [23] are as low as 45 K and 63 K, respectively, which greatly limits their practical applications. Alternatively, 2D Janus TMDCs with hetero chalcogenide elements are found to show novel electronic and magnetic properties due to their broken structural symmetry [24]. In addition, robust ferromagnetic and half-metallic characters are identified for Janus FeXY (X, Y = Cl, Br, and I, X ≠ Y) monolayers [25]. The 2D VSSe was found to be a highly stable room-temperature FM SC with valley polarization feature [20]. The 2D MnSSe was revealed to be high T_C FM half-metal, in which the magnetization easy axis can be tuned by hole and electron doping [26]. Research on the Janus structure then reached a high point, aiming to explore materials with better performance.

In this work, by using the first-principles method, we predict two high-temperature 2D Janus FM SCs, namely, V₃Se₃X₂ (X = S, Te) monolayers. Both systems are predicted to be thermodynamically stable. Interestingly, the ferromagnets of both structures are found to be robust based on the V–S/Se/Te–V superexchange interaction and their T_Cs are about 406 K and 301 K for V₃Se₃S₂ and V₃Se₃Te₂, respectively. Moreover, the electronic and magnetic properties of both systems can be flexibly modulated under external in-plane biaxial strains.

2. Results and Discussion

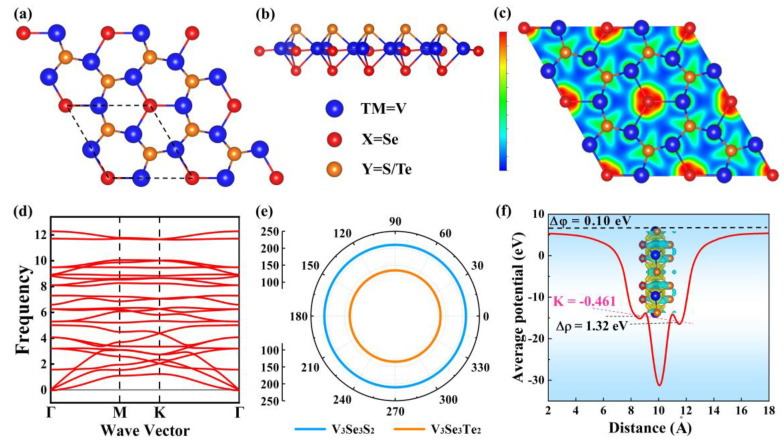
Figure 1a,b presents the crystal structure of monolayer V₃Se₃X₂ (X = S, Te), which is a three-atomic-layer thickness incorporating V, Se, and X atoms. Their space group is P3m1, and the lattice constants are 5.76 Å and 5.95 Å for the V₃Se₃S₂ and V₃Se₃Te₂ monolayers, respectively, in which, the V-V and the V-Se bond lengths in the middle plane are around 3.00~3.12 Å and 2.44~2.47 Å, and the V-S/Te and V-Se bond lengths out of the middle plane are around 2.31~2.67 Å. To address the structural stability and experimental feasibility of both V₃Se₃X₂ monolayers, we have calculated their cohesive energies (E_coh) and formation energies (E_f) based on the following equations:

$$E_f={\displaystyle \frac{E_{V3Se3X2}-(3{\mu }_V+3{\mu }_{Se}+2{\mu }_X)}{n}}$$ (1)

$$E_{coh}={\displaystyle \frac{E_{V3Se3X2}-\left(3E_V+3E_{Se}+2E_X\right)}{n}}$$ (2)

Figure 1.

The (a) top view and (b) side view of the V₃Se₃S₂ (V₃Se₃Te₂) monolayer. (c) The calculated electron localization function (ELF) of the V₃Se₃S₂ monolayer for the (001) plane. (d) Phonon dispersion spectrum of V₃Se₃S₂ monolayer. (e) Young’s modulus of V₃Se₃S₂ (Blue) and V₃Se₃Te₂ (Orange). (f) Average electrostatic potential of the V₃Se₃S₂ monolayer.

Here, E_V3Se3X2, μ_V, μ_Se, and μ_Y are the total energy of V₃Se₃X₂ monolayers, and the energies of V, Se, and S/Te atoms in their bulk crystals, respectively. E_V, E_Se, and E_X are the energies of isolated V, Se, and S/Te atoms. The calculated E_cohs of both systems are −4.96 eV/atom and −4.52 eV/atom, respectively, comparable to that of the MoS₂ (−4.53 eV/atom) and MoSe₂ (−5.07 eV/atom) monolayers [27]. In addition, the E_fs are −0.99 eV and −0.83 eV for V₃Se₃S₂ and V₃Se₃Te₂, respectively; the negative values ensure their fabrication feasibility in the experiment. Figure 1c shows the electron localization function (ELF) of the V₃Se₃S₂ monolayer, from which we can see that the electrons are mainly delocalized around each atom, indicating their obvious ionic characters. The average electrostatic potential and charge density difference (CDD) plot of the V₃Se₃S₂ monolayer is shown in Figure 1f. Clearly, the electrostatic potential of the S atom layer is greater than that of Se atom layer, due to the fact that the electronegativity of the S atom is greater than that of the Se atom. As a result, more electrons are found to be transferred from V atoms to S atoms than Se atoms.

The phonon spectra of the V₃Se₃S₂ and V₃Se₃Te₂ monolayers are illustrated in Figure 1d and Figure S1 in the Supporting Information (SI); the absence of imaginary frequencies in the Brillouin zone confirms the dynamical stabilities of both systems. In addition, the thermal stability of the V₃Se₃X₂ (X = S, Te) monolayers is assessed by AIMD simulations at 300 K for 6 ps. As illustrated in Figure S2, the energies of the V₃Se₃X₂ (X = S, Te) monolayers fluctuate within a narrow range during the simulation, and the final snapshot demonstrates that the structures remain well-preserved, indicating excellent thermal stability. Additionally, the mechanical stabilities for both systems are evaluated by calculating Young’s modulus and the Poisson ratio. The calculated elastic constants for the V₃Se₃S₂/V₃Se₃Te₂ monolayers are C₁₁ = 247.90/193.33 N/m, C₁₂ = 96.92/106.56 N/m, C₂₂ = 247.90/193.33 N/m, and C₆₆ = 75.49/43.38 N/m, respectively, which satisfy the Born stability criterion (C₁₁, C₆₆ > 0, C₁₁–C₂₂ > 0 and C₁₁ + 2C₁₂ > 0), indicating their mechanical stabilities. Young’s modulus and Poisson’s ratio as a function of θ angle (the angle between a certain direction and x-axis) are shown in Figure S3 for both the monolayers. It is found that Young’s modulus for the V₃Se₃S₂ and V₃Se₃Te₂ monolayers are isotropic with Young’s modulus for 210.01 N/m² and 134.59 N/m², respectively; in contrast, Poisson’s ratio for both systems is anisotropic.

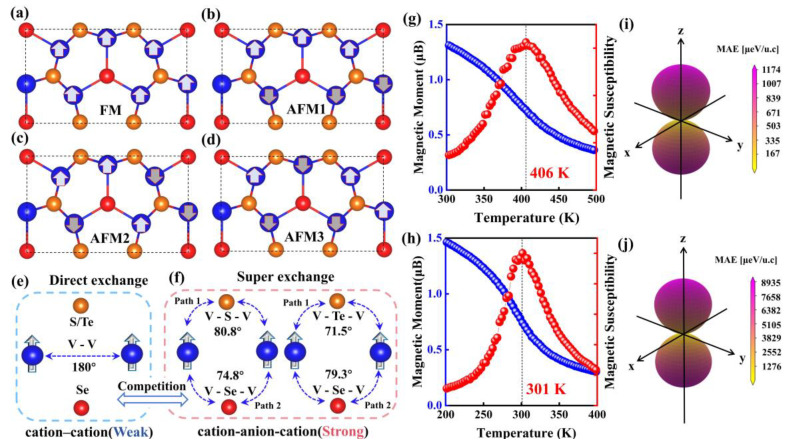
To determine the magnetic ground states of both V₃Se₃X₂ (X = S, Te) monolayers, four magnetic configurations, namely, FM, AFM1, AFM2, and AFM3 are considered, as depicted in Figure 2a–d. Upon comparison, the FM orderings are the favored magnetic states for all the structures, which are lower in energy than AFM1, AFM2, and AFM3 by 0.080, 0.064, and 0.044 eV/atom, respectively, for V₃Se₃S₂ and by 0.064, 0.046, and 0.026 eV/atom for V₃Se₃Te₂. The FM ordering in both V₃Se₃S₂ and V₃Se₃Te₂ monolayers originate from the competition between direct and superexchange interactions (see Figure 2e,f). Direct exchange interactions are based on the overlap of wave functions between two neighboring magnetic ions, which usually leads to AFM coupling. [28] As the distance between two neighboring V atoms is as long as 3.00 and 3.12 Å, longer than that in bulk V (2.62 Å), the direct exchange interactions in both systems are very weak. On the other hand, the superexchange paths are mediated by X or Y atoms (Path 1, 2), as shown in Figure 2f, in which the V-Se-V/V-Y-V angles are around 80° and 75°, close to 90°. Therefore, the superexchange interactions determine the FM couplings of magnetic ions according to the Goodenough–Kanamori–Anderson (GKA) rule. Considering the Coulomb exchange interaction between S/Te p orbitals and the fact that the bond angle of V(I)–S/Te–V(II) is 80.8° in V₃Se₃S₂ and 71.5° in V₃Se₃Te₂ (relatively close to 90°), it can be inferred that the superexchange interaction brings a strong FM order [29,30]. As shown in Figure 2f, there are two kinds of V–Se–V/V-Y-V superexchange coupling pathways in each monolayer (Paths 1, 2) due to the presence of Se and Y elements. In V₃Se₃S₂, the electrons mainly hop between V(I) d_x2/V(II) d_z2 via S p states, as shown in Figure 2a,b, which implies that electrons favor path 1. In V₃Se₃Te₂, the electrons mainly hop between V(I) d_x2/V(II) d_z2 via Te p states, as shown in Figure 2c,d, implying path 1 is again more favored.

Figure 2.

(a–d) FM and AFM orderings. (e,f) illustrations of the V–V direct-exchange, V–S/Se/Te–V superexchange. The magnetic moment and Magnetic susceptibility of the V atom as a function of temperature for the (g) V₃Se₃S₂ and (h) V₃Se₃Te₂ monolayer, respectively. The magnetocrystalline anisotropy energy (MAE) for (i) V₃Se₃S₂ and (j) V₃Se₃Te₂ monolayer.

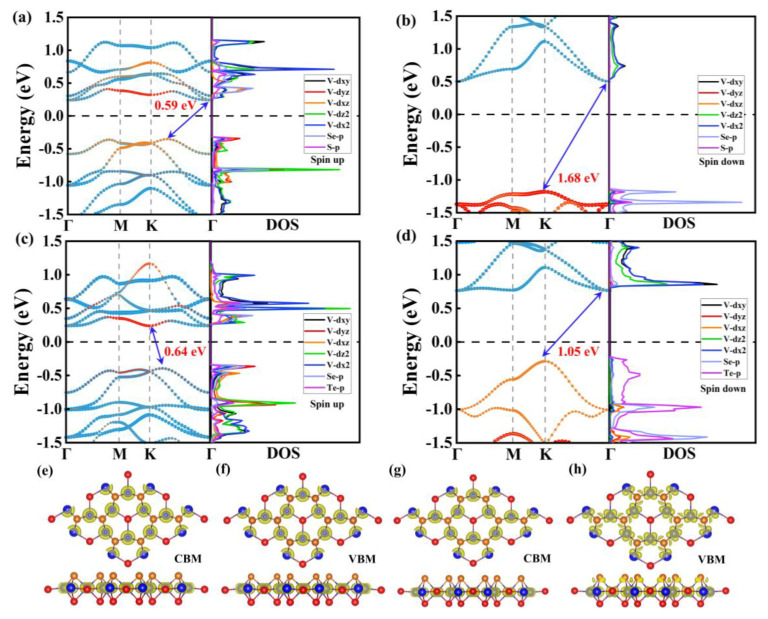
To further investigate the electronic properties of both V₃Se₃X₂ monolayers, we have calculated the spin-resolved band structures and density of states (DOS) (Figure 3a–d). Notably, the V₃Se₃S₂ monolayer is an FM SC with a direct bandgap of 0.59 eV, while the V₃Se₃Te₂ monolayer exhibits an FM SC character with an indirect gap of 0.53 eV. Of particular interest, the conduction band minimum (CBM) and the valence band maximum (VBM) of the V₃Se₃Te₂ monolayer are fully spin-polarized and occupied with opposite spin electrons, indicating a typical bipolar magnetic semiconductor (BMS) feature, as shown in Figure 3c,d [31,32,33]. As can be seen from the DOS in Figure 3a,b, the VBM and CBM are both mainly contributed to by the d_x2–d_z2 orbits of the V atom and p orbits of S and Te, respectively.

Figure 3.

Bands and DOS of SL V₃Se₃S₂ in (a) spin-up and (b) spin-down channels. Bands and DOS of SL V₃Se₃Te₂ in (c) spin-up and (d) spin-down channels. (e) CBM and (f) VBM of SL V₃Se₃S₂. (g) CBM and (h) VBM of SL V₃Se₃Te₂.

Generally, the Curie temperature (T_C) also strongly correlates with the magnetic anisotropic energy (MAE), while it is also the key to the practical application of materials in spintronics. We use the classic Heisenberg model to investigate the magnetic couplings [34,35], the spin Hamiltonian can be considered as

$$H=E_0-J_1{\sum }_{i,j} S_i{S}_j-J_2{\sum }_{i,k} S_i{S}_k-J_3{\sum }_{i,u} S_i{S}_u-A(S_i^z{)}^2$$ (3)

Here, E₀ is the energy without considering the interaction between magnetic atoms V. J₁, J₂, and J₃ represent the first-nearest, second-nearest, and third-nearest spin exchange coupling parameters. S_i, S_j, S_k, and S_u stand for the spin vector, and S_i^z is the spin component. A is an anisotropy energy parameter [28,32,36]. The values of J₁, J₂, and J₃ are computed to be 14.14, 36.16, and 5.14 meV for V₃Se₃S₂ and 3.80 meV, 38.76 meV, and 5.98 meV for V₃Se₃Te₂, respectively. A 10 × 10 supercell and periodic boundary conditions are adopted for the MC simulation. The magnetic moment and magnetic susceptibility are mapped out as functions of temperature in Figure 2g,h. The estimated transition temperatures for SL V₃Se₃S₂ and V₃Se₃Te₂ monolayers are ~406 K and ~301 K, respectively, which are higher than those of CrX₃ (X = Cl, Br, I) monolayers [18,37,38] and the Cr₂Ge₂Te₆ bilayer [17]. The main reason for a relatively high T_C is the large positive magnetic exchange parameter and large MAE, which is also inseparable from the strong hybridization between V and the Te/Se/S atom.

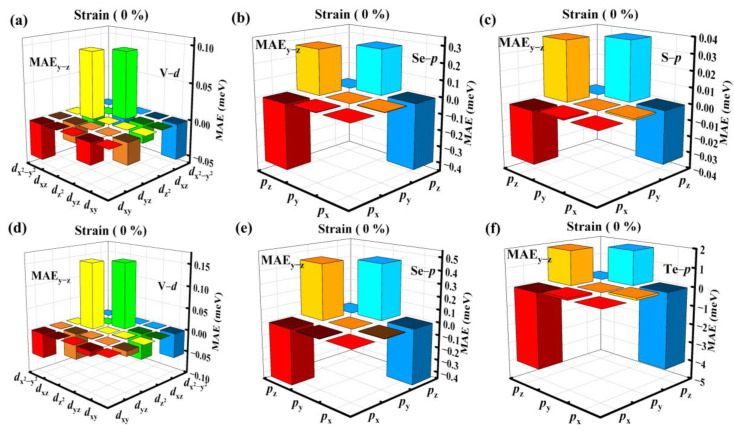
The MAEs are calculated to check the magnetic easy axis of each system as E_MAE = |E_in-plane − E_out-of-plane|, which is defined as the difference between the energy of in-plane and out-plane magnetization directions. As shown in Figure 2e,f, it is found that the MAE values of V₃Se₃S₂ and V₃Se₃Te₂ are 196 and 1489 μeV per V atom, larger than that of CrS₂ (88.5 μeV per Cr) and CrSe₂ (664.0 μeV per Cr) [13]. Their magnetization directions are both in-plane, such large MAEs have rarely been observed in 2D magnetic materials. To further analyze the origin of such large MAEs, orbital resolved MAEs are displayed in Figure 4a–f, illustrating that for the V₃Se₃S₂ monolayer, the coupling strength between the p_y and p_z orbitals of the Se atom is the largest, next is the coupling between the d_xz and V d_z2 orbitals of the V atom. It can be seen that the Se p_z orbital has a big influence on MAE, contributing to the negative part. In addition, the coupling strength between the Se p_y and Se p_z orbitals is also strong with a positive value, but slightly weaker than that of the Se p_z orbitals. For the V₃Se₃Te₂ monolayer, the Te p_z orbital makes the biggest contribution to the MAE, with the coupling between the Se p_y and Se p_z orbitals coming next. As for the V d orbitals, it is the coupling of the d_z2 and d_xz orbitals that dominates, similar to that of the V₃Se₃S₂ monolayer. However, the value is relatively small compared to that of the Se p and Te p orbitals, making little impact on the total MAE value.

Figure 4.

Orbital resolved MAE for (a–c) V₃Se₃S₂ and (d–f) V₃Se₃Te₂, respectively.

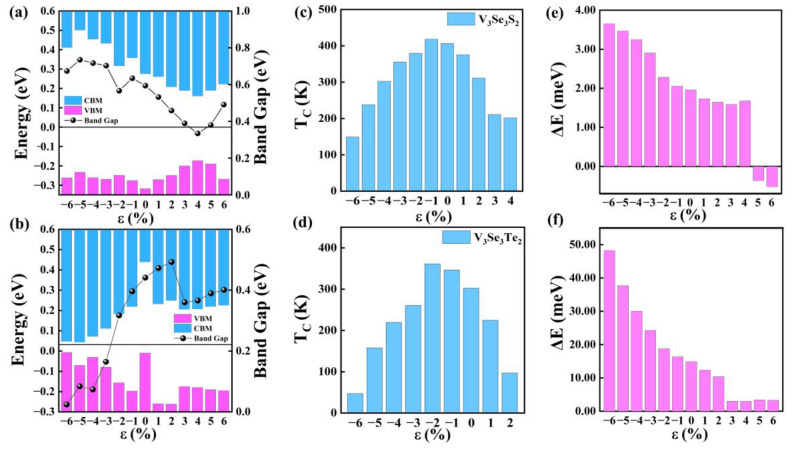
Furthermore, the effect of biaxial strains on the electronic and magnetic properties of V₃Se₃X₂ monolayers is explored (see Figures S4 and S5). It is clear that the V₃Se₃S₂ monolayer keeps the FM SC character in the range from −6% compressive strain to 4% tensile strain, and, under −5% and 6% tensile strain, it is changed to be an AFM BMS (see Figure S4). On the other hand, the V₃Se₃Te₂ monolayer transitioned to be an AFM SC under 3% tensile strain (see Figure S5). Moreover, the band gap of the V₃Se₃S₂ monolayer decreases with the external strains, ranging from −6% to 4%, and goes up slightly under tensile strains, from 4% to 6%, where the VBM experiences a little fluctuation and the CBM gets closer to the Fermi surface (see Figure 5a and Figure S4). For the V₃Se₃Te₂ monolayer, the FM BMS property is maintained under strains from −6% to 2%; remarkably, the V₃Se₃Te₂ monolayer undergoes a FM SC to AFM SC transition under 3% tensile strain (see Figure S5). Unlike the V₃Se₃S₂ monolayer, the band gap of the V₃Se₃Te₂ monolayer increases monotonously with the external strain, where the VBM and CBM get away from the Fermi surface (see Figure 5b).

Figure 5.

Band alignment scheme VBM of the (a) V₃Se₃S₂ monolayer and (b) V₃Se₃S₂ monolayer. (c,d) Curie temperature (T_C) of the V₃Se₃S₂ and V₃Se₃Te₂ monolayers under different strains. MAE = E_out-plane − E_in-plane of the (e) V₃Se₃Te₂ monolayer and (f) V₃Se₃Te₂ monolayer plotted as a function of strain.

Finally, the influence of biaxial strains on the Curie temperature (T_C) of the V₃Se₃S₂ and V₃Se₃Te₂ monolayers is also studied. It is observed that the T_Cs of both materials decrease under tensile strain, while they initially increase and then decrease under compressive strain (see Figure 5c,d). Notably, the T_Cs of the V₃Se₃S₂ and V₃Se₃Te₂ monolayers reach 418 K and 361 K when subjected to −1% and −2% compressive strains, respectively. This behavior demonstrates the tunability of the electronic properties of V₃Se₃Y₂ (Y = S, Te) monolayers through strain engineering, thereby enhancing their potential applications in spintronic devices. Moreover, the variation of the magnetic anisotropy energies (MAE) are analyzed and presented in Figure 5e,f. It is observed that the MAE of V₃Se₃S₂ consistently decreases within the range of −6% to 3% strain and slightly goes up at 4% strain. However, it goes below 0 meV at 5% to 6%, owing to the transition from FM SC to AFM SC. The MAE of V₃Se₃Te₂ experiences a sharper decrease when subjected to strains from −6% to 2% and experiences a sudden decrease upon reaching a tensile strain of 3% due to the phase transition from FM SC to AFM SC.

3. Computational Methods

All the calculations are performed via the density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP) [39]. The Perdew–Burke–Ernzerhof (PBE) [40] method based on the generalized gradient approximation (GGA) [41,42] is used to treat the exchange-correlation functional, and the electronic interaction is treated by the projector augmented wave (PAW) method [43]. To consider the Coulomb and exchange interaction of V 3d electrons, the PBE+U with U = 3 eV is adopted. The plane-wave energy cutoff is set to 500 eV, and the vacuum layer of 20 Å is employed for the studied systems to eliminate adjacent layer interactions. The geometries are fully relaxed until the force and energy convergence are less than 0.01 eV/Å and 10−6 eV, respectively. A Γ-centered k mesh of 12 × 12 × 1 is used for geometry optimization calculations. The Curie temperature (T_C) of both monolayers is calculated by using the EspinS package [44], in which 10 × 10 × 1 lattices are adopted in the Monte Carlo (MC) simulations, and the spins are randomly rotated in the space. A 3 × 3 × 1 supercell of the V3Se3S2 and V3Se3Te2 monolayers are used to calculate the phonon dispersion spectrum by the PHONOPY code based on the density functional perturbation theory [45].

4. Conclusions

In summary, two types of 2D intrinsic FM SC materials, V₃Se₃S₂ and V₃Se₃Te₂ monolayers, are predicted by density functional theory calculations. Both of them are revealed to have good thermal, dynamic, and mechanical stabilities. Our results show that V₃Se₃S₂ and V₃Se₃Te₂ monolayers show robust ferromagnetism and above room temperature T_C of 406 K and 301 K, respectively. The robust ferromagnetic properties are induced by the V–S/Se/Te–V superexchange interaction. V₃Se₃S₂ monolayer is BMS with band gap of 0.59 eV, and V₃Se₃Te₂ monolayer is an indirect band semiconductor with the band gap of 0.53 eV. When biaxial strain is introduced, a FM SC to AFM SC phase transition is found for both systems with the transition point at 5% and 3% tensile strain for the V₃Se₃S₂ and V₃Se₃Te₂ monolayers, respectively. Our results provide an effective method for designing promising candidates for FM SCs, which also provide opportunities for future spintronic research and applications.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules29163915/s1, Figure S1: Phonon spectra of (a) V₃Se₃S₂ and (b) V₃Se₃Te₂; Figure S2: MD simulation was performed for geometric snapshot of the (a) V₃Se₃S₂ and (b) V₃Se₃Te₂ monolayer at 300 K for 6 ps; Figure S3: Young’s modules of (a) V₃Se₃S₂ and (b) V3Se3Te2 respectively and Poisson’s ratio of (c) V₃Se₃S₂ and (d) V₃Se₃Te₂; Figure S4: Band structures of V₃Se₃S₂ under biaxial strain from −6%~6%; Figure S5: Band structures of V₃Se₃Te₂ under biaxial strain from −6%.

Author Contributions

Data curation, Z.W., A.H.Q., Y.L. (Yujie Liu) and J.Z.; writing—original draft preparation, Z.W., A.H.Q., Y.D. and J.L.; writing—review and editing, Y.W. and T.G.; supervision, X.Z. and Y.L. (Yongjun Liu); project administration—Y.W., T.G. and X.Z. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding Statement

This research received no external funding.