Abstract
This study presents an innovative approach for predicting water and groundwater quality indices (WQI and GWQI) in the Eastern Province of Saudi Arabia, addressing critical challenges of scarcity and pollution in arid regions. Recent literature highlights the increasing attention towards WQI based on water pollution index (WPI) and GWQI as essential tools for simplifying complex hydrogeological data, thereby facilitating effective groundwater management and protection. Unlike previous works, the present research introduces a novel hybrid method that integrates non-parametric kernel Gaussian learning (GPR), adaptive neuro-fuzzy inference system (ANFIS), and decision tree (DT) algorithms. This approach marks the first application of a non-parametric kernel for groundwater quality pollution index prediction in Saudi Arabia, offering a significant advancement in the field. Through laboratory analysis and the combination of various machine learning (ML) techniques, this study enhances prediction capabilities, particularly for unmonitored sites in arid and semi-arid regions. The study’s objectives include feature engineering based on dependency sensitivity analysis to identify the most influential variables affecting WQI and GWQI, and the development of predictive models using ANFIS, GPR, and DT for both indices. Furthermore, it aims to assess the impact of different data portions on WQI and GWQI predictions, exploring data divisions such as (70% / 30%), (60% / 40%), and (80% / 20%) for training and testing phase, respectively. By filling a critical gap in water resource management, this research offers significant implications for the prediction of water quality in regions facing similar environmental challenges. Through its innovative methodology and comprehensive analysis, this study contributes to the broader effort of managing and protecting water resources in arid and semi-arid areas. The result proved that GPR-M1 exhibited exceptional testing phase accuracy with RMSE = 0.0169 for GWQI. Similarly, for WPI, the ANFIS-M1 achieved high testing predictive skills with RMSE = 0.0401. The results emphasize the critical role of data quality and quantity in training for enhancing model robustness and prediction precision in water quality assessment.
Keywords: Machine learning, Water pollution, Groundwater quality, Eastern Province, Saudi Arabia, Environmental monitoring
Subject terms: Ecology, Natural hazards, Risk factors, Engineering
Introduction
Water resources are essential for industrial, agricultural, and domestic sectors. High-quality water reduces treatment costs for industrial and drinking uses and boosts agricultural yields1. However, urbanization, industrialization, intensive agriculture, and population growth rapidly increase water demand1. Assessing and predicting water quality is necessary to determine whether a water resource is suitable for a given purpose and to identify the required treatments or precautions if it is not2. Water resources face threats from natural and anthropogenic pollution sources, affecting their suitability for various uses, including drinking, irrigation, and industrial purposes. Agriculture, consuming up to 80% of water resources, is a major water user and contributor to water pollution, necessitating economically efficient water planning and management for sustainable irrigation1. Farmers typically apply irrigation based on water availability rather than growth-stage-based water demand, but greater water availability only sometimes leads to increased crop yield and water use efficiency3.
Water crises and quality are significant concerns in many nations, particularly in arid and semi-arid regions prone to frequent water shortages. Unfortunately, these areas have traditionally placed limited emphasis on water quality evaluation4. Arid and semi-arid regions face various pressing challenges, including water scarcity and extensive groundwater use for diverse purposes3. During the agricultural revolution, irrigation was used to bridge the gap between rain-fed and irrigated crop production5. However, obstacles to dam construction and other technical complexities have become substantial challenges, especially in regions lacking technical expertise, a predicament worsened in areas with low precipitation or within global desert regions6. Climate change and global warming exacerbate the difficulties related to the onset, cessation, duration, and alteration of seasonal rainfall patterns, making their prediction hard due to their chaotic and fluctuating nature, which is unfavorable for cultivation7.
Considering all water quality parameters comprehensively is impractical due to financial and technical challenges and the inherent variability in water quality8. However, recent improvements in Machine learning (ML) techniques have enabled researchers to collect and analyze large amounts of data effectively, meeting the demanding requirements of comprehensive and wide-scale water quality evaluation9. ML, a branch of artificial intelligence (AI), employs algorithms to analyze data and extract patterns to predict new information10. These advanced data analysis and processing techniques are widely used across various fields due to their high precision, flexible customization, and convenient extensibility9.
The Water Quality Index (WQI) is a crucial tool for assessing the overall quality of water for various purposes, including drinking and irrigation9. This comprehensive and standardized method simplifies complex water quality data into a single value, making it easier to interpret and compare water quality across different locations and periods. Investigating the WQI is fundamental in water resources and environmental engineering11. It involves examining the interplay between water requirements and the composition and extent of potential impurities12. Given the prevailing issues of water scarcity and the sustained imbalance in water distribution, more than one billion individuals globally lack access to clean, safe, and adequate fresh water11. The WQI is valuable for sustainable water resource management as it allows for targeted interventions to improve water quality in areas with poor standards.
Furthermore, it serves as a basis for regulatory and policy decisions regarding water quality standards and management strategies. By combining the WQI with advanced ML models, studies have shown that groundwater quality can be predicted with exceptional accuracy and precision10. This demonstrates the essential role of the WQI as a fundamental tool for managing and conserving groundwater resources. The WQI also plays a vital role in pinpointing locations with subpar water quality and elevated salinity concentrations, particularly for agricultural purposes. Utilizing the WQI, researchers can classify and present the geographical pattern of water quality, providing invaluable knowledge about the suitability of groundwater for irrigation and the necessity for adequate treatment before application6,13. This data is crucial for directing irrigation techniques and ensuring the responsible use of water resources in agriculture.
In recent studies, Gaya et al. evaluated the WQI at the Palla station of the Yamuna River in India using three different models (MLR, ANN, and ANFIS)14. By inputting water quality variables, the AI-powered ANN and ANFIS models outperformed the conventional MLR model by up to 10% during the verification phase15. These models accurately tracked the observed water quality index, with the ANN model showing slightly better performance than ANFIS. Similarly, Abba et al. conducted a study on predicting the WQI at three stations along the Yamuna River in India based on data intelligence models and ensemble ML techniques11. The outcomes conclude that these data intelligence models can predict WQI and help in sustainable water resource management. Previous literature concentrated on surface WQI with little attention on groundwater quality (GWQI)16–21. In 2023, Singh et al. assessed seasonal GWQ for irrigation suitability using ML techniques, including ANN and MLR. The outcomes depicted that ANN outperformed linear MLR models22. Uddin et al. introduced ML models and a new Assessment Trophic Status Index (ATSI) model for evaluating eutrophication in coastal and transitional waters23. Utilizing advanced ML techniques, particularly XGBoost, the model demonstrated remarkable accuracy and efficiency, outperforming existing methods in sensitivity and classification across multiple Irish waterbodies. Similarly, Li et al., employed a gated graph neural network (GGNN) model for enhancing the prediction of water quality within water distribution networks (WDNs). Tested in a real-world WDN, the model successfully predicts water quality across the network, including unmonitored sites, with high accuracy. The research highlighted the importance of strategic sensor placement for improving predictions and marks a significant step towards utilizing ML models for water quality management in WDNs, potentially replacing traditional hydraulic models.
Recent literature has addressed WQI and GWQI extensively24–29. The WQI and GWQI simplify complex hydrogeological information into understandable formats, aiding in effective surface water and groundwater management and protection efforts. Addressing the differences between the present work and the existing literature is essential. Thus, we introduce a novel, hybrid approach combining non-parametric kernel Gaussian learning (GPR), hybrid neuro-fuzzy (ANFIS), and decision tree (DT) algorithms for accurate prediction of water and groundwater quality index in Saudi Arabia’s Eastern Province. This approach uniquely addresses the scarcity and pollution challenges in arid regions. It innovatively applies a non-parametric kernel for groundwater quality pollution, a first-in-the-field laboratory analysis, and combines various ML techniques (ANFIS, DT, GPR) for enhanced prediction capabilities. By focusing on surface water and groundwater quality pollution in an area where such studies are scarce, the present study fills a critical gap, especially in predicting quality at unmonitored sites, offering significant advancements for managing water resources globally in arid and semi-arid areas. The clear aim and objectives of this study are: (i) Feature engineering based on dependency sensitivity analysis to understand the most dominant variables for WPI and GWQI (ii) Design and develop a model to predict WQI and GWQI using ANFIS, GPR, and DT (iii) Determine the influence of different data portions on GWQI and WPI by exploring various data divisions for training and testing phases (e.g., 70% / 30%, 60% / 40%, and 80% / 20%).
Experimental method
Study location and data
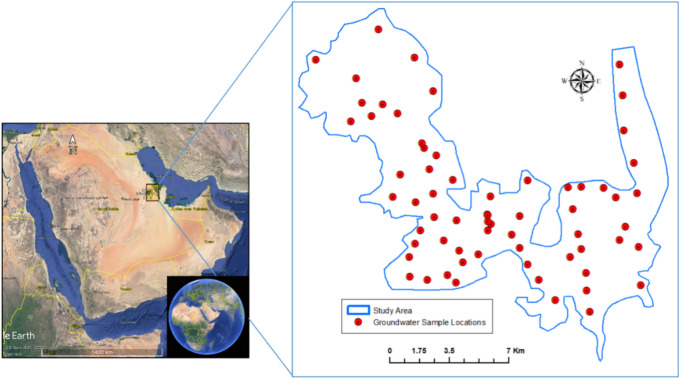
The study area within the Eastern Province of Saudi Arabia encompasses a vast expanse of 672,522 square kilometers and is home to a populace of 5.1 million individuals30. The Al Hassa oasis is located in the Eastern Province of Saudi Arabia, positioned about 320 kilometers east of Riyadh and 70 km west of the Arabian Gulf coastline (Fig. 1). It is positioned at an elevation of roughly 130 to 160 meters above sea level, sloping gradually towards the Gulf coast, between longitudes of 49° 30′ to 49° 50′ E and latitudes of 25° 20′ to 25° 40′ N. The majority of Saudi Arabia is a highly arid area, with an average annual rainfall of only 25 to 150 mm. Over the last twenty years, the Kingdom has undergone significant growth in its agricultural, municipal, and industrial sectors. Groundwater is the primary source of water supply for a variety of uses in the Kingdom, making it essential to manage these resources with great care to prevent any long-term negative impacts on water quality and aquifer productivity31,32. In Saudi Arabia’s Eastern Province, the multi-aquifer system, consisting of the Alat, Khobar, and Umm Er Radhuma (UER) aquifers, serves as the primary water source for irrigation, domestic, and industrial needs. While the UER aquifer caters to domestic and landscape irrigation requirements in residential areas like Dhahran and Al-Khobar, it also provides water to agricultural areas in the region32,33. The Khobar and Alat aquifers, on the other hand, are utilized for domestic and industrial purposes in major cities like Al-Khobar and Dammam, as well as in townships along the coastal belt. The Neogene aquifer, predominantly used for irrigation purposes, is the primary water supply for the Al-Hassa Irrigation and Drainage Project in the Al-Hassa area34,35.
Fig. 1.
Representative case study and sample locations (ArcGIS 10.3/ https://enterprise.arcgis.com/en/portal/10.3/use/deploy-app-portal-obsolete.htm).
Data curation and visualization
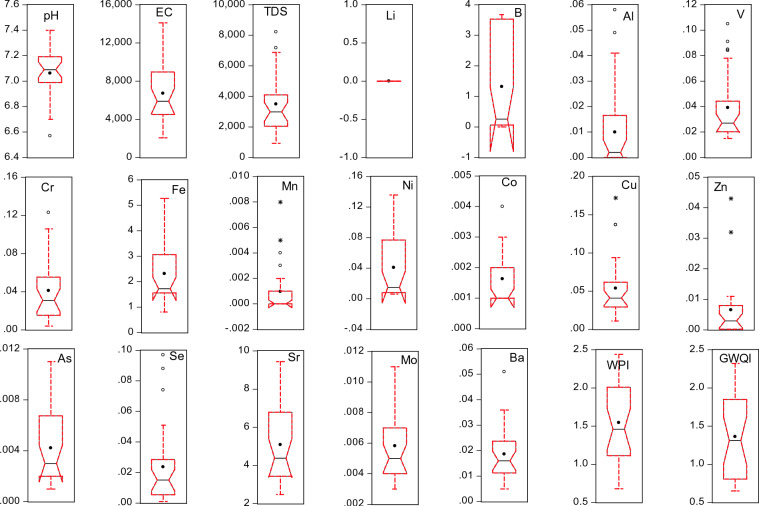
A field investigation was undertaken to assess the physical and chemical properties of groundwater. Measurements of pH, oxidation-reduction potential (ORP), electrical conductivity (EC), total dissolved solids (TDS), turbidity, dissolved oxygen (DO), temperature, and atmospheric pressure were conducted on-site with the use of the Hanna GPS Multiparameter Meter (HI9829). To ensure the removal of any stagnant water, groundwater wells were activated for 15 min before the collection of data. During this investigation, 60 samples from wells within the Neogene aquifer were randomly selected for analysis across the study area. These samples were filtered and stored in a cooler at temperatures below 40 °C in line with the guidelines provided by the US Environmental Protection Agency for sample collection. Acid titration methods were employed to determine bicarbonate levels, while the identification of ions in the groundwater samples was achieved through ion chromatography. The parameters measured for water quality assessment, including pH, electrical conductivity (EC) measured in microsiemens per centimeter (µS/cm), total dissolved solids (TDS), and the concentration of various elements in milligrams per liter (mg/L). These elements are lithium (Li), boron (B), aluminum (Al), vanadium (V), chromium (Cr), iron (Fe), manganese (Mn), nickel (Ni), cobalt (Co), copper (Cu), zinc (Zn), arsenic (As), selenium (Se), strontium (Sr), molybdenum (Mo), and barium (Ba). Additionally, the table includes columns for the Water Pollution Index (WPI) and the Groundwater Quality Index (GWQI), which are indicators of water quality based on the concentrations of the measured elements and compounds. The illustrating distribution of these parameters is presented in Fig. 2.
Fig. 2.
boxplot showing the comprehensive visualization of the mean, median, near outliers, far outliers, whiskers, and staples.
Artificial intelligence applications
Hybrid adaptive neuro-fuzzy inference system (ANFIS)
The ANFIS represents a highly effective neural network methodology that can be employed to tackle function approximation problems effectively36. By utilizing if-then statements that rely on linguistic variables, fuzzy rules can examine the correlation between a system’s inputs and outputs. The ANFIS is a sophisticated multilayer feed-forward network that merges fuzzy reasoning with neural network learning algorithms37. ANFIS can effectively conform to any real continuous function on a compact set and is a powerful tool for modeling non-linear functions, making it an ideal solution for predicting desired outcomes through logical means.
| 1 |
| 2 |
where and are ANFIS inputs, A and B are fuzzy sets, is a first-order polynomial representing the outputs of a Sugeno fuzzy inference system.
Kernel gaussian process regression (k-GPR)
Gaussian process regression (GPR) is a nonparametric model that uses the Gaussian process as prior and then performs prediction analysis on data modeling38. GPR is a non-parametric Bayesian approach to regression, offering a principled way to model complex data without assuming a specific functional form. At its core, GPR embodies the concept of a Gaussian Process (GP), which treats functions as a collection of random variables that have a joint Gaussian distribution. This perspective allows GPR to model the uncertainty about the function underlying the observed data, making it particularly powerful for predictions. A Gaussian process is entirely characterized by its mean function and covariance function , that is,
| 3 |
In the context of regression analysis, the dependent variable is considered as the observation while the independent variable is represented as the Gaussian noise (Mean 0 and Variance )39. By utilizing this information, one can obtain the GPR model.
Decision tree (DT)
Decision Tree (DT) based rule induction is a promising approach to data mining, particularly for predicting groundwater contamination sensitivity, even with limited data and unclear or intricate nonlinear relationships within the dataset40. A DT uses splits to select characteristics that decrease entropy, improving class assignments41. A DT is a hierarchical model that looks like a tree that iteratively divides a dataset into subsets based on their feature attributes, ultimately providing predictions for the pollution index42. A DT can be denoted mathematically as:
| 4 |
where the output of a decision tree for a particular set of input features X is represented by DT(X). The value of J denotes the total number of leaves or terminal nodes in the decision tree, while points to the specific area (leaf) in the feature space that corresponds to the leaf node j; is a constant value assigned to a leaf node j; X is an input feature and is the corresponding region; is an indicator function that equals 1 when X is in and 0 otherwise.
Model validation and performance indicators
The following measures of loss are frequently employed to assess the performance of machine learning models: Root-Mean Square Error (RMSE), Mean Square Error (MSE), Mean Absolute Error (MAE), Coefficient of Determination (R2), and Nash-Sutcliffe efficiency (NSE). According to Moriasi et al.,43, the performance of the model can be classified into four categories: highly commendable (RSR 0.50 or NSE > 0.75), commendable (0.50 < RSR 0.60 or 0.75 NSE > 0.65), satisfactory (0.60 < RSR 0.70 or 0.65 NSE > 0.50), or unsatisfactory (RSR > 0.70 or NSE < 0.50). A lower Mean Absolute Percentage Error (MAPE) is indicative of a higher degree of accuracy in the model, while conversely, a higher MAPE value implies a lower level of accuracy44. Before the modeling process, an external validation technique known as k-fold cross-validation was employed to optimize outcomes, minimize error uncertainty, and enhance the reliability of results45. The mathematical expressions of the performance indicators can be represented as follows:
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
where N = number of data points, = observed and predicted WQI values for observation, and = mean of observed and predicted WQI values.
Water indexes
Water pollution index (WPI)
A measure that indicates the pollution level in a water body, summarizing various pollution indicators into a single value to assess the overall water quality. The computation of the WPI entails several crucial steps to ensure precise evaluation. Initially, we identify vital water quality parameters pertinent to pollution, such as pH, dissolved oxygen, biochemical oxygen demand (BOD), chemical oxygen demand (COD), total suspended solids (TSS), nitrates, phosphates, and heavy metals. These recorded values are standardized to a common scale, usually leveraging reference values or established guidelines. This standardization process normalizes the data, enabling cross-parameter comparability. Subsequently, weights are assigned to each parameter based on their relative significance to overall water quality, discerned through expert assessment or statistical methodologies. Lastly, the normalized values and their respective weights are amalgamated to compute the WPI, furnishing a comprehensive gauge of water pollution.
| 10 |
where is the normalized value of parameter , is the measured concentration of parameter , and is the standard or permissible limit for parameter .
| 11 |
where is the weight assigned to parameter
Groundwater quality index (GWQI)
GWQI is the measure that evaluates groundwater quality, combining different water quality parameters into one value to determine its suitability for various uses such as drinking or irrigation. Calculating the GWQI involves a series of structured steps to evaluate groundwater quality accurately. Specific groundwater quality parameters are initially carefully selected, including pH, TDS, hardness, chloride, sulfate, nitrate, fluoride, and heavy metals. The measured values of these parameters are subsequently standardized to a common scale, often by employing reference values or standard guidelines to ensure comparability. Subsequently, a sub-index is computed for each parameter based on the standardized values. Finally, these sub-indices are aggregated to derive the overall GWQI, offering a comprehensive assessment of groundwater quality.
| 12 |
where is the normalized value of parameter , is the measured value of parameter , is the standard permissible limit for parameter , and is the ideal value for parameter (often taken as 0 for pollutants).
| 13 |
where is the weight assigned to parameter .
| 14 |
Results and discussion
Reliable modelling is paramount for a sustainable environment, this is in line with SDGs-6 aiming to ensure the availability and sustainable management of water and sanitation for all by 2030. This study addresses critical water scarcity and pollution challenges, enhancing water resource management in arid regions and supporting global sustainability and health goals by guiding pollution control and optimizing treatment processes. Additionally, it enhances agricultural productivity and climate change adaptation by ensuring high-quality water resources. However, the study employed a new approach for predicting water and groundwater quality indices (WQI and GWQI) in Saudi Arabia’s Eastern Province, employing a hybrid model that combines non-parametric kernel GPR, ANFIS, and DT.
Preliminary results
The normalization and statistical description of parameters such as EC, TDS, and Co, Sr, V, Cu, As, Se, Mo, and Ba are vital in determining WPI and GWQI because they ensure comparability of data by adjusting for different scales and distributions. Table 1 presents a statistical overview where the mean EC and TDS are relatively high at 6715.784 µS/cm and 3492.384 mg/L respectively, indicating a potential prevalence of mineral-rich water, which could impact the WPI and GWQI with average values of 1.544 and 1.361, suggesting moderate pollution levels. The standard deviations for EC and TDS are 3397.187 µS/cm and 2001.862 mg/L, indicating substantial variability in water quality.
Table 1.
Descriptive statistic of the variables used to determine the WPI and GWQI.
| Parameters | Mean | SD | Kurtosis | Skewness | Minimum | Maximum |
|---|---|---|---|---|---|---|
| EC | 6715.784 | 3397.187 | − 0.583 | 0.511 | 2062.970 | 14114.580 |
| TDS | 3492.384 | 2001.862 | 0.065 | 0.965 | 928.000 | 8226.970 |
| Co | 0.002 | 0.001 | 1.679 | 1.296 | 0.001 | 0.004 |
| Sr | 5.089 | 2.055 | − 0.612 | 0.704 | 2.486 | 9.439 |
| V | 0.039 | 0.027 | 0.405 | 1.305 | 0.015 | 0.105 |
| Cu | 0.054 | 0.040 | 2.680 | 1.681 | 0.011 | 0.172 |
| As | 0.004 | 0.003 | − 0.105 | 1.026 | 0.001 | 0.011 |
| Se | 0.024 | 0.026 | 2.086 | 1.681 | 0.001 | 0.097 |
| Mo | 0.006 | 0.002 | − 0.233 | 0.662 | 0.003 | 0.011 |
| Ba | 0.019 | 0.010 | 2.707 | 1.468 | 0.005 | 0.051 |
| WPI | 1.544 | 0.549 | − 1.288 | − 0.054 | 0.680 | 2.440 |
| GWQI | 1.361 | 0.530 | − 1.147 | 0.266 | 0.650 | 2.320 |
However, trace elements like Co, Sr, and V showed a positive skewness, with values of 1.295, 0.704, and 1.305 respectively, suggesting a distribution with high outliers that could significantly influence the pollution indices. The kurtosis for these elements, with Co at 1.679 and Ba at 2.707, indicates a peaked distribution, highlighting the occurrence of extreme values that may reflect sporadic pollution events. The ranges between minimum and maximum values, such as EC’s 2062.97 to 14114.58 µS/cm and TDS’s 928 to 8226.97 mg/L, further underscore the disparity in water quality across the region. This variability and the presence of extreme values in the water quality parameters are likely to have a pronounced effect on the WQI and GWQI, emphasizing the need for targeted water management strategies to address the areas of concern highlighted by these indices. This process facilitates accurate assessment of water quality by allowing for the aggregation of diverse quality parameters into a single, comprehensible figure that reflects the overall status of water purity and identifies potential health risks associated with water for human consumption and ecosystem health. Moreover, statistical descriptions give insights into the central tendency and variability of each contaminant, helping to discern patterns, trends, and outliers in water quality data, which is essential for effective water management and policymaking.
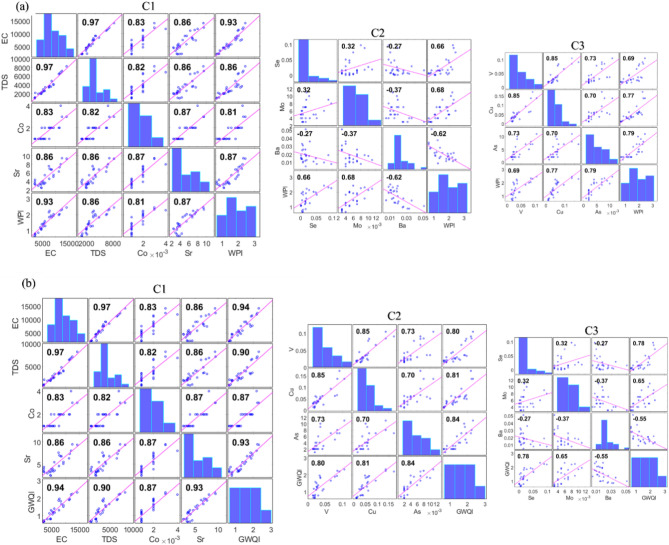
Feature selection using correlation analysis is essential in data-driven models like those predicting WPI and GWQI because it identifies the most significant variables that contribute to the outcome, thereby enhancing model accuracy and efficiency. By analyzing the correlation coefficients, one can establish which parameters have the strongest relationships with the indices, like EC and TDS with WPI (0.9343) and GWQI (0.9387) (see Fig. 3a,b), indicating their strong influence on water quality. This process helps in reducing the dimensionality of the dataset, which not only simplifies the model but also reduces the risk of overfitting, ensuring that the model is generalizable to new, unseen data. Moreover, it can significantly decrease computational costs and improve interpretability by focusing on the most relevant features, leading to clearer insights and more actionable findings. In environmental applications, such focused analysis is crucial for targeted policy-making and efficient resource allocation, enabling stakeholders to address the most impactful factors affecting water quality. For this purpose, we generated three different model combinations to establish the reliable predictive combination for WPI and GWQI for example C1(EC, TDS, Co, and Sr), C2 (V, Cu, and As) and C3(Se, Mo, Ba) as indicated in Fig. 3a,b.
Fig. 3.
Dependency analysis for input variables combinations.
Figure 3 provides insight into how individual water quality parameters relate to the WPI and GWQI. High positive correlation values between the parameters (EC, TDS, Co, Sr, V, Cu, As, Se) and the indices (WPI and GWQI) suggest that these elements have a significant influence on the overall water and groundwater quality. Specifically, EC and TDS show very strong correlations with WPI (0.9343) and GWQI (0.9387), indicating that as the mineral content of the water increases, the indices tend to show worse quality water. Similarly, trace elements such as Sr (mg/L) (0.8711 with WPI, 0.9305 with GWQI) and As (mg/L) (0.7908 with WPI, 0.8419 with GWQI) also show strong positive correlations, suggesting their significant impact on water quality. On the other hand, Ba shows a negative correlation with both WPI (-0.6199) and GWQI (-0.5547), which could indicate that higher Ba (mg/L) concentrations might be associated with better water quality according to these indices, or could reflect a mathematical artifact of the index calculations where Ba behaves inversely to other parameters due to its geochemical properties or the weight assigned to it in the index calculation. The lower correlation of Mo (mg/L) with WPI (0.6763) and GWQI (0.6477) compared to other parameters suggests that molybdenum has a lesser but still notable effect on the indices. The coefficients reveal that while all parameters influence WPI and GWQI, elements such as EC, TDS, Sr, and As(mg/L) are more dominant factors. This detailed statistical relationship is crucial for refining WPI and GWQI calculations and for prioritizing which water quality parameters should be monitored more closely to assess and manage water pollution effectively.
Predictive insight for different data partition of WPI
The predictive accuracy of each model was evaluated using various metrics, including R2, R, MSE, and RMSE with different data partitions including 70%/30%, 60%/40% and 80%/20% training and testing phases respectively, and the accuracy of the models in forecasting the WQI was used to assess their performance. In Table 2, the predictive accuracy of ANFIS, GPR, and DT models for the WQI was evaluated using the 70/30 training and testing phase. In the training phase, ANFIS-M1 exhibited the best performance with an R2 value of 0.9935, an R-value of 0.9968, and the lowest MSE (0.0016) and RMSE (0.0404) scores among all three models (GPR-M2 and DT-M1). Likewise, during the testing phase, ANFIS-M1 maintained its superior performance with the highest R2 (0.9945), R (0.9973), and the lowest MSE (0.0016) and RMSE (0.0401) scores compared to the other models. On the other hand, GPR-M2 performed moderately well with lower R2 and R values and higher MSE and RMSE scores compared to ANFIS-M1 in both the training and testing phases. DT-M1 consistently performed the worst among the three models, with the lowest R2 and R values and the highest MSE and RMSE scores in both the training and testing phases. Conclusively, ANFIS-M1 demonstrated superior predictive accuracy compared to GPR-M2 and DT-M1 in both the training and testing phases, as evidenced by its higher R2 and R values and lower MSE and RMSE scores.
Table 2.
Predictive accuracy of WPI for 70/30.
| Training Phase (70%) | Testing Phase (30%) | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | R | MSE | RMSE | R2 | R | MSE | RMSE | |
| ANFIS-M1 | 0.9935 | 0.9968 | 0.0016 | 0.0404 | 0.9945 | 0.9973 | 0.0016 | 0.0401 |
| ANFIS-M2 | 0.9074 | 0.9526 | 0.0234 | 0.1529 | 0.9135 | 0.9558 | 0.0255 | 0.1597 |
| ANFIS-M3 | 0.8763 | 0.9361 | 0.0313 | 0.1768 | 0.9840 | 0.9920 | 0.0047 | 0.0687 |
| GPR-M1 | 0.9708 | 0.9853 | 0.0074 | 0.0859 | 0.9797 | 0.9898 | 0.0060 | 0.0773 |
| GPR-M2 | 0.9783 | 0.9891 | 0.0055 | 0.0741 | 0.9736 | 0.9867 | 0.0078 | 0.0882 |
| GPR-M3 | 0.7822 | 0.7822 | 0.7822 | 0.7822 | 0.9117 | 0.9548 | 0.0260 | 0.1614 |
| DT-M1 | 0.9128 | 0.9554 | 0.0220 | 0.1484 | 0.8697 | 0.9326 | 0.0384 | 0.1960 |
| DT-M2 | 0.8088 | 0.8994 | 0.0483 | 0.2198 | 0.8094 | 0.8997 | 0.0562 | 0.2371 |
| DT-M3 | 0.8744 | 0.9351 | 0.0317 | 0.1781 | 0.8944 | 0.9458 | 0.0311 | 0.1765 |
Significant are in value [bold].
Table 3 shows that, in both the 60/40 training and testing phases, ANFIS-M1 reliably performs better than GPR-M2 and DT-M1 in terms of R2, R, MSE, and RMSE. In the training phase, the ANFIS-M1 model outperformed other models by achieving the highest R2 value of 0.9962, followed by GPR-M2 with 0.9801 and DT-M1 with 0.9111. Similarly, it possessed the highest R-value of 0.9981, followed by GPR-M2 with 0.9900 and DT-M1 with 0.9545. Moreover, ANFIS-M1 exhibited the lowest MSE of 0.0010, followed by GPR-M2 with 0.0052 and DT-M1 with 0.0233. While In terms of RMSE, ANFIS-M1 had the lowest value of 0.0317, followed by GPR-M2 with 0.0723 and DT-M1 with 0.1526. In the testing phase, ANFIS-M1 continued to perform well by exhibiting the highest R2 value of 0.9904, followed by GPR-M2 with 0.9713 and DT-M1 with 0.8779. Likewise, it had the highest R-value of 0.9952, followed by GPR-M2 with 0.9856 and DT-M1 with 0.9370. Furthermore, ANFIS-M1 exhibited the lowest MSE of 0.0025, followed by GPR-M2 with 0.0075 and DT-M1 with 0.0321. In terms of RMSE, ANFIS-M1 had the lowest value of 0.0503, followed by GPR-M2 with 0.0869 and DT-M1 with 0.1793. The results demonstrate the superior performance of the ANFIS-M1 model in both the training and testing phases.
Table 3.
Performance results of WPI for 60/40.
| 60/40 | Training phase | Testing phase | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | R | MSE | RMSE | R2 | R | MSE | RMSE | |
| ANFIS-M1 | 0.9962 | 0.9981 | 0.0010 | 0.0317 | 0.9904 | 0.9952 | 0.0025 | 0.0503 |
| ANFIS-M2 | 0.9040 | 0.9508 | 0.0251 | 0.1586 | 0.9150 | 0.9566 | 0.0224 | 0.1496 |
| ANFIS-M3 | 0.8656 | 0.9304 | 0.0352 | 0.1877 | 0.9765 | 0.9882 | 0.0062 | 0.0787 |
| GPR-M1 | 0.9709 | 0.9853 | 0.0076 | 0.0873 | 0.9772 | 0.9885 | 0.0060 | 0.0775 |
| GPR-M2 | 0.9801 | 0.9900 | 0.0052 | 0.0723 | 0.9713 | 0.9856 | 0.0075 | 0.0869 |
| GPR-M3 | 0.7596 | 0.8716 | 0.0630 | 0.2509 | 0.9150 | 0.9565 | 0.0224 | 0.1496 |
| DT-M1 | 0.9111 | 0.9545 | 0.0233 | 0.1526 | 0.8779 | 0.9370 | 0.0321 | 0.1793 |
| DT-M2 | 0.8063 | 0.8979 | 0.0508 | 0.2253 | 0.8083 | 0.8990 | 0.0505 | 0.2247 |
| DT-M3 | 0.8667 | 0.9310 | 0.0349 | 0.1869 | 0.8988 | 0.9481 | 0.0266 | 0.1632 |
Significant are in value [bold].
However, Table 4 assesses the ANFIS, GPR, and DT models for their ability to predict the WQI during the 80/20 training and testing phases. ANFIS-M1 outperformed GPR-M2 and DT-M1 in both the training and testing phases of the study across all evaluated parameters, including R2, R, MSE, and RMSE. In the training phase, ANFIS-M1 demonstrated the highest R2 value of 0.9933, the highest R-value of 0.9967, the lowest MSE of 0.0016, and the lowest RMSE of 0.0395. In the testing phase, ANFIS-M1 exhibited the highest R2 value of 0.9460, the highest R-value of 0.9726, and the lowest MSE of 0.0019.
Table 4.
Performance results of WPI for 80/20.
| 80/20 | Training phase | Testing phase | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | R | MSE | RMSE | R2 | R | MSE | RMSE | |
| ANFIS-M1 | 0.9933 | 0.9967 | 0.0016 | 0.0395 | 0.9460 | 0.9726 | 0.0019 | 0.0436 |
| ANFIS-M2 | 0.8739 | 0.9348 | 0.0295 | 0.1717 | 0.8266 | 0.9092 | 0.0000 | 0.0013 |
| ANFIS-M3 | 0.8823 | 0.9393 | 0.0275 | 0.1658 | 0.8350 | 0.9138 | 0.0053 | 0.0729 |
| GPR-M1 | 0.9674 | 0.9836 | 0.0076 | 0.0872 | 0.9201 | 0.9592 | 0.0041 | 0.0643 |
| GPR-M2 | 0.9684 | 0.9841 | 0.0074 | 0.0860 | 0.9211 | 0.9597 | 0.0008 | 0.0280 |
| GPR-M3 | 0.7713 | 0.8782 | 0.0534 | 0.2312 | 0.7240 | 0.8509 | 0.0156 | 0.1250 |
| DT-M1 | 0.9184 | 0.9583 | 0.0191 | 0.1381 | 0.8711 | 0.9333 | 0.0613 | 0.2476 |
| DT-M2 | 0.7992 | 0.8940 | 0.0469 | 0.2166 | 0.7519 | 0.8671 | 0.0670 | 0.2589 |
| DT-M3 | 0.8823 | 0.9393 | 0.0275 | 0.1658 | 0.8350 | 0.9138 | 0.0494 | 0.2222 |
Significant are in value [bold].
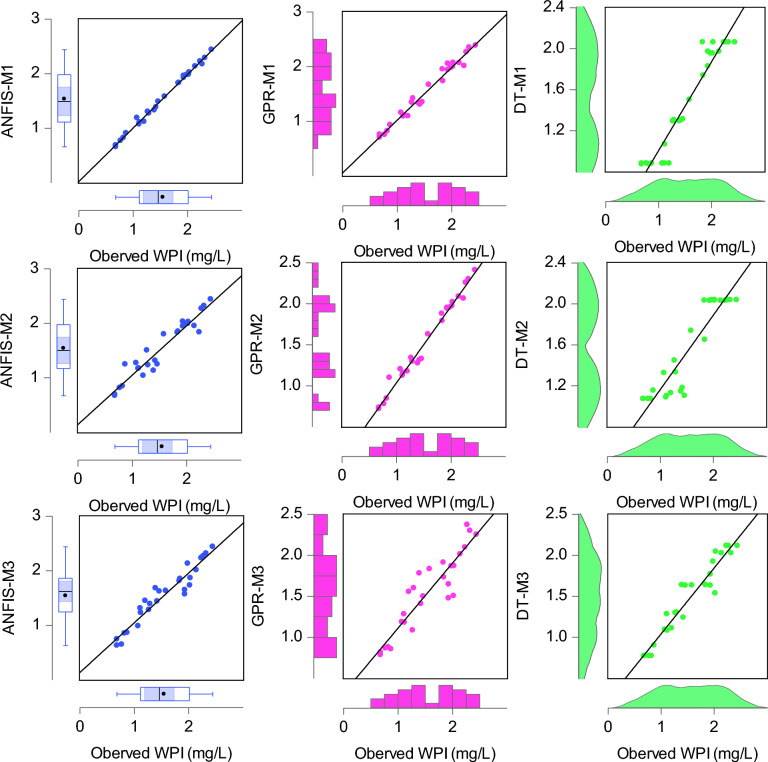
The study employed scatter plots and time series plots to interpret the degree of agreement between the observed and estimated values. These visual representations were utilized to demonstrate the predictive accuracy of the models in estimating the WPI and GWQI. Figure 3 displays scatter plots for the ANFIS, GPR, and DT models, representing the degree of agreement between the observed and predicted WPI values. These plots provide a visual assessment of the predictive accuracy models and performance in estimating the WPI values. The proximity of the points to the diagonal line indicates the level of agreement between the observed and predicted values. Comparing scatter plots of the three models allows for the evaluation of the reliability and accuracy of each model in predicting the WPI. The scatter plots shown in Fig. 4 serve as a valuable tool to visually assess the predictive accuracy of ANFIS, GPR, and DT models in estimating WPI values, enabling the identification of the most effective model for predicting WPI values.
Fig. 4.
Scatter plot between observed WPI and predicted WPI values for the three models.
Predictive insight for 70/30, 60/40 and 80/20 of GWQI
In the training phase, the ANFIS-M1 model exhibited the highest R2 value of 0.9785, followed by GPR-M1 with a value of 0.9922, while the DT-M3 model had a value of 0.9018. This indicates that ANFIS-M1 and GPR-M1 are more strongly correlated with the predicted and actual values, compared to DT-M3. Furthermore, ANFIS-M1 had the highest R-value of 0.9892, followed by GPR-M1 with a value of 0.9961, while DT-M3 had a value of 0.9496. ANFIS-M1 and GPR-M1 outperformed DT-M3 in terms of the linear relationship strength between the predicted and actual values. The MSE of the ANFIS-M1 and GPR-M1 models was the lowest at 0.0000, while that of the DT-M3 model was 0.0014. Equally, the RMSE of the ANFIS-M1 and GPR-M1 models was the lowest at 0.0010 and 0.0025, respectively, while that of the DT-M3 model was 0.0372. During the testing phase, ANFIS-M1 maintained the highest R2 value of 0.9973, followed by GPR-M1 with a value of 0.9991, while DT-M3 had a value of 0.8074. These results indicate that ANFIS-M1 and GPR-M1 have a stronger correlation between the predicted and actual values compared to DT-M3, thus suggesting their suitability for the prediction of the target variable.
In Table 5, the ANFIS-M1 and GPR models outperform the DT models in predicting the GWQI for the 60/40 training and testing phases. During the training phase, GPR-M1 demonstrated the highest performance, with an R2 value of 0.9934, indicating its ability to explain a significant portion of the variance in the data, followed by ANFIS-M1 with 0.9812 and DT-M3 with 0.8915. GPR-M1 also exhibited the strongest linear relationship between predicted and actual values during training, with an R-value of 0.9967, followed by ANFIS-M1 with 0.9905 and DT-M3 with 0.9442. Furthermore, GPR-M1 had the lowest MSE and RMSE, indicating its superior performance in predicting the target variable during training. During the testing phase, GPR-M1 consistently outperformed ANFIS-M1 and DT-M3, with the highest R2, R, and lowest MSE and RMSE, demonstrating its robustness and accuracy in predicting the target variable. These results suggest that GPR-M1 is a promising approach for predicting the target variable, based on its superior performance during both the training and testing phases.
Table 5.
Performance results of GWQI for 60/40.
| 60/40 | Training Phase | Testing Phase | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | R | MSE | RMSE | R2 | R | MSE | RMSE | |
| ANFIS-M1 | 0.9812 | 0.9905 | 0.0000 | 0.0030 | 0.9914 | 0.9957 | 0.0026 | 0.0506 |
| ANFIS-M2 | 0.8938 | 0.9454 | 0.0001 | 0.0119 | 0.9334 | 0.9661 | 0.0197 | 0.1405 |
| ANFIS-M3 | 0.8592 | 0.9269 | 0.0037 | 0.0607 | 0.9756 | 0.9877 | 0.0072 | 0.0851 |
| GPR-M1 | 0.9934 | 0.9967 | 0.0000 | 0.0002 | 0.9967 | 0.9984 | 0.0010 | 0.0312 |
| GPR-M2 | 0.8409 | 0.9170 | 0.0009 | 0.0303 | 0.9174 | 0.9578 | 0.0245 | 0.1564 |
| GPR-M3 | 0.8068 | 0.8982 | 0.0084 | 0.0917 | 0.9538 | 0.9766 | 0.0137 | 0.1170 |
| DT-M1 | 0.8849 | 0.9407 | 0.0002 | 0.0138 | 0.9374 | 0.9682 | 0.0185 | 0.1362 |
| DT-M2 | 0.8866 | 0.9416 | 0.0001 | 0.0091 | 0.8006 | 0.8948 | 0.0591 | 0.2431 |
| DT-M3 | 0.8915 | 0.9442 | 0.0063 | 0.0791 | 0.8464 | 0.9200 | 0.0455 | 0.2134 |
Significant are in value [bold].
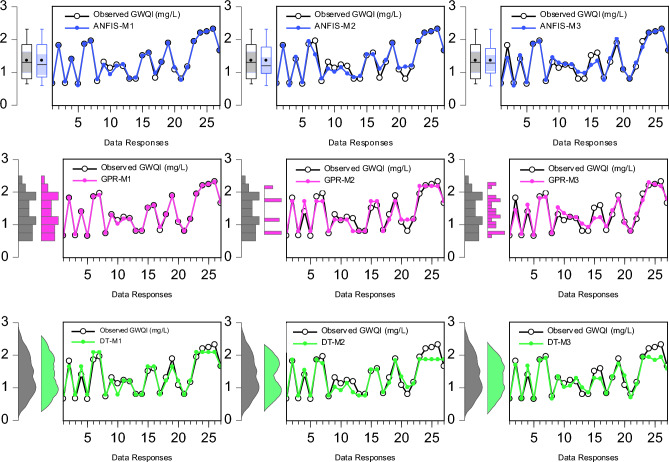
Figure 5 presents a graphical representation of a time series plot that depicts the agreement between the observed and estimated GWQI for three models, namely, ANFIS, GPR, and DT. The time series plot provides a visual representation of the agreement between the observed and estimated GWQI values over time and enables the examination of the temporal patterns and trends in the observed and predicted GWQI values. By comparing the observed and estimated GWQI values over time, the plot allows for the assessment of the ability of the models to capture the variations and fluctuations in groundwater quality and helps to identify systematic deviations or biases in the estimated GWQI values compared to the observed values. This is important for evaluating the overall performance models and reliability in predicting the GWQI. Moreover, the time series plot enables the evaluation of the model’s predictive accuracy in capturing short-term and long-term variations in GWQI and provides a comprehensive view of how well the models track the changes in groundwater quality over the study period. By visually comparing the time series plots for the three models, it is possible to assess the consistency and accuracy of the models in estimating the GWQI values over time and to evaluate the performance of each model in predicting groundwater quality.
Fig. 5.
Time series plot showing the agreement between observed and estimated GWQI.
Table 6 presents the accuracy of ANFIS, GPR, and DT models in predicting GWQI in the 80/20 training and testing phases. During the training and testing phases, ANFIS-M1 exhibited higher R2, R, MSE, and RMSE values compared to GPR-M1 and DT-M1, indicating its superior performance in capturing the underlying patterns in the data and making accurate predictions. ANFIS-M1 specifically demonstrated a higher R2 value of 0.9933 during the training phase and maintained a higher R2 value of 0.9443 in the testing phase compared to GPR-M1 and DT-M1. Additionally, ANFIS-M1 consistently exhibited higher R values, indicating a better fit of the model to the data compared to GPR-M1 and DT-M1. Moreover, the MSE and RMSE values were consistently lower for ANFIS-M1 in both phases, indicating that its predictions were more accurate and closer to the actual values compared to GPR-M1 and DT-M1. Generally, these results suggest that ANFIS-M1 is a more effective modeling approach for capturing the underlying patterns in the data and making accurate predictions compared to GPR-M1 and DT-M1.
Table 6.
Performance results of GWQI for 80/20.
| 80/20 | Training Phase | Testing Phase | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | R | MSE | RMSE | R2 | R | MSE | RMSE | |
| ANFIS-M1 | 0.9933 | 0.9967 | 0.0000 | 0.0030 | 0.9443 | 0.9718 | 0.0019 | 0.0436 |
| ANFIS-M2 | 0.6360 | 0.7975 | 0.0003 | 0.0186 | 0.5870 | 0.7662 | 0.0125 | 0.1116 |
| ANFIS-M3 | 0.6432 | 0.8020 | 0.0000 | 0.0008 | 0.5942 | 0.7709 | 0.0251 | 0.1584 |
| GPR-M1 | 0.7461 | 0.8638 | 0.0007 | 0.0256 | 0.6971 | 0.8349 | 0.0114 | 0.1066 |
| GPR-M2 | 0.5676 | 0.7534 | 0.0009 | 0.0305 | 0.5186 | 0.7202 | 0.0271 | 0.1646 |
| GPR-M3 | 0.5810 | 0.7622 | 0.0001 | 0.0079 | 0.5320 | 0.7294 | 0.0327 | 0.1809 |
| DT-M1 | 0.7130 | 0.8444 | 0.0003 | 0.0160 | 0.6640 | 0.8148 | 0.0501 | 0.2238 |
| DT-M2 | 0.5670 | 0.7530 | 0.0013 | 0.0367 | 0.5180 | 0.7197 | 0.1453 | 0.3811 |
| DT-M3 | 0.6155 | 0.7845 | 0.0015 | 0.0394 | 0.5665 | 0.7526 | 0.1318 | 0.3631 |
Significant are in value [bold].
Comparison of the best division phase
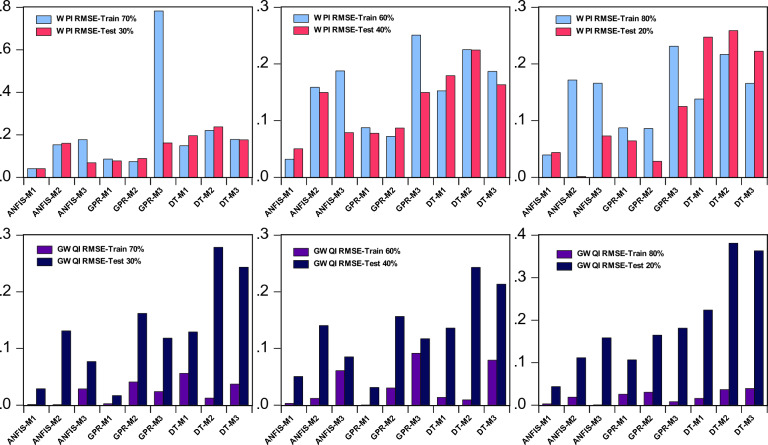
Figure 6 presents a comparative analysis of three predictive models, namely, ANFIS, GPR, and DT, for estimating the WQI and GWQI. The comparison is based on various error metrics such as R2, R, MSE, and RMSE for each model, evaluated across different training and testing phases. The error metrics are fundamental for assessing the accuracy and reliability of the models in predicting the quality of water and groundwater. The comparative analysis provides a comprehensive assessment of the performance of the model and facilitates the identification of the best-performing model based on the overall error metrics. The R2, R, MSE, and RMSE values for each model are compared to determine the model that consistently demonstrates superior predictive accuracy and precision in estimating the WQI and GWQI. Furthermore, the comparison offers insights into the performance variability of the models across different training and testing phases, allowing for a thorough evaluation of their robustness and consistency in predicting water and groundwater quality. The results provide valuable guidance for selecting the most reliable model for predicting the WQI and GWQI values and contribute to the scientific understanding of the efficacy of the ANFIS, GPR, and DT models in predicting water and groundwater quality.
Fig. 6.
Overall error comparison between the models.
To compare the performance results of the WPI prediction models across the tables for the 70/30, 60/40, and 80/20 data splits, we’ll consider several performance criteria. In Table 2 for the 70/30 data split, ANFIS-M1 demonstrates exemplary performance with R² values of 0.9935 in training and 0.9945 in testing, indicating that nearly all the variability in WPI can be explained by the model. However, GPR-M3 seems to have a misprint with repeated values, indicating a possible error in the data. Table 3 shows the results for the 60/40 data split. ANFIS-M1 again shows strong performance with R² values of 0.9962 for training and 0.9904 for testing, albeit with a slight decrease in testing accuracy compared to the 70/30 split. For the 80/20 data split in Table 4, the performance of ANFIS-M1 decreases slightly, with an R² of 0.9933 in training and 0.9460 in testing, suggesting that the model’s ability to generalize decreases with less training data. GPR-M2 shows a consistent training R² value of around 0.968, but the testing R² decreases to 0.9211, indicating a loss in prediction accuracy in the testing phase. Across all data splits, ANFIS models tend to perform better in both training and testing phases than DT models, which consistently show lower R² and higher RMSE values. The performance generally decreases with a smaller proportion of training data, which is expected as models have less information to learn from. The GPR models display robustness in training but exhibit a drop in performance in the testing phase when the training data is reduced, particularly in the 80/20 split. The ANFIS models seem to be the most reliable for WPI prediction across different data splits, maintaining high R² values and low RMSE values in both the training and testing phases. The decrease in performance in the 80/20 split highlights the importance of sufficient training data for model accuracy and generalization (see, Fig. 6).
To compare the performance results of GWQI prediction models across the three tables, we need to look at both the training and testing phases for each data split (70/30, 60/40, 80/20). For the 70/30 data split in Table 7, the models show high predictive accuracy, with ANFIS-M1 and GPR-M1 standing out in both training and testing phases, showing R² values of 0.9785 and 0.9922 during training, and 0.9973 and 0.9991 during testing, respectively. This indicates a very strong fit to the data. In Table 5, for the 60/40 split, we again see high performance in training for ANFIS-M1 and GPR-M1, with R² values of 0.9812 and 0.9934, respectively. The testing phase shows a slight reduction in predictive accuracy compared to the 70/30 split, with R² values of 0.9914 for ANFIS-M1 and 0.9967 for GPR-M1, suggesting that the models are still performing exceptionally well but with a slight performance decrease when the training data is reduced (see Fig. 7).
Table 7.
Predictive accuracy of GWQI for 70/30.
| 70/30 | Training Phase | Testing Phase | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | R | MSE | RMSE | R2 | R | MSE | RMSE | |
| ANFIS-M1 | 0.9785 | 0.9892 | 0.0000 | 0.0010 | 0.9973 | 0.9986 | 0.0008 | 0.0289 |
| ANFIS-M2 | 0.8898 | 0.9433 | 0.0000 | 0.0007 | 0.9440 | 0.9716 | 0.0172 | 0.1311 |
| ANFIS-M3 | 0.8736 | 0.9347 | 0.0008 | 0.0286 | 0.9807 | 0.9903 | 0.0059 | 0.0770 |
| GPR-M1 | 0.9922 | 0.9961 | 0.0000 | 0.0025 | 0.9991 | 0.9995 | 0.0003 | 0.0169 |
| GPR-M2 | 0.8508 | 0.9224 | 0.0017 | 0.0410 | 0.9148 | 0.9564 | 0.0262 | 0.1617 |
| GPR-M3 | 0.8280 | 0.9099 | 0.0006 | 0.0238 | 0.9545 | 0.9770 | 0.0140 | 0.1182 |
| DT-M1 | 0.8847 | 0.9406 | 0.0032 | 0.0562 | 0.9458 | 0.9725 | 0.0166 | 0.1289 |
| DT-M2 | 0.8970 | 0.9471 | 0.0002 | 0.0124 | 0.7476 | 0.8646 | 0.0775 | 0.2784 |
| DT-M3 | 0.9018 | 0.9496 | 0.0014 | 0.0372 | 0.8074 | 0.8985 | 0.0591 | 0.2432 |
Significant are in value [bold].
Fig. 7.
Cumulative probability density function graph for both the observed and simulated WPI and GWQI.
However, Table 6 represents the 80/20 split. Here, the performance drops more notably, especially in the testing phase. ANFIS-M1 shows a decrease in testing phase R² to 0.9443, while GPR-M1 drops to 0.6971. This indicates that with even less training data, the model’s ability to generalize decreases. Comparing across all tables, we observe a trend where the models trained with a higher proportion of data (70/30 split) outperform those with less training data (80/20 split), which is a common occurrence in machine learning where more data generally leads to better model performance. The ANFIS models generally perform better than DT models but are closely matched or sometimes outperformed by the GPR models, particularly in the testing phase, indicating GPR’s robustness in generalization. Furthermore, the RMSE values across all tables tend to increase with a decrease in the training data percentage, reflecting the increased uncertainty or error in the models’ predictions when they are trained with less data. The DT models consistently show higher RMSE values across all splits, suggesting that ANFIS and GPR may be more suitable for predicting GWQI in this context. The DT models consistently yield higher RMSE values across all data splits, suggesting that ANFIS and GPR are more reliable for GWQI prediction in this study. The decrease in R² values and increase in RMSE with smaller training sets highlight the importance of dataset size in model training for reliable groundwater quality prediction. The innovation in the present work significantly reduces the need for continuous field sampling by providing accurate predictions based on existing data, ultimately saving time and resources for policymakers. Similarly, the application of our models can lead to more informed and effective water management policies, potentially preventing costly environmental and public health issues in the long run. By facilitating targeted interventions and efficient resource allocation, the approach offers significant economic and environmental benefits, making the initial efforts and costs a worthwhile investment.
Environmental implication, recommendation, and future studies
The environmental implications of this research are significant, aligning with the Sustainable Development Goals (SDG), particularly SDG 6 (Clean Water and Sanitation) by enhancing the ability to monitor and manage water resources in arid regions effectively. The United Nations (UN) emphasizes the importance of water quality management in combating water scarcity and pollution, critical challenges in arid areas such as the Eastern Province of Saudi Arabia. The World Health Organization (WHO) has set guidelines for water quality that highlight the importance of reliable and accurate water quality monitoring systems to protect human health and the environment. By enabling precise predictions of WQI and GWQI at unmonitored sites, this study supports these guidelines, offering a tool for early detection of pollution and facilitating proactive management strategies. However, the United Nations Children’s Fund (UNICEF) also stresses the importance of clean water for children’s health and development, underscoring the relevance of this research in providing safe water through improved quality monitoring and management. Furthermore, the Environmental Protection Agency (EPA) has developed frameworks for water quality assessment and management, which can benefit from advanced prediction models like the one proposed in this study, enhancing the effectiveness of water pollution control strategies. Recommendations for environmental management include integrating the proposed hybrid model into existing water quality monitoring systems to improve accuracy and reliability in water quality assessment. This integration would enable policymakers and environmental managers to make informed decisions, prioritizing interventions in areas most at risk of pollution. Future studies should focus on expanding the application of this model to other arid and semi-arid regions globally, considering different hydrogeological contexts and pollution sources. Moreover, further research could explore the integration of real-time data from IoT devices into the model, enhancing its predictive capabilities and enabling dynamic water quality management. Lastly, assessing the long-term impacts of improved water quality management on public health and ecosystem resilience would provide valuable insights into the broader implications of this research.
Conclusions
In this study, the current investigation establishes a sophisticated hybrid modelling framework that significantly enhances the prediction of WPI and GWQI in the Eastern Province of Saudi Arabia, a region grappling with the dual challenges of water scarcity and pollution. By amalgamating non-parametric kernel Gaussian learning (GPR), adaptive neuro-fuzzy inference system (ANFIS), and decision tree (DT) algorithms, the research not only pioneers the application of these methods in the context of Saudi Arabia’s hydrogeology but also sets a precedent for their use in similar arid environments worldwide. The comprehensive statistical analysis and machine learning techniques employed herein have shown that models trained with a more substantial proportion of data (e.g., a 70/30 split) yield the most accurate predictions, with GPR-M1 and ANFIS-M1 standing out in their respective indices. These findings reiterate the importance of ample training data in developing robust predictive models and underscore the potential of advanced AI techniques in environmental management. This study’s contribution is manifold: it provides a robust methodological framework for environmental scientists and policymakers, offers actionable insights for effective water resource management, and underscores the broader implications of using AI to safeguard natural resources. By enhancing the capacity to accurately predict WQI and GWQI, this research supports sustainable water management practices that are crucial for the well-being of both human populations and ecosystems in arid regions.
For future research, it is recommended to extend the scope of the current hybrid modeling framework to include real-time data acquisition and the integration of more optimization algorithms and nonlinear feature selection to further refine the predictive accuracy of WPI and GWQI. The incorporation of additional environmental parameters and the use of big data analytics could provide deeper insights into the complex relationships within hydrogeological data. Additionally, expanding the geographic scope to include various arid and semi-arid regions around the world would validate the model’s applicability and robustness across different environmental conditions. Collaborative efforts with local governments and international bodies can facilitate the implementation of these predictive models into water management policies, aiming for a proactive approach to water quality monitoring. Moreover, exploring the socio-economic impacts of improved water quality prediction can guide sustainable development planning. The integration of this research into educational curriculums for environmental science and engineering would also be beneficial, fostering the next generation of researchers in the field of water resource management.
Author contributions
Editor-in-chief, Scientific ReportDear Sir, Author Agreement and Contribution StatementThe authors declare that they have agreed to send and publish their work (if accepted) in the Scientific Report. All authors contributed to the developement of this article.Sincerely, Dr. Sani Isah Abba Department of Chemical Engineering, Prince Mohammad BIn Fahd University, Al Khobar, Saudi Arabia/Water Research Centre, Prince Mohammad Bin Fahd University, Al Khobar, Saudi Arabia saniisaabba86@gmail.com Tel: + 966591019879.
Data availability
The data is vailable upon request through the corrosponding author.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.El Bilali, A. & Taleb, A. Prediction of irrigation water quality parameters using machine learning models in a semi-arid environment. J. Saudi Soc. Agric. Sci.19, 439–451 (2020). [Google Scholar]
- 2.Busico, G. et al. A novel hybrid method of specific vulnerability to anthropogenic pollution using multivariate statistical and regression analyses. Water Res.171, 115386 (2020). 10.1016/j.watres.2019.115386 [DOI] [PubMed] [Google Scholar]
- 3.Li, D. Quantifying water use and groundwater recharge under flood irrigation in an arid Oasis of Northwestern China. Agric. Water Manag.240, 106326 (2020). 10.1016/j.agwat.2020.106326 [DOI] [Google Scholar]
- 4.Batarseh, M. et al. Dataset for the physio-chemical Parameters of Groundwater in the Emirate of Abu Dhabi, UAE. Data Br.38, 107353 (2021). 10.1016/j.dib.2021.107353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zimit, A. Y., Jibril, M. M., Azimi, M. S. & Abba, S. I. Hybrid predictive based control of precipitation in a water-scarce region: A focus on the application of intelligent learning for green irrigation in agriculture sector. J. Saudi Soc. Agric. Sci.10.1016/j.jssas.2023.06.001 (2023). 10.1016/j.jssas.2023.06.001 [DOI] [Google Scholar]
- 6.Bwambale, E., Abagale, F. K. & Anornu, G. K. Data-driven model predictive control for precision irrigation management. Smart Agric. Technol.3, 100074 (2023). 10.1016/j.atech.2022.100074 [DOI] [Google Scholar]
- 7.Emmanuel, A. et al. A review on monitoring and advanced control strategies for precision irrigation. Comput. Electron. Agric.173, 105441 (2020). 10.1016/j.compag.2020.105441 [DOI] [Google Scholar]
- 8.Simões, F., Moreira, A., Bisinoti, M., Gimenez, S. & Santos Yabe, M. . Water quality index as a simple indicator of aquaculture effects on aquatic bodies. Ecol. Indic.8, 476–484 (2008). 10.1016/j.ecolind.2007.05.002 [DOI] [Google Scholar]
- 9.Zhu, M. et al. A review of the application of machine learning in water quality evaluation. Eco-Environ. Health1, 107–116 (2022). 10.1016/j.eehl.2022.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu, Y., Zhao, T., Ju, W. & Shi, S. Materials discovery and design using machine learning. J. Mater.3, 159–177 (2017). [Google Scholar]
- 11.Abba, S. I. et al. Implementation of data intelligence models coupled with ensemble machine learning for prediction of water quality index. Environ. Sci. Pollut Res.27, 41524–41539 (2020). 10.1007/s11356-020-09689-x [DOI] [PubMed] [Google Scholar]
- 12.Islam, S., Rasul, T., Alam, J., Bin, & Haque, M. A. Evaluation of water quality of the Titas river using NSF water quality index. J. Sci. Res.3, 151 (2010). 10.3329/jsr.v3i1.6170 [DOI] [Google Scholar]
- 13.Tiyasha, T., Tung, T. M. & Yaseen, Z. M. Deep learning for prediction of water quality index classification: Tropical catchment environmental assessment. Nat. Resour. Res.30, 1–20 (2021). 10.1007/s11053-021-09922-5 [DOI] [Google Scholar]
- 14.Gaya, M. S. et al. Estimation of water quality index using artificial intelligence approaches and multi-linear regression. IAES Int. J. Artif. Intell.9, 126–134 (2020). [Google Scholar]
- 15.Gaya, M. S. et al. Estimation of Water Quality Index Using Artificial Intelligence Approaches and multi-linear Regression. 9, 126–134 (2020).
- 16.Al-Sulttani, A. O. et al. Proposition of new ensemble data-intelligence models for surface water quality prediction. IEEE Access9, 108527–108541 (2021). 10.1109/ACCESS.2021.3100490 [DOI] [Google Scholar]
- 17.Alrowais, R. et al. Groundwater Quality assessment for drinking and irrigation purposes at Al-Jouf area in KSA using artificial neural network, GIS, and multivariate statistical techniques. Water15, 2982 (2023). 10.3390/w15162982 [DOI] [Google Scholar]
- 18.Abdul Karim, S. A. & Kamsani, N. Water Quality Index Prediction Using Multiple Linear Fuzzy Regression Model: Case Study in Perak River, Malaysia. (2020). 10.1007/978-981-15-3485-0
- 19.Kouadri, S., Elbeltagi, A., Islam, A. R. M. & Kateb, S. Performance of machine learning methods in predicting water quality index based on irregular data set: Application on Illizi Region (Algerian Southeast). Appl. Water Sci.11, 1–20 (2021). 10.1007/s13201-021-01528-9 [DOI] [Google Scholar]
- 20.Machiwal, D., Jha, M. K., Singh, V. P. & Mohan, C. Assessment and mapping of groundwater vulnerability to pollution: Current status and challenges. Earth Sci. Rev.185, 901–927 (2018). 10.1016/j.earscirev.2018.08.009 [DOI] [Google Scholar]
- 21.Sánchez, E. et al. Use of the water quality index and dissolved oxygen deficit as simple indicators of watersheds pollution. Ecol. Indic.7, 315–328 (2007). 10.1016/j.ecolind.2006.02.005 [DOI] [Google Scholar]
- 22.Singh, G., Singh, J., Wani, O. A., Egbueri, J. C. & Agbasi, J. C. Assessment of groundwater suitability for sustainable irrigation: a comprehensive study using indexical, statistical, and machine learning approaches. Groundw. Sustain. Dev.24, 101059 (2024). 10.1016/j.gsd.2023.101059 [DOI] [Google Scholar]
- 23.Uddin, M. G., Nash, S., Rahman, A. & Olbert, A. I. Performance analysis of the water quality index model for predicting water state using machine learning techniques. Process. Saf. Environ. Prot.169, 808–828 (2023). 10.1016/j.psep.2022.11.073 [DOI] [Google Scholar]
- 24.Li, Z., Liu, H., Zhang, C. & Fu, G. Real-time water quality prediction in water distribution networks using graph neural networks with sparse monitoring data. Water Res.250, 121018 (2024). 10.1016/j.watres.2023.121018 [DOI] [PubMed] [Google Scholar]
- 25.Aldrees, A., Khan, M., Taha, A. T. B. & Ali, M. Evaluation of water quality indexes with novel machine learning and shapley additive explanation (SHAP) approaches. J. Water Process. Eng.58, 104789 (2024). 10.1016/j.jwpe.2024.104789 [DOI] [Google Scholar]
- 26.Ding, F. et al. Optimization of water quality index models using machine learning approaches. Water Res.243, 120337 (2023). 10.1016/j.watres.2023.120337 [DOI] [PubMed] [Google Scholar]
- 27.Raheja, H., Goel, A. & Pal, M. Evaluation of groundwater quality for drinking purposes based on machine learning algorithms and GIS. Sustain. Water Resour. Manag.10, 11 (2024). 10.1007/s40899-023-00990-4 [DOI] [Google Scholar]
- 28.Sajib, A. M. et al. Developing a novel tool for assessing the groundwater incorporating water quality index and machine learning approach. Groundw. Sustain. Dev.23, 101049 (2023). 10.1016/j.gsd.2023.101049 [DOI] [Google Scholar]
- 29.Singha, S., Pasupuleti, S., Singha, S. S., Singh, R. & Kumar, S. Prediction of groundwater quality using efficient machine learning technique. Chemosphere276, 130265 (2021). 10.1016/j.chemosphere.2021.130265 [DOI] [PubMed] [Google Scholar]
- 30.Kazmi, Z. A. & Sodangi, M. Integrated analysis of the geotechnical factors impeding sustainable building construction—The case of the eastern province of Saudi Arabia. Sustain13, 6531 (2021). 10.3390/su13126531 [DOI] [Google Scholar]
- 31.Anton, D. Modern eolian deposits of the eastern province of Saudi Arabia. In Developments in Sedimentology vol. 38 365–378 (Elsevier, 1983).
- 32.Benaafi, M. & Abdullatif, O. Sedimentological, mineralogical, and geochemical characterization of sand dunes in Saudi Arabia. Arab. J. Geosci.8, 11073–11092 (2015). 10.1007/s12517-015-1970-9 [DOI] [Google Scholar]
- 33.Yassin, M. A., Usman, A. G., Abba, S. I., Ozsahin, D. U. & Aljundi, I. H. Intelligent learning algorithms integrated with feature engineering for sustainable groundwater salinization modelling: Eastern Province of Saudi Arabia. Results Eng.20, 101434 (2023). 10.1016/j.rineng.2023.101434 [DOI] [Google Scholar]
- 34.Al-Naeem, A. Evaluation of groundwater of Al-Hassa Oasis, Eastern Region Saudi Arabia. Res. J. Environ. Sci.5, 624–642 (2011). 10.3923/rjes.2011.624.642 [DOI] [Google Scholar]
- 35.Alhawas, I. & Hassaballa, A. A. Representation of the spatial association between salinity and water chemical properties in Al-Hassa Oasis. Int. J. Agric. Biol. Eng.13, 168–174 (2020). [Google Scholar]
- 36.Buragohain, M. & Mahanta, C. A novel approach for ANFIS modelling based on full factorial design. Appl. Soft Comput. J.8, 609–625 (2008). 10.1016/j.asoc.2007.03.010 [DOI] [Google Scholar]
- 37.Kisi, O. et al. Modeling groundwater quality parameters using hybrid neuro-fuzzy methods. Water Resour. Manag.33, 847–861 (2019). 10.1007/s11269-018-2147-6 [DOI] [Google Scholar]
- 38.Chen, W. H. et al. Data-driven robust model predictive control framework for stem water potential regulation and irrigation in water management. Control Eng. Pract.113, 104841 (2021). 10.1016/j.conengprac.2021.104841 [DOI] [Google Scholar]
- 39.Fang, S., Hu, R., Yuan, X., Liu, S. & Zhang, Y. Resolution enhancement for lung 4D-CT based on transversal structures by using multiple gaussian process regression learning. Phys. Med.78, 187–194 (2020). 10.1016/j.ejmp.2020.09.011 [DOI] [PubMed] [Google Scholar]
- 40.Yoo, K., Shukla, S. K., Ahn, J. J., Oh, K. & Park, J. Decision tree-based data Mining and rule Induction for Identifying Hydrogeological Parameters that Influence Groundwater Pollution Sensitivity. J. Clean. Prod.122, 277–286 (2016). 10.1016/j.jclepro.2016.01.075 [DOI] [Google Scholar]
- 41.Abba, S. I. et al. Drinking water resources suitability assessment based on pollution index of groundwater using improved explainable artificial intelligence. Sustainability15, 15655 (2023). 10.3390/su152115655 [DOI] [Google Scholar]
- 42.Yaseen, Z. M. The next generation of soil and water bodies heavy metals prediction and detection: New expert system based edge cloud server and federated learning technology. Environ. Pollut.313, 120081 (2022). 10.1016/j.envpol.2022.120081 [DOI] [PubMed] [Google Scholar]
- 43.Moriasi, D. N., Gitau, M. W., Pai, N. & Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE58, 1763–1785 (2015). 10.13031/trans.58.10715 [DOI] [Google Scholar]
- 44.Lu, H. & Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere249, 126169 (2020). 10.1016/j.chemosphere.2020.126169 [DOI] [PubMed] [Google Scholar]
- 45.Abba, S. I., Benaafi, M., Usman, A. G. & Aljundi, I. H. Inverse groundwater salinization modeling in a Sandstone’s aquifer using stand-alone models with an improved non-linear ensemble machine learning technique. J. King Saud Univ. Comput. Inf. Sci.10.1016/j.jksuci.2022.08.002 (2022). 10.1016/j.jksuci.2022.08.002 [DOI] [Google Scholar]
- 46.Baig, N., Abba, S. I., Usman, J., Benaafi, M. & Aljundi, I. H. Ensemble hybrid machine learning to simulate dye/divalent salt fractionation using a loose nanofiltration membrane. Environ. Sci. Adv.2, 1446–1459 (2023). 10.1039/D3VA00124E [DOI] [Google Scholar]
- 47.Usman, J. et al. Intelligent optimization for modelling superhydrophobic ceramic membrane oil flux and oil-water separation efficiency: Evidence from wastewater treatment and experimental laboratory. Chemosphere331, 138726 (2023). 10.1016/j.chemosphere.2023.138726 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data is vailable upon request through the corrosponding author.