How Many Imputations Do You Need? A Two-stage Calculation Using a Quadratic Rule

Abstract

When using multiple imputation, users often want to know how many imputations they need. An old answer is that 2–10 imputations usually suffice, but this recommendation only addresses the efficiency of point estimates. You may need more imputations if, in addition to efficient point estimates, you also want standard error (SE) estimates that would not change (much) if you imputed the data again. For replicable SE estimates, the required number of imputations increases quadratically with the fraction of missing information (not linearly, as previous studies have suggested). I recommend a two-stage procedure in which you conduct a pilot analysis using a small-to-moderate number of imputations, then use the results to calculate the number of imputations that are needed for a final analysis whose SE estimates will have the desired level of replicability. I implement the two-stage procedure using a new SAS macro called %mi_combine and a new Stata command called how_many_imputations.

Overview

Multiple imputation (MI) is a popular method for repairing and analyzing data with missing values (Rubin 1987). Using MI, you fill in the missing values with imputed values that are drawn at random from a posterior predictive distribution that is conditioned on the observed values $Y_{\text{obs}}$. You repeat the process of imputation $M$ times to obtain $M$ imputed data sets, which you analyze as though they were complete. You then combine the results of the $M$ analyses to obtain a point estimate ${\widehat{\text{θ}}}_{\text{MI}}$ and standard error (SE) estimate ${\widehat{SE}}_{\text{MI}}$ for each parameter $\text{θ}$.

Because MI estimates are obtained from a random sample of $M$ imputed data sets, MI estimates include a form of random sampling variation known as imputation variation. Imputation variation makes MI estimates somewhat inefficient in the sense that the estimates obtained from a sample of $M$ imputed data sets are more variable, and offer less power, than the asymptotic estimates that would be obtained if you could impute the data an infinite number of times. In addition, MI estimates can be nonreplicable in the sense that the estimates you report from a sample of $M$ imputed data sets can differ substantially from the estimates that someone else would get if they reimputed the data and obtained a different sample of $M$ imputed data sets.

Nonreplicable results reduce the openness and transparency of scientific research (Freese 2007). In addition, the possibility of changing results by reimputing the data may tempt researchers to capitalize on chance (intentionally or not) by imputing and reimputing the data until a desired result, such as $p\text{<}.05$, is obtained.

The problems of inefficiency and nonreplicability can be reduced by increasing the number of imputations—but how many imputations are enough? Until recently, it was standard advice that $M\text{=2–10}$ imputations usually suffice (Rubin 1987), but that advice only addresses the relative efficiency of the point estimate ${\widehat{\text{θ}}}_{\text{MI}}$. If you also want the SE estimate ${\widehat{SE}}_{\text{MI}}$ to be replicable, then you may need more imputations—as many as $M>200$ in some situations—though fewer imputations may still suffice in many settings (Bodner 2008; Graham, Olchowski, and Gilreath 2007; White, Royston, and Wood 2011).

It might seem conservative to set $M\text{=200}$ (say) as a blanket policy—and that policy may be practical in situations where the data are small and the imputations and analyses run quickly. But if the data are large, or the imputations or analyses run slowly, then you will want to use as few imputations as you can, and you need guidance regarding how many imputations are really needed for your specific data and analysis.

A Quadratic Rule

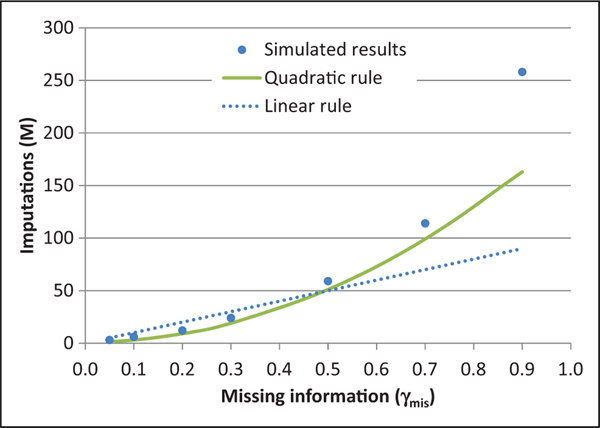
A recently proposed rule is that, to estimate SEs reliably, you should choose the number of imputations according to the linear rule $M=100{\gamma }_{\text{mis}}$ (Bodner 2008; White et al. 2011), where ${\gamma }_{\text{mis}}$ is the fraction of missing information defined below in equation (4). But this linear rule understates the required number of imputations when ${\gamma }_{\text{mis}}$ is large (Bodner 2008) and overstates the required number of imputations when ${\gamma }_{\text{mis}}$ is small (see Figure 1).

Figure 1.

Results of Bodner’s (2008) simulation fitted to the linear rule $M=100{\gamma }_{\text{mis}}$ and to the quadratic rule, which in this situation simplifies to $M=200{\gamma }_{\text{mis}}^2$.

In fact, for replicable SE estimates, the required number of imputations does not fit a linear function of ${\gamma }_{\text{mis}}$. It is better approximated by a quadratic function of ${\gamma }_{\text{mis}}$. A useful version of the quadratic rule (derived later) is:

$$M=1+\frac{1}{2}{\left(\frac{{\gamma }_{\text{mis}}}{\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)}\right)}^2,$$ (1)

where

$$\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)=\frac{SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)}{E\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)},$$ (2)

is the coefficient of variation (CV), which summarizes imputation variation in the SE estimate. The numerator and denominator of the CV are the mean $E\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)$ and standard deviation $SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)$ of ${\widehat{SE}}_{\text{MI}}$ across all possible sets of $M$ imputed data sets, holding the observed values $Y_{\text{obs}}$ constant.

Instead of choosing the CV directly, it may be more natural for you to set a target for $SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)$. For example, if you want to ensure that the SE estimate would typically change by about .01 if the data were reimputed, you might set a target of $SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)=.01$ and calculate the implied target for the CV. I will illustrate this by example later on.

An alternative is to choose $M$ to achieve some desired degrees of freedom $(df)$ in the SE estimate (Allison 2003 footnote 7; von Hippel 2016, table 3). Then, as shown in Degrees of Freedom subsection, the quadratic rule can be rewritten as:

$$M=1+df{\gamma }_{\text{mis}}^2.$$ (3)

Some users will want to aim for replicable SE estimates while others may find it more natural to aim for a target $df$ such as 25, 100, or 200. The two approaches are equivalent. However, estimates of $df$ can be very unstable, as we will see later, and this makes the estimated $df$ a fallible guide for the number of imputations.

A Two-stage Procedure

If you knew both ${\gamma }_{\text{mis}}$ and your desired CV (or your desired $df$), you could plug those numbers into formula (1) (or (13)) and get the required number of imputations $M$. But the practical problem with this approach is that ${\gamma }_{\text{mis}}$ is typically not known in advance. ${\gamma }_{\text{mis}}$ is not the fraction of values that are missing; it is the fraction of information that is missing about the parameter $\text{θ}$ (see equation (4)). ${\gamma }_{\text{mis}}$ is typically estimated using MI (see equation (7)), so estimating ${\gamma }_{\text{mis}}$ requires an initial choice of $M$.

For that reason, I recommend a two-stage procedure.

1. In the first stage, you conduct a small-$M$ pilot analysis to obtain a pilot SE estimate ${\widehat{SE}}_{\text{MI}}$ and a conservative estimate of ${\gamma }_{\text{mis}}$. From the pilot analysis, you use the estimate ${\widehat{SE}}_{\text{MI}}$ and your goal for $SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)$ to estimate your target CV as $\widehat{\text{CV}}=SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)/{\widehat{SE}}_{\text{MI}}$.¹

2. In the second stage, you plug your estimate of ${\gamma }_{\text{mis}}$ and your target CV into the formula (1) to get the required number of imputations $M$. If your pilot $M$ was at least as large as the required $M$, then your pilot analysis was good enough, and you can stop. Otherwise, you conduct a second and final analysis using the $M$ that was recommended by the pilot analysis.

I said that the pilot analysis should be used to get a conservative estimate of ${\gamma }_{\text{mis}}$. Let me explain what I mean by conservative. The obvious estimate to use from the pilot analysis is the point estimate ${\widehat{\gamma }}_{\text{mis}}$, calculated by formula (7), which is output by most MI software. But this point estimate is not conservative since it runs about a 50 percent chance of being smaller than the true value of ${\gamma }_{\text{mis}}$. And if the point estimate ${\widehat{\gamma }}_{\text{mis}}$ is too small, then the recommended number of imputations $M$ will be too small as well. So the approach runs a 50 percent chance of underestimating how many imputations you really need.

A more conservative approach is this: instead of using the pilot analysis to get a point estimate ${\widehat{\gamma }}_{\text{mis}}$, use it to get a 95 percent confidence interval (CI) for ${\gamma }_{\text{mis}}$ and then use the upper bound of the CI to calculate the required number of imputations $M$ from formula (1). Since there is only a 2.5 percent chance that the true value of ${\gamma }_{\text{mis}}$ exceeds the upper bound of the CI, there is only a 2.5 percent chance that the implied number of imputations will be too low to achieve the desired degree of replicability.²

The two-stage procedure for deciding the number of imputations requires a CI for ${\gamma }_{\text{mis}}$. A CI for $logit\left({\gamma }_{\text{mis}}\right)$ is $logit\left({\widehat{\gamma }}_{\text{mis}}\right)\pm z\sqrt{2/M}$, where $z$ is a standard normal quantile (Harel 2007). This CI for $logit\left({\gamma }_{\text{mis}}\right)$ can be transformed to a CI for ${\gamma }_{\text{mis}}$ by applying the inverse-logit transformation to the end points.³

Table 1 gives 95 percent CIs for different values of $M$ and ${\widehat{\gamma }}_{\text{mis}}$ Many of the CIs are wide, indicating considerable uncertainty about the true value of ${\gamma }_{\text{mis}}$, especially when $M$ is small or ${\widehat{\gamma }}_{\text{mis}}$ is close to .50.

Table 1.

Ninety-five Percent CIs for the Fraction of Missing Information ${\gamma }_{\text{mis}}$.

Point Estimate ${\widehat{\gamma }}_{\text{mis}}$	Number of Imputations $M$	95 Percent CI for ${\gamma }_{\text{mis}}$
.1	5	[.03, .28]
	10	[.04, .21]
	15	[.05, .19]
	20	[.06, .17]
.3	5	[.11, .60]
	10	[.15, .51]
	15	[.17, .47]
	20	[.19, .44]
.5	5	[.22, .78]
	10	[.29, .71]
	15	[.33, .67]
	20	[.35, .65]
.7	5	[.40, .89]
	10	[.49, .85]
	15	[.53, .83]
	20	[.56, .81]
.9	5	[.72, .97]
	10	[.79, .96]
	15	[.81, .95]
	20	[.83, .94]

Note: CI = confidence interval.

In the rest of this article, I will illustrate the two-stage procedure and evaluate its properties in an applied example where about 40 percent of information is missing. I then test the two-stage procedure and the quadratic rule by simulation and derive the underlying formulas. I offer a Stata command called how_many_imputations and a SAS macro, called %mi_combine, which recommend the number of imputations needed to achieve a desired level of replicability. The Stata command can be installed by typing ssc install how_many_imputations on the Stata command line. The SAS macro can be downloaded from the Online Supplement to this article, or from the website missingdata.org.

Applied Example

This section illustrates the two-stage procedure with real data. All code and data used in this section are provided in the Online Supplement and on the website missingdata.org.

Data

The SAS data set called bmi_observed contains data on body mass index (BMI) from the Early Childhood Longitudinal Study, Kindergarten cohort of 1998–1999 (ECLS-K). The ECLS-K is a federal survey overseen by the National Center for Education Statistics, U.S. Department of Education. The ECLS-K started with a nationally representative sample of 21,260 U.S. kindergarteners in 1,018 schools and took repeated measures of their BMI in seven different rounds, starting in the fall of 1998 (kindergarten) and ending in the spring of 2007 (eighth grade for most students).

I estimate mean BMI in round 3 (fall of first grade). While every round of the ECLS-K missed some BMI measurements, round 3 missed the most, because in round 3, the ECLS-K saved resources by limiting BMI measurements to a random 30 percent subsample of participating schools. So 76 percent of BMI measurements were missing from round 3—70 percent were missing by design (completely at random), and a further 6 percent were missing (probably not at random) because the child was unavailable or refused to be weighed. The fraction of missing information would be 76 percent if all we had were the observed BMI values at round 3, but we will reduce that fraction substantially by imputation.

(The ECLS-K is a complex random sample, and in a proper analysis, both the analysis model and the imputation model would account for complexities of the sample including clusters, strata, and sampling weights. But in this article, I neglect those complexities and treat the ECLS-K like a simple random sample. I did carry out a more complex analysis that accounted for the sample’s complexities. The two-stage method still performed as expected, but the estimated SEs were 50 percent larger).

Listwise Deletion

The simplest estimation strategy is listwise deletion, which uses only the BMI values that are observed in round 3. The listwise estimate for mean BMI is 16.625 with an estimated SE of .037. There is little bias because the observed values are almost a random sample of the population (over 90 percent of missing values are missing completely at random). But the listwise SE is larger than necessary because it is calculated using just 24 percent of the sample. The results will show that MI can reduce the SE by one-third—an improvement that is equivalent to more than doubling the number of observed BMI values.

Multiple Imputation

Next, I multiply impute missing BMIs. In each MI analysis, I get $M$ imputations of missing BMIs from a multivariate normal model for the BMIs in rounds 1–4.⁴ One implication of this model is that missing BMIs from round 3 are imputed by normal linear regression on BMIs that were observed for the same child in other rounds (Schafer 1997).⁵ The imputation model predicts BMI very well; a multiple regression of round 3 BMIs on BMIs in rounds 1, 2, and 4 has R² =.85, and even a simple regression of round 3 BMIs on round 2 BMIs has R² =.77. The accuracy of the imputed values, and the fact that so many values are missing, ensures that the MI estimates will improve substantially over the listwise deleted estimates (von Hippel and Lynch 2013).

I analyze each of the $M$ imputed data sets as though it were complete; that is, I estimate the mean and SE from each of the $M$ samples. I then combine the $M$ estimates to produce an MI point estimate ${\widehat{\text{θ}}}_{\text{MI}}$ and an SE estimate ${\widehat{SE}}_{\text{MI}}$. I also calculate a point estimate ${\widehat{\gamma }}_{\text{mis}}$, a 95 percent CI for ${\gamma }_{\text{mis}}$, and an estimate $\widehat{df}=(M-1){\widehat{\gamma }}_{\text{mis}}^{-2}$ for the $df$ of the SE estimate. Formulas for all these quantities will be given later, in the Formulas section.

Two-stage Procedure

The two-stage procedure, which I Implemented in SAS code (two_step_example.sas), proceeds as follows.

1. In the first stage, I carry out a small-$M$ pilot analysis and use the upper limit of the CI for ${\gamma }_{\text{mis}}$ to calculate, using formula (1), how many imputations would be needed to achieve my target CV. I chose my CV goal by deciding that I wanted to ensure that the second significant digit (third decimal place) of ${\widehat{SE}}_{\text{MI}}$ would typically change by about 1 if the data were re-imputed. This implies a goal of $SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)$, so that the target CV is $\widehat{\text{CV}}=SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)/{\widehat{SE}}_{\text{MI}}=.001$, where the numerator is .001, and the denominator ${\widehat{SE}}_{\text{MI}}$ is the pilot SE estimate.

2. In the second stage, I carry out a final analysis using the number of imputations that the first stage suggested would be needed to achieve my target CV.

Results With M = 5 Pilot Imputations

I first tried a stage 1 pilot analysis with $M=5$ imputations. The results were an MI point estimate of 16.642 with an SE estimate of .023, which is about one-third smaller than the SE obtained using listwise deletion. The estimated fraction of missing information was .39 with a 95 percent CI of [.15, .69]. The upper bound of the CI implied that $M=125$ imputations should be used in stage 2. In stage 2, the final analysis returned an MI point estimate of 16.650 with an SE estimate of .021. The results of both stages are summarized in the first two rows of Table 2 (Panel A).

Table 2.

One Hundred Replications of the Two-stage Procedure.

Replication	Stage	Imputations	Point Estimate	SE	df	Missing Information Estimate [With 95 Percent Cl]
(A) With $M=5$ pilot imputations
1	1. Pilot	5	16.642	.023	27	.39	[.15, .69]
	2. Final	125	16.650	.021	1,313	.30	[.25, .36]
2	1. Pilot	5	16.659	.026	14	.53	[.25, .80]
	2. Final	219	16.651	.022	1,876	.34	[.30, .38]
…	…	…	…	…	…	…	…
100	1. Pilot	5	16.647	.022	40	.31	[.12, .61]
	2. Final	89	16.651	.022	810	.33	[.27, .40]
Stage 2 summary (across 100 replications)	Mean	97	16.651	.022	840	.34	[.26, .42]
	SD	61	.003	.001	522	.05	[.06, .07]
	Minimum	4	16.633	.020	11	.16	[.06, .30]
	Maximum	266	16.656	.026	2,100	.52	[.36, .81]
(B) With $M=20$ pilot imputations
1	1. Pilot	20	16.654	.021	217	.30	[.18, .44]
	2. Final	45	16.652	.022	451	.31	[.23, .41]
2	1. Pilot	20	16.658	.020	371	.23	[.14, .35]
	2. Final	27	16.647	.022	208	.35	[.24, .48]
…	…	…	…	…	…	…	…
100	1. Pilot	20	16.654	.026	64	.54	[.39, .69]
	2. Final	167	16.650	.022	1,209	.37	[.32, .42]
Stage 2 summary (across 100 replications)	Mean	62	16.652	.022	535	.34	[.26, .43]
	SD	26	.002	.001	233	.04	[.04, .05]
	Minimum	22	16.645	.021	1 18	.25	[.17, .33]
	Maximum	167	16.658	.024	1,352	.45	[.36, .59]

Note: The goal is that the SD of the stage 2 SE estimates should be .001. SE = standard error; SD = standard deviation; df = degrees of freedom.

These results are not deterministic. Imputation has a random component, so if I replicate the two-stage procedure, I will get different results. Table 2 (Panel A) gives the results of a replication (replication 2). The stage 1 pilot estimates are somewhat different than they were the first time, and the recommended number of imputations is different as well (M = 219 rather than 125).

Although the recommended number of imputations changes when I repeat the two-stage procedure, the final estimates are quite similar. The first time I ran the two-stage procedure, our final estimate (and SE) were 16.650 (.021); the second time we ran it, our final estimate (and SE) were 16.651 (.022). The two final point estimates differ by .001, and the final SE estimates differ by .001—which is about the difference that would be expected given my goal of $SD\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)=.001$. By contrast, the two pilot estimates are more different; the pilot point estimates differ by .017 and the pilot SE estimates differ by .003.

The bottom of Table 2 (Panel A) summarizes the stage 2 estimates across 100 replications of the two-stage procedure. (The SAS code to produce the 100 replications is in simulation.sas.) The SD of the 100 SE estimates is .001, which is exactly what I was aiming for. That is reassuring.

Somewhat less reassuring is the tremendous variation in the number of imputations recommended by the pilot. The recommended imputations had a mean of 97 with an SD of 61. One pilot recommended as few as 4 imputations but another recommended as many as 266. The primary⁶ reason for this variation is that the recommended number of imputations is a function of the pilot CI for ${\gamma }_{\text{mis}}$, and that CI varies substantially across replications since the pilot has only $M=5$ imputations.

Results With $\text{M}=20$ Pilot Imputations

One way to reduce variability in the recommended number of imputations is to use more imputations in the pilot. If the pilot uses, say, $M=20$ imputations instead of $M=5$, the pilot will yield a narrower, more replicable CI for ${\gamma }_{\text{mis}}$, and this will result in a more consistent recommendation for the final number of imputations.

Table 2 (Panel B) uses $M=20$ pilot imputation and again summarizes the stage 2 estimates from 100 replications of the two-stage procedure. Again the SD of the 100 stage 2 SE estimates is .001, which is exactly what I was aiming for. And this time, the number of imputations recommended by the pilot is not as variable. The recommended imputations had a mean of 62 with an SD of 26. There is still a wide range—one pilot recommended just 22 imputations and another recommended 167—but with $M=20$ pilot imputations, the range covers just one order of magnitude. The range of recommended imputations covered two orders of magnitude when the pilot used $M=5$ imputations.

With $M=20$ pilot imputations, the recommended number of stage 2 imputations is not just less variable—it is also lower on average. With $M=5$ pilot imputations, the average number of recommended imputations was 97; with $M=20$ pilot imputations, it is just 62. When we increased the number of pilot imputations by 15, we reduced the average number of final imputations by 35. So it wouldn’t pay to lowball the pilot imputations; any time we saved by using $M=5$ instead of $M=20$ imputations in stage 1 gets clawed back double in stage 2.

Why does the recommended number of imputations rise if we reduce the number of pilot imputations? With fewer pilot imputations, we are more likely to get a high pilot estimate of ${\gamma }_{\text{mis}}$, and this leads to a high recommendation for the final number of imputations. With fewer pilot imputations, we are also more likely to get a low pilot estimate of ${\gamma }_{\text{mis}}$, but that doesn’t matter as much. Because the recommended number of imputations increases with the square ${\gamma }_{\text{mis}}^2$, the recommended number of imputations is more sensitive to small changes in the estimate of ${\gamma }_{\text{mis}}$ when that estimate is high than when it is low.

How Many Pilot Imputations Do You Need?

So how many pilot estimates are enough? In a sense, it doesn’t matter how many pilot imputations you use in stage 1, since the procedure almost always ensures that in stage 2, you will use enough imputations to produce SE estimates with the desired level of replicability.

In another sense, though, there are costs to lowballing the pilot imputations. If you don’t use many imputations in the pilot, the number of imputations in stage 2 may be unncecessarily variable, and unnecessarily high on average. This is a particular danger when the true fraction of missing information is high, as it was in our simulation above.⁷

Perhaps the best guidance is to use more pilot imputations when the true value of ${\gamma }_{\text{mis}}$ seems likely to be large. You won’t have a formal estimate of ${\gamma }_{\text{mis}}$ until after the pilot, but you often have a reasonable hunch whether ${\gamma }_{\text{mis}}$ is likely to be large or small. In my ECLS-K example, with 76 percent of values missing, it seemed obvious that ${\gamma }_{\text{mis}}$ was going to be large. I didn’t know exactly how large until the results were in, but I could have guessed that $M=5$ imputations wouldn’t be enough. $M=20$ pilot imputations was a more reasonable choice, and it led to a more limited range of recommendations for the number of imputations in stage 2.

If a low fraction of missing information is expected, on the other hand, then fewer pilot imputations are needed. You can use just a few pilot imputations, and they may be sufficient. If the pilot imputations are not sufficient, then the recommended number of imputations in stage 2 will not vary that much.

Why the Estimated df Is an Unreliable Guide

In the Overview, we mentioned that the number of imputations can also be chosen to ensure that the true $df$ exceeds some threshold, such as 100. This is correct, but basing the number of imputations on the true df is not possible, since the true df is unknown, and basing the number of imputations on the estimated $df$ is a risky business. For example, when I used $M=5$ pilot imputations, about a quarter of my pilot analyses had an estimated $df>100$. So in about a quarter of pilot analyses, I would have concluded that $M=5$ imputations was enough—when clearly it is not enough for an SE with the desired level of replicability. So the estimated $df$ is an unreliable guide to whether you have enough imputations.

To understand this instability, it is important to distinguish between the true $df$ and the estimated $df$. The true $df$ is $df=(M-1){\gamma }_{\text{mis}}^{-2}$ but the estimate is $\widehat{df}=(M-1){\widehat{\gamma }}_{\text{mis}}^{-2}$, and this estimate is very sensitive to estimation error in ${\widehat{\gamma }}_{\text{mis}}$. So the fact that the estimated $df$ exceeds 100 is no guarantee that the true $df$ exceeds 100—and no guarantee that you have enough imputations.

Verifying the Quadratic Rule

The two-stage procedure relies on the quadratic rule (1), so it is important to verify that the rule is approximately correct. In Formulas section, we will derive the quadratic rule analytically. Here, we verify that it approximately fits the results of a simulation published by Bodner (2008).

In his simulation, Bodner varied the true value of ${\gamma }_{\text{mis}}$ and estimated how many imputations $M$ were needed to satisfy a criterion very similar to $\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)=.05$. Figure 1 fits Bodner’s results (2008, table 3, column 2) to our quadratic rule which, with a CV of .05, simplifies to $M=200{\gamma }_{\text{mis}}^2$. Figure 1 also shows a linear rule $M=100{\gamma }_{\text{mis}}$ which others have proposed (Bodner 2008; White et al. 2011).

Clearly, the quadratic rule fits better. The two rules agree at ${\gamma }_{\text{mis}}=.5$, but the linear rule somewhat overstates the number of imputations needed when ${\gamma }_{\text{mis}}<.5$ and substantially understates the number of imputations needed when ${\gamma }_{\text{mis}}>.5$.

While the quadratic rule fits better, it does slightly underpredict the number of imputations that were needed in Bodner’s simulation. Possible reasons for this include the fact that Bodner’s criterion was not exactly $\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)=.05$. In particular,

• Bodner’s criterion did not pertain directly to ${\widehat{SE}}_{\text{MI}}$. Instead, it pertained to the half-width ${\widehat{h}}_{\text{MI}}=t{\widehat{SE}}_{\text{MI}}$ of a 95 percent ${\widehat{\text{θ}}}_{\text{MI}}\pm t{\widehat{SE}}_{\text{MI}}$, where $t$ is the .975 quantile from a $t$ distribution with $\widehat{df}=(M-1){\widehat{\gamma }}_{\text{mis}}$. When ${\gamma }_{\text{mis}}$ is small, $t$ is practically a constant since df is large—so managing the variation in ${\widehat{SE}}_{\text{MI}}$ is equivalent to the variation in ${\widehat{h}}_{\text{MI}}$. But when ${\gamma }_{\text{mis}}$ is large, $t$ contains imputation variation since $df$ may be small, and more imputations may be needed to manage the variation in $t$ along with the variation in ${\widehat{SE}}_{\text{MI}}$. In other words, the quadratic rule may suffice to manage the variation in ${\widehat{SE}}_{\text{MI}}$, but more imputations may be needed to manage the variation in ${\widehat{h}}_{\text{MI}}$, especially when ${\gamma }_{\text{mis}}$ is large.

• Bodner’s criterion also did not pertain directly to the CV of ${\widehat{h}}_{\text{MI}}$. Instead, his criterion was that, across many sets of $M$ imputations, 95 percent of ${\widehat{h}}_{\text{MI}}$ values would be within 10 percent of the mean $E\left(\widehat{h_{MI}}\right)$. This is equivalent to the criterion $\text{CV}\left({\widehat{\overline{h}}}_{\text{MI}}\mid Y_{\text{obs}}\right)=.05$, as $M$ grows and the distribution of ${\widehat{h}}_{\text{MI}}$ approaches normality. But the criteria are not equivalent if $M$ is smaller.

Another consideration is that our expression for $\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)$ is approximate rather than exact. We derive our expression next.

Formulas

In this section, we derive formulas for the number of imputations that are required for different purposes. Some of these formulas were given in the Overview and are now justified. Other formulas will be new to this section.

The number of imputations that is required depends on the quantity that is being estimated. Relatively few imputations are needed for an efficient point estimate ${\widehat{\text{θ}}}_{\text{MI}}$. More imputations are needed for a replicable SE estimate, and even more imputations may be needed for a precise estimate of ${\gamma }_{\text{mis}}$.

Point Estimates

Suppose you have a sample of $N$ cases, some of which are incomplete. MI makes $M$ copies of the incomplete data set. In the $M$ th copy, MI fills in the missing values with random imputations from the posterior predictive distribution of the missing values given the observed values (Rubin 1987).

You analyze each of the $M$ imputed data set as though it were complete and obtain $M$ point estimates ${\widehat{\text{θ}}}_{\text{m}},m=1,\dots ,M$ for some parameter of interest y, such a mean or a vector of regression parameters. You average the $M$ point estimates to get an MI point estimate ${\widehat{\text{θ}}}_{\text{MI}}=\sum _{m=1}^M{\widehat{\text{θ}}}_{\text{m}}/M$.

The true variance of the MI point estimate is $V_{\text{MI}}=V\left({\widehat{\text{θ}}}_{\text{MI}}\right)$. If ${\widehat{\text{θ}}}_{\text{MI}}$ is a scalar, then the square of its SE. If $V_{\text{MI}}$ is a vector, then each component has its own SE and its own $V_{\text{MI}}$.⁸

$V_{\text{MI}}$ reflects two sources of variation: sampling variation due to the fact that we could have taken a different sample of $N$ cases, and imputation variation due to the fact that we could have taken a different sample of $M$ imputations. You can reduce imputation variation by increasing the number of imputations $M$, so that $V_{\text{MI}}$ converges toward a limit that reflects only sampling variation. This is the infinite-imputation variance:$V_{\infty I}={\lim }_{M\to \infty }{V}_{\text{MI}}$. (Throughout this section, the subscript $\infty I$ will be used for the limit of an MI expression as $M\to \infty$.)

Although $V_{\infty I}$ is the lower bound for the variance that you can achieve by applying MI to the incomplete data, $V_{\infty I}$ is still greater than the variance that you could have achieved if the data were complete:$V_{\text{com}}$. The ratio ${\gamma }_{\text{obs}}=V_{\text{com}}/V_{\text{MI}}$ is known as the fraction of observed information, and its complement is the fraction of missing information${\gamma }_{\text{mis}}$:

$${\gamma }_{\text{mis}}=1-V_{\text{com}}/V_{\text{MI}}\text{.}$$ (4)

Note that the fraction of missing information is generally not the same as the fraction of values that are missing. Typically, the fraction of missing information is smaller than the fraction of missing values, though one can contrive situations where it is larger.

Since you have missing values, you are not going to achieve the complete-data variance $V_{\text{com}}$, and since you can’t draw infinite imputations, you are not even going to achieve the infinite-imputation variance $V_{\infty I}$. But how many imputations do you need to come reasonably close to $V_{\infty I}$? The traditional advice is that $M=2-10$ imputations are typically enough. The justification for this is the following formula (Rubin 1987):

$$V_{\text{MI}}=V_{\infty I}\left(1+{\gamma }_{\text{mis}}/M\right),$$ (5)

which says that the variance of an MI point estimate with $M$ imputations is only $\left(1+{\gamma }_{\text{mis}}/M\right)$ times larger than it would be with infinite imputations. For example, even with ${\gamma }_{\text{mis}}=80$ percent missing information, choosing $M=10$ means that the variance of ${\widehat{\text{θ}}}_{\text{MI}}$ is just 8 percent larger (so the SE is only 4 percent larger) than it would be with infinite imputations. In other words, increasing $M$ beyond 10 can only reduce the SE by less than 4 percent.

Variance Estimates

The old recommendation of $M=2-10$ is fine if all you want is an efficient point estimate ${\widehat{\text{θ}}}_{\text{MI}}$. But what you also want an efficient and replicable estimate ${\widehat{V}}_{\text{MI}}$ of the variance $V_{\text{MI}}$, or equivalently an efficient and replicable estimate ${\widehat{SE}}_{\text{MI}}$ of the standard error $S{E}_{\text{MI}}=V_{\text{MI}}^{1/2}?$ Then you may need more imputations—perhaps considerably more.

The most commonly used variance estimator for multiple imputation is:

$${\widehat{V}}_{\text{MI}}={\widehat{W}}_{\text{MI}}+\left(1+\frac{1}{M}\right){\widehat{B}}_{\text{MI}}$$ (6)

(Rubin 1987). Here, ${\widehat{B}}_{\text{MI}}=\sum _{m=1}^M{\left({\widehat{\text{θ}}}_{\text{m}}-{\widehat{\text{θ}}}_{\text{MI}}\right)}^2/(M-1)$ is the between variance—the variance of the point estimates across the $M$ imputed data sets. ${\widehat{W}}_{\text{MI}}=\sum _{m=1}^M{\widehat{W}}_m/M$ is the within variance—the average of the $M$ squared SEs $\left({\widehat{W}}_m={\widehat{SE}}_m^2\right)$ each estimated by analyzing an imputed data set as though it were complete.

The within variance ${\widehat{W}}_{\text{MI}}$ consistently estimates $V_{\text{com}}$, which again is the variance that you would get if the data were complete. Therefore, the fraction of observed information ${\widehat{\gamma }}_{\text{obs}}={\widehat{V}}_{\text{MI}}^{-1}{\widehat{W}}_{\text{MI}}$ can be ratio estimated by the ratio and the fraction of missing information ${\gamma }_{\text{mis}}=1-{\gamma }_{\text{obs}}$ estimated by the complement (Rubin 1987)

$${\widehat{\gamma }}_{\text{mis}}=1-{\widehat{\gamma }}_{\text{obs}},={\widehat{V}}_{\text{MI}}^{-1}{\widehat{B}}_{\text{MI}}(1+1/M).$$ (7)

Notice the implication that ${\widehat{B}}_{\text{MI}}$ tends to be larger (relative to ${\widehat{V}}_{\text{MI}}$) if the true value of ${\gamma }_{\text{mis}}$ is large.

In fact, ${\widehat{B}}_{\text{MI}}$ is the Achilles heel of the variance estimator ${\widehat{V}}_{\text{MI}}$. Since ${\widehat{B}}_{\text{MI}}$ is a variance estimated from a sample of size $M$, if $M$ is small, ${\widehat{B}}_{\text{MI}}$ will be volatile in the sense that a noticeably different value of ${\widehat{B}}_{\text{MI}}$ might be obtained if the data were imputed again. This may not be a problem if ${\gamma }_{\text{mis}}$ is small, but if ${\gamma }_{\text{mis}}$ is large, then ${\widehat{B}}_{\text{MI}}$ will constitute a large fraction of ${\widehat{V}}_{\text{MI}}$, so that ${\widehat{V}}_{\text{MI}}$ will be volatile as well.

The volatility or imputation variation in ${\widehat{V}}_{\text{MI}}$ can be summarized by the coefficient of variation $\text{CV}\left({\widehat{V}}_{\text{MI}}\mid Y_{\text{obs}}\right)$. We can derive a simple approximation for the CV

$$\text{CV}\left({\widehat{V}}_{\text{MI}}\mid Y_{\text{obs}}\right)\underset{M\to \infty }{\to }{\gamma }_{\text{mis}}\sqrt{2/(M-1)}$$ (8)

(von Hippel 2007, appendix A). Then solving for $M$ yields the following quadratic rule for choosing the number of imputations to achieve a particular value of $\text{CV}\left({\widehat{V}}_{\text{MI}}\mid Y_{\text{obs}}\right)$:

$$M\approx 1+2{\left(\frac{{\gamma }_{\text{mis}}}{\text{CV}\left({\widehat{V}}_{\text{MI}}\mid Y_{\text{obs}}\right)}\right)}^2.$$ (9)

This quadratic rule uses the CV of ${\widehat{V}}_{\text{MI}}$, but in practice, you will likely be more interested in the CV of ${\widehat{SE}}_{\text{MI}}$. The two are related by the approximation $\text{CV}\left({\widehat{V}}_{\text{MI}}\right)\approx 2\text{CV}\left({\widehat{SE}}_{\text{MI}}\right)$, which follows from the delta method. And plugging this approximation into equation (9), we get:

$$M\approx 1+\frac{1}{2}{\left(\frac{{\gamma }_{\text{mis}}}{\text{CV}\left({\widehat{SE}}_{\text{MI}}\right)}\right)}^2,$$ (10)

which is the formula (1) that we gave earlier in the Overview.

Degrees of Freedom

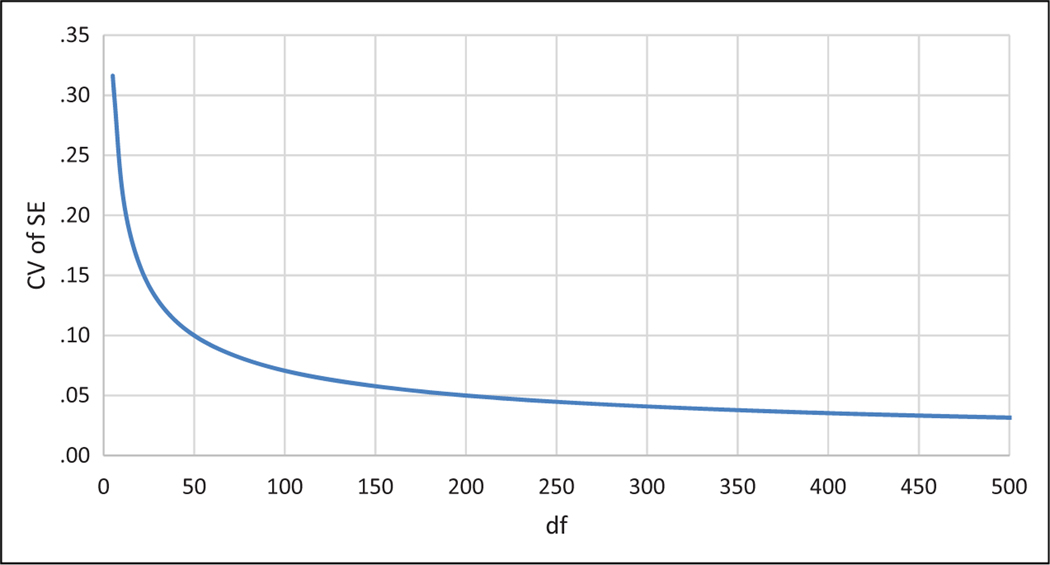
Allison (2003 footnote 7) recommends choosing $M$ to achieve some target degrees of freedom $(df)$. This turns out to be equivalent to our suggestion of choosing $M$ to reduce the variability in ${\widehat{V}}_{\text{MI}}$ and ${\widehat{SE}}_{\text{MI}}$. In large samples, when conditioned on $Y_{\text{obs}}$, ${\widehat{V}}_{\text{MI}}$ follows approximately a ${\chi }^2$ distribution with $df=(M-1){\gamma }_{\text{mis}}^{-2}$ (Rubin 1987).⁹ The CV of such a distribution is $\text{CV}\left({\widehat{V}}_{\text{MI}}\mid Y_{\text{obs}}\right)=\sqrt{2/df}$, which implies the relationship:

$$df=\frac{2}{{\left(\text{CV}\left({\widehat{V}}_{\text{MI}}\mid Y_{\text{obs}}\right)\right)}^2}=\frac{1}{2{\left(\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)\right)}^2}.$$ (11)

So aiming for an SE with $\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)=.05$, for example, is equivalent to aiming for an SE with $df=200$. Figure 2 graphs the relationship between $df$ and $\text{CV}\left({\widehat{SE}}_{\text{MI}}\mid Y_{\text{obs}}\right)$.

Figure 2.

Relationship between the degrees of freedom and the coefficient of variation for a multiple imputation (MI) SE estimate.

If you are aiming for a particular $df$, you can reach it by choosing $M$ according to the following quadratic rule:

$$M=1+df{\gamma }_{\text{mis}}^2,$$ (12)

which we presented earlier as equation (3). It is equivalent to the earlier quadratic rule (10), except that rule (10) was written in terms of the CV while rule (13) is written in terms of the $df$. Rule (13) can also be derived more directly from the definition $df=(M-1){\gamma }_{\text{mis}}^{-2}$.

Again, since ${\gamma }_{\text{mis}}$ is unknown, it makes sense to proceed in two stages. First, carry out a pilot analysis to obtain a conservatively large estimate of ${\gamma }_{\text{mis}}$, such as the upper limit of a 95 percent CI. Then use that estimate of ${\gamma }_{\text{mis}}$ to choose a conservatively large number of imputations $M$, which will with high probability achieve the desired $df$.

Remember that the exact $df$ are unknown since they are a function of the unknown gmis. The $df$ must be estimated by $\widehat{df}=(M-1)/{\widehat{\gamma }}_{\text{mis}}$. While the two-stage procedure can ensure with high probability that the true $df$ achieve the target, the estimated $df$ may be well off the mark. So the estimated $df$ is an unreliable indicator of whether you have enough imputations. We saw this earlier in our simulation.

Conclusion

How many imputations do you need? An old rule of thumb was that $M=2–10$ imputations is usually enough. But that rule only addressed the variability of point estimates. More recent rules also addressed the variability of SE estimates, but those rules were limited in two ways. First, they modeled the variability of SE estimates with a linear function of the fraction of missing information ${\gamma }_{\text{mis}}$. Second, they required the value of ${\gamma }_{\text{mis}}$, which is not known in advance.

I have proposed a new rule that relies on a more accurate quadratic function in which the number of required imputations increases with the square of ${\gamma }_{\text{mis}}$. And since ${\gamma }_{\text{mis}}$ is unknown, I have proposed a two-stage procedure in which ${\gamma }_{\text{mis}}$ is estimated from a small-$M$ pilot analysis, which serves as a guide for how many imputations to use in stage 2. The stage 1 estimate is the top of a 95 percent CI for ${\gamma }_{\text{mis}}$, which is conservative in that it ensures that we are unlikely to use too few imputations in stage 2.

To make this procedure convenient, I have written software for Stata and SAS. For Stata, I wrote the how_many_imputations command. On the Stata command line, install it by typing ssc install how_many_imputations. Then type help how_many_imputations to learn how to use it. For SAS, I wrote the %mi_combine macro, which is available in the online supplement to this article, and on the website missingdata.org. Both the supplement and the website also provide code to illustrate the use of the macro (two_step_example.sas) and to replicate all the results in this article (simulation.sas).

Biography

Paul von Hippel is an associate professor of public policy, data science, and sociology at the University of Texas, Austin. He works on evidence-based policy, education and inequality, and the obesity epidemic. He is an expert on research design and missing data, and a three-time winner of best article awards from the education and methodology sections of the American Sociological Association. Before his academic career, he worked as a data scientist who used predictive analytics to help banks prevent fraud.