Assessing abundance–suitability models to prioritize conservation areas for the dwarf caimans in South America

Abstract

Species–environment relationships have been extensively explored through species distribution models (SDM) and species abundance models (SAM), which have become key components to understand the spatial ecology and population dynamics directed at biodiversity conservation. Nonetheless, within the internal structure of species' ranges, habitat suitability and species abundance do not always show similar patterns, and using information derived from either SDM or SAM could be incomplete and mislead conservation efforts. We gauged support for the abundance–suitability relationship and used the combined information to prioritize the conservation of South American dwarf caimans (Paleosuchus palpebrosus and P. trigonatus). We used 7 environmental predictor sets (surface water, human impact, topography, precipitation, temperature, dynamic habitat indices, soil temperature), 2 regressions methods (Generalized Linear Models—GLM, Generalized Additive Models—GAM), and 4 parametric distributions (Binomial, Poisson, Negative binomial, Gamma) to develop distribution and abundance models. We used the best predictive models to define four categories (low, medium, high, very high) to plan species conservation. The best distribution and abundance models for both Paleosuchus species included a combination of all predictor sets, except for the best abundance model for P. trigonatus which incorporated only temperature, precipitation, surface water, human impact, and topography. We found non‐consistent and low explanatory power of environmental suitability to predict abundance which aligns with previous studies relating SDM‐SAM. We extracted the most relevant information from each optimal SDM and SAM and created a consensus model (2,790,583 km²) that we categorized as low (39.6%), medium (42.7%), high (14.9%), and very high (2.8%) conservation priorities. We identified 279,338 km² where conservation must be critically prioritized and only 29% of these areas are under protection. We concluded that optimal models from correlative methods can be used to provide a systematic prioritization scheme to promote conservation and as surrogates to generate insights for quantifying ecological patterns.

This study identified conservation priorities for the South American dwarf caimans (Paleosuchus palpebrosus and P. trigonatus) relying on robust species distribution and abundance models. We support that environmental suitability and spatial abundance are not always congruent and cannot be considered reliable surrogates for one another, and independently incorporate relevant information to better understand the spatial ecology and population dynamics towards the improvement of systematic conservation planning of biodiversity.

1. INTRODUCTION

The functioning of ecosystems depends on both species' presence and structure of local population dynamics within the species distribution range (Waldock et al., 2022). Thus, the incorporation of local abundance patterns provides fundamental information to understand and predict ecological processes aimed at biodiversity conservation (Cavalcante et al., 2022; Zurell et al., 2022). In spatial ecology, occurrence‐based methods (Species Distribution models (SDM)) have been extensively explored to predict environmental suitability and occupied distribution areas (Guisan et al., 2017; Guisan & Zimmermann, 2000; Peterson et al., 2011). In contrast, abundance‐based methods (Species Abundance Models [SAM]) are scarcer as abundance data, are more difficult to obtain due to economic and temporal cost‐effective challenges, and thus, remained limited or elusive for most taxa (Araújo & Williams, 2000; Carrascal et al., 2015; Sagarin et al., 2006; VanDerWal et al., 2009).

Although SAM are less common than SDM, the “abundance–suitability” relationship has been reviewed previously using the “niche” concept as the sets of environmental states inside a multidimensional hypervolume space, within which a species can survive (Hutchinson, 1957). Under this framework, environmental conditions are assumed to affect the species' habitat suitability and the probability of occurrence, with more favorable environmental conditions driving population dynamics to higher species abundance (Araújo & Williams, 2000; Osorio‐Olvera et al., 2020). However, empirical evidence showed that abundance data are not entirely constrained by the properties of niche theory and rather other ecological factors (e.g., transitory states of population, demographic stochasticity, suitability spatial heterogeneity, and Allee effects) can affect local population dynamics and interfere with the expected abundance–suitability relationship (Osorio‐Olvera et al., 2019; Waldock et al., 2022). Consequently, assessments of the abundance–suitability relationship have failed to detect consistent correlation, suggesting that these patterns are not constrained by the same underlying ecological processes (Dallas & Hastings, 2018; Johnston et al., 2015; Mi et al., 2017). In this context, efforts to identify areas to prioritize species conservation incorporating relevant information from both SDM and SAM must be done so that models are more reflective of the interaction between these two population attributes (Mi et al., 2017; Waldock et al., 2022).

Robust regression‐based methods such as Generalized Linear Models (GLM) and Generalized Additive Models (GAM) have been developed and improved to make ecological inferences based on species' environmental requirements and address some of the major biodiversity shortfalls (Guisan et al., 2002; Pollock et al., 2020; Qiao et al., 2015). GLM are model‐driven as the response variable is expected to follow a parametric distribution along the predictors (e.g., Binomial, Poisson, Negative binomial, Gamma), whereas GAM are data‐driven analysis that apply smaller non‐parametric smoothing functions (basis functions) to each predictor and additively estimates the component response (Guisan et al., 2017). GAM constitute semi‐parametric extensions of GLM, and both use link functions to establish a relationship between predictors and response variables (Wood, 2017; Zuur et al., 2009). Both GLM and GAM have been extensively utilized to predict habitat suitability and, to a lesser extent, abundance patterns, providing information on modeling capabilities (e.g., Guisan et al., 2002; Kosicki, 2020; Oppel et al., 2012; Potts & Elith, 2006) and quantifying general relationships between abundance and suitability patterns (Thuiller et al., 2014; VanDerWal et al., 2009; Weber et al., 2017).

Since protocols to estimate relative abundances have been well standardized for many crocodylian species (Balaguera‐Reina et al., 2017; Grigg & Kirshner, 2015; Rodriguez‐Cordero et al., 2019; Seijas & Chávez, 2000; Zucoloto et al., 2021), these taxa represent a promising group for implementing correlative modeling to assess the spatial ecology of each species. Among the smallest South American crocodylians, both Cuvier's dwarf caiman (Paleosuchus palpebrosus) and the Smooth fronted caiman (Paleosuchus trigonatus) have historically been given marginal attention since they have no commercial value (Ergueta & Pacheco, 1990; Pacheco & King, 1995). Consequently, even though these species are listed as “Least Concern” by the IUCN Red List of Threatened Species and local populations are reported as apparently healthy and abundant throughout their range, much of their spatial ecology, complex habitat use patterns, and quantitative population trends remain relatively unknown (Campos et al., 2019; Magnusson et al., 2019; Marioni et al., 2022).

To address these limitations and to improve our understanding of the spatial ecology of both dwarf caiman species, the main objectives of this research were to: (1) estimate optimal distribution and abundance models to categorize and prioritize conservation areas for the Paleosuchus species across their distribution range, (2) assess whether there is a consistent (either positive or negative) and significant relationship between habitat suitability and species abundance, and (3) define a method to reconcile distribution and abundance models so this information can be integrated to prioritize conservation areas for both Paleosuchus species. We hypothesized that optimized structures and specifications of GLM and GAM would yield a consistent spatial abundance–suitability correlation with a high explanatory capability of suitability to predict species abundance. Furthermore, we expected an agreement between the areas predicted as both highly suitable and abundant that may warrant protection and that can be used as surrogates to promote effective long‐term species conservation planning of the species.

2. METHODOLOGY

2.1. Distribution model data acquisition

We compiled an initial occurrences dataset for distribution modeling from published literature, non‐published databases, the most recent IUCN Red List assessments for the species (Campos et al., 2019; Magnusson et al., 2019), and the Global Biodiversity Information Facility (GBIF) (www.gbif.org; Appendices S1 and S2). GBIF records were obtained via rgbif package (Chamberlain et al., 2023) in R version 4.2.1 (R Core Team, 2022), selected based on record type (human observations, living specimen, preserved specimen, and material sample) and metadata completeness (country, administrative area, reference, year, event date, responsible of specimen record and identification, locality, latitude, longitude, accepted scientific name, uncertainty, counts, and dataset key). We improved the spatial and temporal reliability of our occurrence dataset by excluding duplicated occurrences, records older than 1979, records with an uncertainty higher than 10 km, erroneous coordinates, coordinates out of the natural range, and records with incongruences between specific locality and location coordinates (Anderson et al., 2016; Balaguera‐Reina et al., 2017; Panter et al., 2020; Zizka et al., 2020). Finally, we reduced spatial clustering by overlapping filtered records with a 1 km² raster layer, selected pixels with at least one record, and estimated the centroid of each selected pixel (Anderson & Gonzalez, 2011; Beck et al., 2014; Boria et al., 2014; Veloz, 2009).

We defined the calibration area (geographical extension used for background pseudo‐absences sampling; Phillips et al., 2017) of each species by (1) calculating a convex hull based on peripheral occurrences that were within a distance of 800 km for P. palpebrosus and 700 km and for P. trigonatus, respectively, concentrating the background sampling area around occurrence locations (“background thickening”) and avoid substantial overestimate of the species distribution range (Burgman & Fox, 2003; Vollering et al., 2019), (2) buffering P. palpebrosus and P. trigonatus hulls 40 and 20 km, respectively, assumed as the maximum annual range movement of each species estimated from daily average movement reports (Marioni et al., 2022); and (3) combining previously buffered hulls with the current distribution extent defined reported by the IUCN Red List for each species (Campos et al., 2019; Magnusson et al., 2019; Figure 1a,b). Finally, we selected a modeling background based on 10,000 randomly defined pseudo‐absences within the species calibration area without including locations of species occurrences and without selecting the same pseudo‐absence location more than once. This pseudo‐absence selection method has been shown to produce the most accurate models when implemented within GLM and GAM and evaluated via the True Skill Statistics (TSS) (Barbet‐Massin et al., 2012).

FIGURE 1.

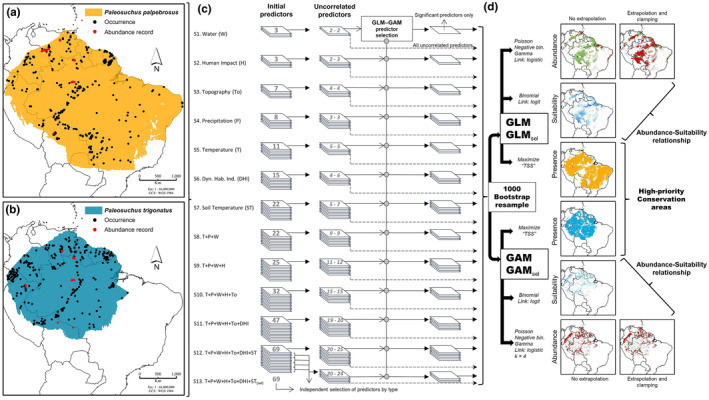
General framework implemented in this study to assess suitability‐abundance relationships and define high‐priority conservation areas for Cuvier's dwarf caiman (Paleosuchus palpebrosus) and Smooth fronted caiman (P. trigonatus). (a) and (B) abundance records, occurrences, and calibration area. (c) Definition of modeling “structure” by selecting different complexity sets of ecological predictors regarding their type and number of variants used during model fitting. The first number of uncorrelated predictors refers to P. palpebrosus, and the second number to P. trigonatus, both calculated within the calibration area, using a Pearson correlation coefficient greater than |.7| to define highly correlated predictors. (d) Definition of modeling “specification” using Generalized Linear Models (GLM) and Generalized Additive Models (GAM) to define distribution (suitability and presence/absence maps) and abundance patterns, establish abundance–suitability relationships, and estimate high‐priority conservation areas for both caiman species throughout their potential distribution range.

2.2. Abundance model data acquisition

We conducted an initial peer‐review literature search via Google Scholar using the following search terms: “Paleosuchus palpebrosus”, “Paleosuchus trigonatus”, “distribution model”, and “relative abundance” (in English, Spanish, and Portuguese). Within the reference section of the previously selected publications, we further searched for unpublished reports and theses and attempted to find them online and through requisition from author/s or University repositories (Tables S1 and S2).

Within the available literature, we then searched for standardized spotlight surveys that were used to estimate the number of caimans observed per kilometer of surveyed transect (ind/km) (Bayliss, 1987; Chabreck, 1966; Magnusson, 1982; Messel et al., 1981; Wood et al., 1985). We compiled any available spatial information associated with abundance reports, such as maps or initial and final survey coordinates. Unrectified transects in maps were digitized and orthorectified based on initial and final survey coordinates, georeferenced imagery, and topographic base‐map layers available in ArcMap v10.8.2 (ESRI, 2021). We did this to reconstruct the potential sampling routes based on historical imagery available in Google Earth Pro v7.3.6.9345 (Google Earth Pro, 2022). We overlapped each digitized transect with a 1 km² raster layer and assigned the corresponding abundance value to each intersecting pixel, as well as its longitudinal and latitudinal centroid coordinates. We excluded both animals classified as “Class I” (referring to hatchlings and neonates) as they vary highly across seasons and years due to the low survival rates (Da Silveira et al., 2008; Waddle et al., 2015), and “eyes only” to avoid species misidentification with other sympatric species within our study area (Marioni et al., 2013) (Appendix S2). Unlike distribution models that estimated the probability of species' occurrence conditioned to environmental predictors (Phillips et al., 2009), abundance models were calibrated without background points since they quantified the relationship between species abundances and environmental conditions (Potts & Elith, 2006).

2.3. Ecological predictors

We considered ecologically relevant and freely available continuous predictors that describe the primary physical environmental regimes (climate, terrain, soil factors, and nutrient availability) (Franklin, 2009) and terrestrial human footprint (Mu et al., 2022). The 69 selected predictors comprised variants of: (1) global surface water (Pekel et al., 2016), (2) human impact on the environment (Center for International Earth Science Information Network—CIESIN—Columbia University, 2018; Mu et al., 2022; Wildlife Conservation Society—WCS,, & Center for International Earth Science Information Network—CIESIN—Columbia University, 2005), (3) topography (Amatulli et al., 2018; Lehner et al., 2008), (4) precipitation, (5) temperature (Karger et al., 2017), (6) dynamic habitat indices (Hobi et al., 2017), and (7) soil temperature (Lembrechts et al., 2021; van den Hoogen et al., 2022) (Table S3). Predictors were used at ~1 km² resolution and clipped based on the calibration area for each Paleosuchus species.

We estimated environmental heterogeneity within the species calibration area based on all 69 ecological predictors. We selected uncorrelated variants (Pearson correlation coefficient r < |.7|) within the calibration area of each Paleosuchus species via the “vifcor” function (using 1000,000 random raster cell values) within the “usdm” R package (Naimi et al., 2014) (Table S4). We spatially rarefied distribution data previously selected as pixel centroids at 1, 3, and 5 km based on high, medium, and low environmental heterogeneity to reduce geographic clustering (Rodriguez‐Cordero et al., 2022) via SDMtoolbox v2.0 (http://www.sdmtoolbox.org; Brown et al., 2017). We did not rarify abundance data due to the low number of records.

2.4. Modeling framework

Model complexity was defined by modifying two parameters: (1) structure (selection of ecological predictors) and (2) specification (selection of alternative modeling parameterization) (Potts & Elith, 2006). For the former, we constructed models using individual and a gradual combination of ecological predictors (Regos et al., 2019), resulting in 12 sets, each with a different number of predictors, and thus, increased the model calibration complexity as the number of predictors increased. We ran Pearson pairwise comparisons in each complexity set to avoid collinearity among predictors and identified predictor pairs with a linear correlation greater than |.7| (Dormann et al., 2013). We excluded the predictor with the highest Variation Inflation Factor (VIF) (Chatterjee & Hadi, 2006) from each highly correlated pair via the “vifcor” function within the “usdm” R package (Naimi et al., 2014). We built an extra ecological predictor set (S13) that initially included all 69 predictors and made two correlation analyses to avoid collinearity by first excluding predictors independently by type, and second, by excluding the highly correlated predictors from the previously selected set (Figure 1c). Considering the latter parameter, we used two regression methods (GLM and GAM) and four parametric distributions: binomial (for distribution models), Poisson, Negative binomial, and Gamma (for abundance models) to comparatively assess the effect of different model specifications (Potts & Elith, 2006). We incorporated the two‐step approach by first modeling distributions with a binary response (e.g., presence/absence), and then, modeling abundances conditional to the binary distribution models (Barry & Welsh, 2002), excluding predictions outside the regions classified as “presence” (Figure 1d).

2.5. Estimating distribution and abundance through GLM and GAM

Initially, GLM and GAM were constructed using all uncorrelated predictors with each of the 13 predictor sets. Then, GLM complexity was reduced by sequentially excluding predictors until reaching the minimum Akaike Information Criteria (AIC) (Zuur et al., 2009), using the “step” function from the “stats” package (version 4.2.2). For GAM, the selection of the smooth component and predictor selection was achieved using the “double penalty shrinkage approach” (Marra & Wood, 2011), by selecting the argument “select = TRUE” in the “gam” function from the “mgcv” package (version 1.8.2) (Wood, 2017).

We produced species distribution models (suitability and presence/absence) based on the outputs from the GLM using a binomial error distribution and a “logit” link, via “glm” function from the “stats” package. For GAM we used a binomial parametric distribution using the restricted maximum likelihood (REML), low‐rank thin‐plate splines (bs = “tp”) via the “gam” function from the “mgcv” package (Marra & Wood, 2011; Wood, 2017), and a basis complexity (k) = 4 as it approximates to a third‐degree polynomial as suggested by Guisan et al. (2017) and Hastie et al. (2017). For all our distribution models, we applied an internal iteratively 5‐fold cross‐validation analysis, randomly selecting 80% of occurrences for calibration and the remaining 20% for model evaluation, via the “crossvalSDM” function from the “mecofun” package (Zurell, 2020). We evaluated model performance using minimum reliable predictability values for the receiver operator characteristics (ROC) of the area under the curve (AUC = 0.7), and true skill statistics (TSS = 0.4) (Araújo et al., 2005; Ruete & Leynaud, 2015). Lastly, we estimated binary responses (presence/absence) using the threshold that maximized the model TSS (sensitivity + specificity −1) (Allouche et al., 2006; Fielding & Bell, 1997).

For species abundance models, we estimated regression coefficients for both GLM and GAM by bootstrapping the data 1000 times using the “boot” function from the “boot” package approach (Canty & Ripley, 2021; Efron & Tibshirani, 1998). The bootstrapping approach allowed us to resample the modeling data and provide the least biased estimates of regression coefficients (Potts & Elith, 2006). We did this because of the low number of abundance records, which limited the obtention of an independent evaluation dataset for species abundance models. For GLM, each resample was fitted with a “logistic” link with Poisson and Gamma parametric distributions, via the “glm” functions from “stats” package (Davison & Hinkley, 1997), and Negative Binomial parametric distribution via the “glm.nb” function from “MASS” package (Venables & Ripley, 2002). For GAM, each resample was fitted using Poisson, Negative Binomial, and Gamma distributions with a “logistic” link, via the “gam” functions from “mgcv” package (Wood, 2017). We used transect length as an “offset” parameter when fitting both GLM and GAM to account for differences in length. The average of the 1000 regression coefficients for each predictor was used to estimate GLM and GAM abundance values. We used Pearson's correlation coefficient (r > .7) as an indicator of agreement between observed (y‐axis) and predicted (x‐axis) values and fitted a simple linear regression to provide information on predictions' bias and consistency (Piñeiro et al., 2008; Potts & Elith, 2006).

We projected abundance estimations into the “presence” area defined by distribution models, conditioning the suitability response to the projected area where the species was predicted to be present (Barry & Welsh, 2002). Due to the skewed distribution of projected abundances as a result of the “logistic” link and extreme predictor values, we bootstrapped projected values 100 times to estimate the “inner fences”, defined as the minimum and maximum percentiles (25th percentile [Q1]‐(1.5*inter‐quartile range) and 75th percentile [Q3] + (1.5*inter‐quartile range), respectively) based on Adjusted Boxplot, which is a robust method to detect outliers within skewed datasets (Hubert & Vandervieren, 2008; Seo, 2006). Outlier detection was done via “do” (“mosaic” R package) and “adjboxStat” (“robustbase” R package) functions (Maechler et al., 2023; Pruim et al., 2017). To explore the implications of different model projections, we constrained our predicted abundances to remain within the range of the minimum and maximum percentiles via two methods: (1) “no extrapolation” by discarding values outside the range of the minimum and maximum percentiles and (2) “extrapolation and clamping” by replacing values that were greater or less than the maximum and minimum percentile with the respective limit values (Cobos et al., 2019; Elith et al., 2011).

Additionally, as suggested by Liu et al. (2019), the relative importance of ecological predictors driving species abundances was analyzed via the loss of predictive power excluding each ecological predictor at a time and calculating the mean explained deviance reduction. For distributional models, we used permutation‐based variable‐importance evaluation by applying the Pearson correlation between the original predictions and predictions where one variable has been 100 times randomly permutated (i.e., if the correlation is high, the variable is not important for the model), via the “bm_VariablesImportance” function of the “biomod2” (version 4.2–5‐2) R package (Thuiller et al., 2024).

2.6. Estimating abundance–suitability relationship

The abundance–suitability relationship was performed in two ways: (1) we related models that were constructed using the same ecological predictors and (2) we selected the best distribution and abundance models independently of the ecological predictors used as inputs. For the former step, we selected optimal distributional models (AUC > 0.7 and TSS > 0.4) restricting suitability estimations to the regions classified as “presence” by the binary predictions. For abundance, we selected models with high consistency between observed and predicted values (Pearson's coefficient r > .7), clipped predictions to the region previously classified as “presence”, and rescaled abundances to continuous values from 0 to 1 (representing low to high abundances, respectively). Finally, suitable and abundance outcome maps were used to test for spatial correlation (Pearson's correlation coefficient analysis) using 2,000,000 raster values for P. palpebrosus and 1,000,000 raster values for P. trigonatus, which correspond to ~10% of the total number of raster pixels in the “presence” extent. For the latter step, we used the region classified as “presence” by the distributional model to clip both suitability and abundance outcome maps. We rescaled the abundance predictions (0–1) and tested for spatial autocorrelation which provided the significance and abundance variation explained by suitability predictions.

2.7. Conservation areas prioritization

We binarized the best continuous distribution and abundance models for each of the Paleosuchus species using the threshold that maximized the model TSS (sensitivity + specificity −1) classifying areas as “1” or “highly suitable” as well as classified areas above the median threshold (2nd quartile) as “1” or “highly abundant”, respectively. We then overlapped and summed both suitability and abundance binarized maps (Cavalcante et al., 2022) to create a consensus SDM‐SAM model that we categorized as low (1 = single species present), medium (2 = one species present with high predicted abundances, or both species present), high (3 = both species present with one of them predicted to be abundant), and very high (4 = both species present with high predicted abundances) conservation priorities. Subsequently, we identified critical areas where the conservation of Paleosuchus species should be highly prioritized by (1) calculating a minimum convex hull that connected all fragmented areas classified as “very high”, (2) selecting areas classified as “high” within the extent of the hull, and (3) combining both previously selected classified “high” and “very high” priority areas. We used this rationale as we focused on preserving areas where species can be considered in good conditions (both present and abundant), and maintain connectivity to serve as refugia, as well as sources for sustaining viable subpopulations in other locations. Finally, we quantified how much of the critical areas are included within areas with any protection category defined by the United Nations Environment Programme and the International Union for Conservation of Nature categories system (www.protectedplanet.net; UNEP‐WCMC & IUCN, 2024).

3. RESULTS

3.1. Distribution and abundance through GLM and GAM

For distribution models, we initially collected 1697 occurrence records for Paleosuchus palpebrosus and 2055 for P. trigonatus, from which 405 and 386 were selected after data cleaning, respectively (Figure 1a,b). With these data, we estimated 52 distributional binomial models for each Paleosuchus species based on identical modeling structures and specifications. A total of 23 (44.2%) models showed minimally optimal predictive performance (both AUC > 0.7 and TSS > 0.4) for P. palpebrosus, with the best distributional model achieved via GAM including all predictor sets (GAM‐S13, AUC = 0.830, TSS = 0.548). For P. trigonatus, 18 (34.6%) models showed reliable AUC and TSS values with the highest predictive performance achieved via GAM and including all predictor sets (GAM_sel‐S12, AUC = 0.808, TSS = 0.490). We also found that optimal models for both Paleosuchus species were yielded when using combinations of ecological predictor sets. The single exception was for P. palpebrosus, where model S5 (“Temperature” [T] variants only) achieved optimal performance via GAM and GAM_sel. Regarding model specification, our results showed that optimal distributional GAM resulted in higher predictive performances than GLM, except for models S2 and S8 for P. trigonatus, where both GLM and GLM_sel had higher predictive accuracy than their counterpart GAM and GAM_sel (Figure 2; Tables S5 and S6).

FIGURE 2.

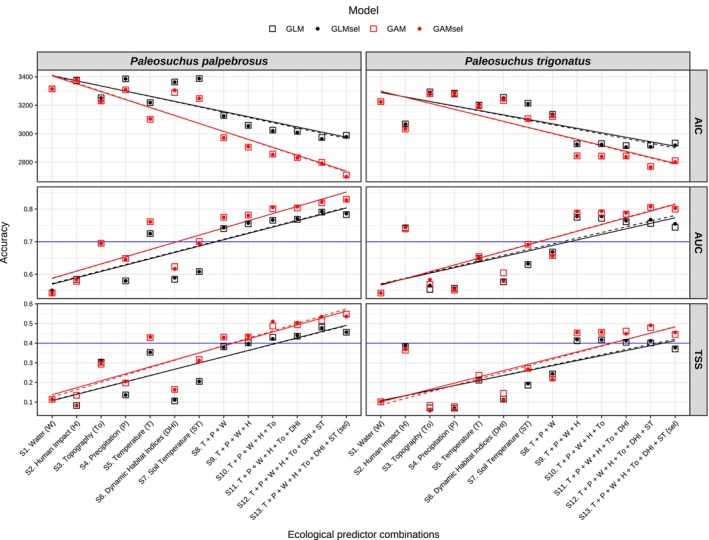
Evaluation of distribution model performances measured by the Akaike Information Criteria (AIC), receiver operator characteristics of the Area Under the Curve (AUC), and the True Skill Statistics (TSS). Sets of predictors (x‐axis) are ordered by increasing complexity regarding the number of predictor variants from left to right, accounting for individual predictor types (models S1–S7) and a gradual combination of different predictor types (models S8–S13). AIC shows how informative the model is based on the number of parameters and complexity. The lower the AIC, the better the model fits the data. AUC and TSS correspond to independent‐threshold and dependent‐threshold metrics, respectively. The blue line corresponds to the minimum levels of reliability for model predictability performance based on the AUC (0.7) and TSS (0.4). Black and red lines correspond to linear fits for Generalized Linear Models (GLM) and Generalized Additive Models (GAM), respectively. Solid lines correspond to models that used all uncorrelated predictors in each predictor set (denoted as “GLM” and “GAM”), whereas dashed lines correspond to models that used uncorrelated predictors, from which most significant were selected to be fitted in each model (denoted as “GLM_sel” and “GAM_sel”).

For abundance models, we gathered 44 and 43 counting transects for P. palpebrosus and P. trigonatus, respectively. After overlapping each digitized transect with a 1 km² raster layer, we obtained 670 abundance records within 272 intersecting pixels for P. palpebrosus and 942 abundance records within 276 pixels for P. trigonatus. We estimated 87 abundance models (42 GLM and 45 GAM) for P. palpebrosus and 71 models (35 GLM and 36 GAM) for P. trigonatus, based on the sets of predictors combinations that we used to construct minimally optimal distribution models (AUC > 0.7 and TSS > 0.4). Our results showed higher levels of abundance variations being explained via GAM than GLM, with predictive performance increasing as the number of predictors increased in the model structure. For P. palpebrosus, the average explained deviance was 71.3% for GLM and 78% for GAM, whereas for P. trigonatus, the average explained deviance was 62.1% for GLM and 66.8% for GAM. Despite the higher levels of deviance explained by GAM than GLM, the former algorithm showed higher discrepancies between predicted and observed abundances (Pearson's correlation r < .7). Thus, 22 (48.9%) and 25 (69.4%) GAM models were excluded for P. palpebrosus and P. trigonatus, respectively, whereas only 2 GLM (5.7%) were excluded for P. trigonatus. Furthermore, GLM showed a higher average correlation between predicted and observed abundances (r = .92 for P. palpebrosus and r = .78 for P. trigonatus) than GAM (r = .89 for P. palpebrosus and r = .77 for P. trigonatus). The highest consistency between observed and predicted values was obtained via Poisson GLM using all predictors sets (GLM_sel‐S12, r = .95) for P. palpebrosus, and via Poisson GAM using temperature, precipitation, water, human impact on the environment, and topography variants (GAM_sel‐S10, r = .85) for P. trigonatus (Figure 3a; Tables S7 and S8).

FIGURE 3.

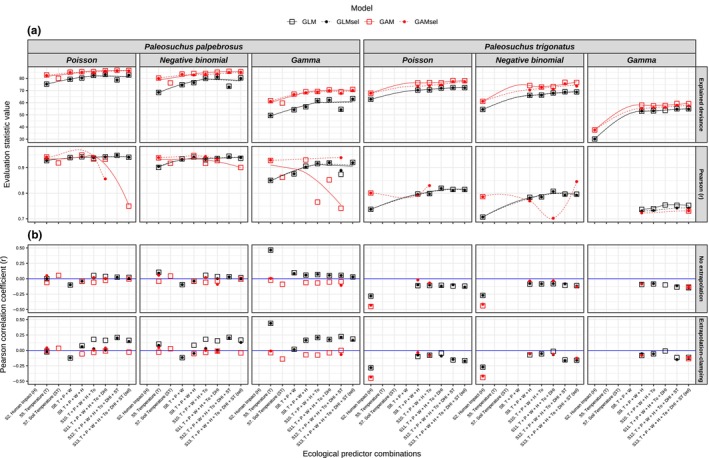
(a) Top facets correspond to the amount of variation (percentage) explained by different ecological predictor sets with different specifications during model calibration. The bottom facets indicate the consistency between observed and predicted abundances via Pearson's correlation coefficient (r). Models with r < .7 were excluded from the analysis. Black and red lines correspond to loess smoother fits for Generalized Linear Models (GLM) and Generalized Additive Models (GAM), respectively. Solid lines correspond to models that used all uncorrelated predictors in each predictor set (“GLM” and “GAM”), whereas dashed lines correspond to models that used uncorrelated and significant selected predictors that were fitted into each model (“GLM_sel” and “GAM_sel”). (b) Correlation coefficients between optimal abundance and suitability models that had significant correlations (p < .05). Top facets correspond to abundance projections via the “no extrapolation method”, whereas bottom facets correspond to projections via the “extrapolation and clamping” method. The blue line represents the non‐correlation value (0), above and below which correlations between suitability and abundance were significantly positive and negative, respectively. Sets of predictors (x‐axis) are ordered by increasing complexity regarding the number of predictor variants from left to right, accounting for individual predictor types (models S1–S7) and a gradual combination of different predictor types (models S8–S13). The set of predictors in models S1, S3, S4, and S6 were not included in the analysis since no distributional models achieved minimally optimal evaluation parameters (AUC > 0.7 and TSS > 0.4).

3.2. Abundance–suitability relationship

The assessment of the relationship between distribution and abundance models that used the same ecological predictor inputs was restricted to 110 optimal models. Our results showed low Pearson correlation coefficients (|r| < .7) and yielded mixed evidence between positive and negative abundance–suitability relationships. Regarding the analysis using abundance predictions via the “no extrapolation” method, we found four non‐significant relationships, whereas 37 and 69 models had significantly positive and negative abundance–suitability relationships, respectively. Considering the “extrapolation and clamping” method, we found one non‐significant relationship, 42 had positive and 67 had negative correlations (Figure 3b).

We found similar results when restricting the analysis to the best predictive performance models in terms of non‐consistent and low explanatory power between abundance and suitability. For P. palpebrosus, the best distributional model (GAM‐S13; AUC = 0.830, TSS = 0.548) and abundance (Poisson GLM_sel‐S12; r = .949) models were constructed using a combination of all predictor types. For the former model, we found that “elevation” and “precipitation seasonality” predictors were most critical, whereas for the latter, “mean monthly precipitation amount of the warmest quarter” and “soil temperature seasonality”, were the most important predictors that affected species occurrence. The correlation between the best distributional and abundance models (GAM‐S13 and Poisson GLM_sel‐S12, respectively) was significantly positive for both “no extrapolation” (r = .009, p < .001, CI 95% = 0.007 and 0.011) and “extrapolation and clamping” (r = .094, p < .001, CI 95% = 0.091 and 0.095) methods (Figure S2).

For P. trigonatus, the best distributional model (GAM_sel‐S12; AUC = 0.809, TSS = 0.493) included a combination of all predictor types, with “isothermality” and “human footprint” being the most important predictors. The best abundance model (Poisson GAM_sel‐S10; r = .853) incorporated a combination of 5 predictor types (temperature, precipitation, global surface water [excluded after variable selection], human impact on the environment, and topography) with “temperature seasonality” and “mean monthly precipitation amount of the coldest quarter” being the most influential predictor variants. The abundance–suitability correlation yielded significantly negative outcomes for “no extrapolation” (r = −.013, p < .001, CI 95% = −0.015 and −0.011) and “extrapolation and clamping” (r = −.020, p < .001, CI 95% = −0.022 and −0.018) abundance predictive methods (Figure S2). These results suggested that high habitat suitability and species abundance are not always congruent, and suitability has low explanatory power of abundance patterns. Variable importance and partial response curves of the selected distribution and abundance models are found in Appendix S1 (Figures S3–S7).

3.3. Conservation areas prioritization

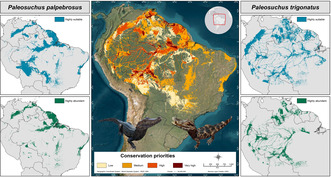
Even though correlation analysis showed that distribution and abundance models are not correlated, we extracted and combined the most relevant information from them to create a consensus model that allowed us to estimate areas to be prioritized for species conservation. We estimated a potential distribution area of 1,993,865 km² for P. palpebrosus in which at least 50.3% are areas with highly abundant populations of the species (1,003,578 km²). For P. trigonatus, the potential distribution was estimated at 1,368,089 km² with a core area of 683,174 km² (~49.9%) in which the species is predicted to be highly abundant. We identified 2,790,583 km² to be categorized into different levels of conservation priorities for the targeted taxa, with 1,105,079 km² (39.6%) classified as “low” (single species present), 1,192,809 km² (42.7%) as “medium” (one species present and abundant or both species present), 414,674 km² (14.9%) as “high” (both species present with one being abundant), and 78,021 km² (2.8%) as “very high” (both species present and abundant) (Figure 4; Table 1). We delineated critical conservation areas encompassing 279,338 km² where the conservation of Paleosuchus species should be highly prioritized, distributed within Brazil (165,622 km², 59.3%), Venezuela (59,929 km², 20.4%), Bolivia (14,721 km², 5.3%), Peru (12,397 km², 4.4%), Suriname (10,054 km², 3.6%), Colombia (6548 km², 2.3%), Guyana (6101 km², 2.2%), French Guiana (5344 km², 1.9%), and Ecuador (1623 km², 0.6%). We showed that 29% (81,684 km²) of critical conservation areas are under protection, whereas 71% (197,653 km²) are found outside protected areas (Figure 5).

FIGURE 4.

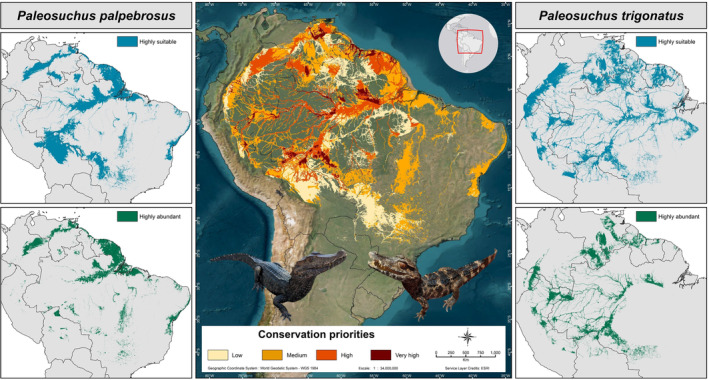
Geographic projection of the prioritization of conservation areas for Paleosuchus palpebrosus and P. trigonatus estimated via selecting and then combining the best predictive performance distributional and abundance models. Regions predicted as “Highly suitable” (in blue) correspond to areas classified as “presence” based on Binary dependent‐threshold models that maximized the True Skill Statistic (TSS). Regions where the species are predicted to be “highly abundant” (in green) were obtained from continuous species abundance models that were binarized using the median (2nd quartile) as a classifier threshold. Conservation priorities correspond to the number of binarized models that agreed on highly suitable habitats and where the species is predicted to be highly abundant, with values of low (single species present), medium (one species present with high predicted abundances or both species present only), “high” (both species present with one of them predicted to be highly abundant), and “very high” (both species present with high predicted abundances). Left: P. palpebrosus; Right: P. trigonatus. Photo credit: Andre Rocha.

TABLE 1.

Difference between the extent of the areas estimated for the conservation priorities of Paleosuchus palpebrosus and Paleosuchus trigonatus based on ecological suitability and species abundance.

Conservation priority	Area (km2)
	Bolivia	Brazil	Colombia	Ecuador	French Guiana	Guyana	Peru	Suriname	Paraguay	Trinidad & Tobago	Venezuela
Low	269,861	566,140	92,837	27,005	2605	22,036	35,472	21,381	735	18	66,989
Medium	35,382	675,119	86,250	27,490	48,121	36,406	100,147	26,813	106	794	156,181
High	17,323	204,694	69,929	1366	26,481	1151	11,649	28,328	—	—	53,753
Very high	4672	43,804	868	330	1287	4976	3484	6957	—	—	11,643
TOTAL	327,238	1,489,757	249,884	56,191	78,494	64,569	150,752	83,479	843	814	288,566

FIGURE 5.

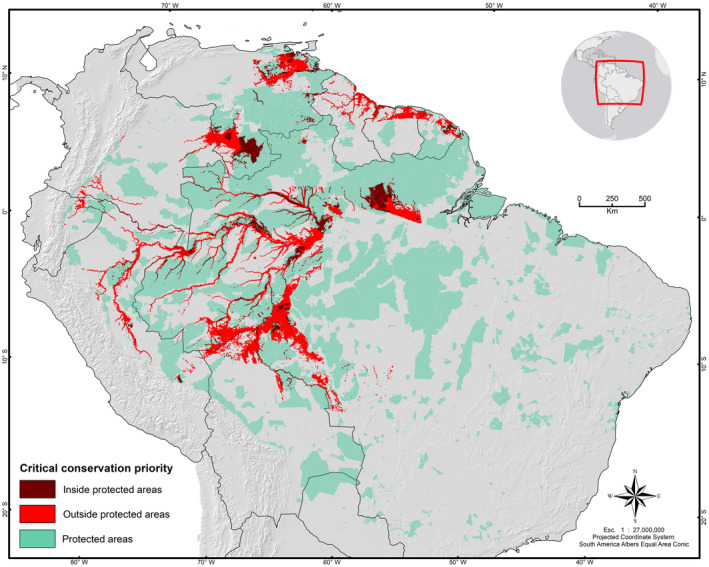
Geographic projection of critical conservation areas that are currently under protection (in brown) and that are found outside protected areas (in red) based on the United Nations Environment Programme and the International Union for Conservation of Nature Protected Areas categories system (in green) (www.protectedplanet.net; UNEP‐WCMC & IUCN, 2024).

4. DISCUSSION

Our study is the first attempt to identify conservation priorities for two crocodylian species with low knowledge of their spatial ecology, relying on robust distribution models and predicting abundances conditional to species presence. Due to the underdevelopment of abundance‐based models relative to occurrence‐based models, guidance on modeling abundance spatial variation (varying both model structure and regression analysis specifications) remains scarce (Waldock et al., 2022), and was not tested thoroughly for any crocodylian species besides this current study. Thus, the robustness of our approach constitutes a useful tool for managers and conservation practitioners that can guide future conservation planning and provide insights in spatial ecology and biogeography.

Our prioritization approach was restricted to the best distributional and abundance models. For Paleosuchus palpebrosus, we selected GAM‐S13 for distribution and Poisson GLMsel‐S12 for abundance. Both models used a combination of all predictor types as inputs (temperature, precipitation, global surface water, human impact on the environment, topography, dynamic habitat indices, and soil temperature). For P. trigonatus, GAM_sel‐S12 optimized distribution predictions and included a combination of all predictor types, whereas Poisson GAMsel‐S10 was selected as the best abundance model, which incorporated a combination of 4 predictor types (temperature, precipitation, human impact on the environment, and topography). From this perspective, we estimated 2,790,583 km² that were categorized as low (39.6%), medium (42.7%), high (14.9%), and very high (2.8%) conservation priorities, and identified 279,338 km² where conservation effort for Paleosuchus species should be highly prioritized, distributed in Brazil (59.3%), Venezuela (20.4%), Bolivia, Peru, Suriname, Colombia, Guyana, French Guiana, and Ecuador (20.3%) where the conservation of the targeted taxa should be highly prioritized.

We argue that biodiversity conservation is best met by managing single species instead of entire ecosystems since this method provides explicit analytical and monitoring data to assess the success of conservation efforts (Mace et al., 2007). However, the information used for analyzing conservation efforts must be robust and descriptive of the species' natural conditions or at least the uncertainty of the metric must be understood. For instance, a study on prioritization models and assessment of protected areas' effectiveness in the conservation of worldwide crocodylians suggested that both Paleosuchus species are well represented within protected areas (Lourenço‐de‐Moraes et al., 2023), which implies that there is no need for conservation efforts in this regard for these species. However, our study showed that around 71% of the areas where the species can be considered in good condition based on habitat suitability and abundance modeling are outside of any category of protection and do not have any type of regularized protection to ensure their conservation. In this example, the broad differences between Lourenço‐de‐Moraes et al. (2023) and our analysis derived from the quality of the data used as the former study relied conclusions on IUCN Red List distribution polygons which are highly inaccurate to describe the actual species distribution and has no consideration of any other population attribute, whereas the latter used a robust method that accurately defined what could be described as the distribution of both species based on presence and abundance. Thus, since conservation efforts need evidence‐based planning, we emphasize the importance of the development of finer‐scale strategies and incorporating relevant species‐specific data in consensus models to prioritize the allocation of flexible funding to promote species conservation efforts and minimize biodiversity loss (Brooks et al., 2006). Furthermore, crocodylians are considered flagship and umbrella species, and thus, efficient conservation actions might protect a large number of coexisting species and their local environments (Lourenço‐de‐Moraes et al., 2023).

In our study, we also explored the capacity of suitability habitat models to predict abundance patterns within the species distributional range focused on developing a finer‐scale conservation strategies framework. However, we failed to detect a consistent relationship between abundance and suitability since regardless of the use of GLM, GAM, and the individual or gradual combination of ecological predictor types yielded mixed evidence between weak positive and negative relationships. These results were not affected by whether spatial correlation was assessed between single independent abundance and suitable models with the best predictive performance. Consequently, our findings support that environmental suitability and spatial abundance are not always congruent (Waldock et al., 2022), cannot be considered reliable surrogates for one another (Dallas & Hastings, 2018), and independently incorporate relevant information to better understand the spatial ecology and population dynamics towards the improvement of systematic conservation planning.

Similarly to most vertebrate taxa around the world, we were confronted with limited data and had a lower geographic representation of abundances compared with species occurrence (Araújo & Williams, 2000). Although abundance in crocodylian populations has been collected based on standardized methods (Bayliss, 1987; Chabreck, 1966; Magnusson, 1982; Messel et al., 1981; Wood et al., 1985) and have been improved based on new technologies, specific habitats, and ecological information required (e.g., Balaguera‐Reina et al., 2018; Fujisaki et al., 2011; Fukuda et al., 2013; Pacheco, 1996; Sai et al., 2016; Thorbjarnarson et al., 2000), non‐commercially valuable species such as the dwarf caimans have only been given marginal attention (Ergueta & Pacheco, 1990; Pacheco & King, 1995). Consequently, since small sample sizes may yield erroneous density estimations (Yañez‐Arenas et al., 2014) or estimate overconfident models (Waldock et al., 2022), the scarcity of abundance data for crocodylian species that are not subject to management and sustainable use programs constitutes a major constraint to filling knowledge gaps on species abundance distribution patterns.

To overcome this shortcoming, we implemented the method suggested by Welsh et al. (1996) and Barry and Welsh (2002) where distributional patterns were initially modeled, followed by abundance estimation conditional to the presence of the species. Although this strategy might be useful to reduce uncertainty, we emphasize the need to further explore the effect of sample size on abundance‐based models. For example, these caveats could be explored with future studies that include other species from the Alligatoridae family whose abundances have been better monitored, such as Caiman yacare (Campos et al., 2020), Caiman crocodilus (Balaguera‐Reina & Velasco, 2019), or Alligator mississippiensis (Elsey et al., 2019). We highlight the relevance of assessing entire assemblages (Hidasi‐Neto et al., 2020), to account for ecological constraints of estimation methods, and incorporate a thorough integrative analysis to obtain comparable data to understand species distribution and abundances patterns (Araújo & Williams, 2000; Balaguera‐Reina et al., 2018). Furthermore, we highlight the need to continue the collection of abundance data or explore potential methods to reduce bias when making density estimations (e.g., Yañez‐Arenas et al., 2014). Future research and conservation efforts could be improved by incorporating major threats not only to crocodylian species but also to other wildlife, such as climate change and habitat degradation. Nonetheless, this approach would only be useful if both current ecological predictors and threats could be accurately predicted into the future (Araújo et al., 2002).

Our findings showed that individual sets of predictors led to low predictive performances, whereas the gradual combination of different sets of predictors and the increase of predictor variants consistently increased the accuracy of distributional models (Figure 2). As expected, our results are consistent with studies that showed significant effects of model structure and the choice of explanatory variables on model performance and transferability (Pratt et al., 2022; Zarzo‐Arias et al., 2022). Interestingly, many studies that implemented distribution models used the same sets of predictors without assessing the effects of different combinations (Regos et al., 2019). To ensure the ecological significance and transferability success of Species Distribution Models (SDM) and Ecological Niche Models (ENM), the selection of predictors needs to avoid the assumption of a fitted equilibrium (Guisan & Theurillat, 2000; Jones et al., 2016), and account for both direct and indirect contingent nature of species‐predictor relationships (Austin, 2007; Gillson et al., 2013).

Overall, we found that both GLM and GAM increased their predictive performance when gradually combining different sets of predictors. Moreover, it would be expected that GAM would yield better predictions than GLM because even though they are both parameterized to fit a linear parametric distribution, GAMs automatically select the polynomial transformation via “smoothers” applied to some predictors (Guisan et al., 2002). Nonetheless, for distribution models, we found that GAM had higher discriminatory power between areas of presence and absence (lowest AIC and highest AUC and TSS) (Figure 2; Tables S5 and S6), whereas GLM performed consistently better for abundance models, yielding higher correlations between observed and predicted values (Figure 3; Tables S7 and S8). Similar patterns were found in other studies, suggesting that GLMs could estimate abundance patterns more accurately than GAM (Waldock et al., 2022; Yu et al., 2013). However, Oppel et al. (2012) found opposite results, indicating better performance of GLM for distributional data and GAM for abundance data. We suggest that this difference might be due to the targeted species (migratory seabird Puffinus mauretanicus), ecosystem (Balearic archipelago in the western Mediterranean), and ecological predictors (dynamic oceanographic data) used by Oppel et al. (2012). Consequently, we can conclude that depending on the distributional patterns of the species records (e.g., occurrences and abundance locations), the optimal modeling method (structure and specification) might differ depending on the target species and ecological predictor selection (Yoon & Lee, 2021; Zarzo‐Arias et al., 2022).

We found that the selection process of uncorrelated predictors and identification of significant predictors while model fitting were important considerations to increase the predictive ability for both GLM and GAM. Nevertheless, studies have shown that high accuracy produced by the increase in the number of predictors might result in overfitting models, variable redundancy, and increased uncertainty (Beaumont et al., 2005; Synes & Osborne, 2011). These effects might be problematic when the main objective of the models is the extrapolation of distributions to novel environmental conditions. To overcome these issues, we recommend using other evaluation parameters besides the AUC (e.g., calculate omission and commission errors separately) (Synes & Osborne, 2011) or to evaluate model performance against independent data (e.g., occurrences and environmental conditions not included during model calibration) (Araújo et al., 2005). Although these suggestions may be included in future studies, herein, however, we attempted to make an exploratory analysis comparing the trade‐off between different model structures and specifications using the same current available occurrence and abundance dataset.

This study was able to find evidence to support our hypothesis that the incorporation of additional predictors besides commonly used temperature and precipitation would improve the prediction accuracy of the species realized niche within the limits of the calibration dataset. Nevertheless, complexity might decrease the model's predictive performance within novel environments, and thus affect the interpretability of distribution and abundance estimations. Therefore, the degree of complexity for distribution and abundance models must balance out both calibration accuracy and performance of predictions (interpretability; Venables & Dichmont, 2004). For distribution models, we suggest the incorporation of more relevant predictors when using GLM and GAM if both the amount and representativeness of sampling locations are appropriate. For abundance models, we suggest using GLM for inferences when dealing with scarcity of data and novel environments, since our results showed uniform estimations regardless of model structure and specifications. Future studies including a detailed assessment of regression models' performance and transferability to novel environments is also warranted, incorporating species and entire assemblages with high‐quality abundance estimates.

Finally, this work supports previous studies in that presence‐based distribution and abundance models should systematically guide sustainable management planning and conservation prioritization efforts (Cavalcante et al., 2022; Lourenço‐de‐Moraes et al., 2023; Pollock et al., 2020; Waldock et al., 2022), not only to protect crocodylian species but to prevent widespread loss of concurrent biodiversity and their habitats. Although our findings and datasets are directly related to both Paleosuchus species, the same principles should be relevant for other crocodylian species and even other vertebrates, assuming that the amount, quality, and representativeness of predictors are minimally optimal for these assessments. Having considered our research's strengths and limitations, it is important to emphasize that spatial biodiversity models constitute a critical tool to potentially overcome shortfalls that are yet to be explored (e.g., scarcity of data and sampling gaps across the taxon's geographic distribution extent).

AUTHOR CONTRIBUTIONS

Andrés L. Rodriguez‐Cordero: Conceptualization (lead); data curation (lead); formal analysis (lead); investigation (lead); methodology (lead); visualization (lead); writing – original draft (lead); writing – review and editing (lead). Sergio A. Balaguera‐Reina: Conceptualization (equal); formal analysis (equal); investigation (equal); methodology (equal); supervision (equal); writing – review and editing (equal). Brandon A. Gross: Investigation (equal); validation (equal); writing – review and editing (equal). Margaret Munn: Data curation (equal); validation (equal). Llewellyn D. Densmore III: Funding acquisition (lead); investigation (equal); supervision (lead); validation (equal); writing – review and editing (equal).

Supporting information

Appendix S1.

Appendix S2.

Appendix S3.

Rodriguez‐Cordero, A. L. , Balaguera‐Reina, S. A. , Gross, B. A. , Munn, M. , & Densmore, L. D. III (2024). Assessing abundance–suitability models to prioritize conservation areas for the dwarf caimans in South America. Ecology and Evolution, 14, e70235. 10.1002/ece3.70235

DATA AVAILABILITY STATEMENT

The occurrences database, links for the ecological predictors, R script, and relevant information used in this article are available in Appendices S1, S2, and S3.