Abstract
Heterogeneous thermocatalysis of formic acid dehydrogenation by metals in solution is of great importance for chemical storage and production of hydrogen. Insightful understanding of the complicated formic acid dehydrogenation kinetics at the metal-solution interface is challenging and yet essential for the design of efficient heterogeneous formic acid dehydrogenation systems. In this work, formic acid dehydrogenation kinetics is initially studied from a perspective of electrochemistry by decoupling this reaction on Pd catalyst into two short-circuit half reactions, formic acid oxidation reaction and hydrogen evolution reaction and manipulating the electrical double layer impact from the solution side. The pH-dependences of formic acid dehydrogenation kinetics and the associated cation effect are attributed to the induced change of electric double layer structure and potential by means of electrochemical measurements involving kinetic isotope effect, in situ infrared spectroscopy as well as grand canonical quantum mechanics calculations. This work showcases how kinetic puzzles on some important heterogeneous catalytic reactions can be tackled by electrochemical theories and methodologies.
Subject terms: Electrochemistry, Energy, Heterogeneous catalysis
pH-dependent rate determining steps and cation effects for thermocatalytic formic acid dehydrogenation at Pd/solution interfaces are analyzed electrochemically based on the coupling of formic acid oxidation reaction and hydrogen evolution reaction.
Introduction
Heterogeneous catalysis is the core sector in the chemical industry that produces enormous quantity of chemical materials annually. Most of the heterogeneous catalytic processes take place at the solid-gas interface, and the theories and methodologies to investigate the heterogeneous catalysis are built on the classic context accordingly. However, there are also important heterogeneous catalytic reactions proceeding at the solid-liquid interface (specifically, the metal-solution interface) that are distinct from those at the gas-solid interface1–3. Regular heterogeneous catalytic theories are incapable of describing the complex chemical behaviors at the metal-solution interface, and a framework for mechanistic study of such heterogeneous catalysis is highly demanded.
Among such catalytic reactions, thermocatalytic formic acid dehydrogenation (FAD, , )4 on a metallic catalyst deserves special attention in that the production and storage of hydrogen by means of heterogeneous catalysis is one of the top priorities in energy chemistry5,6. The high volumetric capacity (53 g H2/L) and its low toxicity and flammability under ambient conditions make formic acid a promising hydrogen energy carrier7,8. With input of renewable power, FA can be facilely and massively produced from electroreduction of CO29. As a liquid, it can be safely stored and transported to the end-consumers. When hydrogen is in need, FA undergoes a spontaneous and selective dehydrogenation process to release hydrogen gas on Pd-based catalysts in aqueous formic acid-formate solutions at mild temperatures (referred herein to thermocatalytic FAD or FAD unless otherwise specified)10–14.
FAD at the metal-gas interface has been well understood by theoretical calculations15–17, which suggests sequential cleavage of O-H and C-H bonds of FA on the metal surface without any charged species or charge transfer steps as depicted in the top left of Fig. 1a. In contrast, the FAD at the metal-solution interface involves the deprotonation of FA in the bulk solution to formate prior to adsorption onto the metal surface18–22, with charged species and charge transfer steps. The thermocatalytic investigations of FAD have so far been overwhelmingly limited to the development of catalysts by tuning composition, structure and metal-support interaction as well as the test of additives in the solution. Among them, decreasing the Pd particle size to enrich the active sites (e.g., the Pd(0)-Pd(II) interface)23 and modifying the support with alkaline groups (e.g., amines) to facilitate the deprotonation of FA14 are two effective tactics for developing FAD catalysts.
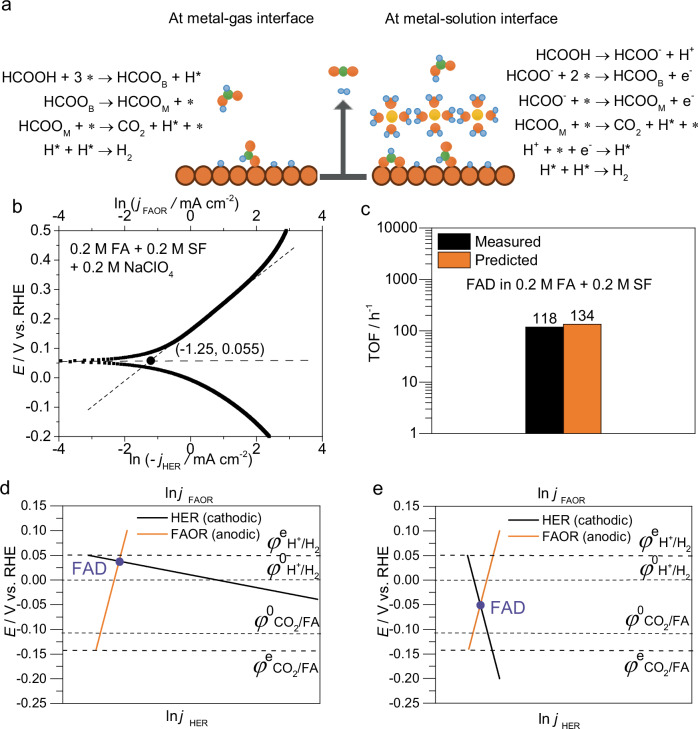
Fig. 1. FAD mechanism at metal-gas and metal-solution interfaces.
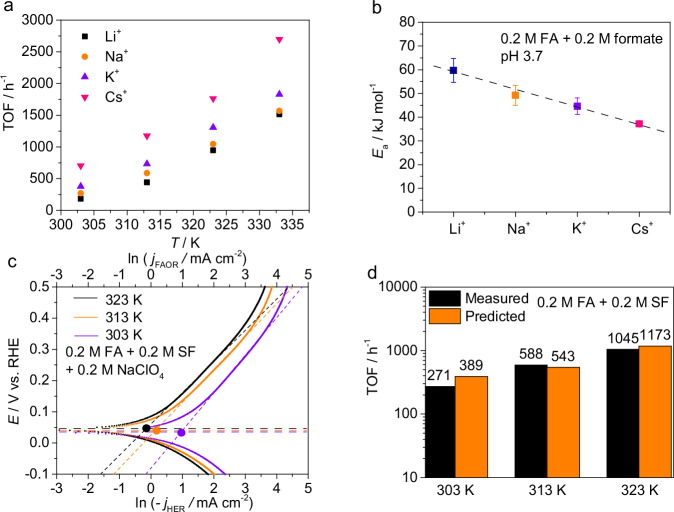
a Elementary steps of FAD at metal-gas and metal-solution interfaces. b Evans diagram for FAD in 0.2 M FA + 0.2 M NaHCOO(SF) + 0.2 M NaClO4 at pH3.7. c The measured value of FAD reaction rate as compared to the value predicted by the Evans diagram method in b. d A typical schematic plot of the Evans diagram where FAOR is relatively sluggish. e A typical schematic plot of the Evans diagram on FAD with similar reaction rate of FAOR and HER. φ0 refers to the potential when the second term on the right side of Eq. 1 or 2 is zero. Source data are provided as a Source Data file.
Virtually no attention has been paid to the metal-solution interface for FAD. Therefore, the mechanism of thermocatalytic FAD is far from clear in terms of the rate determining step (RDS) and its deciding interfacial factors. Among others, the combinative desorption of hydrogen () has been suggested as the RDS of FAD based on apparent activation energy determination and DFT calculations on neat Pd(111)20,21, whereas, the C-H bond cleavage step as the RDS based on kinetic isotopic effect (KIE) and reaction order of formate24. The major hurdle against clear mechanistic clarification arises from the fact that such a spontaneous FAD at the Pd catalyst /solution interface involves coupled reactions as well as electrical double layer (EDL) effect. Unfortunately, such essential and yet puzzling points have been largely ignored in FAD thermocatalysis.
In this work, we tackle the thermocatalysis of FAD on Pd catalysts in aqueous formic acid-formate solutions using methodologies and theories rooted in interfacial electrochemistry. An electrochemical mechanistic paradigm is put forward by disentangling the FAD into two electrochemical half reactions at a mixed potential, namely, formic acid oxidation reaction (FAOR, ) and hydrogen evolution reaction (HER, ), and then coupling the kinetic features of the two half reactions to comprehensively understand the overall FAD kinetics. pH-dependent RDSs for the FAOR, HER and FAD in acidic, neutral and alkaline solutions are determined by KIE measurements, respectively, and grand canonical quantum mechanics (GCQM) calculations to evaluate the energy barriers of the elementary steps of FAOR and HER at a constant potential. The influence of the EDL structure on FAD kinetics is studied by cation effects on the two half reactions. An insightful mechanistic understanding of FAD at the Pd-solution interface is projected to guide the design of efficient FAD systems.
Results and discussion
Disentangling FAD into two electrochemical half reactions
A mixed potential theory originating from classical corrosion electrochemistry has been put forward to address the thermochemical catalytic reaction at metal/solution interfaces, including small organic molecules oxidation, hydrogen peroxide production and nitrophenol hydrogenation25–30. In these studies, the thermocatalytic reactions were regarded as the coupling of two independent half reactions. And by measuring respectively the current densities of the half reactions in isolation, the mixed potential and the reaction rates for the overall thermocatalytic reactions can be quantitatively predicted by this model. For example, the thermocatalytic oxidation of formic acid (2HCOOH + O2 = 2CO2 + 2H2O) was regarded as the coupling of FAOR and oxygen reduction reaction (ORR: O2 + 4e− + 4H+ = 2H2O), the FAOR current density (jFAOR) was measured without O2, and the ORR current density (jORR) measured without HCOOH as a function of potential (E)25. In a j-E diagram involving the two half reactions, the potential at which jFAOR = -jORR is the mixed potential for the overall oxidation of formic acid while the current density jFAOR = -jORR corresponds to the reaction rate of oxidation of formic acid in consideration of Faraday’s Law on electrolysis. This diagram is also known as the Wagner-Traud diagram in classic electrochemistry, which is often used to quantify the kinetics of electroless metal plating31.
As for the heterogeneous FAD in solutions, the overall reaction can be deemed as the combination of two half cell reactions: FAOR and HER. The standard electrode potential for the redox couple of H+(aq.)/H2(g) is 0 V vs SHE while that of CO2(g) /HCOOH(aq.) is around −0.11 V vs SHE32. Therefore, HER and FAOR reactions may take place spontaneously to form a short circuit galvanic cell on a metal catalyst to yield the mixed potential, which is equivalent to the stabilized open circuit potential (OCP) for FAD in a deaerated solution. However, since the reactant for kinetically facile HER is proton or water which is a ubiquitous species in aqueous solution, one cannot directly measure with confidence the net FAOR current density in isolation of HER around the OCP. Thus, the Wagner-Traud diagram based method is no longer suited for predicting the reaction rate of FAD. In fact, in a latest work published by others during the revision of this work, Wagner-Traud diagram was directly applied to predict FAD reaction rates with one order of magnitude smaller than the measured ones33.
To address this issue, a method based on the Evans diagram which is widely used in corrosion electrochemistry is invoked in this work. The key point of such a method involves the Tafel straight line extrapolation on the polarization curves of the two half reactions31, where the crossing point yields the mixed potential (OCP) and the short-circuit current. A representative Evans diagram for FAD in a FA/SF mixed solution (pH3.7) is shown in Fig. 1b, in which 0.2 M NaClO4 was added as a supporting electrolyte to minimize the solution resistance without changing the reaction kinetics. Ideally, both FAOR and HER current densities on the Tafel extrapolation lines would yield the FAD reaction rate at the mixed potential. Practically, we found that the Tafel equation fits well for the current density of FAOR between 0.15 and 0.3 V, while a significant deviation of HER current density from the Tafel equation was recorded in the whole potential range, given the fact that the HER current density was drastically influenced by the reoxidation of H2 at low overpotentials and slow diffusion of H2 in the supported catalyst layer at high overpotentials34. Therefore, we used the Tafel extrapolation line of FAOR rather than that of HER at OCP in the Evans diagram to derive the FAD reaction rate in Fig. 1b. Indeed, the FAD reaction rate was satisfactorily predicted by this method, as shown Fig. 1c. In other words, we have demonstrated that the mixed potential theory in electrochemistry can be applied in dealing with thermocatalytic FAD kinetics.
In addition, the relative biases of the mixed potential (or OCP) from the equilibrium potentials of the two redox couples can be used to gauge the kinetically sluggish half reaction. For instance, Fig. 1d is a schematic of that the FAD rate is mainly determined by the FAOR rate as judged by the more proximity of the OCP to the equilibrium potential φe(H+/H2). And if the OCP locates around the middle of φe(H+/H2) and φe(CO2/HCOOH), the FAOR and HER half reactions are expected to exhibit comparable kinetics (see Fig. 1e). Note that
| 1 |
| 2 |
where and are the partial pressures of product gases in the catalyst layer, and is the concentration of formic acid; R, T and F are gas constant, Kelvin temperature and Faraday constant, respectively.
pH-dependent RDSs for electrochemical half reactions
To unravel the RDS of thermocatalytic FAD in solutions of varying pHs, we first deal with the RDSs of the two electrochemical half reactions FAOR and HER individually. The KIE factor is a critical term for identifying an RDS35, usually an H/D KIE factor value larger than 1.4 indicates that the C-H/D (or O-H/D) bond cleavage step is an RDS for the specific reaction. For the FAOR on Pd, a pH-dependent shift of RDS is revealed by KIE measurements as shown in Fig. 2a–d. From the peak oxidation current density, the C-H/D KIE factors are determined to be 3.8, 3.3 and 1.4 while the O-H/D KIE factors are 2.0, 1.4 and 1.2 for pH1, 3.7 and 13, respectively. In electrochemistry, it is well accepted that FAOR reaction undergoes the formate pathway as the major pathway in a wide range of pH with deprotonation of formic acid facilely occurring in the bulk solution via the conjugate acid-base equilibrium36, i.e.,
| 3 |
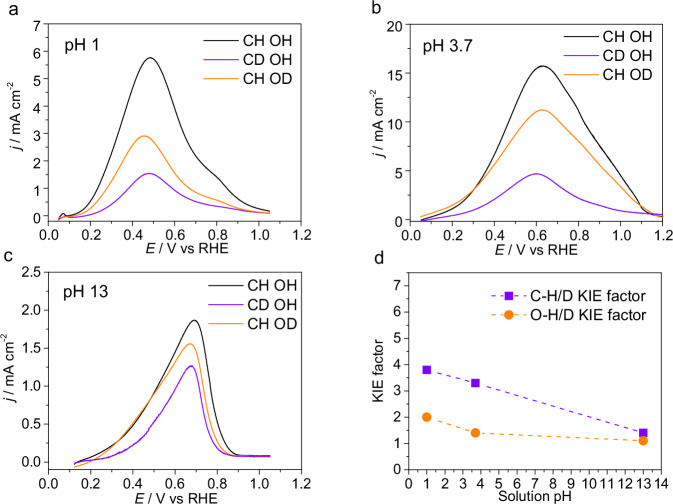
Fig. 2. KIE measurements of FAOR on Pd/C catalysts.
Linear sweep voltammograms on Pd/C in solutions containing (a) 0.1 M HClO4 + 0.1 M HCOOH at pH1, (b) 0.2 M HCOOH + 0.2 M NaHCOO + 0.2 M NaClO4 at pH3.7 and (c) 0.1 M NaOH + 0.1 M NaHCOO at pH13. Label C-H(C-D) refers to (deuterated) formate/formic acid, and O-H(O-D) refers to (deuterated) water. The scan rate is set at 10 mV/s and the rotating speed of the RDE at 1600 rpm. d The plots of KIE factors for C-H/D and O-H/D against solution pH for FAOR, where the dotted lines are used for the guide of eyes. Source data are provided as a Source Data file.
which is consistent with the low O-H/D KIE factors from pH1 to pH13 in the above measurement. It may be necessary to point out that a relatively higher O-H/D KIE factor of 2.0 observed at pH1, as an exception, may be due to the coexistence of a parallel formic acid pathway in a strong acidic solution37, which starts with a slow deprotonation on surface sites via . In addition, the high O-H/D KIE factor of 2.0 may also be caused by the smaller dissociation constant (Kw) of D2O than H2O, which suppress the deprotonation of formic acid38.
The subsequent breaking of the C-H bond occurs in the formate pathway (as depicted in Fig. 1a). High C-H/D KIE factors at pH1 and pH3.7 indicate that the C-H bond breaking is an RDS for the formate pathway of FAOR. Further increasing pH changes the kinetics of the formate pathway through a change of the interfacial electric potential. For a given potential versus RHE, the corresponding potential versus SHE decreases with increasing pH,
| 4 |
leading to a more negatively charged surface39,40. Considering that the proton is not involved in the formate adsorption step,
| 5 |
the driving force for the anionic formate adsorption decreases with increasing pH, and step 3 turns kinetically sluggish at higher pH. As a result, the RDS changes from being C-H cleavage relevant to irrelevant with increasing pH, as demonstrated by the decreasing C-H/D KIE factor from 3.8 at pH1 to 1.4 at pH13 in Fig. 2d. Such kinetic feature of FAOR on Pd is consistent with that on Pt(111) reported by Chen’s group41,42.
On the other hand, since a large number of literature reports have already dealt with the pH dependent kinetics of HER on Pd electrodes43–46, we just simply summarize and testify the main consensus herein. The HER on Pd in an acidic solution is kinetically facile with a determined exchange current density of 0.84 mA cm−2 in H2-saturated 0.1 M HClO4 and controlled by mass transport of hydrogen as shown in Supplementary Fig. 1a, b43. In contrast, the reaction rate in an alkaline solution is generally over two magnitudes of order lower than that in an acidic solution on a noble metal44. The RDS for HER on Pd in alkaline solutions is the Volmer step (), with a Tafel slope of ~125 mV dec−1 as shown in Supplementary Fig. 1c45,46. Furthermore, Supplementary Fig. 1d, e shows a primary O-H/D KIE factor of 5.7 for HER on Pd in an alkaline solution, in agreement with the Volmer step-controlled HER process. Considering that water is the reactive precursor in a neutral or alkaline solution, it can be inferred that the Volmer step is the RDS for HER on Pd in a neutral solution as well.
Electrochemical origins of pH dependent FAD kinetics
As depicted in Fig. 1, the kinetics of FAD is expected to be collectively determined by those of FAOR and HER, which is actually confirmed by the KIE results for FAD as shown in Fig. 3a, b and Supplementary Fig. 2. At pH1 and pH3.7, the C-H/D KIE factors for FAD are 4.5 and 4.0, in proximity to the counterparts for FAOR, while the O-H/D KIE factors for FAD are 1.1 and 0.9, consistent with the fast kinetics of HER in acidic media. Moreover, the OCP values remain at 23 and 33 mV vs RHE, close to the equilibrium potential φe(H+/H2), see Fig. 3c. The primary KIE on C-H/D (KIE factor equals to 2.5) and secondary KIE on O-H/D (KIE factor equals to 1.1) at pH 3.7 are further verified in Fig. 3d, e, we can conclude that the overall FAD kinetics is controlled by the C-H bond cleavage of the half reaction FAOR in acidic media.
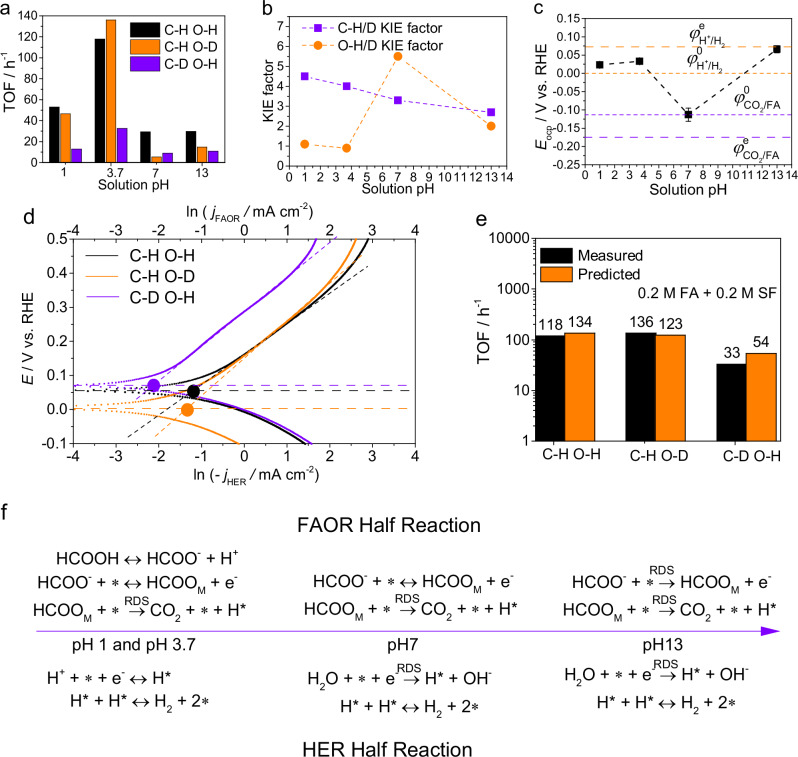
Fig. 3. Determination of RDS of FAD on Pd/C catalysts.
a Initial TOFs for FAD on Pd at different solution pHs. pH1 solution: 0.1 M HClO4 + 1.0 M HCOOH, pH3.7 solution: 0.2 M HCOOH + 0.2 M NaHCOO, pH~7 solution: 1.0 M NaHCOO, and pH13 solution: 0.1 M KOH + 1.0 M KHCOO. Labels C-H and C-D refer to the use of HCOOH/HCOO− and DCOOH/DCOO−, and O-H and O-D to the use of H2O and D2O in the measurements, respectively. Test condition: 298 K for pH1, 3.7 and ~7, and 333 K for pH13. b KIE factors of C-H/D and O-H/D for FAD at different pHs calculated from the data obtained in a. c Open circuit potentials (Eocp) measured at the catalyst surface during FAD (without deuteration) at different pHs at 298 K, the dotted lines are used for the guide of eyes. d Evans diagrams for KIE measurements of FAD in solutions of pH3.7. e Comparisons between measured FAD reaction rates (adapted from data in a) and predicted FAD reaction rates by the Evans diagram method (adapted from data in d). f Scheme of pH-dependent RDS for FAD as analyzed by the mixed potential theory. The chemical equilibrium among CO2, bicarbonate and carbonate in solutions is neglected in this scheme. φ0 refers to the potential when the second term on the right side of Eq. 1 or 2 is zero. Source data are provided as a Source Data file.
With an increase of solution pH, two major events take place. One is the exhaustion of hydronium ions, and the other is the decreasing Pd electrode potential vs SHE that favors the adsorption of cation species but disfavors the adsorption of anions. In a solution of pH~7, the O-H/D and C-H/D KIE factors for FAD are 5.5 and 3.3, respectively. The drastic increase of the O-H/D KIE factor for FAD from 0.9 to 5.5 with pH increased from 3.7 to 7 can be attributed to the sluggish O-H cleavage of H2O in the half reaction HER in a neutral solution, which is corroborated by the dramatically negative shift of OCP to −113 mV vs RHE approaching φe(CO2/HCOO−). Furthermore, a C-H/D KIE factor of 3.3 for FAD indicates that C-H bond cleavage in the half reaction FAOR is another RDS for the overall FAD. In other words, both half reactions are kinetically sluggish in a neutral solution. Given that the 1.0 M NaHCOO solution does not exhibit a pH buffering capacity, the fluctuation of surface pH prevents the meaningful electrochemical FAOR and HER measurements. Instead, the kinetically sluggish O-H cleavage of H2O to form adsorbed H during FAD in a neutral solution is verified by an isotope labeled in situ mass spectrometric measurement, as shown in Supplementary Fig. 3. It turns out that the inter-exchange H* + D+ = H+ + D* due to H* = H+ + e− and D+ + e− = D* on Pd is facile and reversible in an acidic solution while the inter-exchange is slow and rate-limiting in a neutral solution during FAD. This result lends additional support to our conclusions that C-H bond cleavage is the only RDS for the FAD in an acidic solution while both C-H and O-H cleavages jointly contribute to the RDS for the FAD in a neutral solution.
With the solution pH increased to 13, a second transition of the RDS against pH for the overall FAD may occur due to the energetically unfavorable adsorption of formate anions on Pd as detailed in the prior section (see Eq. (5)). In fact, compared to the counterparts measured at pH~7, the O-H/D and C-H/D KIE factors for the FAD at pH13 decrease to 2.0 and 2.8, respectively, suggesting that additional RDS (i.e., formate adsorption) for the FAD should not be neglected at pH13 where an equivalently very negative potential vs SHE applies to Pd surface. This proposal is corroborated by the observation that the OCP is again positively shifted towards φe(H+/H2) at 66 mV vs RHE, indicating that FAOR is kinetically more sluggish than HER. In other words, three separate RDSs, two from FAOR and one from HER, jointly determine the overall FAD kinetics at pH13. Notably, a complex multistep reaction may contain more than one RDSs whose contribution to the overall reaction rate can be quantified by a term called degree of rate control47.
The reaction mechanism of FAD with identified RDSs at different pHs is summarized in Fig. 3f, in light of the analytical paradigm by disentangling FAD into two coupled half reactions at a mixed potential. Now we are able to settle the long-lasting argument about the RDS for thermocatalytic FAD. Specifically, the proposal that C-H cleavage is the sole RDS for FAD24 is true only in acidic solutions. And this proposal should be modified accordingly in neutral and alkaline solutions: in a pH7 solution besides the C-H cleavage as one RDS, H2O dissociation to adsorbed H should be involved as the other RDS at pH7 while in a pH13 solution, besides the above two RDSs, the formate adsorption acts as another RDSs. As for the proposal that combinative hydrogen formation step is the RDS for FAD20,21, the electrochemical research paradigm enables us to rule out this possibility at all pHs given that the HER kinetics measurements (see Supplementary Fig. 1) have shown that is a fast step at Pd electrode regardless of solution pH. The clarification of the complicated FAD mechanism benefits the practical catalyst design: to enhance the FAD performance in an acidic solution, a target catalyst should be able to expedite FAOR, more specifically, promote the C-H cleavage; to achieve a high FAD performance in a neutral or alkaline solution, a target catalyst is required to advance both FAOR and HER, more specifically, facilitate formate adsorption, C-H cleavage and water dissociation.
Notably, Pd can absorb H to form stable Pd-H phases with α-PdH being transformable to β-PdH at a potential negative of 55 mV vs RHE22,48. The measured OCP values indicate that β-PdH prevails at pH1, 3.7 and ~7 during FAD, whereas α-PdH may exist in the bulk Pd during FAD at pH13. The presence of PdH phases during FAD is in accordance with a calculated Pourbaix diagram of Pd(111)49. In this work, the presence of α-PdH and β-PdH phases during FAD is mimicked by modeling different coverages of H* on Pd(111) as shown in the following GCQM calculations.
GCQM calculations
To corroborate with the mechanistic understanding of the FAD reaction from the perspective of the interfacial electrochemistry, Grand Canonical quantum mechanics (GCQM) calculations were performed, in which the applied electric potential was kept constant, and the energy barriers for the two electrochemical half reactions were calculated. The free energy profiles of the C-H bond dissociation in FAOR and the Volmer step in HER from GCQM calculations are shown in Fig. 4. Here, these two processes at 0 V vs RHE are compared at pH values of 1, 7 and 13.
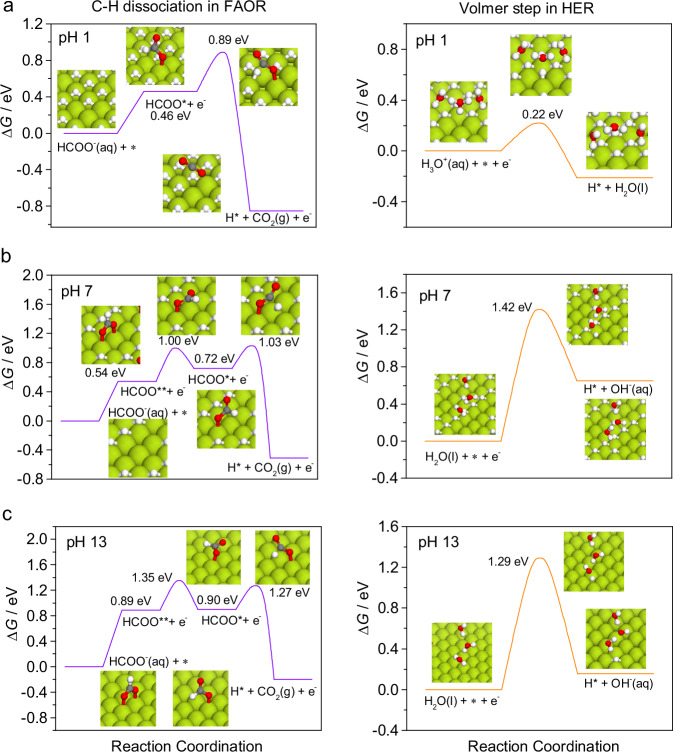
Fig. 4. GCQM Calculations of the energy barriers of FAD on Pd at different pHs.
Free-energy profiles for the C-H dissociation in formic acid oxidation and the Volmer step in hydrogen evolution at 0 V (vs RHE): a under pH1 over 0.66 ML H* preadsorbed Pd(111), b pH7 over 0.44 ML H* preadsorbed Pd(111) and c pH13 over clean Pd(111). The structures for intermediates and transition states are shown in the panels. The green, gray, red and white balls represent palladium, carbon, oxygen and hydrogen atoms, respectively. Source data are provided as a Source Data file.
To simulate the Pd electrode towards realistic conditions at pH1, a Pd(111) surface with 0.66 monolayer (ML) of pre-adsorbed H* was selected as model to mimic the high coverage of H* at the steady state based on experimental observation50. The monodentate formate HCOOM (HCOO*) is found to be more stable than the bidentate HCOOB (HCOO**), with an adsorption free energy of 0.46 eV for a dissolved formate ion to surface HCOOM. The free energy barrier for the subsequent dehydrogenation is 0.43 eV, and the effective activation free energy for C-H dissociation is 0.89 eV. Under the same condition, the activation free energy for proton adsorption to form H* is only 0.22 eV, remarkably lower than that of the C-H dissociation. Therefore, the C-H dissociation in FAOR is kinetically slow while the Volmer step is fast, in good agreement with the KIE experiment for FAD.
At pH7, considering that the -PdH is observed in the experiment, a 0.44 ML H* pre-adsorbed Pd(111) surface model was selected to mimic the moderate coverage of H* at the steady state based on experimental observation48. One can find from Fig. 4b that the bidentate HCOOB is more stable than the monodentate HCOOM under this condition. To undergo C-H dissociation, a free energy barrier of 0.46 eV should firstly be overcome to transform the bidentate structure to the monodentate, followed with a higher barrier to achieve C-H bond dissociation. The effective activation free energy for C-H dissociation here is 1.03 eV. As expected, the Volmer step for O-H dissociation becomes more difficult at pH7 with a free energy barrier of 1.42 eV. This corresponds to a larger KIE factor of O- H/D than that of C-H/D as measured in the experiment, suggesting that O-H cleavage becomes an RDS (see Fig. 3). In addition, even the clean surface model (i.e., a zero coverage of H*) was considered here (see Supplementary Fig. 4), the results are also consistent with the KIE experiments.
At pH13, considering that the -PdH is observed in the experiment, a clean Pd(111) surface model was used here to mimic the low coverage of H* at the steady state based on experimental observation48. With a negative shift of potential vs SHE, the more negatively charged surface retards the adsorption of formate anions. The adsorption free energy for HCOOB is as high as 0.89 eV, and the free energy barrier for its transformation to HCOOM is 0.46 eV for the subsequent C-H bond cleavage to proceed. The effective activation free energy for the C-H dissociation in FAOR is 1.35 eV. For the Vomer step involving O-H dissociation in HER under the same situation, the activation free energy is 1.29 eV, slightly lower than that of the C-H dissociation, in good agreement with the slightly larger KIE factor for C-H/D than O-H/D in the experiment. Noteworthy, implicit solvation model was involved throughout all the simulations, a brief discussion on the effectiveness of the model can be found in the paragraphs related to Supplementary Fig. 4.
As mentioned above, the electric potential was kept constant during the GCQM simulations, which is different from conventional constant-charge QM simulations based on electric-neutral systems. We further performed charge analysis on the surface adsorbates to gain deeper insights into the charge transfer during the reactions as shown in Supplementary Fig. 5. On one hand, it can be found that for the Volmer process in HER at pH7 and pH13, approximately one electron transfer occurs from the initial state (3H2O) to the final state (2H2O + OH−) and partial electron (0.5~0.6 e−) transfer from the initial state to the transition state, which is in accordance with an ideal symmetric factor of 0.5 for HER. On the other hand, for the C-H dissociation in FAOR, the electron transfer upon adsorption of formate from solution to surface is far below 1 (approximately 0.2 e−), indicating that HCOOM is a partially negatively charged species. Therefore, the symmetric factor may deviate from 0.5 in FAOR, in accordance with the Tafel slope of over 200 mV/dec as shown in the following section.
Interfacial cation effect on thermocatalytic FAD
It is known that in electrochemical realm cation effect impacts the structure of the electric double layer (EDL, the compact layer in this work)51. Except in very diluted electrolytes, the interfacial potential drop is mainly restricted within the EDL whose thickness determines the local electric field strength52. In general, at potentials negative of the potential of zero charge (pzc), the surface bears net negative charges, such that hydrated cation species pile up in the compact layer of EDL. Small cations exhibit stronger hydration energies and tend to form larger hydrated cations; therefore, the hydration energies and radii of hydrated cations follow the order of Li+ > Na+ > K+ > Cs+ and the electric field strength in the EDL follows the order of Li+ < Na+ < K+ <Cs+53,54. For charged reactive species like formate anion in this work, the columbic interaction between the interfacial electric field and the reactive species may alter the reaction kinetics55,56.
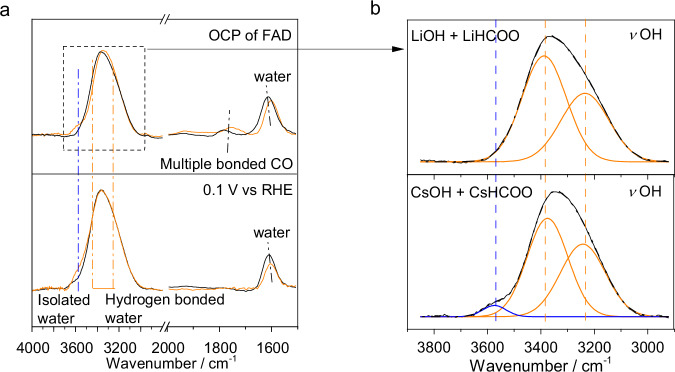
Cation effect has been utilized to promote the thermocatalytic FAD performance21, yet its physiochemical origin has not been clarified. To observe the spontaneously formed EDL structure during the thermocatalytic FAD reaction at OCP, in situ attenuated total reflectance surface-enhanced infrared ab-sorption spectroscopy (ATR-SEIRAS) measurement was conducted to examine the interfacial water structure change during FAD on a Pd film in a pH13 solution containing either Li+ or Cs+ cations. The ATR-SEIRA spectra for the Pd-solution interface acquired at OCPs in 0.1 M LiOH + 0.1 M LiHCOO and 0.1 M CsOH + 0.1 M CsHCOO solutions are shown in the upper panel of Fig. 5a. The band for interfacial water can be deconvoluted into three independent components. The bands at ~3200 and ~3400 cm−1 are due to the symmetric and asymmetric O-H stretching vibrations of water molecules in H-bond networks, respectively, whereas the band at ~3600 cm−1 to the O-H stretching vibration of isolated water molecules57. The frequency for the latter is obviously higher in 0.1 M CsOH + 0.1 M CsHCOO compared to that in 0.1 M LiOH + 0.1 M LiHCOO as highlighted in Fig. 5b. In addition, the δH−O−H band for the scissoring mode of interfacial water at ~1610 cm−1 redshifts by 10 cm−1 in 0.1 M CsOH + 0.1 M CsHCOO as compared to that in 0.1 M LiOH + 0.1 M LiHCOO. To mimic the cation dependent EDL structure for the FAD, in situ ATR-SEIRAS spectra for a Pd electrode in 0.1 M LiOH or 0.1 M CsOH at a controlled potential close to the OCP, or 0.1 V vs RHE (electrochemical realm) are also presented in the lower panel of Fig. 5a, similar spectral change for the interfacial water was indeed observed. The above spectral features indicate that the as-formed interfacial electric field in a Cs+-containing electrolyte is stronger than that in a Li+-containing electrolyte for the FAD, consistent with the proposal that a stronger EDL field results in more isolated water at the Pd-solution interface57. In one word, the fact of cation-tuned EDL structure and field strength at the Pd electrode-electrolyte interface can be extended to manipulate the thermocatalysis of the FAD at the Pd catalyst-solution interface.
Fig. 5. ATR-SEIRA spectra on Pd film in alkaline solutions with different cation species in the absence and presence of formate.
a The lower panel shows the ATR-SEIRA spectra collected in 0.1 M LiOH (or 0.1 M CsOH) on Pd film electrode at 0.1 V vs RHE, the reference spectrum is taken in the same electrolyte at 1.0 V vs RHE respectively. The upper panel shows the in situ ATR-SEIRAS spectra collected in 0.1 M LiOH + 0.1 M LiHCOO (or 0.1 M CsOH + 0.1 M CsHCOO) on Pd film 3 min after injection of formate, the reference spectrum is taken in the electrolyte before the injection of formate. b Deconvolution of the IR bands for interfacial water (νO-H) in the selected region of a. Source data are provided as a Source Data file.
To understand how the EDL changes the kinetics of the thermocatalytic FAD process, we first electrochemically examine how the cation induced EDL structure change affect the kinetics of FAOR and HER on Pd/C, see Supplementary Fig. 6. Note that the pzc for Pd(111) is around 0.17, 0.33 and 0.89 V vs RHE at pH1, 3.7 and 13, respectively58,59. For FAOR, the cation effect at pH1 is insignificant due to positively charged Pd surface at the working potentials; From pH3.7 to 13, the FAOR peak current density follows the order of Li+ < Na+ < K+, suggesting that a smaller hydrated cation induces a stronger EDL field to stabilize the reactive species HCOOM through columbic interaction60, as net charge analysis (Supplementary Fig. 5) and Tafel analysis (Supplementary Fig. 7) have both suggested that adsorbed is a partially negatively charged species whose free energy is tunable in an electric field61–63. Furthermore, mass transport determines HER at Pd electrode in an acidic solution as mentioned above and shown in Supplementary Fig. 1, leading to an insignificant cation effect as well; In contrast, HER in a neutral to basic solution follows the order of Li+ > Na+ > K+ > Cs+ (Supplementary Fig. 6d), similar to that reported for HER at Pt and Ir electrodes. It is known that the water structure-breaking cations like K+ and Cs+ break the continuity of the hydrogen bond network in the EDL to deteriorate the alkaline HER kinetics whereas the water structure-making cations like Li+ and Na+ promote the alkaline HER kinetics64–67.
Now we can turn to the cation-tuned EDL effect on overall FAD kinetics. Figure 6a, b and Supplementary Fig. 8 show the reaction rates of FAD against cation entities measured at different solution pHs. At pH1, no cation effect can be observed within error, consistent with the above-mentioned insignificant cation effect on both FAOR and HER. At pH3.7, the FAD reaction rate increases in the order of Li+ < Na+ < K+ < Cs+, in accordance with the significant cation effect on FAOR and insignificant effect on HER at this pH. The fact that the cation effect on FAD originates from the cation effect on FAOR is verified by the Evans diagrams as shown in Fig. 6c, d. At pH~7, the FAD reaction rate follows the order of Li+ < Na+ < K+ > Cs+, where the maximum occurs with K+. Given that C-H cleavage of adsorbed formate in FAOR and O-H cleavage of water in HER reaction are both rate limiting for the overall FAD reaction at pH7, the net cation effect on FAD inherits from antithetic cation effects on FAOR (Li+ < Na+ < K+ < Cs+) and HER (Li+ > Na+ > K+ > Cs+). At pH13, FAD reaction rate reverts to the order Li+ < Na+ < K+ < Cs+, same as the cation effect on FAOR since FAOR is kinetically more sluggish than HER for FAD at pH13 as judged from Fig. 3c. In one word, the cation effect on FAD indeed originates from the cation effect on the kinetically sluggish electrochemical half reaction(s).
Fig. 6. Cation effect measurements for FAD on Pd/C catalyst.
a Cation dependent TOFs for FAD in solutions of different pHs: 0.1 M HClO4 + 1.0 M HCOOH + 0.1 M MClO4 (0.1 M HClO4 + 1.0 M HCOOH for the H+-only solution) for pH 1, 0.2 M HCOOH + 0.2 M MHCOO for pH3.7, 1.0 M MHCOO for pH~7, and 0.1 M MOH + 1.0 M MHCOO for pH13. Temperature condition: 298 K for pH1, 3.7 and ~7, and 333 K for pH13. (M+ stands for cation species). b TOFs for FAD in K+ or NH4+ contained solutions: 0.2 M HCOOH + 0.2 M MHCOO for pH3.7, 1.0 M MHCOO for pH~7. The dotted lines are used for the guide of eyes. c Evans diagrams showing cation effects on FAD in solutions of pH3.7. d Comparisons between measured FAD reaction rates (adapted from data in a) and predicted FAD reaction rates in Evans diagrams (adapted from data in c). e In situ ATR-SEIRA spectra at the Pd/C-solution interface during FAD in solutions containing different cations: 0.2 M HCOOH + 0.2 M HCOO− (colored lines) and 2 M HCOOH (the black line), a.u. stands for absorption unit. The reference spectra were taken before the injection of solutions. Source data are provided as a Source Data file.
Ammonium cation (NH4+) is a type of cations that not only influence the EDL field strength but also serve as Brønsted acid, and it has been widely utilized in thermocatalytic FAD. Notably, its much favorable effect on thermocatalytic FAD can be explained by the same scenario as well. As shown in Fig. 6b, the FAD rate in a NH4+-containing solution approximately equals to that in a K+ -containing solution at pH3.7, which may be attributed to a similar EDL field intensities induced by NH4+ and K+, given that the ionic radius and hydration energy of NH4+ are close to those of K+68. Moreover, NH4+ (pKa 9.3) is a stronger Brønsted acid than H2O (pKa15.7)69–71, assisting the HER in a pH~7 solution more than K+ does. In other words, ammonium cation promotes both half reactions FAOR and HER, which can explain a much higher thermocatalytic FAD rate in a NH4+ -contained solution than in a K+-contained solution at pH~7 in Fig. 6b. Practically, organic amines have been widely tested as additives to accelerate FAD in acidic and neutral solutions by trial-and-errors72. Based on the above understanding of cation effect on FAD, screening guidelines for ammine additives may be proposed: 1) the protonated target ammine cation (i.e., organic ammonium) at the Pd-solution interface should have a strong EDL field strength to promote C-H cleavage, and along this line, a smaller size of hydrated organic ammonium is preferred; 2) in an ammonium formate solution (pH~7), in order to promote the HER, the target ammine cation should be a stronger Brønsted acid and a water structure-making cation.
To further verify the origin of this cation effect on FAD at the molecular level, in situ ATR-SEIRA spectra were obtained on Pd/C in different cation-contained 0.2 M HCOOH + 0.2 M HCOO− solutions (colored lines) and neat 2 M HCOOH solution (without any alkali-cations, black line) at 298 K. The peaks at 1350 cm−1 and 1380 cm−1 can be attributed to aqueous HCOO−, the 1398-cm−1 peak to aqueous HCOOH, and the 1452-cm−1 peak to aqueous NH4+11. The peaks ranging from 1320 to 1340 cm−1 were assigned to adsorbed HCOO*, showing the cation-dependent frequency. Specifically, in 2.0 M FA solution (pH ~1.7) without any alkali cations, the 1338-cm−1 peak was assigned to bidentate formate HCOOB on Pd73. In 0.2 M HCOOH + 0.2 M HCOO− solutions with varying cations (pH 3.7), the peaks centered at 1320 to 1330 cm−1 to monodentate formate HCOOM on Pd74. Interestingly, as the hydrated cation radius decreases from Li+ to Cs+, the peak is redshifted from 1330 cm−1 to 1320 cm−1. In one word, the spectral observation indicates that HCOO* adsorption configuration and energy indeed can be tuned by the structure and strength of the EDL, a stronger electric field in the EDL favors the adsorption of reactive HCOOM* species for FAD.
To find out the cation effect (and thus EDL field effect) on FAD kinetics from thermocatalytic perspective, FAD reaction rates in different cation-contained solutions at pH3.7 are measured as a function of temperature to yield the apparent activation energies using Arrhenius equation. As shown in Fig. 7a, the cation effect on FAD reaction rate follows the order Cs+ > K+ > Na+ > Li+ from 303 K to 333 K and in Fig. 7b, the apparent activation energies follow the order Li+ (60 kJ/mol) > Na+ (49 kJ/mol) > K+ (44 kJ/mol) > Cs+ (37 kJ/mol). Indeed, the apparent activation energy data obtained from a traditional thermocatalytic measurement are consistent with the cation effect on FAD kinetics, and Fig. 7c, d indicate that the temperature dependent FAD reaction rates are in line with the temperature dependent FAOR/HER current densities as revealed by the Evans diagrams.
Fig. 7. Temperature dependent FAD reaction rates.
a TOF for FAD in different cation-contained 0.2 M HCOOH + 0.2 M HCOO− solutions at 303, 313, 323 and 333 K. b Apparent activation energies for FAD in different cation-contained solutions, the error bars indicate the errors of the linear fitting in the Arrhenius plots. c Evans diagrams showing temperature effect on FAD in solutions of pH3.7. d Comparisons between measured FAD reaction rates (adapted from data in a) and predicted FAD reaction rates by Evans diagrams (adapted from data in c). Source data are provided as a Source Data file.
Spontaneous FAD on metal catalyst in aqueous solution is a thermocatalytic reaction involving coupled electrochemical reactions and EDL effect. In this work, we have initially succeeded in pinning down essential and yet challenging issues of the FAD at the Pd-solution interface by decoupling FAD into two short-circuit half reactions FAOR and HER on Pd sites, the FAD reaction rates can be quantitatively predicted by the Evans diagrams as exemplified in acidic solutions where FAD reaction rates is controlled by the anodic reaction FAOR. In addition, the relative biases of the mixed potential (or OCP) from the equilibrium potentials of the two redox couples were used to gauge the kinetically sluggish half reaction. The mechanistic insight was otherwise unable to be revealed by traditional thermocatalysis methodology. The reported research paradigm can be extended to FAD on other metal catalysts in aqueous solutions.
Guided by the electrochemical mixed potential theory, we have applied KIE measurement, isotope labeling mass spectroscopy and GCQM calculations to clarify the lasting debate on the assignment of RDS for the FAD in solutions of varying pH. The mechanistic findings for FAD are disclosed as follows: In an acidic solution, the C-H cleavage step is determined to be the sole RDS; In a neutral solution, H2O dissociation to H* is the other RDS besides the C-H cleavage; In an alkaline solution, in addition to the above two RDSs, the formate adsorption acts as another RDS; In all pH solutions under investigation, the 2H* to H2 as the RDS for FAD can be excluded. And a design principle of a Pd-based catalyst for FAD has been proposed accordingly, that is, the target catalyst should be able to expedite the RDS for FAD in a given pH solution.
The interfacial structure and electric field play a vital role in the FAD reaction and can be readily tuned by cations in a solution for a given catalyst. We have confirmed in ATR-SEIRAS measurements that the cation effect on the FAD reaction arises from the spontaneously formed EDL. Moreover, the cation effect on FAD has been clarified to originate from the cation effect on the relatively sluggish electrochemical half reaction(s). The cation effect on FAD is insignificant at pH1 given that Pd is positively charged at mixed potential. With increasing pH, the Pd surface turns negatively charged, thus hydrated cations are enriched in the EDL, leading to significant cation-dependent FAD. At pH3.7 and 13, FAOR is the kinetically sluggish half reaction as compared to HER, the FAD rate follows the same order as FAOR due to the electrostatic interaction between the cation-dependent EDL field and the key intermediate HCOOM, that is, Li+ < Na+ < K+ < Cs+. Such modulation on adsorption energies of HCOO* by interfacial EDL strength has been verified by in situ ATR-SEIRAS data, demonstrating that the IR peak of HCOO* is red-shifted as the hydrated cation entities changes from H+ (1338 cm−1) to Li+ (1330 cm−1) and further to Cs+ (1320 cm−1). While at pH~7, FAOR and HER kinetics are sluggish and comparable but exhibit opposite cation effects, i.e., Li+ < Na+ < K+ < Cs+ for FAOR, and Li+ > Na+ > K+ > Cs+ for HER (due to their different roles in disrupting water hydrogen bond networks in the EDL), the antithetic cation effects on two half reactions account for the observed order Li+ < Na+ < K+ > Cs+ for the overall FAD at pH~7. Along this line, screening guidelines for cation additives in FAD was proposed: in general, a candidate should form a strong EDL field; and be a strong Brønsted acid and a water structure-making cation in a pH~7 solution.
Methods
Chemicals
Perchloric acid (HClO4, 70%, 99.999% trace metal basis, Sigma-Aldrich), sodium hydroxide (NaOH, 99.99%, Sigma-Aldrich), potassium hydroxide (KOH, 99.95%, Sigma-Aldrich), sodium formate (NaHCOO, >99.0%, ACS grade, Sigma-Aldrich), sodium formate-d (NaDCOO, 99 atom% D, Sigma-Aldrich), formic-d acid (DCOOH, 98% D, 95 weight% in water, Sigma-Aldrich), lithium hydroxide monohydrate (LiOH·H2O, 99.995% metal basis, Aladdin), cesium hydroxide monohydrate (CsOH·H2O, 99.95% metal basis, Aladdin), ammonium formate (NH4HCOO, ultra-pure, >99.0%, Aladdin), formic acid (HCOOH, >96%, ACS grade, Aladdin), sulfuric acid (H2SO4, 98%, GR, Sinopharm), deuteride oxide (D2O, 99.9 atom% D, Innochem). The solution/electrolyte used for each measurement is listed in Supplementary Tables 1 and 2. Formate salts used in the measurements were prepared by mixing equivalent amount of formic acid to the metal hydroxides. It should be noted that in this paper, the deuterium purities of the reagent in the KIE measurements fall in the range of 98–99.9%, which are high enough for qualitative analysis of RDS.
Synthesis of Pd/C catalysts
5 wt.% Pd supported on XR-72 carbon (5 wt.% Pd/C) was synthesized by a NaBH4 reduction method19. H2PdCl4 (0.1575 mmol), sodium citrate (Na3Cit·2H2O, 370.6 mg) were dissolved and mixed in ultrapure water (40 mL) to yield a yellow solution, and carbon powder (Vulcan XC-72, 318 mg) was added into the solution and sonicated for 20 min and vigorously stirred for another 1 h to yield a blackish slurry. Then, 10 mL solution of Na2CO3 (60 mg) and NaBH4 (40 mg) was added dropwise to the suspension under 750-rpm stirring by a peristaltic pump at 0.5 mL min–1. The suspension was kept under stirring for another 4 h. After the suspension was filtered and washed with ultrapure water for 5 times, it was dried in a vacuum oven at 343 K overnight to yield the 5 wt.% Pd/C. The TEM, EDS, SEM and XRD characterizations of the as-prepared Pd/C catalyst are shown in Supplementary Fig. 9, and the TEM characterizations of the used Pd/C catalyst after FAOR and HER measurements at 323 K are shown in Supplementary Fig. 10.
General procedure for FAD test
For each test, 80 mg of Pd/C catalyst was added to a three-neck flask placed in a temperature-controlled water bath. Before each test, Argon was bubbled through the flask for over 15 min to remove the dissolved oxygen. The necessity of deaeration is illustrated in Supplementary Fig. 11. After turning off the Argon stream, 10 mL of formic acid/formate salt solution was quickly injected into the flask under magnetic stirring, and the generated gas was collected by means of water displacement. The temperature for FAD was controlled at 298 K for all tested solution except for the alkaline solution (pH13) where FAD was carried out at 333 K to expedite the hydrogen production.
Analysis of FAD product by GC
For each test, 80 mg of Pd/C catalyst was added to a three-neck flask placed in a temperature-controlled water bath. Before each test, Argon was bubbled through the flask for over 15 min to remove the dissolved oxygen. While holding the Argon stream at a rate of ~50 sccm, 10 mL of formate reagent was quickly injected into the flask under magnetic stirring and generated gas was connected into a GC equipped with FID and TCD.
Analysis of isotope labeled FAD product by in situ mass spectrometer
For each test, 40 mg of Pd/C catalyst was added to a three-neck flask placed in a temperature-controlled water bath. Before each test, Argon was bubbled through the flask for over 15 min to remove the dissolved oxygen. While holding the Argon stream at a rate of ~50 sccm, 10 mL of formic acid/formate reagent was quickly injected into the flask under magnetic stirring and the gas was flown into a mass spectrometer by filtering out water vapor. Mass spectrometer was operated in a differential mode with a time resolution of ~0.1 s. Signal channels for m/z = 2, 3 and 4 were turned on to measure relative signal intensities of H2, HD and D2 in the gas products.
Calculation of FAD reaction rate
The initial TOF value is measured to show the reaction rate of FAD,
| 6 |
where P0 is the atmospheric pressure (101.3 kPa), V is the generated volume of (H2 + CO2) gas, R is the universal gas constant (8.314 m3 Pa mol–1 K–1), T is the temperature of water bath for gas collection (room temperature), t is the time duration for production of 40 mL of gas from FAD, nPd and is the overall mole numbers of Pd atoms in catalysts. In acidic solution (pH1 and pH3.7), k = 0.5, indicating that the partial pressure of H2 in the gas mixture is 0.5 atm. However, the proportion of H2 in the generated gas no longer equals to 0.5 in neutral and alkaline solution due to dissolution of CO2. The values of k were measured by GC as shown in Supplementary Figs. 12 and 13. At pH~7, k = 0.9 and at pH13, k = 1.0. In addition, t is adjusted to the time duration for production of 10 mL of gas from FAD at pH~7 and 13. The KIE factor is defined as the ratio of the TOF values before and after deuteration, that is, TOFC-H/TOFC-D (or TOFO-H/TOFO-D).
General procedure for electrochemical test
For each test, a fresh prepared catalyst ink was obtained by mixing Pd/C with water, isopropanol and Nafion solution. The ink was deposited on a glassy carbon electrode to prepare a Pd/C film electrode. After electrochemically cleaning the catalyst layer, the electrochemical measurement was carried out in a freshly prepared and deaerated electrolyte solution. Ohmic compensation was conducted during all the electrochemical measurements at a level of 80%. For FAOR on Pd/C at pH 3.7, due to the high ohmic drop in the electrolyte, another post-measurement ohmic compensation is conducted at a level of ~10%. The detailed procedures for electrochemical tests are described in Supplementary Note 1. The KIE factor is the ratio of current density before and after deuteration, that is, jC-H/jC-D (or jO-H/jO-D).
Preparation of the catalyst ink
2 mg of Pd/C catalyst was mixed with 800 μL water, 200 μL isopropanol and 120 μL 5% Nafion solution. The mixture was sonicated to attain a homogeneous black ink.
Activation of Pd/C film electrode
Typically, 10 μL of the Pd/C catalyst ink was deposited on a Φ 5 mm glass carbon electrode. After evaporation of the solvent, the as-deposited Pd/C film electrode was electrochemically cleaned between 0.05 and 1.05 V vs RHE in 0.1 M HClO4 solution with a carbon rod and a home-made reversible hydrogen electrode (RHE) serving as the counter electrode and reference electrodes, respectively.
Evans diagrams for FAD reactions
To generate the Evans diagrams for FAD, we measured the apparent FAOR and HER current densities by electrochemical measurements carried out on a Pd/C catalyst layer-coated RDE. For FAOR, the linear sweep voltammetry was started from the OCP to 0.6 V; For HER, the linear sweep voltammetry was started from the OCP to −0.2 V. Tafel fitting was performed on a polarization curve of FAOR to estimate the net FAOR current densities at sufficiently high overpotentials. The current densities on the extrapolated Tafel straight line at the mixed potential yielded the overall FAD reaction rate. Test conditions: scan rate of 10 mV/s and rotation rate of 1600 rpm in an Ar-sparged solution. Ar stream kept flowing vigorously through the headspace of the electrolytic cell chamber during the measurements. The current density was converted to the overall FAD reaction rate by using
| 7 |
where is the above-mentioned current density at the mixed potential in the Evans diagrams, A is the electrode area, F is the Faraday constant and is the mole number of Pd used in the Evans diagram measurement.
ATR-SEIRAS measurement on water structures at Pd-solution interface
The ATR-SEIRAS measurement was conducted by using a Thermo Scientific Nicolet iS50 FT-IR spectrometer equipped with a HgCdTe (MCT) detector at well-controlled room temperature/humidity. The gold film chemically deposited on the basal plane of a hemicylindrical Si prism served as the IR reflective window. And the Pd film was electrodeposited on the Au film. And each spectrum was taken with the p-polarized IR radiation. Typically, a spectrum of the solution/Pd interface at 1.1 V was taken as a reference spectrum. The ultimate spectra shown in the figure are the differential spectra shown in absorbance units (a.u.), which is calculated as , where Rr and Rs are the reference and sample spectra, respectively. Subtraction of atmospheric species signals has been conducted to enhance the signal noise ratio of the spectra.
In situ ATR-SEIRAS measurement on Pd/C during FAD
The preparation of the IR reflective window and data processing are the same as those specified in the former section except that Pd/C catalyst layer was evenly coated on the Au film with a diameter of 1 cm at a loading of 80 μg of 5 wt.% Pd/C. The reference spectra were taken at the Pd/C catalyst-air interface before injection of desired solutions. The sample spectra were taken at 1 min after the injection of the solutions.
GCQM calculations
All the structures were optimized in VASPsol75,76 implemented in the Vienna Ab-initio Simulation Package (VASP) code77,78, using Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional79. The DFT-D3 method of Grimme et al.80 was selected to include the long-range van der Waals interactions in the calculations. To obtain the reaction pathway and transition states, the VTST package81 with climbing image nudged elastic band (CI-NEB)82 was used including solvation. To simulate the adsorption and reaction processes, a four-layer 3 × 3 Pd(111) slab was employed with the top two Pd layers relaxed. The vacuum height was set around 15 Å to prevent the interaction between periodic structures. A 3 × 3 × 1 k-point grid generated with the Monkhorst–Pack scheme was used78. The energy cutoff was set as 400 eV. The convergence criteria were set as 0.05 eV/Å for force on each atom and 10−4 eV and 10−7 eV for energy in adsorption structure optimization and for CI-NEB simulations, respectively.
GCQM calculations were performed with the open-source software jDFTx83, which could accurately describe the continuum solvation and include constant potentials for electrochemical reactions. Based on the optimized structures from VASPsol, the grand canonical potential kinetics (GCP-K) method84–87 developed by Goddard and co-workers along with the CANDLE implicit solvation model88 were adopted to obtain the free energies as a function of potential (U). All the key settings are the same with those in the simulations using VASP. The method to calculated the adsorption free energy of formate anion from solution onto electrode surface is shown in Supplementary Note 2, along with Supplementary Fig. 14 showing the thermodynamic cycle for the reaction. And the Calculation details for the GCP-K method is shown in Supplementary Note 3, along with Supplementary Fig. 15 and Supplementary Tables 3–5.
Supplementary information
Source data
Acknowledgements
We thank Prof. Shaowei Chen at UCSC for valuable suggestions on our manuscript. This work was supported by the National Key R&D Program of China (2022YFA1503803), the NSFC (21733004) and the Shanghai Science & Technology Innovation Action Plan (22dz1205500), these fundings were received by W.-B. Cai. B.Y. acknowledges the funding support from the National Natural Science Foundation of China (21991152, 21991150). We also thank the HPC Platform of ShanghaiTech University for computing time.
Author contributions
These authors contributed equally: X. Qin and J. Li. X. Qin carried out the experiments. J. Li carried out the GCQM calculation. T.-W. Jiang, X.-Y. Ma and K. Jiang supported the spectroscopic measurements. B. Yang supervised the GCQM calculation, and W.-B. Cai supervised the experiments. W.-B. Cai, S. Chen and X. Qin came up with the original idea of this manuscript. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
All data generated in this study are provided in the Supplementary Information and Source Data file. Source data are provided with this paper.
Competing interests
The authors declare no competing interest.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
11/7/2024
A Correction to this paper has been published: 10.1038/s41467-024-53936-5
Contributor Information
Bo Yang, Email: yangbo1@shanghaitech.edu.cn.
Wen-Bin Cai, Email: wbcai@fudan.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51926-1.
References
- 1.Lin, L. et al. Heterogeneous Catalysis in Water. JACS Au1, 1834–1848 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wesley, T. S., Roman-Leshkov, Y. & Surendranath, Y. Spontaneous Electric Fields Play a Key Role in Thermochemical Catalysis at Metal-Liquid Interfaces. ACS Cent. Sci.7, 1045–1055 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Steinmann, S. N. & Michel, C. How to Gain Atomistic Insights on Reactions at the Water/Solid Interface? ACS Catal.12, 6294–6301 (2022). [Google Scholar]
- 4.Jessop, P. G., Ikariya, T. & Noyori, R. Homogeneous Hydrogenation of Carbon Dioxide. Chem. Rev.95, 259–272 (1995). [Google Scholar]
- 5.Sordakis, K. et al. Homogeneous Catalysis for Sustainable Hydrogen Storage in Formic Acid and Alcohols. Chem. Rev.118, 372–433 (2018). [DOI] [PubMed] [Google Scholar]
- 6.Wei, D. et al. Toward a Hydrogen Economy: Development of Heterogeneous Catalysts for Chemical Hydrogen Storage and Release Reactions. ACS Ener. Lett.7, 3734–3752 (2022). [Google Scholar]
- 7.Kar, S., Rauch, M., Leitus, G., Ben-David, Y. & Milstein, D. Highly Efficient Additive-Free Dehydrogenation of Neat Formic Acid. Nat. Catal.4, 193–201 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wei, D., Sang, R., Sponholz, P., Junge, H. & Beller, M. Reversible Hydrogenation of Carbon Dioxide to Formic Acid Using a Mn-pincer Complex in the Presence of Lysine. Nat. Energy7, 438–447 (2022). [Google Scholar]
- 9.Zelocualtecatl Montiel, I. et al. CO2 Conversion at High Current Densities: Stabilization of Bi(III)-Containing Electrocatalysts under CO2 Gas Flow Conditions. ACS Catal.12, 10872–10886 (2022). [Google Scholar]
- 10.Chen, Z. et al. Designing a Robust Palladium Catalyst for Formic Acid Dehydrogenation. ACS Catal.13, 4835–4841 (2023). [Google Scholar]
- 11.Jiang, K., Xu, K., Zou, S. Z. & Cai, W. B. B-Doped Pd Catalyst: Boosting Room-Temperature Hydrogen Production from Formic Acid-Formate Solutions. J. Am. Chem. Soc.136, 4861–4864 (2014). [DOI] [PubMed] [Google Scholar]
- 12.Wang, N. et al. In Situ Confinement of Ultrasmall Pd Clusters within Nanosized Silicalite−1 Zeolite for Highly Efficient Catalysis of Hydrogen Generation. J. Am. Chem. Soc.138, 7484–7487 (2016). [DOI] [PubMed] [Google Scholar]
- 13.Li, Z. & Xu, Q. Metal-Nanoparticle-Catalyzed Hydrogen Generation from Formic Acid. Acc. Chem. Res.50, 1449–1458 (2017). [DOI] [PubMed] [Google Scholar]
- 14.Masuda, S., Mori, K., Futamura, Y. & Yamashita, H. PdAg Nanoparticles Supported on Functionalized Mesoporous Carbon: Promotional Effect of Surface Amine Groups in Reversible Hydrogen Delivery/Storage Mediated by Formic Acid/CO2. ACS Catal.8, 2277–2285 (2018). [Google Scholar]
- 15.Yoo, J. S., Abild-Pedersen, F., Nørskov, J. K. & Studt, F. Theoretical Analysis of Transition-Metal Catalysts for Formic Acid Decomposition. ACS Catal.4, 1226–1233 (2014). [Google Scholar]
- 16.Bhandari, S., Rangarajan, S. & Mavrikakis, M. Combining Computational Modeling with Reaction Kinetics Experiments for Elucidating the In Situ Nature of the Active Site in Catalysis. Acc. Chem. Res.53, 1893–1904 (2020). [DOI] [PubMed] [Google Scholar]
- 17.Ding, C., Shen, T. H., Yang, Y. Q. & Xu, X. Involvement of the Unoccupied Site Changes the Kinetic Trend Significantly: A Case Study on Formic Acid Decomposition. ACS Catal.10, 5153–5162 (2020). [Google Scholar]
- 18.Zhang, S., Jiang, B., Jiang, K. & Cai, W.-B. Surfactant-Free Synthesis of Carbon-Supported Palladium Nanoparticles and Size-Dependent Hydrogen Production from Formic Acid–Formate Solution. ACS Appl. Mater. Interfaces9, 24678–24687 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Qin, X. X. et al. Mechanistic Analysis-Guided Pd-Based Catalysts for Efficient Hydrogen Production from Formic Acid Dehydrogenation. ACS Catal.10, 3921–3932 (2020). [Google Scholar]
- 20.Kim, Y. & Kim, D. H. Understanding the Effect of Pd Size on Formic Acid Dehydrogenation via Size-Controlled Pd/C Catalysts Prepared by NaBH4 Treatment. Appl. Catal. B-Environ.244, 684–693 (2019). [Google Scholar]
- 21.Kim, Y., Kim, S. H., Ham, H. C. & Kim, D. H. Mechanistic Insights on Aqueous Formic Acid Dehydrogenation over Pd/C Catalyst for Efficient Hydrogen Production. J. Catal.389, 506–516 (2020). [Google Scholar]
- 22.Luque, G. C., de Chialvo, M. R. G. & Chialvo, A. C. Influence of Spontaneous Decomposition on the Electrochemical Formic Acid Oxidation on a Nanostructured Palladium Electrode. Electrochem. Commun.70, 69–72 (2016). [Google Scholar]
- 23.Meng, Q. et al. Revealing the True Origin of Size-Dependent Pd/C Catalytic Behavior towards Formic Acid Decomposition. Chin. Chem. Lett.34, 107221 (2023). [Google Scholar]
- 24.Navlani-Garcia, M., Mori, K., Nozaki, A., Kuwahara, Y. & Yamashita, H. Investigation of Size Sensitivity in the Hydrogen Production from Formic Acid over Carbon-Supported Pd Nanoparticles. Chemistryselect1, 1879–1886 (2016). [Google Scholar]
- 25.Ryu, J. et al. Thermochemical Aerobic Oxidation Catalysis in Water can be Analysed as Two Coupled Electrochemical Half-Reactions. Nat. Catal.4, 742–752 (2021). [Google Scholar]
- 26.Peng, M., Xiao, D. & Ma, D. An Electrified Insight into the Thermocatalysis in Water. Joule5, 2768–2771 (2021). [Google Scholar]
- 27.Adams, J. S., Kromer, M. L., Rodriguez-Lopez, J. & Flaherty, D. W. Unifying Concepts in Electro- and Thermocatalysis toward Hydrogen Peroxide Production. J. Am. Chem. Soc.143, 7940–7957 (2021). [DOI] [PubMed] [Google Scholar]
- 28.Cheng, G. et al. Importance of Interface Open Circuit Potential on Aqueous Hydrogenolytic Reduction of Benzyl Alcohol over Pd/C. Nat. Commun.13, 7967 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wilson, N. M. & Flaherty, D. W. Mechanism for the Direct Synthesis of H2O2 on Pd Clusters: Heterolytic Reaction Pathways at the Liquid–Solid Interface. J. Am. Chem. Soc.138, 574–586 (2016). [DOI] [PubMed] [Google Scholar]
- 30.An, H., Sun, G., Hülsey, M. J., Sautet, P. & Yan, N. Demonstrating the Electron–Proton-Transfer Mechanism of Aqueous Phase 4-Nitrophenol Hydrogenation Using Unbiased Electrochemical Cells. ACS Catal.12, 15021–15027 (2022). [Google Scholar]
- 31.Noam, E. & Eliezer, G. Physical Electrochemistry: Fundamentals, Techniques, and Applications, (Wiley-VCH, 2019).
- 32.Bratsch, S. G. Standard Electrode Potentials and Temperature Coefficients in Water at 298.15 K. J. Phys. Chem. Ref. Data18, 1–21 (1989). [Google Scholar]
- 33.Qi, X. et al. Potential–Rate Correlations of Supported Palladium-Based Catalysts for Aqueous Formic Acid Dehydrogenation. J. Am. Chem. Soc.146, 9191–9204 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wan, C. et al. Unraveling and Resolving the Inconsistencies in Tafel Analysis for Hydrogen Evolution Reactions. ACS Cent. Sci.10, 658–665 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Simmons, E. M. & Hartwig, J. F. On the Interpretation of Deuterium Kinetic Isotope Effects in C-H Bond Functionalizations by Transition-Metal Complexes. Angew. Chem. Int. Ed.51, 3066–3072 (2012). [DOI] [PubMed] [Google Scholar]
- 36.Joo, J., Uchida, T., Cuesta, A., Koper, M. T. M. & Osawa, M. Importance of Acid-Base Equilibrium in Electrocatalytic Oxidation of Formic Acid on Platinum. J. Am. Chem. Soc.135, 9991–9994 (2013). [DOI] [PubMed] [Google Scholar]
- 37.Zhou, Y.-W. et al. Boosting Electrocatalytic Oxidation of Formic Acid on SnO2-Decorated Pd Nanosheets. J. Catal.399, 8–14 (2021). [Google Scholar]
- 38.Wiberg, K. B. The Deuterium Isotope Effect. Chem. Rev.55, 713–743 (1955). [Google Scholar]
- 39.Cheng, T., Wang, L., Merinov, B. V. & Goddard, W. A. III Explanation of Dramatic pH-Dependence of Hydrogen Binding on Noble Metal Electrode: Greatly Weakened Water Adsorption at High pH. J. Am. Chem. Soc.140, 7787–7790 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Kastlunger, G. et al. Using pH Dependence to Understand Mechanisms in Electrochemical CO Reduction. ACS Catal.12, 4344–4357 (2022). [Google Scholar]
- 41.Zhang, M.-K. et al. Mechanistic Implication of the pH Effect and H/D Kinetic Isotope Effect on HCOOH/HCOO– Oxidation at Pt Electrodes: A Study by Computer Simulation. ACS Catal.11, 6920–6930 (2021). [Google Scholar]
- 42.Wei, Y. et al. The Mechanisms of HCOOH/HCOO– Oxidation on Pt Electrodes: Implication from the pH Effect and H/D Kinetic Isotope Effect. Electrochem. Commun.81, 1–4 (2017). [Google Scholar]
- 43.Durst, J., Simon, C., Hasché, F. & Gasteiger, H. A. Hydrogen Oxidation and Evolution Reaction Kinetics on Carbon Supported Pt, Ir, Rh, and Pd Electrocatalysts in Acidic Media. J. Electrochem. Soc.162, F190–F203 (2014). [Google Scholar]
- 44.Markovića, N. M., Sarraf, S. T., Gasteiger, H. A. & Ross, P. N. Hydrogen Electrochemistry on Platinum Low-Index Single-Crystal Surfaces in Alkaline Solution. J. Chem. Soc. Faraday Trans.92, 3719–3725 (1996). [Google Scholar]
- 45.Marković, N. M., Grgur, B. N. & Ross, P. N. Temperature-Dependent Hydrogen Electrochemistry on Platinum Low-Index Single-Crystal Surfaces in Acid Solutions. J. Phys. Chem. B101, 5405–5413 (1997). [Google Scholar]
- 46.Zhu, S. et al. The Role of Ruthenium in Improving the Kinetics of Hydrogen Oxidation and Evolution Reactions of Platinum. Nat. Catal.4, 711–718 (2021). [Google Scholar]
- 47.Campbell, C. T. The Degree of Rate Control: A Powerful Tool for Catalysis Research. ACS Catal.7, 2770–2779 (2017). [Google Scholar]
- 48.Rau, M. S., Quaino, P. M., Gennero de Chialvo, M. R. & Chialvo, A. C. Hydrogen Oxidation Reaction: Evidences of Different Electrocatalytic Activity between α and β Pd–H. Electrochem. Commun.10, 208–212 (2008). [Google Scholar]
- 49.Landers, A. T. et al. Dynamics and Hysteresis of Hydrogen Intercalation and Deintercalation in Palladium Electrodes: A Multimodal In Situ X-ray Diffraction, Coulometry, and Computational Study. Chem. Mater.33, 5872–5884 (2021). [Google Scholar]
- 50.Marković, N. M. & Ross, P. N. Surface Science Studies of Model Fuel Cell Electrocatalysts. Surf. Sci. Rep.45, 117–229 (2002). [Google Scholar]
- 51.Monteiro, M. C. O., Dattila, F., López, N. & Koper, M. T. M. The Role of Cation Acidity on the Competition between Hydrogen Evolution and CO2 Reduction on Gold Electrodes. J. Am. Chem. Soc.144, 1589–1602 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Frumkin, A. Wasserstoffüberspannung und Struktur der Doppelschicht. Z. f.ür. Physikalische Chem.164A, 121–133 (1933). [Google Scholar]
- 53.Ye, K. et al. Resolving local reaction environment toward an optimized CO2-to-CO conversion performance. Energ. Environ. Sci.15, 749–759 (2022). [Google Scholar]
- 54.Ringe, S. et al. Understanding Cation Effects in Electrochemical CO2 Reduction. Energ. Environ. Sci.12, 3001–3014 (2019). [Google Scholar]
- 55.Mortensen, J. J., Hammer, B. & Nørskovi, J. K. A Theoretical Study of Adsorbate–Adsorbate Interactions on Ru(0001). Surf. Sci.414, 315–329 (1998). [Google Scholar]
- 56.Chen, L. D., Urushihara, M., Chan, K. & Nørskov, J. K. Electric Field Effects in Electrochemical CO2 Reduction. ACS Catal.6, 7133–7139 (2016). [Google Scholar]
- 57.Wang, Y.-H. et al. In situ Raman Spectroscopy Reveals the Structure and Dissociation of Interfacial Water. Nature600, 81–85 (2021). [DOI] [PubMed] [Google Scholar]
- 58.El-Aziz, A. M., Kibler, L. A. & Kolb, D. M. The Potentials of Zero Charge of Pd(111) and Thin Pd Overlayers on Au(111). Electrochem. Commun.4, 535–539 (2002). [Google Scholar]
- 59.Xu, P., von Rueden, A. D., Schimmenti, R., Mavrikakis, M. & Suntivich, J. Optical Method for Quantifying the Potential of Zero Charge at the Platinum–Water Electrochemical Interface. Nat. Mater.22, 503–510 (2023). [DOI] [PubMed] [Google Scholar]
- 60.Zhu, X., Huang, J. & Eikerling, M. pH Effects in a Model Electrocatalytic Reaction Disentangled. JACS Au3, 1052–1064 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ferre-Vilaplana, A., Perales-Rondon, J. V., Feliu, J. M. & Herrero, E. Understanding the Effect of the Adatoms in the Formic Acid Oxidation Mechanism on Pt(111) Electrodes. ACS Catal.5, 645–654 (2015). [Google Scholar]
- 62.Wang, P., Steinmann, S. N., Fu, G., Michel, C. & Sautet, P. Key Role of Anionic Doping for H2 Production from Formic Acid on Pd(111). ACS Catal.7, 1955–1959 (2017). [Google Scholar]
- 63.Limaye, A. M., Zeng, J. S., Willard, A. P. & Manthiram, K. Bayesian Data Analysis Reveals No Preference for Cardinal Tafel Slopes in CO2 Reduction Electrocatalysis. Nat. Commun.12, 703 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wang, P.-Y., Zhou, J.-F., Chen, H., Peng, B. & Zhang, K. Activation of H2O Tailored by Interfacial Electronic States at a Nanoscale Interface for Enhanced Electrocatalytic Hydrogen Evolution. JACS Au2, 1457–1471 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Xue, S. et al. Influence of Alkali Metal Cations on the Hydrogen Evolution Reaction Activity of Pt, Ir, Au, and Ag Electrodes in Alkaline Electrolytes. ChemElectroChem5, 2326–2329 (2018). [Google Scholar]
- 66.Monteiro, M. C. O., Goyal, A., Moerland, P. & Koper, M. T. M. Understanding Cation Trends for Hydrogen Evolution on Platinum and Gold Electrodes in Alkaline Media. ACS Catal.11, 14328–14335 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Li, P. et al. Hydrogen Bond Network Connectivity in the Electric Double Layer Dominates the Kinetic pH Effect in Hydrogen Electrocatalysis on Pt. Nat. Catal.5, 900–911 (2022). [Google Scholar]
- 68.Marcus, Y. Ionic Radii in Aqueous Solutions. Chem. Rev.88, 1475–1498 (1988). [Google Scholar]
- 69.Jackson, M. N., Jung, O., Lamotte, H. C. & Surendranath, Y. Donor-Dependent Promotion of Interfacial Proton-Coupled Electron Transfer in Aqueous Electrocatalysis. ACS Catal.9, 3737–3743 (2019). [Google Scholar]
- 70.Jackson, M. N. & Surendranath, Y. Donor-Dependent Kinetics of Interfacial Proton-Coupled Electron Transfer. J. Am. Chem. Soc.138, 3228–3234 (2016). [DOI] [PubMed] [Google Scholar]
- 71.Ledezma-Yanez, I. et al. Interfacial Water Reorganization as a pH-Dependent Descriptor of the Hydrogen Evolution Rate on Platinum Electrodes. Nat. Energy2, 17031 (2017). [Google Scholar]
- 72.Bi, Q.-Y., Lin, J.-D., Liu, Y.-M., Huang, F.-Q. & Cao, Y. Promoted Hydrogen Generation from Formic Acid with Amines Using Au/ZrO2 Catalyst. Int. J. Hydrog. Energ.41, 21193–21202 (2016). [Google Scholar]
- 73.Miyake, H., Okada, T., Samjeské, G. & Osawa, M. Formic Acid Electrooxidation on Pd in Acidic Solutions Studied by Surface-Enhanced Infrared Absorption Spectroscopy. Phys. Chem. Chem. Phys.10, 3662–3669 (2008). [DOI] [PubMed] [Google Scholar]
- 74.Nelson, N. C., Nguyen, M.-T., Glezakou, V.-A., Rousseau, R. & Szanyi, J. Carboxyl Intermediate Formation via an in situ-Generated Metastable Active Site during Water-Gas Shift Catalysis. Nat. Catal.2, 916–924 (2019). [Google Scholar]
- 75.Mathew, K., Kolluru, V. S. C., Mula, S., Steinmann, S. N. & Hennig, R. G. Implicit Self-Consistent Electrolyte Model in Plane-Wave Density-Functional Theory. J. Chem. Phys.151, 234101 (2019). [DOI] [PubMed] [Google Scholar]
- 76.Mathew, K., Sundararaman, R., Letchworth-Weaver, K., Arias, T. A. & Hennig, R. G. Implicit Solvation Model for Density-Functional Study of Nanocrystal Surfaces and Reaction Pathways. J. Chem. Phys.140, 084106 (2014). [DOI] [PubMed] [Google Scholar]
- 77.Kresse, G. & Furthmüller, J. Efficiency of ab-initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comp. Mater. Sci.6, 15–50 (1996). [DOI] [PubMed] [Google Scholar]
- 78.Kresse, G. & Furthmüller, J. Efficient Iterative Schemes for ab initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
- 79.Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett.77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- 80.Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys.132, 154104 (2010). [DOI] [PubMed] [Google Scholar]
- 81.Sheppard, D., Xiao, P., Chemelewski, W., Johnson, D. D. & Henkelman, G. A Generalized Solid-State Nudged Elastic Band Method. J. Chem. Phys.136, 074103 (2012). [DOI] [PubMed] [Google Scholar]
- 82.Henkelman, G., Uberuaga, B. P. & Jónsson, H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys.113, 9901–9904 (2000). [Google Scholar]
- 83.Sundararaman, R. et al. JDFTx: Software for Joint Density-Functional Theory. SoftwareX6, 278–284 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Yan, E. et al. Experimental and Theoretical Comparison of Potential-dependent Methylation on Chemically Exfoliated WS2 and MoS2. ACS Appl. Mater. Interfaces14, 9744–9753 (2022). [DOI] [PubMed] [Google Scholar]
- 85.Liu, C. et al. Oxygen evolution reaction over catalytic single-site Co in a well-defined brookite TiO2 nanorod surface. Nat. Catal.4, 36–45 (2021). [Google Scholar]
- 86.Hossain, M. D., Huang, Y., Yu, T. H., Goddard, W. A. III. & Luo, Z. Reaction mechanism and kinetics for CO2 reduction on nickel single atom catalysts from quantum mechanics. Nat. Commun.11, 2256 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Huang, Y., Nielsen, R. J. & Goddard, W. A. III. Reaction Mechanism for the Hydrogen Evolution Reaction on the Basal Plane Sulfur Vacancy Site of MoS2 Using Grand Canonical Potential Kinetics. J. Am. Chem. Soc.140, 16773–16782 (2018). [DOI] [PubMed] [Google Scholar]
- 88.Sundararaman, R. & Goddard, W. A. III. The Charge-Asymmetric Nonlocally Determined Local-Electric (CANDLE) Solvation Model. J. Chem. Phys.142, 064107 (2015). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated in this study are provided in the Supplementary Information and Source Data file. Source data are provided with this paper.