Improving Biological Joint Moment Estimation During Real-World Tasks with EMG and Instrumented Insoles

Abstract

Objective:

Real-time measurement of biological joint moment could enhance clinical assessments and generalize exoskeleton control. Accessing joint moments outside clinical and laboratory settings requires harnessing non-invasive wearable sensor data for indirect estimation. Previous approaches have been primarily validated during cyclic tasks, such as walking, but these methods are likely limited when translating to non-cyclic tasks where the mapping from kinematics to moments is not unique.

Methods:

We trained deep learning models to estimate hip and knee joint moments from kinematic sensors, electromyography (EMG), and simulated pressure insoles from a dataset including 10 cyclic and 18 non-cyclic activities. We assessed estimation error on combinations of sensor modalities during both activity types.

Results:

Compared to the kinematics-only baseline, adding EMG reduced RMSE by 16.9% at the hip and 30.4% at the knee (p<0.05) and adding insoles reduced RMSE by 21.7% at the hip and 33.9% at the knee (p<0.05). Adding both modalities reduced RMSE by 32.5% at the hip and 41.2% at the knee (p<0.05) which was significantly higher than either modality individually (p<0.05). All sensor additions improved model performance on non-cyclic tasks more than cyclic tasks (p<0.05).

Conclusion:

These results demonstrate that adding kinetic sensor information through EMG or insoles improves joint moment estimation both individually and jointly. These additional modalities are most important during non-cyclic tasks, tasks that reflect the variable and sporadic nature of the real-world.

Significance:

Improved joint moment estimation and task generalization is pivotal to developing wearable robotic systems capable of enhancing mobility in everyday life.

I. Introduction

Accurate estimation of human joint moments using wearable sensors could provide a useful signal for health monitoring [1], [2] and exoskeleton control [3], [4] during real-world activities. The gold standard approach to quantify joint moment is through inverse dynamics enabled by optical motion capture and in-ground force plates [5]. However, these systems are not accessible outside of the lab; thus, recent efforts have explored methods for estimating joint moments directly from wearable sensors. Three main categories of approaches have emerged as possible wearable alternatives: analytical models driven by inertial measurement units (IMUs) and instrumented insoles [6], electromyography (EMG)-driven models [7], and machine learning data-driven models [6], [8]. Deep learning methods have shown great promise in accurately estimating joint moments with a limited sensor suite of kinematic sensors [4], [9] and do not require the same assumptions entailed by analytical methods [6]. However, this approach, as well as its alternatives, have mostly been tested during limited tasks such as walking and running or on a few individual alternate tasks [6]. The question remains whether these approaches will be viable on highly dynamic, constantly changing tasks.

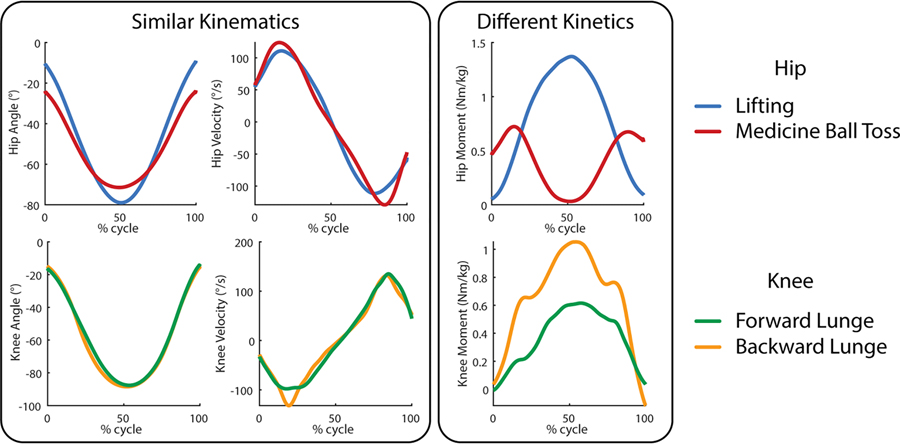
The machine learning biological moment estimation approach has a potential weakness in these unique non-cyclic activities. Most of the current approaches use only kinematic sensor inputs such as joint angles and IMUs [4], [8]. However, changes in a person’s kinematics do not directly predict changes in their joint moment, especially in these unique activities because similar kinematic patterns do not necessarily result in similar kinetic patterns. Although studies have shown promising results in estimating ground reaction forces directly from kinematic sensors during standard cyclic activities [9], [10], these relationships may not hold in the same way during unusual cyclic and non-cyclic tasks as shown in Fig. 1 [11]. Thus, a kinematic-based machine learning model is potentially lacking distinguishing information for tasks with similar kinematics but differing torques or vice versa.

Fig. 1.

Several non-cyclic tasks that demonstrate similar kinematic profiles but different kinetic profiles at the hip and knee. The curves are subject average profiles drawn from Scherpereel et. al.

To add this missing information, there are two potential avenues inspired by both the current musculoskeletal modeling techniques and the alternate approaches to moment estimation. The inverse approach uses ground reaction forces traced up the kinematic chain to the joint of interest to estimate joint moments. This line of reasoning has given rise to the gold standard of inverse dynamics [5] and the analytical models for moment estimation. The forward approach notes that fundamentally muscle activations lead to muscle forces which are ultimately responsible for the resulting torque exerted on the joint. This line of thinking has inspired EMG-driven modeling techniques [12], [13]. Although current real-time wearable systems cannot directly measure 3D ground reaction forces [14] or muscle forces and activation [15], the substitute wearable sensors, pressure insoles and EMG, have the potential to provide insight into kinetic changes in human movement.

Pressure insoles estimate the vertical ground reaction force (vGRF) and center of pressure (COP) within the reference frame of the foot [16]. Pressure insoles have recently grown in popularity for wearable robotic technologies [17], specifically for discrete gait event detection and even locomotion mode recognition [18]. More recently, analytical methods for moment estimation have used continuous signals from insoles as a surrogate for force plates, but their success is varied [19]. Only a few studies have examined insoles in machine learning approaches, two for estimating internal loading [20], [21] and a single study using vGRF as an input in hip moment estimation for a single treadmill walking speed [22]. An analysis of the benefits of insoles on deep learning moment estimation has yet to be explored.

Electromyography (EMG) has the capacity to encode information about muscle activation, which relates to muscle forces and thereby joint moments. Thus, information from surface EMG signals could provide a machine learning model with the ability to distinguish between situations where the mapping between kinematics and kinetics may be highly nondeterministic. EMG inputs in deep learning models have conventionally been used for gesture recognition on upper limbs, but have also been beneficial for angle and force/torque estimation [23]. On upper limbs, various types of neural networks have been used to estimate forces at the wrist [24] as well as multi-degree-of-freedom torques at the wrist [25]. Work on lower limbs has included using deep learning for estimation of gait events with EMG [26] as well as several attempts to estimate biological moments with EMG and neural networks [27]–[29]. In 2008, Hahn and O’Keefe used a neural network with EMG, kinematics, and other subject information as inputs to estimate lower-limb joint moments [27]. More recent studies have used EMG as well as kinematics to estimate ankle moments [28] and all three lower-limb joints [29] using deep learning models. The benefits and feasibility of estimating biological moment during unique non-cyclic tasks has yet to be examined and a direct comparison of the benefits of EMG over kinematic sensors alone has yet to be performed.

In this study, a deep learning joint moment estimation approach was used to estimate joint moments in both common, time-repeatable cyclic activities as well as unique non-cyclic activities. Using subject dependent models, we analyzed the benefits of adding EMG, simulated instrumented insoles, and both as compared to a purely kinematic sensor baseline. Sensors were chosen to replicate those most accessible to two devices: a hip exoskeleton and a knee exoskeleton, and the associated joint moment was selected as the appropriate estimation label. Our main hypothesis was that EMG and simulated insoles, both individually and together, would improve joint moment estimation on left-out-tasks as compared to the kinematic-only baseline. This is due to the additional information that these sensors provide to distinguish between tasks with similar kinematics but different torques. Our secondary hypothesis was that the benefit of adding these sensors would be higher for the unique non-cyclic activities over the cyclic activities. Because the model architecture received time history information, we expect that the cyclic tasks will be easier to model without additional information from EMG or simulated insoles than the non-cyclic activities.

II. Methods

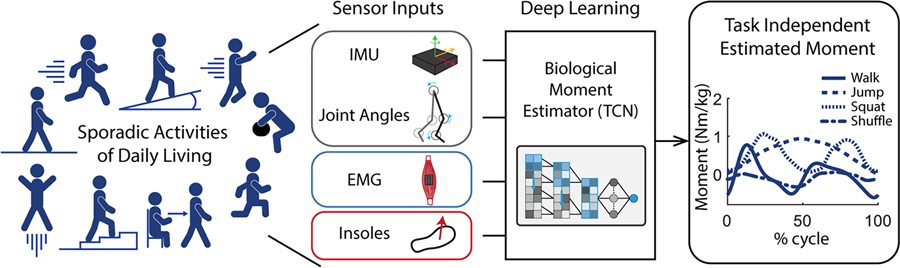
This study utilized a temporal convolutional network (TCN) [4] in concert with different sensor inputs (EMG, virtual insoles) to create models that estimate joint moments based on wearable sensor data. This allowed a rigorous examination of the benefits of including EMG, instrumented insoles, or both in estimating joint moments for unique tasks. Due to the left-out-task training approach, our results represent the expected benefit during truly novel tasks. Our experimental approach is outlined in Fig. 2.

Fig. 2.

Overview of our approach for estimating biological joint moments on a task independent basis. Wearable signals were collected over many different tasks of daily living and then used as inputs to a temporal convolutional network (TCN) to estimate biological moment.

A. Network Architecture

The network was designed based on the TCN introduced by Bai et. al. [30]. This model architecture was chosen based on its ability to incorporate significant time history information without excessive model complexity, as well as previous data demonstrating its ability to accurately predict biological moments [4]. Inputs to the model are sequences of time-history data where the length of time history is determined by the kernel size for the convolutional layers as well as the depth of the network. Dilated causal convolution is used to increase the size of the input time series. The kernel size for the convolutional layers was set to four, and we chose a depth of five layers. Each layer consisted of a set of two convolutions with weight normalization and rectified linear unit (ReLU) activation functions with a dropout term to avoid overfitting. Each hidden layer consisted of fifty nodes. This particular architecture represents an effective time history of 0.93s given a 200Hz sampling rate. The details of the generic TCN architecture are included in Bai et. al. [30]. The depth, kernel size, learning rate, and dropout are parameters that were set based on previous testing with this network for estimating hip moments from purely mechanical sensors [4]. This network architecture employed input-level sensor fusion where information from the various sensor modalities (EMGs, joint angles, IMUs, and virtual insoles) were allowed to influence each other from the beginning of the network.

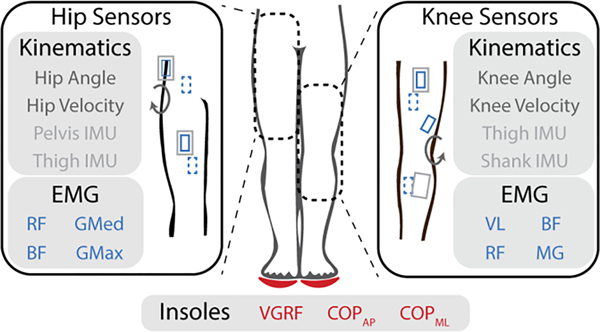
Inputs consisted of only the sensors relevant to the specific exoskeleton (hip or knee). For a sensor suite simulating a knee exoskeleton, the baseline kinematic sensors included knee angle, knee velocity, a shank IMU, and a thigh IMU similar to Lee et al. [31]. EMG inputs consisted of four channels of EMG from knee spanning muscles: vastus lateralis (VL), rectus femoris (RF), biceps femoris (BF), and medial gastrocnemius (MG). For a system simulating a hip exoskeleton, the baseline kinematic sensors included hip angle, hip velocity, a thigh IMU and a pelvis IMU inspired by a combination of research devices [32], [33]. EMG inputs consisted of four channels of EMG from hip spanning muscles: rectus femoris (RF), gluteus medius (GMed), gluteus maximus (GMax), and biceps femoris (BF). For both analyses, virtual insoles consisted of vGRF in the frame of the foot as well as COP for both the anteroposterior and mediolateral directions. This is summarized in Fig. 3.

Fig. 3.

Detailed view of sensors and locations used as inputs to the model. Angles were computed using motion capture trajectories and wearable sensors were placed for the surface electromyography (EMGs) and the inertial measurement units (IMUs). Dotted sensor symbols indicate the posterior side. Insoles were simulated based on vertical ground reaction force (vGRF) and center of pressure (mediolateral: COP_ML and anterior-posterior: COP_AP) transformed from the force plate to the reference frame of the foot. EMG sensors for the hip included: rectus femoris (RF), gluteus medius (GMed), biceps femoris (BF), and gluteus maximus (GMax). For the knee, BF and RF were again used as well as the vastus lateralis (VL), and medial gastrocnemius (MG).

Training was performed in mini-batches for 15 epochs. To choose this number, we trained models similar to those presented here (subject-dependent models with kinematic sensors to estimate knee joint moment) with a completely separate dataset [34]–[37] to determine the average point at which the models stopped improving. Model weights were initialized to random values. Mean squared error was used for the loss function.

B. Data Overview

The data used in this experiment consist of bilateral data for 12 subjects performing various unique tasks. These tasks included conventional biomechanics tasks (e.g., walking, running, ramps and stairs), athletic maneuvers (e.g., lunges), tasks of daily living (e.g., sit-to-stand, turns, and lifting), and responses to external perturbations (e.g., tug of war and walking over obstacles). The dataset was divided into 10 cyclic and 18 non-cyclic task groups. This study was approved under Georgia Tech Institutional Review Board H17240 (07/12/2017). We have open-sourced these data and further details on the groupings and data collection methods can be found in that publication [11].

The mocap joint angles (VICON, UK), IMUs (Avanti Wireless EMG, Delsys, Natick, MA), and virtual insole data (Bertec Corporation, Columbus, Ohio) from the dataset at 200Hz were fed directly into the model (Angles: rad, velocity: rad/s, IMU data: Accel Gs Gyro rad/s, Insoles: Force N/kg COP m). For EMG processing, the raw EMG signal was centered by subtracting the mean, then bandpass filtered between 30 and 300 Hz using a 4th order forward-reverse Butterworth filter. Then the signal was rectified and lowpass filtered at 6Hz with another 4^th order forward-reverse Butterworth filter. This envelope was then downsampled to match the frequency of the rest of the mechanical sensors (200 Hz). We scaled the magnitude of the EMG envelope to be similar to the magnitudes of the other input signals by changing the units (constant scaling factor of 10,000) because we chose not to use feature normalization in keeping with Molinaro et al. [4]. This was performed for each channel of EMG. Other additional EMG features such as EMG frequency features (short time Fourier transform analysis and wavelet analysis) were tested, but no substantial improvement in estimation error was obtained so these were not included in the final analyses. Labels for the model were joint moments calculated with inverse dynamics based on kinematics from motion capture, ground reaction forces from in-ground and treadmill force plates, and a subject specific model created in OpenSim [11]. The joint moments were scaled by subject mass (Nm/kg) to allow easier comparison across participants.

To increase the data available for training the model, the left leg data were mirrored to match the coordinate system of the right leg allowing a single leg model that can be trained and tested on both legs. This strategy has been used for kinematic sensors [38]. To verify that we could use a similar strategy for EMG, we ran a direct comparison between models trained separately for the left and right leg and models trained with both right and left leg data. We found that training with combined right and left leg EMG did not decrease performance of the estimator.

C. Model Training/Testing and Evaluation

To train and test these models, a leave-one-group-out cross-fold validation was performed. Groups of trials were left out such as walking (at three speeds), running (for two speeds), sitting (two chair heights), declined walking (two inclination angles), etc. Training was then performed on all of the held-in tasks for the given subject, and the model was used to predict the torques of the left-out group of tasks. This was then folded across all of the task groups and performed individually for each subject to yield the final results. To evaluate the model’s performance and compare different approaches, root mean squared error (RMSE) was calculated between the ground-truth joint moment labels and the estimated labels to demonstrate the overall performance of the model. To further evaluate how well the shape of the estimate matched the ground truth moment, R² was calculated based on a best fit line between the ground truth joint moment and the estimate for each participant and task group (e.g. walk) as a whole (subtasks within each task such as walking speeds are combined before computing a single best fit line). Mean absolute error (MAE) at peak joint moments was also examined. These were then compared between models and across subjects to establish the benefits of the different approaches.

While this examination of left-out-task performance provides a rigorous comparison of the impact of sensor additions, the question remains whether all of these tasks are necessary to achieve the observed accuracy and if not, which tasks are the most important to include when generalizing to left out tasks. To answer these questions, a forward task selection algorithm was used to sequentially select the most important task for improving the model’s ability to generalize to the rest of the tasks. To select the initial task, a model was trained using each individual task from each participant as the training set and then testing on the rest of the tasks for that participant. The task that produced the lowest moment estimation RMSE on the rest of the tasks across participants was selected. After this initial iteration, the following tasks were selected by sequentially testing each of the remaining tasks (those not chosen yet) and choosing the specific task that, when added to the training set, resulted in the greatest reduction in RMSE for the rest of the remaining tasks as compared to not including that specific task. This was performed for the sensor case that included all sensor types (kinematics, EMG, and insoles).

Statistics across different sensor input types and task types (cyclic and noncyclic) were computed using a two-way repeated measures analysis of variance (ANOVA) test with a significance level of α = 0.05. Participants were the random factor while sensor combinations and task types were the independent variables. Moment estimation RMSE was the dependent variable and was first averaged across trials within the same task group and same participant and then averaged across task groups within the same participant. This means that we compare a single value per participant per sensor set. To further explore these effects, we ran separate simple main effect one-way ANOVAs for each task delineation (all, cyclic, and non-cyclic) at each joint (hip and knee) to compare the four sensors combinations (kinematics, kinematics + EMG, kinematics + insoles, kinematics + EMG + insoles). To parse out pairwise differences between different sensor additions, we applied paired t-tests with Bonferroni correction for the six possible comparisons. On each individual task, we ran comparisons between sensor combinations. Due to the number of comparisons, we controlled the false discovery rate (q < 0.05) using the method proposed by Benjamini & Hochberg [39]. This test controls for both the comparison of sensors within task and its use across tasks. To test the second hypothesis, the difference in RMSE with respect to the kinematic baseline was computed for each task and sensor addition within each subject (1).

$$\begin{array}{l}RMSEDifference\left(sensor\right)\\ =RMS{E}_{kinematics+sensor}\\ -RMS{E}_{kinematics}\end{array}$$ (1)

The difference was then averaged separately across cyclic and non-cyclic tasks within each subject. The reduction in RMSE for cyclic and non-cyclic activities was compared with a paired t-test for each sensor combination. This tested whether adding additional sensors showed more benefit during noncyclic tasks than cyclic tasks. All statistical analyses were performed in Matlab (MathWorks, Natick, MA).

III. Results

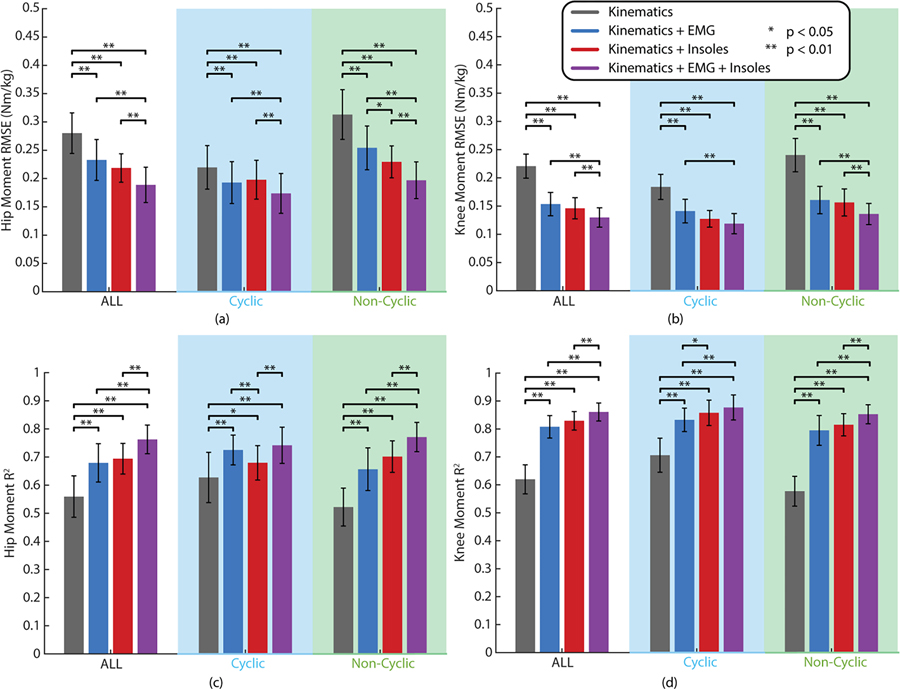
Our two-way ANOVA across sensor additions and task types (with subjects as a fixed effect) revealed statistically significant decreases in RMSE from adding different sensor inputs in the deep learning model for both the hip (F=91.70, dfM=3, dfE=33, p < 0.01) and knee (F=204.64, dfM=3, dfE=33, p < 0.01). It also revealed a statistically significant difference between cyclic and non-cyclic tasks at both the hip (F=32.49, dfM=1, dfE=11, p < 0.01) and knee (F=34.51, dfM=1, dfE=11, p < 0.01) and a significant interaction effect between sensors and task type at both the hip (F=45.43, dfM=3, dfE=33, p < 0.01) and knee (F=16.49, dfM=3, dfE=33, p < 0.01). Because of these significant effects, we further explored these differences with simple main effects ANOVAs across sensor additions for different task types (all, cyclic, and non-cyclic) each of which showed statistical significance at both the hip and knee (p < 0.01). These were followed up by pairwise multiple comparisons tests as shown in Fig. 4a&b. When comparing results across all tasks, the models with EMG (Hip RMSE: 0.233 Nm/kg, Knee RMSE: 0.154 Nm/kg), simulated insoles (Hip RMSE: 0.219 Nm/kg, Knee RMSE: 0.146 Nm/kg), and EMG + insoles (Hip RMSE: 0.189 Nm/kg, Knee RMSE: 0.130 Nm/kg) all showed statistically significant reductions in joint moment estimation error as compared to the kinematic baseline (Hip RMSE: 0.280 Nm/kg, Knee RMSE: 0.221 Nm/kg). This was also the case when broken down between cyclic and non-cyclic tasks. Similar results can be seen for R² in Fig. 4c&d where an increase in R² indicates a better match between the shape of the estimate and the shape of the ground truth moment. Again, a two-way ANOVA revealed statistically significant effects for sensors (hip: F=99.26, dfM=3, dfE=33, p < 0.01; knee: F=215.27, dfM=3, dfE=33, p < 0.01), tasks (hip: F=9.04, dfM=1, dfE=11, p = 0.012; knee: F=15.84, dfM=1, dfE=11, p < 0.01), and the interaction effect (hip: F=35.60, dfM=3, dfE=33, p < 0.01; knee: F=21.79, dfM=3, dfE=33, p < 0.01) with significant simple main effects ANOVAs (p < 0.01). Across all tasks, R² significantly increased when adding EMG (Hip R²: 0.68, Knee R²: 0.81), insoles (Hip R²: 0.69, Knee R²: 0.83), and both EMG and insoles (Hip R²: 0.76, Knee R²: 0.86) as compared to the kinematic only baseline (Hip R²: 0.56, Knee R²: 0.62). This also held when separated into cyclic and non-cyclic tasks. Across task groups, models with EMG + insoles had lower estimation error and a higher R² value than models with either EMG or insoles individually (p < 0.01). When broken down into cyclic and non-cyclic tasks, this held for the non-cyclic tasks (p < 0.01), but not in cyclic task RMSE at the knee or R² at either joint. No statistically significant difference was detected between adding EMG versus adding insoles across all tasks. However, when broken down by cyclic and non-cyclic, there was a detectable difference in RMSE between adding EMG and insoles at the hip during non-cyclic tasks and in R² at the knee for cyclic activities (p < 0.05), both favoring insoles over EMG. However, the opposite can be seen favoring EMG over insoles for R² at the hip. Similar results are shown in the online supplement for mean absolute error at the peak joint moments.

Fig. 4.

Summary of results from comparing different sensor inputs in a deep learning model for joint moment estimation. Hip (a) and knee (b) moment estimation errors (RMSE) across sensor additions are presented for all of the tasks and then broken down into cyclic and non-cyclic tasks. The corresponding R² value for the hip (c) and knee (d) are also shown. Error bars represent the standard deviation across the 12 subjects.

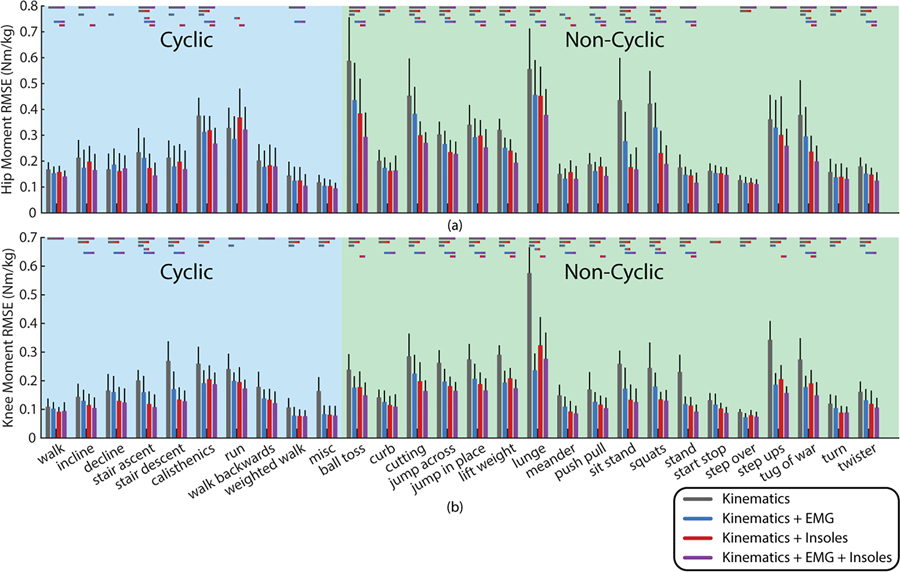
The results for specific task groups for both the hip and knee are shown in Fig. 5 broken into cyclic and non-cyclic tasks to show the performance differences on each specific task group. Performance on different task groups varies significantly based on the complexity of the task, but more of the non-cyclic tasks demonstrate statistically significant differences based on sensor additions than the cyclic tasks. Changes relative to kinematics for each individual task are provided in the online supplement.

Fig. 5.

Results broken down by task groups for the hip (a) and the knee (b). This is shown based on the performance for each left out task from a model trained on the other tasks. Lines above the bars show the standard deviation across the 12 subjects. Statistically significant comparisons as determined by controlling the false rate of discovery are indicated with colored bars above each task.

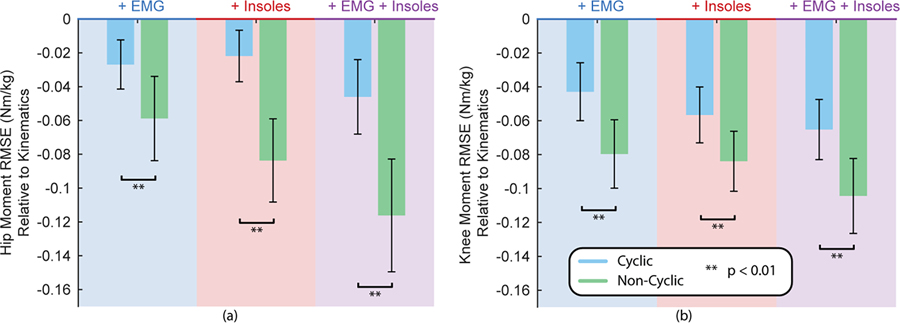
The results from the reduction in RMSE of noncyclic versus cyclic tasks are shown in Fig. 6. All three additional sensor combinations showed a statistically significant improvement in the noncyclic activities as compared to the cyclic activities for both hip and knee (p < 0.01).

Fig. 6.

RMSE difference relative to the kinematic baseline for each sensor addition during non-cyclic tasks and cyclic tasks for the hip (a) and the knee (b). Error bars represent standard deviation across the 12 subjects. Asterisks indicate statistical significance.

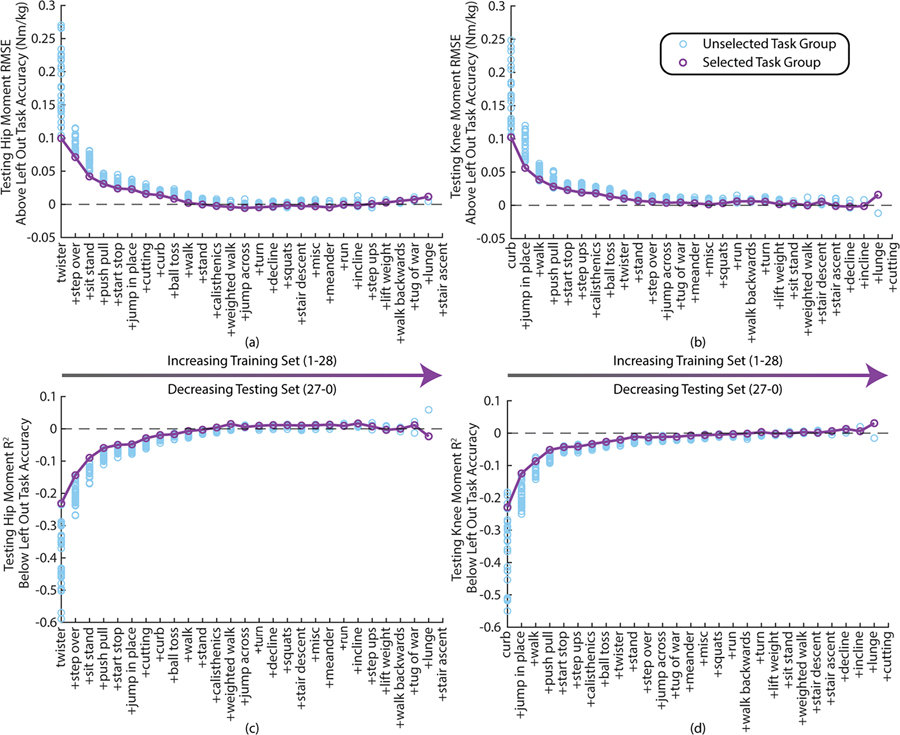
Task selection optimization results are presented in Fig. 7a&b for the hip and knee. The performance of kinematic +EMG + insole models trained with the tasks up to that iteration are subtracted from the corresponding participant and task results presented in Fig. 5. Thus, zero represents performance equivalent to the performance from Fig. 4–5 with many fewer tasks in the training set. At the hip, RMSE drops to within 5% of the RMSE of the average left-out-task accuracy for this sensor set in the first 9 tasks and for the knee this occurs within the first 11 tasks. A similar result can be seen for R² in Fig. 7c&d.

Fig. 7.

Task optimization performance compared to the corresponding leave one task out performance are shown in terms of moment estimation error (RMSE) for the hip (a) and the knee (b) and also in terms of R² for the hip (c) and knee (d). Each datapoint represents the average performance on a given task group across all 12 participants when including kinematics, EMG, and insoles. Error bars were omitted for visual clarity.

IV. Discussion

As hypothesized, adding kinetic sensor information in the form of EMG or insoles significantly aided in estimating joint moments using a deep learning model. This contributes a formal comparison of these unique sensor modalities that has not yet been explored, and it expands joint moment estimation to unique non-cyclic activities where we show that these additional sensor inputs are more essential.

In general, EMG or insoles added additional information that improved model performance. For RMSE during non-cyclic tasks at the hip and R² during cyclic tasks at the knee there are statistical difference between adding only EMG versus adding only insoles. This indicates that either the EMG added less relevant information for these tasks at that joint compared to the insoles or that the EMG information could not be utilized as well without the added information from the insoles. The opposite can be seen for the hip R² during cyclic tasks. This contrasts with our assumption that proximal joints would benefit less from insoles given that ground reaction forces must be traced farther up the kinematic chain, and unmeasured shear forces have a larger effective moment arm. The counterintuitive result for RMSE at the hip may be due to the fact that fewer EMGs were available for direct sagittal plane actuation at the hip and the only accessible hip flexor muscle (rectus femoris) is a biarticular muscle where placement may play a role in which action (hip flexion or knee extension) is captured more clearly in the signal [40].

Including both EMG and insoles compared to either on their own showed significant benefits overall, but this difference was more substantial in the non-cyclic activities than the cyclic activities. This demonstrates that the information provided by these modalities is unique, though they may contain some overlapping information. The lack of significance for some comparisons during cyclic activities may reflect that the model cannot benefit from this additional information due to the repeatable nature of the activity. Thus, the time history embedded in the model architecture may provide enough information to accurately predict moments without the need for as much additional information.

The task-by-task breakdown demonstrates that more statistically significant differences are detectible in the non-cyclic tasks than in the cyclic tasks. This may be due to the fact that these activities lie more often on the extremes of the sensor input ranges. Thus, when left out of training, these tasks require the model to extrapolate to new unique conditions which may be easier with more information. Particularly at the hip, the most commonly heretofore tested tasks like walking, running, stairs, and ramps do not show significant improvements with additional sensing while the less commonly tested cyclic and non-cyclic activities do. This may explain the lack of apparent benefit to including EMG at the hip and knee in Camargo et al. [29].

Differences between cyclic and non-cyclic activities are hinted at in the previous analyses but to further elucidate this effect, we compared the relative improvement of these sensor additions from non-cyclic to cyclic tasks. In all cases, adding additional sensors had a statistically larger reduction in moment estimation error during the non-cyclic activities than during cyclic activities. This is most likely due to the inherently more challenging nature of non-cyclic tasks as highlighted by the similar kinematics but different kinetics shown in Fig. 1.

The task optimization results demonstrate that while the above analyses used 27 tasks as the training set and then evaluated performance on the left-out task, similar performance can be achieved with only ~10 tasks in the training set. Also, although the ordering differs, seven out of the first ten tasks are shared between the hip and the knee optimizations. These results indicate that this moment estimation approach could be feasible for real-time implementation while promising a small subset of tasks necessary for task generalization. Again, non-cyclic tasks are more highly represented in the most important tasks than are the cyclic tasks.

A direct comparison to current joint estimation models is difficult because this study explores subject dependent models trained on many unique tasks in a left-out-task group manner whereas other studies examine small subsets of tasks with subject independent models and without full task withholding. However, it is useful to note that even with tasks completely withheld and the requirement that the model generalize to a wide range of tasks, the accuracy of the models presented here is in line with other studies examining joint moment estimation. Molinaro et al. reported hip moment estimation errors of 0.13 Nm/kg for walking, ramps and stairs with slight increases due to left out slopes and speeds [4]. This is slightly better than the kinematic baseline presented here perhaps due to our training paradigm leaving out the entire walking group at once and using a subject dependent model with much less training data. Our results for walking (0.070 range normalized RMSE for the hip and 0.063 for the knee) are also slightly above Hossain et al. who included more sensors [9] but lower than Mundt et. al. [41]. Thus, our performance on cyclic tasks has similar error magnitudes to previous studies that do this without generalizing to new tasks. For the non-cyclic tasks, only a few papers have examined tasks that could be similar, but the ranges are again comparable. Chaaban et al. presented knee extension moment estimation during jumping of 0.028 (normalized to BW*HT) for an independent model with only thigh IMUs [42] whereas our results for a similar activity are lower at 0.0143 but with both thigh and shank IMUs. Thus, while our model can estimate many more tasks than previous deep learning approaches, it still maintains comparable accuracy for similar activities, showing the great extensibility of deep learning. Beyond comparisons to deep learning approaches, our results can be compared to both analytical and EMG-driven approaches with similar restrictions as above prohibiting a direct comparison. To compare to analytical models, Wang et al. present results using IMUs and instrumented insoles for several cyclic and non-cyclic activities. Across subjects their error was 0.37 Nm/kg at the knee and 0.85 Nm/kg at the hip which are much higher than those presented here even with only kinematic sensors [19]. To compare to EMG-driven models, Sartori et al. reported their lowest errors of 23.75 Nm at the knee and 26.06 Nm at the hip for the stance phase of walking, side-stepping, cross-stepping, and running combined. Although there is no direct comparison, our results averaged across running and walking for the entire gait cycle are 17.9 Nm for the hip and 12.0 Nm for the knee with kinematics and EMG. These results demonstrate that the key contributions from our analyses rest upon baseline results that fit well within the current literature.

There are several limitations of this work. First, these models are subject dependent due to the nature of EMG as a very subject specific signal. Future work could explore the usefulness of EMG in independent systems but this was beyond the scope of this work and likely would still necessitate some subject specific data incorporated through adaptive or transfer learning approaches [43], [44]. Second, although the IMUs and EMGs were real sensors, the insole portion of this analysis was run with simulated insoles. This means that these results represent the best possible case for the benefit of instrumented insoles. Real-time studies with physical insoles may reveal that the current state-of-the-art sensors may not provide as much benefit as shown here. To maintain as fair a comparison as possible, we also present the best-case EMG results by using non-causal filtering techniques. Real-time estimation would require causal filtering techniques which may result in a slight decrease in performance, but that decrease can be mitigated by optimizing the filtering strategy. Third, if this strategy were applied to exoskeleton control, changes in kinematics and possible interaction noise in sensor signals could have an impact on model performance.

V. Conclusion

This study demonstrates that EMG and insoles can provide highly useful information in estimating joint moments for wearable systems. While they show some benefit in normal cyclic activities like walking and running, the situations where these additional sensors become highly important is during unique non-cyclic activities where the relationship between kinematics and kinetics may be highly nondeterministic. This study provides pivotal information for device designers choosing sensor inputs for both wearable robotic devices and health monitoring devices. This study also provides another step to encourage scientists in these fields to begin testing on more activities than just the conventional gait lab activities in order to advance technologies that can be deployed in real-world scenarios.