Analysis of a stochastic SEI_uI_rR epidemic model incorporating the Ornstein-Uhlenbeck process

Abstract

This article aims to analyze a stochastic epidemic model $SE{I}_u{I}_{r}R$ (Susceptible-exposed-undetected infected-detected infected (reported -recovered) assuming that the transmission rate at which people undetected become detected is perturbed by the Ornstein–Uhlenbeck process. Our first objective is to prove that the stochastic model has a unique positive global solution by constructing a nonnegative Lyapunov function. Afterward, we provide a sufficient criterion to prove the existence of an ergodic stationary distribution of the mode by constructing a suitable series of Lyapunov functions. Subsequently, we establish sufficient conditions for the extinction of the disease. Finally, a series of numerical simulations are carried out to illustrate the theoretical results.

1. Introduction

Mathematical modeling has the potential to play a significant role in solving the problem of the spread of epidemics. Vaccination programs, physical separation and disease eradication efforts could all benefit from mathematical analysis of epidemic models. In recent years, mathematical models have been developed to analyze infectious diseases such as Covid 19, HIV/AIDS and influenza [17], [24], [26], [38], [43], [45], [47]. In the context of epidemic modeling, the widely used deterministic models are SIR (Susceptible-Infectious-Recovered) and SEIR (Susceptible-Exposed-Infectious-Recovered) models [7], [9], [20], [27], [28], [29], [34], [36], [42], among others. These deterministic models have provided invaluable insights into infection rates, healthcare system demands, and potential intervention effectiveness. However, to capture the memory and hereditary properties of biological systems more accurately, Proportional Caputo Fractional Derivative models are increasingly recognized as necessary [1], [2], [3], [4], [5], [6], [19], [37].

However, the intricacies of real-world dynamics and the inherent variability in human behavior introduce an element of randomness that cannot be ignored. From variations in individual susceptibility and contact patterns to the uncertainty surrounding the emergence of new viral strains, randomness permeates every aspect of the pandemic's progression. This realization has led to the evolution of epidemic modeling beyond deterministic analyses, prompting researchers to embrace stochastic processes and probabilistic methods to capture the unpredictable nature of the virus's spread [10], [13], [16], [39], [50]. Zhou et al. [49] formulated a stochastic SIR epidemic model with nonlinear incidence rate and general stochastic noises. Su and Zhang [41] proposed a stochastic SEI epidemic model in which the transmission rates are general functions and satisfy the log-normal Ornstein-Uhlenbeck process. Song and Zhang [40] studied a stationary distribution and the exponential extinction of a stochastic SVEIS epidemic model. Gatyeni et al. [18] suggested and analyzed a model incorporates the vital dynamics to capture the dynamics of COVID-19 infection using the South African setting in addition to optimizing the control strategies. Based on the work done by Gatyeni et al. [18] and El hadj Moussa et al. [15], we consider an $SE{I}_u{I}_{r}R$ epidemic model as follows:

$$\{\begin{array}{c}\frac{dS(t)}{dt}=\mathrm{\Delta }-\beta (v_1{I}_u+v_2{I}_r)S-\mu S,\hfill \\ \frac{dE(t)}{dt}=\beta (v_1{I}_u+v_2{I}_r)S-(\sigma +\mu )E,\hfill \\ \frac{d{I}_u(t)}{dt}=\sigma (1-\rho )E-(\mu +d_1+\delta +{\gamma }_{I_u})I_u,\hfill \\ \frac{d{I}_r(t)}{dt}=\sigma \rho E+\delta I_u-(\mu +d_2+{\gamma }_{I_r})I_r,\hfill \\ \frac{dR(t)}{dt}={\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r-\mu R,\hfill \end{array}$$ (1)

where $S(t)$ denotes susceptible population, $E(t)$ represents exposed people, $I_u(t)$ represents undetected infected people, $I_r(t)$ represents the detected infected people (or reported), and $R(t)$ denotes the recovered people. Assuming all parameters to be constant and positive, their respective descriptions are provided in Table 1. It is feasible to achieve that system (1) possesses a positive invariant region [15], [18]:

$$\mathrm{\Gamma }=\{(S,E,I_u,I_r,R)\in {\mathbb{R}}_{+}^5,0\le S+E+I_u+I_r+R\le \frac{\mathrm{\Delta }}{\mu }\}.$$

The expression for the basic reproduction number of system (1) is provided as follows:

$${\mathcal{R}}_0={\mathcal{R}}_1+{\mathcal{R}}_2+{\mathcal{R}}_3,$$

where

$${\mathcal{R}}_1=\frac{\sigma \beta S_0{v}_1(1-\rho )}{(\sigma +\mu )(\delta +{\gamma }_{I_u}+\mu +d_1)},{\mathcal{R}}_2=\frac{\sigma \beta S_0{\nu }_2\rho }{(\sigma +\mu )({\gamma }_{I_r}+\mu +d_2)},{\mathcal{R}}_3=\frac{\sigma \beta S_0{v}_2(1-\rho )\delta }{(\sigma +\mu )(\delta +{\gamma }_{I_u}+\mu +d_1)({\gamma }_{I_r}+\mu +d_2)},$$

which plays a crucial role in determining the occurrence of the disease, in a situation where $S_0=\frac{\mathrm{\Delta }}{\mu }$.

Table 1.

Description of state parameters of the model (1).

Parameter	Description
Δ	Birth rate
μ	Natural death rate
β	Disease transmission rate
ρ	Proportion of E which becomes undiagnosed
v1	Transmissibility relative to undetected people
v2	Transmissibility relative to detected people
δ	The transmission rate at which undetected people become detected
d1	Disease related death rate in Iu compartment
d2	Disease related s death rate in Ir compartment
σ	Incubation rate Fitted
${\gamma }_{I_u}$	Recovery rate of people in Iu compartment
${\gamma }_{I_r}$	Recovery rate of people in Ir compartment

Furthermore, the system's (1) relevant threshold dynamics can be described in the following manner:

• •If ${\mathcal{R}}_0<1$. The system (1) exhibits a disease-free equilibrium $E(S_0,0,0,0,0)=(\frac{\mathrm{\Delta }}{\mu },0,0,0,0)$, which is locally asymptotically stable within the region Γ.
• •If ${\mathcal{R}}_0\ge 1$. The system (1) possesses a globally asymptotically stable endemic equilibrium $X^{⁎}=(S^{⁎},E^{⁎},I_u^{⁎},I_r^{⁎},R^{⁎})$ within the region Γ.

Lately, an increasing number of researchers have shown a significant interest in investigating the dynamic behavior of epidemiological models incorporating stochastic perturbations, as it has become evident that the utilization of stochastic modeling techniques provides a more accurate representation of infectious diseases [21], [23], [31], [32].

Until now, multiple methods exist for incorporating stochastic perturbations into deterministic models. Among these approaches, one of the widely adopted strategies assumes that the system's parameters follow an Itô process known as the Ornstein-Uhlenbeck process, [8], [33], [46], [51], [52].

Motivated by the aforementioned discussions, this study considers the analysis of a stochastic $SE{I}_u{I}_{r}R$ (Susceptible-exposed-undetected infected-detected infected (reported)-recovered) epidemic model by incorporating the Ornstein-Uhlenbeck process, as outlined in the following manner:

$$d\delta (t)={\rho }_1[\overline{\delta }-\delta (t)]dt+{\sigma }_{1}dB(t),$$

where $\overline{\delta }$ is measure the long-time mean level of the infection rate δ, ${\rho }_1$ is the speeds of reversion, $B(t)$ is independent standard Brownian motion parameter defined on a complete probability space $(\mathrm{\Omega },\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbf{P})$ with a filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ satisfying the usual conditions, and ${\sigma }_1$ represents the intensity of $B(t)$. Typically, it is assumed that all parameters in the stochastic model are nonnegative to examine the necessity of incorporating positivity into the discussion, variable $\max \{\delta (t),0\}$ is used instead of variable $\delta (t)$ in [31]. Consequently, the ensuing stochastic model is derived as follows:

$$\{\begin{array}{c}dS(t)=[\mathrm{\Delta }-\beta (v_1{I}_u+v_2{I}_r)S-\mu S]dt,\hfill \\ dE(t)=[\beta (v_1{I}_u+v_2{I}_r)S-(\sigma +\mu )E]dt,\hfill \\ d{I}_u(t)=[\sigma (1-\rho )E-(\mu +d_1+\max \{\delta (t),0\}+{\gamma }_{I_u})I_u]dt,\hfill \\ d{I}_r(t)=[\sigma \rho E+\max \{\delta (t),0\}{I}_u-(\mu +d_2+{\gamma }_{I_r})I_r]dt,\hfill \\ dR(t)=[{\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r-\mu R]dt,\hfill \\ d\delta (t)={\rho }_1[\overline{\delta }-\delta (t)]dt+{\sigma }_{1}dB(t).\hfill \end{array}$$ (2)

For convenience and clarity, we introduce the following notation conventions:

${\mathbb{R}}_{+}^m=\{(x_1,...,x_m)|x_b\ge 0,1\le b\le m\},p_1\vee p_2=\max \{p_1,p_2\}$ for any $p_1,p_2\in \mathbb{R}$. Consider ${\mathbb{1}}_D$ as the indicator function for set D. If Q is a vector or matrix, we represent its transpose as $Q^T$.

The main innovations and contributions of this paper are given as follows:

• •This paper introduces and investigates a novel stochastic epidemic model $SE{I}_u{I}_{r}R$ with the incorporation of Ornstein–Uhlenbeck process to perturb the transmission rate δ.
• •The model stochastic considered is more realistic and biologically meaningful framework for describing the transmission rate δ at which undetected people become detected, because this rate can be subject to fluctuations and uncertainties in real-world scenarios. For example, it can depend on factors like changes in testing capabilities, public health interventions, or population behavior. By modeling δ as a stochastic process, the model can account for these variations in detection rates over time.
• •By employing novel Lyapunov functions, we establish the existence of a unique global solution of the model for any initial condition, we describe the sufficient conditions for establishing an ergodic stationary distribution and we proceed to define the sufficient criteria for extinction of the disease.

The rest of the paper is arranged as follows: In Section 2, we establish the existence of a unique global solution of system (2) for any initial condition. Section 3 outlines sufficient conditions for establishing a distinctive ergodic stationary distribution through the utilization of the stochastic Lyapunov method. In Section 4, we proceed to delineate the sufficient criteria for the extinction of the disease. In addition, numerical simulations are given in Section 5 to illustrate the results of the previous analysis. The last section concludes the paper.

2. The global solution's existence and uniqueness

Before delving into the properties of the epidemic system, it is crucial to establish whether the solution it exhibits is globally valid or not, and this theorem addresses the issue of the existence and uniqueness of the global solution for system (2) under any given initial value.

Theorem 2.1

If there is an initial value${(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))}^T\in {\mathbb{R}}_{+}^5\times \mathbb{R}$, the system(2)has a unique solution${(S(t),E(t),I_u(t),I_r(t),R(t),\delta (t))}^T$. That is,${(S(t),E(t),I_u(t),I_r(t),R(t),\delta (t))}^T$is defined for$\forall t\ge 0$and remains in${\mathbb{R}}_{+}^5\times \mathbb{R}$almost surely (a.s.).

Proof 2.1

Since that all the coefficients of system (2) satisfy the local Lipschitz conditions, there will exist a unique local solution ${(S(t),E(t),I_u(t),I_r(t),R(t),\delta (t))}^T$ on the interval $[0,{\varrho }_e)$ for any initial value ${(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))}^T\in {\mathbb{R}}_{+}^5\times \mathbb{R}$, where ${\varrho }_e$ denotes the time of explosion [35]. So, to prove that this solution is global, it suffices to prove that: ${\varrho }_e=\infty$ a.s. Letting $D_n=(1/n,n)\times (1/n,n)\times (1/n,n)\times (1/n,n)\times (1/n,n)\times (1/n,n)$, for any ${(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))}^T\in {\mathbb{R}}_{+}^5\times \mathbb{R}$, one easily obtains a sufficiently large integer $j_0$ to satisfy $(S(0),E(0),I_u(0),I_r(0),R(0),\exp \delta (0))\in D_{j_0}$. In this sense, for every integer $j\ge j_0$, a stopping time set ${\varrho }_j$ is defined by [35]:

$$\begin{gathered} {\varrho }_j=\inf \{t\in [0,{\varrho }_e):\min \{S(t),E(t),I_u(t),I_r(t),R(t),e^{\delta (t)}\}\le \frac{1}{j} \\ \text{or}\max \{S(t),E(t),I_u(t),I_r(t),R(t),e^{\delta (t)}\}\ge j\} \end{gathered}$$

Where we assume in our paper that $\inf \varnothing =\infty$ (with ∅ representing the empty set) and ${\varrho }_{\infty }={\lim }_{j\to \infty }{\varrho }_j$, whence ${\varrho }_{\infty }\le {\varrho }_e$ a.s. If ${\varrho }_{\infty }=\infty$ a.s. is true, then ${\varrho }_e=\infty$ a.s. and ${(S(t),E(t),I_u(t),I_r(t),R(t),\delta (t))}^T\in {\mathbb{R}}_{+}^5\times \mathbb{R}$ a.s. for all $t\ge 0$. So we must prove that ${\varrho }_{\infty }=\infty$ a.s. To prove the latter, we use the proof backwards, assuming that it is false. It means there is a pair of constants $(\epsilon ,T_1)\in ((0,1),{\mathbb{R}}_{+})$ such that:

$$\mathbf{P}\{{\varrho }_{\infty }\le T\}>\epsilon .$$

Consequently, there exists an integer $j_1\ge j_0$ such that

$$\mathbf{P}\{{\varrho }_j\le T\}:=\mathbf{P}\left\{{\mathrm{\Pi }}_j\right\}\ge \epsilon \forall j\ge j_1.$$ (3)

Define the function $U:{\mathbb{R}}_{+}^5\times \mathbb{R}\to {\mathbb{R}}_{+}$ by

$$U(S,E,I_u,I_r,R,\delta )=(S-1-\ln S)+(E-1-\ln E)+(I_u-1-\ln I_u)+(I_r-1-\ln I_r)+(R-1-\ln R)+\frac{{\delta }^2}{2}.$$

Applying the Itô's formula [35], we obtain

$$dU(S,E,I_u,I_r,R,\delta )=\mathcal{L}U(S,E,I_u,I_r,R,\delta )dt+{\sigma }_1\delta dB(t).$$ (4)

Where $\mathcal{L}U:{\mathbb{R}}_{+}^5\times \mathbb{R}\to {\mathbb{R}}_{+}$ is defined by

$$\mathcal{L}U=\mathrm{\Delta }+5\mu +\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}+\max \{\delta (t),0\}+\beta (v_1{I}_u+v_2{I}_r)-\mu S-\mu E-\mu I_u-d_1{I}_u-\mu I_r-d_2{I}_r-\mu R-\frac{\mathrm{\Delta }}{S}-\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}-\frac{\sigma (1-\rho )E}{I_u}-\frac{\sigma \rho E}{I_r}-\frac{\max \{\delta (t),0\}{I}_u}{I_r}-\frac{{\gamma }_{I_u}{I}_u}{R}-\frac{{\gamma }_{I_r}{I}_r}{R}+{\rho }_1\overline{\delta }\delta -{\rho }_1{\delta }^2\le \mathrm{\Delta }+5\mu +\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}+\left|\delta \right|+\beta (v_1{I}_u+v_2{I}_r)+{\rho }_1\overline{\delta }\delta -{\rho }_1{\delta }^2.$$ (5)

Based on model (2) we have

$$\frac{d(S+E+I_u+I_r+R)}{dt}=\mathrm{\Delta }-\mu (S+E+I_u+I_r+R)-(d_1{I}_u+d_2{I}_r)\le \mathrm{\Delta }-\mu (S+E+I_u+I_r+R).$$

Consequently, this suggests that

$$S(t)+E(t)+I_u(t)+I_r(t)+R(t)\le \{\begin{array}{c}S(0)+E(0)+I_u(0)+I_r(0)+R(0),\text{ if }S(0)+E(0)+I_u(0)+I_r(0)+R(0)\ge \frac{\mathrm{\Delta }}{\mu },\hfill \\ \frac{\mathrm{\Delta }}{\mu },\text{ if }S(0)+E(0)+I_u(0)+I_r(0)+R(0)<\frac{\mathrm{\Delta }}{\mu }\hfill \end{array}\le {\Upsilon }_1.$$ (6)

Where

$${\Upsilon }_1:=\sup \{S(0)+E(0)+I_u(0)+I_r(0)+R(0),\frac{\mathrm{\Delta }}{\mu }\}.$$

Substituting (6) into (5) leads to that

$$\mathcal{L}U\le \mathrm{\Delta }+5\mu +\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}+\beta (v_1+v_2){\Upsilon }_1+\underset{\delta \in \mathbb{R}}{\sup }\{-{\rho }_1{\delta }^2+|\delta |+{\rho }_1\overline{\delta }\delta \}:={\Upsilon }_2.$$ (7)

In this case, ${\Upsilon }_2$ represents a positive constant which is independent of the variables $S,E,I_u,I_r,R$ and δ.

Consequently, by inetegrating both sides of equation (4) from 0 to ${\varrho }_j\wedge T$ for any $j\ge j_1$, and then taking the mathematical expectations lead to

$$0\le \mathit{E}U(S({\varrho }_j\wedge T),E({\varrho }_j\wedge T),I_u({\varrho }_j\wedge T),I_r({\varrho }_j\wedge T),R({\varrho }_j\wedge T),\delta ({\varrho }_j\wedge T))=\mathit{E}U(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))+\mathit{E}\underset{0}{\overset{{\varrho }_j\wedge T}{\int }}\mathcal{L}U(S(\xi ),E(\xi ),I_u(\xi ),I_r(\xi ),R(\xi ),\delta (\xi ))d\xi \le \mathit{E}U(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))+{\Upsilon }_{2}T.$$ (8)

Similarly, based on (3), it can be deduced that for all $\zeta \in {\mathrm{\Pi }}_j$, at least one of the variables $S,E,I_u,I_r,R$ and δ must be either $\frac{1}{j}$ or j, ensuring that $U(S({\varrho }_j,\zeta ),E({\varrho }_j,\zeta ),I_u({\varrho }_j,\zeta ),I_r({\varrho }_j,\zeta ),R({\varrho }_j,\zeta ),\delta ({\varrho }_j,\zeta ))$ will not be less than

$$(j-1-\ln j)\wedge \frac{{\ln }^{2}j}{2}\text{ or }(\frac{1}{j}-1+\ln j)\wedge \frac{{\ln }^{2}j}{2}.$$

Based on (3) and (8), we have

$$\mathbb{E}U(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))+{\Upsilon }_{2}T\ge \mathbb{E}U(S({\varrho }_j\wedge T),E({\varrho }_j\wedge T),I_u({\varrho }_j\wedge T),I_r({\varrho }_j\wedge T),R({\varrho }_j\wedge T),\delta ({\varrho }_j\wedge T))\ge \mathbb{E}\left[{\mathbb{1}}_{{\mathrm{\Pi }}_j(\zeta )}U(S({\varrho }_j\wedge T),E({\varrho }_j\wedge T),I_u({\varrho }_j\wedge T),I_r({\varrho }_j\wedge T),R({\varrho }_j\wedge T),\delta ({\varrho }_j\wedge T))\right]\ge \mathbf{P}({\mathrm{\Pi }}_j(\zeta ))U(S({\varrho }_j,\zeta ),E({\varrho }_j,\zeta ),I_u({\varrho }_j,\zeta ),I_r({\varrho }_j,\zeta ),R({\varrho }_j,\zeta ),\delta ({\varrho }_j,\zeta ))\ge \epsilon [(j-1-\ln j)\wedge (\frac{1}{j}-1+\ln j)\wedge \frac{{\ln }^{2}j}{2}].$$ (9)

Considering the unlimited nature of j, as j approaches positive infinity, a contradiction appears.

$$+\infty <\mathbb{E}U(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))+{\Upsilon }_{2}T=+\infty .$$

That is to say ${\varrho }_{\infty }=\infty$ a.s. The demonstration is finished.

Remark 2.1

From the conditions provided in the proof of Theorem 2.1, we can deduce that if $S(0)+E(0)+I_u(0)+I_r(0)+R(0)<\frac{\mathrm{\Delta }}{\mu }$

$$\Sigma =\{(S,E,I_u,I_r,R,\delta )\in {\mathbb{R}}_{+}^5\times \mathbb{R},0\le S+E+I_u+I_r+R\le \frac{\mathrm{\Delta }}{\mu }\}$$

is positively invariant for system (2).

3. Ergodic stationary distribution

In the present section, our primary focus is on establishing adequate requirements for the existence of a stationary ergodic distribution, which, in turn, indicates the significant persistence of the susceptible population, exposed individuals, undetected infected individuals, and detected infected individuals. To achieve this objective, we introduce the following theorem.

Let us consider a b-dimensions nonlinear stochastic differential equation (SDE):

$$dV(t)=h_1(V(t))dt+h_2(V(t))dB(t).$$ (10)

With the initial value $V(0)\in {\mathbb{R}}^b$, where $B(t)$ is a b-dimensional Brownian motion defined on the complete probability space $(\mathrm{\Omega },\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbf{P})$. Moreover, $h_1:{\mathbb{R}}^b\to {\mathbb{R}}^b$ and $h_2:{\mathbb{R}}^b\to {\mathbb{R}}^{b\times n}$ are Borel measurable.

The following lemma is useful to prove the next theorem.

Lemma 3.1

(See[14], Theorem 2.2) Assume the presence of a bounded closed domain$\mathbf{A}\subset {\mathbb{R}}^b$with a regular boundary Λ. For any initial value$V(0)\in {\mathbb{R}}^b$, if

$$\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbf{P}(s,V(s),\mathbf{A})ds>0\mathit{\text{a.s.}}$$

Where$P(s,V(s),.)$signifies the transition probability of$V(t)$, then a solution exists for system(10)that possesses the Feller property. Moreover, system(10)accommodates at least one stationary distribution$\mathrm{\Theta }(.)$on${\mathbb{R}}^b$.

Theorem 3.1

Let ${\mathcal{R}}_0^s=\frac{S_0}{(\sigma +\mu )}(\frac{\sigma \beta v_1(1-\rho )}{(\overline{\delta }+{\gamma }_{I_u}+\mu +d_1)}+\frac{\sigma \beta {\nu }_2\rho }{({\gamma }_{I_r}+\mu +d_2)}+\frac{\sigma \beta v_2(1-\rho ){\left(\frac{1}{\sqrt{\pi }}{\int }_{-\frac{\overline{\delta }\sqrt{{\rho }_1}}{{\sigma }_1}}^{\infty }{(\frac{{\sigma }_1}{\sqrt{{\rho }_1}}y+\overline{\delta })}^{\frac{1}{4}}{e}^{-y^2}dy\right)}^4}{(\overline{\delta }+{\gamma }_{I_u}+\mu +d_1)({\gamma }_{I_r}+\mu +d_2)})-(\frac{\sigma \beta v_1(1-\rho )\mathrm{\Delta }}{\mu {(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})}^2}+\frac{\sigma \beta v_2(1-\rho )\mathrm{\Delta }{\left(\frac{1}{\sqrt{\pi }}{\int }_{-\frac{\overline{\delta }\sqrt{{\rho }_1}}{{\sigma }_1}}^{\infty }{(\frac{{\sigma }_1}{\sqrt{{\rho }_1}}y+\overline{\delta })}^{\frac{1}{4}}{e}^{-y^2}dy\right)}^4}{\mu {(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})}^2(\mu +d_2+{\gamma }_{I_r})})\frac{{\sigma }_1}{2\sqrt{\pi {\rho }_1}(\sigma +\mu )}>1$ . Suppose the initial values $(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))\in {\mathbb{R}}_{+}^5\times \mathbb{R}$ then, the solution $(S(t),E(t),I_u(t),I_r(t),R(t),\delta (t))$ of system (2) possesses a single stationary distribution $\mathrm{\Theta }(.)$ with the ergodic property.

Proof 3.1

Establish the Lyapunov function in the following manner:

$$\overline{\mathcal{W}}(S,E,I_u,I_r,R,\delta )=\tilde{N}{\mathcal{W}}_0(S,E,I_u,I_r,R)+{\mathcal{W}}_1(S,E,I_u,I_r)+{\mathcal{W}}_2(S,E,I_u,I_r,R)+W_3(\delta )$$

Where

$${\mathcal{W}}_0(S,E,I_u,I_r,R,\delta )=-2\ln E-(a_1+a_2+a_3)\ln S-(a_4+a_5)\ln I_u-(a_6+a_7)\ln I_r+(a_1+a_2+a_3)\beta R,{\mathcal{W}}_1(S,E,I_u,I_r)=-\ln S-\ln E-\ln I_u-\ln I_r,{\mathcal{W}}_2(S,E,I_u,I_r,R)=-\ln (\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R),{\mathcal{W}}_3(\delta )=\frac{{\delta }^2}{2}.$$

The positive constants $a_1$, $a_2$, $a_3$, $a_4$, $a_5$, $a_6$ and $a_7$ will be determined later, while $\tilde{N}$ is a suitably large positive constant satisfying the given condition

$$-\tilde{N}(\sigma +\mu )({\mathcal{R}}_0^s-1)+{\Upsilon }_3\le -2$$ (11)

and

$${\Upsilon }_3:=\underset{\delta \in \mathbb{R}}{\sup }\{-\frac{{\rho }_1}{2}{\delta }^2+|\delta |+{\rho }_1\overline{\delta }\delta \}+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_2+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}<\infty .$$ (12)

Indeed, $\overline{\mathcal{W}}(S,E,I_u,I_r,R,\delta )$ exhibits continuity, conforming to

$$\underset{m\to \infty ,(S,E,I_u,I_r,R,\delta )\in \Sigma ﹨D_m}{\lim \inf }\overline{\mathcal{W}}(S,E,I_u,I_r,R,\delta )=+\infty .$$

Consequently, a non-negative $C^2$-function $\mathcal{W}(S,E,I_u,I_r,R,\delta )$ is provided as follows

$$\mathcal{W}(S,E,I_u,I_r,R,\delta )=\overline{\mathcal{W}}(S,E,I_u,I_r,R,\delta )-\overline{\mathcal{W}}(S_0,E_0,I_{u_0},I_{r_0},R_0,{\delta }_0).$$

Where $(S_0,E_0,I_{u_0},I_{r_0},R_0,{\delta }_0)\in \Sigma$ is the minimum point of $\overline{\mathcal{W}}(S,E,I_u,I_r,R,\delta )$.

By Applying Itô's formula [35] to ${\mathcal{W}}_0$ and the arithmetic-geometric men inequality

$$\frac{b_1+b_2+...+b_n}{n}\ge {(b_1{b}_2...b_n)}^{\frac{1}{n}}\text{ For any }{b}_n>0\text{and }n\in \mathbb{N},$$

we obtain

$$\mathcal{L}{\mathcal{W}}_0=-(\frac{a_1+a_2+a_3}{S})(\mathrm{\Delta }-\beta (v_1{I}_u+v_2{I}_r)S-\mu S)-\frac{2}{E}(\beta (v_1{I}_u+v_2{I}_r)S-(\sigma +\mu )E)-(\frac{a_4+a_5}{I_u})(\sigma (1-\rho )E-(\mu +d_1+\max \{\delta (t),0\}+{\gamma }_{I_u})I_u)(\frac{a_6+a_7}{I_r})(\sigma \rho E+\max \{\delta (t),0\}{I}_u-(\mu +d_2+{\gamma }_{I_r})I_r)-(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r-\mu R)\le (-\frac{a_1\mathrm{\Delta }}{S}-\frac{a_4\sigma (1-\rho )E}{I_u}-\frac{\beta v_1{I}_{u}S}{E})+a_1\mu +a_4(\mu +d_1+\max \{\delta (t),0\}+{\gamma }_{I_u})+(-\frac{a_2\mathrm{\Delta }}{S}-\frac{a_6\sigma \rho E}{I_r}-\frac{\beta v_2{I}_{r}S}{E})+a_2\mu +a_6(\mu +d_2+{\gamma }_{I_r})+(-\frac{a_3\mathrm{\Delta }}{S}-\frac{a_5\sigma (1-\rho )E}{I_u}-\frac{a_7\max \{\delta ,0\}{I}_u}{I_r}-\frac{\beta v_2{I}_{r}S}{E})+a_3\mu +a_5(\mu +d_1+\max \{\delta (t),0\}+{\gamma }_{I_u})+a_7(\mu +d_2+{\gamma }_{I_r})+(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+2(\sigma +\mu )\le -3\sqrt[3]{a_1{a}_4\sigma \beta v_1(1-\rho )\mathrm{\Delta }}+a_1\mu +a_4(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})-3\sqrt[3]{a_2{a}_6\sigma \beta v_2\rho \mathrm{\Delta }}+a_2\mu +a_6(\mu +d_2+{\gamma }_{I_r})-4\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }\tilde{\delta }}+a_3\mu +a_5(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})+a_7(\mu +d_2+{\gamma }_{I_r})+(a_4+a_5)A(t)\vee 0+2(\sigma +\mu )+(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r),$$ (13)

with

$$\tilde{\delta }=\max \{\delta (t),0\}\text{and}A(t)=\delta (t)-\overline{\delta }.$$

Concerning the equation corresponding to the sixth position in system (2), that is

$$d\delta (t)={\rho }_1[\overline{\delta }-\delta (t)]dt+{\sigma }_{1}dB(t).$$

Based on the references [11], [31], [48], [51] it can be inferred that the process $\delta (t)$ exhibits the ergodic property and it is expected to undergo weak convergence towards the invariant density

$$f(y)=\frac{\sqrt{{\rho }_1}}{\sqrt{\pi }{\sigma }_1}{e}^{-\frac{{\rho }_1{(y-\overline{\delta })}^2}{{\sigma }_1^2}},y\in \mathbb{R}.$$

Having incorporated the ergodic theorem [30], the aforementioned leads us to the following conclusion

$$\underset{-\infty }{\overset{\infty }{\int }}{(y\vee 0)}^{\frac{1}{4}}f(y)dy=\underset{0}{\overset{\infty }{\int }}{y}^{\frac{1}{4}}f(y)dy=\underset{0}{\overset{\infty }{\int }}{y}^{\frac{1}{4}}\frac{\sqrt{{\rho }_1}}{\sqrt{\pi }{\sigma }_1}{e}^{-\frac{{\rho }_1{(y-\overline{\delta })}^2}{{\sigma }_1^2}}dy=\frac{1}{\sqrt{\pi }}\underset{-\frac{\overline{\delta }\sqrt{{\rho }_1}}{{\sigma }_1}}{\overset{\infty }{\int }}{(\frac{{\sigma }_1}{\sqrt{{\rho }_1}}y+\overline{\delta })}^{\frac{1}{4}}{e}^{-y^2}dy.$$ (14)

Likewise, in the case of the stochastic differential equation

$$dA(t)={\rho }_{1}A(t)dt+{\sigma }_{1}dB(t).$$

The ergodic property of $A(t)$ and its eventual weak convergence to the invariant density can be readily derived

$$g(y)=\frac{\sqrt{{\rho }_1}}{\sqrt{\pi }{\sigma }_1}{e}^{-\frac{{\rho }_1{y}^2}{{\sigma }_1^2}},y\in \mathbb{R}.$$

Drawing upon the ergodic theorem [30], we arrive at the following conclusion

$$\underset{-\infty }{\overset{\infty }{\int }}(y\vee 0)g(y)dy=\underset{0}{\overset{\infty }{\int }}yg(y)dy=\underset{0}{\overset{\infty }{\int }}y\frac{\sqrt{{\rho }_1}}{\sqrt{\pi }{\sigma }_1}{e}^{-\frac{{\rho }_1{y}^2}{{\sigma }_1^2}}dy=\frac{{\sigma }_1}{2\sqrt{\pi {\rho }_1}}.$$ (15)

Substituting (14) and (15) into (13) leads to that

$$\mathcal{L}{\mathcal{W}}_0\le -3\sqrt[3]{a_1{a}_4\sigma \beta v_1(1-\rho )\mathrm{\Delta }}+a_1\mu +a_4(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})-3\sqrt[3]{a_2{a}_6\sigma \beta v_2\rho \mathrm{\Delta }}+a_2\mu +a_6(\mu +d_2+{\gamma }_{I_r})-4\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }\hat{\delta }}+(4\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }\hat{\delta }}-4\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }\tilde{\delta }})+a_3\mu +a_5(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})+a_7(\mu +d_2+{\gamma }_{I_r})+2(\sigma +\mu )+(a_4+a_5)\frac{{\sigma }_1}{2\sqrt{\pi {\rho }_1}}+(a_4+a_5)(A(t)\vee 0-\underset{0}{\overset{\infty }{\int }}yg(y)dy)+(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r).$$ (16)

Where

$$\hat{\delta }={(\underset{-\infty }{\overset{\infty }{\int }}{(y\vee 0)}^{\frac{1}{4}}f(y)dy)}^4={\left(\frac{1}{\sqrt{\pi }}\underset{-\frac{\delta \sqrt{{\rho }_1}}{{\sigma }_1}}{\overset{\infty }{\int }}{(\frac{{\sigma }_1}{\sqrt{{\rho }_1}}y+\overline{\delta })}^{\frac{1}{4}}{e}^{-y^2}dy\right)}^4.$$

Let

$$\begin{gathered} a_1\mu =a_4(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})=\frac{\sigma \beta v_1(1-\rho )\mathrm{\Delta }}{\mu (\mu +d_1+\overline{\delta }+{\gamma }_{I_u})},a_2\mu =a_6(\mu +d_2+{\gamma }_{I_r})=\frac{\sigma \beta v_2\rho \mathrm{\Delta }}{\mu (\mu +d_2+{\gamma }_{I_r})} \\ {a}_3\mu =a_5(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})=a_7(\mu +d_2+{\gamma }_{I_r})=\frac{\sigma \beta v_2(1-\rho )\mathrm{\Delta }\hat{\delta }}{\mu (\mu +d_1+\overline{\delta }+{\gamma }_{I_u})(\mu +d_2+{\gamma }_{I_r})}. \end{gathered}$$

Consequently, we acquire

$$\begin{gathered} a_1=\frac{\sigma \beta v_1(1-\rho )\mathrm{\Delta }}{{\mu }^2(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})},a_4=\frac{\sigma \beta v_1(1-\rho )\mathrm{\Delta }}{\mu {(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})}^2} \\ {a}_2=\frac{\sigma \beta v_2\rho \mathrm{\Delta }}{{\mu }^2(\mu +d_2+{\gamma }_{I_r})},a_6=\frac{\sigma \beta v_2\rho \mathrm{\Delta }}{\mu {(\mu +d_2+{\gamma }_{I_r})}^2} \\ {a}_3=\frac{\sigma \beta v_2(1-\rho )\mathrm{\Delta }\hat{\delta }}{{\mu }^2(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})(\mu +d_2+{\gamma }_{I_r})},a_5=\frac{\sigma \beta v_2(1-\rho )\mathrm{\Delta }\hat{\delta }}{\mu {(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})}^2(\mu +d_2+{\gamma }_{I_r})},a_7=\frac{\sigma \beta v_2(1-\rho )\mathrm{\Delta }\hat{\delta }}{\mu (\mu +d_1+\overline{\delta }+{\gamma }_{I_u}){(\mu +d_2+{\gamma }_{I_r})}^2}. \end{gathered}$$

Consequently, as a result

$$\mathcal{L}{\mathcal{W}}_0\le -\frac{\sigma \beta v_1(1-\rho )\mathrm{\Delta }}{\mu (\mu +d_1+\overline{\delta }+{\gamma }_{I_u})}-\frac{\sigma \beta v_2\rho \mathrm{\Delta }}{\mu (\mu +d_2+{\gamma }_{I_r})}-\frac{\sigma \beta v_2(1-\rho )\mathrm{\Delta }\hat{\delta }}{\mu (\mu +d_1+\overline{\delta }+{\gamma }_{I_u})(\mu +d_2+{\gamma }_{I_r})}+2(\sigma +\mu )+(a_4+a_5)\frac{{\sigma }_1}{2\sqrt{\pi {\rho }_1}}+4\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }}(\sqrt[4]{\hat{\delta }}-\sqrt[4]{\tilde{\delta }})+(a_4+a_5)(A(t)\vee 0-\underset{0}{\overset{\infty }{\int }}yg(y)dy)+(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)\le -(\sigma +\mu )({\mathcal{R}}_0^s-1)+\sigma +\mu +(a_4+a_5)(A(t)\vee 0-\underset{0}{\overset{\infty }{\int }}yg(y)dy)+(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r).$$ (17)

Where

$${\mathcal{R}}_0^s=\frac{S_0}{(\sigma +\mu )}(\frac{\sigma \beta v_1(1-\rho )}{(\overline{\delta }+{\gamma }_{I_u}+\mu +d_1)}+\frac{\sigma \beta {\nu }_2\rho }{({\gamma }_{I_r}+\mu +d_2)}+\frac{\sigma \beta v_2(1-\rho )\hat{\delta }}{(\overline{\delta }+{\gamma }_{I_u}+\mu +d_1)({\gamma }_{I_r}+\mu +d_2)})-(a_1+a_5)\frac{{\sigma }_1}{2\sqrt{\pi {\rho }_1}(\sigma +\mu )}.$$

Analogously, employing Itô's formula [35] to ${\mathcal{W}}_1$, ${\mathcal{W}}_2$, and ${\mathcal{W}}_3$, respectively, yields the following results

$$\mathcal{L}{\mathcal{W}}_1=-\frac{\mathrm{\Delta }}{S}+\beta (v_1{I}_u+v_2{I}_r)+\mu -\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}+\sigma +\mu -\frac{\sigma (1-\rho )E}{I_u}+(\mu +d_1+\max \{\delta (t),0\}+{\gamma }_{I_u})-\frac{\sigma \rho E}{I_r}-\frac{\max \{\delta (t),0\}{I}_u}{I_r}+(\mu +d_2+{\gamma }_{I_r})\le -\frac{\mathrm{\Delta }}{S}-\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+|\delta |+4\mu +\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}$$ (18)

$$\mathcal{L}{\mathcal{W}}_2=\frac{1}{\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R}(\mathrm{\Delta }-\mu S-\mu I_u-\mu I_r-d_1{I}_u-d_2{I}_r-\mu R)\le \mu -\frac{d_1{I}_u+d_2{I}_r}{\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R}$$ (19)

and

$$\mathcal{L}{\mathcal{W}}_3={\rho }_1\overline{\delta }\delta -{\rho }_1{\delta }^2+\frac{{\sigma }_1^2}{2}.$$ (20)

By (17), (18), (19) and (20), we get

$$\mathcal{L}\mathcal{W}\le -\tilde{N}(\sigma +\mu )({\mathcal{R}}_0^s-1)+4\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }}(\sqrt[4]{\hat{\delta }}-\sqrt[4]{\tilde{\delta }})+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+\tilde{N}(a_4+a_5)(A(t)\vee 0-\underset{0}{\overset{\infty }{\int }}yg(y)dy)-\frac{\mathrm{\Delta }}{S}-\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}-\frac{d_1{I}_u+d_2{I}_r}{\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R}+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2-\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}:=\mathbf{H}(S,E,I_u,I_r,R;\delta )+4\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }}(\sqrt[4]{\hat{\delta }}-\sqrt[4]{\tilde{\delta }})+\tilde{N}(a_4+a_5)(A(t)\vee 0-\underset{0}{\overset{\infty }{\int }}yg(y)dy).$$ (21)

Where

$$\mathbf{H}(S,E,I_u,I_r,R;\delta )=-\tilde{N}(\sigma +\mu )({\mathcal{R}}_0^s-1)+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)-\frac{\mathrm{\Delta }}{S}-\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}-\frac{d_1{I}_u+d_2{I}_r}{\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R}+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2-\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}.$$ (22)

Following that, we define a suitable bounded subset $\hat{E}$ is described by

$$\hat{E}=\{{(S,E,I_u,I_r,R)}^T\in \Sigma ,S\ge \epsilon ,I_u\ge \epsilon ,I_r\ge \epsilon ,E\ge {\epsilon }^3,S+E+I_u+I_r+R\le \frac{\mathrm{\Delta }}{\mu }-{\epsilon }^2,|\delta |\le \frac{1}{\epsilon }\}.$$

Let ε be a sufficiently small positive constant that fulfills the following conditions.

$$-\frac{\mathrm{\Delta }}{\epsilon }+{\Upsilon }_4\le -1$$ (23)

$$\epsilon \le \frac{1}{\tilde{N}\beta (a_1+a_2+a_3)(v_1+v_2+{\gamma }_{I_u}+{\gamma }_{I_r})}$$ (24)

$$-\frac{\beta (v_1+v_2)}{\epsilon }+{\Upsilon }_4\le -1$$ (25)

$$-\frac{d_1+d_2}{\epsilon }+{\Upsilon }_4\le -1$$ (26)

$$-\frac{{\rho }_1}{2{\epsilon }^2}+{\Upsilon }_4\le -1.$$ (27)

Where

$${\Upsilon }_4:=\underset{\delta \in \mathbb{R}}{\sup }\{-\frac{{\rho }_1}{2}{\delta }^2+|\delta |+{\rho }_1\overline{\delta }\delta \}+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}.$$ (28)

We can then partition the set $\Sigma ﹨\hat{E}$ into the following five subsets ${\hat{E}}_i^c,i=1,2,3,4,5$, where

$${\hat{E}}_1^c=\{{(S,E,I_u,I_r,R,\delta )}^T\in \Sigma ,S<\epsilon \}$$

$${\hat{E}}_2^c=\{{(S,E,I_u,I_r,R,\delta )}^T\in \Sigma ,I_u<\epsilon ,I_r<\epsilon \}$$

$${\hat{E}}_3^c=\{{(S,E,I_u,I_r,R,\delta )}^T\in \Sigma ,E<{\epsilon }^3,I_u\ge \epsilon ,I_r\ge \epsilon \}$$

$${\hat{E}}_4^c=\{{(S,E,I_u,I_r,R,\delta )}^T\in \Sigma ,S+E+I_u+I_r+R>\frac{\mathrm{\Delta }}{\mu }-{\epsilon }^2,I_u\ge \epsilon ,I_r\ge \epsilon \}$$

$${\hat{E}}_5^c=\{{(S,E,I_u,I_r,R,\delta )}^T\in \Sigma ,|\delta |>\frac{1}{\epsilon }\}.$$

It is then obvious that,

$$\Sigma ﹨\hat{E}=\bigcup _{i=1}^5{\hat{E}}_i^c.$$

We shall now proceed to establish the proof that $\mathbf{H}(S,E,I_u,I_r,R;\delta )\le -1$ on ${\hat{E}}^c$.

Put differently, we must verify its fulfillment across the aforementioned five regions

• •
  Case 1. For any ${(S,E,I_u,I_r,R,\delta )}^T\in {\hat{E}}_1^c$, according to (22), we get

  $$\mathbf{H}(S,E,I_u,I_r,R,\delta )\le -\frac{\mathrm{\Delta }}{S}+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{\mathrm{\Delta }}{S}+\tilde{N}(a_1+a_2+a_3)\beta (v_1+v_2)\frac{\mathrm{\Delta }}{\mu }+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}+{\gamma }_{I_r})\frac{\mathrm{\Delta }}{\mu }+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{\mathrm{\Delta }}{\epsilon }+{\Upsilon }_4\le -1.$$ (29)

  Which follows from (23) and (28)
• •
  Case 2. For any ${(S,E,I_u,I_r,R,\delta )}^T\in {\hat{E}}_2^c$, by (22), we obtain

  $$\mathbf{H}(S,E,I_u,I_r,R,\delta )\le -\tilde{N}(\sigma +\mu )({\mathcal{R}}_0^s-1)+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\tilde{N}(\sigma +\mu )({\mathcal{R}}_0^s-1)+{\Upsilon }_3+\tilde{N}\beta (a_1+a_2+a_3)(v_1+v_2+{\gamma }_{I_u}+{\gamma }_{I_r})\epsilon \le -1.$$ (30)

  Which follows from (11) and (24).
• •
  Case 3. For any ${(S,E,I_u,I_r,R,\delta )}^T\in {\hat{E}}_3^c$, from (22) it follows that

  $$\mathbf{H}(S,E,I_u,I_r,R,\delta )\le -\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}+\tilde{N}(a_1+a_2+a_3)\beta (v_1+v_2)\frac{\mathrm{\Delta }}{\mu }+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}+{\gamma }_{I_r})\frac{\mathrm{\Delta }}{\mu }+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{(v_1+v_2){\epsilon }^2}{{\epsilon }^3}+{\Upsilon }_4\le -\frac{(v_1+v_2)}{\epsilon }+{\Upsilon }_4\le -1.$$ (31)

  Which results from (25).
• •
  Case 4. For any ${(S,E,I_u,I_r,R,\delta )}^T\in {\hat{E}}_4^c$, in view of (22), we obtain

  $$\mathbf{H}(S,E,I_u,I_r,R,\delta )\le -\frac{d_1{I}_u+d_2{I}_r}{\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R}+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{d_1{I}_u+d_2{I}_r}{\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R}+\tilde{N}(a_1+a_2+a_3)\beta (v_1+v_2)\frac{\mathrm{\Delta }}{\mu }+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}+{\gamma }_{I_r})\frac{\mathrm{\Delta }}{\mu }+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{(d_1+d_2)\epsilon }{{\epsilon }^2}+{\Upsilon }_4\le -\frac{(d_1+d_2)}{\epsilon }+{\Upsilon }_4\le -1.$$ (32)

  Which results from (26).
• •
  Case 5. For any ${(S,E,I_u,I_r,R,\delta )}^T\in {\hat{E}}_5^c$, in view of (22), we have

  $$\mathbf{H}(S,E,I_u,I_r,R,\delta )\le -\frac{{\rho }_1}{2}{\delta }^2+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{{\rho }_1}{2}{\delta }^2+\tilde{N}(a_1+a_2+a_3)\beta (v_1+v_2)\frac{\mathrm{\Delta }}{\mu }+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}+{\gamma }_{I_r})\frac{\mathrm{\Delta }}{\mu }+{\rho }_1\overline{\delta }\delta -\frac{{\rho }_1}{2}{\delta }^2+|\delta |+\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\le -\frac{{\rho }_1}{2{\epsilon }^2}+{\Upsilon }_4\le -1.$$ (33)

  Which follows from (27).

Drawing from the evidence presented in inequalities (29), (30), (31), (32) and (33), a straightforward conclusion can be reached, establishing the existence of a sufficiently small ε that satisfies The following condition

$$\mathbf{H}(S,E,I_u,I_r,R,\delta )\le -1\text{for any}{(S,E,I_u,I_r,R,\delta )}^T\in {\hat{E}}^c.$$ (34)

So we have

$$\mathbf{H}(S,E,I_u,I_r,R,\delta )\le {\Upsilon }_5<\infty \text{for any}{(S,E,I_u,I_r,R,\delta )}^T\in {\mathbb{R}}_{+}^5\times \mathbb{R}.$$ (35)

Where

$$\begin{gathered} {\Upsilon }_5:=\underset{(S,E,I_u,I_r,R,\delta )\in {\mathbb{R}}_{+}^5\times \mathbb{R}}{\sup }\{-\tilde{N}(\sigma +\mu )({\mathcal{R}}_0^s-1)+\tilde{N}(a_1+a_2+a_3)\beta (v_1{I}_u+v_2{I}_r)+\tilde{N}(a_1+a_2+a_3)\beta ({\gamma }_{I_u}{I}_u+{\gamma }_{I_r}{I}_r)-\frac{\mathrm{\Delta }}{S}-\frac{\beta (v_1{I}_u+v_2{I}_r)S}{E}-\frac{d_1{I}_u+d_2{I}_r}{\frac{\mathrm{\Delta }}{\mu }-S-E-I_u-I_r-R} \\ +{\rho }_1\overline{\delta }\delta \frac{{\rho }_1}{2}{\delta }^2-\frac{{\rho }_1}{2}{\delta }^2+\delta +\frac{\beta \mathrm{\Delta }(v_1+v_2)}{\mu }+6\mu +2\sigma +d_1+d_2+{\gamma }_{I_u}+{\gamma }_{I_r}+\frac{{\sigma }_1^2}{2}\}. \end{gathered}$$

By integrating equation (21) over the interval $[0,t]$ for any initial values $(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))\in \Sigma$ and subsequently calculating the mathematical expectation, the following expression is obtained

$$0\le \frac{\mathbb{E}\mathcal{W}(S(t),E(t),I_u(t),I_r(t),R(t),\delta (t))}{t}=\frac{\mathbb{E}\mathcal{W}(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))}{t}+\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbb{E}(\mathcal{L}\mathcal{W}(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s)))ds\le \frac{\mathbb{E}\mathcal{W}(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))}{t}+\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbb{E}(\mathbf{H}(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s)))ds+4\tilde{N}\sqrt[4]{a_3{a}_5{a}_7\sigma \beta v_2(1-\rho )\mathrm{\Delta }}\mathbb{E}[\underset{-\infty }{\overset{\infty }{\int }}{(y\vee 0)}^{\frac{1}{4}}f(y)dy-\frac{1}{t}\underset{0}{\overset{t}{\int }}{(\delta (s)\vee 0)}^{\frac{1}{4}}ds]+\tilde{N}\mathbb{E}[\frac{1}{t}\underset{0}{\overset{t}{\int }}(A(s)\vee 0)ds-\underset{0}{\overset{\infty }{\int }}yg(y)dy].$$ (36)

Utilizing the ergodic properties of both $\delta (t)$ and $A(t)$, along with the strong law of large numbers as demonstrated in [35], we derive the following

$$\underset{t\to \infty }{\lim }\mathbb{E}[\underset{-\infty }{\overset{\infty }{\int }}{(y\vee 0)}^{\frac{1}{4}}f(y)dy-\frac{1}{t}\underset{0}{\overset{t}{\int }}{(\delta (s)\vee 0)}^{\frac{1}{4}}ds]=0\text{a.s.}$$

and

$$\underset{t\to \infty }{\lim }\mathbb{E}[\frac{1}{t}\underset{0}{\overset{t}{\int }}(A(s)\vee 0)ds-\underset{0}{\overset{\infty }{\int }}yg(y)dy]=0\text{a.s.}$$

Therefore, by applying the inferior limit to both sides of (36), we deduce the subsequent outcome

$$0\le \underset{t\to \infty }{\lim \inf }\frac{\mathbb{E}\mathcal{W}(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))}{t}+\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbb{E}(\mathbf{H}(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s)))ds=\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbb{E}(\mathbf{H}(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s)))ds\text{a.s.}$$ (37)

Furthermore, in accordance with to (34) and (35), it follows that we obtain

$$\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbb{E}(\mathbf{H}(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s)))ds=\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbb{E}(\mathbf{H}(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))){\mathbf{1}}_{{(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))}^T\in \hat{E}}ds+\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbb{E}(\mathbf{H}(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))){\mathbb{1}}_{{(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))}^T\in (\Sigma ﹨\hat{E})}ds\le {\Upsilon }_5\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}{\mathbb{1}}_{{(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))}^T\in \hat{E}}ds-\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}{\mathbb{1}}_{{(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))}^T\in (\Sigma ﹨\hat{E})}ds\le -1+({\Upsilon }_5+1)\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}{\mathbb{1}}_{{(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))}^T\in \hat{E}}ds.$$ (38)

Consequently, from (37) and (38) lead to the conclusion that

$$\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}{\mathbb{1}}_{{(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))}^T\in \hat{E}}ds\ge \frac{1}{{\Upsilon }_5+1}>0\text{a.s.}$$ (39)

Considering the event probability definition and the application of Fatou's lemma [12], [31], [51]. The result (39) is equivalent to

$$\underset{t\to \infty }{\lim \inf }\frac{1}{t}\underset{0}{\overset{t}{\int }}\mathbf{P}(s,S(s),E(s),I_u(s),I_r(s),R(s),\delta (s),\hat{E})ds\ge \frac{1}{{\Upsilon }_5+1}>0\text{a.s.}$$ (40)

Where $\mathbf{P}(s,S(s),E(s),I_u(s),I_r(s),R(s),\delta (s),\hat{E})$ is the transition probability of ${(S(s),E(s),I_u(s),I_r(s),R(s),\delta (s))}^T$ belonging to set $\hat{E}$. Thus, we have fulfilled the conditions of Lemma 3.1 and thus the system (2) has at least one stationary distribution $\mathrm{\Theta }(.)$ on ${\mathbb{R}}_{+}^5\times \mathbb{R}$ which has the Feller property. This completes the proof.

4. Extinction of the disease

Within this portion, we will set forth the sufficient conditions for the complete eradication of the disease.

Theorem 4.1

Consider the solution$(S(t),E(t),I_u(t),I_r(t),R(t),\delta (t))$to system(2)with initial value$(S(0),E(0),I_u(0),I_r(0),R(0),\delta (0))\in {\mathbb{R}}_{+}^5\times \mathbb{R}$. If

$${\mathcal{R}}_0^{EX}=\sqrt[3]{\frac{{\mathcal{R}}_3}{2}+\sqrt{{\left(\frac{{\mathcal{R}}_3}{2}\right)}^2+{\left(\frac{{\mathcal{R}}_1+{\mathcal{R}}_2}{3}\right)}^3}}+\sqrt[3]{\frac{{\mathcal{R}}_3}{2}-\sqrt{{\left(\frac{{\mathcal{R}}_3}{2}\right)}^2+{\left(\frac{{\mathcal{R}}_1+{\mathcal{R}}_2}{3}\right)}^3}}<1$$

and

$$\psi =\min \{\sigma +\mu ,\mu +d_1+\overline{\delta }+{\gamma }_{I_u},\mu +d_2+{\gamma }_{I_r}\}({\mathcal{R}}_0^{EX}-1)+(\frac{v_1(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}^{EX}}{{\mathcal{R}}_0^{EX}(\mu +d_2+{\gamma }_{I_r})S_0{v}_1+\overline{\delta }{S}_0{v}_2}+\frac{(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}_0^{EX}}{S_0})\underset{0}{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}|l-s_0|\mathrm{\Theta }(l,\delta )dld\delta +(\frac{v_2(\mu +d_1\overline{\delta }+{\gamma }_{I_u}){\mathcal{R}}_0^{EX}}{v_1(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}_0^{EX}+\overline{\delta }{v}_2}+1)\frac{{\sigma }_1}{\sqrt{\pi {\rho }_1}}\mathit{\text{is negative}}.$$

Then${\lim }_{t\to \infty }E(t)=0,{\lim }_{t\to \infty }{I}_u(t)=0,{\lim }_{t\to \infty }{I}_r(t)=0$a.s.

Specifically, the disease undergoes exponential extinction with a almost surely.

Proof 4.1

Based on the first equation of system (2), we have:

$$dS(t)\le (\mathrm{\Delta }-\mu S)dt$$

Let the following auxiliary logistical equation be

$$dL(t)=(\mathrm{\Delta }-\mu L)dt.$$ (41)

Assume that $L(t)$ represents the solution of (41) with the initial condition $L(0)=S(0)>0$. Referring to the theorem shown in [25], we obtain $S(t)\le L(t)$, for any $t\ge 0$ a.s.

Furthermore, B it is readily apparent that a three-dimensional matrix possesses a non-negative eigenvector on the left and ${\mathcal{R}}_0^{EX}({\vartheta }_1,{\vartheta }_2,{\vartheta }_3)=({\vartheta }_1,{\vartheta }_2,{\vartheta }_3)B$ and

$$B=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{\beta S_0{v}_1}{\sigma +\mu }\hfill & \hfill \frac{\beta S_0{v}_2}{\sigma +\mu }\hfill \\ \hfill \frac{\sigma (1-\rho )}{\mu +d_1+\overline{\delta }+{\gamma }_{I_u}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{\sigma \rho }{\mu +d_2+{\gamma }_{I_r}}\hfill & \hfill \frac{\overline{\delta }}{\mu +d_2+{\gamma }_{I_r}}\hfill & \hfill 0\hfill \end{array}\right)$$

Define a $C^2$-lyapunov function $\text{Ģ}(E,I_u,I_r)$ by

$$\text{Ģ}(E,I_u,I_r)={\alpha }_{1}E+{\alpha }_2{I}_u+{\alpha }_3{I}_r.$$

Where

$${\alpha }_1=\frac{{\vartheta }_1}{\sigma +\mu },{\alpha }_2=\frac{{\vartheta }_2}{\mu +d_1+\overline{\delta }+{\gamma }_{I_u}},{\alpha }_3=\frac{{\vartheta }_3}{\mu +d_2+{\gamma }_{I_r}}.$$

Which implies

$$\mathcal{L}(\ln \text{Ģ})=\frac{1}{\text{Ģ}}[{\alpha }_1(\beta (v_1{I}_u+v_2{I}_r)S-(\sigma +\mu )E)+{\alpha }_2(\sigma (1-\rho )E-(\mu +d_1+\tilde{\delta }+{\gamma }_{I_u})I_u)+{\alpha }_3(\sigma \rho E+\tilde{\delta }{I}_u-(\mu +d_2+{\gamma }_{I_r})I_r)]=\frac{1}{\text{Ģ}}[{\alpha }_1(\beta (v_1{I}_u+v_2{I}_r)S_0-(\sigma +\mu )E)+{\alpha }_2(\sigma (1-\rho )E-(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})I_u)+{\alpha }_3(\sigma \rho E+\overline{\delta }{I}_u-(\mu +d_2+{\gamma }_{I_r})I_r)]+\frac{{\alpha }_1(\beta (v_1{I}_u+v_2{I}_r)(S-S_0)}{\text{Ģ}}+\frac{{\alpha }_2(\overline{\delta }-\tilde{\delta })I_u}{\text{Ģ}}+\frac{{\alpha }_3(\tilde{\delta }-\overline{\delta })I_u}{\text{Ģ}}\le \frac{1}{\text{Ģ}}[\frac{{\vartheta }_1}{\sigma +\mu }(\beta (v_1{I}_u+v_2{I}_r)S_0-(\sigma +\mu )E)+\frac{{\vartheta }_2}{\mu +d_1+\overline{\delta }+{\gamma }_{I_u}}(\sigma (1-\rho )E-(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})I_u)+\frac{{\vartheta }_3}{\mu +d_2+{\gamma }_{I_r}}(\sigma \rho E+\overline{\delta }{I}_u-(\mu +d_2+{\gamma }_{I_r})I_r)]+\frac{{\alpha }_1(\beta (v_1{I}_u+v_2{I}_r)(L-S_0)}{\text{Ģ}}+\frac{{\alpha }_2|\tilde{\delta }-\overline{\delta }|I_u}{\text{Ģ}}+\frac{{\alpha }_3|\tilde{\delta }-\overline{\delta }|I_u}{\text{Ģ}}\le \frac{1}{\text{Ģ}}({\vartheta }_1,{\vartheta }_2,{\vartheta }_3)(B{(E,I_u,I_r)}^T-{(E,I_u,I_r)}^T)+\frac{{\alpha }_1(\beta (v_1{I}_u+v_2{I}_r)(L-S_0)}{\text{Ģ}}+\frac{({\alpha }_2+{\alpha }_3)|\tilde{\delta }-\overline{\delta }|I_u}{\text{Ģ}}\le \frac{1}{\text{Ģ}}({\mathcal{R}}_0^{EX}-1)({\vartheta }_{1}E+{\vartheta }_2{I}_u+{\vartheta }_3{I}_r)+\frac{{\alpha }_1\beta ({\alpha }_3{v}_1+{\alpha }_2{v}_2)}{{\alpha }_2{\alpha }_3}|L-S_0|+\frac{({\alpha }_2+{\alpha }_3)}{{\alpha }_2}|\tilde{\delta }-\overline{\delta }|\le \frac{1}{\text{Ģ}}({\mathcal{R}}_0^{EX}-1)({\alpha }_1(\sigma +\mu )E+{\alpha }_2(\mu +d_1\overline{\delta }+{\gamma }_{I_u})I_u+{\alpha }_3(\mu +d_2+{\gamma }_{I_r})I_r)+\frac{{\alpha }_1\beta ({\alpha }_3{v}_1+{\alpha }_2{v}_2)}{{\alpha }_2{\alpha }_3}|L-S_0|+\frac{({\alpha }_2+{\alpha }_3)}{{\alpha }_2}|\tilde{\delta }-\overline{\delta }|\le \min \{\sigma +\mu ,\mu +d_1+\overline{\delta }+{\gamma }_{I_u},\mu +d_2+{\gamma }_{I_r}\}({\mathcal{R}}_0^{EX}-1)+{\chi }_1|L-S_0|+{\chi }_2|\tilde{\delta }-\overline{\delta }|.$$ (42)

Where

$${\chi }_1:=\frac{v_1(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}^{EX}}{{\mathcal{R}}^{EX}(\mu +d_2+{\gamma }_{I_r})S_0{v}_1+\overline{\delta }{S}_0{v}_2}+\frac{(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}_0^{EX}}{S_0}$$

$${\chi }_2=\frac{v_2(\mu +d_1\overline{\delta }+{\gamma }_{I_u}){\mathcal{R}}_0^{EX}}{v_1(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}_0^{EX}+\overline{\delta }{v}_2}+1.$$

Upon integrating both sides of (42) over the interval $[0,t]$ and subsequently dividing by t, it follows that

$$\frac{\ln \text{Ģ}(E(t),I_u(t),I_r(t))}{t}\le \frac{\ln \text{Ģ}(E(0),I_u(0),I_r(0))}{t}+\min \{\sigma +\mu ,\mu +d_1+\overline{\delta }+{\gamma }_{I_u},\mu +d_2+{\gamma }_{I_r}\}({\mathcal{R}}_0^{EX}-1)+{\chi }_1\frac{1}{t}\underset{0}{\overset{t}{\int }}|L(s)-S_0|ds+{\chi }_2\frac{1}{t}\underset{0}{\overset{t}{\int }}|\tilde{\delta }(s)-\overline{\delta }|ds.$$ (43)

Considering Theorem 3.1 along with the strong law of large numbers [30], [31], [35], [51], we can conclude that the process $(L(t),\delta (t))$ possesses a distinct stationary distribution $\mathrm{\Theta }(.,.)$ and exhibits the property of ergodicity so

$$\underset{t\to \infty }{\lim }\frac{1}{t}\underset{0}{\overset{t}{\int }}|L(s)-S_0|ds=\underset{0}{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}|l-S_0|\mathrm{\Theta }(l,\delta )dld\delta ,$$ (44)

and

$$\underset{t\to \infty }{\lim }\frac{1}{t}\underset{0}{\overset{t}{\int }}|\tilde{\delta }(s)-\overline{\delta }|ds=\underset{-\infty }{\overset{\infty }{\int }}|\tilde{\delta }(y)-\overline{\delta }|f(y)dy=\frac{{\sigma }_1}{\sqrt{\pi {\rho }_1}}.$$ (45)

Applying the upper limit to both sides of (43) and consolidating it with (44) and (45), we arrive at

$$\underset{t\to \infty }{\lim \sup }\frac{\ln \text{Ģ}(E(t),I_u(t),I_r(t))}{t}\le \min \{\sigma +\mu ,\mu +d_1+\overline{\delta }+{\gamma }_{I_u},\mu +d_2+{\gamma }_{I_r}\}({\mathcal{R}}_0^{EX}-1)+{\chi }_1\underset{0}{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}|l-S_0|\mathrm{\Theta }(l,\delta )dld\delta +{\chi }_2\frac{{\sigma }_1}{\sqrt{\pi {\rho }_1}}:=\psi \mathbf{\text{a.s.}}$$

and if ψ is negative, we can deduce from this:

$$\underset{t\to \infty }{\lim \sup }\frac{\ln E(t)}{t}<0,\underset{t\to \infty }{\lim \sup }\frac{\ln I_u(t)}{t}<0\text{and}\underset{t\to \infty }{\lim \sup }\frac{\ln I_r(t)}{t}<0\mathbf{\text{a.s}}\text{.}$$

This entails that

$$\underset{t\to \infty }{\lim }E(t)=0,\underset{t\to \infty }{\lim }{I}_u(t)=0\text{and}\underset{t\to \infty }{\lim }{I}_r(t)=0\mathbf{\text{a.s}}.$$

This finalizes the theorem's proof.

5. Numerical results

Using the advanced technique outlined by Milstein in reference [22], the discretized equation corresponding to system (2) can be derived

$$\{\begin{array}{c}S[j+1]=S[j]+(\mathrm{\Delta }-\beta (v_1{I}_u[j]+v_2{I}_r[j])S[j]-\mu S[j])\mathrm{\Delta }t,\hfill \\ E[j+1]=E[j]+(\beta (v_1{I}_u[j]+v_2{I}_r[j])S[j]-(\sigma +\mu )E[j])\mathrm{\Delta }t,\hfill \\ I_u[j+1]=I_u[j]+(\sigma (1-\rho )E[j]-(\mu +d_1+\max (\delta [j],0)+{\gamma }_{Iu})I_u[j])\mathrm{\Delta }t,\hfill \\ I_r[j+1]=I_r[j]+(\sigma \rho E[j]+\max (\delta [j],0)I_u[j]-(\mu +d_2+{\gamma }_{Ir})I_r[j])\mathrm{\Delta }t,\hfill \\ R[j+1]=R[j]+({\gamma }_{Iu}{I}_u[j]+{\gamma }_{Ir}{I}_r[j]-\mu R[j])\mathrm{\Delta }t,\hfill \\ \delta [j+1]=\delta [j]+{\rho }_1(\overline{\delta }-\delta [j])\mathrm{\Delta }t+{\sigma }_1\sqrt{\mathrm{\Delta }t}{\iota }_j.\hfill \end{array}$$ (46)

In accordance with the jth iteration of Equation (46), denoted as $(S[j],E[j],I_u[j],I_r[j],R[j],\delta [j])$, where Δt represents the positive time increment, ${\iota }_j$ signifies independent Gaussian random variables adhering to the $N(0,1)$ distribution for $j=1,...,n$. Realistic parameter values are selected from established sources, and the biological parameters are comprehensively listed in Table 2.

Table 2.

Values of parameters of stochastic model (2).

Parameters	values	Source
Δ	0.1	Assumed
μ	0.0399	Assumed
β	0.6594	[44]
ρ	0.2929	[44]
v1	0.3958	[18]
v2	0.4941	[18]
$\overline{\delta }$	0.1	Estimated
d1	0.0290	[44]
d2	0.4897	[44]
σ	0.5732	[18]
${\gamma }_{I_u}$	0.0458	[44]
${\gamma }_{I_r}$	0.0806	[44]

In this section, our primary focus is on confirming the validity of the following two outcomes:

• 1.The condition for ${\mathcal{R}}_0^s>1$ leads to the existence of a distinctive ergodic stationary distribution.
• 2.Model (2) undergoes exponential extinction when ${\mathcal{R}}_0^{EX}<1$ and $\psi <0$.

Example 5.1

Given the values $\beta =0.6594,{\rho }_1=0.1$ and ${\sigma }_1=0.02$, a calculation yields

$${\mathcal{R}}_0^s=\frac{S_0}{(\sigma +\mu )}(\frac{\sigma \beta v_1(1-\rho )}{(\overline{\delta }+{\gamma }_{I_u}+\mu +d_1)}+\frac{\sigma \beta {\nu }_2\rho }{({\gamma }_{I_r}+\mu +d_2)}+\frac{\sigma \beta v_2(1-\rho ){\left(\frac{1}{\sqrt{\pi }}{\int }_{-\frac{\overline{\delta }\sqrt{{\rho }_1}}{{\sigma }_1}}^{\infty }{(\frac{{\sigma }_1}{\sqrt{{\rho }_1}}y+\overline{\delta })}^{\frac{1}{4}}{e}^{-y^2}dy\right)}^4}{(\overline{\delta }+{\gamma }_{I_u}+\mu +d_1)({\gamma }_{I_r}+\mu +d_2)})-(\frac{\sigma \beta v_1(1-\rho )\mathrm{\Delta }}{\mu {(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})}^2}+\frac{\sigma \beta v_2(1-\rho )\mathrm{\Delta }{\left(\frac{1}{\sqrt{\pi }}{\int }_{-\frac{\overline{\delta }\sqrt{{\rho }_1}}{{\sigma }_1}}^{\infty }{(\frac{{\sigma }_1}{\sqrt{{\rho }_1}}y+\overline{\delta })}^{\frac{1}{4}}{e}^{-y^2}dy\right)}^4}{\mu {(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})}^2(\mu +d_2+{\gamma }_{I_r})})\frac{{\sigma }_1}{2\sqrt{\pi {\rho }_1}(\sigma +\mu )}\approx 2.54697>1.$$

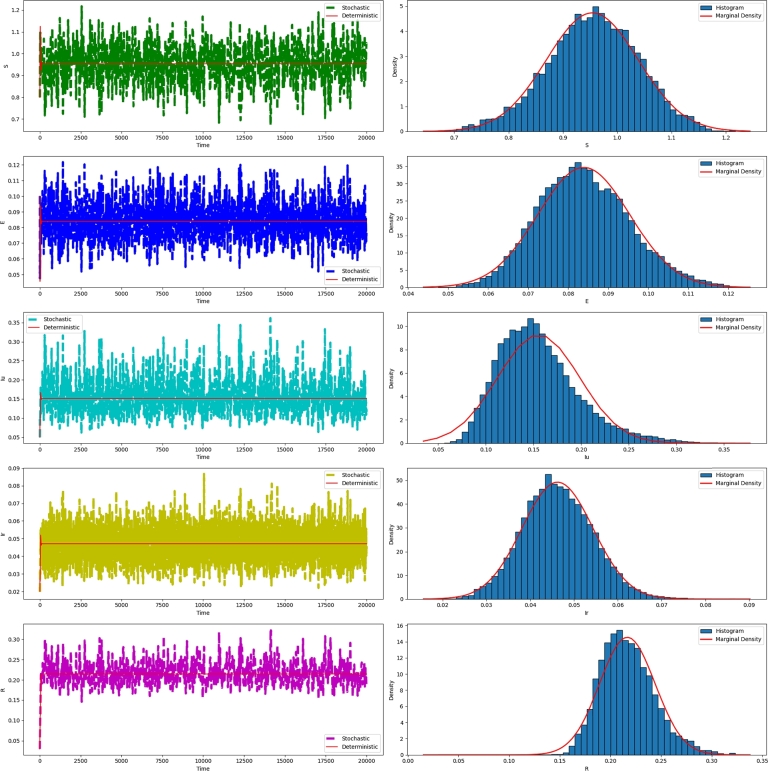
According to Theorem 3.1, we deduce the existence of a singular stationary distribution $\mathrm{\Theta }(.)$ with ergodic properties, as depicted in Fig. 1.

It's clear that the Fig. 1 illustrates a stationary distribution of a solution of the system, $(S(t),E(t)$, ${I_u(t),I_r(t),R(t),\delta (t))}^T$, which means that the disease will last for a long time.

Example 5.2

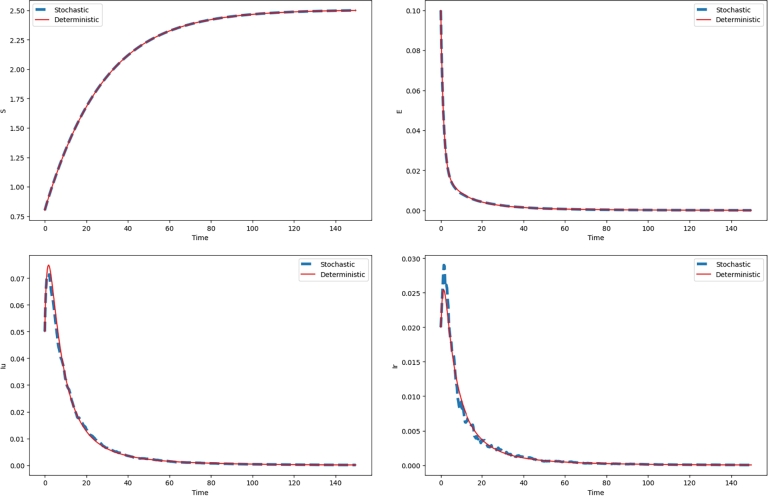
Assume that $\beta =0.2,{\rho }_1=4$ and ${\sigma }_1=0.08$, then we similarly compute that

$${\mathcal{R}}_0^{EX}=\sqrt[3]{\frac{{\mathcal{R}}_3}{2}+\sqrt{{(\frac{{\mathcal{R}}_3}{2})}^2+{(\frac{{\mathcal{R}}_1+{\mathcal{R}}_2}{3})}^3}}+\sqrt[3]{\frac{{\mathcal{R}}_3}{2}-\sqrt{{(\frac{{\mathcal{R}}_3}{2})}^2+{(\frac{{\mathcal{R}}_1+{\mathcal{R}}_2}{3})}^3}}\approx 0.16<1$$

and

$$\psi =\min \{\sigma +\mu ,\mu +d_1+\overline{\delta }+{\gamma }_{I_u},\mu +d_2+{\gamma }_{I_r}\}({\mathcal{R}}_0^{EX}-1)+(\frac{v_1(\mu +d_1+\overline{\delta }+{\gamma }_{I_u})(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}^{EX}}{{\mathcal{R}}^{EX}(\mu +d_2+{\gamma }_{I_r})S_0{v}_1+\overline{\delta }{S}_0{v}_2}+\frac{(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}_0^{EX}}{S_0})\underset{0}{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}|l-S_0|\mathrm{\Theta }(l,\delta )dld\delta +(\frac{v_2(\mu +d_1\overline{\delta }+{\gamma }_{I_u}){\mathcal{R}}_0^{EX}}{v_1(\mu +d_2+{\gamma }_{I_r}){\mathcal{R}}_0^{EX}+\overline{\delta }{v}_2}+1)\frac{{\sigma }_1}{\sqrt{\pi {\rho }_1}}\approx -0.003.$$

The implications of Theorem 4.1 readily demonstrate that the infected population will undergo exponential extinction, thereby guaranteeing the eradication of the disease outbreak. The graphs in Fig. 2 representing the curves of the populations $S(t)$, $E(t)$, $I_u(t)$ and $I_r(t)$ confirm this result.

The Fig. 2 presents the extinction dynamics of the disease, showing a steady and continuous decline in the number of exposed E, undetected infected $I_u$, and infected $I_r$ individuals over time. This trend ultimately leads to the disease's eradication.

Figure 1.

The left illustration depicts the simulated evolution of the solution (S(t),E(t),I_u(t),I_r(t),R(t)) for the models (1) and (2) using the given parameter values β = 0.6594,ρ₁ = 0.1, and σ₁ = 0.02. The right displays the frequency histogram and probability densities for S, E, I_u, I_r and R of model (2).

Figure 2.

The simulations of the solution (S(t),E(t),I_u(t),I_r(t),R(t)) of the deterministic model (1) and the stochastic model (2) with the parameter values β = 0.2,ρ₁ = 4, and σ₁ = 0.08.

6. Conclusion

In this paper we analyzed a novel stochastic $SE{I}_u{I}_{r}R$ model with the Ornstein–Uhlenbeck process to describe the transmission rate from undetected to detected individuals. We proved the theoretical results by constructing a series of suitable Lyapunov functions. In the first, we gave the theoretical result that the stochastic $SE{I}_u{I}_{r}R$ system (2) has a unique global positive solution and proved it. Then, we established sufficient criteria for the existence of stationary distribution and exposed the effects of the Ornstein–Uhlenbeck process on the existence of stationary distribution. Specifically, if ${\mathcal{R}}_0^s>1$ and the parameters δ of the Ornstein–Uhlenbeck process meet certain conditions, the system (2) exists with a stable distribution. In addition, we derived the sufficient conditions when ${\mathcal{R}}_0^{EX}<1$ for the extinction of the disease. We used numerical simulation to simulate and verify the theoretical results in the paper.

CRediT authorship contribution statement

Mhammed Mediani: Writing – original draft, Visualization, Methodology, Investigation. Abdeldjalil Slama: Writing – original draft, Validation, Conceptualization. Ahmed Boudaoui: Writing – review & editing, Writing – original draft, Validation, Conceptualization. Thabet Abdeljawad: Writing – review & editing, Supervision, Investigation, Formal analysis, Conceptualization.

Declaration of Competing Interest

The authors declare that there is no conflict of interest in this work.

Data availability

The data that supports the findings of this study are available within the article.