Three-dimensional atomic insights into the metal-oxide interface in Zr-ZrO₂ nanoparticles

Abstract

Metal-oxide interfaces with poor coherency have specific properties comparing to bulk materials and offer broad applications in heterogeneous catalysis, battery, and electronics. However, current understanding of the three-dimensional (3D) atomic metal-oxide interfaces remains limited because of their inherent structural complexity and the limitations of conventional two-dimensional imaging techniques. Here, we determine the 3D atomic structure of metal-oxide interfaces in zirconium-zirconia nanoparticles using atomic-resolution electron tomography. We quantitatively analyze the atomic concentration and the degree of oxidation, and find the coherency and translational symmetry of the interfaces are broken. Atoms at the interface have low structural ordering, low coordination, and elongated bond length. Moreover, we observe porous structures such as Zr vacancies and nano-pores, and investigate their distribution. Our findings provide a clear 3D atomic picture of metal-oxide interface with direct experimental evidence. We anticipate this work could encourage future studies on fundamental problems of oxides, such as interfacial structures in semiconductor and atomic motion during oxidation process.

A detailed understanding of metal-oxide interfaces is essential for uncovering their intrinsic properties. Here, the authors investigate the 3D atomic structure of metal-oxide interfaces in Zr-ZrO₂ nanoparticles using atomic-resolution electron tomography.

Introduction

Most metals spontaneously form an oxidation layer on their surfaces. The metal-oxide interface plays a critical role in broad applications ranging from heterocatalysis^1,2, batteries^3,4, and electronics^5,6. The thermodynamics and kinetics of oxidation processes have been extensively studied over the years^7–9. Plenty of research has been focused on the metal’s work function¹⁰, the transport of metal or oxygen species^11–13, and the rate of oxidation¹⁴. A number of theories have been proposed in these studies to understand the oxidation behavior. For example, the Kirkendall effect is used to explain the formation of oxidized pores^15–17; Wagner et al. proposed the law of oxidation kinetics in which the oxidation rate is controlled by the transport of ions under electrochemical potential gradient based on several assumptions^12,14,18. However, owing to the lack of direct observation of the three-dimensional (3D) metal-oxide interface at nanoscale or atomic scale, most of the theories are based on the ideal atomistic interface model. Properties of the interface, including catalytic activity, phonon dispersion, and electron transportation, are strongly related to the local atomic arrangements of the metal-oxide interface, such as coordination numbers and atomic bond lengths^19–24. It is, therefore, essential to determine the 3D atomic arrangements and understand the detailed oxidation structure of metal.

With the recent development in aberration-corrected transmission electron microscopy (TEM), local structures of metal-oxide interfaces such as Cu-Cu₂O^25,26, Ag-Ag₂O²⁷, and Ni-NiO²⁸ have been studied at nanoscale or atomic scale; several of them were probed in-situ by atomic-resolution imaging and theoretical simulation^25–29. Semi-coherent and incoherent interfaces between metal and oxide have been observed at sub-Å resolution from two-dimensional (2D) projections²⁶. Luo et al. discovered the periodic dislocation in Cu-Cu₂O semi-coherent interface, suggesting the mechanism of strain release by defects between metal and oxide²⁵. Zhu et al. tracked the formation of voids in Ni-NiO nanoparticles at nanoscale, identifying a two-stage oxidation mechanism including early-stage nucleation and then the Wagner oxidation²⁸. However, since the oxidized interfaces are usually non-epitaxial and inherently disordered due to the lattice mismatch, the atomic arrangements between some metals and their oxidation layer cannot be clearly elucidated using high-resolution TEM or crystallography. Conventional 3D characterization methods such as atom probe tomography^30,31, electron tomography^28,32–35, and depth sectioning^36,37 have been used to study the 3D morphological structures of the metal-oxide interfaces, and these techniques could overcome the limitation of single images, which only provide the projected information of the 3D structures in 2D. However, the resolution of these techniques is limited to nanometer scale. Thus, determining the 3D atomic arrangements of the metal-oxide interface remains a major challenge. Although it remains notoriously difficult to image and identify each of the oxygen atoms of oxides in 3D, especially in annular dark-field scanning transmission electron microscopy (ADF-STEM) mode, atomic-resolution electron tomography (AET), which is an effective tool for determining the 3D atomic structure of nanomaterials^32–35, can in principle resolve the positions of heavy metal atoms in oxides and therefore give important structural information on this long-standing problem.

Here, using Zr-ZrO₂ as a model system, we determined the 3D atomic structure of the metal-oxide interface using AET. We chose Zr-ZrO₂ for two reasons. First, Zr can form oxide spontaneously in air, and the oxidation process is moderate¹⁰; second, the Zr-O bonding is strong among all the common metal oxides, and ZrO₂ has excellent chemical stability. The Zr-ZrO₂ interface can maintain its atomic structures after electron irradiation at a dose rate of 6 × 10⁵ e Å⁻², which is essential for electron tomography experiments. By determining all the Zr atomic positions in Zr-ZrO₂ nanoparticles (NPs), we obtained the 3D atomic structure of a partially oxidized Zr NP; it has an uncommon face-centered cubic (FCC) Zr metal crystal nucleus as the core and amorphous/crystalline ZrO₂ as the shell. The degree of oxidation decreases while Zr packing density increases from the oxide surface to the metal core. Instead of forming a coherent interface, most of the atoms at the Zr-ZrO₂ interfaces connect with each other semi-coherently or incoherently. We discovered a bidirectional distortion including bending and twisting at the semi-coherent metal-oxide interface. Moreover, we identified numbers of voids in the oxides including Zr vacancies, nano-pores, and large pores; the oxidation process is related to the distribution of the voids. These findings expand our understanding of the atomic structures of metal-oxide interfaces with poor coherency, encourage future studies on oxidation process at 3D atomic resolution, and further inspire the designing and modeling of atomic metal-oxide interface in surface engineering, heterogeneous catalysis, and semiconductors.

Results

Atomic structures of Zr-ZrO₂ nanoparticles in 3D

NPs made of different monatomic metals with both disordered and crystalline structures can be achieved using fast-cooling vitrification process^38,39. Zr NPs were synthesized using pulse laser ablation of pure Zr target (purity > 99.95%) in ethanol (Methods). This technique can provide a very high temperature to melt and vaporize the metal target and fast cooling to yield nanoparticles which have a large variety of morphologies³⁸ including amorphous, partially amorphous, and crystalline metal nanoparticles (Supplementary Fig. 1a). By naturally oxidizing the freshly prepared Zr NPs in air, we obtained Zr-ZrO₂ NPs at different stages of the oxidation process. Some of the Zr-ZrO₂ NPs have an oxidized shell and a metal core (Supplementary Fig. 1c,e). To confirm the oxidation, we have employed high-resolution ADF-STEM and energy dispersive spectroscopy (EDS) to characterize the Zr-ZrO₂ NPs (Supplementary Figs. 1, 2); it is notable that the edges of the NPs have a high degree of oxidation since the oxygen signal of EDS at the edge are stronger while ADF-STEM intensities are weaker. The line profiles of Zr elemental intensity are particularly high at the core of the nanoparticles, also indicating the nanoparticles have a metallic Zr core and ZrO₂ shell.

In this study, we selected Zr-ZrO₂ particles with a suitable size (≈ 10 nm) and various of metal-oxide interfaces to perform AET experiments. We resolved the 3D atomic structures of all Zr atoms in several Zr-ZrO₂ NPs using AET. In short, tomography tilt series (Supplementary Figs. 3–8) were acquired from three Zr-ZrO₂ NPs at different stages of the oxidation process using an aberration-corrected TEM in ADF-STEM mode (Supplementary Table 1). After imaging processing including denoising, background subtracting, and alignment (Methods), the tilt series were reconstructed using the Real Space Iterative Reconstruction (RESIRE) algorithm⁴⁰. Supplementary Fig. 9 and Supplementary Movie 1 show the volume rendering of raw reconstructions of these NPs. The 3D atomic coordinates of all Zr were traced from the computed reconstructions (Methods). We chose a partially oxidized Zr-ZrO₂ (named Zr1) as our main interest to elucidate the metal-oxide interfaces. The other two particles are fully oxidized without obvious metal core (named as Zr2 and Zr3; Supplementary Fig. 10).

Since the image contrast of atoms in ADF-STEM mode is sensitive to the atomic number, the oxygen atoms are too light, and our current imaging parameters are not sufficient enough to detect oxygen (Supplementary Tables 1, 2). To verify the contrast contribution of oxygen in 2D ADF-STEM images, we have constructed a slab model of cubic ZrO₂ which is 8-nm-thick (similar thickness comparing to Zr NPs); and then performed the multi-slice simulation along the [100] zone axis. The contrasts of oxygen columns in the simulated images are very low, making the column of oxygen atoms barely seen (Supplementary Fig. 11). To further validate our reconstruction and verify the contrast contribution of oxygen in 3D, we have performed multi-slice simulation of the tilt series and computed 3D reconstruction to show the oxygen contrast in 3D. The same number of projections have been generated from the experimental model with filling oxygens (Methods). By performing the same image processing, reconstruction, and atom tracing procedures, we obtained a multi-slice atomic model. We estimated that 97.2% of atoms were identified correctly with a 3D precision of ≈ 28 pm by comparing the experimental model with the multi-slice one (Supplementary Fig. 12). From either 3D reconstructed volume or traced atomic positions, we cannot distinguish the oxygen atoms in ZrO₂ regions due to the low intensities of the oxygen atoms (Supplementary Figs. 13, 14). These results reveal the low contrast of oxygen atoms, both in 2D ADF-STEM images and 3D AET reconstruction.

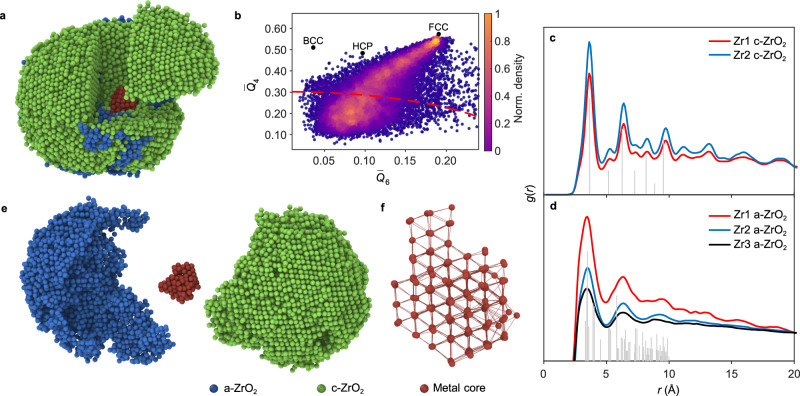
Figure 1a and Supplementary Movie 2 show the experimental 3D atomic model of Zr1, with ordered crystalline grains and disordered structures in the particle. We calculated the normalized bond orientational order (BOO) parameters for all the atoms to quantify the disorder (Fig. 1b and Methods); about 32% of all the Zr atoms are disordered. The particle has complicated phases, composed of a central metal grain, crystalline oxide grains (c-ZrO₂), and an amorphous oxide phase (a-ZrO₂) (Fig. 1d and Supplementary Movie 3). We calculated the Zr-Zr partial pair distribution functions (PDFs) of the atoms in c-ZrO₂ and a-ZrO₂ separately (Methods). The c-ZrO₂ shows a well-matched cubic phase ZrO₂ structure instead of monoclinic phase ZrO₂ in both Zr1 and Zr2 (Fig. 1c). The PDFs of the a-ZrO₂ atoms in all three NPs exhibit similar shape; and the first peak position is located at 3.45 Å, which is close to the first peak position of monoclinic phase ZrO₂ (Fig. 1c). All the positions of main peaks and valleys in our Zr-Zr PDFs obtained from the atomic coordinates of our a-ZrO₂ structures agree with those obtained from synchrotron X-ray diffraction⁴¹. The most populated Zr-Zr bond lengths in c-ZrO₂ and a-ZrO₂ are 3.6 Å and 3.45 Å, respectively (Supplementary Fig. 15). Interestingly, there is a small Zr metal core inside Zr1, confirmed by polyhedron template matching⁴² and atomic concentration analysis (Methods). Figure 1e shows the atomic structure of the pure Zr metal core viewing from 〈110〉 direction. The metal core has a distorted FCC structure with an averaged Zr-Zr bond length of 3.3 Å, slightly longer than the standard value in Zr metal (3.2 Å). These observations are different from the bulk behavior, where Zr typically forms hexagonal close-packed (HCP) or body-centered cubic (BCC) structures and usually forms monoclinic phase ZrO₂ after natural oxidation⁴³. This discrepancy highlights the distinctive behavior of materials at the nanoscale.

Fig. 1. Atomic structures of Zr-ZrO₂ nanoparticles in 3D.

a Experimental 3D atomic model of the Zr1 NP with a-ZrO₂ in blue, c-ZrO₂ in green and metal core in red. b Normalized BOO parameters of all atoms. The red dashed curve is a criterion to distinguish the disordered atoms (32% in total, atoms below the curve) and ordered atoms (68% in total, atoms above the curve). The standard BCC, HCP and FCC parameters are marked as black dots for reference. c, d Zr-Zr PDFs of the c-ZrO₂ (c) and a-ZrO₂ (d), with Zr1 in red, Zr2 in blue and Zr3 in black. The gray peaks show the peak positions of the standard PDF of cubic phase ZrO₂ (c) and monoclinic phase ZrO₂ (d) for comparison. e The NP consists of a-ZrO₂, c-ZrO₂ and a metal core grain. f Magnified atomic structure of the pure Zr metal core viewing from 〈110〉 direction. Source data are provided as a Source Data file.

Atomic concentration and the degree of oxidation

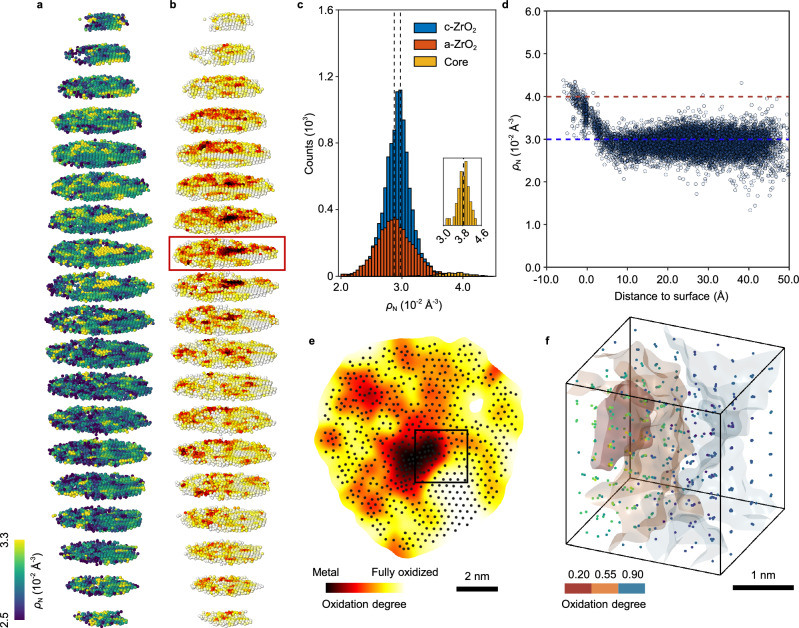
To compare the local atomic packing density of Zr in all phases, we obtained the compactness of the NP by determining the Zr atomic concentration (ρ_N) of all the regions present in Zr1 NP (Methods). Figure 2a shows the 3D ρ_N distribution of Zr1. The low packing density regions are not related to any voids in the NP as we exclude all the voids from consideration when performing calculation (Methods). The averaged ρ_N of the metal core is 3.85 × 10⁻² Å⁻³ (Fig. 2c), close to the ρ_N of ideal close-packed metallic Zr (3.9 × 10⁻² Å⁻³). The ρ_N of oxides (both c-ZrO₂ and a-ZrO₂ phases) are significantly lower than that of pure metal, being 2.92 × 10⁻² Å⁻³ and 2.89 × 10⁻² Å⁻³, respectively. They are comparable to the ρ_N of ideal cubic phase ZrO₂ (3.0 × 10⁻² Å⁻³). We also observed 3D local ρ_N heterogeneity in the oxides, particularly distributed around the metal-oxide interfaces. Figure 2d shows the ρ_N distribution as a function of the distance from the surface of the metal core (metal to c-ZrO₂). The gradual decrease in ρ_N suggests the metal-oxide interfaces are atomically smooth. The packing density gradient is attributed to the gradual change of the degree of oxidation of the Zr metal. Our PDFs and Zr-Zr bond length analysis suggest that c-ZrO₂ is the cubic phase, and a-ZrO₂ mainly forms the tetrahedral structure locally⁴¹; oxygen should be located in tetrahedral sites in both phases (Supplementary Fig. 16). Next, we quantified the degree of oxidation by geometrically filling oxygen into the tetrahedral sites based on a reasonable Zr-specific knowledge (Methods). Since EDS measurements in other similar Zr-ZrO₂ NPs suggest the oxide grain is almost fully oxidized, which is confirmed by our atomic concentration analysis, to satisfy the stoichiometric ratio of ZrO₂, oxygen can be filled in eight tetrahedral sites (5.5 ų) of the oxide (Supplementary Fig. 16a); but those tetrahedral sites (4.2 ų) in Zr metal are too small (Supplementary Fig. 16b). Figure 2b and Supplementary Movie 4 show the 3D oxidation maps of Zr1. The degree of oxidation distributions in all the phases are shown in Fig. 2e and Supplementary Fig. 17, where the degree of oxidation increases along with the decrease of Zr ρ_N. The c-ZrO₂ and a-ZrO₂ grains are almost fully oxidized in their surfaces; and they become less oxidized as closer to their interfaces with the central Zr core (Fig. 2e). The experimentally measured tetrahedral sites in the central Zr core are too small to be filled with oxygen, confirming the core is barely oxidized. There could be some heterogeneity in the degree of oxidation in some of the oxide grains, which makes the oxidation maps non-uniform. To further validate our oxygen filling method and partial oxidation, we have performed integrated differential phase-contrast STEM (iDPC-STEM) imaging on a similar nanoparticle with a known structure, the cubic ZrO₂ phase (Methods, Supplementary Fig. 18a, b). This technique provides improved sensitivity to light elements such as oxygens⁴⁴. The line profiles of the iDPC image show the contrasts of different oxygen columns are different, indicating partial oxidation and non-uniform oxygen filling in this cubic ZrO₂ grain (Supplementary Fig. 18c). A cubic cutout of the 3D oxidation maps reveals that the degree of oxidation is strongly correlated to the atomic packing density of Zr; a highly oxidized region always has a lower Zr ρ_N (Fig. 2f). It’s notable that some other Zr NPs are completely oxidized to cubic phase ZrO₂ and/or amorphous ZrO₂ (Supplementary Fig. 19) even from the same batch of oxidation. These results indicate the oxidation process is kinetics controlled, in which we observed several intermediate states of oxidized Zr-ZrO₂.

Fig. 2. Atomic concentration and the degree of oxidation of Zr-ZrO₂ NP.

a, b Atomic concentration ρ_N distribution (a) and the degree of oxidation (b) of all the atoms in Zr1. Each slice has a thickness of 5.3 Å. To increase the signal-to-noise ratio, we convolved the degree of oxidation with a 2-Å-wide 3D Gaussian kernel, but this also reduces the 3D spatial resolution of oxidation map to ≈ 4 Å. c Distribution of ρ_N in c-ZrO₂ (blue), a-ZrO₂ (red) and metal core (yellow) phase. c-ZrO₂ has a slightly larger ρ_N distribution by 1% (dashed lines) than a-ZrO₂. The inset figure shows the magnified histogram of metal core. d The ρ_N distribution of metal/c-ZrO₂ as a function of the distance from the surface of metal core. The dashed lines show the standard ρ_N in Zr metal (red) and cubic phase ZrO₂ (blue). e A slice through the Zr1 NP as the red rectangle marked in (b), showing the degree of oxidation at different regions. f 3D surface rendering of local degree of oxidation and corresponding atomic concentration ρ_N, showing the strong correlation. The cutout is 25 × 25 × 25 ų. Source data are provided as a Source Data file.

3D atomic metal-oxide interfaces

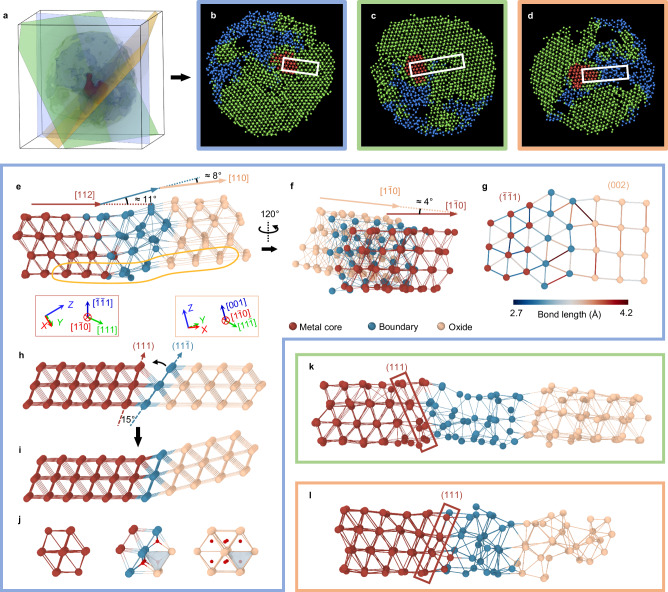
Coherency of the metal-oxide interface affects many properties, including strain, diffusion, and band structure^26,45,46. It is difficult to identify the atomic arrangement of semi-coherent or incoherent metal-oxide interfaces from 2D projected images. To probe the 3D structure of metal-oxide interface at atomic level, we focus on the atomic Zr-Zr bonding of the interfaces with a range of ≈ 10 Å based on the packing density between metal core and oxide phases (Fig. 2d). Figure 3a presents the 3D surface renderings of three major phase, showing the contour of metal core, c-ZrO₂, and a-ZrO₂ phase. Three slices with four atomic layers in thickness through the metal core show the Zr-Zr bonding of metal-oxide interfaces (Fig. 3b–d). We found several types of interfaces, including semi-coherent and incoherent interfaces between metal and c-ZrO₂, and incoherent interfaces between metal and a-ZrO₂. The white rectangles in Fig. 3b–d highlight three cutouts from the atomic structures of a semi-coherent (Fig. 3e) and an incoherent interface (Fig. 3k) between metal and c-ZrO₂, and an incoherent interface (Fig. 3l) between metal and a-ZrO₂, respectively. The layer-by-layer slices of the raw reconstruction volume of these interfaces are shown in Supplementary Figs. 20–22, indicating the consistency between the raw reconstruction and the traced atomic model.

Fig. 3. 3D atomic metal-oxide interfaces.

a–d 3D surface renderings of three major phases, showing the contour (a) of metal core (red), c-ZrO₂ (green) and a-ZrO₂ (blue) of Zr1. Three planes go through the Zr1 in different directions. The sliced atomic models (4-atom-layers thick) highlights three different types of interfaces, i.e., metal/c-ZrO₂ semicoherent interface between (b; in blue frame), metal/c-ZrO₂ incoherent interface (c; in green frame), and metal/a-ZrO₂ incoherent interface (d; in orange frame). e–g Experimental semicoherent interface structures specified by the rectangle region in (b). e The semicoherent interface viewing from metal [$1\overline{1}0$] direction. There is a bending of ≈ 11° between metal and interfacial layers in metal [112] direction (angle between red line and blue line), and a bending of ≈ 8° between interfacial layers and c-ZrO₂ in oxide [110] direction (angle in blue line and ivory line). The coordination tripods in red and ivory boxes shows the spatial crystal orientation of metal and oxide, respectively. f The semicoherent interface viewing from metal [101] direction (by rotating the cutout in (e) 120° counter clockwise), showing a twisting of ≈ 4° in metal [$1\overline{1}0$] direction (angle between red line and ivory line). g One atomic plane extracted from the semicoherent interface (the highlighted area in red in e), viewing from metal [$\overline{1}\overline{1}1$] direction. In this direction, the oxide shows the (002) plane. The color of the atomic bonding shows the Zr-Zr bond length. h The ideal model of an interface structure between ideal FCC Zr metal and ideal cubic ZrO₂, showing a 15° of wedge if no bending exists. To minimize the interfacial energy and maintain the coherency, a bending of 15° (i) is needed. The structure changed from metal to oxide shows in (j). The oxygen atoms are colored in red. k, l Incoherent interface structures specified by the rectangle region in (c, d), showing the metal/c-ZrO₂ (k) and metal/a-ZrO₂ interface (l). In (e–l), the metal atoms, interface atoms and oxide atoms are colored in deep red, blue and ivory, respectively. The Zr atoms are bonded with their first-nearest Zr neighbors and linked with lines (Methods).

In the semi-coherent interface, four layers of metal Zr atoms (marked in deep red) from the metal [$1\overline{1}0$] direction correspond to four layers of Zr atoms (marked as ivory) in the oxide (Fig. 3e). To see the atomic connections in a single corresponding layer, one plane in the cutout is extracted and viewed from [$\overline{1}\overline{1}1$] direction of metal (Fig. 3g, Supplementary Fig. 23). Metal ($\overline{1}\overline{1}1$) plane is almost coplanar with oxide (002) plane; and the interface is about two atomic layers in thickness (blue atoms in Fig. 3g) and primarily connects metal (111) face with oxide ($11\overline{1}$) face. The Zr-Zr bond lengths increase from the metal side (≈ 3.3 Å) to the oxide side (≈ 3.6 Å). The interface has a long Zr-Zr distance, which is due to partial oxidation. Moreover, there is an angular mismatch of ≈ 11° between metal planes and the interfacial planes in metal [112] direction (oxide [110] direction), making the interface bending towards the oxide (Fig. 3e). To better illustrate the origin of the angular mismatch, we build an ideal model of Zr crystal grain and connect it to a cubic phase ZrO₂ from the same crystal orientation (Fig. 3h). Since the metal and oxide grains have different crystal orientations, there is a 15° of wedge through direct connection (angular mismatch in Fig. 3h). To minimize the interfacial energy while maintaining the coherency, the oxide has to adopt a bending of 15° to fill the wedge (Fig. 3i). At the interface, the maximum numbers of filling oxygen are four instead of eight (Fig. 3j), which means the interface is partially oxidized and the maximum stoichiometric ratio is ZrO. Besides, it is notable that there is a gap angle of ≈ 8° between the Zr (100) planes in the oxide and those in the interface (Fig. 3e), alleviating the overall strain in the whole NPs. By rotating this cutout 120° counterclockwise, we observed another angular mismatch of ≈ 4° between the metal ($\overline{1}\overline{1}1$) planes and oxide (002) planes in metal [$1\overline{1}0$] direction (oxide [$1\overline{1}0$] direction; Fig. 3f), which is perpendicular to metal [112] direction. It is considerable to have an angular mismatch when two adjacent crystal grains have different crystal plane spacing. The (111) spacing of Zr metal is 2.694 Å, while the (200) spacing of Zr oxide is 2.546 Å. To compensate for the spacing mismatch and to maintain the coherency, a certain degree (≈ 4°) of twisting between metal and oxide is preferred (Supplementary Fig. 24)⁴⁷.

Most of the metal-oxide interfaces are incoherent in the whole particle. Figure 3k, l shows the incoherent interfaces of metal/c-ZrO₂ and metal/a-ZrO₂, respectively. Although the atomic bonding becomes more distorted and disordered in the incoherent interfaces between metal and c-ZrO₂, most of the metal core {111} faces still correspond to oxide {111} faces (Fig. 3k and Supplementary Fig. 25). Zr atoms form an incoherent boundary with lower coordination number and longer bond length than crystalline region (Supplementary Figs. 26, 27). Those metal-oxide incoherent interfaces introduce a number of defects which are distributed around the metal core. Many Zr defects are found in those incoherent interfaces. These observations indicate that when a semi-coherent interface forms, a significant amount of strain could occur due to lattice and/or angular mismatch during oxidation. Once the strain caused by bending or twisting is too large, some of the semi-coherent interfaces could possibly turn to disordered structures through amorphization⁴⁸, where the coherency of the interface is completely broken.

Porous structures during oxidation

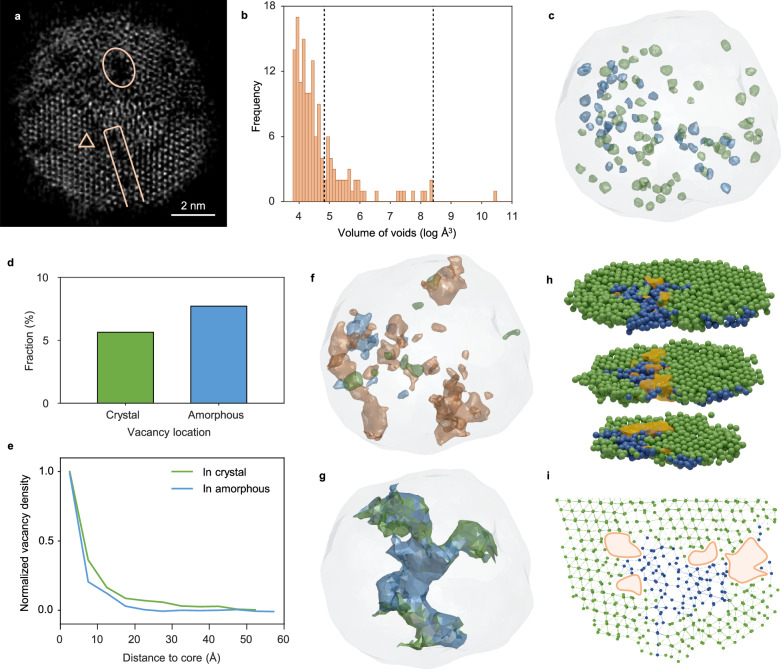
Porous structures of the oxide film formed on the surface of metal are usually associated with metal corrosion^{11,17,27–29}. We observed numbers of porous structures in the Zr-ZrO₂ particles. Figure 4a shows a 2.4 Å-thick slice from the reconstruction volume of Zr1; in which a significant number of voids, such as Zr vacancies (triangle), nano-pores (rectangle), and the largest pore (circle), are observed in the particle. From the 3D intensity and surface renderings of three consecutive atomic layers, a single Zr vacancy defect can be clearly located (Supplementary Fig. 28). To determine all the voids and evaluate their occupied volume, we employed Voronoi analysis by measuring the distance of Voronoi vertices to atoms (Methods). Figure 4b shows the histogram of volume distribution of all the voids, which we define as Zr vacancies, nano-pores, and a significantly large nanoscale pore throughout the particle. The porosity is 17% and 14% in Zr1 and Zr2, respectively. Figure 4c and Supplementary Movie 5 show the distribution of all Zr vacancies in Zr1. No vacancy is found in the metal core. More than 110 vacancies are distributed in the particle, and all the Zr vacancies contribute 8.4% of the total porosity. Slightly more vacancies are found in a-ZrO₂ than in c-ZrO₂ (Fig. 4d). We plot the density of Zr vacancies from the boundary of the metal core to the surface of the particle (Fig. 4e). Most of the vacancies are distributed in the range of 15 Å between metal core and oxide, which corresponds to the region where Zr packing density exponentially decreases (Fig. 2d). It’s notable that we exclude the vacancies from calculating the Zr packing density, the lower ρ_N of interface is independent with the rich vacancies surrounding the metal core. We found 41 nano-pores in the volume range between 125 and 4500 ų. They are mostly irregular and with a relatively large length-to-radius ratio. Figure 4f and Supplementary Movie 5 show the distribution of all nano-pores; they mostly sit at the boundaries between c-ZrO₂ and a-ZrO₂ regions. The largest pore is more than 34000 ų and penetrates throughout the whole particle, providing a possible pathway for further oxidation (Fig. 4g and Supplementary Movie 5). This pore predominantly sits in the a-ZrO₂ regions, connecting and separating all three phases; it terminates at the c-ZrO₂ region, releasing a large amount of strain. It’s interesting that the Zr-Zr bonds are significantly distorted at the boundary between two c-ZrO₂ domains (Fig. 4h, i), where some of the Zr atoms turn to be completely amorphous to release strain. Several nano-pores are coincidentally observed at this region near the small amorphous ZrO₂ domain. These findings indicate that when the strain reaches a certain point, possibly higher than the fracture point, the Zr-Zr crystal bonding could turn distorted and amorphous first, and then rupture to form defects to release the strain. It is generally believed that a compact layer of amorphous oxide at the micrometer scale can protect the interior of metal from further oxidation in aluminum^49,50. While our results reveal that in zirconium oxide, the amorphous oxide regions are substantially more porous than those in the crystalline regions, the voids would further advance the oxidation of Zr metal. We observed a variety of voids, which are highly related to the structure of the incoherent interface in Zr NPs from the atomic scale to the nanometer scale. The rearrangements of all the atom positions, including distortion, amorphization, and the rupture of bonding, are possibly due to the massive mass transportation during oxidation at the metal-oxide interfaces facilitated by these voids.

Fig. 4. Porous structures during oxidation.

a A 2.4 Å-thick slice from the reconstructed volume of Zr1, with vacancy (triangle), nano-pores (rectangle) and the largest pore (circle) highlight. b Volume distribution of all the voids. We define the voids with volume no larger than filling two Zr atoms (125 ų, Methods) as vacancies, the voids with volume between 125 and 4500 ų as nano-pores. We consider the largest pore with volume of 34,000 ų independently as it touches and separates all three phases. Dashed lines show the boundaries between three types of voids we define. c The surface renderings of all vacancies in c-ZrO₂ (in green) and a-ZrO₂ (in blue). The outline of whole NP is plotted with gray contour. d, e Statistics of vacancies. The fractions of vacancies in c-ZrO₂ and a-ZrO₂ show in (d). The radially normalized density distributions of vacancies as a function of distance from the surface core to the surface show in (e). f The surface renderings of all nano-pores in c-ZrO₂ (in green), in a-ZrO₂ (in blue) and in between c-ZrO₂ and a-ZrO₂ (in orange). g The surface rendering of the largest pore. The boundary atoms composed of amorphous and crystalline atoms are colored by blue and green, respectively. h One interface between two c-ZrO₂ regions with distorted interfacial Zr-Zr bonds, amorphous region and nano-pores. The crystal and amorphous atoms distinguished by BOO analysis are colored as green and blue, respectively. The contour of the nano-pore is colored as orange. i One representative slice shows a 7.8 Å-thick (≈ five atomic layers) cross section of the nano-pores and surrounding atoms. Source data are provided as a Source Data file.

Discussion

In conclusion, we determined the 3D atomic structure of metal-oxide interfaces in Zr-ZrO₂ NP using atomic-resolution electron tomography. We quantitatively measured the atomic packing density and the degree of oxidation from our experimental model of the metal-oxide interface. The degree of oxidation from metal to oxide increases gradually, resulting in a diffuse interface between FCC Zr core and ZrO₂. The Zr metal connects with its oxide via {111} planes; and the semi-coherent interface has severe distortion, including bending and twisting. The significant stress in the interface is relieved through low coordination and defects. Numbers of defects, including vacancies and nano-pores, together leverage the mass transportation during oxidation. We anticipate that our findings will fulfill the dearth of 3D atomic structure of metal-oxide interface and advance the study of fundamental problems of metal-oxide interfaces such as oxidation kinetics, diffusion, and defect evolution in variety of materials.

Methods

Synthesis of zirconium nanoparticles

The Zr NPs were synthesized in liquid using laser ablation methods. An all-solid-state ultraviolet laser with a wavelength of 355 nm was employed for laser ablation in ethanol, with a pulse width of 7 ps, a max pulse energy of 18 μJ, a repetition frequency of 800 kHz, and a beam spot diameter of 20 μm. Before being placed in a clean beaker, the bulk Zr target (purity > 99.95%) was washed by acetone (99.5%) and ethanol (99.9%). The dissolved oxygen in liquid is eliminated to the minimization by nitrogen flow for 60 min with a flow rate of 4 L min⁻¹. Then, the Zr target was submerged into ethanol and the laser beam was accurately focused vertically on the surface of the bulk Zr through the ethanol in a closed chamber. The laser ablation was continued for 1 min, and the produced Zr NPs were dispersed using ultrasonic agitation and subsequently isolated via centrifugation to be collected in the ethanol solution. The freshly prepared Zr NPs were then placed in air for one month to obtain a naturally oxidized layer several nanometers thick. The detailed methods of synthesis are described in ref. ³⁹. The final Zr-ZrO₂ NPs were drop cast onto 7-nm-thick Si₃N₄ membranes using an atomizer for TEM experiment.

Electron microscopy and atomic-resolution electron tomography

EDS maps were collected on an aberration-corrected Thermo Fisher Scientific Themis Z microscope at 300 kV in Analytical Instrumentation Center at Peking University. The iDPC-STEM imaging was conducted using aberration-corrected TEM (Thermo Fisher Themis Z) operated at 300 kV. The convergence semi-angle is 15 mrad. The collection angle is 6.3–24.7 mrad. The last measured current is 19 pA. The dwell time for each pixel is 10 μs. The pixel size is 0.088 × 0.088 Ų. The iDPC-STEM images were filtered by a Gaussian filter with a sigma of 20 pixels, which is a common image-processing step directly conducted in Velox software.

Tomographic tilt series were acquired by an aberration-corrected Thermo Fisher Scientific Titan microscope at 300 kV at the Electron Microscopy Laboratory of Peking University. The acceleration voltage was 300 kV and the imaging mode was ADF-STEM mode. Detailed parameters for data acquisition are listed in Supplementary Table 1. Each tomographic tilt series was acquired at the dose rate of < 5 × 10⁵ e Å⁻². For each tilt angle, three sequential images with a dwell time of 2 to 4 μs were acquired and registered using normalized cross-correlation, and then averaged to enhance the signal-to-noise ratio.

Acquired images were drift-corrected, denoised, and aligned before reconstruction. Linear drift from the sample or stage was corrected during the image registration. Three sequential frames of images at each tilt angle were used to estimate and compensate for the drift due to thermal vibration or instability of the stage. We computed the cross-correlation coefficient between the images to estimate the drift direction and drift speed. Then, we recovered the images by interpolating the raw images with drift-corrected pixel positions. This drift correction method has been used in many other image processing^35,51. Block-matching and 3D filtering (BM3D) is employed to denoise the images after drift correction⁵². And then, the background was estimated using the discrete Laplacian function of MATLAB and subtracted. In the direction perpendicular to the tilt axis, the images were aligned by maximizing the cross-correlation between the common lines. Along the tilt axis, the images were aligned using the center-of-mass method.

After image processing, the 3D reconstruction was computed from experimental tilt series using RESIRE algorithm⁴⁰.

After reconstruction, atom tracing was performed to determine the 3D atomic coordinates. First, we interpolated reconstructed volume with spline method. All the local maxima in the reconstruction were identified as the rough atomic coordinates. Then, the coordinates were optimized according to the local volume of 1.7 Å × 1.7 Å × 1.7 Å with a polynomial fitting method. To separate the non-atoms from the potential atoms, K-means clustering method was employed based on the integrated intensity of the local volume (1.7 Å × 1.7 Å × 1.7 Å). For every potential atom, a minimum distance of 2 Å to its nearest atom should be satisfied. The value of the cutoff is chosen based on the measurement deviation of atom positions. The standard error (σ) of the deviation is measured by the blurring width of reconstruction volume (that is, the standard deviation of the Gaussian-shaped volume of an atom) at the atom sites. The distribution of σ is 0.357 ± 0.004 Å, as Supplementary Fig. 29 shows. So, the cutoff is determined according to the “3σ” criterion (in statistics) to be 3.2 Å − 3 × 0.357 Å ≈ 2 Å. The 3.2 Å is the standard Zr-Zr bond length in metal. By carefully comparing the individual atom in the potential atomic models with the reconstructed volume, we manually corrected the atomic coordinates of unidentified or misidentified atoms. The manual correction has been routinely applied during the atom tracing and refinement in protein crystallography⁵³. Specifically, we have manually removed unphysically too close atoms, which are 112 (0.73%) atoms for Zr1, 168 (0.75%) atoms for Zr2, and 93 (0.7%) atoms for Zr3.

Calibration of the pixel size of the ADF-STEM image

The pixel size calibration procedure is shown in Supplementary Fig. 30. A FIB sample of silicon is rotated to the [110] zone axis. Calibration images are taken at the same magnification with the same pixel size as the tomography experiments use (normally ≈ 35.8 pm). To correct any potential image distortion caused by sample drift, we take 20 to 50 frames for each image. The dwell time of one pixel in each frame is only 200 to 500 ns, which significantly alleviates the image stretching due to the drift. For each image, all frames are aligned and then averaged. The brightest spots of the fast Fourier transform (FFT) are precisely located using 2D gaussian fit. The distances of these points to the center of FFT are the countdowns of the lattice spacing of the image in the real space. Thus, we can get the lattice constants measured in this image. By comparing it to the standard lattice constants of Si, we can calibrate the pixel size in this magnification. We take multiple Si images at different scan rotation angles and then determine the mean value of the real pixel size.

Calculation of PDF

We calculated the PDF curve from experimental 3D atomic model by

$$g\left(r\right)=\frac{1}{N^2}{\sum }_{i=1}^N{\sum }_{j=1}^N⟨\delta \left(\mid {\mathbf{r}}_{ij}\mid -r\right)⟩$$ 1

where N is the total number of atoms; δ is the Dirac delta function; 〈⋅〉 is the notation for expectation value; |r_ij| is the distance between the i-th atom and the j-th atom. To get a smoother PDF curve, a Gaussian kernel function with a σ of 1.5 Å was applied to convolute with original g(r). Finally, the PDF was scaled to approach one at the large pair distances. Using this procedure, we calculate the c-ZrO₂ and a-ZrO₂ separately in three NPs. From the PDF, we determined the first valley position as 4.5 Å, corresponding to the first-nearest-neighbor shell distance. The distance was used as a cutoff for BOO and alpha shape calculation (see the sections below).

Local BOO parameters

We calculated the normalized local BOO parameters to distinguish the order and disorder of all the atoms. The normalized BOO parameter is defined as $\sqrt{{\overline{Q}}_4^2+{\overline{Q}}_6^2}/\sqrt{{\overline{Q}}_{4\text{FCC}}^2+{\overline{Q}}_{6\text{FCC}}^2}$, where the ${\overline{Q}}_4$ and ${\overline{Q}}_6$ values were computed based on the procedure described in ref. ⁵⁴, using 4.5 Å (the first-nearest-neighbor shell distance) as a constraint. The ${\overline{Q}}_{4\text{FCC}}$ and ${\overline{Q}}_{6\text{FCC}}$ are the reference values of the standard FCC structure. We separated the amorphous part from crystalline part according to the criterion of the normalized BOO less than 0.5³⁴.

Determination of voids

Delaunay triangulation and Voronoi tessellation were performed to determine the voids. Delaunay triangulation, Voronoi tessellation, and alpha shape were performed with the built-in functions of MATLAB (namely, ‘delaunayTriangulation’, ‘voronoin’, and ‘alphaShape’). The initial spatial region of NP was calculated by alpha shape with α = 4.5 Å (the first-nearest-neighbor shell distance). Then, we calculated the space that accommodates at least one Zr atom in the initial particle region with the following steps:

1. The initial particle region was divided into tetrahedra by Delaunay triangulation.

2. We determined whether a tetrahedron is void. We calculated the radius of the circumscribed sphere for each tetrahedron. The radius represents the maximized sphere that can fit within the NP without intersecting with the center of any atom. Tetrahedra with a radius larger than 3.19 Å were classified as voids. This criterion of radius was obtained based on the standard cubic phase of ZrO₂ with one vacancy.

3. We grouped neighboring voids together to form larger voids. Two voids that share a common face are considered neighboring and thus combined into a single, larger void. The volume of these larger voids was calculated by summing the volumes of each void component.

4. We classified the voids into vacancies, nano-pores and the largest pore based on volume. We define the voids with volume filling one or two Zr atoms (45–125 ų) as vacancies, the voids with volume between 125 and 4500 ų as nano-pores. The largest pore with volume of 34000 ų was considered independently.

Finally, the contours of voids were displayed with Laplacian smoothing conducted by GIBBON⁵⁵.

Atomic concentration

Topological bonds were determined based on the Voronoi tessellation. Two atoms are considered topologically bonded if their corresponding Voronoi polygons share a common face. In constructing the Voronoi polygons, we removed those surfaces with area less than 1% of the total area of the polygon surfaces⁵⁶. Additionally, this bond must also be shorter than 4.5 Å, corresponding to the first-nearest-neighbor shell distance. The atomic concentration was calculated by ρ_N = 1/V, where V is the volume of Voronoi cell of an atom.

Degree of oxidation

Our current oxygen filling is based on geometric frustration of the tetrahedra sites formed by Zr atoms. One prior assumption for this geometric frustration is as long as the volume of any tetrahedra site is large enough (4.68 ų), it would be filled with oxygen atoms. This assumption is based on a fact that Zr is a highly oxygenophilic metal, it is relatively easy to form Zr-O bonds to oxidize Zr metal. Although it cannot give us the precise information about where all the oxygen atoms exactly are, we believe it could still give us a fairly good estimation of the degree of oxidation based on the reasonable Zr-specific knowledge. The oxidation state was then determined using Delaunay triangulation. First, the distortion of Delaunay tetrahedra was considered. The distortion parameter was calculated by $\delta =\left(e_{\max }/e_{\text{avg}}\right)-1$, where $e_{\max }$ and $e_{\text{avg}}$ are the maximum and average edge lengths of tetrahedron³³. We removed the tetrahedron with a distortion parameter larger than 0.255. Then, the volume of the remaining Delaunay tetrahedra was calculated. If the volume of a tetrahedron is larger than 4.68 ų (the averaged tetrahedron volume of FCC Zr lattice and c-ZrO₂ lattice), an oxygen atom was placed inside. Finally, the degree of oxidation for each Zr atom was calculated by the fraction of its surrounding tetrahedra that accommodated one oxygen atom.

Author contributions

J.Z. conceived the idea and directed the study. Z.L., Z.X., and Y.Z. performed TEM experiment and acquired the data. Y.Z. and S.H. performed the imaging processing, reconstructions, and atom tracing. Y.Z., Z.L., S.H. conducted/discussed data analysis under the direction of J.Z.; T.X. and Y.-E.Z. synthesized Zr NPs under the direction of H.-B.K. and W.-H.W.; Y.Z., Z.L., and J.Z. wrote the manuscript. All authors commented on the manuscript.

Peer review

Peer review information

Nature Communications thanks Robert Hovden, Ryo Ishikawa, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data that support the findings of this study, including the raw tilt series, raw reconstructions, and traced atom positions, are available from Zenodo⁵⁷ and from the corresponding authors upon request. Source data are provided with this paper.

Code availability

The codes used in this study are available from Zenodo⁵⁷ and from the corresponding authors upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-52026-w.