Validation of the TOPAS Monte Carlo toolkit for HDR Brachytherapy Simulations

Abstract

Purpose:

The goal of this work is to validate the user-friendly Geant4-based MC toolkit TOPAS for brachytherapy applications.

Methods:

Brachytherapy simulations performed with TOPAS were systematically compared with published TG-186 reference data. The photon emission energy spectrum, the air-kerma strength, and the dose-rate constant of the MBDCA-WG generic Ir-192 source were extracted. For dose calculations, a track-length estimator (TLE) was implemented. The four Joint AAPM/ESTRO/ABG MBDCA-WG test cases were evaluated through histograms of the local and global dose difference volumes. A prostate, a palliative lung, and a breast case were simulated. For each case, the dose ratio map, the histogram of the global dose difference volume, and cumulative dose volume histograms were calculated.

Results:

The air-kerma strength was (9.772 ± 0.001) ×10⁻⁸ U Bq⁻¹ (within 0.3% of the reference value). The dose-rate constant was 1.1107 ± 0.0005 cGy h⁻¹ U⁻¹ (within 0.01% of the reference value). For all cases, at least 96.9% of voxels had a local dose difference within [−1%, 1%] and at least 99.9% of voxels had a global dose difference within [−0.1%, 0.1%]. The implemented TLE scorer was more efficient than the default analog dose scorer by a factor of 237. For all clinical cases, at least 97.5% of voxels had a global dose difference within [−1%, 1%]. Dose volume histograms were consistent with the reference data.

Conclusion:

TOPAS was validated for HDR brachytherapy simulations following the TG-186 recommended approach for model-based dose calculation algorithms. Built on top of Geant4, TOPAS provides broad access to a state-of-the-art MC code for brachytherapy simulations.

Introduction

Traditionally, dosimetry in brachytherapy is based on the TG-43 formalism that computes the dose distribution considering precalculated data of a single source centered in an infinite water medium (1, 2). There are some limitations in this formalism since the true patient geometry is not considered. For example, the dose distribution in a breast treatment is substantially modified by the presence of lung and the air outside the patient (3–5). For breast implants, isodose contours lower than 60% of the prescribed dose are overestimated by 5%-10% in treatment planning system calculations (4). Another problem is that specific materials are not considered, for instance, the tungsten shielding of a gynecological or rectal applicator (3). For these reasons, model-based dose calculation algorithms (MBDCAs) such as the collapsed-cone superposition-convolution algorithms (6–9) and the grid-based Boltzmann solvers of the differential linear Boltzmann transport equation (10–15) are recently being applied in the clinic (16, 17). MBDCAs account for the absorbed dose differences between water and tissue, the attenuation differences between water and tissue, the radiation interaction in the source and applicator materials, and the change in scattered radiation due to the patient geometry (3). These algorithms require validation and according to TG-186, the only way to fully validate the MBDCAs is through the use of a validated Monte Carlo (MC) code or a combination of MC simulations and experimental measurements (16). Experimental measurements are much more difficult than for other treatment modalities and uncertainties of 1 mm in dosimeter positioning can lead to differences of the order of 20% or more close to the source (3, 16, 18–20). On the other hand, the MC method accurately models the fundamental physical processes by simulating the discrete particle interactions and it is considered the gold standard for dose calculations in brachytherapy (16, 21, 22).

Based on general purpose MC toolkits, there are codes optimized for brachytherapy simulations such as BrachyDose (23) and egs_brachy (24) based on EGSnrc (25), BrachyGUIDE (26) and HDRMC (27) based on MCNP (28), ALGEBRA (29) and RapidBrachyMCTPS (30) based on Geant4 (31), and MCPI (32) based on PTRAN (18). Traditionally, MC codes are complex and necessitate coding knowledge that limit their pool of users. TOPAS (TOol for PArticle Simulation) is a user-friendly MC toolkit that wraps and extends the general-purpose MC code Geant4 (33, 34). Users interact with TOPAS through simple text files to create complex geometries and simulations. This paradigm allows users to perform simulations with no need of writing any Geant4/C++ code. The toolkit was originally developed for proton therapy and now is available in many different areas of radiation therapy and imaging research (34). Starting in the 3.2 version series, simulations with volumetric sources were adopted by TOPAS enabling accurate brachytherapy simulations. With its much-simplified approach to simulation and geometry description, and built-in features such as compatibility with DICOM files and the layered mass geometry method (35), TOPAS might be a natural choice for various dose calculation and clinical development tasks. The purpose of this study is to validate TOPAS for high dose-rate (HDR) brachytherapy applications. Results obtained with TOPAS were systematically compared with published TG-186 reference data. More specifically the photon emission energy spectrum, the air-kerma strength, and the dose-rate constant of the MBDCA-WG generic Ir-192 source were extracted (36); the Joint AAPM/ESTRO/ABG MBDCA-WG test cases were evaluated (36, 37); and three different patient geometries were studied (9).

Materials and Methods

Monte Carlo code

TOPAS version 3.2 (Geant4 version 10.5) released in July 2019 was used in this work. Geant4 provides different physics lists to model electromagnetic processes useful for medical applications (38). These physics lists are distributed in several modules called physics list constructors. The g4em-livermore (in TOPAS nomenclature) physics list constructor that uses the EPDL97, EEDL97, and EADL97 libraries (Lawrence Livermore Laboratory) was included in the simulations (39). This constructor models the photons and electrons interactions down to about 250 eV. The accuracy of the Livermore models implemented in an older version of Geant4 (version 8.0, released in 2005) was shown elsewhere (40). Nevertheless, substantial improvements (e.g. Goudsmith-Saunderson model for elastic electron interactions, multithreading capability, unification of physics list in constructors, etc) had been implemented in Geant4 (41) and calls for verification. TOPAS was run on Compute Canada high performance computing clusters (42). Nodes of 32 cores Intel E5-2683 v4 Broadwell 2.1 GHz and 40 cores Intel Gold 6148 Skylake 2.4 GHz were used for simulations.

TOPAS includes an extension mechanism in which users are allowed to implement new classes and methods in their simulations. Through this mechanism, a linear track-length estimator (TLE) method for dose scoring was implemented (43). The TLE technique approximates the absorbed dose as electronic (collisional) kerma. For a photon traversing a voxel, the absorbed dose is:

$$D=\text{Φ}E\frac{{\mu }_{\mathit{en}}}{\rho }=\frac{L}{V}E\frac{{\mu }_{\mathit{en}}}{\rho },$$ (1)

where $L$ is the track length (the distance travelled in the voxel), V is the voxel volume, $E$ is the photon energy, and ${\mu }_{\mathit{en}}/\rho$ is the mass energy absorption coefficient. With this method, the dose along the voxels a photon encounters in its path between successive collisions is accounted for, resulting in a drastic variance reduction. The TLE method requires no tracking of secondary electrons, hence energy is deposited locally (44). Secondary electrons are only relevant very close to the source. For Ir-192, the dose may be approximated as electronic kerma within 1% at distances greater than 2 mm (45). Since the mass energy absorption coefficient is selected according to the voxel material, the calculated dose corresponds to dose to medium in medium $\left(D_{m,m}\right)$, as recommended by TG-186 (16). TOPAS calculates the statistical information (mean, variance, or standard deviation) following a stable algorithm from Donald E. Knuth, 2014 (46).

Data of the generic MBDCA-WG Ir-192 source

The generic MBDCA-WG Ir-192 brachytherapy source (36) was modeled. Parameters extracted with TOPAS such as the photon energy emission spectrum, the air-kerma strength and the dose-rate constant were compared with the reference data (36, 47). The photon energy spectrum was extracted with the source surrounded by vacuum except for an air cell of 10 × 10 × 0.05 cm³ located at 100 cm from the source along the transverse axis of the source. The initial photon spectrum was taken from the National Nuclear Data Center (48, 49) considering an average of 2.3002 photons/Bq. A low energy limit of 10 keV was used. The electron spectrum was not considered. Secondary electrons were not tracked and the local energy deposition by electrons was considered. The cut-off value for photons was 50 μm. The total of generated photons was 10¹¹. Based on the energy spectrum, the air-kerma strength was estimated (2). With the source located at the geometric center of a 40 cm side water cube (as per AAPM/ESTRO HEBD recommendations (20)), the dose-rate constant was extracted (2) by scoring the dose to water, using the implemented TLE method, in a 1 mm³ voxel located at 1 cm from the source centre along the transverse axis of the source. The number of generated photons were 10⁹.

Water cube phantom tests

The four Joint AAPM/ESTRO/ABG MBDCA-WG test cases (36, 37) were simulated and compared with the reference data (MCNP6 MC code (50)) from the AAPM/IROC Houston Source Registry (47). The aforementioned cases are well-defined voxelized models proposed for MBDCA commissioning and dose comparisons. Case 1 “TG-43” was designed to approximate TG-43 conditions where the generic MBDCA-WG Ir-192 source is centered in a 51.1 cm side water cube. Case 2 “source centered in water” refers to a 20.1 cm side water cube centered in a 51.1 cm side air cube; the generic source is centered in the water cube. Case 3 “source displaced” uses the case 2 phantom but the source is displaced 7 cm along the positive x axis. Case 4 “source centered in applicator” also uses the case 2 phantom but the source is centered in the TG-186 shielded applicator (37). For all cases, the dose was scored in a centered 20.1 cm side cube using 1 mm³ voxels with the implemented TLE scorer. The number of emitted photons were 5×10¹⁰ yielding statistical uncertainties of < 0.2% measured at 10 cm from the source. The comparison was performed through histograms of the local and global dose difference ratio volumes. The local dose difference ratio was defined as ${\text{Δ}D}_{\mathit{LOCAL}}(\text{\%})=100\times \frac{D(r)-D_{\mathit{ref}}(r)}{D_{\mathit{ref}}(r)}$ where $D(r)$ is the TOPAS dose and $D_{\mathit{ref}}(r)$ is the reference MCNP6 dose at any point. The global dose difference ratio was defined as ${\text{Δ}D}_{\mathit{GLOBAL}}(\text{\%})=100\times \frac{D(r)-D_{\mathit{ref}}(r)}{D_{\mathit{ref}}\left(r_{\mathit{ref}}\right)}$ where $D_{\mathit{ref}}\left(r_{\mathit{ref}}\right)$ is the reference MCNP6 dose at the reference point. Note that the local dose difference ratio is with respect to each voxel of the reference volume, whereas the global dose difference ratio is with respect to a unique relevant reference point. The reference point for case 1 and 2 was located at (−1 cm,0,0), for case 3 at (6 cm,0,0), and for case 4 at (−2.3 cm,0,0). Dose volumes were normalized to the corresponding reference point before calculations. In all cases, voxels within the source and/or applicator were omitted from the analysis. Also, TOPAS datasets were visually presented as scaled relative dose maps according to $\left(D(r)\times {\left(r-r_s\right)}^2\right)/\left(D\left(r_{\mathit{ref}}\right)\times {\left(r_{\mathit{ref}}-r_s\right)}^2\right)$ where r_s is the source position equal to (0,0,0) for cases 1, 2 and 4, and (7 cm,0,0) for case 3.

The variance reduction provided by the TLE method was studied. The relative standard deviation was calculated as a function of the number of histories for the implemented TLE scorer and the default analog TOPAS dose scorer DoseToMedium (DTM). The generic source was centered in a 51.1 cm side water cube (test case 1 geometry). The standard deviation and the mean value of the absorbed dose were extracted in a 1 mm³ voxel located at 1 cm along the source transverse plane. The number of histories were varied from 10⁵ to 10¹⁰. The relative efficiency of the TLE scorer with respect to the DTM scorer was calculated as ${ϵ}_{\mathit{TLE}/\mathit{DTM}}=t(\mathit{DTM}){\sigma }_{\mathit{\text{rel}}}^2(\mathit{DTM})/t(\mathit{TLE}){\sigma }_{\mathit{\text{rel}}}^2(\mathit{TLE})$ where $t$ is the computation time and ${\sigma }_{\mathit{rel}}^2$ is the estimated relative variance for both scorers.

Clinical cases

Three clinical cases were studied: a prostate case, a palliative lung case, and a breast case. These cases were previously used to validate a commercial treatment planning system (9) and they represent a good range in heterogeneity and scatter conditions of HDR brachytherapy treatments. The prostate case was a 19×19×20.8 cm³ volume of 104 CT slices with 2 mm slice thickness. The pixel spacing was 0.371 mm in the x and y directions. The patient included the prostate (target), bladder, urethra, and rectum segmented volumes. The cortical bone was segmented by histogram thresholding. Seventeen catheters with 111 active dwell positions were simulated. Prescription dose was 15 Gy to the clinical target volume (CTV) in a single fraction. The lung case was a 35×35×20.4 cm³ volume of 136 CT slices with 1.5 mm slice thickness. The pixel spacing was 0.684 mm in the x and y directions. The patient included the lungs and bronchus segmented volumes. One catheter went through the bronchus to the left lung with 19 active dwell positions. Prescription dose was 5 Gy at 1 cm from the catheter wall. The breast case was a 50×50×9 cm³ volume of 72 CT slices with 1.25 mm slice thickness. The pixel spacing was 0.977 mm in the x and y directions. The patient included the left lung, ribs, and target segmented volumes. Seven channels with 45 active dwell positions in a SAVI applicator (51) were simulated. Prescription dose was 3.4 Gy to the CTV.

Clinical cases were simulated with the microSelectron-HDR v2 Ir-192 source model. Spectrum and energy limit were the same as in section Data of the generic MBDCA-WG Ir-192 source. Patient geometries were created from segmented structures, and TG-186 materials (16) were assigned following the scheme of table 2 in ref (9). Note that this scheme simulated worst-case scenarios by assigning air to structures such as rectum (prostate case), lung (lung and breast cases), and struts (breast case). For TOPAS simulations, each structure had assigned an integer identification number and each of these numbers assigned a specific material. This imaging to material converter is known as ByIntegerID in TOPAS. Source position, orientation and number of generated photons were varied, using the TOPAS Time Feature system, according to each dwell position and time. The source was inserted in the CT geometry using the layered mass geometry method (35) which is included in TOPAS. For all cases, the number of generated photons were 10⁹. Dose was scored using the TLE scorer in a dose grid cloned by TOPAS from the reference RT Dose DICOM file. The dose grid was aligned with the CT geometry. TOPAS results were compared with the reference data (9) (ALGEBRA MC code (29)). Dose ratio maps (TOPAS/ALGEBRA) were calculated and visually presented with the isodose lines of each dose map. Since the dose grids were identical, histograms of the ${\text{Δ}D}_{\mathit{GLOBAL}}$ difference were calculated as well. Cumulative dose volume histograms (DVH) were calculated for the segmented volumes.

Results

MBDCA-WG Ir-192 source data

The air-kerma strength of the generic MBDCA-WG source was $S_K=(9.772\pm 0.001)\times {10}^{-8}{\text{UBq}}^{-1}$, and the dose-rate constant was $\text{Λ}=1.1107\pm 0.0005{\text{cGyh}}^{-1}{\text{U}}^{-1}$. Reported uncertainties considered one standard deviation. Figure 1 presents the energy fluence photon spectrum and its comparison with the reference data (36).

FIGURE 1.

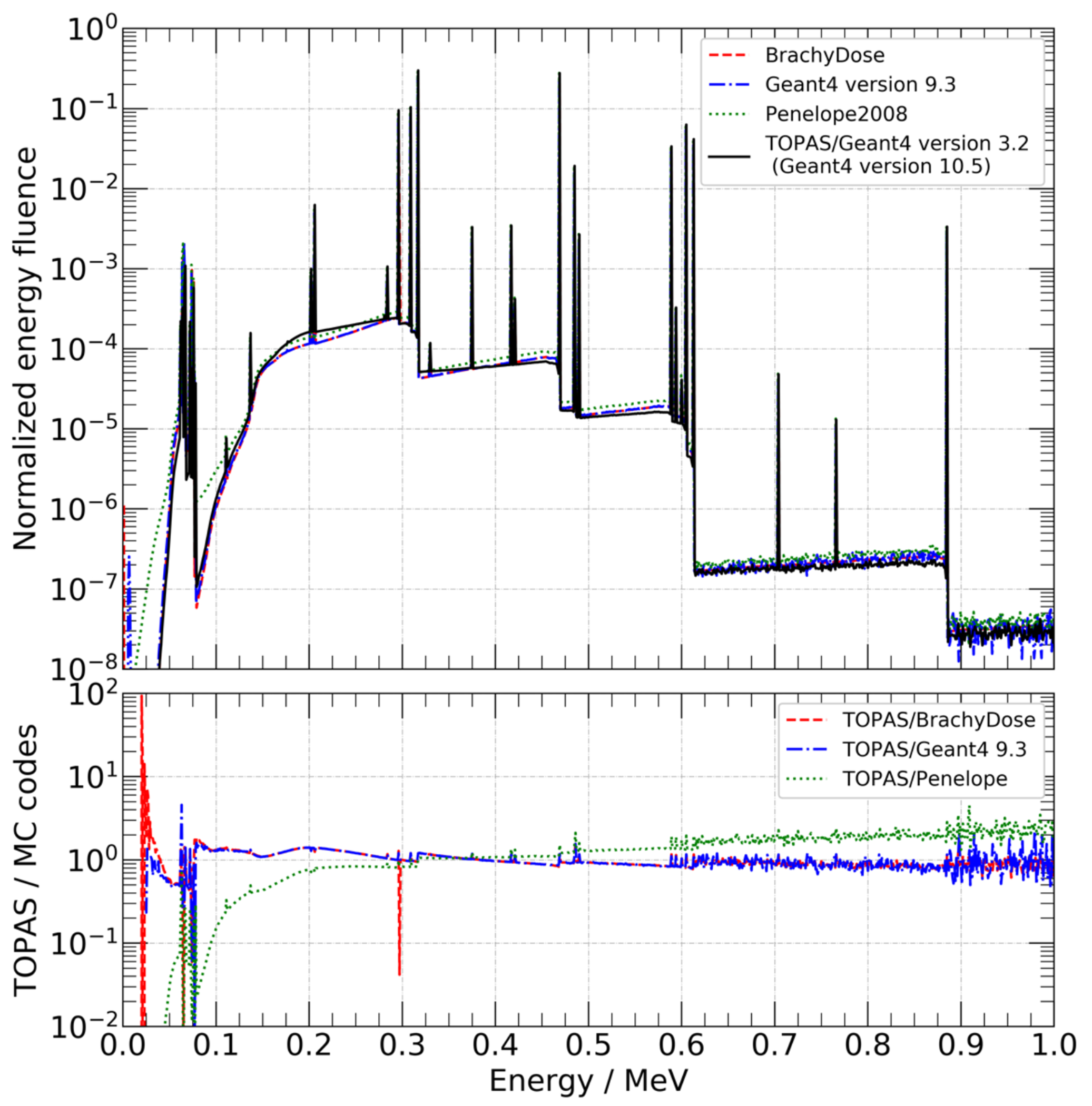
Top panel: energy fluence photon spectrum exiting the source capsule obtained with TOPAS and compared with the reference data (Ballester et. al. 2015 (36), personal communication with F. Ballester). Bottom panel: ratio of TOPAS/Geant4 to other codes. In all codes, the energy bin is 1 keV.

Water cube phantom tests

Results of test cases 1-2 are found as supplementary material. Results of test cases 3-4 are presented in figure 2 and 3. To illustrate the dose distribution obtained with TOPAS, two representative planes are depicted, z = 0 cm in top-left panels and y = 0 cm in middle-left panels. In top-right and middle-right panels, the visual comparison between TOPAS and MCNP6 is presented as the ${\text{Δ}D}_{\mathit{LOCAL}}$ ratio corresponding the same representative planes. Bottom-left panels contain the ${\text{Δ}D}_{\mathit{LOCAL}}$ histogram between −5% and 5% and bottom-right panels contain the ${\text{Δ}D}_{\mathit{GLOBAL}}$ histogram between −0.4% and 0.4%. White regions in test case 4 represents the applicator. The relative efficiency of the TLE scorer was ${ϵ}_{\mathit{TLE}/\mathit{DTM}}$ = 237. The average calculation time for tests cases, when scoring with the TLE, was 44 ± 5 s per 10⁶ histories for 32 cores Intel E5-2683 v4 Broadwell of speed 2.1GHz.

FIGURE 2.

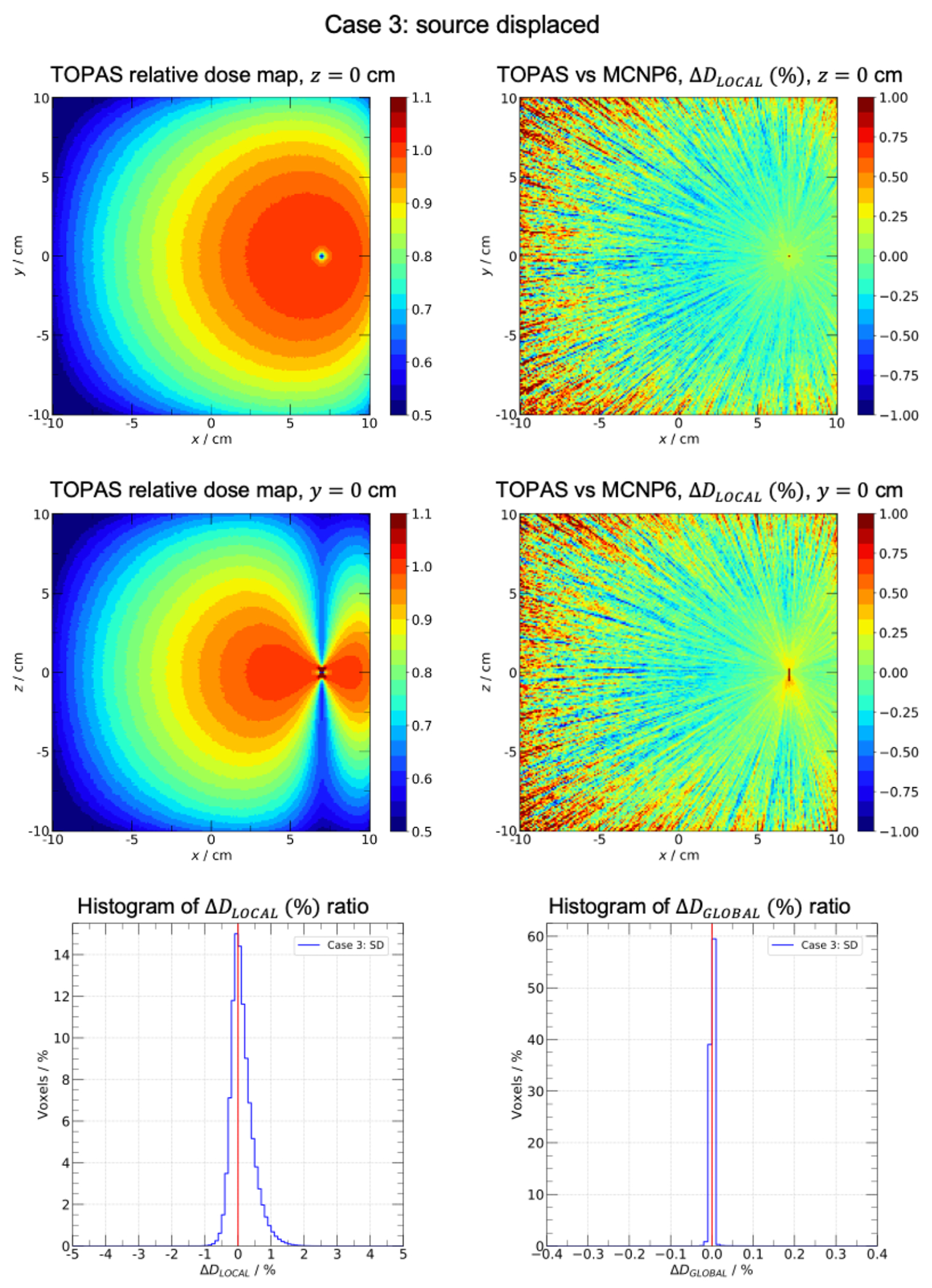
Case 3: source displaced. Water cube of side 20.1 cm centered in a 51.1 cm side air cube. The generic MBDCA-WG Ir-192 source is displaced 7 cm along the positive x axis. Top-left and middle-left panels: TOPAS scaled relative dose maps in planes z = 0 and y = 0. Top-right and middle-right panels: local dose difference ratio ${\text{ΔD}}_{\mathrm{LOCAL}}$ (%) in planes z = 0 and y = 0. Bottom-left and bottom-right panels: histograms of ${\text{ΔD}}_{\mathrm{LOCAL}}$ (%) and ${\text{ΔD}}_{\mathrm{GLOBAL}}$ (%) ratios, respectively.

FIGURE 3.

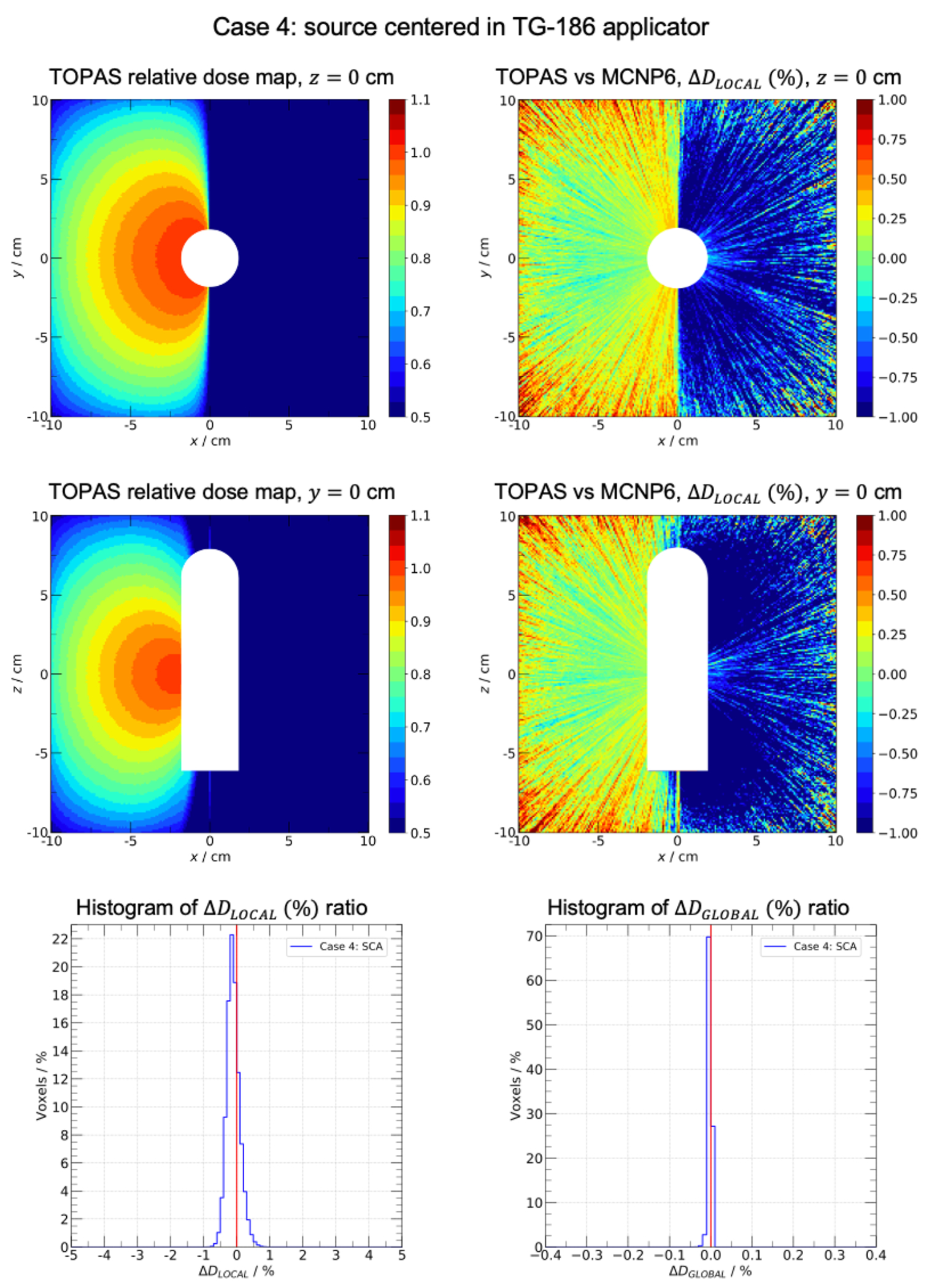
Case 4: source centered in applicator. Water cube of side 20.1 cm centered in a 51.1 cm side air cube. The generic MBDCA-WG Ir-192 source is centered in the TG-186 shielded applicator. Top-left and middle-left panels: TOPAS scaled relative dose maps in planes z = 0 and y = 0, white regions represent the applicator position. Top-right and middle-right panels: local dose difference ratio ${\text{ΔD}}_{\mathrm{LOCAL}}$ (%) in planes z = 0 and y = 0. Bottom-left and bottom-right panels: histograms of ${\text{ΔD}}_{\mathrm{LOCAL}}$ (%) and ${\text{ΔD}}_{\mathrm{GLOBAL}}$ (%) ratios, respectively.

Clinical cases

Results of prostate and palliative lung cases are presented in figure 4 and 5. Results of breast case are found as supplementary material. Representative slices of the dose distributions obtained with TOPAS are depicted in the top-left panels. In top-right panels, the dose ratio maps TOPAS/ALGEBRA are presented along with the isodose lines obtained from dose maps. Bottom-left panels contain the histograms of the global dose difference ratio ${\text{Δ}D}_{\mathit{GLOBAL}}$ between −4% and 4%. The cumulative DVHs for segmented structures are presented in the bottom-right panels. Table 1 contains dosimetry metrics extracted from the DVHs for prostate and breast cases. The calculation time was 6.3, 6.9, and 19.5 min per 10⁶ histories for breast, lung, and prostate cases for 40 cores Intel Gold 6148 Skylake of speed 2.4 GHz.

FIGURE 4.

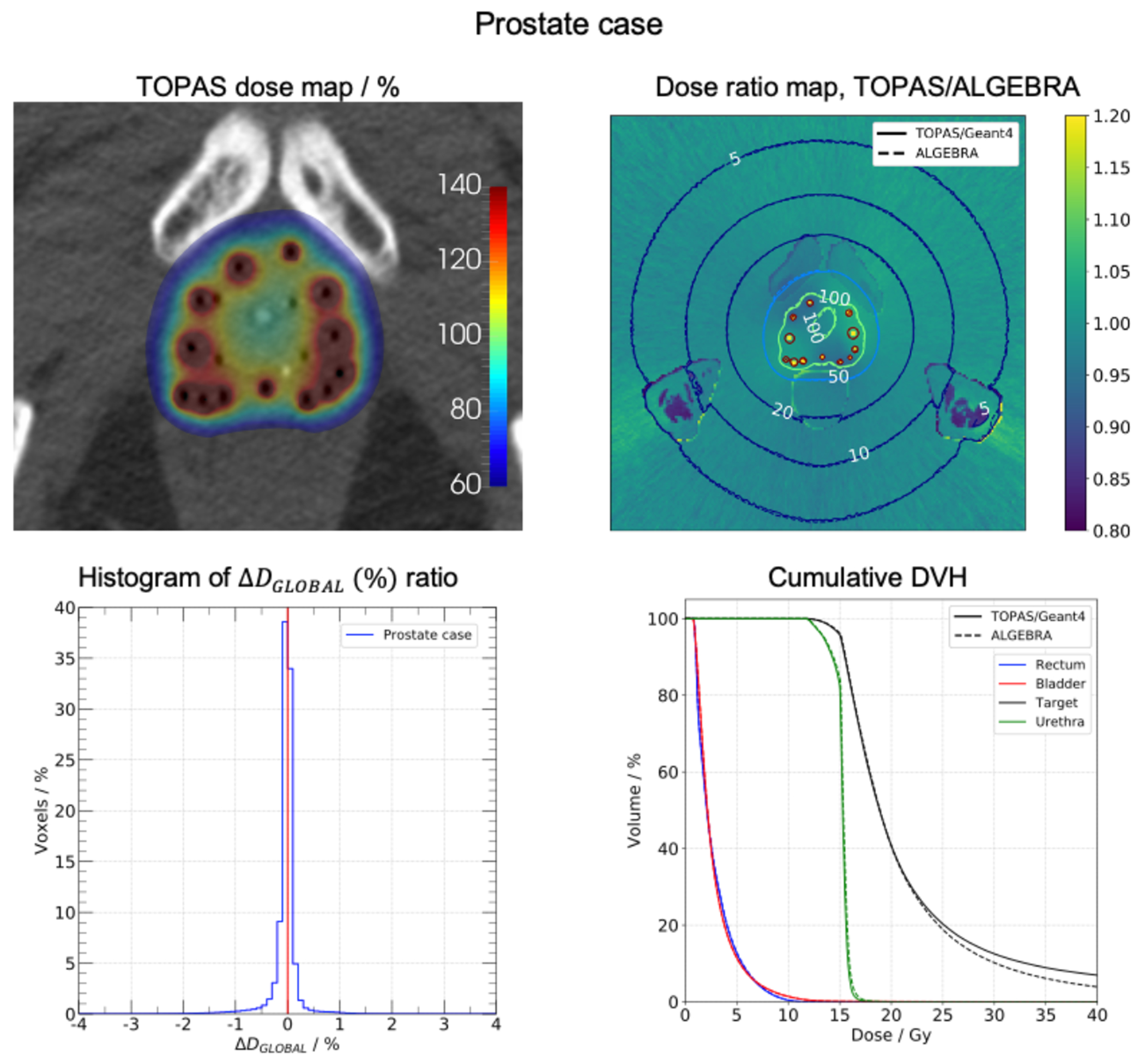
Prostate case. Top-left: dose map obtained with TOPAS. Top-right: dose ratio map TOPAS/ALGEBRA, the isodose lines of each dose map are shown. Bottom-left panel: histogram of ${\text{ΔD}}_{\mathrm{GLOBAL}}$ (%) ratio. Bottom-right panel: cumulative DVH for segmented structures.

FIGURE 5.

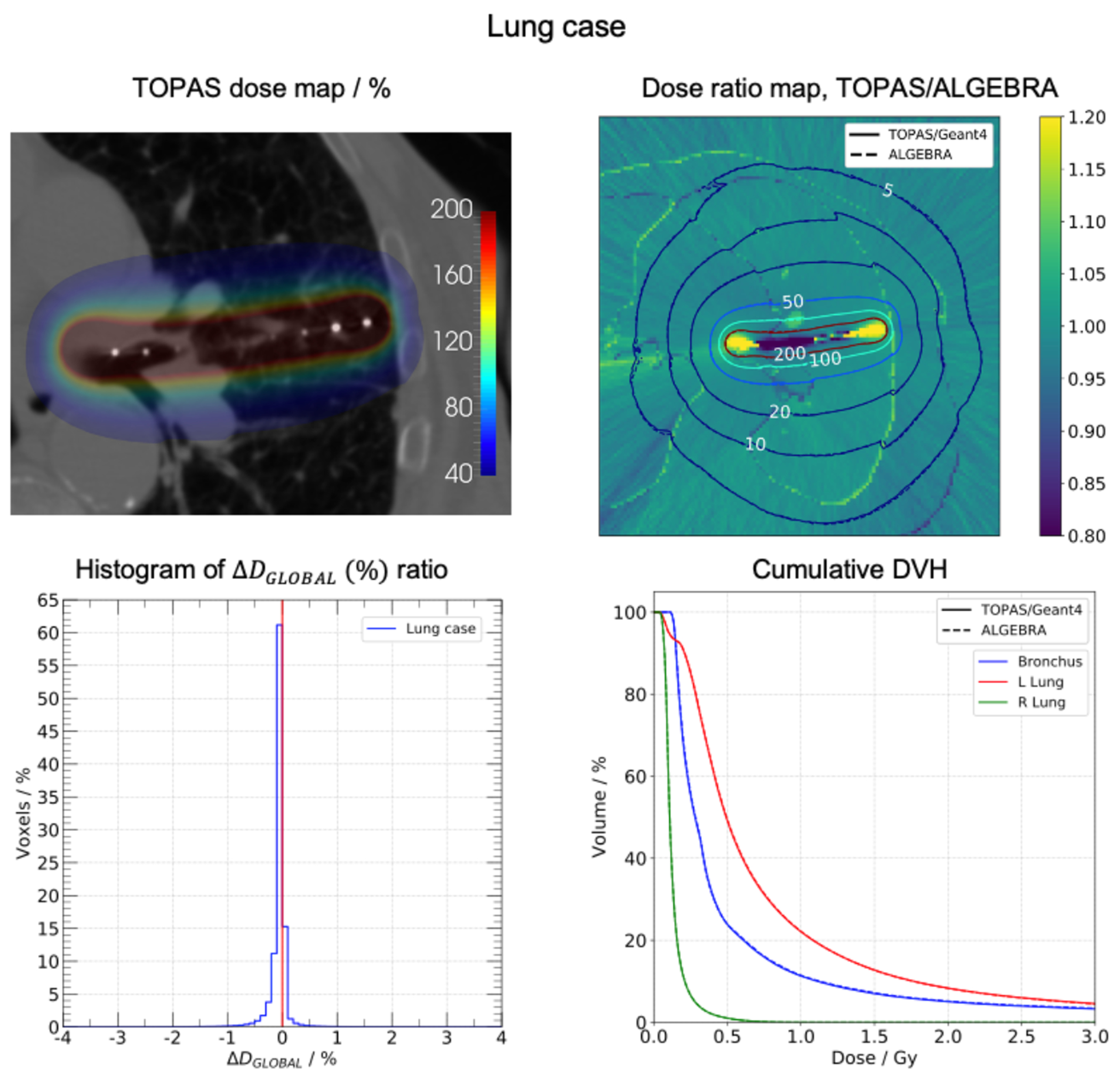
Lung case. Top-left: dose map obtained with TOPAS. Top-right: dose ratio map TOPAS/ALGEBRA, the isodose lines of each dose map are shown. Bottom-left panel: histogram of ${\text{ΔD}}_{\mathrm{GLOBAL}}$ (%) ratio. Bottom-right panel: cumulative DVH for segmented structures.

Table 1.

DVH metrics for prostate and breast cases

	ALGEBRA	TOPAS/Geant4
Prostate (Rx = 15 Gy)
V100 (%)	96.1	95.6
V150 (%)	27.0	27.4
V200 (%)	10.2	12.5
D90 (Gy)	15.5	15.5
D50 (Gy)	18.9	18.9
Rectum D2cc (Gy)	7.6	7.5
Breast (Rx = 3.4 Gy)
V100 (%)	80.8	80.3
V150 (%)	37.9	38.0
V200 (%)	19.3	18.9
D90 (Gy)	3.1	3.0
D50 (Gy)	4.5	4.5

DVH = dose-volume histogram; TOPAS = TOol for PArticle Simulation.

Discussion

Generic MBDCA-WG source data

The air-kerma strength showed an agreement of 0.3% with respect to the reference (36). The dose-rate constant was within 0.01% of the reference value (36). In figure 1, it is possible to see the differences among MC codes in predicting the photon spectrum exiting the source. The main variations are explained by the different approaches used to obtain the spectra. The reference work counted photons to calculate the radiant energy whereas, the present work calculated fluence as the track-length density. Note that the Geant4 9.3 simulation used the so-called standard physics list, whereas TOPAS 3.2/Geant4 10.5 used the Livermore physics list. In general, the recommended physics list for medical physics applications is the standard physics list option 4 which was developed to provide the most accurate Geant4 physics models, irrespective of CPU performance (38). Similar to the standard physics list option 4, the Livermore physics list uses the same model for low-energy gammas and electrons at the energy range useful for brachytherapy applications. Hence, brachytherapy simulations using the standard physics list option 4 or the Livermore physics list are expected to be equivalent within statistical uncertainties. Interested readers are referred to the report on G4-Med, a benchmarking and regression testing system of Geant4 for medical physics applications (38). Despite the differences seen in the photon energy emission spectrum, they were not significant as confirmed by the air-kerma strength and dose-rate constant results.

Water cube phantom tests

Test case 1 evaluated TOPAS under TG-43 conditions. 99.9% of voxels had a local dose difference ratio within ±1% with the maximum of the distribution at 0.2%. For the global dose difference ratio, 99.9% of voxels were within ±0.1% with the maximum of the distribution at 0.01%. The reader should note the difference between evaluating the TG-43 dosimetry parameters and the evaluation performed for test case 1. Evaluating the TG-43 parameters involves calculations in several points of interest covering the range of r and θ to be used in clinical practice, whereas evaluating test case 1 compares locally and globally a full voxelized volume of clinically relevant size. Test case 2 assessed TOPAS under non-TG43 scatter conditions by using a smaller water phantom than in case 1. 99.5% of voxels had a local dose difference ratio within ±1% with the maximum of the distribution at 0.1%. For the global dose difference ratio, 99.9% of voxels were within ±0.1% with the maximum of the distribution at 0.01%.

The dose distribution presented a fall-off near the water phantom edges as well as border effects near the corners. This behavior was consistent with the presence of the water-air interfaces. Test case 3 (figure 2) evaluated a more complex scatter condition scenario, with the source displaced near the phantom edge. 96.9% of voxels had a local dose difference ratio within ±1% with the maximum of the distribution at 0.1%. For the global dose difference ratio, 99.9% of voxels were within ±0.1% with the maximum of the distribution at 0.01%. The loss of lateral equilibrium near the water-air interface is well illustrated in the dose map distributions. In addition, fluctuations were seen in regions far from the displaced source due to the decrease of particle fluence. Test case 4 (figure 3) assessed the effect of a shielded applicator on the dose distribution. 99.9% of voxels had a local dose difference ratio within ±1% with the maximum of the distribution at 0.2%. For the global dose difference ratio, 99.9% of voxels were within ±0.1% with the maximum of the distribution at 0.01%. For all 4 cases, differences within statistical uncertainties are expected when comparing TOPAS dose distributions with the reference dataset (37). From the original work of Ballester et. al. (36), the uncertainty budget shows an expected uncertainty of the MC simulation of the order of 0.25%, therefore the uncertainty of the difference is the order of 0.4%. All four cases simulated with TOPAS showed excellent agreement and are compatible with the reference data within uncertainties.

The implemented track-length estimator method reduced the number of histories required to reach a reasonable statistical uncertainty. Results showed that for the same uncertainty, the TLE scorer requires about 277 times less histories than the analog DoseToMedium scorer, with a 1% level reached at 14.4M histories. This behavior is expected since the analog scorer only deposits the dose at the interaction points. When using the TLE scorer, the penalty in computation time was relatively small by a factor of 1.17 for the same number of histories.

Clinical cases

In prostate case (figure 4), isodose lines indicated that TOPAS yielded a dose distribution nearly identical to the ALGEBRA one. Minor deviations were seen in the bone marrow region due to differences in material assignment. The original work assigned cortical bone material to the entire bone structure, including the bone marrow (9). The present work assigns water rather than cortical bone material to this bone marrow. Deviations are explained by the different composition and density of assigned materials. The maximum of the histogram was at −0.1%, and 97.5% of voxels had a global dose difference ratio within ±1%. The target DVHs showed clear differences for volumes less than 30%. These variations corresponded to the source dwell position regions as can be seen in the dose ratio map. In the reference work (9), the model source was not included in the geometry hierarchy and phase space files were used for simulations. In contrast, source geometry was included in TOPAS simulations resulting in the discussed differences. From the prostate results of table 1, TOPAS V₁₀₀ exhibited a difference of −0.5% with respect the reference. V₁₅₀ and V₂₀₀ were greater than reference values by 0.4% and 2.3%, respectively. D₉₀ and D₅₀ presented equal values. Rectum D_2cc had a small difference of 0.1 Gy. Urethra, bladder, and rectum DVHs were compatible.

In the palliative lung case (figure 5), TOPAS dose distribution matched the ALGEBRA distribution. Variations in the 5% isodose lines were small but discernible. In the body-lung interfaces, jagged lines were exhibited. Differences in the dose ratio map were seen in the source dwell positions regions. However, these variations were not visualized in the left lung DVH because of the small volume portion that the region represents. The maximum of the histogram was at −0.1% and 98.5% of the voxels had a global dose difference ratio within ±1%. Bronchus and lungs DVHs were equivalent.

In the breast case, noticeable shifts were seen in the TOPAS isodose lines, especially in the 20% and 10% lines. The dose ratio map exhibited heterogeneities in the struts sector, more specifically in the source dwell position regions. The breast case presents complex conditions of heterogeneity and scattering because of the body-air interfaces. Due to these conditions, variations are emphasized. The maximum of the histogram was at −0.1% and 98.1% of voxels had a global dose difference ratio within ±1%. PTV DHVs showed minor differences especially for volumes greater than 80%. From the breast results of table 1, TOPAS V₁₀₀, V₁₅₀, and V₂₀₀ had minor differences of −0.5%, 0.1%, and −0.4% with respect to the reference values. D₉₀ values were close with a 0.1 Gy difference. D₅₀ presented equal values. Ribs DVHs showed a small shift in concordance with the isodose lines behavior. Lung DVHs were compatible and variations were masked by the small values of absorbed dose in the relatively large lung volume.

The prostate, lung, and breast cases presented a good mix of challenges that TOPAS can encounter in clinical geometries (table 1 and figure 4–5). The prostate case showed abrupt shifts in the rectum interface since all the rectum was assigned to air as a worst-case scenario (air density equals to 0.0012 g/cm³). Noticeable changes were also visualized in the cortical bone regions which had density of 1.92 g/cm³. The lung case demonstrated the source positioned in an air volume surrounded by water. Body-air interfaces showed the expected abrupt shifts. The breast case presented the biggest challenge due to the air outside the breast, in the struts, and in the lung. The complex conditions of the breast case were exhibited in the isodose lines of the dose ratio map. Results such as the dose ratio maps, the histograms of the global dose difference ratio, and the cumulative DHVs, showed that TOPAS performed well with voxelized clinical geometries, and the calculated dose volumes were equivalent to those of ALGEBRA.

Conclusions

In this study, the TOPAS Monte Carlo toolkit was validated for HDR brachytherapy applications. TOPAS is capable of handling the 3D geometries of sources, applicators and patient geometries using its much-simplified user interface for simulations. Overall, brachytherapy simulations made with TOPAS showed excellent agreement with the reference data. The photon energy emission spectrum, air-kerma strength and dose-rate constant of the MBDCA-WG Ir-192 source are equivalent to the reference data. The four Joint AAPM/ESTRO/ABG MBDCA-WG test cases simulated with TOPAS are equivalent with the reference AAPM/IROC Houston Source Registry reference data. The test cases agreed with the MC reference data within [1%, 1%] locally for at least 96.9% of voxels and within [0.1%, 0.1%] globally for at least 99.9% of voxels. The versatile extension mechanism allows to implement a track-length estimator method for dose scoring which provides an efficiency improvement of a factor of 237 over the default analog scorer (case 1 geometry). TOPAS is able to simulate voxelized clinical geometries with complex conditions in heterogeneity and scattering. Clinical cases agreed with the MC reference data within [1%, 1%] globally for at least 97.5% of voxels. These results show TOPAS to be a state-of-the-art MC toolkit for brachytherapy simulations having a much-simplified set-up for particle simulation and geometry description compared with the underlying Geant4 code.