Abstract
This study focused on the challenges posed by the fluctuating demand for COVID-19 vaccines, considering factors such as side effects, religious objections, and absenteeism, which result in the accumulation of excess vaccines. Recognizing the resulting social, economic, and environmental issues, this study investigated the application of a lateral transshipment policy for the management of the inventory of short-term vaccines, considering related unpredictabilities. A discrete event simulation built on foundational principles derived from a mixed-integer linear programming model was employed to explore the dynamics of mRNA-based vaccine distribution among two hospitals based on lateral transshipment and reordering policies. Through the simulation of various scenarios over periods of 1-30 days, transshipment based on the availability policy is employed to determine the quantity of vaccines to be transshipped, constrained to vial amounts, and the (s, S) inventory system for reordering. The results of this study underscore the efficacy of lateral transshipment, particularly in situations where demand discrepancies exist between hospitals, thereby revealing its superiority over non-transshipment strategies within 7 days.
Keywords: Vaccine, Lateral transshipment, Uncertainty, Discrete event simulation, Inventory
Subject terms: Health policy, Health services
Introduction
In late 2019, COVID-19 emerged as a novel virus, distinct from the six known species, that prompted global health and industrial challenges. Over 178 million COVID-19 cases and 3.84 million deaths associated with COVID-19 have been recorded worldwide1. Governments adopted strategies, such as social distancing and teleworking, to mitigate its spread, while the pharmaceutical industry worked on accelerating vaccine development. The development of vaccines against infectious diseases is among the most effective strategies for mitigating their effects. However, this achievement is not sudden; rather, it is the culmination of decades of scientific research and technological advancement2. The urgency of the pandemic has sparked remarkable global efforts. By November 2020, more than 210 potential vaccines were in the pipeline, with 11 advancing to Phase 3 clinical trials3. A key factor in this rapid progress was the adoption of cutting-edge technologies such as mRNA in the vaccine development process4. Among these rapid and competitive developments, the Pfizer-BioNTech vaccine is considered to be up to 95% effective against severe diseases or death1.
mRNA vaccines introduce the viral antigen gene in mRNA form into the body, which then produces antigen proteins and stimulates an immune response. However, these vaccines face a significant challenge. The main component, that is, mRNA, is susceptible to degradation by RNA-degrading enzymes (RNases)5. This vulnerability necessitates special storage and transportation conditions such as ultralow-temperature freezing to maintain stability, thus highlighting the need for meticulous management in terms of storage, transportation, and hygiene6,7. Therefore, the specific guidelines for handling vaccines, particularly after thawing, necessitate several key protocols8:
Vaccines should be administered on the same day they are thawed.
Once opened, the vaccines must be discarded after a specified period.
Any excess vaccine should not be gathered for use; instead, it should be disposed of appropriately.
Vaccines should not be transported to other hospitals once they have been opened.
The production of vaccines has surged dramatically because of the development of mRNA technology and its effectiveness against COVID-19, as reflected in the increase in demand9. By June 25, 2021, the worldwide battle against COVID-19 had achieved significant progress, with the production and global distribution of more than 2.88 billion vaccine doses. Through an international vaccination campaign, approximately 1.77 billion people in 213 countries were administered at least one vaccine dose10. Despite the clinical superiority of mRNA vaccines in combating COVID-19, public skepticism, fueled by misinformation, religious beliefs, or personal concerns11, resulted in erratic vaccination rates. Consequently, studies have focused on conducting extensive research on vaccine hesitancy owing to its profound effect on vaccination rates12–14.
Overproduction and underconsumption, which are primarily attributed to vaccine hesitancy, present significant challenges in supply chain management. Consequently, governments face either a surplus or shortage of vaccines15, which complicates inventory planning and distribution. In terms of supply chain and inventory management, residual vaccines are plagued by several problems, thus highlighting the need for efficient vaccine redistribution. These problems include:
Wastage and expiry Residual vaccines, or surplus vaccine doses, can be problematic in cases of more supply than demand. This can result in wastage if the vaccines expire before use. Vaccine shelf life and storage requirements (e.g., cold chain maintenance) play significant roles in this.
Equity issues Wealthier countries or regions may have surplus vaccines, whereas poorer regions struggle to obtain sufficient doses. This inequality poses ethical and public health challenges on a global scale.
Public health implications Unused vaccines indicate a missed opportunity to control the spread of the virus. High rates of vaccination are vital to achieving herd immunity and reducing the overall impact of the pandemic.
As previously mentioned, vaccine characteristics underscore their perishable nature which means that it has a limited lifetime16 after thawed. The intricacies of the vaccination process require high precision. In practical scenarios, medical factors such as allergies and side effects17, coupled with social factors such as personal beliefs and instances of missed appointments18, contribute to the unpredictability of vaccination schedules, or, essentially, the demand for vaccines. This uncertainty complicates the realization of just-in-time vaccination strategies and thus leads to residual vaccination costs. For example, the Irish Health Service Executive reported that €95,000,000 was spent on unused COVID-19 vaccines last year19. Consequently, there is a critical need for effective inventory management to optimize and satisfy the fluctuating demand for vaccination.
This study aimed to enhance the efficiency of vaccine inventory management via lateral transshipment. This process, which typically involves the transfer of products between retailers within the same organization, is adaptable to healthcare services. Hospitals administering vaccines may operate independently and are, conventionally, competitors; however, their involvement in vaccination transcends competitive dynamics owing to the overarching goal of public health services. Vaccination scheduling in these hospitals is conducted on an hourly basis through an online platform, where individuals with appointments are expected to adhere to their designated times. We extended the above to analyze the economic effects of a redistribution policy when two hospitals have unequal vaccine stocks and designed mathematical models and simulations that reflected the characteristics of the vaccine and vaccination operations. However, several detailed assumptions are necessary to incorporate the characteristics of vaccines and vaccination into the model. Here are the details of the problem while modeling.
Each individual is entitled to one dose of the vaccine.
The demand for appointments at each clinic varies randomly, following a uniform distribution with an average of and a standard deviation of .
Patients arriving within their scheduled time are vaccinated within an hour. The vaccination schedules are simply considered as first-come-first-served manner.
Hospitals operate on a fixed daily schedule.
Backorders are not accounted for; a shortage of vaccines at any given time incurs an underage cost.
The underage cost is also applicable if an appointment cannot be fulfilled owing to a vaccine shortage.
Vaccine suppliers maintain sufficient stock; thus, their inventory levels are not a concern during reorders.
Vaccine orders placed with a provider are delivered 2 h after ordering.
In the case of lateral transshipment to a nearby hospital, the vaccine is delivered within 1 h of transshipment.
Demand for booking vaccines is calculated in dose units, whereas inventory adjustments and lateral transshipment is conducted in vial units.
Each hospital starts with an initial stock of vaccine vials.
The administration of second doses is not considered in this model.
Unused vaccine doses are discarded after one business day.
During vaccination, hospitals thaw and prepare the necessary number of vials as required.
mRNA vaccines require extra care in terms of transportation, including cold chain management and storage20. Therefore, in situations with unstable demand owing to the aforementioned social factors, the redistribution system of mRNA vaccines is more affected from temporal and physical perspectives. Thus, this study focused on mRNA vaccines and proposed a lateral transshipment policy aimed at optimizing vaccine distribution. This policy ensured an adequate supply while minimizing waste and environmental impacts. Lateral transshipment is often implemented in situations where retailers are in proximity to each other, facilitating the transportation of products within a considerably shorter timeframe. This enhances customer satisfaction and reduces order losses at relatively low costs21.
Methodologies such as mixed-integer linear programming (MILP) and discrete event simulation (DES) with lateral transshipment policies have been employed to solve problems related to the specific characteristics of vaccines. These approaches have been utilized in numerous studies to address various challenges in industrial and healthcare settings, including health and inventory management. MILP is a mathematical optimization technique that determines the optimal solution for a given problem based on a user-defined mathematical model. Although it can theoretically determine the optimal solution, actual adaptation to the field is challenging owing to its dimensionality. Consequently, the more responsive framework, DES, is frequently used in the field of inventory management. DES models the operation of a system as a sequence of discrete events over time. Each event occurs at a specific instant and signifies a change in the system state22. In contrast to continuous simulation, which models a system’s changes in a continuous time frame, DES jumps from one event to the next.
Under these two methodological pillars, inventory management is aimed at satisfying demand while minimizing costs. Such objectives optimize the stocking levels of on-hand items to consider the trade-off between inventory costs and demands, where inventory costs are mostly considered for holding, ordering, and underage costs. Considerable interest in inventory management has resulted in the consideration of stochastic models, such as newsvendors23 for a classical inventory issue that has been extensively studied in operations management24,25. DeYong26 extended this problem to include price setting using the newsvendor model, highlighting the importance of demand uncertainty in determining the optimal price. Watters27 explored the role of new communication technologies in electronic news delivery and emphasized the need for comprehensive and personalized news delivery. Besbes28 further examined the newsvendor problem in the context of decision-making, considering the trade-off between data quality and quantity.
Rastegar29 and Tavana30 proposed MILP models for equitable vaccine distribution in developing countries, focusing on influenza and COVID-19 vaccines, respectively. These models consider factors such as the vaccine type, storage requirements, and vulnerable populations. Sarigol31 introduced a multi-objective order allocation model with product substitution to minimize the number of inefficiently vaccinated individuals, postponed vaccinations, and purchasing costs. Thul32 proposed a stochastic optimization model for allocating vaccines and testing kits, considering uncertainty and resource scarcity. Wen33 utilized mixed-integer programming (MIP) to address the challenge of allocating COVID-19 vaccines across diverse groups. They revealed that enhancing the budget resulted in higher vaccination rates, thus enabling more individuals to receive the vaccine and facilitating the attainment of herd immunity with the available vaccine supply. These studies primarily concentrated on the vaccination operations of hospital groups, long-term operations, and factors concerning vaccine recipients, such as age, sex, underlying medical conditions, and the cost of vaccines. In contrast, the present study focused on the effectiveness of a vaccine redistribution policy among individual hospitals, particularly when surplus vaccines are in stock at smaller, non-major hospitals, and assessed its impact on public health.
Alshammari34 and Arora35 developed mathematical models to predict vaccination effectiveness, focusing on vaccination thresholds and the delay in the pandemic rise time, respectively. Kim36 introduced a compartmental model that considered the emergence of mutant viruses and the impact of multiple vaccinations on disease transmission. Vázquez-Abad37 used a hybrid simulation model to examine the effects of vaccination policies on healthcare systems. Çaglayan38 attempted to enhance pandemic management, strategizing, and readiness by developing a tool for capacity and workforce planning. This tool, designed using a simulation-based approach, aims to facilitate the implementation and dissemination of mAb treatments for COVID-19.
Collectively, these studies highlighted the crucial role of vaccination in controlling the spread of COVID-19 and the need for further research to optimize vaccination strategies. Despite numerous studies on various aspects of vaccination, our study specifically focused on the operational aspects of vaccine distribution during the COVID-19 pandemic. We focused on the act of vaccination itself and the critical aspect of managing the vaccine inventory. Thus, this study developed and examined a policy for managing vaccine inventory efficiently, addressing the cumulative imbalanced inventory levels caused by discrepancies between supply and demand over operational time buckets, and checking the feasibility of this phrase. A simulation was conducted to analyze the effects of the proposed policy over both short (less than a week) and longer (from 1 week to less than a month) periods to assess its effectiveness over time.
Lateral transshipment redistributes stock from retailers with excess stock to retailers that cannot satisfy customer demands or those facing significant losses owing to high risk39. There are two types of lateral transshipments: proactive and reactive. Proactive transshipment involves the prescheduled redistribution of stock among all points in an echelon to minimize handling costs, which is particularly beneficial in the retail sector, where such costs are significant. However, reactive transshipment is triggered by immediate stock shortages at one point, while others have adequate stock. This strategy is more suited to environments where the transshipment costs are lower than the costs of holding excessive inventory and failing to meet immediate demand40. Firoozi41 propose a scenario-based model for a two-stage multi-echelon system, demonstrating the benefits of lateral transshipments and multiple sourcing in reducing costs in 2020. Achamrah42 examine a two-level spare parts supply chain, incorporating transshipment and substitution under stochastic demands, highlighting their effectiveness in improving supply chain performance and Farghadani-Chaharsooghi and Karimi43 propose a robust optimization model for PRP incorporating outsourcing, lateral transshipment, and demand uncertainty, developing matheuristic algorithms for large-scale problems. Paul44 reported that it lowered the costs of slow-moving items with demand driven by nonhomogeneous or homogeneous Poisson processes. Naseraldin45 integrated lateral transshipments into a location inventory model to optimize the number and locations of retail outlets. Paterson40 conducted a comprehensive review of the literature on lateral transshipments, highlighting the influence of inventory system elements on transshipment methods. Several studies have focused on lateral transshipment policies for discrete events. Banerjee46 and Hachicha47 demonstrated the superiority of lateral transshipment approaches over non-transshipment. Liu48 reported that different transshipment network structures could significantly impact performance, with the “complete link” structure being the most effective. A lateral transshipment policy was employed to tailor the specific attributes of vaccines in the vaccine inventory DES with demands following a uniform distribution, and its impact effectiveness was analyzed.
As COVID-19 transitions from a pandemic to an endemic phase, the insights gained from our study remain pertinent. The strategies and methodologies outlined here are applicable to the current situation and can serve as a valuable reference for managing vaccine distribution in response to future outbreaks of infectious diseases, such as the Zika virus and Mycoplasma pneumonia. This study provides a deeper understanding of efficient vaccine inventory management during critical health crises.
Results
As mentioned in the introduction, the experiments reflect the problem setting of vaccine management, vaccination operations in hospitals, and vaccine transport between hospitals. The details of the applying assumptions to the model are described in the methods section. Experiments were conducted in two hospitals, considering two cases wherein the distribution of vaccine appointment demands were similar and different. For each scenario, the effectiveness of the policy was analyzed based on various changes in parameters. The mean, standard deviation, and specific parameters for the demand distributions of the two hospitals, denoted by and , respectively, are presented in Table 1. Two DES techniques, without lateral transshipment (DES-NLT) and with lateral transshipment (DES-LT), were employed to assess the short-term effectiveness and measure long-term efficiency. The vaccine administration demand for each hospital followed a probability distribution. To compare the effectiveness, the model was run 1,000 times, with averages considered for each cost and the total cost. The study was differentiated into two scenarios based on the nature of the demand distribution: one wherein both hospitals had differing demand distributions (Case 1), and another wherein they were similar (Case 2). Various parameters were adjusted to observe the resultant policy implications, including changes in vaccine vial size |I|, the initial stock of each hospital, and the associated costs. In Case 1, the demand for each hospital was determined by generating random numbers within 0–20 and 0–10, 2000 times, and the mean and standard deviation were calculated. Case 2 followed the same procedure, generating random numbers within 0–17 and 0–15. The Python Numpy package was used to generate demand from a uniform distribution49. Simulations were performed using Python SimPy50. The study period was segmented into intervals ranging from 1-30 days. To prevent excessively large fluctuations, the demand occurrences were confined within the range of each uniform distribution. The parameters used in the experiments and the demand statistics for Case 1 and Case 2 are summarized in Tables 2 and 3.
Table 1.
Default parameters of the simulation model.
| Parameters | Values |
|---|---|
| 15 | |
| 20 | |
| |I| | 5 |
| p | 30 |
| c | 45 |
| 55 | |
| 10 | |
| 400 |
Table 2.
All parameters used in the experiment.
| Parameter | Hospitals |
|---|---|
| (5,20), (15,20), (20,5), (20,15), (20,20) | |
| (5,5), (5,7), (7,5), (7,7) | |
| 3, 5, 7, 9 |
Table 3.
Demand statistics for each cases used in the experiment.
| Case 1 | Case 2 | |||
|---|---|---|---|---|
| Hospital | Hospital | Hospital | Hospital | |
| Mean | 10.5176 | 5.4951 | 11.108 | 9.956 |
| Std. | 1.4997 | 1.5 | 2.0175 | 2.5662 |
Case 1: Distinct mean and standard deviation
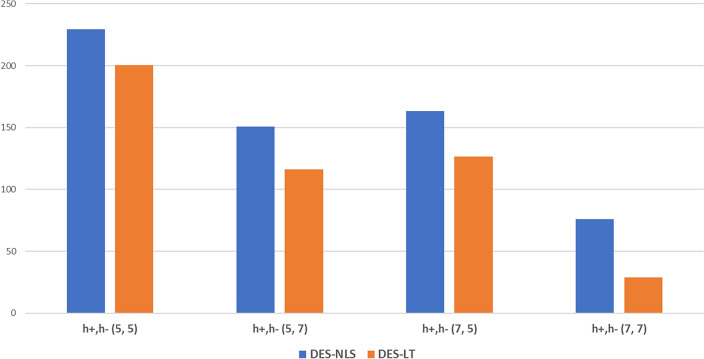
Figure 1 presents the total cost for a two-day operational period at varying initial inventory levels and under different demand distributions. The data indicate a reduction in total costs when implementing the proposed policy. On average, the difference between NLT and LT costs was 30 when the LT policy was applied. Notably, the costs were minimized when both hospitals started with seven vials each. Typically, an increase in initial inventory decreases the total costs. Specifically, it was observed that the cost was lower when the inventory levels are (5,7), as opposed to (7,5), suggesting a more efficient allocation when hospital had a higher initial inventory relative to demand and hospital had a lower one. This trend underscores the effectiveness of resource management policies.
Fig. 1.
Average total costs of Case 1 based on initial inventory over a two-day operation period.
Table 4 presents the variation in total cost with change in the initial inventory levels, particularly focusing on the inventory setup. In the shorter term (1, 2, and 3 days), the policy resulted in a decrease in the total costs. With an initial inventory of seven vials each, DES-LT was more effective than DES-NLT and generated a cost-benefit during the one-day experiment. At the 7-day mark (equivalent to 1 week), the total costs of DES-NLT and DES-LT exhibited similar tendencies. However, over longer periods (10, 20, and 30 days), the effectiveness of the LT policy decreased. For the one-day trial, there was an average 64% reduction in total costs compared with the NLT policy. The initial inventory of seven vials at both hospitals generally resulted in lower costs across all the periods examined. The policy proved economically beneficial in a one-day trial, with cost reductions of 62% and 23% by the end of three days for the two hospitals, respectively. By the end of the week, the policy had maintained its effectiveness. Thus, the policy demonstrated efficiency for shorter durations, particularly when the demand distributions between the two hospitals varied.
Table 4.
Results of the total cost for Case 1 with initial inventory variations.
| (5, 5) | (5, 7) | (7, 5) | (7, 7) | |||||
|---|---|---|---|---|---|---|---|---|
| Days/policies | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT |
| 1 | 183.5 | 136.24 | 98.93 | 52.98 | 102.96 | 51.56 | 15.43 | − 36.02 |
| 2 | 229.21 | 200.63 | 150.75 | 116.16 | 163.26 | 126.42 | 75.73 | 28.72 |
| 3 | 280.48 | 250.81 | 203.75 | 162.18 | 202.06 | 185.19 | 133.22 | 102.66 |
| 7 | 478.55 | 478.6 | 424.89 | 430.38 | 410.34 | 412.84 | 326.62 | 347.21 |
| 10 | 652 | 684.76 | 595.37 | 619.52 | 586.37 | 622.3 | 529.44 | 537.28 |
| 20 | 1201.14 | 1356.62 | 1137.92 | 1280.48 | 1109.27 | 1250.06 | 1017.55 | 1156.04 |
| 30 | 1705.02 | 1954.36 | 1637.19 | 1886.45 | 1593.07 | 1847.65 | 1520.74 | 1767.75 |
Cases where LT outperformed NLT are in bold. Minus values indicate revenue.
Table 5 details the costs for each period for hospitals and with initial inventories of seven and five vials, respectively, as listed in Table 4. At the one-day duration, the total cost decreased to 49.92% of NLT, with smaller decreases to 22.57% and 8.35% as days are increased to two and three days respectively. Similarly, overage cost decreased by 11%, 9.84%, and 7.09%, and reorder cost decreased by 2% for each day. The increased number of vaccinations due to the LT policy resulted in an increase in revenue and a decrease in total costs. When the LT policy is advantageous, the average overage, underage, and reorder costs are lower than under the NLT policy. Thus, lateral transshipment mitigated issues related to surplus vaccines and missed appointments owing to fluctuating demand. Moreover, it appeared to reduce the frequency of both excessive and insufficient vaccine doses, resulting in fewer reorders compared with the NLT policy. Thus, lateral transshipment was the primary factor influencing the economic effect (or cost reduction). A comparison of the total costs under the NLT and LT policies in Table 5 revealed that the total cost was significantly influenced by average underage and reorder costs. These two factors are critical for analyzing the policy’s impact, particularly when hospitals have different demand distributions.
Table 5.
Comparison results between two policies with initial inventory of 7 and 5 vials for each hospital. Note that the values are in average.
| (7, 5) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Policies | DES-NLT | DES-LT | |||||||
| Days/costs | Overage | Underage | Reorder | Total | Overage | Underage | Reorder | Transshipment | Total |
| 1 | 57.81 | 588.14 | 1312.63 | 102.96 | 51.45 | 572.04 | 1287.66 | 12.17 | 51.56 |
| 2 | 118.05 | 1330.8 | 2631.75 | 163.26 | 106.43 | 1332.62 | 2578.4 | 23.95 | 126.42 |
| 3 | 174.23 | 2064.7 | 3938.22 | 202.06 | 161.88 | 2082.16 | 3863.2 | 35.58 | 185.19 |
| 7 | 405.66 | 5020.56 | 9203.15 | 410.34 | 368.1 | 5093.94 | 9009.22 | 83.94 | 412.84 |
| 10 | 578.37 | 7253.62 | 13136.64 | 586.37 | 525.32 | 7377.48 | 12852.18 | 120.04 | 622.295 |
| 20 | 1158.53 | 14660.68 | 26264.7 | 1109.27 | 1057.38 | 14918.22 | 25736.15 | 240.66 | 1250.06 |
| 30 | 1738.95 | 22016.24 | 39363.83 | 1593.08 | 1595.87 | 22403.3 | 38606.81 | 360.42 | 1847.65 |
Cases where LT outperformed NLT are in bold. Minus values indicate revenue.
On day 30, the NLT policy demonstrated clear superiority in terms of total cost across 1000 repetitions, even though the LT policy achieved better overage and reorder costs. This suggests that the NLT policy may be more suitable for long-term operations overall. However, there were instances where the NLT policy performed significantly worse than the LT policy, occurring 2-3 times more frequently (Supplementary Table S1, S2 in Supplementary material). This discrepancy was found to result from extreme variations in cumulative demand sampled from the given distribution, which magnified the relative benefits of the LT policy in those specific cases.
Tables 6 and 7 present the total costs with changes in and and the variations in total costs with different doses per vial, respectively. Initially, the proposed policy demonstrated superior inventory management compared to the comparative policy on days one, two, and three. However, from day seven onwards, the lateral transshipment policy became ineffective when was equal to or greater than . Specifically, when was lower, a larger gap between and (i.e., a higher ) tended to reduce the total costs. This indicated that the total cost decreased more when than when . In and , for lower underage costs, the difference (profit conversion) was usually two or greater. This is particularly evident in the case of during the 10-day experiment, wherein the LT policy proved to be more effective. Moreover, Table 5 indicates that the average underage cost was approximately 10 times that of the average overage cost. Therefore, lowering significantly reduced costs and increased profitability, which highlights the importance of managing underage costs. Regarding the demand distributions and doses per vial, the case of yielded the most effective results with greater robustness than the others.
Table 6.
Total cost of Case 1 variations as change.
| (5, 20) | (15, 20) | (20, 5) | (20, 15) | (20, 20) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Days/policies | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT |
| 1 | 72.41 | 26.38 | 116.13 | 61.35 | -322.27 | -365.66 | -22.22 | -68.89 | 128.35 | 93.29 |
| 2 | 68.90 | 53.30 | 156.14 | 103.73 | -789.77 | -833.22 | -135.06 | -181.77 | 191.94 | 163.54 |
| 3 | 102.23 | 116.20 | 213.55 | 184.05 | -1281.89 | -1324.49 | -259.88 | -304.2 | 275.11 | 252.61 |
| 7 | 180.54 | 278.78 | 430.55 | 446.43 | -3204.31 | -3230.14 | -686.07 | -686.95 | 552.38 | 554.68 |
| 10 | 315.89 | 389.78 | 589.66 | 644.68 | -4643.81 | -4653.54 | -1020.28 | -995.12 | 768.72 | 805.28 |
| 20 | 315.89 | 814.12 | 1119.8 | 1257.66 | -9471.18 | -9470.08 | -2180.12 | -1980.69 | 1501.20 | 1626.76 |
| 30 | 473.92 | 1255.02 | 1682.04 | 1917.51 | -14350.19 | -14334.45 | -3263.52 | -3027.46 | 2176.92 | 2397.78 |
Cases where LT outperformed NLT are in bold. Minus values indicate revenue.
Table 7.
Total cost variations of Case 1 with accord to the change values of doses per vial (|I|).
| doses per vial (|I|) | 3 | 5 | 7 | 9 | ||||
|---|---|---|---|---|---|---|---|---|
| Days/policies | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT |
| 1 | 1469.41 | 1512.51 | 105.28 | 62.55 | 175.02 | 222.30 | -75.17 | 50.36 |
| 2 | 2783.57 | 2904.10 | 156.35 | 118.83 | 460.42 | 675.70 | 21.46 | 462.60 |
| 3 | 4087.16 | 4284.16 | 207.07 | 178.31 | 750.33 | 1148.30 | 142.11 | 955.39 |
| 7 | 9323.61 | 9820.69 | 417.33 | 411.58 | 1891.87 | 2999.90 | 551.44 | 2671.90 |
| 10 | 13235.64 | 13974.00 | 588.46 | 620.23 | 2759.90 | 4392.48 | 842.45 | 4012.65 |
| 20 | 26316.01 | 27804.91 | 1087.65 | 1198.48 | 5594.07 | 9020.85 | 1833.04 | 8373.35 |
| 30 | 39419.97 | 41697.90 | 1619.40 | 1844.58 | 8506.25 | 13682.72 | 2904.66 | 12801.79 |
Cases where LT outperformed NLT are in bold. Minus values indicate revenue.
As |I| decreased, the cost decreased and vice-versa. An increase in |I| is associated with an increase in the initial inventory. If the default parameters are and , this implies a 40% reduction in the initial inventory for the default parameter setting; if , this implies an 80% increase. Therefore, as |I| increases, the total cost decreases, and consequently, profits may be made. The LT policy transports vaccines to satisfy vaccine shortages in hospitals. However, the unit of vaccine shortage is a dose, whereas the unit of transported vaccine is a vial. Therefore, an appropriate |I| that is neither excessively large nor small is required. We have shown that a value of five out of three, five, seven, and nine was appropriate.
Case 2: Homogenous mean and standard deviation
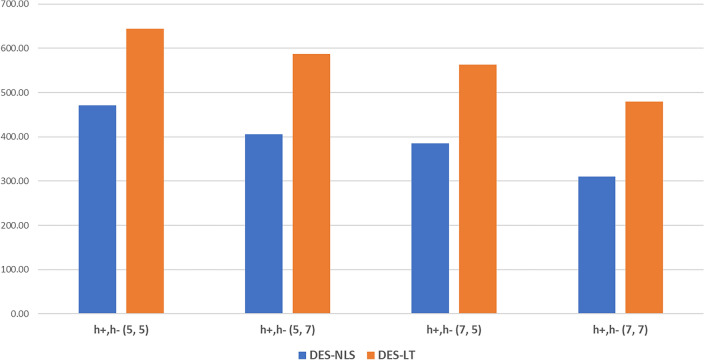
Figure 2 illustrates the average total cost influenced by the initial inventory on the second day of the experiment, under circumstances wherein both hospitals experienced similar demand patterns. Herein, the LT policy did not have any significant effect, in contrast to the outcomes observed in Case 1. When the initial inventories were either (5, 7) or (7, 5), the cost difference was minimal. With an increase in the total vaccine inventory, the total cost decreased, which was attributed to the enlarged size of the inventory itself. Table 8 echoes the trends observed in Fig. 2, indicating that the LT policy was less effective across all periods under similar demand conditions.
Fig. 2.
Average total cost of Case 2 based on initial inventory over a 2-day operation period.
Table 8.
Results of the total cost for Case 2 with initial inventory variations.
| (5, 5) | (5, 7) | (7, 5) | (7, 7) | |||||
|---|---|---|---|---|---|---|---|---|
| Days/Policies | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT |
| 1 | 343.95 | 392.50 | 265.79 | 324.65 | 257.11 | 306.27 | 170.92 | 229.66 |
| 2 | 470.98 | 644.34 | 405.74 | 586.88 | 384.59 | 562.67 | 309.67 | 479.92 |
| 3 | 624.93 | 915.50 | 539.75 | 823.66 | 515.44 | 810.14 | 455.07 | 757.77 |
| 7 | 1195.50 | 1959.64 | 1093.37 | 1868.10 | 1094.49 | 1885.15 | 994.94 | 1757.35 |
| 10 | 1587.71 | 2708.39 | 1513.85 | 2618.97 | 1522.73 | 2658.37 | 1423.61 | 2537.67 |
| 20 | 2962.35 | 5308.98 | 2917.03 | 5250.27 | 2946.88 | 5248.71 | 2893.23 | 5217.35 |
| 30 | 4500.79 | 7963.10 | 4333.62 | 7786.61 | 4261.00 | 7788.22 | 4271.37 | 7791.38 |
This diminished effectiveness is attributed to homogeneous demand distribution, resulting in a disproportionate reduction in inventory. Table 9 presents the average costs when each hospital began with seven vials. In Case 2, it is evident that the reorder costs significantly affected policy effectiveness. Although the average overage and underage costs by policy did not exhibit significant enhancement, the difference in reorder costs by policy increased as the experimental period increased. Further experiments with , also showed that the LT policy did not verify its extensive effectiveness in this case.
Table 9.
Comparison results between two policies with an initial inventory of 7 vials for each hospital.
| (7, 7) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Policies | DES-LT | DES-NLT | |||||||
| Days Costs | Overage | Underage | Reorder | Total | Overage | Underage | Reorder | Transshipment | Total |
| 1 | 49.67 | 994.72 | 1602.48 | 170.92 | 51.21 | 971.54 | 1690.26 | 18.23 | 229.66 |
| 2 | 101.66 | 2139.36 | 3202.65 | 309.67 | 101.88 | 2114.94 | 3387.23 | 35.78 | 479.92 |
| 3 | 152.22 | 3304.10 | 4794.90 | 455.07 | 152.75 | 3292.28 | 5068.36 | 54.44 | 757.77 |
| 7 | 356.85 | 7896.10 | 11185.68 | 994.94 | 355.95 | 7900.78 | 11814.44 | 124.65 | 1757.35 |
| 10 | 506.67 | 11369.48 | 15980.69 | 1423.61 | 514.02 | 11377.52 | 16891.49 | 179.23 | 2537.67 |
| 20 | 945.00 | 23500.00 | 32010.00 | 2893.23 | 930.00 | 22920.00 | 34430.00 | 370.00 | 5217.35 |
| 30 | 1532.69 | 34474.74 | 47931.84 | 4271.37 | 1537.22 | 34561.28 | 50730.68 | 540.12 | 7791.38 |
Note that the values are in average.
In contrast to Case 1, the results varied according to the number of doses per vial, as shown in Table 10. Similar to the observations in Case 1, as the number of doses per vial (|I|) increased, the costs generally decreased and profits increased. In particular, the largest decrease was seen when |I| increased from 3 to 5. The total cost decreased by an average of 11 times for NLS and 7 times for LT. This trend is attributable to the fact that larger initial inventories resulted in lower costs and higher profits. For doses three, five, and seven, the disparity in total costs between the policies widened with the length of the experimental period. However, for |I|=9, the NLT policy generated higher revenue than the LT policy during the initial setup period, ranging from one day to 1 week, with no significant change in the differential as time progressed. This pattern was not observed at the other doses. Notably, in 10, 20, and 30 days of the experiment, the total revenue of the LT policy exceeded that of the NLT. Thus, in scenarios with similar demand, this shows that the LT policy can be more effective over the long term, with a larger inventory and an increased number of doses per vial.
Table 10.
Total costs variations of Case 2 with accord to the change values of doses per vial (|I|).
| doses/vial (|I|) | 3 | 5 | 7 | 9 | ||||
|---|---|---|---|---|---|---|---|---|
| Days | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT | DES-NLT | DES-LT |
| 1 | 2088.08 | 2240.44 | 268.215 | 325.65 | -490.07 | -475.02 | -997.25 | -957.61 |
| 2 | 3914.24 | 4188.05 | 406.62 | 587.08 | -1361.60 | -1292.96 | -1910.02 | -1891.92 |
| 3 | 5775.54 | 6182.97 | 536.31 | 835.80 | -2261.98 | -2147.51 | -2882.86 | -2853.89 |
| 7 | 13138.70 | 13992.30 | 1095.02 | 1886.50 | -5836.76 | -5562.89 | -6725.16 | -6704.70 |
| 10 | 18650.31 | 19909.26 | 1535.53 | 2655.17 | -8426.21 | -8065.46 | -9617.88 | -9653.23 |
| 20 | 37054.73 | 39428.50 | 2956.62 | 5229.66 | -17362.00 | -16538.70 | -19076.40 | -19136.90 |
| 30 | 55388.43 | 59055.24 | 4345.75 | 7814.31 | -26242.40 | -25019.90 | -28581.00 | -28713.60 |
Cases where LT outperformed NLT are in bold. Minus values indicate revenue.
To further test the realism of the model, we varied the lateral transshipment time from 1 to 2 hours, i.e. whether it comes within an hour or not. The parameter settings were set as and for the default parameters. Table 11 shows the results for Case 1. Similar to the Case 1 experiment, the cost decreases by day 3. For 1, 2, and 3 days, the proposed policy reduces the NLT cost by 40.45%, 19.45%, and 9.17%, respectively. The cost seemed to increase within 5% compared to Table 5 in Case 1. The LT policy determines the lateral transshipment to maximize the demand at that time. However, if it fails to arrive within one hour, the demand is not satisfied, so it incurs additional underage cost (penalty), which increases the cost. On the other hand, for the days being greater than 3, i.e., days being longer than a week, the LT policy was not superior to NLT, where the trend is inline with the previous experiment.
Table 11.
Comparison Case 1 results between two policies with initial inventory of 7 and 5 vials for each hospital when lateral transshipment time has variation. Note that the values are in average.
| (7, 5) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Policies | DES-NLT | DES-LT | |||||||
| Days/costs | Overage | Underage | Reorder | Total | Overage | Underage | Reorder | Transshipment | Total |
| 1 | 57.08 | 583.68 | 1309.88 | 94.52 | 53.64 | 571.4 | 1287.66 | 12.23 | 56.29 |
| 2 | 115.08 | 1328.96 | 2631.75 | 164.39 | 103.97 | 1336.62 | 2570.04 | 24.98 | 132.41 |
| 3 | 174.48 | 2070.8 | 3936.46 | 216.43 | 158.4 | 2096.8 | 3842.41 | 37.3 | 196.59 |
| 7 | 408.06 | 5031.96 | 9181.92 | 430.17 | 367.91 | 5146.3 | 8973.91 | 86.94 | 504.03 |
| 10 | 574.7 | 7261.08 | 13120.58 | 586.91 | 529.58 | 7423.36 | 12826.77 | 121.9 | 683.33 |
| 20 | 1156.7 | 14652.86 | 26250.84 | 1119.59 | 1053.84 | 15025.7 | 25654.75 | 246.22 | 1430.75 |
| 30 | 1735.14 | 22083.96 | 39373.18 | 1638.4 | 1582.71 | 22642.82 | 38486.69 | 370.96 | 2116.17 |
Cases where LT outperformed NLT are in bold. Minus values indicate revenue.
Discussion
The proposed lateral transshipment policy was demonstrated to be effective for relatively short periods, such as 1, 2, 3, and 7 days, particularly when each hospital experienced distinct demand distributions. A significant portion of the total cost was consistently attributed to underage and reorder costs across the different scenarios. Thus, demand often exceeded initial stock, indicating the potential to reduce costs by maintaining an adequate inventory level. The strategy and timing of the reordering significantly influenced the overall cost. Specifically, the implemented reorder policy requested twice the average demand in doses, factoring in arrival time, whenever the available stock fell below 1.5 times the average demand for each hospital, with a restocking time of 2 h. This frequent reordering in response to the demand surpassing inventory levels resulted in increased volumes and costs of reorders, coupled with a higher count of underage doses during the 2 h shortages. Moreover, the effect of these factors became more pronounced for experimental periods extending beyond 10 days.
This study introduced a lateral transshipment policy similar to the (s, S) reorder policy. To minimize the total costs, strategies that consider the specific characteristics of vaccines must be devised. The effectiveness of the policy was determined by variations in |I| (doses per vial) and , (overage and underage costs per dose), with the profitability of vaccinations being a significant factor. In the lateral transshipment policy, parameters such as p, , and were considered; as p ( price per dose) increased, the number of transported vials varied. Costs were influenced by changes in the doses per vial. Thus, the experiments tested the variations in , , and |I| independently; however, future strategies should consider varying these factors together with p.
We did not compare our results with those of the MILP for two reasons. First, the computation process of MILP is time-intensive. Even with identical parameter settings, the computation time required to compute varies significantly across the different demand distributions, and this variability persists even over the shortest experimental durations. As our simulation was executed 1000 times, replicating it with MILP for more complex experimental durations is impractical because of the extensive computation time required. Second, the operational dynamics of the simulations conducted differed from those of the MILP. In our simulation, decisions were made on an hourly basis without foresight of future demand. In contrast, MILP knows the demand at every interval, allowing for optimal solution calculation. This fundamental difference renders any direct comparison of the two approaches not particularly insightful. Thus, replicating the simulation policy using MILP is challenging owing to these computational demands. Consequently, we did not consider the MILP’s solutions. Nevertheless, the MILP’s discrete-time constraints offered a valuable structure for designing our DES and guided us in aligning our simulation framework with that of the MILP, including the reordering and LT policies.
To mitigate sudden demand spikes, we conducted experiments within of the mean of the uniform distribution, and the current policies resembled rule-based approaches. In addition, in the context of demand, under-aged and over-aged doses were measured in doses, whereas the amounts of reordering and LT were calculated in vials, which resulted in further complexity and reduced the policy effectiveness with more unstable distributions. Thus, future research should explore dynamic or robust policies using reinforcement learning and Markov decision process (MDP)-based simulations to accommodate a wider range of demand scenarios51,52.
Conclusion
Vaccines have emerged as a critical measure against COVID-19; however, uncertainties in demand owing to factors such as side effects, religious objections, and absenteeism have caused unstable vaccine demand, resulting in excess vaccines and subsequent social, economic, and environmental challenges. This study evaluated the effectiveness of a lateral transshipment policy in managing the inventory of short-term vaccines in such stochastic situations. Inheriting the basic knowledge of the nature of the problem from the MILP model, this study modeled a DES with lateral transshipment and reordering policies for mRNA-based vaccines across two hospitals, accompanied by a DES of the scenario. Consequently, various timeframes ranging from 1 to 30 days were tested.
The lateral transshipment policy employed lateral transshipment based on the availability (TBA) policy46 to decide on the quantity to transfer, either less than or equal to a vial’s amount. Whereas, the reorder policy was structured around the (s, S) inventory system. The transshipment strategy proved beneficial, particularly when demand distributions varied among hospitals, showing greater effectiveness than the no-transshipment approach for up to seven days. The impact of the policy was assessed based on factors such as the profitability of vaccination, costs associated with surpluses or shortages of vaccines, and the availability of doses per vial. Overall, lateral transshipment was more effective than non-transshipment.
However, the complexity involved in tailoring the policies to the unique characteristics of vaccines, determining strategies on a per-dose basis, and applying these strategies on a per-vial basis resulted in instances where rule-based or similar transport policies were less effective. Consequently, there is a need for advanced policy research, particularly the application of MDP-based simulation with reinforcement learning which can be employed for learning-based adaptive control53 in the DES context, to develop more sophisticated and effective strategies.
Methods
To address the inventory management challenges, we employed MILP and DES. Both methods offer advantages in problem integration by combining the MILP with lateral transshipment. Because of the computational difficulty, simulations are the preferred approach. The discrete operation of the inventory in a simulation facilitated the incorporation of aspects of this method. Our research methodology was structured into two distinct phases. The first stage involved designing a mathematical inventory management model that minimized costs under uncertain demand conditions. The second stage focused on analyzing the lateral transshipment policy through simulations that replicated the same environmental conditions and included lateral transshipment variables.
Mixed integer linear programming
The parameters and decision variables used in MILP are shown in the following Tables 12 and 13:
Table 12.
IP parameters.
| Notations | Description |
|---|---|
| H | Set of hospitals, |
| I | Set of doses, |
| J | Set of vials, |
| N | Operation hours a day, |
| K | Set of day |
| T | Set of time slots, |
| p | Price each customer pays for a single vaccine dose |
| c | Cost of the single vaccine vial |
| Cost of the single vial reorder | |
| Cost of the single lateral transshipment of a vial | |
| Overage cost of a single vaccine dose | |
| Underage cost of a single vaccine dose | |
| Holding cost | |
| Demand of hospital h following normal distribution at time slot t, | |
| Initial vaccine vials for hospital h, | |
| M | Large number |
| Mean of demand of hospital h | |
| Standard deviation of demand of hospital h |
Table 13.
Decision variables.
| Notations | Description |
|---|---|
| 1 if dose i of vial j is used at hospital h at time slot t, 0 otherwise | |
| A binary indicator whether the vial j is opened at hospital h at time slot t | |
| Number of vials at hospital h at time slot t, | |
| Number of vials to reorder for hospital h at time slot t, | |
| Direction of transshipment from to at time slot t when transshipment is implemented 1, 0 otherwise. | |
| Number of vials to transship from hospital to at time slot t | |
| Overaged dose at hospital h at time slot t | |
| Underaged dose at hospital h at time slot t | |
| Profit | Total profit by vaccinating customers |
| Total reorder cost of reordered vials | |
| Total lateral transshipment cost of transshipped vials | |
| Total overage cost of left doses after operation hours | |
| Underage cost cost of unvaccinated doses (people) after an hour |
In our model, time slots T represent the hospital’s operating hours, spanning n hours over k days, resulting in when . The reorder cost encompasses the per- vial usage and transshipment costs. In the case of lateral transshipment, the cost incurred is solely for transportation purposes. We regard profit as a social benefit that prevents the spread of epidemic diseases through vaccination. Each vaccine vial contained |I| doses, denoted by |I|. Let p, , and represent the revenue per dose when vaccinated, cost per dose when not administered, and cost per dose for leftover vaccines, respectively. Here, p symbolizes the benefit, and and represent the penalties. The objective of this problem was to maximize the number of vaccinated people and minimize the number of unvaccinated individuals. Thus, it minimized the total costs incurred during vaccination. Therefore, the importance hierarchy was 54. Minimizing costs in this context equates to maximizing revenue. The initial inventory for each hospital was measured in vials. Considering the vaccine appointment demands of two hospitals, and , each with their respective means and standard deviations , we formulated a problem that incorporated lateral transshipment.
The specific objective and constraint expressions for this problem are as follows.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
| 21 |
| 22 |
| 23 |
| 24 |
| 25 |
| 26 |
| 27 |
| 28 |
| 29 |
| 30 |
| 31 |
| 32 |
| 33 |
The objective function (1) in our model was designed to minimize the total vaccination cost over the period . This function comprised several costs, including reordering, lateral transshipment, underage, overage, profit, and holding. To minimize costs, the objective function was formulated as the total cost subtracted from profit.
Constraints (2–6) describe the costs involved in the objective function. Profit was calculated as the total number of doses sold during the period minus the total cost associated with the vials used for vaccination. The cost per used vial, along with transportation costs, was included to represent the cost of reordering. denotes the transportation cost of transported vials. and represent the costs per dose for overage and underage vaccines, respectively. Equation (7) addresses the underage dose that occurs if the demand of a hospital is lower than the number of doses administered, resulting in leftover doses. Constraint (8) defines the overage dose, which is the quantity of vaccine remaining at the end of the day, and is thus discarded. The calculations of the overage dose amount and associated costs are included here. Constraints (9) and (10) establish the relationship between the vial and dose. Through the binary variables x and y and a large number denoted by M, the model ensured that if any dose was used, the corresponding vial was considered open; if no dose was used, the vial count remained 0.
Constraints (11–14) establish the directional nature of lateral transshipment, indicating that it is unidirectional rather than bidirectional. Equations (15–18) depict the dynamics of the vaccine inventory over period T. For example, at (the first hour of day 1), the vaccine inventory was reduced from its initial level by the scheduled doses plus vials sent to other hospitals and increased by vials received from other hospitals. At , the inventory from the previous hour was adjusted by subtracting the demand and adding the transported vials. Constraints (15–16) are delineated separately to accommodate the indexing notation for reorders.
Constraint (17) pertains to inventory updates for the final hour of the day. Alongside constraint (18), which addresses hours other than 1 and 2, these constraints account for the exclusion of vaccines opened in the last hour and overage vaccines that are required to be discarded. Constraint (18) updates the vaccine inventory for times t excluding 1 and 2, thus increasing the inventory by the vials ordered 2 h prior and those received from other hospitals and decreasing it by the vials transported and doses administered. Because the inventory is measured in doses, Constraint (19) specifies the quantity of vaccine vials in the hospital. Equation (20) relates to reordering, which requires 2 h, and stipulates that no orders can be placed after hour each day. Constraints (21–33) define the settings and ensure the non-negativity of each decision variable.
Discrete event simulation with lateral transshipment policy
The potential complexity of daily problems that may not be solvable within the given time limit (3600 s) using MILP and DES was utilized for policy analysis. The simulation environment mirrored the mathematical formulation by incorporating a lateral transshipment policy. Both MILP and DES operated under the assumption that the demand for vaccine appointments at two hospitals, and , followed a uniform distribution with respective means and standard deviations . Further, it was considered that the same individuals attended appointments at consistent times. This study focused on reactive lateral transshipments. The lateral transshipment policy extended Banerjee’s TBA policy to accommodate the specific characteristics of vaccines46.
The DES process was structured into six distinct phases: appointment visits, detection of vaccine stockout, execution of lateral transshipment, renewal of vaccine stock, reorder decisions, and finality of the day’s operations. This approach provided a comprehensive understanding of the dynamics involved in vaccine distribution and management under various demand scenarios.
The parameters of the simulation are shown in Table 14, which contain the same meaning with the proposed MILP.
Table 14.
Parameters in DES.
| Notations | Description | Unit |
|---|---|---|
| Vaccine inventory for hospital h at time t | dose | |
| Estimated vaccine inventory for hospital h at time t | dose | |
| Estimated vaccine inventory for hospital h at time t | dose | |
| Shortage of vaccine for hospital h at time t | dose | |
| Transportable vaccine inventory for hospital h at time t | vial | |
| Shortage of vaccine for hospital h at time t | vial |
Step 1. Appointment visit
Patients with appointments, as determined using a uniform distribution model, arrive at the hospital.
Step 2. Detection of vaccine stockout
The vaccine inventory is calculated for each hospital after completing all appointments have been fulfilled.
| 34 |
If across different hospitals is negative, the process moves to Step 3; otherwise, it proceeds to Step 4.
Step 3. Execution of lateral trans-shipment
Step 3.1. Decision on lateral transshipment
Assess the quantity of the vaccine that can be transported and the extent of vaccine dose shortage.
| 35 |
| 36 |
Because transportation is conducted in vials, Eqs. (36) and (37) can be expressed as Eqs. (38) and (39), respectively:
| 37 |
| 38 |
In the proposed model, the variable was always rounded down and was rounded up. This rounding approach was because of the constraint in our problem setting, where balance adjustments could not be made through vial units. If the value for hospitals capable of transporting vaccines and the value for hospitals experiencing vaccine shortages are both nonzero, the process advances to Step 3.2. However, if either of these values is zero, the procedure proceeds directly to Step 4.
Step 3.2. Decision on lateral transshipment quantity
When transporting vaccine vials from hospital to hospital , the quantity transported is determined as follows:
| 39 |
The amount of transshipment is determined under the two conditions.
, then The transshipment amount does not change. Proceed to the next step.
, then The decision to transport one fewer vaccine vial involves an evaluation of the trade-off between the revenue generated and the residual cost incurred if the vaccine is transferred to another hospital against the overage cost associated with the movement of one less vaccine. This assessment balances the financial implications of either keeping or reallocating the vaccine to optimize resource utilization and cost-efficiency.
Step 4. Renewal of the vaccine stock
Update the hospital vaccine inventory after lateral transshipment.
| 40 |
Step 5. Making reorder decisions
The reordering strategy is based on the (s, S) policy55. When the current inventory at any hospital drops below 1.5 times the average demand measured in doses, a reorder is initiated for twice the average demand calculated in dose vials, while also considering the time required for the order to arrive. If the expected arrival time of the reordered vaccines falls outside the hospital’s operational hours, a reorder request is not executed.
| 41 |
Step 6. Finality of the day’s operation
If it is the final hour of the day, calculate and account for the cost of any surplus dose, retaining only the vial, and then proceed back to step 1. Should this not be the end of the day, Step 1 should be repeated immediately. As the day concludes, any dose left in a partially used vial is disposed of, resulting in an incurred cost for the excess.
| 42 |
Because demand is derived from a probabilistic distribution, we determine the impact of policies by averaging the results from numerous iterations. Figure 3 illustrates the overall process of the simulation.
Fig. 3.
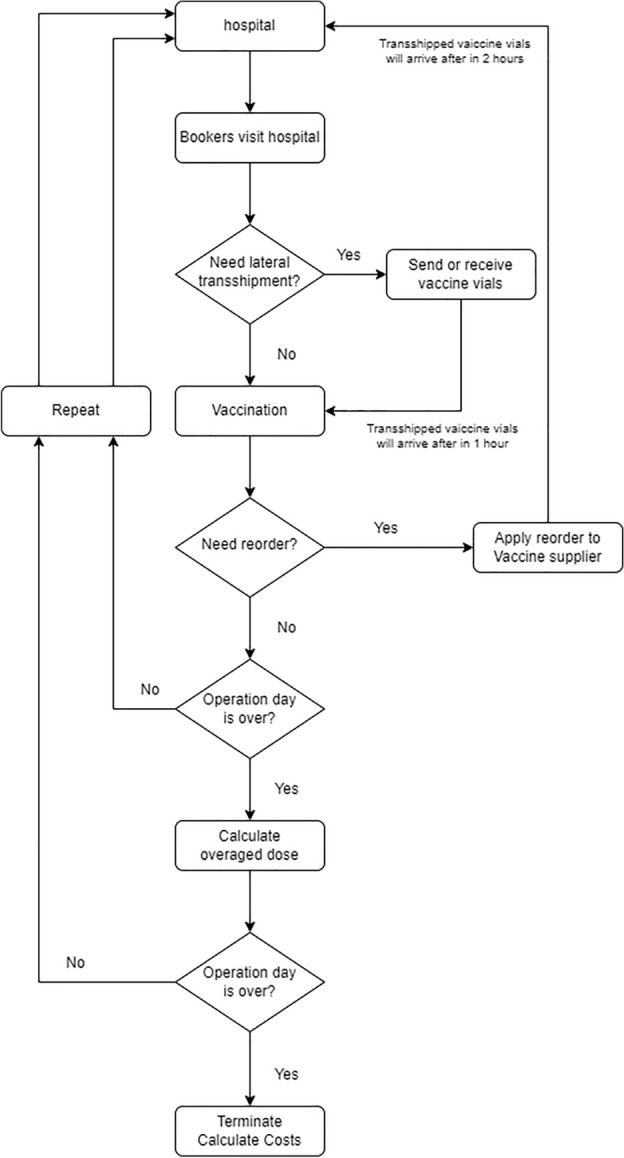
Discrete event simulation overview.
Supplementary Information
Author contributions
T.C. conceived and conceptualized the idea regarding the problem and acquired the funding. H.C. formulated the mathematical model and designed experiments. H.K. designed discrete event simulation and performed formal analysis through computational experiments. H.K wrote the manuscript and T.C. and H.C. did the review and editing. All authors reviewed the manuscript.
Funding
This research was supported by Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea government (MOTIE) (P0020649, The Competency Development Program for Industry Specialist) and the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. NRF-2021R1F1A105930213).
Data availability
The datasets generated during the current study are not publicly available due to that the data is randomly sampled from an uniform distribution following a mean and standard deviation reported in this paper, but are available from the corresponding author on reasonable request.
Competing declarations
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Hyungjoo Cha, Email: hyungjoo_cha@korea.ac.kr.
Taesu Cheong, Email: tcheong@korea.ac.kr.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-71322-5.
References
- 1.Hubbard, S. & Bais, R. Assessing unused residual Pfizer-BioNTech COVID-19 vaccine: A community observational study. medRxiv 2021–08 (2021).
- 2.Fauci, A. S. The story behind COVID-19 vaccines (2021). [DOI] [PubMed]
- 3.Seneviratne, S., Jayarajah, U., Abeysuriya, V., Rahman, A. & Wanigasuriya, K. COVID-19 vaccine landscape. (2020).
- 4.Yan, Y. et al. The COVID-19 vaccines: Recent development, challenges and prospects. Vaccines9, 349 (2021). 10.3390/vaccines9040349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schoenmaker, L. et al. mRNA-lipid nanoparticle COVID-19 vaccines: Structure and stability. Int. J. Pharm.601, 120586. 10.1016/j.ijpharm.2021.120586 (2021). 10.1016/j.ijpharm.2021.120586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Holm, M. R. & Poland, G. A. Critical aspects of packaging, storage, preparation, and administration of mRNA and adenovirus-vectored COVID-19 vaccines for optimal efficacy. Vaccine39, 457 (2021). 10.1016/j.vaccine.2020.12.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Uddin, M. N. & Roni, M. A. Challenges of storage and stability of mRNA-based COVID-19 vaccines. Vaccines9, 1033 (2021). 10.3390/vaccines9091033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Control, K. D. & Agency, P. COVID-19 vaccination information for healthcare providers. https://ncv.kdca.go.kr/board.es?mid=a12101000000 &bid=0031. (Accessed on 12/29/2023).
- 9.Rosenberg, E. S. et al. COVID-19 vaccine effectiveness in New York state. N. Engl. J. Med.386, 116–127 (2022). 10.1056/NEJMoa2116063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mathieu, E. et al. A global database of COVID-19 vaccinations. Nat. Hum. Behav.5, 947–953 (2021). 10.1038/s41562-021-01122-8 [DOI] [PubMed] [Google Scholar]
- 11.Al-Rashid, M., Al-Hamad, A., Al-Hamad, A. & Yasin, Y. Myths, misconceptions, and hesitancy in people residing in Qatar toward mRNA COVID-19 vaccines: An experience exchange from Qatar University Health Center. In Qatar Medical Journal, vol. 2022, 20 (HBKU Press Qatar, 2022). [DOI] [PMC free article] [PubMed]
- 12.Pierri, F. et al. Online misinformation is linked to early COVID-19 vaccination hesitancy and refusal. Sci. Rep.12, 5966 (2022). 10.1038/s41598-022-10070-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lee, S. K., Sun, J., Jang, S. & Connelly, S. Misinformation of COVID-19 vaccines and vaccine hesitancy. Sci. Rep.12, 13681 (2022). 10.1038/s41598-022-17430-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rudloff, J. P., Hutmacher, F. & Appel, M. Post-truth epistemic beliefs rooted in the dark factor of personality are associated with higher COVID-19 vaccination refusal. Sci. Rep.13, 4254 (2023). 10.1038/s41598-023-31079-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Musamih, A. et al. Blockchain-based solution for COVID-19 vaccine waste reduction. J. Clean. Prod.372, 133619 (2022). 10.1016/j.jclepro.2022.133619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cheong, T. Joint inventory and transshipment control for perishable products of a two-period lifetime. Int. J. Adv. Manuf. Technol.66, 1327–1341 (2013). 10.1007/s00170-012-4411-x [DOI] [Google Scholar]
- 17.Ganesan, S. et al. Vaccine side effects following COVID-19 vaccination among the residents of the UAE—an observational study. Front. Public Health10, 876336 (2022). 10.3389/fpubh.2022.876336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vaccination no-shows: Why are thousands of appointments going unfilled? | CTV News. https://www.ctvnews.ca/health/coronavirus/vaccination-no-shows-why-are-thousands-of-appointments-going-unfilled-1.5377278. (Accessed on 12/29/2023).
- 19.Unused Covid-19 vaccines worth €95m discarded by HSE last year-the irish times. https://www.irishtimes.com/health/2023/04/24/unused-vaccines-worth-95m-discarded-by-hse-last-year/. (Accessed on 12/29/2023).
- 20.Fahrni, M. L. et al. Management of COVID-19 vaccines cold chain logistics: A scoping review. J. Pharm. Policy Pract.15, 16 (2022). 10.1186/s40545-022-00411-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li, Z., Li, H. & Xu, X. Efficient lateral transshipment policy for multi-retailer system. In 2019 IEEE/SICE International Symposium on System Integration (SII), 756–763 (IEEE, 2019).
- 22.Olson, D. L. Software process simulation. In Bidgoli, H. (ed.) Encyclopedia of Information Systems, 143–153, 10.1016/B0-12-227240-4/00163-5 (publisherElsevier, addressNew York, 2003).
- 23.Qin, Y., Wang, R., Vakharia, A. J., Chen, Y. & Seref, M. M. The newsvendor problem: Review and directions for future research. Eur. J. Oper. Res.213, 361–374 (2011). 10.1016/j.ejor.2010.11.024 [DOI] [Google Scholar]
- 24.Porteus, E. L. The newsvendor problem. Building intuition: Insights from basic operations management models and principles 115–134 (2008).
- 25.Cheong, T. & Kwon, K. The robust min-max newsvendor problem with balking under a service level constraint. S. Afr. J. Ind. Eng.24, 83–97 (2013). [Google Scholar]
- 26.DeYong, G. D. The price-setting newsvendor: Review and extensions. Int. J. Prod. Res.58, 1776–1804 (2020). 10.1080/00207543.2019.1671624 [DOI] [Google Scholar]
- 27.Watters, C. R., Shepherd, M. A. & Burkowski, F. J. Electronic news delivery project. J. Am. Soc. Inf. Sci.49, 134–150 (1998). [DOI] [Google Scholar]
- 28.Besbes, O., Ma, W. & Mouchtaki, O. Quality vs. quantity of data in contextual decision-making: Exact analysis under newsvendor loss. arXiv preprintarXiv:2302.08424 (2023).
- 29.Rastegar, M., Tavana, M., Meraj, A. & Mina, H. An inventory-location optimization model for equitable influenza vaccine distribution in developing countries during the covid-19 pandemic. Vaccine39, 495–504 (2021). 10.1016/j.vaccine.2020.12.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tavana, M., Govindan, K., Nasr, A. K., Heidary, M. S. & Mina, H. A mathematical programming approach for equitable COVID-19 vaccine distribution in developing countries. Ann. Oper. Res. 1–34 (2021). [DOI] [PMC free article] [PubMed]
- 31.Sarigol, I., Ozdemir, R. G. & Bayraktar, E. Covid 19 vaccine order allocation: an optimization model with substitution. J. Humanit. Logist. Supply Chain Manag.13, 125–139 (2023). 10.1108/JHLSCM-09-2021-0094 [DOI] [Google Scholar]
- 32.Thul, L. & Powell, W. Stochastic optimization for vaccine and testing kit allocation for the COVID-19 pandemic. Eur. J. Oper. Res.304, 325–338 (2023). 10.1016/j.ejor.2021.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wen, Z., Yue, T., Chen, W., Jiang, G. & Hu, B. Optimizing COVID-19 vaccine allocation considering the target population. Front. Public Health10, 1015133 (2023). 10.3389/fpubh.2022.1015133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Alshammari, F., Mustafa, A., Omer, E. & Omer, F. A simulation model of COVID-19 epidemic based on vaccination and treatment. Eur. J. Pure Appl. Math.16, 2450–2460 (2023). 10.29020/nybg.ejpam.v16i4.4805 [DOI] [Google Scholar]
- 35.Arora, C. et al. Mathematical modelling to predict the effect of vaccination on delay and rise of COVID-19 cases management. Mathematics11, 821 (2023). 10.3390/math11040821 [DOI] [Google Scholar]
- 36.Kim, Y. R., Choi, Y.-J. & Min, Y. A model of COVID-19 pandemic with vaccines and mutant viruses. PLoS ONE17, e0275851 (2022). 10.1371/journal.pone.0275851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vázquez-Abad, F. J., Dufresne, D. & Park, G.-B. Impact of vaccination policies for covid-19 using hybrid simulation. In 2022 Winter Simulation Conference (WSC), 545–556 (IEEE, 2022).
- 38.Çaglayan, Ç. et al. Staffing and capacity planning for SARS-CoV-2 monoclonal antibody infusion facilities: A performance estimation calculator based on discrete-event simulations. Front. Public Health9, 770039 (2022). 10.3389/fpubh.2021.770039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tagaras, G. & Cohen, M. A. Pooling in two-location inventory systems with non-negligible replenishment lead times. Manage. Sci.38, 1067–1083 (1992). 10.1287/mnsc.38.8.1067 [DOI] [Google Scholar]
- 40.Paterson, C., Kiesmüller, G., Teunter, R. & Glazebrook, K. Inventory models with lateral transshipments: A review. Eur. J. Oper. Res.210, 125–136 (2011). 10.1016/j.ejor.2010.05.048 [DOI] [Google Scholar]
- 41.Firoozi, M., Babai, M. Z., Klibi, W. & Ducq, Y. Distribution planning for multi-echelon networks considering multiple sourcing and lateral transshipments. Int. J. Prod. Res.58, 1968–1986 (2020). 10.1080/00207543.2019.1639841 [DOI] [Google Scholar]
- 42.Achamrah, F. E., Riane, F. & Limbourg, S. Spare parts inventory routing problem with transshipment and substitutions under stochastic demands. Appl. Math. Model.101, 309–331 (2022). 10.1016/j.apm.2021.08.029 [DOI] [Google Scholar]
- 43.Farghadani-Chaharsooghi, P. & Karimi, B. A robust optimization approach for the production-routing problem with lateral transshipment and outsourcing. RAIRO-Oper. Res.57, 1957–1981 (2023). 10.1051/ro/2023083 [DOI] [Google Scholar]
- 44.Paul, A. & Yenipazarli, A. A note on lateral transshipment under point-process driven demand. Oper. Res. Lett.41, 159–163 (2013). 10.1016/j.orl.2012.12.005 [DOI] [Google Scholar]
- 45.Naseraldin, H. & Herer, Y. T. A location-inventory model with lateral transshipments. Naval Res. Logist.58, 437–456 (2011). 10.1002/nav.20461 [DOI] [Google Scholar]
- 46.Banerjee, A., Burton, J. & Banerjee, S. A simulation study of lateral shipments in single supplier, multiple buyers supply chain networks. Int. J. Prod. Econ.81, 103–114 (2003). 10.1016/S0925-5273(02)00366-3 [DOI] [Google Scholar]
- 47.Hachicha, W., Afli, A. & Elleuch, F. Evaluating emergency lateral transshipment policies using simulation-based approaches. In 2013 International Conference on Advanced Logistics and Transport, 470–475 (IEEE, 2013).
- 48.Liu, H. Simulation of lateral transshipment in order delivery under e-commerce environment. Int. J. Simul. Process Model.11, 51–65 (2016). 10.1504/IJSPM.2016.075080 [DOI] [Google Scholar]
- 49.Harris, C. R. et al. Array programming with NumPy. Nature585, 357–362. 10.1038/s41586-020-2649-2 (2020). 10.1038/s41586-020-2649-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Overview — simpy 4.1.1 documentation. https://simpy.readthedocs.io/en/latest/. (Accessed on 01/17/2024).
- 51.Chong, J. W., Kim, W. & Hong, J. Optimization of apparel supply chain using deep reinforcement learning. IEEE Access10, 100367–100375 (2022). 10.1109/ACCESS.2022.3205720 [DOI] [Google Scholar]
- 52.Khan, M. A. et al. Effective demand forecasting model using business intelligence empowered with machine learning. IEEE Access8, 116013–116023 (2020). 10.1109/ACCESS.2020.3003790 [DOI] [Google Scholar]
- 53.Seo, D.-W., Chang, K., Cheong, T. & Baek, J.-G. A reinforcement learning approach to distribution-free capacity allocation for sea cargo revenue management. Inf. Sci.571, 623–648 (2021). 10.1016/j.ins.2021.04.092 [DOI] [Google Scholar]
- 54.Cristea, M., Cristea, C., Tirnovan, R.-A. & Fagarasan, C. Optimal sizing of electrical energy storage system for a household with a grid-connected PV system using inventory model. In 2020 International Conference and Exposition on Electrical And Power Engineering (EPE), 067–071 (IEEE, 2020).
- 55.Zheng, Y.-S. & Federgruen, A. Finding optimal (s, S) policies is about as simple as evaluating a single policy. Oper. Res.39, 654–665 (1991). 10.1287/opre.39.4.654 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during the current study are not publicly available due to that the data is randomly sampled from an uniform distribution following a mean and standard deviation reported in this paper, but are available from the corresponding author on reasonable request.