Confined antiskyrmion motion driven by electric current excitations

Abstract

Current-driven dynamics of topological spin textures, such as skyrmions and antiskyrmions, have garnered considerable attention in condensed matter physics and spintronics. As compared with skyrmions, the current-driven dynamics of their antiparticles – antiskyrmions − remain less explored due to the increased complexity of antiskyrmions. Here, we design and employ fabricated microdevices of a prototypical antiskyrmion host, (Fe_0.63Ni_0.3Pd_0.07)₃P, to allow in situ current application with Lorentz transmission electron microscopy observations. The experimental results and related micromagnetic simulations demonstrate current-driven antiskyrmion dynamics confined within stripe domains. Under nanosecond-long current pulses, antiskyrmions exhibit directional motion along the stripe regardless of the current direction, while the antiskyrmion velocity is linearly proportional to the current density. Significantly, the antiskyrmion mobility could be enhanced when the current flow is perpendicular to the stripe direction. Our findings provide novel and reliable insights on dynamical antiskyrmions and their potential implications on spintronics.

Antiskyrmions, like skyrmions, are a form of topological spin texture, with a topological charge of opposite sign to the equivalent skyrmion with the same polarity. While antiskyrmions have been less explored, they offer some potential advantages for applications, and here, Guang et al demonstrate antiskyrmion motion within stripe domains.

Introduction

Magnetic skyrmions^1–3 and antiskyrmions^2,4 are topologically nontrivial spin textures that have garnered significant attention due to their particle-like properties and unique dynamic behaviors. These topological spin textures hold great promise as information carriers for applications of storage and memory for the capability of nanometric size, non-volatile, and low threshold density for current drive⁵. One important intrinsic origin of these spin textures is the Dzyaloshinskii-Moriya interaction⁶ (DMI), an antisymmetric spin exchange interaction arising from spin-orbit coupling in inversion-symmetry broken system. Since the small-angle neutron scattering measurement on a hexagonal skyrmion lattice in bulk MnSi¹ and the following Lorentz transmission electron microscopy (LTEM) observation on magnetic topology of skyrmions in Fe_0.5Co_0.5Si³, extensive studies on skyrmions have been conducted, in particular on their dynamical features, including thermally induced skyrmion diffusions^7–9, field-controlled transformations of skyrmion states¹⁰, and current-driven motion of skyrmions^11–16.

While a wide range of skyrmion-hosting materials have been discovered¹⁷, rare antiskyrmion-hosting materials have been explored^4,18–23, which exhibit tetragonal structure with D_2d (Mn_1.4Pt_0.9Pd_0.1Sn^4,18, Mn_1.4PtSn¹⁹) or S₄ [(Fe_0.63Ni_0.3Pd_0.07)₃P^20–23] crystal symmetry. In stark contrast to the skyrmion-hosting materials with a unique DMI vector, the aforementioned antiskyrmion materials have anisotropic DMI vectors, resulting in fertile spin textures in a, such as elliptical skyrmions, square-shaped antiskyrmions constituted by alternative Bloch lines and Bloch domain walls, and non-topological bubbles in external magnetic fields. Due to the competition between the anisotropic DMI and dipole-dipole interactions, antiskyrmions in these materials also possess rich three-dimensional structures^18,22. In addition to square-shaped antiskyrmions, a recent report claimed that the arc-shaped antiskyrmion appears in a prototypical skyrmion-hosting helimagnet FeGe with a single DMI vector²⁴.

On the other hand, the spintronics field shows an increasing interest in topological spin textures emerged in the helical phase background. For example, recent studies have revealed that interstitial skyrmions within helical stripes exhibit enhanced mobility compared to skyrmions in a ferromagnetic background in FeGe¹⁶. Moreover, H-shaped skyrmions (or half-skyrmion pairs) in a helical background may demonstrate better stability and mobility in comparison with interstitial skyrmions^25,26.

Skyrmion and antiskyrmion carry opposite topological charges, $Q=-1$ and +1, as given by $Q=\frac{1}{4\pi }\int \mathbf{m}\cdot \left({\partial }_x\mathbf{m}\times {\partial }_y\mathbf{m}\right)dxdy$, where m represents the unit vector of the local spin. Note here that the field reversed can rise to an opposite sign topological charge in topological spin textures. Therefore, it is expected that their emergent properties, which are determined by the topological charge, may also differ from each other. For example, in analogy to the skyrmion Hall motion^12,27, theoretical simulations have predicted a current-driven antiskyrmion Hall motion with a characteristic Hall angle relative to the applied current direction and induced by the effective Magnus force²⁸. Note that the sign of both the topological Hall effect of conduction electrons and (anti)skyrmion Hall effect are determined by the topological charge $Q$, and they should be opposite for skyrmions ($Q=-1$) and antiskyrmions ($Q=+1$). Indeed, a recently reported sign reversal in the topological Hall effect in a Heusler thin film magnet was attributed to the transformation between skyrmions and antiskyrmions²⁹. Current-driven skyrmion dynamics have been well characterized, including studies of skyrmion motion in confined geometries^30–32 and with various current orientations relative to the sample geometry³³. However, the current-driven motion of an antiskyrmion embedded in stripe domains of a helical phase background, which contains four Bloch lines, has rarely been experimentally reported. The main reason is that, compared to skyrmions, creating and stabilizing antiskyrmions in experiments is challenging as it usually requires a precise control of intrinsic magnetic parameters, such as anisotropic DMI and anisotropy, which is technically demanding. Also, existing techniques and tools for studying skyrmions may not be directly applicable to the observation and manipulation of antiskyrmions due to their different magnetic properties.

Despite these challenges, there is a growing interest in antiskyrmions and their dynamics. Comprehensive studies on antiskyrmions are not only critical for the expansion of the fundamental understanding of topological phenomena, but also important for the design and development of future spintronic devices based on different topological spin textures.

Here, we have demonstrated the dynamical behaviors of antiskyrmions confined into stripes under nanosecond current-pulse excitations in FNPP using in situ LTEM. The confined antiskyrmions, which are efficiently generated in stripe-shape channels by tuning the magnitude and direction of external magnetic fields, remain even at zero field as a metastable state. The in situ LTEM results show that (1) the antiskyrmions move along the stripes regardless of whether the current flows parallel or perpendicular to the stripes, indicating that the Hall motion of such confined antiskyrmions is completely suppressed when the current is parallel to the stripes; (2) the antiskyrmion velocity is linearly proportional to the current density; (3) an enhancement in the antiskyrmion velocity has been revealed when the current flows perpendicular to the stripes.

Micromagnetic simulations for current-driven antiskyrmions in FNPP nanostripes

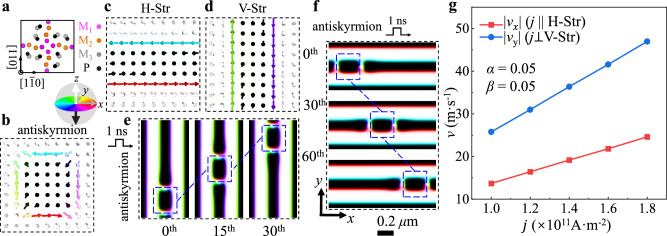
We focus on current-driven antiskyrmion dynamics in the tetragonal FNPP (space group I$\overline{4}$). The crystal structure of FNPP along the [001] crystal axis is drawn schematically in Fig. 1a. The square-shaped antiskyrmions (Fig. 1b) are stabilized in FNPP by applying an external magnetic field^22,34 of several hundred milliteslas (mTs)²⁰. Antiskyrmions thus created can remain robust even after reducing the field to zero at room temperature^23,34. In this study, we target metastable antiskyrmions embedded in a helical background and confined within the stripes. These stripes make it possible to investigate the antiskyrmion dynamics in a confined geometry with current flow parallel or perpendicular to the stripes. To simplify the text description, we denoted the stripes aligned along the $\left[1\overline{1}0\right]$ and [$110$] crystal axes as horizontal (H-Str) and vertical (V-Str), respectively, as shown in Fig. 1c, d.

Fig. 1. Simulated current-driven antiskyrmion motion in helical stripes.

a Crystal structure of M₃P ((Fe_0.63Ni_0.3Pd_0.07)₃P) with $I\overline{4}$ (S₄ symmetry) space group along the [$001$] axis. The M₁ (light purple), M₂ (orange), and M₃ (gray) denote three inequivalent M atomic sites for Fe, Ni, or Pd. Schematic of the real-space structure of an antiskyrmion (b), horizontal helical stripe (c, H-Str), and vertical helical stripe (d, V-Str). The colors and arrows in (b–f) indicate the vector fields coded by the color wheel shown below (a). The white and black colors indicate up ($+z$) and down ($-z$) magnetizations perpendicular to the plane. Snapshots of the real-space trajectory of an antiskyrmion embedded in a stripe by applying current pulses (e) perpendicular (j$\perp$V-Str) and (f) parallel (j$\parallel$H-Str) to the helical background stripes. The scale bar is 0.2 μm. g The antiskyrmion velocity |${\overline{v}}_x$| and |${\overline{v}}_y$| versus j for j$\perp$V-Str (red squares) and j$\parallel$H-Str (blue circles).

Current-driven motion of antiskyrmion via the spin transfer torque (STT) effect can be described by the Thiele equation^30–33:

$$\mathbf{G}\times \left({\mathbf{v}}_{\mathrm{s}}-{\mathbf{v}}_{\mathrm{d}}\right)+\mathcal{D}\left(\beta {\mathbf{v}}_{\mathrm{s}}-\alpha {\mathbf{v}}_{\mathrm{d}}\right)+\mathbf{F}=\mathbf{0},$$ 1

which is comprised of three distinct terms. The first term describes the gyrotropic effect, where G = (0, 0, 4πQ). Here, v_d is the drift velocity of the spin texture, and the conduction electron velocity v_s can be defined in terms of the current density j as v_s = −(gPμ_B/2eM_s) j, where ɡ is the Landé g-factor, μ_B is the Bohr magneton, e is the elementary charge, M_s is the saturation magnetization, and P is the spin polarization ratio of the conduction electrons. The second term encompasses the dissipative forces and includes the Gilbert damping coefficient α, non-adiabatic STT parameter β, and the dissipative tensor $\mathcal{D}$, which is determined by the shape of the topological spin texture. The third term F accounts for the forces exerted on the spin textures related to external fields, boundary confinement, and impurities.

Skyrmions confined within micrometer-scale geometries have been observed to exhibit distinctive velocity-current density relationships depending on the direction of the current with respect to the device boundary³³. Specifically, when the current flows along the boundary, the velocity scales as v_d $\propto$ (β/α) j, and when current flows perpendicular to the boundary, it scales as v_d $\propto$ $-$(4πQ/α) j³³. Note that the skyrmion dynamics in helical background has been studied, and it was found an H-shaped skyrmion and anti-H-shaped skyrmion move in opposite directions along the current flow direction²⁶. However, in the case of current-driven antiskyrmion dynamics confined by a stripe domain, the relationship remains uncharted and has not yet been fully understood. We performed the simulations first for the current-driven dynamics of antiskyrmions at the two states which are embedded in H-Str and in V-Str, respectively. For both states, current pulses with the duration of 1 ns and the magnitude |j| = 1.0 × 10¹¹A m⁻² flow along the horizontal axis (the x-axis indicated in Fig. 1f). The values of α and β for the simulation are set to 0.05. Representative snapshots of the simulations displayed in Fig. 1e, f depict the current-driven motions of an antiskyrmion embedded in (e) V-Str and (f) H-Str under an external field ${\mu }_{0}H=50\mathrm{mT}$ (along +$\widehat{z}$), revealing that the antiskyrmion is confined to one-dimensional motion by the stripe domains independent of the current flow direction. A clear linear dependence of the antiskyrmion velocity on the current density emerges in both cases as shown in Fig. 1g. Furthermore, a significant enhancement in antiskyrmion velocity is present for the $j\perp$ V-Str case, suggesting that the confining magnetic stripe domains may play a role similar to the sample edge in the confined skyrmion dynamics discussed above²⁷.

The formations of antiskyrmions confined within helical stripe domains in FNPP

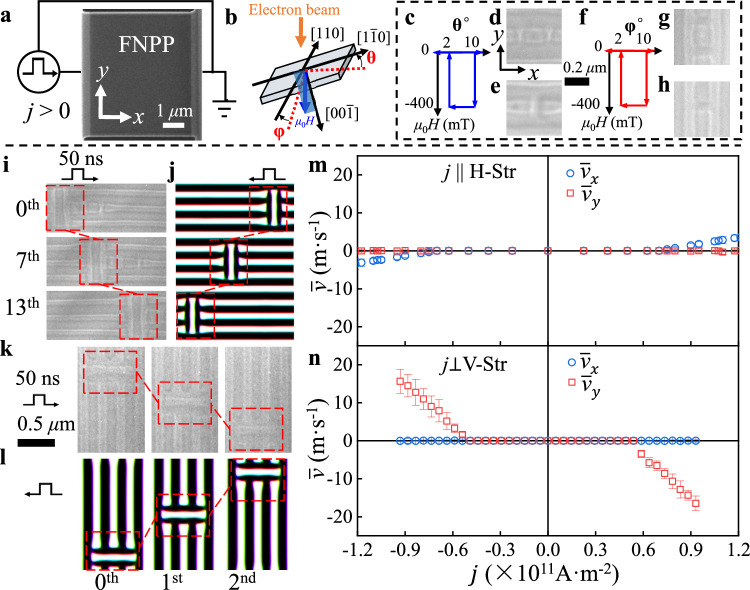
To experimentally confirm the antiskyrmion dynamics predicted by the aforementioned micromagnetic simulations in FNPP, we fabricated a two-terminal device using a focused ion beam (FIB) method (see Supplementary Note 1). The experimental setup is schematically illustrated in Fig. 2a. We manufactured a rectangular FNPP device, with its edges aligned along the $\left[1\overline{1}0\right]$ and [$110$] crystal axes, respectively, defined as the +x and +y directions in Fig. 2a. The positive pulse current direction is defined as the +x axis. Figure 2b shows the orientation of the device on a double-tilt holder capable of applying electric current to the device within the transmission electron microscope. We then employed LTEM to characterize magnetic configurations and their dynamics within the device.

Fig. 2. In situ Lorentz transmission electron microscopy (LTEM) measurements of current-driven antiskyrmion motion in stripes.

a A scanning electron microscope (SEM) image of a two-terminal device. The scale bar in (a) is 1 μm. b The schematic of the device orientations with respect to the electron beam and external field. c, f Schematic drawings show the procedure to generate antiskyrmions (d, g) or half antiskyrmion pairs (HAPs) (e, h) in the H-Str (d, e) or in V-Str (g, h). The scale bar for images in (d, e, g, h) is 0.2 μm. i, k LTEM images observed after sequential current-pulse applications showing the current-driven antiskyrmion (marked by the red rectangular dashed line) motion in H-Str (i) and in V-Str (k) for positive current (i, left panels; k, top panels) and ${\mu }_{0}H=-50\mathrm{mT}$. Micromagnetic simulation results for negative (j, right panels; l, bottom panels) current and ${\mu }_{0}H=-50\mathrm{mT}$. The current densities in (i–l) are 0.95 × 10¹¹ A m⁻², 0.20 × 10¹¹ A m⁻², 0.73 × 10¹¹ A m⁻², and 1.00 × 10¹¹ A m⁻², respectively, and the current-pulse width is 50 ns. The scale bar for images in (i–l) is 0.5 μm. m, n The corresponding average antiskyrmion velocity $\overline{v}$ versus current density $j$ in (i, k). The error bars in both plots represent the standard deviation from the mean of multiple trials.

To create an antiskyrmion embedded in H-Str, the following experimental procedure (illustrated in Fig. 2c) was employed: (1) tilt the sample holder by approximately 10° (the θ-value), (2) increase the magnetic field to ${\mu }_{0}H=-400\mathrm{mT}$, (3) return the sample holder to its original orientation with a roughly 2° tilt, and (4) reduce ${\mu }_{0}H$ to 0 mT and tilt the sample holder to 0°. An antiskyrmion embedded in a H-Str is obtained, as shown in a defocused LTEM micrograph (Fig. 2d). Similarly, an antiskyrmion embedded in V-Str can be generated by tilting the device plate at the angle φ, as shown in Fig. 2f. Representative antiskyrmion is shown in Fig. 2g.

For a rectangular antiskyrmion, we can define a major axis length $l_{Asky}=n{\lambda }_{hel}$, where ${\lambda }_{hel}$ is the helical period of the studied system. Interestingly, in addition to typical square-shape antiskyrmion (n = 1), antiskyrmions with different elongation factor n within helical stripe domains (see Supplementary Notes 4 and 5) can also be created. These antiskyrmions with different n exhibit different current-driven dynamics, which will be discussed in the next section.

The geometry, unidirectional current, and external field effects on antiskyrmion dynamics

To drive the antiskyrmion dynamics while minimizing the Joule heating, we employed a short current-pulse width of 50 ns (see Note 2 in Supplementary). The current pulse is first applied to a single square-shaped antiskyrmions. Although n = 1 antiskyrmions can be readily generated within a single H-Str stripe, the critical current density required to move them is close to that beyond which the antiskyrmion will be annihilated (see Note 3 in Supplementary).

In contrast, the elongated antiskyrmions (n > 1) with their longer axis perpendicular to the background helices, can move at a lower threshold current density than that required for driving antiskyrmions with the square shape. For example, Fig. 2i shows that an antiskyrmion with $n=3$ embedded in H-Str moves at |j| = 0.95 × 10¹¹ A m⁻² (pulse width: 50 ns). The motion of antiskyrmions ($n=3$) embedded in V-Str under ${\mu }_{0}H=-50\mathrm{mT}$ and a 50 ns current-pulse width with flowing currents of |j| = 0.73 × 10¹¹ A m⁻² are also shown in the LTEM micrographs in Fig. 2k. A significant enhancement of $v_d$ is observed when the elongated antiskyrmion is embedded in V-Str (j $\perp$ V-Str) compared to that in H-Str (j || H-Str).

To better understanding the antiskyrmion dynamics embedded in both H-Str and V-Str cases, micromagnetic simulations were performed for antiskyrmions ($n=3$), as shown in Fig. 2j, l. The simulation results are well consistent with experimental observations of antiskyrmion dynamics upon the current reversals, as shown in Supplementary Note 6. The unidirectional motion perpendicular to the current flow and along the V-Str ($v_d\perp j$) can be ascribed to the Magnus force, which is perpendicular to the current flow as described theoretically with the Thiele equation discussed above²⁷. The experimental results agree well with the micromagnetic simulation results to fix the formula as v_d $\propto$ $-$(4πQ/α) j for the antiskyrmion in V-Str (j $\perp$ V-Str), compared with v_d $\propto$ (β/α) j for the antiskyrmion in H-Str (j$\parallel$H-Str). As the damping parameter α and non-adiabatic spin-transfer torque strength parameter β are usually very small and close to each other, we could have difference with 4π/α = 251 and β/α = 1, if we assume α = β = 0.05. However, the simulation for elongated antiskyrmion (n = 3) in j ⊥ V-Str shows a velocity that is only 1.5 times compared to that in j || H-Str, as shown in Supplementary Note 7. This difference may possibly ascribe to the difference in other parameters, such as the dissipative tensor, which is subject to the antiskyrmion geometry.

To quantitatively understand the relationship between $v_d$ and $j$ in these two cases, we performed a systemically study of the antiskyrmion motion over a wide range of $j$ in pinned and flow regimes for antiskyrmions. Figure 2m, n shows the distinctive average velocity of the antiskyrmion ($n=3$) as the j$\parallel$H-Str and j $\perp$ V-Str, respectively. Notably, the results indicate a larger threshold current density (|j_c| ~ 0.73 × 10¹¹ A m⁻²) for driving the antiskyrmion in H-Str than that for the antiskyrmion in V-Str (|j_c| ~ 0.49 × 10¹¹ A m⁻²). At j = 0.94 × 10¹¹ A m⁻², it shows the velocity of elongated antiskyrmion (n = 3) in j ⊥ V-Str is about 9.3 times faster than that in j || H-Str. The results reveal that the current flow direction is a critical factor in designing antiskyrmion-based spintronics devices with confined geometries.

The effect of pulse width on antiskyrmion dynamics has also been investigated experimentally. We examined the elongated antiskyrmions (n = 4) with respect to the pulse width at 0 mT in both j$\parallel$H-Str and j ⊥ V-Str configuration (Supplementary Note 2). The results indicate a non-linear increase in antiskyrmion velocity with increasing pulse width. When the current exceeds a critical value, the transformation of it was observed that antiskyrmions can transition into non-topological bubbles, or be annihilation of antiskyrmion occurs.

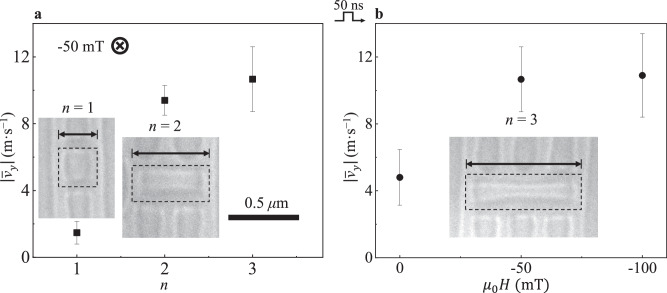
Figure 3a shows the average antiskyrmion velocity $\mid {\overline{v}}_y\mid$ versus $n$ for antiskyrmions embedded in V-Str at j = 0.78 × 10¹¹ A m⁻². We observed that antiskyrmions with n = 2 and n = 3 exhibit onset motion above |j_c| ~ 0.5 × 10¹¹A m⁻² and that the increase of $n$ leads to faster motions of antiskyrmions. The same geometric effect on the dynamical antiskyrmions (n = 2 and n = 3) embedded in H-Str has also been revealed with flowing current of |j_c| ~ 0.7 × 10¹¹ A m⁻² (see Supplementary Note 8).

Fig. 3. Effects of antiskyrmion shape and external field on antiskyrmion dynamics.

a The average antiskyrmion velocity in a V-Str background versus the elongation factor $n$ defined as the ratio of the antiskyrmion length $l_{Asky}$ to the helical period ${\lambda }_{hel}$ at j = 0.78 × 10¹¹ A m⁻² under ${\mu }_{0}H\mathit{=}-50\mathrm{mT}$. b The average velocity of $n=3$ antiskyrmions versus ${\mu }_{0}H$ at j = 0.78 × 10¹¹ A m⁻². The inset images in (a, b) are LTEM images of n = 1, 2, and 3 antiskyrmions, respectively. The scale bar for inset images in (a, b) is 0.5 μm. The error bars in both plots represent the standard deviation from the mean of multiple trials.

In addition to the geometric effect on antiskyrmion dynamics, the external field H has been observed to modify the size and stability of spin textures³⁴, thereby potentially affecting their dynamics³⁵ (Supplementary Notes 6). The observed results reveal that above $∣j_c∣$ the velocity of antiskyrmion continues increasing in proportion to $j$, irrespective of the direction of ${\mu }_{0}H$. However, an increased magnetic field results in faster antiskyrmion motions, as shown in Fig. 3b. Our simulation results also confirmed this phenomenon that the antiskyrmion at −100 mT shows 15% velocity enhancement compared to the one at −50 mT in j $\perp$ V-Str, however, the velocity for antiskyrmion in j || H-Str remains almost unchanged at −100 mT and −50 mT (Supplementary Notes 9). These results show that the antiskyrmion velocity can be tuned by both their geometric shapes and the external magnetic field. As for higher field, e.g., −150 mT, we found antiskyrmions are easy to transform into non-topological bubbles under pulse current stimulations and therefore, leading to the complicated dynamical phenomena. We have also conducted the experiment for current-driven isolated antiskyrmion in the ferromagnetic background. Such an isolated antiskyrmion transformed into a non-topological bubble before its motion driven by currents (Supplementary Notes 10).

Current-driven dynamics of half-antiskyrmion pairs

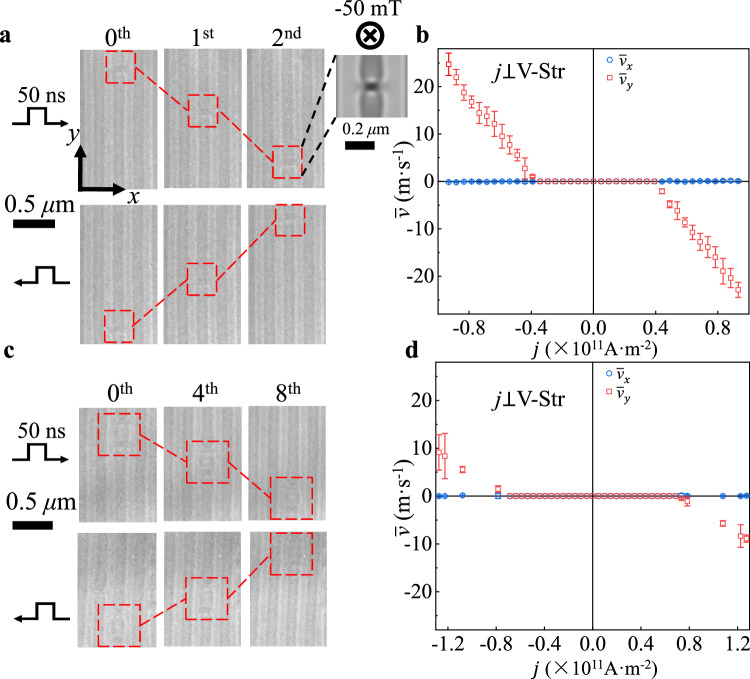
In addition to the formation of an antiskyrmion in stripes with the method in Fig. 2c, f, a half-antiskyrmion pair (HAP) embedded in the H-Str and V-Str shows up, as shown in Fig. 2e, h, respectively. Here, the HAP, which has the same topological charge (Q = +1) as the antiskyrmion, can be regarded as a combination of two antimerons³⁶. We also perform the topological charge calculation of the HAP and antiskyrmion using micromagnetic simulation (see Supplementary Note 11). Note here that HAPs are distinguished with half skyrmion pairs^16,25 or H-shaped skyrmion²⁶ due to the presence of four Bloch lines in real space, even though they may carry the same unit of topological charge. The critical current density required for moving the HAPs embedded in H-Str is also as high as that needed to annihilate them, similarly like the antiskyrmion in the H-Str (see Supplementary Note 3). Unlike antiskyrmions embedded in V-Str, HAPs in V-Str exhibit current-driven motion with a markedly enhanced velocity and lower threshold current density. Figure 4a presents representative LTEM images of a HAP configuration at |j| = 0.63 × 10¹¹ A m⁻² under ${\mu }_{0}H=-50\mathrm{mT}$, revealing that HAPs move along the same direction as their antiskyrmion counterparts under an electric current flow. To elucidate the difference between the current-driven motions of HAPs and antiskyrmions, we conducted an experiment probing the HAP velocity as a function of current density. Figure 4b shows a critical current density of |j_c| ~ 0.4 × 10¹¹ A m⁻² for moving the HAP, about 20% lower than that for driving elongated antiskyrmions (n = 3) in j ⊥ V-Str. In contrast, a squared antiskyrmion in a V-Str domain exhibits step-by-step motion (Fig. 4c) with sequences of pulse currents at relatively lower current densities (Fig. 4d) compared to the drive of a squared antiskyrmion in the H-Str. Interestingly, the current-induced deformation of antiskyrmion is observed from a square shape into a rectangle shape along the current-flow direction due to the strong pinning effect in the present device (see Supplementary Note 8). Moreover, the HAP velocity at j = 0.78 × 10¹¹ A m⁻² is 16.0 m s⁻¹, 49% larger than the antiskyrmion ($n=3$) velocity with j ⊥ V-Str.

Fig. 4. The current-driven dynamics of a HAP and an antiskyrmion (n = 1).

a, c LTEM images of a HAP and an antiskyrmion observed by sequential current-pulse applications, respectively. The scale bar for images in (a, c) is 0.5 μm. The |j| is 0.63 × 10¹¹ A m⁻² and 0.78 × 10¹¹ A m⁻² in (a, c), flowing along the +x (upper panels) and opposite direction (−x, lower panels). A simulated LTEM image for the HAP is shown in the upper right panel of (a). The scale bar for the simulated LTEM image is 0.2 μm. b, d The HAP and antiskyrmion velocity averaged over several trials plotted as a function of j, respectively. All data were obtained under ${\mu }_{0}H\mathit{=}-50\mathrm{mT}$. The error bars in both plots represent the standard deviation from the mean of multiple trials.

To gain deeper insights into the underlying mechanisms governing HAP dynamics, we also conducted experiments at various ${\mu }_{0}H$ (Supplementary Note 12). The results reveal that the ${\mu }_{0}H$ can also affect HAPs dynamics. However, it is noteworthy that the velocity of HAPs decreases with the increase in ${\mu }_{0}H$, as opposed to that observed for antiskyrmions. The reason could be that the increase in ${\mu }_{0}H$ leads to a compression between adjacent half antiskyrmions, and thus reduces the size of the HAP. The efficiency of STTs in driving the HAP decreases with the decreasing size of HAP.

In summary, we have experimentally demonstrated the real-space observations of current-driven antiskyrmion motions in FNPP at room temperature. The antiskyrmions can be reproducibly generated within a stripe domain background and electrically driven while confined within the stripe domains. The velocity of antiskyrmions shows a linear dependence on the current density with current flows parallel or perpendicular to the stripes. Importantly, the antiskyrmion motion is enhanced when the current is flowed perpendicular to the stripes. Our results evidence antiskyrmion as a prototype carrier for racetrack-type memory^37–39. These findings can potentially propel antiskyrmions to the forefront of future practical spintronic applications.

Methods

Sample preparation

A single crystal of (Fe_0.63Ni_0.3Pd_0.07)₃P (FNPP) was synthesized via the self-flux method utilizing Fe, Ni, Pd, and red phosphorous P. The two terminal devices composed of (001) thin plates of FNPP with dimensions of 0.16 μm × 4.9 μm × 6 μm for one device and 0.16 μm × 4.3 μm × 2.5 μm for another device, were fabricated with the focused ion beam technique (NB5000, Hitachi).

In situ measurement

Real-space observations of antiskyrmions were performed by transmission electron microscopes (JEM-2100F and JEM-2800, JEOL) equipped with a double-tilt current capable holder (Fusion select, Protochips). An external magnetic field was applied normally to the device-plate plane by controlling the objective-lens current of the microscope. The pulsed voltage was provided by an arbitrary function generator (AFG 31252, Tektronix). The pulse currents were manually triggered at intervals exceeding 2 s.

Data analysis

The LTEM videos are recorded during the sequential current-pulse excitations. The average velocities of antiskyrmions and HAPs are calculated over several trials (at least 4 trials) at each current density. The error bars of the velocity represent the standard deviation from the mean of multiple trials.

Micromagnetic simulations

Micromagnetic simulations were performed using the functional micromagnetics package−Object Oriented MicroMagnetic Framework (OOMMF)⁴⁰. The current-driven spin dynamics were simulated by solving the Landau-Lifshitz-Gilbert equation augmented with adiabatic and non-adiabatic spin-transfer torques:

$$\frac{d\mathbf{M}}{dt}=-{\gamma }_0\mathbf{M}\times \mathit{\times }{\mathbf{H}}_{\mathrm{eff}}\mathit{+}\frac{\alpha }{M_{\mathrm{S}}}\left(\mathbf{M}\times \mathit{\times }\frac{d\mathbf{M}}{dt}\right)+\frac{u}{M_{\mathrm{S}}^2}\left(\mathbf{M}\times \frac{\partial \mathbf{M}}{\partial x}\times \mathbf{M}\right)-\frac{\beta u}{M_{\mathrm{S}}}\left(\mathbf{M}\times \frac{\partial \mathbf{M}}{\partial x}\right)$$ 2

where M is the magnetization, M_S = |M_S| is the saturation magnetization, t is the time, γ₀ is the absolute gyromagnetic ratio, and α is the damping parameter. ${\mathbf{H}}_{\mathrm{eff}}=-{\mu }_0^{-1}\partial \epsilon /\partial \mathbf{M}$ is the effective field, and $u=∣{\gamma }_0\hslash /{\mu }_{0}e∣\left(jP/2M_{\mathrm{S}}\right)$ is the conduction electron velocity, where ${\mu }_0$ is the vacuum permeability constant, $\hslash$ is the reduced Planck constant, e is the electron charge, j is the applied current density, and P is the spin polarization rate. The total system energy includes the ferromagnetic exchange interaction, anisotropic DMI, uniaxial magnetic anisotropy, external magnetic field, and demagnetization energy terms. The average energy density is expressed as:

$$\epsilon =A{\left[\nabla \left(\frac{\mathbf{M}}{M_{\mathrm{S}}}\right)\right]}^2+\frac{D}{M_{\mathrm{S}}^2}\left[\mathbf{M}\cdot \left(\widehat{x}\times \frac{\partial \mathbf{M}}{\partial x}\right)-\mathbf{M}\cdot \left(\widehat{y}\times \frac{\partial \mathbf{M}}{\partial y}\right)\right]-\frac{K}{M_{\mathrm{S}}^2}{\left(\widehat{z}\cdot \mathbf{M}\right)}^2-{\mu }_0\mathbf{M}\cdot \mathbf{H}\mathit{-}\frac{{\mu }_0}{2}\mathbf{M}\cdot {\mathbf{H}}_{\mathrm{d}},$$ 3

where A and D denote the ferromagnetic exchange and anisotropic DMI constants, respectively. K is the uniaxial magnetic anisotropy constant. H is the applied external magnetic field. H_d is the demagnetization field.

The intrinsic magnetic parameters are adopted from ref. ²⁰ the saturation magnetization M_s = 417 kA m⁻¹, the exchange constant A = 8.1 pJ m⁻¹, the anisotropic DMI constant D = 0.25 mJ m⁻², and the uniaxial anisotropy constant K = 3.1 × 10⁴ J m⁻³. The default sample size is 2000 × 600 × 160 nm³ or 600 × 2000 × 160 nm³, which depends on the current injection direction. The mesh size is set to 5 × 5 × 32 nm³. The periodic boundary condition is applied in the x or y direction, depending on the current injection geometry. We assumed that the damping parameter α = 0.05 and β = 0.05. The spin polarization rate is set to P = 1 for simplicity, so that the driving force is simply proportional to the applied current density, i.e., u ~ j. The initial state is an antiskyrmion or HAP placed at the center of the sample with a helical background, which is relaxed at an out-of-plane field of B_z = −50 mT or 50 mT before flowing the current through the device.

Author contributions

Y.G. and X.Z. Yu conceived the project. Y.G. fabricated the bulk materials, performed the Lorentz TEM measurements, analyzed LTEM data with L.C.P., F.S.Y. and X.Z. Yu. Y.G., F.S.Y. and X.Z. Yu wrote the manuscript. X.Z. and M.M. carried out the micromagnetic simulations assisted with data analyses. K.K. and Y. Taguchi prepared the FNPP alloy. D.N. measured the damping parameter of FNPP using ferromagnetic resonance. All authors discussed the data and commented on the manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The authors declare that the main data supporting the findings of this study are available within the article and its Supplementary Information files. Extra data are available from the corresponding author upon reasonable request.

Code availability

The micromagnetic simulator OOMMF used in this work is publicly accessible at http://math.nist.gov/oommf.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-52072-4.