Abstract
Nonhuman primates (NHPs) exhibit complex and diverse behavior that typifies advanced cognitive function and social communication, but quantitative and systematical measure of this natural nonverbal processing has been a technical challenge. Specifically, a method is required to automatically segment time series of behavior into elemental motion motifs, much like finding meaningful words in character strings. Here, we propose a solution called SyntacticMotionParser (SMP), a general-purpose unsupervised behavior parsing algorithm using a nonparametric Bayesian model. Using three-dimensional posture-tracking data from NHPs, SMP automatically outputs an optimized sequence of latent motion motifs classified into the most likely number of states. When applied to behavioral datasets from common marmosets and rhesus monkeys, SMP outperformed conventional posture-clustering models and detected a set of behavioral ethograms from publicly available data. SMP also quantified and visualized the behavioral effects of chemogenetic neural manipulations. SMP thus has the potential to dramatically improve our understanding of natural NHP behavior in a variety of contexts.
Subject terms: Computational models, Dynamical systems
Data-driven machine learning algorithm, Syntactic Motion Parser, automatically decomposes primate’s natural motion dynamics into its inherent component.
Introduction
In humans and other primates, complex and dynamical behavioral sequences consisting of gaze, facial expressions, postures, and body movements serve as expressions of internal states such as emotion and intention (i.e. nonverbal expression), which are fundamental for normal social life1,2. Nonhuman primates (NHPs), such as macaque and marmoset monkeys, have been shown to interact socially through such nonverbal expressions while they perform higher cognitive/motor functions, thus providing unique opportunities for modeling human brain function in healthy and diseased contexts3,4. Several NHP models of emotional and social communication dysfunction have been studied using pharmacological interventions and genetic modifications in adolescence or adulthood5–8. In addition, recent advances in techniques for genetic manipulation, such as chemogenetics, have allowed reversible manipulation of activity in specific brain circuits of freely moving monkeys, opening up valuable avenues for understanding the neural mechanisms that govern internal states9–11. However, previous NHP studies have focused on measuring behavioral indicators based on the experimenters’ hypotheses, running the risk of overlooking changes in animal behavior that are beyond the scope of the prediction. Thus, advancing our understanding of the brain mechanisms that underlie internal states requires a quantitative, data-driven recapture of natural NHP behavior12,13; however, the lack of a method for doing this has created a bottleneck in this research field.
Recent developments in video-based motion-tracking systems have enabled the automated acquisition of large-scale behavioral data9,14–16. These data can be analyzed by machine learning to automatically segment and extract recurrent behaviors (ethograms) from the data, thus replacing human observation. Programmatically, this means automatically determining the starting and ending points of all data segments corresponding to a given ethogram, even for non-predetermined behavior. Several studies have proposed ethogram-detection algorithms, but each has certain limitations. Ballesta et al. proposed a method for automatically detecting ethograms17; however, it requires manually set ad hoc extraction parameters for the predetermined target ethograms, making it unsuitable as an objective means of evaluating natural NHP behavior. Other studies have automatically classified NHP behavior by using a simple clustering method that has been successfully applied to rodents and insects to look at NHP body postures that correspond to different ethograms14,15. This method may be useful for studying NHPs in a confined range of research interests, such as when all postures in the data can be completely mapped to a set of ethograms of interest. However, comprehensive NHP behavioral analysis must target a broad range of ethograms that are beyond the scope of these posture-based classification methods—including temporally dynamic changes in multiple postures (e.g., jumps, turns, and catching prey), as well as complex and abstract changes, such as those that occur during social play18–20.
Another framework for unsupervised behavioral data segmentation is one that fits a generative model to time series of data. In this scenario, observed behavioral parameters are modeled as probabilistic implements of a sequence of categorical and reproducible latent states (motion motifs)21,22. This framework has shown promise in analyzing behavioral data from rodents, fish, and insects to identify novel ways of capturing prey23, sorting neuropharmacological effects24, and mapping animal internal states by simultaneously recording neural activity 25–27. This technique is also gaining prominence in the fields of computer vision and human robotics as a way to computationally estimate the meaning of behavior28–30. However, to the best of our knowledge, such an algorithm has not been verified as appropriate for NHPs, likely because the current algorithms were not developed or optimized to target the complexity and diversity of NHP behavioral ethograms. In addition, even if the current algorithms were available for NHPs, they remain somewhat subjective; in the case of unsupervised behavior segmentation, determining the number of latent motif classes (class size) has a significant impact on the results, but has usually been left to the subjective judgment of the researchers14,31. Ideally, the optimal class size should also be determined in an unsupervised manner32,33.
Here, we propose a new framework called SyntacticMotionParser (SMP), which allows for quantitative and automatic parsing of NHP behavior into a set of motion motifs. Using SMP, three-dimensional (3D) motion-tracking data can be described as a stochastic generative process of motion motifs, each of which is optimally segmented by unsupervised machine learning (Fig. 1a). Specifically, the internal variability of individual motifs is regressed by a Gaussian process (GP) and simultaneously clustered by its hyperparameters, while the class size is automatically optimized by a Bayesian nonparametric model with hierarchical Dirichlet process (HDP) (Fig. 1b). We demonstrate that SMP can characterize and describe different styles of common marmoset (Callithrix jacchus) feeding behavior. SMP was also able to extract several ethograms unique to rhesus monkeys (Macaca mulatta) from publicly available motion-tracking data and describe their patterns and temporal sequences14. Critically, SMP was also able to automatically detect and describe the changes in marmoset behavior that resulted from chemogenetic manipulation of specific neural circuits9, without any prior information.
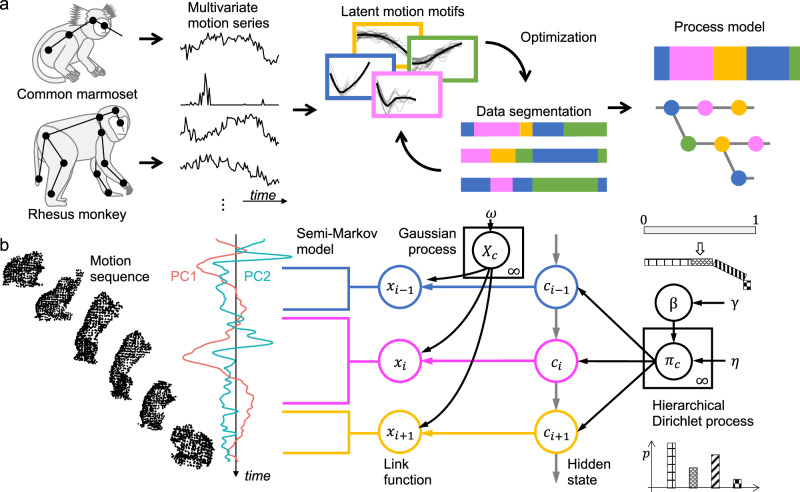
Fig. 1. Dynamic temporal segmentation of NHP motion time series using a generative model.
a Illustration of the generative description workflow of NHP behavior. The input behavior series is segmented into a set of latent motion motifs, which are partially reproducible trends of multivariate motion parameters. The properties of motion motifs and their probabilistic interconnectedness, i.e., “the grammar of behavior,” are optimized by data-driven machine learning and generatively describe behavior as a stochastic process model. b A graphical model of dynamical decomposition of monkey behavior using the nonparametric Bayesian model, SMP. The two major principal component scores (PC1 and PC2) extracted from the multivariate time series of monkey behavior were optimally segmented by this model into a time series of discretely labeled hidden state c, using GP as the nonlinear regression link function, a hidden semi-Markov model for estimating the temporal breakpoints, and HDP including the stick-breaking process for estimating state class size. NHP nonhuman primate, SMP SyntacticMotionParser, GP Gaussian process, HDP hierarchical Dirichlet process.
Results
Unsupervised detection of latent motion motifs from free-feeding marmoset behavior
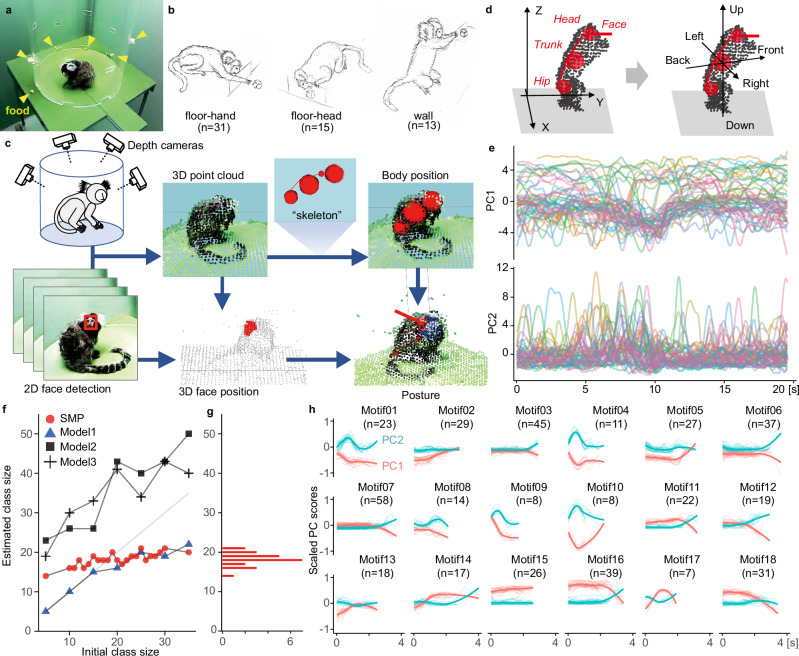
We first assessed the ability of SMP’s computational segmentation to identify changes in internal states. Internal states were inferred from simple goal-directed behaviors, which included stereotyped and reproducible motion series such as searching, discovering, approaching, and eating. We recorded free-feeding behavior of four adult marmosets, during which they fed wherever, whenever, and however they wanted (Fig. 2a, b, Supplementary Fig. 1). Using an original marker-less motion-tracking system9,34,35, the marmoset behavior was semi-automatically captured as 3D trajectories of the four body parts (Face, Head, Trunk, and Hip; Fig. 2c, d and Supplementary Movie 1). For the SMP analysis, we manually extracted trajectory data (approx. 20 s) centered on the timing of feeding based on video clips (N = 51, total duration = 993 s; Supplementary Table 1, Supplementary Fig. 2). We assumed that these 20-s instances of feeding behavior would consist of a few motion motifs, each lasting several seconds. We applied SMP to the 1st and 2nd principal component (PC) scores for all of the free-feeding data, including 3D trajectories of body parts (13 parameters) (Fig. 2e, Supplementary Table 2). SMP successfully segmented the data into about 430 motion motifs (433.8 ± 5.2, mean ± sd) across simulations with various initial simulation class sizes (random seed, n = 23). The resulting number of motif classes converged to a unimodal posterior distribution with a median value of 18, which indicates the optimal class size (Fig. 2f, g, red). Analysis of the seven simulations that yielded 18 motif classes revealed that the 1st and 2nd PC scores of the motifs were similar regardless of the initial class size (Supplementary Fig. 3). Figure 2h shows 18 motion motifs that were characterized by a distinct set of PC-score dynamics, and which were segmented by SMP with an initial class size of 22 (which was used in the subsequent analyses). These motion motifs were commonly observed in the four marmosets without significant individual unique distribution bias (X-sq = 62.99, df = 51, p value = 0.121, Pearson’s Chi-squared test, Supplementary Table 3). Successful convergence of dynamic motion segmentation appeared to result from the combination of GP and HDP inherent in SMP; the GP works as a link function that represents dynamic postural changes, while the HDP optimizes the class size36–38. To benchmark SMP performance, we compared it with the performance of other statistical models. When using GP as a link function, but not using HDP, the resulting class size depended on the initial value, and the optimal class size was not determined (Fig. 2f, Model1). Although simulations with an excessive number of initial class sizes—18 or more in this case—did result in final class sizes that converged to a value which was similar to that obtained by SMP using HDP (Fig. 2f), these results indicate that this model (Model1) required repetitive simulations with different initial values to reach the final converged values, which increased the computational cost. When using HDP with a different link function (autocorrelation and static; Fig. 2f, Models 2 and 3, respectively), the class size again depended on the initial value and no information about optimal class size was provided. Thus, SMP that incorporates both HDP and GP demonstrated a significant advantage in simultaneously providing flexible regression to explain free-feeding behavior and guaranteeing unsupervised convergence of an optimal class size of motion motifs inherent in the data.
Fig. 2. Motion tracking and computational segmentation in freely moving common marmosets.
a Experimental setup for marmoset free-feeding behavior. Yellow arrowheads indicate the location of the food reward. b Illustrations showing the subtypes of feeding behavior: using hands to take food from the floor (floor-hand, left), using head and mouth directly (floor-head, middle), and taking food from the wall (wall, right). c Data-flow diagram of the marker-less motion-tracking system. The positions of marmoset body parts, Head, Neck, Trunk, and Hip were estimated by a skeleton model fitting. The Face position was also estimated by the projection of the face rectangle on RGB images to the point cloud. See also Supplementary Movie 1. d The posture parameters were transformed from distance-from-the center coordinates (left) to Trunk-centered coordinates (right). e Time series of the first and second principal component scores (PC1 and PC2) with 10 Hz resolution for a total of 1020 s of data comprising 51 sets of 20-s data. f Using between 5 and 35 for the initial class size for the simulation, the class size of the inherent motion motifs during the free-feeding behavior was estimated by four statistical models: the proposed SMP method (HDP + GP, red), Model1 (GP, blue), Model2 (HDP + linear regression, square), and Model3 (HDP, cross). g Using SMP, the number of motif classes converged to a unimodal posterior distribution with a median of 18. h Examples of a set of 18 motion motifs estimated by SMP simulation with 22 initial classes. SMP SyntacticMotionParser, HDP hierarchical Dirichlet process, GP Gaussian process.
SMP can describe and reproduce sequences of motion motifs from goal-directed marmoset behavior
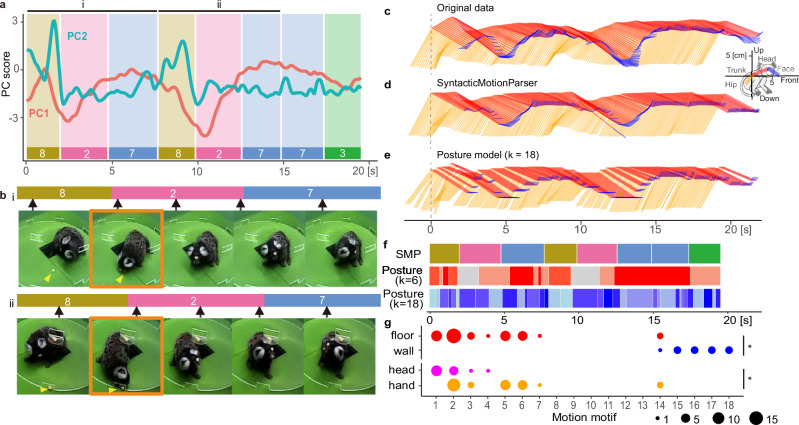
Having shown that SMP performed consistently in unsupervised segmentation of marmoset free-feeding behavior, we next investigated how feeding behavior can be described with a sequence of motion motifs detected by SMP. Figure 3a presents a 20-s data sample that included two feedings. SMP decomposed these data into a sequence of eight motion motifs from four classes. Because each motion motif represents typical body motion trajectories that are transformed into temporal dynamics of two PCs (Fig. 2h), corresponding body motion parameters can be retrieved by inverse calculation from the mean value of the PC scores. For example, when a series of movements represented by motifs 2, 3, 7, and 8 were reconstructed in the order of observation, marmoset behavior was able to be retrieved as the dynamic relative positions of the Face, Head, Trunk, and Hip (Fig. 3d, Supplementary Movie 2), similar to those from the original data (Fig. 3b, c). When we attempted a similar reproduction of movements using a standard posture model (the 2D uniform manifold approximation and projection; UMAP)18,19 with the k-means clustering method, the motions were unnatural and resembled a stop-motion animation of static postures stitched together (Fig. 3e). With the same initial class size as that of the SMP (k = 18), the posture model decomposed the data into significantly shorter sub-second fragments (UMAP: n = 2076, 0.3 ± 0.53 s, median ± sd; SMP: n = 438, 2.3 ± 0.59 s; BM statistic = −177.48, df = 2451.8, p value < 2.2e-16) (Fig. 3f). These results demonstrate that SMP is unique in that it allows for a simple description of the multi-second dynamical structure observed during feeding behavior.
Fig. 3. Example of marmoset behavior smoothly described by SMP-derived motion motifs.
a Example of behavior segmentation. The curve trends represent the 1st and 2nd principal component scores (PC1 and PC2) of the motion parameters. The bottom lines and background rectangles represent the resulting eight segmented motion motifs with four types (motif 8, 2, 7, and 3). b Two sequential images of marmoset free-feeding behaviors with three-segment arrays “8-2-7”, where the labels (i) and (ii) correspond to those in (a). Black arrows indicate the position of the video frame in the segment represented by the upper bar. Yellow arrowheads indicate the location of the food reward. Orange rectangles indicate the images in which feeding occurred. c Time series of the original body movement trajectory during the data from (a), with the X-axis representing time and the front-back direction, and the Y-axis representing the up-down direction. The Face-Head, Head-Trunk, and Trunk-Hip are color-coded in blue, red, and orange, respectively. d The time series of the ideal body motion trajectory, which was pieced together from the eight motion motifs provided by SMP. e Time series connecting the six representative postures provided by the posture model, calculated by clustering the two-dimensional UMAP scores of all data using the k-means hierarchical clustering method (k = 18). See also Supplementary Movie 2. f Segmentation results of the motion sequence c using the proposed SMP method and the posture models (k = 6 and 18). g Dot plots showing the distribution of motion motifs in response to food placed on the wall and floor and in feeding approaches to food placed on the floor (floor-hand and floor-head). Size indicates the number of observations. *p value < 0.05 by Pearson’s Chi-squared test.
SMP motion motifs quantitatively characterized classification by observation
As shown in Fig. 3a, SMP described feeding behavior as a specific sequence of motion motifs (e.g., 8–2–7). Because feeding behaviors can be classified manually into three subtypes according to food position and approach strategy (floor-hand, floor-head, and wall; Fig. 2b; Supplementary Table 1), we next asked whether SMP-derived motion motifs would correspond to different feeding subtypes. Analysis revealed differences in motion motifs according to where the food was located (wall vs. floor), indicating that significantly different motifs were employed in the feeding segment (n = 58, X-sq = 51.9, df = 11, p value = 2.84e-08, Fig. 3g, top). We also found significant differences according to approach (floor-hand vs. floor-head), indicating that different motifs were employed depending on the approach strategy (n = 46, X-sq = 26.2, df = 8, p value = 9.85e-4, Fig. 3g, bottom). For comparison, we assessed the distribution of posture clusters during feeding using a conventional posture model (k-means with UMAP) with k = 18. Although the distributions of posture clusters at feeding times differed significantly between wall and floor (n = 58, X-sq = 58, df = 12, p = 5.21e-08, Pearson’s Chi-squared test), they did not significantly differ between floor-head and floor-hand (n = 46, X-sq = 7.58, df = 7, p = 0.371, Pearson’s Chi-squared test; Supplementary Table 3). Compared with the posture-based methods, when given data that was manually and roughly clipped to the timing of specific events, SMP provided a description that better reflected the dynamics of the actual behavior (Fig. 3c–e). We also compared SMP performance with manual segmentation by experts. Segmentations of feeding behavior varied more among the experts and tended to be larger grained than those derived by SMP (Supplementary Fig. 4). Thus, SMP consistently detected smaller, fine-grained differences in behavioral features than the conventional posture model or human annotation could, meaning it has a higher behavioral resolution.
Using SMP to identify ethograms in freely moving macaques
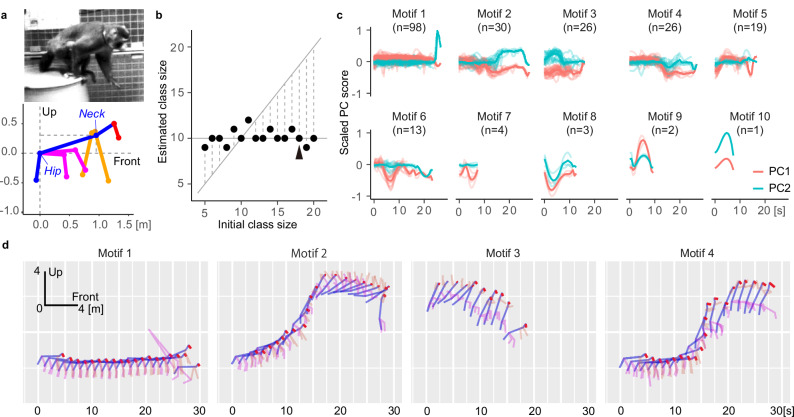
Having demonstrated the effectiveness of SMP analysis of marmoset behavior during a goal-directed paradigm, we next applied SMP to data from freely moving NHPs to test whether it could extract what animals are doing (i.e., ethograms), in a data-driven manner. For this purpose, we used OpenMonkeyStudio, an open data source of macaque monkey behaviors14, which consists of 3D trajectories of 13 key landmarks on a macaque body captured by multiple synchronized cameras (Fig. 4a, top). Similar to the data preprocessing in the marmoset analysis, the Front-Up coordinates were aligned to the Head-Hip axis (Hip-centered) to determine what each animal was doing rather than where it was (Fig. 4a, bottom). We assumed that the macaque behavior would comprise several kinds of motion motifs, each lasting around 15 s. The SMP segmented the 1st and 2nd PC scores (Supplementary Table 5) into about 230 motion motifs (234.2 ± 6.5, mean ± sd) in 16 random-seed simulations with various initial class sizes. The motifs comprised 10 classes whose sizes did not vary depending on the initial values of the simulation (Fig. 4b). Figure 4c shows the PC waveforms of motion motifs that resulted from SMP extraction with an initial class size of 18, which were replicated using different initial class sizes (Supplementary Fig. 5). By inverse-calculating the postural parameters from the average trend of the PC waveforms, SMP resynthesized the ideal motion represented by each motion motif, as exemplified in Fig. 4d: walking (motif 1), climbing up and holding on upside down (motif 2), stepping down (motif 3), and climbing up and staying (motif 4), which are common motion ethograms observed in macaques. Furthermore, less common ethograms were also captured as independent classes, such as long-distance jumps along walls and to the floor (motif 8 and motif 9; Fig. 4c, Supplementary Movie 3). These results demonstrate the versatility of SMP for detecting ethograms in freely moving NHPs from any dataset, with only a minimum assumption of their duration.
Fig. 4. Independent macaque behavior was segmented into ethograms by SMP.
a Macaque image (top; adapted from OpenMonkeyStudio14) and corresponding posture keypoint coordinates, which have been rescaled as Hip-centered with the x–y plane including the Hip-Neck vector (bottom). b The median posterior distribution of class sizes was 10. c Example of the trends for the 1st and 2nd principal components (PC1 and PC2) of each motion motif with initial class size = 18 (arrowhead in b). d The synthesized ideal body trajectories in major motions are calculated by the inverse operation of PC analysis. Motion motifs 1–4 represent walking, climbing up and holding upside down, stepping down, and climbing up and staying, respectively (see also Supplementary Movie 3).
Using SMP to characterize behavioral change induced by circuit manipulation
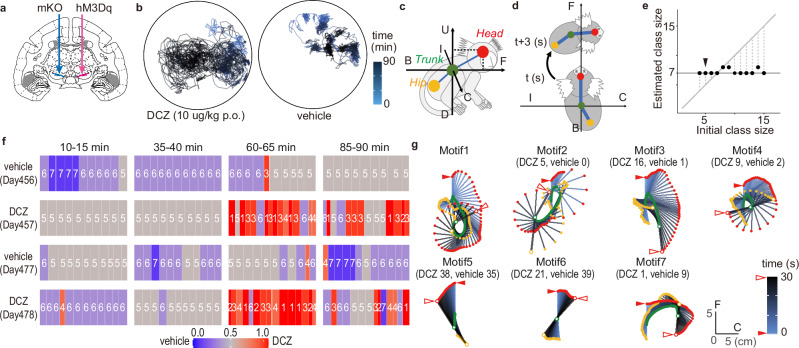
To identify how activity within a specific brain circuit can cause specific natural behaviors, we must be able to establish a method for unsupervised detection of behavioral changes. We therefore tested whether SMP could detect and characterize behavioral changes in free-moving marmosets that we induced by chemogenetic neural manipulation in our previous study9. Marmosets that expressed the excitatory chemogenetic receptor hM3Dq in the unilateral substantia nigra (SN) spun themselves around in the direction contralateral to the activated SN, and this behavior began about 45 min after eating the chemogenetic activator (deschloroclozapine, DCZ) (Fig. 5a, b). Although this behavioral change can be quantified by counting the number of rotations, its characterization is not simple, as it is difficult to describe rotation behavior using conventional static postures in a series of snapshot images. We asked whether SMP could effectively capture this phenotype without any assumptions. We analyzed two sessions of 5-min motion-tracking data at four certain time windows (10–15, 35–40, 60–65, and 85–90 min) after DCZ or vehicle consumption. We used 3D trajectories of the Head, Trunk, and Hip, and their velocities in the postural coordinates where the Head was frontal and the Trunk was centered (Fig. 5c, d), and applied PC analysis to reduce their dimensions to two (Supplementary Table 6). With multiple initial class sizes, SMP consistently extracted seven classes of motion motifs (approx. 30-s) from the data (Fig. 5e; Supplementary Fig. 6). Temporal distribution of these motifs indicated that more than 90% of motifs 1–4 appeared later than 60 min after DCZ administration (Fig. 5f, red). Visualization of the reconstructed body movements through inverse PC analysis revealed that motion motifs 1–4 characterized the nature of the contralateral rotation with dynamical postural changes, which were clearly dissociable from normal directional changes (motifs 5 and 6 ipsilateral and contralateral, respectively) or exploratory behavior (motif 7) (Fig. 5g, Supplementary Movie 4). The DCZ-induced contralateral body rotation was consistently detected even when a longer initial value of motif length was used for the simulation (i.e., approximately 90-s ranging 75 to 150 s) (Supplementary Fig. 7a, d). These results demonstrate that without any prior information, SMP could successfully capture and describe changes in unconstrained behavior that were induced by circuit manipulation. Importantly, it also indicated when and how the behavioral effects appeared, highlighting another advantage of this method in studying the causal relationship between natural behavior and brain function in NHPs.
Fig. 5. SMP characterized contralateral rotation behavior induced by chemogenetic manipulation.
a Illustration of viral vector injection locations adapted from Mimura et al.9. AAV vectors expressing excitatory DREADD hM3Dq were injected into the unilateral substantia nigra (SN, red arrow). As a control, an AAV vector expressing a fluorescent marker (mKO) was injected into the contralateral SN (blue arrow). b Example of the top view of the Head trajectory of the marmoset after deschloroclozapine (DCZ; 10 μg/kg, per os (p.o.)) and vehicle administration. c Illustration of the posture coordinate. The horizontal mapping of the Head through the center of the Trunk was defined as the front-back (F-B) axis, and the axes orthogonal to the F-B axis horizontally and vertically were defined as the ipsilateral-contralateral (I-C) and vertical up-down (U-D) axes, respectively. d Body coordinates were used to determine relative positions every 3 s. e Estimation result of motion-motif class size. SMP was applied to four 5-min time windows each from two 90-min sessions after DCZ and vehicle p.o. The result was 7 kinds of motion motifs. f Example of a motion-motif sequence detected by SMP with initial class size = 5 (arrowhead in (e)). The time at which the motif was observed is indicated by tiles and color-coded by the percentage of occurrences in the DCZ data. The days since vector injection are shown below the dosing conditions. g The top view illustration of the body trajectories is represented by the motion motifs in (f). Observed numbers in the DCZ and vehicle groups are under the motif numbers. The red and white arrowheads indicate the starting and ending points of the Head track, respectively. The Head, Trunk, and Hip positions are color-corded as (c), with white at the ending points. The body positions are drawn at 0.5-s intervals with a gradation from blue to black from start to end (see also Supplementary Movie 4).
Discussion
Here, we describe a novel computational framework, SMP, that quantitatively and automatically parses natural NHP behaviors into motion motifs, which can be used as meaningful metrics, like ethograms. As illustrated by its application to three NHP datasets in two monkey species, SMP is versatile and effective for quantifying and characterizing behaviors by simply adjusting the temporal window for motifs of interest, and not changing the model or process. SMP can also automatically detect and describe behavioral changes induced by neuronal manipulation. These results demonstrate that data-driven SMP not only performs as well as human observations, but can outperform them in detecting nuanced behaviors that manual methods may overlook. Thus, SMP can be widely applied for motion description and quantification of NHPs, offering the potential to dramatically improve our understanding of natural NHP behavior and the underlying brain functions in both normal and disease states.
Recent advances in machine learning allow for the collection of large-scale posture data, measured and estimated automatically from videos of freely moving NHPs9,14–16. At the same time, frame-by-frame classification of posture information can be used to detect ethograms from streaming behavior data14. Although this type of classification has been shown to be effective in rodents39, it may not be sufficient in NHPs because their natural ethograms are typically longer and more complex, which makes it more likely that the same postures occur in different contexts, as happens when climbing up and down. Indeed, in our demonstration, the conventional posture-classification method could not capture and reproduce NHP motion motifs because these methods transform inherently smooth and dynamic postural changes in a given ethogram into a constrained combination of static states, i.e., specific postures represented by k-means clusters in UMAP scores (Fig. 3e, f). In the case of rodents and insects, attempts have been made to address this issue by refining the conventional posture model to account for the semantic context33,40. The results are like stop-motion animations, forcing complex and computationally expensive modifications to reproduce natural actions. Unlike these static posture models, our proposed SMP can provide dynamic and reproducible motion motifs—which are inherent in the behavior—as basic units. Using a probabilistic estimation of the type and occurrence of motifs through data-driven learning, SMP automatically parses streaming behavioral data into a series of motion motifs (or ethograms). This is similar to the way in which sentence structure analysis in natural written language processing directly searches for meaningful morphemes like words, omitting detailed consideration of the smallest static unit, the character. SMP clearly distinguished climbing up from climbing down as different behavioral “words”, even though these two actions are indistinguishable in principle by posture alone (Fig. 4, Supplementary Movie 3). Thus, by estimating the grammar and syntax of NHP behavior, motion parsing might allow researchers to understand the internal state of animals or the functional significance of the behavior in terms of social communication and the underlying brain mechanisms, similar to what has already been shown to be effective for time-series correlation analysis with neural activity in rodents24,26.
Our results also demonstrate that SMP represents a major advance in how the behavioral effects of neural manipulation can be evaluated. While conventional methods have long relied on subjectively defined ethograms or task-controlled behavior, SMP employs automatic detection and description of changes in natural behavior, such as the frequency and type of motion motifs. Our demonstration showed that SMP can isolate and resynthesize abnormal contralateral turning that was triggered by chemogenetic neuronal manipulation, even under severe constraints such as limited tracking points that lacked facial coordinates (Fig. 5, Supplementary Movie 4). When chemogenetics is applied to NHP brain circuits that govern complex behaviors (e.g., the dorsolateral prefrontal cortex and caudate nucleus)41, SMP may be able to detect resulting behavioral changes not only as abnormal motifs, but also as abnormalities in motion-motif sequences (e.g., “8-2-7” in feeding behavior in Fig. 3) or their transition structures. In addition, by building a large dataset of natural NHP behavior, we can address behavioral variations across individuals. Our results suggest that SMP holds enormous potential for quantifying and describing behavioral changes far beyond what can be measured by conventional observational or task-based methods.
SMP implements two extensions to its generative model, HPD and GP, which address the following two major issues related to statistical estimation of latent states. The first issue is determining how many latent states exist in the behavioral data, which is always a problem when labeling discrete data elements as “characters” or “words”. Because the class size (the number of latent motion motif classes) is usually given as an ad hoc fixed parameter42, researchers have struggled to determine which is the most likely result when running simulations under a variety of conditions, each returning a plausible result14. The HDP is theoretically guaranteed to yield a single estimated class size for any initial value in an ideal situation with infinite iterations, which eliminates the need to select an optimal result36–38. Our comparison of multiple initial values was not for a posteriori sorting as in previous studies33, but rather it was to confirm that sufficient iterations were performed for convergence. In fact, all of our simulations returned a simple unimodal posterior distribution of the class sizes after 50 iterations (Figs. 2f, g, 4b, and 5e), from which the most likely class size was uniquely and automatically determined. The second issue is related to the link function of the latent state model. In a typical latent state model, each state is assumed to be static, as is the posture, which is why a link function is needed to regress and represent complex internal variability such as motion. We chose GP as the regression link function because it has been used in human behavior analyses29,30,43, and because it allows for more flexible regression than conventional auto-regressive filtering or Bernoulli generalized linear models25,26.
By incorporating both GP and HDP, SMP is able to automatically estimate all parameters, except for the three hyperparameters (ω, γ, and η) and the motif length for initial value of the simulation (min, max, and mean of initial motif duration). The parameter ω controls error coefficients within a motif, where a smaller ω would result in greater variance, permitting a broader range of movements to be classified under a single motif. The other hyperparameters γ and η are related to HDP; γ is the sparsity of the underlying state transition matrix and η is the expected number of different hidden states (Fig. 1b). Throughout this study, we showed that the basic parameter settings are efficient for NHP behavior quantification, and that the values were similar to those that we observed in our human motion analysis29. The hyperparameters might need to be tuned for data with different variance assumptions. In particular, the state interval parameters are the major adjustment factors that directly reflect the temporal extent of the motion motifs of interest. As we have shown (Supplementary Fig. 7a, d), increasing the interval reduces the redundancy of the classified motifs, while maintaining the detectability of specific behaviors. Although there are no theoretical limitations on the intervals, longer intervals increase computational cost and decrease the frequency of reproducible GP regression curves. Therefore, when trying different intervals, we recommend that the parameterized frame length first be fixed and the time resolution of the data be adjusted, as we demonstrated. While a similar latent model with HDP and GP was able to identify human motion as accurately as manual annotation29, the current study is the first application of this type of model extension for exploratory behavior quantification in NHPs, for which the GP kernel function was optimized. Although SMP with the parameter set used in this study is expected to work for analyzing freely-moving primate behavior for over several tens of minutes, further parameter optimization might be necessary to handle longer duration data, such as daily natural behavior logs within home cages lasting several days to months.
SMP will open the door to quantitative, rigorous, and comprehensive research of natural monkey behavior, which is needed in a wide range of scientific disciplines, including neuroscience, ethology, and developmental and evolutionary biology. Application of SMP also has a potential use in drug development and engineering brain-machine interfaces and other clinical devices. Neural recording and circuit manipulation of NHPs in free-moving conditions9,44 would bear real fruit when combined with computational behavioral description. SMP overcomes the motion annotation bottleneck of NHP experiments and automatically describes the diversity and complexity of dynamic natural behavior and the behavioral changes associated with brain circuit manipulation, thereby increasing the value of NHPs in the fields of neuroscience and psychology by opening a new behavioral research field—natural nonverbal processing.
Materials and methods
Animals
Four laboratory-bred adult common marmosets were used (2 males, 2 females; 1.4–6.4 years old; 290–400 g, Supplementary Table 1). Each cage was exposed to a 12/12-h light-dark cycle. Room temperature and humidity were maintained at 27–30 °C and 40%–50%, respectively. All experimental procedures were performed in accordance with the Guide for the Care and Use of Nonhuman Primates in Neuroscience Research (Japan Neuroscience Society; https://www.jnss.org/en/animal_primates) and were approved by the Animal Ethics Committee of the National Institutes for Quantum Science and Technology (#11-1038).
Behavior testing
Behavior experiments were conducted in a sound-attenuated room (O’hara & Co., Ltd., Tokyo, Japan; 2.4 m (h) × 1.2 m (w) × 1.6 m (d)), which was apart from the colony room. Vocalizations from the colony room could not be detected in the experimental room. The temperature was maintained at 27–30 °C and relative humidity was 30%–40%. The internal space of the sound-attenuated room was ventilated and illuminated with fluorescent lighting. The experiments were performed between 11:00 and 16:00.
Before the experimental sessions, each subject was transferred individually from the colony room to the experimental room in a small transport chamber (O’hara & Co., Ltd., Tokyo, Japan; 300 mm (h) × 100 mm (w) × 100 mm (d)). Once in the experimental room the transport chamber was placed under a table with a green top (O’hara & Co., Ltd., Tokyo, Japan; 0.5 m × 0.5 m × 0.5 m), upon which rested a cylindrical test chamber made from transparent acrylic (0.4 m (r) × 0.5 m (h)). The bottom of the test chamber had a door that when opened allowed the marmoset to enter from the transport chamber (Supplementary Fig. 1a). The test chamber had 16 feeding ports (30 mm × 15 mm) located at 45-degree intervals on the floor (8 ports) and on the wall at heights of 150 mm and 200 mm (4 each, alternately arranged). Platforms (30 mm × 15 mm) were set up on the outside of the wall ports where food rewards could be placed (Supplementary Fig. 1b). For 3D data acquisition, 4 depth cameras (RealSense Depth Camera R200, Intel, Santa Clara, USA) were placed around the chamber at 90-degree intervals (Supplementary Fig. 1b), and were connected in parallel to a PC (Windows 10, 64-bit) using USB-C cables (U3S1A01C12-050, Newnex Technology, Santa Clara, USA; the distance was 1-5 m). The subjects were allowed to adapt to the transport procedure and experimental environment for two consecutive days before behavioral testing.
Each behavioral test started when a marmoset entered the test chamber from the transport chamber through the floor entrance, and movements were recorded until they finished eating all the food placed in the feeding ports, or until 30 min has passed. Subjects freely moved around the test chamber and, whenever they wanted, ate 7–9 pieces of sponge cake (approximately 2 g each); one cake was located on the near side of the entrance to entice them to enter the chamber, two on the wall ports, two on the near side of the floor ports, and the others 3 cm from the floor ports (Fig. 2a, Supplementary Fig. 1b). Observed feeding behaviors were manually classified into three subtypes: using hands to take food from the floor (floor-hand), using head and mouth directly (floor-head), and taking food from the wall (wall) (Fig. 2b, Supplementary Table 1). Fifty-one sets of 20-s data (10 s before and after eating) were used for analysis (Supplementary Table 1). Subjects were returned to the colony room after the end of the recording session. The experiments were performed once a day for each subject.
Marmoset marker-less 3D motion-tracking system
Our motion-tracking system software package for depth camera calibration, 3D data acquisition, and fundamental setup for physical simulation is available online (3DTracker-FAB, https://www.3dtrack.org). This motion-tracking system allowed us to robustly estimate the 3D trajectory of marmoset body parts as the positions of skeleton model parts (Head, Neck, Trunk, Hip) fitted by the physical simulation to the 3D point data of marmoset body shape (3D point cloud)9,34. The Face position was estimated by projecting the rectangle of the marmoset face area onto the 3D point cloud. This face area was detected frame-by-frame on 2D-RGB images by an object recognition algorithm YOLO335. To achieve sufficient accuracy, the YOLO3 detector was trained to detect marmoset face regions using 2,000 manually detected faces from two of the four marmosets (Marmo1 and Marmo2). 3D points inside the projected face rectangle were filtered to be less than 2.5 cm from the center of the Head, and the average position of these 3D points was defined as the Face position (Fig. 2c). Estimated error of Face position is reported in Supplementary Fig. 8.
Behavioral data under chemogenetic neuronal manipulation
We used behavioral data obtained from an adult male marmoset that received a viral vector injection in the unilateral SN for expressing an excitatory Designer Receptor Exclusively Activated by a Designer Drug (DREADD) (AAV2.1-hSyn1-hM3Dq-IRES-AcGFP)9. Using this DREADD setup, SN neurons are excited when the receptor is activated by administration of the agonist DCZ (HY-42110, MedChemExpress, NJ, USA; 3 μg/kg, orally). Two sets of free-moving behavior data ( ~ 60 min) following either DCZ or vehicle alone (saline with 2.5% dimethyl sulfoxide FUJIFILM Wako Pure Chemical., Osaka, Japan) were used.
Data preprocessing
All data preprocessing was performed using R version 4.0.3 (www.r-project.org) and the R packages tidyverse (version 1.3.0)45, data.table (version 1.13.2), patchwork (version 1.1.1), and magick (version 2.7.0).
Marmoset behavioral analysis
For free-feeding behavior analysis, the trajectory of body parts (Face, Head, Trunk, and Hip) was filtered with a locally estimated scatterplot smoothing filter using the stats::loess() function with span = 1/30 and downsampled to 10 Hz. Then, the spatial movement speed of each body part was calculated and the data coordinates were transformed frame-by-frame to make them posture-centered. Specifically, distance-from-center coordinates were transformed into posture coordinates with the Trunk’s center and the vector from Trunk to Head contained in the front-up quadrant. As a result, we used a set of 13 posture parameters (Face [x, y, z, v], Head [x ≡ 0, y, z, v], Trunk [x ≡ 0, y ≡ 0, z, v], and Hip [x, y, z, v], Fig. 2d). For SMP analysis, PC1 and PC2, which retained 69% of the data’s variance (Supplementary Table 2), were calculated using the stats::prcomp() function in R with scale = TRUE (Fig. 2e), and then scaled to a maximum absolute value of 1.
The same procedures were used for the data obtained after chemogenetic neuronal manipulation, except that instead of the Face position, we included the relative velocity of body parts into the SMP analysis, which was calculated from the postures at t + 3 s (Fig. 5d) and normalized by the coordinates of the body at time t and the distances between these parts. Thus, the analysis of the neuronal manipulation data used a set of 26 parameters (Head [x, y, z ≡ 0], Trunk [x ≡ 0, y ≡ 0, z ≡ 0], Hip [x, y, z], their positions at t + 3 s [x, y, z], their velocities [x, y, z, and absolute value]).
We used PC1 and PC2, which retained 48% of the data’s variance (Supplementary Table 6). To validate that these two PCs were the optimal choice, we also compared the results of the SMP analysis when using different numbers of PCs (Supplementary Fig. 7b, c, e, f).
Macaque behavioral analysis
For this analysis, we used published 3D macaque tracking data captured by OpenMonkeyStudio14. From the published data, we extracted 3,534 s of data that was divided into 29 subsets with few missing frames (frame gap ≤ 20 frames) and sufficient duration (d ≥ 100 s). Then, the extracted data were transformed frame-by-frame from distance-from-center coordinates to posture coordinates with the Hip’s center and the vector from Hip to Neck contained in the front-up quadrant. These posture-coordinated parameters were interpolated in 2/3 Hz using the stats::loess() function with a span set to one-fifth of the data fragment length. As a result, we use 5,452 video frames with 36 posture parameters ([x, y, z] coordinates of 13 body keypoints with Hip_x, Hip_z, Neck_z scaled to zero, Fig. 4a). For SMP analysis, the PC1 and PC2 extracted from the 36-parameter data, which retained 46% of the data’s variance (Supplementary Table 5), were calculated using the stats::prcomp() function with scale = TRUE.
Computational segmentation
The joint probability distribution of motion-motif length and class can be estimated by a blocked Gibbs sampler in which all motion motifs and their classes in the observed data (PC scores) are sampled. First, all data are randomly divided into motion motifs and classified. Next, motion motifs obtained by a part of the data are excluded from the dataset, and the model parameters are updated. By iterating this procedure, the parameters can be optimized. Parameter estimation in each iteration is described as forward filtering-backward sampling, which can be considered a maximum likelihood estimation process.
In the forward filtering step, the probability α that a data point given time step t is the ending point of a motion motif of length k classified as motif class c was calculated as follows:
| 1 |
where si denotes time series PC score at time step i, C denotes the maximum number of motion-motif classes, K denotes the maximum length of motion motifs, and ptrans (c|c’) denotes posterior transition probability from motif c’ to c.
The is a predictive distribution of a Gaussian process of class c fitted to PC score s at the time step from t-k to k, and is computed as follows:
| 2 |
where Xc denotes a set of segments that are classified into class c. The variation within a segment is regressed on data fragments belonging to the same class c as follows:
| 3 |
The class ci of the ith motion motif is determined by the (i-1)th segment and transition probability πc, which is generated from a Dirichlet process (DP) using β and parameterized by η as follows:
| 4 |
This β is an infinite-dimensional multinomial distribution, and its parameters were constructed by repeatedly breaking a stick, the length of which is one, with a ratio vk sampled from a beta distribution, as follows:
| 5 |
| 6 |
This stick-breaking process is also the DP, so the two-phase DP to generate c is called an HDP. In both the macaque and marmoset behavior analyses, the parameters were set to ω = 10.0, η = 10.0, and γ = 1.0, and the length of the motion motifs for the initial value of the simulation was set to be around 30 frames (min = 10, max = 70). This model was reported as HDP-GP-HSMM for human motion analysis29. To evaluate the impact of motif length variation on the results, the motif length was set to an average of 90 frames, ranging from 75 to 150, for the marmoset neural manipulation data (Supplementary Fig. 7a, d). For exploratory behavior analysis in NHPs, we optimized the kernel function with comparison as follows:
In addition, after learning the parameters for the data by iterating the model 100 times, the Viterbi algorithm estimated the most likely path of the latent state in the data. That is, all possible α in the data were obtained, and the most probable of all possible state sequences, combined with the learned transition probabilities, was adopted as the posterior state sequence.
Posture model
For comparisons, the conventional posture model was estimated as described below. PC1 and PC2 scores, which were scaled to have a maximum absolute value of 1 to match the input of SMP, were mapped to two dimensions using the umap.UMAP() function in Python 3.746. Posture clusters were detected on the UMAP scores using the stats::kmeans() function in R. The representative posture for each cluster was the average of the data contained in each class.
Manual motion segmentation
Five trained observers manually segmented four sets of 20-s (approximately) RGB video data clips captured from four separate angles simultaneously. The clips showed marmoset free-feeding behavior, was part of the data used for SMP analysis. Observers were instructed to segment the clips into motifs lasting 2–10 seconds.
Synthesis of typical body motion sequences
The inverse operation of PC analysis was used to synthesize a typical posture series from the estimated PC coordinates. In each motif class, the typical PC waveforms (Fig. 2h, and Fig. 4c) were calculated within 10 Hz by moving the average for all PCs. These typical PCs were multiplied by the pseudo-inverse matrix of the eigenvector for the PC analysis of the test data that was calculated using MASS::ginv() function in R. Finally, the resulting values were inversely standardized using the mean and variance values of the data to synthesize the posture parameters. In the cases of marmoset free-feeding behavior and macaque ethogram detection, the postural information is displayed side-by-side along the time axis (Fig. 3c–e, Fig. 4d). The results of neural manipulation analysis visualized the motif’s internal variability by integrating the velocity relative to the initial position (Fig. 5g).
Statistical analysis
Pearson’s Chi-square test, implemented with the rstatix::chisq_test() function in R, was used to compare intervals containing constant-specific timing among feeding subtypes and to test for differences in motion motif distributions among individuals. The Brunner–Munzel test, implemented with the lawstats::brunner.munzel.test() function in R, was used to compare the median value of motif length.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Description of Additional Supplementary Materials
Acknowledgements
We thank J. Kamei, R. Yamaguchi, Y. Matsuda, Y. Sugii, K. Yamashita, Y. Iwasawa, M. Nakano, and M. Fujiwara for their technical assistance. We also thank Drs. K. Shimatani (Institute of Statistical Mathematics), S. Nakamura (Tokyo University of Agriculture and Technology), and T. Taniguchi (Ritsumeikan University) for their comments on an earlier version of the manuscript. This study was supported by MEXT/JSPS KAKENHI Grant Numbers JP17H06040, JP19H04996, 22K07338 (to KM), 22H05157 (to JM), JP17H02219 (to TH), and JP20H05955 and JP24H00069 (to TM), AMED under Grant Numbers JP20dm0107146 (to TM), JP20dm0307007 (to TH), JP20dm0207072 (to MH), and Takeda Science Foundation (to JM and HN).
Author contributions
Conceptualization: K.M. and T.M. Formal analysis: K.M., D.M., and T.N., Investigation: K.M., and J.M. Resources: K.M., J.M., T.N. and T.M. Writing (original draft): K.M. and T.M. Visualization: K.M. Supervision: T.M. Project administration: K.M. Funding acquisition: K.M., T.H., M.H., J.M., H.N. and T.M. Writing (review and editing): all authors.
Peer review
Peer review information
Communications Biology thanks Steve Chang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Joao Valente.
Data availability
The data generated in this study have been deposited in the Open Science Framework database (10.5281/zenodo.13337942). All other data are available from the corresponding authors on reasonable request.
Code availability
Custom code generated in this study is available at GitHub repository (10.5281/zenodo.13337942).
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Koki Mimura, Email: mimura.koki@qst.go.jp.
Takafumi Minamimoto, Email: minamimoto.takafumi@qst.go.jp.
Supplementary information
The online version contains supplementary material available at 10.1038/s42003-024-06786-2.
References
- 1.Fröhlich, M. & van Schaik, C. P. The function of primate multimodal communication. Anim. Cogn.21, 619–629 (2018). 10.1007/s10071-018-1197-8 [DOI] [PubMed] [Google Scholar]
- 2.Kret, M. E., Prochazkova, E., Sterck, E. H. M. & Clay, Z. Emotional expressions in human and non-human great apes. Neurosci. Biobehav. Rev.115, 378–395 (2020). 10.1016/j.neubiorev.2020.01.027 [DOI] [PubMed] [Google Scholar]
- 3.Bauman, M. D. & Schumann, C. M. Advances in nonhuman primate models of autism: Integrating neuroscience and behavior. Exp. Neurol.299, 252–265 (2018). 10.1016/j.expneurol.2017.07.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ferretti, V. & Papaleo, F. Understanding others: emotion recognition abilities in humans and other animals. Genes Brain Behav. 10.1111/gbb.12544 (2018). [DOI] [PubMed]
- 5.Nelson, E. E. & Winslow, J. T. Non-human primates: model animals for developmental psychopathology. Neuropsychopharmacology34, 90–105 (2009). 10.1038/npp.2008.150 [DOI] [PubMed] [Google Scholar]
- 6.Alexander, L. et al. Fractionating blunted reward processing characteristic of anhedonia by over-activating primate subgenual anterior cingulate cortex. Neuron101, 307–320.e6 (2019). 10.1016/j.neuron.2018.11.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Watanabe, S. et al. Functional and molecular characterization of a non-human primate model of autism spectrum disorder shows similarity with the human disease. Nat. Commun.12, 5388 (2021). 10.1038/s41467-021-25487-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Feng, G. et al. Opportunities and limitations of genetically modified nonhuman primate models for neuroscience research. Proc. Natl Acad. Sci.117, 24022–24031 (2020). 10.1073/pnas.2006515117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mimura, K. et al. Chemogenetic activation of nigrostriatal dopamine neurons in freely moving common marmosets. iScience24, 103066 (2021). 10.1016/j.isci.2021.103066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Oyama, K. et al. Chemogenetic dissection of the primate prefronto-subcortical pathways for working memory and decision-making. Sci. Adv.7, eabg4246 (2021). 10.1126/sciadv.abg4246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Roseboom, P. H. et al. Evidence in primates supporting the use of chemogenetics for the treatment of human refractory neuropsychiatric disorders. Mol. Ther.29, 3484–3497 (2021). 10.1016/j.ymthe.2021.04.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Miller, C. T. et al. Natural behavior is the language of the brain. Curr. Biol.32, R482–R493 (2022). 10.1016/j.cub.2022.03.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mathis, M. W. & Mathis, A. Deep learning tools for the measurement of animal behavior in neuroscience. Curr. Opin. Neurobiol.60, 1–11 (2020). 10.1016/j.conb.2019.10.008 [DOI] [PubMed] [Google Scholar]
- 14.Bala, P. C. et al. Automated markerless pose estimation in freely moving macaques with OpenMonkeyStudio. Nat. Commun.11, 4560 (2020). 10.1038/s41467-020-18441-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lauer, J. et al. Multi-animal pose estimation, identification and tracking with DeepLabCut. Nat. Methods19, 496–504 (2022). 10.1038/s41592-022-01443-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Labuguen, R. et al. MacaquePose: a novel “in the wild” macaque monkey pose dataset for markerless motion capture. Front. Behav. Neurosci.14, 581154 (2021). 10.3389/fnbeh.2020.581154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ballesta, S., Reymond, G., Pozzobon, M. & Duhamel, J.-R. A real-time 3D video tracking system for monitoring primate groups. J. Neurosci. Methods234, 147–152 (2014). 10.1016/j.jneumeth.2014.05.022 [DOI] [PubMed] [Google Scholar]
- 18.Bauman, M. D. The development of mother-infant interactions after neonatal amygdala lesions in rhesus monkeys. J. Neurosci.24, 711–721 (2004). 10.1523/JNEUROSCI.3263-03.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Graham, K. E., Hobaiter, C., Ounsley, J., Furuichi, T. & Byrne, R. W. Bonobo and chimpanzee gestures overlap extensively in meaning. PLOS Biol.16, e2004825 (2018). 10.1371/journal.pbio.2004825 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ngo, V. et al. Active vision during prey capture in wild marmoset monkeys. Curr. Biol.32, 3423–3428.e3 (2022). 10.1016/j.cub.2022.06.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kennedy, A. The what, how, and why of naturalistic behavior. Curr. Opin. Neurobiol.74, 102549 (2022). 10.1016/j.conb.2022.102549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McCullough, M. H. & Goodhill, G. J. Unsupervised quantification of naturalistic animal behaviors for gaining insight into the brain. Curr. Opin. Neurobiol.70, 89–100 (2021). 10.1016/j.conb.2021.07.014 [DOI] [PubMed] [Google Scholar]
- 23.Marques, J. C., Li, M., Schaak, D., Robson, D. N. & Li, J. M. Internal state dynamics shape brainwide activity and foraging behaviour. Nature577, 239–243 (2020). 10.1038/s41586-019-1858-z [DOI] [PubMed] [Google Scholar]
- 24.Wiltschko, A. B. et al. Revealing the structure of pharmacobehavioral space through motion sequencing. Nat. Neurosci.23, 1433–1443 (2020). 10.1038/s41593-020-00706-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ashwood, Z. C. et al. Mice alternate between discrete strategies during perceptual decision-making. Nat. Neurosci.25, 201–212 (2022). 10.1038/s41593-021-01007-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Calhoun, A. J., Pillow, J. W. & Murthy, M. Unsupervised identification of the internal states that shape natural behavior. Nat. Neurosci.22, 2040–2049 (2019). 10.1038/s41593-019-0533-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Luxem, K. et al. Identifying behavioral structure from deep variational embeddings of animal motion. Commun. Biol.http://biorxiv.org/lookup/doi/10.1101/2020.05.14.095430 (2020). [DOI] [PMC free article] [PubMed]
- 28.Kuniyasu, R., Nakamura, T., Taniguchi, T. & Nagai, T. Robot concept acquisition based on interaction between probabilistic and deep generative models. Front. Comput. Sci.3, 618069 (2021). 10.3389/fcomp.2021.618069 [DOI] [Google Scholar]
- 29.Nagano, M. et al. Sequence Pattern Extraction by Segmenting Time Series Data Using GP-HSMM with Hierarchical Dirichlet Process. in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 4067–4074 (IEEE, 2018). 10.1109/IROS.2018.8594029.
- 30.Wang, J. M., Fleet, D. J. & Hertzmann, A. Gaussian process dynamical models for human motion. IEEE Trans. Pattern Anal. Mach. Intell.30, 283–298 (2008). 10.1109/TPAMI.2007.1167 [DOI] [PubMed] [Google Scholar]
- 31.Berman, G. J., Choi, D. M., Bialek, W. & Shaevitz, J. W. Mapping the stereotyped behaviour of freely moving fruit flies. J. R. Soc. Interface11, 20140672 (2014). 10.1098/rsif.2014.0672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hooten, M. B. & Hobbs, N. T. A guide to Bayesian model selection for ecologists. Ecol. Monogr.85, 3–28 (2015). 10.1890/14-0661.1 [DOI] [Google Scholar]
- 33.Huang, K. et al. A hierarchical 3D-motion learning framework for animal spontaneous behavior mapping. Nat. Commun.12, 2784 (2021). 10.1038/s41467-021-22970-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Matsumoto, J. et al. A 3D-video-based computerized analysis of social and sexual interactions in rats. PLoS ONE8, e78460 (2013). 10.1371/journal.pone.0078460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Redmon, J., Divvala, S., Girshick, R. & Farhadi, A. You only look once: unified, real-time object detection. Preprint at http://arxiv.org/abs/1506.02640 (2016).
- 36.Beal, M., Ghahramani, Z. & Rasmussen, C. The infinite hidden Markov model. in Advances in Neural Information Processing Systems (eds. Dietterich, T., Becker, S. & Ghahramani, Z.) vol. 14 (MIT Press, 2001).
- 37.Fox, E. B., Sudderth, E. B., Jordan, M. I. & Willsky, A. S. A sticky HDP-HMM with application to speaker diarization. Ann. Appl. Stat. 5, (2011).
- 38.Teh, Y. W., Jordan, M. I., Beal, M. J. & Blei, D. M. Hierarchical Dirichlet Processes. J. Am. Stat. Assoc.101, 1566–1581 (2006). 10.1198/016214506000000302 [DOI] [Google Scholar]
- 39.Segalin, C. et al. The Mouse Action Recognition System (MARS) software pipeline for automated analysis of social behaviors in mice. eLife10, e63720 (2021). 10.7554/eLife.63720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ning, J. et al. Behavioral signatures of structured feature detection during courtship in Drosophila. Curr. Biol.32, 1211–1231.e7 (2022). 10.1016/j.cub.2022.01.024 [DOI] [PubMed] [Google Scholar]
- 41.Oyama, K. et al. Chemogenetic disconnection between the orbitofrontal cortex and the rostromedial caudate nucleus disrupts motivational control of goal-directed action. J. Neurosci.42, 6267–6275 (2022). 10.1523/JNEUROSCI.0229-22.2022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wiltschko, A. B. et al. Mapping sub-second structure in mouse behavior. Neuron88, 1121–1135 (2015). 10.1016/j.neuron.2015.11.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nakamura, T. et al. Segmenting continuous motions with hidden semi-Markov models and Gaussian processes. Front. Neurorobotics11, 67 (2017). 10.3389/fnbot.2017.00067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kondo, T. et al. Calcium transient dynamics of neural ensembles in the primary motor cortex of naturally behaving monkeys. Cell Rep.24, 2191–2195.e4 (2018). 10.1016/j.celrep.2018.07.057 [DOI] [PubMed] [Google Scholar]
- 45.Wickham, H. et al. Welcome to the tidyverse. J. Open Source Softw.4, 1686 (2019). 10.21105/joss.01686 [DOI] [Google Scholar]
- 46.McInnes, L., Healy, J. & Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. Preprint at http://arxiv.org/abs/1802.03426 (2020).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of Additional Supplementary Materials
Data Availability Statement
The data generated in this study have been deposited in the Open Science Framework database (10.5281/zenodo.13337942). All other data are available from the corresponding authors on reasonable request.
Custom code generated in this study is available at GitHub repository (10.5281/zenodo.13337942).