Resolving intermediates during the growth of aluminum deuteroxide (Hydroxide) polymorphs in high chemical potential solutions

Abstract

Aluminum hydroxide polymorphs are of widespread importance yet their kinetics of nucleation and growth remain beyond the reach of current models. Here we attempt to unveil the reaction processes underlying the polymorphs formation at high chemical potential. We examine their formation in-situ from supersaturated alkaline sodium aluminate solutions using deuteration and time-resolved neutron pair distribution function analyses, which indicate the formation of individual Al(OD)₃ layers as an intermediate particle phase. These layers ultimately stack to form gibbsite- or bayerite-like layered heterostructures. Ex-situ characterization of the recovered precipitates using ²⁷Al magic angle spinning nuclear magnetic resonance spectroscopy, Raman, X-ray diffraction, and scanning electron microscopy, suggests the presence of additional intermediate states, an amorphous compound bearing both tetrahededrally- and penta-coordinated Al³⁺. These observations reveal the complex pathways to form Al(OD)₃ monolayers via either transient pentacoordinate species or amorphous-to-ordered transitions. The subsequent crystallization of admixed gibbsite/bayerite is followed by an Al(OD)₃ monolayer attachment process.

Aluminum hydroxide polymorphs play a key role in industrial aluminum production, yet their nucleation and growth kinetics remain beyond the reach of current models. Here, the authors study polymorph formation in situ from supersaturated alkaline sodium aluminate solutions using time-resolved neutron pair distribution function and complementary spectroscopy analyses, which indicate the formation of individual Al(OD)₃ layers as an intermediate particle phase.

Introduction

Mineral growth and dissolution are of widespread importance across natural systems and industry. However, predicting rates of these processes still often relies upon phenomenological models that are based on fits to macroscopic observables. Identifying the underlying mechanistic pathways is essential for making conceptual advances in system predictability. For nucleation and growth, this includes understanding aspects such as the formation of oligomeric precursors to nucleation, and the assembly of nanoparticles as building blocks during crystal growth^1–4. Differentiating between classical and nonclassical nucleation, beyond the thermodynamic arguments, inevitably relies on molecular-level insights at the relevant timescale and the ability to resolve the structure and (meta)stability of critical nuclei or amorphous precursors during the reaction process^4–7. However, capturing the intermediate and/or end states, some of which are kinetically controlled (e.g., intermediates need to exchange with ions in solution to move to the next stage) and some thermodynamically controlled (e.g., free energy barriers favor nucleation of intermediates when the chemical potential is high), at the atomic scale is challenging, even using state-of-the-art tools, e.g., refs. ^3,8–11. The demanding signal-to-noise ratio (sensitivity), in practice, represents a persistent barrier to identifying signals from intermediate species, including candidate cluster growth units, which are often short-lived and may only possess short-range order (i.e., roughly 3–5 atomic shells), making them difficult to differentiate from matrix/background signals.

For example, reactions in highly concentrated sodium aluminate solutions (brines) are one of the important subjects of research in aluminum chemistry. These solutions are central to the Bayer process in the alumina industry^12,13, where alkaline sodium hydroxide solutions (NaOH_(aq)) are used for the selective extraction of aluminum from bauxite ores. Concentrated caustic alkaline aluminate solutions are also important for the retrieval and processing of radioactive waste at the Department of Energy’s legacy nuclear sites, e.g., Hanford^14,15, where chemical conditions must be tuned to stabilize the solutions and prevent precipitation in processing pipes^16,17. The Na₂O-Al₂O₃-H₂O ternary system is studied here as a simple representation of radioactive waste solutions (minus other soluble oxyanion species, such as nitrate, nitrite, sulfate, carbonate, and phosphate), and in this ternary system, we have learned that the metastability, nucleation kinetics, and growth phase(s) can be controlled by varying the Na⁺/Al³⁺ mole ratios¹⁸.

The thermodynamically controlling Al³⁺-bearing solid phases from alkaline sodium aluminate solutions are known, but the mechanism of Al³⁺ coordination change upon going from dissolved species to the solid phase is unknown. To date, only two forms of tetrahedrally-coordinated aluminate dissolved species have been identified, the Al(OH)₄⁻ monomer and the µ₂-oxo Al₂O(OH)₆²⁻ dimer^18–20. The existence of higher-order oligomeric species remains difficult to confirm experimentally. At low [NaOH] (less than ~10 molality, m), these monomers and dimers are thus considered as active species responsible for coordination transformation from tetrahedral-Al³⁺ in solution to octahedral-Al³⁺ in precipitating solids during crystallization of aluminum hydroxide (Al(OH)₃ :gibbsite or its structural polymorphs)^4,18. When the Na⁺/Al³⁺ mole ratios are greater than ~1 and the total [NaOH] is above ~10 m, the sodium aluminate salts, monosodium aluminate hydrate (MSA: Na₂[Al₂O₃(OH)₂]·1.5H₂O) or nonasodium aluminate hydrate (NSA: Na₉[Al(OH)₆]₂(OH)₃·6H₂O) are solubility-controlling phases^18,21. The MSA structure is composed of tetrahedral aluminate sheets, each sharing three corners (as bridging µ₂-oxygens) and one unbridged hydroxy apex^22–24, forming an open two-dimensional structure, with the general formula of [Al₂O₃(OH)₂]_n²ⁿ⁻. The open structure results in large interstitial sites between the sheets, which can be occupied by Na⁺ and H₂O molecules. The NSA structure is built with isolated Al(OH)₆³⁻ octahedral complexes that are linked together by the OH⁻, Na⁺ and H₂O molecules^22,25. If specific aluminate complexes, comprising part or all elements of the solid structure, need to be in solution in order to facilitate nucleation reactions, they would be octahedral Al(OH)_x(H₂O)_6-x^(3-x) species for Al(OH)₃ and NSA, and large negatively charged tetrahedral aluminate oligomers consisting of a high ratio of µ₂-oxygen sites for MSA. Unless these assumed complexes, or other potential transition states, such as pentacoordinate or amorphous aluminate compounds, can be characterized, our mechanistic understanding of crystallization of Al³⁺-bearing solid phases from alkaline sodium aluminate solutions remains unclear.

Building upon our understanding of the structure and reactivity of alkaline aluminate solutions, and how these interactions influence the constituents and structures of precipitated aluminum hydroxy (an)hydrates^4,18, we targeted a specific concentration (in a deuterated form), where the solution is supersaturated with respect to aluminum deutroxide (Al(OD)₃) as the primary phase, and deuterated MSA as the secondary phase. Deuteration was chosen to enhance our ability to discern key precursor species using neutron total scattering methods. This deuterated/supersaturated sodium aluminate solution, with a composition of 9 m [Al³⁺] + 9.9 m [Na⁺] + 36.9 m [OD⁻] (in 55.51 mole of D₂O), contains ~70% monomers (Al(OD)₄⁻) and ~30% dimers (Al₂O(OD)₆²⁻), based on our previous study¹⁸. The timescale of each reaction step is important to identify the signature of key intermediates and the kinetics of the nucleation-crystallization reaction. Here, the composition was selected to match the requisite time resolution between a neutron experiment and the reaction kinetics with the initial intent to observe the transformation from tetrahedral-Al³⁺ in solution to octahedral-Al³⁺ in aluminum deutroxide crystals and/or to resolve intermediate states along the reaction processes. A similar experimental concept on matching the requisite time resolution to the reaction kinetics, for better signal-to-noise ratios, using synchrotron X-rays to resolve intermediate structural signatures during the aqueous reaction of Fe²⁺ and S²⁻ to the precipitation of FeS (mackinawite) was presented by Beauvais et al.¹¹. Here, we aimed to follow the crystallization pathways of aluminum deutroxides from their solute state, using both in-situ and ex-situ approaches. This includes neutron total scattering and complementary ²⁷Al magic angle spinning nuclear magnetic resonance (MAS NMR) spectroscopy for in-situ homogeneous nucleation measurements, and a combination of ²⁷Al MAS NMR, Raman, X-ray diffraction (XRD), and scanning electron microscopy (SEM) imaging for ex-situ characterization of recovered precipitating solids. The goal of our study was to fill several gaps in the understanding of: (i) the nucleation pathways that lead to the formation of edge-sharing Al(OD)₆ octahedral monolayers during the initial stages of precipitation, (ii) the layer stacking and deuterium-bond (D-bond) cross-linkage between layers, necessary for the formation of Al(OD)₃ polymorphs (e.g., gibbsite vs. bayerite), and (iii) the role of the counterions (Na⁺ in this case) and to what extent amorphous compounds, composed of predominantly tetrahedral aluminate species, impede nucleation and growth mechanisms.

Results and discussion

In-situ observation of homogeneous nucleation and growth

To characterize the intermediate states leading to the formation of aluminum deutroxides, the aqueous reaction of NaOD-aluminate was studied in situ using neutron total scattering and pair distribution function (PDF) analysis. The PDF G(r) data, obtained from Fourier transformation of the collected/normalized scattering structure factor S(q), provides a localized view on the probability of finding pairs of atoms separated by some distance, r. The method is thus well suited to understand nanoscale and disordered phases, and if the data requisite times match the reaction kinetics, time-resolved PDF analysis can provide insight into structural evolution, such as nucleation and growth events. Figure S1 (in Supplementary Information, SI) displays infrared camera images captured during the neutron total scattering experiments over a period of 36 h, starting from a homogenous solution to the formation of precipitates. The images reveal a slow nucleation and growth reaction, where cloudiness appears during the first 16 h, then the precipitates begin to fall to the bottom of the tube during the subsequent 16–36 h. To capture structural signals from transient solution phase species, and reduce coherent diffraction signals from crystalline products, the neutron hot-zone was focused on the solution phase, and not the precipitates at the bottom of the tube (Fig. S1). The measured scattering structure factor S(q), corresponding to these infrared images, is given in Fig. S2a, emphasizing small intensity changes (~1–2%) and the practical sensitivity issues underlying in-situ total scattering experiments for probing nucleation and growth reactions. Other studies that probe such small intensity changes in total scattering can be found in refs. ^11,26–28.

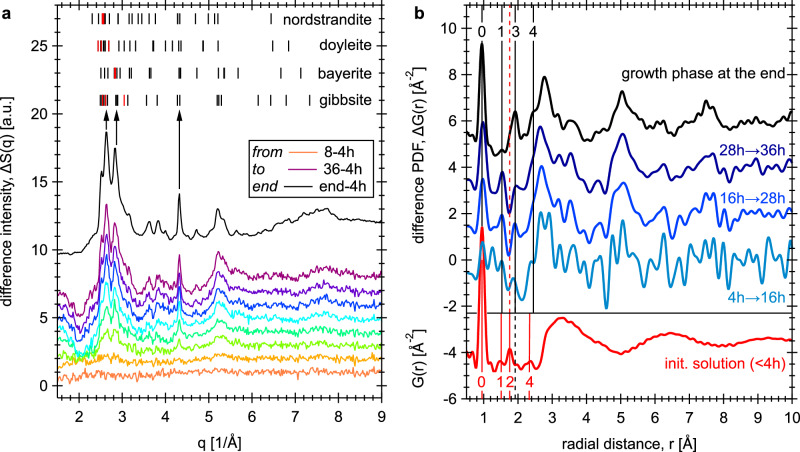
The ΔS(q) datasets were created by subtracting the first 4 h of collected data (as homogeneous solution signals) from each of the following time datasets (Fig. 1a). As seen in Fig. 1a, the ΔS(q) datasets indicate the formation of nanoscale solids over time, with Bragg reflections in the position agreeing with those expected for Al(OD)₃ polymorphs, including gibbsite, bayerite, doyleite and/or nordstrandite (in the sequence of decreasing thermodynamic stability^29,30). These four polymorphs share the same layer structure, consisting of edge-sharing Al(OD)₆ octahedra forming an Al(OD)₃ dioctahedral layer. They differ from one another by the intralayer H/D-bonding orientations and the interlayer shift vectors, which together lead to variations in the geometry and strength of interlayer H/D-bonding (see their structures in Fig. S3). The intensity profile for the endpoint of the experiment (black curve in Fig. 1a) shows non-uniform peak broadening features, where the 4.32 Å⁻¹ reflection is noticeably narrower than the observed reflections at q values of ~3.63, ~3.83, ~4.72, and ~5.21 Å⁻¹. The 4.32 Å⁻¹ peak is mainly the 330 reflection of gibbsite, bayerite or nordstrandite, or the 30$\overline{3}$ reflection of doyleite. Within the space group of gibbsite³¹, bayerite³² and nordstrandite²⁹, each Al(OD)₃ layer lies in the ab-plane and the layer stacking direction is along the c-axis. In the structure of doyleite²⁹, the layer is in the ac-plane and the stacking direction is along the b-axis (Fig. S3). Therefore, based on the layer stacking directions in each of the structures, the sharpness of the 4.32 Å⁻¹ peak is related to the mean crystallite dimension of the layers. Other peaks, including the main reflections near 2–3.4 Å⁻¹, are composed of mixed hkl indices, and thus the extent of broadening varies depending on the Miller index-l (in gibbsite, bayerite and nordstrandite) or -k (in doyleite) components. Commonly, non-uniform peak broadening in powder diffraction data is an indicative of anisotropic crystallite (or domain) size/strain line broadening³³. For example, anisotropic crystallite size can result from crystal growth, where specific bonding interactions produce layered or columnar structures. Atomic dislocation-induced strain in comparison is a typical example of anisotropic strain broadening in a crystal³⁴. Here, only the 4.32 Å⁻¹ reflection is noticeably narrower than other reflections, and its Miller index nicely matches to the expected intralayer lattice plane in the four Al(OD)₃ polymorphs. Thus, the observed non-uniform peak broadening and dependency on Miller indices for the 4.32 Å⁻¹ reflection suggest the lack of translational order along the stacking direction^33,35,36, e.g., random or turbostratic stacking, or finite-sized nanoparticles with anisotropic dimensions^37–39, e.g., suspended monolayers.

Fig. 1. In-situ observation of nucleation and growth events using neutron total scattering.

a Difference ΔS(q) curves every 4 h relative to the first 4 h dataset, showing the reaction progression as indicated by increasing peak intensities. The short ticks at the top of the plot indicate the expected neutron Bragg reflections (of the top 25 peak intensities) for the four Al(OD)₃ polymorphs. In each phase, the three most intense reflections are highlighted by red short ticks. These Bragg reflections are calculated using crystal structure data of Balan et al.³¹ for gibbsite, Zigan et al.³² for bayerite, and Demichelis et al.²⁹ for doyleite and nordstrandite. b Averaged difference PDF ΔG(r) datasets (blues and black curves) obtained at four different time intervals. The PDF of the initial solution structure (completed at/within 4 h after the solution was made) is shown by the red curve in the bottom panel. The vertical black and red lines indicate the relationship of PDF peaks between datasets (see texts for details). See also Fig. S2b, c for plots with extended q and r ranges, respectively.

The difference PDF ΔG(r) were obtained via Fourier transformation of the ΔS(q) intensities (using q_max of 28 Å⁻¹) into the real-space signal (Fig. 1b). To reduce Fourier truncation ripples, a Lorch modification function was applied to each ΔS(q) to smooth derived ΔG(r) data. To improve signal-to-noise ratio, ΔG(r) datasets in time windows between 4–16, 16–28, and 28–36 h were then averaged, resulting in an 8–12 h interval for three ΔG(r) segments (Fig. 1b). These intermediate ΔG(r) curves show similar features to the signals obtained at the endpoint of the experiment, with overall intensities increasing with reaction time. In the initial solution PDF data (red curve in Fig. 1b), our previous geometric modeling¹⁸ indicates that: (i) peak-0 at ~0.97 Å is the intramolecular O-D bonds in D₂O, OD^- and aluminate ions, (ii) peak-1 at ~1.51 Å is mostly the intramolecular D-D distances of a D₂O molecule, and (iii) peak-2 and -4 at ~1.79 and ~2.2–2.5 Å, respectively, correspond mainly to the intramolecular Al-O bonds and Al-D distances in tetrahedrally-coordinated aluminate species. These four peaks, and the aluminate-water and water-water correlations at longer distances, represent the initial solution structure, and are removed by the difference analysis. Therefore, the observed difference PDF ΔG(r) curves (top panel of Fig. 1b) represent the residual signals that contain pair-wise correlations involving primarily nucleating species, and their transformation into crystalline products.

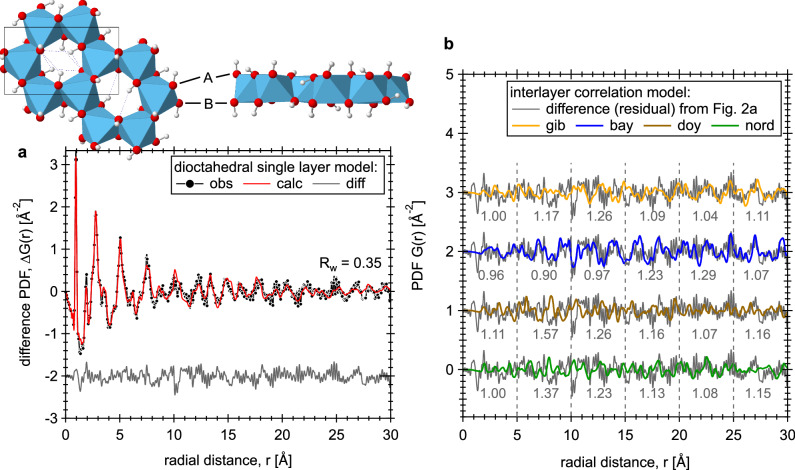
To interpret the structure of the growth phase, a single two-dimensional Al(OD)₃ layer model was developed and tested to fit the PDF data observed at the endpoint of the experiment (Fig. 2a). This model consists of an isolated Al(OD)₃ layer created from the gibbsite structure³¹, and no interlayer atom-atom correlations within the r-range being modeled (up to 30 Å; details are given in Section 1 of SI). Based on fitting results, peak intensities labeled 0, 3 and 4 (black) for the four sets of ΔG(r) data (Fig. 1b) correspond to the first coordination shell of O-D (~0.97 Å), Al-O (~1.91 Å), and Al-D (~2.3–2.5 Å) distances in an Al(OD)₆ octahedron. The relatively broad peaks/oscillations centered at ~2.7, ~5.0 and ~7.5 Å mainly reflect the ordered O-O + O-D distances in the Al(OD)₃ dioctahedral layer (e.g., in the dioctahedral layer the hexagonal cavities are patterned ~5 Å apart; see the insert structure in Fig. 2a). Note that peak-3 (Fig. 1b) also contains the intralayer D-bonds (~2–2.3 Å), which lie approximately in the ab-plane and point towards the vacant sites (Fig. 2a; insert structure). Accordingly, the growth reaction can be expressed as simply: 0.54Al(OD)₄⁻ + 0.23Al₂O(OD)₆²⁻ + 1.1Na⁺ + 0.1OD⁻ + 0.23D₂O → xAl(OD)_3(s) + (1-x)Al(OD)₄⁻ + 1.1Na⁺ + (0.1+x)OD⁻, where the variable x defines the amount of precipitates (see the experimental section for solution composition). The intensity variations for the peak at ~1.53 Å (black peak-1 in Fig. 1b) do not match the Al(OD)₃ layer structural correlations. Considering that neutron PDF is sensitive to changes involving D-bearing species, this peak likely corresponds to D-bonding interactions between the deuteroxide-O_d and water-D_w sites (i.e., OD⁻ solvation correlations¹⁸), due to the change in solution composition upon precipitation. Alternatively, the ~1.53 Å peak could correspond to inner-sphere sorption of Na⁺ to the surface O-sites of the Al(OD)₃ layer, e.g., to the side of the hexagonal cavities, as predicted by molecular dynamics simulations of the gibbsite-NaOH_(aq) interface⁴⁰. The 4-to-16 h ΔG(r) data (light blue curve in Fig. 1b) also suggests a slightly shorter Al-O bonds than expected for Al-O bonds in octahedrally-coordinated configuration, i.e., the peak centered at 1.85 Å is in between the red dashed line (1.79 Å) for Al-O in tetrahedral aluminate species and the black solid line (1.91 Å) for Al-O in octahedral configuration. This intermediate Al-O bond length (between 1.79 and 1.91 Å) may indicate the presence of pentacoordinate species formed early in the reaction.

Fig. 2. 2D Al(OD)₃ single layer model fit and comparison of the residual with four interlayer correlation models.

a The black circles and the red curve show the observed and calculated PDFs, respectively, and the gray curve at the bottom shows the difference (residual) between the two (R_w = 0.35). The observed PDF data is obtained at the end of neutron experiment. The inset structural plot illustrates the top and side views of an Al(OD)₃ single layer. O atoms are shown as red spheres, D as white spheres, and Al as blue octahedra. The unit cell is outlined by black box, and intralayer D-bonds are shown as blue dashed lines. The A and B sites for the surface terminal-OD groups are also indicated. b The gray curve is the residual to the single layer model fit, and was repeated four times to facilitate comparison to the calculated interlayer correlations in all four types of Al(OD)₃ polymorphs. R_w values, calculated for every 5 Å segments of the residual data, are given at the bottom of the plot. See also Fig. S4 for the simulated neutron PDFs of Al(OD)₃ polymorphs. Here, crystal structure data of Balan et al.³¹ for gibbsite, Zigan et al.³² for bayerite, and Demichelis et al.²⁹ for doyleite and nordstrandite were used.

The residual from the fit of the single layer Al(OD)₃ model to the data (Fig. 2b) shows features that could correspond to: (i) solute ions and water molecules coordinated around the layer, and (ii) correlations associated with interlayer stacking. For (i), we expect the weak oscillating residual signal, restricted to the short r range (<10 Å), due to disordering of surface-bound water/ion species (see other examples in refs. ^40–42). For (ii) on the evaluation of interlayer stacking, the residual data is compared with the calculated interlayer correlations (Fig. S4c; details are given in Section 2 of SI) for all four Al(OD)₃ polymorphs. As shown in Fig. 2b, on the basis of R_w analysis (in every 5 Å segments of the data), features in the residual curve correspond to the stacking patterns in either gibbsite or bayerite, but not to stacking patterns in nordstrandite and doyleite. Below ~15 Å, the residual curve corresponds to the bayerite stacking correlation, but between ~15–25 Å, the gibbsite stacking correlation model shows a better match to the overall oscillating widths and intensities (Fig. 2b). This indicates that individual Al(OD)₃ nanolayers are intermediary particles that stack together by oriented attachment to form gibbsite- or bayerite-like layered heterostructures.

Additional in-situ characterization using ²⁷Al MAS NMR was performed on a sodium aluminate solution of the same concentration (separately prepared) to follow the growth of gibbsite/bayerite phases over 2 weeks period. The ²⁷Al nucleus is quadrupolar, with a spin of 5/2, and the chemical shift of the resonance is sensitive to the Al³⁺ coordination environment. For Al³⁺, the isotropic chemical shift is 0 to 20 ppm in octahedral coordination, 30 to 50 ppm in pentacoordination, and 60 to 80 ppm in tetrahedral coordination⁴³. As shown in Fig. S6a, only a single Lorentzian line shape corresponding to tetrahedrally-coordinated aluminate species in solution can be observed initially. After ~3 days, signal intensity in the octahedral region starts to show, which displays a quasi-Lorentzian line attributing to the slow spinning rate. Under the performed acquisition conditions (see Section 3 of SI), individual resonances for bayerite-like or gibbsite-like nanolayers remain unresolved, and instead, a single octahedral resonance is observed, representing the combined octahedral coordination in both polymorphs. The relative integrated intensity of the octahedral Al³⁺ signal increases to about 3.5% in 2 weeks period (Fig. S6b). We note the variation in the induction time between the two in-situ measurements under the same solution concentration. If one considers the stochastic nature of nucleation and the formed nuclei have to grow to appreciable sizes before they can be detected experimentally, studies have shown that variation in the induction times determined from a large number of measurements under well-defined/identical conditions typically results an exponential distribution function^44,45. Thus, ruling out concentration errors, variation in the induction times observed here may result from differences between neutron and NMR experiment conditions, such as temperature and solution volume used. Another possibility for such variation could originate from multiple nucleation and growth processes, i.e., not a single nucleation/growth mechanism. That is during the initial stage of precipitation, the individual Al(OD)₃ layers could be formed by monomer-by-monomer addition to a candidate nucleus (classical nucleation), or they could grow from an amorphous phase that facilitates the coordination change of tetrahedral Al³⁺ to octahedral Al³⁺ (nonclassical nucleation). Ex-situ characterization of precipitates is performed to differentiate between these two potential pathways.

Ex-situ characterization of precipitates

Precipitates were retrieved, via vacuum filtration, from sodium aluminate solutions after the neutron experiment at three different time points: 6 days, 45 days, and 3 months. Based on a combination of XRD characterization and ²⁷Al MAS NMR spectroscopy, a clear signature of an amorphous phase was identified. The presence of an amorphous phase is expected, given the chemical complexity and high chemical potential of the starting solution. Quantitative phase analysis (Table 1) using the Rietveld method on XRD data showed that the precipitate is comprised of gibbsite and bayerite (consistent with in-situ neutron PDF analysis), and an amorphous phase (see XRD patterns in Figs. S7a, b and S8). The amount of gibbsite, bayerite and amorphous phase remained approximately constant across the time series. Raman spectra of the three precipitates also show band positions in the OD stretching vibration region corresponding to a mixture of gibbsite/bayerite (Fig. S9).

Table 1.

Results of XRD phase identification and Rietveld quantification (e.s.d. values in parentheses)

Sample	Phase abundance in wt%
	Gibbsite	Bayerite	Amorphousa	MSAb
6 days – filtered	quantification is not performedc			--
45 days – filtered	42 (3)	22 (5)	35 (5)	--
3 months – filtered	40 (4)	25 (2)	35 (4)	--
3 months – D2O washed	72 (4)	26 (4)	2 (3)	--
3 months – ETOD washed	35 (3)	3.8 (5)	48 (2)	13 (1)

^aAmorphous phase fraction was quantified using 10 wt% TiO₂ (rutile) as an internal standard.

^bMSA is monosodium aluminate hydrate.

^cDue to the sample preparation errors (see Fig. S7), quantitative analysis for gibbsite, bayerite and amorphous phase content in the 6-days sample is subject to a great uncertainty and is not reported.

The coordination state of Al³⁺ in the amorphous phase was determined using solid-state²⁷Al MAS NMR. The ²⁷Al MAS NMR spectra (Fig. 3) indicate that Al³⁺ is present in tetrahedral, penta and octahedral coordinations over the course of the experiment. This is to our knowledge the first time that a pentacoordinated Al³⁺ signal has been resolved during nucleation and growth of gibbsite/bayerite from a supersaturated alkaline aluminate solution. Previously, pentacoordinated species have only been reported in amorphous aluminum hydroxides precipitated at near neutral pH, or in alumina produced from the calcination of aluminum hydroxide^46–48 and aluminum oxyhydroxide⁴⁹.

Fig. 3. Ex-situ characterization of precipitates at three time points.

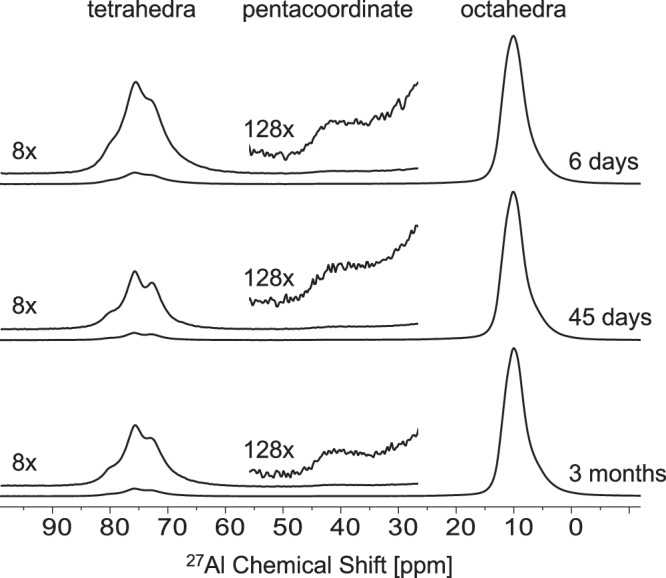
Single pulse, direct excitation ²⁷Al MAS NMR spectra for precipitates collected/filtered after 6 days, 45 days, and 3 months. Vertical magnifications of select regions (8× in tetrahedra and 128× in pentacoordinate) are offset.

The precipitates retrieved via vacuum filtration were then washed with either deuterated water (D₂O) or deuterated ethanol (ETOD) at room temperature. ETOD was used to prevent dissolution of high soluble compounds, such as amorphous phases, during the washing step. The ²⁷Al MAS NMR spectrum of the precipitate washed with D₂O has only an octahedral resonance (Fig. 4) corresponding to gibbsite and/or bayerite, which is expected as these phases are poorly soluble in water (solubilities of 10^−8.1 and 10^−7.9 m^50,51, respectively, in pure water at 25 °C). The ²⁷Al MAS NMR spectrum for the precipitate washed with ETOD had both octahedral and tetrahedral resonances, suggesting that ETOD preserved the amorphous phase, which then partially crystallized into tetrahedral MSA, according to the XRD results (Table 1 and Fig. S7c). The pentacoordinated species was not observed in precipitates washed with either D₂O or ETOD. The wt% proportion of the phases was dependent on the washing process (Table 1), and different amounts of gibbsite and bayerite resulted in a subtle increase in the shoulder of the octahedral resonance near 5 ppm (Fig. 4).

Fig. 4. Effects of washing procedures on phase alternations.

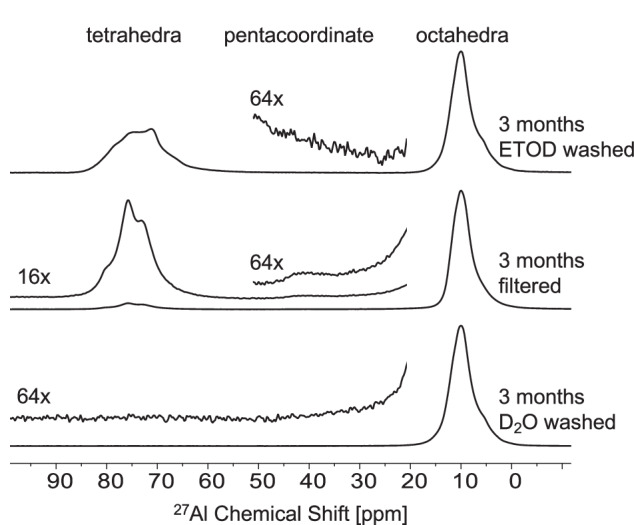
Single pulse, direct excitation ²⁷Al MAS NMR spectroscopy of precipitates after 3 months that were washed with D₂O, filtered only, or washed with ETOD. Vertical magnifications of select regions are offset. The filtered only sample is reproduced from Fig. 3 for comparison.

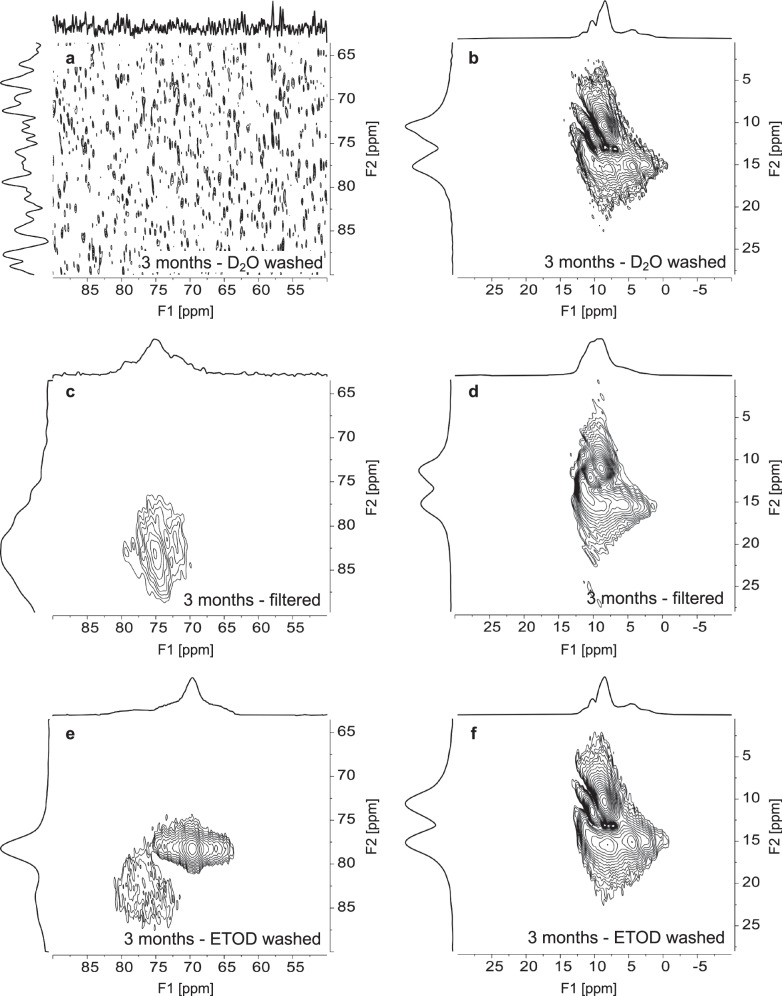
To better resolve ²⁷Al resonances, ²⁷Al triple quantum MAS NMR (3QMAS NMR) spectroscopy was performed (Fig. 5). 3QMAS NMR spectroscopy reduces the second order quadrupolar broadening in MAS NMR spectra of quadrupolar nuclei by correlating multiple quantum coherences with their conversion into single quantum coherence⁵². This NMR acquisition results in two-dimensional spectra, where unique resonances that are often superimposed in one-dimensional spectra can be better resolved. However, the technique has low sensitivity compared to single pulse spectra (Figs. 3 and 4), so the less abundant pentacoordinated species is below the limit of detection in the 3QMAS NMR data. The ²⁷Al 3QMAS NMR spectra of the solids washed with ETOD exhibit at least two tetrahedral environments (Fig. 5e). The first resonance, at an F1 dimension of 69.7 and an F2 dimension of 78.3 ppm, exhibits a well-defined quadrupolar line shape and similar to the resonance for protonated MSA²², in agreement with the XRD data. The second tetrahedral resonance is broad and shows no discernable quadrupolar line shape features, which can be attributed to tetrahedral aluminum in an amorphous phase. Only the second tetrahedral resonance corresponding to the amorphous phase is present in the spectrum for the filtered-only sample (Fig. 5c), and there are no tetrahedral resonances in the D₂O washed sample (Fig. 5a). In the octahedral region, the ²⁷Al 3QMAS NMR spectra shows three peaks (Figs. 5b, d, f). These can be assigned to the two Al sites in gibbsite and the two Al sites in bayerite, with partial overlap resulting in three peaks⁴³. While the differences in wt. % of gibbsite and bayerite observed in XRD may be attributed to some changes in the octahedral region of the 3QMAS NMR spectra between the filtered and samples washed with ETOD or D₂O, these could also potentially mask subtle contributions of octahedrally-coordinated amorphous species.

Fig. 5. Verification of multiple Al³⁺ coordination states in precipitates.

²⁷Al 3QMAS NMR spectroscopy of samples washed with D₂O, filtered only, or washed with ETOD, respectively, at a field strength of 14.1 T. The tetrahedral region is shown in (a), (c), and (e). The octahedral region is shown in (b), (d), and (f).

The ex-situ NMR results indicate that transformation of Al³⁺ coordination from tetrahedral in solution to octahedral in aluminum deuteroxide may proceed either through, or in the presence of, an amorphous phase. This amorphous phase found in the current studied solutions is distinguished from other amorphous phases produced from neutralizing aqueous, acidic solutions of aluminum nitrate⁵³. The amorphous phase is very sensitive to washing procedures, which may induce crystallization into gibbsite, bayerite, or monosodium aluminate hydrate (MSA). SEM images (Fig. S10), showing the morphology of aggregated solids, support XRD (Table 1) and NMR (Figs. 3–5) data. Washing with D₂O precipitates show platelet aggregates resembling typical gibbsite morphology^53,54, while precipitates washed with ETOD form smoother, more globular aggregates resembling an amorphous phase (Fig. S10). Note that there might have some potential impacts on products morphology with D⁵⁴, the exact isotope effects of D for H on the morphology and rates of precipitation are however beyond the scope of this work.

Multiple nucleation and growth processes

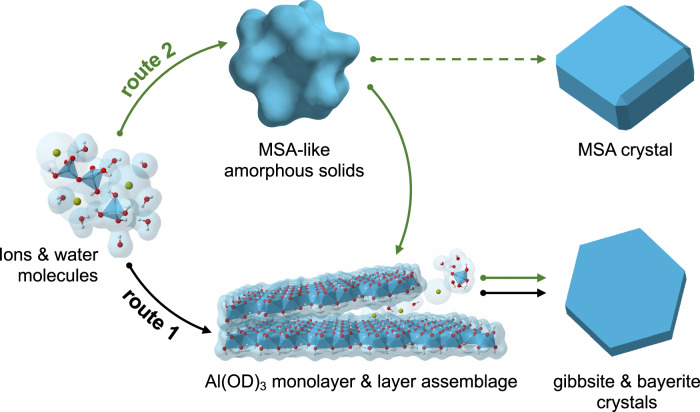
Combining both in-situ and ex-situ observations, Fig. 6 illustrates the proposed multiple reaction pathways for gibbsite/bayerite nucleation and growth from alkaline sodium aluminate solutions. The starting supersaturated solution contains a distribution of aluminate species featuring tetrahedral Al³⁺ coordination, i.e., monomers, dimers, and possibly larger oligomers, all of which can play a role in nucleation and growth. In route 1, the formation of Al(OD)₃ monolayers may start by monomer-by-monomer addition to form octahedrally-coordinated Al³⁺ nuclei, followed by the development of these nuclei into individual nanolayers visible to the naked eye (Fig. 6). This process is a classical nucleation and growth pathway in which the Al³⁺ coordination changed from tetrahedral in small aluminate species to octahedral in nanoplatelets is endergonic. The pentacoordinate Al³⁺ species found with solid state NMR spectroscopy, potentially bridges Al³⁺ coordination changes from tetrahedral solution species to octahedral Al³⁺ nuclei and/or is present at the edge of the nuclei. However, its presence is poorly abundant and not clearly resolvable via both the in-situ neutron total scattering and NMR approaches. At this stage of the reaction, the development of Al(OD)₃ monolayers, instead of direct growth of gibbsite/bayerite nanocrystals, are preferred likely due to the effects of: (i) the bond-valence sum requirements⁵⁵ between OD⁻ and octahedrally-coordinated Al³⁺ (i.e., 0.5 bond valences for each OD⁻ group in bridging two octahedrally coordinate Al³⁺, forming a neutral charged Al(OD)₃ layer), and (ii) the stabilization of layers by interaction with surrounding water molecules, Na⁺, and/or OD⁻, which together act as steric forces preventing direct D-bonding between layers⁴⁰. With time, the crystalline Al(OD)₃ monolayer intermediates ultimately assemble into gibbsite/bayerite structures by particle attachment and alignment processes.

Fig. 6. Schematic of multiple nucleation and growth processes.

Gibbsite/bayerite formation from alkaline sodium aluminate solutions. The final faceted crystals are illustrative representations of final bulk crystal states. The exact crystal morphologies (SEM images in Fig. S10) are more complicated than the illustrations presented here.

The amorphous precipitates observed via ex-situ characterization suggest the presence of an alternative nonclassical pathway to gibbsite/bayerite crystallization (Fig. 6, route 2), via aggregation of Na⁺-aluminate oligomeric precursors. This amorphous compound consists mainly tetrahedral Al³⁺ bridged together by μ₂-oxygene (i.e., similar to both the Al₂O(OH)₆2⁻ dimer and the MSA phase), and with some minor pentacoordinated Al³⁺. Association of pentacoordinate Al³⁺ species with the amorphous surface or as a part of oligomeric network formers would potentially provide a lower energy pathway enhancing Al³⁺ coordination transformation (from tetrahedra to octahedra) and growth of the Al(OD)₃ monolayers. Once the monolayers are formed, the subsequent layer assemblages can be expected, i.e., the processes likely similar to the fabrication of multilayer assemblies based on D/H bonding using the existing surfaces/seedings⁵⁶.

Alternatively, the two nucleation pathways leading to the formation of Al(OD)₃ monolayers, could be independent events. That is, the amorphous phases may not contribute substantially to the Al(OD)₃ layer nucleation and growth. The fact that we are able to observe amorphous materials from the precipitates after several months of dispersion in the solution suggests that the oligomeric precursors for the nucleation of amorphous intermediates may impede Al(OD)₃ layer formation via consuming active aluminate monomers/dimers species to form complex Na⁺-aluminate-D₂O networks. This creates a dynamically arrested state for part of aluminate species within the amorphous network, where aluminate species may become active again upon dissolution of amorphous precipitates. Particularly, if the free energy barriers to form gibbsite/bayerite from amorphous phase are too high to overcome, this would entail that the amorphous phase would eventually transfer only to the MSA salt (due to structure similarity) given a long reaction time or upon partial dehydration (Fig. 6; green dashed line).

The precipitation of Al(OD)₃ polymorphs (gibbsite vs. bayerite) from supersaturated alkaline aluminate solutions must also be addressed. In the past, using solubility data to reflect metastable equilibria^50,51,57, the tendency for bayerite formation (with respective to gibbsite) is generally understood as a result of metastable precipitate from supersaturated solutions. However, many of the thermodynamic properties of Al(OD/H)₃ polymorphs are controlled by modes of stacking of the Al(OD/H)₃ layers^29,30. Thus, layer-by-layer assembly of Al(OD)₃ monolayers must play a significant role in polymorphism and phase selection. In the Al(OD)₃ monolayers, the surface -OD groups are in hexagonal close packing arrangements, and therefore the -OD groups are positioned differently on each side of the surfaces, termed A vs. B sites (Fig. 2a; top insert). In the processes of layer attachment, the likelihood of A-site termination seeing another A-site termination (A-A, or equivalently B-B) is the same as A-site termination seeing B-site termination (A-B or B-A). Hence, from a statistical point of view, the A-B stacking sequences (in bayerite, doyleite and nordstrandite) have the same occurrence probability as the A-A stacking sequences (in gibbsite). The lack of doyleite and nordstrandite phases indicates that the controlling reactions at the interfaces between two monolayers are complicated, involving not only the dynamics of water and ions in the interfacial region, but also the orientational movements of the terminal -OD groups, and their D-bond cross-linkage strength upon attachment. Our findings on gibbsite/bayerite-like layered heterostructures may provide insights into the development of mechanistic descriptions for layer assembly processes. A few of theoretical works dedicated to connect molecular-scale details and energy barriers for layer-layer interactions in aluminum (oxy)hydroxide systems can be found in refs. ^58–63.

Conclusions

Although our mechanistic understanding of gibbsite (the stable thermodynamic phase) nucleation and growth pathways from the supersaturated sodium alkaline solution remains inconclusive, we have shown evidence that the precipitation is not a simple reaction involving the direct growth of ordered gibbsite somatoids from supersaturated solutions. Instead, it is accompanied by formation of bayerite and amorphous metastable phases. Key intermediate states, including pentacoordinate Al³⁺ species, Al(OD)₃ monolayers, and amorphous species, highlight a complex interplay of classical and nonclassical models of nucleation and growth. Cryogenic transmission electron microscopy to isolate layer formation and assemblage processes, and theoretical simulations using our newly developed reactive force field⁶⁴ and a semiempirical model²⁰ to study aluminate oligomerization and transition between different coordination states, are underway to provide a complete understanding of nucleation and growth processes at the molecular level.

Methods

Solution preparation

Deuterated sodium aluminate solution was generated by quantitative dissolution of degreased Al wire (99.999% grade) in 40 wt% stock NaOD solutions (in D₂O; Sigma-Aldrich, 372072, 99.5 atom % D), with selective D₂O water (Cambridge Isotope Laboratories, inc., DLM-6-S-50, 99.96 atom % D) addition or removal (by evaporation at elevated temperatures) as needed to achieve the desired concentration of 9 m [Al³⁺] + 9.9 m [Na⁺] + 36.9 m [OD⁻] (in 55.51 moles of D₂O). Here, concentration units are listed as molality (m), moles of solute per 55.51 moles of solvent (i.e., 1.11 kg of D₂O). This solution is exactly the same solution studied in our previous work (termed s0.1)¹⁸. Its composition corresponds roughly to speciation of 4.8 m [Al(OD)₄⁻] + 2.1 m [Al₂O(OD)₆²⁻] + 9.9 m [Na⁺] + 0.9 m [OD⁻_excess], where the monomeric Al(OD)₄⁻ and the dimeric Al₂O(OD)₆²⁻ solution species have relative abundance of ~70% and ~30%, respectively, according to our previous Raman study¹⁸. The [OD⁻_excess] represents the excess amount of OD⁻ species that is not consumed by Al(OD)₄⁻ and Al₂O(OD)₆²⁻ formation. Thus, the solution has stoichiometric expression of 0.54Al(OD)₄⁻ + 0.23Al₂O(OD)₆²⁻ + 1.1Na⁺ + 0.1OD⁻_excess. During the preparation, an ultra-high purity, Ar-filled glovebox were used to protect solution against CO₂ capture known to be significant for concentrated NaOD solutions at ambient conditions and to prevent isotope exchange of H₂O for D₂O and OH^- for OD^- that can occur upon exposure to ambient atmospheric conditions.

Neutron total scattering measurement

Neutron total scattering data was collected at the NOMAD beamline at the Spallation Neutron Source, Oak Ridge National Laboratory⁶⁵. A thin-walled vessel, incorporating commercially-available 5 mm diameter Wilmad fused quartz NMR tubes and PTFE Swagelok seals, was used as the sample cell. Approximately 3 ml of solution was loaded into the sample cell in an Ar environment at ambient pressure, and was quickly transported to the beamline for neutron total scattering measurements. The sample vessel was mounted vertically in the NOMAD linear sample changer with an argon cryostream fixed below the aligned sample position. Scattering data were collected in 24 min frames at 290 K in an Argon atmosphere over the ~36 h duration of the experiment. Sequential groups of ten datasets were averaged prior further analysis, resulting in a 4 h data segment interval. The beamline’s auto-reduction software⁶⁵ was used to normalize collected data, subtract background and container scattering signals, and produce histograms appropriate for PDF analysis. PDF patterns were calculated via Fourier transformation of the S(q) data utilizing a q_max of 28 Å⁻¹ and a Lorch modification function was applied to smooth data.

Nuclear magnetic resonance spectroscopy

In-situ ²⁷Al MAS NMR spectra were acquired on an 11.7467 T NMR spectrometer using a 7.5 mm HX probe at ~20 °C and a spinning rate of 100 Hz. Ex-situ single-pulse direct excitation ²⁷Al MAS NMR spectra were obtained with a Bruker NMR spectrometer at a field strength of 14.1 T. ²⁷Al triple quantum MAS (3QMAS) NMR spectra were also acquired at a field strength 14.1 T using a 2.5 mm MAS probe with the z-filter, ²⁷Al 3QMAS pulse sequence (mp3qzqf). Please see Section 3 of the supporting text for details on acquisition parameters.

X-ray diffraction

Powder X-ray diffraction was performed on a Rigaku SmartLab SE diffractometer using Cu-Kα radiation (λ = 1.5418 Å) with generator settings of 44 mA and 40 keV. Data were obtained at a scan rate of 0.9 °2θ/min with a step size of 0.01° from 2–100 °2θ using a position-sensitive D/teX ultra-detector with 250 individual detection elements. To quantify an amorphous fraction, 10 wt% rutile (TiO₂ standard reference material #674) was added as a crystalline internal standard. To ensure homogenous distribution of the rutile standard and to minimize CO₂ adsorption, the sample and standard were mixed in an agate mortar and pestle in an N₂ glovebox, and samples were loaded into zero-background cavity holder. Rietveld refinement was performed using TOPAS Software (Bruker ASX). Details about sample preparation and X-ray Rietveld-internal standard refinements are given in Section 4 of the supporting text.

Raman spectroscopy

Raman spectroscopy was performed using a Horiba LabRam HR spectrometer with a Nikon Ti-E inverted microscope using a 632.81 nm continuous laser light source focused through a 40x microscope objective. Spectra were collected between a range of 100–4000 cm⁻¹ with a resolution of 1 cm⁻¹. For each sample, ten spectra were collected with a 30 s exposure time and then averaged. Raman spectra were collected on the filtered supernatant of the original solution (following neutron experiment) and on the solution prepared for the time point study (prior/after precipitation).

Author contributions

H.-W.W., E.T.N., T.R.G., and M.B. made substantial contributions to the experimental design, acquisition and data analysis. H.-W.W. performed in-situ neutron total scattering and PDF analysis. E.T.N., T.R.G., and M.B. conducted ex-situ characterizations using NMR, Raman, XRD, and SEM measurements. M.P., J.G.R., G.K.S., J.J.D.Y., K.M.R., and C.I.P. discussed the results and edited the manuscript. G.K.S., J.J.D.Y., K.M.R., and C.I.P. also supervised the work. The manuscript was prepared by H.-W.W., E.T.N., and T.R.G. with input from all authors.

Peer review

Peer review information

Communications Chemistry thanks David Stephen Wragg and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The article and Supplementary Information contain all the data necessary to support the study’s findings and conclusions. Any relevant data, including neutron/X-ray diffraction and Raman, are available from the authors upon reasonable request. Tabulated source data for ²⁷Al MAS NMR spectra in Figs. 3–5 and in Fig. S6a is provided in Supplementary Data 1.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s42004-024-01285-1.