Influenza virus shedding and symptoms: Dynamics and implications from a multiseason household transmission study

Abstract

Isolation of symptomatic infectious persons can reduce influenza transmission. However, virus shedding that occurs without symptoms will be unaffected by such measures. Identifying effective isolation strategies for influenza requires understanding the interplay between individual virus shedding and symptom presentation. From 2017 to 2020, we conducted a case-ascertained household transmission study using influenza real-time RT-qPCR testing of nasal swabs and daily symptom diary reporting for up to 7 days after enrolment (≤14 days after index onset). We assumed real-time RT-qPCR cycle threshold (Ct) values were indicators of quantitative virus shedding and used symptom diaries to create a score that tracked influenza-like illness (ILI) symptoms (fever, cough, or sore throat). We fit phenomenological nonlinear mixed-effects models stratified by age and vaccination status and estimated two quantities influencing isolation effectiveness: shedding before symptom onset and shedding that might occur once isolation ends. We considered different isolation end points (including 24 h after fever resolution or 5 days after symptom onset) and assumptions about the infectiousness of Ct shedding trajectories. Of the 116 household contacts with ≥2 positive tests for longitudinal analyses, 105 (91%) experienced ≥1 ILI symptom. On average, children <5 years experienced greater peak shedding, longer durations of shedding, and elevated ILI symptom scores compared with other age groups. Most individuals (63/105) shed <10% of their total shed virus before symptom onset, and shedding after isolation varied substantially across individuals, isolation end points, and infectiousness assumptions. Our results can inform strategies to reduce transmission from symptomatic individuals infected with influenza.

Significance Statement.

Individuals infected with influenza are encouraged to avoid contact with others for a period following symptom onset. This action should reduce the likelihood of onward transmission if infectious virus shedding is associated with symptom presentation. We modeled influenza virus shedding and symptom dynamics in participants of a multiseason household transmission study. On average, children <5 years shed more virus for longer durations and experienced elevated influenza-like illness symptoms compared with older age groups. Most shedding took place after symptom onset, and estimated shedding that might remain after a period of avoiding contact with others depended on how the end of this period was defined. Our results can help inform strategies to reduce transmission from symptomatic individuals infected with influenza.

Introduction

Seasonal influenza causes substantial morbidity and mortality in the United States each year (1). Measures to mitigate this burden include pharmaceutical interventions, such as vaccination, and nonpharmaceutical interventions, such as case isolation. The latter is designed to reduce exposure to virus shedding from symptomatic individuals, thereby reducing the potential for onward transmission. The U.S. Centers for Disease Control and Prevention (CDC) recommends symptomatic individuals stay at home and avoid contact with others until 24 h after fever resolution and the improvement of symptoms, or for 5 days following symptom onset if they do not experience fever (2, 3). However, transmission will be unaffected by such mitigation measures if it occurs in the absence of symptoms (for example, prior to symptom onset or from asymptomatic individuals) or after the recommended duration has passed. Understanding how the timing and progression of influenza symptoms relate to influenza virus shedding and transmission is crucial to determining the potential impact of different strategies for reducing onward transmission from symptomatic individuals (4, 5).

Studies of influenza transmission within households provide valuable information on the natural history of infection (6). Individual virus shedding and infection progression can be followed through routine PCR testing of household members and recording of symptoms that arise (7, 8). Such information can be used to characterize patterns of virus shedding from asymptomatic and symptomatic individuals, and to estimate household secondary attack rates and influenza vaccine effectiveness (9–13). Individual-level data can also be modeled to explore potential differences by age or vaccination status that may impact the effectiveness of isolation (14–18). Such insights have improved our understanding of effective isolation measures for SARS-CoV-2 but are limited for influenza (19–21).

Here we modeled individual-level data from a household transmission study conducted across three influenza seasons in the United States. We used cycle threshold (Ct) values obtained from real-time RT-qPCR testing of individual nasal swab specimens to infer longitudinal virus shedding dynamics, and used symptom diaries to assess the relative timing and progression of influenza-associated symptoms. We then identified differences in shedding and symptom presentation by age and vaccination status, and estimated levels of presymptomatic shedding and shedding that may remain once a mitigation measure, such as isolation, has ended. Our findings can help inform effective strategies to reduce transmission from symptomatic individuals infected with influenza.

Materials and methods

Study

We conducted a case-ascertained household transmission study during the 2017–2018, 2018–2019 and 2019–2020 influenza seasons. Households were enrolled following the recruitment of index cases with laboratory-confirmed influenza virus infection from clinics or testing sites in Wisconsin and Tennessee. Households enrolled within 7 days of the index illness onset date were eligible to participate and followed for up to 7 days after enrollment. Participants provided demographic information including age and vaccination status at enrollment. Written informed consent was obtained for all participants. Study protocols and procedures were reviewed and approved by the Institutional Review Boards at the Marshfield Clinic Research Institute and Vanderbilt University. CDC determined these activities were conducted consistent with applicable federal law and CDC policy (see 45 C.F.R. part 46; 21 C.F.R. part 56). The study has been described in detail elsewhere (9, 22); information relevant for the current analysis is summarized below.

Virus shedding

Nasal swabs were collected daily from participants (either by study staff or self-/adult-collected) and tested for influenza by real-time RT-qPCR. Testing was performed using the CDC Human Influenza Virus Real-Time RT-PCR Diagnostic Panel and Influenza A/B Typing Kit at Marshfield Clinic Research Institute or Vanderbilt University Medical Center. We inferred that real-time RT-qPCR Ct values were an indicator of virus shedding and hereafter refer to samples with PCR positive Ct values as reflecting shed virus (23). Since a positive Ct value does not necessarily reflect infectious virus, our Ct analyses relate to the total viral genomic material an individual may shed, not solely that which is infectious. We explore different assumptions about the relationship between Ct measurements and infectious virus in our analyses below.

Ct values are inversely proportional to viral load such that higher Ct values reflect lower amounts of viral material in a sample. Although Ct values can differ by collection method and laboratory procedures, we took the following steps to mitigate such effects. Forty-five cycles were performed for each reaction and samples with Ct values <40 were assumed positive for the purpose of this analysis (24, 25). All negative tests were assigned a value of 40. When individuals had a self- and staff-collected test result on the same day, the Ct values were significantly correlated (correlation = 0.6, P < 0.0001) and so we used the result from the self-collected swab for consistency. We also found no evidence of systematic differences in Ct dynamics by testing site (Figure S1) and thus combined data from both sites in all analyses. Further details of the testing procedures are provided in the Supplementary material.

Symptom scores

Symptom diaries identifying the presence of eight possible signs and symptoms associated with influenza infection (fever, cough, sore throat, runny nose, nasal congestion, fatigue, shortness of breath, and wheezing) were self-/adult-administered daily (Figure 1A). We translated these diaries into a quantitative score, S_ILI, that measured the sum of influenza-like illness (ILI) signs or symptoms reported on each day as

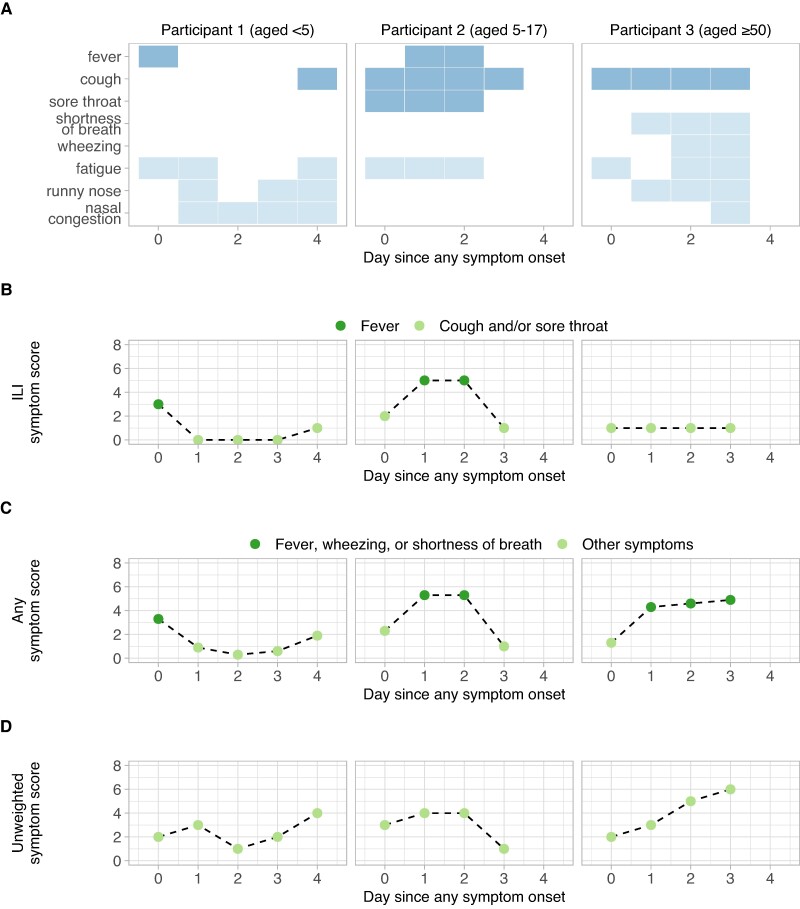
Fig. 1.

Translation of symptom diaries to symptom scores. A) Symptom diary reports from a child aged <5 years (Left panel), a child aged 5–17 (Middle) and an adult aged ≥50 (Right). ILI signs or symptoms (fever, cough, sore throat) reported on a given day are highlighted in dark blue in the top three rows; all other reported symptoms are shown in light blue in the lower rows. Diary reports from (A) are translated to ILI symptom scores, S_ILI (B), any symptom scores, S_ANY (C), and unweighted symptom scores, S_UNW (D). In (B) and (C), colors indicate the presence of fever (B), or the presence of fever, wheezing, or shortness of breath (C).

$${\mathrm{S}}_{\mathrm{ILI}}=3(\mathrm{fever})+\mathrm{sore}\mathrm{throat}+\mathrm{cough},$$

where fever, sore throat, and cough equal 1 on days they were reported and 0 on days they were not (Figure 1B). Fever was weighted more heavily as a proxy for increased clinical severity (26–28). We also defined an alternative score, S_ANY, that accounted for any sign or symptom assessed in the diaries. In this score, shortness of breath and wheezing were more heavily weighted, in addition to fever, to include greater lower respiratory tract involvement as a proxy for severity (Figure 1C) (26, 27, 29). A value of 3 was assigned if at least one of fever, shortness of breath, or wheezing were reported; this value did not increase if more than one was reported. Additional symptoms that were not included in the ILI definition (nasal congestion, runny nose, and fatigue) were each weighted by 1/3, so that

$$\begin{array}{rl}{\mathrm{S}}_{\mathrm{ANY}}& =3(\mathrm{fever}\mathrm{or}\mathrm{shortness}\mathrm{of}\mathrm{breath}\mathrm{or}\mathrm{wheezing})+\mathrm{sore}\mathrm{throat}\\ & +\mathrm{cough}+1/3(\mathrm{runny}\mathrm{nose}+\mathrm{nasal}\mathrm{congestion}+\mathrm{fatigue}).\end{array}$$

The weights for S_ILI and S_ANY were chosen to allow for back-translation of scores to the presence or the absence of fever, shortness of breath, or wheezing. For example, S_ILI > 2 can only occur if fever is reported and 2 ≥ S_ILI > 1 can only occur if cough and sore throat are reported without fever. Similarly, S_ANY > 3 can only occur if fever, shortness of breath, or wheezing are among the reported symptoms; this would not be the case if runny nose, nasal congestion, or fatigue were weighted by 1 instead of 1/3. Finally, we defined an unweighted score, S_UNW, that was simply the number of signs or symptoms reported on any given day (Figure 1D) (10). We compared this with S_ILI and S_ANY to assess the sensitivity of our results to the choice of scoring weights.

Model

We assumed viral shedding over time within an infected individual was proportional to the density of a continuous probability distribution, f_v(t, a_v, b_v). Here, a_v and b_v are the distribution parameters, and t represents the number of days since ILI symptom onset (for analysis of individuals reporting ILI symptoms); since any symptom onset (for analysis of individuals reporting any symptoms); or since first positive test (for analysis of asymptomatic individuals). To allow variation in the magnitude and timing of shedding, we modeled the amount of virus shed at time t, $V(t)$, by

$$V(t)=h_v{f}_v(t-d_v,a_v,b_v),$$

where $h_v$ > 0 is a magnitude scaling factor and $d_v$ a shift in time. Similarly, we modeled the symptom score (S_ILI, S_ANY, or S_UNW) of a symptomatic infected individual as

$$W(t)=h_w{f}_w(t-d_w,a_w,b_w),$$

where t represents days since ILI symptom onset (for S_ILI) or days since any symptom onset (for S_ANY and S_UNW). We investigated three plausible distributions for $f_v$ and $f_w$: lognormal, gamma, and Weibull distributions (4, 11, 19, 30). Since Ct values are bounded by 40 with higher values reflecting lower levels of detected virus, we fit the Ct data with a transformed function,$\hat{V}(t)=40-V(t)$.

Model fitting and covariate analysis

Household contacts with at least two Ct values <40 were included in the modeling analysis. To mitigate the impact of symptoms that were consistently reported due to causes other than influenza, we discarded all data from individuals who reported symptoms on 3 or more days before testing positive, when those days also coincided with a negative test. For analysis of symptomatic infection, we included individuals whose first swab (positive or negative) was on or before symptom onset, and t = 0 anchored all trajectories at symptom onset. For analysis of asymptomatic infection, we could not use time since symptom onset as a common anchor point. We therefore only included individuals with “incident” infection (i.e. those with a recorded negative test before their first positive test). This allowed us to use time since first positive test as a common anchor point that was at, or near, the onset of virus shedding (Figure S2).

We fit $\hat{V}(t)$ and $W(t)$ to the Ct and symptom score data, respectively, using a nonlinear mixed-effects framework (31, 32). We assumed both variables were normally distributed with constant error terms, and ensured model residuals were normally distributed using the Shapiro–Wilk test (33). Each parameter was assigned a fixed effect and an individual-level random effect; the latter captured variation between participants. We assumed a, b, and h were lognormally distributed to ensure positivity, and d was normally distributed to allow positive or negative shifts in time. All parameters were assumed to be independent, and we explored models that stratified one or more parameters by candidate covariates for age group, vaccination status, virus type (influenza A or B), and season. The importance of each covariate–parameter relationship was evaluated using ANOVA (31, 32).

The fit of each candidate model (lognormal, gamma, or Weibull) was compared using Akaike Information Criterion (AIC), where lower AIC values reflect greater statistical support (34). For the model with lowest AIC, we simulated Ct and symptom trajectories for each individual using the fitted parameter estimates. We then calculated key summary metrics, including the duration of shedding (or duration of symptoms), the timing of peak shedding (or timing of peak symptom scores), and the area under each curve. We tested for associations between these summary metrics and each candidate covariate (listed above) using the nonparametric Kruskal–Wallis test and controlled the false-discovery rate using the Benjamini–Hochberg correction. Further details on summary metric calculations are provided in the Supplementary material.

Due to sample size, we did not perform additional stratifications by multiple covariates when testing for associations with the summary metrics described above. Instead, to distinguish covariates with the greatest independent influence on trajectory dynamics from those acting primarily through collinearity with other covariates, we performed hierarchical partitioning (35, 36). Hierarchical partitioning provides a systematic way to assess the independent influence of a particular covariate on a dependent variable, after accounting for the effects of other covariates (additional details are provided in the Supplementary material). Statistical significance was assessed by comparing results to those obtained through 500 random permutations of the covariates.

Implications for isolation impact

We estimated the extent of shedding that would occur before and after a period of isolation by first calculating the proportion of total shedding that had occurred up to any given day, t, as $F_v(t)$, where $F_v$ is the cumulative distribution of the best-fitting model for viral shedding, $f_v$. The proportion of shedding that would have occurred prior to symptom onset and isolation (i.e. presymptomatic shedding) is $F_v(0)$, and the proportion of shedding that would still occur if isolation ended on day t_i is $1-F_v(t_i)$. These estimates account for the magnitude of shedding, in addition to the duration, and are thus more informative than estimates of shedding duration alone.

The value of t_i represents the duration of isolation and was initially assigned for each individual to align with CDC recommendations for staying at home: t_i was set to 24 h after fever resolution for those who experienced fever, and 5 days after symptom onset for those who did not experience fever (2, 3). For those who did not experience fever, we also investigated t_i equal to 3 or 7 days after symptom onset as alternative durations of isolation. We did not have information on individual symptom improvement and so could not account for the timing of improvement in our analysis.

The “back translation” property of S_ILI was used to identify individuals who experienced fever (i.e. attained S_ILI >2) and to determine the time of fever resolution (i.e. when the fitted S_ILI trajectory first decreased below 2 after attaining its peak). Note that the fitted S_ILI trajectories are a continuous representation of a discrete scoring system and so although fever is assigned a value of 3 in S_ILI, anything greater than 2 (i.e. anything above the score assigned for cough + sore throat) is interpreted as possible fever for the purpose of this analysis. In general, S_ILI >2 was a faithful indicator of those who experienced fever (Supplementary material).

Given that Ct values reflect total viral genomic material in a specimen rather than infectious shed virus (i.e. virus with onward transmission potential) we also sought to translate our estimates of viral shedding remaining following the end of isolation to estimates of infectious shedding, or transmission potential, remaining. First, we defined several candidate functions, $g_v(t)$, to describe the proportion of Ct-measured virus that is infectious at any given time. These included (i) a worst-case scenario in which 100% of Ct-measured virus is infectious for the entire duration of shedding; (ii) a best-case scenario in which 100% of Ct-measured virus is infectious until 4 days post symptom onset, and then 0% for the remainder; and (iii) an intermediate scenario in which the infectious percentage of Ct-measured virus decreases linearly from 0 to 7 days following symptom onset (10, 30, 37, 38). These functions were designed for illustrative purposes and are not an exhaustive list of possible infectious virus dynamics. We then estimated the percentage of transmission potential remaining at time t_i as $(1-G_f(t_i))\times 100\text{\%}$, where $G_f(t)$ is the cumulative distribution of $g_v(t)\times f_v(t)$. Assuming secondary infections caused by an infectious individual are distributed in proportion to their infectious shedding distribution, the number of secondary infections generated following the end of isolation can be approximated as $R_t\times (1-G_f(t_i))$, where $R_t$ is the effective reproduction number.

Model fitting and parameter estimation were conducted using Monolix 2021R2 and the lixoftConnectors and Rsmlx packages in R 4.0.3 (Table S1) (39–42). Downstream analyses and plotting were conducted with the hier.part, tidyverse, here, patchwork, ggpubr, and scico packages (43–48). Further methodological details are provided in the Supplementary material.

Results

We identified 119 household contacts with PCR-detectable influenza virus infection and at least two Ct values <40 that were suitable for analysis (Figure S2). Three individuals reported symptoms on at least 3 days with a negative test, before testing positive, and were subsequently excluded. Of the remaining 116, 108 (93%) reported at least one symptom and 105 (91%) reported at least one ILI symptom (fever, cough, or sore throat) during study follow-up (Table S2). Most infections were caused by influenza A viruses (86/116; 74%), and 48 (41%) individuals were vaccinated with the current season's influenza vaccine. Additional characteristics partitioned by age and vaccination status or ILI symptoms are provided in Table S3.

For individuals experiencing at least one ILI symptom (N = 105), a Weibull distribution with shape parameter (a_v) and magnitude parameter (h_v) modified by age provided the best-fit to the Ct data, whereas a Weibull distribution with scale parameter (b_w) modified by age and magnitude (h_w) modified by vaccination status provided the best-fit to the S_ILI scores (Table S4, Figures S3–S5). Results were similar when fitting to the Ct and S_ANY (or S_UNW) observations from those who reported any symptom (N = 108; Table S5, Figures S5–S8). These findings suggest viral shedding dynamics differ by age, and symptom score dynamics differ by age and vaccination status.

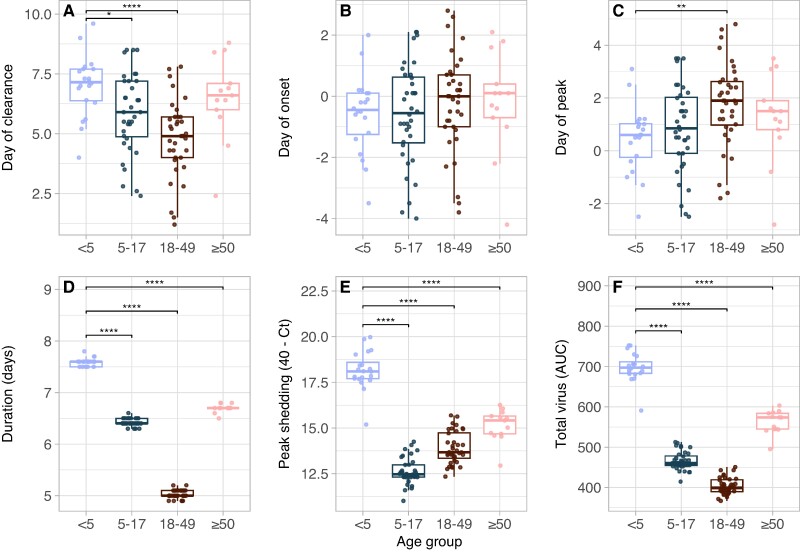
To investigate further, we tested whether age or vaccination status was associated with any trajectory summary metrics. First, we found that young children (aged <5 years) shed significantly more total virus (P < 0.0001), had higher peaks in shedding (P < 0.0001), and had longer durations of shedding (P < 0.0001) relative to other age groups (Figure 2, Figure S9). Children aged <5 years also experienced higher peaks in S_ILI than adults aged ≥50 years and shorter durations of S_ILI than adults ≥18 years (Figure S10, P < 0.01). Conversely, there were no differences in peak symptom score by age when using S_ANY or S_UNW (Figures S11 and S12). This may be driven by the contribution of wheezing and shortness of breath to S_ANY and S_UNW: older individuals, who were less likely to experience fever (Figure S10), were still assigned higher symptom scores if they reported these additional symptoms (Figure S11). Thus, the S_ANY or S_UNW scores may be more sensitive to symptom progression in older individuals.

Fig. 2.

Children aged <5 years shed more virus than other age groups. Associations between age group and viral shedding summary metrics for individuals experiencing ILI symptoms: A) day of shedding clearance relative to ILI onset; B) day of shedding onset relative to ILI onset; C) day of peak shedding relative to ILI onset; D) duration of shedding in days; E) Peak value of shedding attained (transformed as 40—Ct); and F) total virus shed, as measured by the area under the fitted shedding curve. AUC, area under the curve. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.

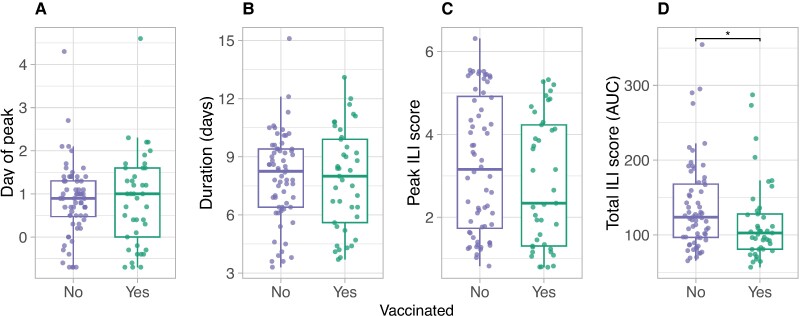
There were no significant associations between vaccination status and the viral shedding metrics (Figure S13). This is unlikely to be confounded by age as the hierarchical partitioning analysis also found no independent effect of vaccination status on the viral shedding summary metrics (Figure S14). In contrast, vaccinated individuals experienced lower total S_ILI scores (P = 0.02) than unvaccinated individuals (Figure 3). Hierarchical partitioning confirmed that this observation was unlikely to be confounded by age (Figure S14). Results were similar for S_UNW, although vaccinated individuals also experienced shorter durations in S_UNW symptom scores (P < 0.001) (Figure S15). Conversely, we found no systematic relationship between the summary metrics and vaccination status for S_ANY (Figure S16).

Fig. 3.

Vaccinated individuals experience lower S_ILI scores. Associations between current season vaccination status and S_ILI summary metrics: A) day of peak S_ILI score relative to ILI onset; B) duration of S_ILI scores in days; C) peak S_ILI score attained; and D) total S_ILI score, as measured by the area under the fitted S_ILI symptom curve. AUC, area under the fitted symptom score curve. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.

Among the other covariates tested (virus type and season), we found an association between season and the time of shedding: infections from 2017–2018 experienced later peaks in shedding (P < 0.01) than infections from 2018–2019 and from 2019–2020 (Figure S17A). However, the hierarchical partitioning analysis suggested this association may be confounded by age (Figure S14), since children <5 were not represented in the 2017–2018 data (Figure S1) and may experience earlier peaks in shedding (Figure 2). We did not detect any associations between shedding or symptom scores among individuals with influenza A and influenza B infections (Figure S14), or between shedding among individuals who reported higher ILI scores (peak S_ILI >2) and those who reported lower scores (peak S_ILI ≤2) (Figure S17B).

Finally, we fit Ct data from 71 individuals with incident infection to compare shedding dynamics during asymptomatic and symptomatic infection (Figures S2 and S18). Asymptomatic individuals experienced substantially shorter durations of shedding than symptomatic individuals, in addition to lower peak and total shedding levels (Figure S19). We did not include additional covariates or formally test these results due to the sample size (8 asymptomatic infections and 63 symptomatic infections).

Implications for isolation impact

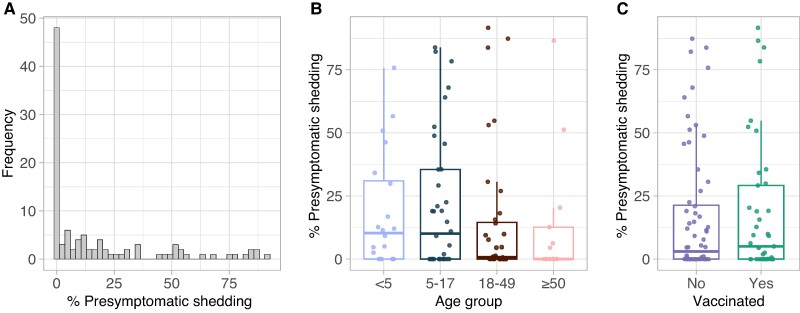
Any shedding that occurs prior to symptom onset (‘presymptomatic shedding’) will reduce the effectiveness of isolation measures. In this study, we estimated that most individuals (60%; 63/105) shed less than 10% of their total virus before the onset of an ILI symptom, although 15% (16/105) shed more than 50% before onset (Figure 4A). Individuals in the latter group had no characteristic in common with respect to age, vaccination status, type of infecting virus, or season of infection (Table S6). Across all individuals there was a nonsignificant reduction in average presymptomatic shedding among adults ≥18 years compared to children <18 years (P = 0.2; Figure 4B), and no relationship with vaccination status (Figure 4C).

Fig. 4.

Presymptomatic shedding is heterogeneous. A) Distribution of presymptomatic shedding across all individuals with ILI symptoms (N = 105). B) Association between presymptomatic shedding and age group. C) Association between presymptomatic shedding and vaccination status. Presymptomatic shedding was estimated as the percentage of total virus shedding that occurred prior to ILI symptom onset. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.

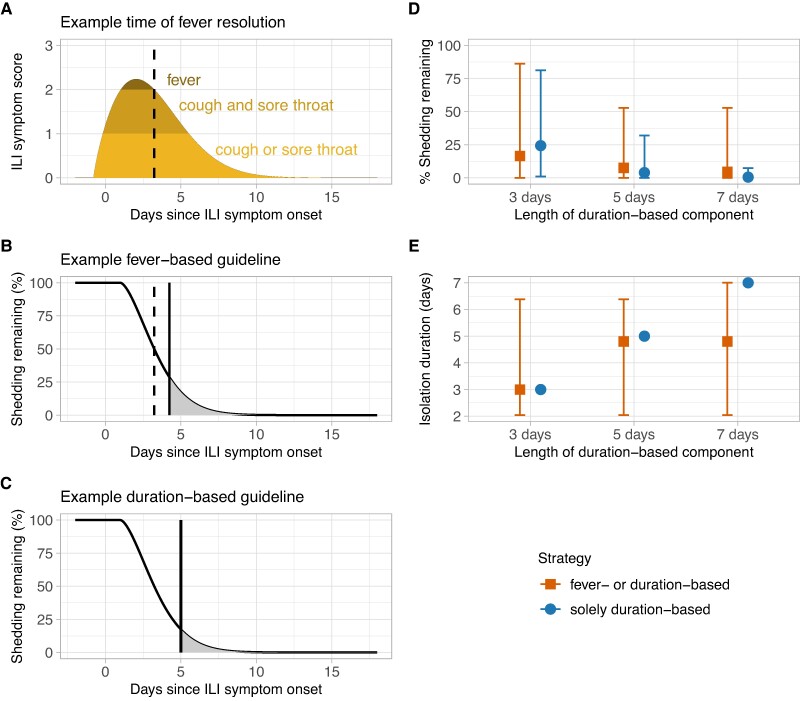
In addition to presymptomatic shedding, shedding may also persist after isolation has ended (“post-isolation shedding”). Current recommendations advise symptomatic individuals infected with influenza viruses to stay at home and avoid contact with others until 24 h after fever resolution and improvement of symptoms, or 5 days following symptom onset if they do not experience fever (2, 3). We henceforth refer to the former as a “fever-based” strategy and the latter as a “duration-based” strategy. For those following the fever-based strategy (i.e. those who experienced fever), we calculated the percentage of shedding remaining 1 day after fever resolution (Figure 5, A and B). For those who did not experience fever and instead followed the duration-based strategy, we calculated the percentage of shedding remaining 5 days after ILI symptom onset (starting from day 0; Figure 5C). We also considered shedding remaining 3 or 7 days after ILI symptom onset. We then combined estimates across all individuals following the fever- and duration-based strategies to explore post-isolation shedding distributions at the population-level. In this study, the median percentage of shedding remaining after isolation was 16.5%, 7.5%, or 4.6% depending on whether individuals without fever isolated for 3, 5, or 7 days, respectively, and there was substantial inter-individual variation (Figure 5D). The corresponding median lengths of time spent in isolation were 3, 4.8, and 4.8 days, respectively (Figure 5E). If all symptomatic participants instead followed a solely duration-based strategy (i.e. everyone isolated for 3, 5, or 7 days following ILI symptom onset regardless of fever presentation), estimates of shedding were generally similar, or lower than, the combination of fever-based and duration-based strategies, and inter-individual variation was reduced (Figure 5D). However, the corresponding median lengths of time spent in isolation were equal to, or greater than, that of the combined strategies (Figure 5E). We observed similar patterns when partitioning estimates by age group and vaccination status (Figure S20). Notably, adults ≥50 years were less likely to experience fever (Figure S10) and thus more likely to isolate for a fixed duration of 3, 5, or 7 days.

Fig. 5.

Duration-based isolation strategies are effective in reducing shedding remaining after isolation from symptomatic individuals but may require individuals to isolate for longer. A, B) Example ILI symptom (A) and shedding remaining (B) trajectories from a child aged 5–17 years following a fever-based isolation strategy. The dashed vertical line represents the time of fever resolution, and the solid vertical line represents the end of recommended isolation. C) Corresponding shedding remaining trajectory for the same child following a duration-based isolation strategy that ends 5 days after ILI symptom onset. D, E) Estimates of shedding remaining (D) and duration of isolation in days (E) for different possible isolation strategies. A combined fever- or duration-based strategy indicates that individuals with fever isolate until 24 h after fever resolution and individuals without fever isolate for 3, 5, or 7 days after ILI symptom onset. A solely duration-based strategy indicates that all individuals isolate for 3, 5, or 7 days after ILI symptom onset, regardless of whether they experience fever or not. Points represent the median and error bars are the 90^th percentiles.

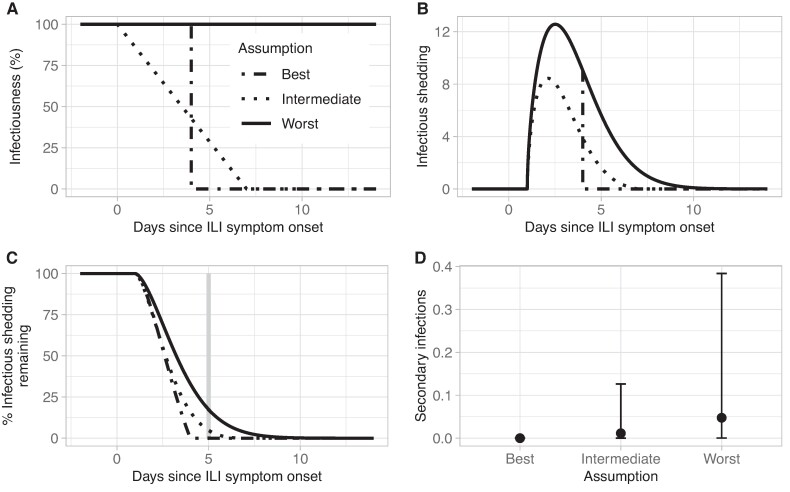
Ct trajectories reflect the dynamics of total viral RNA in a sample rather than infectious virus (i.e. virus with onward transmission potential). We therefore explored how estimates of shedding remaining could be translated to estimates of infectious shedding, or transmission potential, remaining by defining three candidate functions, $g_V(t)$, to describe the proportion of Ct-measured virus that is infectious at any given time: (i) a worst-case scenario in which all shed virus was assumed infectious; (ii) a best-case scenario in which all shed virus was infectious until 4 days after ILI symptom onset and 0% was infectious following that time; and (iii) an intermediate scenario in which the infectiousness of shed virus decayed linearly from 0 to 7 days after ILI symptom onset (Figure 6, A and B) (10, 30, 37, 38). Unsurprisingly, estimates of infectious shedding remaining depended on the assumed infectiousness function, $g_V(t)$: for an example individual ending isolation 5 days after ILI symptom onset, the percentage of infectious virus remaining was 0, 4 and 17% in the best, intermediate, and worst-case scenarios, respectively (Figure 6C). Translating these estimates to the potential number of secondary infections generated per infected individual following the end of a 5-day duration-based isolation strategy (assuming R_t = 1.2 (49)) resulted in projections ranging from 0 to 0.56 across symptomatic participants, equivalent to 0–56 new infections per 100 symptomatic-infected individuals (Figure 6D). Given the strong assumptions underlying each infectiousness function, these results are presented for illustration purposes only.

Fig. 6.

Framework for translating viral shedding to estimates of onward transmission potential. A) Example functions for the percentage of shed virus that is infectious at any time, g_v(t). B) Example application of functions for g_v(t) shown in (A) to the fitted Ct trajectory of the individual shown in Figure 5B. The worst-case scenario reflects the original fitted Ct trajectory. C) Corresponding estimates of the percentage of infectious shedding remaining for the same individual and the same functions for g_v(t) shown in (A). The gray vertical line indicates the end of a 5-day duration-based isolation strategy. D) Estimates of transmission potential remaining across all symptomatic individuals following the end of a 5-day duration-based isolation strategy, expressed as the number of secondary infections caused by each individual when R_t = 1.2. Points represent the median and error bars are the 90^th percentiles.

Discussion

The effectiveness of isolation strategies for individuals with symptomatic influenza virus infection depends in part on the dynamics of virus shedding in relation to symptom timing and severity. We fit nonlinear mixed-effects models to data from an influenza household transmission study and identified differences in shedding by age and symptom scores by age and vaccination status. We also found relatively low levels of presymptomatic, asymptomatic, and post-isolation shedding, which could have important implications for the effectiveness of influenza control through isolation.

Young children are thought to play a central role in influenza transmission within households due to increased susceptibility and infectivity (6, 16, 50). Here, we found that young children aged <5 years shed more virus than all other age groups and experienced higher peaks and longer durations of shedding. A previous study also found children (aged ≤18 years) experienced longer durations of shedding than adults, although there was no difference in shedding levels at symptom onset (30). The difference between the latter result and our identified association with peak shedding levels may be influenced by how age groups were partitioned. The significantly higher peak shedding in children aged <5 years found in this study would have likely been obscured if young children and adolescents (aged 5–17 years) had been analyzed together as previously reported (30). In addition to differences in shedding dynamics, we identified age-related differences in symptom duration and severity. The former increased with age and has been reported previously (7). The latter was influenced by the chosen symptom score: S_ILI scores tended to decrease with age whereas S_ANY and S_UNW scores did not. This is likely due to the inclusion of wheezing and shortness of breath in S_ANY and S_UNW, which may offer a more sensitive description of symptom burden in older adults for whom fever is less common.

In contrast to age, we found no difference in shedding dynamics by vaccination status. This suggests vaccination did not reduce transmission potential in participants with breakthrough infections. Our finding aligns with results from a previous household transmission study (37) and can help inform mathematical modeling studies which must typically make assumptions regarding the infectiousness of breakthrough infections in vaccinated individuals relative to unvaccinated individuals. Despite similar shedding profiles, vaccinated infected participants did experience lower total S_ILI scores than their unvaccinated counterparts. This effect was likely driven by a reduction in fever, given that the association was present with S_UNW (which also includes an independent term for fever) but not with S_ANY (in which wheezing or shortness of breath can compensate for the absence of fever). Our results are consistent with a meta-analysis that found influenza-infected vaccinated individuals were significantly less likely to develop fever than infected unvaccinated individuals, but equally likely to develop other symptoms including cough, headache, sore throat, wheezing, fatigue, and nasal congestion (51). More generally, our findings highlight the importance of considering multiple scoring metrics when analyzing individual symptom dynamics.

In addition to identifying individual differences in shedding and symptom dynamics, we explored the potential impact of these dynamics on the effectiveness of influenza isolation measures by estimating levels of presymptomatic and post-isolation shedding from symptomatic individuals, and by comparing shedding dynamics of symptomatic individuals with those of asymptomatic individuals (who would not be reached by isolation recommendations). We found presymptomatic shedding levels were relatively low for most participants, consistent with previous work (52). However, 15% experienced more than 50% of their shedding prior to symptom onset, suggesting isolation could miss a substantial proportion of transmission in a small fraction of individuals. With respect to post-isolation shedding, although longer durations of isolation will generally favor greater reductions in shedding, this effect must be balanced with the financial and emotional burdens associated with adhering to such measures for prolonged periods (53). Notably, we found that isolation of all symptomatic persons for a fixed duration of time after ILI symptom onset, regardless of the presence of fever (the solely duration-based strategy), may be as effective in reducing shedding compared with a combined strategy informed by current recommendations for staying at home (which had different recommendations for people experiencing fever). However, the solely duration-based strategy could be associated with a greater median length of time spent in isolation, which may outweigh the benefits of reduced shedding in some circumstances. Further work is needed to assess the relative benefits and costs associated with different isolation strategies for influenza.

Finally, we found that asymptomatic infections were rare and shed substantially less virus, for shorter periods of time, than symptomatic infections. Although the sample size was small, these findings support previous analyses (13, 52) and suggest that transmission from symptomatic individuals could comprise the majority of seasonal influenza transmission. There may also be implications for mathematical modeling studies which often assume symptomatic and asymptomatic infections are equally transmissible (54). Overall, our results suggest prompt isolation of symptomatic individuals could be an effective measure for influenza control due to generally low levels of presymptomatic transmission, virus shedding after isolation, and shedding from asymptomatic individuals.

There are several limitations to this study. First, shedding trajectories were fit to Ct values which detect total viral RNA in a sample rather than infectious shed virus. Quantifying the latter would require additional data, such as viral culture, that were not available for this study. Given that influenza viral culture measures decline more rapidly than total shed virus (37), our estimates of presymptomatic and post-isolation shedding are likely upper bounds on infectious virus shedding. Although these can still be useful for planning purposes (23), modeling dynamics of infectious virus, and assessing whether these differ by age and/or other covariates, is a critical avenue for future work. Similarly, when estimating the number of secondary infections that occur after isolation, we assumed these were distributed in proportion to an individual's estimated infectious shedding distribution. Although this may be largely consistent with transmission in community settings, where isolation guidance is most applicable, it does not account for typically higher rates of exposure and susceptible depletion that can occur within households.

Second, we used symptom diaries to quantify symptom onset and severity, which may include reports of symptoms caused by factors other than influenza virus infection (henceforth referred to as nonspecific symptoms). For example, individuals may be more likely to report fatigue and runny nose which have many other causes. Reporting of nonspecific symptoms may contribute to the high frequency of symptomatic infection identified in this study compared to others (55–57). In addition, our estimates of presymptomatic shedding (which depend on the time of reported symptom onset) may be underestimated if nonspecific symptoms were reported before influenza-specific symptoms. To mitigate these impacts, we used definitions that closely track influenza-related symptoms (for example, ILI), and excluded data from individuals who reported symptoms on three or more days with a corresponding negative influenza test, before their first positive test. However, our symptom score trajectories may still be biased towards earlier and/or higher values.

Third, we did not have information on the timing of symptom improvement among the participants of our study. Current recommendations advise individuals with fever to stay at home and avoid contact with others until 24 h after the improvement of symptoms, in addition to fever resolution. Including this additional recommendation may increase our estimates of isolation duration, and decrease our estimates of post-isolation shedding, among participants who experience other symptoms that improve after the resolution of fever. We expect information on symptom improvement to become available in future household transmission studies and could therefore be included in subsequent applications of our modeling framework.

Finally, we used a phenomenological approach to fit the functional forms of the shedding and symptom score data, rather than developing a mechanistic model to explain underlying virus replication and cell infection dynamics (58–61). This choice was motivated by data availability: fitting an appropriate and identifiable mechanistic model for influenza virus infection requires information on viral load and various immune cell populations that were not captured in this study. Although our approach cannot estimate within-host parameters such as viral growth rates and infected cell lifetimes, we are still able to capture shedding and symptoms score trajectories and explore differences in their relative timing and magnitude.

In this work, we have illustrated how phenomenological modeling of data routinely collected during household transmission studies can elucidate virus shedding and symptom dynamics within individuals and identify differences by age and vaccination status. Our framework can also be used to estimate the impact of isolation in reducing influenza virus transmission, and thus inform effective strategies for influenza isolation.

Supplementary Material

Supplementary material is available at PNAS Nexus online.

Funding

These research studies were supported by the Centers for Disease Control and Prevention (grant 5U01IP001078 awarded to the Marshfield Clinic Research Institute, grant 5U01IP001083 awarded to Vanderbilt University Medical Center).

Preprints

This manuscript was posted on a preprint: https://doi.org/10.1101/2024.03.04.24303692.

Data Availability

The data reported in the present study are not publicly available due to privacy restrictions but are available upon reasonable request to the authors. The Monolix software used to fit the data is freely available at https://lixoft.com/products/monolix/.

Disclaimer

The findings and conclusions in this report are those of the authors and do not necessarily represent the views of the Centers for Disease Control and Prevention.