Semi-automated finite element analyses of surgically treated acetabular fractures to investigate the biomechanical behaviour of patient-specific compared to conventional implants

Abstract

Background

In acetabular fracture surgery, understanding the biomechanical behaviour of fractures and implants is beneficial for clinical decision-making about implant selection and postoperative (early) weightbearing protocols. This study outlines a novel approach for creating finite element models (FEA) from actual clinical cases. Our objectives were to (1) create a detailed semi-automatic three-dimensional FEA of a patient with a transverse posterior wall acetabular fracture and (2) biomechanically compare patient-specific implants with manually bent off-the-shelf implants.

Methods

A computational study was performed in which we developed three finite element models. The models were derived from clinical imaging data of a 20-year-old male with a transverse posterior wall acetabular fracture treated with a patient-specific implant. This implant was designed to fit the patient's anatomy and fracture configuration, allowing for optimal placement and predetermined screw trajectories. The three FEA models included an intact hemipelvis for baseline comparison, one with a fracture fixated with a patient-specific implant, and another with a conventional implant. Two loading conditions were investigated: standing up and peak walking forces. Von Mises stress and displacement patterns in bone, implants and screws were analysed to assess the biomechanical behaviour of fracture fixation with either a patient-specific versus a conventional implant.

Results

The finite element models demonstrated that for a transverse posterior wall type fracture, a patient-specific implant resulted in lower peak stresses in the bone (30 MPa and 56 MPa) in standing-up and peak walking scenario, respectively, compared to the conventional implant model (46 MPa and 90 MPa). The results suggested that patient-specific implant could safely withstand standing-up and walking after surgery, with maximum von Mises stresses in the implant of 156 MPa and 371 MPa, respectively. The results from the conventional implant indicate a likelihood of implant failure, with von Mises stresses in the implant (499 MPa and 1000 MPa) exceeding the yield stress of stainless steel.

Conclusion

This study presents a workflow for conducting finite element analysis of real clinical cases in acetabular fracture surgery. This concept of personalized biomechanical fracture and implant assessment can eventually be applied in clinical settings to guide implant selection, compare conventional implants with innovative patient-specific ones, optimizing implant designs (including shape, size, materials, screw positions), and determine whether immediate full weight-bearing can be safely permitted.

Supplementary Information

The online version contains supplementary material available at 10.1186/s13018-024-04957-9.

Background

Acetabular fractures can occur due to high- or low- energy trauma and have a substantial impact on physical functioning, social activities, and work life due to their prolonged rehabilitation duration. Approximately 40% of these injuries require complex open reduction and internal fixation (ORIF) surgery [1]. The primary objective of ORIF is anatomical reconstruction of the acetabular articular surface, aimed at mitigating the risk of progressive osteoarthritis and the subsequent necessity for a total hip arthroplasty (THA) [2, 3]. Following surgical internal fixation, questions emerge regarding fracture stability and the permissible amount of postoperative weight-bearing. The current lack of understanding concerning the type of fixation on biomechanical stability and healing properties leads to a cautious approach to postoperative rehabilitation. Thus, rehabilitation protocols commonly state an initial period of approximately six weeks of non-weight-bearing, followed by a gradual increment in weight-bearing capacity. Additionally, the general biomechanical uncertainties surrounding fractures and fixation methods, as well as the large inter-patient differences, give rise to clinical questions concerning optimal fracture reduction, implant selection, implant dimensions, screw lengths, and screw locations. Gaining insights into these aspects is mandatory because it will enhance decision-making in both implant choice and possible earlier weight-bearing rehabilitation strategies, ultimately contributing to an improvement in patient care and quicker return to society.

The current standard approach to surgical treatment involves the utilization of conventional commercially available implants. These osteosyntheses often involve multiple manual bending manoeuvres during surgery to conform the implant’s shape to the patient’s bone structure. Despite concerted efforts, achieving a perfect anatomical fit between the implant surface and the adjacent bone, along with optimal screw positions, remains a challenge. Importantly, this process of conforming the implant through manual bending, creates a generation of plastic deformation (e.g. exceeding the yield stress) and induces residual stresses in the implant, thereby elevating the risk of implant failure [4, 5] and affecting fatigue resistance [6]. The biomechanical characteristics of the pelvic bone, screws, and fixation materials can be explored through Finite Element Analysis (FEA). FEA is a mathematical tool facilitating the examination of deformations and stress analysis within, in this case, the pelvic anatomical region. Despite the inherent simplifications in FEA simulations in relation to real-world scenarios, their outcomes offer valuable insights for surgical and postoperative treatment. The current literature has extensively documented the use of FEA in this domain. Most studies focus on specific anatomical structures or boundary conditions [7–11], evaluating the biomechanical stability of novel hip replacement prostheses [12–14] and exploring diverse fixation constructs for various conditions including acetabular fractures [15–24], sacroiliac fractures [25] and pelvic ring injuries [26–32]. These studies provide valuable insights into the application of implants before surgery, enabling the prediction of material behavior postoperatively. Nevertheless, comparing findings across these studies poses challenges due to heterogeneity in boundary conditions, loading scenarios, and considerations of anatomical structures. Employing identical models and boundary conditions is crucial for gaining insights into differences in implant choice and design, as well as preoperatively investigating possibilities for early, and possibly even patient-specific, weight-bearing protocols. Thereby improving patients’ surgical treatment, rehabilitation and safety.

We hypothesized that an optimal implant fit, comprising precisely pre-planned screw trajectories, accurate fracture repositioning and a patient-specific implant design will result in favourable clinical outcomes and allows for a personalized treatment approach. Recently, our group introduced patient-specific osteosynthesis for complex acetabular fractures into clinical practise [33–35]. Patient-specific implants are designed to precisely conform to the patient’s unique anatomy as well as the fracture pattern, with the aim of enhancing fracture reduction during surgery and minimizing the likelihood of requiring total hip arthroplasty. We have been able to design, produce and use this implant within 5 days in our clinic. However, the biomechanical performance of patient-specific implants has not yet been thoroughly investigated in comparison to conventional implants. Although different FEAs of patient-specific osteosyntheses have been conducted [23, 24], these studies lack to include real clinical patient data, relying instead on manually simulated fractures, and fail to contain a comparison between conventional and patient-specific implants. Therefore, this study aimed to achieve two primary objectives: (1) to develop a comprehensive semi-automatic three-dimensional FEA of a transverse posterior wall acetabular fracture and (2) to biomechanically compare patient-specific implants to manually bent off-the-shelf osteosynthesis materials while investigating the stresses in the bone and fixation material directly post-operatively during standing up and walking. This was investigated with various computational FEA of a patient who was treated in our clinic for an acetabular fracture. Moreover, the workflow aims to showcase the potential for optimizing patient-specific implants, taking into account real fractures and potentially improving the way we treat patients.

Materials and method

The present study encompasses development of a patient-specific computational analyses, notably FEA, conducted on the hemipelvis of a patient treated for an acetabular fracture in our hospital in 2022. Thus, a real fracture pattern was analysed opposed to a manually created straight fracture often seen in literature. Three distinct models were developed: the contralateral intact hemipelvis, alongside two models featuring fracture reduction. Among these, one model integrated a patient-specific implant, while the other incorporated a manually bent off-the-shelf implant. The intact model served as a benchmark for comparative analysis against existing literature, representing the healthy anatomical structure. The results from the healthy model were compared to literature models with similar boundary conditions, to verify our results. The models remained consistent in configuration, diverging only in the implant type, facilitating a comparative investigation between patient-specific and conventional implants for posterior acetabular fracture surgery. Certain segments of the fabrication process were scripted for both FEA simulations, with a focus on expediting workflow to enhance clinical relevance, thereby prioritizing efficiency crucial for timely clinical interventions. Specifically, the current investigation entailed a comparative assessment of the postoperative load-bearing capacity across bone, implant, and screws during standing and walking, evaluating stress distributions within the aforementioned components. This workflow can be seen as a proof-of-concept to investigate real fractures, taken from the CT scan, and investigate the best surgical approach by incorporating a personalised biomechanical validation for the implant choice (e.g. patient-specific or conventional) or implant design.

Developing a finite element model based on real patient data

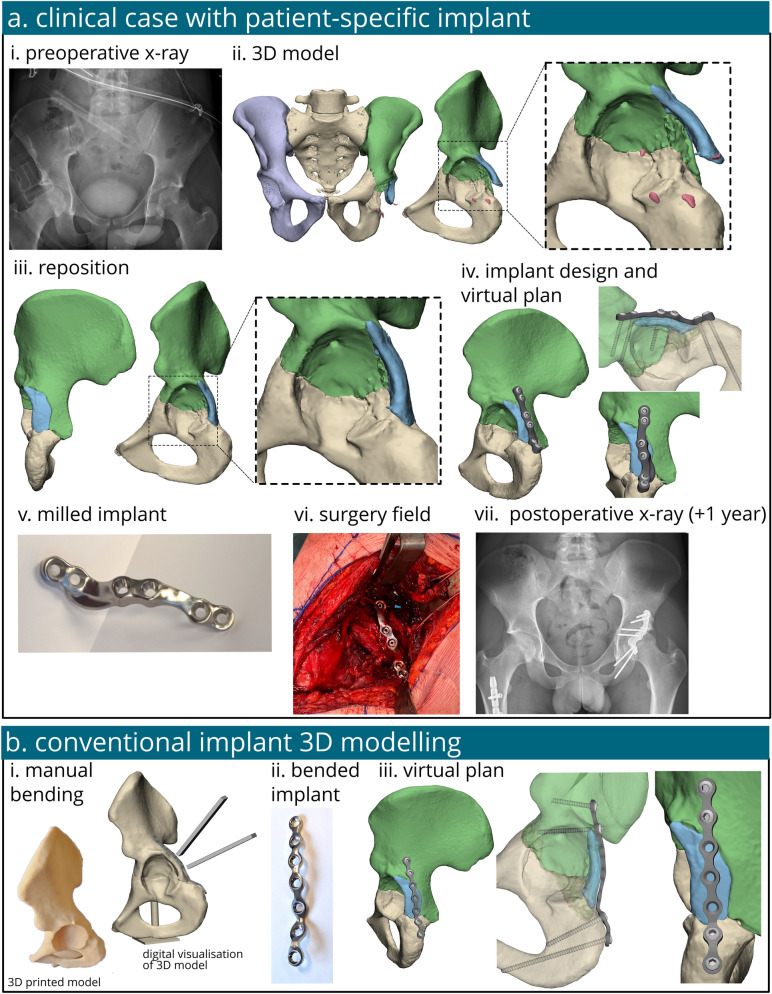
The models were created utilizing the data obtained from a 20-year-old male patient, measuring 180 cm in height and weighing 58 kg, who suffered from polytrauma. He sustained a transverse juxtatectal acetabular fracture accompanied by a posterior wall fragment (AO/OTA classification fracture 62B1.3) on his left acetabulum, resulting from high energy trauma (radiograph Fig. 1a–i). We used this case and this specific type of fracture for our model because, from a clinical perspective, personalized biomechanical evaluation of this injury could potentially optimize future treatment (i.e. optimize implant designs and assess feasibility for early weight-bearing). Surgical treatment consisted of open reduction and internal fixation (ORIF) with a patient-specific implant. In the case under study, two screws were safely positioned in the central region of the implant. These screws were placed to fixate the bone fragment without penetrating the hip joint, ensuring safe placement. Conversely, a safe placement of the screws in this location was not possible in the conventional implantation due to the risk of joint penetration. The main difference between the two implants is that the patient-specific implant achieves a perfect fit to the bone, following its curvature and allowing for the predetermined placement of the screw locations. In contrast, the manually bent implant is an off-the-shelf straight implant that requires bending manoeuvres to fit the bone, preventing a perfect fit, although an appropriate fit is still possible. Both models utilize 3.5 mm cortical screws for fixation. The screws penetrate both cortical bone layers, necessitating different lengths for each screw. Postoperative management included strict adherence to a non-weight-bearing protocol of 6 weeks, followed by a gradual 6-week progression to weight-bearing, aligning with the standard of care. At the one-year follow-up, the patient had an uncomplicated recovery, successfully resuming occupational activities, work, and sports, reporting an absence of pain or discomfort. The complete workflow for the designing, production and clinical application of a patient-specific implant including all relevant clinical imaging is illustrated in Fig. 1a.

Fig. 1.

The workflow of the treatment and analysis of a patient with an acetabular fracture treated with either a patient-specific implant or a conventional off-the-shelf implant. The case taken for the computational analysis was those of a patient treated in our institution for an acetabular fracture surgically managed with a patient-specific implant. The process started with an x-ray (a-i) followed by 3D modelling and bone segmentation of the CT scan (a-ii) and repositioning of the bone fragments (a-iii). A patient-specific implant was created (a-iv), milled out of titanium (a-v) and placed during surgery (a-vi). At one year follow-up the x-ray showed good clinical results (a-vi). The conventional implant was also 3D modelled for comparison, it was manually bended on a 3D printed model (b-i), scanned (b-ii) and virtually placed in 3D (b-iii)

Finite element modelling

A computed tomography (CT) scan with a slice thickness of 0.6 mm was performed of the patient’s pelvic region. The acquired Digital Imaging and Communications (DICOM) files were imported into Mimic Version 25.0 (Materialise, Leuven, Belgium) for further analysis. Employing a threshold of 226-1500 Hounsfield Units (HU), the affected hemipelvis underwent segmentation. Subsequently, fragments of the fractured hemipelvis were segmented separately (Fig. 1a-ii). The segmented regions were then converted into stereolithography (STL) files and imported into 3-matic Version 17.0 (Materialise, Leuven, Belgium).

Following established methodologies from prior clinical studies [33, 34], the subsequent steps for the 3D virtual surgery plan and fabrication of the patient-specific osteosynthesis were initiated as standard of care. The bone fragments were virtually repositioned to their anatomically correct orientation and location (Fig. 1a-iii). In a multidisciplinary meeting, the optimal screw trajectories and locations for the patient-specific implant were determined based on the 3D reconstruction of the fracture. The patient underwent treatment with a patient-specific implant, designed in-house by our engineers with 3-Matic software version 17.0 (Materialise, Leuven, Belgium), Solidworks Professional software version 2020 (Dassault Systèmes Solidworks), and the Geomagic package for Solidworks (3D Systems) (Fig. 1a-iv). 3-Matic was utilized to determine the shape of the implant, Geomagic was employed to convert the models into CAD files, and SolidWorks was used to finalize the design by adding the appropriate screw holes. The patient-specific implants were fabricated from a medical-grade titanium alloy utilizing a 5-axis milling machine at Witec Medical B.V. in the Netherlands. The corresponding surgical drilling guides were produced at Oceanz (Ede, The Netherlands) under the ISO 13485:2016 standard. The manufacturing process was completed within a timeframe of 3 days. The workflow for designing and producing a patient-specific pelvic osteosynthesis plate tailored to the fracture type has been introduced and previously described by our group [33].

The fractured bone fragment models, intact hemipelvis, femur head, and the patient-specific implant were derived from the patient data. However, in order to facilitate a comparative biomechanical evaluation of two implants, a 3D model of the conventional implant was needed. The shape and placement of the conventional implant were determined by merging repositioned bone fragments and subsequently 3D printing them using polyamide powder through selective laser sintering techniques. A conventional 7-hole straight plate (DePuy Synthes, Raynham, MA, USA) was manually contoured onto the 3D print to replicate intraoperative bending of the implant, enhancing its fit to the adjacent bones (Fig. 1b-i). The contoured implant was then optically scanned with an Artec Space Spider (artec 3D, Luxembourg, Luxembourg) to produce a STL-file. The plate was digitally reconstructed in Solidworks Professional software, version 2020 (Dassault Systèmes Solidworks), using STL file from the manually-bent implant as a template, enabling stepwise virtual bending of the implant within Solidworks using the flexing features (Fig. 1b-iii). This step was undertaken to eliminate scanner artifacts and ensure the implant had a proper surface for subsequent steps. However, this reconstruction was performed without accounting for the potential influence of the bending process on the structural integrity and properties of the implant. The implant’s STL-file was used in the virtual plan of the conventional implant (Fig. 1b-iii). To finalize the models for FEA, additional 3D structures such as cartilage layers and screws were manually created. An anatomical femoral head and a cartilage layer was utilized to apply the hip joint force, as it yields more accurate outcomes compared to using a perfectly spherical model [8]. Cartilage layers were individually designed for each fragment using a semi-hemisphere and subtracting the acetabular bone and femur head. To streamline computational efficiency without significantly compromising accuracy, screws were modelled as simplified rods fixed to the bone, as per previous literature [8, 9]. The threaded portion of the screws was depicted as rod-like structures with a diameter of 3.5 mm, while the screw heads were modelled as hemispheres with a diameter of 8 mm [36, 37]. Boolean subtraction was employed to subtract the screws from the bone.

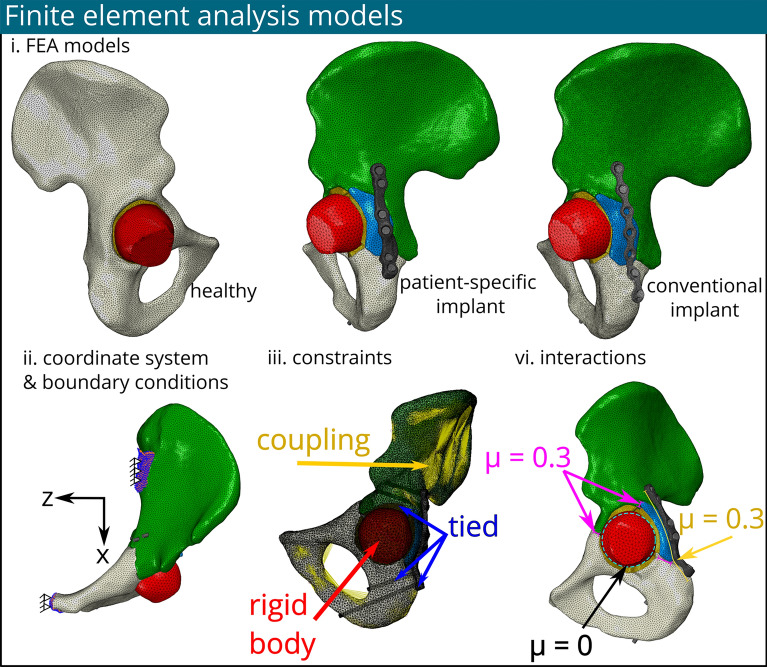
To reduce geometric complexity, all bony parts underwent wrapping and smoothing processes wherever feasible. Subsequently, each part underwent meshing using the remesh function available in 3-Matic (Materialise, Leuven, Belgium), resulting in surface and volume meshes comprised of 10-node tetrahedral elements (C3D10). The number of elements of each part is reported in Appendix A. Following meshing, the repositioned bone parts were duplicated and reverted back to their original positions before repositioning. The translations back to their original fractured positions were needed to align the meshed 3D models to their CT scan location. This alignment facilitated assignment of material properties based on the corresponding CT scan data for each fragment. Since the 3D models needed to be translated back to their repositioned position for the FEA, a transformation matrix (T) was needed. Utilizing 3-Matic, these transformation matrices were generated for each bone fragment, and used in further steps. Subsequently, all volume meshes, along with the assigned surfaces, were exported as ABAQUS input files (Fig. 2).

Fig. 2.

Three different finite element models were fabricated (e.g. a healthy model, with a patient-specific implant and with a conventional implant) after meshing and material assignment in the Materialise software. The cartilage layer was modelled per bone part and illustrated in orange, the femur is illustrated in red (i). Their coordinate system & boundary conditions (ii), constraints (iii) and, interactions (vi) are identical for all models

Material assignment

In this study, all materials were assumed to possess heterogeneous, elastic and isotropic properties. The component models were imported into Mimics, wherein material properties were assigned using the FEA-module. For bone material characterization, HU acquired from the CT scan were used. Elements exhibiting HU values below 226 were excluded from categorization as cancellous or cortical bone and were instead assigned material properties of Young's modulus (E) = 100 MPa, v = 0.3 and bone density ($\rho$) = 0.1 kg/m³. Regions with HU in the range of 226–815 were identified as cancellous bone, which is in the range of previous reported threshold HU values for cancellous bone [8, 38, 39]. The bone density was calculated using Eq. 1 and employed to derive the Young's modulus for the cancellous (Eq. 1) [13]. The cancellous bone was partitioned into 10 sections per part, with Young's modulus values ranging from 3181 to 6123 MPa across all bone parts for both the patient-specific and conventional implant models.

$$\begin{array}{cc}\hfill \rho & =0.00069141\times \text{HU}+1.026716\hfill \\ \hfill E& =2017.3\times {\rho }^{2.46}\hfill \\ \hfill \end{array}$$ 1

Cortical bone was assigned a Young’s modulus of 17 GPa [40]. These material properties were attributed based on the volume meshes obtained from the original locations before repositioning, extracted from CT scans. Utilizing the previously exported transformation matrix (T), Python scripting in Abaqus facilitated the relocation of bone parts to their respective re-positional locations, as detailed in Appendix B. The femur was assigned a Young's modulus of 20 GPa alongside a Poisson's ratio of 0.3. The material properties of the cartilage layer were obtained from existing literature [7, 11], with a Young's modulus of 10.35 MPa and a Poisson's ratio of 0.45. The material properties of the patient-specific implant were derived based on the manufactured medical-grade titanium alloy, featuring a Young's modulus of 114 GPa and a Poisson's ratio of 0.3. The models of screws and the conventional implant were assigned to be the stainless steel, characterized by a Young's modulus of 200 GPa and a Poisson's ratio of 0.3.

Boundary conditions, constraints and interactions

The entire process of assigning parameters and conditions within Abaqus was automated using Python scripting. This methodological approach facilitated expedited and replicable assignments for reposition of the bone fragments employing the transformation matrix, as well as for defining boundary and loading conditions, constraints, and interactions. Such systematic automation ensured a standardized and systematic implementation of the finite element model. The Python scripts were customized to accommodate the specific requirements of our study, thereby allowing for seamless integration of complex structural and biomechanical nuances into the Abaqus simulation framework.

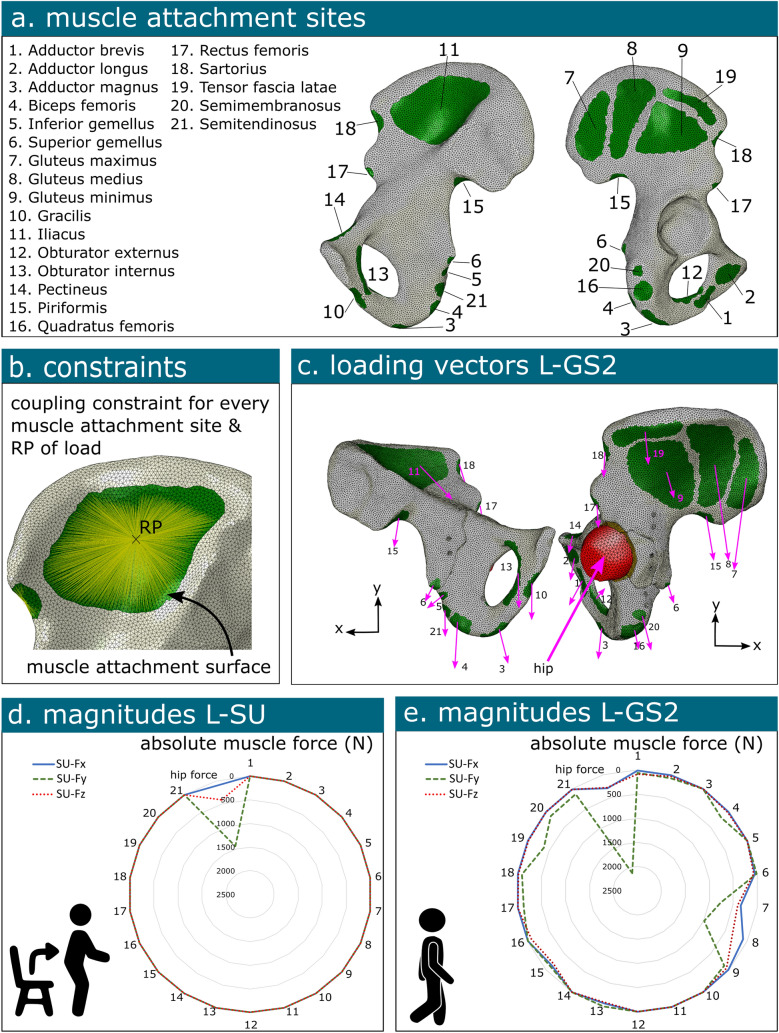
Prior research state that the ligamentous sacroiliac and pubic symphysis joints could be rigidly fixed in space [9] (Fig. 2.ii). Thus, movement was restricted in all directions at these boundary conditions. The cartilage-pelvic bone interface was connected using a tie constraint. In order to ensure the connection between muscle attachment sites and their corresponding anatomical surfaces, a continuum distributing coupling constraint was implemented. This methodology entailed the selection of a pivotal reference point situated approximately at the middle of every muscle attachment site surface, and which was subsequently connected to its corresponding surface. Additionally, a reference point was chosen at the centre of the mass of the femoral head. This reference point was connected to the elements of the femoral head using a rigid body constraint, ensuring structural integrity and coherence within the biomechanical model. The interaction between the articular surface of the femoral head and the cartilage layer was modelled as a frictionless surface-to-surface interaction. Screws were tied to the bone, assuming proper bone-grip [36, 37]. A penalty contact with a friction coefficient of 0.3 was applied between the fracture line surfaces [25, 26]. Similarly, a penalty contact methodology, featuring a friction coefficient of 0.3, was deployed to regulate interactions between the implant and bone surfaces [14]. The interaction between the implant and the screw heads was assumed to be tied [19] (Fig. 2-iii).

Load applications

The coordinate system was manually assigned according to the conventions outlined by Dostal and Andrews [41]. Specifically, the X-axis was defined from posterior to anterior, the Y-axis from inferior to superior, and the Z-axis laterally to the right side of the body, following a right-handed orthogonal reference frame. Various loading conditions were systematically examined to assess the response of the models. The first loading condition (referred to as L-SU) simulates the initial postoperative phase, simulating stage where an individual might be standing up. This condition reproduces the peak hip reaction force measured at the femur head, as observed by Bergman et al. [42]. It reflects an immediate postoperative scenario during recover, such as when the patient transitions between different positions (e.g., bed to chair) without using additional support. The second loading condition (referred to L-GS2) replicates the peak forces experienced during the walking phase, specifically targeting the second phase of the gait cycle. This assessment aims to ascertain the feasibility of walking during the postoperative period, while also serving as a conservative scenario assuming insufficient bone remodelling has occurred.

Notably, twenty-one muscles associated with walking were considered in the analysis [40]. The loads were applied at designated reference points corresponding to the surfaces of the muscle attachment sites. The magnitudes of these muscle forces, in conjunction with the hip joint force, were derived from the study by Dalstra and Huiskes spanning all eight loading phases within a normal gait cycle [40]. The specific contributions of these forces in all three dimensions were calculated based on the directions derived from proximal and distal insertion points as reported by Dostal and Andrews [41]. Furthermore, the hip joint force was determined using data from Bergmann et al. [43], who reported an average peak force of 2.38 times body weight at the hip joint, potentially escalating to 3 times body weight during other daily activities (Fig. 3).

Fig. 3.

Illustration of the loading conditions on the hemipelvis. The muscle attachment sites (a) are connected to a corresponding reference point (RP) using a coupling constraint (b). The directions of the muscle force (c) and the magnitude of the involved muscles forces at the reference points and/or hip reaction force is illustrated for loading condition standing up (L-SU) (d) and loading condition of gait step 2 (L-GS2) (e)

Validation

In order to ascertain the precision and reliability of the finite element model developed in this study, a series of rigorous verification procedures were systematically executed. These procedures encompassed comparing the model's results against established analytical solutions or experimental data in literature, thereby facilitating an assessment of its congruence. Moreover, the simulated healthy intact hemipelvis model (i.e., the contralateral side), was subjected to inspection, wherein its predictions concerning bone stresses and displacement were compared to existing literature, thus serving to validate its performance.

Furthermore, a sensitivity analysis was systematically conducted to evaluate the impact of various input parameters on the model's response. Specifically, a sensitivity analysis was conducted to investigate the influence of element size on the von Misses stress distributions results derived from the finite element analysis pertaining to the healthy model. Element sizes of 1 mm, 2 mm, and 3 mm for the bone were examined, and their impact on the accuracy and convergence of the results was evaluated. This examination ultimately facilitated the identification of an optimal element size that not only ensured reliable predictions but also upheld computational efficiency.

Results

The sensitivity analysis indicated that the 1 mm mesh size provided detailed results but required extensive computational resources and time (over 55 h). Moreover, it was expected that the fractured model would significantly increase the computational resource requirements, making it difficult to work with. The 3 mm element size, while computationally efficient (under 30 min of computational analysis), showed some deviations in the results. Moreover, the 3 mm element size was expected to face challenges with the complex geometry of the fractured model, including screw holes, and the application of patient-specific material properties. The 2 mm mesh size was found to offer an optimal balance, providing accurate results comparable to the 1 mm mesh size while significantly reducing the computational load to approximately 4.5 h allowing for the preferred geometric shapes. Based on the findings of the sensitivity analysis of the current study, the 2 mm element size was selected for the bone parts for the detailed FEA study of the fracture models.

Von Mises stress healthy bone

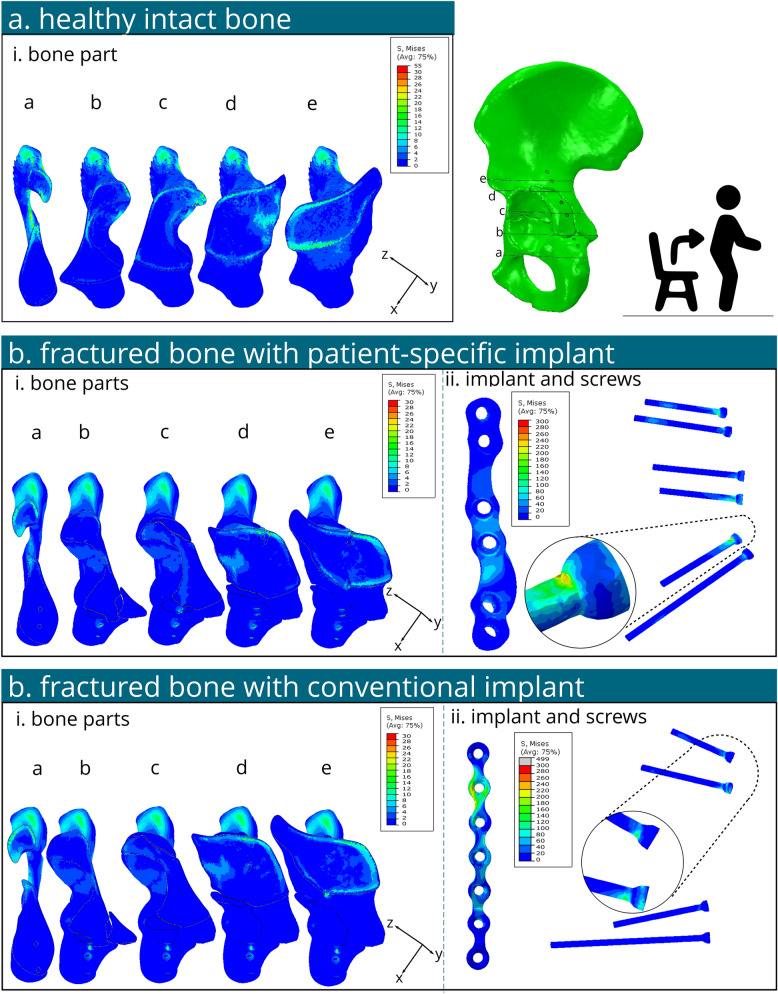
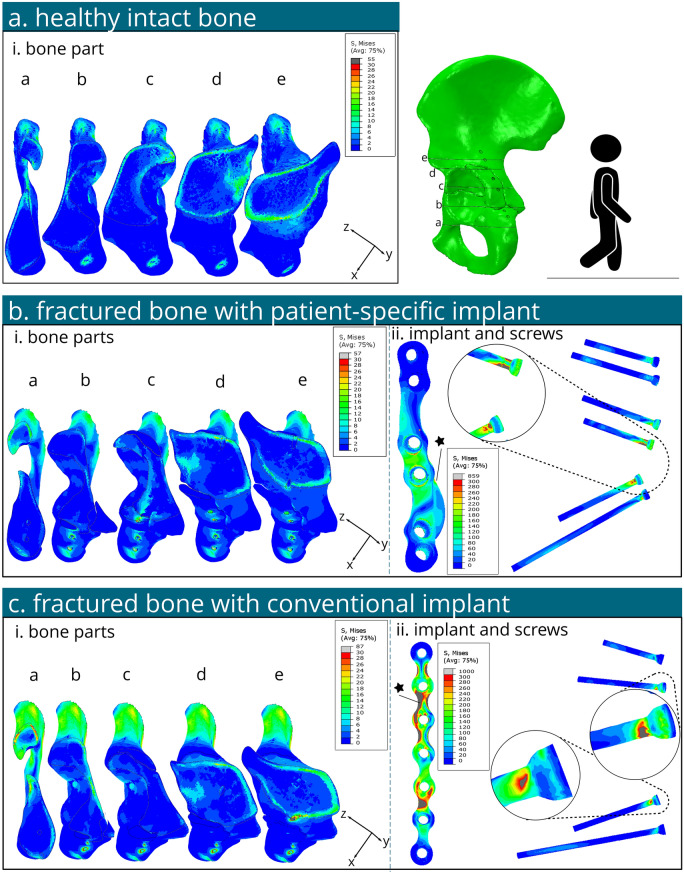
The peak von Mises stress in the intact hemi pelvis was found about 30–40 MPa near the greater sciatic notch for both L-SU and L-GS2 (Figs. 4a and 5a). Another additional peak stress of about 55 MPa was located above the acetabulum's roof with L-GS2. Stresses of 7.5–15 MPa were noted in the cortical bone above the acetabulum for both conditions, slightly higher for L-GS2. Stresses in the upper ilium and ischium were low (< 10 MPa) under both conditions.

Fig. 4.

Several contour plots of the von Mises stress on the bone and fixation material under standing up loading conditions (L-SU). a Von Mises stresses illustrated in cross sections a- e of the healthy intact contralateral hemipelvis bone. b Von Mises stresses of the bone (i) and implant and screws (ii) of the fractured model with a patient-specific implant. c Von Mises stresses of the bone (i) and implant and screws (ii) of the fractured model with a conventional implant

Fig. 5.

Several contour plots of the von Mises stress on the bone and fixation material under peak walking loading conditions (e.g. the second phase of gait walking) (L-GS2) . a Von Mises stresses illustrated in cross sections a - e of the healthy intact contralateral hemipelvis bone. b Von Mises stresses of the bone (i) and implant and screws (ii) of the fractured model with a patient-specific implant. c Von Mises stresses of the bone (i) and implant and screws (ii) of the fractured model with a conventional implant. Stars illustrate the location of the peak stresses for each implant respectively

Von Mises stress for loading condition of standing-up (L-SU)

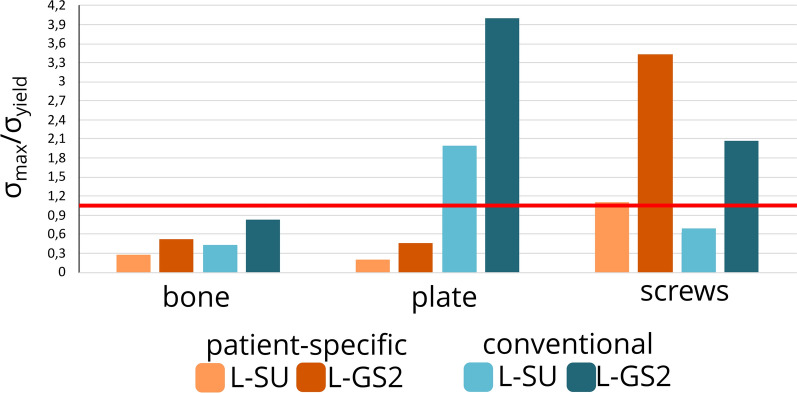
For the patient-specific implant under L-SU (Fig. 4b), maximum bone stress was approximately 30 MPa near the greater sciatic notch. Stresses of 7.5–15 MPa were observed in the cortical bone above the acetabulum. The implant's highest stress reached 156 MPa near the second screw hole distally, with an average stress of 13 MPa in the implant. Screws showed a peak stress of 275 MPa at the head of the second screw distally. All stress levels in the bone, implant, and screws remained below their yield stress thresholds; 108 MPa [41], 875 MPa [42], 250 MPa and 250 MPa [43], for the bone, patient-specific implant, conventional implant and screws, respectively (Fig. 6).

Fig. 6.

Graph of the maximum calculated von Mises stress divided by their respective yield stress of the loading condition standing up (L-SU) and second gait step for walking (L-GS2) for models with either implant. The yield stress of bone, patient-specific implant, conventional implant and screws are 108 MPa [44], 875 MPa [45], 250 MPa and 250 MPa [46], respectively. The red line represent the maximum stress allowed without exceeding the yield stress

For the conventional implant under L-SU (Fig. 4c), the bone's maximum von Mises stress was about 46 MPa at the greater sciatic notch. Von Mises stresses in the range of 10–20 MPa were found in the cortical bone above the acetabulum. The conventional implant's highest stress was 499 MPa at the second screw hole distally, with an average stress of 32 MPa. The maximum screw stress was 174 MPa at the head of the second screw hole distally. The stress magnitudes in the bone and screws were below their respective yield stress, the stresses in the implant exceeded it around the tie constraint of the second screw hole distally (Fig. 6).

Von Mises stress for loading condition of gait step two (L-GS2)

For the patient-specific implant under L-GS2 (Fig. 5b), maximum bone stress was about 56 MPa near the first and third screw holes distally. Stresses of 5–25 MPa were observed above the acetabulum. The implant's highest stress reached 371 MPa near the second screw hole distally (see star in Fig. 5b-ii), with an average stress in the implant of 25 MPa. The screws' peak stress was 859 MPa at the head of the second screw distally, between two tie constraints. Stress in the bone and implant stayed below yield stress, but the screw stress exceeded it (Fig. 6).

For the conventional implant under L-GS2 (Fig. 5c), the maximum bone stress was approximately 90 MPa near the third screw hole distally. Stresses of 5–30 MPa were found in the cortical bone above the acetabulum. The implant's highest stress was 1000 MPa between the second and third screw holes distally, with an average stress in the implant of 112 MPa. The maximum von Mises stress in the screws was 519 MPa at the head of the most proximal screw, between two tie constraints. Bone stress was below yield stress, but stresses in the implant and screws exceeded their yield stress (Fig. 6).

Displacement

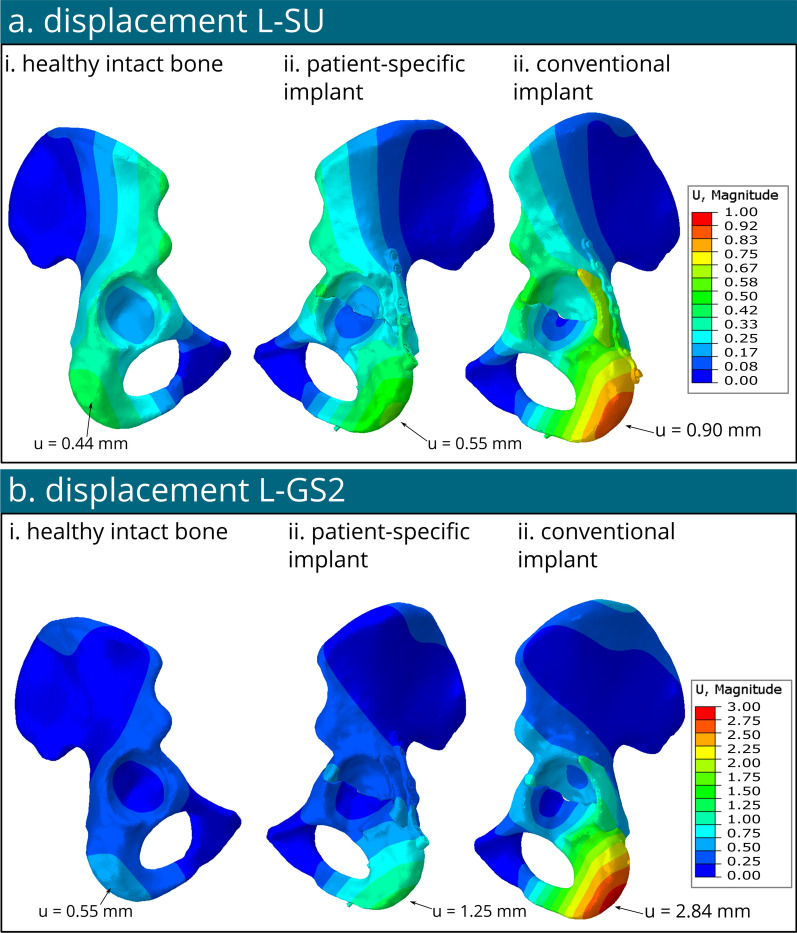
Figure 7 illustrates the plot contours depicting displacement. In the case of the healthy model, the maximum displacement measured 0.44 mm for the L-SU and 0.55 mm for L-GS2, with both peaks observed at the ischium bone region. For the model with the patient-specific implant, the maximum displacement reached 0.55 mm for the L-SU and 1.25 mm for the L-GS2, also located at the ischium bone site. Finally, with the model with the conventional implant, the maximum displacement was 0.90 mm for the L-SU and 2.84 mm for the L-GS2, both concentrated at the ischium bone region.

Fig. 7.

Displacement contour plots in mm of the healthy bone, model with patient-specific implant and model with conventional implant under loading condition standing up (L-SU) (a) and loading condition of gait step 2 (L-GS2) (b)

Discussion

The first aim of this study was to develop a comprehensive semi-automatic three-dimensional FEA model of a real transverse posterior wall acetabular fracture, which was successful. This streamlined workflow allowed us to investigate real fractures and shows potential for optimizing patient-specific implants as well as evaluating the stress levels within the osteosyntheses material. It also facilitates exploring considerations for early postoperative weight-bearing, effectively bridging the gap between biomechanical engineering and clinical surgery. Our goal of modelling real fractures, opposed to manually created fractures as presented in previous studies [23, 24], was achieved. Our model was used to investigate and compare two types of implants for a transverse acetabular fracture with a posterior wall fragment; a patient-specific implant and a conventional one (e.g. off-the-shelf implants). The biomechanical behaviour of our patient-specific implants immediately after surgery had not yet been investigated and compared to conventionally used implants. In this study, the stresses in the bone and osteosynthesis materials were investigated for the loading conditions standing up (L-SU) and the peak forces for walking (L-GS2). The findings indicated that the patient-specific implant resulted in lower stress concentrations in the bone under both loading conditions, and the bone and implant could safely withstand standing-up and walking. The results from the conventional implant indicated it was safe for standing-up, however some elements around the screw hole exceeded their yield stress which was possibly caused by the tie constraint. However, stresses in the implant exceeded the yield stress of stainless steel under walking loading conditions, indicating a high risk of implant failure. The innovative part of our model included the utilization of real clinical case featuring real authentic fracture patterns, as opposed to artificially generated linear fractures. Moreover, this study was one of the first to compare the biomechanical behaviour of the patient-specific implant to the conventional implants for the same fracture. Facilitated by a semi-automatic workflow, the process guaranteed reproducibility and made it a fast-track workflow, possibly rendering it well-suited for clinical applications in the future.

Using our semi-automated workflow, we were able to investigate various scenarios. Our methodology featured a transformation matrix, enabling the repositioning of bone fragments to their anatomical locations, while retaining their HU-based material properties. Additionally, uniform boundary conditions and constraints were applied across all models using scripts, facilitating comprehensive analysis. This approach provided valuable insights into a clinical case under different loading conditions, such as standing up and peak forces of walking, for both patient-specific and conventional fixation implants. The results of von Mises stress in the healthy model under L-GS2 (Fig. 5b) were in agreement with the previous in-vivo studies of healthy pelvic models under similar loading condition to the current study [8, 40]. The observation of low stress concentration found in the low ischium (Fig. 5a-i.a) agrees with the previously-reported 1–5 MPa measurements in the literature [8, 47]. In the current study, the maximum stresses in the cancellous bone (< 10 MPa) were found to be significantly lower than those in the cortical bone (~ 55 MPa) (clearly visible is Figs. 4 and 5), but higher than those reported in other similar studies (< 0.5 MPa) [47]. The reason behind this disparity between the results of maximum stress in this study and the other work [46] might be due to the difference in the material assignment strategies. The current study utilized element-based material properties pertinent to the HU, calculated from the patients’ CT images, while Phillips et al. [47] used separate cortical and cancellous bones. Accordingly, the higher stresses found in the cancellous bone might be explained due to the patient-specific material properties of the bone taking into account the patient’s bone quality and differences. Nevertheless, the finding of stress locations and ranges within the cortical bone of the hemipelvis (Fig. 5a) aligns with the literature [40, 47, 48]. Although high stress concentrations in our models were found near the fixed boundary conditions and related to the rigid fixation of the hemipelvis (e.g., sacro-iliac joint and pubic bones, see Figs. 4 and 5). These high stress concentrations could be disregarded, because they were due to the modelling assumption of the encastre boundary conditions and not located within the region of interest around the acetabulum. Furthermore, the results of maximum von Mises stress of 56 and 90 MPa observed in the bone, as depicted in Fig. 5b and c, were comparable with the magnitudes of 102 and 162 MPa reported by Terzini et al. [21] for a hip model with a virtually-created transverse and t-shaped acetabular fracture in the bone under single leg stance loading conditions. However, it should be noted that muscle forces were not taken into account in their model, which could explain the small differences in the observed stress values [21]. Additionally, the observed maximum displacement of 1.25 mm for the patient-specific implant and 2.84 mm for the conventional implant in this study, shown in Fig. 7b and c, are consistent with previously reported values of 0.96–1.18 mm [21]. These displacements occurred at the ischium bone, comparable to the observation reported by Terzini et al. [21] for a model under single leg stance loading conditions. It should be noted, however, that muscle forces were not considered in their model, which could explain the slight differences in the observed stress values. Yildirim et al. [22] reported maximum displacement of 0.0326–0.077 mm. Their lower magnitudes than the current results of maximum displacement can be explained due to the multiple implants and incisions, as well as lower loads (~ 400 N) their model was involved. Previously reported FEA studies including posterior acetabular fracture [19, 20] simulated full pelvic bone models with virtually created fractures, thus straight lines and not from a real clinical case. Since their loading conditions were significantly lower than ours (600 N [20] and 1200 N [19] versus > 2000 N in our study), their simulations resulted in lower stress concentrations, however these were observed at similar regions.

The results of all simulations allow us to gain insights into the material behaviour under certain loading conditions of both fixation methods. By comparing the maximum von Mises stress of a part to their respective yield stress (Fig. 6), we can predict whether material failure might occur. When the maximum stress exceeds the yield stress of a material, it means that the applied force has caused the material to undergo permanent deformation, rather than returning to its original shape once the force is removed. The maximum von Mises stresses in the bone and the implant of the patient-specific model under both standing up and peak walking loading conditions remained below their respective yield stresses of 108 MPa for cortical bone [44] and 875 MPa for titanium [45]. For the bone of the conventional implant model, the maximum von Mises stresses under L-SU loading condition were all below their respective yield stress (see Fig. 6). Merely several elements of the conventional implant under L-SU were exceeding the yield stress, but this could be caused by the tie constraint of the screws. Under L-GS2 scenario, however, only the bone stresses were found to be below the yield stress, i.e., 108 MPa [44], but the stresses within the conventional implant exceeded the yield stress in two regions of the implant that were manually bent to fit the patient anatomy (see Fig. 5c-ii), reaching 1000 MPa (see star Fig. 5c-ii). This manual bending prior to surgery means that plastic deformation happened in the bent parts of the implant, indicating weaker stiffness and reduced yield stress. Given that the effect of bending was not incorporated into the material definition of the conventional implant in the current analyses, it is presumed that the stresses in the conventional implant would be even higher at these regions than the current results. This observation of high stress concentrations found in the conventional implant (Fig. 6c-i) under L-GS2, indicates that walking directly postoperatively for a patient with the aforementioned transverse acetabular fracture and a posterior fragment (OTA classification fracture 62B1.3) treated with a conventional posterior implant may cause implant failure. On the other hand, the results of von Mises stress in the patient-specific fracture model (Fig. 6) suggest safe weight-bearing postoperatively. Nevertheless, the maximum stress values in the screws were found to be 859 MPa for the patient-specific implant and 519 MPa for the conventional implant, that exceeded their yield stress of approximately 250 MPa [46] under peak walking forces (L-GS2). This detection of higher stress values in the screw models than the yield stress might be explained due to the tie constraint definition between the screws and the adjacent bones and the simplification of the screw models, resulting in potential computational artifacts and elevated stresses. This theory is aligned with the clinical observation of no screw breakages in similar surgery interventions, leading to the assumption of lower stresses in the screws in real-life scenarios. The peak stresses observed in the screws were higher in the patient-specific model when compared with the conventional model. It's worth noting, however, that these peak stress points were predominantly concentrated at the two screws situated within the posterior fragment. This placement, while feasible in the patient-specific implant, poses challenges in the conventional counterpart due to safety concerns. Therefore, direct comparison between the two screw models becomes more complex. Furthermore, the results of the displacement, i.e., 0.55 mm and 1.25 mm for the patient-specific implant model for L-SU and L-GS2, respectively, versus 0.90 mm and 2.84 mm for the model with the conventional implant, illustrated more stability for the patient-specific implant model under both standing up and walking loading conditions (Fig. 7). This is combination with the higher stresses seen in the bone and implants for both models, suggest that the patient-specific implant is biomechanically superior to the conventional implant for this type of fracture.

This computational study is not without limitations. First, FEA inherently simplify real-world scenarios to expedite computational processes and reduce anatomical complexity. The representation of screws in the model was simplified as rod with tie constraints to the bone, assuming a secure attachment to the bone. This was reported to limited effect on the outcomes (< 5%) compared to more accurate threaded models [36] or friction based interactions [37]. However, it is important to recognize that in clinical practice, factors such as reduced bone quality due to age or osteoporosis may lead to instances of poor screw grip or slippage during surgery, which are not fully accounted for with this simplified modeling. Given the young age and good bone quality of our patient, our assumption regarding good screw purchase was considered correct. In our current study, the screw was tied to both the bone and the implant, merely allowing movement at the screw between the bone and the implant, possible resulting in induced computational higher stresses, which were assumed to be computational artifacts. Since material failure at these locations is not seen in our clinical practice, further investigations should be made regarding this region of the screw. Secondly, this comparative computational study utilized generalized loading conditions for activities such as standing up and walking, sourced from existing literature [8, 40–43]. Comparing the results of either the patient-specific or conventional model to the current literature is challenging due to the variety of modelling approaches, fracture type, fixation methods and different loading conditions. While patient-specific modelling and material properties were integrated into the model, it is acknowledged that the loading conditions used may not precisely reflect individual variations in body weight, muscle forces, and the altered gait patterns post-injury. Given the comparative nature of our study, employing these generalized loading conditions was considered appropriate. However, for future investigations focusing on early postoperative weight-bearing, the incorporation of more personalized, patient-specific loading conditions is recommended to enhance the accuracy and relevance of the findings. Additionally, exploring gait patterns observed in previous patients who underwent similar acetabular surgeries, along with potential postoperative gait pattern alterations, could improve the understanding of the issue. Finally, this study provides valuable insights through a single patient case, there is need for broader quantitative evaluations encompassing inter-patient variability to comprehensively understand load transfer across fractured hemi pelvises. These studies would be essential due to the observed differences in pelvic anatomy [49], variations in acetabulum across populations [50] and the need to investigate the disparities in fracture patterns [51, 52]. This study serves as a proof-of-concept, illustrating the workflow for conducting FEA of real clinical cases in acetabular fracture surgery. Subsequent investigations involving larger cohorts and consideration of patient characteristics will be essential for addressing questions related to early postoperative weight-bearing.

Conclusion

Our study introduces a semi-automatic workflow for conducting computational analyses using finite element analysis (FEA) on real clinical cases in acetabular fracture surgery. With this method, we performed a biomechanical evaluation of patient-specific versus conventional implants in the surgical management of transverse acetabular fractures with posterior wall involvement. Primary results suggest that the patient-specific implant could withstand the forces generated by standing up and walking, and the stresses within the bone were lower as compared to the conventional implant model. This personalized approach of biomechanical fracture and implant evaluation could be translated into clinical settings to guide implant selection, compare conventional implants with innovative patient-specific ones, optimize implant designs (including shape, size, materials, and screw positions), and determine whether immediate full weight-bearing is safe to allow.

Abbreviations

ORIF

Open reduction internal fixation

THA

Total hip arthroplasty

FEA

Finite element analysis

CT

Computer tomography

DICOM

Digital imaging and communications in medicine

HU

Hounsfield units

STL

Stereolithography

C3D10

10-Node tetrahedral elements

L-SU

Loading standing up

L-GS2

Loading gait step phase 2

Appendix A

See the Table 1.

Table 1.

Number of elements per 3D part for the model with the patient-specific implant and the model with the conventional implant

	Number of elements	Number of elements
	Patient—specific implant model	Conventional implant model
Bone part 1	505.229	539.319
Bone part 2	182.359	198.590
Bone part 3	8.105	10.000
Cartilage part 1	18.072	26.341
Cartilage part 2	20.160	32.137
Cartilage part 3	2.748	2.073
Implant	407.600	57.234
Screws	94.074	47.115
Femur	91.506	30.103
Total	1.329.853	921.653

Appendix B

Author contributions

This study represents a great deal of effort, resources, and dedication of the authors. All the authors have contributed materially to the elements below: Conceptualization: M.O., Z.K., K.D., F.W., F.IJ. Methodology: M.O., Z.K., F.W., F.IJ. Formal analysis and investigation: M.O., Z.K., J.K., F.IJ. Writing—original draft preparation: M.O., Z.K., F.IJ. Writing—review and editing: F.W., K.D., J.K., J.V. Funding acquisition: J.K., F.IJ. Resources: M.O., J.V., F.IJ. Supervision: F.W., J.K., J.V., F.IJ.

Funding

This study is supported, within the Just Transition Fund program IMPACT-implants, co-financed by the European Union, with co-financing from the Ministry of Economic Affairs and Climate and coordinated by Samenwerkingsverband Noord-Nederland (SNN).

Data availability

No datasets were generated or analysed during the current study.

Declarations

Competing interests

The authors declare no competing interests.