Abstract
Traditional assays for counting bacteriophages and their lysogens are labor-intensive and perturbative to the host cells. Here, we present a high-throughput infection method in a microplate reader, where the growth dynamics of the infected culture is measured using the optical density (OD). We find that the OD at which the culture lyses scales linearly with the logarithm of the initial phage concentration, providing a way of measuring phage numbers over nine orders of magnitude and down to single-phage sensitivity. Interpreting the measured dynamics using a mathematical model allows us to infer the phage growth rate, which is a function of the phage-cell encounter rate, latent period, and burst size. Adding antibiotic selection provides the ability to measure the rate of host lysogenization. Using this method, we found that when E. coli growth slows down, the lytic growth rate of lambda phages decreases, and the propensity for lysogeny increases, demonstrating how host physiology influences the viral developmental program.
Subject terms: Bacteriophages, Phage biology, Bacteriology, Microbiology techniques
Traditional assays for counting bacteriophages and their lysogens are labor-intensive and perturbative to the host cells. Here, the authors present a high-throughput method that can be used to estimate the number of phages in a sample, by measuring growth dynamics of the infected culture in a microplate reader.
Introduction
An essential element in laboratory studies of bacteriophages is the counting of phages and of cells undergoing lysogeny. The protocols for performing these tasks typically consist of the following steps: (i) pre-infection cell growth, (ii) incubation for phage adsorption, (iii) triggering phage genome injection, (iv) post-infection cell recovery, and (v) measurement of the infection outcome1–3. The procedure involves centrifugation, incubation without aeration, and temperature changes, thus strongly perturbing the pre-infection cellular state. Consequently, the impact of host physiology on infection outcome—often of significant interest4–6—is hard to evaluate. Furthermore, measuring this outcome typically relies on plating and requires multiple dilutions to obtain countable numbers of plaques or colonies. These low-throughput steps hinder scaling up the experiments, in turn limiting the ability to perform systematic sampling of parameters of interest.
In this work, we aim to overcome these deficiencies by devising a high-throughput assay (Fig. 1) where phage infection takes place under uninterrupted cell growth in a microplate reader, and the infection outcome is monitored using the culture’s growth dynamics, read continuously from the optical density (OD). Multiple samples under different infection conditions, e.g., multiplicity of infection (MOI) or growth media, can be assayed simultaneously. The post-infection growth dynamics can be used to estimate the number of phages in an unknown sample. Interpreted using a model for the coupled kinetics of bacterial and viral populations, the measured dynamics further allow inferring the phage-cell encounter rate, latent period, and burst size. Finally, adding a single step of antibiotic selection provides the ability to measure the probability of host lysogenization. Combining these tools to characterize the infection of E. coli by phage lambda, we found that as bacterial growth slows down, the lytic growth rate of the phage too decreases, and the propensity to enter and maintain the lysogenic state increases.
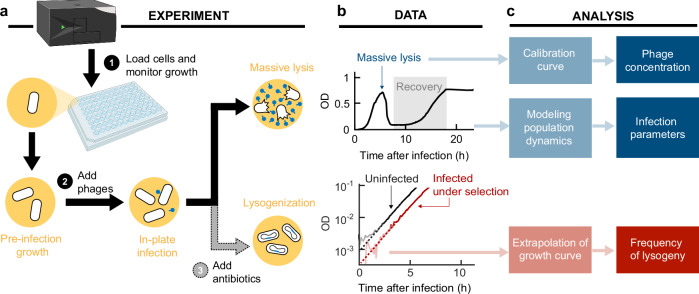
Fig. 1. A high-throughput method for counting phages and lysogenic cells in a microplate reader.
a Experimental pipeline. Bacterial cultures are grown and infected in a microwell plate reader, where the optical density (OD) is continuously measured. To count phages and infer infection parameters, no additional experimental manipulation is needed. To measure the frequency of lysogeny, a step of antibiotic selection is added. Created with BioRender.com, released under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International license. b Representative data. Growth curves of E. coli cultures, infected by (top) obligately lytic phage (λts at 37 oC), and (bottom) temperate phage (λts at 30oC) under antibiotic selection. Data shown in this panel are provided in the Source Data file. c Analysis. Top, the OD at massive lysis is used to establish a calibration curve for measuring phage concentration in an unknown sample. Middle, the entirety of the growth curve is interpreted using a mathematical model for the coupled dynamics of bacterial and phage populations, enabling the inference of infection parameters. Bottom, extrapolation of the growth curves to the time of infection allows measuring the frequency of lysogenization.
Results
The optical density (OD) at which massive lysis begins is used to measure the initial phage concentration
We developed our protocol using bacteriophage lambda, owing to the system’s incomparable knowledge base7 and our lab’s experience with it8–10. Pre-infection E. coli cultures (MG1655) were grown in LBM (LB supplemented with 10 mM MgSO4) in microplate wells at constant temperature (37 oC) and aeration, and samples of phage (λ cI857 bor::kanR, hereafter λts, obligately lytic at 37 oC, ref. 11) were directly added to the cultures during exponential phase (see “Methods”). The absorbance at 595 nm (optical density, OD) of each culture, which can be converted to bacterial concentration12,13, was recorded by the microplate reader throughout the experiment. A typical growth curve is shown in Fig. 1b. After an initial increase due to cell growth, a drop in OD is observed, reflecting the well-documented phenomenon of massive lysis14,15. Following a pause, the OD rises again and eventually reaches saturation. The measured growth curves are highly reproducible across biological repeats (Supplementary Fig. 1). Curves with the same qualitative characteristics were obtained using several lambda and E. coli strains, various growth media, as well as phages T4, T5, and P1vir (Supplementary Fig. 2; see Supplementary Table 1 for list of bacterial and phage strains used in this study).
When using the protocol above to infect bacteria of a given density by varying concentrations of phages, we observed that different initial conditions resulted in clearly distinguishable growth curves (Fig. 2a). In particular, the OD at which massive lysis begins (denoted hereafter “lysis OD”) scales linearly with the logarithm of the initial phage concentration (Fig. 2a). This linear scaling, which holds over 9 orders of magnitude, provides a simple means of counting phages: A calibration curve is first obtained using serial dilution of a phage sample with known concentration, and then used to convert the lysis OD of an unknown sample to its phage concentration; no dilution or plating is needed. A monotonic relation between lysis OD and initial phage concentration was also found in other lambda strains (both obligately lytic and temperate), other growth media, and in phages T4, T5, and P1vir (Supplementary Fig. 3), suggesting that the method for phage counting is broadly applicable.
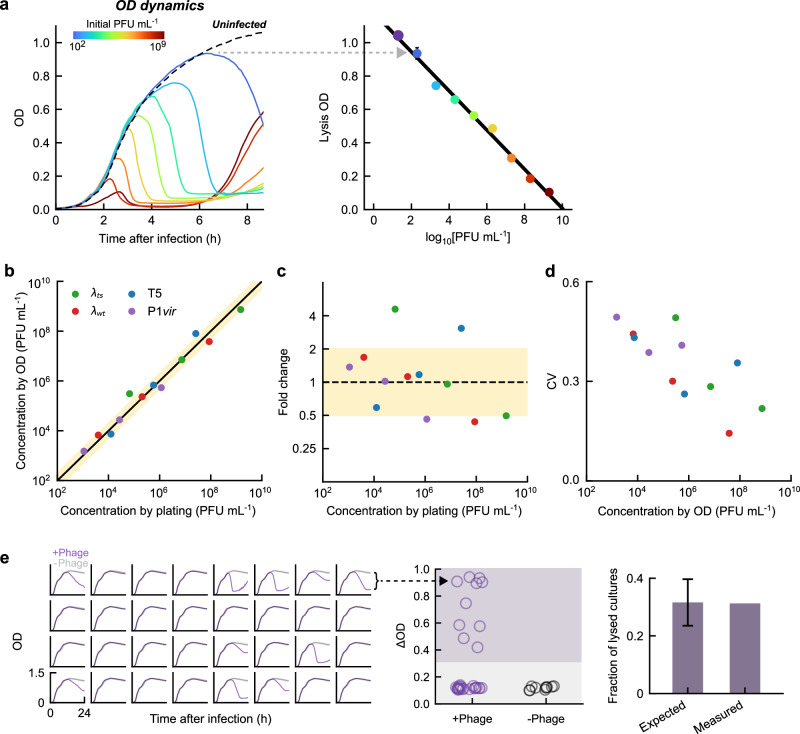
Fig. 2. The optical density (OD) at which massive lysis begins is used to measure the initial phage concentration.
a OD-based phage counting. Left, solid lines, growth curves of E. coli MG1655 cultures at 37 oC in LBM, infected by different concentrations of λts (different colors). Dashed line, growth curve of an uninfected culture. Right, the OD at which the culture lyses scales linearly with the logarithm of the initial phage concentrations over 9 orders of magnitude. Colored markers, data; error bars, standard errors of the mean (SEM) from n = 4 culture replicates. Black line, linear fit. b Comparison of phage concentrations measured using the OD-based method and traditional plaque assay. Samples of λts, λwt, T5, and P1vir (green, red, blue, and purple, respectively), each phage at three different concentrations, were enumerated using the two methods. Markers, mean from n = 2 culture replicates. Black line, y = x. Yellow shading, fold change ≤ 2 from the black line. c The accuracy of OD-based phage counting. The fold change between the phage concentrations measured using the OD-based method and the plaque assay, calculated using the data in panel (b), is plotted. Markers, mean from n = 2 culture replicates. Yellow shading, fold change ≤ 2. d The precision of OD-based phage counting. The coefficient of variation (CV) between the culture replicates (n = 2) for each sample is plotted. e Single-phage sensitivity of the counting assay. Left, purple lines, growth curves of n = 32 cell cultures, each infected by ≈0.4 PFU, at 37 oC in LBM supplemented with 0.2% maltose. In each subplot, the growth curve of an uninfected sample (averaged over n = 10 culture replicates) is shown in gray. Middle, the difference in OD between the first local maximum and the subsequent minimum for each culture (denoted ΔOD). Cultures are considered lysed if ΔOD > 0.3 (purple shading). Right, the expected fraction of wells with non-zero phage numbers, estimated from plating, and the measured fraction of lysed cultures. Error bar, SEM. All data shown in this figure are provided in the Source Data file.
To evaluate the accuracy of the method, we measured phage concentrations in samples of four different phages: temperature-sensitive lambda (λts), wild-type lambda (λ cIwt bor::kanR, hereafter λwt), T5, and P1vir, each phage at three different concentrations, using both the OD-based protocol and standard plaque counting (Fig. 2b; see “Methods”). We found that the values obtained from the OD-based method are typically within two-fold of those obtained via plating, and at worse within four-fold (Fig. 2c). The variation among culture replicates of the same sample covered a comparable range (Fig. 2d). Thus, the OD-based method can reliably distinguish unknown samples having an approximately two-fold difference in phage concentration. Both the accuracy and precision can be moderately improved by interpolating between adjacent calibration points rather than using a single line (Supplementary Fig. 4; see “Methods”). In terms of its sensitivity, the assay can detect the presence of even a single phage: When the average number of infecting phages per well was less than one, the fraction of lysed cultures matched the expected fraction of wells with non-zero phage numbers (Fig. 2e; see “Methods”). Thus, our phage counting method involves no cost in sensitivity as compared to traditional plaque plating.
A mathematical model captures the growth dynamics of bacteria and phages and allows inference of infection parameters
Motivated by the interpretive power of the lysis OD with regards to the initial phage numbers, we reasoned that additional infection parameters may be encoded by the entirety of the measured curve16. To infer these parameters, we performed infection at different MOIs and followed the bacterial OD over time. To interpret the data, we formulated a mathematical model describing the coupled dynamics of four species: nutrients (N), uninfected cells (U), infected cells (I), and phages (P), through three biological processes: cell growth, phage-cell encounters, and cell lysis17 (Fig. 3a; see “Methods” for the full model description and parameterization). We then proceeded to identify the associated kinetic schemes and parameters as follows.
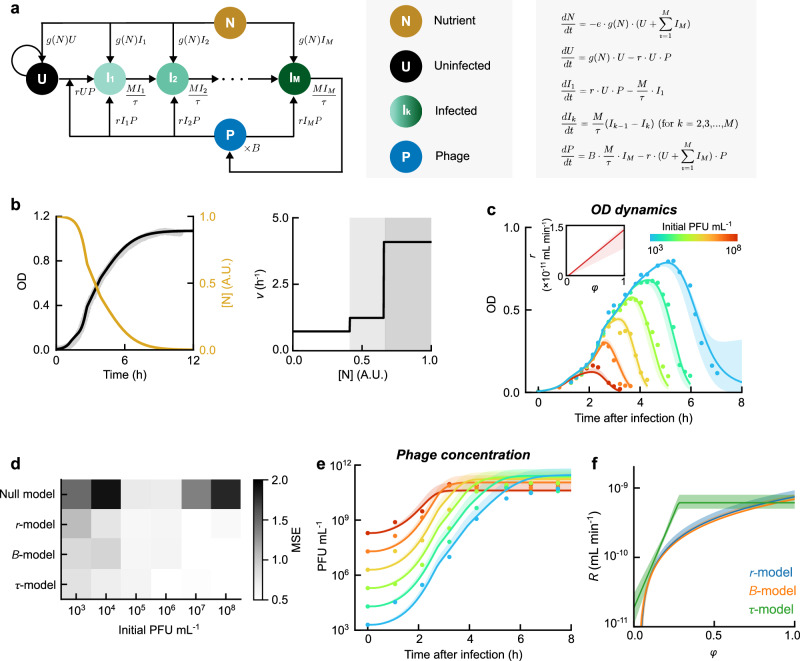
Fig. 3. A mathematical model captures the growth dynamics of phages and bacteria and allows inference of infection parameters.
a Model schematic and equations. Circles, species tracked by the model. Arrows, transitions between species. The transition rates are indicated next to the corresponding arrows. b Parameterization of bacterial growth. The OD of E. coli MG1655 cultures at 37 oC in LBM was followed over time. Left, a model describing nutrient-dependent growth (black) captures the OD dynamics of uninfected cultures (gray; n = 4 culture replicates); gold, the inferred time-dependent nutrient abundance. Right, the maximum growth rate v at different stages of nutrient consumption (white and gray shading). c A model where the rate of phage-cell encounter (r) depends on the bacterial growth rate captures the measured OD dynamics in cultures infected by lambda phages. The dependence of r on the normalized instantaneous growth rate of the host cells (ϕ) is described by: r = max(0, rk · ϕ + r0). Colored markers, data from infection at different initial phage concentrations. Colored lines, best fit of the model. Colored shading, fits by the ensemble of parameters. Inset, the fitted dependence of r on ϕ. For other model variants, see Supplementary Fig. 7. d The mean squared error (MSE) of the different model variants when fitting to the measured OD dynamics. e The model variant where r depends on the bacterial growth rate successfully predicts the phage concentration over time in the infected cultures. Colored markers, data from infection at different initial phage concentrations. Colored lines, predictions of the best-fit model; shading, predictions by the ensemble parameters. For other model variants, see Supplementary Fig. 7. f The dependence of the relative growth rate of the viral population (R) on the relative growth rate of the host cells (ϕ). Colored markers, predictions of the best-fit model; shading, predictions by the ensemble of parameters. All data shown in this figure are provided in the Source Data file.
(i) Cell growth: We assumed that the instantaneous growth rate g depends on available nutrients via the Monod equation18: g(N) = vN/(N + K), where the single species N represents the pool of growth-limiting substrates in the medium. When multiple substrates are present, as in complex media such as LBM (ref. 13.), they are consumed sequentially, resulting in several growth phases, each characterized by specific values of the maximal growth rate v and Monod constant K (refs. 19,20). These parameters were inferred from the measured growth curve of an uninfected cell culture, accounting for the reduced cell size during slower growth13,21 (Fig. 3b, Supplementary Figs. 5, 6; see “Methods”).
(ii) Phage infection: Phages and cells encounter each other with a rate constant r. Following refs. 22,23, we assumed that an infected cell goes through M intermediate states (I1, I2, …, IM) before lysis, with equal transition rates (= M/τ) from one state to the next. Consequently, the time between infection and cell lysis (the latent period) follows an Erlang distribution with mean τ and shape parameter M. The number of phages released from an infected cell (the lytic burst size) is denoted as B. For the sake of parsimony, our model ignores several documented features, including the increase in cell size following infection8, the contribution of cell debris to bacterial OD (ref. 24), and the loss of infectious phage particles due to, e.g., degradation17. These simplifying assumptions are discussed in “Methods”.
We first fitted the model to the OD dynamics measured from cultures grown in LBM and infected by phage lambda (λts) at 6 different MOIs (Fig. 3c). The change in cell size along the growth curve13,21 results in a non-constant conversion factor between OD (the measured variable) and cell density (the model output). To allow fitting, we used our parametrization of cell growth above to describe how the cell’s molar absorptivity varies as a function of nutrient abundance (“Methods”), then used this relation to convert the model output to OD and fitted this observable to the data.
The best-fit values for r, B, and τ were obtained by minimizing the mean squared error (MSE) using simulated annealing25. We then used Markov chain Monte Carlo (MCMC, ref. 26) to obtain an ensemble of parameters. An initial (“null”) model, where the three infection parameters (r, B, and τ) are held constant, failed to capture the experimental data (Supplementary Fig. 7). Motivated by reports regarding the impact of the host’s growth rate on the infective cycle of several phages27–29, we tested three alternative models (denoted “r-model”, “B-model”, and “τ-model”), in which one of the parameters (r, B, τ) is a linear function of the cell’s normalized instantaneous growth rate (ϕ = g(N)/max(g(N))). These models all captured the data similarly well (see Fig. 3c, d, Supplementary Fig. 7, and Supplementary Table 3). Model fitting thus indicates that infection parameters depend on the instantaneous growth rate. While the procedure did not pinpoint through which parameter the dependence arises, the three model variants yielded comparable estimates of the parameters (within ~3 fold range) during fast cell growth (doubling time ≲ 30 min, Supplementary Fig. 8). Furthermore, the ensemble-averaged parameters were consistent with values reported in the literature11,30,31 and with our measurements using standard phage protocols (Supplementary Fig. 9; see “Methods”).
To evaluate the predictive power of our model, we next used the inferred parameters to calculate the phage kinetics in the same cultures whose OD was measured above. We tested these predictions by sampling the cultures at 10 time points along the experiment (“Methods”) and quantifying the phage concentrations using our OD-based method (Fig. 2 above). We found that, regardless of whether r, B, or τ was set to depend on the cell’s growth rate, model predictions closely captured the phage data (Fig. 3e and Supplementary Fig. 7; see “Methods”). Thus, the uncertainty in the model structure and parameters did not diminish its predictive power. This success of our model mirrors the performance of other so-called “sloppy” models in systems biology32, where individual parameters are poorly constrained but the ensemble of parameters nevertheless leads to accurate predictions.
Utilizing a similar procedure, our model was also able to capture the OD dynamics of infected cell cultures in minimal media (M9 minimal broth supplemented with 0.4% glucose or 0.4% maltose, M9Glu and M9Mal; see Supplementary Fig. 10). When analyzing infection in these media, we observed that the best-fit parameters tended to lie on a single plane in the space of (log10r, log10B, τ) (Supplementary Fig. 10), suggesting that the three parameters were constrained beyond their individual uncertainties. Motivated by this observation, we defined the parameter , which describes the relative growth rate of the viral population (“Methods”). The parameter g*, which is inferred from the plane of conserved parameters, is of the same order as the bacterial growth rate in the experiment (“Methods”). As expected, R exhibited lower uncertainty than the individual infection parameters (Supplementary Fig. 10). Revisiting the infection in LBM, we found that the dependence of R on the instantaneous growth rate, as inferred from the three models where r, B, or τ change with the growth rate, followed a single upward trend (Fig. 3f). Furthermore, this trend mirrored the reported behavior of the viral growth rate in T4 (refs. 27,28) (Supplementary Fig. 11). The parameter R thus provides a means of interpreting our model’s results despite the uncertainty in its structure and parameters.
As noted above, the post-infection dynamics continue beyond the lytic collapse. One noticeable feature is the subsequent recovery of culture growth (Fig. 1b). This recovery is observed for all phages examined, including λts (obligately lytic at 37 oC) and the virulent phages T4 and T5 (Supplementary Fig. 2), thus does not reflect the growth of lysogenic cells (discussed below). Rather, growth recovery likely reflects the emergence of a resistant population33,34. Consistent with this interpretation, adding to our model above a first-order transition from uninfected (sensitive) to resistant cells34 captured the observed growth recovery (Supplementary Fig. 12). The inferred rate of switching into resistance, (5.5 ± 0.9) × 10−8 per min, was comparable with a previously reported value34.
Imposing antibiotic selection after a single infection cycle allows counting of lysogens
While the analysis above illuminated the lytic cycle of infecting phages, our OD-based assay also provides the means to identify when the alternative, lysogenic route is chosen. Comparing the OD dynamics of cultures infected by temperate and virulent phages, we noticed that the degree of population collapse during massive lysis was markedly different in the two cases: Cultures infected by wild-type lambda phage (λwt) showed a smaller drop in OD compared to those infected by the obligately lytic strain (λts at 37 oC, Fig. 4a). We reasoned that the higher survival in cultures infected by wild-type phage reflects the presence of lysogenic cells, which then resume growth and are immune to further infections35. This interpretation was confirmed by the antibiotic resistance (kanR, conferred by the prophages) of the surviving cells following infection by λwt (Supplementary Fig. 13). Merely counting these surviving cells is insufficient to infer the frequency of lysogeny per infection, since the number reflects the entire history of the infected culture, during which the infection conditions—e.g., growth rate and MOI—continuously change. Since these conditions are expected to influence the propensity to lysogenize8,36,37, it would be more informative to measure the occurrence of lysogeny after a single infection cycle, during which the infection parameters are well-defined.
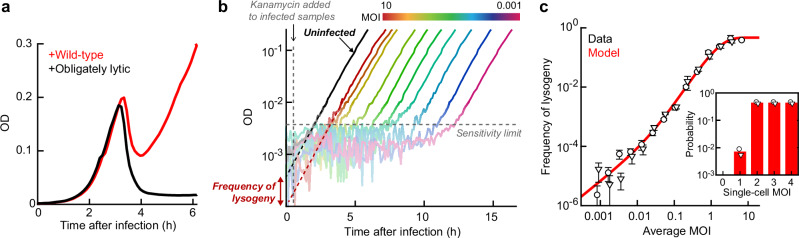
Fig. 4. Imposing antibiotic selection after a single infection cycle allows counting of lysogens.
a Difference in the population collapse between cultures infected by a temperate phage (λwt, red) and obligately lytic mutant (λts, black). Cultures of E. coli MG1655, grown at 37 oC in LBM, were both infected at multiplicity of infection (MOI) of approximately 10. b Using the growth curves under antibiotic selection to infer the fraction of cells undergoing lysogeny. Black line, OD of an uninfected culture without selection. Lines in other colors, OD of cultures infected by λts with different MOIs, under kanamycin selection. All cultures were grown in LBM at 30 oC. Dashed lines, extrapolation of the OD back to t = 0, to infer the initial cell density. c The frequency of lysogeny as a function of MOI (adjusted for the fraction of phage-infected cells). Circles and triangles, data obtained in n = 2 independent runs of the experiment; each sample in each run was measured using n = 3 culture replicates. Error bars, SEM between the culture replicates. Red line, model fit. Inset, the inferred probability of lysogenization as a function of the single-cell MOI. All data shown in this figure are provided in the Source Data file.
To achieve this goal, we again utilized the lambda strain carrying an antibiotic resistance cassette (λts, cI857 bor::kanR). Following 15 min of microplate infection at 30 oC (where λts exhibits wild-type phenotype11), the culture was diluted 250-fold into fresh medium, reducing further infection3,38. After an additional 45 min of growth, kanamycin was added, allowing only lysogenic cells (carrying the resistance-encoding prophage) to grow8,10,37 (Supplementary Fig. 14; see “Methods”). The growth curves under selective media were then extrapolated back to the time of dilution to infer the initial abundance of lysogens (Fig. 4b). To validate our experimental approach, we used it to measure the frequency of lysogeny of MG1655 by λts as a function of MOI (adjusted for the fraction of cells infected within 15 min; see “Methods”). The measured curve (Fig. 4c) recapitulates data obtained using a standard lysogenization protocol10. The data can be further used to infer the corresponding single-cell MOI response, by utilizing the Poissonian statistics of phage-cell encounters36. While similar inference was performed previously8,10, the higher throughput of the new protocol facilitates a finer sampling of MOI values, in turn constraining the single-cell relation better. Specifically, while earlier analysis indicated that infection by a minimum of two phages is required for lysogeny10,36, we were able to identify a non-zero probability of lysogenization during single-phage infection (Fig. 4c, inset). This finding may help reconcile the bulk data with the gradual MOI response observed in single-cell experiments8.
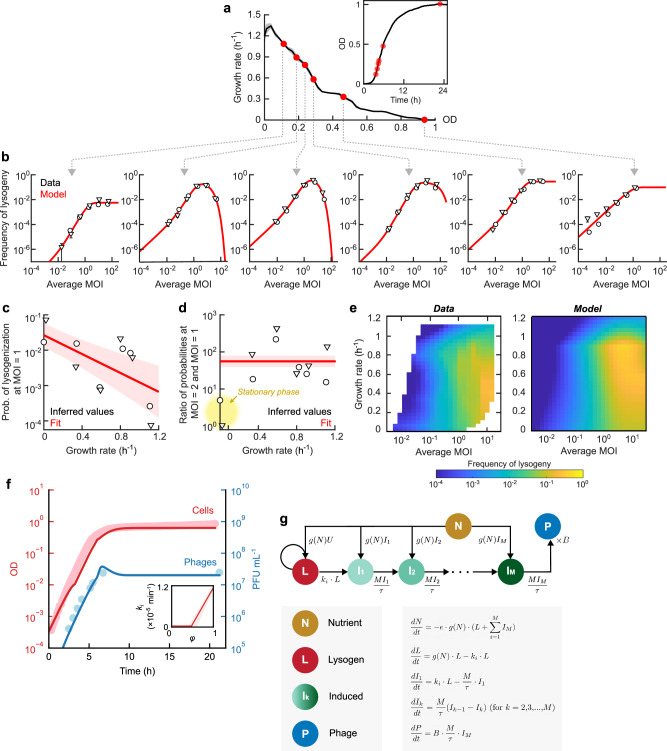
The propensity to enter and maintain lysogeny increases as bacterial growth slows down
Finally, we combined the tools devised above to investigate how the propensities at which lambda enters and exits the lysogenic state change with the host’s growth rate. To probe the probability of lysogenization as a function of growth rate, we performed infection at different stages of cell growth (Fig. 5a) and utilized the lysogen counting method (Fig. 4 above) to measure the frequency of lysogeny at varying MOIs (see “Methods”). The lysogeny-vs.-MOI curve at each growth rate (Fig. 5b) was then used to infer the single-cell propensity to lysogenize (Supplementary Fig. 15 and Supplementary Table 4; see “Methods”). Our analysis revealed that, upon infection by a single phage, the propensity to lysogenize decreases approximately exponentially with growth rate (Fig. 5c). This finding is consistent with previous reports of increased lysogenization in stationary37,39 and starved cells36,40, but places them in the broader context of growth-rate dependent lysogenization—often presumed41 but (to the best of our knowledge) not previously shown. Upon co-infection by two phages, the probability of lysogenization in growing cells increases 40–80 fold (Fig. 5d), suggesting that viral self-counting drives the cell fate choice10. However, this feature is absent in stationary cells, where higher MOI does not significantly increase lysogenization (Fig. 5d and Supplementary Fig. 16). Utilizing the inferred single-cell lysogenization curves allowed us to reproduce the experimentally measured “fate diagram”10 depicting the population-averaged frequency of lysogeny as a function of MOI and bacterial growth rate (Fig. 5e).
Fig. 5. The propensity to enter and maintain lysogeny increases as bacterial growth slows down.
a Performing infection at different growth rates. Black line, the growth rate, as a function of OD, of an uninfected culture of E. coli MG1655 grown at 30 oC in LBM; gray shading, SEM from n = 3 culture replicates. Red markers, the growth rate at which lambda phages (λts) were added. Inset, the growth curve of the same culture. b The frequency of lysogeny as a function of MOI (adjusted for the fraction of phage-infected cells), measured at different bacterial growth rates. Circles and triangles, data obtained in n = 2 independent runs of the experiment; each sample in each run was measured using n = 2 culture replicates. Error bars, SEM between the culture replicates. Red lines, model fits. c The inferred probability of lysogenization in cells with MOI = 1 as a function of growth rate. Markers, fitted values from the two independent runs of the experiment (shown in panel b). Red line, exponential fit, serving as a guide to the eye. Red shading, fitting uncertainty obtained by bootstrapping. d The inferred ratio of lysogenization probabilities at MOI = 2 and MOI = 1, as a function of growth rate. Markers, fitted values from the two independent runs of the experiment (shown in panel b). Red line, linear fit, serving as a guide to the eye. Red shading, fitting uncertainty obtained by bootstrapping. Stationary cells (yellow highlight) do not exhibit an increase in the probability of lysogeny between MOI = 1 and MOI = 2. e The frequency of lysogeny as a function of MOI and growth rate. Left, interpolated experimental data. Right, model prediction. f The OD (red) and the concentration of free phages (blue) during growth of lysogens. MG1655 λts was grown at 30 oC in LBM supplemented with 0.2% glucose. Markers, experimental data. Lines, fit of a model where the rate of phage-cell encounter (r) depends on the bacterial growth rate. Inset, the inferred rate of spontaneous induction (ki) as a function of the normalized instantaneous bacterial growth rate (ϕ). For other model variants, see Supplementary Fig. 17. g Schematic and equations of the model used for capturing the data in panel (f). Circles, species tracked by the model. Arrows, transitions between species. The transition rates are indicated next to the corresponding arrows. All data shown in this figure are provided in the Source Data file.
After examining the choice to enter lysogeny, we aimed to identify how the reverse process, i.e., spontaneous induction where lysogenic cells stochastically switch to the lytic pathway11,41, depends on the bacterial growth rate. To that end, we tracked the growth of lysogenic cells over 24 h (MG1655 λts, grown at 30 oC in LB supplemented with 10 mM MgSO4 and 0.2% glucose, the latter added to reduce phage adsorption to cells14,42). At various time points, corresponding to different bacterial growth rates, phages were extracted11 and enumerated using our phage counting method (Fig. 2 above; see “Methods”). The coupled growth dynamics of lysogenic bacteria and released phages (Fig. 5f) were interpreted using a mathematical model (Fig. 5g) analogous to that in Fig. 3 above. Here, we modeled spontaneous induction as a first-order transition from lysogenic cells (L) to induced cells (I1) with rate constant ki. The latent period was modeled as before, with induced cells undergoing several intermediate states (I2, …, IM) until lysis (see “Methods” for the full model, and Supplementary Table 5 for parameter values). The model was able to capture the OD and phage dynamics (Fig. 5f and Supplementary Fig. 17) under the assumption that the spontaneous induction rate is a linear function of the growth rate, increasing from approx. 0 in slow-growing cells (doubling time ≥ 70 min) to ≈1.1 × 10−5 induction events per minute for early-exponential cells (doubling time ≈ 30 min) (insets of Fig. 5f and Supplementary Fig. 17). The latter value is similar to the estimate by ref. 11, but, as in the case of lysogenization above, our inference generalizes it across the entire growth curve of the culture. The inferred trend is also consistent with the recent report that the rate of spontaneous SOS activation, the driver of lytic induction11, increases with growth rate43.
Discussion
The simple pipeline presented here (Fig. 1 above) enables the counting of bacteriophages in unknown samples and the inference of phage-cell encounter rate, latent period, burst size, and frequencies of entering and exiting dormancy. Streamlining the infection protocol necessitated a removal of several steps commonly included, in particular, cell concentration via centrifugation to accelerate phage adsorption, and a temperature upshift to synchronize phage entry1–3. Despite these shortcuts, the infection procedure yielded reproducible dynamics, which were interpretable through the use of mathematical modeling as described above. The simplified procedure has the added benefits of reduced perturbation to host physiology and the capacity to systematically scan infection parameters in a high-throughput manner.
Our phage counting method (Fig. 2 above) is logarithmic in nature, in that the measured feature (lysis OD) reflects the logarithm of the initial phage concentration. We consider this an advantage: When using traditional plaque counting to quantify an unknown phage sample, one has to plate serial dilutions of the sample to arrive at a countable number of plaques per plate1–3. This serial dilution is a bottleneck in the quantification of samples, one that our approach overcomes by offering a dynamic range of multiple orders of magnitude (e.g., 9 for lambda in LBM, Fig. 2a). If a more precise measurement is needed, one can conceivably combine the two approaches, using the OD-based method to infer the order of magnitude and to choose the appropriate dilution for plaque counting.
Interpreted using a model for the coupled kinetics of bacterial and viral populations, our data indicates a correlation between the lytic growth rate of the viral population and the growth rate of the bacterial hosts (Fig. 3 above). The finding that viral growth rate is higher in faster-growing cells suggests that the physiology of the host constrains viral development, consistent with previous reports in phage T4 (refs. 27,28) (Supplementary Fig. 11). Our current measurements for lambda were done under conditions where the bacterial growth rate changes over time. We therefore cannot rule out a possible dependence on the growth history of the culture, arising through, e.g., the residual activity of metabolic pathways used by the cells in response to previous nutrient substrates44, or the accumulation of secreted signaling molecules and metabolites45–47, which may change the chemical properties of the growth medium over time48,49.
Beyond the characterization of lytic reproduction, our analysis of the rates for entering and exiting lysogeny suggests that viral dormancy is prioritized as the growth of the bacterial host slows down: during infection, the probability of lysogenization increases in slower-growing cells (Fig. 5c); once lysogeny is established, slower-growing cells exhibit a lower rate of spontaneous induction into the lytic state (Fig. 5f). As above, our measurements cannot distinguish between the effect of the instantaneous growth rate and the cumulative growth history of the culture. However, the idea that slow growth promotes lysogeny coheres with the accepted view for lambda41 and other temperate phages6, premised on the rationale that slower growing cells would have reduced capacity for a successful lytic reproduction. The data presented here provides a quantitative test for this narrative. In terms of its mechanistic underpinnings, multiple regulatory interactions feed from the signaling molecules encoding information on cellular growth (ppGpp, cAMP), through cellular proteases (FtsH, Lon, RecA) and ribonucleases (RNase III), into the phage decision circuitry7,50. Our data suggests that, as long speculated, these myriad regulatory interactions enable the phage to sense and respond to its host’s growth rate, providing yet another example for temperate phages’ ability to process information in order to choose their developmental path optimally5,51,52.
The dominant feature in the growth curves of infected cultures was a single peak followed by massive lysis, a feature whose quantitative characteristics were used for the inference of infection parameters. However, more complex dynamics were observed, reproducibly, under certain infection conditions. Whereas some of the additional growth features—the survival of lysogens, and the growth recovery of resistant cells—were addressable by our model, other features remain outside it. Notably, multiple cycles of growth and lysis were observed following infection at high concentrations of lambda, T4, and T5 (Supplementary Fig. 18). These repeated cycles suggest a transient cellular state of insusceptibility to phage infection34,53,54, and highlight the potential role of population heterogeneity, a subject that merits further investigation. We expect even richer dynamics to emerge under infection scenarios that involve additional phage-host interactions, such as phage-mediated quorum sensing55–57, or, conversely, bacterial anti-phage systems58–60. We believe that the approach presented here, combining high-throughput infection with modeling-based interpretation, will prove valuable in illuminating such cases.
Methods
Bacterial strains and phages
All strains used in this study are listed in Supplementary Table 1. In most experiments involving phage lambda, we used a temperature-sensitive phage strain, λ cI857 bor::kanR, hereafter λts, and an isogenic strain without the cI mutation, λ cIwt bor::kanR, hereafter λwt. Phages carrying the cI857 allele cannot establish or maintain lysogeny at 37 °C or above11. We therefore used λts at 38 oC ± 0.5 °C as an obligately lytic variant of lambda, and λwt as the corresponding wild-type variant. Both phage strains also harbor a kanamycin resistance cassette, which was used to select for lysogenic cells. Other phages (T4, T5, and P1vir) were used as described in “Phage preparation” below.
Growth media and conditions
Growth media
The medium used in most experiments was LB (Lennox formulation)2, comprising (w/v) 1% tryptone (BD Biosciences), 0.5% yeast extract (BD Biosciences), and 0.5% NaCl (Fisher Scientific); the pH was adjusted using 1 mM NaOH (Fisher Scientific). LBM is LB supplemented with 10 mM MgSO4 (Fisher Scientific). LBMM and LBGM are LBM supplemented with 0.2% maltose (Fisher Scientific) or 0.2% glucose (Fisher Scientific)11. In experiments involving T5 and P1vir phages, LB was supplemented with 1 mM or 5 mM CaCl2 (Fisher Scientific), respectively61,62.
Other media used in this study are as follows. Tryptone broth (TB) is composed of (w/v) 1% tryptone and 0.8% NaCl, and TBM is TB supplemented with 10 mM MgSO4. Minimal media are based on the M9 minimal salts broth media without a carbon source (Teknova). M9Mal and M9Glu are M9 broth supplemented with 0.4% maltose or 0.4% glucose, respectively. For the plaque formation assay10,63, NZYM medium was prepared using (w/v) 2.2% NZYM powder (Teknova); the pH was adjusted using 10 mM NaOH.
Agar plates and soft agar were prepared by supplementing the liquid medium with (w/v) 1.5% and 0.7% agar (BD Biosciences), respectively10.
Growth conditions
To prepare overnight cell cultures, fresh colonies on LB agar plates (supplemented with 50 μg mL−1 kanamycin, Fisher Scientific, for lysogenic strains) were inoculated into 2 mL of medium (as specified for each experiment below) in 14 mL round-bottom test tubes (Falcon). Overnight cultures were grown for approx. 16 h at 30 oC with aeration (220 rpm shaking). The overnight cultures were diluted into experimental (“overday”) culture as described in each experiment below.
Measuring the optical density
Throughout this work, we used two different instruments to measure the optical density (OD): (i) When growing cells in bulk cultures, a SmartSpec Plus spectrophotometer (Bio-Rad) was used to measure the OD at a wavelength of 600 nm and a path length of 1 cm. The corresponding values are denoted below as ODspec. (ii) During growth in the plate reader, the instrument (TECAN Infinite F200 Pro or TECAN M Nano) measured the OD at 595 nm and a path length determined by the depth of liquid in the well (≈ 3 mm in our experiments). We denoted these values, used in the analysis of growth dynamics, simply as “OD”. The two measurements differ by a scaling factor, ODspec ÷ OD = 4.51 ± 0.05.
Phage preparation
Preparing lambda phages
We followed the protocols in refs. 11,40 to produce crude phage lysates. For the temperature-sensitive λts, we performed a heat induction of the lysogens. Briefly, an overnight culture of MG1655 λts was diluted 1000-fold into LBGM in a baffled Erlenmeyer flask, and incubated at 30 oC with mild shaking (180 rpm). Upon reaching ODspec ≈ 0.4, the culture was incubated in a water bath at 42 oC with 180 rpm shaking for 15 min, then at 37 oC with 180 rpm shaking for 1 h until ODspec dropped below 0.05. For λwt, we performed a chemical induction using mitomycin C (MMC, Fisher Scientific). Briefly, an overnight culture of MG1655 λwt was diluted 1000-fold into LBGM in a baffled Erlenmeyer flask, and incubated at 37 oC with mild shaking (180 rpm). At ODspec ≈ 0.4, 10 μg mL−1 of MMC was added to the culture. The flask was wrapped in foil, and incubation (37 oC, 180 rpm shaking) was resumed for 2–3 h. Lysis was determined to be complete when the ODspec dropped below 0.2.
Following either heat or MMC induction, the lysed culture was supplemented with 5% chloroform, and incubated at room temperature (RT) for 15 min. The lysate was centrifuged at 4000 × g for 10 min at 4 oC to pellet the debris, and the clear supernatant was extracted, supplemented with 0.3% chloroform, and stored at 4 oC until use. Standard plaque formation assays were performed, using NZYM agar, to determine the phage titers (≈1010 plaque-forming units, PFU mL−1).
When higher titers were required, we used the crude induction lysates (produced using heat induction) to perform phage precipitation using polyethylene glycol (PEG), followed by resuspension of the phage pellets in SM buffer (Teknova) as described in ref. 64. These additional steps increased the phage titer to ≈ 1011 PFU mL−1.
Preparing other phages
Phages T4, T5, and P1vir were produced by infecting cell cultures, as described in ref. 2. Briefly, cultures of MG1655 were grown at 37 oC in LB (supplemented with 1 mM CaCl2 for T5, as described in ref. 61, or 5 mM CaCl2 for P1vir, as described in ref. 62). When the culture reached ODspec ≈ 0.2, approximately 107 PFUs of T4, T5, or P1vir were added to the cultures. The infected cultures were incubated at 37 oC without shaking for 15 min, then shaking was resumed until lysis was observed (approximately 3–4 h). Chloroform treatment and centrifugation were then performed as described for lambda phages.
Microplate-based infection assay for measuring phage concentrations
Calibration curves using known phage concentrations
To perform the calibration assay for infection by λts in LBM, a 10-fold serial dilution of λts phages, with concentrations spanning from 6 × 102 PFU mL−1 to 6 × 1011 PFU mL−1, was prepared in SM buffer. An overnight culture of MG1655 in LB was diluted 1:500 into LBM in a baffled Erlenmeyer flask. The culture was then grown at 37 oC with 220 rpm shaking. Upon reaching ODspec ≈ 0.1, the culture was diluted 1:10 into LBM and aliquoted into a clear 48-well flat-bottom microplate (COSTAR), with each well containing 500 μL of culture. As negative controls for cell growth, some wells containing blank LBM were included in the microplate. The microplate was then placed into the plate reader, incubated at 38 oC with shaking (orbital mode, 1 mm amplitude), and the OD was recorded every 5 min. After 30 min of growth in the plate reader, 10 μL of phages at different concentrations were added to each well. We included two replicates for each phage concentration. As negative controls for phage infection, we included two uninfected cultures to which blank SM buffer was added. After phage addition, incubation was resumed for at least 12 h.
The average OD in the wells with blank LBM was first subtracted from all OD measurements. Next, we identified the first local maximum in the growth curve for each culture, which, for infected cultures, corresponds to the onset of massive lysis. We term this OD value the “lysis OD”. For lambda phages infecting cells in LBM medium, the relationship between the lysis OD and the logarithm of the initial phage concentration is approximately linear (Fig. 2a). The calibration curve was obtained by fitting a linear equation:
| 1 |
where y is the lysis OD and x is the logarithm base 10 of the initial phage concentration in PFU mL−1.
We also performed the calibration assay for infection in other growth media, other lambda strains, and other phages. For infections in complex media (LB, LB supplemented with CaCl2, and TBM), the calibration curves were analyzed using Eq. (1). For infections in minimal media (M9Glu and M9Mal), the lysis OD was found to be approximately a power function of the initial phage concentration. The calibration curve was obtained by fitting the following equation:
| 2 |
where y and x are defined the same way as in Eq. (1). All calibration curves under different infection conditions are shown in Supplementary Fig. 3.
Measuring phage concentrations in unknown samples
For a sample with unknown phage concentration, the infection protocol was performed, and the lysis OD was identified, using the procedure described above. The calibration curve (Eq. (1)), obtained using the same host strain, phage strain, and infection condition, was used to calculate the unknown phage concentration corresponding to this lysis OD.
Measuring phage concentrations in samples extracted from infected cultures
To measure the phage concentrations in the infected cultures during cell growth (Fig. 3e), we extracted phages as follows. At each time point (before phage addition, then at 1, 2, 3, 4, 5, 6, 7, 8, and 20 h after phage addition), 5 µL of the infected cultures were taken from the wells and diluted into 495 μL of LBM media (a 1:100 dilution). Then, 25 μL of chloroform (final concentration, 5%) was added to each culture, followed by vortexing for 10 s, to lyse the cells11. Phage lysates were stored at 4 oC, and the phage counting procedure was used to measure the phage concentration in each sample.
Quantifying the precision and accuracy of the phage counting method
Sample preparation and infection
To quantify the precision and accuracy of our phage-counting method, we subjected samples of four different phages (λts, λwt, T5, and P1vir), each phage at three different concentrations, to a single-blind test. Here, one person prepared the unknown samples by diluting the phage stocks in SM buffer to reach different target concentrations, and used the plaque formation assay to measure the phage concentrations in these samples. If the target concentration was more than approx. 104 PFU mL−1, duplicate dilution series (in SM) were prepared to reach approx. 104 PFU mL−1. Each dilution series, or the original unknown sample if there was no further dilution, was plated on replicate agar plates, and the number of plaques was counted to calculate the phage concentration. Another person received the unknown phage samples and performed the OD-based measurement to measure the phage concentrations. The concentration of each unknown sample was measured using duplicate cultures, and the calibration curve (of the same phage, bacterial host, and growth condition) was obtained using the same microplate as the unknown samples.
Data analysis
The comparison between the plaque-based and OD-based counts, the latter inferred using a single fitted line through the lysis OD values of all calibration samples (Eq. (1)), is shown in Fig. 2b. To evaluate the accuracy of the method (Fig. 2c), we calculated the fold change between phage concentrations measured using the OD-based method and the plaque assay:
| 3 |
To evaluate the precision of the method, for each unknown sample, we quantified the coefficient of variation (CV) of the OD-based phage counts between the replicate cultures. This result is shown in Fig. 2d.
In Supplementary Fig. 4, we present the accuracy and precision of the method following an alternative analysis, where we interpolated between the two points on the calibration curve that immediately precede and succeed the lysis OD of each unknown sample, and used this interpolation to infer the phage concentrations in the sample.
Detecting single phages using the OD-based method
Sample preparation and infection
A solution of λts was diluted in SM to reach a concentration of ≈104 PFU mL−1. The concentration was confirmed using a plaque assay on NZYM agar plates10. Immediately before infection, the phage solution was further diluted 1:200 in SM (thus reaching 38 PFU mL−1, or 0.38 PFU in 10 μL on average—measured using the plaque assay). Cells were cultured in LBMM and aliquoted into a 48-well microplate as described above in “Microplate-based infection assay for measuring phage concentrations”. After 30 min of growth in the plate reader, 10 μL of phage solution (containing, on average, 0.38 PFU) were added to each culture well. We included 32 replicates of cultures with phages and 10 replicates without phages. After phage addition, incubation was resumed, and the OD was recorded for 48 h.
When the same assay was performed in LBM, we noticed that the fraction of lysed cultures (analyzed as described below) was lower than our theoretical expectation. We reasoned that the cultures in LBM had entered the stationary phase before massive lysis occurred. To extend the range of OD over which the cultures can grow before saturation, we therefore used LBMM in this assay instead.
Predicting the expected number of lysed cultures
We denoted the average number of phage particles in 10 μL as λ (dictated by the experimental design). The number of phage particles in each of the 10 μL aliquots (X) is expected to follow the Poisson distribution:
| 4 |
The probability that there is a non-zero number of phage particles in that aliquot volume, π0, is:
| 5 |
with λ = 0.38, π0 = 0.316.
Among N independent cultures, the number of cultures containing a non-zero number of phage particles (Y) follows the Binomial distribution:
| 6 |
Using Eq. (6), we calculated the expected number of Y in N = 32 independent cultures. The expected fraction of lysed cultures, Y/N, and the SEM obtained from bootstrapping, are shown in Fig. 2e, right.
Identifying lysed cultures
Massive lysis was identified as described above in “Microplate-based infection assay for measuring phage concentrations”. We note that for uninfected cells over 48 h of growth, the OD displayed a minor decline during the stationary phase, presumably due to cell death65. However, this decline is not as drastic as that in massive lysis (Fig. 2e, left). Therefore, to quantitatively distinguish massive lysis from the death phase, we calculated the difference in OD between the first local maximum and the subsequent minimum for each culture (denoted ΔOD). For the infected samples, the values of ΔOD fell into two distinct groups (Fig. 2e, middle). One group (ΔOD < 0.3, arbitrarily chosen) was similar to the uninfected cultures, and was classified as unlysed. The other (ΔOD ≥ 0.3) was recorded as lysed. The measured fraction of lysed cultures (10 out of 32 cultures) is shown in Fig. 2e, right.
Performing a binomial test
We defined π0 as in Eq. (5), and π as the observed probability that the 10 µL phage aliquot leads to massive lysis. If a single phage leads to massive lysis, π should be equal to π0. We performed a two-tailed binomial test66 to test the following hypothesis: H0: π = π0. Denoting the observed number of lysis events in N infected cultures as k, we calculated the two-tailed p-value as follows:
| 7 |
where was defined as . With N = 32 and k = 10, the calculated p-value was 0.849; as a result, we accepted the null hypothesis and concluded that our assay can detect single phages at the expected efficiency.
Modeling the OD dynamics of phages and bacteria during infection
We aimed to capture the population dynamics, up to but excluding the recovery of bacterial growth (Fig. 1b). Following refs. 17,34, we used a set of ordinary differential equations (ODE) to describe the dynamics of nutrient resources (N), uninfected cells (U), infected cells (I), and free phages (P). The assumptions of the model, shown in Fig. 3a, are summarized below.
- Cell growth: As in ref. 18, we assumed the instantaneous growth rate of uninfected cells g(N) depends on the nutrients (N), in the following manner:
where K is the Monod constant and v is the maximal growth rate under a given nutrient.8 Phage-cell encounter: We assumed that phages (P) and cells (U and I) encounter each other with a second-order rate constant r The encounter of phages and uninfected cells (U) results in the production of infected cells (I) (ref. 17).
Nutrient consumption: The infected cells (I) are assumed to consume nutrient resources even if they do not grow and divide. Therefore, the rate of resource consumption is proportional to the combined densities of uninfected and infected cells, the instantaneous growth rate g(N), and a conversion efficiency parameter e that relates cell growth to nutrient consumption17.
Cell lysis: We assumed the infected cells go through M intermediate states (I1, I2, …, IM) before lysis, and the transition rates from one state to the next are identical (M/τ) (refs. 22,23). The exit from the last state (IM) leads to cell lysis. Therefore, the time between infection and cell lysis (the latent period) follows an Erlang distribution with mean τ and shape parameter M. The larger M is, the narrower the latent period distribution.
Phage release: The number of phages released upon cell lysis (burst size67) is denoted as B.
Taken together, the population dynamics of nutrient resources, bacterial cells, and free phages obey the following equations (Eq. (9)):
| 9 |
Parameterization of cell growth
We assumed nutrients are consumed sequentially19,20 through X phases. In each phase (i), cell growth is controlled by one limiting substrate via substrate-specific vi and Ki, where i = 1, 2, …, X. The transition between these phases is defined by the thresholds θi, where θ0 = 1 (the first growth phase with maximum nutrient), and θX (the final growth phase) = 0. When N decreases below θi, the substrate i is considered exhausted, and cells begin to consume substrate i + 1. We also assumed that the conversion factor from cell growth to nutrient consumption is e. Therefore, the dynamics of nutrients and cells in the absence of infection are described by the following equations (Eq. (10)):
| 10 |
We scanned X from 1 to 3, and fitted the model above to the OD dynamics of uninfected cultures with initial conditions N(0) = 1 and , where OD(t) is the measured OD of uninfected cultures at time t and ε(t) is the relative molar absorptivity of the cell (normalized for the optical path length). Fitting was performed by minimizing the following objective function using a simulated annealing algorithm25:
| 11 |
where is the model-predicted density of uninfected cells and T0 is the set of time points where OD was measured.
For minimal media (M9Glu and M9Mal), we note that cell growth took place at an approximately constant growth rate up to massive lysis, irrespective of the initial phage concentration (Supplementary Figs. 3h, i). Therefore, we assumed a constant ε0 = 10−9 CFU−1 mL (ref. 13) over time, where OD = 1 corresponds to 109 colony-forming units per mL (CFU mL−1). As expected, the growth in M9Glu and M9Mal was describable using X = 1, with a single set of v and K (Supplementary Fig. 6). The fitted values of v and K are shown in Supplementary Table 2, and the errors were obtained from repeated runs of simulated annealing (N = 10).
For LB-based media (i.e., LBM, LBGM), we expected ε to change with the cell size21, hence, with the growth rate13. Since in our model, the growth rate is a function of the nutrient concentration N, we chose to describe ε as a function of N. To do so, we first utilized the data by Sezonov et al. 13, which measured ODspec and cell concentration for E. coli cells along the growth in LB at 37 oC (Supplementary Fig. 5a). We obtained ε(t) by converting ODspec to OD (as described above in “Measuring the optical density”) and dividing it by the measured cell concentration at the corresponding time point. Then, we fitted Eq. (11) to the data and found that X = 3 well captures the growth in LBM (Fig. 3b) and growth in LBGM up to and including the first plateau in OD (Supplementary Fig. 6). The fitted values of vi, Ki and θi are shown in Supplementary Table 2, and the errors were obtained from repeated runs of simulated annealing (N = 10). By combining ε(t) (Supplementary Fig. 5a) and the nutrient profile N(t) (obtained from the growth model, Supplementary Fig. 5b), we obtained a relation between ε and N (i.e., ε(N)), which was approximated by a polynomial model (Supplementary Fig. 5c).
Parameterization of the number of intermediate infected states (M)
We sought to find the optimal value of M (see Eq. (9)) to model the infection dynamics by phage lambda. Considering a population of synchronously infected cells, we described the dynamics immediately after the infection using the following equation:
| 12 |
where Ii describes the different states of the infected cells between phage-cell encounter and cell lysis (i = 1, 2, …, M).
To estimate M, we fitted the mean latent period τ and burst size B to the phage dynamics from a one-step experiment, where cells were synchronously infected (Supplementary Fig. 9). In this experiment, the phage concentrations measured at each time point, denoted as PFU(t), reflect both the free phages and the infected cells, both of which formed plaques. Therefore, the initial conditions for the model-predicted species are I1 = PFU(0), Ii(0) = 0 for i = 2, 3, …, M, and P(0) = 0. We then scanned M from 1 to 16 (Supplementary Fig. 19a); for each M, we minimized the following objective function using simulated annealing:
| 13 |
where To is the set of time points where phage concentrations were measured, is the predicted phage concentration, and is the predicted infected cell concentration.
As shown in Supplementary Fig. 19b, as M becomes larger, the residual becomes smaller, and the fitted B and τ converge. For the sake of saving computational time, we chose M = 5 for all the following models. We confirmed that increasing M value results in no significant changes to the model inference (see “Examining alternative model assumptions” below).
Parameterization of phage-cell encounter rate, latent period, and burst size
General strategy
After cell growth has been parameterized and M has been chosen, the remaining parameters in Eq. (9) are the phage-cell encounter rate r, latent period τ, and burst size B. This section describes the procedure of inferring these parameters for models where they are held constant (i.e., for infection in minimal media, and the null model for infection in LBM). For the case where r, B, or τ changes with bacterial growth rate, the details are described below in “Characterizing the dependence of infection parameters on growth rate”.
Briefly, to estimate r, B, and τ, we performed simulated annealing to find a best-fit parameter, followed by a Markov Chain Monte Carlo (MCMC) search to obtain an ensemble of parameters. Below are the details.
Obtaining the best-fit parameters
We fitted Eq. (9) to the OD dynamics of cultures infected at different MOIs. For infection in LBM, the OD dynamics of cultures infected at six different phage concentrations (1.2 × 108, 1.2 × 107, 1.2 × 106, 1.2 × 105, 1.2 × 104, and 1.2 × 103 PFU mL−1) were used for fitting. For infection in M9Glu, the OD dynamics of cultures infected at five phage concentrations (7.4 × 106, 7.4 × 105, 7.4 × 104, 7.4 × 103, and 7.4 × 102 PFU mL−1) were used for fitting. For infection in M9Mal, the OD dynamics of cultures infected at six phage concentrations (7.4 × 106, 7.4 × 105, 7.4 × 104, 7.4 × 103, 7.4 × 102, and 7.4 × 101 PFU mL−1) were used for fitting.
We used j to index the infection conditions (i.e., initial phage concentrations), and the system was initialized with N(0) = 1, , Ii (0) = 0 for i = 1, 2, 3,…, M. Fitting was then performed by minimizing the following objective function using simulated annealing:
| 14 |
where J is the total number of infection conditions, , and are the model-predicted dynamics of nutrient, uninfected cells and infected cells for infection condition j, and ODj(t) is the measured OD dynamics. To,j is the set of time points where the measured OD concentrations were used for fitting, and |To,j| is the total number of time points. To reduce the computational burden, for infection by λts in LBM, only the data points whose second-order time-derivative (approximated using the centered finite differences) is greater than 3.5 × 10−5 were used in fitting. The values of the best-fit parameters for all infection conditions are listed in Supplementary Table 3.
Obtaining the ensemble of parameters
We then performed an MCMC search using the Python package ‘emcee’, employing a uniform prior (the range of the prior is described in Supplementary Table 3) and initializing from the best-fit values. Each chain was run with 100 walkers over 6000 iterations, with a burn-in period of 3300-iterations. The chains were further thinned, and every 20th sample was retained. The resulting chain contained 13,500 samples for each parameter, and the distributions are shown in Supplementary Fig. 8 (for infection in LBM) and Supplementary Fig. 10 (for infection in minimal media). We further sampled 200 instances from the resulting chains, while ensuring that each parameter fell within the 95% confidence interval of its marginal distribution. The resulted samples constitute the ensemble of parameters, which was used for the following purposes:
Demonstrating the agreement of the model with the data. See Supplementary Fig. 7a for modeling OD dynamics in LBM with the null model and Supplementary Fig. 10a, b for modeling OD dynamics in minimal media.
Predicting the phage dynamics. See “Predicting phage dynamics for infection in LBM” below for method description, and Supplementary Fig. 7d for phage dynamics prediction in LBM with the null model.
Characterizing the relative growth rate of the viral population (R). See “Characterizing the relative growth rate of the viral population” below for method description and Supplementary Figs. 10e–h for characterizing R for infection in minimal media.
The values for the best-fit parameters, the range of the prior, and the range of the ensemble of parameters for the above models are provided in Supplementary Table 3.
Characterizing the dependence of infection parameters on growth rate
As shown in Supplementary Fig. 7a, when assuming a constant phage-cell encounter rate r, latent period τ, and burst size B, the model failed to capture the OD dynamics for infection in LBM. Motivated by previous reports regarding the impact of host’s growth rate on the infection cycle of several phages27–29, we tested three alternative models (denoted as “r-model”, “B-model”, and “τ-model”), in which one of the parameters (r, B, τ) is a linear function of the cell’s normalized instantaneous growth rate (ϕ = g(N)/max(g(N))). For LBM, max(g(N)) = v1/(1 + K1) = 0.035 min−1. The specific model assumptions are listed below:
r-model: B and τ are constant, and r = max(0, rk · ϕ + r0), where rk and r0 are the slope and intercept of the linear function.
B-model: r and τ are constant, and B = max(0, Bk · ϕ + B0), where Bk and B0 are the slope and intercept of the linear function.
τ-model: r and B are constant, and τ = max(20, τk · ϕ + τ0), where τk and τ0 are the slope and intercept of the linear function.
We fitted each model to the OD dynamics of cultures infected in LBM and obtained the ensemble of parameters using the method described above in “Parameterization of phage-cell encounter rate, latent period and burst size”. The fitting results are shown in Fig. 3c (for the “r-model”), Supplementary Fig. 7b (for the “B-model”) and Supplementary Fig. 7c (for the “τ-model”). The range of the ensemble of parameters for those models is provided in Supplementary Table 3.
Predicting phage dynamics for infection in LBM
We used the infection parameters in LBM to predict the phage dynamics and compared it with the measured concentrations of phages extracted from the same cultures. We assumed that the intracellular phage particles only get mature in the terminal infected state (M). Since the extracted phages contain both free (released) and intracellular phage particles, the predicted phage concentration is given by:
| 15 |
The model predictions are shown in Fig. 3e (for the “r-model”) and Supplementary Figs. 7d–f (for the null model, “B-model” and “τ-model”).
Characterizing the relative growth rate of the viral population
Examining infection parameters for minimal media and defining R
To assess whether the infection parameters are further constrained, we analyzed the infection in minimal media and plotted the ensemble of parameters sampled from MCMC (as described above in “Parameterization of phage-cell encounter rate, latent period and burst size”) in the space of (log10r, log10B, τ). We noticed that they lie approximately on a single plane, described by τ = α × [log10r + log10B] + β (see Supplementary Figs. 10e, f). Motivated by this observation, we defined a new parameter, R:
| 16 |
where g* denotes a characteristic growth rate (see below), obtained by fitting the expression to the data.
To test if R exhibits a lower uncertainty than the individual infection parameters, we calculated the coefficient of variation (CV) for the individual infection parameters and R. Notably, in most cases, the CV of R is smaller than the CV of individual infection parameters, except for the CV of τ in M9Glu (= 0.012, slightly smaller than the CV of R, = 0.015). This supports the idea that R is a robust quantity that constrains the individual infection parameters. The distribution and CV of infection parameters and R in minimal media are shown in Supplementary Figs. 10c, d, 10g, h.
Interpreting R as the relative growth rate of viral population
To motivate the interpretation of R as the relative growth rate of the viral population, we used the following simplified model. We assumed an exponentially growing bacterial population U(t) with growth rate g*. When phage loss due to adsorption is negligible, the production of phages at time t can be accounted for by the encounter of bacteria and phages at time t − τ and the subsequent release of free phages by the infected cells:
| 17 |
We further assumed that before massive lysis, the effect of infection on bacterial concentration is negligible. We therefore have U(t − τ) = U(t)/exp(τ ⋅ g*). Plugging this expression into Eq. (17), we found:
| 18 |
Therefore, R can be interpreted as a rate parameter that describes the relative growth rate of viral population (normalized for cell concentration). Consistent with this interpretation, the fitted parameter g*, which was inferred from the plane of conserved parameters (Supplementary Figs. 10g, h), is of the same order of magnitude as the bacterial growth rate: for M9Mal, g* is 0.052 min−1, and the bacterial growth rate is 0.010 min−1; for M9Glu, g* is 0.035 min−1, and the bacterial growth rate is 0.012 min−1. However, the derivation above relies on simplified assumptions regarding cell growth and infection. Further theoretical investigation is needed to derive the growth rate of phages, in analogy to the approach undertaken for chemostat growth in refs. 27,68.
Examining the relative growth rate of lambda phages in LBM
To further investigate whether R effectively constrains infection parameters in LBM, we plotted R, obtained from the ensemble of parameters from the three models (“r-model”, “B-model”, and “τ-model”), as a function of the normalized instantaneous growth rate (ϕ). We found that R(ϕ) exhibited a consistent increasing trend with the growth rate across all three models (see Fig. 3f).
Examining the relative growth rate of T4 phage in different growth conditions
We also examined the relative growth rate of T4 phages under different growth conditions, as reported in the literature. Two studies investigating the infection parameters of T4 phages as a function of bacterial growth rate yielded seemingly conflicting results. Nabergoj et al. 27, which assessed the individual infection parameters of T4 at varying bacterial growth rates in a chemostat, observed a decrease in r and τ with the bacterial growth rate, and an increase in B. Hadas et al. 28, which examined these parameters in batch cultures with different carbon sources, reported an increasing trend in r and B with the bacterial growth rate, along with a non-monotonic trend in τ.
We sought to reconcile these findings by examining whether R could offer a unified explanation for both studies. To this end, we plotted R as a function of bacterial growth rate (g) for both studies. For Nabergoj et al.27, we utilized the fitted relationships of r, B, and τ as functions of growth rate (ref. 27) to calculate R, using Eq. (16). For Hadas et al.28, we used their measured parameters to compute R, from the following growth conditions: LB supplemented with 0.4% glucose (LBG), LBG supplemented with penicillin (LBG+Pn), and M9 minimal medium supplemented with 0.4% glucose (Glu), 0.4% glycerol (Gly), or 0.4% acetate (Acet). The results, depicted in Supplementary Fig. 11, suggest a consistent increasing trend of R with bacterial growth rate across both studies.
Modeling bacterial recovery
We aimed to incorporate the recovery after massive lysis into the model. Following ref. 17, we assumed that three processes contribute to this recovery: (1) Growth of cells that are resistant to phage infection; (2) Conversion from lysed cells to debris, which contributes to the measured OD; and (3) Recycling of nutrients from cell debris into the nutrients, which foster cell growth. We denoted the resistant population as R and cell debris as D. We assumed that the resistant cells were produced from uninfected cells (U) with a first-order transition rate km (refs. 17,34), and all lysed cells were converted to cell debris instantaneously. The content of each lysed cell was recycled as nutrients (N) with a conversion factor kf. Finally, we assumed that the debris from each lysed cell contributed to OD with a 10% molar absorptivity of an intact cell (see “Examining alternative model assumptions” below for derivation). The model schematic is shown in Supplementary Fig. 12a.
Accordingly, we modified Eq. (9) to describe the dynamics of nutrients (N), uninfected cells (U), infected cells (Ii), free phages (P), resistant cells (R) and cell debris (D):
| 19 |
Since g was parameterized from the OD dynamics of uninfected cultures, and r, B and τ were parameterized from early-stage infection data using the “r-model” (as described above), the only remaining unknown parameters are km and kf. We fitted km and kf by minimizing the following objective function:
| 20 |
We then obtained the ensemble of parameters using the method described above in “Characterizing the dependence of infection parameters on growth rate” and predicted the phage dynamics using the method described above in “Predicting phage dynamics for infection in LBM”. The fitting results are shown in Supplementary Fig. 12b. The predictions are shown in Supplementary Fig. 12c.
Examining model assumptions
Ignoring the inactivation of infectious phage particles
While some models have incorporated the inactivation of infectious phage particles due to non-infective processes such as degradation69, our model omitted this term. Examination of measured phage concentrations over time (see Supplementary Fig. 12c) revealed no significant drop in phage concentration following massive lysis. For instance, for infection in LBM with an initial phage concentration of ~103 PFU mL−1 (where the phage concentration displayed the greatest reduction among the six infection conditions examined), the phage concentration decreased from 4.1 × 1010 PFU mL−1 at t = 8 h to 1.4 × 1010 PFU mL−1 at t = 20 h, corresponding to a 3.9% inactivation per hour. Given that our model focuses on infection over a shorter time scale (the initial ~6 h), we contend that the effects of phage particle inactivation are negligible.
Ignoring the contribution of cell debris to OD
When modeling early-stage infection, our model also ignored the contribution of cell debris to bacterial OD (ref. 24), since we consider that contribution to be small. For instance, for infection in LBM with an initial phage concentration of ~103 PFU mL−1, the lysis OD and the minimal OD after massive lysis were approximately 0.8 and 0.1, respectively (see Supplementary Fig. 12c). Thus, even assuming that the latter OD solely originates from debris released from the peak, each dead cell’s contribution to OD is ~12% that of a live cell. For the sake of simplicity, we neglected this contribution.
Evaluating the effect of assuming M = 10
While our model used M = 5 to represent the number of intermediate infected states (see Eq. (9)), previous models have used other values, e.g., M = 8 (ref. 23) and M = 10 (ref. 22). To evaluate the effect of a larger M value, we assumed M = 10 and fitted the OD dynamics of infected cultures in LBM using the “r-model”. Examining the fitting results, we found that there is minimal change in the distribution of r, B, τ compared to the model with M = 5 (see Supplementary Fig. 19d). Furthermore, the inferred value of the relative growth rate of the viral population, R, only displayed a small shift (from 3 × 10−10 mL−1 min−1 at M = 5 to 4 × 10−10 mL−1 min−1 at M = 10), and the quality of fitting the OD dynamics, and of predicting phage dynamics, were not improved (see Supplementary Figs. 19c, 19d, 19f). Therefore, to reduce computational time when fitting the data, we decided not to use a larger M value.
Evaluating the effect of cell elongation after infection
It was previously reported that cells elongate upon infection8. However, our model assumed that infected cells contribute to OD in the same manner as uninfected cells. Here, we explored the hypothesis that the increased contribution to OD by infected cells would impact model inference.
To do so, we used the data in ref. 21, where the molar absorptivity (ε) of ampicillin-treated E. coli cells (~ 30 μm long) was reported to be 3-fold that of the exponentially growing cells. We used the 3-fold factor in our model as the upper bound for the change in ε of infected cells. Specifically, we assumed that the molar absorptivity of infected cells (ε(Ii(t))) grows exponentially with their infection state (i), with the terminal state (M) having a 3-fold ε of the corresponding uninfected cells under the same growth condition:
| 21 |
We then fitted the OD dynamics of infected cultures in LBM with the r-model by minimizing the following objective function:
| 22 |
We found that incorporating this feature led to a modest ~2 fold change in the inferred values of r and B, and no change in τ, compared to the original model where infected and uninfected cells have the same molar absorptivity (see Supplementary Fig. 20c). Furthermore, the inferred value of the relative growth rate of the viral population, R, was almost unchanged, and the quality of fitting the OD dynamics, and of predicting phage dynamics, were not improved (see Supplementary Figs. 20a, b, d). Consequently, for simplicity, we decided not to incorporate any change in absorptivity of infected cells.
Quantifying the proportion of lysogens among surviving cells in phage-infected cultures
To verify that the surviving cells in cultures infected by λwt were lysogens, we leveraged the fact that λwt harbors a kanamycin resistance cassette11. After the cell culture infected at an initial phage concentration of ≈ 2 × 107 PFU mL−1 had exhibited massive lysis, the culture was extracted and diluted 4 × 104-fold using 1 × PBS. Diluted cells were plated on agar plates made using LB or LB supplemented with 50 μg mL−1 kanamycin. The numbers of colonies were used to calculate the total number of cells in the infected culture and the number of lysogenic cells (resistant to kanamycin). The results, shown in Supplementary Fig. 13, indicated that >99% of the surviving cells were lysogens.
Measuring the number of phages released by lambda lysogens at different growth rates
This assay is modified from ref. 11. Briefly, an overnight culture of MG1655 λts in LB, supplemented with 50 µg mL−1 kanamycin, was centrifuged, and the supernatant (containing free phages released during overnight growth) was removed. The cell pellet was resuspended in the same volume of fresh LBGM, and further diluted 1000-fold in LBGM. 500 μL of this diluted culture was aliquoted into replicate wells in a clear 48-well flat-bottom microplate (COSTAR). The plate was incubated for 24 h at 30 oC with shaking.
We sampled the bacterial cultures when they were first inoculated, and when the blank-subtracted OD reached approximately 0.01, 0.02, 0.04, 0.25, 0.30, 0.50, and 1.00. At each time point, the entire 500 µL of the cultures from two wells were extracted, and 25 μL of chloroform (final concentration, 5%) was added to each sample, followed by vortexing for 10 s. Phage lysates were stored at 4 oC, and the OD-based phage counting procedure was used to measure the phage concentrations, with the calibration curve obtained by infection of the same phage strain in LBM (Fig. 2a).
Modeling spontaneous induction
We assumed the lysogenic cells (L) switch to the induced state (Ii) with a first-order transition rate ki (the spontaneous induction rate), and that ki is a linear function of the normalized instantaneous cell growth rate (ϕ): . The induced cells undergo M intermediate states (I1, I2, …, IM) before reaching lysis, similar to the infected cells in models that describe infected cultures (see “Modeling the OD dynamics of phages and bacteria during infection” above). The released phages get adsorbed to the glucose-grown cells at a rate 10-fold lower than that of cells grown in maltose-supplemented medium42. The model schematic is shown in Fig. 5g. Accordingly, we modified Eq. (9) to describe the dynamics of nutrients (N), lysogens (L), induced cells (Ii) and free phages (P):
| 23 |
To parameterize the growth rate, the growth curves of cultures in LBGM up to and including the first plateau were fitted to Eq. (10). The data was well described by three growth phases (X = 3) (Supplementary Fig. 6). The fitted parameter values are listed in Supplementary Table 2.
We then parameterized Eq. (23) using the “r-model”, “B-model” and “τ-model” respectively. For each model, the parameters for r, B and τ were obtained from the fitting of the corresponding model to infection dynamics in LBM. The remaining parameters ( and ) were fitted to the measured dynamics of OD and phage concentration, by minimizing the following objective function:
| 24 |
where is the model-predicted dynamics of lysogenic cells, P(t) is the measured phage dynamics, Tp is the set of time points where the phage concentrations are measured, and |Tp| is the total number of time points. The other notations are the same as in Eq. (14).
Additionally, we tested an alternative set of models where no phage adsorption is allowed, following the same fitting strategy as above. The fitting result are shown in Fig. 5f (for “r-model” with phage adsorption) and Supplementary Fig. 17 (for other models), with the fitting parameters provided in Supplementary Table 5.
We found that, in the absence of phage adsorption, all three models (“r-model”, “B-model” and “τ-model”) reproduce the data, and the fitted induction rates ki all increase with the growth rate (see Supplementary Figs. 17a–c). When adsorption is introduced, the “B-model” cannot reproduce the data, while the “r-model” and “τ-model” are able to do so. For the latter two models, the inferred induction rate ki increases with growth rate, exhibiting a similar trend to the models without adsorption (see Fig. 5f for “r-model” and Supplementary Figs. 17d, e for “B-model” and “τ-model”). Therefore, regardless of whether phage adsorption is included in the model, the fitting results suggest that the spontaneous induction rate increases with the bacterial growth rate.
Measuring the frequency of lysogeny as a function of MOI and growth rate
Infecting at different MOIs at a given growth rate
For this assay, we adapted the bulk lysogenization protocol from refs. 8,10, but instead of plating for colonies to measure the concentration of cells, we used the growth dynamics of the infected bacterial cultures as described below. This assay was used to produce the data shown in Fig. 4b, c.
A 2-fold dilution series of λts (harboring a kanamycin resistance cassette) was prepared in LBM. The concentrations of phages in this dilution series ranged from ≈ 5 × 107 PFU mL−1 to ≈ 2 × 1011 PFU mL−1. To prepare cells, an overnight culture of MG1655 in LB was diluted 1:500 into LBM in a baffled Erlenmeyer flask. This culture was grown at 30 oC with aeration (220 rpm shaking). Upon reaching ODspec ≈ 0.1, 500 μL of the culture was aliquoted into different wells of a clear 48-well flat-bottom microplate (COSTAR). This plate (“infection plate”) was incubated for 30 min at 30 oC with shaking in a plate reader, where the OD was recorded every 5 min.
After 30 min, 10 μL of phages at different concentrations were added to different wells, resulting in infected bacterial cultures at multiplicity of infection, MOI, ranging from ~0.02 to ~100. As negative controls for phage infection, we included uninfected cultures, to which blank SM buffer was added. The infection plate was incubated with shaking at 30 oC for 15 min to allow phages to infect cells. Then, 2 μL of each sample was diluted into 500 μL of LBM in another 48-well microplate (“detection plate”), pre-warmed at 30 oC. The detection plate was incubated with shaking at 30 oC for 45 min. Then, each sample was supplemented with kanamycin (final concentration, 50 μg mL−1), and incubated for 24 h.
For the uninfected samples, some wells were supplemented with 50 μg mL−1 kanamycin, serving as a negative control for infection, whereas some were not subjected to selection, providing an estimate for the total density of cells in the infection mixture (analyzed as described below).
Infecting at different MOIs and growth rates
This assay was used to produce the data shown in Fig. 5b. To obtain cells at different growth rates, we first prepared a culture of MG1655 in LBM at 30 oC. At ODspec ≈ 0.1, this culture was diluted into fresh LBM in different baffled Erlenmeyer flasks (5 cultures, dilution ratios ranging from 1:50 to undiluted). These cultures with different initial ODspec were grown at 30 oC for 3 h (final ODspec ranging from ~0.2 to ~2.5). Then, 200 μL of these cultures and the overnight culture (ODspec ≈ 5), were aliquoted into different wells of a 96-well “infection plate”, yielding 6 infection series at different growth rates. These cultures were grown for 30 min at 30 oC before phage addition.
Infection was performed using phages in a 5× dilution series (6 levels, ranging from ≈ 8 × 107 PFU mL−1 to ≈ 2 × 1011 PFU mL−1). The infected samples were grown for 30 min; then, 1 μL of each sample in the infection plate was diluted into 200 μL of pre-warmed LBM supplemented with 50 μg mL−1 kanamycin in another 96-well microplate (“detection plate”). The detection plate was incubated with shaking at 30 oC for 24 h. The detection plate also contained the uninfected control cultures with and without kanamycin selection. Here, kanamycin selection was introduced immediately after the dilution step. Growth in fresh medium without kanamycin selection was omitted to ensure that the density of lysogens we measured reflected lysogenization at the original growth rates.
Data analysis
The growth rate at which infection was performed, g, was calculated by fitting the following equation to the growth curves of each sample during the 30-minute duration before phages were added.
| 25 |
where N0 is the initial cell concentration, and g is the growth rate. Fitting was performed in logarithmic space.
Following previous studies8,10, we defined the frequency of lysogeny as the fraction of kanamycin-resistant lysogenic cells (L0) among all cells in the infected cultures (T0):
| 26 |
We inferred L0 and T0 by extrapolating the growth curves of the infected cell cultures under selection L(t), and the uninfected without selection T(t) to t = 0, defined as the time the samples in the infection plate were diluted into the detection plate (Fig. 4b). This was done by fitting Eq. (25) to L(t) and T(t) for OD between ~0.02 and ~0.1. We note that in this case, the parameter g reflects the growth rate in the detection plate, not the growth rates at which infection was performed.
Inferring the single-cell probability of lysogenization
Model description
Following refs. 8,10,17,36, we assumed the following:
(1) Phage-cell encounters follow Poisson statistics. As a result, the single-cell MOI, n, is described by the following distribution:
| 27 |
where M is the average MOI in the infection mixture, and a is a scaling factor that accounts for the infection efficiency and the accuracy in measuring phage and cell concentrations.
(2) The probability of lysogenization, Qn, is a function of the single-cell MOI, n. Unlike refs. 8,10,36 which assumed coinfection by at least MOI* phages is required for lysogeny, we adopted the more general approach described in ref. 17, which allows for non-zero probability of lysogenization at n < MOI*:
| 28 |
The observed frequency of lysogeny, flysogeny, as a function of the average MOI, M, is found by summing the product of Pn and Qn over all possible values of n:
| 29 |
We scanned the value of MOI* from 1 to 3, and found that MOI* = 2 best captured the lysogenization data by wild-type, replication-competent lambda phages in exponentially growing cells (consistent with refs. 10,36). For MOI* = 2, Eq. (29) becomes:
| 30 |
Eq. (30) was used to fit the lysogeny data shown in Fig. 4c.
Incorporating the reduced frequency of lysogeny at high MOI
At some growth rates, we observed a reduction in the frequency of lysogeny at very high MOI (consistent with previous reports8,36). To capture this reduction, we introduced into Eq. (29) an additional repression term, Rn, which decreases the probability of lysogenization when a cell is infected at high n values. We parameterized Rn as an exponential decay with a rate of k:
| 31 |
For up to n = MOI*, Rn = 1, thus the single-cell probability of lysogenization is simply Qn. With this additional term, Eq. (29) becomes:
| 32 |
and Eq. (30) becomes:
| 33 |
For MOI* = 1 (used to fit data in stationary cells in Supplementary Fig. 16), the frequency of lysogeny is:
| 34 |
Model fitting
To capture the lysogeny-vs.-MOI curve measured at each bacterial growth rate, fitting was performed by minimizing the following objective function:
| 35 |
where are the model-predicted frequencies of lysogeny, and flysogeny are the experimentally measured values. Fitting was performed in logarithmic space because the MOI and the frequencies of lysogeny span several orders of magnitude. We also imposed a constraint of q1 ≤ q2. Fitting results are shown in Figs. 4c and 5b, with the average MOI rescaled using the parameter a as done in ref. 10.
We note that the best-fit values of the parameter a, when plotted as a function of the bacterial density, are in agreement with the theoretically predicted efficiency of phage adsorption38 (Supplementary Fig. 21a). This agreement lends further credence to our measurements and the fitting procedure.
Predicting the frequency of lysogeny as a function of both MOI and growth rates
To predict the parameters a, q1, q2, and k at an arbitrary growth rate g, the best-fit values of these parameters at each sampled growth rate were used to fit the following phenomenological expressions:
| 36 |
The results of these parameterizations are shown in Supplementary Fig. 21b (for q1, also reproduced in Fig. 5c), and the parameter values (with bootstrap standard errors) are shown in Supplementary Table 4.
To predict the frequency of lysogeny as a function of both MOI (M) and growth rate (g), we scanned the MOI between 10−3 and 100, and the growth rate between 0 and 1.25 h−1. For each growth rate (g), the parameter values in Supplementary Table 4 and Eq. (36) were used to calculate the values of a, q1, q2, and k These parameter values and Eqs. (27), (31), and (33) were used to calculate the predicted frequency of lysogeny for different MOI values (M). The “fate diagram”, depicting the frequency of lysogeny as a function of both MOI and growth rates, is shown in Fig. 5e.
This model prediction was compared with the experimental data (Fig. 5e). Here, the sampled data points (6 growth rates, each with 6 MOI values) were interpolated using the triangulation-based natural neighbor method and further smoothed using a 2D median filter, as done in ref. 70.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Source data
Acknowledgements
We are grateful to S. Maslov, K. Sneppen, and all members of the Golding lab for their generous advice. Work in the Golding lab is supported by the National Institutes of Health grant R35 GM140709, the National Science Foundation grant 2243257 (NSF Science and Technology Center for Quantitative Cell Biology), and by the Alfred P. Sloan Foundation grant G-2023-19649, all to I.G. We gratefully acknowledge the computing resources provided by the Computational and Integrative Biomedical Research Center of Baylor College of Medicine.
Author contributions
Conceptualization: Y.G., T.V.P.N, I.G.; methodology: Y.G., T.V.P.N, E.H., I.G.; investigation: Y.G., T.V.P.N.; formal analysis: Y.G., T.V.P.N.; visualization: Y.G., T.V.P.N.; funding acquisition: I.G.; supervision: I.G.; writing—original draft: Y.G., T.V.P.N., I.G.; writing—review & editing: Y.G., T.V.P.N., E.H., I.G.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Data availability
All data and statistics underlying the figures of this publication are provided in the Source Data file. In addition, raw datasets generated in this study (required to run the custom Python and MATLAB scripts; see Code Availability) have been deposited at https://github.com/gengyuncong/PhageCounting. Source data are provided with this paper.
Code availability
Custom scripts (written in Python 3.8.5 using Jupyter Notebook and MATLAB 2020a–2023b) developed in this study for data analysis and model fitting have been deposited at https://github.com/gengyuncong/PhageCounting.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Yuncong Geng, Thu Vu Phuc Nguyen.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-51913-6.
References
- 1.Adams, M. H. Bacteriophages. (Interscience Publishers, New York, 1959).
- 2.Sambrook, J. & Russell, D. W. Molecular Cloning: A Laboratory Manual. (Cold Spring Harbor Laboratory Press, Cold Spring Harbor, N.Y, 2001).
- 3.Clokie, M. R. J. & Kropinski, A. M. Bacteriophages: Methods and Protocols. (Humana Press, New York, 2009).
- 4.Dennehy, J. J. What ecologists can tell virologists. Annu. Rev. Microbiol.68, 117–135 (2014). 10.1146/annurev-micro-091313-103436 [DOI] [PubMed] [Google Scholar]
- 5.Correa, A. M. S. et al. Revisiting the rules of life for viruses of microorganisms. Nat. Rev. Microbiol.19, 501–513 (2021). 10.1038/s41579-021-00530-x [DOI] [PubMed] [Google Scholar]
- 6.Silveira, C. B., Luque, A. & Rohwer, F. The landscape of lysogeny across microbial community density, diversity and energetics. Environ. Microbiol.23, 4098–4111 (2021). 10.1111/1462-2920.15640 [DOI] [PubMed] [Google Scholar]
- 7.Casjens, S. R. & Hendrix, R. W. Bacteriophage lambda: early pioneer and still relevant. Virology479–480, 310–330 (2015). 10.1016/j.virol.2015.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zeng, L. et al. Decision making at a subcellular level determines the outcome of bacteriophage infection. Cell141, 682–691 (2010). 10.1016/j.cell.2010.03.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Golding, I. Single-cell studies of phage λ: hidden treasures under Occam’s rug. Annu. Rev. Virol.3, 453–472 (2016). 10.1146/annurev-virology-110615-042127 [DOI] [PubMed] [Google Scholar]
- 10.Yao, T., Coleman, S., Nguyen, T. V. P., Golding, I. & Igoshin, O. A. Bacteriophage self-counting in the presence of viral replication. Proc. Natl Acad. Sci. USA118, e2104163118 (2021). 10.1073/pnas.2104163118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zong, C., So, L., Sepúlveda, L. A., Skinner, S. O. & Golding, I. Lysogen stability is determined by the frequency of activity bursts from the fate‐determining gene. Mol. Syst. Biol.6, 440 (2010). 10.1038/msb.2010.96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Allen, J. P. Biophysical Chemistry. (Wiley-Blackwell Pub, Oxford; Hoboken, NJ, 2008).
- 13.Sezonov, G., Joseleau-Petit, D. & D’Ari, R. Escherichia coli Physiology in Luria-Bertani Broth. J. Bacteriol.189, 8746–8749 (2007). 10.1128/JB.01368-07 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hendrix, R. W. Lambda II. (Cold Spring Harbor Laboratory, Cold Spring Harbor, N.Y, 1983).
- 15.Young, R. Bacteriophage lysis: mechanism and regulation. Microbiol Rev.56, 430–481 (1992). 10.1128/mr.56.3.430-481.1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maynard, N. D. et al. A forward-genetic screen and dynamic analysis of lambda phage host-dependencies reveals an extensive interaction network and a new anti-viral strategy. PLoS Genet6, e1001017 (2010). 10.1371/journal.pgen.1001017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Weitz, J. Quantitative Viral Ecology: Dynamics of Viruses and Their Microbial Hosts. (Princeton University Press, Princeton; Oxford, 2015).
- 18.Monod, J. The growth of bacterial cultures. Annu. Rev. Microbiol.3, 371–394 (1949). 10.1146/annurev.mi.03.100149.002103 [DOI] [Google Scholar]
- 19.Aidelberg, G. et al. Hierarchy of non-glucose sugars in Escherichia coli. BMC Syst. Biol.8, 133 (2014). 10.1186/s12918-014-0133-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pokhilko, A. Monitoring of nutrient limitation in growing E. coli: a mathematical model of a ppGpp-based biosensor. BMC Syst. Biol.11, 106 (2017). 10.1186/s12918-017-0490-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stevenson, K., McVey, A. F., Clark, I. B. N., Swain, P. S. & Pilizota, T. General calibration of microbial growth in microplate readers. Sci. Rep.6, 38828 (2016). 10.1038/srep38828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mitarai, N., Brown, S. & Sneppen, K. Population dynamics of phage and bacteria in spatially structured habitats using phage λ and Escherichia coli. J. Bacteriol.198, 1783–1793 (2016). 10.1128/JB.00965-15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brown, S., Mitarai, N. & Sneppen, K. Protection of bacteriophage-sensitive Escherichia coli by lysogens. Proc. Natl Acad. Sci. USA119, e2106005119 (2022). 10.1073/pnas.2106005119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hazan, R., Que, Y.-A., Maura, D. & Rahme, L. G. A method for high throughput determination of viable bacteria cell counts in 96-well plates. BMC Microbiol.12, 259 (2012). 10.1186/1471-2180-12-259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kirkpatrick, S., Gelatt Jr, C.D. & Vecchi, M.P. Optimization by simulated annealing. Science220, 671–680 (1983). [DOI] [PubMed]
- 26.Foreman-Mackey, D., Hogg, D. W., Lang, D. & Goodman, J. emcee: The MCMC Hammer. Preprint at 10.48550/ARXIV.1202.3665 (2012).
- 27.Nabergoj, D., Modic, P. & Podgornik, A. Effect of bacterial growth rate on bacteriophage population growth rate. MicrobiologyOpen7, e00558 (2018). 10.1002/mbo3.558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hadas, H., Einav, M., Fishov, I. & Zaritsky, A. Bacteriophage T4 development depends on the physiology of its host Escherichia coli. Microbiology143, 179–185 (1997). 10.1099/00221287-143-1-179 [DOI] [PubMed] [Google Scholar]
- 29.You, L., Suthers, P. F. & Yin, J. Effects of Escherichia coli physiology on growth of phage T7 in vivo and in silico. J. Bacteriol.184, 1888–1894 (2002). 10.1128/JB.184.7.1888-1894.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang, I.-N. Lysis timing and bacteriophage fitness. Genetics172, 17–26 (2006). 10.1534/genetics.105.045922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shao, Y. & Wang, I.-N. Effect of late promoter activity on bacteriophage λ fitness. Genetics181, 1467–1475 (2009). 10.1534/genetics.108.098624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gutenkunst, R. N. et al. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol.3, e189 (2007). 10.1371/journal.pcbi.0030189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bohannan, B. J. M. & Lenski, R. E. Linking genetic change to community evolution: insights from studies of bacteria and bacteriophage. Ecol. Lett.3, 362–377 (2000). 10.1046/j.1461-0248.2000.00161.x [DOI] [Google Scholar]
- 34.Chaudhry, W. N. et al. Leaky resistance and the conditions for the existence of lytic bacteriophage. PLoS Biol.16, e2005971 (2018). 10.1371/journal.pbio.2005971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hao, N., Agnew, D., Krishna, S., Dodd, I. B. & Shearwin, K. E. Analysis of infection time courses shows CII levels determine the frequency of lysogeny in phage 186. Pharmaceuticals14, 998 (2021). 10.3390/ph14100998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kourilsky, P. Lysogenization by bacteriophage lambda: I. Multiple infection and the lysogenic response. Molec. Gen. Genet.122, 183–195 (1973). 10.1007/BF00435190 [DOI] [PubMed] [Google Scholar]
- 37.St-Pierre, F. & Endy, D. Determination of cell fate selection during phage lambda infection. Proc. Natl Acad. Sci.105, 20705–20710 (2008). 10.1073/pnas.0808831105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Moldovan, R., Chapman-McQuiston, E. & Wu, X. L. On kinetics of phage adsorption. Biophys. J.93, 303–315 (2007). 10.1529/biophysj.106.102962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kobiler, O., Koby, S., Teff, D., Court, D. & Oppenheim, A. B. The phage λ CII transcriptional activator carries a C-terminal domain signaling for rapid proteolysis. Proc. Natl Acad. Sci. USA99, 14964–14969 (2002). 10.1073/pnas.222172499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Reichardt, L. F. Control of bacteriophage lambda repressor synthesis after phage infection: the role of the N, cII, cIII and cro products. J. Mol. Biol.93, 267–288 (1975). 10.1016/0022-2836(75)90132-1 [DOI] [PubMed] [Google Scholar]
- 41.Ptashne, M. A Genetic Switch: Phage Lambda Revisited. (Cold Spring Harbor Laboratory Press, Cold Spring Harbor, N.Y, 2004).
- 42.Schwartz, M. The adsorption of coliphage lambda to its host: effect of variations in the surface density of receptor and in phage-receptor affinity. J. Mol. Biol.103, 521–536 (1976). 10.1016/0022-2836(76)90215-1 [DOI] [PubMed] [Google Scholar]
- 43.Jaramillo‐Riveri, S. et al. Growth‐dependent heterogeneity in the DNA damage response in Escherichia coli. Mol. Syst. Biol.18, e10441 (2022). 10.15252/msb.202110441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Basan, M. et al. A universal trade-off between growth and lag in fluctuating environments. Nature584, 470–474 (2020). 10.1038/s41586-020-2505-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lin, W.-H. & Jacobs-Wagner, C. Connecting single-cell ATP dynamics to overflow metabolism, cell growth, and the cell cycle in Escherichia coli. Curr. Biol.32, 3911–3924.e4 (2022). 10.1016/j.cub.2022.07.035 [DOI] [PubMed] [Google Scholar]
- 46.Lazazzera, B. A. Quorum sensing and starvation: signals for entry into stationary phase. Curr. Opin. Microbiol.3, 177–182 (2000). 10.1016/S1369-5274(00)00072-2 [DOI] [PubMed] [Google Scholar]
- 47.Xavier, K. B. & Bassler, B. L. Regulation of uptake and processing of the quorum-sensing autoinducer AI-2 in Escherichia coli. J. Bacteriol.187, 238–248 (2005). 10.1128/JB.187.1.238-248.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sánchez-Clemente, R. et al. Study of pH changes in media during bacterial growth of several environmental strains. In Proceedings2, 1297 (2018).
- 49.Ratzke, C. & Gore, J. Modifying and reacting to the environmental pH can drive bacterial interactions. PLoS Biol.16, e2004248 (2018). 10.1371/journal.pbio.2004248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Golding, I., Coleman, S., Nguyen, T. V. P. & Yao, T. Decision making by temperate phages. in Encyclopedia of Virology 88–97 (Elsevier, 2021).
- 51.Golding, I. Decision making in living cells: lessons from a simple system. Annu. Rev. Biophys.40, 63–80 (2011). 10.1146/annurev-biophys-042910-155227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ofir, G. & Sorek, R. Contemporary phage biology: from classic models to new insights. Cell172, 1260–1270 (2018). 10.1016/j.cell.2017.10.045 [DOI] [PubMed] [Google Scholar]
- 53.Schrag, S. J. & Mittler, J. E. Host-parasite coexistence: the role of spatial refuges in stabilizing bacteria-phage interactions. Am. Naturalist148, 348–377 (1996). 10.1086/285929 [DOI] [Google Scholar]
- 54.Pearl, S., Gabay, C., Kishony, R., Oppenheim, A. & Balaban, N. Q. Nongenetic individuality in the host–phage interaction. PLoS Biol.6, e120 (2008). 10.1371/journal.pbio.0060120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Erez, Z. et al. Communication between viruses guides lysis–lysogeny decisions. Nature541, 488–493 (2017). 10.1038/nature21049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Silpe, J. E. & Bassler, B. L. A host-produced quorum-sensing autoinducer controls a phage lysis-lysogeny decision. Cell176, 268–280.e13 (2019). 10.1016/j.cell.2018.10.059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Aframian, N. et al. Dormant phages communicate via arbitrium to control exit from lysogeny. Nat. Microbiol.7, 145–153 (2021). 10.1038/s41564-021-01008-5 [DOI] [PubMed] [Google Scholar]
- 58.Kronheim, S. et al. A chemical defence against phage infection. Nature564, 283–286 (2018). 10.1038/s41586-018-0767-x [DOI] [PubMed] [Google Scholar]
- 59.Hampton, H. G., Watson, B. N. J. & Fineran, P. C. The arms race between bacteria and their phage foes. Nature577, 327–336 (2020). 10.1038/s41586-019-1894-8 [DOI] [PubMed] [Google Scholar]
- 60.Georjon, H. & Bernheim, A. The highly diverse antiphage defence systems of bacteria. Nat. Rev. Microbiol.21, 686–700 (2023). [DOI] [PubMed]
- 61.Bonhivers, M. & Letellier, L. Calcium controls phage T5 infection at the level of the Escherichia coli cytoplasmic membrane. FEBS Lett.374, 169–173 (1995). 10.1016/0014-5793(95)01101-J [DOI] [PubMed] [Google Scholar]
- 62.Zhang, K., Young, R. & Zeng, L. Bacteriophage P1 does not show spatial preference when infecting Escherichia coli. Virology542, 1–7 (2020). 10.1016/j.virol.2019.12.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Min, T. L. et al. High-resolution, long-term characterization of bacterial motility using optical tweezers. Nat. Methods6, 831–835 (2009). 10.1038/nmeth.1380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zeng, L. & Golding, I. Following Cell-fate in E. coli After Infection by Phage Lambda. JoVE 3363. 10.3791/3363-v (2011). [DOI] [PMC free article] [PubMed]
- 65.Moat, A. G., Foster, J. W. & Spector, M. P. Microbial Physiology. (Wiley-Liss, New York, 2002).
- 66.Sprent, P. & Smeeton, N. C. Applied Nonparametric Statistical Methods. (Chapman & Hall/CRC, Boca Raton, 2007).
- 67.Ellis, E. L. & Delbrück, M. The growth of bacteriophage. J. Gen. Physiol.22, 365–384 (1939). 10.1085/jgp.22.3.365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Bull, J. J. Optimality models of phage life history and parallels in disease evolution. J. Theor. Biol.241, 928–938 (2006). 10.1016/j.jtbi.2006.01.027 [DOI] [PubMed] [Google Scholar]
- 69.Campbell, A. Conditions for the existence of bacteriophage. Evolution15, 153 (1961). 10.2307/2406076 [DOI] [Google Scholar]
- 70.Kaplan, S., Bren, A., Zaslaver, A., Dekel, E. & Alon, U. Diverse two-dimensional input functions control bacterial sugar genes. Mol. Cell29, 786–792 (2008). 10.1016/j.molcel.2008.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data and statistics underlying the figures of this publication are provided in the Source Data file. In addition, raw datasets generated in this study (required to run the custom Python and MATLAB scripts; see Code Availability) have been deposited at https://github.com/gengyuncong/PhageCounting. Source data are provided with this paper.
Custom scripts (written in Python 3.8.5 using Jupyter Notebook and MATLAB 2020a–2023b) developed in this study for data analysis and model fitting have been deposited at https://github.com/gengyuncong/PhageCounting.