Abstract
Diffusion-weighted Magnetic Resonance Imaging (dMRI) is increasingly used to study the fetal brain in utero. An important computation enabled by dMRI is streamline tractography, which has unique applications such as tract-specific analysis of the brain white matter and structural connectivity assessment. However, due to the low fetal dMRI data quality and the challenging nature of tractography, existing methods tend to produce highly inaccurate results. They generate many false streamlines while failing to reconstruct the streamlines that constitute the major white matter tracts. In this paper, we advocate for anatomically constrained tractography based on an accurate segmentation of the fetal brain tissue directly in the dMRI space. We develop a deep learning method to compute the segmentation automatically. Experiments on independent test data show that this method can accurately segment the fetal brain tissue and drastically improve the tractography results. It enables the reconstruction of highly curved tracts such as optic radiations. Importantly, our method infers the tissue segmentation and streamline propagation direction from a diffusion tensor fit to the dMRI data, making it applicable to routine fetal dMRI scans. The proposed method can facilitate the study of fetal brain white matter tracts with dMRI.
Keywords: Tractography, Fetal brain, Diffusion MRI, Machine learning
1. Introduction
1.1. Background and motivation
The human brain undergoes dramatic microstructural and macrostructural developments in utero (Silbereis et al., 2016; Bayer and Altman, 2005). It can be argued that the fetal period is the most dynamic and critical stage in brain development (Collin and Van Den Heuvel, 2013; Dubois et al., 2014). Processes such as neurogenesis, synapse formation, neural migration, and axonal growth all begin before birth. These processes form the brain microstructure and lay the foundations for the formation and development of the structural brain connectome (Takahashi et al., 2012; Song et al., 2017), which will continue its rapid development in the first few months and years after birth. Various diseases and insults can interrupt normal fetal brain development and result in lifelong neurodevelopmental and psychiatric disorders (Donofrio et al., 2011; Lynch, 2009; Linnet et al., 2003). Therefore, quantitative assessment of normal and abnormal fetal brain development is very useful. Not only can it enhance our understanding of the development of the brain’s cognitive capabilities, but it can also facilitate the diagnosis, management, and treatment of neurological disorders at their earliest stage (Song et al., 2018; Huang et al., 2009; Kasprian et al., 2013; Xu et al., 2014; Millischer et al., 2022).
Diffusion-weighted magnetic resonance imaging (dMRI) has played an increasingly prominent role in studying the development of fetal brain (Ouyang et al., 2019; Huang et al., 2006, 2009; Jakab et al., 2015). Although it lacks the spatial resolution of postmortem histological analysis, dMRI is non-invasive, significantly faster, and cheaper, enables assessment of the whole brain in utero in 3D, and allows studying large populations. In addition to assessing local tissue microstructure, fetal dMRI can also be used to trace virtual streamlines with tractography techniques. The streamlines provide a visual and quantitative representation of the nerve fibers connecting different areas of the central nervous system. Two important practical applications of tractography include tract-specific analysis of the brain white matter and quantitative structural connectivity assessment.
Tractography-generated streamlines can be used to identify and study specific white matter tracts. Accurate delineation of these tracts is needed in clinical studies and medical research. For example, changes in the micro-structural properties of specific tracts are commonly used in studying brain development and disorders. The majority of manual and automatic methods for segmenting these tracts depend on tractography (Suarez et al., 2012; Garyfallidis et al., 2018; Siless et al., 2020; Karimi, 2024).
Tractography is also the main computation in structural connectivity analysis. Structural connectivity is widely used in neuroscience and medicine to study normal and abnormal brain development (Collin and Van Den Heuvel, 2013; Bullmore and Bassett, 2011). The accuracy and reproducibility of quantitative structural connectivity depend greatly on the accuracy of tractography.
Although dMRI-based tractography suffers from significant challenges, constant technical advancements have improved its accuracy and reproducibility (Sotiropoulos and Zalesky, 2019; Jones et al., 2013). Moreover, our understanding of the capabilities and limitations of tractography have improved (Jones, 2010; Yang et al., 2021). As a result, tractography has been increasingly employed in medical applications and neuroscience research (Glasser and Rilling, 2008; Essayed et al., 2017; Ciccarelli et al., 2008; Lo et al., 2010). However, most recent technical developments and medical applications have focused on post-natal and adult brains. Comparatively, fetal tractography has received far less attention. Fetal brain dMRI suffers from persistent challenges such as low signal-to-noise ratio, imaging artifacts, short scan times, unpredictable motion, and rapid brain development (Tymofiyeva et al., 2014; Khan et al., 2019; Wilson et al., 2021). These factors have made it challenging to analyze fetal dMRI data and to compute the desired results with the same level of accuracy, detail, and reproducibility as in adult brains. Consequently, compared with postnatal and adult brain imaging, fetal dMRI has remained at a primitive stage (Dubois et al., 2014; Jakab et al., 2017; Qiu et al., 2015). In particular, in-utero fetal brain tractography has been much less utilized.
Most prior works on fetal tractography have focused on one or a few selected tract bundles and have shown low success rates and limited accuracy in reconstructing the full extent of the tracts (Song et al., 2018; Kasprian et al., 2008; Mitter et al., 2015b; Zanin et al., 2011; Takahashi et al., 2014; Kolasinski et al., 2013; Ouyang et al., 2019; Huang et al., 2006, 2009; Jakab et al., 2015, 2017). They have mostly applied standard tractography methods with streamline propagation and stopping criteria based on ad-hoc rules such as turning angles or thresholds on fractional anisotropy (FA). This approach can be especially suboptimal for the developing brain, where white matter tracts mature at different rates. The shape and microstructural makeup (hence diffusivity values and FA) of white matter tracts change over time and at different rates for different tracts (Vasung et al., 2019; Kolasinski et al., 2013; Song et al., 2015; Takahashi et al., 2012). To cope with this difficulty, it has been common to empirically adjust FA and angle thresholds in ad-hoc ways to reconstruct different tracts (Millischer et al., 2022; Mitter et al., 2015b). Many studies have resorted to painstaking manual placement of multiple regions of interest (ROIs) to ensure the desired tracts are reconstructed and reduce false positive streamlines (Song et al., 2015; Millischer et al., 2022; Jaimes et al., 2020a; Kasprian et al., 2008). High-quality anatomical images and/or diffusion parameter maps are needed for precise ROI placement (Mitter et al., 2015b; Zanin et al., 2011; Machado-Rivas et al., 2021a). However, even for postmortem fetal brain tissue, where higher quality dMRI data can be acquired, existing tractography methods tend to produce incomplete and noisy results and often fail to reconstruct the full extent of even the major white matter tracts (Takahashi et al., 2014; Song et al., 2015; Takahashi et al., 2012; Kolasinski et al., 2013; Vasung et al., 2010).
Despite their limitations, prior works have demonstrated that tractography has a unique potential for studying normal and abnormal brain development in utero (Huang et al., 2009; Wilson et al., 2021; Kasprian et al., 2008; Mitter et al., 2015b; Zanin et al., 2011; Mitter et al., 2015a; Xu et al., 2014). Past studies have successfully used tractography of the fetal brain to: (1) chart the normal maturation of different white matter tracts and to gain new insights into the timing and speed of tract-specific microstructural changes in utero (Zanin et al., 2011; Hooker et al., 2020; Machado-Rivas et al., 2021b); (2) analyze structural connectivity of the fetal brain (Limperopoulos et al., 2010; Jaimes et al., 2020b); and (3) characterize, classify, and understand the clinical heterogeneity of various brain malformations that begin in the fetal period such as agenesis of corpus callosum (Jakab et al., 2015; Meoded et al., 2011; Kasprian et al., 2013; Millischer et al., 2022). Hence, there is a critical and urgent need for methods and resources to enable accurate and reproducible tractography of the fetal brain. Accurate tractography can advance the field of fetal brain imaging in multiple ways by facilitating qualitative and quantitative assessment of the development of white matter tracts and of the structural connectome.
1.2. Contributions of this work
This paper introduces a new method for fetal brain tractography that leverages tissue segmentation to ensure reconstruction of anatomically valid streamlines. Accurate tissue segmentation enables the implementation of precise streamline seeding and stopping rules that effectively remove spurious streamlines. A deep learning method is developed to compute accurate tissue segmentations. Streamline tracking is performed based on local fiber orientations computed with a diffusion tensor model, which makes the method applicable to single-shell dMRI scans. We tested our method on a set of independent scans and found that it produced significantly more accurate results than a standard tractography technique. Unlike recent methods that work on unique, high-quality data (Wilson et al., 2023, 2021), our method can be applied to more typical dMRI scans. We release our software to enable other research groups to use this method as a benchmark for future studies.
2. Methods
2.1. Imaging data acquisition and preprocessing
In-utero fetal MRI scans for this work were acquired as part of a prospective research study at Boston Children’s Hospital in Boston, MA, between 2013 and 2019. The research was approved by the Institutional Review Board (IRB) and adhered to the Health Insurance Portability and Accountability Act (HIPAA). Participants were recruited in advance and provided written consent before each fetal MRI examination. Only pregnancies between 23 and 36 weeks of gestational age (GA) with mothers between 18 and 45 years were included in this work. The exclusion criteria included contraindications to MRI, any form of high-risk pregnancy, fetal brain anomalies, and maternal comorbidities such as diabetes, hypertension, or substance abuse.
Three Tesla (3T) MRI scanners (Skyra and Prisma, Siemens Medical Solutions) with 16-channel body matrix and spine coils were used to obtain the images. The field of view and number of slices varied based on maternal and fetal dimensions. T2-weighted Half-Fourier Single Shot Turbo Spin Echo (HASTE) fetal brain images were obtained for structural sequences. We acquired multiple images in orthogonal planes with the following acquisition parameters: TR of 1400–2000 ms, TE of 100–120 ms, in-plane resolution of 0.9–1.1 mm, 2 mm slice thickness with no inter-slice space, and 2- or 4-slice interleaved acquisition. For diffusion-weighted images, we obtained 2–8 echo-planar diffusionweighted images, each along orthogonal planes with respect to the fetal head. Each of these acquisitions included one or two images and 12–24 diffusion-sensitized images at . The acquisition parameters for diffusion-weighted images were TR of 3000–4000 ms, TE of 60 ms, in-plane resolution of 2 mm, and slice thickness of 2–4 mm.
All studies were assessed manually for the availability of at least two diffusion-weighted scans without excessive motion-induced artifacts, distortion, and signal loss that could hinder successful motion correction and registration between diffusion-weighted and structural T2-weighted scans. We used a previously validated pipeline (Marami et al., 2016) to process each subject’s diffusion and structural MRI data. This pipeline includes the reconstruction of structural and diffusionweighted volumes with a Kalman filtering-based motion tracking and slice-to-volume registration algorithm (Marami et al., 2016). It registers the dMRI measurements for each subject into a standard atlas space and produces consistent measurements that consist of scattered q-space data in each voxel. We chose an isotropic voxel size of 1.2 mm for the reconstructed dMRI data. These motion-corrected dMRI volumes were used in the subsequent analysis steps described below.
We excluded subjects that were reconstructed with significant errors or unusually low data quality. This decision was made by an expert via visual inspection of mean diffusivity (MD), color fractional anisotropy, and diffusion tensor glyphs to ensure correctness of the direction of principal eigenvectors. As a result, we used 94 fetal scans to develop and validate our new methods (see Fig. 1). From the 94 scans, we randomly selected 11 subjects, one for every gestational age from weeks 23 to 33, to be segmented manually. These 11 manually-labeled scans were used for final independent validation of the deep learning-based tissue segmentation. The remaining 83 subjects were used to train the deep learning method. To assess the quality of the resulting tractography, we randomly selected 27 subjects, two per gestational age from weeks 23 to 36, except for week 34, which had only one test case (see Section 2.5 for more information).
Fig. 1.

Histogram of the number of fetal scans at different gestational ages. The blue bars show the number of scans used as training data for the deep learning model; pale green depicts the number of subjects used as test data for the deep learning model; and orange depicts the number of subjects used for tractography evaluations.
Fig. 2 shows a schematic representation of the data processing and computational steps that are applied to compute a whole-brain tractogram in this work. The main steps include local fiber orientation estimation, tissue segmentation, and anatomically constrained tractography, which are described in the following sections.
Fig. 2.
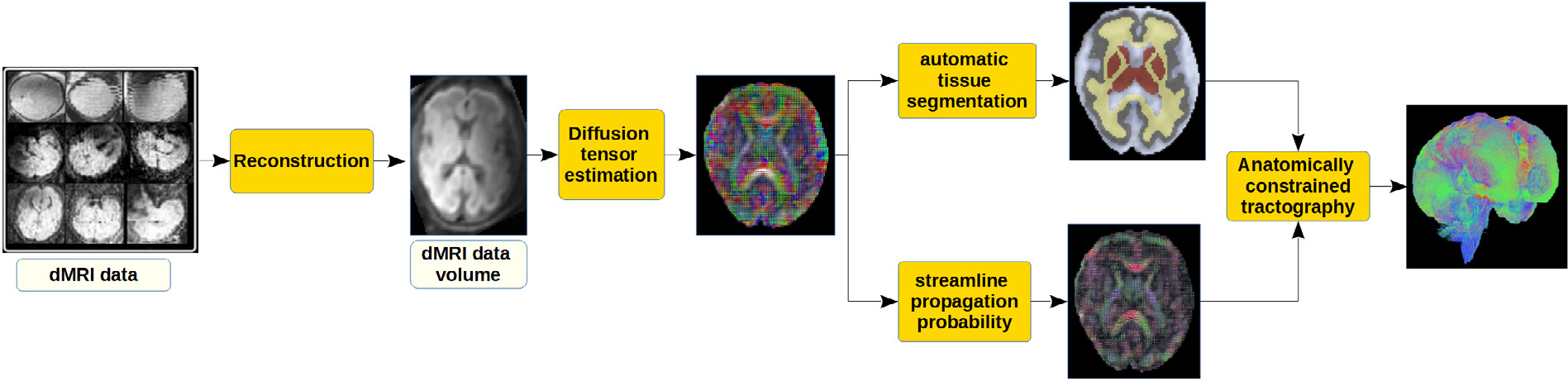
A schematic representation of the data processing steps to compute a whole-brain tractogram in this work. Super-resolved reconstruction of dMRI data volumes is performed using the method described in Marami et al. (2016).
2.2. Estimation of local fiber orientation
Streamline tractography builds upon a voxel-wise estimation of local fiber orientations. It is well known that the accuracy of fiber orientation estimation is one of the main factors influencing the accuracy of tractography (Rheault et al., 2020; Yeh et al., 2021). For post-natal and adult brains, this need has given rise to advanced methods to compute complex fiber configurations in each voxel, such as crossing fibers and asymmetric fiber orientation distributions (Seunarine and Alexander, 2014; Feng and He, 2020). For fetal dMRI, because of the far lower measurement quality, the application of these methods is challenging and rarely attempted. With standard fetal dMRI scans, the diffusion tensor is the most complex model that can be reliably estimated (Dubois et al., 2014; Khan et al., 2019; Jakab et al., 2017). Therefore, we used the tensor model to estimate local fiber orientations in this work.
Given the diffusion signal in a voxel, we estimate the diffusion tensor in that voxel using a weighted linear least squares method (Koay et al., 2006). We then computed the diffusion orientation distribution function (dODF) from the diffusion tensor (D) using the following equation (Aganj et al., 2010; Descoteaux, 2008).
| (1) |
In this equation, is the unit vector denoting the orientation along which the dODF is computed, and denotes the determinant of .
Low diffusion anisotropy in fetal white matter leads to a high prevalence of spurious streamlines with standard tractography techniques. To alleviate this problem, we introduce an ad-hoc but simple and effective method to sharpen the estimated dODF. Specifically, we compute the streamline propagation probability as , i.e., by raising the dODF to power . This operation increases the relative magnitude of along the directions where dODF is larger and reduces its relative magnitude along the directions where dODF is smaller, thereby effectively increasing the anisotropy of . Fig. 3 shows example diffusion tensors and streamline propagation probability maps computed with this approach. We compute for unit vectors on a discrete sphere with 724 uniformly-spaced points.
Fig. 3.

Example diffusion tensors and the corresponding streamline propagation probability maps (p(u)) for three fetuses at three different gestational ages (GAs).
2.3. Segmentation of the brain tissue
Anatomically constrained tractography requires accurate brain tissue segmentation in the dMRI space (Smith et al., 2012). Given the lower spatial resolution and contrast of dMRI, this segmentation is usually obtained via segmenting the anatomical MRI and registering the segmentation to the dMRI space. However, the registration is challenging because the contrast, spatial resolution, and image distortions can differ greatly between the two modalities. Registration errors can significantly impact the accuracy of tractography. Therefore, direct tissue segmentation based on the dMRI data is highly desirable. However, this task is challenging due to the varying contrast of dMRI acquisitions, low SNR, and low spatial resolution. To tackle these challenges, classical machine learning methods such as fuzzy c-means clustering with spatial constraints (Wen et al., 2013), sparse representation of the dMRI signal in dictionaries (Yap et al., 2015), and support vector machines (Ciritsis et al., 2018) have been used in prior works to address this task. More recently, deep learning methods have been attempted by several studies and have shown better results (Golkov et al., 2016; Zhang et al., 2021, 2020, 2015). However, all these prior works have been reported for post-natal and adult brains.
Due to the inferior image quality, rapid brain development, and paucity of training data, segmentation of the fetal brain tissue is significantly more challenging (Makropoulos et al., 2018). Existing works have focused on the segmentation of anatomical MRI images. Several research groups have performed segmentation of the cortical gray matter on T2 images (Dou et al., 2020; Dumast et al., 2021). Segmentation of other tissue types and structures, such as the white matter, ventricles, and cerebellum, has also been addressed by a few recent studies (Fidon et al., 2021; Payette et al., 2023; Karimi et al., 2023). However, segmentation within the dMRI space remains unexplored in the literature. To address this gap, we developed and validated a deep learning method for fast, accurate, and reproducible segmentation of fetal brain tissue directly in dMRI.
2.3.1. Generation of training and test labels
To create a training dataset, we adopted a multi-atlas segmentation strategy by leveraging existing segmentations on high-quality diffusion tensor atlases of fetal brains (Calixto et al., 2023). These atlases have been computed at one-week intervals between 23 and 35 gestational weeks and comprise 12 structures/labels for fetuses under 31 gestational weeks and 11 labels for fetuses aged 31 weeks and above, as shown in Fig. 4. This difference stems from the presence of two transient zones in younger fetuses, namely the subplate and intermediate zones. Note that due to spatial resolution constraints, in our labels, the intermediate zone also contains the ventricular zone and the subventricular zone. Using these atlases, for each fetus, we generated the segmentations by following these steps:
Fig. 4.

Depiction of two diffusion tensor atlases at two different gestational weeks, namely 30 and 35 weeks. The left panel shows manually annotated labels, while the right panel shows the converted labels to the five-tissue-type (5TT) format. The 5TT image is used for anatomically constrained tractography. Please note that the bottom part of the brainstem is converted to a “gray matter” to ensure adequate termination of the streamlines in tractography computation. In the standard 5TT specification, one of the channels is reserved for pathological tissue, which is not shown in the images on the right side because these brains do not include pathological tissue.
The three closest atlases, in terms of gestational weeks (that is, atlases at weeks , , and , for a fetus that is closest to age ) were registered to the subject’s brain. This was performed using a deformable diffusion tensor-based registration technique (Zhang et al., 2006).
The computed registration transformations were used to align the atlas tissue segmentations to the subject fetal brain using a generic interpolator for labeled images (Schaerer et al., 2014). The probabilistic STAPLE algorithm (Akhondi-Asl and Warfield, 2013) was then applied to fuse these segmentations into a final tissue segmentation prediction for the fetus.
Automatic segmentations were reviewed and revised as needed by a board-certified neuroradiologist with fellowship training in pediatric neuroradiology. We excluded automatic segmentations with significant errors, and we ensured the accuracy of the remaining segmentations by having two research fellows with medical training carry out manual refinements where needed.
The resulting tissue segmentation map is then converted to the five-tissue-type (5TT) maps that include five labels: white matter, cortical gray matter, sub-cortical gray matter, CSF, and any pathological tissue. Note that the pathological tissue label is not used in our dataset since we only used healthy brains. Example tissue segmentation maps and 5TT maps are shown in Fig. 4. The 5TT maps are used for anatomically constrained tractography.
The above four-step procedure was used to generate segmentation labels for the 83 fetuses in the training set. For the 11 fetuses in the independent test set, on the other hand, as we mentioned above, an expert manually generated the tissue segmentations by following the same approach as that used for the atlases (Calixto et al., 2023). These manual segmentations were subsequently revised as needed by two neuroradiologists with fellowship training in pediatric neuroradiology. This ensured optimal ground truth labels for validation of the new methods.
2.3.2. Deep learning model development
An important first decision in developing the automatic tissue segmentation model is the choice of the model input. For this application, we decided to compute the model input from the diffusion tensor, , as . In this equation, is the eigenvector associated with the largest eigenvalue and FA is fractional anisotropy. Hence, the input is a three-channel image where each voxel shows the orientation of the highest diffusion, modulated by fractional anisotropy. This representation nicely summarizes the diffusion tensor. The decision to compute the model input from the diffusion tensor has the advantage of improving the method’s generalizability to scans with varying numbers of measurements and different data preprocessing pipelines. Given the fact that the diffusion tensor can be reliably estimated with typical fetal scans, this choice maximizes the method’s applicability. Other informative parameters can be extracted from the diffusion tensor that may be useful for segmenting the tissue. In our experiments, in addition to , we also explored the mean diffusivity (MD) as model input.
Fig. 5 shows our proposed segmentation method. In brief, the method works on image cubes that are partitioned into patches of size voxels. The prediction target is the tissue classification map for the center patch, shown as red in the figure. As input, the network uses the 3-patch and 5-patch neighborhood of the target patch location. Note that the target (center) patch itself is not included in the input context. Therefore 33 − 1, and 53 − 1 patches are used as input to the network.
Fig. 5.

Schematic representation of the tissue segmentation method. (a) A cube from the image is considered. (b) The cube is partitioned into 3D patches. The goal is to predict the tissue segmentation map for the center patch. We consider (33−1)-patch and (53−1)-patch neighborhoods around this center patch, which we denote as and , respectively. (c) Each patch in and is projected into and positional encodings are added to the projections, resulting in sequences and . These projection and positional encoding operations are denoted jointly with Ⓔ. (d) A vision transformer encoder () computes representations and from and . Loss function encourages similarity between these representations. (e) Representation is passed to two decoders, and , which respectively compute the input content and tissue segmentation for the center patch. Loss functions and penalize errors in the input and segmentation predictions for the center patch.
We denote the (33 − 1)- and (53 − 1)-patch inputs as and , respectively. They provide two different “views” of the input image context to the network for performing the desired prediction task. Our method, described in detail below, is based on two mainstream approaches in recent self-supervised machine learning (Balestriero et al., 2023):
Information restoration, which is a very common self-supervised training technique in computer vision and natural language processing (Bao et al., 2021; Pathak et al., 2016). A highly successful recent application in computer vision is the masked autoencoding method proposed in He et al. (2022). In essence, in this approach a part of the image is masked and the model is trained to predict/restore the masked part, thereby learning the structure of the image. This approach also underlies recent breakthroughs in natural language processing that have given rise to models such as BERT and ChatGPT.
Multi-view invariance, which has become a key component of recent self-supervised machine learning methods (Bachman et al., 2019; Chen et al., 2020). This approach works by training the model to learn features that are invariant to simple data transforms. The idea is that simple transforms, such as flipping/magnifying an image, do not change the semantic content of the image. Therefore, the model should compute similar features upon such data transforms. This way, the model can learn the structure of the signal/image without any annotations. In most computer vision applications, data augmentations such as image flip, resize, and random noise are used to generate different views of an image or image patch. In this work, we use input contexts of different sizes. As described below, our method encourages the network to learn similar representations from both input contexts (one larger than the other) for predicting the tissue classification. We think this is a more appropriate approach in this work because operations such as flipping, resizing, or noise manipulation for diffusion tensor images are not trivial and requires extra caution (Zhang et al., 2006; Taquet et al., 2015).
The network itself consists of encoder and decoder sections. The encoder includes five standard vision transformer (ViT) encoder modules (Dosovitskiy et al., 2020). The two decoder sections are 3-layer MLPs of fully-connected layers with ReLU activations. As shown in Fig. 5, each input patch is first projected into , followed by fixed sinusoidal positional encodings similar to Vaswani et al. (2017). These operations (projection and positional encoding) are denoted jointly with Ⓔ in Fig. 5. This creates two input sequences and that are passed through the encoder to compute the representations and . The representation is passed to the two decoders: (1) computes the input image content (i.e., the FA-weighted direction of the major eigenvector) for the center patch; (2) computes the tissue classification for that patch.
Supervised training.
The supervised objective is to achieve accurate tissue classification. We use the cross-entropy loss for this purpose:
| (2) |
where and represent the predicted and ground truth tissue segmentation maps for the center patch.
Self-supervised training.
The self-supervised objective that we propose encourages: (1) the representations ( and ) computed by the encoder for the two input contexts ( and ) to be similar; and (2) the learned representations are useful for predicting the masked input. We achieve this using the following loss functions:
| (3) |
| (4) |
The first term in , based on cosine distance, encourages high similarity between the representations, where and are normalized and . The second term is similar to loss functions proposed by canonical correlation analysis-based techniques such as Barlow Twins (Zbontar et al., 2021) and VICReg (Bardes et al., 2021). In this term, is the cross-correlation of the representations, computed along the batch dimension:
| (5) |
where denotes the data sample index within a batch and is the batch size. This term encourages decorrelation of different elements of the representations computed from the two inputs. It is a standard technique to avoid dimensional collapse, which is the most common pitfall in self-supervised machine learning (Balestriero et al., 2023). As in Zbontar et al. (2021), we normalize the representations such that they have a mean of zero across the batch size and a unit norm for each data sample.
The second self-supervised loss, , encourages accurate prediction of the center image patch. In this equation, and represent, respectively, the predicted and true image content for the center patch. Note that in both Eqs. (4) and (2), the total loss for each patch is the voxel-wise sum for all voxels in the patch.
The combined loss function used to train the model is a weighted sum of the supervised and self-supervised loss terms:
| (6) |
The inclusion of self-supervised training objectives has several advantages. First, based on the results of recent works in computer vision, they are expected to improve the performance on the main task, i.e., tissue classification. Second, self-supervised learning has been shown to be an effective technique for reducing the impact of label noise (Zheltonozhskii et al., 2022; Ghosh and Lan, 2021). This can be important in this work because the inherently low contrast in fetal dMRI leads to inevitable label noise, even in manual annotations. Moreover, self-supervised learning enables us to use additional unlabeled data. In this work, we used 129 preterm newborn subjects scanned between 26 and 36 gestational weeks from the developing Human Connectome Project (dHCP) neonatal dataset (Bastiani et al., 2019). For training with these unlabeled data, we dropped the supervised loss term from the combined loss .
We empirically set the hyper-parameters as follows: , and patch side length voxels. To train the network using the combined loss, we used the Adam optimization method (Kingma and Ba, 2014) with an initial learning rate of 0.001. We reduced the learning rate by a factor of 0.90 after a training epoch if the validation loss did not decrease. Training with the labeled and unlabeled data was performed in tandem and alternately. Specifically, odd training iterations used a batch of unlabeled data from the dHCP neonatal dataset, and even training iterations used a batch of labeled training data from our fetal scans. We used a batch size of 50. The network was implemented in TensorFlow 1.4 and run on an NVIDIA RTX A6000 GPU on a Linux machine with 128 GB of memory and 20 CPU cores.
2.4. Streamline tracing
The method developed in this work was based on the anatomicallyconstrained tractography framework (Smith et al., 2012). For streamline propagation, we use the 2nd-order integration over fiber orientation distributions (iFOD2) algorithm (Tournier et al., 2010) implemented in MRtrix3 (Tournier et al., 2019). Streamlines are launched at the boundary of white matter and (cortical and sub-cortical) gray matter. Any streamline that violates the rules of anatomically-constrained tractography is discarded. The main steps of the algorithm are summarized in Algorithm 1.

For streamline propagation with iFOD2 we used a step size of 0.6 mm and angle threshold of 20°. We aimed to reconstruct various projection, association, and commissural fibers while minimizing the number of U-fibers. As the range of valid streamline lengths varies depending on the brain size, we set the maximum streamline length based on the total brain volume (in mm3) to reduce overly long erroneous streamlines. This strategy was helpful in avoiding unrealistic but anatomically valid streamlines (e.g., a streamline that starts at the brainstem, traverses the internal capsule, crosses over to the contralateral hemisphere via the corpus callosum, and then loops back to the brainstem through the contralateral internal capsule). On the other hand, setting a proper minimum length effectively reduced short association fibers, which typically do not contribute to major fiber bundles. The lower and upper thresholds were determined by initially performing global tractography on a few selected subjects and examining the results. Initially, the minimum streamline length was set at 15 mm and the maximum at 190 mm. After extracting 11 tracts, as listed below, we recorded the shortest streamline length of each tract for every subject. The lowest value among all tracts for every subject was then chosen as the minimum length threshold. Following that, we recorded the 95th percentile of streamline lengths for every tract. The highest value among all tracts for every subject was then selected as the upper limit. These values were utilized in combination with the subject’s brain volume to derive the equations presented below.
| (7) |
2.5. Evaluation
We compared our proposed segmentation method with Attention U-Net (Oktay et al., 2018). In order to assess the impact of segmentation approach and model input, we trained and tested Attention U-Net with two different inputs: (1) our proposed input explained in Section 2.3.2, and (2) Mean diffusivity (MD). We evaluated the accuracy of the automatic tissue segmentation method in terms of Dice similarity coefficient (DSC), 95th percentile of the Hausdorff distance (HD95), and average symmetric surface distance (ASSD). An expert also visually inspected the segmentation maps computed by the automatic method.
To assess the performance of the new anatomically constrained tractography method, we applied it to compute whole-brain tractograms for 27 randomly selected subjects, with two subjects per gestational age from weeks 23 to 36, except for week 34, where only one subject had at least one tract reconstruction in the additional comparison methods (see below). We generated 5 million streamlines for each brain, and two neuroradiologists with specialized training in pediatric neuroradiology and six years of experience in fetal imaging visually inspected the whole brain tractograms.
Additionally, we compared our results with previously established techniques. Thus, we computed whole-brain tractograms for the 27 subjects, implementing the iFOD2 algorithm with standard settings, the Fiber Assignment by Continuous Tracking (FACT) algorithm (Mori et al., 1999), and the 2nd order Runge–Kutta (rk2) algorithm (Basser et al., 2000). For FACT and rk2, we set the maximum angle to 35, which we found to give the best results among different angles (15 to 45) tested in our experiments.
We automatically extracted eleven different tracts (see below) using TractQuerier and the definitions provided by Wassermann et al. (2016). Aside from the tissue segmentations, this method requires cortical gray matter parcellations. To achieve this, we utilized ANTs’ symmetric deformable registration (Avants et al., 2008) to register a previously parcellated T2 atlas of the fetal brain (which can be found at: http://www.crl.med.harvard.edu/research/fetal_brain_atlas/) to the MD map of each subject (using the age-corresponding atlas). The extracted tracks were Anterior Thalamic Radiation (ATR), Genu and Isthmus of the Corpus Callosum (CC 2 and CC 6, respectively), Cortico-Spinal Tract (CST), Frontal Aslant Tract (FAT), Fronto-Pontine Tract (FPT), Inferior Occipito-Frontal fascicle (IFO), Inferior Longitudinal Fascicle (ILF), Middle Longitudinal Fascicle (MLF), Optic Radiations (OR), and Uncinate Fascicle (UF).
Subsequently, two neuroradiologists (independent of each other) assessed each tract generated by our proposed method and the three other methods. Each radiologist rated every tract (four representations for every method and ten tracts per subject for 27 subjects) using a Likert scale ranging from 1 to 5 based on the specifications shown in Table 1. The raters were blinded to which method corresponded to each visualization. The readers were provided with mean diffusivity and fractional anisotropy maps, and no limitations were imposed on window-level setting adjustments.
Table 1.
Likert scale used to rate the tractography results.
| Score | Quality | Description |
|---|---|---|
| 1 | Not reconstructed | The tract failed to be reconstructed. |
| 2 | Poor | The tract is present but significantly deviates from the expected anatomical pathway or includes incorrect routes. It may also suffer from very sparse streamline density, making the tract challenging to identify confidently. |
| 3 | Fair | The tract generally follows the correct pathway with some deviations. The route is plausible, but minor inaccuracies in streamline alignment or density may affect its clarity or anatomical accuracy. |
| 4 | Good | The tract closely adheres to the expected anatomical pathway with minimal deviations. The route accuracy is high, and the density of streamlines is sufficient to clearly define the tract’s structure without excessive sparsity or overcrowding. |
| 5 | Excellent | The tract matches the expected anatomical pathway with no deviations. Streamline density is optimal, providing a detailed, clear, and anatomically precise representation of the tract. |
To assess the differences in reconstruction quality between the different methods, we used a mixed-effects model while accounting for random effects due to “Subject”, “Tract”, and “Rater”. The fixed effect in the model was the tractography method. Following the model fitting, we performed post-hoc pairwise comparisons using Tukey’s Honest Significant Difference (HSD) test to determine statistically significant differences between the methods. The results were adjusted for multiple comparisons using the single-step method. To evaluate if GA had an impact on the ratings (and thus on the reconstruction quality), we used a mixed-effects model while accounting for random effects attributed to “Subject”, “Tract”, and “Rater”. Because FACT, rk2, and iFOD2 without ACT often failed to reconstruct the tracts, and we aimed to compare the quality of successful reconstructions, the mixed-effects models were only fed with data in which the tract has been reconstructed. Thus, tracts with a Likert score rating of 1 were discarded. We measured inter-rater reliability using Cohen’s kappa statistic.
We also compared our proposed method with FACT in terms of sensitivity to the angle threshold, which is one of the main settings in every tractography algorithm. Tractography results, especially for the fetal brain, can be highly sensitive to angle threshold setting, requiring careful adjustment to ensure reconstruction of the tracts of interest. Therefore, a method that is less sensitive to this setting is highly desirable as it can improve the tractography accuracy and reduce the need for manual adjustment of the angle setting for every subject/tract. In order to perform this comparison, we applied our method with three angle thresholds of 15°, 20°, and 25°, and we applied FACT with three angle thresholds of 25°, 30°, and 35°. These angles were selected to ensure the best overall tractography accuracy for the two methods. We converted the tracts to binary masks by following these steps: (1) Compute tract density maps, where each voxel shows the number of streamlines crossing that voxel; (2) Compute a density threshold as the 1% percentile of the non-zero densities; (3) Exclude voxels where the tract density is below the threshold. Other non-zero voxels represent the binary mask of the extracted tract. After computing the binary masks, we computed pair-wise DSC, HD95, ASSD, and relative volume difference (VolDiff) between the three tracts reconstructed with the three angle thresholds to quantify the sensitivity of the method to angle threshold. We define VolDiff between two binary masks and as .
3. Results
Out of 230 fetal dMRI examinations available in the retrospective studies, 53 (23%) were excluded due to very poor dMRI data quality. From the remaining 177 scans, 76 (33%) were not successfully reconstructed with our Kalman filtering-based motion tracking and slice-to-volume registration method (Marami et al., 2016). Moreover, 7 (3%) of the scans that were successfully reconstructed were excluded due to poor post-reconstruction data. Therefore, 94 (40%) scans were included in this study.
3.1. Assessment of automatic brain tissue segmentation
Fig. 6 shows example fetal brain tissue segmentation results computed by the deep learning method compared with the manuallygenerated ground truth. They show that the automatic method can accurately segment all four tissue types. Visual assessments by an expert confirmed that the computed segmentations were free of any major errors.
Fig. 6.

Examples of segmentations predicted by our proposed method in three subjects at three different gestational ages (GA). Each panel shows the manual segmentation on the left, overlaid on the mean diffusivity (MD) map, and the segmentation error map of the proposed method on the right. GM stands for gray matter, and CSF stands for corticospinal fluid.
Table 2 presents quantitative segmentation performance metrics for the four tissue types. The average DSC for white matter, cortical gray matter, sub-cortical gray matter, and CSF was, respectively, 0.89, 80.830, 0.837, and 0.841. These values are in the range of performance metrics reported for the state-of-the-art segmentation methods applied on fetal T2 MRI in recently-published studies (Payette et al., 2023; Fidon et al., 2021; Dou et al., 2020; Dumast et al., 2021). For white matter, for example, the DSC values achieved by several deep learning methods in a recent study (Payette et al., 2023) were in the range 0.85–0.90, while for our method in this work it was 0.898 ± 0.024. Similarly, surface distance error quantified in terms of HD95 and ASSD are comparable with the results of recent deep learning methods for T2 segmentation (Payette et al., 2023), including our own work (Karimi et al., 2023). These results indicate that the proposed method is able to segment the fetal brain tissue with satisfactory accuracy in dMRI, which has an inherently lower signal quality than T2.
Table 2.
Segmentation performance metrics for the proposed method. Note that higher values of DSC and lower values of HD95 and ASSD are desirable. HD95 and ASSD are in millimeters.
| Cortical gray matter | Sub-cortical gray matter | White matter | Cerebrospinal fluid | ||
|---|---|---|---|---|---|
|
| |||||
| Proposed method | DSC | 0.841 ± 0.022 | 0.848 ± 0.024 | 0.900 ± 0.016 | 0.858 ± 0.020 |
| HD95 | 1.035 ± 0.020 | 1.044 ± 0.030 | 0.921 ± 0.023 | 1.001 ± 0.023 | |
| ASSD | 0.241 ± 0.062 | 0.224±0.060 | 0.201 ± 0.055 | 0.229 ± 0.061 | |
|
| |||||
| Attention U-Net (input: u) | DSC | 0.811 ± 0.026 | 0.815 ± 0.027 | 0.851 ± 0.020 | 0.813 ± 0.019 |
| HD95 | 1.099 ± 0.024 | 1.066 ± 0.030 | 0.984 ± 0.029 | 1.070 ± 0.029 | |
| ASSD | 0.247 ± 0.068 | 0.248 ± 0.064 | 0.217 ± 0.067 | 0.266 ± 0.069 | |
|
| |||||
| Attention U-Net (input: MD) | DSC | 0.812 ± 0.030 | 0.807 ± 0.027 | 0.840 ± 0.023 | 0.805 ± 0.022 |
| HD95 | 1.100 ± 0.023 | 1.081 ± 0.033 | 1.004 ± 0.031 | 1.095 ± 0.027 | |
| ASSD | 0.247 ± 0.064 | 0.256 ± 0.069 | 0.228 ± 0.063 | 0.269 ± 0.068 | |
The segmentation performance of our method was also consistently better than Attention U-Net on all four tissue types in terms of DSC, HD95, and ASSD. In terms of DSC, our method achieved 2.9%, 3.3%, 4.9%, and 4.5% higher average for cortical gray matter, sub-cortical gray matter, white matter, and cerebrospinal fluid, respectively. Paired t-tests showed that for all four tissue types this difference was statistically significant with . Moreover, as shown in Table 2, Attention U-Net trained with as input also achieved overall better segmentation accuracy than when trained with MD as input, except for segmentation of the cortical gray matter where the results were similar.
3.2. Assessment of extracted tracts
We extracted a total of 11 tracts. Fig. 7 displays seven selected tracts for a visual comparison between our proposed method and FACT. Our proposed method had the highest percentage of successful tract reconstructions, averaging 99.9%. Our method was the only one that was able to reconstruct the FAT tract. Therefore, FAT was not included in any of the subsequent analyses. The second best method in terms of reconstruction success rate was iFOD 2 with 72.2%, followed by FACT with 55.6%, and rk2 with 52.2%. Fig. 8C displays the reconstruction success rate for each tract by every method. Our proposed method also had the highest quality ratings, averaging 4.27, followed by iFOD2 with 1.80, FACT with 1.72, and rk2 with 1.68. Fig. 8 A shows a detailed average of the quality scores for each tract for every method, while Fig. 8B shows the distribution of the ratings. Most ratings for our proposed method were “good” or “excellent”, while the ratings of tract reconstructions for the other methods were either “poor” or the tract was not reconstructed at all.
Fig. 7.

A visual comparison of seven different tracts reconstructed by the proposed method and FACT for three fetal brains at three different gestational ages (GA). Tracts are overlaid on the mean diffusivity (MD) maps. The following tracts are shown: Genu of the Corpus Callosum (CC_2), Cortico-Spinal Tract (CST), Frontal Aslant Tract (FAT), Fronto-Pontine Tract (FPT), Inferior Occipito-Frontal fascicle (IFO), Inferior Longitudinal Fascicle (ILF), and Optic Radiations (OR). A white asterisk on an image means the tract was not reconstructed by that method.
Fig. 8.

Comparison of the tractography methods. (A) Heatmap displaying the average ratings for each tractography method across different tracts. Each cell is annotated with the average rating value. (B) Bar plot showing the percentage distribution of reconstruction quality ratings for each tractography method. (A) and (B) share the same legend of ratings categorized from “(1) Not reconstructed” to “(5) Excellent”. (C) Heatmap quantifying the percentage of successful tract reconstructions by each method. Percentages are shown on the plot, increasing brightness with higher success rates. (D) Scatter plot with fitted lines illustrating how ratings vary with gestational age for each tractography method. Points are jittered to prevent overplotting, and lines indicate trends, providing insights into how method effectiveness might change over the gestational period.
The linear mixed-effects model analysis indicated significant differences in the ratings assigned to different tractography methods. The random effects variance was relatively small, indicating that while there were some variations between subjects, tracts, and raters, they were not the dominant sources of variability in the ratings. In the subsequent Tukey HSD tests, the pairwise comparisons among the tractography methods yielded the following results:
Proposed vs. FACT: The Proposed method was significantly superior to FACT, showing a substantial increase in ratings (
Proposed vs. rk2: The Proposed method significantly outperformed the rk2 method ().
Proposed vs. iFOD2: The Proposed method also showed significant improvement over the iFOD2 method (.
iFOD2 vs. FACT: iFOD2 was rated significantly lower than FACT (Estimate = −0.18, p < 0.001)
iFOD2 vs. rk2: iFOD2 was rated significantly lower than rk2 (
We also assessed the effect of GA in the ratings, as shown in Fig. 8D, and found that there was no significant association between the ratings and the GA .
Table 3 summarizes the results of the experiment to quantify the impact of angle threshold setting on the reconstruction of the tracts for the proposed method and FACT. In this experiment, the tracts were converted to binary masks, as described in Section 2.5, and several metrics of agreement/disagreement between pairs of tracts reconstructed with different angle thresholds were computed. The values in Table 3 represent the summary for all 11 tracts considered. These results show that the new method is highly robust to the setting. Changing the angle threshold between 15° and 25° had a small impact on the tract reconstruction results, with a mean pair-wise DSC of 0.941 for all tracts. For all four evaluation criteria shown in Table 3, the results for our method were significantly () better compared with FACT.
Table 3.
Results of the experiment to assess the robustness of tractography methods to angle threshold setting. The values shown are computed pair-wise between the tracts reconstructed with different angle thresholds. Note that higher values of DSC and VolDiff and lower values of HD95 and ASSD are desirable.
| DSC | HD95 (mm) | ASSD (mm) | VolDiff | |
|---|---|---|---|---|
|
| ||||
| Proposed method | 0.941 ± 0.042 | 0.815 ± 0.027 | 0.208 ± 0.103 | 0.083 ± 0.032 |
| FACT | 0.605 ± 0.119 | 1.664 ± 0.157 | 0.751 ± 0.195 | 0.279 ± 0.122 |
4. Discussion
This paper introduces the development and validation of an anatomically constrained fetal brain tractography method. Our method relies on the classification/segmentation of brain tissue into white matter, cortical and subcortical gray matter, and cerebrospinal fluid. These segmentations are automatically computed by a deep learning method directly in the dMRI space, a valuable capability not reported in prior works. The segmentation method only requires the diffusion tensor map as the input. The same diffusion tensor map is used to infer the streamline propagation direction for computing the tractogram. We convert the diffusion tensor into a sharpened diffusion orientation distribution function that helps minimize the probability of computing spurious streamlines and enables advanced probabilistic tractography methods such as iFOD2.
Our automatic segmentation method outperforms multi-atlas-based approaches. In our previous work, we achieved a DSC of 0.75 ± 0.17 for cortical gray matter, 0.69–0.86 ± 0.14 for sub-cortical gray matter structures, and 0.70–0.87 ± 0.15 for white matter structures (Calixto et al., 2023). The new deep learning method far surpasses this method, with higher average DSC values and narrower standard deviations for all tissue types. Moreover, multi-atlas-based automatic segmentation for this data typically takes 15–25 min per subject, while our deep learning approach usually has an inference time of 3–5 s. Surface distance errors presented in Table 2 show that HD95 (representing large surface distance errors) for white matter, cortical gray matter, and sub-cortical gray matter are all approximately 1 mm, while the ASSD (representing average surface distance errors) are approximately 0.20–0.25 mm. These numbers suggest that our method can be used for accurate seeding and stopping operations that are essential for anatomically constrained tractography.
Accurate tissue classification enables us to: (1) Launch the streamlines at seed points on the boundary between white matter and gray matter, and (2) Effectively remove the spurious and anatomically invalid streamlines and only preserve valid streamlines based on their paths and endpoints. Effective use of anatomical information enables us to avoid premature termination of valid streamlines or generation of implausible streamlines that are prevalent in fetal tractography, as observed in this study with FACT. Standard tractography methods rely purely on the local diffusion tensor information for streamline propagation and termination (e.g., based on FA). This can lead to high false positive and false negative rates because of the low fetal dMRI data quality, which can give rise to noisy and inaccurate diffusion tensor estimates.
We evaluated the new method on a set of independent test subjects and compared the results to tractography generated using FACT. Our manual extraction of the tracts followed established criteria regarding where streamlines should start and pass through and which structures to avoid (Wassermann et al., 2016). We followed the same tract definitions and extraction procedures for all tractography methods. Expert evaluations showed that our method consistently outperformed the other methods in terms of expert scores. Our method was consistently successful in reconstructing prominent white matter tracts. A visual comparison of the tracts reconstructed by our method and the results on adult brains recently produced with the Human Connectome Project data (Wasserthal et al., 2018) show that our results on fetal brains are qualitatively comparable with adult brains.
The three compared methods failed to reconstruct many of the tracts, as summarized in Fig. 8. Moreover, as shown in the examples for FACT in Fig. 7, these competing methods were often limited in their ability to reconstruct a sufficient number of streamlines for the reconstructed tracts. While some cases in our method (like the FPT tract for the fetus at GA of 30 in Fig. 7) exhibited less dense frontal fibers than anticipated, our approach achieved a very high success rate. The ratings assigned to the tracts reconstructed with our method by two independent experts were far higher than those for the other three tractography methods. Furthermore, our approach successfully reconstructed the tracts with high-curvature sections, such as the optic radiations and the lateral projections of the CST.
Comparing our results with those of prior works on in-utero fetal tractography reveals significant advancements in the anatomical accuracy and completeness of neural tracts, addressing limitations observed in earlier research. Here, we detail these comparisons for specific tracts, underscoring the enhancements our method provides. It is worth noting that comparisons for the ATR, FAT, and MLF are absent, as no previous work has extracted them on fetuses.
Corpus Callosum: Prior investigations have focused on specific segments of the corpus callosum (Jaimes et al., 2020a; Machado-Rivas et al., 2021b; Wilson et al., 2021; Kasprian et al., 2008; Zanin et al., 2011; Mitter et al., 2015b). Our approach stands out in its ability to consistently generate tracts connecting both the medial and lateral surfaces of the frontal lobes within the forceps minor. Furthermore, our streamlines terminate accurately at the gray matter — white matter interface without prematurely ending or crossing the cortical plate and ending into the CSF.
CST: Earlier studies have encountered difficulties in fully extracting the CST, often resulting in premature termination of streamlines (Kasprian et al., 2008; Zanin et al., 2011) or failure to capture lateral projections (Jaimes et al., 2020a; Machado-Rivas et al., 2021b). Unlike these studies, our approach consistently captures the complete intracranial CST, avoiding inaccuracies such as streamline termination in the CSF or implausible crossing through deep gray matter structures (Wilson et al., 2021).
FPT: Limited research has depicted the FPT in fetuses. Our findings show more extensive tract delineation, reaching all intended frontal targets without the premature termination observed in prior works (Mitter et al., 2015b).
IFO: Unlike other works, our tracts reach all expected cortical targets (Song et al., 2015; Jaimes et al., 2020a; Machado-Rivas et al., 2021b), terminate at the junction of gray matter and white matter (Mitter et al., 2015b) and, most importantly, traverse the expected path through the external capsule.
ILF: Our work surpasses previous works (Song et al., 2015; Jaimes et al., 2020a) on generating a fuller tract that reaches all cortical targets and has results comparable to those of Machado-Rivas et al. (2021b) and Wilson et al. (2021) However, it is worth noting that in the two works above, only some branches of the ILF are visualized. They miss the branch connecting the cuneus to the anterior mesial temporal gyri.
OR: Unlike prior attempts, our method ensures that optic radiation streamlines do not prematurely terminate (Zanin et al., 2011) and exclusively traverse white matter to reach the occipital lobe, avoiding aberrant terminations (Wilson et al., 2021) or ventricular crossings (Corroenne et al., 2023) noted in earlier studies.
UF: While our findings align with the trajectory observed in previous studies for the UF (Jaimes et al., 2020a; Mitter et al., 2015b), we additionally note that our tracts achieve expected orbital targets, indicating an improvement over prior works.
4.1. Limitations
Our study has some limitations. Firstly, the sample size of 94 fetuses is relatively small due to the challenges of subject recruitment, fetal imaging, and the moderate success rate of the dMRI reconstruction pipeline. Moreover, generating manual segmentation labels on 3D images is very time-consuming. We evaluated our tissue segmentation method and the complete tractography technique on, respectively, 11 and 27 test subjects and found statistically significant improvements compared with the competing techniques. Nonetheless, increasing the data size for method development and validation will be useful.
Secondly, our data was obtained from a single center and we employed an in-house pipeline for preprocessing of the dMRI data. Validation of data from other centers can help assess the generalizability of our method. Additionally, evaluating our method with different quality or multi-shell dMRI data can also be useful. As we have pointed out above, some recent works have used unique high-quality data that include multi-shell densely-sampled q-space measurements (Wilson et al., 2023, 2021). In typical clinical or research fetal studies, acquiring such data is not possible given the time constraints. Our method, on the other hand, has been designed to work with the more typical fetal dMRI scans that may include as few as 24 measurements in a single shell. We think this is a significant advantage of our method because HCP-style data are very rare in fetal studies. Nonetheless, applying our method to higher-quality data will be useful in highlighting its potential advantages and limitations compared with existing techniques.
Another limitation of our evaluations was that our data included healthy subjects only. Future works can study the performance of our method on abnormal fetal brains. Lastly, we anticipate that our method can lead to significant improvements in the accuracy and reproducibility of structural connectivity analysis, which is a main application of tractography. We aim to pursue this line of investigation in our future work.
5. Conclusions
Our study has demonstrated the feasibility of anatomicallyconstrained tractography of the fetal brain. The new method proposed in this work presents a significant stride toward improving the accuracy of fetal brain tractography. The higher tract reconstruction success rate and accuracy offered by our method can enhance the accuracy of dMRIbased studies of the fetal brain white matter in utero. It can also enable reliable quantitative assessment of the structural connectivity of the fetal brain. Ultimately, these new capabilities can enable important scientific and clinical applications and lead to a better understanding of brain development at its earliest stage.
Acknowledgments
This research was supported in part by the National Institute of Neurological Disorders and Stroke, United States under award numbers R01 NS128281 and R01 NS106030; the Eunice Kennedy Shriver National Institute of Child Health and Human Development, United States under award numbers R01 HD110772 and R01 HD109395; the National Institute of Biomedical Imaging and Bioengineering, United States under award numbers R01 EB031849, R01 EB032366, R01 EB018988, and R01 EB013248; the Office of the Director of the NIH under award number S10 OD0250111; the Rosamund Stone Zander Translational Neuroscience Center, Boston Children’s Hospital; the Office of Faculty Development at Boston Children’s Hospital; and a scholarship from the American Roentgen Ray Society, United States. The content of this publication is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Footnotes
Declaration of competing interest
None.
CRediT authorship contribution statement
Camilo Calixto: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing, Visualization. Camilo Jaimes: Conceptualization, Formal analysis, Investigation, Supervision, Writing – review & editing. Matheus D. Soldatelli: Formal analysis, Investigation, Methodology, Validation, Writing – original draft. Simon K. Warfield: Formal analysis, Investigation, Supervision, Writing – review & editing. Ali Gholipour: Data curation, Formal analysis, Funding acquisition, Investigation, Project administration, Resources, Supervision, Writing review & editing. Davood Karimi: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Writing – original draft, Writing – review & editing.
Data availability
Data will be made available on request.
References
- Aganj Iman, Lenglet Christophe, Sapiro Guillermo, Yacoub Essa, Ugurbil Kamil, Harel Noam, 2010. Reconstruction of the orientation distribution function in singleand multiple-shell q-ball imaging within constant solid angle. Magn. Reson. Med. 64 (2), 554–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akhondi-Asl Alireza, Warfield Simon K., 2013. Simultaneous truth and performance level estimation through fusion of probabilistic segmentations. IEEE Trans. Med. Imaging 32 (10), 1840–1852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants Brian B, Epstein Charles L, Grossman Murray, Gee James C, 2008. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 12 (1), 26–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachman Philip, Hjelm R. Devon, Buchwalter William, 2019. Learning representations by maximizing mutual information across views. Adv. Neural Inf. Process. Syst. 32. [Google Scholar]
- Balestriero Randall, et al. , 2023. A cookbook of self-supervised learning. arXiv preprint arXiv:2304.12210. [Google Scholar]
- Bao Hangbo, Dong Li, Piao Songhao, Wei Furu, 2021. Beit: Bert pre-training of image transformers. arXiv preprint arXiv:2106.08254. [Google Scholar]
- Bardes Adrien, Ponce Jean, LeCun Yann, 2021. Vicreg: Variance-invariance-covariance regularization for self-supervised learning. arXiv preprint arXiv:2105.04906. [Google Scholar]
- Basser Peter J, Pajevic Sinisa, Pierpaoli Carlo, Duda Jeffrey, Aldroubi Akram, 2000. In vivo fiber tractography using DT-MRI data. Magn. Reson. Med. 44 (4), 625–632. [DOI] [PubMed] [Google Scholar]
- Bastiani Matteo, et al. , 2019. Automated processing pipeline for neonatal diffusion MRI in the developing human connectome project. NeuroImage 185, 750–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayer Shirley A., Altman Joseph, 2005. The Human Brain During the Second Trimester. CRC Press. [Google Scholar]
- Bullmore Edward T., Bassett Danielle S., 2011. Brain graphs: graphical models of the human brain connectome. Annu. Rev. Clin. Psychol. 7, 113–140. [DOI] [PubMed] [Google Scholar]
- Calixto Camilo, Machado-Rivas Fedel, Karimi Davood, Cortes-Albornoz Maria C, Acosta-Buitrago Lina M, Gallo-Bernal Sebastian, Afacan Onur, Warfield Simon K, Gholipour Ali, Jaimes Camilo, 2023. Detailed anatomic segmentations of a fetal brain diffusion tensor imaging atlas between 23 and 30 weeks of gestation. Hum. Brain Mapp. 44 (4), 1593–1602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Ting, Kornblith Simon, Norouzi Mohammad, Hinton Geoffrey, 2020. A simple framework for contrastive learning of visual representations. In: International Conference on Machine Learning. PMLR, pp. 1597–1607. [Google Scholar]
- Ciccarelli Olga, Catani Marco, Johansen-Berg Heidi, Clark Chris, Thompson Alan, 2008. Diffusion-based tractography in neurological disorders: concepts, applications, and future developments. Lancet Neurol. 7 (8), 715–727. [DOI] [PubMed] [Google Scholar]
- Ciritsis Alexander, Boss Andreas, Rossi Cristina, 2018. Automated pixel-wise brain tissue segmentation of diffusion-weighted images via machine learning. NMR Biomed. 31 (7), e3931. [DOI] [PubMed] [Google Scholar]
- Collin Guusje, Van Den Heuvel Martijn P., 2013. The ontogeny of the human connectome: development and dynamic changes of brain connectivity across the life span. Neuroscientist 19 (6), 616–628. [DOI] [PubMed] [Google Scholar]
- Corroenne R, Grevent D, Salomon LJ, 2023. Tractography of fetal visual pathway. Ultras. Obstet. Gynecol. 62 (4), 614–615. [DOI] [PubMed] [Google Scholar]
- Descoteaux Maxime, 2008. High Angular Resolution Diffusion MRI: from Local Estimation to Segmentation and Tractography (Ph.D. thesis). Université Nice Sophia Antipolis. [Google Scholar]
- Donofrio Mary T., Limperopoulos Catherine, et al. , 2011. Impact of congenital heart disease on fetal brain development and injury. Curr. Opin. Pediatr. 23 (5), 502–511. [DOI] [PubMed] [Google Scholar]
- Dosovitskiy Alexey, Beyer Lucas, Kolesnikov Alexander, Weissenborn Dirk, Zhai Xiaohua, Unterthiner Thomas, Dehghani Mostafa, Minderer Matthias, Heigold Georg, Gelly Sylvain, et al. , 2020. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929. [Google Scholar]
- Dou Haoran, Karimi Davood, Rollins Caitlin K, Ortinau Cynthia M, Vasung Lana, Velasco-Annis Clemente, Ouaalam Abdelhakim, Yang Xin, Ni Dong, Gholipour Ali, 2020. A deep attentive convolutional neural network for automatic cortical plate segmentation in fetal MRI. IEEE Trans. Med. Imaging 40 (4), 1123–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubois Jessica, Dehaene-Lambertz Ghislaine, Kulikova Sofya, Poupon Cyril, Hüppi Petra S, Hertz-Pannier Lucie, 2014. The early development of brain white matter: a review of imaging studies in fetuses, newborns and infants. Neuroscience 276, 48–71. [DOI] [PubMed] [Google Scholar]
- Dumast Priscille de, Kebiri Hamza, Atat Chirine, Dunet Vincent, Koob Mériam, Cuadra Meritxell Bach, 2021. Segmentation of the cortical plate in fetal brain MRI with a topological loss. In: Uncertainty for Safe Utilization of Machine Learning in Medical Imaging, and Perinatal Imaging, Placental and Preterm Image Analysis. Springer, pp. 200–209. [Google Scholar]
- Essayed Walid I, Zhang Fan, Unadkat Prashin, Cosgrove G Rees, Golby Alexandra J, O’Donnell Lauren J, 2017. White matter tractography for neurosurgical planning: A topography-based review of the current state of the art. NeuroImage: Clin. 15, 659–672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Yuanjing, He Jianzhong, 2020. Asymmetric fiber trajectory distribution estimation using streamline differential equation. Med. Image Anal. 63, 101686. [DOI] [PubMed] [Google Scholar]
- Fidon Lucas, Aertsen Michael, Mufti Nada, Deprest Thomas, Emam Doaa, Guf fens Frédéric, Schwartz Ernst, Ebner Michael, Prayer Daniela, Kasprian Gregor, et al. , 2021. Distributionally robust segmentation of abnormal fetal brain 3D MRI. In: Uncertainty for Safe Utilization of Machine Learning in Medical Imaging, and Perinatal Imaging, Placental and Preterm Image Analysis. Springer, pp. 263–273. [Google Scholar]
- Garyfallidis Eleftherios, Côté Marc-Alexandre, Rheault Francois, Sidhu Jasmeen, Hau Janice, Petit Laurent, Fortin David, Cunanne Stephen, Descoteaux Maxime, 2018. Recognition of white matter bundles using local and global streamline-based registration and clustering. NeuroImage 170, 283–295. [DOI] [PubMed] [Google Scholar]
- Ghosh Aritra, Lan Andrew, 2021. Contrastive learning improves model robustness under label noise. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 2703–2708. [Google Scholar]
- Glasser Matthew F., Rilling James K., 2008. DTI tractography of the human brain’s language pathways. Cerebral Cortex 18 (11), 2471–2482. [DOI] [PubMed] [Google Scholar]
- Golkov Vladimir, Dosovitskiy Alexey, Sperl Jonathan I, Menzel Marion I, Czisch Michael, Sämann Philipp, Brox Thomas, Cremers Daniel, 2016. Q-space deep learning: twelve-fold shorter and model-free diffusion MRI scans. IEEE Trans. Med. Imaging 35 (5), 1344–1351 [DOI] [PubMed] [Google Scholar]
- He Kaiming, Chen Xinlei, Xie Saining, Li Yanghao, Dollár Piotr, Girshick Ross, 2022. Masked autoencoders are scalable vision learners. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 16000–16009. [Google Scholar]
- Hooker Jeffrey D, Khan Majid A, Farkas Amy B, Lirette Seth T, Joyner David A, Gordy David P, Storrs Judd M, Roda Manohar S, Bofill James A, Smith Andrew D, et al. , 2020. Third-trimester in utero fetal brain diffusion tensor imaging fiber tractography: a prospective longitudinal characterization of normal white matter tract development. Pediatr. Radiol. 50, 973–983. [DOI] [PubMed] [Google Scholar]
- Huang Hao, Xue Rong, Zhang Jiangyang, Ren Tianbo, Richards Linda J, Yarowsky Paul, Miller Michael I, Mori Susumu, 2009. Anatomical characterization of human fetal brain development with diffusion tensor magnetic resonance imaging. J. Neurosci. 29 (13), 4263–4273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Hao, Zhang Jiangyang, Wakana Setsu, Zhang Weihong, Ren Tianbo, Richards Linda J, Yarowsky Paul, Donohue Pamela, Graham Ernest, van Zijl Peter CM, et al. , 2006. White and gray matter development in human fetal, newborn and pediatric brains. Neuroimage 33 (1), 27–38 [DOI] [PubMed] [Google Scholar]
- Jaimes Camilo, Machado-Rivas Fedel, Afacan Onur, Khan Shadab, Marami Bahram, Ortinau Cynthia M, Rollins Caitlin K, Velasco-Annis Clemente, Warfield Simon K, Gholipour Ali, 2020a. In vivo characterization of emerging white matter microstructure in the fetal brain in the third trimester. Hum. Brain Mapp. 41 (12), 3177–3185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaimes C, Rofeberg V, Stopp C, Ortinau CM, Gholipour A, Friedman KG, Tworetzky W, Estroff J, Newburger JW, Wypij D, et al. , 2020b. Association of isolated congenital heart disease with fetal brain maturation. Am. J. Neuroradiol. 41 (8), 1525–1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakab András, Kasprian Gregor, Schwartz Ernst, Gruber Gerlinde Maria, Mitter Christian, Prayer Daniela, Schöpf Veronika, Langs Georg, 2015. Disrupted developmental organization of the structural connectome in fetuses with corpus callosum agenesis. Neuroimage 111, 277–288. [DOI] [PubMed] [Google Scholar]
- Jakab András, Tuura Ruth, Kellenberger Christian, Scheer Ianina, 2017. In utero diffusion tensor imaging of the fetal brain: a reproducibility study. NeuroImage: Clin. 15, 601–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones Derek K., 2010. Challenges and limitations of quantifying brain connectivity in vivo with diffusion MRI. Imaging Med. 2 (3), 341 [Google Scholar]
- Jones Derek K., Knösche Thomas R., Turner Robert, 2013. White matter integrity, fiber count, and other fallacies: the do’s and don’ts of diffusion MRI. Neuroimage 73,239–254. [DOI] [PubMed] [Google Scholar]
- Karimi Davood, 2024. Diffusion MRI with machine learning. arXiv preprint arXiv:2402.00019. [Google Scholar]
- Karimi Davood, Rollins Caitlin K, Velasco-Annis Clemente, Ouaalam Abdelhakim, Gholipour Ali, 2023. Learning to segment fetal brain tissue from noisy annotations. Med. Image Anal. 85, 102731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasprian Gregor, Brugger Peter C, Schöpf Veronika, Mitter Christian, Weber Michael, Hainfellner Johannes A, Prayer Daniela, 2013. Assessing prenatal white matter connectivity in commissural agenesis. Brain 136 (1), 168–179. [DOI] [PubMed] [Google Scholar]
- Kasprian Gregor, Brugger Peter C, Weber Michael, Krssák Martin, Krampl Elisabeth, Herold Christian, Prayer Daniela, 2008. In utero tractography of fetal white matter development. Neuroimage 43(2), 213–224. [DOI] [PubMed] [Google Scholar]
- Khan Shadab, Vasung Lana, Marami Bahram, Rollins Caitlin K, Afacan Onur, Ortinau Cynthia M, Yang Edward, Warfield Simon K, Gholipour Ali, 2019. Fetal brain growth portrayed by a spatiotemporal diffusion tensor MRI atlas computed from in utero images. NeuroImage 185, 593–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma Diederik P., Ba Jimmy, 2014. Adam: A method for stochastic optimization. In: Proceedings of the 3rd International Conference on Learning Representations. ICLR. [Google Scholar]
- Koay Cheng Guan, Chang Lin-Ching, Carew John D, Pierpaoli Carlo, Basser Peter J, 2006. A unifying theoretical and algorithmic framework for least squares methods of estimation in diffusion tensor imaging. J. Magn. Reson. 182 (1), 115–125. [DOI] [PubMed] [Google Scholar]
- Kolasinski James, Takahashi Emi, Stevens Allison A, Benner Thomas, Fischl Bruce, Zöllei Lilla, Grant P Ellen, 2013. Radial and tangential neuronal migration pathways in the human fetal brain: anatomically distinct patterns of diffusion MRI coherence. Neuroimage 79, 412–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Limperopoulos Catherine, Tworetzky Wayne, McElhinney Doff B, Newburger Jane W, Brown David W, Robertson Richard L Jr., Guizard Nicolas, McGrath Ellen, Geva Judith, Annese David, et al. , 2010. Brain volume and metabolism in fetuses with congenital heart disease: evaluation with quantitative magnetic resonance imaging and spectroscopy. Circulation 121 (1), 26–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linnet Karen Markussen, Dalsgaard Søren, Obel Carsten, Wisborg Kirsten, Henriksen Tine Brink, Rodriguez Alina, Kotimaa Arto, Moilanen Irma, Thomsen Per Hove, Olsen Jørn, et al. , 2003. Maternal lifestyle factors in pregnancy risk of attention deficit hyperactivity disorder and associated behaviors: review of the current evidence. Am. J. Psychiatry 160 (6), 1028–1040. [DOI] [PubMed] [Google Scholar]
- Lo Chun-Yi, Wang Pei-Ning, Chou Kun-Hsien, Wang Jinhui, He Yong, Lin Ching-Po, 2010. Diffusion tensor tractography reveals abnormal topological organization in structural cortical networks in Alzheimer’s disease. J. Neurosci. 30 (50), 16876–16885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch John Kylan, 2009. Epidemiology and classification of perinatal stroke. Semin. Fetal Neonatal Med. 14 (5), 245–249. [DOI] [PubMed] [Google Scholar]
- Machado-Rivas F, Afacan O, Khan S, Marami B, Rollins CK, Ortinau C, Velasco-Annis C, Warfield SK, Gholipour A, Jaimes C, 2021a. Tractography of the cerebellar peduncles in second-and third-trimester fetuses. Am. J. Neuroradiol. 42 (1), 194–200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado-Rivas Fedel, Afacan Onur, Khan Shadab, Marami Bahram, Velasco-Annis Clemente, Lidov Hart, Warfield Simon K, Gholipour Ali, Jaimes Camilo, 2021b. Spatiotemporal changes in diffusivity and anisotropy in fetal brain tractography. Hum. Brain Mapp. 42 (17), 5771–5784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makropoulos Antonios, Counsell Serena J., Rueckert Daniel, 2018. A review on automatic fetal and neonatal brain MRI segmentation. NeuroImage 170, 231–248. [DOI] [PubMed] [Google Scholar]
- Marami Bahram, Scherrer Benoit, Afacan Onur, Erem Burak, Warfield Simon K, Gholipour Ali, 2016. Motion-robust diffusion-weighted brain MRI reconstruction through slice-level registration-based motion tracking. IEEE Trans. Med. Imaging 35 (10), 2258–2269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meoded A, Poretti A, Tekes A, Flammang A, Pryde S, Huisman TAGM, 2011. Prenatal MR diffusion tractography in a fetus with complete corpus callosum agenesis. Neuropediatrics 42 (03), 122–123. [DOI] [PubMed] [Google Scholar]
- Millischer A-E, Grevent D, Sonigo P, Bahi-Buisson N, Desguerre I, Mahallati H, Bault J-P, Quibel T, Couderc S, Moutard M-L, et al. , 2022. Feasibility and added value of fetal DTI tractography in the evaluation of an isolated short corpus callosum: Preliminary results. Am. J. Neuroradiol. 43 (1), 132–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitter Christian, Jakab András, Brugger Peter C, Ricken Gerda, Gruber Gerlinde M, Bettelheim Dieter, Scharrer Anke, Langs Georg, Hainfellner Johannes A, Prayer Daniela, et al. , 2015a. Validation of in utero tractography of human fetal commissural and internal capsule fibers with histological structure tensor analysis. Front. Neuroanat. 9, 164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitter Christian, Prayer Daniela, Brugger Peter C, Weber Michael, Kasprian Gregor, 2015b. In vivo tractography of fetal association fibers. PLoS One 10 (3), e0119536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori Susumu, Crain Barbara J, Chacko Vadappuram P, Van Zijl, Peter CM, 1999. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol.: Off. J. Am. Neurol. Assoc. Child Neurol. Soc. 45 (2), 265–269. [DOI] [PubMed] [Google Scholar]
- Oktay Ozan, Schlemper Jo, Folgoc Loic Le, Lee Matthew, Heinrich Mattias, Misawa Kazunari, Mori Kensaku, McDonagh Steven, Hammerla Nils Y, Kainz Bernhard, et al. , 2018. Attention u-net: Learning where to look for the pancreas. arXiv preprint arXiv:1804.03999. [Google Scholar]
- Ouyang Minhui, Dubois Jessica, Yu Qinlin, Mukherjee Pratik, Huang Hao, 2019. Delineation of early brain development from fetuses to infants with diffusion MRI and beyond. Neuroimage 185, 836–850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pathak Deepak, Krahenbuhl Philipp, Donahue Jeff, Darrell Trevor, Efros Alexei A, 2016. Context encoders: Feature learning by inpainting. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 2536–2544. [Google Scholar]
- Payette Kelly, Li Hongwei Bran, de Dumast Priscille, Licandro Roxane, Ji Hui, Siddiquee Md Mahfuzur Rahman, Xu Daguang, Myronenko Andriy, Liu Hao, Pei Yuchen, et al. , 2023. Fetal brain tissue annotation and segmentation challenge results. Med. Image Anal. 88, 102833. [DOI] [PubMed] [Google Scholar]
- Qiu Anqi, Mori Susumu, Miller Michael I., 2015. Diffusion tensor imaging for understanding brain development in early life. Annu. Rev. Psychol. 66, 853–876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rheault Francois, Poulin Philippe, Caron Alex Valcourt, St-Onge Etienne, Descoteaux Maxime, 2020. Common misconceptions, hidden biases and modern challenges of dMRI tractography. J. Neural Eng. 17 (1), 011001. [DOI] [PubMed] [Google Scholar]
- Schaerer Joël, Roche Florent, Belaroussi Boubakeur, 2014. A generic interpolator for multi-label images. Insight J. 950. [Google Scholar]
- Seunarine Kiran K., Alexander Daniel C., 2014. Multiple fibers: beyond the diffusion tensor. In: Diffusion Mri. Elsevier, pp. 105–123. [Google Scholar]
- Silbereis John C, Pochareddy Sirisha, Zhu Ying, Li Mingfeng, Sestan Nenad, 2016. The cellular and molecular landscapes of the developing human central nervous system. Neuron 89 (2), 248–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siless Viviana, Davidow Juliet Y, Nielsen Jared, Fan Qiuyun, Hedden Trey, Hollinshead Marisa, Beam Elizabeth, Bustamante Constanza M Vidal, Garrad Megan C, Santillana Rosario, et al. , 2020. Registration-free analysis of diffusion MRI tractography data across subjects through the human lifespan. NeuroImage 214, 116703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith Robert E, Tournier Jacques-Donald, Calamante Fernando, Connelly Alan, 2012. Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information. Neuroimage 62 (3), 1924–1938. [DOI] [PubMed] [Google Scholar]
- Song Jae W, Gruber Gerlinde M, Patsch Janina M, Seidl Rainer, Prayer Daniela, Kasprian Gregor, 2018. How accurate are prenatal tractography results? A postnatal in vivo follow-up study using diffusion tensor imaging. Pediatr. Radiol. 48, 486–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Limei, Mishra Virendra, Ouyang Minhui, Peng Qinmu, Slinger Michelle, Liu Shuwei, Huang Hao, 2017. Human fetal brain connectome: structural network development from middle fetal stage to birth. Front. Neurosci. 11, 561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Jae W, Mitchell Paul D, Kolasinski James, Ellen Grant P, Galaburda Albert M, Takahashi Emi, 2015. Asymmetry of white matter pathways in developing human brains. Cerebral Cortex 25 (9), 2883–2893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sotiropoulos Stamatios N., Zalesky Andrew, 2019. Building connectomes using diffusion MRI: why, how and but. NMR Biomed. 32 (4), e3752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suarez Ralph O, Commowick Olivier, Prabhu Sanjay P, Warfield Simon K, 2012. Automated delineation of white matter fiber tracts with a multiple region-of-interest approach. Neuroimage 59(4), 3690–3700 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi Emi, Folkerth Rebecca D, Galaburda Albert M, Grant Patricia E, 2012. Emerging cerebral connectivity in the human fetal brain: an MR tractography study. Cerebral Cortex 22 (2), 455–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi Emi, Hayashi Emiko, Schmahmann Jeremy D, Grant P Ellen, 2014. Development of cerebellar connectivity in human fetal brains revealed by high angular resolution diffusion tractography. Neuroimage 96, 326–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taquet Maxime, Scherrer Benoit, Warfield Simon K., 2015. A framework for the analysis of diffusion compartment imaging (dci). In: Visualization and Processing of Higher Order Descriptors for Multi-Valued Data. Springer, pp. 271–297. [Google Scholar]
- Tournier J, Donald Calamante, Fernando Connelly, Alan, et al. , 2010. Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions. In: Proceedings of the International Society for Magnetic Resonance in Medicine. Vol. 1670, John Wiley & Sons, Inc, New Jersey. [Google Scholar]
- Tournier J-Donald, Smith Robert, Raffelt David, Tabbara Rami, Dhollander Thijs, Pietsch Maximilian, Christiaens Daan, Jeurissen Ben, Yeh Chun-Hung, Connelly Alan, 2019. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. Neuroimage 202, 116137. [DOI] [PubMed] [Google Scholar]
- Tymofiyeva O, Hess CP, Xu D, Barkovich AJ, 2014. Structural MRI connectome in development: challenges of the changing brain. Brit. J. Radiol. 87 (1039), 20140086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasung Lana, Huang Hao, Jovanov-Milošević Nataša, Pletikos Mihovil, Mori Susumu, Kostović Ivica, 2010. Development of axonal pathways in the human fetal frontolimbic brain: histochemical characterization and diffusion tensor imaging. J. Anat. 217 (4), 400–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasung Lana, Turk Esra Abaci, Ferradal Silvina L, Sutin Jason, Stout Jeffrey N, Ahtam Banu, Lin Pei-Yi, Grant P Ellen, 2019. Exploring early human brain development with structural and physiological neuroimaging. Neuroimage 187, 226–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaswani Ashish, Shazeer Noam, Parmar Niki, Uszkoreit Jakob, Jones Llion, Gomez Aidan N, Kaiser Łukasz, Polosukhin Illia, 2017. Attention is all you need. In: Advances in Neural Information Processing Systems. pp. 5998–6008 [Google Scholar]
- Wassermann Demian, Makris Nikos, Rathi Yogesh, Shenton Martha, Kikinis Ron, Kubicki Marek, Westin Carl-Fredrik, 2016. The white matter query language: a novel approach for describing human white matter anatomy. Brain Struct. Funct. 221, 4705–4721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wasserthal Jakob, Neher Peter, Maier-Hein Klaus H., 2018. TractSeg-fast and accurate white matter tract segmentation. NeuroImage 183, 239–253. [DOI] [PubMed] [Google Scholar]
- Wen Ying, He Lianghua, von Deneen Karen M., Lu Yue, 2013. Brain tissue classification based on DTI using an improved fuzzy C-means algorithm with spatial constraints. Magn. Reson. Imaging 31 (9), 1623–1630. [DOI] [PubMed] [Google Scholar]
- Wilson Siân, Pietsch Maximilian, Cordero-Grande Lucilio, Christiaens Daan, Uus Alena, Karolis Vyacheslav R, Kyriakopoulou Vanessa, Colford Kathleen, Price Anthony N, Hutter Jana, et al. , 2023. Spatiotemporal tissue maturation of thalamocortical pathways in the human fetal brain. Elife 12, e83727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson Siân, Pietsch Maximilian, Cordero-Grande Lucilio, Price Anthony N, Hutter Jana, Xiao Jiaxin, McCabe Laura, Rutherford Mary A, Hughes Emer J, Counsell Serena J, et al. , 2021. Development of human white matter pathways in utero over the second and third trimester. Proc. Natl. Acad. Sci. 118 (20) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Gang, Takahashi Emi, Folkerth Rebecca D, Haynes Robin L, Volpe Joseph J, Grant P Ellen, Kinney Hannah C, 2014. Radial coherence of diffusion tractography in the cerebral white matter of the human fetus: neuroanatomic insights. Cerebral Cortex 24 (3), 579–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Joseph Yuan-Mou, Yeh Chun-Hung, Poupon Cyril, Calamante Fernando, 2021. Diffusion MRI tractography for neurosurgery: the basics, current state, technical reliability and challenges. Phys. Med. Biol. 66 (15), 15 TR01. [DOI] [PubMed] [Google Scholar]
- Yap Pew-Thian, Zhang Yong, Shen Dinggang, 2015. Brain tissue segmentation based on diffusion MRI using 10 sparse-group representation classification. In: Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015: 18th International Conference, Munich, Germany, October 5–9, 2015, Proceedings, Part III 18. Springer, pp. 132–139. [PMC free article] [PubMed] [Google Scholar]
- Yeh Chun-Hung, Jones Derek K, Liang Xiaoyun, Descoteaux Maxime, Connelly Alan, 2021. Mapping structural connectivity using diffusion MRI: Challenges and opportunities. J. Magn. Reson. Imaging 53 (6), 1666–1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanin Emilie, Ranjeva Jean-Philippe, Confort-Gouny Sylviane, Guye Maxime, Denis Daniele, Cozzone Patrick J, Girard Nadine, 2011. White matter maturation of normal human fetal brain. An in vivo diffusion tensor tractography study. Brain Behav. 1 (2), 95–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zbontar Jure, Jing Li, Misra Ishan, LeCun Yann, Deny Stéphane, 2021. Barlow twins: Self-supervised learning via redundancy reduction. In: International Conference on Machine Learning. PMLR, pp. 12310–12320. [Google Scholar]
- Zhang Fan, Breger Anna, Cho Kang Ik Kevin, Ning Lipeng, Westin Carl-Fredrik, O’Donnell Lauren J, Pasternak Ofer, 2021. Deep learning based segmentation of brain tissue from diffusion MRI. NeuroImage 233, 117934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Fan, Breger Anna, Ning Lipeng, Westin Carl-Fredrik, O’Donnell L, Pasternak Ofer, 2020. Deep learning based brain tissue segmentation from novel diffusion kurtosis imaging features. In: Annual Meeting of the International Society for Magnetic Resonance in Medicine. [Google Scholar]
- Zhang Wenlu, Li Rongjian, Deng Houtao, Wang Li, Lin Weili, Ji Shuiwang, Shen Dinggang, 2015. Deep convolutional neural networks for multi-modality isointense infant brain image segmentation. NeuroImage 108, 214–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Hui, Yushkevich Paul A, Alexander Daniel C, Gee James C, 2006. Deformable registration of diffusion tensor MR images with explicit orientation optimization. Med. Image Anal. 10 (5), 764–785. [DOI] [PubMed] [Google Scholar]
- Zheltonozhskii Evgenii, Baskin Chaim, Mendelson Avi, Bronstein Alex M, Litany Or, 2022. Contrast to divide: Self-supervised pre-training for learning with noisy labels. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. pp. 1657–1667. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.


