Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jul 17;128(35):8504–8511. doi: 10.1021/acs.jpcb.4c03162

Conformational Landscape of NADH and Ion Binding in Water/DMSO Mixtures via 31P NMR Spectroscopy

Jiaqi Lu †, Florin Teleanu †,‡,§, Huijing Zou †, Chengtong Zhang †, Andrew Hollingsworth ∥, Alexej Jerschow †,*
PMCID: PMC11382270  PMID: 39018118

Abstract

graphic file with name jp4c03162_0007.jpg

This study reports on the conformational states of nicotinamide adenine dinucleotide (NADH) in water/DMSO mixtures and examines the influence of ion binding. We observe evidence of conformational changes through a series of NMR techniques, including 31P NMR relaxation (R1 and R2), chemical exchange saturation transfer (CEST), and diffusion-ordered spectroscopy (DOSY) experiments. The observed variation of the conformational states is indicative of the solvent’s influence on NADH’s structural flexibility. The experimental findings, in combination with viscosity data, are shown to be in line with findings from earlier molecular dynamics studies. The reported observations emphasize the critical role of the solvent environment in determining the conformational states of NADH and similar molecules with relevance for the biophysiological context. The results found herein can help in studying the biophysical behavior of NADH and similar biomolecules and their associated metabolic pathways under various solvent conditions.

Introduction

Nicotinamide adenine dinucleotides (NAD) are coenzymes present in the intracellular space and form a redox equilibrium between oxidized (NAD+) and reduced (NADH) states. In mitochondria, they serve in metabolic processes such as the tricarboxylic acid cycle and the electron transport system where NADH assists in producing adenosine triphosphate (ATP).1 Both coenzymes are involved in a chemical exchange between two molecular conformations, known as “folded” (F) and “unfolded” (U) as depicted in Figure 1.2 Recent spectroscopic and structural evidence point toward a preference for the unfolded state when binding to the active sites of enzymes which allows for stronger host–guest interactions due to the increased molecular surface.3−7 As a result, perturbations of the freely available, unbounded U/F species arising from temperature,8,9 pH,10,11 solvent,7,12 or chemical gradients13,14 can impact the global enzymatic rates of energy metabolism leading to cellular malfunction. Fluorescence and nuclear magnetic resonance (NMR) spectroscopy have been used to study conformational exchange on time scales spanning several orders of magnitude by monitoring the lifetimes of nonequilibrium electronic or nuclear spin states.15,16 Previous studies investigated the changes in time-resolved fluorescence emission17−19 and/or the NMR spectral changes20−23 of NAD+/NADH in pure solvents such as water or methanol.

Figure 1.

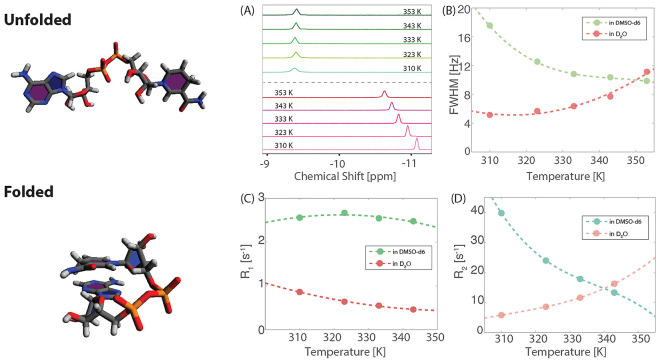
Figure 1

Open in a new tab

Two conformations of NADH marked as “Unfolded” and “Folded” alongside the temperature dependence of 31P NMR results for 30 mM NADH in pure deuterated solvents: DMSO-d6 and D2O. (A) Below the dashed line: 1D NMR spectra of 30 mM NADH in pure D2O at temperatures ranging from 310 to 353 K, demonstrating line broadening with increasing temperature. Above the dashed line: 1D NMR spectra of 30 mM NADH in pure DMSO-d6 over the same temperature range, exhibiting line narrowing as temperature increases. (B) Line widths for NADH as a function of temperature, displaying a monotonic increase in pure D2O and a monotonic decrease in pure DMSO-d6. (C) Spin–lattice relaxation rate (R1) as a function of temperature, showing a monotonic decrease in pure D2O and a local maximum in pure DMSO-d6. (D) Spin–spin relaxation rate (R2) as a function of temperature, following the same trend as the line widths in (B): a monotonic increase in D2O and a monotonic decrease in DMSO-d6.

Here, we probe the conformational landscape of NADH accessed by changing the relative composition of a deuterated bicomponent D2O/DMSO-d6 solvent mixture at different temperatures by means of 31P NMR spectroscopy. The reason for choosing this approach is 2-fold: the pyrophosphate moiety acts as a pivot around which the folding–unfolding dynamics is expected to take place by changing the dihedral angle subtended by the P=O double bonds; thus, the 31P resonance and NMR relaxation rates are expected to be sensitive to the global conformation providing a cleaner biomarker for in vivo studies compared to 1H NMR spectroscopy. Second, a gradual shift of the conformational equilibrium is afforded by tuning the solvent mixture. Notably, DMSO, being an aprotic solvent, probes the influence of polarity, while D2O probes effects due to hydrogen bonding and hydrogen exchange.24−27 Our findings suggest that the two solvents induce different conformations as suggested by the opposite trends in the ps–ns tumbling rates of NADH probed by 1D spectroscopy and relaxometry studies. Changes are observed when altering the solvent mixture, and evidence is provided for suggesting the presence of an intermediate “semifolded” state.28

Experimental Section

Materials and Methods

NADH (Grade II, disodium salt, MW 709.4), DMSO-d6 (99.9 atom % D, contains 0.03% TMS, MW 84.17), D2O (99.9 atom % D, MW 20.03), magnesium chloride (MW 95.211), calcium chloride (MW 110.98), and aluminum chloride (MW 133.34) were acquired from Sigma-Aldrich. All samples were prepared at room temperature. Each sample comprised 30 mM NADH with or without equivalent concentration of metal chloride salts dissolved in 1000 μL of binary solvent, utilizing D2O and 100% DMSO-d6 mixed in varying ratios. pDs corresponding to the volume fractions of DMSO-d6 of 1 to 0 were measured as 12.2, 12.0, 11.0, 10.73, 9.84, 9.74, 8.54, 8.2, 8.14, 7.93, and 8.3. The 30 mM NADH sample in 90% DMSO-d6 and 10% D2O exhibited pD values of 10.45 when 30 mM MgCl2 was added, 11.14 for 30 mM CaCl2, and 9.39 for 30 mM AlCl3. Solutions were pipetted into a Wilmad-LabGlass 5 mm high-throughput NMR tube for NMR analysis.

NMR Experiments

Solution NMR relaxation experiments were performed on a Bruker Avance NEO 500 MHz spectrometer with a CryoProbe Prodigy BBO probe, using Wilmad-LabGlass 5 mm high-throughput NMR tubes. T1 relaxation was measured with a standard inversion–recovery pulse sequence, and T2 relaxation was measured using a Carr–Purcell–Meiboom–Gill (CPMG) sequence. Delays varied between 2 and 5 s depending on sample conditions (temperature, pD, solvents)

NMR Relaxation Measurements

31P T1 and T2 delays were chosen such that the final two points of the T1 curves were fully recovered, and the final points for T2 curves had less than 5% of the initial intensity. T1 relaxation times were determined by employing the TopSpin 4.0.7 T1/T2 dynamics module. T2 relaxation times were determined by monoexponential fitting in MATLAB. The full width at half-maximum (FWHM) was determined by deconvolution of Lorentzian line width employing the TopSpin 4.0.7 DCON command. For each spectrum, a single scan was acquired with 10,240 size of the FID to cover a spectral window of 6579 Hz (32.5 ppm). An AU program was used to automate temperature increments and equilibration (10 min for each temperature). Autoshimming was applied continuously before and between the measurements.

Chemical Exchange Saturation Transfer (CEST)

31P CEST experiments were performed on a Bruker 500 MHz (11.7 T) NMR spectrometer equipped with a broadband observe (BBO) probe. The 90° pulse duration ranged from 11 to 12 μs depending on the ionic strength of the solution. Saturation was performed by continuous-wave (cw) irradiation of 5 s duration with field strengths of 1.16–11.6 μT (corresponding to nutation frequencies of 20–200 Hz). In Figure 2, nutation frequencies from 20 to 200 Hz for 5 s were used. The recycling delay was set to 5 s. Following cw irradiation, a 90° pulse was used for spectral readout. The temperature dependence of CEST was measured at 310, 323, 333, and 343 K with nutation frequencies of 20, 30, 40, 50, 100, 150, and 200 Hz. At each frequency offset, a single scan was acquired. The scanned offset frequency ranged from −40 to 40 ppm with various step sizes of 1, 0.25, and 0.1 ppm, as detailed in the work of Lu et al.29,30 As posited by Bolik-Coulon et al.,31 we consider the transverse relaxation rate of the spin in its ground state, denoted as R2,G. 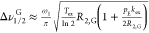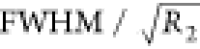When R2,G significantly exceeds the product of the population of excited states, pE, and the exchange rate, kex, i.e., R2,G ≫ pEkex, where pE represents the population of the excited states and kex is the sum of the forward and reverse exchange rates between the ground and excited states, the CEST line width can be approximated as follows: Inline graphic, where Tex denotes the length of the irradiation period. Consequently, in the absence of exchange, the ratio of the chemical exchange saturation transfer line width (FWHM) to the square root of the transverse relaxation rate R2, Inline graphic, plotted as a function of irradiation power, should remain constant. Conversely, in the presence of exchange, this ratio is expected to increase with the exchange rate.

Figure 2.

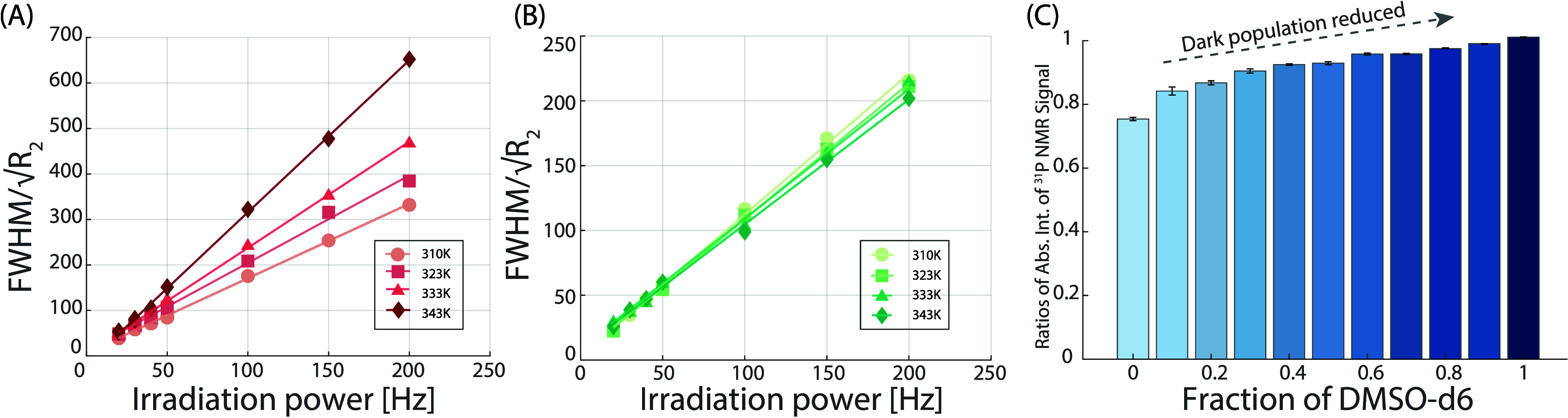
Figure 2

Open in a new tab

31P chemical exchange analysis for 30 mM NADH in pure deuterated solvents of DMSO-d6 and D2O. (A) Investigation of the irradiation power dependence on 31P CEST line widths, normalized by the square root of the spin–spin relaxation rate (FWHM/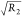Inline graphic), at temperatures of 310, 323, 333, and 343 K in pure D2O. The increasing slope observed at these temperatures signifies an enhancement in the chemical exchange rate with increasing temperature. (B) A parallel analysis conducted in pure DMSO-d6. The uniform slopes across the studied temperatures indicate a negligible chemical exchange in this solvent. (C) Variation in the ratio of the absolute integral of the 31P signal from 1D NMR spectra in 30 mM NADH solutions, using binary mixed solvents of DMSO-d6 and D2O measured from 298 K to 343 K and adjusted for the temperature dependence as discussed in the main text.. An increasing ratio with a higher fraction of DMSO-d6 suggests that the presence of DMSO-d6 reduces the “dark” population of NADH in the solution.

Diffusion Ordered Spectroscopy (DOSY)

31P DOSY measurements were acquired on a 500 MHz Bruker spectrometer with a single gradient along the z-axis. DOSY is an experimental that uses the pulsed field gradient NMR (PFG-NMR) technique to extract diffusion coefficients for each NMR signal present in a sample. The DOSY pulse sequence used to measure the diffusion coefficients for each sample was stegp1s. The signal attenuation as a function of the gradient strength, g, and the diffusion coefficient, D, is given as ψ(g,D) = exp(−Dg2γ2δ2(Δ – δ/3)), where γ is the gyromagnetic ratio of the nucleus, δ is the width of the gradient pulse, and Δ is the time between gradient pulses.32 The fitting was done automatically in Topspin 4.0.7.

All DOSY measurements were taken at 298 K. Eight scans with a 90° pulse were acquired with 10,240 data points to cover a spectral window of 6579 Hz (32.5 ppm). For diffusion measurements, the gradient strength was linearly spaced with 16 values such that the final spectrum had an intensity less than 5% of the initial one. The decays were then fit using the TopSpin 4.0.7 T1/T2 relaxation module to extract the diffusion coefficient. The delay δ ranged from 2.5 to 6 ms, and the Δ ranged from 250 to 550 ms, depending on the solution conditions. The gyromagnetic ratio, γ, of 31P is 10.84 × 107 rad T–1 s–1. The Stokes–Einstein relation was then used to determine the hydrodynamic diameter (dH), as shown in Figure 5A,C.

Figure 5.

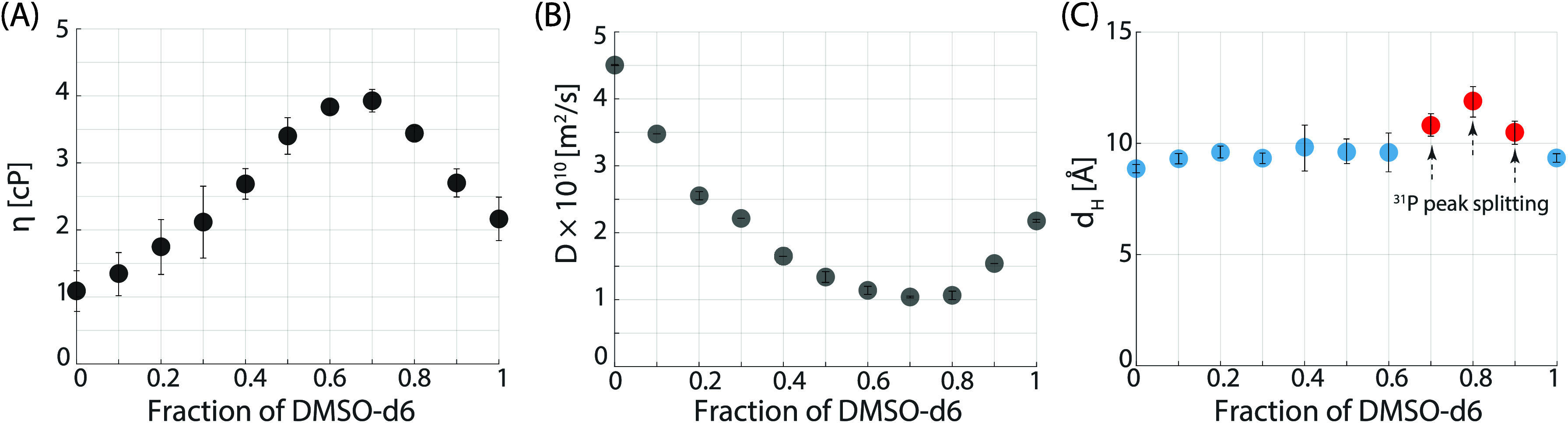
Figure 5

Open in a new tab

Comprehensive analysis of dynamic viscosity (η), diffusion coefficient (D), and hydrodynamic diameter (dH). (A) Dynamic viscosity measurements of binary mixed solvents at 298 K. (B) 31P DOSY results for 30 mM NADH in the binary mixed solvents. (C) Hydrodynamic diameter extracted from the diffusion coefficients in (B) for 30 mM NADH in the binary mixed solvents, providing a quantitative measure of the molecular size of NADH in various solvent compositions. Arrows indicate specific points where 31P peak splitting from a singlet to a doublet of doublets is observed, specifically at 70%, 80%, and 90% DMSO-d6 concentrations.

Ab Initio Structures

The structures from Figure 1 (and Figure S3) were generated by geometry optimization at the DFT level of theory using ORCA software utilizing BP86 functional and Karlsruhe split-valence with polarization basis set (def2-SVP) and continuous model for water solvent. The resulting geometries converged successfully and are true local energy minima (no imaginary frequencies). In order to converge toward either “folded” or “unfolded” structure, the initial geometries were chosen to be similar to the anticipated one.

Viscosity and Density Measurements

In this study, the kinematic viscosities (ν) of binary solvents composed of DMSO-d6 and D2O were measured at 25 ± 0.5 °C using an Ubbelohde viscometer type 531 01, capillary 0a (Schott-Geräte GmbH) inside a temperature-controlled room (Sterling Environments, Inc.). The binary solvent mixtures were prepared with varying ratios of DMSO-d6, ranging from 0 to 1 in volume fraction, with each sample having a total volume of approximately 20 mL. Prior to measurements, the Ubbelohde viscometer (nominal cell constant 0.005 mm2/s2) was cleaned and dried following standard procedures and then calibrated with deionized (DI) water of known viscosity at the target temperature of 25 °C to ensure precision in readings.33 The viscometer was filled with sample, taking special care to avoid bubble formation, and the fluid within the reservoir was equilibrated to ambient temperature for 10 min. For each measurement, a liquid volume—defined exactly between two measuring marks located directly above the capillary—flowed through the 530 μm internal diameter, 9 cm long capillary. The recorded flow time (efflux time) is directly related to the sample viscosity and was measured a minimum of three times for each sample to establish data reproducibility. The kinematic viscosity of each mixture was calculated using the standard formula ν = Kt, where K is the calibration constant of the viscometer and t is efflux time.

The density (ρ) of each batch of binary solvent mixtures, composed of DMSO-d6 and D2O of varying ratios, was determined using a digital density meter (Anton Paar DMA 4500M). Samples were injected into a U-shaped borosilicate glass tube that was vibrated at its characteristic frequency electronically. The detected eigenfrequency is related directly to the particular sample’s density. The tube was filled with DI water and air of known densities to determine the two calibration constants. All measurements were conducted at a controlled temperature of 25.0 °C, and sample volumes of 3 mL were used for each run. Density readings were recorded promptly after each sample was loaded into the instrument. To ensure accurate results, the density of each sample was measured ten times. The average of these readings was calculated to represent the density of that sample. This process was repeated for each mixture.

The dynamic viscosities (η) of the binary solvent mixtures composed of DMSO-d6 and D2O were calculated by utilizing the Hagen–Poiseuille equation. Using the measured density and kinematic viscosity of each mixture, the dynamic viscosity was calculated with the formula η = ρν, where the resulting unit for dynamic viscosity is Pascal-seconds (Pa·s) = 103 centipoise (cP). Kinetic and end effect corrections were not considered but are assumed to be negligible due to the reasonably long efflux times. This calculation was performed for each binary solvent mixture of given sample composition. The measurements of density and calculated dynamic viscosity are shown in Figure 5B,C.

Results and Discussion

The temperature dependence of the 31P NMR 1D spectra of NADH in pure solvents, D2O (purple-red) or DMSO-d6 (blue-green), already highlights the differences in the induced conformational preference (Figure 1A). The spectra contain a pair of strongly coupled doublets that resemble a singlet-like peak due to a small chemical shift difference between the two 31P nuclei. This effect is understood by inspecting the molecular structure noting the very similar electronic environment around both 31P atoms (see the “Unfolded” and “Folded” conformations of NADH in Figure 1). With two identical pentose rings on both sides, the first difference in molecular connectivity is reached only 7–8 bonds farther away from the pyrophosphate group. Consequently, it is expected that 31P spectra will preserve their singlet-like splitting patterns in both folded and unfolded states as only strong intra- or intermolecular interactions around the pyrophosphate group, such as H-bonding, can selectively alter the electronic environment (see below). The temperature dependence of the 31P chemical shift in the D2O sample (approximately −11 ppm) indicates the presence of conformational dynamics, the resulting spectra being the chemical exchange-weighted average of both U and F states. By contrast, the DMSO-d6 spectra show no temperature dependence, suggesting the presence of a single species. Previous time-resolved fluorescence studies provided convincing proof for the existence of a 50/50 folded/unfolded equilibrium of NADH in water at room temperature, while changing the solvent can lead to a preference of one state over the other. Cadena-Caicedo et al., for example, studied the folded and unfolded states of NADH by experiments in water and methanol solutions.18

31P relaxometry data (Figure 1B–D) indicate that the unfolded state is dominant in DMSO-d6 which is in line with interpretations of 1H spectra34 shown in Figure S3: as the fraction of DMSO-d6 decreases, the splitting and shifting of the HN4 peak suggests a dynamic equilibrium between folded and unfolded states of NADH in varying solvent environments. In the folded state, one of the HN4 protons is closer to the adenine ring, which alters its chemical shift due to the influence of additional electronic ring current effects. Conversely, in the unfolded state, the environment around both HN4 protons is more similar, leading to less pronounced chemical shift differences, which was observed in pure DMSO-d6. The longitudinal (R1) and transverse (R2) relaxation rates of 31P in the DMSO-d6 sample follow the expected temperature dependence behavior: R1 describes a concave parabola with a maximum corresponding to the condition τCω0 = 1, where τC is the rotational correlation time of the molecule and ω0 is the Larmor frequency of the 31P nucleus (201.86 MHz for a 11.7 T magnet); R2 decreases monotonically as τC decreases (temperature increases). For the D2O sample, the R1 values decrease with increasing temperature, suggesting that the maximum value can be reached by further cooling the sample. The fact that the two solvents impose different temperature values for the τCω0 = 1 condition can be accounted for by the larger viscosity of DMSO-d6 and the different hydrodynamic radii of the folded and unfolded states (see below). Most surprisingly, the transverse rate increases with increasing temperature for the water-abundant mixtures, a phenomenon which further points toward chemical exchange between different states, as also described for other organic phosphates in very recent studies.29,30

Another technique that is often use to probe the existence of low-concentration states (“dark states”) in exchange with a more abundant species is chemical exchange saturation transfer (CEST).35,36 Here, we employed the method from ref (37) and obtain further evidence to support our finding regarding NADH dynamics in D2O and DMSO-d6 (Figure 2A,B). The dispersion profile of 31P CEST line widths as a function of irradiation power at different temperatures (normalized by the square root of the spin–spin relaxation rate (FWHM/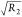Inline graphic) indicates the presence of chemical exchange for the water sample, but not for the DMSO-d6 sample.

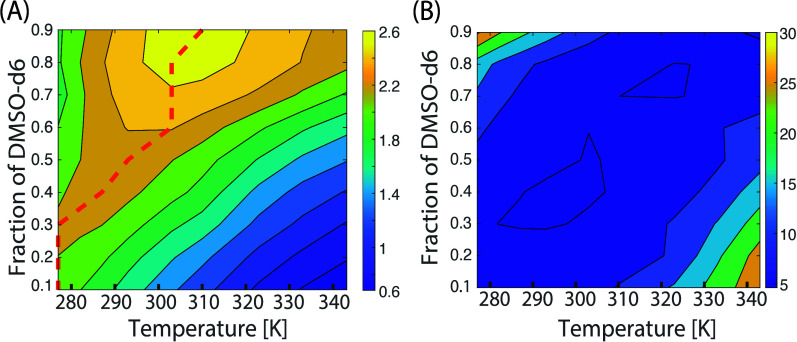
As a next step, we investigated the impact of the bicomponent mixture composition in order to further probe the conformational landscape of NADH: starting from pure DMSO-d6 solvent, where only the U state is assumed to be prevalent, gradually increasing the D2O ratio impacts several observables such as the 31P chemical shift, the splitting pattern, the relaxation rates, and the diffusion constant. These changes are interpreted in terms of the water’s impact on NADH conformation which promotes chemical exchange between U and F states. Notably, a nonmonotonic upfield shift of 31P resonances is observed (Figure 3A) with extreme values at −8.7 ppm (in pure DMSO-d6) and −11 ppm (in pure D2O). In parallel, for a specific range of solvent ratios (Figure 3B), the resulting splitting patterns point toward an enhanced difference in terms of electronic environments for the two 31P nuclei leading to a larger chemical shift difference. This effect can be attributed to intramolecular interactions in the form of H-bonds involving pyrophosphate’s oxygen atoms and nicotinamide protons or intermolecular interactions with D2O–DMSO-d6 complexes. Previous MD studies7,28 point toward the former case while stable water–DMSO complexes have also been reported in the literature.24,26,27 Noting that 31P spectra show a temperature and mixture composition dependence and considering the hypothesized presence of invisible “dark states”, we measured the ratio of peak integrals from 298 to 343 K for different D2O/DMSO-d6 fractions (Figure 2C) and adjusted for the temperature dependence of the magnetization (1/T Curie factor). In the case of pure DMSO-d6 solvent, there is no variation of the resulting peak integral, suggesting that all 31P spins in the sample correspond to the same chemical species, i.e., the large peak corresponding to the unfolded state without exchange with a hidden pool. Adding water leads to a drop in the peak integral from low to high temperatures, proving that the 31P spins are distributed among multiple species, i.e., the abundant unfolded and “dark” folded states giving rise to chemical exchange-averaged spectra.

Figure 3.

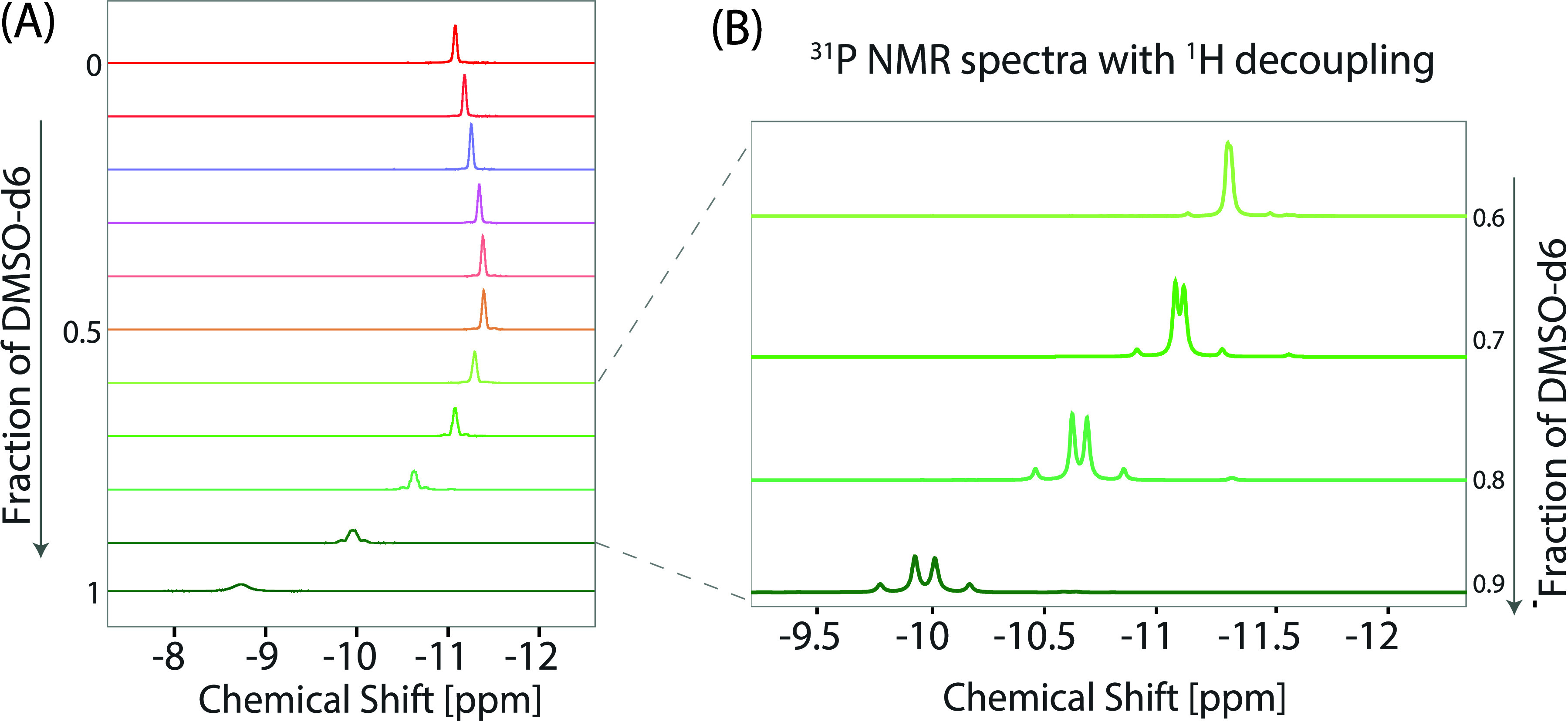
Figure 3

Open in a new tab

31P NMR results of 30 mM NADH in binary mixed solvents of DMSO-d6 and D2O at 298 K. (A) 1D NMR spectra of 30 mM NADH in binary mixtures, with varying DMSO-d6 fractions ranging from 1 (pure DMSO-d6) to 0 (pure D2O), displayed in descending order (bottom to top) with increments of 0.1. These spectra exhibit line narrowing as the fraction of DMSO-d6 decreases. Significantly, 31P peak splitting is observed at specific concentrations, particularly at 90%, 80%, and 70% DMSO-d6. The 31P chemical shift was calibrated with 85% H3PO4. (B) 31P NMR spectra with 1H decoupling, highlighting the evolution of peak patterns: a doublet of doublets is observed at DMSO-d6 concentrations of 90%, 80%, and 70%, which then disappears at a concentration of 60% DMSO-d6.

The relaxation data shown in Figure 4 highlight two different phenomena: first, due to the nonlinearity of viscosity as a function of D2O/DMSO-d6 composition (see Figure 5A), the rotational correlation time, and thus relaxation rates, do not always follow a monotonic trend when changing the solvent fraction. The maximum value of 31P R1 shifts to higher temperatures (red dashed line) due to the slowdown of molecular tumbling as the fraction of the more viscous solvent increases. Based on previous measurements from literature, we can predict the viscosity of each mixture composition over the temperature range used in our experiments (Figure S1). Starting from these values, we use a simple relaxation model based on the common spin interactions that can impact 31P magnetization in order to fit the measured R1 and R2 data (see Part 1 of the Supporting Information). For the case of pure DMSO-d6 at room temperature, a rotational correlation time of τC = 1/ω0 ≈ 0.8 ns is estimated, which corresponds to a hydrodynamic radius of 7.24 Å (using Stokes’ law) for the unfolded state. The transverse relaxation rate R2 follows a monotonic decrease with the DMSO-d6 fraction and increasing temperature (for the case of pure DMSO-d6) while mixtures with abundant water content show a clear deviation from the expected behavior. Normally, as temperature and tumbling rate increase, R2 values should decrease, as predicted by our model. Our results can be explained in terms of an increasing chemical exchange rate between the two (or more) U/F chemical sites which have been proposed in previous reports.9,17 Thus, the two maxima shown in Figure 4B can be explained by a decrease of the tumbling rate (due to low temperature and DMSO’s higher viscosity) and an increased chemical exchange rate for the water-rich mixtures at high temperatures.

Figure 4.

Figure 4

Open in a new tab

31P relaxation characteristics of 30 mM NADH in binary mixed solvents of DMSO-d6 and D2O, with DMSO-d6 fractions ranging from 0.1 to 0.9, across temperatures from 277 to 343 K. (A) Spin–lattice relaxation rate (R1) as a function of temperature. The dashed line indicates the maximum R1 values observed at each solvent fraction. (B) Spin–spin relaxation rate (R2) as a function of temperature, showing an increase in R2 correlating with both higher fractions of DMSO-d6 and increased temperature.

To gain insight into the size of the U/F states, we conducted 31P DOSY experiments as well as independent viscosity measurements (Figure 5). Using the Stokes–Debye–Einstein equation, we were able to infer the hydrodynamic diameter for NADH at room temperature for all D2O/DMSO-d6 mixtures (Figure 5C). The values are constant, around 10 Å, with a clear increase for certain compositions (red dots) which correlate with the different splitting pattern observed in the 31P 1D spectra (Figure 3B). These findings support the existence of an intermediate “semifolded” state where the two 31P nuclei have different chemical environments due to either intramolecular H bonding or solvent interactions, while the molecule undergoes a significant change of the overall conformation.

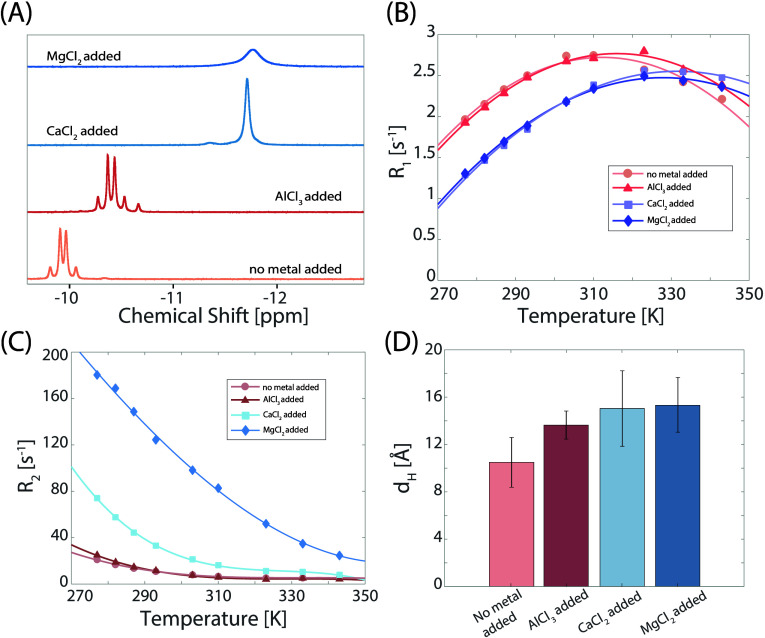
Further investigation of this conformation was conducted for a D2O/DMSO-d6 = 1/9 sample by adding metal ions in an attempt to induce either one of the known folded or unfolded states upon chelation. Figure 6A shows the different 31P 1D spectra. Little effect is observed for Al3+ addition, when compared to addition of Ca2+ or Mg2+. The upfield shift induced by addition of the latter two indicates a preference for the folded state (similar to increasing the water content) which is paralleled by the collapse of the pair of doublets into a singlet-like pattern. The temperature profile of the longitudinal relaxation rate further suggests a large effect of Ca2+ and Mg2+ binding by shifting the maximum R1 value to higher temperature which translates to an increase of the molecular size. This effect can be accounted for by the coordination of extra solvent molecules to the metal which slows down the overall molecular tumbling as also reflected by the increase in R2 and hydrodynamic radii for the Ca2+/Mg2+ complexes (Figure 6C,D).

Figure 6.

Figure 6

Open in a new tab

31P NMR analysis of 30 mM NADH in 90% DMSO-d6 and 10% D2O, with and without 30 mM metal chloride salts. (A) 31P 1D NMR spectra variations: without metal chloride salts, the NADH peak appears as a doublet of doublets. Addition of 30 mM AlCl3 results in slight shielding (0.46 ppm) but retains the doublet of doublet structure. With 30 mM CaCl2, the peak transitions to a singlet with greater shielding (approximately 1.77 ppm), similar to the case with 30 mM MgCl2, though the MgCl2 added one has a broader line width. (B) Spin–lattice relaxation (R1) behavior: NADH shows a local maximum in R1 both with and without metal chloride salts added. The R1 profiles of NADH without metal and with AlCl3 track each other. The addition of CaCl2 or MgCl2 alters the R1 profile, delaying the appearance of the local maximum. (C) Spin–spin relaxation (R2) behavior: all R2 curves exhibit a monotonic decrease. The profiles in the absence of metal chloride salts and with AlCl3 are similar, while the addition of MgCl2 or CaCl2 significantly enlarges R2. (D) Hydrodynamic diameter (dH) extracted from the measured diffusion coefficients and dynamic viscosity in Figure 5A; all metal chloride salts increase NADH size, in the order of AlCl3 < CaCl2 < MgCl2.

Based on our findings about NADH’s different conformations under different solvent conditions in this study, we expect that such phenomena should be taken into consideration in the biological context. DMSO has been widely used in chemistry, biology, and medicine by serving as an efficient cell cryoprotectant as well as a carrier for drug therapy and for the in vivo administration of water-insoluble compounds.38,39 Our observations suggest that NADH may adopt various conformations depending on the environment and the presence of cations, which could significantly impact its enzymatic binding. Enzymes that interact with NADH could have different affinities and activities depending on whether NADH is in a fully folded, semifolded, or extended conformation. This conformational flexibility might be critical in biological systems where NADH participates in numerous metabolic pathways. Additionally, metal ion concentration changes in cellular environments often play roles of stabilizing certain biomolecular structures or facilitating enzymatic reactions. The presence of metal cations might stabilize specific NADH conformations, thereby modulating its biological activity. Understanding these conformational dynamics in different environments enhances our knowledge of NADH’s functionality and its role in cellular metabolism.

Conclusion

As described in previous literature, both NAD+ and NADH can exist in a chemical equilibrium between two conformations, folded and unfolded, which in turn dictates the rate of binding to enzymes where typically the latter state is preferred. By means of 31P NMR, we have explored the conformational landscape of NADH in a bicomponent mixture of deuterated water and dimethyl sulfoxide showing strong solvent-induced changes of the 3D structure. Several observable characteristics for 31P nuclei, such as chemical shifts and relaxation rates, can be used to assess the conformational state of NADH. Potential applications may even include in vivo studies where 31P NMR could be a better alternative than 1H NMR due to the reduced spectral overlap. Relaxometry and diffusion studies offer a glimpse into the overall tumbling rate and size of NADH conformers pointing toward a multisite chemical exchange equilibrium involving folded, semifolded, and unfolded states.

Acknowledgments

We acknowledge funding from the US National Science Foundation, Award No. CHE 2108205, to A.J., the support from The Margaret and Herman Sokol Fellowship to J.L., and the Fulbright Fellowship from Romanian-U.S. Fulbright Commission to F.T.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.4c03162.

  • Viscosity profiles for DMSO–D2O mixtures across different temperatures and compositions; comparison of theoretical and actual R2/R1 relaxation ratios under varying conditions, indicating discrepancies; 1H NMR spectral changes in NADH due to different DMSO–D2O solvent compositions, reflecting conformational shifts (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp4c03162_si_001.pdf (455.7KB, pdf)

References

  1. Nelson D. L.; Lehninger A. L.; Cox M. M.. Lehninger Principles of Biochemistry; Macmillan: 2008. [Google Scholar]
  2. Sarma R. H.; Ross V.; Kaplan N. O. Investigation of the conformation of β-diphosphopyridine nucleotide (β-nicotinamide adenine dinucleotide) and pyridine dinucleotide analogs by proton magnetic resonance. Biochemistry 1968, 7, 3052–3062. 10.1021/bi00849a005. [DOI] [PubMed] [Google Scholar]
  3. Vishwasrao H. D.; Heikal A. A.; Kasischke K. A.; Webb W. W. Conformational Dependence of Intracellular NADH on Metabolic State Revealed by Associated Fluorescence Anisotropy. J. Biol. Chem. 2005, 280, 25119–25126. 10.1074/jbc.M502475200. [DOI] [PubMed] [Google Scholar]
  4. König K.; Berns M. W.; Tromberg B. J. Time-resolved and steady-state fluorescence measurements of β-nicotinamide adenine dinucleotide-alcohol dehydrogenase complex during UVA exposure. J. Photochem. Photobiol. B: Biol. 1997, 37, 91–95. 10.1016/S1011-1344(96)07327-7. [DOI] [PubMed] [Google Scholar]
  5. Blacker T. S.; Duchen M. R. Investigating mitochondrial redox state using NADH and NADPH autofluorescence. Free Radic. Biol. Med. 2016, 100, 53–65. 10.1016/j.freeradbiomed.2016.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hammen P. K.; Allali-Hassani A.; Hallenga K.; Hurley T. D.; Weiner H. Multiple conformations of NAD and NADH when bound to human cytosolic and mitochondrial aldehyde dehydrogenase. Biochemistry 2002, 41, 7156–7168. 10.1021/bi012197t. [DOI] [PubMed] [Google Scholar]
  7. Smith P. E.; Tanner J. J. Conformations of nicotinamide adenine dinucleotide (NAD+) in various environments. J. Mol. Recognit. 2000, 13, 27–34. . [DOI] [PubMed] [Google Scholar]
  8. Malcolm A. D.Methods in Enzymology; Elsevier: 1980; Vol. 66, pp 8–11. [DOI] [PubMed] [Google Scholar]
  9. McDonald G.; Brown B.; Hollis D.; Walter C. Effects of environment on the folding of nicotinamide-adenine dinucleotides in aqueous solutions. Biochemistry 1972, 11, 1920–1930. 10.1021/bi00760a029. [DOI] [PubMed] [Google Scholar]
  10. Barrett T. W. pH-induced modification of NAD and NADH solutions detected by Raman spectroscopy. J. Raman Spectrosc. 1980, 9, 130–133. 10.1002/jrs.1250090212. [DOI] [Google Scholar]
  11. Blumenstein M.; Raftery M. A. Phosphorus-31 and carbon-13 nuclear magnetic resonance studies of nicotinamide-adenine dinucleotide and related compounds. Biochemistry 1972, 11, 1643–1648. 10.1021/bi00759a017. [DOI] [PubMed] [Google Scholar]
  12. Catterall W. A.; Hollis D. P.; Walter C. F. Nuclear magnetic resonance study of the confirmation of nicotinamide-adenine dinucleotide and reduced nicotinamide-adenine dinucleotide insolution. Biochemistry 1969, 8, 4032–4036. 10.1021/bi00838a021. [DOI] [PubMed] [Google Scholar]
  13. Czeisler J. L.; Hollis D. P. Studies of the interaction of adenine and nicotinamide ring systems in aqueous solution by high resolution nuclear magnetic resonance. Biochemistry 1975, 14, 2781–2785. 10.1021/bi00683a035. [DOI] [PubMed] [Google Scholar]
  14. Riddle R. M.; Williams T. J.; Bryson T. A.; Dunlap R. B.; Fisher R. R.; Ellis P. D. Nuclear magnetic resonance studies on pyridine dinucleotides. 6. Dependence of the carbon-13 spin-lattice relaxation time of 1-methylnicotinamide and nicotinamide adenine dinucleotide as a function of pD and phosphate concentration. J. Am. Chem. Soc. 1976, 98, 4286–4290. 10.1021/ja00430a046. [DOI] [PubMed] [Google Scholar]
  15. Korenchan D. E.; Lu J.; Levitt M. H.; Jerschow A. 31 P nuclear spin singlet lifetimes in a system with switchable magnetic inequivalence: Experiment and simulation. Phys. Chem. Chem. Phys. 2021, 23, 19465–19471. 10.1039/D1CP03085J. [DOI] [PubMed] [Google Scholar]
  16. Korenchan D. E.; Lu J.; Sabba M.; Dagys L.; Brown L. J.; Levitt M. H.; Jerschow A. 31 P spin–lattice and singlet order relaxation mechanisms in pyrophosphate studied by isotopic substitution, field shuttling NMR, and molecular dynamics simulation. Phys. Chem. Chem. Phys. 2022, 24, 24238–24245. 10.1039/D2CP03801C. [DOI] [PubMed] [Google Scholar]
  17. Gorbunova I. A.; Sasin M. E.; Rubayo-Soneira J.; Smolin A. G.; Vasyutinskii O. S. Two-Photon Excited Fluorescence Dynamics in NADH in Water–Methanol Solutions: The Role of Conformation States. J. Phys. Chem. B 2020, 124, 10682–10697. 10.1021/acs.jpcb.0c07620. [DOI] [PubMed] [Google Scholar]
  18. Cadena-Caicedo A.; Gonzalez-Cano B.; López-Arteaga R.; Esturau-Escofet N.; Peon J. Ultrafast fluorescence signals from β-dihydronicotinamide adenine dinucleotide: resonant energy transfer in the folded and unfolded forms. J. Phys. Chem. B 2020, 124, 519–530. 10.1021/acs.jpcb.9b10012. [DOI] [PubMed] [Google Scholar]
  19. Heiner Z.; Roland T.; Leonard J.; Haacke S.; Groma G. I. Kinetics of Light-Induced Intramolecular Energy Transfer in Different Conformational States of NADH. J. Phys. Chem. B 2017, 121, 8037–8045. 10.1021/acs.jpcb.7b04753. [DOI] [PubMed] [Google Scholar]
  20. Patel D. J. 220 MHz Proton Magnetic Resonance Spectrum of NADH. Nature 1969, 221, 1239–1241. 10.1038/2211239a0. [DOI] [PubMed] [Google Scholar]
  21. Zens A. P.; Williams T. J.; Wisowaty J. C.; Fisher R. R.; Dunlap R. B.; Bryson T. A.; Ellis P. D. Nuclear magnetic resonance studies on pyridine dinucleotides. II. Solution conformational dynamics of nicotinamide adenine dinucleotide and nicotinamide mononucleotide as viewed by proton T1 measurements. J. Am. Chem. Soc. 1975, 97, 2850–2857. 10.1021/ja00843a040. [DOI] [PubMed] [Google Scholar]
  22. Zens A. P.; Bryson T. A.; Dunlap R. B.; Fisher R. R.; Ellis P. D. Nuclear magnetic resonance studies on pyridine dinucleotides. 7. The solution conformational dynamics of the adenosine portion of nicotinamide adenine dinucleotide and other related purine containing compounds. J. Am. Chem. Soc. 1976, 98, 7559–7564. 10.1021/ja00440a019. [DOI] [PubMed] [Google Scholar]
  23. Oppenheimer N. J.; Davidson R. M. 15N nuclear magnetic resonance studies of [1–15N]nicotinamide adenine dinucleotides. Org. Magn. Reson. 1980, 13, 14–16. 10.1002/mrc.1270130104. [DOI] [Google Scholar]
  24. Borin I. A.; Skaf M. S. Molecular association between water and dimethyl sulfoxide in solution: A molecular dynamics simulation study. J. Chem. Phys. 1999, 110, 6412–6420. 10.1063/1.478544. [DOI] [Google Scholar]
  25. Catalán J.; Díaz C.; García-Blanco F. Characterization of Binary Solvent Mixtures of DMSO with Water and Other Cosolvents. J. Org. Chem. 2001, 66, 5846–5852. 10.1021/jo010415i. [DOI] [PubMed] [Google Scholar]
  26. Luzar A.; Chandler D. Structure and hydrogen bond dynamics of water–dimethyl sulfoxide mixtures by computer simulations. J. Chem. Phys. 1993, 98, 8160–8173. 10.1063/1.464521. [DOI] [Google Scholar]
  27. Perera A.; Mazighi R. On the nature of the molecular ordering of water in aqueous DMSO mixtures. J. Chem. Phys. 2015, 143, 154502. 10.1063/1.4933204. [DOI] [PubMed] [Google Scholar]
  28. Volkov D. A.; Gorbunova I. A.; Vasyutinskii O. S. Conformational states of NADH in water–alcohol solutions studied by molecular dynamics simulations. J. Photochem. Photobiol., A 2024, 449, 115422. 10.1016/j.jphotochem.2023.115422. [DOI] [Google Scholar]
  29. Lu J.; Straub J. S.; Nowotarski M. S.; Han S.; Xu X.; Jerschow A. Spectroscopically dark phosphate features revealed by chemical exchange saturation transfer. NMR Biomed. 2024, 37, e5057 10.1002/nbm.5057. [DOI] [PubMed] [Google Scholar]
  30. Straub J. S.; Nowotarski M. S.; Lu J.; Sheth T.; Jiao S.; Fisher M. P. A.; Shell M. S.; Helgeson M. E.; Jerschow A.; Han S. Phosphates form spectroscopically dark state assemblies in common aqueous solutions. Proc. Natl. Acad. Sci. U. S. A. 2023, 120, e2206765120 10.1073/pnas.2206765120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Bolik-Coulon N.; Hansen D. F.; Kay L. E. Optimizing frequency sampling in CEST experiments. J. Biomol. NMR 2022, 76, 167–183. 10.1007/s10858-022-00403-2. [DOI] [PubMed] [Google Scholar]
  32. Johnson C. Diffusion ordered nuclear magnetic resonance spectroscopy: principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 1999, 34, 203–256. 10.1016/S0079-6565(99)00003-5. [DOI] [Google Scholar]
  33. Hall H. T.; Fuoss R. M. Empirical Analysis of Viscosity Data1. J. Am. Chem. Soc. 1951, 73, 265–269. 10.1021/ja01145a089. [DOI] [Google Scholar]
  34. Tropp J.; Redfield A. G. Proton magnetic resonance of NADH in water-methanol mixtures. Conformational change and behavior of exchangeable proton resonances as a function of temperature. J. Am. Chem. Soc. 1980, 102, 534–538. 10.1021/ja00522a016. [DOI] [Google Scholar]
  35. van Zijl P. C.; Yadav N. N. Chemical Exchange Saturation Transfer (CEST): what is in a name and what isn’t? Magn. Reson. Med. 2011, 65, 927–948. 10.1002/mrm.22761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Zhou J.; Zijl P. C. M. v. Chemical exchange saturation transfer imaging and spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2006, 48, 109–136. 10.1016/j.pnmrs.2006.01.001. [DOI] [PubMed] [Google Scholar]
  37. Bolik-Coulon N.; Hansen D. F.; Kay L. E. Optimizing frequency sampling in CEST experiments. J. Biomol. NMR 2022, 76, 167–183. 10.1007/s10858-022-00403-2. [DOI] [PubMed] [Google Scholar]
  38. Moskot M.; Jakóbkiewicz-Banecka J.; Kloska A.; Piotrowska E.; Narajczyk M.; Gabig-Cimińska M. The role of dimethyl sulfoxide (DMSO) in gene expression modulation and glycosaminoglycan metabolism in lysosomal storage disorders on an example of mucopolysaccharidosis. Int. J. Mol. Sci. 2019, 20, 304. 10.3390/ijms20020304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Gironi B.; Kahveci Z.; McGill B.; Lechner B.-D.; Pagliara S.; Metz J.; Morresi A.; Palombo F.; Sassi P.; Petrov P. G. Effect of DMSO on the mechanical and structural properties of model and biological membranes. Biophys. J. 2020, 119, 274–286. 10.1016/j.bpj.2020.05.037. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp4c03162_si_001.pdf (455.7KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES