Abstract
The turning process remains one of the most widely used manufacturing methods in the industry due to its high flexibility and production rates. Despite being an extensively used technique, the impact of this machining process on the surface integrity of the components has not yet been resolved in the literature, although it is well known that it can have a major influence on their final life. With the aim of providing new insights in the field, an extensive experimental campaign was designed on a 42CrMo4 quenched and tempered steel (in the following 42CrMo4+QT) using the response surface method. As inputs of this experimental design, the principal machining parameters were selected: feed rate (mm/rev), cutting speed (m/min), depth of cut (mm) and insert radius (mm). Meanwhile the main outputs measured where the surface roughness (µm) and the longitudinal residual stresses (MPa). In parallel, the turning operation of each specimen was monitored and the forces (X, Y and Z), current consumption of the main lathe motor, sound pressure and tool holder accelerations were recorded.
Keywords: Machining, Monitoring, Alloyed steel, Response surface method
Specifications Table
| Subject | Manufacturing Engineering; Mechanical Engineering. |
| Specific subject area | Assess the impact of the turning process on the surface integrity of a 42CrMo4+QT steel and develop phenomenological models to predict surface roughness and residual stress. |
| Type of data | Table, Graph and Figure. Raw, Filtered and Processed. |
| Data collection | Superficial residual stress was evaluated using an X-ray diffractometer Stresstech 3000-G3R while surface roughness was measured by means of a confocal microscope Leica DCM3D. Regarding the turning process monitoring task, the forces in the 3-axis, the principal motor current consumption, the sound pressure and tool holder accelerations, were recorded employing a National Instruments data acquisition card and an ad-hoc LabView software. |
| Data source location |
|
| Data accessibility | Repository name: MaRoReS (Machining, Roughness and Residual Stresses generated in turning of 42CrMo4+QT steel) [1] Data identification number: 10.17632/z9w23xvhbt.1 Direct URL to data: https://data.mendeley.com/datasets/z9w23xvhbt/1 |
1. Value of the Data
-
•
The data here will allow a better understanding of the influence of the manufacturing process on the surface integrity of 42CrMo4+QT, allowing the recognition of the key factors among those studied in this work (feed rate, cutting speed, depth of cut and insert radius).
-
•
The data collected during the extensive experimental campaign carried out by the authors will allow the development of phenomenological predictive models to assess the residual stresses and roughness generated in a 42CrMo4+QT steel based on the turning conditions, hence improving the existing knowledge in the field and laying the foundations for the manufacture of this steel to maximize the life of the components in service.
-
•
By monitoring the turning process of each of the specimens, additional information on the forces, accelerations or sound measured during machining is included, allowing complex models to be established relating these parameters to residual stresses and the generation of surface roughness.
2. Background
The influence of turning parameters on surface integrity has been recognized in the literature, although the relationship between the manufacturing process and the surface finish is not direct, existing some discussion about the importance of each of the cutting parameters on it.
On the one hand, the influence of cutting parameters on roughness has been studied in several comprehensive reviews, agreeing that among all the parameters, feed rate, cutting speed, depth of cut and tool radius are the most influential ones [[2], [3], [4]]. On the other hand, residual stress generated during manufacturing due to thermomechanical load is related to feed rate and insert tip radius, while the impact of depth of cut and cutting speed is questionable [5,6]. Furthermore, although some analytical equations have been proposed in the literature to assess the impact of turning in the surface integrity, they need to be revised for those complex machining scenarios where the tool does not work in the best conditions.
With the aim of developing predictive phenomenological models to appraise the impact of machining in the surface integrity, an extensive experimental campaign has been designed in this work, extending the existing knowledge in the field.
3. Data Description
The data presented in this manuscript belong to the extensive experimental campaign developed by the authors on the influence of the main turning parameters on the surface integrity of a 42CrMo4+QT steel. This experimental campaign was designed using the response surface methodology, a technique widely used in the design of experiments in many areas of knowledge due to its potential for the subsequent analysis of the results and the establishment of relationships between different parameters under study [7,8].
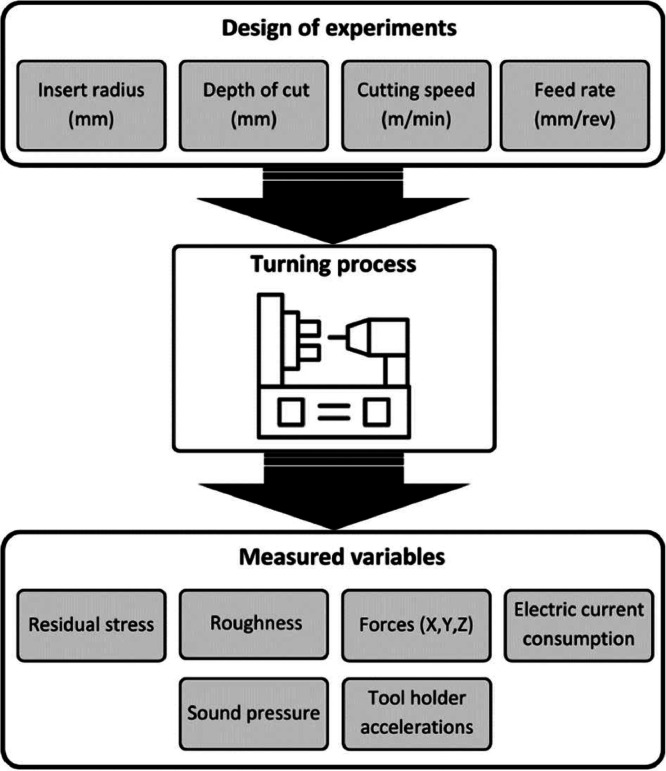
The presented dataset has the following format. Firstly, in the web repository a folder named “Raw Data” can be found. Within this folder, three more sub-folders are placed: “Residual Stress Measurements”; “Roughness Measurements”; and “Turning Process Monitoring” in which the raw results obtained from the evaluation of the residual stress, the surface roughness, and the monitoring of the turning process can be found. A more detailed classification based on the insert tip radius is used, leading to two more folders for each of the above mentioned folders with the information corresponding to the specimens machined with each of the tool insert radii used in the experimental campaign (0.4 mm and 0.8 mm respectively). Fig. 6 shows a general scheme of the experimental campaign developed, highlighting both the input variables (here insert radius, feed rate, depth of cut and cutting speed) used for the design of experiments that give rise to each of the machining scenarios, and the variables measured in the post-manufacturing stage.
Fig. 6.
General scheme of the input variables and the variables collected in the experimental campaign designed.
Regarding the raw residual stress data, three measurements were taken on each specimen, each equispaced 45°. As for the files generated in the evaluation, and following the criteria explained above, the experimental results are divided into two .txt files, one for each tool radius used in the experimental campaign (0.4 and 0.8 mm). Table 1 shows the results stored in the “0.4 mm Insert radius Residual stress Raw.txt” file, corresponding to the raw data obtained after measuring the residual stresses in the specimens machined with the 0.4 mm insert by means of a X-ray diffractometer, while Table 2 presents the analogous results for the specimens machined with the 0.8 mm tool. The principal stresses are there referred to the 0° orientation.
Table 1.
Experimental results of residual stress measurements carried out according to the scheme shown in Fig. 7(a) for 0.4 mm insert radius machined specimens.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Principal stresses |
||
|---|---|---|---|---|---|---|---|
| σmax (MPa) | σmin (MPa) | φ (angle) | |||||
| 1 | 0.4 | 0.05 | 138 | 0.15 | 599.7 | 363.9 | 46.6 |
| 2 | 0.4 | 0.05 | 138 | 0.15 | 714.8 | 435.0 | 46.1 |
| 3 | 0.4 | 0.10 | 107 | 0.10 | 406.2 | 79.9 | 41.5 |
| 4 | 0.4 | 0.10 | 107 | 0.10 | 398.6 | 62.4 | 41.2 |
| 5 | 0.4 | 0.10 | 107 | 0.20 | 763.8 | 414.2 | 59.8 |
| 6 | 0.4 | 0.10 | 107 | 0.20 | 722.6 | 406.7 | 58.3 |
| 7 | 0.4 | 0.10 | 169 | 0.20 | 756.4 | 432.5 | 43.9 |
| 8 | 0.4 | 0.10 | 169 | 0.20 | 788.0 | 457.9 | 45.1 |
| 9 | 0.4 | 0.10 | 169 | 0.10 | 567.2 | 170.6 | 40.4 |
| 10 | 0.4 | 0.10 | 169 | 0.10 | 324.7 | 20.8 | 35.3 |
| 11 | 0.4 | 0.15 | 76 | 0.15 | 677.8 | 332.5 | 52.4 |
| 12 | 0.4 | 0.15 | 76 | 0.15 | 285.8 | 56.1 | 26.7 |
| 13 | 0.4 | 0.15 | 138 | 0.05 | −275.2 | −478.6 | 4.7 |
| 14 | 0.4 | 0.15 | 138 | 0.05 | −246.2 | −513.7 | 2.1 |
| 15 | 0.4 | 0.15 | 138 | 0.15 | 272.3 | 90.5 | 31.9 |
| 16 | 0.4 | 0.15 | 138 | 0.15 | 697.0 | 353.5 | 51.3 |
| 17 | 0.4 | 0.15 | 138 | 0.15 | 732.3 | 353.9 | 46.5 |
| 18 | 0.4 | 0.15 | 138 | 0.15 | 598.9 | 272.5 | 42.5 |
| 19 | 0.4 | 0.15 | 138 | 0.15 | 630.9 | 320.3 | 42.3 |
| 20 | 0.4 | 0.15 | 138 | 0.15 | 751.9 | 386.4 | 51.6 |
| 21 | 0.4 | 0.15 | 138 | 0.25 | 801.6 | 466.5 | 58.5 |
| 22 | 0.4 | 0.15 | 138 | 0.25 | 799.7 | 476.4 | 56.8 |
| 23 | 0.4 | 0.15 | 200 | 0.15 | 661.9 | 255.9 | 42.6 |
| 24 | 0.4 | 0.15 | 200 | 0.15 | 606.4 | 207.0 | 38.7 |
| 25 | 0.4 | 0.20 | 107 | 0.10 | 500.1 | 125.9 | 44.9 |
| 26 | 0.4 | 0.20 | 107 | 0.10 | 491.1 | 122.7 | 46.1 |
| 27 | 0.4 | 0.20 | 107 | 0.20 | 647.7 | 291.0 | 53.2 |
| 28 | 0.4 | 0.20 | 107 | 0.20 | 786.6 | 388.2 | 59.7 |
| 29 | 0.4 | 0.20 | 169 | 0.20 | 679.6 | 219.0 | 52.5 |
| 30 | 0.4 | 0.20 | 169 | 0.20 | 695.3 | 274.0 | 52.7 |
| 31 | 0.4 | 0.20 | 169 | 0.10 | 606.5 | 187.7 | 39.5 |
| 32 | 0.4 | 0.20 | 169 | 0.10 | 603.4 | 186.6 | 41.3 |
| 33 | 0.4 | 0.25 | 138 | 0.15 | 752.6 | 357.7 | 51.2 |
| 34 | 0.4 | 0.25 | 138 | 0.15 | 748.6 | 343.6 | 49.1 |
Table 2.
Experimental results of residual stress measurements carried out according to the scheme shown in Fig. 7(a) for 0.8 mm insert radius machined specimens.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Principal stresses |
||
|---|---|---|---|---|---|---|---|
| σmax (MPa) | σmin (MPa) | φ (angle) | |||||
| 35 | 0.8 | 0.05 | 138 | 0.15 | 495.5 | 227.7 | −50.8 |
| 36 | 0.8 | 0.05 | 138 | 0.15 | 669.8 | 356.8 | −48.1 |
| 37 | 0.8 | 0.10 | 107 | 0.10 | 175.8 | −95.3 | −47.4 |
| 38 | 0.8 | 0.10 | 107 | 0.10 | −19.3 | −279.6 | −71.4 |
| 39 | 0.8 | 0.10 | 107 | 0.20 | 759.7 | 398.7 | −32.1 |
| 40 | 0.8 | 0.10 | 107 | 0.20 | 533.4 | 277.4 | −37.3 |
| 41 | 0.8 | 0.10 | 169 | 0.20 | 650.1 | 334.3 | −41.0 |
| 42 | 0.8 | 0.10 | 169 | 0.20 | 746.9 | 415.2 | −39.3 |
| 43 | 0.8 | 0.10 | 169 | 0.10 | 416.5 | 34.3 | −41.4 |
| 44 | 0.8 | 0.10 | 169 | 0.10 | 413.1 | 77.9 | −43.6 |
| 45 | 0.8 | 0.15 | 76 | 0.15 | 249.3 | −8.5 | −42.2 |
| 46 | 0.8 | 0.15 | 76 | 0.15 | 450.0 | 98.6 | −39.2 |
| 47 | 0.8 | 0.15 | 138 | 0.05 | −290.5 | −613.1 | −49.9 |
| 48 | 0.8 | 0.15 | 138 | 0.05 | −439.5 | −664.2 | −49.8 |
| 49 | 0.8 | 0.15 | 138 | 0.15 | 370.9 | 136.7 | −56.2 |
| 50 | 0.8 | 0.15 | 138 | 0.15 | 502.0 | 204.2 | −43.7 |
| 51 | 0.8 | 0.15 | 138 | 0.15 | 330.0 | 112.7 | −59.2 |
| 52 | 0.8 | 0.15 | 138 | 0.15 | 689.1 | 324.3 | −38.8 |
| 53 | 0.8 | 0.15 | 138 | 0.15 | 681.7 | 314.2 | −38.6 |
| 54 | 0.8 | 0.15 | 138 | 0.15 | 523.3 | 237.7 | −50.3 |
| 55 | 0.8 | 0.15 | 138 | 0.25 | 782.9 | 439.1 | −33.5 |
| 56 | 0.8 | 0.15 | 138 | 0.25 | 824.3 | 506.9 | −32.7 |
| 57 | 0.8 | 0.15 | 200 | 0.15 | 509.6 | 171.0 | −45.1 |
| 58 | 0.8 | 0.15 | 200 | 0.15 | 662.3 | 287.4 | −42.0 |
| 59 | 0.8 | 0.20 | 107 | 0.10 | 188.4 | −65.4 | −51.6 |
| 60 | 0.8 | 0.20 | 107 | 0.10 | 253.8 | −17.9 | −62.0 |
| 61 | 0.8 | 0.20 | 107 | 0.20 | 770.2 | 413.8 | −32.1 |
| 62 | 0.8 | 0.20 | 107 | 0.20 | 690.7 | 343.6 | −34.4 |
| 63 | 0.8 | 0.20 | 169 | 0.20 | 697.4 | 355.5 | −43.4 |
| 64 | 0.8 | 0.20 | 169 | 0.20 | 649.6 | 290.0 | −36.2 |
| 65 | 0.8 | 0.20 | 169 | 0.10 | 182.6 | −65.4 | −52.9 |
| 66 | 0.8 | 0.20 | 169 | 0.10 | 573.2 | 187.3 | −45.8 |
| 67 | 0.8 | 0.25 | 138 | 0.15 | 89.0 | −91.9 | 20.3 |
| 68 | 0.8 | 0.25 | 138 | 0.15 | 593.9 | 255.4 | 51.0 |
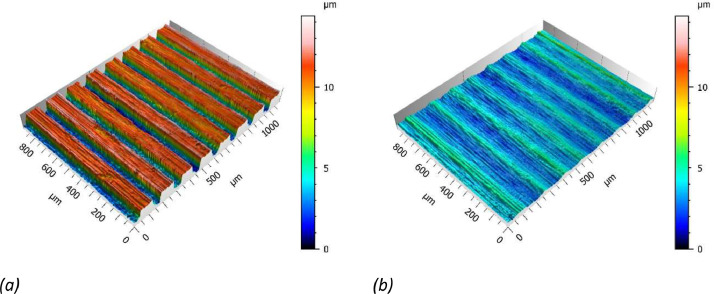
The scheme followed for the classification of the roughness data is analogous to the previous one, although, due to the measurement method used, two types of file have been stored for each of the measurements taken. The first of these files (.plu), allows a three-dimensional reconstruction of the measured surface, which greatly facilitates the results evaluation task. As an example, Fig. 1 shows the results obtained when evaluating files 45_01.plu (a) and 46_01 (b), both machined with the 0.8 mm radius tool. The second type of data in the aforementioned folder, with .dat extension, contains all information related to the performed roughness measurements in terms of roughness parameters (Ra, Rq, Rz, etc.) and the configuration of the measuring device. The existence of three files per specimen (i.e. 01_01.dat, 01_02.dat and 01_03.dat) is justified by having made three roughness measurements per sample.
Fig. 1.
Three-dimensional representation of the surfaces of 2 different test specimens obtained from .plu files: (a) 45_01.plu (0.8 mm); and (b) 46_01.plu (0.8 mm).
In the third sub-folder found in this repository (“Turning Process Monitoring”) the raw data recollected during the machining process of each sample can be found. In order to establish a bi-univocal relationship between each of the files and the machining conditions, a specific coding has been implemented. Thus, for instance, the first file found in the subfolder “0.4 mm Insert radius Turning monitoring Raw.zip” is named “1_r04_d005_s138_f015.txt,” which states that the data stored in this file corresponds to the specimen machined with an insert radius of 0.4 mm, with a depth of cut of 0.05 mm, a cutting speed of 138 m/min and a feed rate of 0.15 mm/rev.
Within each of these text files, the monitored data is structured in columns, where the first column shows the time history in seconds, the second column shows the current consumption of the lathe in millivolts, the third and fourth columns show the accelerations measured in the tool holder in g, the fifth column shows the sound in Pa, and finally, the remaining three columns show the forces in X, Y and X, respectively, in volts. At this point, is important to note that the former values, were not registered in their real units (e.g. forces in Newtons) and need, therefore, to be transformed to their real scale.
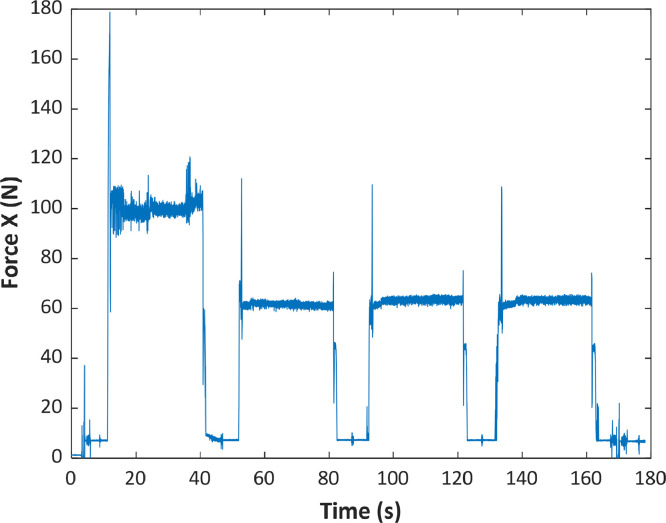
Fig. 2 displays the results of plotting the lathe Force X against the time for the specimen 11 machined with the 0.4 mm insert tip radius. A more exhaustive analysis of the above graph shows four regions whose associated force values are higher (60N-100 N) than those of the other regions, each of these high regions corresponding to the different machining passes. It is important to note that, although the first wave may seem anomalous, it is within the expected range, as it is the first finishing pass after roughing. As explained later, in order to analyse the monitored data, a filtering of the measured signals, which guarantees the elimination of both the first wave and the low areas of the signal, is required.
Fig. 2.
X-axis force measured during machining.
Lastly, the web repository contains the “Filtered Data” folder, whose structure is analogous to the one originally proposed to store the raw results. Within the folder, again, three sub-folders can be found: “Residual Stress Measurements”; “Roughness Measurements”; and “Turning Process Monitoring”, containing the results obtained after the filtering process of the residual stress, the surface roughness, and the monitoring of the turning process, respectively. In turn, each of these sub-folders is divided into two more folders with the information corresponding to the specimens machined with each of the tool radii used in the experimental campaign (0.4 mm and 0.8 mm).
Based on the data presented in Table 1, Table 3 shows both the longitudinal residual stresses (σL) and the radial residual stress (σC), calculated employing the MATLAB code developed by the authors (“Residual Stress Transformation Code.mlx”) which is placed within the sub-folder “Residual Stress Measurements”.
Table 3.
Circumferential and longitudinal residual stresses according to Fig. 7(b) for the measured specimens machined with the 0.4 mm radius tool.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Residual stress (RS) measurements |
|
|---|---|---|---|---|---|---|
| Longitudinal RS σL (MPa) |
Radial RS σR (MPa) |
|||||
| 1 | 0.4 | 0.05 | 138 | 0.15 | 488.4 | 475.2 |
| 2 | 0.4 | 0.05 | 138 | 0.15 | 580.3 | 569.5 |
| 3 | 0.4 | 0.10 | 107 | 0.10 | 223.2 | 262.9 |
| 4 | 0.4 | 0.10 | 107 | 0.10 | 208.3 | 252.7 |
| 5 | 0.4 | 0.10 | 107 | 0.20 | 675.3 | 502.7 |
| 6 | 0.4 | 0.10 | 107 | 0.20 | 635.4 | 493.9 |
| 7 | 0.4 | 0.10 | 169 | 0.20 | 588.2 | 600.7 |
| 8 | 0.4 | 0.10 | 169 | 0.20 | 623.5 | 622.4 |
| 9 | 0.4 | 0.10 | 169 | 0.10 | 337.2 | 400.6 |
| 10 | 0.4 | 0.10 | 169 | 0.10 | 122.3 | 223.2 |
| 11 | 0.4 | 0.15 | 76 | 0.15 | 549.3 | 461.0 |
| 12 | 0.4 | 0.15 | 76 | 0.15 | 102.5 | 239.4 |
| 13 | 0.4 | 0.15 | 138 | 0.05 | −477.2 | −276.6 |
| 14 | 0.4 | 0.15 | 138 | 0.05 | −513.3 | −246.6 |
| 15 | 0.4 | 0.15 | 138 | 0.15 | 141.3 | 221.5 |
| 16 | 0.4 | 0.15 | 138 | 0.15 | 562.7 | 487.8 |
| 17 | 0.4 | 0.15 | 138 | 0.15 | 553.0 | 533.2 |
| 18 | 0.4 | 0.15 | 138 | 0.15 | 421.5 | 449.9 |
| 19 | 0.4 | 0.15 | 138 | 0.15 | 461.0 | 490.2 |
| 20 | 0.4 | 0.15 | 138 | 0.15 | 610.9 | 527.4 |
| 21 | 0.4 | 0.15 | 138 | 0.25 | 710.1 | 558.0 |
| 22 | 0.4 | 0.15 | 138 | 0.25 | 702.8 | 573.3 |
| 23 | 0.4 | 0.15 | 200 | 0.15 | 441.9 | 475.9 |
| 24 | 0.4 | 0.15 | 200 | 0.15 | 363.1 | 450.3 |
| 25 | 0.4 | 0.20 | 107 | 0.10 | 312.3 | 313.7 |
| 26 | 0.4 | 0.20 | 107 | 0.10 | 314.0 | 299.8 |
| 27 | 0.4 | 0.20 | 107 | 0.20 | 519.7 | 419.0 |
| 28 | 0.4 | 0.20 | 107 | 0.20 | 685.2 | 489.6 |
| 29 | 0.4 | 0.20 | 169 | 0.20 | 508.9 | 389.7 |
| 30 | 0.4 | 0.20 | 169 | 0.20 | 540.6 | 428.7 |
| 31 | 0.4 | 0.20 | 169 | 0.10 | 357.1 | 437.1 |
| 32 | 0.4 | 0.20 | 169 | 0.10 | 368.2 | 421.8 |
| 33 | 0.4 | 0.25 | 138 | 0.15 | 597.5 | 512.8 |
| 34 | 0.4 | 0.25 | 138 | 0.15 | 575.0 | 517.2 |
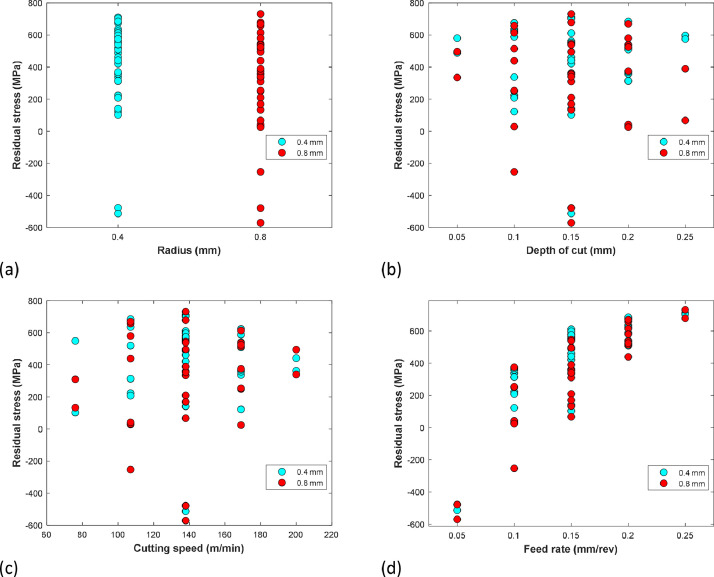
Fig. 3 shows graphically the influence of each of the cutting parameters studied here on the measured residual surface tension, showing that the feed rate is the most influential one, which is in accordance with most of the authors, as reported in some of the most cited reviews in the field [2,9]. Regarding the rest of the parameters, there is still some discussion in the literature depending on the material studied and the machining conditions themselves. For example, while most investigations in the literature report significant effects of cutting speeds [10], some researchers claim that this parameter has no impact on the generated residual stresses [11] (Table 4).
Fig. 3.
Influence of the four cutting parameters studied on the longitudinal residual stress: (a) Influence of insert raidus, (b) Influence of Depth of cut, (c) Influence of Cutting speed (m/min), and (d) Influence of feed rate (mm/rev).
Table 4.
Circumferential and longitudinal residual stresses according to Fig. 7(b) for the measured specimens machined with the 0.8 mm radius tool.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Residual stress (RS) measurements |
|
|---|---|---|---|---|---|---|
| Longitudinal RS σL (MPa) |
Radial RS σR (MPa) |
|||||
| 35 | 0.8 | 0.05 | 138 | 0.15 | 334.7 | 388.5 |
| 36 | 0.8 | 0.05 | 138 | 0.15 | 496.4 | 530.2 |
| 37 | 0.8 | 0.10 | 107 | 0.10 | 28.9 | 51.6 |
| 38 | 0.8 | 0.10 | 107 | 0.10 | −253.1 | −45.8 |
| 39 | 0.8 | 0.10 | 107 | 0.20 | 657.8 | 500.6 |
| 40 | 0.8 | 0.10 | 107 | 0.20 | 439.4 | 371.4 |
| 41 | 0.8 | 0.10 | 169 | 0.20 | 514.2 | 470.2 |
| 42 | 0.8 | 0.10 | 169 | 0.20 | 613.8 | 548.3 |
| 43 | 0.8 | 0.10 | 169 | 0.10 | 249.4 | 201.4 |
| 44 | 0.8 | 0.10 | 169 | 0.10 | 253.7 | 237.3 |
| 45 | 0.8 | 0.15 | 76 | 0.15 | 133.0 | 107.8 |
| 46 | 0.8 | 0.15 | 76 | 0.15 | 309.6 | 239.0 |
| 47 | 0.8 | 0.15 | 138 | 0.05 | −479.3 | −424.3 |
| 48 | 0.8 | 0.15 | 138 | 0.05 | −570.6 | −533.1 |
| 49 | 0.8 | 0.15 | 138 | 0.15 | 209.2 | 298.4 |
| 50 | 0.8 | 0.15 | 138 | 0.15 | 359.9 | 346.3 |
| 51 | 0.8 | 0.15 | 138 | 0.15 | 169.7 | 273.0 |
| 52 | 0.8 | 0.15 | 138 | 0.15 | 545.9 | 467.5 |
| 53 | 0.8 | 0.15 | 138 | 0.15 | 538.7 | 457.2 |
| 54 | 0.8 | 0.15 | 138 | 0.15 | 354.2 | 406.8 |
| 55 | 0.8 | 0.15 | 138 | 0.25 | 678.2 | 543.8 |
| 56 | 0.8 | 0.15 | 138 | 0.25 | 731.7 | 599.5 |
| 57 | 0.8 | 0.15 | 200 | 0.15 | 339.7 | 340.9 |
| 58 | 0.8 | 0.15 | 200 | 0.15 | 494.4 | 455.3 |
| 59 | 0.8 | 0.20 | 107 | 0.10 | 32.5 | 90.5 |
| 60 | 0.8 | 0.20 | 107 | 0.10 | 42.0 | 193.9 |
| 61 | 0.8 | 0.20 | 107 | 0.20 | 669.6 | 514.4 |
| 62 | 0.8 | 0.20 | 107 | 0.20 | 579.9 | 454.4 |
| 63 | 0.8 | 0.20 | 169 | 0.20 | 536.0 | 516.9 |
| 64 | 0.8 | 0.20 | 169 | 0.20 | 524.2 | 415.4 |
| 65 | 0.8 | 0.20 | 169 | 0.10 | 24.8 | 92.4 |
| 66 | 0.8 | 0.20 | 169 | 0.10 | 374.9 | 385.6 |
| 67 | 0.8 | 0.25 | 138 | 0.15 | 67.2 | −70.1 |
| 68 | 0.8 | 0.25 | 138 | 0.15 | 389.5 | 459.8 |
In this way, a similar situation seems to occur with the depth of cut [10,12]. Among all cutting parameters, cutting depth has a minor effect on residual stresses in machining processes and may be neglected compared to the effects of cutting speed and feed rate. However, some researchers have reported contrary results [13].
Table 5 shows the experimental roughness results, evaluated in terms of the average roughness parameter, Ra, as it is one of the most widely used at industrial level. Note that here, the authors have selected Ra as the parameter of interest, but given the simplicity of the proposed analysis, an identical evaluation can be made for any other roughness parameter available in the .dat files (Rq, Rp, Rv, Rt, Rpm, RzISO, RmaxISO, etc.) by simply calculating the average value of the parameter of interest measured on each of the specimens. Within the sub-folder “Roughness Measurements” found in the folder “Filtered Data”, the results of the Ra evaluation can be found both for 0.4 and 0.8 mm insert radius tool, named “0.4 mm Insert radius Roughness Filtered.txt” and “0.8 mm Insert radius Roughness Filtered.txt”, respectively (Table 6, Table 7, Table 8).
Table 5.
Evaluation of Ra (µm) roughness parameter for 0.4 mm insert tool radius.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Ra roughness measurements |
|||
|---|---|---|---|---|---|---|---|---|
| 01 (µm) |
02 (µm) |
03 (µm) |
Mean (µm) |
|||||
| 1 | 0.4 | 0.05 | 138 | 0.15 | 0.856 | 0.854 | 0.863 | 0.858 |
| 2 | 0.4 | 0.05 | 138 | 0.15 | 1.070 | 1.060 | 1.105 | 1.078 |
| 3 | 0.4 | 0.10 | 107 | 0.10 | 0.420 | 0.413 | 0.393 | 0.409 |
| 4 | 0.4 | 0.10 | 107 | 0.10 | 0.563 | 0.562 | 0.549 | 0.558 |
| 5 | 0.4 | 0.10 | 107 | 0.20 | 1.142 | 1.095 | 1.163 | 1.133 |
| 6 | 0.4 | 0.10 | 107 | 0.20 | 1.180 | 1.177 | 1.198 | 1.185 |
| 7 | 0.4 | 0.10 | 169 | 0.20 | 1.159 | 1.168 | 1.140 | 1.156 |
| 8 | 0.4 | 0.10 | 169 | 0.20 | 1.154 | 1.122 | 1.144 | 1.140 |
| 9 | 0.4 | 0.10 | 169 | 0.10 | 0.655 | 0.673 | 0.593 | 0.640 |
| 10 | 0.4 | 0.10 | 169 | 0.10 | 0.562 | 0.550 | 0.570 | 0.561 |
| 11 | 0.4 | 0.15 | 76 | 0.15 | 0.753 | 0.760 | 0.763 | 0.759 |
| 12 | 0.4 | 0.15 | 76 | 0.15 | 0.843 | 0.798 | 0.777 | 0.806 |
| 13 | 0.4 | 0.15 | 138 | 0.05 | 0.291 | 0.313 | 0.314 | 0.306 |
| 14 | 0.4 | 0.15 | 138 | 0.05 | 0.664 | 0.611 | 0.696 | 0.657 |
| 15 | 0.4 | 0.15 | 138 | 0.15 | 0.801 | 0.793 | 0.793 | 0.796 |
| 16 | 0.4 | 0.15 | 138 | 0.15 | 0.856 | 0.853 | 0.839 | 0.849 |
| 17 | 0.4 | 0.15 | 138 | 0.15 | 0.660 | 0.685 | 0.679 | 0.675 |
| 18 | 0.4 | 0.15 | 138 | 0.15 | 0.692 | 0.689 | 0.689 | 0.690 |
| 19 | 0.4 | 0.15 | 138 | 0.15 | 0.910 | 0.878 | 0.875 | 0.888 |
| 20 | 0.4 | 0.15 | 138 | 0.15 | 0.869 | 0.869 | 0.872 | 0.870 |
| 21 | 0.4 | 0.15 | 138 | 0.25 | 1.671 | 1.601 | 1.596 | 1.623 |
| 22 | 0.4 | 0.15 | 138 | 0.25 | 1.685 | 1.668 | 1.693 | 1.682 |
| 23 | 0.4 | 0.15 | 200 | 0.15 | 0.578 | 0.590 | 0.594 | 0.587 |
| 24 | 0.4 | 0.15 | 200 | 0.15 | 0.612 | 0.601 | 0.576 | 0.596 |
| 25 | 0.4 | 0.20 | 107 | 0.10 | 0.477 | 0.483 | 0.474 | 0.478 |
| 26 | 0.4 | 0.20 | 107 | 0.10 | 0.574 | 0.576 | 0.571 | 0.574 |
| 27 | 0.4 | 0.20 | 107 | 0.20 | 0.971 | 1.018 | 1.017 | 1.002 |
| 28 | 0.4 | 0.20 | 107 | 0.20 | 1.062 | 1.059 | 1.100 | 1.074 |
| 29 | 0.4 | 0.20 | 169 | 0.20 | 1.101 | 1.114 | 1.117 | 1.111 |
| 30 | 0.4 | 0.20 | 169 | 0.20 | 1.087 | 1.102 | 1.085 | 1.091 |
| 31 | 0.4 | 0.20 | 169 | 0.10 | 0.419 | 0.434 | 0.442 | 0.432 |
| 32 | 0.4 | 0.20 | 169 | 0.10 | 0.469 | 0.443 | 0.467 | 0.460 |
| 33 | 0.4 | 0.25 | 138 | 0.15 | 0.751 | 0.732 | 0.723 | 0.735 |
| 34 | 0.4 | 0.25 | 138 | 0.15 | 0.793 | 0.768 | 0.789 | 0.783 |
Table 6.
Evaluation of Ra (µm) roughness parameter for 0.8 mm insert tool radius.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Ra roughness measurements |
|||
|---|---|---|---|---|---|---|---|---|
| 01 (µm) |
02 (µm) |
03 (µm) |
Mean (µm) |
|||||
| 35 | 0.8 | 0.05 | 138 | 0.15 | 0.791 | 0.812 | 0.797 | 0.800 |
| 36 | 0.8 | 0.05 | 138 | 0.15 | 1.060 | 1.054 | 1.092 | 1.069 |
| 37 | 0.8 | 0.10 | 107 | 0.10 | 0.494 | 0.460 | 0.476 | 0.477 |
| 38 | 0.8 | 0.10 | 107 | 0.10 | 0.550 | 0.549 | 0.555 | 0.551 |
| 39 | 0.8 | 0.10 | 107 | 0.20 | 0.743 | 0.735 | 0.728 | 0.735 |
| 40 | 0.8 | 0.10 | 107 | 0.20 | 0.778 | 0.783 | 0.771 | 0.777 |
| 41 | 0.8 | 0.10 | 169 | 0.20 | 0.722 | 0.737 | 0.730 | 0.730 |
| 42 | 0.8 | 0.10 | 169 | 0.20 | 0.723 | 0.743 | 0.715 | 0.727 |
| 43 | 0.8 | 0.10 | 169 | 0.10 | 0.575 | 0.522 | 0.536 | 0.544 |
| 44 | 0.8 | 0.10 | 169 | 0.10 | 0.462 | 0.474 | 0.469 | 0.468 |
| 45 | 0.8 | 0.15 | 76 | 0.15 | 3.326 | 3.202 | 3.176 | 3.235 |
| 46 | 0.8 | 0.15 | 76 | 0.15 | 0.634 | 0.623 | 0.616 | 0.624 |
| 47 | 0.8 | 0.15 | 138 | 0.05 | 0.303 | 0.313 | 0.306 | 0.307 |
| 48 | 0.8 | 0.15 | 138 | 0.05 | 0.326 | 0.250 | 0.250 | 0.275 |
| 49 | 0.8 | 0.15 | 138 | 0.15 | 0.470 | 0.501 | 0.494 | 0.488 |
| 50 | 0.8 | 0.15 | 138 | 0.15 | 0.550 | 0.540 | 0.576 | 0.555 |
| 51 | 0.8 | 0.15 | 138 | 0.15 | 0.414 | 0.401 | 0.404 | 0.406 |
| 52 | 0.8 | 0.15 | 138 | 0.15 | 0.420 | 0.405 | 0.404 | 0.410 |
| 53 | 0.8 | 0.15 | 138 | 0.15 | 0.479 | 0.470 | 0.476 | 0.475 |
| 54 | 0.8 | 0.15 | 138 | 0.15 | 0.560 | 0.571 | 0.563 | 0.565 |
| 55 | 0.8 | 0.15 | 138 | 0.25 | 0.865 | 0.822 | 0.874 | 0.854 |
| 56 | 0.8 | 0.15 | 138 | 0.25 | 0.898 | 0.911 | 0.896 | 0.902 |
| 57 | 0.8 | 0.15 | 200 | 0.15 | 0.696 | 0.722 | 0.715 | 0.711 |
| 58 | 0.8 | 0.15 | 200 | 0.15 | 0.590 | 0.607 | 0.604 | 0.600 |
| 59 | 0.8 | 0.20 | 107 | 0.10 | 0.402 | 0.387 | 0.366 | 0.385 |
| 60 | 0.8 | 0.20 | 107 | 0.10 | 0.453 | 0.439 | 0.491 | 0.461 |
| 61 | 0.8 | 0.20 | 107 | 0.20 | 1.252 | 1.264 | 1.262 | 1.259 |
| 62 | 0.8 | 0.20 | 107 | 0.20 | 0.671 | 0.717 | 0.691 | 0.693 |
| 63 | 0.8 | 0.20 | 169 | 0.20 | 0.443 | 0.449 | 0.444 | 0.445 |
| 64 | 0.8 | 0.20 | 169 | 0.20 | 0.468 | 0.469 | 0.460 | 0.466 |
| 65 | 0.8 | 0.20 | 169 | 0.10 | 0.547 | 0.538 | 0.534 | 0.540 |
| 66 | 0.8 | 0.20 | 169 | 0.10 | 0.375 | 0.382 | 0.358 | 0.372 |
| 67 | 0.8 | 0.25 | 138 | 0.15 | 0.375 | 0.358 | 0.368 | 0.367 |
| 68 | 0.8 | 0.25 | 138 | 0.15 | 0.531 | 0.549 | 0.525 | 0.535 |
Table 7.
Average value of the forces in the three axes and of the current consumed by the lathe for the specimens machined with the 0.4 mm insert tip radius.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Turning process monitoring |
|||
|---|---|---|---|---|---|---|---|---|
| Force X (N) |
Force Y (N) |
Force Z (N) |
Current (A) |
|||||
| 1 | 0.4 | 0.05 | 138 | 0.15 | 41.673 | 60.573 | 21.434 | 9.083 |
| 2 | 0.4 | 0.05 | 138 | 0.15 | 41.422 | 55.547 | 19.800 | 9.053 |
| 3 | 0.4 | 0.10 | 107 | 0.10 | 38.978 | 43.202 | 26.637 | 11.639 |
| 4 | 0.4 | 0.10 | 107 | 0.10 | 44.870 | 63.900 | 25.919 | 11.627 |
| 5 | 0.4 | 0.10 | 107 | 0.20 | 63.336 | 91.264 | 32.111 | 11.713 |
| 6 | 0.4 | 0.10 | 107 | 0.20 | 62.732 | 91.650 | 31.799 | 11.640 |
| 7 | 0.4 | 0.10 | 169 | 0.20 | 66.996 | 87.049 | 34.330 | 8.075 |
| 8 | 0.4 | 0.10 | 169 | 0.20 | 66.046 | 90.405 | 33.676 | 8.101 |
| 9 | 0.4 | 0.10 | 169 | 0.10 | 49.385 | 59.757 | 29.059 | 7.844 |
| 10 | 0.4 | 0.10 | 169 | 0.10 | 49.209 | 63.941 | 23.212 | 7.817 |
| 11 | 0.4 | 0.15 | 76 | 0.15 | 62.582 | 100.795 | 37.915 | 13.971 |
| 12 | 0.4 | 0.15 | 76 | 0.15 | 63.647 | 111.934 | 37.835 | 13.972 |
| 13 | 0.4 | 0.15 | 138 | 0.05 | 37.376 | 39.940 | 24.900 | 9.127 |
| 14 | 0.4 | 0.15 | 138 | 0.05 | 48.876 | 59.784 | 27.847 | 9.082 |
| 15 | 0.4 | 0.15 | 138 | 0.15 | 61.138 | 97.351 | 34.069 | 9.113 |
| 16 | 0.4 | 0.15 | 138 | 0.15 | 53.180 | 75.430 | 32.158 | 9.109 |
| 17 | 0.4 | 0.15 | 138 | 0.15 | 65.491 | 93.390 | 37.436 | 9.078 |
| 18 | 0.4 | 0.15 | 138 | 0.15 | 64.813 | 95.427 | 35.927 | 9.084 |
| 19 | 0.4 | 0.15 | 138 | 0.15 | 65.286 | 98.675 | 36.125 | 9.081 |
| 20 | 0.4 | 0.15 | 138 | 0.15 | 57.077 | 73.649 | 38.234 | 9.036 |
| 21 | 0.4 | 0.15 | 138 | 0.25 | 82.196 | 126.715 | 46.128 | 9.177 |
| 22 | 0.4 | 0.15 | 138 | 0.25 | 79.582 | 125.298 | 45.395 | 9.159 |
| 23 | 0.4 | 0.15 | 200 | 0.15 | 72.325 | 91.753 | 39.286 | 7.682 |
| 24 | 0.4 | 0.15 | 200 | 0.15 | 71.485 | 92.786 | 40.267 | 7.646 |
| 25 | 0.4 | 0.20 | 107 | 0.10 | 54.141 | 90.364 | 35.991 | 11.642 |
| 26 | 0.4 | 0.20 | 107 | 0.10 | 53.593 | 89.682 | 34.269 | 11.623 |
| 27 | 0.4 | 0.20 | 107 | 0.20 | 84.661 | 140.501 | 44.124 | 11.606 |
| 28 | 0.4 | 0.20 | 107 | 0.20 | 76.734 | 115.173 | 49.474 | 11.631 |
| 29 | 0.4 | 0.20 | 169 | 0.20 | 89.799 | 117.947 | 52.733 | 8.323 |
| 30 | 0.4 | 0.20 | 169 | 0.20 | 86.109 | 112.166 | 53.093 | 8.284 |
| 31 | 0.4 | 0.20 | 169 | 0.10 | 58.787 | 89.179 | 36.876 | 7.929 |
| 32 | 0.4 | 0.20 | 169 | 0.10 | 58.653 | 87.638 | 36.189 | 7.905 |
| 33 | 0.4 | 0.25 | 138 | 0.15 | 71.237 | 112.791 | 49.349 | 9.160 |
| 34 | 0.4 | 0.25 | 138 | 0.15 | 76.304 | 132.177 | 48.496 | 9.155 |
Table 8.
Average value of the forces in the three axes and of the current consumed by the lathe for the specimens machined with the 0.8 mm insert tip radius.
| Run | Factor Ir: Insert radius (mm) |
Factor Dc: Depth of cut (mm) |
Factor Cs: Cutting speed (m/min) |
Factor Fr: Feed rate (mm/rev) |
Turning process monitoring |
|||
|---|---|---|---|---|---|---|---|---|
| Force X (N) |
Force Y (N) |
Force Z (N) |
Current (A) |
|||||
| 35 | 0.8 | 0.05 | 138 | 0.15 | 32.412 | 57.719 | 22.452 | 9.130 |
| 36 | 0.8 | 0.05 | 138 | 0.15 | 32.632 | 54.193 | 22.361 | 9.115 |
| 37 | 0.8 | 0.10 | 107 | 0.10 | 29.555 | 47.126 | 28.383 | 11.757 |
| 38 | 0.8 | 0.10 | 107 | 0.10 | 34.888 | 65.673 | 30.999 | 11.753 |
| 39 | 0.8 | 0.10 | 107 | 0.20 | 50.282 | 70.953 | 30.892 | 11.793 |
| 40 | 0.8 | 0.10 | 107 | 0.20 | 57.406 | 91.437 | 30.645 | 11.793 |
| 41 | 0.8 | 0.10 | 169 | 0.20 | 64.704 | 94.675 | 36.307 | 8.187 |
| 42 | 0.8 | 0.10 | 169 | 0.20 | 61.216 | 84.054 | 32.949 | 8.183 |
| 43 | 0.8 | 0.10 | 169 | 0.10 | 40.707 | 62.509 | 26.523 | 7.895 |
| 44 | 0.8 | 0.10 | 169 | 0.10 | 43.039 | 63.950 | 26.336 | 7.882 |
| 45 | 0.8 | 0.15 | 76 | 0.15 | 53.278 | 77.666 | 40.333 | 13.978 |
| 46 | 0.8 | 0.15 | 76 | 0.15 | 61.090 | 105.365 | 33.760 | 13.980 |
| 47 | 0.8 | 0.15 | 138 | 0.05 | 38.925 | 64.243 | 29.238 | 9.048 |
| 48 | 0.8 | 0.15 | 138 | 0.05 | 45.374 | 71.574 | 29.269 | 9.030 |
| 49 | 0.8 | 0.15 | 138 | 0.15 | 64.127 | 98.812 | 35.613 | 9.244 |
| 50 | 0.8 | 0.15 | 138 | 0.15 | 68.375 | 100.659 | 44.035 | 9.211 |
| 51 | 0.8 | 0.15 | 138 | 0.15 | 62.255 | 96.224 | 32.824 | 9.161 |
| 52 | 0.8 | 0.15 | 138 | 0.15 | 61.272 | 94.665 | 32.811 | 9.151 |
| 53 | 0.8 | 0.15 | 138 | 0.15 | 60.291 | 92.190 | 33.937 | 9.155 |
| 54 | 0.8 | 0.15 | 138 | 0.15 | 63.634 | 112.106 | 42.878 | 9.201 |
| 55 | 0.8 | 0.15 | 138 | 0.25 | 79.882 | 127.650 | 41.905 | 9.239 |
| 56 | 0.8 | 0.15 | 138 | 0.25 | 78.907 | 125.357 | 38.860 | 9.231 |
| 57 | 0.8 | 0.15 | 200 | 0.15 | 65.029 | 94.976 | 36.874 | 7.913 |
| 58 | 0.8 | 0.15 | 200 | 0.15 | 62.986 | 89.963 | 37.478 | 7.849 |
| 59 | 0.8 | 0.20 | 107 | 0.10 | 67.596 | 123.165 | 74.399 | 11.800 |
| 60 | 0.8 | 0.20 | 107 | 0.10 | 57.704 | 97.486 | 29.742 | 11.711 |
| 61 | 0.8 | 0.20 | 107 | 0.20 | 82.291 | 135.903 | 36.908 | 11.652 |
| 62 | 0.8 | 0.20 | 107 | 0.20 | 77.933 | 134.579 | 45.562 | 11.769 |
| 63 | 0.8 | 0.20 | 169 | 0.20 | 86.114 | 137.287 | 50.642 | 8.308 |
| 64 | 0.8 | 0.20 | 169 | 0.20 | 85.320 | 140.201 | 62.409 | 8.259 |
| 65 | 0.8 | 0.20 | 169 | 0.10 | 67.167 | 99.101 | 53.134 | 8.093 |
| 66 | 0.8 | 0.20 | 169 | 0.10 | 67.511 | 89.080 | 38.583 | 8.002 |
| 67 | 0.8 | 0.25 | 138 | 0.15 | 86.671 | 158.813 | 63.192 | 9.273 |
| 68 | 0.8 | 0.25 | 138 | 0.15 | 68.177 | 110.583 | 49.337 | 9.193 |
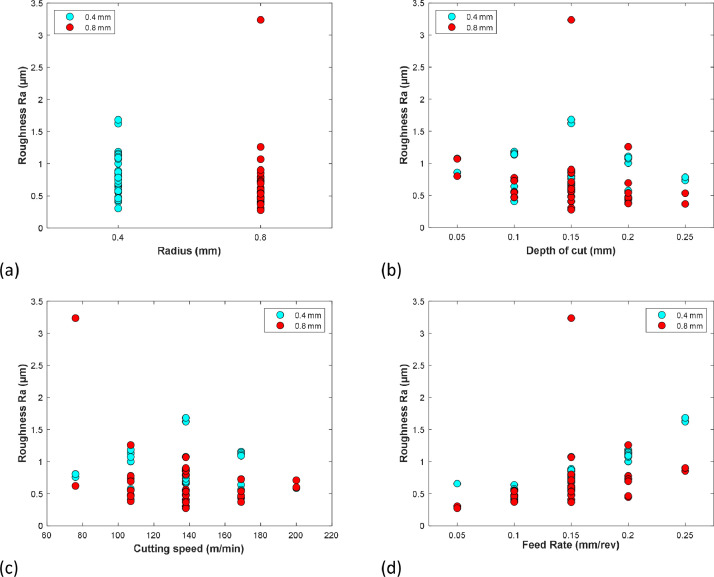
As previously done for the longitudinal residual stress, the relationships between the main turning parameters and the average Ra surface roughness measured on the specimens have been plotted (see Fig. 4). The obtained results are in clear agreement with the literature, showing how the feed rate is the determining parameter in the generation of surface roughness [2]. In general lines, most authors agree that feed rate and residual stress had significant effects in reducing the surface roughness, while the depth of cut had the least effect [14].
Fig. 4.
Influence of the four cutting parameters studied on the Ra roughness parameter: (a) Influence of insert radius, (b) Influence of Depth of cut, (c) Influence of Cutting speed (m/min), and (d) Influence of feed rate (mm/rev).
As mentioned before, the signals monitored during machining (current, accelerations, sound, and forces) require a filtering process before analysis, whereby the data recorded corresponding to the time between cutting passes are eliminated. For this purpose, an ad-hoc MATLAB code has been developed based on the state-level function, specifically programmed to identify signal high and low levels, allowing the subsequent evaluation of the results by eliminating the influence of the low part of the signal and thus, favoring the subsequent calculation of a representative value for each signal. The results of this filtering can be found in the last sub-folder called “Monitoring of the turning process,” following the same coding as in the case of the “Raw data,” while the MATLAB codes are found in the first one (see “MATLAB analysis codes”).
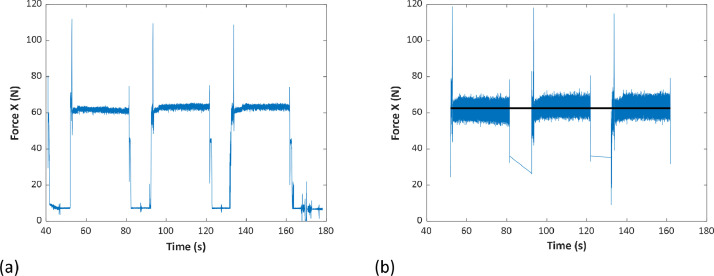
The following paragraphs are devoted to a more detailed explanation of the aforementioned MATLAB codes. Initially, the “Filter 1.m” code is used to read the raw data measured on the lathe, whose shape, in the case of the X forces, is shown in Fig. 5. Once the data is loaded, the code is able to identify the start and end of each of the high parts of the waves which correspond, as mentioned above, to the start and end of each machining pass and, therefore, to the region of interest. In addition, the initial section of the wave is also removed, leaving the final finishing passes as the region of interest (see Fig. 5(a)).
Fig. 5.
Result of the forces on the X-axis after filtering the data: (a) After removal of the first wave after roughing, and (b) After removing the lower regions of the waveforms corresponding to the time between passes.
Once the filtering is done, the reference value for each of the recorded variables can be obtained using the “Filter 2.m” code. Fig. 5(b) shows the results for the case of the X-axis forces, where the mean value of the X-force is represented by a black line. The noise observed in both Fig. 5(a) and (b) is related to the entry and exit of the tool from the workpiece and the high data acquisition frequency during the process. An analogous calculation is performed for the rest of the variables (Y-force, Z-force, accelerations, sound, and current), although each of these variables, due to their different waveforms, requires a unique analysis. For example, RMS (root mean square value) seems to be a good analysis method to obtain a representative value for the current consumed during machining, while frequency domain analysis methods may be necessary to select a representative value for the sound.
4. Experimental Design, Materials and Methods
In this section, a more detailed explanation of the design of experiments is given, as well as the equipment used for batch fabrication and data collection, hence facilitating the reproducibility of the work presented here.
After a thorough review of the state of the art in the field, feed rate, cutting speed, depth of cut and tool radius were identified as the main machining parameters [2,9,15,16]. Due to the technical characteristics of the lathe available for this work (see Table 9), the ranges of each of the parameters shown in the Table 10 were selected while the selected cutting inserts are those shown in Table 11. Furthermore, these parameters have been chosen in order to force the tool to work in conditions outside its correct machining range, forcing complex machining scenarios.
Table 9.
JATOR TAJ-42 CNC lathe technical specifications.
| CNC lathe Jator TAJ-42 | |
|---|---|
| Machine software | Fagor 8055 T |
| Main speed engine power | 11/15 kW |
| Max. spindle speed | 3000 rpm |
| Spindle nose | DIN 55,026 (A5) |
| Bar trough | 42 mm |
| Automatic tool changer | 12 tools |
| Working area (Z/X) | 500/200 mm |
| Rapid feed (Z/X) | 15/12 m/min |
Table 10.
Machining parameters ranges selected for the turning process.
| Experimental campaign parameters | |
|---|---|
| Insert radius (mm) | 0.4 and 0.8 |
| Depth of cut (mm) | 0.05–0.25 |
| Cutting speed (m/min) | 76–200 |
| Feed rate (mm/rev) | 0.10–0.25 |
Table 11.
Insert technical specifications.
| Insert specifications | ||
|---|---|---|
| Insert manufacturer | Sandvik Coromant | Sandvik Coromant |
| Reference | DCMX 11 T3 04-WF 4325 | DCMX 11 T3 08-WF 4425 |
| Tip radius (mm) | 0.4 | 0.8 |
| Main cutting edge angle (°) | 93 | 93 |
| Recommended depth of cut (mm) | 0.3–3.0 | 0.3–3.0 |
| Recommended cutting speed (m/min) | 345–475 | 305–420 |
| Recommended feed rate (mm/rev) | 0.07–0.30 | 0.12–0.40 |
Once the parameters under study were selected, a central composite design of experiments was implemented using DesignExpert V13 software, leading to the machining of 68 specimens, 34 with an insert tip radius of 0.4 mm and 34 with an insert tool radius of 0.8 mm. This type of design consists of central points (normally between 4 and 6), which enable the correct fit of the model to be analyzed and the pure experimental error estimation. These central points are extended with axial or star points, by means of which the quadratic effects can be analyzed. Thanks to this design, the first and second order terms can be efficiently estimated [17]. The coding of the factorial points (code level) and the minimum and maximum values of the four selected factors (star points of the CCD design), can be found at Table 12. In the aforementioned Table 12, it is important to note that the variable ‘Insert radius’, being of categorical type, does not have an associated coding level, but simply takes two possible values, in the case studied here 0.4 mm (minimum value) and 0.8 mm (maximum value).
Table 12.
Model input parameters.
| Input | Type | Factor | Units | Min | Max | Code level |
||
|---|---|---|---|---|---|---|---|---|
| −1 | 0 | +1 | ||||||
| Feed rate | Numerical | Fr | mm/rev | 0.05 | 0.25 | 0.1 | 0.15 | 0.2 |
| Cutting speed | Numerical | Cs | m/min | 76 | 200 | 107 | 138 | 169 |
| Depth of cut | Numerical | Dc | mm | 0.05 | 0.25 | 0.1 | 0.15 | 0.2 |
| Insert radius | Categorical | Ir | mm | 0.4 | 0.8 | – | – | – |
Subsequently, surface residual stresses were measured utilizing an Stresstech 3000-G3R X-ray diffractomer, which setup can be seen in Table 13 following the recommendations proposed in NTI guide [18]. As explained above, three measurement were made according with the scheme shown in Fig. 7a), each equispaced 45°. The subsequent analysis leads to the residual stresses in both longitudinal and radial orientation (see Fig. 7b)). In parallel, surface roughness was evaluated using a Leica DCM3 confocal microscope, configured in accordance with the UNE-EN-ISO-21,920–3 standard [19] (see Table 14). Regarding lathe monitoring, a National Instruments data acquisitions system in combination with a LabView software has been used to collect all the data measured during the turning process. Table 15 shows the reference of the equipment used.
Table 13.
Experimental parameters for residual stress measurements.
| Stresstech 3000-G3R X-ray diffractomer setup | |
|---|---|
| Maximum voltaje (kV) | 30 |
| Exposure time (s) | 20 |
| Tilt Ψ (°) | 5 points between −45°/ +45° |
| Noise reduction | Parabolic |
| Filter of Kα radiation | Vanadium |
| Maximun intensity (mA) | 6.7 |
| Collimator diameter (mm) | 2 (Short type) |
| Goniometric rotation (measurement direction) Ø (°) | 0 |
| Peak adjustment | Pseudo-Voigt |
Fig. 7.
Residual stresses measurements: (a) Orientation of the residual stress measurements carried out on previously machined 42CrMo4+QT specimens, and (b) Arrangement of the residual stresses on the machined specimens.
Table 14.
Experimental parameters for roughness measurements.
| Leica DCM3 confocal microscope setup | |
|---|---|
| Used standard | UNE-EN-ISO-21,920–3 [19] |
| Objective magnification | 10x |
| Measured parameter | Ra |
| Selected Cutt-off (λc) (mm) | 0.80 |
| Evaluation length (mm) | 5.60 |
| Evaluation width (mm) | 0.95 |
| Evaluation area (mm2) | 5.32 |
Table 15.
Adquisition system used during the turning process.
| Data acquisitions system | |
|---|---|
| Procurement module | NI 9269/NI 9234 |
| Acquisition chassis | NI cDAQ-9174 |
Finally, Table 16 shows the correction factors needed to convert the measured forces, sound, acceleration and current consumption to their actual unit scales.
Table 16.
Conversion scales required for measurements monitored in non-international units.
| Parameter | Register Units | SI Units | Conversion Scale |
|---|---|---|---|
| Current consumption | Volts (V) | Ampere (A) | 100 mV/A |
| Acceleration X | Gravity (g) | Metres/ second2 (m/s2) | 9.8 (m/s2)/g |
| Force X | Volts (V) | Newton (N) | 100 N/V |
| Force Y | Volts (V) | Newton (N) | 100 N/V |
| Force Z | Volts (V) | Newton (N) | 100 N/V |
Limitations
The dataset shared in this work has been collected on a 42CrMo4+QT steel, so the extrapolation of these results to other steels whose chemical composition and properties are different is not straightforward. Furthermore, the predictive models developed from these results may not be accurate for other cutting conditions not included in the design space used here.
Ethics Statement
The authors have read and follow the ethical requirements for publication in Data in Brief. The authors confirm that the present work does not involve human subjects, animal experiments, or any data collected from social media platforms.
CRediT authorship contribution statement
D. Díaz-Salamanca: Conceptualization, Methodology, Data curation, Formal analysis, Validation, Writing – original draft. S. Álvarez Álvarez: Conceptualization, Formal analysis, Validation, Writing – original draft. M. Muñiz-Calvente: Conceptualization, Methodology, Resources, Funding acquisition, Data curation, Formal analysis, Validation, Supervision, Project administration, Writing – review & editing. P. Ebrahimzadeh: Conceptualization, Methodology, Data curation, Formal analysis, Validation, Writing – review & editing. I. Llavori: Conceptualization, Methodology, Resources, Funding acquisition, Data curation, Formal analysis, Validation, Writing – review & editing. A. Zabala: Conceptualization, Methodology, Resources, Funding acquisition, Data curation, Formal analysis, Validation, Writing – review & editing. P. Pando: Resources, Funding acquisition, Investigation, Writing – review & editing. C. Suárez Álvarez: Conceptualization, Methodology, Data curation, Writing – review & editing. I. Fernández-Pariente: Conceptualization, Methodology, Data curation, Formal analysis, Validation, Writing – review & editing. M. Larrañaga: Conceptualization, Methodology, Resources, Funding acquisition, Data curation, Formal analysis, Validation, Writing – review & editing. J. Papuga: Conceptualization, Methodology, Resources, Funding acquisition, Validation, Writing – review & editing.
Acknowledgements
This work was supported by the University of Oviedo [UNOV-22-RLD-UE-5]; the Government of the Basque Country, Spain [PIBA 2023/1/0052]; the Spanish Government [TED2021-130306B-100 and PID2021-124245OA-I00]; and the Czech Science Foundation [23-06130K].
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data Availability
References
- 1.Diaz Salamanca D., Álvarez Álvarez S., Muniz Calvente M., Ebrahimzadeh P., Llavori I., Zabala A., Pando P., Suárez C., Fernández-Pariente I., Larrañaga M., Papuga J. 2024. MaRoReS (Machining, Roughness and Residual Stresses Generated in Turning of 42CrMo4+QT steel) p. 1. [DOI] [Google Scholar]
- 2.Saini S., Ahuja I.S., Sharma V.S. Residual stresses, surface roughness, and tool wear in hard turning: a comprehensive review. Mater. Manuf. Process. 2012;27:583–598. doi: 10.1080/10426914.2011.585505. [DOI] [Google Scholar]
- 3.Petropoulos G.P. Surf. Integr. Mach. 2008. Surface texture characterization and evaluation related to machining; pp. 37–66. C.N.P., J.P.D. [DOI] [Google Scholar]
- 4.Nee C.Y., Saad M.S., Mohd Nor A., Zakaria M.Z., Baharudin M.E. Optimal process parameters for minimizing the surface roughness in CNC lathe machining of Co28Cr6Mo medical alloy using differential evolution. Int. J. Adv. Manuf. Technol. 2018;97:1541–1555. doi: 10.1007/s00170-018-1817-0. [DOI] [Google Scholar]
- 5.Bassanini G., Bisi A., Capello E. Residual stresses and surface roughness in turning. J. Eng. Mater. Technol. 1999:346–351. http://asme.org/terms [Google Scholar]
- 6.Capello E. Residual stresses in turning: Part I: influence of process parameters. J. Mater. Process. Technol. 2005;160:221–228. doi: 10.1016/J.JMATPROTEC.2004.06.012. [DOI] [Google Scholar]
- 7.Weisberg S. 4th ed. Wiley; 2014. Applied Linear Regression. [Google Scholar]
- 8.Box S., Hunter G., Hunter W. Statistics for experimenters. Technometrics. 1978;21:387–388. doi: 10.1080/00401706.1979.10489788. [DOI] [Google Scholar]
- 9.Elsheikh A.H., Shanmugan S., Muthuramalingam T., Thakur A.K., Essa F.A., Ibrahim A.M.M., Mosleh A.O. A comprehensive review on residual stresses in turning. Adv. Manuf. 2022;10:287–312. doi: 10.1007/s40436-021-00371-0. [DOI] [Google Scholar]
- 10.Gunnberg F., Escursell M., Jacobson M. The influence of cutting parameters on residual stresses and surface topography during hard turning of 18MnCr5 case carburised steel. J. Mater. Process. Technol. 2006;174:82–90. doi: 10.1016/j.jmatprotec.2005.02.262. [DOI] [Google Scholar]
- 11.Saini S., Ahuja I.S., Sharma V.S. Modelling the effects of cutting parameters on residual stresses in hard turning of aisi h11 tool steel. Int. J. Adv. Manuf. Technol. 2013;65:667–678. doi: 10.1007/s00170-012-4206-0. [DOI] [Google Scholar]
- 12.Dahlman P. The influence of rake angle, cutting feed and cutting depth on residual stresses in hard turning. J. Mater. Process. Technol. 2004;147:181–184. doi: 10.1016/j.matprotec.2003.12.014. [DOI] [Google Scholar]
- 13.Xueping Z., Erwei G., Liu C.Richard. Optimization of process parameter of residual stresses for hard turned surfaces. J. Mater. Process. Technol. 2009;209:4286–4291. doi: 10.1016/j.jmatprotec.2008.10.011. [DOI] [Google Scholar]
- 14.Davim J.P., Gaitonde V.N., Karnik S.R. Investigations into the effect of cutting conditions on surface roughness in turning of free machining steel by ANN models. J. Mater. Process. Technol. 2008;205:16–23. doi: 10.1016/j.jmatprotec.2007.11.082. [DOI] [Google Scholar]
- 15.Santhosh A.J., Tura A.D., Jiregna I.T., Gemechu W.F., Ashok N., Ponnusamy M. Optimization of CNC turning parameters using face centred CCD approach in RSM and ANN-genetic algorithm for AISI 4340 alloy steel. Results Eng. 2021;11 doi: 10.1016/j.rineng.2021.100251. [DOI] [Google Scholar]
- 16.Lalwani D.I., Mehta N.K., Jain P.K. Experimental investigations of cutting parameters influence on cutting forces and surface roughness in finish hard turning of MDN250 steel. J. Mater. Process. Technol. 2008;206:167–179. doi: 10.1016/j.jmatprotec.2007.12.018. [DOI] [Google Scholar]
- 17.Ebrahimzadeh P., Martínez L.B.P., Pariente I.F., Varela F.J.B. Optimization of shot-peening parameters for steel AISI 316L via response surface methodology (RSM): introducing two novel mechanical aspects. Int. J. Adv. Manuf. Technol. 2024 doi: 10.1007/s00170-024-13274-8. [DOI] [Google Scholar]
- 18.A National Measurement Good Practice Guide . 2010. Determination of Residual Stresses by X-ray Diffraction - Issue 2. [DOI] [Google Scholar]
- 19.UNE . 2023. Spanish Standard UNE-EN ISO 21920-3 Geometrical Product Specifications (GPS) Surface Texture : Profile Part 3 : Specification Operators. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.