Abstract
The hypothesis that genomic regions rich in non-protein-coding RNAs (ncRNAs) can be identified using local variations in single-base and dinucleotide statistics has been investigated. (G+C)%, (G–C)% difference, (A–T)% difference and dinucleotide-frequency statistics were compared among seven classes of ncRNAs and three genomes. Significant variations were observed in (G+C)% and, in Methanococcus jannaschii, in the frequency of the dinucleotide ‘CG’. Screening programs based on these two base-composition statistics were developed. With (G+C)% screening alone, a 1% fraction of the M.jannaschii genome containing all 44 known transfer RNAs, ribosomal RNAs and signal recognition particle RNAs could be identified. When (G+C)% combined with CG dinucleotide-frequency screening was used, 43 of the 44 known M.jannaschii structural ncRNAs were again identified, while the number of presumably false hits overlapping a known or putative protein-coding gene was reduced from 15 to 6. In addition, 19 candidate ncRNAs were identified including one with significant homology to several known archaeal RNaseP RNAs.
INTRODUCTION
Non-protein-coding RNAs (ncRNAs) are known to play significant roles in biological systems. Along with the familiar transfer RNAs (tRNAs) and ribosomal RNAs (rRNAs), ncRNAs contribute to gene splicing, RNA nucleotide modification, protein transport and regulation of gene expression (1). Consequently, identifying ncRNAs is an important task. Conventional protein gene-finding programs such as Genscan are not designed to locate ncRNAs. In cases where detailed characterization of the ncRNA gene families is possible, specialized RNA gene-finding programs have been quite successful (2–5). In addition, promising new ncRNA search algorithms based on comparative genomics have been proposed (6–8). Nevertheless, the goal of locating ncRNAs, when detailed characterizations of the target RNA sequences are unavailable, remains difficult to achieve.
One intriguing approach (9) is that, for some genomes, the local percentage of GC bases (G+C)% may serve as a filter to screen for ncRNA-rich regions. Genomic variations in base-composition statistics, such as (G+C)%, and their application to searching for protein-coding genes have been studied for many years (reviewed in 10). In particular, it is well known that thermophiles maintain the stability of ncRNAs by increasing their (G+C)% (11,12). It is also known that thermophiles generally use mechanisms other than (G+C)% elevation to maintain the stability of their genomic DNA (13,14). Based on these ideas, Rivas and Eddy proposed ncRNA gene-finding based on (G+C)% (9). They also suggested this approach may be applicable even in non-thermophiles—such as Caenorhabditis elegans—which have differing ncRNA and genomic (G+C)% (9). However, the feasibility of such an approach has not been clear since other investigations (15–17) have indicated that base composition alone is not sufficient to predict RNA folding and hence the occurrence of ncRNAs in the genome.
Other base-composition statistics besides (G+C)% might also be expected to vary between ncRNAs and their genomic background. For example, the single-strand G minus C excess, (G–C)%—also known as the ‘G–C% Chargaff difference’—has long been known to be very small for a wide range of organisms (18). Similarly small values have been observed for (A–T)% Chargaff differences. Moreover, at least in Escherichia coli, these approximate G=C and A=T single-strand frequency equalities—known as ‘Chargaff’s Second Law’—have been observed on the local level as well (18).
On the other hand, RNAs may be subject to constraints causing deviation from Chargaff’s Second Law. For example, recent work suggests that non-zero Chargaff differences may mark the presence of protein-coding messenger RNAs (mRNAs) (19). Moreover, G/U base pairs are more commonly found in RNA structure than C/A base pairs, which might lead to local violations of Chargaff’s Second Law.
Relative dinucleotide frequencies might also be anticipated to vary between ncRNAs and the genomic background. Though dinucleotide frequencies vary widely among species, they tend to be relatively constant within the genome of any single species (10). However, ncRNAs are subject to structural constraints that may influence their dinucleotide composition. ncRNAs typically form folded structures whose stacking energies—and consequently whose conformation—depend on their dinucleotide composition (20–21). As a result, one might expect that ncRNA dinucleotide frequencies would display characteristic atypical values relative to the genomic background.
The present work investigates the feasibility of using local base-composition statistics to distinguish between ncRNA-rich and ncRNA-poor regions of the genome. The goal is to partition a genomic region into two components—one well defined component with high probability of containing ncRNAs and the other component with low probability of containing ncRNAs. To assess the feasibility of this approach, base-composition statistics from a variety of ncRNAs were compiled. Similar statistics were acquired from three test genomes (Methanococcus jannaschii, Plasmodium falciparum and C.elegans) and were compared with the values found from the RNA sequences. Lastly, for the case where the largest RNA-genome variations were observed—specifically, for (G+C)% and ρ(CG) in M.jannaschii—two programs were developed to apply these statistical variations to genome-wide searching for ncRNA genes. Using these programs led to the identification of 36 known tRNAs, six known rRNAs and one known signal recognition particle RNA in M.jannaschii. In addition, 19 putative ncRNAs including one with homology to several RNaseP RNAs were identified.
MATERIALS AND METHODS
Data sources
Sequence data for cytoplasmic tRNAs (22), rRNAs (23,24), riboregulator RNAs (25), small nuclear RNAs (snRNAs) and small cytoplasmic RNAs (http://mbcr.bcm.tmc.edu/smallRNA/), small nucleolar RNAs (snoRNAs) (http://rna.wustl.edu/snoRNAdb/), signal recognition particle RNAs (SRP RNAs) (26), and RNA pseudoknots (27) were obtained from the public databases.
Genomic data for M.jannaschii, P.falciparum and C.elegans were downloaded from the NCBI GenBank genomes databases (ftp://ftp.ncbi.nih.gov/genomes/) in April 2001.
Base-composition statistics calculated
For each sequence, the following statistics were computed:
(G+C)% = 100 (nG + nC)/(nA + nC + nG + nT)
(G–C)% Chargaff difference = 100 (nG – nC)/(nG + nC)
(A–T)% Chargaff difference = 100 (nA – nT)/(nA + nT)
ρ(AB) = [f(AB)/f(A)*f(B)] = (L * nAB)/(nA * nB)
where L is the sequence length, nB and nAB are the number of occurrences of base ‘B’ or the dinucleotide AB, respectively, and f(B) or f(AB) is the frequency of occurrence of base B or dinucleotide AB [e.g. f(B) = nB / L]. [We use Karlin et al.’s (10) variable ρ rather than their variable ρ* to measure dinucleotide frequencies since we are interested in observing the effects of RNA genes that will be present on only one of the two DNA strands.]
It should be noted that a systematic, positive (G–C)% difference in ncRNAs would not necessarily imply a positive genomic (G–C)% difference at an ncRNA gene since the ncRNA gene might be on the negative strand. However, any systematic non-zero ncRNA Chargaff differences of either sign would imply non-zero genomic Chargaff differences near an ncRNA gene. Moreover, if the absolute value of the local Chargaff difference indicated the presence of an ncRNA, then the sign of the difference could serve as an indicator of the strand on which the ncRNA was located. Similarly, systematic ncRNA dinucleotide variations (except for dinucleotides that are their own reverse complements) would result in somewhat different genomic signatures depending on which strand the ncRNA were located.
Base-composition statistical averages
RNA data were grouped by RNA type and by species. In most cases, M.jannaschii, P.falciparum, C.elegans and Homo sapiens RNA sequences were used. For those RNA classes for which the databases contained limited or no data for M.jannaschii, P.falciparum, C.elegans and H.sapiens, RNA sequence data from other organisms or groups of organisms were used, as noted in the text and tables.
For genomic averages, 1000 random samples of 100 bp each were selected per chromosome. In addition, tests were performed to check for any local base-composition variations along the length of a chromosome. For example, for chromosome I of C.elegans, the entire chromosomal sequence was divided into 49 regions of 294 kb each, and base-composition statistics for 1000 random samples of 100 bp were calculated for each of the 49 regions.
For each group of sequences (whether RNAs or genomic samples), means and standard deviations (SDs) of each of the base-composition statistics were calculated. For the genomic sequences, parameter means and SDs for each of the chromosomal subregions were also calculated. Statistical significance of population differences between parameter-means was determined using Student t-test comparisons with 95% confidence levels.
Algorithms and training of ncRNA search programs
Two ncRNA search algorithms were implemented. The first approach (‘Program I’) is based solely on scoring local (G+C)% values. (G+C)% of a subsequence is scored using a log odds (LOD) score (9):
LOD = CAT(nA + nT) + CGC(nC + nG)
where
CAT = log2[(A+T)% in RNA genes/(A+T)% in genome]
and
CGC = log2[(G+C)% in RNA genes/(G+C)% in genome]
The second search algorithm (‘Program II’)identifies possible ncRNAs using a combination of (G+C)% and ρ(CG) values. The (G+C)% component of this algorithm is identical to Program I; however, any putative hit must also have a value of ρ(CG) larger than a specified cut-off value.
Both programs have a few adjustable parameters: the window lengths to be tried while searching for a hit, the minimum RNA length, and the LOD cut-off scores to indicate the beginning and end of a ‘hit’. Program II has one additional parameter: the cut-off value for ρ(CG).
The adjustable parameters were chosen by training the programs on a 20 kb subsequence of the M.jannaschii sequence (from 850 000 to 870 000) which has six annotated tRNA genes and one annotated rRNA gene. Using this training data, the following parameter values were selected for Program I (and subsequently used for the scan of the entire genome): minimum RNA length = 40 bp; window length range = 25–100 bp; minimum LOD value for the start of a hit = 19; and minimum LOD value for the continuation of a hit = 13. After training Program II with the same training set, the cut-off value for ρ(CG) was set equal to 0.5 and the minimum LOD value for the start of a hit was set equal to 15, with the other parameters having the same values they had for Program I.
Assessment of the search programs
Both search programs were run against the M.jannaschii genome with the resulting hits compared with known RNAs as annotated in the GenBank ‘.gbk’ database file at ftp://ftp.ncbi.nih.gov/genomes/. Sequence segments that scored above the scoring threshold and that did not overlap any GenBank annotated gene—as well as 60 bp extensions of those sequences—were input to the NCBI BLAST program (28) and run against the NCBI non-redundant nucleotide database (NRDB). In most cases, default BLAST parameters were used. A few BLAST searches were performed with non-default wordsize, match or mismatch values. Changing the BLAST parameter values did not result in any additional, noteworthy BLAST hits.
RESULTS
Two significant base-composition variations were observed between RNAs and the background genome: (G+C)% and, in M.jannaschii, ρ(CG). For example, in M.jannaschii RNA mean (G+C)% is 63.1%, while background (G+C)% is 31.4% (Table 1). In C.elegans RNA mean (G+C)% is 53.5%, while background (G+C)% (on chromosome I) is 35.9%. ρ(CG) in M.jannaschii RNAs is 0.75 while background ρ(CG) is 0.34 (Table 1). These differences between RNA and genome values for (G+C)% and ρ(CG) in M.jannaschii formed the basis for the RNA gene-finding algorithms.
Table 1. Base-composition statistics for RNAs and genomes.
| No. of sequences used | (G+C)% | ρ(CG) | (G–C)% difference | (A–T)% difference | |
|---|---|---|---|---|---|
| (A) Average RNA base-composition statistics | |||||
| M.jannaschii | 48 | 63.1 (7.3) | 0.75 (0.24) | 8.1 (9.7) | –3.3 (12.9) |
| Plasmodium | 59 | 32.1 (7.2) | 0.94 (0.56) | 12.7 (6.3) | –1.6 (4.1) |
| C.elegans | 59 | 53.5 (8.2) | 0.96 (0.23) | 6.8 (10.1) | –9.6 (11.4) |
| H.sapiens | 186 | 48.7 (9.1) | 0.60 (0.41) | 7.5 (11.8) | –5.8 (13.0) |
| (B) Genomic base-composition statistics | |||||
| M.jannaschii | 31.4 (6.9) | 0.34 (0.47) | 1.4 (36.9) | –0.34 (18.8) | |
| P.falciparum Chr. II | 20.0 (8.4) | 0.75 (1.3) | 0.73 (34.5) | –1.7 (24.0) | |
| C.elegans Chr. I | 35.9 (8.8) | 1.03 (0.68) | 0.65 (25.0) | –0.61 (19.6) |
This table summarizes the differences in mean-value base-composition statistics between ncRNAs and the genomic background in M.jannaschii, P.falciparum and C.elegans. SDs are shown in parentheses. Statistics for RNAs of several Plasmodium species were averaged together since there are only a limited number of P.falciparum RNA sequences in the RNA databases. (A) Average base-composition statistics among ncRNAs. The low (32.1%) value for (G+C)% in Plasmodium in contrast to the high (>48%) (G+C)% value for the other genomes is striking. One also notes the positive (G–C)% values and negative (A–T)% values, possibly resulting from the occurrence of G-U ‘wobble’ pairs in the ncRNAs. (B) Base-composition statistics for three test genomes: M.jannaschii, P.falciparum chromosome II and C.elegans chromosomes (results for other C.elegans and P.falciparum chromosomes were similar—data not shown). One notes the differences in genome mean values from the RNA values of (G+C)% for M.jannaschii and C.elegans and for ρ(CG) for M.jannaschii. Data for dinucleotide frequencies other than ρ(CG) did not show systematic differences between RNAs and the genomic background (data not shown). Genomic (G–C)% and (A–T)% differences are seen to be very close to zero (as expected from ‘Chargaff’s Second Law’) which is different from the RNA values shown in (A). However, the table also shows the large SDs for (G–C)% and (A–T)% relative to their mean values, implying that using these differences to distinguish RNAs from the background would be difficult.
However, we observed that RNA (G+C)% is not elevated in all species: Plasmodium-RNA mean (G+C)% is 32.1% (Table 1) indicating that—despite its low background (G+C)% (e.g. 20.0% for P.falciparum chromosome II)—Plasmodium is not a promising candidate for RNA gene-finding based on (G+C)%.
We also observed consistently positive ncRNA (G–C)% values and negative (A–T)% values (Table 1). It is possible that these result from the occurrence of G-U ‘wobble’ pairs in the ncRNAs. However, the differences between RNA and the background values for the Chargaff differences as well as for the dinucleotide variations—other than for ρ(CG)—were all smaller than, or comparable with, the corresponding individual population SDs (Tables 1 and 2; not all data shown). Consequently, these parameters were deemed unsuitable for a ncRNA gene-finder.
Table 2. Variations in (C+G)% and ρ(CG) statistics among differing RNA classes.
| RNA | Species | (C+G)% | ρ(CG) |
|---|---|---|---|
| tRNAs (cytoplasmic) | M.jannaschii | 66.2 | 0.72 |
| Plasmodium | 25.6 | 0.88 | |
| C.elegans | 58.8 | 0.92 | |
| H.sapiens | 58.0 | 1.00 | |
| rRNAs | M.jannaschii | 63.8 | 0.87 |
| Plasmodium | 36.0 | 0.98 | |
| C.elegans | 48.0 | 1.04 | |
| H.sapiens | 60.3 | 1.03 | |
| SRP RNAs | M.jannaschii | 65.7 | 0.66 |
| C.elegans | 56.8 | 1.07 | |
| H.sapiens | 58.3 | 0.48 | |
| Small nuclear RNAs | C.elegans | 43.1 | 1.01 |
| H.sapiens | 44.3 | 0.90 | |
| sno- and sno-like RNAs | M.jannaschii | 48.7 | 0.83 |
| H.sapiens | 44.2 | 0.38 | |
| Riboregulator RNAs | H.sapiens | 47.6 | 0.33 |
| All eukaryotes | 44.4 | 0.46 | |
| Pseudoknot RNAs | All bacteria | 52.0 | 0.86 |
| All viruses | 51.8 | 0.98 |
This table shows some of the variations in (C+G)% and ρ(CG) values among different classes of RNAs for M.jannaschii, Plasmodium (multiple species combined because of limited data), C.elegans and H.sapiens. For the riboregulator and pseudoknot databases, which contain limited or no data for these species, RNA sequence data from other groups of organisms are shown. The base-composition variations shown in the table indicate which ncRNA types are more likely to be detected by a RNA gene-finder based on (C+G)% and ρ(CG). For example, one notes that (C+G)% is only 48.7% in M.jannaschii snoRNAs and 43.1% in C.elegans snRNAs. Consequently these RNAs would be more difficult to detect using a (C+G)% detector than the more G+C rich tRNAs, rRNAs and SRP RNAs.
The results of testing Programs I and II against the M.jannaschii genome are shown in Tables 3 and 4. Both programs identify a set of sequence regions that are predicted to contain a high percentage of structural RNAs. Together, these regions consist of <1% of the M.jannaschii genome. With Program I, this 1% subsequence contains all 43 annotated tRNAs and rRNAs in the GenBank ‘.gbk’ file as well as the single M.jannaschii SRP RNA in the SRP RNA database (20). Program II has slightly lower sensitivity, finding 43 of the 44 annotated tRNAs, rRNAs and SRP RNAs [a tRNA at location 637 982 with ρ(CG) = 0.28 is missed].
Table 3. Results of (G+C)% + ρ(CG) screening on M.jannaschii.
| Method | Annotated RNAs found | Annotated RNAs missed | Total no. of other hits | Other hits overlapping >50% putative protein gene | Putative protein genes with BLASTX hits to multiple species |
|---|---|---|---|---|---|
| (G+C)% alone | 44 | 0 | 41 | 15 | 6 |
| (G+C)% and ρ(CG) | 43 | 1 | 28 | 6 | 1 |
Summary of results of scanning the M.jannaschii genome for ncRNAs using (G+C)% or (G+C)% combined with ρ(CG). Annotated RNAs include tRNAs, rRNAs and SRP RNAs of which only six tRNA genes and one rRNA gene were included in the training set. One notes adding ρ(CG) screening causes one RNA to be missed while reducing the number of putative hits overlapping a protein gene from 15 to 6, of which only one shows homology using BLASTX to exons from multiple other species. Further details are in the text.
Table 4. Candidate M.jannaschii ncRNAs.
| ID no. | Genomic start position | Genomic end position | G+C% | ρ(CG) |
|---|---|---|---|---|
| cnr1 | 118060 | 118190 | 54.8 | 0.95 |
| cnr2 | 291952 | 291992 | 63.4 | 1.16 |
| cnr3 | 325022 | 325062 | 53.7 | 1.00 |
| cnr4 | 412566 | 412606 | 56.1 | 0.63 |
| cnr5 | 465392 | 465533 | 61.0 | 0.51 |
| cnr6 | 471565 | 471605 | 61.0 | 0.56 |
| cnr7 | 537593 | 537711 | 56.1 | 0.86 |
| cnr8 | 543830 | 543896 | 53.0 | 0.86 |
| cnr9 | 638309 | 638411 | 56.9 | 0.72 |
| cnr10 | 643488 | 643698 | 57.6 | 0.71 |
| cnr11 | 873579 | 873622 | 53.5 | 0.64 |
| cnr12 | 951834 | 951959 | 56.8 | 0.68 |
| cnr13 | 986076 | 986116 | 61.0 | 1.11 |
| cnr14 | 1129093 | 1129170 | 52.0 | 0.90 |
| cnr15 | 1131997 | 1132037 | 53.7 | 1.03 |
| cnr16 | 1137151 | 1137191 | 56.1 | 0.63 |
| cnr17 | 1204222 | 1204262 | 56.1 | 1.33 |
| cnr18 | 1606179 | 1606219 | 63.4 | 0.75 |
| cnr19 | 1659426 | 1659497 | 50.0 | 0.69 |
List of 21 candidate ncRNAs identified by combined (G+C)% + ρ(CG) screening. Positions along the M.jannaschii genome as well as values for the statistical parameters are shown. Strand location is not determined by the present methods, since (C+G)% and ρ(CG) are identical for both strands. Three of the candidate ncRNAs (cnr1, cnr7 and cnr 12) consist of two immediately-adjacent ‘hits’ presumably resulting from a single ncRNA and combined in the table. Cnr10 is homologous to several RNaseP genes.
The primary difference between the results of the two programs is that Program I yields nine more ‘hits’ that overlap a putative protein-coding gene than does Program II (Table 3). Running NCBI BLASTX searches against the NCBI non-redundant protein database with these nine sequences showed that five of them have strong homologies (E < 10e–5) to exons of multiple (five or more) other species (data not shown). This result suggests that most—if not all—of the nine additional overlapping hits are false-positives for ncRNAs, which in turn implies that using ρ(CG) together with (G+C)% results in higher specificity than using (G+C)% alone. In contrast, when the six sequences identified by both Program I and Program II that overlap putative protein genes were run with BLASTX, only one showed significant homology to exons of other species.
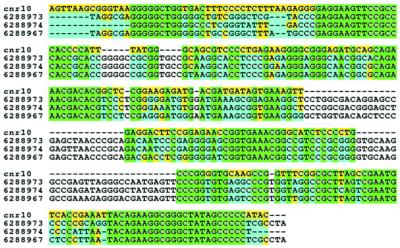
In addition to finding the known tRNAs, rRNAs and SRP RNAs, Program II identified 22 additional ‘hits’. Among these hits were three pairs of hits located within 40 bp of each other and likely to be parts of three longer ncRNAs (shown as cnr1, cnr7 and cnr12 in Table 4). Consequently there are a total of 19 candidate, novel ncRNAs which are listed with their genomic start and end locations in Table 4. Since these locations were determined solely on the basis of elevated (C+G)% and ρ(CG), they indicate only the approximate end points of the candidate ncRNAs. A predicted strand is not determined by the present methods, since (C+G)% and ρ(CG) are identical for both strands. BLAST searches with these 19 sequences identified one sequence, cnr10 in Table 4, as homologous (E-values < 10e–11) to RNaseP RNAs (rnpB) of Methanococcus vannielii, Methanococcus thermolithotrophicus and Methanococcus maripaludis. Figure 1 shows a Clustal W (29) multiple alignment of cnr10 and its surrounding sequence with the three homologous RNaseP genes.
Figure 1.
Alignment of cnr10 and RNAaseP genes from M.vannielii (AF192357/GBBCT:6288966), M.thermolithotrophicus (AF192355/GBBCT:6288964) and M.maripaludis (AF192354/GBBCT:6288963). The RNAaseP sequences are partial sequences obtained from the specified GenBank records.
A next step in determining which, if any, of the candidate ncRNAs is real might be to look for promoter and terminator sequences adjacent to the putative RNAs in a manner similar to the method of Argaman et al. (8). However, archaeal promoters and terminators are far less well characterized than those in bacteria, and consequently we have not attempted to implement such a search. Experimental testing—such as northern analyses or microarray expression profiling under various growth conditions—is needed to determine whether these putative ncRNAs are transcribed.
DISCUSSION
The present work has shown that in M.jannaschii it is possible to locate structural ncRNAs solely on the basis of local variations of genomic base composition. In M.jannaschii, these base-composition variations led to identifying 36 known tRNAs, six known rRNAs and one known SRP RNA. In addition, 19 putative ncRNAs including one with homology to several RNaseP RNAs were identified. Although the method worked well at identifying tRNAs, rRNAs and SRP RNAs—which all have mean RNA (G+C)% >60%—it failed to find any of the eight M.jannaschii C-D snoRNA-like genes. These RNAs have mean (G+C)% = 49% (Table 2). Similarly, one notes in Table 2 that for snRNAs (G+C)% is 43.1% in C.elegans and 44.3% in H.sapiens. For riboregulator RNAs, (G+C)% is 47.6% in H.sapiens and 44.4% in all eukaryotes. Consequently, the present method is also likely to be less successful at identifying snRNAs and riboregulator RNAs.
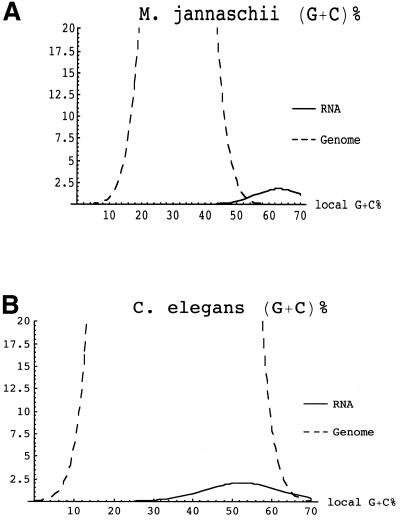
It would be desirable if the present approach could be applied to additional genomes. However, this will be challenging, since most genomes have higher background (G+C)% than M.jannaschii. For example, background genomic (G+C)% is ∼34% in C.elegans and 39% in Saccharomyces cerevisiae, compared with 29% in M.jannaschii (9). Although the mean genomic (G+C)% value of C.elegans (34%) is still quite different from the C.elegans RNA (G+C)% values (∼53%, see Table 1), the problem is that the random fluctuations of genomic (G+C)% are also large (∼8% SDs, see Table 1). Consequently, finding ncRNAs in C.elegans on the basis of (G+C)% alone is not feasible. Figure 2 illustrates the problem. The situation in S.cerevisiae is even less encouraging, since background (G+C)% = 39%, while typical (G+C)% for tRNAs is only 54% (9). Even in P.falciparum—which initially appeared promising because of its low mean background (G+C)% of 20%—identifying ncRNAs using (G+C)% is not likely to be feasible because of the low mean RNA (G+C)% of 32% in Plasmodium species (Table 1). Consequently, at this point, it appears that success with this method will be restricted to species like M.jannaschii which have high RNA (G+C)% (a constraint common among hyperthermophiles) as well as low genomic (G+C)%.
Figure 2.
Separation of RNAs and genomic background using G+C%. Vertical axes indicate estimated relative number of 100 bp subsequences. Note that the peak of the curve for the number of genomic sequences is truncated. RNA estimate assumes ratio of protein coding genes to ncRNA genes is approximately equal to that in S.cerevisiae. Graphs are shown as normally distributed for the purpose of illustration—the actual distribution of G+C% may vary. (A) M.jannaschii RNA and genome G+C% distributions are separated enough to enable discrimination between RNA and background populations. (B) C.elegans chromosome X. Although C.elegans ncRNA and genomic G+C% population means are significantly different, ncRNA distribution cannot be distinguished from that of the background by G+C% alone.
We had initially thought that other base-composition parameters—such as Chargaff differences and dinucleotide frequencies—might offer additional statistical signatures with which to differentiate ncRNAs from the background. However, with the exception of ρ(CG) in M.jannaschii, we were unable to find any other base-composition variations between ncRNAs and the background that were large enough to be usefully incorporated into an RNA gene-finder.
We had also hoped to improve our results by restricting the ncRNA searches to genomic regions with relatively high (A+T)%. This idea is based on evidence for ‘isochores’ in chromosomes of vertebrates (30), and, more recently, also in chromosomes of non-vertebrate eukaryotes (31). Isochores are 100–300 kb regions with relatively homogenous, local (G+C)% mean values which may vary by as much as 3–4% from the overall genomic (G+C)% mean (29). For example, we computed over a set of 49 regions of 100 kb on C.elegans chromosome I, that mean (G+C)% ranges from 33.3 to 40.3%. Consequently, (G+C)%-based ncRNA screening might be improved if the search was restricted to isochores with elevated (A+T)%. However, we have also found that isochore base-composition homogeneity does not extend down to the length of typical RNAs—i.e. ∼100 bp. As a result, the strategy of focusing on high (A+T)% isochores appears unlikely to significantly improve the performance of (G+C)%-based screening programs.
The present approach can be compared with other recent methods for ncRNA gene-finding. The most similar is that of Klein and Eddy (http://ismb00.sdsc.edu/posters/poster-list.html) who use a hidden Markov model (HMM) based on (G+C)% alone to search for ncRNAs in M.jannaschii and other high (A+T)% thermophillic organisms. After the present work was completed and submitted for publication, Klein, Misulovin and Eddy presented a detailed description of their method and the results of an experimental search for the ncRNAs that they predict (ftp://ftp.genetics.wustl.edu/pub/eddy/papers/2002-klein-archaea/preprint.pdf).
There are three principal differences between their approach and the one taken in this work. First, Klein’s model is based solely on (G+C)% variations. By additionally using ρ(CG), the present method eliminates potential false positives that overlap known and putative protein-coding regions. Secondly, different assumptions were made regarding ncRNA lengths. In the present work, the only ncRNA length restriction is that ‘hits’ must be >40 bases long. Klein et al. make more restrictive assumptions—not only must the ncRNA length be >50 bases, but they also set their HMM transition probabilities so that the average ncRNA length will be approximately 100 bases. Finally, Klein’s approach is implemented using an HMM while the present method uses a scanning, base-counting window. Although fundamentally similar, algorithm operation and dependence on model parameters are easier to interpret in base-counting methods than in HMMs. Specifically, in addition to the ncRNA length and base-count cut-offs common to both approaches, HMMs require a set of transition-probability parameters; determining the sensitivity of the HMM results to varied assumptions in these parameters may not be easy to predict.
It is interesting to compare Klein et al.’s predictions and experimental results with the predictions of the present work. Klein et al. experimentally verify four of the nine M.jannaschii ncRNAs that they predict. We note that all four of the experimentally confirmed ncRNAs are also identified by the present approach (Klein’s mja2, mja3, mja6 and mja7 correspond to our cnr1, cnr3, cnr12 and cnr14, respectively). In addition, two other unconfirmed candidates (Klein’s mja4 and mja9, corresponding to our cnr4 and cnr19) are predicted by both approaches. Klein’s mja1 is not predicted by the present work because it is located on the M.jannaschii extrachromosomal segment which was not analyzed in the present work. More interesting are Klein’s mja5 and mja8 which were rejected by the base-composition gene-finder because, in both cases, ρ(CG) < 0.50. We note that both of these loci overlap putative protein-coding regions in M.jannaschii, one of which (mja5) has significant (e < 0.002) homology with methyl transferase and other proteins in Methanosarcina barkeri, Methanothermobacter thermautotrophicus and Methanosarcina mazei. On the other hand, Table 4 includes 13 candidate ncRNAs not predicted by Klein et al. and consequently not experimentally tested by them.
One intriguing aspect of Klein et al.’s work is their combination of a (G+C)% based HMM with a comparative genomics gene-finder (6). By using this combined approach, they can decrease the number of false positives that might be generated by using (G+C)% scanning alone. As mentioned above, we expect our gene-finder to have a lower false positive rate than Klein’s since we use ρ(CG) in addition to (G+C)%. Nevertheless, combining a comparative genomics approach with our base-composition scanner should also be helpful in lowering the overall false-positive rate.
A different class of ncRNA gene-finders that can be compared with the present approach is represented by the comparative genomics methods (6–8). These powerful methods have found several ncRNAs in E.coli and show promise of being applicable to other species. Their principal limitation is the requirement of two—or preferably more—fully sequenced genomes of closely related species. RNAs that are not shared by related species will not be found by these methods. Moreover, it is not clear how well these methods will scale when applied to larger genomes with lower gene densities than E.coli.
It is interesting to speculate whether base-composition RNA-gene-scanning could have applicability in other genomes if used in combination with a structure-based RNA gene-finding approach such as that of Rivas et al. (6) or Eddy and Durbin (32). Since such structure-based RNA-gene-finders can be computationally demanding, it may be useful to have a rapid method to serve as an initial screen to eliminate part of the genomic background. For example, preliminary tests on short (1–2 MB) regions of the C.elegans genome identified a 5% (non-contiguous) subregion containing 80% of the GenBank-annotated tRNAs and rRNAs (data not shown). Though preliminary, these results suggest that in some genomes, such as C.elegans, base-composition scanning—though not sufficiently specific to identify ncRNAs by itself—may still be useful as a prescreening tool prior to the application of more discriminating, but computationally more demanding, RNA gene-finding programs.
Acknowledgments
ACKNOWLEDGEMENTS
We are grateful to Dr T. Lowe for many helpful discussions and comments on this manuscript, and for bringing the work of Klein and Eddy to our attention. An earlier version of this work was presented as a poster at ISMB 2001, http://ismb01.cbs.dtu.dk/GeneFinding.html#A301.
REFERENCES
- 1.Eddy S.R. (1999) Noncoding RNA genes. Curr. Opin. Genet. Dev., 9, 695–699. [DOI] [PubMed] [Google Scholar]
- 2.Lowe T.M. and Eddy,S.R. (1999) A computational screen for methylation guide snoRNAs in yeast. Science, 283, 1168–1171. [DOI] [PubMed] [Google Scholar]
- 3.Lowe T.M. and Eddy,S.R. (1997) tRNAscan-SE: a program for improved detection of transfer RNA genes in genomic sequence. Nucleic Acids Res., 25, 955–964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fichant G.A. and Burks,C. (1991) Identifying potential tRNA genes in genomic DNA sequences. J. Mol. Biol., 220, 659–671. [DOI] [PubMed] [Google Scholar]
- 5.Pavesi A., Conterio,F., Bolchi,A., Dieci,G. and Ottonello,S. (1994) Identification of new eukaryotic tRNA genes in genomic DNA databases by a multistep weight matrix analysis of transcriptional control regions. Nucleic Acids Res., 22, 1247–1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rivas E., Klein,R.J., Jones,T.A. and Eddy,S.R. (2001) Computational identification of noncoding RNAs in E. coli by comparative genomics. Curr. Biol., 11, 1369–1373. [DOI] [PubMed] [Google Scholar]
- 7.Wassarman K.M., Repoila,F., Rosenow,C., Storz,G. and Gottesman,S. (2001) Identification of novel small RNAs using comparative genomics and microarrays. Genes Dev., 15, 1637–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Argaman L., Hershberg,R., Vogel,J., Bejerano,G., Wagner,E.G., Margalit,H. and Altuvia,S. (2001) Novel small RNA-encoding genes in the intergenic regions of Escherichia coli. Curr. Biol., 11, 941–950. [DOI] [PubMed] [Google Scholar]
- 9.Rivas E. and Eddy,S.R. (2000) Secondary structure alone is generally not statistically significant for the detection of noncoding RNAs. Bioinformatics, 16, 583–605. [DOI] [PubMed] [Google Scholar]
- 10.Karlin S., Campbell,A.M. and Mrazek,J. (1998) Comparative DNA analysis across diverse genomes. Annu. Rev. Genet., 32, 185–225. [DOI] [PubMed] [Google Scholar]
- 11.Galtier N. and Lobry,J.R. (1997) Relationships between genomic G+C content, RNA secondary structures and optimal growth temperature in prokaryotes. J. Mol. Evol., 44, 632–636. [DOI] [PubMed] [Google Scholar]
- 12.Hurst L.D. and Merchant,A.R. (2001) High guanine-cytosine content is not an adaptation to high temperature: a comparative analysis amongst prokaryotes. Proc. R. Soc. Lond. B Biol. Sci., 268, 493–497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Grove A. and Lim,L. (2001) High-affinity DNA binding of HU protein from the hyperthermophile Thermotoga maritima. J. Mol. Biol., 311, 491–502. [DOI] [PubMed] [Google Scholar]
- 14.Friedman S.M., Malik,M. and Drlica,K. (1995) DNA supercoiling in a thermotolerant mutant of Escherichia coli. Mol. Gen. Genet., 248, 417–422. [DOI] [PubMed] [Google Scholar]
- 15.Seffens W. and Digby,D. (1999) mRNAs have greater negative folding free energies than shuffled or codon choice randomized sequences. Nucleic Acids Res., 27, 1578–1584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schultes E.A., Hraber,P.T. and LaBean,T.H. (1999) Estimating the contributions of selection and self-organization in RNA secondary structure. J. Mol. Evol., 49, 76–83. [DOI] [PubMed] [Google Scholar]
- 17.Workman C. and Krogh,A. (1999) No evidence that mRNAs have lower folding free energies than random sequences with the same dinucleotide distribution. Nucleic Acids Res., 27, 4816–4822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bell S.J. and Forsdyke,D.R. (1999) Accounting units in DNA. J. Theor. Biol., 197, 51–61. [DOI] [PubMed] [Google Scholar]
- 19.Lao P.J. and Forsdyke,D.R. (2000) Thermophilic bacteria strictly obey Szybalski’s transcription direction rule and politely purine-load RNAs with both adenine and guanine. Genome Res., 10, 228–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Freier S., Kierzek,R., Jaeger,J., Sugimoto,N., Caruthers,M., Neilson,T. and Turner,D. (1986) Improved free-energy parameters for predictions of RNA duplex stability. Proc. Natl Acad. Sci. USA, 83, 9373–9377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xia T., SantaLucia,J.,Jr, Burkard,M.E., Kierzek,R., Schroeder,S.J., Jiao,X., Cox,C. and Turner,D.H. (1998) Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson–Crick base pairs. Biochemistry, 37, 14719–14735. [DOI] [PubMed] [Google Scholar]
- 22.Sprinzl M., Horn,C., Brown,M., Ioudovitch,A. and Steinberg,S. (1998) Compilation of tRNA sequences and sequences of tRNA genes. Nucleic Acids Res., 26, 148–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Van de Peer Y., De Rijk,P., Wuyts,J., Winkelmans,T. and De Wachter,R. (2000) The European small subunit ribosomal RNA database. Nucleic Acids Res., 28, 175–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wuyts J., De Rijk,P., Van de Peer,Y., Winkelmans,T. and De Wachter,R. (2001) The European Large Subunit Ribosomal RNA Database. Nucleic Acids Res., 29, 175–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Erdmann V.A., Barciszewska,M.Z., Szymanski,M., Hochberg,A., de Groot,N. and Barciszewski,J. (2001) The non-coding RNAs as riboregulators. Nucleic Acids Res., 29, 189–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gorodkin J., Knudsen,B., Zwieb,C. and Samuelsson,T. (2001) SRPDB (Signal Recognition Particle Database). Nucleic Acids Res., 29, 169–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.van Batenburg F.H., Gultyaev,A.P. and Pleij,C.W. (2001) PseudoBase: structural information on RNA pseudoknots. Nucleic Acids Res., 29, 194–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Altschul S.F., Gish,W., Miller,W., Myers,E.W. and Lipman,D.J. (1990) Basic local alignment search tool. J. Mol. Biol., 215, 403–410. [DOI] [PubMed] [Google Scholar]
- 29.Thompson J.D., Higgins,D.G. and Gibson,T.J. (1994) CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res., 22, 4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bernardi G. (2000) Isochores and the evolutionary genomics of vertebrates. Gene, 241, 3–17. [DOI] [PubMed] [Google Scholar]
- 31.Nekrutenko A. and Li,W.H. (2000) Assessment of compositional heterogeneity within and between eukaryotic genomes. Genome Res., 10, 1986–1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Eddy S.R. and Durbin,R. (1994) RNA sequence analysis using covariance models. Nucleic Acids Res., 22, 2079–2088. [DOI] [PMC free article] [PubMed] [Google Scholar]