Rational design of metal–organic cages to increase the number of components via dihedral angle control

Abstract

The general principles of discrete, large self-assemblies composed of numerous components are not unveiled and the artificial formation of such entities is a challenging topic. In metal–organic cages, design strategies for tuning the coordination directions in multitopic ligands by the bend and twist angles were previously developed to solve this problem. In this study, the importance of remote geometric communications between components is emphasized, realizing several types of metal–organic assemblies based on dihedral angle control in multitopic ligands although they have the same coordination directions. Self-assembly of a tritopic ligand with dihedral angles θ = 36.5° and a cis-protected Pd(II) ion affords M₉L₆ and M₁₂L₈ cages as kinetic and thermodynamic products, respectively, whereas an M₁₂L₈ sheet is formed when θ = 90°. Geometric analyses of strains in the subcomponent rings reveals that remote geometric communications among neighboring multitopic ligands through coordination bonds are key for large assemblies.

General design principles for self-assembly of discrete, large metal-organic cages composed of numerous components are challenging to develop. Here, the authors use remote geometric communications between components to realize several types of metal–organic assemblies based on dihedral angle control in multitopic ligands.

Introduction

Molecular self-assembly is a powerful strategy for creating structurally well-defined large entities from small building blocks using reversible interactions between them and has been widely observed in nature, such as DNA origami^1–3, protein assemblies^4–6, and lipid bilayers^7,8. Because of the reversibility of the interactions between the building blocks, the molecular self-assembly tends to reach thermodynamic equilibrium, where the products are determined by the Maxwell-Boltzmann distribution. Because the translational and rotational freedoms of the building blocks in self-assemblies composed of numerous building blocks are largely restricted compared with those in the disassembled state, the formation of such entities is entropically less favorable. Therefore, under the assumption that environmental effects such as solvation and templation are negligible, increasing the number of components in the self-assemblies enhances the entropic penalty. Consequently, when the enthalpic gains arising from the interactions between the building blocks (enthalpy change per component) are the same, assemblies composed of fewer components are thermodynamically advantageous, and the construction of self-assemblies with many building blocks under thermodynamic control is challenging. As observed in virus capsids^9,10, general principles that enable the self-assembly of discrete structures composed of numerous building blocks must exist; however, no details are known beyond the geometric and electrostatic complementarity among the components.

Metal–organic cages^11–13 are a well-established class of artificial self-assembled structures composed of multitopic ligands (L) and transition metal ions (M). The formation of M–L coordination bonds is the dominant enthalpic driving force of self-assembly. The geometric consistency between the coordination direction in the multitopic ligand and the coordination geometry of the metal centers determines the assembled structure. Metal–organic cages composed of many components were realized by precisely designing the bend angle of 4-pyridyl-based rigid ditopic ligands for a series of M_nL_2n assemblies (n = 2–48)^14–31. Recently, it was reported that twisting a multitopic ligand, which alters the coordination direction of the ligand, enables the construction of a large molecular self-assembly^32–34. In both cases, the change in the coordination directions in the multitopic ligands causes enthalpic destabilization of the self-assemblies consisting of fewer components, resulting in the thermodynamically most stable assemblies composed of more building blocks.

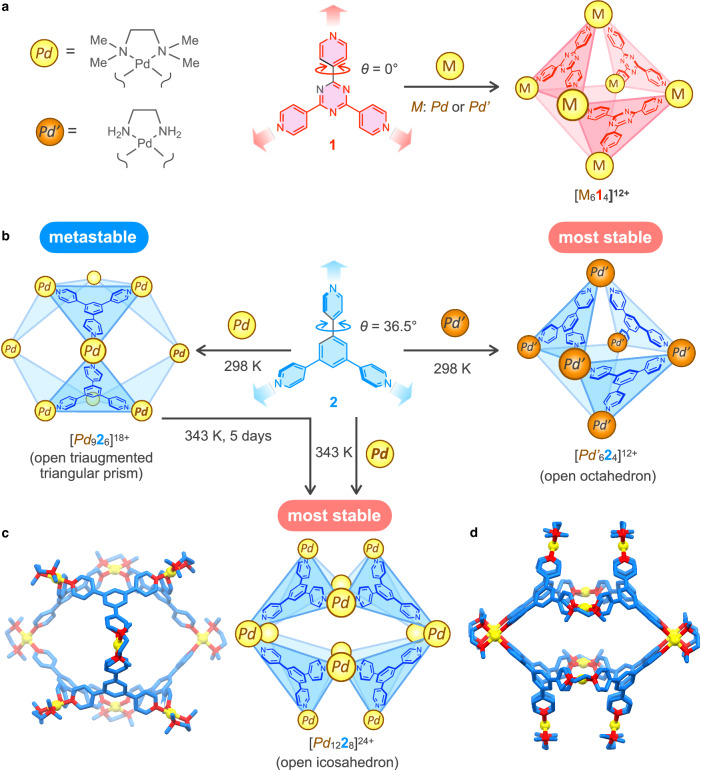
The self-assembly of the M₆L₄ open octahedron from the cis-protected square-planar Pd(II) ion (M: Pd²⁺ or Pd’²⁺) and tritopic ligand 1 was reported (Fig. 1a)^35,36. Because the cis-protected Pd(II) ion has two binding sites, the assembled structures that satisfy the full occupations of the two building blocks have the general formula of M_3nL_2n. The minimum structure, M₃L₂, cannot be formed from Pd²⁺ and 1 because of the large strain. Such a strain is not found in the second minimum structure, M₆L₄. Thus, M₆L₄ was chosen in the thermodynamic selection process even if larger structures than M₆L₄, M_3nL_2n (n ≥ 3), also do not have large strains because of the above-mentioned entropic reason. The question is whether the assembled structures can be controlled by other changes in multitopic ligands while retaining the original coordination directions. Let us consider the self-assembly of Pd²⁺ and tritopic ligand 2 (Fig. 1b), whose structure is basically the same as 1 except for the dihedral angle (θ) between the 4-pyridyl rings and the central ring (θ for 1 is 0°, while θ for 2 is larger than 0°). Because the coordination directions in 2 are the same as those in 1, the assembly of the M₆L₄ open octahedron was expected from 2.

Fig. 1. Assembled structures from tritopic ligand 1 or 2 and cis-protected Pd(II) ions.

a Self-assembly of the [M₆1₄]¹²⁺ open octahedron from triazine-based tritopic ligand 1^35,36. b Self-assembly of the [Pd₉2₆]¹⁸⁺ open triaugmented triangular prism and the [Pd₁₂2₈]²⁴⁺ open icosahedron from benzene-based tritopic ligand 2 and Pd²⁺, whereas [Pd’₆2₄]¹²⁺ open octahedron was formed with Pd’²⁺ instead of Pd²⁺. c Energy-minimized structure of [Pd₉2₆]¹⁸⁺ by DFT calculations using B3LYP/def2-SV(P) level of theory. d Crystal structure of [Pd₁₂2₈]²⁴⁺. Color labels: Yellow = Pd; Blue = C; Red = N. Hydrogen atoms are omitted for clarity.

Herein, we report that the dihedral angle change in tritopic ligands with three 4-pyridyl rings attached to a central aromatic ring afforded different self-assemblies of M_3nL_2n (n = 3 and 4). Metal-complexation of tritopic ligand 2 with θ around 36° gave an M₉L₆ open triaugmented triangular prism³⁷ as a kinetic product, and an M₁₂L₈ open icosahedron³⁸ was produced as the thermodynamically most stable product (Fig. 1b–d). In contrast, the self-assembly of tritopic ligand 3 with a mesitylene moiety as the central ring to set θ > 70° afforded an M₁₂L₈ square sheet structure. Geometric analyses of M_nL_n (n = 2–4) subcomponent rings found in these assemblies revealed that a subcomponent ring(s) with small strain is(are) selected for each θ, resulting in the formation of self-assemblies composed of a larger number of building blocks (M₉L₆ and M₁₂L₈) by increasing θ. Remote geometric communication among the tritopic ligands through a cis-protected Pd(II) center connecting them, which is realized by fixing the relative orientation around the Pd(II) center, is key for reflecting the change in θ to the assembled structure, even though there is no contact among the tritopic ligands in the assemblies. These results imply that such a high level of design of building blocks is a hidden factor that enables the creation of large self-assemblies in nature.

Results

Self-assembly of an M₁₂L₈ cage

The self-assembly of tritopic ligand 2 and Pd²⁺ was conducted in CH₃NO₂ at 363 K in the presence of NO₃^– for 5 days, resulting in a broad ¹H NMR spectrum at thermodynamic equilibrium (Fig. 2a). Downfield shift of H^a signals indicates the coordination of the 4-pyridyl groups in 2 to a Pd(II) center. ¹H diffusion-ordered spectroscopy (DOSY) measurement indicated that all ¹H signals of 2 have the same diffusion coefficient (2.0 × 10^–10 m² s^–1), indicating the formation of a single assembly with a diameter of 35.6 Å, which is larger than the M₆L₄ open octahedron.

Fig. 2. ¹H NMR spectra of the [Pd₁₂2₈]²⁴⁺ open icosahedron and the [Pd₉2₆]¹⁸⁺ open triaugmented triangular prism (500 MHz, CD₃NO₂).

a [Pd₁₂2₈]²⁴⁺ at 298 K. b ¹H DOSY spectrum of [Pd₁₂2₈]²⁴⁺. c [Pd₁₂2₈]²⁴⁺ at 353 K. The dynamic motion in [Pd₁₂2₈]²⁴⁺, which caused the broadening of the ¹H NMR spectrum at 298 K, is schematically shown on the right. d Free ligand 2 at 298 K. e [Pd₉2₆]¹⁸⁺ at 298 K. f ¹H DOSY spectrum of [Pd₉2₆]¹⁸⁺.

Single crystals were obtained by slow diffusion of methanol into the reaction mixture for 8 days. Single-crystal X-ray analysis revealed the structure of an [Pd₁₂2₈]²⁴⁺ open icosahedron (Fig. 1d, Supplementary Fig. 1, and Methods section). Eight tritopic ligands 2 are connected by twelve Pd²⁺ and occupy eight faces of a distorted icosahedron. According to the crystal structure of [Pd₁₂2₈]²⁴⁺, all eight tritopic ligands 2 are chemically equivalent, and all H^c protons should be identical. In contrast, because of the distortion of the open icosahedron, the H^a and H^b protons in the 4-pyridyl rings of 2 are placed under two environments (denoted as a^A, a^B, b^A, and b^B in Fig. 2b). Thus, the observation of two types of H^a protons by ¹H NMR spectroscopy is consistent with the crystal structure of [Pd₁₂2₈]²⁴⁺. Variable-temperature (VT) ¹H NMR measurements of a solution of [Pd₁₂2₈]²⁴⁺ indicated that broad H^a and H^b signals at 298 K became sharp at 353 K, showing only one set of signals due to fast chemical exchange between a^A and a^B protons by dynamic motion in [Pd₁₂2₈]²⁴⁺ (Fig. 2c). Thermodynamic parameters for the dynamic motion were determined by the Eyring plot (Supplementary Fig. 2) to obtain ΔH^‡ = 81.9 kJ mol^–1 and ΔS^‡ = 60.0 J mol^–1 K^–1. A large positive entropy change is probably due to the stabilization of the transition state by solvent and/or counter anions. Cold spray ionization Fourier transform ion cyclotron resonance (CSI FT-ICR) mass spectrometry showed the signals of ionic species for [Pd₁₂2₈(BF₄)_x]^(24–x)+ (x = 13–19) (Supplementary Fig. 3). The [Pd₁₂2₈]²⁴⁺ open icosahedron was further characterized by ¹³C NMR, heteronuclear multiple quantum correlation (HMQC), and heteronuclear multiple bond coherence (HMBC) spectroscopy (Supplementary Figs. 4–6).

Self-assembly of an M₉L₆ cage

Careful monitoring of the self-assembly of 2 and Pd²⁺ in CH₃NO₂ without NO₃^– at 343 K indicated that a different structure was assembled as a kinetic species almost quantitatively (96%) in 2 days. The ¹H NMR spectrum is much more complicated than expected from the highly symmetrical M₆L₄ open octahedron and M₁₂L₈ open icosahedron (Fig. 2e). ¹H DOSY measurement indicated that all ¹H NMR signals for 2 belong to a single species with a diffusion coefficient of 2.4 × 10^–10 m² s^–1 (Fig. 2f), which is larger than that of the [Pd₁₂2₈]²⁴⁺ open icosahedron, indicating the formation of a discrete assembled structure smaller than [Pd₁₂2₈]²⁴⁺. An M₉L₆ open triaugmented triangular prism³⁷ meets this requirement (Fig. 1b). All ¹H NMR signals for 2 in the new assembly were assigned by (H,H)-COSY and (H,H)-NOESY spectroscopy (Supplementary Figs. 7, 8). A characteristic feature of the ¹H NMR spectrum is that although three chemically inequivalent H^a protons were observed, H^c protons were observed as two signals in a 1:2 ratio. This signal pattern is consistent with a [Pd₉2₆]¹⁸⁺ open triaugmented triangular prism, in which all six chemically equivalent tritopic ligands 2 are desymmetrized into C_2v symmetry. The H^a and H^b protons in the 4-pyridyl ring A were observed as two sets (a1–a2 and b1–b2) because of the slow rotation of ring A on the NMR time scale (Fig. 2e). The chemical exchange between these signals observed by (H,H)-exchange spectroscopy (EXSY) (Supplementary Fig. 8) is consistent with the two sets of protons belonging to the same pyridyl ring A. In contrast, only one set of H^a and H^b signals was observed for ring B because the exchange of the inner and outer protons in ring B is possible by tilting ring B instead of flipping (180° rotation of) it against the N₄ plane of Pd²⁺, unlike flipping the ring required for the exchange between H^a and H^b protons in ring A. VT ¹H NMR measurements of a solution of [Pd₉2₆]¹⁸⁺ showed that the a1, a2, b1, and b2 signals gradually broadened as the temperature increased and finally coalesced at 363 K because of the rotation of ring A on the NMR time scale (Supplementary Fig. 9). In contrast, the H^c protons were observed as two sets of signals in a 1:2 ratio even at high temperature, indicating that tritopic ligand 2 in the assembled structure maintained C_2v symmetry at 363 K.

[Pd₉2₆]¹⁸⁺ is kinetically so stable that any decomposition of [Pd₉2₆]¹⁸⁺ was not observed at 298 K for 3 days and that heating at 363 K for 60 h caused only a 19% decrease of [Pd₉2₆]¹⁸⁺ without formation of [Pd₁₂2₈]²⁴⁺ (Supplementary Fig. 10). The conversion of [Pd₉2₆]¹⁸⁺ into [Pd₁₂2₈]²⁴⁺ proceeded in the presence of NO₃^– by heating at 363 K for 60 h (Supplementary Fig. 10). These results indicate that [Pd₉2₆]¹⁸⁺ is metastable and that NO₃^– promotes the equilibration of the system due to its coordination ability.

Good quality single crystals of [Pd₉2₆]¹⁸⁺ could not be obtained, and crystallization of a solution of [Pd₉2₆]¹⁸⁺ in the presence of NO₃^– afforded single crystals of the [Pd₁₂2₈]²⁴⁺ open icosahedron, preventing the characterization of [Pd₉2₆]¹⁸⁺ by X-ray analysis. The energy-minimized structure of [Pd₉2₆]¹⁸⁺ obtained by density functional theory (DFT) calculation shows that an M₉L₆ open triaugmented triangular prism can be constructed without significant distortion (Fig. 1c).

CSI FT-ICR mass spectrometry showed the signals of ionic species for [Pd₉2₆(BF₄)_x(NO₃)_yF_z]^{(18–x–y–z)+} (x, y, z) = (3,7,4) (4,6,4), (5,5,4), (8,4,2), (3,6,4), (7,4,2), (8,3,2) (Supplementary Fig. 11). The signal intensity of these mass signals was low, probably because of fragmentation of the metastable [Pd₉2₆]¹⁸⁺ during the ionization process. The [Pd₉2₆]¹⁸⁺ open triaugmented triangular prism was further characterized by ¹³C NMR, HMQC, and HMBC spectroscopy (Supplementary Figs. 12–14).

Geometric analysis

The self-assembly of the [Pd₁₂2₈]²⁴⁺ open icosahedron and the [Pd₉2₆]¹⁸⁺ open triaugmented triangular prism is contrary to the expectation that tritopic ligand 2, whose coordination directions are the same as those of 1, affords an M₆L₄ open octahedron. A question is why larger structures such as M₉L₆ and M₁₂L₈ were assembled with only the dihedral angles changed, retaining the same coordination directions as 1. DFT calculations of [Pd₆2₄]¹²⁺, [Pd₉2₆]¹⁸⁺, and [Pd₁₂2₈]²⁴⁺ showed that their total energies normalized as a Pd₃2₂ unit are in the order [Pd₁₂2₈]²⁴⁺ <[Pd₉2₆]¹⁸⁺ <[Pd₆2₄]¹²⁺ (Supplementary Table 1), which is consistent with the experimental results; however, the reason for this is unclear.

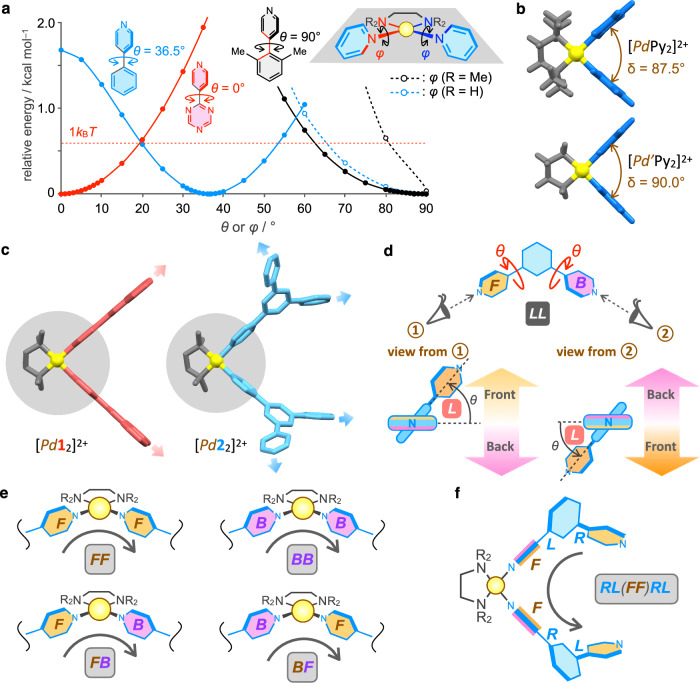
To understand how the dihedral change in the tritopic ligand affected self-assembly, first, the geometries of the building blocks (2 and Pd²⁺) were investigated by DFT calculations. The energy-minimized structure of 4-pyridylbenzene shows that the optimal dihedral angle (θ) is 36.5° (a blue solid line in Fig. 3a). The deviation from the optimal θ value destabilizes the structure. The red broken line in Fig. 3a indicates the energy level of 1 k_BT at room temperature. Regarding the cis-protected square-planar geometry of the Pd(II) center, DFT calculations of [PdPy₂]²⁺ were conducted. The optimal N^TMEDA–Pd–N^Py–C dihedral angle (φ) is 90°, and decreasing φ from 90° causes large destabilization (a black broken line in Fig. 3a), which indicates that the arrangement of the two pyridyl rings is sterically restricted by N,N,N’,N’-tetramethylethylenediamine (TMEDA) for Pd²⁺. The optimal N^Py–Pd–N^Py angle (δ) for [PdPy₂]²⁺ is 87.5° (Fig. 3b), which is slightly smaller than the ideal 90° due to the steric effect of the methyl groups in TMEDA. The three angles (θ, φ, and δ) are the deterministic factors of the assembled structures that should be considered in addition to the coordination directions of 2.

Fig. 3. Conformation analysis of building blocks and precursory complexes.

a Change in the relative energy of 4-pyridyl-1,3,5-triazine, 4-phenylpyridine, and 4-(2,6-dimethylphenyl)pyridine by change of θ and change in the relative energies of [PdPy₂]²⁺ and [Pd’Py₂]²⁺ by change of φ. b Energy-minimized structures of [PdPy₂]²⁺ and [Pd’Py₂]²⁺ by DFT calculations using B3LYP/SDD (Pd), D95** (other atoms) level of theory. Color labels: Yellow = Pd; Gray = cis-protecting group; Blue = pyridine. c Energy-minimized structures of [Pd1₂]²⁺ and [Pd2₂]²⁺ by DFT calculations. Color labels: Yellow = Pd; Gray = TMEDA; Red = 1; Blue = 2. The structures highlighted by gray-filled circles are very similar. d Definition of L and R for the dihedral change (θ) and F (front) and B (back) faces of the pyridyl rings in the ligand. When θ = 0° and 90°, there is no discrimination between L and R. e Definition of the relative orientation of the ligands connected by a cis-protected Pd(II) ion. f Example of the notation of the conformation ID for [PdL₂]²⁺. It is arbitrary from which side to read, so LR(FF)LR is the other notation of this conformation.

The effect of the dihedral angle (θ) in 2 was discussed by comparing the optimized structures of mononuclear [Pd1₂]²⁺ and [Pd2₂]²⁺ (Fig. 3c). The Pd(4-Py)₂ moieties highlighted in filled gray circles are very similar between [Pd1₂]²⁺ and [Pd2₂]²⁺ and are essentially the same as the structure of [PdPy₂]²⁺ (Fig. 3b). The structural difference between [Pd1₂]²⁺ and [Pd2₂]²⁺ is due to the arrangement of the 1,3-di(4-pyridyl)benzene moiety, which is caused by the difference in θ between 1 and 2. Therefore, although the coordination directions of the three nitrogen atoms in 1 and 2 are the same, the coordination directions of the four free pyridyl rings in [Pd1₂]²⁺ and [Pd2₂]²⁺ are different (red and blue bold arrows in Fig. 3c), which is caused by the fixation of the configuration in the Pd(4-Py)₂ structure. In other words, the fixed value of φ enables remote geometric communications between the tritopic ligands through the connecting part (Pd²⁺), which energetically differentiates the assembled structures by a change in θ.

Reason why M₆L₄ was not formed from 2

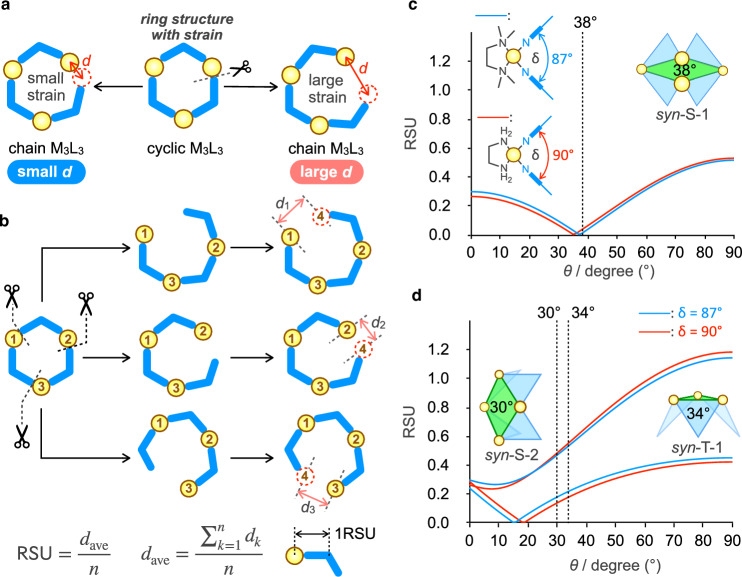
The reason why the [Pd₆2₄]¹²⁺ open octahedron was not assembled is discussed on the basis of the structural change of a subcomponent M₃L₃ ring in the M₆L₄ open octahedron by change of θ (Fig. 4a). M₆L₄ is formed by connecting the three free coordination sites in the M₃L₃ ring with a free ligand L by three M. The optimized structure of [Pd₃1₃]⁶⁺ from 1 with θ = 0° shows that the three free pyridyl groups are properly positioned to bind the fourth L. Increasing θ value forces the three free pyridyl rings in [Pd₃L₃]⁶⁺ outward, and those in [Pd₃2₃]⁶⁺ are far from each other. Therefore, the large strain caused in the M₆L₄ open octahedron by increasing θ under the fixed φ value is the reason why [Pd₆2₄]¹²⁺ was not formed.

Fig. 4. Geometric analysis of the subcomponent rings in the [Pd_3nL_2n]⁶ⁿ⁺ (n = 2–4) cages.

a Structure change in the syn-T-1 conformation of [Pd₃L₃]⁶⁺ by change of θ. The energy-minimized structures of [Pd₃1₃]⁶⁺ and [Pd₃2₃]⁶⁺ are shown on the right. Color labels: Yellow = Pd; Blue = C; Red = N. Hydrogen atoms are omitted for clarity. b Subcomponent rings in the [Pd_3nL_2n]⁶ⁿ⁺ (n = 2–4) cages. The average θ values were obtained from the crystal structures or energy-minimized structures. The conformation IDs and RSU values of the subcomponent rings are listed in Table 1. The definition of RSU is shown in Fig. 5b.

Strain analysis of subcomponent rings

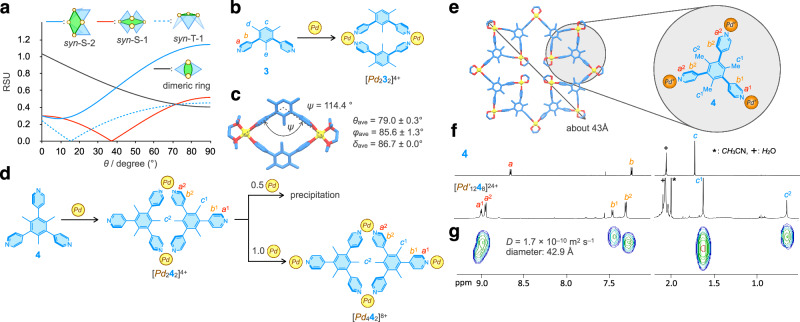
Next, we discuss why the [Pd₁₂2₈]²⁴⁺ open icosahedron is thermodynamically the most stable, whereas the [Pd₉2₆]¹⁸⁺ open triaugmented triangular prism is metastable. We focus on the subcomponent rings in the assembled structures (Fig. 4b). The M₁₂L₈ open icosahedron has only one type of conformation of M₄L₄ square in which all four free pyridyl groups are pointed toward the same side (syn-S-1). The M₉L₆ open triaugmented triangular prism has triangular and square subcomponents (syn-T-1 and syn-S-2). The M₆L₄ open octahedron contains triangles (syn-T-1) and squares (1,3-alt-S) as the subcomponent rings.

To analyze each subcomponent ring M_nL_n, the ditopic ligand L (1,3-di(4-pyridyl)benzene) was considered (Fig. 3d). The conformations of the ligand can be classified based on the screw sense concerning two dihedral angles (θ) (Fig. 3d). The clockwise rotation of θ indicates R, while the counterclockwise rotation of θ indicates L, and the conformation of the ligand can be indicated by two letters, such as LL. Next, the faces of the two pyridyl rings (F and B) are defined according to Fig. 3d. Four combinations of two pyridyl rings coordinating to a cis-protected Pd(II) center are possible (Fig. 3e). The conformational isomers of Pd_xL_y can be expressed using four types of letters (R, L, B, and F). For example, the PdL₂ structure shown in Fig. 3f is indicated as RL(FF)RL. According to this notation rule, the conformation IDs of the subcomponent rings in the crystal structures of [Pd₆1₄]¹²⁺ and [Pd₁₂2₈]²⁴⁺ and the optimized structure of [Pd₉2₆]¹⁸⁺ were determined (Table 1).

Table 1.

Ring strain per unit of subcomponent rings in Pd_3nL_2n cages

cage	subcomponent ringa	θ / °	RSUb
[Pd614]12+	syn-T-1 RL(FF)RL(FF)RL(FF)c	0	0.243
	1,3-alt-S RR(FF)RR(BB)RR(FF)RR(BB)	0	0.284
[Pd926]18+	syn-T-1 RL(FF)RL(FF)RL(FF)	34d	0.220
	syn-S-2 RR(FB)RL(BB)RR(FB)RL(BB)	30d	0.470
[Pd1228]24+	syn-S-1 RR(FF)LL(BB)RR(FF)LL(BB)	38e	0.010

^aSchematic representation of the structures is shown in Fig. 4b.

^bDefinition of the ring strain per unit (RSU) is shown in Fig. 5b.

^cConformation ID of the subcomponent ring. The definitions of L and R for the counterclockwise and clockwise rotation of the dihedral change (θ) and F (front) and B (back) faces of the pyridyl rings in the ligand, as shown in Fig. 3d–f. When θ = 0° and 90°, there is no discrimination between L and R.

^dAverage θ was obtained from the energy-minimized structure.

^eAverage θ was obtained from the crystal structure³⁸.

Strain in the subcomponent rings is purely estimated using the following method (Fig. 5a, b). Now, we consider the situation where an M–L coordination bond in an M₃L₃ ring is broken to form a chain structure without strain. When the ring strain is large, both terminals in the chain structure are largely separated from each other to relieve the strain. Thus, the distance between both ends in the M₄L₃ chain (d in Fig. 5a) can be used to evaluate the ring strain. In an M₃L₃ ring, there are three ways to form the M₄L₃ chain, and three d values are obtained from each M₄L₃ chain. The normalized ring strain in an M_nL_n ring per ML unit (RSU) is defined as d_ave/n (Fig. 5b). The effect of θ on the strain in the subcomponent rings M_nL_n was systematically analyzed by considering all possible mathematically generated conformations (see details in the Methods section).

Fig. 5. Strain analysis of M_nL_n rings.

a A concept of evaluating ring strain from the distance, d, between both ends in the chain structure obtained by breaking an M–L bond. The yellow circle and blue boomerang indicate a cis-protected Pd(II) ion and a ditopic ligand with a bend angle of 120°, respectively. b Definition of the ring strain per unit (RSU) for M_nL_n rings. The unit of RSU is the distance, and 1RSU is the distance between the centers of M and L. c Change in the RSU values of syn-S-1 in an M₁₂L₈ open icosahedron for Pd²⁺ (δ = 87°) and Pd’²⁺ (δ = 90°) by change of θ. A broken line indicates θ_ave = 38° for syn-S-1 found in the crystal structure. d Change in the RSU values of syn-S-2 and syn-T-1 in an M₉L₆ open triaugmented triangular prism for Pd²⁺ (δ = 87°) and Pd’²⁺ (δ = 90°) by change of θ. Broken lines indicate θ_ave = 30° and 34° for syn-S-2 and syn-T-1 in the energy-minimized structure of [Pd₉2₆]¹⁸⁺, respectively.

Strain analysis of Pd₁₂L₈

The change in RSU for the subcomponent square found in [Pd₁₂2₈]²⁴⁺, syn-S-1, is shown in Fig. 5c. The average θ value in the crystal structure of [Pd₁₂2₈]²⁴⁺ is 38°, which is slightly larger than the optimal value of θ for 4-pyridylbenzene (36.5°). It was found that the RSU of syn-S-1 for θ = 38° is 0.010 (Table 1), which is very close to the minimum RSU value at θ = 37°, and that syn-S-1 is the subcomponent square whose RSU is the smallest among the possible syn-M₄L₄ squares in the rage 37° ≤ θ ≤ 44°. Note that the RSU values of syn-T-1 and 1,3-alt-S in the [Pd₆1₄]¹²⁺ open octahedron (θ = 0°) are 0.243 and 0.284, respectively (Table 1). The strain in the [Pd₁₂2₈]²⁴⁺ open icosahedron is much smaller than that in [Pd₆1₄]¹²⁺. The small strain in [Pd₁₂2₈]²⁴⁺ is the reason why [Pd₁₂2₈]²⁴⁺ is thermodynamically the most stable, even though the number of components in [Pd₁₂2₈]²⁴⁺ is twice that of [Pd₆1₄]¹²⁺.

Strain analysis of Pd₉L₆

The changes in RSU of the subcomponent rings in [Pd₉2₆]¹⁸⁺ are shown in Fig. 5d. The average θ for syn-S-2 and syn-T-1 in the energy-minimized structure of [Pd₉2₆]¹⁸⁺ are 30° and 34°, respectively, and their RSU values are 0.470 and 0.220 (Table 1), which is much larger than RSU of syn-S-1 in [Pd₁₂2₈]²⁴⁺ at 38° (0.010). Therefore, a larger ring strain in [Pd₉2₆]¹⁸⁺ than in [Pd₁₂2₈]²⁴⁺ is the reason why [Pd₉2₆]¹⁸⁺ was obtained as a metastable assembly. The θ-dependence of RSU of syn-S-2 and syn-T-1 indicates that the ring strains are relieved by decreasing θ, and that approximately 20° is the best value to minimize the ring strains. The average θ values, 30° and 34°, are between 20° and the ideal θ for the free ligand, 36.5°. Considering that a total of six and eight rotatable pyridyl rings exist in syn-S-2 and syn-T-1, a large deviation of θ from the ideal 36.5° in all the rotatable parts significantly destabilizes the subcomponent rings, so these θ values would be taken to balance the two criteria. Smaller θ for syn-S-2, 30°, than θ for syn-T-1, 34°, would be due to a decrease in the large strain of syn-S-2.

Effect of cis-protecting group

The self-assembly of 2 and Pd’²⁺, in which ethylenediamine (en) is the cis-protecting group instead of TMEDA, produced neither M₉L₆ nor M₁₂L₈ but afforded a [Pd’₆2₄]¹²⁺ open octahedron (Fig. 1d). The [Pd’₆2₄]¹²⁺ open octahedron was characterized by ¹H NMR, ¹H DOSY, and mass spectroscopy (Supplementary Fig. 16). Unfortunately, single crystals of [Pd’₆2₄]¹²⁺ were not obtained. The assembly of the [Pd’₆2₄]¹²⁺ open octahedron indicates that not only θ but also φ is the important factor affecting the assembled structures. The cis-protecting group of a Pd(II) center alters φ and δ (Fig. 3b, c). DFT calculations indicate that the bite angle δ for [Pd’Py₂]²⁺ is 90°, which is slightly larger than that for [PdPy₂]²⁺, 87.5° (Fig. 3c). The effect of δ on RSU for the subcomponent rings of the assemblies is small (Fig. 5c, d), indicating that slight change in δ is not the reason for the formation of [Pd’₆2₄]¹²⁺.

Because the four N-methyl groups in TMEDA are replaced with hydrogens in en, the less steric effect of en allows a wider range of φ (Fig. 3a); therefore, the restriction of φ being 90° is relieved in the en-protected Pd(II) center, which enables [Pd’2₂]²⁺ to adopt a structure similar to that of [Pd1₂]²⁺ (Fig. 4a) by changing φ. In other words, in the case of en, variable φ values cancel the effect of θ, diminishing the geometric communication among the tritopic ligands. This idea was confirmed by comparing the DFT-optimized structures of the [Pd₆2₄]¹²⁺ and [Pd’₆2₄]¹²⁺ open octahedrons. Both cage structures have similar average θ values; 22.6 ± 1.9° for [Pd₆2₄]¹²⁺ and 27.5 ± 1.5° for [Pd’₆2₄]¹²⁺. In contrast, the φ values in [Pd₆2₄]¹²⁺ and [Pd’₆2₄]¹²⁺ show a larger difference; 82.0 ± 2.8° for [Pd₆2₄]¹²⁺ and 70.9 ± 7.2° for [Pd’₆2₄]¹²⁺ (Supplementary Fig. 16d), indicating that φ in [Pd’₆2₄]¹²⁺ is largely deviated from the ideal 90°. The small φ values in [Pd’₆2₄]¹²⁺ relieve the strain in subcomponent rings of [Pd’₆2₄]¹²⁺ caused by the dihedral angle θ being about 30°. Consequently, the fixed φ value is the key factor for differentiating the strain in the M_3nL_2n subcomponent rings caused by the θ change.

Strain analysis of Zn₁₂L₈

A similar M₁₂L₈ open icosahedron structure composed of 2 and a tetrahedral Zn(II) center, ZnCl₂ (Zn), was reported in solid state (Fig. 6a)^38,39. Because Zn(II) ions adopt tetrahedral coordinate, δ for Zn₁₂2₈ is larger than 90°, and the average δ in the crystal structure is 102.8 ± 0.6°. The θ and φ in the crystal structure are 26.1 ± 9.0° and 84.1 ± 13.4°, respectively. The energy-minimized structure of the Zn₃2₃ ring shows that the three free pyridyl rings are separated (Fig. 6b). Note that the Zn₃1₃ ring also shows a similar spreading structure (Fig. 6b), indicating that the large ring strain in the Zn₆L₄ open octahedron (L = 1 or 2) is because of large δ regardless of θ.

Fig. 6. Strain analysis of the Zn₁₂2₈ open icosahedron.

a Schematic representation of the Zn₁₂2₈ open icosahedron. Zn indicates ZnCl₂. θ_ave, φ_ave, and δ_ave were obtained from the crystal structure³⁸. b Energy-minimized structure of Zn₃2₃ by molecular mechanics calculations. Color labels: Purple = Zn; Blue = C; Red = N; Green = Cl. Hydrogen atoms are omitted for clarity. c Relative energy of mononuclear complexes by changing φ. φ_min indicates φ in the energy-minimized structure. d Change in the RSU values of syn-S-1 and syn-S-3 in an M₁₂L₈ open triaugmented triangular prism for M (δ = 103°) by change of θ. syn-S-3 is the subcomponent ring found in the crystal structure of Zn₁₂2₈³⁸. syn-S-1 is the same conformation as the subcomponent ring found in [Pd₁₂2₈]²⁴⁺. A broken line indicates θ_ave = 26.1° found in the crystal structure of Zn₁₂2₈. e Change in the RSU values of syn-S-2 and syn-T-1 in an M₉L₆ open triaugmented triangular prism for M (δ = 103°) by change of θ.

The subcomponent square in the crystal structure of Zn₁₂2₈ is syn-S-3, in which one pyridyl ring rotates oppositely compared with syn-S-1 in [Pd₁₂2₈]²⁴⁺, so the conformation ID of syn-S-3 is different from that of syn-S-1 by two letters (Fig. 6d). The changes in the RSU values of syn-S-1 and syn-S-3 are shown in Fig. 6d. The ring strain in syn-S-3 is larger than that in syn-S-1 in the range 0° ≤ θ ≤ 70°. The reason why syn-S-3 with a larger strain was adopted in the crystal structure of Zn₁₂2₈ is probably crystal packing. The RSU of syn-S-1 (δ = 103°) at the optimal θ (37°) is 0.15, which is larger than that at δ = 87° (RSU = 0.010, θ = 38°); therefore, the ring strain in Pd₁₂2₈ is much smaller than that in Zn₁₂2₈.

The changes in the RSU values of the subcomponent rings in M₉L₆ (δ = 103°) were calculated (Fig. 6e). The RSU of syn-S-2 was greater than 0.4 for θ > 20°, whereas the RSU of syn-T-1 was negligible around optimal θ = 36.5°. Therefore, Zn₉2₆ is largely destabilized by the strain in the square parts of Zn₉2₆ and is less stable than Zn₁₂2₈. Because the complexation of 2 with ZnCl₂ caused immediate precipitation³⁸ and the resulting solid was not soluble in both polar and apolar solvents, thermodynamic discussion in the solution state was impossible. Thus, [Zn(TMEDA)]²⁺ (Zn’²⁺) was used as the metal source instead of ZnCl₂ to solve the solubility problem. The complexation of 2 with Zn’²⁺ in CD₃NO₂ did not cause precipitation, and a slight downfield shift of the ¹H NMR signals of 2 indicated the formation of coordination bonds between 2 with Zn’²⁺ (Supplementary Fig. 17a). ¹H DOSY measurement of the resulting solution showed a diffusion coefficient of 6.7 × 10^–10 m² s^–1 (Supplementary Fig. 17b), which is comparable to that of the free ligand 2 (6.7 × 10^–10 m² s^–1) and larger than that of [Pd₁₂2₈]²⁴⁺ (2.0 × 10^–10 m² s^–1). This result indicates that the equilibrium seldom shifts to the Zn’₁₂L₈ open icosahedron in solution, probably because of the weak Zn’–pyridine bond.

Note that φ in the crystal structure of Zn₁₂2₈ shows a large deviation (84.1 ± 13.4°), which is likely due to the small steric effect of the two Cl atoms in the tetrahedral Zn(II) center, whereas θ values of 2 in the cage are close to the ideal value of 36.5°⁴⁰. DFT calculations showed that destabilization by deviation of φ from the optimal φ for ZnCl₂Py₂ is much smaller than that for [PdPy₂]²⁺ (Fig. 6c), which indicates that remote geometric communication among tritopic ligands 2 via the Zn–Py coordination bonds is weak. The Zn₁₂2₈ open octahedron was assembled because of the destabilization of smaller assemblies (Zn₆2₄ and Zn₉2₆) by strain arising from large δ. This strategy is the same as that for the assembly of large [Pd_nL_2n]²ⁿ⁺ assemblies by increasing the bend angle of the ditopic ligand; δ in Zn_3n2_2n assemblies corresponds to the bend angle of L in [Pd_nL_2n]²ⁿ⁺. [Pd₁₂2₈]²⁴⁺ and Zn₁₂2₈ are structurally similar, but their formation origins are different.

Self-assembly of ligands with large dihedral angles

The next question is what assembly is produced when θ is greater than 40°. Methyl groups are introduced into the benzene ring to increase θ. DFT calculations indicate that the optimal θ for 4-(2,6-dimethylphenyl)pyridine is 90° (a black solid line in Fig. 3a). The RSU values of syn-T-1, syn-S-1, and syn-S-2 for the subcomponent rings in Pd₉L₆ and Pd₁₂L₈ increase with increasing θ, but the RSU of the Pd₂L₂ ring decreases as θ increases (Fig. 7a) and becomes the smallest among the four at θ > 74°. Thus, a Pd₂L₂ ring is expected when methyl groups are introduced in the central ring. To test this idea, the self-assembly of mesitylene-based ditopic ligand 3 was performed (Fig. 7b). A 1:1 mixture of Pd²⁺ and 3 afforded a clean ¹H NMR spectrum, suggesting the formation of a single species (Supplementary Fig. 18). The [Pd₂2₂]⁴⁺ ring structure was unambiguously characterized by its single-crystal structure (Fig. 7c), where the bend angle of the ditopic ligands (ψ) was smaller than the ideal 120°, 114.4°, indicating a slight distortion, which is consistent with the large RSU of 0.416 at θ = 79°.

Fig. 7. Self-assembly of ligands with a large θ and cis-protected Pd(II) ions.

a Change in the RSU values of syn-S-1, syn-S-2, syn-T-1, and dimeric ring for Pd²⁺ (δ = 87°) by change of θ. The conformation of the dimeric ring whose RSU is the smallest at each θ is taken and their RSU values are plotted. b Formation of a [Pd₂3₂]⁴⁺ ring from the mesitylene-based ditopic ligand 3 and Pd²⁺. c Crystal structure of [Pd₂3₂]⁴⁺. Color labels: Yellow = Pd; Blue = C; Red = N. Hydrogen atoms are omitted for clarity. d Self-assembly of 4 and Pd²⁺ at different stoichiometry. e Energy-minimized structure of [Pd’₁₂4₈]²⁴⁺ composed of an M₂L₂ dimeric ring by molecular mechanics calculations. Color labels: Yellow = Pd; Blue = C; Red = N. Hydrogen atoms are omitted for clarity. f ¹H NMR spectra of 4 and the [Pd’₁₂4₈]²⁴⁺ square sheet (500 MHz, CD₃NO₂, 298 K). g ¹H DOSY spectrum of [Pd’₁₂4₈]²⁴⁺ (500 MHz, CD₃NO₂, 298 K).

Next, the self-assembly of tritopic ligand 4 and Pd²⁺ was investigated (Fig. 7d). The formation of the [Pd₁₂4₈]²⁴⁺ square sheet, where four molecules of the dimeric ring, [Pd₂4₂]⁴⁺, are connected by four Pd²⁺, was expected. 1:1 complexation of 4 and Pd²⁺ showed a characteristic ¹H NMR spectrum of the [Pd₂4₂]⁴⁺ ring, where two sets of H^a, H^b, and H^c signals in a 1:2 integration ratio were observed (Supplementary Fig. 19a). The diffusion coefficients of these signals determined by ¹H DOSY spectroscopy are the same (Supplementary Fig. 19b), indicating the formation of a single species with diameter of about 20.8 Å. Addition of 0.5 equiv. of Pd²⁺ to a solution of [Pd₂4₂]⁴⁺ to set the stoichiometry [Pd]/[4] = 1.5 caused precipitation, whereas addition of 1.0 equiv. of Pd²⁺ ([Pd]/[4] = 2) afforded a clear solution, whose ¹H NMR spectrum showed a downfield shift of the a2 signal (Supplementary Fig. 19c), indicating the formation of Pd–N coordination bonds at the free pyridyl rings in [Pd₂4₂]⁴⁺ to form [Pd₄4₂]⁸⁺. [Pd₄4₂]⁸⁺ was characterized by ¹H DOSY (Supplementary Fig. 19d), (H,H)-COSY, (H,H)-NOESY, ¹³C NMR, heteronuclear single quantum coherence (HSQC) and HMBC spectroscopy (Supplementary Figs. 20–24).

The precipitate produced at [Pd]/[4] = 1.5 may have oligomeric chain structures. Molecular modeling of the [Pd₁₂4₈]²⁴⁺ square sheet shows steric repulsion between the four TMEDA groups gathered in the center of the square (Supplementary Fig. 25), which may prevent the formation of the square sheet. When en is used as the cis-protecting group, such steric repulsion is not observed in the [Pd’₁₂4₈]²⁴⁺ square sheet by molecular modeling (Fig. 7e). Self-assembly of 4 and Pd’²⁺ in a 2:3 ratio gave a ¹H NMR spectrum in which both a1 and a2 showed downfield shift, indicating that all of the pyridyl groups make a Pd(II)–N coordination bond (Fig. 7f). The ¹H DOSY spectrum indicated the formation of a single species with a diameter of 42.9 Å (Fig. 7g), which is consistent with the size of the [Pd’₁₂4₈]²⁴⁺ square sheet (43 Å). According to the modeling structure of [Pd’₁₂4₈]²⁴⁺ square sheet, tritopic ligand 4 should be desymmetrized to C₁; three 4-pyridyl groups in 4 are chemically inequivalent. Therefore, each H^a, H^b, and H^c proton is expected to be observed as three signals in a 1:1:1 ratio, which is not consistent with the observation of their signals in a 1:2 ratio (Fig. 7f). The environments of two types of 4-pyridyl groups of the [Pd’₂4₂]⁴⁺ ring parts (a2 protons) in the square sheet might be magnetically identical. CSI FT-ICR mass measurement of the solution detected the signals for [Pd’₁₂4₈]²⁴⁺ square sheet as several ionic species of [Pd’₁₂4₈(BF₄)_x(NO₃)_yF₆]^{(18–x–y)+} (x, y) = (1,13), (2,12), (3,11), (0,13), (1,12), (2,11), (10,2), (11,1), (12,0), (11,0) (Supplementary Fig. 26). The [Pd’₁₂4₈]²⁴⁺ square sheet was further characterized by (H,H)-COSY, (H,H)-NOESY, ¹³C NMR, HSQC, and HMBC spectroscopy (Supplementary Figs. 27–31). Consequently, the introduction of three methyl groups in the central benzene ring to increase θ altered the assembled structure from the M₁₂L₈ open icosahedron to the M₁₂L₈ square sheet.

Narcissistic self-sorting behavior

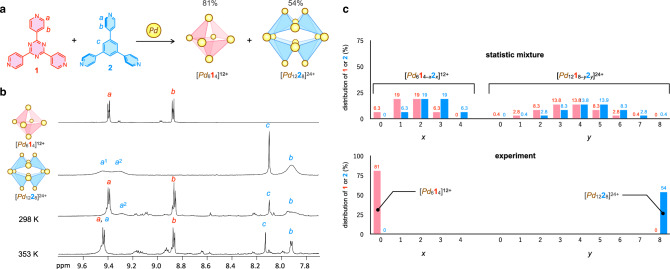
Finally, self-sorting of the tritopic ligands, 1 and 2, was investigated in the self-assembly of Pd_3nL_2n cages to evaluate the effect of the dihedral angle (θ) for the recognition between the two ligands with the same coordination direction. Although many examples of narcissistic self-sorting have been reported in molecular self-assembly^41–53, the self-sorting of building blocks with high structural similarity is still challenging and such examples are scarce⁵⁴. Tritopic ligands 1 and 2 are structurally the same except for a difference in the dihedral angle, θ (Fig. 1a, b). Tritopic ligands 1 and 2 were complexed with Pd²⁺ under thermodynamic control (heating at 363 K), resulting in intense ¹H NMR signals of [Pd₆1₄]¹²⁺ and [Pd₁₂2₈]²⁴⁺ (Fig. 8b). The yields of [Pd₆1₄]¹²⁺ and [Pd₁₂2₈]²⁴⁺ determined by ¹H NMR with the internal standard were 81% and 54%, respectively. The number of possible isomers of an M₆L₄ open octahedron composed of 1 and 2 is 5 and that of an M₁₂L₈ open icosahedron is 23, including an enantiomer (Supplementary Figs. 32 and 33). If there is no discrimination between the two ligands, the yields of [Pd₆1₄]¹²⁺ and [Pd₁₂2₈]²⁴⁺ based on 1 and 2 are calculated to be 6.25 and 0.39%, respectively (Fig. 8c and Supplementary Fig. 34). The difference in θ between 1 and 2 was well recognized in self-sorting, affording the homoleptic [Pd₆1₄]¹²⁺ and [Pd₁₂2₈]²⁴⁺ cages in much higher yields than those calculated for the statistical mixture. This indicates the power of remote geometric communications stemming from fixed φ.

Fig. 8. Narcissistic self-sorting of M₆L₄ and M₁₂L₈ cages from tritopic ligands 1 and 2 with the same coordination direction and Pd²⁺.

a A reaction scheme of the narcissistic self-sorting. The yields were determined based on tritopic ligands (1 or 2). b ¹H NMR spectra of a mixture of 1, 2, Pd²⁺, and NO₃^– in a 1:1:3:1 ratio (500 MHz, CD₃NO₂/CDCl₃/CD₃OD = 7/3/2 (v/v/v)) after the convergence measured at 298 K and 353 K. NO₃^– was added to accelerate the equilibration of the system. ¹H NMR spectra of [Pd₆1₄]¹²⁺ and [Pd₁₂2₈]²⁴⁺ at 298 K are shown for comparison. c Distribution of the tritopic ligands (1 and 2) in the [Pd₆L₄]¹²⁺ and [Pd₁₂L₈]²⁴⁺ for a statistical mixture and experimental result (the yields of [Pd₆1₄]¹²⁺ and [Pd₁₂2₈]²⁴⁺). Only the distributions of 1 and 2 in the homoleptic assemblies are shown in the experimental result. Calculation of the distributions of 1 and 2 for a statistical mixture is shown in Supplementary Fig. 34.

Discussion

Although it has been recognized that the interactions among the building blocks in terms of shape and electrostatic complementarity are key for creating discrete, large self-assemblies in nature, a deeper understanding of the essence of the interactions is necessary to reveal the general principles. Simple artificial systems are a good toy model for abstracting the essential parts underlying complicated phenomena. It was found in this research that cis-protected Pd(II)-based self-assemblies are determined not only by the coordination direction of the multitopic ligand (L) and the coordination geometry of the metal ion (δ) but also by the dihedral angle (θ) in L. A narrow range of φ around 90° for Pd²⁺ enables propagation of the difference of θ in the multitopic ligand to neighboring multitopic ligands via cis-protected Pd(II) ions. There is no direct contact among the tritopic ligands in the Pd_3nL_2n (n = 2–4) assemblies, but remote geometric communications are realized through the connecting part (Pd²⁺) by fixing φ. This is the reason why larger assemblies, [Pd₁₂2₈]²⁴⁺ and [Pd₉2₆]¹⁸⁺, were assembled from the benzene-based tritopic ligand 2 (θ = 36.5°), whereas an M₆L₄ open octahedron was assembled from the triazine-based 1 (θ = 0°). The results obtained from a simple self-assembly system suggest that remote geometric communications among building blocks are a hidden important factor enabling giant assemblies in nature. Such a new perspective would allow us to rationally design large self-assemblies based on a higher level of geometric communication among the building blocks beyond the mere design of the shape of the building block itself.

Note that metastable [Pd₉2₆]¹⁸⁺ was produced in 96% yield, which must be realized by a pathway-dependent kinetic origin. Kinetic control can sometimes be involved in molecular self-assembly in nature^55–57, but the understanding of kinetic control does not go beyond a kinetic trap. The advantage of kinetic control is that assemblies that are not thermodynamically most stable are accessible, which expands the possibility of molecular self-assembly. Understanding the self-assembly pathway to [Pd₉2₆]¹⁸⁺ would lead to the general principles of kinetic control in molecular self-assembly⁵⁸, which would enable us to rationally design kinetic assemblies. We have just started working on this issue.

Methods

General information

¹H NMR spectra were recorded using a Bruker AV-500 (500 MHz) spectrometer. All ¹H NMR spectra were referenced using a residual solvent peak, CDCl₃ (δ 7.26), CD₃NO₂ (δ 4.33). Electrospray ionization time-of-flight (ESI-TOF) mass spectra were obtained using a Waters Xevo G2-S Tof mass spectrometer and Bruker micrOTOF II-KE02. CSI FT-ICR Mass spectra were obtained using Bruker scimaX. Single-crystal X-ray analyses were conducted by Rigaku VariMax and SuperNova. Ligands 1^59,60, 2^61,62, and 4⁶³ were prepared according to the literature. Molecular mechanics calculations were performed using Materials Studio software (BIOVIA) with the universal force field.

Materials

Unless otherwise noted, all solvents and reagents were obtained from commercial suppliers (TCI Co., Ltd., WAKO Pure Chemical Industries Ltd., KANTO Chemical Co., Inc., and Sigma-Aldrich Co.) and were used as received. Deuterated solvents were used after dehydration with Molecular Sieves 4 Å.

Synthesis of 2,4,6-tri(4-pyridyl)-1,3,5-triazine (1)

18-Crown-6 (200 mg, 0.76 mmol) and KOH (45 mg, 0.8 mmol) were added to EtOH (4 mL), stirring at room temperature for 20 min. Then, 4-cyanopyrine (2.0 g, 19 mmol) was added to the reaction mixture, heating at 200 °C for 6 h. After cooling down to room temperature, pyridine (24 mL) was added to the reaction mixture, stirring for 5 min. The precipitation was obtained after filtration, washing with pyridine (10 mL) and toluene (10 mL). The solid was dissolved to 2 M. HCl aq. (24 mL) and collected into the filtrate. After the addition of NH₃ aq. to the solution, until precipitation was generated. After filtration, tritopic ligand 1 was obtained as an off-white powder (0.51 g, 1.6 mmol, 25%). ¹H NMR (500 MHz, CD₃NO₂/CDCl₃/CD₃OD = 7/3/2 (v/v/v), 298 K): δ 8.91 (dd, J = 1.5 and 4.3 Hz, 6 H), 8.71 (dd, J = 1.5 and 4.3 Hz, 6 H).

Synthesis of 1,3,5,-tri(4-pyridyl)-benzene (2)

In a 100-mL sealed tube flask, 1,3,5-tribromobenzene (0.3 g, 0.95 mmol, 1 eq.), 4-pyridyl-boronic acid (0.47 g, 3.8 mmol, 4 eq.), Na₂CO₃ (3.0 g, 29 mmol, 30 eq.), Pd(PPh₃)₄ (0.17 g, 0.14 mmol, 15 mol%) were mixed under inert atmosphere in dioxane (30 mL) and H₂O (20 mL). The resulting mixture was stirred at 110 °C for 2 days. After evaporation of the mixture, the residue was added to H₂O (50 mL), and extraction was performed using CHCl₃ (40 mL, three times). The organic layer was dried over anhydrous MgSO₄, and the solvent was removed by evaporation to obtain the crude product. After purification by silica gel column chromatography (Eluent: 5% CH₃OH containing CHCl₃ solution), tritopic ligand 2 was obtained as a colorless solid (0.22 g, 0.70 mmol, 73%). ¹H NMR (500 MHz, CDCl₃, 298 K): δ 8.76 (dd, J = 1.5 and 4.4 Hz, 6 H), 7.92 (s, 3 H), 7.61 (dd, J = 1.5 and 4.4 Hz, 6 H).

Synthesis of 4,4’,4”-(2,4,6-trimethylbenzene-1,3,5-triyl)tripyridine (4)

In a 100-mL sealed tube flask, 1,3,5-tribromo-2,4,6-trimethylbenzene (357 mg, 1.0 mmol, 1 eq.), 4-pyridyl-boronic acid (1.23 g, 10 mmol, 10 eq.), K₃PO₄ (2.55 g, 12 mmol, 12 eq.), Pd₂(dba)₃ (20.1 mg, 22 µmol, 0.022 eq.), and SPhos (18.1 mg, 44 µmol, 0.044 eq.) were mixed under inert atmosphere in n-butanol (40 mL). The resulting mixture was stirred at 80 °C for 3 days. After cooling to room temperature, the reaction mixture was filtered, and the filtrate was evaporated to remove the solvent. The residue was added to H₂O (10 mL), and extraction was performed using CHCl₃ (20 mL, three times). The organic layer was dried over anhydrous MgSO₄, and the solvent was removed by evaporation to yield a yellow solid. After purification by silica gel column chromatography (Eluent: AcOEt), tritopic ligand 4 was obtained as a colorless solid (0.15 g, 0.42 mmol, 42%). ¹H NMR (500 MHz, CD₂Cl₂, 298 K): δ 8.65 (dd, J = 1.5 and 4.3 Hz, 6 H), 7.14 (dd, J = 1.5 and 4.3 Hz, 4 H), 1.67 (s, 9 H).

Self-assembly of the [Pd₁₂2₈]²⁴⁺ open icosahedron

In a vial, [Pd(CH₃CN)₂](BF₄)₂ (12 mg, 24.2 µmol) was added to a solution of tritopic ligand 2 (5.0 mg, 16 µmol) in CH₃NO₂ in the presence of n-Bu₄N·NO₃ (2.5 mg, 8.1 µmol). The solution was heated at 363 K for 5 days. After cooling to room temperature, the solvent was removed by evaporation, and the residue was washed three times with CHCl₃ (1.0 mL). The pale brown solid was dried in vacuo to obtain [Pd₁₂2₈]²⁴⁺ (15 mg, quant.). ¹H NMR (500 MHz, CD₃NO₂, 353 K) δ 9.39 (d, J = 6.0 Hz, 48 H), 8.13 (s, 24 H), 7.94 (d, J = 6.0 Hz, 48 H), 3.28 (m, 48 H), 2.98 (s, 72 H), 2.84 (s, 72 H). ¹³C NMR (125 MHz, CD₃NO₂, 353 K): δ 153.2, 153.1, 140.2, 130.6, 127.4, 52.1, 51.9.

Self-assembly of the [Pd₉2₆]¹⁸⁺ open triaugmented triangular prism

In an NMR tube with [2.2]paracyclophane as an internal standard, [Pd(CH₃CN)₂](BF₄)₂ (0.86 mg, 1.8 µmol), tritopic ligand 2 (0.37 mg, 1.2 µmol), and CH₃NO₂ (480 µL) were added. The solution was then heated at 343 K for 2 days to obtain [Pd₉2₆]¹⁸⁺ in 96% NMR yield. ¹H NMR (500 MHz, CD₃NO₂, 298 K): δ 9.21 (d, J = 6.0 Hz, 12 H), 9.15 (d, J = 6.0 Hz, 12 H), 9.10 (d, J = 6.0 Hz, 12 H), 8.08 (d, J = 1.5 Hz, 12 H), 7.95 (d, J = 6.5 Hz, 24 H), 7.66 (dd, J = 2.0, 6.0 Hz, 12 H), 7.58 (s, 6 H), 3.28 (m, 36 H), 3.03 (s, 36 H), 2.97 (s, 36 H), 2.73 (s, 36 H). ¹³C NMR (125 MHz, CD₃NO₂, 298 K): δ 153.0, 152.7, 152.5, 139.8, 139.6, 132.7, 128.8, 127.4, 127.0, 126.8, 105.5, 105.1, 51.9, 51.8, 51.5.

Self-assembly of the [Pd₂3₂]⁴⁺ ring

In an NMR tube with [2.2]paracyclophane as an internal standard, 1 equiv. of [Pd(CH₃CN)₂](BF₄)₂ (1.2 µmol) was added to a solution of 3 (1.2 µmol) in CD₃NO₂ (490 µL). After heating the solution at 343 K for 1 h, the [Pd₂3₂]⁴⁺ ring was obtained in 92% yield. ¹H NMR (500 MHz, CD₃NO₂, 298 K): δ 9.14 (dd, J = 1.5, 5.5 Hz, 8 H), 7.40 (dd, J = 1.5 and 5.5 Hz, 8 H), 7.14 (s, 2 H), 3.20 (s, 8 H), 2.85 (s, 12 H), 2.06 (s, 12 H), 0.64 (s, 6 H). ¹³C NMR (125 MHz, CD₃NO₂, 298 K): δ 155.9, 152.6, 136.7, 136.4, 133.3, 130.3, 130.2, 51.7, 20.8, 20.3, 13.9.

Self-assembly of the [Pd₂4₂]⁴⁺ ring

In an NMR tube with [2.2]paracyclophane as an internal standard, 1 equiv. of [Pd(CH₃CN)₂](BF₄)₂ was added to a solution of 4 in CD₃NO₂ (500 µL). After heating at 343 K for 4 h, the [Pd₂4₂]⁴⁺ ring was obtained quantitatively. ¹H NMR (500 MHz, CD₃NO₂, 298 K): δ 9.17 (dd, J = 1.5 and 5.5 Hz, 8 H), 8.65 (dd, J = 1.5 and 4.5 Hz, 4 H), 7.46 (d, J = 1.5 and 5.0 Hz, 8 H), 7.21 (d, J = 1.5 and 4.5 Hz,4 H), 3.18 (s, 8 H), 2.83 (s, 24 H), 1.77 (s, 12 H), 0.71 (s, 6 H). ¹³C NMR (125 MHz, CD₃NO₂, 298 K): δ 155.9, 152.8, 151.4, 139.3, 137.0, 134.1, 133.1, 130.2, 126.1, 79.2, 51.7, 21.0, 19.3, 13.9.

Self-assembly of the [Pd’₁₂4₈]²⁴⁺ square sheet

In an NMR tube with [2,2]paracyclophane as an internal standard, [Pd’(CH₃CN)₂](BF₄)₂ (0.76 mg, 1.8 μmol) was added to a solution of 4 (0.42 mg, 1.2 µmol) in CD₃NO₂ (500 µL) by titration at 343 K. After the convergence of the self-assembly, the [Pd’₁₂4₈]²⁴⁺ square sheet was obtained in 90% NMR yield. ¹H NMR (500 MHz, CD₃NO₂, 298 K): δ 8.99 (d, J = 6.5 Hz, 16 H), 8.94 (d, J = 6.5 Hz, 32 H), 7.44 (d, J = 6.5 Hz, 16 H), 7.28 (d, J = 6.5 Hz, 32 H), 3.10 (br, 48 H), 1.62 (s, 48 H), 0.65 (s, 24 H). ¹³C NMR (125 MHz, CD₃NO₂, 298 K): δ 153.2, 137.4, 133.6, 132.6, 129.4, 129.2, 48.6, 47.8, 21.0, 19.1.

Single-crystal X-ray analyses

Single crystals of the [Pd₁₂2₈]²⁴⁺ open icosahedron suitable for X-ray crystallographic analysis were obtained by vapor diffusion of CH₃OH in a CH₃NO₂ solution of [Pd₁₂2₈]²⁴⁺ at room temperature after 15 days. A crystal was immersed in and coated with FluorolubeⓇ (SIGMA-ALDRICH Corp.), and then mounted on a MicroMountTM (MiteGen LLC). The diffraction data of the single crystal were collected on a Rigaku VariMax with a Hybrid Photon Counting Detector at 93 K, using Mo Kα (λ = 0.71075 Å).

Single crystals of [Pd₂3₂]⁴⁺ were obtained at the interface between the two phases with CH₃NO₂ (100 µL) as a buffer solvent placed between them at room temperature for 15 days. One phase was a solution of 3 (5 mg, 18.2 µmol) and n-Bu₄N·NO₃ (2.8 mg, 9.1 µmol) in CH₃NO₂ (200 µL), and the other phase was a solution of [Pd(CH₃CN)₂](BF₄)₂ (8.7 mg, 18.2 µmol) in CH₃NO₂ (200 µL). A crystal was immersed in and coated with immersion oil (Cargille Corp.), and then mounted on a SuperNova single-crystal X-ray diffractometer with an Eos CCD detector (Rigaku Oxford Diffraction) at 180 K, using Cu Kα (λ = 1.54184 Å) radiation monochromated by multilayer mirror optics. Bragg spots were integrated using the CrysAlisPro program package (Rigaku Oxford Corporation). An empirical absorption correction based on the multi-scan method using spherical harmonics was implemented in the SCALE3 ABSPACK scaling algorithm. The structure was solved by an intrinsic phasing method on the SHELXT program⁶⁴ and refined by a full-matrix least-squares minimization on F2 executed by the SHELXL program⁶⁵ using the Olex2 software package (OlexSys Ltd.)⁶⁶ and the ShelXle graphical user interface⁶⁷. Thermal displacement parameters were refined anisotropically for all non-hydrogen atoms. The data were corrected for scattered electron density in large solvent voids using the PLATON SQUEEZE method⁶⁸. The crystal structures are shown in Figs. 1d, 7d and Supplementary Fig. 35. The crystallographic data are summarized in Supplementary Table 2.

DFT calculations

The optimized structures of 2-(4-pyridyl)-1,3,5-triazine, 4-phenylpyridine, 4-(2,6-dimethylphenyl)pyridine, [PdPy₂]²⁺,[Pd’Py₂]²⁺, [Pd1₂]²⁺, [Pd2₂]²⁺ ZnPy₂ were obtained using the B3LYP functional^69,70 implemented in the Gaussian16 program package⁷¹. The SDD basis set⁷² was used for the Pd and Zn atoms, and the D95** basis set⁷³ was used for the calculations of the H, C, N, and Cl atoms. The 6-31 G** basis set^74,75 was employed for the calculations of 2-(4-pyridyl)-1,3,5-triazine, 4-phenylpyridine and 4-(2,6-dimethylphenyl)pyridine. To determine the relative energies depending on θ in the ligands and φ in [PdPy₂]²⁺, [Pd’Py₂]²⁺, and ZnPy₂ (Figs. 3a and 6c), geometrical optimizations were performed by fixing the corresponding dihedral angle by inserting opt = modredundant keyword into the input file. Optimized structures and their energies were obtained using B3LYP/def2-SV(P) level of theory in [Pd₆2₄](BF₄)₁₂, [Pd₉2₆](BF₄)₁₈, [Pd₁₂2₈](BF₄)₂₄, and [Pd’₆2₄](BF₄)₁₂. After optimization, single-point calculations were carried out with various functionals of LC-OLYP, M06, and ωB97X, taking into account an implicit solvent effect as a polarizable continuum model (PCM) of nitromethane (ε = 36.562). The cartesian coordinates of the optimized structures are listed in Supplementary Data 1.

Geometric analysis

For the calculation of RSU, it is necessary to determine the distance between the ends of the M_nL_n chain. Given that one end is situated at the origin of the global coordinate system, it suffices to ascertain the coordinates of the other end in the global coordinate system. When there exist coordinate systems A and B with bases ${}^{\mathrm{A}}\mathbf{e}_x{,}^{\mathrm{A}}{\mathbf{e}}_y{,}^{\mathrm{A}}{\mathbf{e}}_z$ and ${}^{\mathrm{B}}\mathbf{e}_x{,}^{\mathrm{B}}{\mathbf{e}}_y{,}^{\mathrm{B}}{\mathbf{e}}_z$ respectively, and the rotation matrix between them is denoted as $R_{\mathrm{AB}}$ i.e.,

$$\left(\genfrac{}{}{0ex}{}{\mathrm{B}}{}{\mathbf{e}}_x{,}^{\mathrm{B}}{\mathbf{e}}_y{,}^{\mathrm{B}}{\mathbf{e}}_z\right)=\left(\genfrac{}{}{0ex}{}{\mathrm{A}}{}{\mathbf{e}}_x{,}^{\mathrm{A}}{\mathbf{e}}_y{,}^{\mathrm{A}}{\mathbf{e}}_z\right)R_{\mathrm{AB}}$$ 1

the coordinates of a vector $\mathbf{r}$ expressed as ${}^{\mathrm{B}}\mathbf{x}={\left(\genfrac{}{}{0ex}{}{\mathrm{B}}{}x{,}^{\mathrm{B}}y{,}^{\mathrm{B}}z\right)}^{\mathrm{T}}$ in coordinate system B can be calculated in coordinate system A as ${}^{\mathrm{A}}\mathbf{x}=R_{\mathrm{AB}}\genfrac{}{}{0ex}{}{\mathrm{B}}{}\mathbf{x}$.

$$\because \mathbf{r}=\left({\genfrac{}{}{0ex}{}{\mathrm{A}}{}\mathbf{e}}_x{,}^{\mathrm{A}}{\mathbf{e}}_y{,}^{\mathrm{A}}{\mathbf{e}}_z\right)\left(\begin{array}{c}\hfill \genfrac{}{}{0ex}{}{\mathrm{A}}{}x\hfill \\ \hfill {}^{\mathrm{A}}y\hfill \\ \hfill {}^{\mathrm{A}}z\hfill \end{array}\right)=\left({\genfrac{}{}{0ex}{}{\mathrm{B}}{}\mathbf{e}}_x{,}^{\mathrm{B}}{\mathbf{e}}_y{,}^{\mathrm{B}}{\mathbf{e}}_z\right)\left(\begin{array}{c}\hfill \genfrac{}{}{0ex}{}{\mathrm{B}}{}x\hfill \\ \hfill {}^{\mathrm{B}}y\hfill \\ \hfill {}^{\mathrm{B}}z\hfill \end{array}\right)=\left({\genfrac{}{}{0ex}{}{\mathrm{A}}{}\mathbf{e}}_x{,}^{\mathrm{A}}{\mathbf{e}}_y{,}^{\mathrm{A}}{\mathbf{e}}_z\right)R_{\mathrm{AB}}\left(\begin{array}{c}\hfill \genfrac{}{}{0ex}{}{\mathrm{B}}{}x\hfill \\ \hfill {}^{\mathrm{B}}y\hfill \\ \hfill {}^{\mathrm{B}}z\hfill \end{array}\right)$$ 2

Note that vectors are quantities independent of coordinate systems. The vectors represented by $\mathbf{r}$ here and later, such as $\overrightarrow{\mathrm{AB}}$, fall into this category. On the other hand, coordinates are representations of vectors that depend on the choice of coordinate systems and are expressed by arranging the components of the basis. Coordinates will be denoted by $\mathbf{x}$.

Each unit is assigned points A, B, and C, and coordinate systems A, B₁, B₂, and C, as illustrated in Fig. 9a–d. Because the positions of the coordinate systems do not affect the subsequent calculations, the coordinate systems can be located anywhere. Only the orientation of coordinate systems is crucial. Two dihedral angles between the rings in the ligand, denoted as θ₁ and θ₂, are defined as shown in Fig. 9a–d (0 ≤ θ₁, θ₂ ≤ 90°). To specify the rotation direction of the dihedral angles (R or L), integers j and k are introduced as follows.

$$j=\left\{\begin{array}{c}\hfill +1\left(\mathrm{rotation}\mathrm{direction}\mathrm{of}{\theta }_1\mathrm{is}R\right)\hfill \\ \hfill -1\left(\mathrm{rotation}\mathrm{direction}\mathrm{of}{\theta }_1\mathrm{is}L\right)\hfill \end{array}\right)$$ 3

$$k=\left\{\begin{array}{c}\hfill +1\left(\mathrm{rotation}\mathrm{direction}\mathrm{of}{\theta }_2\mathrm{is}R\right)\hfill \\ \hfill -1\left(\mathrm{rotation}\mathrm{direction}\mathrm{of}{\theta }_2\mathrm{is}L\right)\hfill \end{array}\right)$$ 4

Fig. 9. Definition of inner points and coordinates for ditopic ligands with cis-protected metal ions.

The ditopic ligand is depicted as a model of 1,3-di-4-pyridylbenzene. Two cis-protected metal ions with a bent ditopic ligand are shown (a–d). a RR, b RL, c LR, and d LL configurations. Points A and C are located at the center of the metal ions, whereas point B is located at the center of the middle hexagon in the ditopic ligand. The four coordinates are shown as the x, y, and z axes. The cis-protecting groups are omitted. Definitions of L and R are shown in the main text (Fig. 3d). A metal center with two coordinating rings is shown (e–h). e type FF, f type FB, g type BF, and h type BB. The point C_i is shown in the center of the Pd(II) ion, and the two coordinates are shown in the center of the coordinating rings. The coordinate is defined such that the front face of the coordinating ring is placed on the positive side of the z-axis. The cis-protecting ligand was omitted. Definitions of F and B are shown in the main text (Fig. 3d).

Definitions of L and R are shown in the main text (Fig. 3d).

What is ultimately required is only the transformation matrix between coordinate systems A and C, and the displacement vector between points A and C. Other coordinate systems, such as B₁ and B₂, are essentially not crucial. To determine the transformation matrix from A to C, the auxiliary coordinate systems B₁ and B₂ are introduced. Note that the z-axis of coordinate systems A and C always protrudes towards the front face.

Let the rotation matrix from A to B₁ be denoted as $R_{\mathrm{A}{\mathrm{B}}_1}$, from B₁ to B₂ as $R_{{\mathrm{B}}_1{\mathrm{B}}_2}$, and from B₂ to C as $R_{{\mathrm{B}}_2\mathrm{C}}$. Each matrix can be expressed as follows:

$$R_{\mathrm{A}{\mathrm{B}}_1}\left(j,{\theta }_1\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos {\theta }_1\hfill & \hfill -j\sin {\theta }_1\hfill \\ \hfill 0\hfill & \hfill j\sin {\theta }_1\hfill & \hfill \cos {\theta }_1\hfill \end{array}\right)$$ 5

$$R_{{\mathrm{B}}_1{\mathrm{B}}_2}\left(j\right)=\left(\begin{array}{ccc}\hfill -\cos 120^{\circ }\hfill & \hfill -j\sin 120^{\circ }\hfill & \hfill 0\hfill \\ \hfill j\sin 120^{\circ }\hfill & \hfill -\cos 120^{\circ }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$ 6

$$R_{{\mathrm{B}}_2\mathrm{C}}\left(j,k,{\theta }_2\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -jk\cos {\theta }_2\hfill & \hfill j\sin {\theta }_2\hfill \\ \hfill 0\hfill & \hfill -j\sin {\theta }_2\hfill & \hfill -jk\cos {\theta }_2\hfill \end{array}\right)$$ 7

Since consecutive rotations can be expressed as the product of rotation matrices, the rotation matrix from A to C, denoted as $R_{\mathrm{AC}}$, can be expressed as follows:

$$R_{\mathrm{AC}}\left(j,k,{\theta }_1,{\theta }_2\right)=R_{\mathrm{A}{\mathrm{B}}_1}\left(j,{\theta }_1\right)R_{{\mathrm{B}}_1{\mathrm{B}}_2}\left(j\right)R_{{\mathrm{B}}_2\mathrm{C}}\left(j,k,{\theta }_2\right)$$ 8

Let us now determine the components of the vector $\overrightarrow{\mathrm{AC}}$ as seen in the local coordinate system A. As $\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}$ holds, it is necessary to express the right-hand side components $\overrightarrow{\mathrm{AB}}$ and $\overrightarrow{\mathrm{BC}}$ as coordinates seen from coordinate system A.

Since $∣\overrightarrow{\mathrm{AB}}∣=∣\overrightarrow{\mathrm{BC}}∣=1$ by definition, $\overrightarrow{\mathrm{AB}}$ is expressed in coordinate system A as ${}^{\mathrm{A}}\mathbf{x}_{\overrightarrow{\mathrm{AB}}}={\left(1,0,0\right)}^{\mathrm{T}}$, and $\overrightarrow{\mathrm{BC}}$ is expressed in the B₂ coordinate system as ${}^{{\mathrm{B}}_2}\mathbf{x}_{\overrightarrow{\mathrm{BC}}}={\left(1,0,0\right)}^{\mathrm{T}}$. When converted to coordinates in the A system, $\overrightarrow{\mathrm{BC}}$ is expressed as ${}^{\mathrm{A}}\mathbf{x}_{\overrightarrow{\mathrm{BC}}}=R_{{\mathrm{AB}}_2}\genfrac{}{}{0ex}{}{{\mathrm{B}}_2}{}{\mathbf{x}}_{\overrightarrow{\mathrm{BC}}}=R_{\mathrm{A}{\mathrm{B}}_1}{R}_{{\mathrm{B}}_1{\mathrm{B}}_2}\genfrac{}{}{0ex}{}{{\mathrm{B}}_2}{}{\mathbf{x}}_{\overrightarrow{\mathrm{BC}}}=R_{\mathrm{A}{\mathrm{B}}_1}{R}_{{\mathrm{B}}_1{\mathrm{B}}_2}{\left(1,0,0\right)}^{\mathrm{T}}$. Therefore, the components of $\overrightarrow{\mathrm{AC}}$ as seen in the local coordinate system A are indicated as follows:

$$\genfrac{}{}{0ex}{}{\mathrm{A}}{}{\mathbf{x}}_{\overrightarrow{\mathrm{AC}}}=\genfrac{}{}{0ex}{}{\mathrm{A}}{}{\mathbf{x}}_{\overrightarrow{\mathrm{AB}}}+\genfrac{}{}{0ex}{}{\mathrm{A}}{}{\mathbf{x}}_{\overrightarrow{\mathrm{BC}}}={\left(1,0,0\right)}^{\mathrm{T}}+R_{\mathrm{A}{\mathrm{B}}_1}{R}_{{\mathrm{B}}_1{\mathrm{B}}_2}{\left(1,0,0\right)}^{\mathrm{T}}$$ 9

Consider two units, labeled as unit $i$ and unit $i+1$. The two units are connected, and the unit numbers are indicated with superscripts in the alphabet (e.g., point A in unit $i$ is denoted as point ${\mathrm{A}}^i$, and the coordinate system of unit $i$ is represented as coordinate system ${\mathrm{A}}^i$). Figure 9e–h shows an enlarged view of the junction part. φ was set to 90° throughout the calculation, which was demonstrated by DFT calculations (Fig. 3a) as the most stable for pyridyl groups coordinating to cis-protected Pd(II) center with TMEDA. While points ${\mathrm{C}}^i$ and ${\mathrm{A}}^{i+1}$ represent the same point, the coordinate systems ${\mathrm{C}}^i$ and ${\mathrm{A}}^{i+1}$ have different orientations.

Let the bite angle be denoted as δ (0° < δ < 180°). Additionally, to specify the relative orientations (F or B) of the connecting units, we defined integers $l$ and $m$ as follows:

$$l=\left\{\begin{array}{c}\hfill +1\left(\mathrm{orientation}\mathrm{of}\mathrm{unit}i\mathrm{is}F\right)\hfill \\ \hfill -1\left(\mathrm{orientation}\mathrm{of}\mathrm{unit}i\mathrm{is}B\right)\hfill \end{array}\right)$$ 10

$$m=\left\{\begin{array}{c}\hfill +1\left(\mathrm{orientation}\mathrm{of}\mathrm{unit}i+1\mathrm{is}F\right)\hfill \\ \hfill -1\left(\mathrm{orientation}\mathrm{of}\mathrm{unit}i+1\mathrm{is}B\right)\hfill \end{array}\right)$$ 11

Definitions of F and B are shown in the main text (Fig. 3d).

The rotation matrix $R_{{\mathrm{C}}^i{\mathrm{A}}^{i+1}}$ can be expressed as follows:

$$R_{{\mathrm{C}}^i{\mathrm{A}}^{i+1}}\left(l,m,\delta \right)=\left(\begin{array}{ccc}\hfill -\cos \delta \hfill & \hfill 0\hfill & \hfill -m\sin \delta \hfill \\ \hfill 0\hfill & \hfill lm\hfill & \hfill 0\hfill \\ \hfill l\sin \delta \hfill & \hfill 0\hfill & \hfill -lm\cos \delta \hfill \end{array}\right)$$ 12

The specific form of the coordinates $\genfrac{}{}{0ex}{}{{\mathrm{A}}^{i+1}}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^{i+1}{\mathrm{C}}^{i+1}}}$ in the coordinate system ${\mathrm{A}}^{i+1}$ for $\overrightarrow{{\mathrm{A}}^{i+1}{\mathrm{C}}^{i+1}}$ is already known. The representation of $\overrightarrow{{\mathrm{A}}^{i+1}{\mathrm{C}}^{i+1}}$ in the coordinate system ${\mathrm{A}}^i$ is obtained by multiplying ${\genfrac{}{}{0ex}{}{{\mathrm{A}}^{i+1}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^{i+1}{\mathrm{C}}^{i+1}}}$ from the left with the rotation matrix $R_{{\mathrm{A}}^i{\mathrm{A}}^{i+1}}$. Therefore, the calculation is given by ${\genfrac{}{}{0ex}{}{{\mathrm{A}}^i}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^{i+1}{\mathrm{C}}^{i+1}}}=R_{{\mathrm{A}}^i{\mathrm{A}}^{i+1}}\cdot {\genfrac{}{}{0ex}{}{{\mathrm{A}}^{i+1}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^{i+1}{\mathrm{C}}^{i+1}}}=R_{{\mathrm{A}}^i{\mathrm{C}}^i}{R}_{{\mathrm{C}}^i{\mathrm{A}}^{i+1}}\cdot {\genfrac{}{}{0ex}{}{{\mathrm{A}}^{i+1}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^{i+1}{\mathrm{C}}^{i+1}}}$.

Let us consider a chain consisting of n units (Unit 1, Unit 2,…, Unit n). The point A of Unit 1 (i.e., point ${\mathrm{A}}^1$) is located at the origin of the global coordinate system, and the orientation of the local coordinate system of Unit 1 (i.e., coordinate system ${\mathrm{A}}^1$) coincides with the global coordinate system.

Using the previously calculated ${\genfrac{}{}{0ex}{}{{\mathrm{A}}^i}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^i{\mathrm{C}}^i}},R_{{\mathrm{A}}^i{\mathrm{C}}^i}$, and $R_{{\mathrm{C}}^i{\mathrm{A}}^{i+1}}$, the position vector of the chain’s endpoint (i.e., point ${\mathrm{C}}^n$) in the global coordinate system can be expressed in terms of components as follows.

$$\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^n}}=\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}+\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}+\dots +\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^n{\mathrm{C}}^n}}=\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}+R_{{\mathrm{A}}^1{\mathrm{A}}^2}\genfrac{}{}{0ex}{}{{\mathrm{A}}^2}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}+\dots +R_{{\mathrm{A}}^1{\mathrm{A}}^2}{R}_{{\mathrm{A}}^2{\mathrm{A}}^3}\dots R_{{\mathrm{A}}^{n-1}{\mathrm{A}}^n}\genfrac{}{}{0ex}{}{{\mathrm{A}}^n}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^n{\mathrm{C}}^n}}=\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}+R_{{\mathrm{A}}^1{\mathrm{C}}^1}{R}_{{\mathrm{C}}^1{\mathrm{A}}^2}\genfrac{}{}{0ex}{}{{\mathrm{A}}^2}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}+\dots +R_{{\mathrm{A}}^1{\mathrm{C}}^1}{R}_{{\mathrm{C}}^1{\mathrm{A}}^2}{R}_{{\mathrm{A}}^2{\mathrm{C}}^2}{R}_{{\mathrm{C}}^2{\mathrm{A}}^3}\dots R_{{\mathrm{A}}^{n-1}{\mathrm{C}}^{n-1}}{R}_{{\mathrm{C}}^{n-1}{\mathrm{A}}^n}\genfrac{}{}{0ex}{}{{\mathrm{A}}^n}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^n{\mathrm{C}}^n}}$$ 13

Example

The method described above is employed to determine the distance between the endpoints of the M₃L₂ chain, illustrated through a specific example using the RR(FF)RL chain whose dihedral angles are all 30°. In this chain, the ditopic ligands with conformations RR and RL are connected to a cis-protected Pd(II) center with an FF relative orientation. Initially, the first unit (RR with both dihedral angles at 30°) is placed at the origin of the global coordinate system (i.e., ${\theta }_1=30^{\circ },{\theta }_2=30^{\circ },j=+1,k=+1$).

First, compute $R_{{\mathrm{A}}^1{\mathrm{B}}_1^1}$, $R_{{\mathrm{B}}_1^1{\mathrm{B}}_2^1}$ and $R_{{\mathrm{B}}_2^1{\mathrm{C}}^1}$ as follows.

$$R_{{\mathrm{A}}^1{\mathrm{B}}_1^1}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos {\theta }_1\hfill & \hfill -j\sin {\theta }_1\hfill \\ \hfill 0\hfill & \hfill j\sin {\theta }_1\hfill & \hfill \cos {\theta }_1\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{3}/2\hfill & \hfill -1/2\hfill \\ \hfill 0\hfill & \hfill 1/2\hfill & \hfill \sqrt{3}/2\hfill \end{array}\right)$$ 14

$$R_{{\mathrm{B}}_1^1{\mathrm{B}}_2^1}=\left(\begin{array}{ccc}\hfill -\cos 120^{\circ }\hfill & \hfill -j\sin 120^{\circ }\hfill & \hfill 0\hfill \\ \hfill j\sin 120^{\circ }\hfill & \hfill -\cos 120^{\circ }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill -\sqrt{3}/2\hfill & \hfill 0\hfill \\ \hfill \sqrt{3}/2\hfill & \hfill 1/2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$ 15

$$R_{{\mathrm{B}}_2^1{\mathrm{C}}^1}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -jk\cos {\theta }_2\hfill & \hfill j\sin {\theta }_2\hfill \\ \hfill 0\hfill & \hfill -j\sin {\theta }_2\hfill & \hfill -jk\cos {\theta }_2\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\sqrt{3}/2\hfill & \hfill 1/2\hfill \\ \hfill 0\hfill & \hfill -1/2\hfill & \hfill -\sqrt{3}/2\hfill \end{array}\right)$$ 16

Next, the components of the vector $\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}$ as viewed from the local coordinate system ${\mathrm{A}}^1$, denoted as $\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}$, is calculated as follows:

$$\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}{\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}={\left(1,0,0\right)}^{\mathrm{T}}+R_{{\mathrm{A}}^1{\mathrm{B}}_1^1}{R}_{{\mathrm{B}}_1^1{\mathrm{B}}_2^1}{\left(1,0,0\right)}^{\mathrm{T}}=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)+\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{3}/2\hfill & \hfill -1/2\hfill \\ \hfill 0\hfill & \hfill 1/2\hfill & \hfill \sqrt{3}/2\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill -\sqrt{3}/2\hfill & \hfill 0\hfill \\ \hfill \sqrt{3}/2\hfill & \hfill -1/2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 3/2\hfill \\ \hfill 3/4\hfill \\ \hfill \sqrt{3}/4\hfill \end{array}\right)~\left(\begin{array}{c}\hfill 1.5\hfill \\ \hfill 0.75\hfill \\ \hfill 0.43\hfill \end{array}\right)$$ 17

Finally, the components of the position vector of point ${\mathrm{C}}^1$ as seen from the global coordinate system, denoted as ${\genfrac{}{}{0ex}{}{\mathrm{global}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}$, is computed. Since the local coordinate system ${\mathrm{A}}^1$ of Unit 1 is equivalent to the global coordinate system,

$${\genfrac{}{}{0ex}{}{\mathrm{global}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}={\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}=\left(\begin{array}{c}\hfill 3/2\hfill \\ \hfill 3/4\hfill \\ \hfill \sqrt{3}/4\hfill \end{array}\right)~\left(\begin{array}{c}\hfill 1.5\hfill \\ \hfill 0.75\hfill \\ \hfill 0.43\hfill \end{array}\right)$$ 18

For calculations for subsequent units, the rotation matrix $R_{{\mathrm{A}}^1{\mathrm{C}}^1}$ from the global coordinate system to the ${\mathrm{C}}^1$ coordinate system is calculated as follows.

$$R_{{\mathrm{A}}^1{\mathrm{C}}^1}=R_{{\mathrm{A}}^1{\mathrm{B}}_1^1}{R}_{{\mathrm{B}}_1^1{\mathrm{B}}_2^1}{R}_{{\mathrm{B}}_2^1{\mathrm{C}}^1}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{3}/2\hfill & \hfill -1/2\hfill \\ \hfill 0\hfill & \hfill 1/2\hfill & \hfill \sqrt{3}/2\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill -\sqrt{3}/2\hfill & \hfill 0\hfill \\ \hfill \sqrt{3}/2\hfill & \hfill 1/2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\sqrt{3}/2\hfill & \hfill 1/2\hfill \\ \hfill 0\hfill & \hfill -1/2\hfill & \hfill -\sqrt{3}/2\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill 3/4\hfill & \hfill -\sqrt{3}/4\hfill \\ \hfill 3/4\hfill & \hfill -1/8\hfill & \hfill 3\sqrt{3}/8\hfill \\ \hfill \sqrt{3}/4\hfill & \hfill -3\sqrt{3}/8\hfill & \hfill -5/8\hfill \end{array}\right)~\left(\begin{array}{ccc}\hfill 0.5\hfill & \hfill 0.75\hfill & \hfill -0.43\hfill \\ \hfill 0.75\hfill & \hfill -0.13\hfill & \hfill 0.65\hfill \\ \hfill 0.43\hfill & \hfill -0.65\hfill & \hfill -0.63\hfill \end{array}\right)$$ 19

Next, consider connecting a new Unit 2 (RL with both dihedral angles at 30°) to the tip (point C) of Unit 1 (i.e., ${\theta }_1=30^{\circ },{\theta }_2=30^{\circ },j=1,k=-1$). The relative orientation between the units is FF, and the bite angle is set at 90° (i.e., $l=1,m=1,\delta =90^{\circ }$).

First, calculate $R_{{\mathrm{A}}^2{\mathrm{B}}_1^2}$, $R_{{\mathrm{B}}_1^2{\mathrm{B}}_2^2}$, $R_{{\mathrm{B}}_2^2{\mathrm{C}}^2}$, and $R_{{\mathrm{C}}^1{\mathrm{A}}^2}$ as follows.

$$R_{{\mathrm{A}}^2{\mathrm{B}}_1^2}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos {\theta }_1\hfill & \hfill -j\sin {\theta }_1\hfill \\ \hfill 0\hfill & \hfill j\sin {\theta }_1\hfill & \hfill \cos {\theta }_1\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{3}/2\hfill & \hfill -1/2\hfill \\ \hfill 0\hfill & \hfill 1/2\hfill & \hfill \sqrt{3}/2\hfill \end{array}\right)$$ 20

$$R_{{\mathrm{B}}_1^2{\mathrm{B}}_2^2}=\left(\begin{array}{ccc}\hfill -\cos 120^{\circ }\hfill & \hfill -j\sin 120^{\circ }\hfill & \hfill 0\hfill \\ \hfill j\sin 120^{\circ }\hfill & \hfill -\cos 120^{\circ }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill -\sqrt{3}/2\hfill & \hfill 0\hfill \\ \hfill \sqrt{3}/2\hfill & \hfill 1/2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$ 21

$$R_{{\mathrm{B}}_2^2{\mathrm{C}}^2}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -jk\cos {\theta }_2\hfill & \hfill j\sin {\theta }_2\hfill \\ \hfill 0\hfill & \hfill -j\sin {\theta }_2\hfill & \hfill -jk\cos {\theta }_2\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{3}/2\hfill & \hfill 1/2\hfill \\ \hfill 0\hfill & \hfill -1/2\hfill & \hfill \sqrt{3}/2\hfill \end{array}\right)$$ 22

$$R_{{\mathrm{C}}^1{\mathrm{A}}^2}=\left(\begin{array}{ccc}\hfill -\cos \delta \hfill & \hfill 0\hfill & \hfill -m\sin \delta \hfill \\ \hfill 0\hfill & \hfill lm\hfill & \hfill 0\hfill \\ \hfill l\sin \delta \hfill & \hfill 0\hfill & \hfill -lm\cos \delta \hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$$ 23

Next, calculate the components of the vector $\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}$ as viewed from the local coordinate system ${\mathrm{A}}^2$, denoted as ${\genfrac{}{}{0ex}{}{{\mathrm{A}}^2}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}$:

$${\genfrac{}{}{0ex}{}{{\mathrm{A}}^2}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}={\left(1,0,0\right)}^{\mathrm{T}}+R_{{\mathrm{A}}^2{\mathrm{B}}_1^2}{R}_{{\mathrm{B}}_1^2{\mathrm{B}}_2^2}{\left(1,0,0\right)}^{\mathrm{T}}=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)+\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{3}/2\hfill & \hfill -1/2\hfill \\ \hfill 0\hfill & \hfill 1/2\hfill & \hfill \sqrt{3}/2\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill -\sqrt{3}/2\hfill & \hfill 0\hfill \\ \hfill \sqrt{3}/2\hfill & \hfill 1/2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 3/2\hfill \\ \hfill 3/4\hfill \\ \hfill \sqrt{3}/4\hfill \end{array}\right)~\left(\begin{array}{c}\hfill 1.5\hfill \\ \hfill 0.75\hfill \\ \hfill 0.43\hfill \end{array}\right)$$ 24

Subsequently, the coordinates of the vector $\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}$ as seen from the global coordinate system (i.e., the local coordinate system ${\mathrm{A}}^1$) can be computed as follows.

$${\genfrac{}{}{0ex}{}{\mathrm{global}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}={\genfrac{}{}{0ex}{}{{\mathrm{A}}^1}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}=R_{{\mathrm{A}}^1{\mathrm{C}}^1}{R}_{{\mathrm{C}}^1{\mathrm{A}}^2}{\genfrac{}{}{0ex}{}{{\mathrm{A}}^2}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}=\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill 3/4\hfill & \hfill -\sqrt{3}/4\hfill \\ \hfill 3/4\hfill & \hfill -1/8\hfill & \hfill 3\sqrt{3}/8\hfill \\ \hfill \sqrt{3}/4\hfill & \hfill -3\sqrt{3}/8\hfill & \hfill -5/8\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill 3/2\hfill \\ \hfill 3/4\hfill \\ \hfill \sqrt{3}/4\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 1/2\hfill & \hfill 3/4\hfill & \hfill -\sqrt{3}/4\hfill \\ \hfill 3/4\hfill & \hfill -1/8\hfill & \hfill 3\sqrt{3}/8\hfill \\ \hfill \sqrt{3}/4\hfill & \hfill -3\sqrt{3}/8\hfill & \hfill -5/8\hfill \end{array}\right)\left(\begin{array}{c}\hfill -\sqrt{3}/4\hfill \\ \hfill 3/4\hfill \\ \hfill 3/2\hfill \end{array}\right)~\left(\begin{array}{c}\hfill -0.30\hfill \\ \hfill 0.56\hfill \\ \hfill -1.6\hfill \end{array}\right)$$ 25

Therefore, the components of the position vector of point ${\mathrm{C}}^2$ as viewed from the global coordinate system (i.e., the local coordinate system ${\mathrm{A}}^1$) are given by the following:

$${\genfrac{}{}{0ex}{}{\mathrm{global}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^2}}={\genfrac{}{}{0ex}{}{\mathrm{global}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^1{\mathrm{C}}^1}}+{\genfrac{}{}{0ex}{}{\mathrm{global}}{}\mathbf{x}}_{\overrightarrow{{\mathrm{A}}^2{\mathrm{C}}^2}}~\left(\begin{array}{c}\hfill 1.5\hfill \\ \hfill 0.75\hfill \\ \hfill 0.43\hfill \end{array}\right)+\left(\begin{array}{c}\hfill -0.30\hfill \\ \hfill 0.56\hfill \\ \hfill -1.6\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 1.2\hfill \\ \hfill 1.3\hfill \\ \hfill -1.2\hfill \end{array}\right)$$ 26

Therefore, the distance between the endpoints of the chain (tilt angle = 30°, bite angle = 90°, conformation id = RR(FF)RL is found to be

$$\overrightarrow{∣{\mathrm{A}}^1{\mathrm{C}}^2∣}~\sqrt{{1.2}^2+{1.3}^2+{\left(-1.2\right)}^2}=2.1.$$ 27

Author contributions

S.H. conceived the project. T.A. performed all experiments. T.A., M.H., and H.S. performed DFT calculations. T.A. and K.T. performed geometric analyses. K.T. created a program to calculate RSU and strain analyses. S.H., T.A., and K.T. prepared the manuscript and the Supplementary Information, and all authors discussed the results and commented on the manuscript.

Peer review

Peer review information

Nature Communications thanks Javier Marti-Rujas and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The authors declare that all data supporting the findings of this study are available within the paper and its supplementary information files. Crystallographic data for the structures reported in this Article have been deposited at the Cambridge Crystallographic Data Centre (CCDC), under deposition numbers 2313022 (for the [Pd₁₂2₈]²⁴⁺ open icosahedron) and 2313023 (for the [Pd₂3₂]⁴⁺ ring). Copies of the data can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/. Calculated cartesian coordinates in this study are provided as Supplementary Data 1. All additional data were available from the corresponding author.

Code availability

All original code (RSU project) in this study has been deposited in Zenodo at the following: 10.5281/zenodo.10677305⁷⁶ The data were available under the MIT license and is publicly accessible as of the date of publication.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-50972-z.