High-performance hydrogen evolution reaction in quadratic nodal line semimetal Na₂CdSn

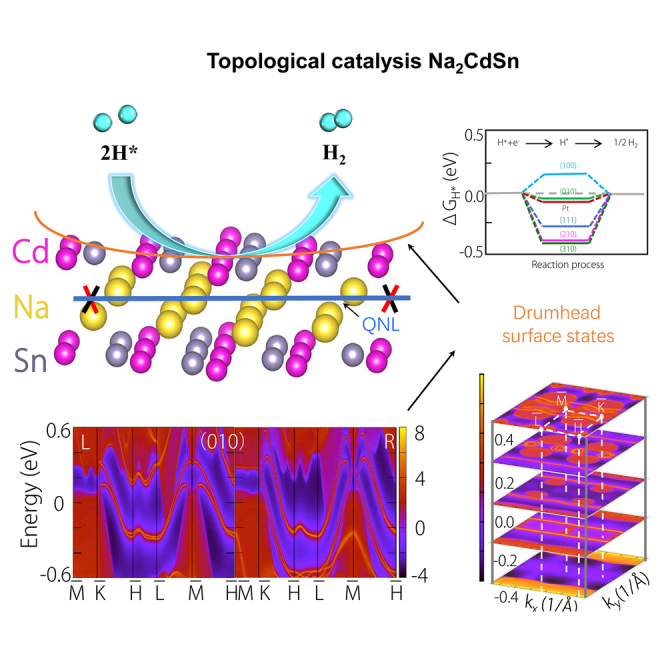
Summary

Topological nodal line semimetals (TNLSMs), which exhibit one-dimensional (1D) band crossing in their electronic band structure, have been predicted to be potential catalysts in electrocatalytic processes. However, the current studies are limited to the TNLSMs where the dispersion around the nodal line is linear in all directions. Here, the potential application of the quadratic nodal line (QNL) semimetal Na₂CdSn in hydrogen evolution reaction is explored. Based on the bulk-boundary correspondence, we find that the topological surface states (TSSs) of the QNL are extended in the entire Brillouin zone. A linear relationship between the density of states of the TSSs and the Gibbs free energy is established in Na₂CdSn. Remarkably, the best performance of Na₂CdSn can be comparable to that of the noble metal Pt. Therefore, our work not only identifies an innovative type of topological catalyst with a QNL state but also confirms the relationship between TSSs and catalytic performance.

Graphical abstract

Highlights

• •An ideal quadratic nodal line semimetal Na₂CdSn is theoretically predicted
• •Na₂CdSn exhibits a higher theoretical hydrogen evolution activity than Pt
• •The surface states cause a high surface DOS, which significantly reduces the ΔG_H
• •A linear relationship between ΔG_H and surface states is established

Physics; Quantum physics

Introduction

Topological materials, distinguished by nontrivial topological surface states (TSSs), have recently garnered significant research attention.^1,2,3 These TSSs form a frontier in current topological materials research, serving as stable electron sources for chemical reactions.^4,5,6 Importantly, the topological protection afforded by TSSs imparts high resilience to materials against surface contamination, defects, and morphological changes.^7,8,9,10,11 Hence, topological materials are predicted to be promising catalysts in electrochemical reductions, including CO₂¹² and N₂¹³ reduction, hydrogen evolution reaction (HER),^{14,15,16,17,18,19,20,21,22,23,24} and oxygen evolution reaction.^25,26,27 Notably, topological catalysts offer advantages beyond electron source stability. Their catalytic performance correlates strongly with TSSs,¹⁸ determined by the crystalline symmetry of materials rather than noble metals.^28,29,30 This feature suggests potential cost-effective alternatives. Additionally, the inherent topological nature imparts robustness to these catalysts, ensuring performance in challenging environments. So far, while several topological materials have shown potential as catalysts, the ongoing search for topological catalysts remains a pressing task. This urgency arises from the diverse classifications within the realm of topology, presenting an expansive landscape that necessitates continued exploration to identify and understand the catalytic potential of various topological materials.

The determination of TSSs types is governed by the bulk topology of materials. For instance, Weyl/Dirac semimetals, characterized by zero-dimensional (0D) band crossings in their bulk band structures, exhibit one-dimensional (1D) surface states known as Fermi arcs.^{31,32,33,34,35} Nodal line semimetals, featuring 1D band crossings, showcase 2D surface states named drumhead surface states, constrained by the projection of the nodal line.^{36,37,38,39,40,41} Additionally, the nature of TSSs is intricately linked to the dispersion around band crossings. For instance, double/triple Weyl semimetals, with quadratic/cubic dispersion in-plane, manifest two/three Fermi arcs.^{42,43,44,45,46} In the case of nodal line semimetals, besides the linear dispersion, Yu et al. have demonstrated the existence of high-order nodal lines with high-order dispersions such as quadratic and cubic dispersion, as shown in Figure S1 in supporting information. Distinct from the nodal line with linear dispersion, the higher-order nodal line could have surface states span the entire surface Brillouin zone.^47,48 Consequently, compared to traditional topological semimetals, topological semimetals with high-order dispersion are expected to have higher surface density of states (SDOSs).

So far, several nodal line semimetals have been introduced as catalysts in the HER process. For example, the 2D nodal line metal Cu₂Si has demonstrated a Gibbs free energy as low as 0.195 eV in HER reactions.⁴⁹ Additionally, double Dirac nodal line semimetals, with large topological surface densities of states (DOSs), exhibit Gibbs free energy values comparable to that of Pt, approximately 0.09 eV, positioning them at the top of the volcano plot for catalytic activity.⁵⁰ However, while these nodal lines exhibit linear dispersion around the line, the catalytic performance of nodal lines with quadratic dispersion has not yet been investigated.

Most recently, Zhang et al. have established that TSSs serve as a universal descriptor for predicting the catalytic performance of topological materials.¹⁸ Specifically, they identified a linear relationship between the SDOSs of topological materials and the Gibbs free energy—a crucial factor assessing catalytic ability. This conclusion has been validated not only in topological semimetals with 0D⁵¹ and 1D⁵² band crossings but also in nodal chain semimetals characterized by nodal loops forming a chain.⁵³ Notably, there is a lack of results related to topological semimetals with high-order dispersion. Nevertheless, the exploration of the catalytic performance of innovative topological semimetals not only underscores the significance of TSSs but also unveils promising candidates for catalyzing electrochemical reductions.

In this work, we propose Na₂CdSn, a nodal line semimetal exhibiting quadratic dispersion along its nodal line, as a promising catalyst for the HER. The quadratic dispersion characteristic enables its TSSs to extend across the entire Brillouin zone, creating a substantial energy window around the Fermi level. Our investigation reveals that these TSSs exhibit different projected areas on various surfaces, and a notable linear relationship is established between the Gibbs free energy and the TSS area. Particularly, the (010) surface, characterized by the largest TSS area, exhibits a lower Gibbs free energy compared to other surfaces, even outperforming the classical Pt catalyst, signifying superior catalytic performance. Furthermore, the considerable energy window around the Fermi level enables the persistent catalytic ability of Na₂CdSn upon electron doping across a broad region. On the other hand, when the TSSs extend completely beyond the Fermi level, the catalytic performance of Na₂CdSn drops. Moreover, as the topological nature of Na₂CdSn is intrinsically tied to its crystalline symmetry, any disruption of this symmetry leads to a sharp decline in catalytic performance by suppressing TSSs. This work not only identifies an innovative nodal line semimetal with quadratic dispersion but also anticipates its promising role in the HER process, thereby expanding the potential applications of topological materials.

Results

Topological features of Na₂CdSn

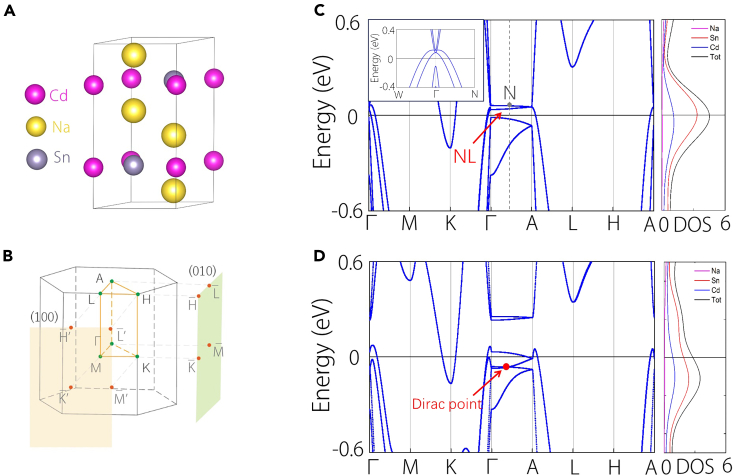
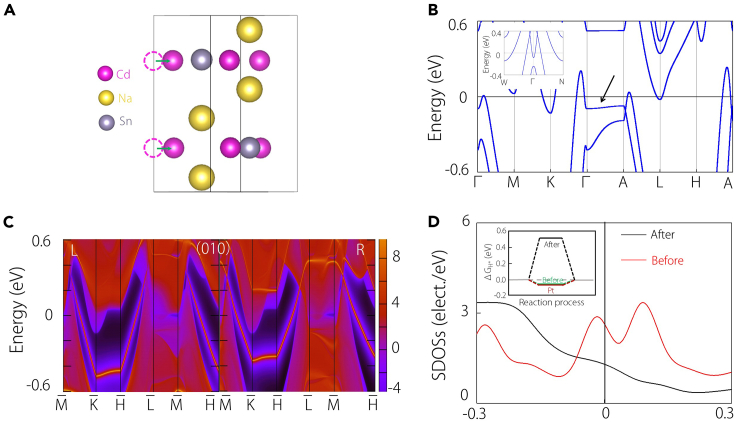
The existing material Na₂CdSn features a hexagonal structure with space group P63/mmc (No. 194) (Figure 1A). Na₂CdSn has been synthesized in the experiment.⁵⁴ The optimized parameters are given as a = b = 5.08 Å and c = 10.16 Å. In this configuration, Cd and Sn atoms occupy the same plane, forming a honeycomb lattice layer, and subsequently, an ABAB-stacking along the c-axis. The interlayer separation along the c-axis measures 5.05 Å, with an atomic distance of 2.91 Å between Cd and Sn. Two Na atoms are positioned both above and below the center of the Cd and Sn hexagonal ring. This arrangement resembles the distribution of C atoms in hexagonal diamonds, with Na atoms across the honeycomb layer at a distance of 3.329 Å. In addition, its Brillouin zone with high-symmetry points labeled is shown in Figure 1B.

Figure 1.

Crystal structure and electronic structures

(A) Crystal structure for Na₂CdSn.

(B) Brillouin zone (BZ) of Na₂CdSn and the corresponding surface projection along the (100) and (010) directions.

(C and D) Electronic band structures for Na₂CdSn without/with considering SOC, alongside with the corresponding density of states (DOS). The inset in (C) shows the dispersion relationship of nodal line along Γ-A path.

The band structure without spin-orbital coupling (SOC) obtained from density functional theory calculations is presented in Figure 1C, accompanied by the corresponding DOS analysis. The DOS clearly indicates that the system exhibits metallic behavior, with the low-energy states near the Fermi level primarily originating from the Sn and Cd atoms. Examining the band structure reveals the presence of nodal lines along the Γ-A path near the Fermi level. Notably, the dispersion transverse to the nodal line is observed to be quadratic, rather than linear. To corroborate this observation, a zoomed-in representation of the band structure normal to the nodal line is illustrated in the inset figure of Figure 1C, demonstrating a quadratic dispersion for any arbitrary point on the Γ-A path.

From a symmetric perspective, the origin of the quadratic nodal line (QNL) lies in its symmetry protection. Specifically, any k-point (denoted as P) on the Γ-A path exhibits invariance under the C_6v point group generated by C_6z and M_z. In addition, the nonmagnetic ground state permits the existence of time-reversal symmetry (T), with the point P remaining invariant under the combined operation TM_z. Along this path, [C_6z, H(P)] = 0, allowing the band eigenstates to be chosen as C_6z eigenstates. Considering a basis state corresponding to the Γ5 representation of the point group, the symmetry operations at P point under this basis can be expressed as

$$C_{6z}=-\frac{1}{2}{\sigma }_0+i\frac{\sqrt{3}}{2}{\sigma }_z,\mathcal{T}{M}_z={\sigma }_x\mathcal{K}\text{,}$$

where $\mathcal{K}$ stands for the complex conjugation and ${\sigma }_i\left(i=x,y,z\right)$ is the Pauli matrix. The effective Hamiltonian is required to be invariant under these operations, namely,

$$C_{6z}H\left(\mathit{k}\right)C_{6z}^{-1}=H\left(R_{6z}\mathit{k}\right),\left(\mathcal{T}{M}_z\right)H\left(\mathit{k}\right){\left(\mathcal{T}{M}_z\right)}^{-1}=H\left(-\mathit{k}\right)\text{.}$$

To be noted, we consider the dispersion around the nodal line, such as k is in plane ($k_z=0$). Consequently, the effective Hamiltonian takes the following form:

$$H\left(\mathit{k}\right)=\left(c_0+c{k}_{\parallel }^2\right)+\alpha k_{+}^2{\sigma }_{+}+h.c.,$$

where $\alpha$ is a complex parameter and $k_{\parallel }=\sqrt{k_x^2+k_y^2}$, $k_{\pm }=k_x\pm i{k}_y$, and ${\sigma }_{\pm }={\sigma }_x\pm i{\sigma }_y$. Thus, we conclude that the doubly degenerate line along Γ-A path is a QNL.

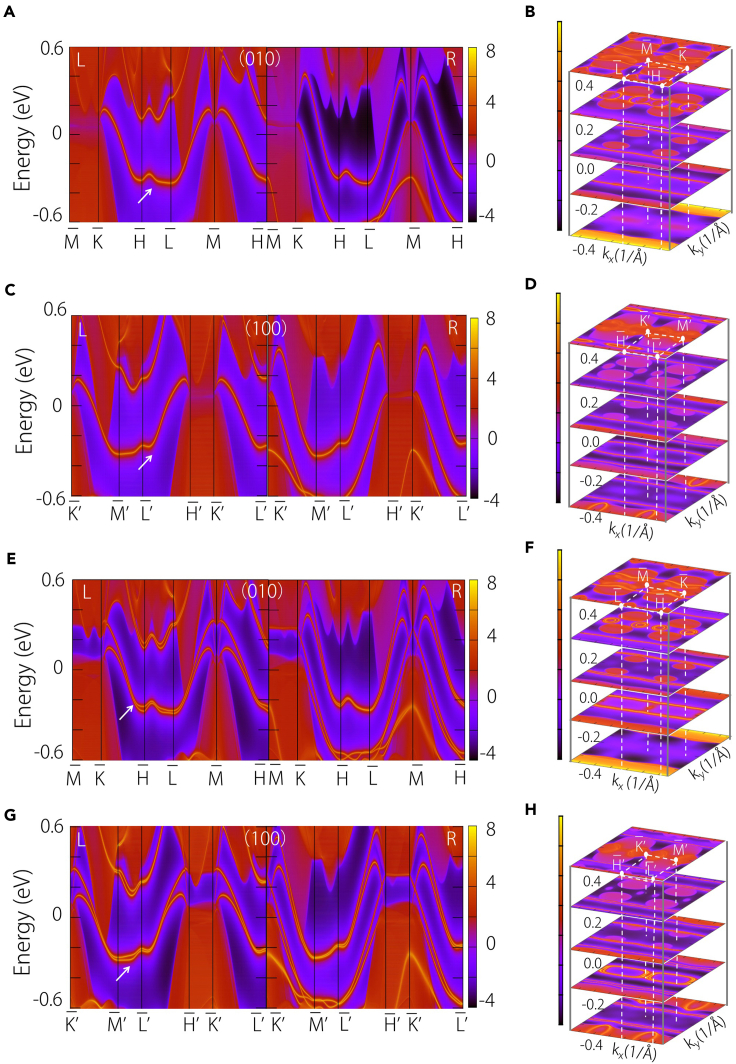
It has been demonstrated that materials featuring conventional linear nodal lines exhibit “drumhead” surface states, where the surface states are confined within the projection of the nodal line. In contrast, the QNL presents a distinct surface state, as highlighted in the study by Yu et al. and Zhang et al.,^47,48 where the surface state can extend across the entire surface Brillouin zone. From a topological perspective, this nontrivial surface state results from a nontrivial Zak phase. In our study, we confirmed that the QNL serves as a transition point where the Zak phase changes sign, leading to surface states spanning the vertical surface Brillouin zone. This confirmation is illustrated in the surface spectra presented in Figures 2A and 2C. Notably, these surface states penetrate the Fermi level, creating a sizable energy window, as indicated in Figures 2B and 2D.

Figure 2.

Topological surface states and energy slices

(A, C, E, and G) Projected spectrum on the (010) and (100) surfaces without/with SOC in Na₂CdSn, where the arrows represent the drumhead and Fermi arc surface states of the quadratic nodal line and Dirac point.

(B, D, F, and H) The slices under different energy values (−0.4 to 0.4 eV).

Upon the inclusion of spin-orbit coupling, the QNL transforms into a quadratic Dirac point, and the number of surface states doubles, as depicted in Figures 1D and 2E–2G. Remarkably, the surface states continue to span the entire surface Brillouin zone. Importantly, the substantial energy window persists, as demonstrated in Figures 2F and 2H.

Considering the significant impact of surface states on the catalytic performance of topological materials, especially in catalytic activity, one may contemplate the influence of surface states spanning the entire surface Brillouin zone on catalytic performance. In the following discussion, we shall discuss the catalytic performance of Na₂CdSn.

Catalytic performance of Na₂CdSn and relationship to its topology

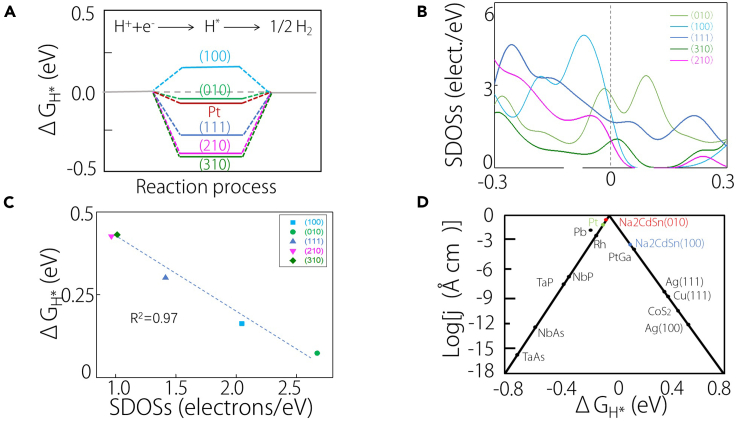
A critical parameter for assessing the catalytic performance in the HER process is the Gibbs free energy value (ΔG_H∗). As the absolute value of ΔG_H∗ approaches zero, the catalyst’s performance improves. For example, the classical catalyst Pt has a ΔG_H∗ value of about 0.09 eV.⁵⁵ With the extension of surface states throughout the vertical surface Brillouin zone, these two surfaces are anticipated to exhibit a lower ΔG_H∗ compared to other surfaces. To validate this expectation, we calculated ΔG_H∗ in Figure 3A, revealing that the ΔG_H∗ of (010) is even smaller than that of Pt, and the ΔG_H∗ of (100) is comparable to it. In stark contrast, other surfaces display higher ΔG_H∗ values. The study by Zhang et al. has illuminated the pivotal role of SDOSs in influencing the catalytic performance of topological materials.¹⁸ Their findings suggest that superior catalytic performance correlates with a higher SDOS. In alignment with this, our calculations of the SDOSs, as depicted in Figure 3B, confirm this conclusion. Notably, the (010) and (100) surfaces indeed exhibit a higher SDOS, emphasizing their potential for enhanced catalytic performance.

Figure 3.

HER performance of different surfaces

(A) Gibbs free energy of (100), (010), (111), (210), and (310) surfaces for Na₂CdSn and metal Pt.

(B) Surface DOS values of (100), (010), (111), (210), and (310) surfaces for Na₂CdSn.

(C) Linear relationship between surface DOS values and Gibbs free energy of (100), (010), (111), (210), and (310) surfaces.

(D) Volcano map of Na₂CdSn, pure metals (Pt, Pb, Ag, and Cu) and some other topological materials (TaAs family, PtGa, and CoS₂).

Additionally, our exploration reveals a linear relationship between the SDOS and the ΔG_H∗ value, as illustrated in Figure 3C. This outcome serves to validate the notion that an elevated SDOS is conducive to an enhanced catalytic performance in topological materials. Remarkably, the catalytic performance of the Na₂CdSn (010) surface, as depicted in the volcano trend, even surpasses that of Pt. Similarly, the catalytic performance of the (100) surface demonstrates notable efficacy, outperforming numerous other catalysts, as illustrated in Figure 3D. In the volcano diagram, we can see that the performance of Na₂CdSn not only outperforms that of the classical precious metal catalyst Pt but also shows significant advantages over other topological materials, such as CoS₂, which features both Weyl points and nodal lines,⁵⁶ and the classical Weyl semimetallic catalyst PtGa.⁵⁷ The unique topological feature of Na₂CdSn gives it a higher hydrogen evolution efficiency than most topological catalysts. Additionally, Na₂CdSn does not contain any precious components, which will greatly reduce catalytic costs.

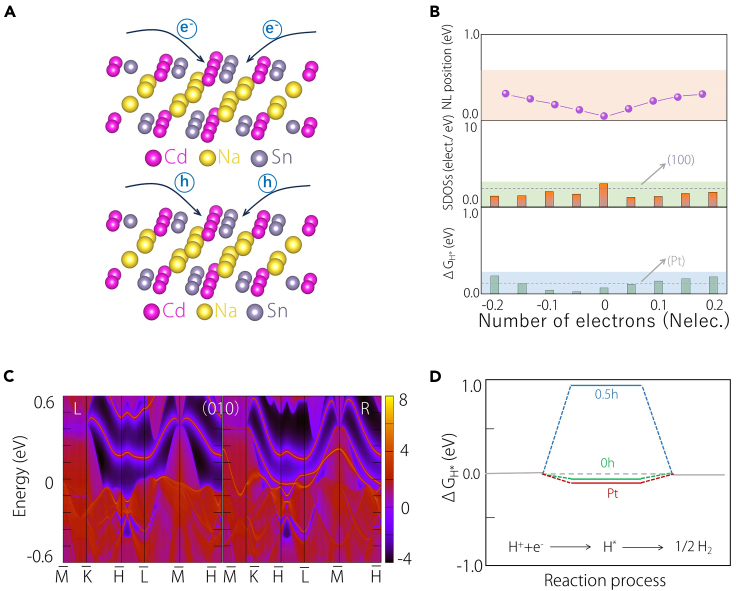
Preserving the crystalline symmetry of Na₂CdSn is crucial for maintaining its topological phases. When doping electrons or holes, the crystalline symmetry persists, but its electronic band structure shifts around the Fermi level. For clarity, the energy position of the QNL at an arbitrary point (N) undergoes variations with lightly doping electrons/holes (Figures 4A and 4B). Simultaneously, the SDOS, represented by ΔG_H∗ on the (010) surface, fluctuates during doping (Figure 4B). Despite these fluctuations, the SDOS remains comparable to that of (100), ensuring the persistence of catalytic performance. Importantly, the ΔG_H∗ values throughout the doping process remain competitive with Pt (Figure 4B). The value of ΔG_H∗ remains stable within 0.1 eV, suggesting a good catalytic performance. However, when TSSs are lifted above the Fermi level, the catalytic performance undergoes a dramatic decrease. To illustrate this, we intentionally shift the TSS above the Fermi level through heavy hole doping (Figures S2–S4). As depicted in Figure 4C, with the introduction of 0.5 holes, the TSS is entirely elevated, particularly along the left boundary where it extends above the Fermi level. Consequently, ΔG_H∗ undergoes a substantial increase, rising from 0.074 to 0.89 eV, as shown in Figure 4D. Thus, the energy window also plays a crucial role in determining the catalytic performance.

Figure 4.

Tuning the QNL and HER performance by electrons and holes doping

(A) Schematic diagram of electrons/holes doping into Na₂CdSn lattice.

(B) Changes of QNL positions, surface DOS values, and Gibbs free energy, when electrons and holes are doped into Na₂CdSn lattice.

(C) Projection spectrum on the (010) surface of Na₂CdSn doped with 0.5 hole.

(D) Gibbs free energy of Na₂CdSn by doping 0 and 0.5 holes.

On the contrary, when TSSs are disrupted, it is anticipated that the catalytic performance will degrade. In the Na₂CdSn lattice, all of Cd atoms are located at the hinges of lattices; we move Cd1 and Cd2 atoms (Figure 5A) from (0, 0, 0.75) to (0.11, 0.06, 0.75), then the 3-fold rotation symmetry is broken. Consequently, the QNL on Γ-A is destroyed, as shown in Figure 5B. Simultaneously, the TSS is suppressed. The TSS calculation on the (010) surface, presented in Figure 5C, illustrates a significant reduction in the SDOS compared to the original state (Figure 5D). Consequently, its ΔG_H∗ is lifted from 0.074 to 0.58 eV, shown in the inset of Figure 5D, and the catalytic performance diminishes compared to the pre-symmetry-breaking condition. This result is line with our assumption that the topology signature, TSS, plays a significant role in determining the catalytic performance of topological catalysts.

Figure 5.

Tuning the QNL and HER performance by moving atoms

(A) Schematic diagram by moving Cd atoms in Na₂CdSn.

(B) Electronic band structure after moving Cd atoms. The inset shows the dispersion relationship by breaking QNL.

(C) Projected spectrum on the (010) surface by breaking QNL.

(D) Changes of surface DOS values before and after breaking QNL. The inset shows the change of Gibbs free energy before and after breaking QNL.

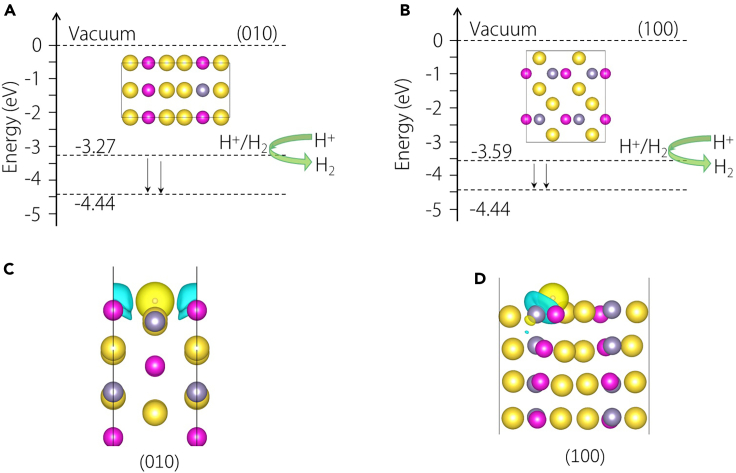
Beyond the TSS and its associated energy window, the matching of energy levels also significantly influences the HER activity. Figure 6A illustrates the energy difference between the Fermi level (−3.27 eV) corresponding to the vacuum and the standard redox potential (−4.44 eV) of the HER for the Na₂CdSn (010) surface, which is −1.17 eV. In contrast, such an energy difference on the (100) surface is −0.85 eV, as shown in Figure 6B. A lower overpotential is advantageous for driving the exchange of electrons at the catalyst-electrolyte interface. Examining the charge differential density of Na₂CdSn in the HER reaction, as depicted in Figures 6C and 6D, reveals that Cd/Sn atoms are involved in transferring electrons to H atoms on the (010)/(100) surfaces. This electron transfer is a crucial aspect of the HER reaction.

Figure 6.

Overpotential and charge density difference

(A and B) The overpotential on the (010) and (100) surfaces, respectively.

(C and D) Charge density difference on the (010) and (100) surfaces, respectively.

We have unveiled that the catalytic performance of Na₂CdSn is dependent on its topology. For traditional transition metal catalysts, such as Pt, the catalytic performance is characterized by the d-band center theory,⁵⁸ making the catalytic ability strongly dependent on the elemental composition. In comparison, from a topological perspective, the catalytic properties of topological materials are strongly associated with the TSSs, which are determined by their crystalline symmetry rather than the specific elements constituting the material. For concreteness, the presence of C_6z and TM_z symmetries in Na₂CdSn results in the formation of a QNL in its bulk electronic band structure. This unique band structure leads to TSSs that span the entire Brillouin zone. Such TSSs not only provide a high SDOS but also offer stable and highly mobile channels for electron transfer. This significantly influences the adsorption and desorption processes in catalytic reactions. These characteristics suggest that topological materials may exhibit excellent catalytic performance.

Discussion

In our study, we conducted a comprehensive investigation into the catalytic performance of Na₂CdSn materials and explored the relationship between its topological properties and catalytic activity. We discovered that Na₂CdSn stands out as an excellent topological catalyst. Its remarkable catalytic performance can be attributed to its unique topology, specifically the presence of QNL, leading to a surface state that traverses the entire surface Brillouin zone. This surface state significantly affects the SDOS, which is a key factor determining the catalytic performance of Na₂CdSn. A more extended surface state correlates strongly with a higher surface state density, ultimately resulting in an extremely low Gibbs free energy of Na₂CdSn. Moreover, the surface states penetrate the Fermi level, creating a broad energy window around it, which also has a substantial impact on the catalytic performance of Na₂CdSn. Conversely, disrupting the surface states or shifting them above the Fermi level suppresses catalytic activity of Na₂CdSn. In addition, we identified three other material candidates with QNL in their electronic band structures, showcasing lower Gibbs free energies comparable to that of Pt but without the need for noble metals (Table 1; Figure S5). Therefore, our work establishes a foundation for further research on the application of QNL materials in the HER, aiming to develop high-performance HER catalysts without relying on precious metals.

Table 1.

The lattice parameters, Gibbs free energy, potential, and experimental synthesis of some QNL materials

Material	Lattice parameters (Å)	|ΔGH∗| (eV)	Potential (eV)	Experiment
Na2CdSn	a = b = 5.08, c = 10.16	0.074	−3.27	Yes
Na2MgPb	a = b = 5.15, c = 10.20	0.166	−3.18	Yes
KHgAs	a = b = 4.62, c = 10.25	0.12	−3.12	Yes
K2NaAs	a = b = 5.38, c = 10.66	0.159	−1.75	No

Limitations of the study

Sodium and tin, integral components of Na₂CdSn, are highly reactive and prone to oxidation. To address this issue, we can implement surface passivation techniques to protect the material from oxidation. This may involve depositing a thin layer of inert material or a protective oxide layer on the surface of Na₂CdSn to prevent direct exposure to air or reactive species. Alternatively, surface functionalization techniques can be employed to modify the surface chemistry of Na₂CdSn, enhancing its resistance to oxidation. This might include grafting functional groups or ligands onto the surface to passivate reactive sites and improve stability. Although these techniques may be complicated compared with traditional catalysts, studying about topological catalysts featuring QNL paves the way for developing such catalysts.

Resource availability

Lead contact

Further information and requests for resources should be directed to the lead contact, Ying Liu (ying_liu@hebut.edu.cn).

Materials availability

This study did not generate new unique reagents.

Data and code availability

This article includes all datasets/code generated or analyzed during this study.

Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (no. 12374039), the Natural Science Foundation of Hebei Province (no. A2024205006) 2024 Research Projects of Higher Education Institutions in Hebei Province (no. JZX2024023), the State Key Laboratory of Reliability and Intelligence of Electrical Equipment of Hebei University of Technology (no. EERI_OY2021006), and S&T Program of Hebei (225676163GH).

Author contributions

Conceptualization, Y.L. and W.M.; methodology, X.Z., X.D., and G.L.; investigation, Z.L., Z.H., and L.W.; writing – original draft, Z.L.; writing – review and editing, W.M. and Y.L.; funding acquisition, Y.L., X.Z., and W.M.; supervision, G.L. and X.Z.

Declaration of interests

The authors declare no competing interests.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Vienna ab initio simulation package	Kresse et al.59	https://www.vasp.at/
Wanniertools	Wu et al.60	https://www.wanniertools.org/

Method details

In our study, we performed first-principles calculations utilizing the density functional theory (DFT)⁶¹ and employed the projector augmented wave (PAW) method, which is implemented in the Vienna ab initio simulation package (VASP).⁵⁹ For the exchange-correlation functional, we opted for the generalized gradient approximation (GGA) and utilized the Perdew-Burke-Ernzerhof (PBE)⁶² parameterization. To eliminate any potential interactions between periodic images, we introduced a vacuum space with a thickness of 20 Å. The cutoff energy for the plane-wave basis was set at 400 eV. We conducted a thorough optimization of both the lattice parameters and ionic positions until the residual force acting on each atom reached values lower than 0.01 eV/Å. Additionally, our convergence criterion for energy calculations was established at 10⁻⁶ eV, ensuring precise and reliable results. From the maximally localized Wannier func tions^63,64 and the WannierTools package,⁶⁰ the topological features of the topological surface states for the Na₂CdSn were calculated.

In the HER reaction, HER can be summarized into the following three steps. The first step is the Volmer reaction, in which electrons transfer to protons and form H atoms adsorbed on the catalyst surface, described as:

$$H^{+}+e^{-}+\ast \to H^{\ast }$$

Among them, $\ast$ and $H^{\ast }$ represent the catalyst and the catalyst adsorbed with $H^{+}$, respectively. Then, H₂ desorption can be achieved through Tafel reaction or Heyrovsky reaction, which can be described as follows:

$$2H^{\ast }\to H_2+2\ast$$

$$H^{+}+e^{-}+H^{\ast }\to H_2+\ast$$

Among them, $H^{\ast }$ still serves as an intermediate. Therefore, the HER rate is highly correlated with the binding conditions between intermediates and active sites. Therefore, hydrogen adsorption $\Delta G_{H\ast }$ is a key parameter for characterizing HER activity. parameter $\Delta G_{H\ast }$ can be obtained using this formula⁶⁵:

$$\Delta G_{H\ast }=\Delta E_H+\Delta E_{ZPE}-T\Delta S_H$$

Among $\Delta E_H$ is the adsorption energy of H, $\Delta E_{ZPE}$ and $\Delta S_H$ represents the zero point energy and entropy changes between the absorbed H and the gas H.

For the H adsorption process, this article investigates it by cutting 3D Na₂CdSn into a 2D slab model and then adsorbing one H atom on different sites of the slab model. We tested slab models of various sizes of Na₂CdSn and the results showed that when using 1 × 1 × 6 model and Use of 1 × 1 × 8 model, its $\Delta G_{H\ast }$ The value of has hardly changed. In addition, we also considered the catalytic performance of different surfaces, including the (100) and (010) surfaces, and fully considered the stability of different sites on each surface, and found the most stable adsorption site for our subsequent research work.

All calculations for adsorption kinetics and surface DOS studies were repeated three times. Use the determination coefficient (R²) to determine the relationship between Gibbs free energy and surface DOS. All other calculations are repeated three times, and the data is represented as the mean.

Quantification and statistical analysis

All calculations for adsorption kinetics and surface DOS studies were repeated three times. Use the determination coefficient (R²) to determine the relationship between Gibbs free energy and surface DOS. All other calculations are repeated three times, and the data is represented as the mean.

Published: August 12, 2024