Abstract
To solve the problem of a large amount of fly ash accumulation and study the axial compression and bearing capacity prediction of the self-compacting fly ash concrete filled circle steel tube (SCCFST) columns, eight specimens are designed to explore the impact of concrete strength grade, internal structural measures, and additional parameters. The stress, progression of deformation, and failure mode of each specimen are observed during the loading process. The load–displacement curves, load-strain curves, characteristic load and displacement, ductility, and stiffness degradation are analyzed. The findings revealed that shear deformation occurred predominantly in the middle and upper portions of the steel tubes. Enhancing the strength of the concrete or adopting internal structural measures could increase the bearing capacity and ductility of the specimens. The peak load and ductility could be increased by up to 17.6 and 53.6%, respectively. The proposed unified calculation equation for the axial compression bearing capacity of SCCFST columns demonstrates notable reliability and precision. Furthermore, these tests offer valuable references for the engineering application of various forms of SCCFST columns, which are of significant importance in practical engineering.
Keywords: Self-compacting fly ash concrete circle filled steel tube columns, Axial compression performance, Characteristic load, Failure mode, Bearing capacity calculation
Subject terms: Civil engineering, Applied mathematics
Introduction
Self-compacting concrete (SCC) is widely utilized in high-rise and long-span structures due to its excellent characteristics, such as vibration-free construction and high fluidity1–4. The integration of fly ash into SCC, when poured into steel tubes, forms a composite column that effectively combines the benefits of both steel and SCC5. This method eliminates the need for formwork and vibration6, adapting well to the complexities of engineering projects. And the use of fly ash in the engineering projects not only can improve the performance of the SCC, but also can realize the resource utilization of solid waste. It also facilitates the adaptation of the structure to combined loads and environmental factors, thus maintaining high load-bearing capacity over extended periods7–10. Numerous scholars have investigated the performance of concrete-filled steel tubular columns under various conditions. Huang et al.11 focused on the number of tie bars as a research variable, designing 17 concrete-filled steel tubular column samples to examine their ultimate load under repeated axial compression. Han et al.12 analyzed the mechanical properties of these columns under long-term loads, noting an increase in stiffness over time. Azevedo et al.13 conducted axial compression tests on recycled aggregate concrete-filled steel tubular columns, finding that both the slenderness ratio and the size of the constraint effect significantly influence the cross-sectional response. Hui et al.14 examined the impact of corrosion degree on the load bearing capacity of recycled concrete filled steel tube (CFST) columns. Cao et al.15 studied these columns under cyclic axial compression, observing failure modes similar to those under monotonic loads. Yu et al.16 conducted experiments on 28 high-strength SCCFST columns, discovering shear failure in circular short columns. Ahmed et al.17 performed numerical simulations of the axial compression of SCCFST columns with varying parameters, concluding that the compressive strength of the concrete and the yield stress of the steel tube significantly affect the axial compression performance of the columns. Wang et al.18–22 studied the axial and eccentric compressive behaviors of SCC filled thin-walled steel tube columns and the ultimate capacity prediction. Furthermore, various scholars23–25 have, through extensive experimental research, that the strength predictions for standard concrete-filled steel tubular columns also apply to SCCFST columns.
Self-compacting concrete and self-compacting concrete filled steel tube have been fully studied and there are many engineering applications. But the study of resource utilization of bulk solid waste, especially fly ash has not been studied deep enough. In order to solve the problem of resource utilization of fly ash, this study tests eight SCCFST columns under axial compression, varying parameters such as the strength grade of the concrete and the internal structure. Observations are made of the structural behavior and failure mode of each specimen. Parameters such as the load–displacement curve, the load-strain curve, and the stiffness degradation curve are obtained. The impact of each variable on the axial bearing capacity, stiffness, and ductility of the columns is analyzed. Based on this research, a simplified formula is proposed to calculate the axial bearing capacity of SCCFST columns, providing valuable information for related projects. These conclusions can promote the engineering application of fly ash self-compacting concrete.
Test overviews
Test materials
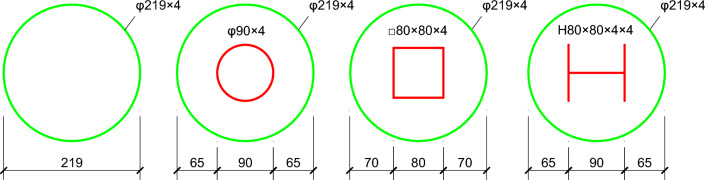
In these tests, all steel pipes are ordinary Q235 steel tubes of the same batch, with a thickness of 4 mm. The mechanical properties of steel include a yield strength of 296 MPa, an ultimate strength of 371 MPa, an elongation of 32.8%, and a yield ratio of 0.799. The nominal diameter (D) of the steel tube is 219 mm, with a nominal wall thickness (T) of 4 mm and a consistent height (L) for each specimen of 700 mm. Internal construction measures include a 90 mm diameter circular steel tube, an 80 × 80 mm square steel pipe, and a 90 × 90 × 4 × 4 mm H beam.
The components of SCC include fly ash, cement, coarse aggregate, fine aggregate, water, and a water reducing agent. The cement used is P.O. 42.5 ordinary Portland cement; the fly ash is grade II; the coarse aggregate is continuously graded gravel with a particle size of 5–20 mm; the fine aggregate is natural river sand with a fineness modulus of 2.3 and a standard sieve of 2.36 mm standard sieve; the water reducer is a high-efficiency polycarboxylate superplasticizer with a 30% water reduction efficiency. The water for the mixture is obtained from laboratory tap water. The composition of each group is detailed in Table 1.
Table 1.
Mix proportion of SCC (unit: kg/m3).
| Type | Water cement ratio | Cement | Fly ash | Coarse aggregate | Fine aggregate | Water | Reducer |
|---|---|---|---|---|---|---|---|
| FA40 | 0.37 | 291.9 | 194.6 | 950 | 809.6 | 180 | 4.87 |
| FA60 | 0.31 | 309.6 | 206.4 | 909 | 774 | 160 | 7.74 |
Specimen design
In this experiment, the concrete strength grade and internal structural measures were considered the primary variables. Eight SCCFST specimens were designed and fabricated. The internal structure is depicted in Fig. 1, and the detailed parameters are outlined in Table 2.
Fig. 1.
Internal structure of specimen (unit: mm).
Table 2.
Design parameters for each specimen.
| Specimens | L × D × t (mm) | Strength grade of concrete | Internal structure form | Total section area (mm2) | Total steel area (mm2) | Steel ratio (%) |
|---|---|---|---|---|---|---|
| FA40-C | 700 × 219 × 4 | C40 | – | 37,668 | 2702 | 7.2 |
| FA40-C–C | 700 × 219 × 4 | C40 | Circular steel tube | 37,668 | 3782 | 10.0 |
| FA40-C-H | 700 × 219 × 4 | C40 | H-shaped steel | 37,668 | 3782 | 10.0 |
| FA40-C-S | 700 × 219 × 4 | C40 | Square steel tube | 37,668 | 3918 | 10.4 |
| FA60-C | 700 × 219 × 4 | C60 | – | 37,668 | 2702 | 7.2 |
| FA60-C–C | 700 × 219 × 4 | C60 | Circular steel tube | 37,668 | 3782 | 10.0 |
| FA60-C-H | 700 × 219 × 4 | C60 | H-shaped steel | 37,668 | 3782 | 10.0 |
| FA60-C-S | 700 × 219 × 4 | C60 | Square steel tube | 37,668 | 3918 | 10.4 |
Loading device and loading scheme
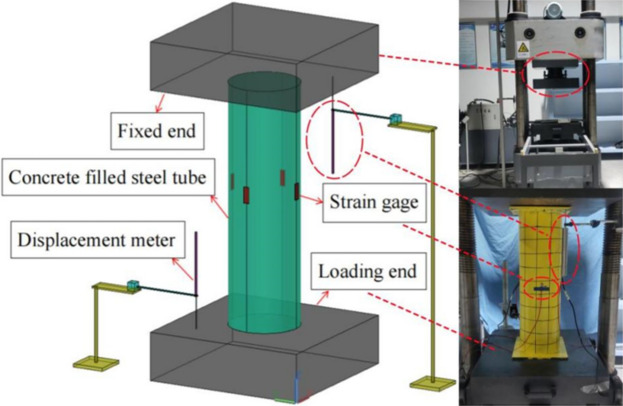
The test was conducted using a 5000 kN electro-hydraulic servo universal testing machine. The loading schematic and loading device is illustrated in Fig. 2.
Fig. 2.
Loading schematic and loading device.
To measure strain, four strain gauges, alternating in vertical and horizontal orientations, were positioned at half the radius of the outer steel pipe at intervals of 90° along the circumferential direction. An additional strain gauge of identical specification was placed for temperature compensation. A displacement meter was arranged at both ends of the specimen to record the displacement changes. The test loading comprised two stages: preloading and formal loading. Initially, preloading involved applying and maintaining 10% of the estimated ultimate load for 1 min. During this period, data acquisition was verified to confirm the normal operation of the equipment before unloading and proceeding to the formal loading stage. Formal loading included a displacement-controlled protocol that employs a continuous loading method at a rate of 0.4 mm/min. When the longitudinal displacement reached 50 mm, the steel pipe welds cracked and the bearing capacity decreased significantly, prompting the cessation of loading and the conclusion of the test.
Test results and analysis
Experimental phenomena
The failure modes of each circular steel tube specimen are depicted in Fig. 3.
Fig. 3.
Destruction mode of the circular steel tube specimen.
It can be seen from Fig. 3 that:
The specimen shear deformation concentrates in the middle and upper portions of the steel tube, manifesting itself as transverse buckling deformation in these regions, accompanied by a noticeable shear failure. Internal structural measures negligibly influence the deformation and failure mode of the SCCFST columns. However, these measures enhance the specimen's load-bearing capacity and stiffness, reduce or prevent multilayer shear failure, and delay specimen deformation to an extent. Increasing the internal concrete strength only increases the load bearing capacity of the specimen.
The failure modes of concrete-filled steel tubular column specimens predominantly display shear failure, including transverse buckling deformation. From the beginning of loading to peak load, the specimens’ transition from elastic to elastic–plastic stages, with negligible deformation during this phase. The intermittent micro-sounds emerge at approximately 70% of the peak load, resulting from internal concrete crushing and fracturing under load. After peak load, vertical displacement continues to escalate. At 15–20 mm displacement, bulging deformation becomes visibly evident on the surface of the specimen, intensifying with further displacement. When the vertical displacement reaches 25–30 mm, the specimen's shear failure mode of the specimen becomes distinctly visible. With an increase in continued displacement, surface buckling and shear deformation become more pronounced. Specimens such as FA40-C and FA60-C, lacking internal structural reinforcement, exhibit lower stiffness. Their internal concrete is more prone to crushing and recombination under load, demonstrating weaker deformation resistance and leading to multilevel shear failure.
Continuous observation and real-time monitoring of the specimen's deformation were conducted. When deformation became visible, the knocking method was used to assess the hollowing of the sample. It was observed that there was minimal hollowing in the deformation process of the circular steel tube column filled with concrete, indicating a strong bond between the concrete and the steel tube. Under load, the concrete broke and refilled the hollow areas, allowing the specimen to maintain a certain bearing capacity even with significant deformation.
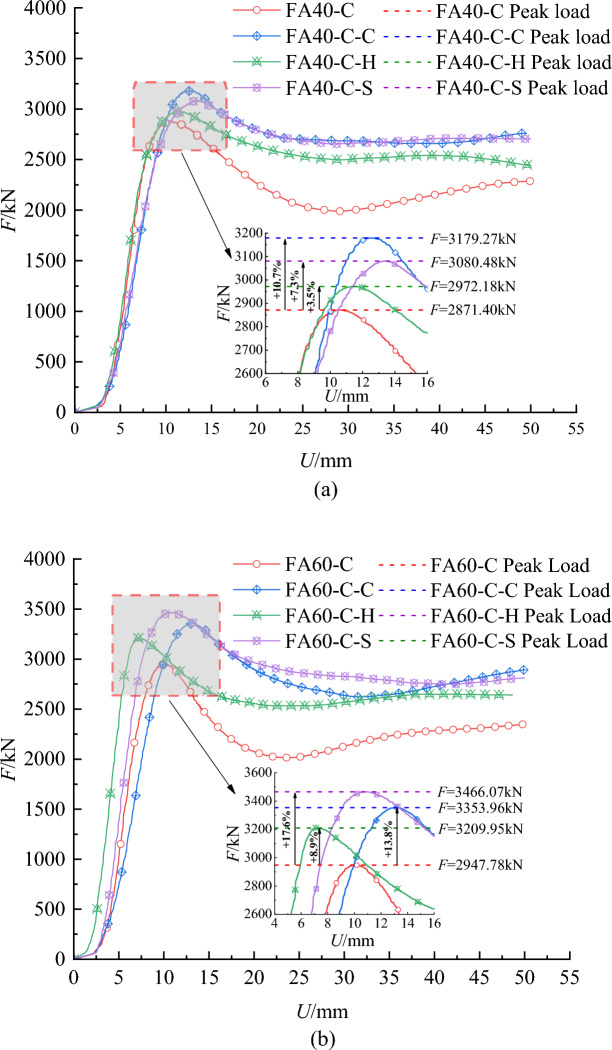
Load–displacement curve
The load–displacement curve for the specimen appears in Fig. 4. In the figure, F denotes the specimen's load, directed vertically upward, with compression being positive; u represents the specimen's vertical displacement, positive in the upward direction.
Fig. 4.
Load–displacement curve of each specimen.
It can be seen from Fig. 4 that:
The load–displacement curves are similar. Before peak load, load and displacement correlate almost linearly, with an inconspicuous yield stage. Post-peak load, the SCCFST column specimens begins to decline variably. After dropping to a specific load, the bulging of the specimen enlarges the stress area, slightly enhancing the load. In general, this has an insignificant impact on the performance of the specimen bearing, and excessive deformation at this stage renders a continuous bearing unsuitable.
Increasing concrete strength and adding internal structural measures moderately affect the load-bearing capacity of the specimen. Comparison with FA40-C, FA40-C-C, FA40-C-H, and FA40-C-S, the peak load of FA60-C, FA60-C-C, FA60-C-H, and FA60-C-S increase by 2.7, 5.5, 8.0 and 12.5%, respectively. Compared to specimens without internal structural measures, those with structural measures exhibit superior bearing performance. Specimens with square and circular steel tube internal structural measures outperform those with H-shaped steel internal structures in bearing performance.
Analysis of characteristic load and ductility
To study the deformation and failure mechanism of SCCFST columns under axial load, characteristic parameters such as yield load, maximum load, maximum load and corresponding displacement of each sample were analyzed. The impact of concrete strength grade, outer steel tube type, and internal structure form was examined. A summary of each characteristic parameter is presented in Table 3. The ultimate load in this test is defined as meeting one of the following conditions: (1) The bearing capacity of the sample decreased to 85% of the maximum load; (2) After reaching the maximum load, the bearing capacity was maintained or slightly increased after the decrease. The minimum load during this phase was selected as the ultimate load; (3) The surface deformation of the specimen was significant, making it unsuitable for future load bearing. The ultimate displacement is the displacement corresponding to the ultimate load under these conditions.
Table 3.
Characteristic load and characteristic displacement.
| Numbers | Yield load (kN) | Yield displacement (mm) | Peak load (kN) | Peak displacement (mm) | Ultimate load (kN) | Ultimate displacement (mm) | Ductility factor |
|---|---|---|---|---|---|---|---|
| FA40-C | 2298.86 | 6.41 | 2871.40 | 9.69 | 2440.85 | 16.41 | 2.56 |
| FA40-C-C | 2542.62 | 9.53 | 3179.27 | 13.17 | 2702.41 | 25.45 | 2.67 |
| FA40-C-H | 2379.59 | 7.24 | 2972.18 | 11.32 | 2526.34 | 25.27 | 3.49 |
| FA40-C-S | 2465.03 | 8.52 | 3080.48 | 13.08 | 2682.75 | 25.01 | 2.93 |
| FA60-C | 2359.76 | 7.29 | 2947.78 | 10.21 | 2505.24 | 14.31 | 1.96 |
| FA60-C-C | 2683.59 | 7.84 | 3353.96 | 11.85 | 2850.59 | 19.83 | 2.53 |
| FA60-C-H | 2565.25 | 6.69 | 3209.95 | 8.71 | 2728.26 | 15.50 | 2.32 |
| FA60-C-S | 2774.62 | 6.86 | 3466.07 | 10.62 | 2946.09 | 20.64 | 3.01 |
By combining the load–displacement curves of each specimen and Table 3, the following conclusions are drawn:
The bearing capacity of each steel tube fly ash SCC specimen is maintained at a high level due to the addition of concrete. When subjected to external loads, the steel tube restraint places the fly ash SCC in a three-dimensional stress state within the steel tube, fully utilizing its high compressive strength. Simultaneously, the concrete filling in the steel tube effectively prevents the buckling failure of the steel tube. The steel tube and the fly ash SCC jointly carry the load, maximizing the advantages of both materials. The addition of reasonable internal structural measures also positively impacts the bearing capacity of the sample.
Structural measures influence the bearing capacity of each specimen, but do not play a decisive role. Taking the FA60-C, FA60-C-C, FA60-C-H and FA60-C-S samples as examples, the maximum loads are 2947.78 kN, 3353.96 kN, 3209.95 kN, and 3466.07 kN, respectively. The peak load of FA60-C-C, FA60-C-H, and FA60-C-S with structural measures is 13.8, 8.9 and 17.6% higher than that of FA60-C without structural measures. Further analysis of each group of specimens reveals that different internal structural measures have varying effects on improving the bearing capacity of the specimens. Generally, the inner circular steel tube and inner square steel tube are more effective than the inner H beam.
The influence of the concrete strength grade on the bearing capacity of the sample is relatively minor. When comparing the FA40-C-C and FA60-C-C specimens, the maximum loads are 3179.27 and 3353.96 kN, respectively, which is a difference of only 5.5%, indicating similar constraint effects of steel tubes. More exploration is necessary to determine whether high-strength concrete needs to be matched with larger-sized or thicker-walled specimens to maximize its effect.
The ductility coefficient of each specimen ranges from 1.96 to 3.49, with an average of 2.61. The specimen shows sufficient deformation development from yield to failure and the failure mode is not a sudden brittle failure, indicating good deformation ability. The addition of an internal structure improves the ductility of concrete filled steel tubular columns, and the degree of ductility improvement varies slightly between different structural measures. For example, after adding structural measures, the ductility of concrete filled steel tubular columns in the FA60-C, FA60-C-C, FA60-C-H and FA60-C-S samples increases by 29.1, 18.4 and 53.6%, respectively. The appropriate addition of structural measures can effectively enhance the ductility of concrete-filled steel tubular column specimens.
Load-strain curve
The load-strain curves of the specimens are depicted in Fig. 5, where εv represents the longitudinal strain, and εh indicates the transverse strain. The test’s positive and negative values denote the only direction: the tensile strain is positive and the compressive strain is negative.
Fig. 5.
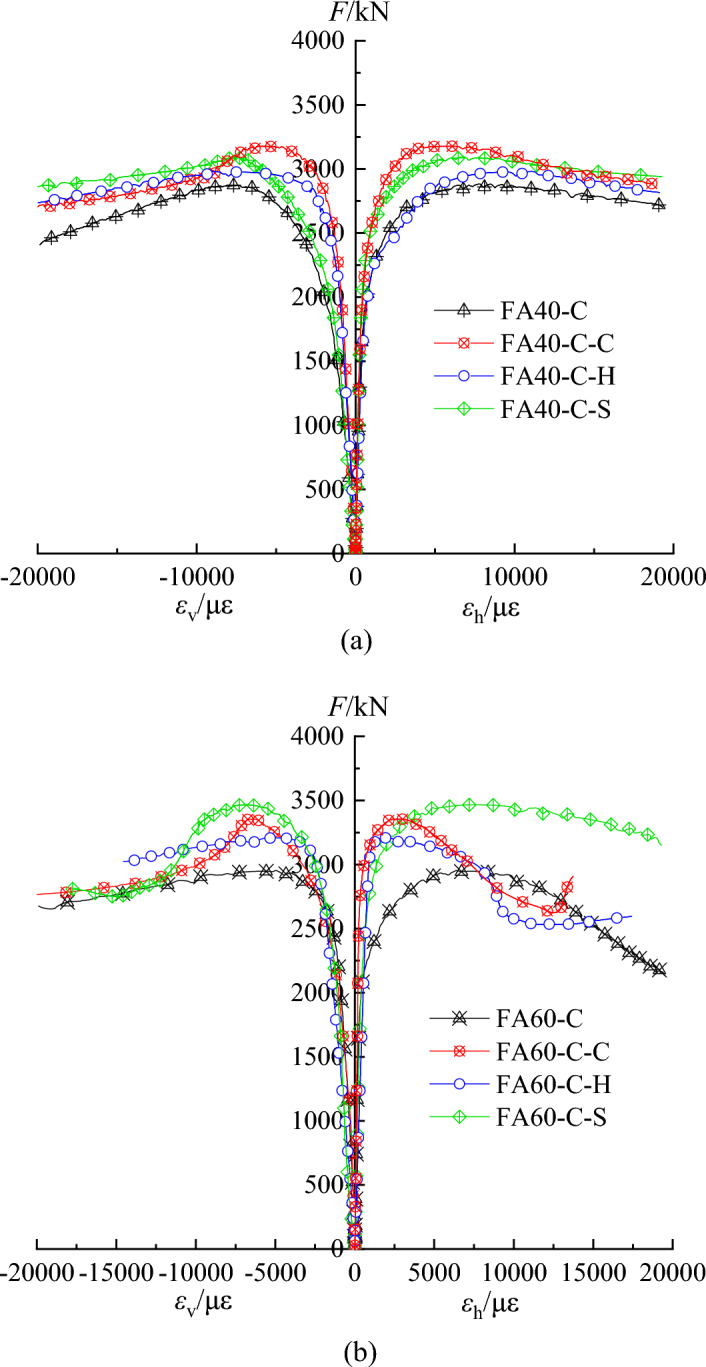
Load-strain curves of each specimen.
The major observations from Fig. 5 include the following:
The specimen's load and strain exhibit certain regularity. As the load escalates, the strain intensifies. Both the transverse and longitudinal strains are approximately symmetrical, signifying the uniformity and regularity of the specimen's deformation. Moreover, the concrete's strength marginally impacts the specimen's strain. An increase in concrete strength correlates significantly with the specimen's bearing capacity, yet the strain exhibits no notable change.
For the SCCFST column specimens, the transverse and longitudinal strains corresponding to the load-strain curve develop synchronously. At the same load, the strains are almost identical. Pre-yield, the strain gradually increases with the load. Post-peak load, the load diminishes, and the strain escalates rapidly.
Internal structural measures can decelerate the strain development in specimens to an extent. For instance, in specimens FA40-C, FA40-C-C, FA40-C-H, and FA40-C-S, incorporating an internal structure reduced the strain at peak load, resulting in relatively minimal deformation.
Stiffness degradation
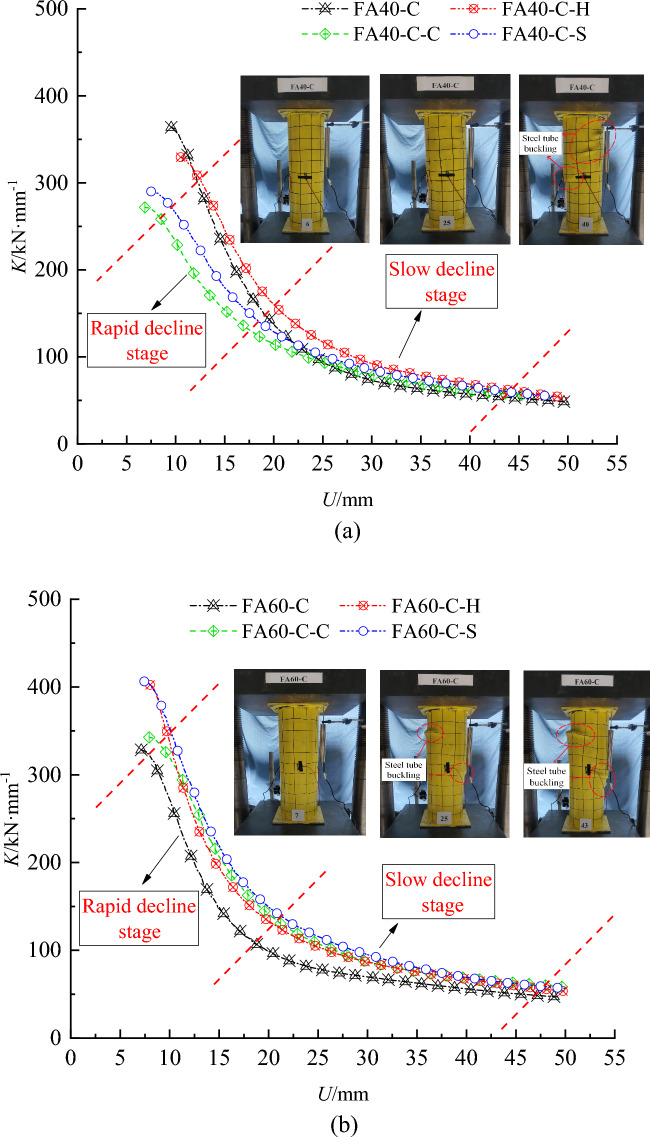
The stiffness reflects a structure's ability to resist elastic deformation under load and characterizes the difficulty of the structure's elastic deformation. It is defined as the load-to-displacement ratio in the macroscopic elastic range, essentially the force required for unit displacement. The stiffness degradation curves for each specimen group are shown in Fig. 6, where K denotes the secant stiffness.
Fig. 6.
Stiffness degradation curve of each specimen.
The following observations can be made from Fig. 6:
The stiffness degradation pattern for each group of SCCFST columns is analogous, categorized into a rapid decline section and a slow decline section. Initially, the stiffness degradation rate is swift; then it decelerates and stabilizes after it decreases to a certain level.
Internal structural measures somewhat influence the initial stiffness of the samples. When the concrete strength grade is C40, samples with structural measures exhibit lower initial stiffness compared to those without internal structures. For example, the initial stiffness of FA40-C exceeds that of FA40-C-C, FA40-C-H and FA40-C-S. On the contrary, in the C60 concrete strength grade group, adding internal structures increases the initial stiffness of the samples. The impact of internal structures on specimen stiffness is not markedly apparent. The overall stiffness of specimens with an inner square steel tube matches closely that of those with an inner H-shaped steel, whereas the initial stiffness of specimens with an inner circular steel tube is lower. Each specimen demonstrates high initial stiffness.
Concrete strength significantly affects the initial stiffness of the specimen. For the concrete strength C40, the initial stiffness values for FA40-C, FA40-C-C, FA40-C-H and FA40-C-S are 363.85, 271.80, 329.54, and 289.98 kN mm−1, respectively. The initial stiffness values of FA60-C, FA60-C-C, FA60-C-H, and FA60-C-S are 328.32, 342.66, 402.44, and 406.32 kN mm−1, respectively. Additionally, the increases in initial stiffness values are − 9.7, 26.1, 22.1, and 40.1%, respectively. Generally, a higher concrete strength grade results in higher initial stiffness for the specimen.
Calculation of the bearing capacity
Existing codes have stipulated the calculation of the bearing capacity of concrete filled steel tubular columns with circular, square, and polygonal outer steel tubes or those filled with steel tubes or steel sections under single and complex stress conditions26–29. This study theoretically analyzes the bearing capacity of such composite structures using the superposition principle, unified theory, and the limit equilibrium principle30–32. It deduces a simplified calculation method for the axial compression bearing capacity of complex SCCFST columns. To simplify the research content and reduce the calculation time, the following assumptions are made:
The basic mechanical properties of the sandwich concrete and the core concrete of the same sample are identical, with the influence of the internal structure on the weakening effect of the overall performance of the concrete being ignored.
The cross sections of each specimen are approximately considered completely symmetric along the axis, which meets the plane section assumption. Under axial load, the longitudinal strain of the outer steel tube, sandwich concrete, inner steel tube (or steel), core concrete, and other components is consistent.
The steel tubes used in this study are all thin-walled, D > > t, allowing the stress effect in the direction of wall thickness of the steel tube to be ignored. It is assumed that the stress along the direction of wall thickness is evenly distributed; the sandwich concrete is subjected to the same extrusion effect of the outer steel tube and the inner steel tube.
- The bonding performance between the steel tube (or steel) and the concrete is considered good. The slip deformation between the steel tube (or steel) and concrete is not considered, with the steel tube adhering to the Von Mises yield condition, the confined concrete adopting the Richart model, and the core concrete following the linear yield condition.
1
where fc is the uniaxial compressive strength of concrete; is the longitudinal stress of the concrete under three-dimensional compression; p is the lateral pressure on the concrete; k represents the lateral pressure coefficient. Reference33 shows that the k-value is generally between 3 and 5.
Superposition principle
Using the superposition principle, the members were simplified into two categories: ordinary concrete-filled steel tubular columns and additional internal structures. At the same time, only the constraint effect of the outer steel tube was considered. The role of the inner steel tube or H-shaped steel was approximated to that of a steel bar, while its constraint on the concrete was ignored. Hence, the internal structure is equivalent to a steel bar of the same area.
The calculation method is as follows:
| 2 |
where NT represents the bearing capacity of the concrete column confined to the outer steel tube confined concrete column; Ns represents the bearing capacity provided by the simplified internal structure to the steel bar; Asi represents the area of the inner steel tube or H-shaped steel. The calculation method is as follows:
| 3 |
| 4 |
Considering the restraint effect of the inner steel tube on the concrete
For ordinary concrete-filled steel tubular columns without internal structure and concrete-filled steel tubular columns with inner H-shaped steel, double-layer concrete-filled steel tubular columns lack a core concrete part. Thus, there is no constraint effect. The calculations of these components are based on the superposition principle. On the contrary, the double-layer concrete-filled steel tube column with a built-in steel tube is divided into four parts: outer steel tube, sandwich concrete, inner steel tube and core concrete. Taking into account the effect of the inner steel tube restraint on the core concrete, the bearing capacities of both the outer and inner concrete-filled steel tubes were calculated separately and then summed.
| 5 |
where No represents the bearing capacity of the concrete column of the outer steel tube, that is, the total area surrounded by the outer steel tube; Ni represents the column of the steel tube column; Aci represents the area of core concrete; is the constraint effect coefficient of the inner steel tube on concrete, . The calculation formula is as follows:
| 6 |
| 7 |
Unified formula for bearing capacity calculation
The selection of these two calculation methods depends on the type of specimen. To simplify the calculation process for different internal structural forms, a unified formula is proposed for the axial compression bearing capacity of complex concrete-filled steel tubular columns as follows:
| 8 |
| 9 |
| 10 |
where P represents the ratio of the core concrete area Aci to the total concrete area Ac, Aci = 0 for samples without core concrete; Q represents the reduction value of the steel constraint effect coefficient; As, Aso, and Asi represent the total area of steel, the outer steel pipe and the area of steel used in internal structure, respectively; q1 and q2 represent the constraint effect coefficient of the outer steel tube and the constraint effect coefficient of the internal structure, respectively.
The values of q1 and q2 depend solely on the type of steel. The q values for the circular steel tube, the square steel tube and the H beam are k/2, kek, and 1, respectively. The term k represents the lateral pressure coefficient. In this experiment, the lateral pressure coefficient is k = 3 and the constraint effect reduction coefficient for the square steel tube is ke = 0.3285. The derivation process is outlined in the following section.
The method to calculate the axial compression bearing capacity of concrete-filled steel tube columns primarily considers the capacities provided by the outer concrete-filled steel tube and the internal H-shaped steel or confined core concrete of the steel tube. Initially, it is assumed that the bearing capacity Ni provided by the H-shaped steel is correlated with the core concrete. This assumption allows for the unification of the bearing capacities provided by H-shaped steel, circular steel tube, and square steel tube in the form of internal structures.
| 11 |
According to Sections “Experimental phenomena” and “Load–displacement curve”:
| 12 |
The constraint effect coefficient is defined by regression and can be obtained:
| 13 |
Expand it to obtain:
| 14 |
Introduces to
| 15 |
By introducing , a unified formula for calculating the bearing capacity of complex forms of SCCFST can be obtained:
| 16 |
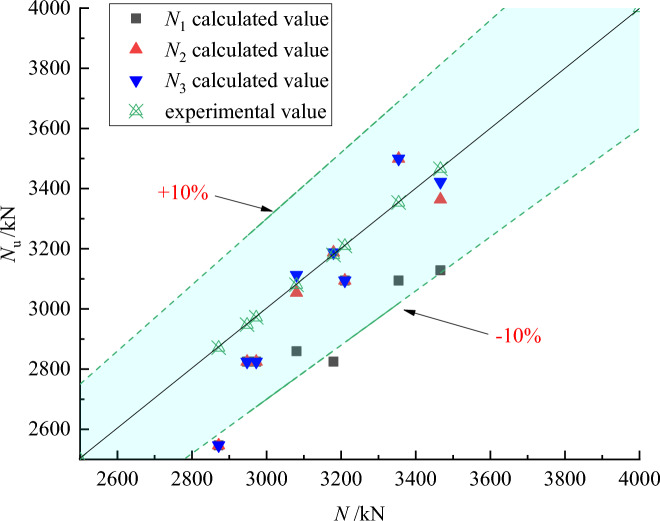
The three methods proposed above were used for the calculation, and the calculation results are summarized as shown in Table 4. In this sense, Nu represents the test results, and N1, N2, and N3 represent the results obtained by the three calculation methods.
Table 4.
Calculation results and test results.
| Numbers | Nu (kN) | N1 (kN) | N1/Nu | N2 (kN) | N2/Nu | N3 (kN) | N3/Nu |
|---|---|---|---|---|---|---|---|
| FA40-C | 2871.40 | 2546.58 | 0.89 | 2546.58 | 0.89 | 2546.58 | 0.89 |
| FA40-C-C | 3179.27 | 2824.66 | 0.89 | 3187.82 | 1.00 | 3187.82 | 1.00 |
| FA40-C-H | 2972.18 | 2824.66 | 0.95 | 2824.66 | 0.95 | 2824.66 | 0.95 |
| FA40-C-S | 3080.48 | 2859.67 | 0.93 | 3054.14 | 0.99 | 3112.45 | 1.01 |
| FA60-C | 2947.78 | 2824.91 | 0.96 | 2824.91 | 0.96 | 2824.91 | 0.96 |
| FA60-C-C | 3353.96 | 3094.39 | 0.92 | 3499.57 | 1.04 | 3499.57 | 1.04 |
| FA60-C-H | 3209.95 | 3094.39 | 0.96 | 3094.39 | 0.96 | 3094.39 | 0.96 |
| FA60-C-S | 3466.07 | 3128.32 | 0.90 | 3364.06 | 0.97 | 3422.37 | 0.99 |
| Mean value | 0.925 | 0.97 | 0.975 | ||||
| Standard deviation | 0.030 | 0.043 | 0.046 | ||||
| Coefficient of variation | 0.032 | 0.045 | 0.047 |
Table 4 and Fig. 7 indicate the following:
Three calculation methods were used: the superposition principle, the constraint effect of the inner steel tube, and the unified calculation principle for complex concrete-filled steel tube structures. These methods calculate the bearing capacities of ordinary concrete-filled steel tubular columns, built-in H-shaped steel concrete-filled steel tubular columns, and built-in steel tube double layer concrete-filled steel tubular columns in this test. The calculated results show strong agreement with the experimental results, demonstrating their applicability and reliability.
The ratio of the N1, N2 and N3 values calculated by the superposition principle to the actual results ranges from 0.89 to 1.04, with most specimen errors remaining within 5%. The mean values of the ratios of the calculated results to the experimental results using the three methods are 0.925, 0.97, and 0.975. The standard deviations are 0.03, 0.043, and 0.046, with coefficients of variation of 0.032, 0.045, and 0.047, respectively. These calculations align well with the experimental results, indicating the feasibility of these methods to calculate the axial compression bearing capacity of complex SCCFST columns. They also offer a reference to calculate the bearing capacity of concrete-filled steel tube columns.
The unified calculation formula simplifies the process of determining the axial compression bearing capacity of various types of concrete filled steel tubular columns, reduces computational costs, and produces results that align closely with the experimental data. In addition, its wide applicability effectively addresses the issue of inconsistent calculation methods for the axial compression bearing capacity of different types of concrete-filled steel tubular columns.
Fig. 7.
Comparison of the experimental value and the calculated value.
Conclusions
Under axial load, SCCFST columns typically exhibit shear failure characteristics. The failure occurs predominantly in the upper part of the specimen. Although internal structural measures mitigate deformation progression, they do not significantly alter macroscopic failure mode. Concrete strength improves the bearing capacity but has limit impact on the failure mode. Internal structural measures can improve the bearing capacity, ductility, and stiffness of the specimens. Compared with FA60-C, the peak loads of FA60-C-C, FA60-C-H, and FA60-C-S increase by 13.8, 8.9 and 17.6%, respectively, and stiffness increase by 29.1, 18.4 and 53.6%, respectively.
At the initial loading stage, the transverse and longitudinal strains are nearly symmetric, indicating that the specimen is in the elastic stage. As the load continues to rise, the specimen enters the plastic stage and the strain escalates rapidly. Internal structural measures can somewhat decelerate the development of the strain, while the strength of the concrete has a negligible effect on the strain. The proposed unified calculation equation for the axial compression bearing capacity of SCCFST columns demonstrates notable reliability and precision with a relative error of less than 10%. The proposed simplified equation could be used for engineering applications of the SCCFST.
Acknowledgements
This study is funded by the National Natural Science Foundation of China (52208226) and Henan Province Key Research and Development Program (241111322000).
Author contributions
C.H.: The proposer and coordinator of the experiment are responsible for the design of the test scheme and the revision of the subsequent papers. Y.Z.: Prepare materials, test collaborators. The whole process of the experiment operation, first draft editing and subsequent paper revision. Z.M.: Explain the operation process of the test instrument, and test cooperation personnel. R.H.: Provide resources, guide, supervise and review thesis writing.
Data availability
The datasets used and analyzed during the current study available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Yu, F., Chen, L., Bu, S. S., Huang, W. & Fang, Y. Experimental and theoretical investigations of recycled self-compacting concrete filled steel tubular columns subjected to axial compression. Constr. Build. Mater.248, 118399. 10.1016/j.conbuildmat.2020.118399118399 (2020). 10.1016/j.conbuildmat.2020.118399118399 [DOI] [Google Scholar]
- 2.Miao, K. et al. Eccentric compression behavior of concrete-filled steel tube columns strengthened by CFRP/steel strip. Eng. Struct.287, 116191 (2023). [Google Scholar]
- 3.Li, S., Liu, Z. Z., Lu, Y. Y. & Zhu, T. Shear performance of steel fibers reinforced self-confinement and self-compacting concrete-filled steel tube stub columns. Constr. Build. Mater.147, 758–775. 10.1016/j.conbuildmat.2017.04.192 (2017). 10.1016/j.conbuildmat.2017.04.192 [DOI] [Google Scholar]
- 4.Akram, T., Memon, S. A. & Obaid, H. Production of low cost self compacting concrete using bagasse ash. Constr. Build. Mater.23(2), 703–712. 10.1016/j.conbuildmat.2008.02.012 (2009). 10.1016/j.conbuildmat.2008.02.012 [DOI] [Google Scholar]
- 5.Wei, Y., Jiang, C. & Wu, Y. F. Confinement effectiveness of circular concrete-filled steel tubular columns under axial compression. J. Constr. Steel Res.158, 15–27. 10.1016/j.jcsr.2019.03.012 (2019). 10.1016/j.jcsr.2019.03.012 [DOI] [Google Scholar]
- 6.Lai, M. H. & Ho, J. C. M. Confinement effect of ring-confined concrete-filled-steel-tube columns under uni-axial load. Eng. Struct.67, 123–141. 10.1016/j.engstruct.2014.02.013 (2014). 10.1016/j.engstruct.2014.02.013 [DOI] [Google Scholar]
- 7.Giakoumelis, G. & Lam, D. Axial capacity of circular concrete-filled tube columns. J. Constr. Steel Res.60(7), 1049–1068. 10.1016/j.jcsr.2003.10.001 (2004). 10.1016/j.jcsr.2003.10.001 [DOI] [Google Scholar]
- 8.Lu, Y. Y., Liu, Z. Z., Li, S. & Li, W. J. Behavior of steel fibers reinforced self-stressing and self-compacting concrete-filled steel tube subjected to bending. Constr. Build. Mater.156, 639–651. 10.1016/j.conbuildmat.2008.02.012 (2017). 10.1016/j.conbuildmat.2008.02.012 [DOI] [Google Scholar]
- 9.Kanagaraj, B., Annad, N., Jerry, R., Raj, E. S. & Lubloy, E. Axial compressive behaviour and physical characteristics of high strength self-compacting geopolymer concrete (HSGC) columns exposed to elevated temperature. Constr. Build. Mater.401, 132866. 10.1016/j.conbuildmat.2023.132866 (2023). 10.1016/j.conbuildmat.2023.132866 [DOI] [Google Scholar]
- 10.Yu, F., Chen, L., Bu, S., Huang, W. & Fang, Y. Experimental and theoretical investigations of recycled self-compacting concrete filled steel tubular columns subjected to axial compression. Constr. Build. Mater.248, 118689. 10.1016/j.conbuildmat.2020.118689 (2020). 10.1016/j.conbuildmat.2020.118689 [DOI] [Google Scholar]
- 11.Li, B. et al. Expansive behavior of high-strength self-stressing and self-compacting concrete: Experimental study and analytical model. Constr. Build. Mater.353, 129080. 10.1016/j.conbuildmat.2022.129080 (2022). 10.1016/j.conbuildmat.2022.129080 [DOI] [Google Scholar]
- 12.Han, L. H. & Huo, J. S. Concrete-filled hollow structural steel columns after exposure to ISO-834 fire standard. J. Struct. Eng.129(1), 68–78. 10.1061/(ASCE)0733-9445(2003)129:1(68) (2003). 10.1061/(ASCE)0733-9445(2003)129:1(68) [DOI] [Google Scholar]
- 13.Azevedo, V. D., Lima, L. D., Vellasco, P. S., Tavares, M. N. & Chan, T. M. Experimental investigation on recycled aggregate concrete filled steel tubular stub columns under axial compression. J. Constr. Steel Res.187, 106930. 10.1016/j.jcsr.2021.106930 (2021). 10.1016/j.jcsr.2021.106930 [DOI] [Google Scholar]
- 14.Hui, C. et al. Experimental investigation and analysis on the axial compressive performance of recycled concrete-filled corroded steel tubular columns. Arch. Civ. Mech. Eng.22, 97. 10.1007/s43452-022-00422-8 (2022). 10.1007/s43452-022-00422-8 [DOI] [Google Scholar]
- 15.Cao, V. V., Le, Q. D. & Nguyen, P. T. Experimental behaviour of concrete-filled steel tubes under cyclic axial compression. Adv. Struct. Eng.23, 74–88. 10.1177/1369433219866107 (2020). 10.1177/1369433219866107 [DOI] [Google Scholar]
- 16.Yu, Q., Tao, Z. & Wu, Y. X. Experimental behaviour of high performance concrete-filled steel tubular columns. Thin Walled Struct.46, 362–370. 10.1016/j.tws.2007.10.001 (2008). 10.1016/j.tws.2007.10.001 [DOI] [Google Scholar]
- 17.Ahmed, M., Sheikh, M., Hadi, M. & Liang, Q. Numerical modeling of self-compacting concrete columns longitudinally reinforced with steel tubes under axial loading. Eng. Struct.270, 114913. 10.1016/j.engstruct.2022.114913 (2022). 10.1016/j.engstruct.2022.114913 [DOI] [Google Scholar]
- 18.Wang, Y. Y., Sun, S. W., Zhang, L. Q. & Jia, Y. D. Compressive behaviors of thin-walled steel tube stub columns filled with self-compacting concrete containing recycled aggregate. Materials16(18), 6088. 10.3390/ma16186088 (2023). 10.3390/ma16186088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang, Y. Y. et al. Eccentric compression behaviors of self-compacting concrete-filled thin-walled steel tube columns. Materials16(18), 6330. 10.3390/ma16186330 (2023). 10.3390/ma16186330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang, Y. Y., Sun, S. W., Zhang, L. Q. & Jia, Y. D. Strength behavior and ultimate capacity prediction of self-compacting concrete-filled thin-walled medium-length steel tubular columns under eccentric compression. Buildings13(11), 2876. 10.3390/buildings13112876 (2023). 10.3390/buildings13112876 [DOI] [Google Scholar]
- 21.Wang, Y. Y., Zhang, L. Q., Jia, Y. D. & Li, L. Experimental study on self-compacting concrete-filled thin-walled steel tube columns. Buildings12(12), 2134. 10.3390/buildings12122134 (2022). 10.3390/buildings12122134 [DOI] [Google Scholar]
- 22.Wang, Y. Y. et al. Axial loading behaviour of self-compacting concrete-filled thin-walled steel tubular stub columns. Adv. Civ. Eng.2021, 8861340. 10.1155/2021/8861340 (2021). 10.1155/2021/8861340 [DOI] [Google Scholar]
- 23.Han, L. H. & Yao, G. H. Experimental behaviour of thin-walled hollow structural steel (HSS) columns filled with self-consolidating concrete (SCC). Thin Walled Struct.42(9), 1357–1377. 10.1016/j.tws.2004.03.016 (2004). 10.1016/j.tws.2004.03.016 [DOI] [Google Scholar]
- 24.Han, L. H., Yao, G. H. & Zhao, X. L. Tests and calculations for hollow structural steel (HSS) stub columns filled with self-consolidating concrete (SCC). J. Constr. Steel Res.61(9), 1241–1269. 10.1016/j.jcsr.2005.01.004 (2005). 10.1016/j.jcsr.2005.01.004 [DOI] [Google Scholar]
- 25.Lachemi, M., Hossain, K. M. A. & Lambros, V. B. Self-consolidating concrete filled steel tube columns—design equations for confinement and axial strength. Struct. Eng. Mech.22(5), 541–562. 10.12989/sem.2006.22.5.541 (2006). 10.12989/sem.2006.22.5.541 [DOI] [Google Scholar]
- 26.GB 50936-2014. Technical Specification for Concrete-Filled Steel Tubular Structures (China Architecture and Building Press, 2014). [Google Scholar]
- 27.CECS 663-2020. Technical Specification for Concrete-Encased Steel Concrete-Filled Steel Tubular Structures (China Architecture and Building Press, 2020). [Google Scholar]
- 28.CECS 188-2019. Technical Specification for Steel Tube-Reinforced Concrete Column Structure (China State Engineering and Construction Press, 2019). [Google Scholar]
- 29.JGJ 138-2016. General Code for Composite Structures (China Architecture and Building Press, 2016). [Google Scholar]
- 30.Ahmed, M., Liang, Q. Q., Patel, V. I. & Hadi, M. N. S. Behavior of eccentrically loaded double circular steel tubular short columns filled with concrete. Eng. Struct.201, 109790. 10.1016/j.engstruct.2019.109790 (2019). 10.1016/j.engstruct.2019.109790 [DOI] [Google Scholar]
- 31.Uenaka, K., Kitoh, H. & Sonoda, K. Concrete filled double skin circular stub columns under compression. Thin Walled Struct.48(1), 19–24. 10.1016/j.tws.2009.08.001 (2010). 10.1016/j.tws.2009.08.001 [DOI] [Google Scholar]
- 32.Han, L. H., Yang, Y. F. & Xu, L. An experimental study and calculation on the fire resistance of concrete-filled SHS and RHS columns. J. Constr. Steel Res.59(4), 427–452. 10.1016/S0143-974X(02)00041-X (2003). 10.1016/S0143-974X(02)00041-X [DOI] [Google Scholar]
- 33.Cai, S. H. Modern Concrete Filled Steel Tubular Structures (China Communication Press, 2007). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and analyzed during the current study available from the corresponding author on reasonable request.