Reconstruction of Phanerozoic climate using carbonate clumped isotopes and implications for the oxygen isotopic composition of seawater

Significance

Over the course of the Phanerozoic, the oxygen isotopic composition of minerals in marine sediments has increased by approximately 8‰. The interpretation of this trend is complicated by uncertainties in formation temperature, δ¹⁸O_seawater and the extent of diagenesis. Here we apply carbonate clumped isotope measurements to exceptionally well-preserved Ordovician rocks from the Baltic Basin and present a framework for interpreting clumped isotope results. We find that the Ordovician had lower δ¹⁸O_seawater values than previously estimated, underscoring the necessity of reevaluating climate records dependent on oxygen isotopes. Our results suggest a potential link between the long-term rise in marine sedimentary rock oxygen isotope composition and changes in global water–rock interactions, shedding light on the Earth’s climatic evolution.

Abstract

The oxygen isotope ratio ¹⁸O/¹⁶O (expressed as a δ¹⁸O_VSMOW value) in marine sedimentary rocks has increased by ~8‰ from the early Paleozoic to modern times. Interpretation of this trend is hindered by ambiguities in the temperature of formation of the carbonate, the δ¹⁸O_seawater, and the effects of postdepositional diagenesis. Carbonate clumped isotope measurements, a temperature proxy, offer constraints on this problem. This thermometer is thermodynamically controlled in cases where carbonate achieves an equilibrium internal distribution of isotopes and is independent of the δ¹⁸O of the water from which the carbonate grew; therefore, it has a relatively rigorous chemical–physics foundation and can be applied to settings where the δ¹⁸O of the water is not known. We apply this technique to an exceptionally well-preserved Ordovician carbonate record from the Baltic Basin and present a framework for interpreting clumped isotope results and for reconstructing past δ¹⁸O_seawater. We find that the seawater in the Ordovician had lower δ¹⁸O_seawater values than previously estimated, highlighting the need to reassess climate records based on oxygen-isotopes, particularly where interpretations are based on assumptions regarding either the δ¹⁸O_seawater or the temperature of deposition or diagenesis. We argue that an increase in δ¹⁸O_seawater contributed to the long-term rise in the δ¹⁸O of marine sedimentary rocks since the early Paleozoic. This rise might have been driven by a change in the proportion of high- versus low-temperature water–rock interaction in the earth’s hydrosphere as a whole.

The oxygen isotope composition of ancient seawater is a longstanding controversy. On timescales of 10⁷ years and longer, it is controlled by weathering on continents as well as hydrothermal alteration along mid-ocean ridges (1, 2). Weathering reactions occurring at near-Earth-surface temperatures are usually associated with large oxygen isotope fractionations that preferentially partition ¹⁸O into residual solids, such as clays, and thus depleting the residual water. If the ocean’s oxygen isotope budget was controlled by low-temperature weathering alone, its oxygen isotope composition (expressed as a δ¹⁸O_VSMOW value) would reach a steady state of −9‰ [roughly 25‰ lower than average residual solids (3)]. In contrast, hydrothermal alteration at the mid-ocean ridges generally occurs at elevated temperatures (~200 to 400 ˚C) where the oxygen isotope fractionation between silicates and water is small (generally within ~2 ‰ of 0). Therefore, if hydrothermal alteration of seafloor basalts and gabbros was the only process affecting the δ¹⁸O_VSMOW of seawater, it would reach a steady state of 6‰ (the value of unaltered mafic igneous rocks). It is often assumed that, at least since the start of the Cenozoic, the weighted average δ¹⁸O_VSMOW of ice-free seawater (i.e., summing across ocean water and glacial ice) has been approximately −1‰ (4), implying that the ocean has been at near steady state with a balance of contributions to its oxygen isotope budget of ~44% weathering and 56% hydrothermal alteration. However, the estimated residence time of the ice-free ocean with respect to its oxygen isotope budget is about 250 My (2), so this balance could have changed over the course of the Earth’s history. Moreover, recent combined oxygen and clumped isotope studies of benthic foraminifera suggest that at least Atlantic deep waters deviated significantly outside this range during the early Cenozoic (5), suggesting that the assumption of globally uniform and steady-state δ¹⁸O of seawater may lead to systematic errors in interpreting paleoclimate records even over relatively short timescales of 10’s of My.

There have been several prior efforts to reconstruct the δ¹⁸O of seawater over timescales of 100’s of My. One of the most well-developed methods uses the oxygen isotope composition of low-Mg calcite fossils, mostly brachiopods, filtered to focus the interpretation on samples that are inferred to preserve their primary isotopic composition with minimal diagenetic modification (1). This record shows an 8‰ increase in δ¹⁸O from the Cambrian to the present and can be interpreted in three different ways: first, it can represent a primary signal that reflects minimal secular change in marine temperatures but a large increase in δ¹⁸O of seawater, presumably caused by a decrease in the contributions of weathering and increase in the contributions of hydrothermal alteration to the oceans oxygen isotope budget (1, 3). Second, the record can be interpreted as a primary signal that reflects a negligible secular change in the δ¹⁸O of seawater but a decrease in surface temperatures by ca 35 °C, perhaps due to generally diminishing pCO₂ over the course of the Phanerozoic. This interpretation has been criticized by some for being implausible (3, 6, 7) as it contradicts with well-documented glacial intervals (8) and biological evolution (9). However, the interpretation has been supported by oxygen isotope studies in coexisting cherts and phosphates (10) and δ¹⁸O and δD studies of cherts (11). Finally, this record could reflect diagenetic alteration of marine carbonate units, which is clearly expressed in early Phanerozoic dolomites having δ¹⁸O values similar to the calcitic fossils in question (12). These end-member interpretations are not mutually exclusive, so the geological record could reflect some combination of temperature change, change in δ¹⁸O of seawater, and diagenesis. One difficulty in resolving among the possible interpretations is that δ¹⁸O values of minerals depend both on temperature and the δ¹⁸O value of the fluid, and both variables are generally unknown in pre-Cenozoic sediments.

Carbonate-clumped isotope measurements offer a potential solution to this problem. It is a temperature proxy (at least, in cases where minerals form at or near isotopic equilibrium) based on the ordering of ¹³C and ¹⁸O atoms into bonds with each other in the same carbonate molecule, in excess of the double rare-isotope substitutions that would occur by random chance (13, 14). [Note that double ¹⁸O substitution can also be used as a temperature proxy but will not be discussed here; (15–17)]. This isotopic “clumping” phenomenon exists due to a thermodynamically controlled homogeneous isotope exchange equilibrium in the carbonate mineral (or perhaps among dissolved carbonate ions from which solid carbonate precipitated). This exchange reaction is independent of the δ¹⁸O of water and δ¹³C of dissolved inorganic carbon (DIC) from which the carbonate grew; therefore, it can be applied to settings where these parameters are not known (14). Carbonate clumped isotope measurements are reported as Δ₄₇ where Δ₄₇=((R⁴⁷_measured/R⁴⁷_stochastic) − 1) * 1,000 and R⁴⁷=[¹⁷O¹³C¹⁷O + ¹⁷O¹²C¹⁸O + ¹⁸O¹³C¹⁶O]/[¹⁶O¹²C¹⁶O]. Previous studies have applied clumped isotope thermometry to fossil carbonates in the Phanerozoic and shown that least altered fossils have clumped isotope temperatures and δ¹⁸O_carbonate values that imply δ¹⁸O_seawater values of −1.6 to 0‰ (18–22).

Here, we present measurements of stable C and O isotopes and clumped isotopes of some of the best-preserved Ordovician carbonate samples studied to date, including brachiopods and micrite fabrics sampled from outcrops and a drill core in the Paleozoic Baltic Basin. The sampling site is a carbonate platform setting and has previously been described extensively (23). The Ordovician (485 to 444 Mya) includes some of the most remarkable changes in biodiversity in the history of life. This time period saw rapid and significant increases in the diversity of marine organisms during the Ordovician Biodiversification (9, 24, 25), which was followed 40 My later by the Late Ordovician Mass Extinction (26). These evolutionary changes have been attributed to an increase in extraterrestrial dust (27), the onset of Gondwanan glaciation and global cooling (19, 28), or changes in ocean ventilation (29). Most previously documented paleoclimate records of this period are from low-latitude sites from the Laurentia paleocontinent. Here, we present a mid-latitude record from the Baltic continent which was situated at nearly 50°S during the Dapingian (~470 to 467 Ma) and migrated to about 20°S by the Hirnantian (445 to 444 Ma; SI Appendix, Fig. S1). The record presented here includes clumped isotope measurements plus a compilation of more than 3,000 previously unpublished carbonate bulk-rock δ¹⁸O_VPDB measurements from 9 outcrop and 29 drill core sections all stratigraphically correlated through the Baltic Basin strata. The Ordovician section of the Baltic Basin is characterized by its uncompact fabrics and thermally immature organic matter (23), suggesting only shallow (~<2 km) burial and maximum burial temperatures below oil window temperatures (~<50 to 60 °C) (30, 31). We examine the isotopic characteristics of these carbonates with the goal of reconstructing seawater temperature and oxygen isotope composition. We also present a framework for interpreting carbonate clumped isotope records and use this model to reconstruct δ¹⁸O_seawater variations with time using both our record and other, previously published records.

We find that the studied Baltica carbonate samples record δ¹⁸O_VPDB values from −7 to −2‰, Δ₄₇-based apparent temperatures from 23 to 61 °C and calculated δ¹⁸O_VSMOW values of water [i.e., calculated using the measured δ¹⁸O of carbonate and the clumped isotope apparent temperature along with a previously determined relationship (32)] from −4 to 5‰ (Figs. 1 and 2 and SI Appendix, Fig. S2). This record includes both samples that record environmentally plausible surface temperatures as well as hotter apparent temperatures associated with burial diagenesis. The lower Δ₄₇-temperatures observed include values lower than other previously measured Ordovician clumped isotope record (Fig. 1); in this sense, we interpret this record as being relatively well preserved and/or sampling a relatively cold climatic environment (perhaps consistent with its relatively high paleolatitude).

Fig. 1.

Δ₄₇-Temperature versus Age of brachiopods and micrites from Baltica in the current study and Laurentia (19, 20, 33, 34). Error bars are 2σ.

Fig. 2.

Calculated δ¹⁸O_water versus Δ₄₇-Temperature of brachiopods and micrites from (A) Baltica in the current study and (B) Laurentia (19, 20, 33, 34). The Baltica, Anticosti, Mid Continent, and Cincinnati Arch records fall along lines close to W/R = 0 while Svalbard and Newfoundland show evidence for more open system diagenesis. In B, several points are about the W/R = 0 line. These points are from the Hirnantian, and we do not include these points in our analysis, as the Hirnatian was a period of extensive glaciation and continental ice formation, and we cannot compensate for the change in ice volume using the approach to paleoclimate interpretations that we have followed here. Please refer to Fig. 1 for the legend.

Previous clumped isotope studies of ancient carbonates typically interpret wide ranges in Δ₄₇-temperatures as reflecting postdepositional alteration superimposed on some initial depositional or earliest diagenetic record and interpret either the lowest (18, 19, 22) or the average (33) apparent temperatures as the formation temperature. However, it is possible that all the Ordovician records, including the one presented here, are subtly altered by postdepositional diagenetic processes, i.e., that none of the apparent temperatures recorded by any of the samples studied reflects depositional conditions alone. This possibility has been present in all prior oxygen and clumped isotope studies of ancient carbonates but is challenging to evaluate and translate into quantitative interpretations of the possible limits on depositional conditions. Below, we develop a different approach to this problem and apply that method to clumped isotope compositions of well preserved Paleozoic marine carbonates.

Diagenetic alteration can occur in open or closed systems. During open system, fluid-dominated, or fluid-buffered diagenesis, the oxygen isotope composition of the mineral (δ¹⁸O_carbonate) and clumped isotope values are both altered through fluid–rock exchange processes such as dissolution and reprecipitation. In contrast, during closed system, rock-buffered diagenesis, the primary mineral δ¹⁸O_carbonate values are preserved while the clumped isotope temperatures can be reset (35). These differences mean that the systematics of combined Δ₄₇-δ¹⁸O data constrain whether bulk δ¹⁸O_carbonate values have been altered by exchange with fluids in an open system (high water/rock ratio) or preserved in a closed system (low water/rock ratio). In addition, scenarios intermediate between these extremes will lead to coupled variations in δ¹⁸O and Δ₄₇ that constrain the extent and water/rock ratio of diagenesis. Results from the Baltic Basin indicate that its carbonate rocks experienced diagenetic alteration under low but variable water/rock ratios ranging between 0 and 2 and averaging ~0.4 (Fig. 2; SI Appendix, Fig. S4). Thus, based on this clumped isotope record, the Baltic Basin samples we investigate largely (but not perfectly) preserve their δ¹⁸O values and were deposited at or below temperatures of 23 °C (the minimum seen in our datasets).

We further investigate the initial formation conditions of our samples (see SI Appendix, Methods for further details). We first divide our record into five stratigraphic stages, the Dapingian, Darriwilian, Sandbian, Katian, and Hirnantian, and examine what range of initial formation temperatures (from −2 °C to the minimum Δ₄₇-temperature in each suite) and δ¹⁸O_seawater (from −10‰ to the minimum δ¹⁸O_seawater in each suite) could be consistent with the observed δ¹⁸O_carbonate and Δ₄₇-temperatures, recognizing that all five suites appear to have been altered along diagenetic vectors under relatively low water/rock ratios (36). Each suite of data defines its own field in a plot of temperature (depositional or diagenetically modified) versus δ¹⁸O of water with which it last equilibrated at that temperature. We then further constrain these calculated fields by only allowing combinations of temperature and δ¹⁸O_water values that correspond to the measured δ¹⁸O_carbonate values. With these added constraints, the range of possible depositional temperatures and δ¹⁸O_seawater during each time period is recorded in Fig. 3. These temperatures and δ¹⁸O_seawater ranges are notable for being relatively cold and low in δ¹⁸O_seawater, as compared to past reconstructions of Paleozoic climate. Although we do not have clumped isotope records exhibiting such low Δ₄₇-temperatures or δ¹⁸O_seawater from other geographic locations where Ordovician marine carbonates are preserved, we cannot rule out these possible initial conditions as it is possible that these samples from prior studies formed under cooler conditions from lower δ¹⁸O waters and then underwent minor diagenetic alteration.

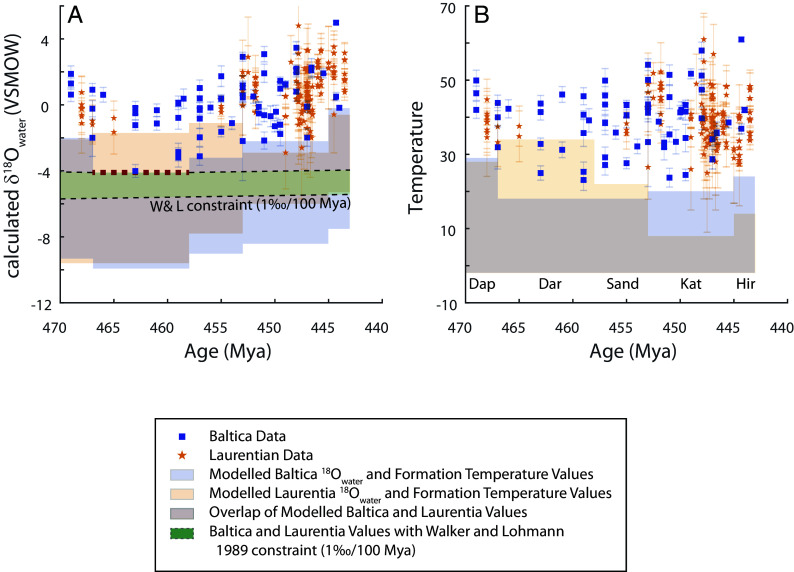
Fig. 3.

Calculated δ¹⁸O_water (A) and measured Δ₄₇-temperature (B) versus age as well as modeled possible formation temperatures and δ¹⁸O_water values. Blue bars are the modeled Baltica δ¹⁸O_water and Temperature values while yellow bars show the modeled Laurentia δ¹⁸O_water and Temperature values. The red bars are where the two overlap. The red dashed line shows the lowest value for the upper bound on δ¹⁸O_water (Baltica record in the Darriwilian). With the additional constraints that Laurentia and Baltica must have had the same δ¹⁸O_water at the same time and δ¹⁸O_water cannot change more than 1‰/100Mya, the green shaded bar records the range of permitted δ¹⁸O_water values. This green shaded bar of permitted δ¹⁸O_water values is used to calculate δ¹⁸O-temperatures in Fig. 4.

We do a similar analysis on the Anticosti, Mid-Continent, and Cincinnati Arch Laurentian records (19, 20, 22, 33) that appear to have undergone diagenesis with water/rock ratios ranging between 0 and 0.6 (Fig. 2) and find that they are consistent with a range of temperature and initial δ¹⁸O_seawater values similar to those reconstructed for Baltica.

We note that the analysis of samples from Baltica in the Darriwilian has the lowest value for the upper bound on δ¹⁸O_seawater (note, we mark this constraint with a bold red dashed line in Fig. 3). Next, we adopt two additional, related constraints: 1) Laurentia and Baltica must have the same δ¹⁸O_seawater at the same time; and 2) δ¹⁸O_seawater cannot change more than 1‰ per 100 million years, due to the large size of the ocean water reservoir—derived from a previously published model of the geochemical cycles controlling δ¹⁸O_seawater (37). Therefore in the Ordovician at 470 Mya, δ¹⁸O_seawater could not have been lower than −5.7‰, assuming a starting point of an ice-free seawater of −1‰. When these constraints are used, they suggest that at 470 Mya, δ¹⁸O_seawater cannot have been higher than −4‰ or lower than −5.7‰. This range of allowable δ¹⁸O_seawater during each time period is indicated with a green shaded bar in Fig. 3.

Our findings of low δ¹⁸O_seawater contrast with suggestions of similar to modern δ¹⁸O_seawater values from previous clumped isotope records (12, 18–21) and ophiolite measurements suggesting constant δ¹⁸O of seawater throughout the Phanerozoic eon (38). The previous calcite clumped isotope derived δ¹⁸O_seawater records are inconsistent with ours because they have assumed that the lowest measured temperature reflects the initial marine precipitation temperature. However, these records can also be explained by growth at lower temperatures and lower δ¹⁸O_seawater values (Fig. 3 and SI Appendix, Fig. S3). There are two possibilities for the discrepancy between this study and previous interpretations of ophiolite records: 1) the ophiolite record may have been decoupled from δ¹⁸O_seawater because of rock-buffered high-temperature hydrothermal alteration (39) or 2) previous modeling studies have indicated that the absence of a δ¹⁸O trend in ophiolite samples does not conflict with changing δ¹⁸O_seawater values (40).

A previous modeling study has also suggested that the δ¹⁸O_seawater in the Ordovician was low, similar to the values that we observe (41). Such low values would be an indication that the balance of fluxes of oxygen-isotope exchange associated with weathering versus hydrothermal alteration reactions were substantially different during the Ordovician. A rise in δ¹⁸O_seawater from the early Paleozoic to the modern requires either an increase in the δ¹⁸O of the rocks being weathered or a decrease in the fractionation associated with crustal alteration. We are not aware of evidence that would support a sustained and substantial increase in the δ¹⁸O of the rocks being weathered over the Phanerozoic, although there are models suggesting that an increased contribution from weathering of continental crust which is isotopically heavier than oceanic crust, possibly driven by the expansion of land plants could lead to an increase in the δ¹⁸O of rocks being weathered (42). The fractionation associated with crustal alteration could have changed if there was an increase in the proportion of high-temperature hydrothermal alternation relative to low-temperature weathering reactions in the hydrosphere’s oxygen isotope budget (3). An increase in high-temperature hydrothermal alteration could be due to deepening oceans or an increase in mid-ocean ridge length, while a decrease in low-temperature weathering reactions could be due to an increased rate of seafloor spreading or subduction over time (37). Previous work has suggested that a progressive increase in authigenic siliceous and carbonate sediment production, at ~550 Ma initiated the blanketing of mid-ocean ridge basalts by pelagic sediments which reduced the interaction between seawater and the crust (3). This reduced interaction between seawater and crust reduced the rate of cooler off-axis ocean-floor alteration and changed the balance toward high-temperature hydrothermal interactions at ridges (37, 40, 43), and thus increased the δ¹⁸O_seawater.

We can use our modeled δ¹⁸O_seawater values (green shaded region in Fig. 3) to calculate temperatures of carbonate precipitation, using the known temperature dependence of the oxygen isotope fractionation between water and carbonate (32) and 3,000 new and previously published δ¹⁸O_carbonate measurements from Baltica. The 3,000 δ¹⁸O_carbonate measurements do not have corresponding clumped isotope data but have a range in δ¹⁸O_carbonate at any given time period that is similar to what is observed in the suite of samples for which we did measure Δ₄₇ values (~3 ‰). Thus, we infer that the samples in this larger database generally experienced extents and conditions of diagenesis resembling those of the better characterized, related samples. We focus our interpretation on the upper 10th decile of the δ¹⁸O_carbonate data, with the assumption that these values will best approximate the δ¹⁸O_carbonate values of these carbonates when they first precipitated from seawater. For a single sample, these constraints are generally weaker than directly approximating temperature using clumped isotope data, but such an approach allows us to use an orders of magnitude larger database of δ¹⁸O_carbonate values which likely includes samples that experienced even less alteration than the clumped isotope dataset and we can therefore put stricter constraints on surface temperature. This exercise also proves an independent test and validation to the constraints put on the δ¹⁸O_seawater—i.e., if the constraints underestimate δ¹⁸O_seawater, we may get impossibly negative temperatures in such a calculation. To calculate δ¹⁸O-derived temperatures, we use a previously published oxygen isotope fractionation between water and inorganic carbonate (32). We note that any diagenetic alteration not accounted for by our data filtering would be expected to shift δ¹⁸O_carbonate values lower, leading to higher inferred temperatures. We find that Ordovician Baltic temperatures based on this large record of δ¹⁸O_carbonate values range from a high of 13 ± 5 °C in the Dapingian to a low of 6 ± 4 °C in the Katian. We do not use our δ¹⁸O_seawater reconstruction to estimate Hirnantian temperatures because this was a period of extensive glaciation and continental ice formation, and we cannot compensate for the change in continental ice volume using the approach to paleoclimate interpretations that we have followed here. These temperature records are largely consistent with conodont-based temperature estimates and other records showing cooling trends over this period (44, 45). We note that a previous compilation (6) has indicated that δ¹⁸O_carbonate increased by ~4‰ in the Ordovician. If we use our δ¹⁸O_seawater reconstruction and its ~2‰ range, then temperature must have decreased by ~10 °C which is consistent with our record (Fig. 4). The cooling trend seen in these records was driven by decreasing atmospheric CO₂ and probably caused by a combination of reduced solid Earth degassing combined with increased silicate weathering either due to progressively more exposed land in the warm and wet tropics (28, 46), or an increase in arc accretion, which may have been an additional cooling mechanism by exhuming and eroding mafic rocks in tropical latitudes, or possibly the rise of plants (28, 42, 46). This cooling could have triggered the Ordovician Biodiversification through the combined effects of cooler oceanic temperatures and increased oceanic oxygen (44).

Fig. 4.

Calculated δ¹⁸O-temperatures based on modeled δ¹⁸O_seawater values (green shaded bar in Fig. 3) for upper decile values of Baltica carbonates (current study) and conodonts (45), as well as upper decile of Laurentia carbonates (22).

Materials and Methods

Samples were analyzed for Δ₄₇ using previously established methods (1, 2, 13, 14). See SI Appendix for further information. Briefly, 7 to 10 mg of samples were drilled from thick sections and digested with phosphoric acid at 90 °C to produce CO₂. The CO₂ was separated from H₂O, trace organics, and other polar contaminants by dry ice/ethanol and liquid nitrogen traps as well as entraining the CO₂ in He and passing over a Porapak Q 120/80 mesh column held at −20 °C. The resulting CO₂ was again purified from He using dry ice/ethanol and nitrogen traps and expanded into the bellows of the mass spectrometer. The evolved CO₂ was analyzed in a dual inlet Finnigan MAT-253 mass spectrometer with the simultaneous collection of ion beams corresponding to masses 44 to 48 to obtain Δ₄₇, Δ₄₈, δ¹³C, and δ¹⁸O values.

δ¹³C_VPDB and δ¹⁸O_VSMOW values of samples and standards were calculated from raw ion currents on masses 44, 45, and 46 of sample and working gases using the “Brand” parameters (3). Raw Δ₄₇ values were then calculated from the differences in R₄₇, δ¹³C_VPDB, and δ¹⁸O_VSMOW values between the reference gas and the derived sample gas. The raw Δ₄₇ value was then corrected for instrument nonlinearity and scale compression based on concurrent measurements of laboratory-equilibrated CO₂ gases of variable δ¹³C_VPDB and δ¹⁸O_VSMOW (13, 14). These gases were used to convert measurements into the interlaboratory absolute reference frame (47). Samples were projected to a 25 °C acid reaction temperature using an acid digestion fractionation factor of 0.092‰. The final accepted Δ₄₇ values were then converted to apparent temperatures using the Bonifacie calibration (5).

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (PDF)

Dataset S02 (PDF)

Dataset S03 (PDF)

Dataset S04 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.