Comparison and classification of photovoltaic system architectures for limiting the impact of the partial shading phenomenon

Abstract

This article proposes a comparison and classification of PV system architectures with the aim of limiting the impact of the partial shading phenomenon which remains one of the most harmful defects during the production of electrical energy with significant consequences on output power, current and voltage. the methodological approach used consists of analyzing in depth the main most recent architectures developed in the current literature with their advantages and disadvantages; then define five partial shading scenarios for different irradiance levels (1000W/m2; 900W/m2; 700W/m2; 500W/m2; 300W/m2), which will then be immediately applied to five other proposed architectures: SP (serial-parallel), BL (Bridge-Link); HC (Honey Comb); TCT (Total-Cross-Tied); TSPL (Triple Series Parallel Ladder); the values obtained at the output with each of its architectures will be used for an in-depth descriptive analysis with PCA (principal component analysis) in statistics but to carry out a comparative analysis between the architectures. All with a Matlab Simulink 2022.b software environment. The results obtained offer a strong positive correlation for TCP and TSPL architectures with better weight compared to other architectures. All in accordance with the IEEE-519-2022 standard. This work is therefore positioned as a contribution to the optimization of the performance of electrical energy production through the use of PV systems which today represent widely used alternatives in the renewable energy register.

1. Introduction

The global energy need has experienced exponential growth in recent years and solar energy is positioned as a source of energy in high demand due to its non-polluting and environmentally friendly nature [1]. several factors such as: the material used in solar panels, Irradiation, shadows and temperature variation in solar cells are likely to reduce the efficiency of solar energy conversion and expose the solar panels and in particular thus their duration of life and their overall performance [2]. Several architectures have therefore been proposed in the current literature in terms of solutions [3]: offer eight varied configurations of PV system connections allowing maximum output power profiles to be obtained; this for 16 PV panel numbers of 10W each with a total capacity of 160 W; This study establishes that the partial shading model determines and influences the nature of losses in the PV system. The PLT architecture is therefore positioned in this study as the one that best resists partial shading. One of the limitations of this study is: The general failure to take into account the variable choice of materials, which is nevertheless crucial to guarantee good performance and optimal conversion of solar energy into electricity. As an additional limitation in this work, the type of partial shading modeling does not allow a comparative study to be carried out simultaneously with other architectures available in the scientific literature which adopt as hypotheses: a percentage coverage of the PV surface or quite simply a variation in the intensity of the solar irradiation level per cell [4]; which offers a bifacial photovoltaic module (BPVM) which now offers great importance in the most recent works due to its high efficiency due to the arrangements to capture the photon on both sides of the module. It was also demonstrated in this work that partial shading significantly affects the performance of polycrystalline photovoltaic modules (PPVMs) and BPVMs. A comparison of the performance of PPVM and BPVM under different partial shading conditions is presented in this paper. Experiments were carried out on polycrystals and BPVMs with 320 W and 395 W respectively. The module performance is analyzed in terms of power extraction percentage, power loss percentage and power extraction per square meter. Partial shading for the front and back faces of the BPVM was developed and the results are presented. Based on the results, the average loss due to partial front shading is 26 % lower in BPVM compared to polycrystalline; However, one of the limitations of this work also comes from the failure to take into consideration a comparative study with existing materials for other PV systems taken under the same operating conditions [5]; which shows that mismatch losses due to partial shading condition (PSC) are not allowed to extract the maximum power from the solar PV array. But the major problem is to discover the occurrence and its distribution of partial shading in the photovoltaic solar generator. Conventional methods temporarily disconnect the load from the PV array and measure the short circuit current (Isc) and use the information to detect partial shading. Frequent disconnection of the solar PV array from the load makes the conventional method impractical in a large solar power plant and even in a stand-alone PV system. A partial detection technique is therefore proposed in the work [5,6] which uses the line voltage difference (Vd) instead of the short circuit. current (Isc) to estimate partial shading. A larger Vd infers the severity of the occurrence of partial shading syndrome in the photovoltaic solar field. By using static reconfiguration and then technically modified torque coupling (MCM), the voltage difference (Vd) is reduced. This guarantees the attack of the PSC. In this technical proposal the load must never be disconnected from the photovoltaic solar generator, to detect partial shading it can be used practically even for an autonomous photovoltaic system. Eight extended partial shading models are simulated using MATLAB Simulink to validate the proposed work and the array size of 120W 3 × 4 polycrystalline photovoltaic panels is used for experimental validation in his work. However, the choice of partial shading modeling in this study does not directly favor a comparative study with existing models for the same operating conditions [6]. propose new photovoltaic panel (PVAT) topologies to improve performance under partial shading conditions (PSC). A total of eight shading models are considered in the analysis for seven types of bay configurations. Based on existing network configurations, six new PVATs are proposed to address the partial shading effect. A 4 × 4.4 kW photovoltaic solar generator composed of panels of 250 W each. The rating is taken into account in this article. The proposed PVATs are simulated in MATLAB/Simulink® to evaluate the performances. The results obtained from the simulation are compared to conventional PVATs and matched to topologies that give the best performance during various identified PSCs. Comparing the results shows that the modified TCT (Total Cross-Tied) configuration works well to extract more power in most PSCs. For the short and wide PSC, the TCT proposed improved the power output of the PVAT by 105 % compared to the existing TCT topology. The proposed method is also experimentally validated using 2 × 2 TCT photovoltaic panel topology and the output waveforms are presented. However, there are known limits as:

• •A lack of classification and direct comparison of its architectures for identical partial shading scenarios.
• •Optimization of current and output voltage power quantities by using metha-heuristic algorithms at the charge controller without first reducing losses in the conversion process at the PV cell level
• •The general failure to take into account the variable choice of material which is nevertheless crucial to guarantee good performance and optimal conversion of solar energy into electricity.

All its limits further crystallize the challenges of the race for control or even the optimization of the production of electrical energy. Two common methods are used to combine multiple photovoltaic modules in a system: series and parallel connection of photovoltaic (PV) modules [7]. Each method has its own advantages and disadvantages, and this will depend on various factors, such as the type of system, the size of the system, and the specific constraints of the solar installation. Series connection of PV modules involves connecting the positive terminals of one module to the negative terminal of the next module, so that the voltage adds up and the current remains constant. Their efficiency is the highest (12–18 %), but due to their manufacturing complexity, they are too expensive [8]. Additionally, connecting PV modules in parallel connects the positive and negative terminals of all modules together, which increases the total system current [9]. Each module operates autonomously, which is an advantage of parallel connection. In addition, they are simpler to design, their manufacturing costs less and their efficiency decreases (from 11 % to 15 %). However, voltage drops in cables can cause overall voltage losses. Additionally, to support this accumulated load, it may be necessary to use larger, more expensive cables [10].

The main contributions in this article in terms of originality are defined around the following points:

• •An in-depth study of several recent architectures or topologies in the literature depending on the size of the panels and the associated mathaheuristic algorithms
• •A modeling and a comparative simulation of the five topologies or architectures for well-defined partial shading scenarios with the ultimate goal of making a classification according to the performance of the quantities obtained at the output.
• •Highlighting the existing link between the variation of the partial shading level in the different scenarios and the production of maximum output power.
• •A principal component analysis for each partial shading scenario for a better analysis of the correlations between the five architectures: SP, BL, HC, TCP, TSPL.

A combination of keywords in search engines provides Fig. 1 which presents the evolution of the documentary trend in terms of quantity and quality. all this further reveals the technical and scientific issues of the problem over time.

Fig. 1.

Documentary quality and quantity.

In the rest of this article, section 2 first presents the most recent architectures in the literature according to the size of the PVs and the algorithms used. Section 3 presents the mathematical modeling of the main one-, two-, and three-diode PV models and includes the Bishop model. A presentation of the main panels will also be made at this level. Section 4 presents the five main architectures SP, BL, HC, TCP, TSPL, which will be tested on several partial shading scenarios defined in advance. Section 5 which will present the results obtained with the five different architectures. An in-depth descriptive analysis will also be carried out at this level. Finally, section 6 will present the conclusion which will recall the originalities in terms of major contributions in the article and especially the impact of the results obtained in the context of development support.

2. Recent architectures of PV topologies

This section presents the main recent architectures developed in the literature depending on the size of PV panels. The different issues are also mentioned in Table 1 according to the topology presented, each time associating the advantages and limits. Table 2 also offers the different types of cells, their efficiency, their advantages and limitations as well. Its main observations made in the literature allow us to position ourselves on the impact of partial shading which reduces the production of electrical energy while causing a reduction in the lifespan of the PV.

Table 1.

Evolution of recent literature on the impact of the partial shading phenomenon.

Réf.	Themes	Goals	Topologies	Size of PV panels	Remarks
[11]	Performance analysis of photovoltaic power plants highlighting the combination of different MPPT algorithms, shading models and connection types	study various combinations of algorithms, connection types and partial obstruction models for efficient photovoltaic installation design	SP, TCT, HC, BL, SP-TCT, BL-TCT, BL-HC et HC-TCT	5 × 5	The study reveals that the Total Cross Tied (TCT) connection type outperforms other types in all PSCs with an average loss of 25.98 %, fill factor of 54.3 % and efficiency of 13.45 %., while the Diagonal and Long Wide models have less effect.
[12]	Performance analysis of monocrystalline, polycrystalline and thin-film materials based on 6 × 6 TCT photovoltaic panels under different partial shading situations	Analyze the performance of photovoltaic panels made of single crystals, polycrystals and thin films	T-C-T	6 × 6	Under uniform radiation conditions, the thin-film TCT photovoltaic generator offers the highest efficiency compared to single-crystal and polycrystal TCT generators.
[13]	A review of maximum power point tracking for photovoltaic systems with and without shading condition	Examine maximum power point tracking (MPPT) techniques in PV systems, focusing on normal and partial shading conditions.			Performance is limited in partial shading.
[14]	Simulation study of the electrical efficiency of different PV module topologies in partially shaded urban scenarios	Propose a simple but effective approach to compare the potential of different module topologies to maximize the electrical performance of partially obstructed photovoltaic systems.	modules with bypass diodes (BPD) and series-parallel modules (SP)	6 × 12	The study demonstrates that the performance of a partially obstructed photovoltaic system, composed of conventional solar modules, can be increased by up to 25 % when obstructed by nearby obstacles.
[15]	A novel MPPT (power point tracking) algorithm based on a modified genetic algorithm specialized in global maximum power point tracking in photovoltaic systems affected by partial shading.	Propose a new MPPT algorithm for photovoltaic systems affected by partial obstructive damage	MPPT algorithm based on a GA (genetic algorithm)		The proposed algorithm does not require predefined configuration and gives the best results than other comparison algorithms.
[16]	Global maximum power point tracking based on ANFIS approach for PV panel configurations under partial shading conditions	design an intelligent MPPT controller that can predict and extract the global maximum power point (GMPP) of a photovoltaic array under partial shading (PSC) conditions, regardless of the configuration used or its size	TCT	4 × 2	The results show that the algorithm can effectively track the overall MPP and is robust to various shading models, with high system efficiency, speed and stability.
[17]	Photovoltaic panel reconfiguration techniques for maximum power optimization under partial shading conditions	This article reviews the main approaches to help solve this problem, evaluating the techniques, advantages and disadvantages.	SP, TCT, BL, HC	4 × 4	This article discusses various PV reconfiguration strategies for different panel topologies, categorizing them into static and dynamic methods. The most common techniques include TCT and SP topologies for partial shading conditions
[18]	A review of techniques for reconfiguring photovoltaic panels for maximum power extraction under partial shading conditions	This article provides a comprehensive review of the main methods used to reconfigure existing photovoltaic panels to solve the problem of obstructing parts.			The adaptive technique requires a statically adaptable solar cell bank, increasing the number of collectors and connection complications. Dynamic approaches result in high costs due to excessive use of sensors, switches, and embedded devices
[19]	Analysis and comparison of different photovoltaic panel configurations under partial shading conditions	Study the performances of different types of PV configurations	S, SP, TCT, BL, HC	6 × 6	The study reveals that TCT provides the best performance in all shading conditions and increases maximum power compared to other configurations.
[20]	A new fixed photovoltaic array configuration to harvest maximum power from shaded modules especially the number of cross-links	This research aims to model and simulate photovoltaic solar panel configurations in various shading scenarios.	S, SP, TCT, BL, HC et TT	7 × 7	The TCT configuration offers the highest peak wind power, but requires more crossings and incurs higher connection costs. In contrast, the TT configuration provides consistent performance under most shading conditions, especially the number of cross connections compared to the TCT configuration.
[21]	Estimation of solar irradiance and optimal localization of power region in photovoltaic energy systems under partially shaded conditions	This work aims to develop a simple and powerful approach to operate PV systems under partial solar charging (PSC)			The proposed system includes a simple solar irradiance estimator, a voltage-current cap on partially obstructed modules, and a neural network for accurate power zone determination, thereby causing the single-task MPPT problem.

Table 2.

main PV cells.

Cell types	Rendering	Benefits	Disadvantages
[22]	Approximately 17 %	Good performance in direct sun, very efficient, stability of energy production	Loss of yield when the temperature rises and high cost, expensive
[23]	12 %	Easy design, affordable cost, suitable for large-scale production	Low yield when temperature rises
[24]	8–10 %	Not very sensitive to high temperatures	Poor performance in full Sun
[25]	1–2 %	Easy to handle, affordable price	High cost, unreliable
[26]	26 %	Less high frequency noise	High cost
[27]	40,7 %	Better yield thanks to the concentrator	The increase in temperature disrupts the proper functioning of the concentrator and therefore reduces efficiency.
[28]	11 %	Simple hardware technology therefore easy to use	System very little developed and less used therefore not reliable
[29]	18,7 %	Fast and less expensive manufacturing process, resistance to heating	Requires few materials but some contain polluting substances

This evolution of the literature also allows us to take into consideration Panel technology: Different types of solar panels (monocrystalline, polycrystalline, thin films, etc.) have different efficiencies, which can influence the overall efficiency of the photovoltaic system.

3. Modeling of PV systems

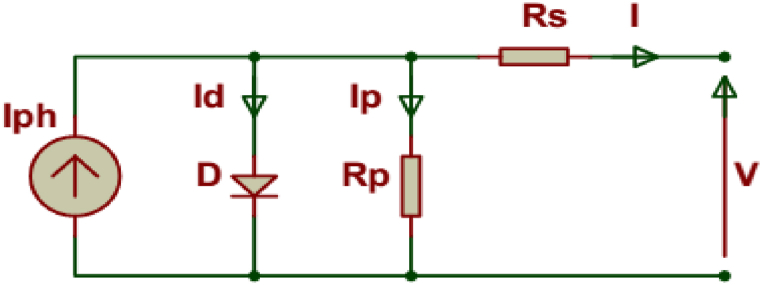
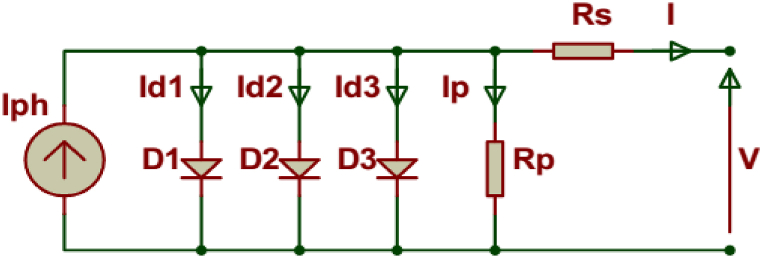
In order to generate an accurate photovoltaic cell design, it is necessary to have a good mathematical model. After that, it can be used as a search strategy to not only estimate the best values for the model, but also for supervision and fault diagnosis [[30], [31], [32], [33]]. In this article the simulation of photovoltaic cells is carried out using the Simulink approach based on electrical circuits. Among the electrical circuit-based models, the ideal single-diode model in Fig. 2 is the one with the lowest computational complexity [[34], [35], [36], [37]]. The one-diode model in Fig. 3 offers the best compromise between simplicity and precision [[38], [39], [40], [41]]. Considering the recombination loss in the depletion region, the more precise two-diode models in Fig. 4 and then the three-diode models in Fig. 5 were introduced [[42], [43], [44], [45]]. Among the different models used to model the normal operation of PVs, in practice, only the single diode (SD) models and the two diode (DD) model are retained for their simplicity and efficiency [46,47].

Fig. 2.

Ideal model of a PV cell.

Fig. 3.

Model of a one-diode PV cell.

Fig. 4.

Figure Model of a two-diode PV cell.

Fig. 5.

Model of a three-diode PV cell.

In practice, a shunt resistor is added to account for the small current leakage caused by the nonlinearity of the semiconductor. In addition a series resistance is also added to model metallic connections and resistance of semiconductor materials [41].

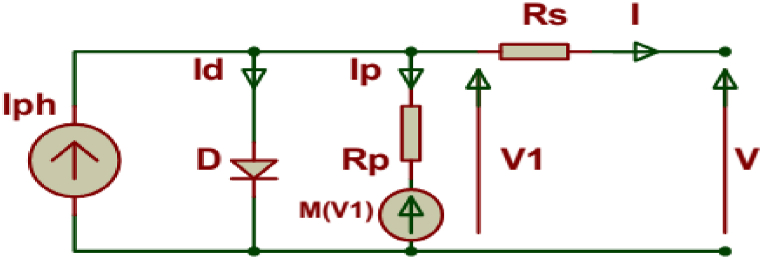
The Bishop model in Fig. 6 makes it possible to model a PV in normal and inverse operation using the Bishop parameters [42].

Fig. 6.

Equivalent circuit for the Bishop model.

Table 3 provides the summary table of the mathematical equations of the models most used in the literature. However, the one-diode model is used in this work for its many advantages.

Table 3.

Summary of the different PV cell models with their number and number of parameters.

Model	Number of diodes	Number of parameters to determine	Model equation
Ideal	1	Iph, I0, n	$\mathit{I}=\mathit{I}\mathit{p}\mathit{h}-\mathit{I}\mathbf{0}\left[\mathit{exp}\frac{\mathit{q}.\mathit{V}\mathit{d}}{\mathit{n}.\mathit{k}.\mathit{T}}\right]-\mathbf{1}$
One diode	1	Iph, I0, n, Rs, Rsh	$\mathit{I}=\mathit{I}\mathit{p}\mathit{h}-\mathit{I}\mathbf{0}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{n}.\mathit{V}\mathit{t}}\right)-\mathbf{1}\right]-\mathit{V}+\frac{\mathit{I}.\mathit{R}\mathit{s}}{\mathit{R}\mathit{s}\mathit{h}}$
Two diodes	2	Iph,I01, I02, n1, n2. Rs, Rsh	$\mathit{I}=\mathit{I}\mathit{p}\mathit{h}-\mathit{I}\mathbf{01}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{n}\mathbf{1}.\mathit{V}\mathit{t}}\right)-\mathbf{1}\right]-\mathit{I}\mathbf{02}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{n}\mathbf{2}.\mathit{V}\mathit{t}}\right)-\mathbf{1}\right]-\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{R}\mathit{s}\mathit{h}}$
Three diodes	3	Ipv,I01, I02, n1, n2. Rs, Rp	$\mathit{I}=\mathit{I}\mathit{p}\mathit{v}-\mathit{I}\mathbf{01}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{n}\mathbf{1}.\mathit{V}\mathit{t}}\right)-\mathbf{1}\right]-\mathit{I}\mathbf{02}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{n}\mathbf{2}.\mathit{V}\mathit{t}}\right)-\mathbf{1}\right]-\mathit{I}\mathbf{03}\left[\mathit{exp}\left(\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{n}\mathbf{3}.\mathit{V}\mathit{t}}\right)-\mathbf{1}\right]-\frac{\mathit{V}+\mathit{I}.\mathit{R}\mathit{s}}{\mathit{R}\mathit{p}}$
Bishop	1	Iph, I0, n, Rs, Rp	$\mathbf{I}=\mathbf{Iph}-\mathbf{I}\mathbf{0}\left[\mathbf{exp}\left(\frac{\mathbf{V}+\mathbf{I}.\mathbf{Rs}}{\mathbf{n}.\mathbf{Vt}}\right)-\mathbf{1}\right]-\frac{\mathbf{V}+\mathbf{I}.\mathbf{Rs}}{\mathrm{Rp}}\left[\mathbf{1}+\mathbf{k}{\left(\mathbf{1}-\frac{\mathbf{V}+\mathbf{I}.\mathbf{Rs}}{\mathrm{Vb}}\right)}^{-\mathbf{n}}\right]$

Fig. 7(a–c) presents the types of photovoltaic cells according to the different technologies. On the other hand, several works in the current literature show the impact of the choice of cell type during production in a partial shade situation.

Fig. 7.

Main types of photovoltaic cells ((a) Monocrystalline cell; (b) Polycrystalline cell (c) Amorphous cell).

4. Simulated architectures and partial shading scenarios

This section presents the five main architectures developed in this work: SP (serial-parallel), BL (Bridge-Link); HC (Honey Comb); TCT (Total-Cross-Tied); TSPL (Triple Series Parallel Ladder); as well as the predefined partial shading scenarios which will be tested on our architectures: considering the Long Narrow (LN), Short Narrow (SN), Short Wide (SW), Long Wide (LW) and Middle (M) shading situations.).

4.1. Modeling of the five architectures or topologies

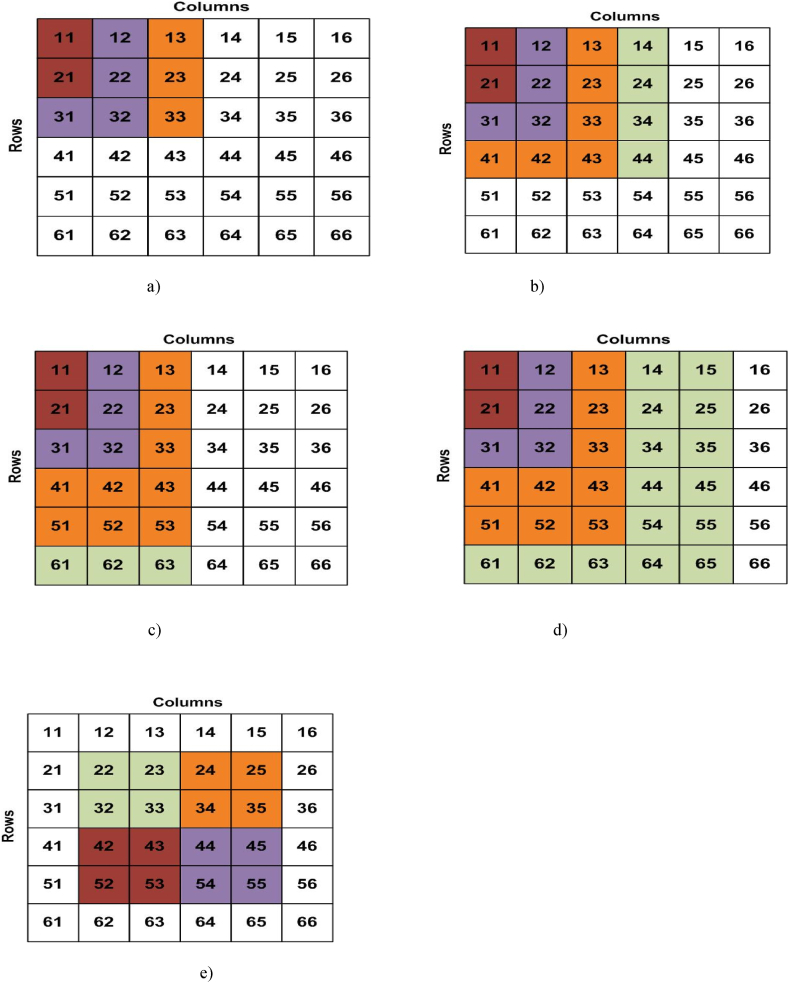
This section presents the five different architectural models developed in this study. They will be used to implement the different partial shading scenarios. One of the objectives of this research is also to evaluate the link between the variation in output power and the variation in shading level. Fig. 8(a–e) presents the different architectures or topologies.

Fig. 8.

Architecture modeling ((a) SP, (b)BL, (c) HC; (d) TCT; (e)TSP-L).

4.2. Scenarios for different partial shading

The shading scenarios used in this work are conditioned by the irradiance levels in Fig. 9. Thus we have defined by hypotheses the irradiances to the colors in Fig. 9 with the values: 1000W/m²; 900W/m²; 700W/m²; 500W/m²; 300W/m²

Fig. 9.

Assignment of solar irradiance levels.

This assignment thus makes it possible to highlight the different distributions for each scenario directly applied to the architectures or topologies; its scenarios are as follows:

Scenario 1: Long Narrow (LN); scenario 2: Short Narrow (SN); scenario 3: Short Wide (SW);

Scenario 4: Long Wide (LW); scenario 5: medium shading situations (M); an illustration is made in Fig. 10(a–e):

Fig. 10.

Different scenarios (a) SN; (b) SW; (c) LN; (d) LW; (e) M.

Table 4 offers the main simulation parameters by integrating all the partial shading scenarios for the five topologies or architectures:

Table 4.

Simulation parameters.

Specifications	Monocrystalline PV Panel
Dimensions of PV panel (mm)	1490 × 990 × 42
No of cells in series	54
Module efficiency	14.6 %
Short circuit current(A)	8.47
Open circuit voltage(V)	34.63
Maximum current(A)	7.96
Maximum voltage(V)	27.01
Nominal Maximum power(W)	215
Model name	D6M215B5A

5. Results and discussions

This step presents the results and discussions for each partial shading scenario applied to the five architectures. A principal component analysis is also proposed by scenarios.

5.1. Short and narrow shading condition

Fig. 11(a1-b1): (a1) and (b1) present the behavior of the five architectures or topologies for scenario 1: SN; the values obtained at output are presented in Table 5 and the TCP and TSPL architectures offer the best results in terms of power, i.e. 6233.07 W and 6183.96 W. Table 6 presents the descriptive statistics for this scenario1.

• •Statistical analysis of scenario 1: SN

Fig. 11.

Scenario1 ((a1) current-voltage; (b1) power-voltage).

Table 5.

Values obtained in output with scenario 1: SN.

	Voc	Isc	Vmp	Imp	Pmp
SP	207.09	51.19	165.19	35.74	5903.13
BL	207.09	51.19	166.57	35.97	5992.26
HC	207.09	51.19	166.57	35.82	5967.21
TCT	206.39	51.19	168.30	37.04	6233.07
TSPL	207.09	51.19	168.30	36.74	6183.96

Table 6.

Descriptive statistics.

Variable	values	Obs. without missing data	Minimum	Maximum	Average	Type Deviation
Voc	5	5	206,390	207,090	206,950	0,313
Vmp	5	5	165,190	168,300	166,986	1,325
Imp	5	5	35,740	37,040	36,262	0,589
Pmp	5	5	5903,130	6233,070	6055,926	144,086

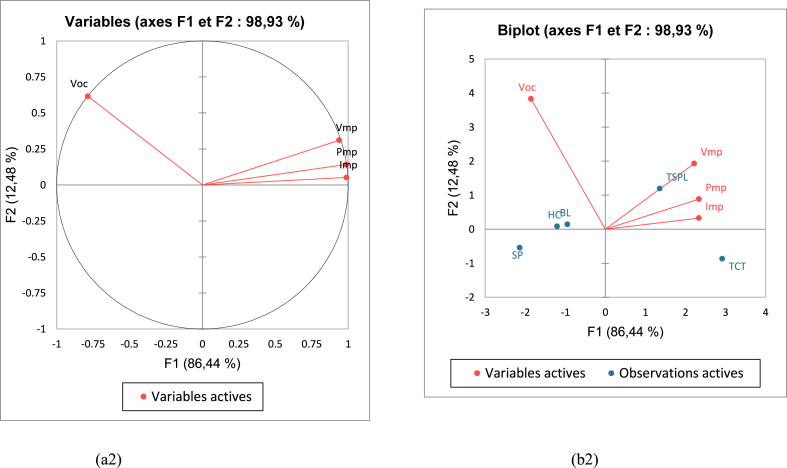
Fig. 12(a2-b2): (a2) and (b2) represent the correlation circle thus F1 and F2 represent respectively the first (86.44 %) and the second (12.48 %) dimension of ACP; the variables Vmp, Imp, Pmp have a strong positive correlation so there is a very strong link between its variables. The Bioplot (b2) confirms that the TCT and TSPL architectures have a better weight and a better correlation with the variables. Table 7, Table 8 confirm this.

Fig. 12.

(a2) correlation circle; (b2) variables and observations of bioplots.

Table 7.

Correlations between variables and factors.

	F1	F2	F3	F4
Voc	−0,786	0,616	−0,051	0,000
Vmp	0,940	0,311	0,143	0,000
Imp	0,990	0,052	−0,134	0,000
Pmp	0,989	0,142	−0,043	0,000

Table 8.

Coordinates of observations.

	F1	F2	F3	F4
SP	−2,135	−0,542	−0,286	0,000
BL	−0,946	0,141	0,094	0,000
HC	−1,201	0,081	0,319	0,000
TCT	2,923	−0,871	0,021	0,000
TSPL	1,360	1,191	−0,148	0,000

5.2. Short wide shading condition

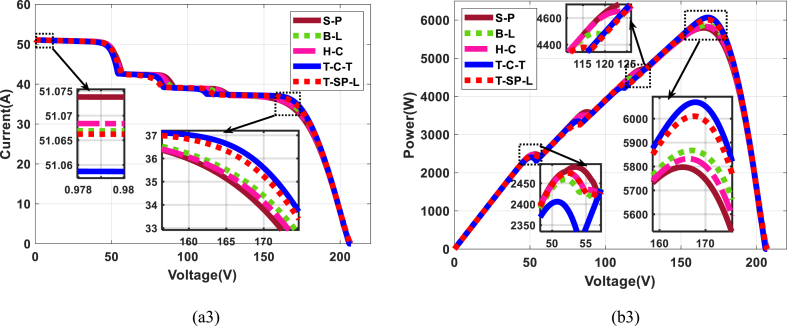
Fig. 13(a3-b3): (a3) and (b3) present the behavior of the five architectures or topologies for scenario 2: SW; the values obtained at the output are presented in Table 9 and the TCT and TSPL architectures offer the best results in terms of power, i.e. 6068.89 W and 6010.34 W. Table 10 presents the descriptive statistics for this scenario 2.

• •Statistical analysis of scenario 2:

Fig. 13.

Scenario 2 ((a3) current-voltage; (b3) power-voltage).

Table 9.

Values obtained in output with scenario 2: SW.

	Voc	Isc	Vmp	Imp	Pmp
SP	207.09	51.19	165.19	35.10	5797.43
BL	206.74	51.19	166.92	35.15	5867.08
HC	206.74	51.19	166.22	35.09	5832.39
TCT	206.05	51.19	167.61	36.21	6068.89
TSPL	207.09	51.19	167.26	35.93	6010.34

Table 10.

Descriptive statistics.

Variable	values	Obs. without missing data	Minimum	Maximum	Average	Type Deviation
Voc	5	5	206,050	207,090	206,742	0,425
Vmp	5	5	165,190	167,610	166,640	0,960
Imp	5	5	35,090	36,210	35,496	0,534
Pmp	5	5	5797,430	6068,890	5915,226	118,020

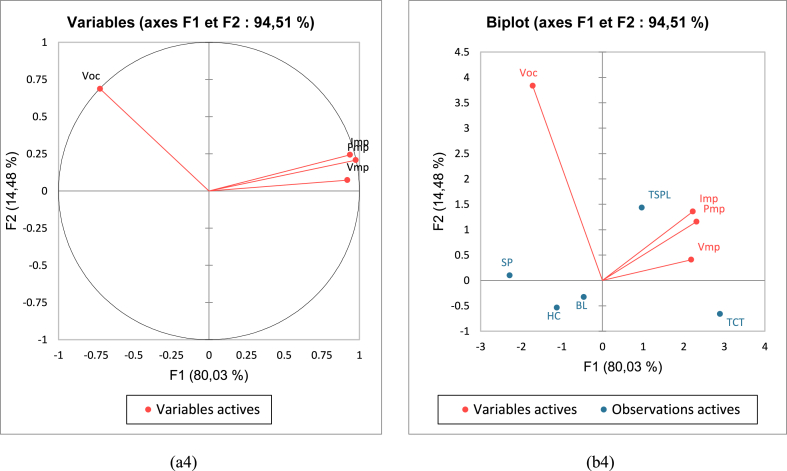
Fig. 14(a4-b4): (a4) and (b4) represent the correlation circle thus F1 and F2 represent respectively the first (80.03 %) and the second (14.48 %) dimension of ACP; the variables Vmp, Imp, Pmp have a strong positive correlation so there is a very strong link between its variables. The Bioplot (b4) confirms that the TCT and TSPL architectures have a better weight and a better correlation with the variables. Table 11, Table 12 confirm this.

Fig. 14.

(a4) Correlation circle; (b4) variables and observations of bioplots.

Table 11.

Correlations between variables and factors.

	F1	F2	F3	F4
Voc	−0,723	0,687	0,069	0,000
Vmp	0,920	0,073	0,385	0,000
Imp	0,938	0,243	−0,246	0,000
Pmp	0,975	0,207	−0,075	0,001

Table 12.

Coordinates of observations.

	F1	F2	F3	F4
SP	−2,283	0,097	−0,639	−0,001
BL	−0,459	−0,329	0,722	−0,001
HC	−1,123	−0,537	0,170	0,001
TCT	2,896	−0,663	−0,359	0,000
TSPL	0,969	1,432	0,107	0,000

5.3. Long narrow shading condition

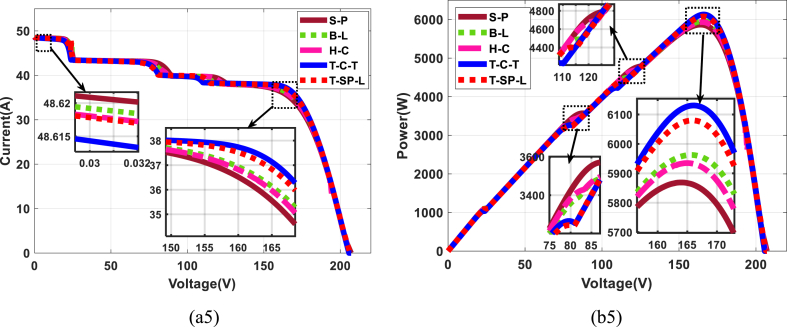
Fig. 15(a5-b5): (a5) and (b5) present the behavior of the five architectures or topologies for scenario 3: LN; the values obtained at the output are presented in Table 13 and the TCT and TSPL architectures offer the best results in terms of power, i.e. 6130.57 W and 6079.91 W. Table 14 presents the descriptive statistics for this scenario 3.

• •Statistical analysis of scenario 3: LN

Fig. 15.

Scenario 3 ((a5) current-voltage; (b5) power-voltage).

Table 13.

Output values obtained with scenario 3: LN.

	Voc	Isc	Vmp	Imp	Pmp
SP	207.09	48.63	163.80	35.83	5868.86
BL	206.74	48.63	165.53	36.02	5962.42
HC	206.74	48.63	164.84	36.00	5934.84
TCT	205.70	48.63	165.88	36.96	6130.57
TSPL	206.74	48.63	165.88	36.65	6079.91

Table 14.

Descriptive statistics.

Variable	Observations	Obs. sans données manquantes	Minimum	Maximum	Average	Type Deviation
Voc	5	5	205,700	207,090	206,602	0,527
Vmp	5	5	163,800	165,880	165,186	0,884
Imp	5	5	35,830	36,960	36,292	0,487
Pmp	5	5	5868,860	6130,570	5995,320	107,448

Fig. 16(a6-b6): (a6) and (b6) represent the correlation circle thus F1 and F2 represent respectively the first (87.27 %) and the second (9.03 %) dimension of ACP; the variables Vmp, Imp, Pmp have a strong positive correlation so there is a very strong link between its variables. the Bioplot (b6) confirms that the TCT and TSPL architectures have a better weight and a better correlation with the variables. Table 15, Table 16 confirm this.

Fig. 16.

(a6) Correlation circle; (b6) variables and observations of biplots.

Table 15.

Correlations between variables and factors.

	F1	F2	F3	F4
Voc	−0,882	0,426	0,202	0,000
Vmp	0,891	0,412	−0,192	0,000
Imp	0,969	−0,066	0,236	−0,001
Pmp	0,990	0,074	0,121	0,001

Table 16.

Coordinates of observations.

	F1	F2	F3	F4
SP	−2,573	−0,512	0,353	−0,001
BL	−0,436	0,533	−0,555	−0,002
HC	−1,029	−0,096	−0,238	0,003
TCT	2,865	−0,752	−0,057	0,000
TSPL	1,173	0,827	0,497	0,000

5.4. Long wide shading condition

Fig. 17(a7-b7): (a7) and (b7) present the behavior of the five architectures or topologies for scenario 4: LW; the values obtained at the output are presented in Table 17 and the TCT and TSPL architectures offer the best results in terms of power, i.e. 5884.46 W and 5835.30 W. Table 18 presents the descriptive statistics for this scenario 4.

• •Statistical analysis of scenario 4: LW

Fig. 17.

Scenario 4: ((a7) courant-tension; (b7) puissance-tension).

Table 17.

Values obtained as output with the scenario 4: LW.

	Voc	Isc	Vmp	Imp	Pmp
SP	207.09	46.92	164.49	34.25	5634.56
BL	206.39	46.92	166.22	34.43	5723.92
HC	206.39	46.92	165.53	34.42	5696.80
TCT	205.70	46.92	166.57	35.33	5884.46
TSPL	206.39	46.92	166.57	35.03	5835.30

Table 18.

Descriptive statistics.

Variable	values	Obs. without missing data	Minimum	Maximum	Average	Type Deviation
Voc	5	5	205,700	207,090	206,392	0,491
Vmp	5	5	164,490	166,570	165,876	0,884
Imp	5	5	34,250	35,330	34,692	0,463
Pmp	5	5	5634,560	5884,460	5755,008	102,551

Fig. 18(a8-b8): (a8) and (b8) represent the correlation circle thus F1 and F2 represent respectively the first (89.81 %) and the second (5.95 %) dimension of ACP; the variables Vmp, Imp, Pmp have a strong positive correlation so there is a very strong link between its variables. The Bioplot (b8) confirms that the TCT and TSPL architectures have a better weight and a better correlation with the variables. Table 19, Table 20 confirm this.

Fig. 18.

(a8) Correlation circle; (b8) variables and observations of biplots.

Table 19.

Correlations between variables and factors.

	F1	F2	F3	F4
Voc	−0,927	0,198	0,318	0,000
Vmp	0,926	−0,282	0,251	−0,001
Imp	0,950	0,311	−0,009	−0,002
Pmp	0,986	0,151	0,072	0,003

Table 20.

Coordinates of observations.

	F1	F2	F3	F4
SP	−2,851	0,571	−0,050	0,002
BL	−0,278	−0,761	0,217	0,005
HC	−0,871	−0,363	−0,367	−0,006
TCT	2,705	0,272	−0,468	0,002
TSPL	1,295	0,281	0,667	−0,003

5.5. Middle shading condition

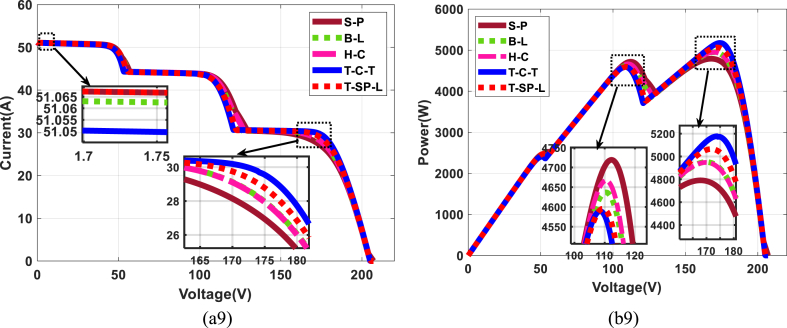
Fig. 19(a9-b9): (a9) and (b9) present the behavior of the five architectures or topologies for scenario 5: M; the values obtained at the output are presented in Table 21 and the TCT and TSPL architectures offer the best results in terms of power, i.e. 5777.27 W and 5065.37W. Table 22 presents the Descriptive Statistics for this scenario 5.

• •Statistical analysis of scenario 5: M

Fig. 19.

Scenario 5 ((a9) current-voltage; (b9) power-voltage).

Table 21.

Values obtained as output with scenario 5: M.

	Voc	Isc	Vmp	Imp	Pmp
SP	207.09	51.19	167.61	28.59	4791.17
BL	205.36	51.19	169.69	29.18	4951.40
HC	205.36	51.19	169.69	29.16	4947.79
TCT	205.36	51.19	173.84	29.78	5177.27
TSPL	205.70	51.19	171.76	29.49	5065.37

Table 22.

Descriptive statistics.

Variable	values	Obs. without missing data	Minimum	Maximum	Average	Type Deviation
Voc	5	5	205,360	207,090	205,774	0,750
Vmp	5	5	167,610	173,840	170,518	2,367
Imp	5	5	28,590	29,780	29,240	0,443
Pmp	5	5	4791,170	5177,270	4986,600	144,480

Fig. 20(a10-b10): (a10) and (b10) represent the correlation circle thus F1 and F2 represent respectively the first (89.41 %) and the second (10.52 %) dimension of ACP; the variables Vmp, Imp, Pmp have a strong positive correlation so there is a very strong link between its variables. the Bioplot (b10) confirms that the TCT and TSPL architectures have a better weight and a better correlation with the variables. Table 23, Table 24 confirm this.

Fig. 20.

(a10) Correlation circle; (b10) variables and observations of bioplots.

Table 23.

correlations between variables and factors.

	F1	F2	F3	F4
Voc	−0,821	0,571	0,010	0,000
Vmp	0,967	0,254	−0,033	0,000
Imp	0,997	0,065	0,038	0,000
Pmp	0,987	0,161	0,002	0,001

Table 24.

Coordinates of observations.

	F1	F2	F3	F4
SP	−3,207	0,650	−0,017	0,000
BL	−0,154	−0,779	0,011	0,001
HC	−0,195	−0,791	−0,027	−0,001
TCT	2,558	0,573	−0,059	0,000
TSPL	0,998	0,347	0,093	0,000

5.6. Discussion

The statistical study in principal component analysis (PCA) in this article takes into account the five architectures presented (SP, BL, HC, TCP, TSPL.) for 6 × 6 monocrystalline (PV) system as input variables; it is important to note that all the data or values are established from the output values obtained with each architecture, that is to say the currents, voltages and powers taken in the different scenarios or operating cases; corresponding to forms of partial shading already defined beforehand by the solar irradiance levels: 1000W/m2; 900W/m2; 700W/m2; 500W/m2; 300W/m2; .This approach therefore allows us to have a precise analysis of the behavior of our five architectures when we apply the different partial shading scenarios; the data sets obtained also make it possible to establish a correlation between the forms of partial shading and the nature of the power losses at the levels of the architectures studied; this observation was also demonstrated by the work of [3]; on the other hand, from the results obtained in this work new mathematical correlation models can be developed in our future work with the ultimate goal of better controlling the impact of partial shading configurations or scenarios in a power loss situation. for a PV architecture. A direct comparison with the work [31] in which serial hybrid architectures also offers better results, confirming that series-parallel coupling improves the performance of the output values depending on the configurations. This observation is also valid in this article with regard to the power, voltage and current values for the T-C-T and T-SP-L architectures with better weight and significance in comparison with other architectures; with a better output production of around 6233.07W for scenario 1. We also see that the performances of the architectures are closely linked to the nature of (a) Monocrystalline cell, (b) Polycrystalline cell, (c) Amorphous cell cell; PV systems; this observation is also made in the work [32] it therefore becomes interesting to analyze the results obtained for the different architectures if at the output we rather have two diodes, three diodes, or the Bishop model.

6. Conclusion

The main objective of this article was to classify and above all compare several architectural topologies of photovoltaic systems with the aim of reducing or limiting the impact of partial shading. Five architectures (SP, BL, HC, TCT, TSPL) were modeled and simulated for five operating scenarios in clearly defined partial shading conditions: Long Narrow (LN), Short Narrow (SN), Short Wide (SW), Long Wide (LW) and Middle (M) shading situations by observing for each operating scenario the power, current and voltage values obtained at the output. Thus allowing a descriptive statistical analysis of the output quantities for better classification and assessment. The essential contributions in this article were:

• •An in-depth study of several recent architectures or topologies in the literature depending on the size of the panels and the associated mathaheuristic algorithms
• •A modeling and a comparative simulation of the five topologies or architectures for well-defined partial shading scenarios with the ultimate goal of making a classification according to the performance of the quantities obtained at the output.
• •Highlighting the existing link between the variation of the partial shading level in the different scenarios and the production of maximum output power.
• •A principal component analysis for each partial shading scenario for a better analysis of the correlations between the five architectures: SP, BL, HC, TCP, TSPL.

The results obtained in this work offer better powers with the TCP and TSPL architectures for the different system simulation scenarios with irradiances; statistical validation establishes a good correlation for its two architectures during the comparative study for each operating scenario. Thus contribute to optimizing the production of electrical energy in several sectors of activity with support for sustainable development, such as:

• (i)On the industrial level with decentralized production plants connected to the standard electricity network with the aim of injecting energy in the event of collapse of the electricity network for cases of heavy demand on certain receivers or loads.
• (ii)In terms of energy quality in accordance with the requirements of the IEEE-519-2022 standard, energy suppliers are required to provide clean energy with a harmonic distortion rate of less than 3 % in single-phase and less than 5 % in three-phase regime. ; the TCP and TSPL architectures can therefore be used to create a harmonic hybrid filter connected to the electrical network with a capacity to optimize the DC voltage of the power inverter which is a very important module of the harmonic hybrid filter.
• (iii)In the automotive industry, which is experiencing significant growth today with the creation of electric vehicles equipped with coverings or frames with photovoltaic cells, with the aim of improving the energy autonomy performance of the vehicle. TCP and TSPL architectures can also be used in this scenario.

As a perspective in future work, it therefore becomes interesting to analyze in depth the behavior of the PV modules according to the results obtained for the different architectures if the output is rather two diodes, three diodes, or the Bishop model. Because the performances of the architectures are closely linked to the nature of: (a) Monocrystalline cell, (b) Polycrystalline cell, (c) Amorphous cell; as established in the scientific literature.

Disclosure statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Ethical approval

This paper does not contain any studies with human participants or animals performed by any of the authors.

Data availability statement

No data was used for the research described in the article.

CRediT authorship contribution statement

Luc Vivien Assiene Mouodo: Writing – original draft, Methodology, Formal analysis. AbdeL-Hamid Mahamat Ali: Validation, Software, Methodology. Alvine Donfang Moteyo: Software, Methodology. Jean Gaston Tamba: Supervision, Software, Methodology, Formal analysis, Conceptualization. Petros Axaopoulos: Supervision, Software, Formal analysis, Data curation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.