Abstract
This study aims to assess the effect of familial structures on the still-missing heritability estimate and prediction accuracy of Type 2 Diabetes (T2D) using pedigree estimated risk values (ERV) and genomic ERV. We used 11,818 individuals (T2D cases: 2,210) with genotype (649,932 SNPs) and pedigree information from the ongoing periodic cohort study of the Iranian population project. We considered three different familial structure scenarios, including (i) all families, (ii) all families with ≥ 1 generation, and (iii) families with ≥ 1 generation in which both case and control individuals are presented. Comprehensive simulation strategies were implemented to quantify the difference between estimates of 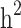 and
and 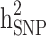 . A proportion of still-missing heritability in T2D could be explained by overestimation of pedigree-based heritability due to the presence of families with individuals having only one of the two disease statuses. Our research findings underscore the significance of including families with only case/control individuals in cohort studies. The presence of such family structures (as observed in scenarios i and ii) contributes to a more accurate estimation of disease heritability, addressing the underestimation that was previously overlooked in prior research. However, when predicting disease risk, the absence of these families (as seen in scenario iii) can yield the highest prediction accuracy and the strongest correlation with Polygenic Risk Scores. Our findings represent the first evidence of the important contribution of familial structure for heritability estimations and genomic prediction studies in T2D.
. A proportion of still-missing heritability in T2D could be explained by overestimation of pedigree-based heritability due to the presence of families with individuals having only one of the two disease statuses. Our research findings underscore the significance of including families with only case/control individuals in cohort studies. The presence of such family structures (as observed in scenarios i and ii) contributes to a more accurate estimation of disease heritability, addressing the underestimation that was previously overlooked in prior research. However, when predicting disease risk, the absence of these families (as seen in scenario iii) can yield the highest prediction accuracy and the strongest correlation with Polygenic Risk Scores. Our findings represent the first evidence of the important contribution of familial structure for heritability estimations and genomic prediction studies in T2D.
Supplementary Information
The online version contains supplementary material available at 10.1186/s40246-024-00669-7.
Keywords: Genome-wide association studies (GWAS), Heritability, Estimated risk values (ERV), Type 2 diabetes, Missing heritability
Introduction
The genetic architecture of complex traits and our ability to map the genes responsible for disease risk have become fundamental topics of study in human genetics. Sharing of common genetic risk factors (e.g., single nucleotide polymorphism or SNP) in relatives results in an increase in the risk of the disorder of those affected. By accepting this fundamental definition, heritability (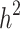 ) is formally defined as the proportion of variation in a particular trait attributable to genetic factors [1]. Reported results from genome-wide association studies (GWAS) provided associated SNPs that can be used to determine the proportion of variance explained by these loci together (
) is formally defined as the proportion of variation in a particular trait attributable to genetic factors [1]. Reported results from genome-wide association studies (GWAS) provided associated SNPs that can be used to determine the proportion of variance explained by these loci together (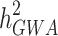 ). The difference between the heritability captured by these known associated SNPs and the one predicted by traditional genetic epidemiology studies is known as missing heritability [2]. The earlier GWASs were underpowered to detect the underlying common genetic variants, and the number of significant associations increased with the increase in sample sizes. By combining quantitative and population genetic concepts, new statistical methods were introduced by using genome-wide marker data simultaneously to evaluate the contribution of common SNPs (with a MAF ≥ 0.01 or 0.05) to variance,
). The difference between the heritability captured by these known associated SNPs and the one predicted by traditional genetic epidemiology studies is known as missing heritability [2]. The earlier GWASs were underpowered to detect the underlying common genetic variants, and the number of significant associations increased with the increase in sample sizes. By combining quantitative and population genetic concepts, new statistical methods were introduced by using genome-wide marker data simultaneously to evaluate the contribution of common SNPs (with a MAF ≥ 0.01 or 0.05) to variance, 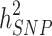 , [3–5]. These polygenic analyses have been successful in identifying hidden heritability, which is known as the difference between
, [3–5]. These polygenic analyses have been successful in identifying hidden heritability, which is known as the difference between 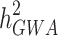 and
and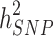 .
. 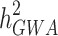 can become closer to
can become closer to 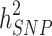 by increasing the sample size of the studied population. For most diseases the difference between
by increasing the sample size of the studied population. For most diseases the difference between 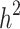 and
and 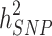 remains to be captured and considered as the still-missing heritability. Many possible explanations are represented for this part of missing, i.e., rare and structural genetic variants, dominance effects, and epistasis. Shared familial environmental factors can induce overestimation of heritability, and this phenomenon can explain some part of still-missing heritability.
remains to be captured and considered as the still-missing heritability. Many possible explanations are represented for this part of missing, i.e., rare and structural genetic variants, dominance effects, and epistasis. Shared familial environmental factors can induce overestimation of heritability, and this phenomenon can explain some part of still-missing heritability.
Heritability estimates help predict the trait of interest using prediction models [6]. Different approaches can be applied to predict the genetic risk of diseases in humans, including (i) pedigree Estimated Risk Values (ERV), which are referred to as “Estimated Breeding Values” or “EBV” in animal and plant breeding [7], (ii) Genomic ERV (GERV), known as “Genomic EBV” or “GEBV” in animal and plant breeding [8], and (iii) Polygenic Risk Scores or PRS [9]. ERV predicts an individual’s genetic risk for a specific trait based on its phenotype, the phenotypic data of its ancestors and relatives, and the pedigree information [7]. GERV is a prediction of the genetic risk of an individual for a specific trait using genome-wide genetic information [8]. GERV is calculated by summing up the effects of individual SNPs across the genome [10]. These SNP effects are estimated from a reference population, including large datasets of individuals with known phenotypes and genotypes [11]. In contrast, PRS predicts an individual’s genetic risk of developing a disease or a trait that utilizes a subset of genetic variants [9]. This approach uses SNPs and combining them into a score that reflects the individual’s genetic risk for that trait [12]. The risk of T2D has already been predicted in different populations using PRS [13–15].
In the GERV approach, the most common method to estimate prediction accuracy is to obtain the correlation between the predicted values and the actual phenotypic values in the testing dataset [16]. Several factors affect genomic prediction accuracy, including linkage disequilibrium (LD) between markers [16], statistical model [17], marker density [3], training population size and composition [18], heritability [19], and genetic architecture of the target trait [20]. Recently, training population composition has received considerable attention [18, 21]. It was shown that training populations with high diversity closely related to the target population which the testing set belongs to could improve prediction accuracies [18]. Despite multiple optimization strategies proposed to gain higher genomic prediction accuracy, the effect of familial structure has not been well investigated. This study aims to investigate the effect of familial structures on the still-missing heritability estimate and prediction accuracy of T2D using ERV and GERV. We analyzed different familial structure scenarios, as a possible contributing factor for still-missing heritability, to investigate the best population composition with the lowest still-missing heritability and the highest genomic prediction accuracy using GERV. The prediction ability of T2D based on the three approaches, ERV, GERV, and PRS, was also compared.
Materials and methods
Study subjects
Individuals participating in the Tehran Lipid and Glucose Study (TLGS), the ongoing periodic cohort study of the Iranian population project, were included in this study. The TCGS population consists of individuals from diverse ethnic backgrounds, providing valuable insights into the diversity of the Iranian population. This ethnic information was gathered through self-reported data and questionnaires detailing the birthplaces of the past three generations [22]. Epidemiological data on non-communicable disorders’ risk factors has been collected from 15,000 participants of TLGS every three years for the past 25 years. All participants in the cohort study executed written informed consent prior to inclusion. TLGS participants were recruited in six phases between October 1, 1999, and April 1, 2018, with approximately three years between each phase. The first phase had 15,005 participants, and the second phase had 3,531 new participants [22, 23]. Here, 14,113 individuals aged > 20 years were selected from the dataset, of which 2,284 and 11 individuals with missing data on diabetes status and body mass index (BMI) were excluded, respectively. We meticulously excluded cases that might have been misclassified as type 2 diabetes. This involved excluding not only patients with Type 1 diabetes and congenital diabetes but also those with monogenic diabetes, particularly Maturity-Onset Diabetes of the Young (MODY) [24]. Therefore, 11,818 individuals, with an age of 45.7 ± 16.8 years, entered the study.
We used the TLGS standard questionnaire to collect demographics, medical, and drug history information. Weight was measured in kilograms and height in meters; subsequently, the BMI of participants was calculated using the formula of 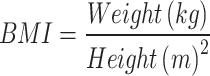 . Moreover, following a 12–14 h overnight fast, blood samples were taken from all study participants to quantify biochemical parameters, including fasting plasma glucose (FPG) and 2-hour postprandial plasma glucose (2hpp). T2D was defined as if one of the following conditions were present: (i) treatment with antidiabetic drugs at least once in 6 phases, (ii) FPG was more than 126 mg/dL, or (iii) 2hpp was more than 200 mg/dL.
. Moreover, following a 12–14 h overnight fast, blood samples were taken from all study participants to quantify biochemical parameters, including fasting plasma glucose (FPG) and 2-hour postprandial plasma glucose (2hpp). T2D was defined as if one of the following conditions were present: (i) treatment with antidiabetic drugs at least once in 6 phases, (ii) FPG was more than 126 mg/dL, or (iii) 2hpp was more than 200 mg/dL.
Genotyping, quality control, and imputation
All individuals were genotyped with HumanOmniExpress-24-v1-0 bead chip (Illumina, San Diego, CA) at deCODE genetic company. This bead chip provided 649,932 SNPs with an average mean distance of 4 Kb for each individual, as MS Daneshpour, et al. [25] described. To find any problem with recorded relationship information, a pedigree check was conducted using S.A.G.E (Statistical Analysis for Genetic Epidemiology) software v6.4 [26]. To perform a parentage check, snp1101 software v1.0 [27] was used to find contradictory information based on recorded parental and genotype platforms’ information [28]. This software checks for Mendelian inconsistencies and calculates the probability of correct parentage assignment. A conservative probability threshold of approximately 0.95 was used to ensure strong confidence in the detected parentage relationships. Any parent-offspring pairs with probabilities below this threshold were flagged for further investigation. We encountered inconsistencies in the parental information for a total of 132 individuals. Specifically, these inconsistencies pertained to the non-biological parent. To address this, we designated these 132 individuals as having unknown parentage with respect to the non-biological parent within the pedigree structure.
Quality control of individuals and genotypes was performed using PLINK software v1.9 [29]. We initiated the quality control (QC) process for both individuals and markers using PLINK software. Initially, we filtered out SNPs and individuals with a missing rate exceeding 20% to eliminate low-quality data, resulting in the removal of 770 SNPs and 11 individuals. This initial step was conducted using a non-stringent threshold. Subsequently, we applied a more stringent criterion by setting a threshold of 2% to exclude SNPs and individuals with more than 2% missing data. This step led to the removal of 17,636 SNPs, but no additional individuals were excluded. In the next phase, we examined sex discrepancies by comparing the recorded sex with genetic data derived from the X chromosome; no discrepancies were observed. To maintain the power of the study, we excluded SNPs with a minor allele frequency (MAF) of less than 0.05, which resulted in the exclusion of 72,500 SNPs. Additionally, markers that significantly deviated from Hardy-Weinberg equilibrium (HWE) were excluded using a p-value threshold of 1e-6, leading to the removal of 1,125 SNP markers. We also removed individuals whose heterozygosity rates deviated by more than ± 3 standard deviations from the mean, which led to the exclusion of 317 individuals. Population stratification was also checked using principal component analysis (PCA) using R software’s SNPRelate package [30]. Finally, the missing genotypes were imputed using Beagle software v5.4 [31].
Statistical analysis
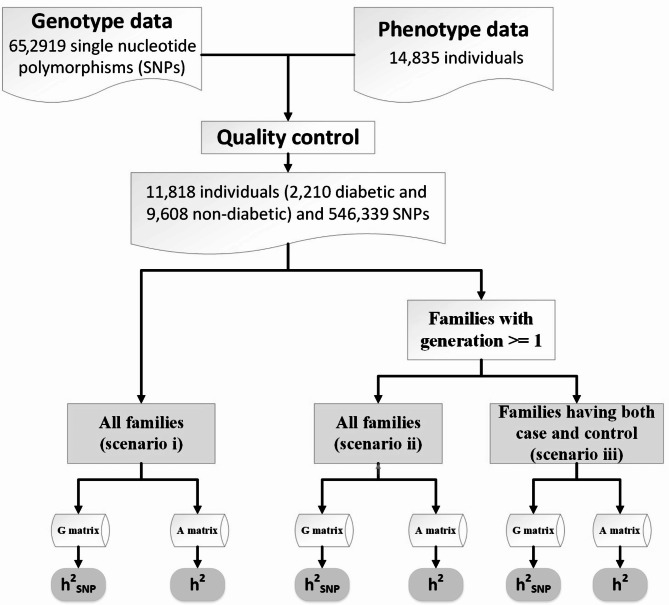
The design of this study is shown in Fig. 1.
Fig. 1.
Flowchart of population selection based on different scenarios. The overall design of this study was based on estimating of heritability based on models using A or G matrix computed using genealogical information or genome-wide common SNPs, respectively
Familial structure scenarios
Three different scenarios were used to investigate the effect of familial structure on still-missing heritability and genomic prediction accuracy (Fig. 1). In the first scenario, all families were used without any limitation (scenario i). In this scenario, of 11,818, we had 1,967 persons within 1,591 families with zero generation and respectively zero and non-zero pedigree- and genomic-based relatedness with the others. We evaluated the effect of these individuals on estimated heritability from pedigree and genome-wide markers in scenario ii by removing them from the data and comparing the results with the scenario i. This results in 9,851 individuals within 2,189 families with ≥ 1 generation. Of all families represented in the scenario ii, we had 1,091 families (3,959 individuals) that only have one disease status, case or control. We hypothesized that presenting families with only one disease status may induce overestimation of heritability in both pedigree- and genomic-based methods. This hypothesis is based on the understanding that heritability is a statistical measure quantifying the proportion of variation in a trait within a population attributable to genetic differences, ranging from 0 to 1. A value of 1 indicates that all observed variation in the trait is due to genetic factors, while a value of 0 suggests that the variation is entirely due to environmental factors. When all members of a family exhibit a particular disease, it implies that the disease is predominantly influenced by genetic factors within that family, resulting in heritability approaching 1. Conversely, if none of the family members have the disease, the heritability would still approach 1, indicating that genetic factors are the primary contributors to the absence of the disease within the family. This phenomenon can lead to an overestimation of heritability especially in pedigree-based estimations, as this method assumes an additive genetic relationship of zero between families, while SNP-based estimations consider non-zero genetic relationships between individuals across families. This hypothesis was tested by constructing scenario iii through removing families with only diabetic (case) or non-diabetic (control) individuals from scenario ii and resulting in 1098 families with both disease status represented within them.
Still-missing heritability estimation
To estimate heritability based on genealogical information (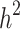 ), a generalized linear model framework was implemented. Each element of the response vector
), a generalized linear model framework was implemented. Each element of the response vector 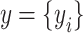 had two possible values, i.e., presence
had two possible values, i.e., presence 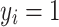 or absence
or absence 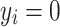 of T2D for the ith individual. We used a probit link function
of T2D for the ith individual. We used a probit link function 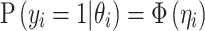 , where
, where 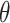 and Φ are a vector of regressors and the standard normal cumulative distribution function, respectively, and
and Φ are a vector of regressors and the standard normal cumulative distribution function, respectively, and 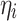 is a linear predictor given by:
is a linear predictor given by:
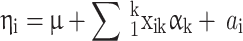 |
1 |
,
where µ is an intercept, 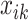 is the covariate of the
is the covariate of the 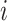 th individual at the
th individual at the 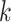 th effect (i.e., sex, age, and BMI),
th effect (i.e., sex, age, and BMI), 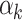 is the
is the 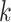 th fixed effect, and
th fixed effect, and 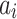 is the random genetic effect of the
is the random genetic effect of the 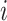 th individual. In this model we assumed a latent normally distributed variable
th individual. In this model we assumed a latent normally distributed variable 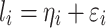 , where
, where 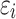 ’s are independent residual terms that follow the standard normal distribution, and a measurement model
’s are independent residual terms that follow the standard normal distribution, and a measurement model 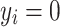 if
if 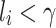 , and 1 otherwise, where γ is a threshold parameter, and
, and 1 otherwise, where γ is a threshold parameter, and 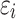 is an independent normal model residual with mean zero and variance set equal to one. In this equation, the vector of random additive genetic effect,
is an independent normal model residual with mean zero and variance set equal to one. In this equation, the vector of random additive genetic effect, 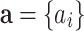 follows a multivariate normal distribution of
follows a multivariate normal distribution of 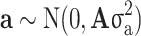 , where
, where 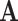 is the covariance matrix computed using pedigree information and
is the covariance matrix computed using pedigree information and 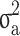 is an additive genetic variance caused by sample relatedness.
is an additive genetic variance caused by sample relatedness.
In order to estimate heritability based on genome-wide common SNPs (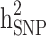 ), we used a linear predictor given by:
), we used a linear predictor given by:
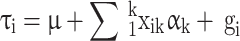 |
2 |
,
which is comparable to model (1); however, 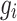 is the random genomic effect which is assumed to have a distribution of
is the random genomic effect which is assumed to have a distribution of  , where
, where 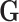 is the genomic relationship matrix constructed based on the method proposed by J Yang, et al. [32] and
is the genomic relationship matrix constructed based on the method proposed by J Yang, et al. [32] and 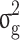 is the genomic variance.
is the genomic variance.
All models were fitted using the Bayesian approach implemented in the R package BGLR [33]. All Bayesian inference was conducted using a Markov chain Monte Carlo (MCMC) approach, Gibbs sampling. To estimate heritability, we ran 350,000 iterations of a Gibbs sampler, where the first 100,000 samples were discarded as burn-in, and the remaining samples were thinned at a thinning interval of 50. Thus, 5,000 posterior samples were used to infer the posterior distribution features. We conducted convergence diagnosis of the Gibbs sampler using a criterion of the accuracy of estimation of a quantile using the R package coda [34].
The 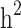 and
and 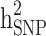 were then estimated by
were then estimated by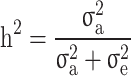 and
and 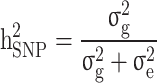 , and the still-missing heritability was calculated by subtracting
, and the still-missing heritability was calculated by subtracting 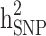 from
from 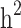 .
.
T2D risk prediction accuracy using ERV and GERV
T2D risk prediction was performed using three models: (i) model (1) above, (ii) model (2) above, and (iii) a fixed model as control, which is comparable to model (1) above, but without the random genetic effect term 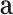 .
.
A 10-repeated 5-fold cross-validation (CV) was conducted to evaluate the prediction models’ performance in each scenario. In each repeat, we randomly divided individuals into 5 subsamples. In each fold of the CV, each subsample was considered the testing set and others the training set. The process followed until every 5 subsets were placed in the testing set precisely once. The entire process was repeated 10 times to reduce the variance of the estimated prediction accuracy. In each CV, for each model, the number of iterations of the Gibbs sampler was 210,000, with the first 60,000 samples discarded as burn-in. A thinning interval of 30 was used.
A receiver operating characteristic (ROC) analysis was used to compare the implemented models under different scenarios based on the area under curve (AUC), sensitivity, and specificity.
Construction and validation of T2D PRS
In the data, we calculated the PRS based on the summary statistics of a previous multi-ancestry GWAS conducted by A Mahajan, et al. [35], which is publicly available on the Diabetes Meta-Analysis of Trans-Ethnic association studies (DIAMANTE) Consortium data download website (http://diagram-consortium.org/downloads.html). Participants in the present study were independent of the DIAMANTE Consortium participants. From the summary statistics data, we removed SNPs with low info-score < 0.8, SNPs with MAF < 0.01, ambiguous SNPs, and SNPs on sex chromosomes.
PRSice software v2.3.3 [36] was used for PRS calculation using the commonly implemented method, LD clumping and p-value thresholding (C + T). As a default setting of the software, we adopted the additive model for PRS calculation, which sums up the dosage of the effective allele carried by an individual (ranging from 0 to 2). PRS was calculated for each individual using the following formulae:
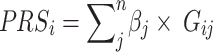 |
3 |
where 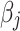 is the effective allele of the
is the effective allele of the 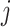 th SNP, which derived from DIAMANTE Consortium GWAS, as the base data,
th SNP, which derived from DIAMANTE Consortium GWAS, as the base data, 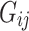 is the number of the effective allele of the
is the number of the effective allele of the 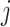 th SNP for the
th SNP for the 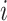 th individual,
th individual, 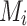 is the number of alleles included in the PRS for the
is the number of alleles included in the PRS for the 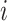 th individual, and
th individual, and 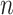 is the number of SNPs.
is the number of SNPs.
To implement C + T, LD clumping was first performed using pairwise LD of 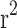 < 0.25 within 200 kb windows. Then, we calculated the PRS in the target data (n = 11,818) using different variant sets based on p-value thresholds between 1 and
< 0.25 within 200 kb windows. Then, we calculated the PRS in the target data (n = 11,818) using different variant sets based on p-value thresholds between 1 and 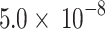 , Model 1 to Model 10, including age, sex, and the first 10 principal components (PCs), to account for population stratification (Table 1). The AUC metric was implemented to measure the capability of the model in discriminating between those having and not having T2D. The value of AUC closer to 1 is good in terms of discriminative performance, and the value of AUC closer to 0.5 means the model’s performance is like random guessing. In addition to AUC, Nagelkerke’s R² was used to establish the part of the variance in the dependent variable that the independent variable in each model could account for. This metric gives us an understanding of the models. The better the value, the more the fit toward the data. The logistic regression models have been compared through these metrics and labelled from model 1 to model 2. Among the models, Model 2 showed the highest performance, with respect to AUC and Nagelkerke’s R² value being the largest and substantially higher than the rest (p < 0.001, #variants = 3026).
, Model 1 to Model 10, including age, sex, and the first 10 principal components (PCs), to account for population stratification (Table 1). The AUC metric was implemented to measure the capability of the model in discriminating between those having and not having T2D. The value of AUC closer to 1 is good in terms of discriminative performance, and the value of AUC closer to 0.5 means the model’s performance is like random guessing. In addition to AUC, Nagelkerke’s R² was used to establish the part of the variance in the dependent variable that the independent variable in each model could account for. This metric gives us an understanding of the models. The better the value, the more the fit toward the data. The logistic regression models have been compared through these metrics and labelled from model 1 to model 2. Among the models, Model 2 showed the highest performance, with respect to AUC and Nagelkerke’s R² value being the largest and substantially higher than the rest (p < 0.001, #variants = 3026).
Table 1.
Performance metrics of logistic regression models (model 1 to Model 10) based on AUC and Nagelkerke’s R². The table highlights each model’s discriminative ability and explanatory power, with PT7 demonstrating superior performance across both metrics
| Model name | P-value threshold | #SNP | AUCa | Betab | P-valuec | Nagelkerke’s R2 d |
|---|---|---|---|---|---|---|
| Model 1 | P < 1 | 94,517 | 0.6396 | 0.7 | 4.97E-34 | 0.2 |
| Model 2 | P < 0.5 | 70,489 | 0.6442 | 0.69 | 2.39E-35 | 0.26 |
| Model 3 | P < 0.2 | 44,054 | 0.6503 | 0.7 | 1.16E-34 | 0.34 |
| Model 4 | P < 0.1 | 29,861 | 0.6527 | 0.71 | 6.62E-28 | 0.37 |
| Model 5 | P < 0.05 | 20,120 | 0.6549 | 0.72 | 5.46E-13 | 0.39 |
| Model 6 | P < 0.01 | 8,439 | 0.6621 | 0.69 | 1.31E-10 | 0.49 |
| Model 7 | P < 0.001 | 3,026 | 0.6632 | 0.7 | 5.78E-12 | 0.5 |
| Model 8 | P < 1E-04 | 1,528 | 0.6574 | 0.69 | 4.72E-12 | 0.43 |
| Model 9 | P < 1E-06 | 660 | 0.6495 | 0.7 | 4.60E-10 | 0.33 |
| Model 10 | P < 5E-08 | 473 | 0.6454 | 0.7 | 7.39E-10 | 0.27 |
aAUC (Area Under the Curve): This represents the ability of the model to distinguish between positive and negative cases. A higher AUC indicates better model performance
bThe coefficient value for the independent variable in the logistic regression model. It indicates the direction and strength of the relationship between the independent variable and the outcome
cThe statistical significance of the Beta coefficient
dIndicates the proportion of variance in the dependent variable that the model explains. Higher values indicate better explanatory power
To compare the prediction ability of PRS, ERV, and GERC, we calculated Spearman’s correlation between estimated ERVs or GERVs and predicted PRS on the target under the three different scenarios for family structure.
Simulation study
A simulation analysis was performed based on the TLGS dataset to quantify the difference between estimates of 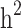 and
and 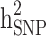 in the three familial structure scenarios. We randomly selected 250 SNPs from the genotype profile of the population and considered them as quantitative trait loci, assigning reference alleles as the effect alleles. The quantitative phenotype of each individual (
in the three familial structure scenarios. We randomly selected 250 SNPs from the genotype profile of the population and considered them as quantitative trait loci, assigning reference alleles as the effect alleles. The quantitative phenotype of each individual (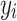 , for the ith individual) with a low (
, for the ith individual) with a low (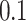 ), moderate (
), moderate (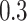 ), and high (
), and high (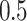 ) heritability (
) heritability (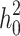 ) was simulated under an additive model by summing the effect sizes of all effect alleles using:
) was simulated under an additive model by summing the effect sizes of all effect alleles using:
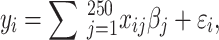 |
where 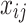 is the number of effect alleles carried by the ith individual at the jth randomly selected SNP,
is the number of effect alleles carried by the ith individual at the jth randomly selected SNP, 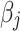 is the simulated effect of the jth SNP, and
is the simulated effect of the jth SNP, and 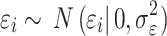 are i.i.d. standard normal residuals, where
are i.i.d. standard normal residuals, where 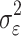 was set to (
was set to (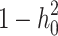 ) to ensure the desired level of heritability of the trait. Different studies have identified various numbers of SNPs (up to more than 400) significantly associated with T2D [35, 37, 38]. Based on the genetic structure of the disease, we assumed a total of 250 SNPs with nonzero effect. Among the candidate genes for T2D, a small number of them were highly replicated in T2D association studies [39]. Moreover, evidence from additional studies, such as the European and East Asian T2D GWAS meta-analyses [40, 41], suggests that specific SNPs located near critical genes associated with T2D demonstrate notably high effect sizes. This made us decide to introduce a small number of SNPs as major quantitative trait loci. Consequently, we assumed 70% of the additive genetic variance was explained by 247 SNPs with a relatively small effect, and the remaining 30% was explained by 3 SNPs with a sizable effect. The simulated
) to ensure the desired level of heritability of the trait. Different studies have identified various numbers of SNPs (up to more than 400) significantly associated with T2D [35, 37, 38]. Based on the genetic structure of the disease, we assumed a total of 250 SNPs with nonzero effect. Among the candidate genes for T2D, a small number of them were highly replicated in T2D association studies [39]. Moreover, evidence from additional studies, such as the European and East Asian T2D GWAS meta-analyses [40, 41], suggests that specific SNPs located near critical genes associated with T2D demonstrate notably high effect sizes. This made us decide to introduce a small number of SNPs as major quantitative trait loci. Consequently, we assumed 70% of the additive genetic variance was explained by 247 SNPs with a relatively small effect, and the remaining 30% was explained by 3 SNPs with a sizable effect. The simulated 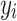 was sorted from big to small and the top
was sorted from big to small and the top 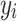 converted to T2D status, with the same prevalence as observed in our TLGS population. All simulation processes were repeated ten times to obtain a robust estimate of the heritability.
converted to T2D status, with the same prevalence as observed in our TLGS population. All simulation processes were repeated ten times to obtain a robust estimate of the heritability.
Results
Table 2 describes the number of families, cases, and controls along with the mean value of the covariates stratified by gender in different scenarios. After applying quality control, 11,818 individuals with 546,339 SNPs remained for further analysis of the T2D phenotype. As expected, the largest number of families (n = 3,780), cases (n = 2,210), and controls (n = 9,608) were included in the analyses when all families, disrespecting the T2D status of their members, were used. Using number of generations = 0 as a threshold (i.e., unrelated couples without children and families with one member), 1,591 families without pedigree relatedness were removed, resulting in all remaining families having pedigree relatedness. In contrast, the scenario in which families (generation ≥ 1) having both diabetic and non-diabetic had the lowest number of families (n = 1,098), cases (n = 1,638), and controls (n = 4,254).
Table 2.
Number of families, cases, and controls, T2D prevalence, and the average of covariates in each scenario
| Generation size | Family type | No. of families (all cases; cases & controls; all controls)a |
T2D prevalence (%) | Sex | Caseb | Controlc | Age (years) | BMI (kg/m2) |
|---|---|---|---|---|---|---|---|---|
| All families | All | 3,780 (368; 1,235; 2,177) | 23.00 | Men | 961 | 4,531 | 46 | 27.06 |
| Women | 1,249 | 5,077 | 45.35 | 28.57 | ||||
| Generation ≥ 1 | All | 2,189 (26; 1,098; 1,065) | 20.87 | Men | 745 | 3,939 | 44.5 | 27.01 |
| Women | 956 | 4,211 | 43.88 | 28.32 | ||||
| Case/control | 1,098 (0; 1,098; 0) | 38.50 | Men | 724 | 2,074 | 45.2 | 27.42 | |
| Women | 914 | 2,180 | 44.07 | 28.85 |
aNo. of families = the total number of families in each scenario; all controls = number of families in which all individuals are negative for T2D; cases&controls = number of families in which both diabetic (case) and non-diabetic (control) individuals are present; all cases = number of families in which all individuals are positive for T2D
bCase = the total number of positive individuals for T2D included in each scenario stratified by gender
cControl = the total number of negative individuals for T2D included in each scenario stratified by gender
Heritability and still-missing heritability
Heritability and still-missing heritability estimates obtained by each scenario are presented in Table 3. Given all scenarios, 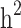 and
and 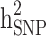 estimates ranged from 0.171 to 0.529 and from 0.095 to 0.334, respectively. We estimated the highest
estimates ranged from 0.171 to 0.529 and from 0.095 to 0.334, respectively. We estimated the highest 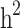 and
and 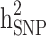 estimates when all families are included in the analysis. When families with generation = 0 were removed from the data (scenarios ii),
estimates when all families are included in the analysis. When families with generation = 0 were removed from the data (scenarios ii), 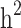 and
and 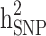 reduced by 15.9% and 5.1%, respectively. This shows that families with no information in their pedigree can affect
reduced by 15.9% and 5.1%, respectively. This shows that families with no information in their pedigree can affect 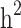 more than
more than 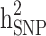 . Further removing families with only cases or only controls (scenario iii), 61.6% and 70% of the
. Further removing families with only cases or only controls (scenario iii), 61.6% and 70% of the 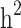 and
and 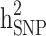 reduced, respectively. In other words, from scenario ii to scenario iii, the magnitudes of
reduced, respectively. In other words, from scenario ii to scenario iii, the magnitudes of 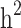 and
and 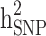 decreased by 0.274 and 0.22, respectively, demonstrating that the families with either case-only or control-only structures have a greater impact on the estimated
decreased by 0.274 and 0.22, respectively, demonstrating that the families with either case-only or control-only structures have a greater impact on the estimated 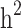 compared to
compared to 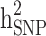 for the studied disease. Consequently, in families (≥ 1 generation) having both diabetic and non-diabetic individuals achieved the lowest
for the studied disease. Consequently, in families (≥ 1 generation) having both diabetic and non-diabetic individuals achieved the lowest 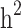 and
and 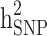 estimates.
estimates.
Table 3.
The estimates of additive genetic variance (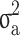 ), genomic variance (
), genomic variance (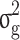 ), heritability (
), heritability (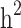 ), genomic heritability (
), genomic heritability (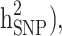 and still-missing heritability of type-2 diabetes (T2D) under different familial structure scenarios
and still-missing heritability of type-2 diabetes (T2D) under different familial structure scenarios
| Generation size | Family type |
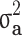 (SDa) (SDa) |
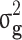 (SD) (SD) |
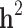 (SD) (SD) |
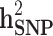 (SD) (SD) |
Still-missing heritability (%b) |
|---|---|---|---|---|---|---|
| All families | All | 0.804 (0.151) | 0.444 (0.061) | 0.529 (0.043) | 0.334 (0.033) | 0.195 (36.9%) |
| Generation ≥ 1 | All | 0.802 (0.175) | 0.464 (0.069) | 0.445 (0.053) | 0.317 (0.032) | 0.128 (28.8%) |
| Case/control | 0.206 (0.053) | 0.105 (0.026) | 0.171 (0.036) | 0.095 (0.021) | 0.076 (44.4%) |
aStandard deviation is calculated by 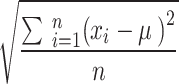 , where
, where 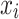 is the posterior value of the parameter from the n = 5,000 sampled iterations,
is the posterior value of the parameter from the n = 5,000 sampled iterations, 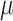 is the estimated posterior means of parameter
is the estimated posterior means of parameter
bProportion of still-missing heritability is calculated by 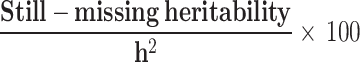
Still-missing heritability ranged from 0.076 to 0.195 among different scenarios. Family structure showed a noticeable effect on still-missing heritability estimates. The highest level of still-missing heritability was estimated when families with generation = 0 were considered in the model. However, the lowest estimate was given by the families (≥ 1 generation) comprising both diabetic and non-diabetic individuals. To eliminate the magnitude of 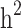 for comparing the still-missing heritability estimates between different family structures, the proportion of still-missing heritability was also represented. Interestingly, the lowest estimated proportion of still-missing heritability was found in scenario ii, suggesting that families with generation ≥ 1 could lead to much smaller estimated proportion of still-missing heritability.
for comparing the still-missing heritability estimates between different family structures, the proportion of still-missing heritability was also represented. Interestingly, the lowest estimated proportion of still-missing heritability was found in scenario ii, suggesting that families with generation ≥ 1 could lead to much smaller estimated proportion of still-missing heritability.
Assessment of T2D prediction
Our results indicate noticeable differences among the AUC, sensitivity, and specificity estimates obtained from different family structures applied to pedigree, genomic, and fixed models (Table 4). Among different scenarios, AUC and sensitivity ranged from 0.510 to 0.737 and 0.435 to 0.029, respectively. The highest AUC (0.737 ± 0.014) and sensitivity (0.435 ± 0.030) were given when T2D was predicted using GERV based on families (≥ 1 generation) comprising both diabetic and non-diabetic individuals. However, using the same input, pedigree-based T2D prediction by ERV obtained slightly lower AUC (0.623 ± 0.013) and sensitivity (0.425 ± 0.029). The fixed model gave the lowest AUC (0.510 ± 0.003) and sensitivity (0.029 ± 0.006) with all families as the input.
Table 4.
The mean (standard deviation) of area under curve (AUC), sensitivity and specificity of type-2 diabetes (T2D) prediction under different familial structure scenarios based on different models
| Generation size | Family type | Modela | AUC | Sensitivity | Specificity |
|---|---|---|---|---|---|
| All families | All | (1) | 0.713 (0.011) | 0.043 (0.009) | 0.984 (0.004) |
| (2) | 0.713 (0.011) | 0.044 (0.009) | 0.983 (0.004) | ||
| Fixed | 0.510 (0.003) | 0.029 (0.006) | 0.990 (0.003) | ||
| Generation ≥ 1 | All | (1) | 0.725 (0.013) | 0.036 (0.010) | 0.990 (0.003) |
| (2) | 0.724 (0.013) | 0.037 (0.011) | 0.989 (0.003) | ||
| Fixed | 0.511 (0.004) | 0.031 (0.008) | 0.992 (0.002) | ||
| Case and control | (1) | 0.736 (0.014) | 0.425 (0.029) | 0.821 (0.017) | |
| (2) | 0.737 (0.014) | 0.435 (0.030) | 0.817 (0.016) | ||
| Fixed | 0.553 (0.010) | 0.189 (0.018) | 0.917 (0.011) |
aModels (1) and (2) represents additive and genomic prediction models, respectively. Fixed model is comparable to model (1) but without the random genetic effect
The correlations between PRS and ERV or GERV ranged from 0.196 to 0.224 (Table 5 and Supplementary file, Figure S1). Using families with generation ≥ 1 and having both cases and controls showed the highest correlation between PRS and both GERV and ERV. In contrast, the lowest correlation was observed between PRS and ERV in both scenario i and ii.
Table 5.
Spearman’s correlation between polygenic risk scores (PRS) and genomic estimated risk values (GERV) or estimated risk values (ERV) obtained from full models (1) and (2)a in different scenarios
| GERV (p-value) | ERV (p-value) | ||
|---|---|---|---|
| All families | All | 0.220 (4.28e− 122) | 0.196 (4.20e− 96) |
| Generation ≥ 1 | All | 0.219 (1.81e− 100) | 0.196 (3.74e− 80) |
| Case/control | 0.224 (1.40e− 63) | 0.210 (3.14e− 56) | |
a Models (1) and (2) represents pedigree-based and genomic prediction models, respectively
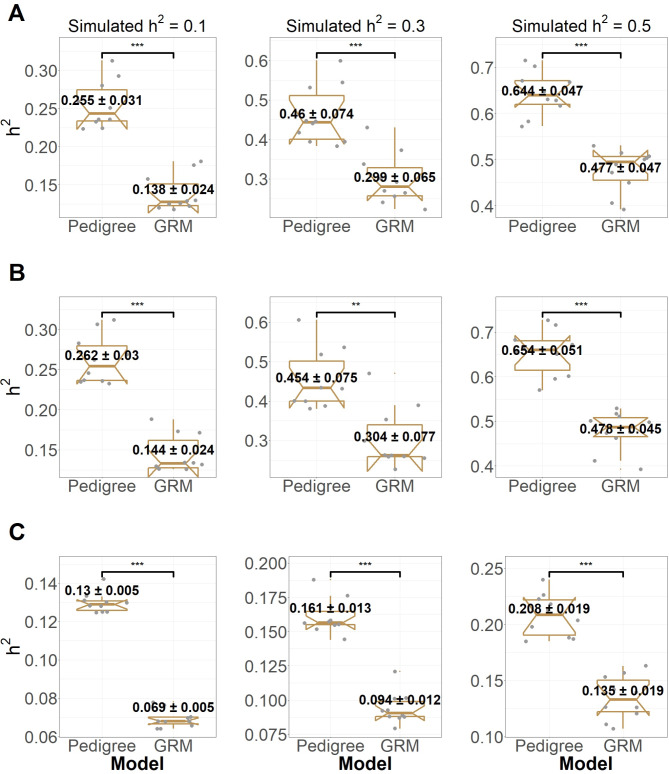
Simulation study
Figure 2 shows the difference between estimates of 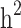 and
and 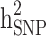 in the three different familial structures based on our simulated data. In scenarios i and ii, the estimated
in the three different familial structures based on our simulated data. In scenarios i and ii, the estimated 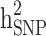 was very close to its moderate and high simulated heritability, while
was very close to its moderate and high simulated heritability, while 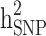 was overestimated in the low simulated heritability estimate scenario. The simulation results showed an overestimation of
was overestimated in the low simulated heritability estimate scenario. The simulation results showed an overestimation of 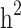 in different levels of simulated heritability for both scenarios i and ii. When only families with both case and control individuals with different heritabilities, scenario iii, were simulated,
in different levels of simulated heritability for both scenarios i and ii. When only families with both case and control individuals with different heritabilities, scenario iii, were simulated, 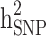 was underestimated. In scenario iii, the estimated
was underestimated. In scenario iii, the estimated 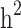 was slightly higher than the simulated low heritability of 0.1. However, for moderate (0.3) and high (0.5) levels of heritability, the estimated
was slightly higher than the simulated low heritability of 0.1. However, for moderate (0.3) and high (0.5) levels of heritability, the estimated 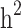 values were significantly lower than the simulated values.
values were significantly lower than the simulated values.
Fig. 2.
Differences between estimated heritability. The heritabilities were estimated based on genealogical information (pedigree) and genomic relationship matrix (GRM) in simulation study for three different familial structures, including all families (A), all families with ≥ 1 generation (B), and families with ≥ 1 generation in which both case control individuals are presented (C). In each plot, mean of estimated heritability based on the two different models was significantly differed at p-value < 0.01 (**) or 0.001 (***) based on a t-test
Discussion
Most diseases of complex origin have a quantitative genetic component contributing to their phenotypic variability. However, a significant part of the genetic component of complex phenotypes has not been discovered and this “still-missing heritability” [3, 39] requires special attention. For example, different explanations have been proposed for the still-missing heritability of T2D. Complex traits like T2D are highly polygenic, and GWAS might not be sufficiently robust in capturing the rare genetic variants with weak effects [42]. Low-frequency rare variants could also explain the missing heritability with large effects [43]. Moreover, twin studies might have overestimated heritability due to genetic interactions [44], gene-environment interactions [45], or violation of environment assumptions [46]. However, extended twin designs, when combined with additional data from other family members, can effectively differentiate the effects of shared environment and resolve confounds related to gene-by-common environment interactions [47]. In contrast, pedigree- or SNP-based heritability estimations typically lack twin data and are often implemented using statistical models that completely ignore shared environmental effects, including only additive and environmental variance components. This was the approach taken in our study. Consequently, our heritability estimates based on pedigree/SNP data may be biased due to the exclusion of shared variances. Nonetheless, this limitation does not affect our primary objective of evaluating the effect of population structure on the still-missing heritability and prediction accuracy, as we compared pedigree- and SNP-based without accounting for shared environment in both cases. It is also possible that the heritability of T2D has been overestimated in previous studies due to epigenetic effects or complex genetic interactions [44]. While the possible explanations for still-missing heritability of T2D were widely discussed [2, 39, 42], the effect of familial structure on the estimate of still-missing heritability of T2D has not been investigated yet. In this study, using three different familial structure scenarios, we showed that the still-missing heritability and prediction of T2D could be remarkably affected by familial structure.
It is well known that common SNPs can explain some proportion of the variation of the trait, and individuals with more genetic similarity estimated with genome-wide allele sharing show more phenotypic similarity in a variance components model [3, 48]. Confounding by population structure can occur because of a shared environment and significantly affect estimation models [49]. In this study, utilizing real data, we demonstrate that this confounding effect may be altered by the estimated similarity between individuals based on SNPs or genealogical information. Specifically, using pedigree information tends to yield a significantly higher estimated heritability compared to SNP information, particularly when representing families with either case-only or control-only structures. Although it has been proposed that for binary traits, such as T2D, additive variance is typically parameterized on an unobserved continuous liability scale to ensure heritability is independent of disease prevalence [50], our findings suggest that this method is inadequate for addressing family structure. Specifically, the absence of families with only case/control in cohort studies may lead to an underestimation of disease heritability in both pedigree-based (except in cases with low heritability) and SNP-based heritability estimations.
The highest still-missing heritability was observed when there were no limitations for families included in the analysis. Based on the simulation study, this relatively high still-missing heritability was mainly due to the overestimation of 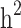 . Another possible reason is that the estimated heritability of families without pedigree relatedness is attributed more to the family structure than based on the genome-wide method (scenario i vs. scenario ii). However, removing these families (i.e., members without pedigree relatedness) slightly reduced the estimated heritability in scenario ii for the real data but not for the simulation study. In contrast, removing families with only case or only control structure drastically reduced the estimated heritability based on both the pedigree and genome-wide methods on both the simulated data and the real data. In other words, cohorts with a high proportion of families with only case and control structure may be susceptible to overestimation of heritability, especially for pedigree-based heritability estimation. We also cannot ignore the potential confounding effect of sample size in our study. The sample size of the different scenarios was not comparable, and with a larger sample size, there is a greater chance of capturing a representative amount of genomic or genetic variation in the population [51, 52]. Therefore, we suggest that further investigation of the familial structure effect on the still-missing heritability using scenarios with comparable sample sizes is important in future studies.
. Another possible reason is that the estimated heritability of families without pedigree relatedness is attributed more to the family structure than based on the genome-wide method (scenario i vs. scenario ii). However, removing these families (i.e., members without pedigree relatedness) slightly reduced the estimated heritability in scenario ii for the real data but not for the simulation study. In contrast, removing families with only case or only control structure drastically reduced the estimated heritability based on both the pedigree and genome-wide methods on both the simulated data and the real data. In other words, cohorts with a high proportion of families with only case and control structure may be susceptible to overestimation of heritability, especially for pedigree-based heritability estimation. We also cannot ignore the potential confounding effect of sample size in our study. The sample size of the different scenarios was not comparable, and with a larger sample size, there is a greater chance of capturing a representative amount of genomic or genetic variation in the population [51, 52]. Therefore, we suggest that further investigation of the familial structure effect on the still-missing heritability using scenarios with comparable sample sizes is important in future studies.
We show that familial structure can impact the predictive ability of the fixed, genetic, and genomic prediction models for T2D. Families with both cases and controls obtained higher sensitivity and lower specificity compared to the all-families scenario. One explanation for the differences in the T2D predictive ability based on different training subsets could be disease prevalence. When disease prevalence is high, like our scenario of families having both cases and controls, genomic prediction models tend to have higher sensitivity but lower specificity [53]. This is because the model may identify many individuals at high risk for the disease, even if they are not, to capture as many true positives as possible. However, this strategy may also result in a high false positive rate, reducing the model’s specificity [53]. Conversely, when disease prevalence is low, such presented in scenarios i and ii; genomic prediction models tend to have high specificity but low sensitivity [53]. This is because the model may be more conservative in its predictions, only identifying individuals at high risk if they have a strong genetic signal for the disease. However, this strategy may also result in a high false negative rate, reducing the sensitivity of the model. The impact of disease prevalence on AUC is less straightforward and may depend on the specific characteristics of the genomic prediction model and the disease being studied. In general, however, as disease prevalence increases, the AUC and accuracy of the model may also increase as the model has more information on the disease and can make more accurate predictions [54].
Another explanation for the differences in the T2D predictive ability by different subsets could be attributed to environmental factors. A study by AV Khera, et al. [55] investigated the prediction accuracy of a polygenic risk score for coronary artery disease in different racial and ethnic groups in the United States. The authors found that the risk score had variable performance across different groups, with higher performance in white individuals and lower in Hispanic and African American individuals. The authors suggested that this could be due to environmental factors such as lifestyle and healthcare access to some extent. Therefore, in our study, some unknown environmental effects might affect the T2D genomic prediction performance in some subsets of our population.
We cannot ignore the effect of sample size on genomic prediction performance. The relationship between sample size and genomic prediction accuracy can be explained by larger sample sizes providing more information on the genetic architecture of the trait being predicted. This additional information reduces the noise in the data and allows for a more accurate estimation of the effects of individual markers on the trait [16]. In contrast, as the sample size decreases as presented in scenario i to scenario iii, genomic and genetic prediction performance increases. This suggests that family structure may play an important role in prediction accuracy alongside disease prevalence. While increasing sample size can improve prediction accuracy up to a certain point, it is also essential to consider other factors, such as genetic diversity and marker density, when designing genomic prediction studies.
PRSs are a popular tool to estimate the risk of developing a specific common disease condition. However, PRS estimates in samples of unrelated participants can be affected by population stratification, assortative mating, and environmentally-mediated parental genetic effects [56, 57]. We show that the family structure can be a potential factor for the interpretation of PRS prediction. For instance, the highest correlation between T2D PRS and GERVs/ERVs was observed when families with both cases and control structure were used for estimating genetic/genomic risk values.
In conclusion, our study reveals that familial structure can play a significant role in the estimate of missing heritability of complex genetic diseases with the occurrence of case or control, such as T2D, and their genomic prediction performance. Specifically, our study shows that families with only case/control structure could overestimate pedigree-based heritability, resulting in a higher still-missing heritability estimate. Additionally, incorporating information about families containing both cases and controls can improve the performance of genomic prediction models in T2D. Our findings emphasize the importance of considering the familial structure for heritability estimations and genomic prediction studies in other diseases with the case/control outcome. Overall, our study highlights the need for further research on the impact of familial structure on genomic prediction and missing heritability.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
The authors would like to express their gratitude to the staff and participants in the TCGS project. Special thanks to deCODE genetics, Inc. (Reykjavik, Iceland) for their scientific support.
Author contributions
M.A.R. and M.A. were responsible for conceptualization, methodology, software, formal analysis, and visualization. S.V., M.A.R. and M.A. wrote the original draft. J.J., H.V., H.H., A.T., A.K. and S.V. were tasked with the validation of the study’s results. J.J., H.V., H.H. and A.T. made significant contributions to review and editing on the report. M.J., D.H., P.R., F.N. and S.T.F. were tasked with conducting the investigation and performing the review and editorial process for the report. H.L., S.M., A.S.Z., M.M.J., L.N.H.B., S.A., M.Z., M.R.M. and S.F.M. were responsible for data curation. F.A. and M.H. contributed to the study by reviewing and editing the report. M.S.D. and M.A. were responsible for project administration, investigation and supervision.
Data availability
No datasets were generated or analysed during the current study.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Maryam Sadat Daneshpour, Email: daneshpour@sbmu.ac.ir.
Mahdi Akbarzadeh, Email: akbarzadeh.ms@gmail.com.
References
- 1.Tenesa A, Haley CS. The heritability of human disease: estimation, uses and abuses. Nat Rev Genet. 2013;14(2):139–49. 10.1038/nrg3377 [DOI] [PubMed] [Google Scholar]
- 2.Eichler EE, Flint J, Gibson G, Kong A, Leal SM, Moore JH, Nadeau JH. Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev Genet. 2010;11(6):446–50. 10.1038/nrg2809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010; 42. [DOI] [PMC free article] [PubMed]
- 4.Yang J, Manolio TA, Pasquale LR, Boerwinkle E, Caporaso N, Cunningham JM, De Andrade M, Feenstra B, Feingold E, Hayes MG. Genome partitioning of genetic variation for complex traits using common SNPs. Nat Genet. 2011;43(6):519–25. 10.1038/ng.823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.So HC, Li M, Sham PC. Uncovering the total heritability explained by all true susceptibility variants in a genome-wide association study. Genet Epidemiol. 2011;35(6):447–56. [DOI] [PubMed] [Google Scholar]
- 6.Visscher PM, Hill WG, Wray NR. Heritability in the genomics era—concepts and misconceptions. Nat Rev Genet. 2008;9(4):255–66. 10.1038/nrg2322 [DOI] [PubMed] [Google Scholar]
- 7.Henderson CR. Best linear unbiased estimation and prediction under a selection model. Biometrics. 1975:423–47. [PubMed]
- 8.Meuwissen TH, Hayes BJ, Goddard M. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157(4):1819–29. 10.1093/genetics/157.4.1819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dudbridge F. Power and predictive accuracy of polygenic risk scores. PLoS Genet. 2013;9(3):e1003348. 10.1371/journal.pgen.1003348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Meuwissen T, Hayes B, Goddard M. Genomic selection: a paradigm shift in animal breeding. Anim Front. 2016;6(1):6–14. 10.2527/af.2016-0002 [DOI] [Google Scholar]
- 11.Hayes BJ, Lewin HA, Goddard ME. The future of livestock breeding: genomic selection for efficiency, reduced emissions intensity, and adaptation. Trends Genet. 2013;29(4):206–14. 10.1016/j.tig.2012.11.009 [DOI] [PubMed] [Google Scholar]
- 12.Duncan L, Shen H, Gelaye B, Meijsen J, Ressler K, Feldman M, Peterson R, Domingue B. Analysis of polygenic risk score usage and performance in diverse human populations. Nat Commun. 2019;10(1):3328. 10.1038/s41467-019-11112-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lello L, Raben TG, Yong SY, Tellier LC, Hsu SD. Genomic prediction of 16 complex disease risks including heart attack, diabetes, breast and prostate cancer. Sci Rep. 2019;9(1):15286. 10.1038/s41598-019-51258-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lei X, Huang S. Enrichment of minor allele of SNPs and genetic prediction of type 2 diabetes risk in British population. PLoS ONE. 2017;12(11):e0187644. 10.1371/journal.pone.0187644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Van Hoek M, Dehghan A, Witteman JC, Van Duijn CM, Uitterlinden AG, Oostra BA, Hofman A, Sijbrands EJ, Janssens ACJ. Predicting type 2 diabetes based on polymorphisms from genome-wide association studies: a population-based study. Diabetes. 2008;57(11):3122–8. 10.2337/db08-0425 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Habier D, Fernando RL, Dekkers J. The impact of genetic relationship information on genome-assisted breeding values. Genetics. 2007;177(4):2389–97. 10.1534/genetics.107.081190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.de Los Campos G, Hickey JM, Pong-Wong R, Daetwyler HD, Calus MP. Whole-genome regression and prediction methods applied to plant and animal breeding. Genetics. 2013;193(2):327–45. 10.1534/genetics.112.143313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Norman A, Taylor J, Edwards J, Kuchel H. Optimising genomic selection in wheat: effect of marker density, population size and population structure on prediction accuracy. G3: Genes Genomes Genet. 2018;8(9):2889–99. 10.1534/g3.118.200311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hayes BJ, Bowman PJ, Chamberlain AJ, Goddard ME. Invited review: genomic selection in dairy cattle: Progress and challenges. J Dairy Sci. 2009;92(2):433–43. 10.3168/jds.2008-1646 [DOI] [PubMed] [Google Scholar]
- 20.McClellan JM, Susser E, King M-C. Schizophrenia: a common disease caused by multiple rare alleles. Br J Psychiatry. 2007;190(3):194–9. 10.1192/bjp.bp.106.025585 [DOI] [PubMed] [Google Scholar]
- 21.Akdemir D, Isidro-Sánchez J. Design of training populations for selective phenotyping in genomic prediction. Sci Rep. 2019;9(1):1446. 10.1038/s41598-018-38081-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Daneshpour MS, Akbarzadeh M, Lanjanian H, Sedaghati-khayat B, Guity K, Masjoudi S, Zahedi AS, Moazzam-Jazi M, Bonab LNH, Shalbafan B. Cohort profile update. Tehran cardiometabolic genetic study, a path toward precision medicine; 2022. [DOI] [PMC free article] [PubMed]
- 23.Azizi F, Madjid M, Rahmani M, Emami H, Mirmiran P, Hadjipour R. Tehran lipid and glucose study (TLGS): rationale and design. Iran J Endocrinol Metabolism. 2000;2(2):77–86. [Google Scholar]
- 24.Asgarian S, Lanjanian H, Anaraki SR, Hadaegh F, Moazzam-jazi M, Bonab LNH, Masjoudi S, Zahedi AS, Zarkesh M, Shalbafan B. From genes to diagnosis: examining the clinical and genetic spectrum of maturity-onset diabetes of the young (MODY) in TCGS. Preprint at https://www.researchsquare.com/article/rs-3927463/v1; 2024. [DOI] [PMC free article] [PubMed]
- 25.Daneshpour MS, Fallah M-S, Sedaghati-Khayat B, Guity K, Khalili D, Hedayati M, Ebrahimi A, Hajsheikholeslami F, Mirmiran P, Tehrani FR. Rationale and design of a genetic study on cardiometabolic risk factors: protocol for the Tehran Cardiometabolic Genetic Study (TCGS). JMIR Res Protocols. 2017;6(2):e6050. 10.2196/resprot.6050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Elston RC, Gray-McGuire C. A review of the’Statistical analysis for genetic Epidemiology‘(SAGE) software package. Hum Genomics. 2004;1(6):1–4. 10.1186/1479-7364-1-6-456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sargolzaei M. SNP1101 user’s guide. Version 1.0. Guelph: HiggsGene Solut. Inc[Google Scholar]; 2014.
- 28.Akbarzadeh M, Moghimbeigi A, Morris N, Daneshpour MS, Mahjub H, Soltanian AR. A Bayesian structural equation model in general pedigree data analysis. Statistical analysis and data mining. ASA Data Sci J. 2019;12(5):404–11.
- 29.Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, De Bakker PI, Daly MJ. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559–75. 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zheng X, Levine D, Shen J, Gogarten SM, Laurie C, Weir BS. A high-performance computing toolset for relatedness and principal component analysis of SNP data. Bioinformatics. 2012;28(24):3326–8. 10.1093/bioinformatics/bts606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Browning BL, Zhou Y, Browning SR. A one-penny imputed genome from next-generation reference panels. Am J Hum Genet. 2018;103(3):338–48. 10.1016/j.ajhg.2018.07.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet. 2011;88(1):76–82. 10.1016/j.ajhg.2010.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pérez P, de Los Campos G. Genome-wide regression and prediction with the BGLR statistical package. Genetics. 2014;198(2):483–95. 10.1534/genetics.114.164442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Plummer M, Best N, Cowles K, Vines K. CODA: convergence diagnosis and output analysis for MCMC. R news. 2006;6(1):7–11. [Google Scholar]
- 35.Mahajan A, Spracklen CN, Zhang W, Ng MC, Petty LE, Kitajima H, Yu GZ, Rüeger S, Speidel L, Kim YJ. Multi-ancestry genetic study of type 2 diabetes highlights the power of diverse populations for discovery and translation. Nat Genet. 2022;54(5):560–72. 10.1038/s41588-022-01058-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Choi SW, O’Reilly PF. PRSice-2: polygenic risk score software for biobank-scale data. Gigascience. 2019;8(7):giz082. 10.1093/gigascience/giz082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mahajan A, Taliun D, Thurner M, Robertson NR, Torres JM, Rayner NW, Payne AJ, Steinthorsdottir V, Scott RA, Grarup N. Fine-mapping type 2 diabetes loci to single-variant resolution using high-density imputation and islet-specific epigenome maps. Nat Genet. 2018;50(11):1505–13. 10.1038/s41588-018-0241-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cai L, Wheeler E, Kerrison ND, Luan Ja, Deloukas P, Franks PW, Amiano P, Ardanaz E, Bonet C, Fagherazzi G, et al. Genome-wide association analysis of type 2 diabetes in the EPIC-InterAct study. Sci Data. 2020;7(1):393. 10.1038/s41597-020-00716-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ali O. Genetics of type 2 diabetes. World J Diabetes. 2013;4(4):114. 10.4239/wjd.v4.i4.114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Suzuki K, Akiyama M, Ishigaki K, Kanai M, Hosoe J, Shojima N, Hozawa A, Kadota A, Kuriki K, Naito M, et al. Identification of 28 new susceptibility loci for type 2 diabetes in the Japanese population. Nat Genet. 2019;51(3):379–86. 10.1038/s41588-018-0332-4 [DOI] [PubMed] [Google Scholar]
- 41.Spracklen CN, Horikoshi M, Kim YJ, Lin K, Bragg F, Moon S, Suzuki K, Tam CHT, Tabara Y, Kwak S-H, et al. Identification of type 2 diabetes loci in 433,540 east Asian individuals. Nature. 2020;582(7811):240–5. 10.1038/s41586-020-2263-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A. Finding the missing heritability of complex diseases. Nature. 2009;461(7265):747–53. 10.1038/nature08494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Stančáková A, Laakso M. Genetics of type 2 diabetes. Novelties Diabetes. 2016;31:203–20. [DOI] [PubMed] [Google Scholar]
- 44.Zuk O, Hechter E, Sunyaev SR, Lander ES. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc Nat Acad Sci. 2012; 109(4):1193–1198. [DOI] [PMC free article] [PubMed]
- 45.Purcell S. Variance components models for gene–environment interaction in twin analysis. Twin Res Hum Genet. 2002;5(6):554–71. 10.1375/136905202762342026 [DOI] [PubMed] [Google Scholar]
- 46.Felson J. What can we learn from twin studies? A comprehensive evaluation of the equal environments assumption. Soc Sci Res. 2014;43:184–99. 10.1016/j.ssresearch.2013.10.004 [DOI] [PubMed] [Google Scholar]
- 47.Keller MC, Medland SE, Duncan LE, Hatemi PK, Neale MC, Maes HH, Eaves LJ. Modeling extended twin family data I: description of the Cascade model. Twin Res Hum Genet. 2009;12(1):8–18. 10.1375/twin.12.1.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lee SH, Wray NR, Goddard ME, Visscher PM. Estimating missing heritability for disease from genome-wide association studies. Am J Hum Genet. 2011;88(3):294–305. 10.1016/j.ajhg.2011.02.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Browning SR, Browning BL. Population structure can inflate SNP-based heritability estimates. Am J Hum Genet. 2011;89(1):191–3. 10.1016/j.ajhg.2011.05.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Falconer DS. The inheritance of liability to certain diseases, estimated from the incidence among relatives. Ann Hum Genet. 1965;29(1):51–76. 10.1111/j.1469-1809.1965.tb00500.x [DOI] [Google Scholar]
- 51.Visscher PM, Wray NR, Zhang Q, Sklar P, McCarthy MI, Brown MA, Yang J. 10 years of GWAS discovery: biology, function, and translation. Am J Hum Genet. 2017;101(1):5–22. 10.1016/j.ajhg.2017.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Speed D, Hemani G, Johnson MR, Balding DJ. Improved heritability estimation from genome-wide SNPs. Am J Hum Genet. 2012;91(6):1011–21. 10.1016/j.ajhg.2012.10.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Daetwyler HD, Villanueva B, Woolliams JA. Accuracy of predicting the genetic risk of disease using a genome-wide approach. PLoS ONE. 2008;3(10):e3395. 10.1371/journal.pone.0003395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Khera AV, Chaffin M, Aragam KG, Haas ME, Roselli C, Choi SH, Natarajan P, Lander ES, Lubitz SA, Ellinor PT. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat Genet. 2018;50(9):1219–24. 10.1038/s41588-018-0183-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Khera AV, Chaffin M, Wade KH, Zahid S, Brancale J, Xia R, Distefano M, Senol-Cosar O, Haas ME, Bick A. Polygenic prediction of weight and obesity trajectories from birth to adulthood. Cell. 2019;177(3):587–96. e589. 10.1016/j.cell.2019.03.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lee JJ, Wedow R, Okbay A, Kong E, Maghzian O, Zacher M, Nguyen-Viet TA, Bowers P, Sidorenko J. Karlsson Linnér R. Gene discovery and polygenic prediction from a genome-wide association study of educational attainment in 1.1 million individuals. Nat Genet. 2018;50(8):1112–21. 10.1038/s41588-018-0147-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Selzam S, Ritchie SJ, Pingault J-B, Reynolds CA, O’Reilly PF, Plomin R. Comparing within-and between-family polygenic score prediction. Am J Hum Genet. 2019;105(2):351–63. 10.1016/j.ajhg.2019.06.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
No datasets were generated or analysed during the current study.