Phase II control charts for monitoring the depth-ratio of ball-bearings involving three normal variables

Abstract

This paper investigates the problem of monitoring the ratio involving three variables, jointly distributed as trivariate normal. The Shewhart-type and two exponentially weighted moving average (EWMA) type schemes for monitoring depth ratio are proposed. The ratio of a normal variable to the average of two other normal variables has wide applications in natural science, production, and engineering. It is defined with slightly different terminology in various contexts, such as depth or aspect ratios. In modern bearing manufacturing, the aspect ratio of width to the average of inner and outer diameters can be an essential indicator of product quality and process stability. While there are many helpful existing charts for monitoring the three components separately or jointly when these characteristics follow a normal distribution, the ratio aspect is often ignored. The Shewhart-type schemes' exact and approximated control limits are considered and analyzed. Numerical results based on Monte-Carlo are conducted using the average run length as a metric with different values of in-control ratio and correlation between the three variables. An application based on the parts manufacturing data illustrates the implementation design of the two control charts. The real-life data analysis shows the efficacy of the proposed monitoring schemes in practice.

1. Introduction

Statistical process monitoring (SPM) is a straightforward but effective tool for quality improvement in industrial and non-industrial processes. Among various SPM procedures, different charting schemes are widely used to detect changes in quality characteristics. Multivariate statistical process monitoring (MSPM) has been commonly applied when more than one correlated characteristic needs to be monitored in tandem. For instance, practitioners typically use the well-known Hotelling's $T^2$ charting scheme (see [32]) to monitor the mean vector of a multivariate normal process. Many high-performing MSPM schemes have been introduced in recent years; see, for example, [16] and [20] and the references therein. However, there are many quality assessment scenarios in production and manufacturing where practitioners are interested in monitoring the stability of the ratio of normal random variables more closely than their mean vector or covariance matrix. In these scenarios, the traditional MSPM schemes are not efficient. Therefore, monitoring the ratio of normal variables has been widely concerned in the literature.

In the statistical literature on distribution theory, the ratio of two normal variables has a long history. See [14,17,18,24] for the early works. To the best of our knowledge, Spisak [35] first discussed the SPM schemes for the ratio of two random variables. Öksoy et al. [31] suggested a set of guidelines for implementing the Shewhart-type scheme to perform online monitoring in the glass industry. More recently, the RZ-Shewhart-type scheme for individual observations was proposed by Celano et al. [7]. In a further follow-up, Celano and Castagliola [9] extended the RZ-Shewhart schemes by considering each subgroup consisting of n ( $\ge 1$) sample units. A study using run rules by incorporating two one-sided limits for monitoring the ratio of two normal variables was proposed by Tran et al. [39]. Celano and Castagliola [8] developed a Phase-II Synthetic-RZ scheme that always offers better statistical sensitivity than the RZ-Shewhart scheme. The use of memory-type control charts, such as those proposed by Alevizakos et al. [3] and Adeoti et al. [2] for non-parametric joint monitoring and count data, can improve the monitoring of small and persistent drifts. To enhance the sensitivity of these schemes for small to moderate ratio shifts, an EWMA and a cumulative sum (CUSUM) schemes for the ratio are proposed (see [37,38]). Further, Tran and Knoth [41] proposed a steady-state ARL-unbiased EWMA scheme for monitoring the ratio of two normal variables. Nguyen et al. [27] and Nguyen et al. [28], respectively, combined variable sampling interval (VSI) with the EWMA scheme and CUSUM scheme to surveil the ratio of the two normal variables.

Tran et al. [40] investigated the effect of measurement errors on the Shewhart-RZ scheme, assuming that the measurement error follows a linear covariate error model. With a similar assumption, Nguyen and Tran [11] investigated the effect of measurement errors on the two one-sided Shewhart and EWMA-type schemes for the ratio of two normal variables. Nguyen et al. [29] extended the linear covariate error model applied in previous studies to a more general situation. They provided a study on the performance of the EWMA schemes for monitoring the ratio in the presence of measurement errors. Finally, a two-sided run sum scheme for the ratio of two normal variables was made by Abubakar et al. [1]. Nguyen et al. [30] investigated the performance of the Phase II Shewhart-type RZ control chart monitoring the ratio of two normal variables whose relationship is captured by a bivariate time series autoregressive model VAR(1). The SPM schemes for the ratio of non-normal distribution variables are also addressed in the literature. Yamauchi and Lee Ho [43] proposed Shewhart and EWMA charts for monitoring the ratio of two Poisson rates. They offered some guidelines indicating which statistics yield the best performance for the practitioners. Erto et al. [12] considered the problem of monitoring the ratio of Weibull percentiles.

In monitoring the ratio of two variables, the underlying joint distribution of the two variables is assumed to follow a bivariate normal distribution. In a real-life situation, the problem may be slightly more complex than the ratio of two variables. This study defines a ratio involving three correlated normal variables: width (Z)-to average diameter ratio. Suppose that X and Y denote the inner and outer diameters; the average is given by $(X+Y)/2$. The width-to-average diameter ratio is $2Z/(X+Y)$. The constant multiplier two may be omitted for monitoring purposes. This ratio could be used in various ways depending on the context and the specific values of X, Y, and Z. One common use would be a relative performance or comparison measure. For example, suppose X represents the sales of a particular product, and Y and Z represent the sales of similar products. In that case, the ratio of X to the average of Y and Z could indicate how well the product performs relative to the others. The ratio between the length and the average width measures the aspect ratio of an object or shape. The aspect ratio is the proportion of an object's length (or height) to its width. It is commonly used in many fields, such as construction, engineering, and design, to ensure that the object or shape has the desired proportions. In construction, for example, the aspect ratio of a building can affect its structural stability, energy efficiency, and aesthetic appeal. In engineering, the aspect ratio of a wing or blade can affect its aerodynamic performance. In design, the aspect ratio of a photograph or image can affect its composition and visual appeal. The ratio between the length and the average width can also be used in geology and geomorphology, as it can be a useful measure of the shape and orientation of landforms such as valleys, rivers, or coastlines. It is important to note that when measuring the ratio between the length and the average width, the units of length and width must be consistent, as the ratio will not be meaningful if they are not.

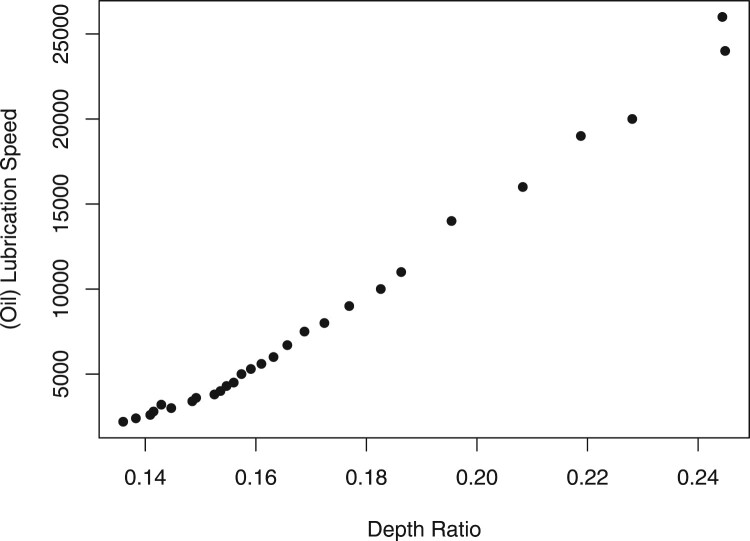
In bearing manufacturing, bore diameter, outer diameter, and width are three essential quality characteristics often individually or jointly monitored. We found that the depth ratio defined by dividing the bearing width (Z) by the average of the bore (X) and outer (Y) diameters has a significant impact on the performance indicators of the bearing. The following figure shows the relationship between depth ratio and Lubrication Speed (The data is obtained from 6300 Series Deep Groove Radial Ball Bearings On Emerson Bearing ¹). It can be seen that the speed increases with the depth ratio (Figure 1). Assuming that when the width gets a little larger, and Bore Diameter or/and Outer Diameter gets a little smaller, the depth ratio may be large enough that the performance of the bearing changes, but the individual variables do not change considerably. Therefore, during the bearing production process, the three variables of the same product type may have engineering tolerance. Still, the depth ratio should be kept stable to ensure the performance of the bearing.

Figure 1.

The relationship between depth ratio and (Oil) Lubrication Speed of the 6300 Series Ball Bearings.

Another example is the bending instability of double-walled carbon nanotubes. Wang et al. [42] found that when the length-to-average diameter ratio exceeds 8.2, the onset characteristic of the bending instability remains the same (i.e. the occurrence of a single kink at the midpoint of the beam). However, the critical bending moment decreases with the increasing length/diameter ratio. Again, the definition of L/D is the same as the depth ratio. It can be seen that in the manufacturing of double-walled carbon nanotubes, control charts can be introduced to improve the quality. Similar situations can be found widely in the nanotube fields. See [36]. In addition to the bearing or nanotube examples, a similar ratio is essential in preparing pre-expanded particles of thermoplastic resins. An aqueous dispersion of thermoplastic resin particles containing a volatile blowing agent is released into a low-pressure zone through an orifice with a length ratio to the average diameter of 4 to 100 (see [26]). We can define the depth ratio of this hole and monitor it to keep the process running stably.

The approach used in this work can be extended to monitoring the ratio in other forms. For example, Sarsam et al. [33] study the effect of height to average diameter ratio on the behaviour of high-performance concrete specimens with different shapes under compression load. The results of testing specimens show that the compressive strength of the specimen increases with decreasing height to average diameter ratio. Therefore, in the concrete industry, it makes sense to use control charts to monitor the shape to guarantee excellent performance of the concrete. In the Polymerase Chain Reaction (PCR), the ratio of depth between two allele sequences Shiina et al. [34], Kulski et al. [22] defined as the average depth of allele 1/average depth of allele 2, should be in the range of 0.6 to 1.6. It is required to make sure that an excellent allelic balance is achieved. Monitoring the depth ratio between two allele sequences in the PCR is essential, which requires a further but straightforward extension of the proposed approach where both the numerator and denominator are averages.

Motivated by these problems, we focus on monitoring the ratio of normal variables with a more complex mathematical structure than X/Y. In this article, we ignore the constant multiplier for simplicity. The monitoring problem in the examples mentioned in this article can be summarised as the ratio of one normal variable to the sum of two normal variables, denoted as $V=Z/(X+Y)$. The distribution of V can be obtained by transforming the trivariate normal random vector. Then some schemes similar to monitoring the ratio of two normal variables can be used to monitor the ratio V. Noting the complexity of the exact ratio distribution, some authors suggested using an approximate version under certain conditions, which are valid in most practical cases. However, Nadarajah and Okorie [25] pointed out that the approximation used in existing literature does not always perform well. Thus, we consider exact as well as approximate distributions for completeness.

In industrial engineering, the quality of manufacturing parts is a fundamental issue. In this paper, we consider a dataset involving parts manufacturing available at https://www.kaggle.com/datasets/gabrielsantello/parts-manufacturing-industry-dataset to illustrate the monitoring of the depth ratio involving three normal variables. The features of this dataset include item No., length, width, height, and operator. The parts' length, width, and height are denoted as X, Y, and Z, respectively. Then the depth ratio V defined previously can be used as an essential parts quality characteristic, as we have seen in the context of ball-bearing in our early discussion. A more detailed discussion on this monitoring problem is deferred to Section 5.

In this study, the average run length (ARL) is used to evaluate the charting parameters and compare the capabilities of the competing SPM schemes in detecting shifts. In-control(IC) ARL, denoted as ${\mathrm{ARL}}_0$, and out-of-control (OOC) ARL, abbreviated as ${\mathrm{ARL}}_1$, are two types of ARL. The value of ${\mathrm{ARL}}_0$ is usually prefixed at a given level, such as 200, 370, or 500, to control the type I error. When comparing the performance of two or more competing schemes, the one with a smaller ${\mathrm{ARL}}_1$ is considered the more effective scheme because it gives the signal faster in a process shift.

The rest of this paper is organised as follows. Section 2 presents the exact and approximation distribution functions of $V=Z/(X+Y)$. Section 3 introduces the Shewhart, EWMA, and the modified one-sided EWMA (MOSE) schemes for ratio V. The methods of ARL computation are also presented in this section. Section 4 is devoted to the performance of the proposed charting schemes for ratio V with different OOC conditions. The comparison of the exact and approximate control limits of the Shewhart schemes is also provided in this section. In Section 5, an example using the parts manufacturing data is offered to illustrate the implementation and show the performance of the proposed control charts. Some conclusions are given in Section 6.

2. The distribution of the ratio

This paper assumes that the three constituent variables jointly follow the trivariate normal distribution to monitor the depth ratio. For example, suppose X, Y and Z be the length, width and depth, respectively. The depth ratio or total depth percentage is $2Z/(X+Y).$ It is enough to monitor $V=Z/(X+Y),$ in practice, ignoring constant multiplier 2. Precisely, we consider $(X,Y,Z)$ follows a trivariate normal distribution, and we may write the random vector $U=(X,Y,Z{)}^{\mathrm{\top }}\sim N(\mu ,\mathbf{\Sigma })$, where

$$\mu =\left(\begin{array}{c}{\mu }_X\\ {\mu }_Y\\ {\mu }_Z\end{array}\right)$$

and variance-covariance matrix

$$\mathbf{\Sigma }=\left(\begin{array}{ccc}{\sigma }_X^2& {\sigma }_{\mathrm{XY}}& {\sigma }_{\mathrm{XZ}}\\ {\sigma }_{\mathrm{XY}}& {\sigma }_Y^2& {\sigma }_{\mathrm{YZ}}\\ {\sigma }_{\mathrm{XZ}}& {\sigma }_{\mathrm{YZ}}& {\sigma }_Z^2\end{array}\right)=\left(\begin{array}{ccc}{\sigma }_X^2& {\rho }_1{\sigma }_X{\sigma }_Y& {\rho }_2{\sigma }_X{\sigma }_Z\\ {\rho }_1{\sigma }_X{\sigma }_Y& {\sigma }_Y^2& {\rho }_3{\sigma }_Y{\sigma }_Z\\ {\rho }_2{\sigma }_X{\sigma }_Z& {\rho }_3{\sigma }_Y{\sigma }_Z& {\sigma }_Z^2\end{array}\right),$$

where ${\rho }_1$, ${\rho }_2$, ${\rho }_3$ are the correlation coefficients between variables X and Y, X and Z, Y and Z, respectively. In this paper, the ratio defined as $V=Z/(X+Y)$ is of our interest.

2.1. The exact distribution of the ratio

Several studies on the distribution of the ratio of X to Y can be found in the literature. In the present paper, the result in Hinkley [18] is used to obtain the exact distribution of the ratio V.

Let

$$\mathbf{D}=\left(\begin{array}{ccc}0& 0& 1\\ 1& 1& 0\end{array}\right).$$

It is easy to note that $\mathrm{rank}(\mathbf{D})=2$. Using Anderson [4], $\mathbf{D}U=(Z,X+Y{)}^{\mathrm{\top }}$ is distributed according to $N(\mathbf{D}\mu ,\mathbf{D}\mathbf{\Sigma }{\mathbf{D}}^{\mathrm{\top }})$, where

$$\begin{array}{rl}\mathbf{D}\mu & =({\mu }_Z,{\mu }_X+{\mu }_Y{)}^{\mathrm{\top }},\\ \mathbf{D}\mathbf{\Sigma }{\mathbf{D}}^{\mathrm{\top }}& =\left(\begin{array}{cc}{\sigma }_Z^2& {\sigma }_{\mathrm{XZ}}+{\sigma }_{\mathrm{YZ}}\\ {\sigma }_{\mathrm{XZ}}+{\sigma }_{\mathrm{YZ}}& {\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}\end{array}\right).\end{array}$$

Consequently, the correlation coefficient between Z and X + Y is

$${\rho }^{\ast }=\frac{{\sigma }_{\mathrm{XZ}}+{\sigma }_{\mathrm{YZ}}}{{\sigma }_Z\sqrt{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}}}.$$

Then, the distribution of the ratio of X to Y, as in Hinkley [18], can be used to obtain the distribution of $V=Z/(X+Y)$. Following the existing research, the cumulative distribution function (c.d.f.) $F_V(v)$ of the ratio V is

$$F_V(v)=L(a,b;c)+L(-a,-b;c)$$ (1)

where,

$$\begin{array}{rl}a& =\frac{{\mu }_Z-({\mu }_X+{\mu }_Y)v}{\eta (v){\sigma }_Z\sqrt{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}}},\\ b& =-\frac{{\mu }_X+{\mu }_Y}{\sqrt{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}}},\\ c& =\frac{\sqrt{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}}-{\rho }^{\ast }{\sigma }_Z}{\eta (v){\sigma }_Z\sqrt{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}}},\\ \eta (v)& =\sqrt{\frac{v^2}{{\sigma }_z^2}-\frac{2{\rho }^{\ast }v}{{\sigma }_Z\sqrt{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}}}+\frac{1}{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathrm{XY}}}},\\ L(h,k;\xi )& =\frac{1}{2\pi \sqrt{1-{\xi }^2}}{\int }_h^{\mathrm{\infty }}{\int }_k^{\mathrm{\infty }}\exp \{-\frac{x^2-2\mathrm{\xi xy}+y^2}{2\sqrt{1-{\xi }^2}}\}\mathrm{d}x\mathrm{d}y.\end{array}$$

Note that $L(h,k,\xi )$ is the standard bivariate normal integral according to Hinkley [18]. In the era of reduced computational facilities, working with the exact c.d.f. of V was complicated in designing a charting scheme. Therefore, many authors used an approximated c.d.f. as discussed in the following subsection. However, it has become much easier to handle the exact distribution with modern computing facilities. So, unlike previous articles on monitoring ratio schemes, this paper considers both exact and approximate distributions of V.

2.2. An approximation of the distribution

This study adopts the method for obtaining the approximate c.d.f. of the ratio X/Y presented in Hayya and Gressis [17] and Celano and Castagliola [9]. They assumed that $P(X+Y\le 0)\approx 0$. For $V=Z/(X+Y)$, $F_V(v)=P(V\le v)=P(Z/(X+Y)\le v)$ is replaced by

$$F_V(v)=P(Z-\mathrm{vX}-\mathrm{vY}\le 0).$$

Since $W=Z-\mathrm{vX}-\mathrm{vY}=(-v,-v,1)U$ is a linear combination of X, Y and Z, the random variable W follows a normal distribution $N({\mu }_W,{\sigma }_W^2)$, with ${\mu }_W={\mu }_Z-v{\mu }_X-v{\mu }_Y$,

$$\begin{array}{rl}{\sigma }_W^2& =(-v,-v,1)\mathbf{\Sigma }\left(\begin{array}{c}-v\\ -v\\ 1\end{array}\right)\\ & =v^2{\sigma }_X^2+v^2{\sigma }_Y^2+{\sigma }_Z^2+2v^2{\sigma }_{\mathrm{XY}}-2v{\sigma }_{\mathrm{XY}}-2v{\sigma }_{\mathrm{YZ}}\\ & =v^2{\sigma }_X^2+v^2{\sigma }_Y^2+{\sigma }_Z^2+2v^2{\rho }_1{\sigma }_X{\sigma }_Y-2v{\rho }_2{\sigma }_X{\sigma }_Z-2v{\rho }_3{\sigma }_Y{\sigma }_Z.\end{array}$$

An approximation for $F_V(v)$ can be conveniently stated as

$$\begin{array}{rl}{F}_V^{\ast }(v)& \simeq \mathrm{\Phi }\left(\frac{0-{\mu }_W}{{\sigma }_W}\right)\\ & =\mathrm{\Phi }\left(\frac{v{\mu }_X+v{\mu }_Y-{\mu }_Z}{\sqrt{v^2{\sigma }_X^2+v^2{\sigma }_Y^2+{\sigma }_Z^2+2v^2{\rho }_1{\sigma }_X{\sigma }_Y-2v{\rho }_2{\sigma }_X{\sigma }_Z-2v{\rho }_3{\sigma }_Y{\sigma }_Z}}\right)\\ & =\mathrm{\Phi }\left(\frac{v{\omega }_{\mathrm{XZ}}/{\gamma }_X+v{\omega }_{\mathrm{YZ}}/{\gamma }_Y-1/{\gamma }_Z}{\sqrt{v^2{\omega }_{\mathrm{XZ}}^2+v^2{\omega }_{\mathrm{YZ}}^2+2v^2{\rho }_1{\omega }_{\mathrm{XZ}}{\omega }_{\mathrm{YZ}}-2v{\rho }_2{\omega }_{\mathrm{XZ}}-2v{\rho }_3{\omega }_{\mathrm{YZ}}+1}}\right),\end{array}$$ (2)

where $\mathrm{\Phi }(x)$ is the c.d.f. of $N(0,1)$. ${\gamma }_X={\sigma }_X/{\mu }_X,{\gamma }_Y={\sigma }_Y/{\mu }_Y$ and ${\gamma }_Z={\sigma }_Z/{\mu }_Z$ are the coefficients of variation of X, Y and Z, respectively, while ${\omega }_{\mathrm{XZ}}={\sigma }_X/{\sigma }_Z$, ${\omega }_{\mathrm{YZ}}={\sigma }_Y/{\sigma }_Z$ are the standard deviation ratios of the variables, respectively.

3. Implementation of the control charts for ratio V

The ratio V is monitored in practice by collecting a set of n independent samples $\{U_{t,1},U_{t,2},\dots ,U_{t,n}\}$ at each sampling period $t=1,2,\dots$, where $U_{t,i}=(X_{t,i},Y_{t,i},Z_{t,i}{)}^{\mathrm{\top }}\sim N({\mu }_{U,t},{\mathbf{\Sigma }}_{U,t}),i=1,2,\dots n$. The mean vector and variance-covariance matrix of $U_{t,i}$ can be presented as

$$\begin{array}{rl}{\mu }_{U,t}& =\left(\begin{array}{c}{\mu }_{X,t}\\ {\mu }_{Y,t}\\ {\mu }_{Z,t}\end{array}\right),\\ {\mathbf{\Sigma }}_{U,t}& =\left(\begin{array}{ccc}{\sigma }_{X,t}^2& {\rho }_{1,t}{\sigma }_{X,t}{\sigma }_{Y,t}& {\rho }_{2,t}{\sigma }_{X,t}{\sigma }_{Z,t}\\ {\rho }_{1,t}{\sigma }_{X,t}{\sigma }_{Y,t}& {\sigma }_{Y,t}^2& {\rho }_{3,t}{\sigma }_{Y,t}{\sigma }_{Z,t}\\ {\rho }_{2,t}{\sigma }_{X,t}{\sigma }_{Z,t}& {\rho }_{3,t}{\sigma }_{Y,t}{\sigma }_{Z,t}& {\sigma }_{Z,t}^2\end{array}\right).\end{array}$$

Similar to Celano and Castagliola [9] and Nguyen et al. [27], some assumptions are necessary for using the approximate distribution. The first assumption is that the initial value of the ratio $v_0$ is equal to ${\mu }_Z/({\mu }_X+{\mu }_Y)$ when the process runs IC. The second assumption is: ${\gamma }_X,{\gamma }_Y,$ and ${\gamma }_Z$ are known constant coefficients of variations. Because many quality characteristics have a dispersion proportional to the population mean, it is a standard practice to use known and constant coefficients of variation. However, to construct a Shewhart-type chart using the exact distribution function assuming known IC process parameters, this assumption is redundant.

Then, the observed statistic is

$$\widehat{V_t}=\frac{\overline{Z_t}}{\overline{X_t}+\overline{Y_t}}=\frac{\sum _{i=1}^n{Z}_{t,i}}{\sum _{i=1}^n{X}_{t,i}+\sum _{i=1}^n{Y}_{t,i}},t=1,2,\dots$$ (3)

It is convenient to demonstrate that $\overline{X_t}\sim N({\mu }_{X,t},{\sigma }_{X,t}/\sqrt{n})$, $\overline{Y_t}\sim N({\mu }_{Y,t},{\sigma }_{Y,t}/\sqrt{n})$, and $\overline{Z_t}\sim N({\mu }_{Z,t},{\sigma }_{Z,t}/\sqrt{n})$. Therefore the coefficients of variation of $\overline{X_t},\overline{Y_t},\overline{Z_t}$ are

$${\gamma }_{\overline{X}}=\frac{{\sigma }_{X,t}}{{\mu }_{X,t}\sqrt{n}}=\frac{{\gamma }_X}{\sqrt{n}},{\gamma }_{\overline{Y}}=\frac{{\sigma }_{Y,t}}{{\mu }_{Y,t}\sqrt{n}}=\frac{{\gamma }_Y}{\sqrt{n}},{\gamma }_{\overline{Z}}=\frac{{\sigma }_{Z,t}}{{\mu }_{Z,t}\sqrt{n}}=\frac{{\gamma }_Z}{\sqrt{n}},$$

and the standard deviation ratios are

$${\omega }_{\mathrm{XZ},t}=\frac{{\mu }_{X,t}}{{\mu }_{Z,t}}\times \frac{{\gamma }_X}{{\gamma }_Z},{\omega }_{\mathrm{YZ},t}=\frac{{\mu }_{Y,t}}{{\mu }_{Z,t}}\times \frac{{\gamma }_Y}{{\gamma }_Z}.$$

It can be found that the standard deviation ratios are independent of sample size n. Let $\gamma =({\gamma }_X,{\gamma }_Y,{\gamma }_Z)$ and $\rho =({\rho }_1,{\rho }_2,{\rho }_3)$. Then, the c.d.f. of $\widehat{V_t}$ can be presented as $F_{\widehat{V_t}}(\widehat{v_t})=F_V(v;n)$, and the approximation can be presented as $F_{\widehat{V_t}}^{\ast }(\widehat{v_t})=F_V^{\ast }(v;n)$.

3.1. Shewhart-type schemes for ratio V

According to Marsaglia [24], the ratio of two arbitrary normal variables leads to a Cauchy-like distribution. Cedilnik et al. [6] showed that the density of the ratio of the bivariate normal distribution with the arbitrary parameters is a product of a Cauchy density and a highly complex function. Analogously, the distribution of $V=Z/(X+Y)$ is related to the Cauchy-type distribution. Thus, the distribution of V has no moments. For this reason, the control limits of the Shewhart-type schemes are defined in terms of probability control limits, i.e.

$$\begin{array}{rl}\mathrm{UCL}& =F_V^{-1}(1-\frac{\alpha }{2};n),\mathrm{LCL}=F_V^{-1}(\frac{\alpha }{2};n);\end{array}$$ (4)

$$\begin{array}{rl}{\mathrm{UCL}}^{\ast }& =F_V^{\ast -1}(1-\frac{\alpha }{2};n),{\mathrm{LCL}}^{\ast }=F_V^{\ast -1}(\frac{\alpha }{2};n),\end{array}$$ (5)

where α is the desired false alarm rate. The UCL and LCL based on the exact c.d.f. are defined in Equation (1), while ${\mathrm{UCL}}^{\ast }$ and ${\mathrm{LCL}}^{\ast }$ based on the approximate c.d.f. are introduced in Equation (2). The central line of the Shewhart-type schemes may be set at the median value, i.e.

$$\mathrm{CL}=F_V^{-1}(0.5;n),C{L}^{\ast }=F_V^{\ast -1}(0.5;n).$$

The run-length variable of the Shewhart-type schemes for the ratio V follows a Geometric distribution $\mathrm{Ge}(\alpha )$ when the process is IC. It is straightforward to get

$${\mathrm{ARL}}_0=\frac{1}{\alpha },{\sigma }_{\mathrm{RL}}^0=\frac{\sqrt{1-\alpha }}{\alpha },$$

where ${\sigma }_{\mathrm{RL}}^{(0)}$ is the standard deviation of the IC run-length distribution.

3.2. EWMA-type scheme for ratio V

In this section, we propose two EWMA-type SPM schemes for monitoring the ratio V. The EWMA-type scheme is based on a weighted average of the current and all the previously observed data, where the weights attached to the data exponentially increase as observation becomes more recent.

3.2.1. Two one-sided EWMA control charts

In this paper, considering the skewness of the distribution of V, the two one-sided EWMA charting schemes are designed to monitor possible shifts in the distribution of V.

First, an upward EWMA scheme is constructed to detect an increase in the ratio V. It is defined as

$$E{V}_t^{+}=max(v_0,(1-\lambda )E{V}_{t-1}^{+}+\lambda \widehat{V_t}),$$ (6)

where $E{V}_0^{+}=v_0$ is the initial value, $\lambda \in (0,1]$ is the smoothing parameter of the EWMA scheme. When λ is chosen to be larger, more weight is assigned to the current observation $V_t$ and less weight is assigned to the previous observations. At this time, the proposed chart is more capable of monitoring large shifts. In contrast, the control chart is more proficient at monitoring small and persistent shifts when the value of λ is chosen small. The scheme gives an OOC signal at sampling time t if $E{V}_t^{+}$ exceeds UCL.

Second, a downward EWMA scheme is designed to detect a decrease in the ratio V and is defined as

$$E{V}_t^{-}=min(v_0,(1-\lambda )E{V}_{t-1}^{-}+\lambda \widehat{V_t}),$$ (7)

with $E{V}_0^{-}=v_0$. The scheme gives an OOC signal at sampling time t if $E{V}_t^{-}$ is less than LCL.

The two one-sided EWMA schemes are combined by running the upward and downward EWMA schemes simultaneously. It is worth noting that the control limits are not considered in the forms involving the mean and standard deviation of V because the distribution of V has, in general, no moments. Section 3.3 introduces the details of control limits computation. According to [13], the ARL of the combined scheme may be approximated using

$$\frac{1}{\mathrm{ARL}}\approx \frac{1}{{\mathrm{ARL}}^{+}}+\frac{1}{{\mathrm{ARL}}^{-}},$$

where ${\mathrm{ARL}}^{+}$ is the ARL of the upward EWMA scheme and ${\mathrm{ARL}}^{-}$ is the ARL of the downward EWMA scheme.

3.2.2. Two one-sided MOSE control charts

Zhang et al. [44] proposed a MOSE charting scheme for monitoring the process coefficient of variation, which performs better than the traditional EWMA scheme. Motivated by their findings, a MOSE scheme for V is designed. The numerical results based on simulation in the subsequent Section show that the MOSE chart for ratio V also performs better than its competitors in various scenarios.

In designing the two one-sided MOSE schemes for ratio V, first, the upward MOSE scheme for each sample $t\ge 1$ is defined as

$$M{Z}_t^{+}=max(v_0,E_t^{+}),$$ (8)

where $E_t^{+}$ is defined as

$$E_t^{+}=(1-{\lambda }^{+})E_{t-1}^{+}+{\lambda }^{+}\widehat{V_t}$$

with $E_0^{+}=v_0$ as the initial value. ${\lambda }^{+}\in (0,1]$ is the smoothing parameter for the MOSE scheme. The scheme gives an OOC signal at sampling time t if $M{Z}_t^{+}$ exceeds UCL.

Similarly, the downward MOSE scheme for each sample $t\ge 1$ can be presented as

$$M{Z}_t^{-}=min(v_0,E_t^{-}),$$ (9)

where $E_t^{-}$ is defined as

$$E_t^{-}=(1-{\lambda }^{-})E_{t-1}^{-}+{\lambda }^{-}\widehat{V_t}$$

with $E_0^{-}=v_0$ as the initial value. The scheme gives an OOC signal at sampling time t if $M{Z}_t^{-}$ is less than LCL.

The two one-sided MOSE schemes are combined by running the upward and downward MOSE charts simultaneously. For convenience, we set ${\lambda }^{+}={\lambda }^{-}=\lambda$ in this article. An alarm is triggered if $M{Z}_t^{+}$ or $M{Z}_t^{-}$ falls outside the control limits as defined above.

3.3. Computation of ARLs

For Shewhart-type schemes, the values of exact control limits can be obtained by solving numerical solution of the equations in accordance to (4)

$$\begin{array}{rl}{F}_V(\mathrm{LCL};n)& =\frac{\alpha }{2},\end{array}$$ (10)

$$\begin{array}{rl}{F}_V(\mathrm{UCL};n)& =1-\frac{\alpha }{2},\end{array}$$ (11)

with the given α (e.g, $\alpha =0.005$, ${\mathrm{ARL}}_0=200$). It is convenient to get fairly accurate results by the function uniroot() in the R program or similar code in other programming languages. According to (5), approximate control limits ${\mathrm{UCL}}^{\ast }$ and ${\mathrm{LCL}}^{\ast }$ can be obtained in the same way.

For the two EWMA-type schemes, the values of control limits can be calculated by Monte Carlo simulation based on 50, 000 replications. We construct both For upper-sided and lower-sided charts with approximately the same ${\mathrm{ARL}}_0$. At the same time, we also ensure that the overall ${\mathrm{ARL}}_0$ of the combined scheme attains the specified value. The algorithm for computing the control limits of the two one-sided MOSE charts is given below. The algorithm for the two one-sided EWMA control charts is very similar.

• Step 1.

  Determine the values of parameters including sample size n, γ and ρ in the IC process. For convenience, the values of IC ${\omega }_{\mathrm{XZ}}={\omega }_{\mathrm{YZ}}=1$ are fixed for all simulations in this article. The smoothing parameter λ and the value of ${\mathrm{ARL}}_0$ are specified. The number of replications is set to 50, 000. Select the initial values of UCL and LCL near the initial value of $v_0$ and denote as $h^{+}\mathrm{and}{h}^{-}$.

• Step 2.

  Generate a sample of size n from a trivariate normal distribution with the corresponding parameters.

• Step 3.

  The upward plotting statistic $M{Z}_t^{+}$ is calculated. If $M{Z}_t^{+}⩽$ $h^{+}$, turn to Step 2. If $M{Z}_t^{+}>h^{+}$, record the corresponding sample number as the one that produces the first OOC signal and denote the number as RL.

• Step 4.

  Repeat Steps 2 and 3 50,000 times and compute the average of RLs as the ${\mathrm{ARL}}_0$ corresponding to $h^{+}$. Then adjust the value of $h^{+}$ until the specified ${\mathrm{ARL}}_0^{+}$ is reached. Finally, set the UCL equal to $h^{+}$.

• Step 5.

  Obtain the value of LCL similarly.

• Step 6.

  Calculate the ${\mathrm{ARL}}_0$ of the combined chart. UCL and LCL are obtained if it is equal to the specified value. In our simulation, the ${\mathrm{ARL}}_0$ of the combined scheme reaches 370 when the ${\mathrm{ARL}}_0$ values of individual one-sided schemes are approximately 745.

When there is a process shift, the performance of the schemes can be evaluated by comparing ${\mathrm{ARL}}_1$. We assume an OOC condition shifts the IC ratio $v_0$ to $v_1=\tau \times v_0$, where $\tau >0$ is the shift size. The following algorithm can be used in R to find the ${\mathrm{ARL}}_1$:

• Step 1.

  Choose the type of charting schemes;

• Step 2.

  Specify the values of $n,\gamma ,\rho$, obtain the value of control limits;

• Step 3.

  Generate the observation $U=(X,Y,Z{)}^{\mathrm{\top }}$ with shift size τ. Then the plotting statistic is calculated by Equation (3) or Equations (6)–(7) or Equations (8)–(9);

• Step 4.

  If the control chart signal, RL is recorded. If not, turn to Step 3;

• Step 5.

  After 50,000 replications of Steps 3 and 4, ${\mathrm{ARL}}_1$ is calculated by averaging the RL values.

In this paper, Monte Carlo method is used to calculate the control limits. However, for the EWMA scheme, a more efficient approach for the calculation of control limits is the Markov chain method proposed by Brook and Evans [5]. The details of the Markov chain method for calculating the control limits of the EWMA scheme are shown in the Appendix.

4. Numerical results and comparisons

This section illustrates the performance of the proposed charting schemes for ratio V for various OOC situations. The shifts in V or the correlation coefficient ρ or both are considered than just the shifts in V. It is well known in the literature that memory-type SPM schemes often perform better than other charting schemes since they use all the historical data. Therefore, the comparison between Shewhart-type and EWMA-type charts is omitted in this section. We first focus on the ${\mathrm{ARL}}_1$ comparison of Shewhart-type schemes with the different types of control limits. Subsequently, we consider the ${\mathrm{ARL}}_1$ comparison of the two EWMA-type schemes and the performance of these charting schemes under a shift in the correlation coefficient. All simulations in this section were run in R on an Intel Core i5-1035G1 CPU. The execution time is several minutes when ARL is 370. For instance, if we set $\gamma =(0.1,0.1,0.1)$, $\rho =(0.4,0.4,0.4)$, n = 5, the LCL and UCL of the EWMA scheme are 0.47927 and 0.52193, respectively. It takes 7.3 minutes to compute the ${\mathrm{ARL}}_0$ of this scheme.

4.1. The performance of Shewhart-type schemes with exact and approximate control limits

4.1.1. The difference between exact and approximate control limits

The control limits for Shewhart-type schemes are based on the c.d.f. of V, so the approximate control limits will be equal to the exact control limits when $P(X+Y\le 0)\to 0$, i.e. when the coefficient of variation of $X+Y$ converges to 0, as discussed in [17,18]. The difference between exact and approximate control limits for Shewhart-type schemes is illustrated through the following simulation. Let mean vector of U belong to set $\{(50,50,50{)}^{\mathrm{\top }},(10,10,10{)}^{\mathrm{\top }},$ $(5,5,5{)}^{\mathrm{\top }},$ $(10/3,10/3,10/3{)}^{\mathrm{\top }},$ $(2.5,2.5,2.5{)}^{\mathrm{\top }},$ $(2,2,2{)}^{\mathrm{\top }}$, $(10,5,10/3{)}^{\mathrm{\top }}$, $(10,10/3,2{)}^{\mathrm{\top }}$, $(10/3,5,10{)}^{\mathrm{\top }}$, $(2,10/3,10{)}^{\mathrm{\top }}\}$, and

$$\begin{array}{rl}\mathbf{\Sigma }& =\left(\begin{array}{ccc}1.0& -0.4& -0.4\\ -0.4& 1.0& -0.4\\ -0.4& -0.4& 1.0\end{array}\right),\left(\begin{array}{ccc}1.0& 0.0& 0.0\\ 0.0& 1.0& 0.0\\ 0.0& 0.0& 1.0\end{array}\right),\left(\begin{array}{ccc}1.0& 0.4& 0.4\\ 0.4& 1.0& 0.4\\ 0.4& 0.4& 1.0\end{array}\right),\\ & \left(\begin{array}{ccc}1.0& 0.8& 0.8\\ 0.8& 1.0& 0.8\\ 0.8& 0.8& 1.0\end{array}\right),\left(\begin{array}{ccc}1.0& 0.4& 0.6\\ 0.4& 1.0& 0.8\\ 0.6& 0.8& 1.0\end{array}\right).\end{array}$$

i.e.

• $\gamma \in \{(0.02,0.02,0.02),(0.1,0.1,0.1)$, $(0.2,0.2,0.2)$, $(0.3,0.3,0.3)$, $(0.4,0.4,0.4)$, $(0.5,0.5,0.5)$, $(0.1,0.3,0.3)$, $(0.1,0.3,0.5)$, $(0.3,0.2,0.1)$, $(0.5,0.3,0.1)\}$;

• $\rho \in \{(-0.4,-0.4,-0.4),(0.0,0.0,0.0),(0.4,0.4,0.4),(0.8,0.8,0.8),(0.4,0.6,0.8)\}$;

• $n\in \{1,5\}$, ${\mathrm{ARL}}_0=370$.

The exact and approximate control limit values can be found in Table 1. When n = 1, the two types of control limits are practically equal if $\gamma =(0.1,0.1,0.1)$ and $(0.2,0.2,0.2)$. If ${\gamma }_X,{\gamma }_Y,{\gamma }_Z>0.2$, the two types of control limits are quite different in most cases. When $\gamma =(0.3,0.3,0.3)$, and $\rho =(-0.4,-0.4,-0.4)$, the control limits may be viewed as almost equal (for example, the exact and approximate UCLs are both 1.71211). But as the positive correlation increases, the gaps between the two types of control limits increase. When $\gamma =(0.3,0.3,0.3)$, the UCLs are 1.63120 and 1.63145 if $\rho =(0.0,0.0,0.0)$ and the UCLs are 1.47952 and 1.48710 if $\rho =(0.4,0.4,0.4)$. The gaps are 0.00025 and 0.00758, respectively. It can be concluded that the approximate values are greater than the exact values, and the approximate control regions are wider in most cases when the two control limits are unequal. For instance, when $n=1,\gamma =(0.4,0.4,0.4),\rho =(0.0,0.0,0.0)$, the exact values are $-0.11810$ and 3.42365 while the approximate values are $-0.10673$ and 3.67615. It is easy to see that the widths of control limits are 3.54175 and 3.78288, respectively. For the unequal coefficient of variation cases, if the values of the components of γ are not large, the approximation is quite accurate. When only ${\gamma }_Z$ is large, the approximations still are pretty good. However, when one of ${\gamma }_X$ or ${\gamma }_Y$ is larger, the approximate control limits are inaccurate or unreliable. It should be noted that when the components of γ and ρ are both too large, the control limit may not be obtained through the approximate distribution function. When $n=5$, there is practically no difference between the exact and approximate control limits for the Shewhart-type schemes in most cases. The reason may be as the sample size n increases, the coefficient of variation decreases, and consequently, the approximate control limits gradually approach the exact values. The only difference is that when $\gamma =(0.5,0.5,0.5)$ and $\rho =(0.8,0.8,0.8)$, the exact and approximate UCLs are 0.77885 and 0.77888. Nevertheless, their difference is practically negligible.

Table 1.

Values of exact and approximate control limits of Shewhart-type schemes for ratio V, with ${\mathrm{ARL}}_0=370$.

		n = 1				n = 5
		exact		appro		exact		appro
γ	ρ	LCL	UCL	LCL	UCL	LCL	UCL	LCL	UCL
(0.02, 0.02, 0.02)	(−0.4, −0.4, −0.4)	0.45774	0.54477	0.45774	0.54477	0.48082	0.51969	0.48082	0.51969
	(0.0, 0.0, 0.0)	0.46412	0.53768	0.46412	0.53768	0.48374	0.51661	0.48374	0.51661
	(0.4, 0.4, 0.4)	0.47205	0.52905	0.47205	0.52905	0.48737	0.51286	0.48737	0.51286
	(0.8, 0.8, 0.8)	0.48372	0.51663	0.48372	0.51663	0.49271	0.50737	0.49271	0.50737
	(0.4, 0.6, 0.8)	0.48354	0.51644	0.48354	0.51644	0.49266	0.50733	0.49266	0.50733
(0.1, 0.1, 0.1)	(−0.4, −0.4, −0.4)	0.30966	0.75507	0.30966	0.75507	0.40867	0.60400	0.40867	0.60400
	(0.0, 0.0, 0.0)	0.33413	0.71300	0.33413	0.71300	0.42189	0.58718	0.42189	0.58718
	(0.4, 0.4, 0.4)	0.36672	0.66209	0.36672	0.66209	0.43862	0.56681	0.43862	0.56681
	(0.8, 0.8, 0.8)	0.41909	0.59074	0.41909	0.59074	0.46388	0.53797	0.46388	0.53797
	(0.4, 0.6, 0.8)	0.41514	0.58487	0.41514	0.58487	0.46302	0.53696	0.46302	0.53696
(0.2, 0.2, 0.2)	(−0.4, −0.4, −0.4)	0.15979	1.12265	0.15979	1.12265	0.32756	0.72397	0.32756	0.72397
	(0.0, 0.0, 0.0)	0.18946	1.03000	0.18946	1.03000	0.35028	0.68704	0.35028	0.68704
	(0.4, 0.4, 0.4)	0.23532	0.90902	0.23532	0.90902	0.38027	0.64245	0.38027	0.64245
	(0.8, 0.8, 0.8)	0.32504	0.72821	0.32504	0.72821	0.42778	0.57993	0.42778	0.57993
	(0.4, 0.6, 0.8)	0.31004	0.68997	0.31004	0.68997	0.42460	0.57539	0.42460	0.57539
(0.3, 0.3, 0.3)	(−0.4, −0.4, −0.4)	0.03668	1.71211	0.03668	1.71211	0.25475	0.86441	0.25475	0.86441
	(0.0, 0.0, 0.0)	0.04893	1.63120	0.04897	1.63145	0.28324	0.80489	0.28324	0.80489
	(0.4, 0.4, 0.4)	0.07248	1.47952	0.07382	1.48710	0.32284	0.73198	0.32284	0.73198
	(0.8, 0.8, 0.8)	0.14804	1.11126	0.15304	1.14560	0.38986	0.62910	0.38986	0.62910
	(0.4, 0.6, 0.8)	0.12596	0.87405	0.12553	0.87447	0.38295	0.61705	0.38295	0.61705
(0.4, 0.4, 0.4)	(−0.4, −0.4, −0.4)	−0.06817	2.84081	−0.06808	2.84205	0.18882	1.03177	0.18882	1.03177
	(0.0, 0.0, 0.0)	−0.11810	3.42365	−0.10673	3.67615	0.21911	0.94908	0.21911	0.94908
	(0.4, 0.4, 0.4)	−0.67335	3.91609	−0.26043	--	0.26415	0.84406	0.26415	0.84406
	(0.8, 0.8, 0.8)	−1.58946	3.16179	--	--	0.34760	0.69127	0.34760	0.69127
	(0.4, 0.6, 0.8)	−0.60587	1.60586	--	--	0.33555	0.66445	0.33555	0.66445
(0.5, 0.5, 0.5)	(−0.4, −0.4, −0.4)	−0.16448	5.73085	−0.16004	6.00294	0.12868	1.23537	0.12868	1.23537
	(0.0, 0.0, 0.0)	−4.84259	9.97458	−0.32562	--	0.15651	1.13373	0.15651	1.13373
	(0.4, 0.4, 0.4)	−8.95535	11.48201	--	--	0.20169	0.99532	0.20169	0.99532
	(0.8, 0.8, 0.8)	−7.16909	8.52497	--	--	0.29667	0.77885	0.29669	0.77888
	(0.4, 0.6, 0.8)	−3.96555	4.96555	--	--	0.27806	0.72194	0.27806	0.72194
(0.1, 0.2, 0.3)	(−0.4, −0.4, −0.4)	0.01917	0.51492	0.01917	0.51492	0.12360	0.33807	0.12360	0.33807
	(0.0, 0.0, 0.0)	0.02213	0.46096	0.02213	0.46096	0.13126	0.32039	0.13126	0.32039
	(0.4, 0.4, 0.4)	0.02629	0.40212	0.02629	0.40212	0.14073	0.30080	0.14073	0.30080
	(0.8, 0.8, 0.8)	0.03254	0.33716	0.03254	0.33716	0.15330	0.27797	0.15330	0.27797
	(0.4, 0.6, 0.8)	0.03078	0.34363	0.03078	0.34363	0.15057	0.28117	0.15057	0.28117
(0.1, 0.3, 0.5)	(−0.4, −0.4, −0.4)	−0.06376	0.46939	−0.06376	0.46939	0.04566	0.27443	0.04566	0.27443
	(0.0, 0.0, 0.0)	−0.07629	0.41007	−0.07629	0.41007	0.04915	0.25706	0.04915	0.25706
	(0.4, 0.4, 0.4)	−0.09385	0.34904	−0.09385	0.34904	0.05336	0.23870	0.05336	0.23870
	(0.8, 0.8, 0.8)	−0.11932	0.28813	0.11932	0.28813	0.05863	0.21909	0.05863	0.21909
	(0.4, 0.6, 0.8)	−0.11090	0.29533	−0.11090	0.29533	0.05729	0.22228	0.05729	0.22228
(0.3, 0.2, 0.1)	(−0.4, −0.4, −0.4)	0.63195	2.45540	0.63195	2.45540	0.90225	1.61756	0.90225	1.61756
	(0.0, 0.0, 0.0)	0.69518	2.54426	0.69518	2.54426	0.93341	1.59778	0.93341	1.59778
	(0.4, 0.4, 0.4)	0.76989	2.67117	0.76990	2.67125	0.96809	1.57497	0.96809	1.57497
	(0.8, 0.8, 0.8)	0.85767	2.86115	0.85776	2.86332	1.00749	1.54797	1.00749	1.54797
	(0.4, 0.6, 0.8)	0.89227	2.30478	0.89227	2.30485	1.03180	1.47774	1.03180	1.47774
( 0.5, 0.3, 0.1)	(−0.4, −0.4, −0.4)	0.85928	6.00059	0.85931	6.00104	1.30515	2.86248	1.30515	2.86248
	(0.0, 0.0, 0.0)	0.93604	9.06171	0.93962	9.26930	1.33698	2.95625	1.33698	2.95625
	(0.4, 0.4, 0.4)	0.98816	16.19793	1.02313	27.36801	1.36853	3.06579	1.36853	3.06579
	(0.8, 0.8, 0.8)	−15.88116	28.50127	1.10654	--	1.39957	3.19429	1.39957	3.19429
	(0.4, 0.6, 0.8)	1.14422	14.23460	1.17172	23.89700	1.45149	2.89053	1.45149	2.89053

Note: the dash ‘--’ means that the value is not available.

These results conclude that small coefficients of variation lead to the approximate distribution being more precise. Nadarajah and Okorie [25] pointed out that the approximate p.d.f of X/Y is not so accurate when the coefficients of variation of both variables are close to 0.2. Similarly, when the values of ${\gamma }_X,{\gamma }_Y,{\gamma }_Z$ are large, $F_V^{\ast }(v)$ also does not perform well. The difference between the two types of control limits will considerably influence the performance of the Shewhart-type schemes when the coefficients of variation are large. The approximate control limits are entirely undesirable in some cases, while the exact control limits will always work. However, in stable and predictable processes, the standard deviation value is significantly smaller than the mean, according to [40]. Therefore, the approximate control limits are applicable in most practical situations with some restrictions on the parameters. In contrast, the exact control limits are more reliable without having any constraints on the parameters.

4.1.2. ARL performance

The control limits based on approximate distribution may affect the performance of the charting scheme, so it is necessary to study the implementation of the Shewhart-type schemes with both exact and approximate control limits. In this subsection, we take the monitoring of upward shifts as an example to illustrate the performance of the two Shewhart-type schemes for ratio V. As can be seen in Section 4.1.1, the exact and approximate control limits for Shewhart type schemes are equal when ${\gamma }_X$, ${\gamma }_Y$ and ${\gamma }_Z$ are small. The two types of control limits are quite different when ${\gamma }_X$, ${\gamma }_Y$, and ${\gamma }_Z$ are large and n = 1. Therefore, the simulation parameters are set as follows:

• $\gamma =(0.3,0.3,0.3)$;

• $\rho \in \{(-0.4,-0.4,-0.4),(0.0,0.0,0.0),(0.4,0.4,0.4),(0.8,0.8,0.8),(0.4,0.6,0.8)\}$;

• $\tau \in \{1.00,1.05,1.10,1.20,1.30,1.40,1.50,1.60,1.80,2.00\}$;

• n = 1 and ${\mathrm{ARL}}_0=370$.

Table 2 shows the simulation results. As can be seen in this table, there is no difference between the ${\mathrm{ARL}}_1$ values based on the two types of control limits when the $\rho =(-0.4,-0.4,-0.4)$. This is because the exact and approximate control limits are equal.

Table 2.

${\mathrm{ARL}}_1$ of Shewhart-type schemes with approximate and exact control limits, with n = 1, $\gamma =(0.3,0.3,0.3)$ and ${\mathrm{ARL}}_0=370$.

	$\rho =(-0.4,-0.4,-0.4)$		(0.0, 0.0, 0.0)		(0.4, 0.4, 0.4)		(0.8, 0.8, 0.8)		(0.4, 0.6, 0.8)
τ	exact	appro	exact	appro	exact	appro	exact	appro	exact	appro
1.00	371.7	371.7	368.8	367.8	369.9	370.8	369.1	373.5	369.8	372.6
1.05	313.0	313.0	324.1	325.4	339.7	340.3	336.1	355.7	282.5	280.8
1.10	255.5	255.5	274.5	275.2	294.5	295.3	307.7	322.9	197.5	199.0
1.20	167.3	167.3	193.2	189.9	221.2	222.8	215.2	244.2	81.8	81.4
1.30	107.7	107.7	128.1	128.2	151.6	158.1	140.8	167.9	30.3	31.3
1.40	67.7	67.7	86.6	85.4	104.0	108.3	85.7	107.9	12.7	12.7
1.50	46.4	46.4	57.7	56.8	69.2	72.7	49.5	63.1	6.1	6.1
1.60	32.1	32.1	39.7	39.9	46.9	48.7	28.2	36.2	3.5	3.5
1.80	17.6	17.6	20.2	20.5	22.5	23.3	9.3	12.3	1.8	1.8
2.00	10.5	10.5	11.9	11.7	11.9	12.2	3.8	4.8	1.3	1.3

When $\rho =(0.0,0.0,0.0)$, the difference of ${\mathrm{ARL}}_1$ caused by different control limits is not obvious. However, the type of control limits significantly influences the value of ${\mathrm{ARL}}_1$ when ${\rho }_1,{\rho }_2,{\rho }_3>0$. It can be concluded that the exact control limits have more advantages over the approximate control limits in these cases. For instance, when $\rho =(0.8,0.8,0.8)$ and $\tau =1.10$, the results for exact and approximate control limits are 336.1 and 355.7. It can be seen that the simulation results are consistent with the conclusion in Section 4.1.1.

4.2. The performance of two EWMA-type schemes

A memory-type EWMA scheme performs well in detecting small to moderate and persistent shifts, and the MOSE scheme has further enhanced performance. In this subsection, we compare the performance of the two one-sided EWMA and MOSE schemes when ${\gamma }_X,{\gamma }_Y,{\gamma }_Z\ge 0.1$, and parameters of the simulations are selected as follows:

• $\gamma \in \{(0.1,0.1,0.1),(0.2,0.2,0.2),(0.3,0.3,0.3),(0.1,0.2,0.3),(0.3,0.2,0.1)\}$;

• ${\rho }_0\in \{(-0.4,-0.4,-0.4),(0,0,0),(0.4,0.4,0.4),(0.8,0.8,0.8),(0.4,0.6,0.8)\}$;

• $\tau \in \{0.90,0.93,0.95,0.97,0.98,0.99,1.00,1.01,1.02,1.03,1.05,1.07,1.1\}$;

• $\lambda =0.2$, $n\in \{1,5\}$, ${\mathrm{ARL}}_0=370$.

The control limits of the two one-sided EWMA and MOSE schemes are obtained by the algorithm outlined in Section 3.3 and are presented in Table 3. Table 4 shows the ${\mathrm{ARL}}_1$ results under different settings when n = 1. Table 5 shows the ${\mathrm{ARL}}_1$ results when n = 5. Now, we briefly discuss the numerical results of Tables 4–5.

Table 3.

Control limits of two EWMA-type schemes for ratio V, with ${\mathrm{ARL}}_0=370$.

		EWMA				MOSE
		n = 1		n = 5		n = 1		n = 5
γ	ρ	LCL	UCL	LCL	UCL	LCL	UCL	LCL	UCL
(0.02, 0.02, 0.02)	(−0.4, −0.4, −0.4)	0.48574	0.51481	0.49355	0.50655	0.48651	0.51412	0.49387	0.50624
	(0.0, 0.0, 0.0)	0.48792	0.51245	0.49455	0.50552	0.48854	0.51190	0.49483	0.50526
	(0.4, 0.4, 0.4)	0.49061	0.50964	0.49577	0.50428	0.49109	0.50918	0.49598	0.50406
	(0.8, 0.8, 0.8)	0.49455	0.50555	0.49755	0.50246	0.49481	0.50527	0.49767	0.50235
	(0.4, 0.6, 0.8)	0.49449	0.50549	0.49754	0.50245	0.49479	0.50522	0.49766	0.50234
(0.1, 0.1, 0.1)	(−0.4, −0.4, −0.4)	0.43359	0.58088	0.46887	0.53393	0.43750	0.57737	0.47057	0.53241
	(0.0, 0.0, 0.0)	0.44291	0.56758	0.47353	0.52855	0.44618	0.56451	0.47487	0.52721
	(0.4, 0.4, 0.4)	0.45472	0.55170	0.47927	0.52193	0.45720	0.54934	0.48032	0.52090
	(0.8, 0.8, 0.8)	0.47302	0.52904	0.48788	0.51253	0.47444	0.52776	0.48850	0.51194
	(0.4, 0.6, 0.8)	0.47211	0.52795	0.48770	0.51233	0.47353	0.52653	0.48830	0.51170
(0.2, 0.2, 0.2)	(−0.4, −0.4, −0.4)	0.37700	0.68480	0.44004	0.57144	0.38562	0.67828	0.44355	0.56837
	(0.0, 0.0, 0.0)	0.39172	0.65555	0.44854	0.55975	0.39882	0.65000	0.45156	0.55712
	(0.4, 0.4, 0.4)	0.41141	0.61906	0.45940	0.54564	0.41713	0.61429	0.46146	0.54355
	(0.8, 0.8, 0.8)	0.44463	0.56674	0.47591	0.52585	0.44793	0.56342	0.47718	0.52457
	(0.4, 0.6, 0.8)	0.44094	0.55883	0.47515	0.52480	0.44411	0.55590	0.47641	0.52364
(0.3, 0.3, 0.3)	(−0.4, −0.4, −0.4)	0.32756	0.83469	0.41334	0.61312	0.34141	0.82359	0.41870	0.60867
	(0.0, 0.0, 0.0)	0.34313	0.79859	0.42489	0.59433	0.35584	0.78780	0.42946	0.59074
	(0.4, 0.4, 0.4)	0.36470	0.74703	0.43983	0.57218	0.37514	0.73723	0.44335	0.56880
	(0.8, 0.8, 0.8)	0.40313	0.64844	0.46373	0.54035	0.41040	0.64076	0.46569	0.53854
	(0.4, 0.6, 0.8)	0.39685	0.60319	0.46215	0.53789	0.40289	0.59697	0.46398	0.53597
(0.1, 0.2, 0.3)	(−0.4, −0.4, −0.4)	0.15077	0.31349	0.18840	0.25983	0.15519	0.30992	0.190325	0.258224
	(0.0, 0.0, 0.0)	0.15476	0.29791	0.19158	0.25443	0.15851	0.29474	0.19312	0.25292
	(0.4, 0.4, 0.4)	0.15971	0.28133	0.19531	0.24847	0.16249	0.27828	0.19661	0.24709
	(0.8, 0.8, 0.8)	0.16556	0.26246	0.20015	0.24138	0.16777	0.25986	0.20113	0.24027
	(0.4, 0.6, 0.8)	0.16412	0.26487	0.19916	0.24240	0.16660	0.26205	0.20015	0.24132
(0.3, 0.2, 0.1)	(−0.4, −0.4, −0.4)	0.98966	1.56001	1.09541	1.33090	1.00581	1.54876	1.10159	1.32566
	(0.0, 0.0, 0.0)	1.01241	1.56819	1.10570	1.32320	1.02812	1.55750	1.11169	1.31851
	(0.4, 0.4, 0.4)	1.03822	1.58148	1.11721	1.31454	1.05241	1.57281	1.12258	1.31009
	(0.8, 0.8, 0.8)	1.06692	1.61014	1.13032	1.30387	1.08053	1.60253	1.13508	1.30040
	(0.4, 0.6, 0.8)	1.08285	1.48660	1.13989	1.28466	1.09334	1.47933	1.14364	1.28138

Table 4.

${\mathrm{ARL}}_1$ of two EWMA-type schemes for ratio V, with n = 1 and ${\mathrm{ARL}}_0=370$.

	$\gamma =(0.02,0.02,0.02)$		$(0.1,0.1,0.1)$		$(0.2,0.2,0.2)$		$(0.3,0.3,0.3)$		$(0.1,0.2,0.3)$		$(0.3,0.2,0.1)$
τ	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE
$\rho =($- $0.4,$- $0.4,$- $0.4)$
0.90	2.1	2.0	21.3	18.1	94.2	72.6	185.4	146.1	171.4	129.7	43.0	34.6
0.93	3.0	2.8	45.5	37.5	163.0	129.5	257.9	215.1	259.8	204.6	84.7	69.8
0.95	4.5	4.3	88.3	72.0	231.8	198.9	307.1	272.2	326.1	278.7	143.7	119.0
0.97	9.9	9.0	182.0	155.2	313.5	280.4	354.0	326.6	356.8	347.8	237.8	209.4
0.98	21.5	18.9	261.4	236.9	342.2	332.1	361.5	349.5	395.0	366.1	293.8	263.0
0.99	86.2	71.3	341.8	321.8	371.5	360.0	368.7	361.5	394.3	377.6	343.2	329.9
1.00	368.7	368.2	375.3	370.1	371.5	368.4	372.6	371.5	373.3	368.8	373.7	368.4
1.01	83.7	72.8	331.8	311.4	358.7	349.0	368.4	359.1	349.4	347.3	376.1	368.6
1.02	22.1	19.6	251.3	228.1	320.9	326.5	345.6	359.5	316.0	319.0	338.5	331.6
1.03	10.3	9.5	177.3	154.8	288.5	282.6	347.6	335.8	280.4	275.2	298.1	281.5
1.05	4.7	4.4	86.5	74.8	209.2	199.6	300.8	291.1	207.3	201.6	200.2	184.2
1.07	3.1	3.0	47.2	41.1	150.6	135.4	250.7	236.0	155.3	144.2	132.7	117.6
1.10	2.2	2.1	23.5	20.8	91.2	82.0	185.4	170.8	96.1	88.8	74.8	65.5
$\rho =(0,0,0)$
0.90	1.8	1.8	15.1	13.2	70.1	55.4	159.5	120.2	151.9	116.6	32.8	27.5
0.93	2.5	2.4	32.3	26.8	133.2	106.2	233.6	189.7	238.3	190.6	67.5	54.3
0.95	3.6	3.4	64.5	52.7	202.0	168.1	286.5	244.4	311.6	269.1	116.9	95.2
0.97	7.6	7.0	149.4	125.7	285.9	260.8	335.3	304.6	374.4	347.2	204.6	182.5
0.98	15.5	13.9	230.4	207.2	335.0	311.2	348.9	333.6	396.8	377.8	267.2	237.8
0.99	63.1	53.3	331.5	309.3	359.3	352.7	366.3	350.7	395.8	382.6	330.0	313.8
1.00	372.5	369.7	367.1	369.7	367.8	368.7	373.5	367.4	371.7	368.9	372.1	367.6
1.01	63.4	53.8	315.5	298.6	348.8	356.7	379.1	367.1	335.8	336.1	387.7	381.4
1.02	15.8	14.3	222.5	199.6	316.1	318.5	366.6	366.8	296.7	298.2	371.1	360.3
1.03	7.8	7.2	143.1	124.0	281.3	271.9	363.4	351.9	257.4	254.2	323.7	311.6
1.05	3.7	3.6	64.8	55.1	190.2	180.9	310.9	307.4	181.6	172.0	232.3	209.5
1.07	2.6	2.5	34.2	29.6	130.0	119.2	272.2	253.2	125.8	116.8	154.6	136.1
1.10	1.9	1.8	16.8	15.3	75.2	67.7	199.3	183.2	75.3	69.8	86.8	76.2
$\rho =(0.4,0.4,0.4)$
0.90	1.4	1.3	9.6	8.7	44.0	35.0	126.2	93.0	132.2	102.9	24.3	20.7
0.93	2.0	1.9	19.4	16.6	88.7	70.6	198.4	152.5	217.8	177.6	48.7	41.5
0.95	2.7	2.6	39.2	32.8	154.1	123.0	255.5	219.5	299.6	261.9	88.3	75.7
0.97	5.1	4.8	104.7	86.1	252.7	217.9	313.4	282.9	376.1	353.4	168.6	151.2
0.98	9.7	8.9	183.0	158.3	312.9	279.2	331.9	318.3	395.6	385.7	230.4	212.9
0.99	38.5	32.2	303.2	279.1	352.4	341.0	360.8	343.6	397.9	390.2	298.0	295.0
1.00	371.5	372.2	373.4	373.9	372.6	371.2	369.6	368.1	367.2	372.0	368.9	372.5
1.01	38.5	32.6	295.1	277.0	350.1	345.3	374.2	382.8	330.7	329.9	398.1	408.2
1.02	9.9	9.1	177.4	154.0	307.3	303.0	376.0	381.2	276.8	272.5	403.6	400.9
1.03	5.3	4.9	102.3	87.2	251.6	236.6	369.9	373.0	220.0	220.4	371.3	363.0
1.05	2.8	2.7	41.2	35.1	154.6	143.1	327.8	327.3	144.0	137.4	267.5	248.8
1.07	2.0	1.9	21.0	18.3	100.6	85.9	283.8	268.5	94.1	86.5	185.8	171.3
1.10	1.4	1.3	10.8	9.9	50.8	44.9	209.7	190.8	54.2	48.0	104.3	96.4
$\rho =(0.8,0.8,0.8)$
0.90	1.0	1.0	4.2	4.0	14.5	12.6	74.3	52.1	109.0	85.8	16.2	14.3
0.93	1.1	1.0	7.0	6.6	31.9	26.4	148.6	107.4	205.1	160.5	32.8	28.3
0.95	1.7	1.6	12.9	11.5	65.4	51.5	225.0	174.0	300.5	241.0	61.5	52.3
0.97	2.6	2.5	37.3	31.4	153.9	125.3	300.1	264.5	394.9	355.8	128.4	115.7
0.98	4.3	4.0	82.2	67.9	231.8	203.4	330.4	310.1	431.9	398.1	193.4	175.6
0.99	12.7	11.4	210.6	185.8	329.1	308.0	357.6	338.3	426.2	409.2	277.3	264.7
1.00	371.8	373.4	368.1	371.1	370.4	369.3	370.9	368.3	368.6	368.1	369.2	368.1
1.01	12.9	11.6	205.5	188.0	336.2	318.2	371.8	375.5	298.5	297.9	439.8	443.3
1.02	4.3	4.1	81.5	69.9	249.2	215.8	356.9	362.7	226.5	220.1	463.6	467.7
1.03	2.7	2.5	37.5	32.9	169.6	139.9	344.0	340.9	169.2	158.0	444.2	439.9
1.05	1.7	1.6	13.5	12.4	74.9	61.3	285.5	278.0	91.5	84.3	349.6	325.1
1.07	1.1	1.1	7.5	7.1	37.8	31.8	229.2	201.2	53.9	49.0	255.0	236.4
1.10	1.0	1.0	4.6	4.3	17.8	15.7	140.5	118.0	29.0	26.4	150.0	136.8
$\rho =(0.4,0.6,0.8)$
0.90	1.0	1.0	4.3	4.1	16.2	14.0	81.6	60.6	114.8	18.1	12.5	11.1
0.93	1.1	1.0	7.4	6.8	36.3	30.1	161.2	123.6	203.8	37.5	24.8	21.8
0.95	1.7	1.6	13.6	12.2	74.9	59.8	248.5	199.6	303.6	72.0	48.1	41.4
0.97	2.7	2.5	39.6	33.2	172.6	143.8	335.5	302.2	402.8	155.2	110.8	96.9
0.98	4.3	4.0	89.1	72.8	263.2	224.8	373.1	345.1	422.3	236.9	174.7	160.4
0.99	12.9	11.5	222.4	193.4	349.2	330.5	374.3	379.8	424.2	321.8	266.9	255.8
1.00	373.6	368.1	372.5	373.4	369.5	372.8	373.5	369.2	371.8	370.1	370.4	372.8
1.01	12.5	11.4	199.3	176.9	296.2	286.8	342.0	331.5	308.1	311.4	430.2	435.7
1.02	4.3	4.0	76.2	64.0	196.1	180.0	293.3	280.4	242.0	228.1	409.4	401.8
1.03	2.7	2.5	35.1	30.1	126.0	109.7	239.1	222.3	177.6	154.8	349.6	324.7
1.05	1.7	1.6	12.9	11.7	53.8	46.4	151.9	131.5	100.1	74.8	220.9	197.7
1.07	1.1	1.1	7.2	6.7	28.3	24.3	91.9	77.2	59.9	41.1	134.9	118.5
1.10	1.0	1.0	4.4	4.1	13.9	12.5	46.6	37.6	31.8	20.8	66.3	58.4

Table 5.

${\mathrm{ARL}}_1$ of two EWMA-type schemes for ratio V, with n = 5 and ${\mathrm{ARL}}_0=370$.

	$\gamma =(0.02,0.02,0.02)$		$(0.1,0.1,0.1)$		$(0.2,0.2,0.2)$		$(0.3,0.3,0.3)$		$(0.1,0.2,0.3)$		$(0.3,0.2,0.1)$
τ	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE	EWMA	MOSE
$\rho =(-0.4,-0.4,-0.4)$
0.90	1.0	1.0	5.2	4.8	16.9	14.5	40.5	32.6	28.5	23.8	9.0	8.1
0.93	1.3	1.2	9.1	8.1	36.7	29.5	83.4	66.7	61.7	50.1	18.2	15.7
0.95	1.9	1.9	17.0	15.0	72.2	57.8	143.5	117.9	117.7	92.0	36.2	30.6
0.97	3.2	3.0	49.4	41.4	160.8	135.6	246.1	218.1	222.8	185.2	94.3	80.2
0.98	5.4	5.0	103.2	86.2	244.5	207.8	313.4	292.3	294.5	263.4	170.6	147.0
0.99	17.6	15.5	237.0	211.8	330.3	314.6	351.6	339.3	354.9	340.1	285.4	267.3
1.00	370.0	368.5	369.5	368.8	373.7	367.7	374.8	368.1	373.0	370.0	369.7	373.9
1.01	17.9	15.8	226.7	206.9	320.1	311.7	348.0	338.1	324.5	324.7	301.5	289.3
1.02	5.4	5.1	104.5	88.5	230.9	213.6	284.7	284.4	243.4	233.9	189.5	165.5
1.03	3.2	3.1	49.9	41.7	149.8	135.6	232.4	212.1	175.8	162.2	110.2	96.6
1.05	2.0	1.9	18.0	16.1	70.9	61.2	136.4	119.0	90.7	79.7	44.1	38.9
1.07	1.4	1.3	9.9	8.9	37.3	33.1	82.1	72.5	50.5	44.3	22.8	20.3
1.10	1.0	1.0	5.6	5.3	19.1	17.0	42.3	37.7	25.4	22.6	11.6	10.7
$\rho =(0,0,0)$
0.90	1.0	1.0	4.1	3.8	12.2	10.8	28.5	23.5	22.7	19.1	7.7	6.8
0.93	1.1	1.0	6.9	6.3	25.4	21.5	62.0	47.6	49.8	40.7	14.7	12.7
0.95	1.7	1.6	12.3	11.2	52.1	42.2	114.6	90.1	95.5	76.5	29.3	24.5
0.97	2.6	2.5	35.1	29.9	130.2	105.0	214.8	184.2	199.5	169.7	79.6	66.0
0.98	4.2	4.0	77.2	64.7	209.8	179.5	283.8	255.9	279.2	251.5	148.7	124.4
0.99	12.6	11.3	203.8	178.2	313.9	292.9	341.6	329.4	354.9	347.7	274.1	248.9
1.00	369.3	367.8	368.7	369.8	373.2	368.6	367.6	372.9	368.0	372.4	372.3	367.4
1.01	12.7	11.6	202.6	179.9	305.0	288.8	336.6	330.4	318.6	303.5	303.6	288.7
1.02	4.3	4.1	78.6	65.1	202.0	180.3	267.6	256.0	216.3	202.8	180.5	160.3
1.03	2.7	2.5	35.2	30.7	124.7	107.9	202.9	189.2	150.5	134.8	103.8	88.9
1.05	1.7	1.6	13.1	11.8	53.6	45.6	110.9	96.7	70.1	62.2	39.5	35.1
1.07	1.1	1.1	7.4	6.9	26.8	24.2	61.9	55.1	38.5	34.2	20.4	18.3
1.10	1.0	1.0	4.5	4.2	13.7	12.4	31.8	27.8	19.3	17.6	10.4	9.7
$\rho =(0.4,0.4,0.4)$
0.90	1.0	1.0	3.0	2.9	7.8	7.1	17.0	14.9	16.5	14.7	6.3	5.7
0.93	1.0	1.0	4.8	4.5	15.2	13.5	37.5	31.0	35.7	30.3	11.4	10.1
0.95	1.2	1.1	7.9	7.3	30.5	26.3	73.3	59.6	74.3	60.3	22.1	19.3
0.97	2.1	2.0	21.1	18.0	85.1	70.8	166.2	138.9	171.1	141.4	61.9	51.5
0.98	3.1	2.9	48.3	40.4	157.6	134.8	250.9	216.0	251.9	229.4	122.2	103.2
0.99	8.1	7.4	155.7	133.9	281.9	265.7	339.1	316.2	351.2	327.9	247.0	221.2
1.00	372.3	369.5	372.7	369.6	368.2	370.6	373.1	368.3	372.2	369.5	372.0	370.0
1.01	8.2	7.5	149.4	128.7	274.4	252.8	330.6	309.7	284.3	271.2	305.2	286.7
1.02	3.2	3.0	47.5	41.6	153.7	134.1	231.2	212.5	189.5	171.4	172.0	151.6
1.03	2.1	2.0	21.2	19.1	85.6	71.7	158.6	136.8	118.0	103.6	94.9	82.1
1.05	1.2	1.1	8.3	7.8	31.6	27.6	75.4	62.4	50.2	44.1	34.7	31.3
1.07	1.0	1.0	5.1	4.7	16.4	14.8	39.6	34.2	26.6	23.4	17.6	16.0
1.10	1.0	1.0	3.2	3.1	8.8	8.1	19.8	17.2	13.5	12.5	9.2	8.5
$\rho =(0.8,0.8,0.8)$
0.90	1.0	1.0	1.9	1.8	3.6	3.4	6.5	6.0	10.8	9.8	4.9	4.5
0.93	1.0	1.0	2.5	2.4	5.9	5.5	12.4	10.8	22.5	19.8	8.4	7.7
0.95	1.0	1.0	3.7	3.4	10.4	9.3	24.2	20.8	47.3	39.4	15.6	13.7
0.97	1.1	1.1	7.5	6.9	29.4	25.0	69.9	57.3	126.0	103.6	43.9	36.9
0.98	1.9	1.8	15.6	13.9	66.5	54.0	137.1	115.3	211.8	182.9	91.0	77.3
0.99	3.7	3.5	63.7	54.3	185.8	161.9	268.7	246.4	339.2	307.3	205.6	188.7
1.00	367.6	368.7	373.8	372.9	373.3	373.3	367.8	369.5	367.9	369.0	368.7	372.5
1.01	3.7	3.5	64.5	54.6	184.8	162.3	262.4	248.8	249.3	232.0	294.3	282.0
1.02	1.9	1.8	15.9	14.6	66.4	56.5	136.5	120.2	137.4	116.9	152.3	139.6
1.03	1.1	1.1	7.8	7.2	29.7	25.8	71.5	60.2	73.7	63.1	82.0	70.5
1.05	1.0	1.0	3.8	3.6	11.1	10.1	26.1	23.1	28.7	25.1	29.2	25.5
1.07	1.0	1.0	2.6	2.5	6.4	5.9	13.4	12.1	15.4	13.6	14.8	13.4
1.10	1.0	1.0	1.9	1.8	4.0	3.7	7.2	6.8	8.3	7.7	7.8	7.3
$\rho =(0.4,0.6,0.8)$
0.90	1.0	1.0	1.9	1.8	3.8	3.5	6.9	6.3	11.7	10.7	3.9	3.7
0.93	1.0	1.0	2.5	2.4	6.2	5.7	13.0	11.6	24.5	21.8	6.6	6.1
0.95	1.0	1.0	3.7	3.5	10.8	9.8	26.3	22.6	52.7	44.1	11.8	10.5
0.97	1.1	1.1	7.7	7.1	30.4	26.3	76.0	62.8	135.0	110.6	32.3	27.4
0.98	1.9	1.8	16.1	14.4	69.8	57.8	149.0	123.3	221.0	195.4	69.3	60.2
0.99	3.7	3.5	64.9	54.9	197.2	169.1	283.1	254.1	336.9	325.1	184.9	162.3
1.00	369.2	372.0	371.6	368.9	371.1	367.2	367.7	369.2	368.7	368.2	370.6	368.1
1.01	3.7	3.5	61.9	52.2	168.1	154.0	246.5	225.8	254.5	241.9	256.7	231.8
1.02	1.9	1.8	15.6	14.1	60.9	52.0	120.3	105.1	143.5	126.5	116.6	98.5
1.03	1.1	1.1	7.6	7.0	27.3	23.7	62.1	52.5	78.7	69.5	55.0	47.1
1.05	1.0	1.0	3.7	3.5	10.4	9.5	22.9	19.8	31.5	27.7	19.4	17.5
1.07	1.0	1.0	2.5	2.4	6.1	5.7	12.0	10.9	16.7	15.1	10.3	9.4
1.10	1.0	1.0	1.9	1.8	3.8	3.6	6.7	6.2	8.8	8.3	5.7	5.4

For both the schemes, as expected, the value of ${\mathrm{ARL}}_1$ decreases as n increases, which means the charting schemes become more efficient in detecting a shift as the test sample size increases. The two charting schemes are more sensitive in the presence of positive correlation among X, Y and Z. For example, if $\gamma =(0.1,0.1,0.1)$, n = 1, $\tau =1.03$ and $\rho =(-0.4,-0.4,-0.4)$, we have the ${\mathrm{ARL}}_1$ value of the two one-sided EWMA charts is 177.3, while ${\mathrm{ARL}}_1=102.3$ if $\rho =(0.4,0.4,0.4)$. The numerical results of the two one-sided MOSE schemes are similar to the two one-sided EWMA schemes.

From Tables 4–5, one may observe that the parameter γ immensely influences both schemes' performance. For example, when $\gamma =(0.1,0.1,0.1),\rho =(0.4,0.4,0.4)$, n = 5 and $\tau =0.97$, ${\mathrm{ARL}}_1$ of the two one-sided EWMA and MOSE schemes are equal to 21.1 and 18.0, respectively; when $\gamma =(0.2,0.2,0.2)$, $\rho =(0.4,0.4,0.4)$, n = 5 and $\tau =0.97$, ${\mathrm{ARL}}_1$ of two one-sided EWMA and MOSE charts are 85.1 and 70.8, respectively. Obviously, the control charts are more sensitive to a smaller coefficient of variation. For unequal coefficients of variation cases, i.e. $\gamma =(0.1,0.2,0.3)$ and $(0.3,0.2,0.1)$, we can conclude that the performance of the schemes is worse when ${\gamma }_Z$ is large, compared to situations when ${\gamma }_X$ is large.

The two one-sided MOSE schemes perform better than the two one-sided EWMA schemes in almost all cases investigated in this article. For instance, when $\gamma =(0.1,0.1,0.1)$, $\rho =(0.4,0.6,0.8)$, n = 5, and $\tau =1.01$, ${\mathrm{ARL}}_1$ values of the two one-sided EWMA and MOSE schemes are 61.9 and 52.2, respectively. It is worth noting that the values of ${\mathrm{ARL}}_1$ for small shifts are great than ${\mathrm{ARL}}_0$ when ${\gamma }_X=0.3$ and n = 1. For instance, the results of the EWMA and MOSE schemes with $\tau =1.01$ are 398.1 and 408.2, respectively, if $\gamma =(0.3,0.2,0.1)$ and $\rho =(0.4,0.4,0.4)$. The results indicate that the ${\mathrm{ARL}}_1$ is biased when ${\gamma }_X$ is large. As expected, EWMA-type charts are more sensitive to small shifts than the Shewhart chart.

For example, let $\gamma =(0.3,0.3,0.3)$, $\rho =(0.4,0.6,0.8)$, n = 1, and $\tau =1.05$. The ${\mathrm{ARL}}_1$ of the Shewhart chart with exact control limits is 282.5, while the ${\mathrm{ARL}}_1$ values of the EWMA and MOSE schemes are 151.9 and 131.5, respectively. However, if τ is 2, additional simulations show that the ${\mathrm{ARL}}_1$ of the two EWMA-type charts are 1.6 and 1.5, respectively, whereas the ${\mathrm{ARL}}_1$ of the Shewhart chart is 1.3. Therefore, the Shewhart-type scheme may perform better for large shifts.

4.3. The performance of proposed control charts with shift of correlation coefficient

In practice, a shift of the correlation coefficient may lead the process to an OOC state. This simulation aims to evaluate the performance of the proposed control charts when the correlation coefficient changes. $\gamma =(0.02,0.02,0.02)$ and $(0.1,0.1,0.1)$ are considered in this section. According to Section 4.1, the exact and approximate control limits of the Shewhart-type schemes are practically equal in these cases. Table 6 shows the ${\mathrm{ARL}}_1$ of the proposed three charts under different parameter settings.

Table 6.

${\mathrm{ARL}}_1$ of three proposed schemes for ratio V with shift of correlation coefficient, with n = 1, 5 and ${\mathrm{ARL}}_0=370$.

	n = 1						n = 5
	$\gamma =(0.02,0.02,0.02)$			$(0.1,0.1,0.1)$			$\gamma =(0.02,0.02,0.02)$			$(0.1,0.1,0.1)$
τ	Shewhart	EWMA	MOSE	Shewhart	EWMA	MOSE	Shewhart	EWMA	MOSE	Shewhart	EWMA	MOSE
$\rho =(-0.4,-0.4,-0.4)$ to $(-0.4,-0.2,-0.4)$
0.90	1.4	2.1	2.0	161.1	22.4	18.6	1.0	1.0	1.0	16.3	5.1	4.8
0.93	3.5	3.0	2.8	276.5	51.2	40.2	1.0	1.3	1.2	49.0	9.2	8.3
0.95	10.8	4.5	4.2	388.6	104.9	81.4	1.2	1.9	1.9	110.1	17.5	15.3
0.97	52.8	10.1	9.0	527.3	246.1	193.1	4.1	3.1	3.0	264.7	55.8	44.7
0.98	136.2	23.4	19.7	569.0	370.0	312.3	15.9	5.3	5.0	400.2	128.7	102.1
0.99	353.5	105.1	83.2	593.4	522.3	471.5	104.7	18.3	16.1	549.6	329.2	275.5
1.00	616.6	601.1	564.1	595.8	590.1	564.3	624.6	602.8	574.0	609.0	590.2	554.1
1.01	340.8	106.5	87.4	575.2	536.1	489.7	103.2	18.6	16.3	525.9	334.6	297.4
1.02	127.1	24.0	20.8	532.5	385.0	329.6	16.0	5.5	5.1	375.1	129.3	108.0
1.03	49.6	10.4	9.7	457.3	250.7	213.8	4.3	3.2	3.1	244.6	58.2	48.6
1.05	11.5	4.7	4.5	332.5	110.6	93.5	1.3	2.0	1.9	101.2	19.3	16.9
1.07	3.9	3.1	3.0	223.8	54.9	47.1	1.0	1.4	1.3	44.3	10.0	9.2
1.10	1.6	2.2	2.1	126.5	25.6	22.5	1.0	1.0	1.0	16.4	5.7	5.3
$\rho =(-0.4,-0.4,-0.4)$ to $(-0.4,-0.6,-0.4)$
0.90	1.4	2.1	2.0	92.9	20.5	17.5	1.0	1.0	1.0	12.5	5.1	4.8
0.93	3.3	3.0	2.8	147.3	42.4	34.9	1.0	1.3	1.2	32.1	9.0	8.2
0.95	8.9	4.5	4.2	191.6	75.7	63.1	1.2	1.9	1.8	66.0	16.7	14.6
0.97	34.2	9.9	9.0	230.3	146.5	128.8	3.8	3.2	3.0	134.6	44.3	37.9
0.98	73.8	20.4	18.0	249.6	192.7	181.2	12.3	5.3	5.0	186.6	85.7	73.9
0.99	161.6	72.3	61.4	250.6	239.1	240.2	60.3	17.1	14.9	230.4	177.7	166.4
1.00	240.6	252.0	254.4	246.3	246.6	253.8	240.9	255.7	258.9	244.5	251.2	258.6
1.01	152.8	70.6	62.9	232.1	226.5	226.4	60.7	16.9	15.3	209.7	167.2	159.5
1.02	69.9	20.8	18.8	216.2	177.2	170.9	12.0	5.4	5.1	163.4	81.0	73.0
1.03	32.8	10.1	9.2	192.8	133.8	118.8	4.0	3.2	3.1	115.1	43.0	38.4
1.05	9.1	4.7	4.4	142.4	70.3	63.3	1.3	2.0	1.9	54.9	17.1	15.3
1.07	3.7	3.1	3.0	106.7	40.7	36.2	1.0	1.4	1.3	28.9	9.4	9.0
1.10	1.6	2.2	2.1	65.1	21.9	19.6	1.0	1.0	1.0	12.3	5.6	5.3
$\rho =(0.4,0.4,0.4)$ to $(0.4,0.6,0.4)$
0.90	1.0	1.3	1.2	91.6	9.8	8.7	1.0	1.0	1.0	4.0	3.0	2.8
0.93	1.2	2.0	1.9	231.8	21.6	17.8	1.0	1.0	1.0	16.1	4.8	4.4
0.95	2.8	2.7	2.6	432.6	51.0	40.1	1.0	1.1	1.1	53.4	8.1	7.4
0.97	18.5	5.1	4.8	787.8	179.3	132.1	1.3	2.1	2.0	224.7	24.1	20.3
0.98	75.8	10.0	9.1	998.2	386.2	289.8	4.2	3.1	2.9	482.4	68.9	53.1
0.99	400.8	52.2	41.0	1233.0	847.1	673.1	51.6	8.4	7.5	1018.0	321.8	245.3
1.00	1462.4	1352.7	1185.3	1301.6	1335.2	1166.7	1505.6	1373.5	1195.4	1444.1	1368.4	1195.7
1.01	389.5	53.3	42.0	1230.7	974.6	815.1	52.8	8.4	7.7	1010.0	345.0	261.8
1.02	72.5	10.4	9.5	1033.1	458.3	361.4	4.4	3.1	3.0	473.3	72.1	57.3
1.03	18.8	5.3	5.0	794.1	213.4	161.3	1.4	2.1	2.0	219.1	25.5	21.7
1.05	3.1	2.8	2.6	409.1	59.4	48.3	1.0	1.2	1.1	52.5	8.7	8.0
1.07	1.3	2.0	2.0	212.9	25.0	21.6	1.0	1.0	1.0	17.0	5.0	4.8
1.10	1.0	1.4	1.3	83.0	11.6	10.3	1.0	1.0	1.0	4.8	3.2	3.1
$\rho =(0.4,0.4,0.4)$ to $(0.4,0.2,0.4)$
0.90	1.0	1.4	1.3	32.6	9.3	8.6	1.0	1.0	1.0	3.4	3.1	2.9
0.93	1.3	2.0	1.9	62.2	17.7	15.8	1.0	1.0	1.0	9.4	4.8	4.5
0.95	2.6	2.7	2.6	95.7	32.3	28.6	1.0	1.2	1.1	20.9	7.9	7.2
0.97	10.2	5.1	4.8	135.1	71.2	64.8	1.4	2.1	2.0	55.1	18.6	16.7
0.98	25.7	9.3	8.7	149.2	108.4	103.2	3.5	3.1	3.0	91.3	38.0	33.8
0.99	76.2	30.9	27.2	160.4	151.5	155.1	20.5	7.9	7.3	131.9	92.9	88.6
1.00	150.9	166.2	174.9	156.5	170.2	177.8	152.4	165.5	174.0	153.6	164.6	174.6
1.01	73.5	31.2	27.8	147.6	137.9	143.6	20.1	8.0	7.4	126.2	89.0	82.5
1.02	25.2	9.6	8.8	131.6	97.5	93.8	3.6	3.2	3.0	81.1	36.9	32.9
1.03	9.8	5.3	4.9	111.4	64.6	59.9	1.5	2.1	2.0	49.9	18.8	16.8
1.05	2.8	2.8	2.7	75.2	31.7	28.2	1.0	1.2	1.2	20.2	8.1	7.5
1.07	1.4	2.0	1.9	48.9	18.3	16.5	1.0	1.0	1.0	9.2	5.0	4.8
1.10	1.0	1.4	1.4	26.6	10.1	9.4	1.0	1.0	1.0	3.9	3.2	3.1

When the correlation coefficients ${\rho }_1$, ${\rho }_2$ and ${\rho }_3$ are negative, and $\tau =1.00$, that is, there is no change in the ratio, the values of ${\mathrm{ARL}}_1$ are greater than 370 if the correlation between X and Z becomes weaker. For example, when $\gamma =(0.02,0.02,0.02)$, n = 1 and ${\rho }_2=-0.4$ shifts to $-0.2$, ${\mathrm{ARL}}_1$ of the three proposed charts are 616.6, 601.1 and 564.1, respectively. The conclusion is the opposite if the correlation between X and Z gets more substantial. Thus, the proposed charts for ratio V are more sensitive to increased negative correlation.

When the correlation coefficients ${\rho }_1$, ${\rho }_2$ and ${\rho }_3$ are positive, and the correlation between X and Z becomes weaker, the values of ${\mathrm{ARL}}_1$ under the unchanged ratio (i.e. $\tau =1.00$) are small than 370. For instance, when $\gamma =(0.1,0.1,0.1)$, n = 5 and ${\rho }_2=0.4$ shifts to 0.2, ${\mathrm{ARL}}_1$ values of the proposed three charts are 153.6, 164.6 and 174, respectively. If the correlation between X and Z becomes stronger, the conclusion is totally opposite. It means all the proposed charts are more sensitive to decreasing positive correlation.

For different schemes, the values of ${\mathrm{ARL}}_1$ without shifts in V are pretty different when other parameters are the same. If ${\rho }_2=-0.4$ shifts to $-0.2$ or ${\rho }_2=0.4$ shifts to 0.6, the ${\mathrm{ARL}}_1$ value of the Shewhart scheme is the largest, while the value of the two one-sided MOSE schemes is the smallest. However, when ${\rho }_2=-0.4$ shifts to $-0.6$ or ${\rho }_2=0.4$ shifts to 0.2, the ${\mathrm{ARL}}_1$ value of the Shewhart chart is the smallest, while the value of the two one-sided MOSE charts is the largest.

5. An illustrative example

This section illustrates the proposed monitoring schemes using the parts manufacturing dataset described in Section 1.

We use the data in a manner that help illustrate various schemes. Noting that the proposed schemes assume true process parameters are unknown, we use the data obtained from operators 1–10 as phase-I samples. We appropriately process the data to eliminate outliers and use the remaining to estimate the process parameters. Subsequently, we use those estimates as true process parameters to illustrate the proposed Phase-II chart. We have mentioned earlier that the current paper deals with the known parameter (Case-K) setup, and its modification for unknown parameters (Case-U) may be considered separately. We consider Phase-II samples from the data of operators 11–20. For illustration purposes, we ignore the operator aspect and consider that these data are items manufactured at ten-time points in a sequence.

It is well known that many statistical procedures are based on specific distributional assumptions, and the proposed monitoring schemes are no exception. So it's essential to provide a goodness-of-fit test before the monitoring. For this purpose, the one-sample Kolmogorov-Smirnov and Cramer-von Mises tests are used to decide whether the dataset follows the distribution defined in Equation (1). The p-values of Kolmogorov-Smirnov and Cramer-von Mises tests for phase-I samples are 0.3535 and 0.4119, respectively. According to the p-values, it can be concluded that the dataset follows the distribution defined in Equation (1). Therefore, the proposed schemes can be used in the parts manufacturing dataset monitoring.

We should first estimate the mean vector and the variance-covariance matrix using the IC samples in phase-I. This paper uses the phase I Lepage scheme proposed by Li et al. [23] to obtain IC samples. Phase I Lepage scheme is a distribution-free chart based on the multi-sample Lepage statistic for Phase I analysis, and it is capable of assessing the stability of both location and scale parameters of the process using a single plotting statistic. The result shows that there is an OOC signal in the data of operator 6. Therefore, we used the data from the remaining nine operators as IC samples. The parameters estimated from the phase-I samples are as follows:

$$\begin{array}{rl}\hat{\mu }& =(100.51,50.04,20.25{)}^{\mathrm{\top }},\\ \hat{\mathbf{\Sigma }}& =\left(\begin{array}{ccc}24.97& 2.83& 1.44\\ 2.83& 6.11& 0.58\\ 1.44& 0.58& 1.22\end{array}\right).\end{array}$$

In phase II, we consider a random subgroup sample of size n = 5 sequentially every time. Essentially, the first subgroup sample is taken from Operator-11, the second from Operator-12 and so on. It reflects a realistic situation ignoring the operator aspect and presuming that the different product features data for the operators are feature data obtained at different time points to inspect process stability. Table 7 presents the data used for phase II monitoring. The control limits of the Shewhart control chart can be obtained from Equations (10)–(11), and the control limits of the EWMA-type control charts are calculated using the Monte Carlo method provided in Section 3.3.

Table 7.

Subgroup sample for phase II monitoring.

Subgroup	Number	Length	Width	Height	Subgroup	Number	Length	Width	Height
1	1	99.00	50.00	18.54	6	1	95.78	52.00	20.71
	2	99.72	49.44	19.97		2	100.54	52.62	20.48
	3	97.98	50.05	21.39		3	98.21	51.32	19.69
	4	103.00	48.59	18.91		4	94.50	47.27	21.67
	5	98.77	49.23	21.15		5	97.82	48.52	20.99
2	1	101.85	49.87	20.97	7	1	98.59	47.47	21.15
	2	94.10	50.48	21.02		2	96.82	49.89	21.86
	3	95.15	49.77	18.81		3	101.24	48.17	19.97
	4	98.08	50.29	21.91		4	96.49	47.98	21.76
	5	95.75	52.17	20.67		5	96.68	51.03	20.10
3	1	97.91	49.17	19.69	8	1	102.77	51.90	19.97
	2	96.81	47.56	21.36		2	98.55	47.74	20.47
	3	96.61	51.74	20.57		3	103.15	48.27	21.64
	4	100.84	52.46	20.85		4	94.86	50.35	20.83
	5	94.19	52.43	18.87		5	97.48	49.70	20.48
4	1	100.99	52.40	21.58	9	1	98.19	51.70	20.26
	2	103.54	50.86	21.15		2	97.88	51.02	21.97
	3	97.87	48.76	21.72		3	98.04	51.18	20.22
	4	97.76	49.64	19.97		4	100.56	51.73	20.92
	5	98.24	51.31	20.53		5	97.07	50.99	18.99
5	1	102.80	52.86	21.01	10	1	101.40	49.13	20.47
	2	98.63	48.07	21.43		2	96.11	52.46	21.38
	3	103.63	47.38	20.95		3	94.16	48.39	21.60
	4	96.70	47.42	20.80		4	100.44	52.45	19.72
	5	103.30	50.12	20.59		5	101.24	49.03	20.96

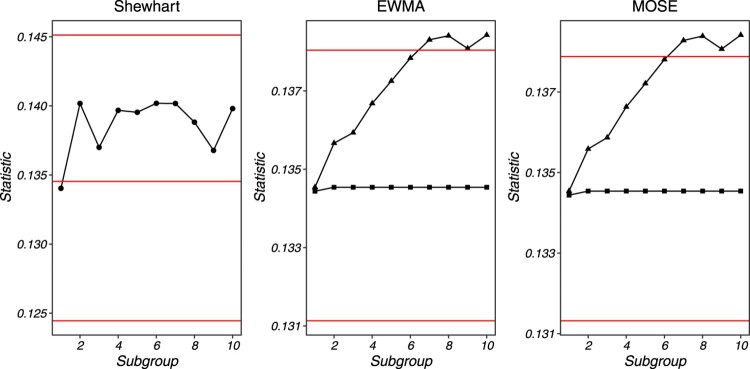
The control limits of the proposed control charts can be obtained according to Section 3.3. As in Section 4, ${\mathrm{ARL}}_0$ is fixed at 370. The LCL and UCL of the Shewhart control chart with these estimated parameters are $0.12445$ and $0.14513$, respectively. The LCL and UCL with $\lambda =0.2$ of the two one-sided EWMA control charts are $0.13113$ and $0.13804$, respectively. While the LCL and UCL with $\lambda =0.2$ of the MOSE scheme are $0.13132$ and $0.13788$, respectively. Figure 2 illustrates the Phase-II monitoring result for ten successive subgroup sample inspections, and Table 8 lists these plotting statistics.

Figure 2.

Proposed schemes for parts manufacturing quality.

Table 8.

Plotting statistics in phase II monitoring.

Subgroup	Shewhart	Downward EWMA	Upward EWMA	Downward MOSE	Upward MOSE
1	0.13403	0.13444	0.13454	0.13444	0.13454
2	0.14017	0.13454	0.13567	0.13454	0.13559
3	0.13700	0.13454	0.13593	0.13454	0.13587
4	0.13968	0.13454	0.13668	0.13454	0.13663
5	0.13954	0.13454	0.13725	0.13454	0.13721
6	0.14019	0.13454	0.13784	0.13454	0.13781
7	0.14017	0.13454	0.13831	0.13454	0.13828
8	0.13882	0.13454	0.13841	0.13454	0.13839
9	0.13678	0.13454	0.13808	0.13454	0.13807
10	0.13981	0.13454	0.13843	0.13454	0.13841

Although the Shewhart control chart does not show any point in the OOC region, a sequence of points lies above the central line, indicating a possible presence of small to moderate persistent shifts in the process. Shewhart scheme is more sensitive to a large shaft without run-rules, while memory-type control charts will be more effective for the small shift. In this example, both the EWMA and MOSE schemes signal at subgroups 7–10, respectively, indicating possible shifts and necessary corrective actions for the manufacturing process. However, it is worth noting that alarms from EWMA-type control charts may be delayed, and the actual shift might have happened earlier.

6. Conclusion

This paper uses the Shewhart and the two one-sided EWMA and MOSE-type SPM schemes to monitor the depth ratio V. The investigation shows that the difference between the exact and approximation control limits of the Shewhart-type schemes can be ignored since the random variables are often non-negative in natural processes. The study further reveals that the two one-sided MOSE schemes perform the best among the three proposed competing schemes in most cases. The data on parts manufacturing provides an illustration of the proposed charting schemes.

The three methods proposed in this paper are designed for different practical problems. Shewhart scheme is simple, easy to use, with low computational cost, and suitable for quickly detecting sudden process shifts, usually of larger magnitude. However, it is not sensitive enough to small or gradual shifts in the process and may result in false alarms. Therefore for high-quality processes, the two EWMA-type schemes are necessary. EWMA charts can use Markov chains to calculate ARL and can get control limits faster. The advantage of the MOSE control chart is that its monitoring performance is better, although it takes more time to calculate the control limits. Hence, in practice, we recommend using the MOSE scheme when the calculation is not a problem. Otherwise, the EWMA scheme is recommended.

The current article presumes that the parameters of the process are known as apriori. However, the standard (true) values of the process parameters to be monitored are seldom known and must be estimated using a sizeable historical sample. More research is highly warranted to investigate the efficacies of the proposed schemes with unknown and estimated parameters. With insufficient historical information, bootstrap-based monitoring schemes are also worth investigating, for example, Chatterjee and Qiu [10] and Khusna et al. [21]. Furthermore, future research should explore developing a self-starting version of our chart, which can simultaneously update parameter estimates using new incoming observations and check for OOC conditions. Following Han et al. [15], future research on designing optimal CUSUM-type schemes, preferably with the dynamic non-random control limit, would be worth exploring. The illustration in Section 5 is based on individual observations, and it will also be interesting to extend the proposed schemes for subgroup samples with equal but subgroup sizes greater than one and unequal subgroup sizes. Like Imran et al. [19], the current work could also be extended to study the zero-state and steady-state performance of the proposed schemes. Furthermore, other SPM schemes, such as run sum schemes and VSI strategy for the ratio V, are also worth studying.

APPENDIX. MARKOV CHAIN METHOD FOR CALCULATING THE CONTROL LIMITS OF THE EWMA SCHEME.

The control interval of an EWMA control chart is divided into several contiguous sub-intervals such that the Markov chain has p + 2 states, where states $0,1,\dots ,p$ belong to the control interval and are transient and state p + 1 coincides with a signal and is absorbing. The transition probability matrix $\mathbf{P}$ of this discrete Markov chain is

$$\mathbf{P}=\left(\begin{array}{cc}\mathbf{Q}& \mathbf{r}\\ {\mathbf{0}}^{\mathrm{\top }}& 1\end{array}\right)=\left(\begin{array}{ccccc}{Q}_{0,0}& Q_{0,1}& \cdots & Q_{0,p}& r_0\\ Q_{1,0}& Q_{1,1}& \cdots & Q_{1,p}& r_1\\ ⋮& ⋮& & ⋮\\ Q_{p,0}& Q_{p,1}& \cdots & Q_{p,p}& r_p\\ 0& 0& \cdots & 0& 1\end{array}\right).$$

where $\mathbf{Q}$ is the $(p+1,p+1)$ matrix of transient probabilities, $\mathbf{0}=(0,0,\dots ,0{)}^{\mathrm{\top }}$ and the $(p+1)$ vector $\mathbf{r}$ satisfies $\mathbf{r}=(\mathbf{1}-\mathbf{Q}\mathbf{1})$ with $\mathbf{1}=(1,1,\dots ,1{)}^{\mathrm{\top }}$. Let $\mathbf{q}$ be the $(p+1,1)$ vector of initial probabilities associated with the p + 1 transient states, that is, $\mathbf{q}=(q_0,q_1,\dots ,q_p{)}^{\mathrm{\top }}$. Concerning the zero-state condition, $\mathbf{q}=(1,0,\dots ,0{)}^{\mathrm{\top }}$.

For the upward EWMA scheme, the interval between $v_0$ and ${\mathrm{UCL}}^{+}=h^{+}>v_0$ is divided into p sub-intervals of width $2\delta$, where $\delta =\frac{h^{+}-v_0}{2p}$. For the downward EWMA scheme, the interval between $v_0$ and ${\mathrm{LCL}}^{-}=h^{-}<v_0$ is divided into p sub-intervals of width $2\delta$, where $\delta =\frac{v_0-h^{-}}{2p}$. Let $d_j,j=1,\dots ,p$ be the midpoint of the jth sub-interval and $d_0=v_0$. When the number p of sub-intervals is sufficiently large, this finite approach provides an effective method that allows the RL properties of the EWMA schemes to be accurately evaluated.

In our study, the element $Q_{i,j},i=0,1,\dots ,p$ of the matrix $\mathbf{Q}$ can be presented as follow:

• when j = 0,

  • °
    for the upward EWMA scheme,

    $$Q_{i,0}=F_{{\hat{V}}_i}\left(\frac{v_0-(1-{\lambda }^{+})d_i}{{\lambda }^{+}}\right),$$
  • °
    for the downward EWMA scheme,

    $$Q_{i,0}=1-F_{{\hat{V}}_i}\left(\frac{v_0-(1-{\lambda }^{-})d_i}{{\lambda }^{-}}\right),$$
• when $j=1,2,\dots ,p$, for both cases,

  $$Q_{\mathrm{ij}}=F_{{\hat{V}}_i}\left(\frac{d_j+\delta -(1-\lambda )d_i}{\lambda }\right)-F_{{\hat{V}}_i}\left(\frac{d_j-\delta -(1-\lambda )d_i}{\lambda }\right),$$

where $F_{{\hat{V}}_i}(\cdot )$ is the c.d.f. of ${\hat{V}}_i$ and λ is either ${\lambda }^{+}$ or ${\lambda }^{-}$.

Then, the ARL of a specified EWMA scheme is equal to

$$\mathrm{ARL}={\mathbf{q}}^{\mathrm{\top }}(\mathbf{I}-\mathbf{Q}{)}^{-1}\mathbf{1}.$$

Funding Statement

This work was supported by the National Natural Science Foundation of China [Grant Nos. 12171328,12201429]; the Beijing Natural Science Foundation [Grant No. Z210003]; the Liaoning BaiQianWan Talents Program; the Natural Science Foundation of Liaoning Province [Grant Nos. 2020-MS-139, 2023-MS-142]; the Scientific Research Fund of Liaoning Provincial Education Department of China [Grant No. LJC202006]; the Project of Science and Research of Hebei Educational Department of China [Grant No. ZD2022020]; the Doctoral Research Start-up Fund of Liaoning Province [Grant No. 2021-BS-142]; the Research on Humanities and Social Sciences of the Ministry of Education [Grant No. 22YJC910009]; and the Research of economic and social development in Liaoning Province [Grant No. 20231s1ybkt-103].

Disclosure statement

No potential conflict of interest was reported by the author(s).