Abstract
The design and synthesis of molecular nanoswitches using organic molecules represent a crucial research field within molecular electronics. To understand the switching mechanisms, it is essential to investigate various factors, such as charge/energy transfer, electron transfer, nonlinear optical properties (NLO), current–voltage (I–V) curves, Joule-like (LJL) and Peltier-like (LPL) intramolecular phenomenological coefficients, as well as the energy levels of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) boundary orbitals. In this Article, a novel approach to designing a molecular nanoswitch and understanding its ON/OFF mechanism is presented, utilizing the quantum theory of atoms in molecules (QTAIM), density functional theory (DFT), and Landauer theory (LT). These analyses contribute significantly to a deep understanding of switching effects within molecular electronic systems.
1. Introduction
Molecular electronics stands out as one of the extensively explored domains within nanotechnology. The challenges within this field include the miniaturization of electronic devices and the establishment of robust molecular junctions at the molecular scale.1−3 The enhancement of electronic circuit efficiency can be achieved through the miniaturization of electronic devices and the development of strong intermolecular connections.4,5 Employing single molecules to build molecular nanoelectronic systems emerges as a promising approach to overcome these challenges.6−8
Nanostructures hold particular significance in the realm of nanoelectronics. Owing to their unique properties and very small dimensions, they find many applications9,10 and play a pivotal role in the fabrication of transistors, sensors, and molecular switches.11−16 Notably, molecular switches have garnered significant attention within nanoelectronic devices due to their broad applications in information storage and signal processing.17−23 The capability of a molecular to switch between ON and OFF states through the application of an external agent, thereby altering its configuration, is a key feature. Consequently, the design and synthesis of modifiable molecules switching between ON/OFF states under the influence of an external stimulus, such as an electric field, stand as remarkable achievements in the field of molecular electronics.24−27
It is well-known that an external electric field (EF) often exerts a significant influence on groups of atoms or molecules, inducing observable changes in both the physical and physicochemical properties of the molecule.28,29 Within this context, the electron transfer properties investigation, at the atomic-molecular scale, emerges as a crucial element in understanding the characteristics of the molecular components, such as molecular wires and switches.30,31 In some molecular switches, quantum effects, notably tunneling, become prominent when the energy gap is sufficiently small. These effects enable electrons to go through energy barriers, significantly influencing switching behavior.32 Hence, the design of a molecular switch necessitates the careful selection of materials with a specific energy gap. In this context, conjugated molecules are particularly intriguing.
In a conjugated molecule or conjugated system, the application of an external electric field (EF) induces displacement of the π electrons within the molecule, resulting in a switch between ON and OFF states.33−36 This study specifically demonstrates the ability of a single conjugated molecule, incorporating tetracyanoquinodimethane (TCNQ) unit, to switch between these two states.37−39
The observed state changes are intricately related to the transfer of π-conjugated bonding electrons along the proposed molecular structure (see Figure 1). The research delves into the electron-transport properties of the molecular switch using the quantum theory of density subordination, the quantum theory of atoms in molecules, and Landauer theory (LT). The single-particle Density Functional Theory (DFT) formulation within a Landauer approach is effective for conducting electronic transport calculations at zero temperature. However, it overlooks crucial temperature-dependent factors such as thermal excitations like electron–phonon interactions, which significantly affect conductance in nanoscale systems. Furthermore, its approximation of electron–electron interactions and inability to predict conductance variations with temperature limit its practical utility. These constraints highlight the necessity for more sophisticated theoretical frameworks capable of accurately modeling electronic transport under realistic, nonzero temperature conditions, particularly in molecular junctions and nanoelectronics where thermal effects are pivotal. Additionally, molecular orbital theory, employed as the first principle, is utilized to predict the feasibility of controlling molecular switching through EFs. This research enable the development of efficient methods for designing structures capable of creating stable molecular electronic devices, with a particular emphasis on single-molecule junctions (electrode-molecule-electrode).
Figure 1.
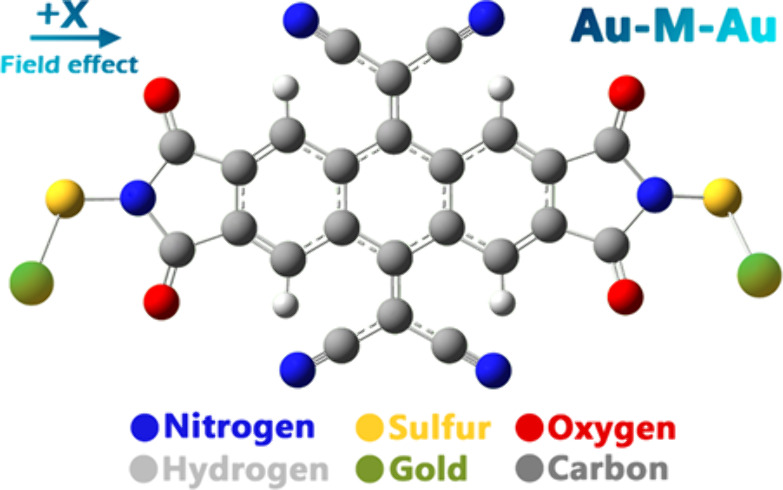
Molecular nanoswitch designed (Au–M–Au).
2. Computational Details
Density Functional Theory (DFT) served as the computational framework for optimizing the geometric arrangement and investigating the impact of an EF on both the structure and electronic characteristics of the designed molecular switch. The computations were conducted using the Gaussian 09 software, employing two distinct levels of theory-B3LYP and M062X-coupled with the 6-311G basis set.40−42 For the gold atoms, which acted as electrodes, the LANL2DZ pseudopotential was applied. Simultaneously, vibrational frequency analyses were performed using the same theoretical approaches.
To evaluate the stability of the proposed structure, the cohesive energy (ECoh) was initially computed using eq 1. ECoh of a solid is a measure of the energy required to separate the constituent atoms within a molecule from one another, transforming them into independent neutral atoms.
| 1 |
Where Etot, represents the total energy of all designed molecules, Ei is the atomic energy, ni is the number of atoms, and n is the total number of all atoms.43
To understand the stability and factors responsible for the positioning of groups within our structure, and to assess the impact of the electric field on the surface of the Au-M-Au molecular nanoswitch on electron density distributions, we utilized the QTAIM topological theory along with NCI analyses.44−52 The QTAIM/NCI results were obtained using the Multiwfn package.53
To investigate the electronic properties of the designed molecular switch, the HOMO and LUMO energy levels and the distance between them were determined. To achieve this, GaussSum03 software was utilized to draw the density of the electronic state (DOS) diagrams. The energy gap was subsequently calculated using eq 2,43 considering the influence of different EFs on the intensity.
| 2 |
Additionally, the polarizability (α) and first hyperpolarizability (β), corresponding to linear and NLO properties, were calculated using eqs 3–5.54,55
• The total electric dipole moment (μtot) in terms of electric dipole moment components (μx, μy, μz) is evaluated as follow:
| 3 |
• The linear static polarizability (α) is the measure of the distortion of a molecule in an electric field. It is a tensor and can be represented in a 3 × 3 real symmetric matrix, i.e., the off-diagonal elements are equal. The polarizability (α) was calculated using the components (αxx, αyy and αzz) by employing the following eq 4.
| 4 |
The quantities αxx, αyy and αzz are known as the principal values of the polarizability tensor.
The first-order hyperpolarizability (β) is the measure of the nonlinear optical activity, which can be of different types such as βvec (β vector), β|| (β parallel), and βtot (β total). A third-rank tensor can be described by a 3 × 3 × 3 matrix. The Kleinman symmetry enables to reduce the 27 components of a 3D matrix into 10 components. Gaussian 09 provides 10 components of this matrix as βxxx, βyxx, βxyy, βyyy, βxxz, βxyz, βyyz, βxxz, βyzz, βzzz, respectively, from which all x, y and z components of β can be calculated. The hyperpolarizability (βtot) can be calculated using the following equation:
| 5 |
Moreover, Landauer’s formula or theory (LT), expressed through eqs 6–8 was employed to predict the current–voltage diagram (I–V curve) of this field-effect molecular switch.
| 6 |
| 7 |
| 8 |
Where
ℏ represents 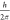 , where
h is the Planck constant. The symbol
φ denotes the potential barrier altitude for tunneling through
the HOMO or LUMO level, which is the same to the energy difference
between the Fermi energy (EF) and the HOMO or LUMO energy
level. The effective mass of the electron is denoted as m* (with m*=0.16
m0, where m0 is the free electron mass), and
α is the symmetry parameter in the potential profile; for a
symmetric case, α is set to 1.56,57 The φ
plays a crucial role in the mechanism of electron transfer in molecular
components. It can be predicted that when φ<EF, with both φ and EF in units of eV, the molecular
switch is in the ON state.
, where
h is the Planck constant. The symbol
φ denotes the potential barrier altitude for tunneling through
the HOMO or LUMO level, which is the same to the energy difference
between the Fermi energy (EF) and the HOMO or LUMO energy
level. The effective mass of the electron is denoted as m* (with m*=0.16
m0, where m0 is the free electron mass), and
α is the symmetry parameter in the potential profile; for a
symmetric case, α is set to 1.56,57 The φ
plays a crucial role in the mechanism of electron transfer in molecular
components. It can be predicted that when φ<EF, with both φ and EF in units of eV, the molecular
switch is in the ON state.
3. Results and Discussion
3.1. Ground State Geometry Optimization and Stability
Initially, the designed molecular switch was optimized with the B3LYP and M062x methods using the 6-311G basis set. Following that, the main stability factors-imaginary frequency and ECoh were examined (see Table 1).
Table 1. First Frequency and Cohesive Energy (kJ mol–1) in the Studied Structure (M).
| method | first frequency | cohesive energy |
|---|---|---|
| B3LYP | 11.38 | 115.82 |
| M062X | 12.44 | 116.04 |
Cohesive energy quantifies the energy required to separate a solid into its constituent atoms, which is crucial for understanding material stability.58,59 Consistent with this concept, the high ECoh and the absence of an imaginary frequency justify the feasibility of forming the designed structure.
3.2. Topological QTAIM Analyses
The QTAIM is a theoretical framework developed to explore the electronic structure of molecules in great precision. It has become an essential tool for evaluating and predicting molecular properties.60−66 Furthermore, quantum chemistry simulations based on QTAIM provide valuable predictions about the performance of molecular switches, offering detailed insights into energy barriers, transition states, and the thermodynamics of their ON/OFF states.
In this article, QTAIM was employed to analyze the strength and other characteristics of chemical bonds. Topological metrics, including electron density and the Laplacian, were used to assess a designed molecular switch subjected to an applied EF of 10 × 10–4 a.u. and 100 × 10–4 a.u. The analysis involved QTAIM67−69 in conjunction with stress tensor analysis, which entails higher derivatives of the total charge density distribution ρ (rB) at the bond critical point (BCP). The ellipticity parameter ε measures the relative accumulation of ρ(rB) in the two directions perpendicular to the bond-path at a BCP, defined as
| 9 |
Where λ1 and λ2 represent the negative eigenvalues of their respective eigenvectors e1 and e2.
Researchers have demonstrated70,71 that the degree of covalent character can be determined from the total local energy density H (rB), defined as follows:
| 10 |
Where G (rB) and V(rB) represent the local kinetic and potential energy densities at a BCP, respectively, in eq 10. In accordance, the Laplacian of electron density (∇2ρ(rB)), serves as a critical descriptor alongside the kinetic energy of the Hamiltonian (H (rB)) to discern the nature of interactions. The following conditions provide insights into these interactions:
∇2ρ(rB)> 0 and H (rB) < 0: it signifies the presence of a Bond Critical Point (BCP) with a discernible covalent character. This is indicated by the positive value of the Laplacian of electron density (∇2ρ(rB)) for a closed-shell BCP with a negative value of H (rB).
∇2ρ(rB)> 0 and H (rB) > 0: it implies a lack of covalent character for the closed-shell BCP.
∇2ρ(rB)< 0 and H (rB) < 0: it denotes a shared-shell BCP.
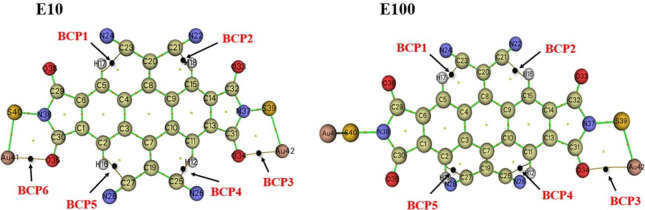
These distinctions provide clarity regarding the nature of interactions in the system, offering insights into the covalent or shared-shell character of the Bond Critical Points. Figure 2-(a, b) displays a topology-graph of electron density for the studied molecular switch at EF of 10 × 10–4 a.u (OFF) (Figure 2-a) and at EF = 100 × 10–4 a.u (ON) (Figure 2-b). Both graphs clearly depict the presence of C23---H17 BCP1, C21---H18 BCP2, C25---H12 BCP4 and C27---H16 BCP5 bond critical points for both the “OFF” and for the “ON” switch performances.
Figure 2.
QTAIM molecular graph showing the different BCPs of the studied compound with the EF 10 × 10–4 a.u. and 100 × 10–4 a.u.
Moreover, the graphs highlight bonds between oxygen (O) and gold (Au), with significantly different electro-negativities. Oxygen is highly electronegative, strongly attracting electrons, while gold is a low electronegativity metal. Bonds between elements with such different electro-negativities are typically ionic or metallic in nature. In this case, metallic interactions between the O34···Au42 and O35···Au41 named BCP3 and BCP6, respectively, are evident (see Figure 2-a). However, for the “ON” switch performance, there is only an O34···Au42 metallic interaction present, as illustrated in Figure 2-b, with the O35···Au41 metallic interaction being absent. Table 2 presents the corresponding topological parameters.
Table 2. Topological Parameters for Each Intramolecular Interaction within the Investigated Compound under an EF of 10 × 10–4 a.u. and 100 × 10–4 a.u (EHB = V(rB)/2 Is Calculated in kJ/mol).
| BCPs | ρ (rB) | ∇2ρ(rB) | G(rB) | V(rB) | H(rB) | ε | λ3σ 10–5 | EHB | RDG 10–15 | ELF | LOL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E10 10–4 a.u | BCP1 | 0.0105 | 0.0405 | 0.0081 | –0.0062 | 0.00194 | 0.8703 | 0.134 | –8,20 | 0.268 | 0.0304 | 0.155 |
| BCP2 | 0.0107 | 0.0413 | 0.0083 | –0.0064 | 0.00796 | 0.8739 | 0.141 | –8,40 | 0.456 | 0.0309 | 0.151 | |
| BCP3 | 0.0286 | 0.1048 | 0.0270 | –0.0270 | –0.00082 | 0.0531 | 9.222 | –35,44 | 1.362 | 0.0748 | 0.221 | |
| BCP4 | 0.0109 | 0.0420 | 0.0085 | –0.0065 | 0.00197 | 0.7895 | 0.130 | –8,58 | 0.373 | 0.0318 | 0.153 | |
| BCP5 | 0.0107 | 0.0410 | 0.0083 | –0.0063 | 0.00195 | 0.8079 | 0.150 | –8,28 | 0.919 | 0.3117 | 0.153 | |
| BCP6 | 0.0287 | 0.1061 | 0.0273 | –0.0281 | –0.00083 | 0.0497 | 9.547 | –36,91 | 0.280 | 0.0742 | 0.220 | |
| E100 10–4 a.u | BCP1 | 0.0132 | 0.0508 | 0.0105 | –0.0083 | 0.00218 | 0.6309 | 0.380 | –10,96 | 0.414 | 0.0394 | 0.168 |
| BCP2 | 0.0115 | 0.0433 | 0.0088 | –0.0068 | 0.00200 | 0.5851 | 0.266 | –8,96 | 0.295 | 0.0349 | 0.160 | |
| BCP3 | 0.0188 | 0.0646 | 0.0157 | –0.0154 | 0.00038 | 0.0119 | 2.003 | –20,21 | 1.113 | 0.0555 | 0.195 | |
| BCP4 | 0.0111 | 0.0427 | 0.0086 | –0.0066 | 0.00199 | 0.8959 | 0.169 | –8,78 | 0.579 | 0.0326 | 0.155 | |
| BCP5 | 0.0117 | 0.0451 | 0.0092 | –0.0072 | 0.00203 | 0.9113 | 0.187 | –9,45 | 1.183 | 0.0342 | 0.158 |
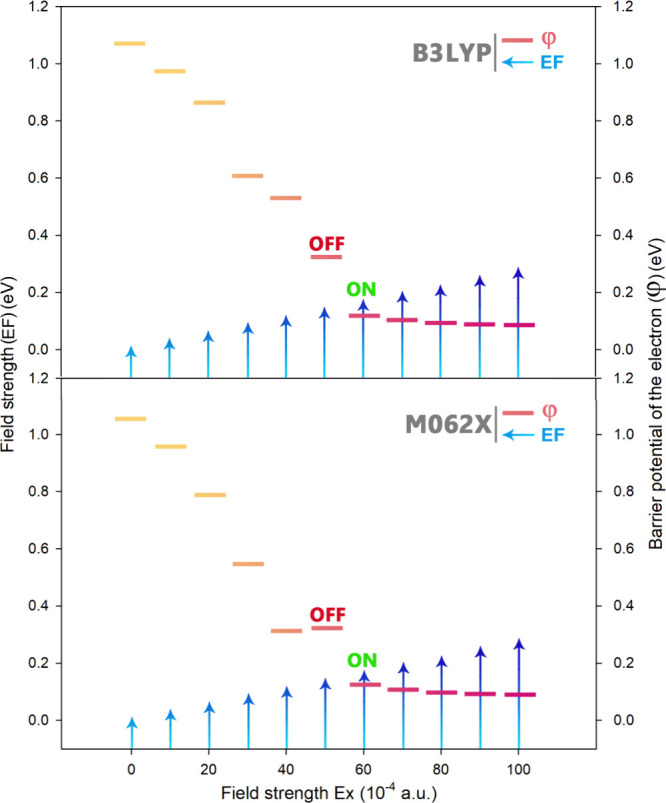
This observation can be attributed to the dynamic movement of electrons between the electrode and the molecule, a phenomenon contingent on the molecular resonant structure and its alterations induced by the applying of an external electric field (EF). Consequently, we anticipate that the switching mechanism of the molecular switch is governed by the displacement of π-conjugated electrons when subjected to an EF.
Our analysis indicates that the total electron densities at all critical points range from 0.0105 au to 0.0287 au for “ON” switch performance and from 0.0111 au to 0.0188 au for “OFF” switch performance.
As shown in Table 2, all H (rB) values of BCPs were positive, except for BCP3 of O34···Au42 and BCP6 of O35···Au41 in the “ON” state, which displayed negative values. According to,72 these findings provide insights into the types of interactions, categorized as follows: ∇2ρ (rB) > 0 and H(rB) > 0 indicate a lack of covalent character for the closed-shell BCP. However, for BCP3 of O34···Au42 and BCP6 of O35···Au41 in the “ON” state, ∇2ρ (rB)>0 and H (rB) < 0 signify a certain degree of covalent character (indicated by the positive value of the Laplacian of electron density) for the closed-shell BCP (negative value of H (rB)).
Furthermore, the examination of the binding energy EHB = V (rB))/2,73 reveals that larger EF values increase the strength of binding for BCP1 (C23---H17), BCP2 (C21---H18), BCP4 (C25---H12), and BCP5 (C27---H16), indicating stabilization of the molecular system. Similarly, the EHB values show that, in this case, BCP3 of O34···Au42 and BCP6 of O35···Au41 are weakened and destabilized by an increase in the EF. As evident in Table 2, the metallic interactions of BCP3 and BCP6 contribute to stabilizing the studied molecular system. The switching function of this molecular switch (M) is anticipated to be executed through the movement of π-conjunction electrons in response to EF.
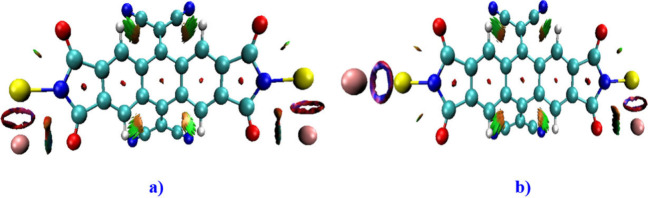
To gain deeper insights into probable intramolecular interactions within the molecular switch (M), we utilized the NCI index.74 This method facilitates the identification and visualization of distinct regions featuring weak interactions in a molecular structure, including van der Waals forces, hydrogen bonding (H–B), and steric effects (refer to Figure 3). The 3D plot of Figure 3(a,b) represent the NCI iso-surfaces obtained by Multiwfn software of the structure in the “OFF” and “ON” configurations. Notably, the presence of steric effects is indicated by red spots at the center of the five rings in the studied compound. At the same time, the NCI plot reveals a repulsive interaction between S and O atoms, depicted by the red region, along with a green spot indicating an S···O interaction. Furthermore, the systematic stability of the molecule is confirmed by C–H···C-type H-bonds, as evident in the NCI analysis. Additionally, the NCI index, employing reduced density gradient (RDG) calculations over this molecular system, highlights significant noncovalent π–π interactions diffusing between gold atoms and O/S atoms. The RDG values in Table 2 indicate that the EF influences the charge distribution.
Figure 3.
NCI iso-surfaces of the studied compound with an EF of 10 × 10–4 a.u. (a, OFF) and 100 × 10–4 a.u. (b, ON).
All these findings underscore the crucial role of the Au atom in stabilizing and fixing electron charge on the molecular system’s surface. This mechanism facilitates efficient charge transfer within the molecule, especially between the Au metal and the molecular components. The capability to visually and quantitatively assess changes in switch topology using QTAIM and NCI analysis provides novel insights into the occurrence of the molecular switch “ON/OFF” phenomenon in the studied molecular system.
3.4. Electron Localization Function (ELF) Analysis
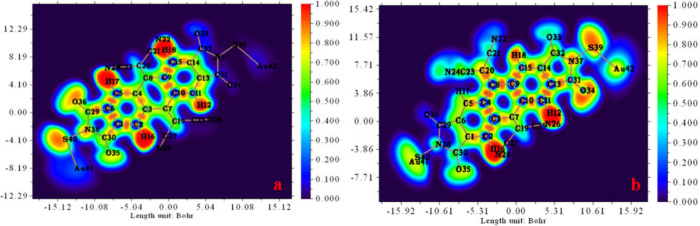
The analysis of ELF stands as a widely accepted approach for characterizing the localization of electrons within a molecular system. Additionally, it is used to disclose additional insights into chemical bonds, electronic structure,75 shell organization, and the identification of charge shift bonds on the molecular surface, all based on kinetic energy density.76 Furthermore, ELF analysis provides easily interpretable images that display clear patterns of chemical bonds and electron localization. Specifically, when the ELF value falls within the 0.5 to 1.0 range, it indicates perfectly localized electrons, while ELF values ranging from 0.0 to 0.5 correspond to delocalized electrons.77 The 2D representation of the ELF iso-surface for the studied compound with the EF of 10 × 10–4a.u. (a) and 100 × 10–4 a.u. (b), generated using the Multiwfn 3.7 program, is illustrated in Figure 4-(a, b).
Figure 4.
ELF analysis of the studied compound with an EF of 10 × 10–4 a.u. (a, OFF) and 100 × 10–4 a.u. (b, ON).
In the ELF map, a discernible transition from blue to red is observed within the 0–1 range. The red regions, signifying the highest ELF values, prominently outline localized electrons around hydrogen atoms H (12, 16, 17, and 18) in the “OFF” position of the studied compound. In the “ON” position, notable changes are evident following the application of an EF (100 × 10–24 a.u.), with the red area now encompassing H12 and H16 atoms, along with N26 and N28 atoms. Furthermore, orange coloring around O36, O35, N38, and S40 falls within the 0.5–0.8 au ELF range for an EF strength of 10 × 10–24 a.u., indicating regions characterized by weak electron localization. Conversely, orange areas are identified on S39, O34, H18, and N37 in the “OFF” position.
Additionally, blue coloring surrounds carbon atoms C (1, 2, 5, 6, 9, 10, 15, 31, and 32), O (33 and 34), Au (41 and 42), and S39 of Au-M-Au. Similarly, nitrogen atoms N7, N9, N10, and N16 exhibit blue coloring, representing delocalized electrons. Notably, in Figure 4-b, changes in delocalized electrons around carbon atoms (2, 3, 4, 8, 9, 11, 13, 14, 15, and 31), oxygen atoms (33 and 36), and nitrogen atom N22 are observed, suggesting the presence of noncovalent bonding, specifically H-bonding, within the molecular arrangement.
The application of an EF induces changes in electron localization/delocalization in the studied compound. These observations highlight the crucial role of the gold (Au) atom in stabilizing and fixing electron charge on the molecular system’s surface. This, in turn, facilitates charge transfer within the molecule, particularly between the Au metal and other molecular components. The capability of ELF analysis to visualize and quantify changes in switch topology provides novel insights into the occurrence of the molecular switch “ON/OFF” phenomenon in the studied molecular system.
3.5. Localized Orbital Locator (LOL) Analysis
LOL topology analyses78 were extensively used for classifying chemical bonds, determining electronic structures, and characterizing molecular binding and chemical structure. These analyses focus on the LOL function, which is associated with the kinetic energy density. LOL maps recognize the maximum-localized orbital gradients when the orbitals overlap in the studied system.79
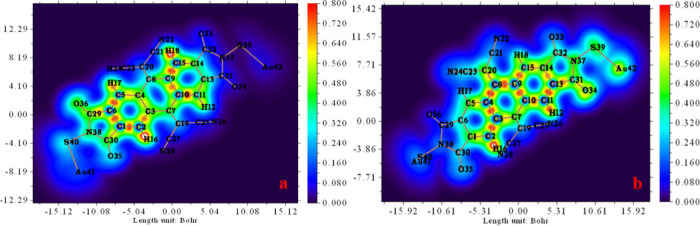
The Multiwfn 3.7 program was utilized to generate the 2D visualization of the Electron Localization Function, ELF, iso-surface for the investigated compound with the EF of 10 × 10–4 a.u. and 100 × 10–4 a.u. The representations are depicted in Figure 5-(a, b), respectively. The color scale of the LOL map ranges from 0 to 0.8, transitioning from blue to red. Referring to Figure 5 (a, b) we observe that the LOL values surpass 0.5 in regions, indicating electron localization as the primary determinant of electron density.
Figure 5.
LOL analysis of the studied compound with an EF of 10 × 10–4 a.u. (a, OFF state) and 100 × 10–4 a.u. (b, ON state).
As depicted in Figure 5-a, small white spots are clearly visible at the center of the red spots, concentrated around hydrogen atoms H16 and H18. This observation indicates that the electron density exceeds the upper limit of 0.8. Comparing the LOL map of the studied compound under an EF of 100 × 10–4 a.u., we note a distinct white spot at the center of the red spot, specifically on H16. However, for H18, the localized orbital locator value decreases, as evidenced by the presence of a green spot overlapping with the H18 atom. The presence of a white color means that the bonds are concentrated within a single localized orbital.80
Moreover, the presence of green spots overlapping with the atoms of the investigated compound indicates the occurrence of van der Waals (VdW) interactions. Furthermore, the blue-colored areas surrounding the atoms, characterized by small LOL values (<0.5), can be interpreted as a depleted electron density region. Hence, in this area, we can categorize the bonds as either weakly covalent or VdW bonds.
As evident from the LOL map of the investigated compound in the “OFF” state (i.e., with EF = 10 × 10–4 a.u.) (Figure 5-a), green spots overlap the atoms O36 and S40, while the blue-colored areas surround the atoms S39 and Au42. However, when a strong external (EF = 100 × 10–4 a.u.) is applied (Figure 5-b), atoms S39 and Au42 are surrounded by green spots, and the O36 and S40 atoms overlap in blue-colored areas. The values presented in Table 2 for LOL further highlight the impact of the EF on the distribution of charges.
The obtained results strongly suggest the presence of noncovalent bonding, including VdW interactions, within the molecular configuration. Additionally, the application of an EF induces changes in electron localization/delocalization within the studied compound. These findings highlight the crucial role played by the Au atom in stabilizing and anchoring electron charge on the molecular system’s surface, facilitating charge transfer within the molecule itself, particularly between the Au metal and molecular components. The above clarify the capability of LOL analysis to effectively visualize and quantify topology changes resulting from the switch. This analytical approach provides innovative insights into the occurrence of the molecular switch’s “ON/OFF” phenomenon within the studied molecular system
3.6. Field Effects on Electronic Properties
In order to investigate the response of the designed molecular switch to the EF, various electronic properties were calculated and examined in the next sections. These properties include the electric dipole moment (μ), polarizability (α), hyperpolarizability tensor (β), electronic spatial extents (ESE), and HOMO and LUMO energy levels, in addition to the energy gap between them (HLG).
3.7. HOMO/LUMO Boundary Orbitals and the Energy Gap (HLG)
The energy levels of the HOMO and LUMO boundary molecular orbitals, along with the energy gap between them (HLG), are crucial factors influencing the conductivity of molecular electronic devices.81,82 To determine the electrical properties of molecular nanoelectronic systems, it is essential to study the behavior of the HOMO and LUMO frontier orbitals’ energy levels following the application of an external electric field (EF). In this context, we report the energy values of HOMO/LUMO boundary orbitals and the energy gap between them (as an indicator of the response to the EF) for the designed nanoswitch at various EF intensities, in Table 3.
Table 3. HOMO and LUMO Energy Levels and Energy Gap (HLG) under the Application of an EF (All Values Are in eV).
| B3LYP
(6-311G) |
M062X
(6-311G) |
|||||
|---|---|---|---|---|---|---|
| field (10–4 a.u.) | HOMO | LUMO | HLG | HOMO | LUMO | HLG |
| 0 | –6.73 | –4.59 | 2.14 | –6.70 | –4.76 | 1.94 |
| 10 | –6.50 | –4.55 | 1.95 | –6.60 | –4.68 | 1.92 |
| 20 | –6.25 | –4.52 | 1.73 | –6.34 | –4.76 | 1.58 |
| 30 | –5.93 | –4.71 | 1.22 | –6.03 | –4.94 | 1.09 |
| 40 | –5.66 | –4.60 | 1.06 | –5.78 | –5.14 | 0.64 |
| 50 | –5.40 | –4.75 | 0.65 | –5.51 | –4.85 | 0.66 |
| 60 | –5.12 | –4.88 | 0.24 | –5.25 | –4.98 | 0.27 |
| 70 | –5.41 | –5.18 | 0.23 | –5.51 | –5.27 | 0.24 |
| 80 | –5.53 | –5.30 | 0.23 | –5.53 | –5.30 | 0.23 |
| 90 | –5.55 | –5.33 | 0.22 | –5.58 | –5.38 | 0.20 |
| 100 | –5.64 | –5.42 | 0.22 | –5.63 | –5.43 | 0.20 |
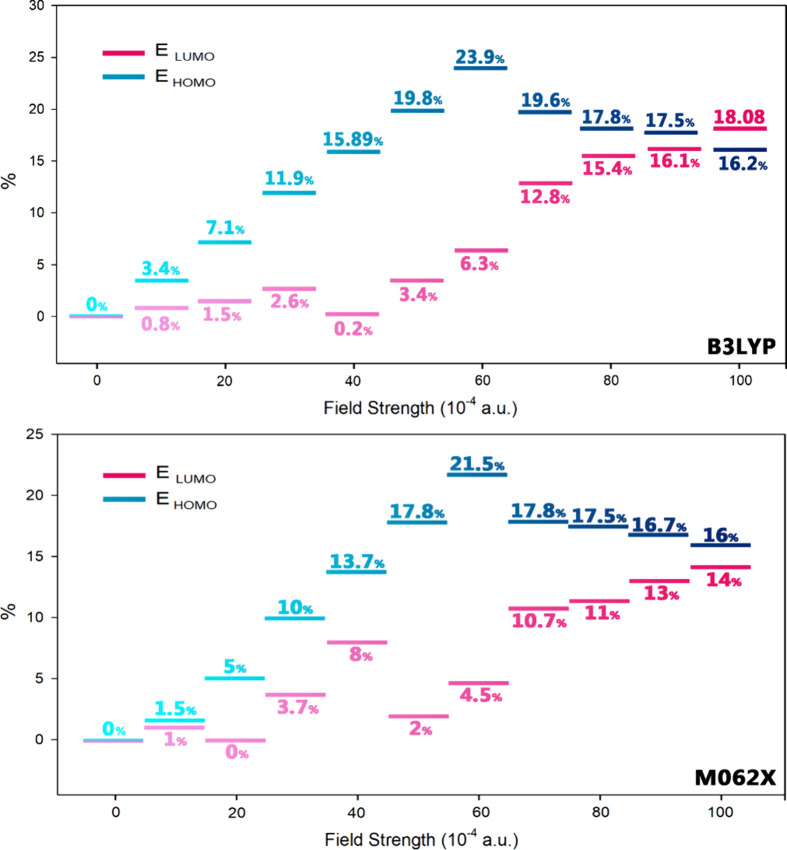
The effect of the EF on the HOMO and LUMO energy levels reveals that as the intensity of the EF increases, the energy level of the LUMO orbitals decreases while the energy level of the HOMO orbitals increases.
According to the results reported in Figure 6, the effect of the EF on the energy levels of the frontier HOMO orbitals is strong, resulting in an increase in the energy of these orbitals, i.e. in an energy gap alteration. An important point in the results reported in Table 3 is the trend of energy gap changes for applied EF exceeding 50 × 10–4 (a.u.). As the EF intensity increases from 50 × 10–4 (a.u.) to 60 × 10–4 (a.u.), a significant decrease in the energy gap is noted. Reducing the energy gap facilitates the phenomenon of quantum tunneling inside the molecule and thus the conductivity of the system increases. Consequently, it is expected that in EF higher than 50 × 10–4 (a.u.), the molecule’s conductivity will notably increase.
Figure 6.
Percentage of energy changes in the HOMO and LUMO boundary orbitals due to the increase in the intensity of the EF (the zero field was considered as a reference).
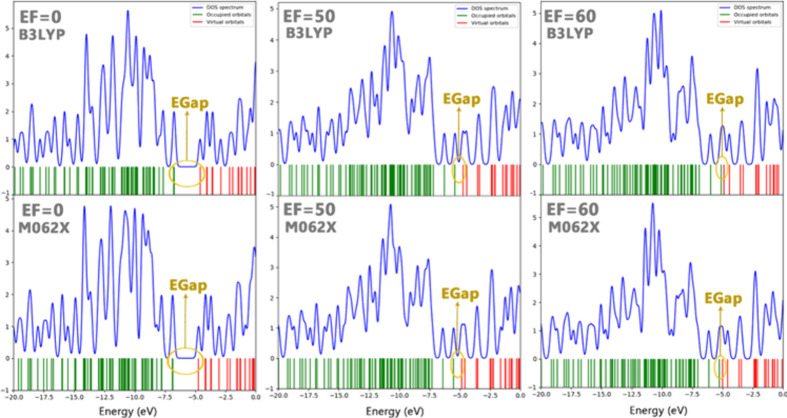
Using the DOS diagrams proves to be an excellent method for illustrating the energy difference between molecular orbitals within chemical bonds.83 An analysis of the field effect on the DOS for the molecular switch reveals that the electron density exhibits an almost linear dependence on the EF intensity (Figure 7). This property signifies the observable and measurable response of the studied molecular switch to the applied field’s properties, such as the direction and intensity. These electronic changes at the molecular (atomic) level indicate that the EF induce the molecular switch resulting in an increase in the distribution (or redistribution) of charge/energy transfer between different intramolecular parts (atomic basins). It is worth noting that by applying intense electric fields (EF), the DOS spectra show broad peaks corresponding to the energy levels of delocalized electrons. The orbital overlap between the HOMO and LUMO would facilitate electron movement, contributing to the compound’s metallic properties.
Figure 7.
EF effect on the DOS diagram of the investigated molecular switch.
3.8. Barrier Potential of the Electron (φ)
The electron transfer potential barrier (φ) is crucial parameter in evaluating the conductivity properties of single molecules in molecular nanoelectronic systems. It represents the potential difference required for the movement of electrons in an EF and is defined as HLG/2. To better understand the ON/OFF mechanism of the designed molecular switch, the relationship between the applied EF and the electron transfer potential is depicted in Figure 8 and Table 4. In this Figure, it is evident that when φ < EF (in units of eV), the electrons freely move between the electrode and the molecule, indicating that the molecular switch is in the ON state.
Figure 8.
Plot of EF intensity versus potential barrier of electron passage for the proposed molecular switch.
Table 4. Calculated Values for the Electron Transfer Potential Barrier (φ) after Applying an External Electric Field (EF).
| B3LYP |
M062X |
|||
|---|---|---|---|---|
| EF (10–4 a.u.) | EF (eV) | φ (eV) | φ (eV) | state |
| 0 | 0.000 | 1.070 | 1.060 | OFF |
| 10 | 0.027 | 0.975 | 0.960 | OFF |
| 20 | 0.054 | 0.865 | 0.790 | OFF |
| 30 | 0.081 | 0.610 | 0.545 | OFF |
| 40 | 0.108 | 0.530 | 0.320 | OFF |
| 50 | 0.136 | 0.325 | 0.330 | OFF |
| 60 | 0.163 | 0.120 | 0.135 | ON |
| 70 | 0.190 | 0.115 | 0.120 | ON |
| 80 | 0.217 | 0.115 | 0.115 | ON |
| 90 | 0.244 | 0.110 | 0.100 | ON |
| 100 | 0.272 | 0.110 | 0.100 | ON |
Additionally, it can be anticipated that the switching mechanism and, consequently, the function of this field-effect molecular switch (Au-M-Au) depend on the molecular resonant structure and its changes resulting from the application of an EF. It is predicted that the switching function of the molecular switch is executed by the movement of π-conjugated electrons when a strong enough EF is applied (refer to Figure 9).
Figure 9.
Switching mechanism (ON/OFF) of the molecular switch studied in this work.
3.9. I–V Characteristic Curve
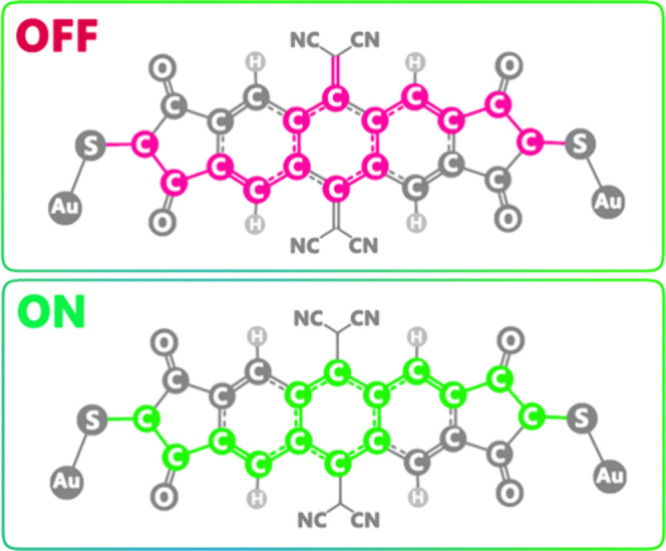
The I–V characteristic curve is used to define the performance of a molecular nanoelectronic device within an electrical circuit.84,85 This curve illustrates the relationship between the current passing through a molecular nanoelectronic component and the voltage applied to its terminals.
In this regard, Landauer’s theory was used to check the conductivity of the designed molecular nanoswitch under the influence of varying EF intensities. Figure 10 shows the I–V curve can be divided into two parts. The first part is related to the application of EF less than 50 × 10–4 (a.u.), while the second part is associated with EF with an intensity greater than 50 × 10–4 (a.u.). It is evident that as the EF increases from 50 × 10–4 (a.u.) to 60 × 10–4 (a.u.), the current passing through the molecular nanoswitch increases surprisingly.
Figure 10.
Current–voltage diagram (I–V curve) of molecular switch (Au–M–Au) under EF intensity.
An EF intensity higher than 50 × 10–4 (a.u.) induces a rapid and facile transfer of electrons from the valence band to the conduction band. This ensures a highly efficient electronic energy/charge transfer between the electrode and the designed molecular switch. In such cases, the molecule’s conductivity increases, and the molecular switch is expected to be in the “ON” position.
3.10. Nonlinear Optical (NLO) Properties
This section focuses on determining the theoretical polarizability of the studied molecular switch, which is crucial in designing nonlinear optical (NLO) materials.86−88 A comprehensive understanding of this property is essential for unraveling the link between molecular structure and nonlinear optical traits, particularly in organic materials recognized for their high polarizability and NLO characteristics.89−97 In this context, to evaluate the NLO properties of the examined nanoswitch, calculations and analyses of dipole moment, polarizability, and hyperpolarizability were conducted at various EF intensities (refer to Table 5).
Table 5. Dipole Moment (μ), Polarizability (α), and First Hyperpolarizability (β) Values for the Designed Molecular Switch.
| B3LYP | ||||
|---|---|---|---|---|
| EF (10–4 a.u.) | dipole (μ) | polar (α) | hyper polar (β) | ON/OFF |
| 0 | 7.567 | 624.390 | 43114.717 | OFF |
| 10 | 7.328 | 634.993 | 42050.539 | OFF |
| 20 | 8.104 | 645.167 | 44663.257 | OFF |
| 30 | 8.104 | 648.539 | 45366.947 | OFF |
| 40 | 11.957 | 658.033 | 46615.486 | OFF |
| 50 | 13.567 | 662.533 | 47858.838 | OFF |
| 60 | 15.614 | 723.905 | 64198.367 | ON |
| 70 | 23.837 | 758.463 | 69254.990 | ON |
| 80 | 27.773 | 744.328 | 75128.241 | ON |
| 90 | 34.713 | 753.287 | 78228.573 | ON |
| 100 | 50.103 | 787.871 | 80782.952 | ON |
| M062X | ||||
|---|---|---|---|---|
| 0 | 7.438 | 619.170 | 43114.652 | OFF |
| 10 | 7.096 | 638.680 | 42922.114 | OFF |
| 20 | 4.334 | 647.588 | 44300.144 | OFF |
| 30 | 8.133 | 654.552 | 45595.523 | OFF |
| 40 | 9.855 | 660.238 | 46728.349 | OFF |
| 50 | 14.072 | 671.245 | 49544.075 | OFF |
| 60 | 15.971 | 729.811 | 65544.279 | ON |
| 70 | 23.762 | 754.354 | 70793.188 | ON |
| 80 | 30.432 | 769.811 | 74544.279 | ON |
| 90 | 37.967 | 774.584 | 78699.540 | ON |
| 100 | 51.022 | 794.969 | 81108.263 | ON |
The results show that the NLO properties increase with the increase in EF, with more significant changes observed for EF above 50 × 10–4 (a.u.) when the switch is ON. The increase in NLO properties with increased EF intensity is due to the more obvious response of the electrons of the material to the applied field. Additionally, the application of an EF can alter the energy levels of the molecular orbitals, influencing the NLO response. Typically, higher EF intensity can induce larger changes in energy levels, thereby enhancing NLO properties.
Polarizability, which measures a material’s response to an EF, is closely related to the energy gap. In EF exceeding 50 × 10–4 a.u. (ON state), as the energy gap decreases (refer to Table 3 and Figure 6), the dipole moment (μ), polarizability (α), and first hyperpolarizability (β) increase significantly, leading to increased NLO responses. The relationship between the energy gap and NLO is crucial for understanding and predicting material behavior in the optics and photonics fields. It also opens possibilities for designing and developing materials with NLO behavior suitable for various technological applications.
3.11. Electronic Spatial Extents (ESE)
The ESE of this molecular switch is calculated in units of 0.001 electrons/bohr3 (see Table 6). ESE is a key concept used for evaluating the cause of over potential in the charging and current transfer processes of an electrode. It serves as a measure of the molecule’s sensitivity to the EF.98,99
Table 6. Effect of the EF on the ESE of the Designed Molecular Switch, (the Percentage of Changes under EF Compared to the Zero Field Was Considered).
| B3LYP |
M062X |
|||
|---|---|---|---|---|
| EF (10–4 a.u.) | ESE (a.u.) | % | ESE (a.u.) | % |
| 0 | 32528.843 | 32201.843 | ||
| 10 | 32635.557 | 0.3 | 32210.099 | 0.02 |
| 20 | 32643.557 | 0.3 | 32469.786 | 0.80 |
| 30 | 32606.115 | 0.2 | 32536.881 | 1.00 |
| 40 | 32639.136 | 0.3 | 32443.216 | 0.70 |
| 50 | 32704.462 | 0.5 | 32466.095 | 0.80 |
| 60 | 32744.398 | 0.6 | 32501.999 | 0.90 |
| 70 | 32791.223 | 0.8 | 32576.157 | 1.10 |
| 80 | 32876.081 | 1.0 | 32592.891 | 1.20 |
| 90 | 32899.220 | 1.1 | 32601.237 | 1.20 |
| 100 | 32957.861 | 1.3 | 32640.923 | 1.30 |
The observed negligible changes in the electronic spatial extent under various EF intensities serve as a positive indicator for this molecular switch in nanoelectronic circuits. This is due to its minimal impact on steric interactions with its neighboring nanoelectronic circuit components.
3.12. Intramolecular Joule-Like and Peltier-Like Coefficients
Quantum mechanics empowers the exploration and design of molecular nanoelectronic components and circuits, enabling the anticipation of their behavior in various conditions, including the presence or absence of electric and magnetic fields. The mutual effects of electric current and heat flow are called thermoelectric effects. Understanding thermoelectric effects such as Joule, Sibeck, and Peltier, especially in managing temperature and electric current for optimal performance in nanoelectronic circuits, is crucial. This represents the ultimate goal of research in this area.100,101
In a molecular model exposed to an EF (with intensity ε), the system can be classified into electron donor/acceptor (n-p-like) parts, and the charge/energy exchange between these parts can be investigated after applying the EF. To understand intramolecular pseudothermoelectric phenomena in a molecular nanoelectronic system, it is essential to segment the system into specific intramolecular sections, as illustrated in Figure 11.
Figure 11.
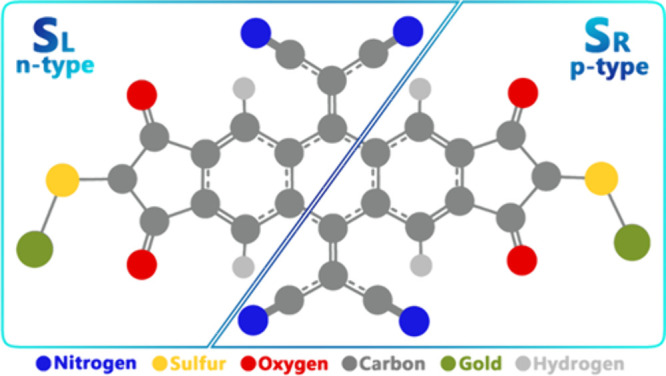
Studied molecular switch was divided into two intramolecular parts (right and left sections).
According to this model, the studied molecular system under investigation was divided into distinct parts, namely the left (SL) and right (SR) parts, which is similar to the division of an n/p type semiconductor thermoelectric system (Figure 11).
By introducing a temperature gradient or generating a potential difference in the E-M-E molecular system, there exists the possibility of charge and energy exchange between the electrode and molecule, leading to intramolecular thermoelectric-like phenomena.102
Considering that Joule’s heat is an even function and Peltier’s heat is an odd function with respect to the change in the direction of the applied field (f/r), therefore, similar to n/p-thermoelectric-like systems, the Joule-like heat (QJL) and Peltier-like heat (QPL), the intramolecular thermoelectric systems, can be given by103
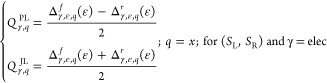 |
11 |
Similarly, the intramolecular Peltier-like (LPL) and Joule-like (LJL) coefficients can be considered as follows:
| 12 |
| 13 |
Here
| 14 |
Where
| 15 |
In addition, it can be shown that the electron kinetic energy of any atomic basin () or substrate based on AIM quantum theory is obtained by the following Equation:
| 16 |
Where N is the number of electrons and dτ is the integral over the spin coordinates of the electrons.104
Intramolecular thermoelectric coefficients (Joule/Peltier-like) were calculated using eqs 11–16 for the studied molecular switch. Results in Figure 12 revealed a higher Joule-like coefficient than the Pelletier-like one. Additionally, the Peltier-like coefficient displayed a nonlinear dependence on the intensity of the applied external electric field (EF).
Figure 12.
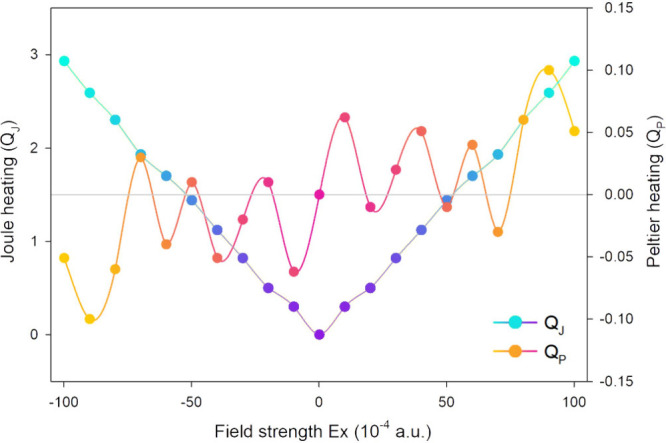
External EF effects on local QPLγ,q and QJLγ,q coefficients (all in a.u.) of the molecular switch studied in this work.
The introduced coefficients appear to provide valuable insights into the control of heat and specific thermoelectric interactions within single molecules and molecular systems. They clarify the emergence of local thermoelectric interferences resulting from the redistribution of electronic energy within the system under the influence of an EF. These findings are expected to be beneficial for the optimal and effective design of thermoelectric systems, enhancing their capability for load and energy transfer.
4. Conclusion
In summary, our study aims to examine the effects of an electric field along the x-axis on the vibrational and electronic properties of a field-effect molecular switch. We employ DFT and AIM methods at two different levels of theory (B3LYP and M062X), utilizing the 6-311G basis set. Quantum Theory of Atoms in Molecules (QTAIM) topological analyses indicate that the switching mechanism of the system under study is controlled by the displacement of π-conjugated electrons at an electric field (EF) strength above 50 × 10–4 (a.u.). 2D-Electron Localization Function and Localized Orbital (2D-ELF-LOL) analyses emphasize the presence of electron occupation sets between electrodes, facilitating efficient charge and energy transfer within the system. These findings highlight the potential of this model for novel nanoelectronic device applications. The analysis of electrical conductivity behavior (I–V diagram) suggests that the application of an electric field (EF) results in the separation of atomic charges, affecting the nonlinear optical (NLO) properties, reducing the HOMO–LUMO gap, and consequently increasing the electrical conductivity of the designed molecular switch. The application of a strong EF in the Au-M-Au system induces significant charge and energy exchange between different atomic layers, leading to notable changes in dipole moment, polarizability, and first hyperpolarizability, particularly for EF values exceeding 50 × 10–4 (a.u.). Furthermore, the impact of the EF on the molecular structure indicates that an EF greater than 50 × 10–4 (a.u.) activates the molecular switch by facilitating the movement of π electrons along the molecule’s length. Moreover, the investigation of the Joule-like (LJL) and Peltier-like (LPL) coefficients revealed that the LJL coefficient shows a linear dependence on the intensity of the applied EF, while the LPL coefficient demonstrates a nonlinear dependence. These findings display the high adaptability of our Au-M-Au system for developing new nanoelectronic modules.
Acknowledgments
The authors extend their sincere appreciation to the Ministry of Higher Education and Scientific Research in Tunisia for the technical and financial support provided for this study, based on an agreement between the Ministry of Higher Education and Scientific Research in Tunisia and the American Chemical Society (ACS).
Data Availability Statement
All data are included in the manuscript.
Author Contributions
H.H., N.A.D., I.C, B.G., B.A, R.S.: conceptualization, methodology, software, data curation, writing—original draft, supervision, validation, writing—review and editing. M.T.C, S. M, H.G.: investigation, validation, and conceptualization. S.P., S.A.: software, data curation, visualization, investigation, review and editing.
The authors declare no competing financial interest.
References
- Zhang X.; Li T. Molecular-Scale Electronics: From Device Fabrication to Functionality. Chin. Chem. Lett. 2017, 28 (11), 2058–2064. 10.1016/j.cclet.2017.09.008. [DOI] [Google Scholar]
- Tsutsui M.; Taniguchi M. Single Molecule Electronics and Devices. Sensors 2012, 12 (6), 7259–7298. 10.3390/s120607259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komoto Y.; Fujii S.; Iwane M.; Kiguchi M. Single-Molecule Junctions for Molecular Electronics. J. Mater. Chem. C 2016, 4 (38), 8842–8858. 10.1039/C6TC03268K. [DOI] [Google Scholar]
- Leary E.; La Rosa A.; Gonzalez M. T.; Rubio-Bollinger G.; Agrait N.; Martin N. Incorporating Single Molecules into Electrical Circuits. The Role of the Chemical Anchoring Group. Chem. Soc. Rev. 2015, 44 (4), 920–942. 10.1039/C4CS00264D. [DOI] [PubMed] [Google Scholar]
- Yong A.; Hao-Li Z. Construction and Conductance Measurement of Single Molecule Junctions. Acta Physico-Chimica Sinica 2012, 28 (10), 2237–2248. 10.3866/PKU.WHXB201209102. [DOI] [Google Scholar]
- Tang C.; Ayinla R. T.; Wang K. Beyond Electrical Conductance: Progress and Prospects in Single-Molecule Junctions. Journal of Materials Chemistry C 2022, 10 (37), 13717–13733. 10.1039/D2TC01155G. [DOI] [Google Scholar]
- Stone I.; Starr R. L.; Zang Y.; Nuckolls C.; Steigerwald M. L.; Lambert T. H.; Roy X.; Venkataraman L. A Single-Molecule Blueprint for Synthesis. Nat. Rev. Chem. 2021, 5 (10), 695–710. 10.1038/s41570-021-00316-y. [DOI] [PubMed] [Google Scholar]
- Li Y.; Yang C.; Guo X. Single-Molecule Electrical Detection: A Promising Route toward the Fundamental Limits of Chemistry and Life Science. Acc. Chem. Res. 2020, 53 (1), 159–169. 10.1021/acs.accounts.9b00347. [DOI] [PubMed] [Google Scholar]
- Sidorenko A. S. Functional Nanostructures for Electronics, Spintronics and Sensors. Beilstein J. Nanotechnol. 2020, 11, 1704–1706. 10.3762/bjnano.11.152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madkour L. H. Nanoelectronic Materials. Adv. Struct. Mater. 2019, 10.1007/978-3-030-21621-4. [DOI] [Google Scholar]
- Kim F. S.; Ren G.; Jenekhe S. A. One-Dimensional Nanostructures of π-Conjugated Molecular Systems: Assembly, Properties, and Applications from Photovoltaics, Sensors, and Nanophotonics to Nanoelectronics. Chem. Mater. 2011, 23 (3), 682–732. 10.1021/cm102772x. [DOI] [Google Scholar]
- Sun L.; Diaz-Fernandez Y. A.; Gschneidtner T. A.; Westerlund F.; Lara-Avila S.; Moth-Poulsen K. Single-Molecule Electronics: From Chemical Design to Functional Devices. Chem. Soc. Rev. 2014, 43 (21), 7378–7411. 10.1039/C4CS00143E. [DOI] [PubMed] [Google Scholar]
- Lee S. U.; Belosludov R. V.; Mizuseki H.; Kawazoe Y. Designing Nanogadgetry for Nanoelectronic Devices with Nitrogen-Doped Capped Carbon Nanotubes. Small 2009, 5 (15), 1769–1775. 10.1002/smll.200801938. [DOI] [PubMed] [Google Scholar]
- Chen L.; Feng A.; Wang M.; Liu J.; Hong W.; Guo X.; Xiang D. Towards Single-Molecule Optoelectronic Devices. Sci. China Chem. 2018, 61 (11), 1368–1384. 10.1007/s11426-018-9356-2. [DOI] [Google Scholar]
- Franco I.; George C. B.; Solomon G. C.; Schatz G. C.; Ratner M. A. Mechanically Activated Molecular Switch through Single-Molecule Pulling. J. Am. Chem. Soc. 2011, 133 (7), 2242–2249. 10.1021/ja1095396. [DOI] [PubMed] [Google Scholar]
- Liu B.; Chen J.; Ouyang Y.; Zhang M.; Tan Y.-Z.; Song F. Single-Electron Transport in H2O@C60 Single-Molecule Transistors. Chinese Phys. B 2023, 32 (6), 063601 10.1088/1674-1056/acc801. [DOI] [Google Scholar]
- Mendes P. M.; Flood A. H.; Stoddart J. F. Nanoelectronic Devices from Self-Organized Molecular Switches. Appl. Phys. A: Mater. Sci. Process. 2005, 80 (6), 1197–1209. 10.1007/s00339-004-3172-2. [DOI] [Google Scholar]
- Sabzyan H.; Farmanzadeh D. Electric Field Effects on the Performance of a Candidate Multipole Molecular Switch: A Quantum Computational Study. J. Comput. Chem. 2007, 28 (5), 922–931. 10.1002/jcc.20606. [DOI] [PubMed] [Google Scholar]
- Burghard M.; Klauk H.; Kern K. Carbon-Based Field-Effect Transistors for Nanoelectronics. Adv. Mater. 2009, 21 (25–26), 2586–2600. 10.1002/adma.200803582. [DOI] [PubMed] [Google Scholar]
- Han Y.; Nickle C.; Zhang Z.; Astier H. P. A. G.; Duffin T. J.; Qi D.; Wang Z.; del Barco E.; Thompson D.; Nijhuis C. A. Electric-Field-Driven Dual-Functional Molecular Switches in Tunnel Junctions. Nat. Mater. 2020, 19 (8), 843–848. 10.1038/s41563-020-0697-5. [DOI] [PubMed] [Google Scholar]
- Taylor J.; Guo H.; Wang J. Ab Initio Modeling of Open Systems: Charge Transfer, Electron Conduction, and Molecular Switching of a ${\mathrm{C}}_{60}$ Device. Phys. Rev. B 2001, 63 (12), 121104 10.1103/PhysRevB.63.121104. [DOI] [Google Scholar]
- Liu W.; Yang S.; Li J.; Su G.; Ren J.-C. One Molecule, Two States: Single Molecular Switch on Metallic Electrodes. WIREs Computational Molecular Science 2021, 11 (4), e1511 10.1002/wcms.1511. [DOI] [Google Scholar]
- Chen Y.; Jung G.-Y.; Ohlberg D. A. A.; Li X.; Stewart D. R.; Jeppesen J. O.; Nielsen K. A.; Stoddart J. F.; Williams R. S. Nanoscale Molecular-Switch Crossbar Circuits. Nanotechnology 2003, 14 (4), 462. 10.1088/0957-4484/14/4/311. [DOI] [Google Scholar]
- Tao N. J. Electron Transport in Molecular Junctions. Nat. Nanotechnol. 2006, 1 (3), 173–181. 10.1038/nnano.2006.130. [DOI] [PubMed] [Google Scholar]
- Fuentes N.; Martin-Lasanta A.; Alvarez de Cienfuegos L.; Ribagorda M.; Parra A.; Cuerva J. M. Organic-Based Molecular Switches for Molecular Electronics. Nanoscale 2011, 3 (10), 4003–4014. 10.1039/c1nr10536a. [DOI] [PubMed] [Google Scholar]
- Ionescu A. M.; Riel H. Tunnel Field-Effect Transistors as Energy-Efficient Electronic Switches. Nature 2011, 479 (7373), 329–337. 10.1038/nature10679. [DOI] [PubMed] [Google Scholar]
- Browne W. R.; Feringa B. L. Chiroptical molecular switches. Molecular Switches 2011, 121–179. 10.1002/9783527634408.ch5. [DOI] [Google Scholar]
- Lu X.; Sun Y.; Hu W. The External Electric Field Effect on the Charge Transport Performance of Organic Semiconductors: A Theoretical Investigation. J. Mater. Chem. A 2021, 9 (37), 21044–21050. 10.1039/D1TA05762F. [DOI] [Google Scholar]
- Goser K.; Glösekötter P.; Dienstuhl J.. Nanoelectronics with Tunneling Devices. In Nanoelectronics and Nanosystems: From Transistors to Molecular and Quantum Devices; Goser K., Glösekötter P., Dienstuhl J., Eds.; Springer: Berlin, 2004; pp 187–208. 10.1007/978-3-662-05421-5_12. [DOI] [Google Scholar]
- Mathew P. T.; Fang F. Advances in Molecular Electronics: A Brief Review. Engineering 2018, 4 (6), 760–771. 10.1016/j.eng.2018.11.001. [DOI] [Google Scholar]
- Chen J.; Wang W.; Klemic J.; Reed M. A.; Axelrod B. W.; Kaschak D. M.; Rawlett A. M.; Price D. W.; Dirk S. M.; Tour J. M.; Grubisha D. S.; Bennett D. W. Molecular Wires, Switches, and Memories. Ann. N.Y. Acad. Sci. 2002, 960 (1), 69–99. 10.1111/j.1749-6632.2002.tb03026.x. [DOI] [PubMed] [Google Scholar]
- Safari R.; Hadi H.; Shamlouei H. R. Quantum Study of Symmetrical/Asymmetrical Charge and Energy Transfer in a Simple Candidate Molecular Switch. Struct Chem. 2023, 34 (1), 59–70. 10.1007/s11224-022-01917-z. [DOI] [Google Scholar]
- Georgiev A.; Deneva V.; Yordanov D.; Völzer T.; Wolter S.; Fennel F.; Lochbrunner S.; Antonov L. Benzothiazol Picolin/Isonicotinamides Molecular Switches: Expectations and Reality. J. Mol. Liq. 2022, 356, 118968 10.1016/j.molliq.2022.118968. [DOI] [Google Scholar]
- Zhang J. L.; Zhong J. Q.; Lin J. D.; Hu W. P.; Wu K.; Xu G. Q.; Wee A. T. S.; Chen W. Towards Single Molecule Switches. Chem. Soc. Rev. 2015, 44 (10), 2998–3022. 10.1039/C4CS00377B. [DOI] [PubMed] [Google Scholar]
- Li Y.; Xu K.; Sun X. Single Molecule Switch Devices: A Minireview. Instrumentation Science & Technology 2020, 48 (5), 518–538. 10.1080/10739149.2020.1740247. [DOI] [Google Scholar]
- Liu W.; Yang S.; Li J.; Su G.; Ren J.-C. One Molecule, Two States: Single Molecular Switch on Metallic Electrodes. WIREs Computational Molecular Science 2021, 11 (4), e1511 10.1002/wcms.1511. [DOI] [Google Scholar]
- Feyer V.; Graus M.; Nigge P.; Zamborlini G.; Acres R. G.; Schöll A.; Reinert F.; Schneider C. M. The Geometric and Electronic Structure of TCNQ and TCNQ+Mn on Ag(0 0 1) and Cu (0 0 1) Surfaces. J. Electron Spectrosc. Relat. Phenom. 2015, 204, 125–131. 10.1016/j.elspec.2015.02.010. [DOI] [Google Scholar]
- Andersson K. Molecular Properties of TCNQ and Anions. Theor. Chem. Acc. 2023, 142 (6), 58. 10.1007/s00214-023-02998-7. [DOI] [Google Scholar]
- Martínez J. I.; Abad E.; Flores F.; Ortega J. Simulating the Organic-Molecule/Metal Interface TCNQ/Au(111). physica status solidi (b) 2011, 248 (9), 2044–2049. 10.1002/pssb.201147136. [DOI] [Google Scholar]
- Hadi H.; Louis H.; Gber T. E.; Ogungbemiro F. O. Molecular Modeling of the Structural, Electronic, Excited State Dynamic, and the Photovoltaic Properties of the Oligomers of n-Corannulene (n = 1–4). Heliyon 2023, 9 (10), e20706 10.1016/j.heliyon.2023.e20706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong K.; Yang J.; Testoff T. T.; Li W.; Wang T.; Liu D.; Zhou X.; Wang L. Electronically Excited State Structures and Stabilities of Organic Small Molecules: A DFT Study of Triphenylamine Derivatives. Chem. Phys. 2021, 549, 111256 10.1016/j.chemphys.2021.111256. [DOI] [Google Scholar]
- Edet H. O.; Louis H.; Gber T. E.; Idante P. S.; Egemonye T. C.; Ashishie P. B.; Oyo-Ita E. E.; Benjamin I.; Adeyinka A. S. Heteroatoms (B, N, S) Doped Quantum Dots as Potential Drug Delivery System for Isoniazid: Insight from DFT, NCI, and QTAIM. Heliyon 2023, 9 (1), e12599 10.1016/j.heliyon.2022.e12599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadi H.; Shamlouei H. R. Molecular Simulation of a Fluorescent Sensor of 2-(1-H-Benzoimidazole)-N-Phenylcarbotiamide for Selective Detection of Ni2+ in Aqueous Media. Mol. Simul. 2022, 48 (18), 1668–1677. 10.1080/08927022.2022.2114600. [DOI] [Google Scholar]
- Abdelaziz B.; Mazouz Z.; Gassoumi B.; El Islam Boukortt N.; Patanè S.; Ayachi S. Molecular engineering of D-π-A-type structures based on nitrobenzofurazan (NBD) derivatives for both organic solar cells and nonlinear optical response. J. Mol. Liq. 2024, 395, 123934 10.1016/j.molliq.2023.123934. [DOI] [Google Scholar]
- Mohammadi M. D.; Abdullah H. Y.; Biskos G.; Bhowmick S. Enhancing the Absorption of 1-Chloro-1,2,2,2-Tetrafluoroethane on Carbon Nanotubes: An Ab Initio Study. Bull. Mater. Sci. 2021, 44 (3), 198. 10.1007/s12034-021-02472-9. [DOI] [Google Scholar]
- Saleh G.; Gatti C.; Lo Presti L. Energetics of Non-Covalent Interactions from Electron and Energy Density Distributions. Computational and Theoretical Chemistry 2015, 1053, 53–59. 10.1016/j.comptc.2014.10.011. [DOI] [Google Scholar]
- Mohammadi M. D.; Salih I. H.; Abdullah H. Y. An Ultimate Investigation on the Adsorption of Amantadine on Pristine and Decorated Fullerenes C59X (X = Si, Ge, B, Al, Ga, N, P, and As): A DFT, NBO, and QTAIM Study. J. Comput. Biophys. Chem. 2021, 20 (01), 23–39. 10.1142/S2737416521500022. [DOI] [Google Scholar]
- Abdelaziz B.; Chérif I.; Gassoumi B.; Patanè S.; Ayachi S. Linear and non-linear optical responses of nitrobenzofurazan-sulfide derivatives: DFT-QTAIM investigation on twisted intramolecular charge transfer. J. Phys. Chem. A 2023, 127 (47), 9895–9910. 10.1021/acs.jpca.3c04277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doust Mohammadi M.; Abdullah H. Y.; Kalamse V.; Chaudhari A. Bromochlorodifluoromethane Interaction with Pristine and Doped BN Nanosheets: A DFT Study. Journal of Environmental Chemical Engineering 2022, 10 (5), 108367 10.1016/j.jece.2022.108367. [DOI] [Google Scholar]
- Doust Mohammadi M.; Abdullah H. Y. The Adsorption of Chlorofluoromethane on Pristine, Al-, Ga-, P-, and As-Doped Boron Nitride Nanotubes: A PBC-DFT, NBO, and QTAIM Study. ChemistrySelect 2020, 5 (39), 12115–12124. 10.1002/slct.202003367. [DOI] [PubMed] [Google Scholar]
- Yurenko Y. P.; Novotný J.; Mitoraj M. P.; Sklenář V.; Michalak A.; Marek R. Nucleic Acid Quadruplexes Based on 8-Halo-9-Deazaxanthines: Energetics and Noncovalent Interactions in Quadruplex Stems. J. Chem. Theory Comput. 2014, 10 (12), 5353–5365. 10.1021/ct5007554. [DOI] [PubMed] [Google Scholar]
- Hadi H.; Gassoumi B.; Nasr S.; Safari R.; Basha A. A.; Imran P. M.; Ghalla H.; Caccamo M. T.; Ayachi S. Design, Transport/Molecular Scale Electronics, Electric Properties, and a Conventional Quantum Study of a New Potential Molecular Switch for Nanoelectronic Devices. ACS Omega 2024, 9 (1), 1029–1041. 10.1021/acsomega.3c07257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu T.; Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33 (5), 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Kumar R.; Yadav S. K.; Seth R.; Singh A. Designing of Gigantic First-Order Hyperpolarizability Molecules via Joining the Promising Organic Fragments: A DFT Study. J. Mol. Model 2023, 29 (1), 5. 10.1007/s00894-022-05401-7. [DOI] [PubMed] [Google Scholar]
- Hadji D.; Champagne B. First Principles Investigation of the Polarizability and First Hyperpolarizability of Anhydride Derivatives. Chemistry Africa 2019, 2 (3), 443–453. 10.1007/s42250-019-00060-3. [DOI] [Google Scholar]
- Smogunov A.; Dal Corso A.; Tosatti E. Magnetic Phenomena, Spin-Orbit Effects, and Landauer Conductance in Pt Nanowire Contacts: Density-Functional Theory Calculations. Phys. Rev. B 2008, 78 (1), 014423 10.1103/PhysRevB.78.014423. [DOI] [Google Scholar]
- Evers F.; Weigend F.; Koentopp M. Conductance of Molecular Wires and Transport Calculations Based on Density-Functional Theory. Phys. Rev. B 2004, 69 (23), 235411 10.1103/PhysRevB.69.235411. [DOI] [Google Scholar]
- Chan B.; Yim W.-L. Accurate Computation of Cohesive Energies for Small to Medium-Sized Gold Clusters. J. Chem. Theory Comput. 2013, 9 (4), 1964–1970. 10.1021/ct400047y. [DOI] [PubMed] [Google Scholar]
- Steenbergen K. G.; Mewes J.-M.; Pašteka L. F.; Gäggeler H. W.; Kresse G.; Pahl E.; Schwerdtfeger P. The Cohesive Energy of Superheavy Element Copernicium Determined from Accurate Relativistic Coupled-Cluster Theory. Phys. Chem. Chem. Phys. 2017, 19 (48), 32286–32295. 10.1039/C7CP07203A. [DOI] [PubMed] [Google Scholar]
- Chérif I.; Raissi H.; Abiedh K.; Gassoumi B.; Caccamo M. T.; Magazu S.; Said A. H.; Hassen F.; Boubaker T.; Ayachi S. Computational Studies on Optoelectronic and Nonlinear Optical Properties of Para-Substituted Nitrobenzofurazan Compound. Materials Today Communications 2023, 35, 106133 10.1016/j.mtcomm.2023.106133. [DOI] [Google Scholar]
- Foroutan-Nejad C.; Andrushchenko V.; Straka M. Dipolar Molecules inside C 70 : An Electric Field-Driven Room-Temperature Single-Molecule Switch. Phys. Chem. Chem. Phys. 2016, 18 (48), 32673–32677. 10.1039/C6CP06986J. [DOI] [PubMed] [Google Scholar]
- Hossain Md. R.; Hasan Md. M.; Nishat M.; Noor-E-Ashrafi; Ahmed F.; Ferdous T.; Hossain Md. A. DFT and QTAIM Investigations of the Adsorption of Chlormethine Anticancer Drug on the Exterior Surface of Pristine and Transition Metal Functionalized Boron Nitride Fullerene. J. Mol. Liq. 2021, 323, 114627 10.1016/j.molliq.2020.114627. [DOI] [Google Scholar]
- Xu T.; Wang L.; Ping Y.; van Mourik T.; Früchtl H.; Kirk S. R.; Jenkins S. Quinone-Based Switches for Candidate Building Blocks of Molecular Junctions with QTAIM and the Stress Tensor. Int. J. Quantum Chem. 2018, 118 (16), e25676 10.1002/qua.25676. [DOI] [Google Scholar]
- Novák M.; Foroutan-Nejad C.; Marek R. Modulating Electron Sharing in Ion-π-Receptors via Substitution and External Electric Field: A Route toward Bond Strengthening. J. Chem. Theory Comput. 2016, 12 (8), 3788–3795. 10.1021/acs.jctc.6b00586. [DOI] [PubMed] [Google Scholar]
- Foroutan-Nejad C.; Marek R. Potential Energy Surface and Binding Energy in the Presence of an External Electric Field: Modulation of Anion−π Interactions for Graphene-Based Receptors. Phys. Chem. Chem. Phys. 2014, 16 (6), 2508–2514. 10.1039/C3CP52671B. [DOI] [PubMed] [Google Scholar]
- Foroutan-Nejad C.; Novák M.; Marek R. Comment on “Some Unexpected Behavior of the Adsorption of Alkali Metal Ions onto the Graphene Surface under the Effect of External Electric Field. J. Phys. Chem. C 2015, 119 (10), 5752–5754. 10.1021/jp511541p. [DOI] [Google Scholar]
- Bader R. F. W.Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, 1994. [Google Scholar]
- Bader R. F. W. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102 (37), 7314–7323. 10.1021/jp981794v. [DOI] [Google Scholar]
- Bader R. F. W. Bond Paths Are Not Chemical Bonds. J. Phys. Chem. A 2009, 113 (38), 10391–10396. 10.1021/jp906341r. [DOI] [PubMed] [Google Scholar]
- Kraka E.; Cremer D. Description of Chemical Reactions in Terms of the Properties of the Electron Density. Journal of Molecular Structure: THEOCHEM 1992, 255, 189–206. 10.1016/0166-1280(92)85010-I. [DOI] [Google Scholar]
- Jenkins S.; Blancafort L.; Kirk S. R.; Bearpark M. J. The Response of the Electronic Structure to Electronic Excitation and Double Bond Torsion in Fulvene: A Combined QTAIM, Stress Tensor and MO Perspective. Phys. Chem. Chem. Phys. 2014, 16 (15), 7115–7126. 10.1039/C4CP00003J. [DOI] [PubMed] [Google Scholar]
- Rozas I.; Alkorta I.; Elguero J. Behavior of Ylides Containing N, O, and C Atoms as Hydrogen Bond Acceptors. J. Am. Chem. Soc. 2000, 122 (45), 11154–11161. 10.1021/ja0017864. [DOI] [Google Scholar]
- Espinosa E.; Lecomte C.; Molins E. Experimental Electron Density Overlapping in Hydrogen Bonds: Topology vs. Energetics. Chem. Phys. Lett. 1999, 300 (5), 745–748. 10.1016/S0009-2614(98)01399-2. [DOI] [Google Scholar]
- Chérif I.; Raissi H.; Abiedh K.; Gassoumi B.; Teresa Caccamo M.; Magazu S.; Haj Said A.; Hassen F.; Boubaker T.; Ayachi S. Photophysical and Nonlinear Optical Properties of Para-Substituted Nitrobenzofurazan: A Comprehensive DFT Investigation. J. Photochem. Photobiol., A 2023, 443, 114850 10.1016/j.jphotochem.2023.114850. [DOI] [Google Scholar]
- Noureddine O.; Issaoui N.; Medimagh M.; Al-Dossary O.; Marouani H. Quantum Chemical Studies on Molecular Structure, AIM, ELF, RDG and Antiviral Activities of Hybrid Hydroxychloroquine in the Treatment of COVID-19: Molecular Docking and DFT Calculations. Journal of King Saud University - Science 2021, 33 (2), 101334 10.1016/j.jksus.2020.101334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janani S.; Rajagopal H.; Muthu S.; Aayisha S.; Raja M. Molecular Structure, Spectroscopic (FT-IR, FT-Raman, NMR), HOMO-LUMO, Chemical Reactivity, AIM, ELF, LOL and Molecular Docking Studies on 1-Benzyl-4-(N-Boc-Amino)Piperidine. J. Mol. Struct. 2021, 1230, 129657 10.1016/j.molstruc.2020.129657. [DOI] [Google Scholar]
- Chérif I.; Raissi H.; Abiedh K.; Gassoumi B.; Caccamo M. T.; Magazu S.; Said A. H.; Hassen F.; Boubaker T.; Ayachi S. Exploration of Intramolecular Charge Transfer in Para-Substituted Nitrobenzofurazan: Experimental and Theoretical Analyses. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2023, 301, 122939 10.1016/j.saa.2023.122939. [DOI] [PubMed] [Google Scholar]
- Silvi B.; Savin A. Classification of Chemical Bonds Based on Topological Analysis of Electron Localization Functions. Nature 1994, 371 (6499), 683–686. 10.1038/371683a0. [DOI] [Google Scholar]
- Tarika J. D. D.; Dexlin X. D. D.; kumar A. A.; Jayanthi D. D.; Rathika A.; Beaula T. J. Insights into Weak and Covalent Interactions, Reactivity Sites and Pharmacokinetic Studies of 4-Dimethylaminopyridinium Salicylate Monohydrate Using Quantum Chemical Computation Method. Computational and Theoretical Chemistry 2021, 1206, 113483 10.1016/j.comptc.2021.113483. [DOI] [Google Scholar]
- Sagaama A.; Issaoui N.; Al-Dossary O.; Kazachenko A. S.; Wojcik M. J. Non Covalent Interactions and Molecular Docking Studies on Morphine Compound. Journal of King Saud University - Science 2021, 33 (8), 101606 10.1016/j.jksus.2021.101606. [DOI] [Google Scholar]
- Dey D.; Roy P.; De D. Electronic Transport Properties of Electrically Doped Cytosine-Based Optical Molecular Switch with Single-Wall Carbon Nanotube Electrodes. IET Nanobiotechnology 2019, 13 (5), 484–492. 10.1049/iet-nbt.2018.5375. [DOI] [Google Scholar]
- OuYang F.; Xu H.; Fan T. All-Carbon Nanoswitch Based on C70 Molecule: A First Principles Study. J. Appl. Phys. 2007, 102 (6), 064501 10.1063/1.2779263. [DOI] [Google Scholar]
- Hadi H.; Louis H.; Gber T. E.; Ogungbemiro F. O. Molecular modeling of the structural, electronic, excited state dynamic, and the photovoltaic properties of the oligomers of n-corannulene (n = 1–4). Heliyon 2023, 9 (10), e20706. 10.1016/j.heliyon.2023.e20706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batool H.; Majid A.; Alkhedher M.; Bulut N.; Al-Adwan I. A DFT Study of Quantum Electronic Transport Properties of InTeCl. Materials Science in Semiconductor Processing 2023, 168, 107842 10.1016/j.mssp.2023.107842. [DOI] [Google Scholar]
- Hadi H.; Safari R. Computational evaluation of some optical and quantum electronics properties (performance) of an organic molecular switch. Optical and Quantum Electronics 2024, 56 (4), 575. 10.1007/s11082-023-06221-6. [DOI] [Google Scholar]
- Islam N.; Chimni S. S. DFT Investigation on Nonlinear Optical (NLO) Properties of Novel Borazine Derivatives. Computational and Theoretical Chemistry 2016, 1086, 58–66. 10.1016/j.comptc.2016.04.016. [DOI] [Google Scholar]
- Manikandan I.; Perumal M. V.; Jayamoorthy K. Synthesis, Characterization, Physico-Chemical and DFT Studies of Potential Organic NLO Materials: Experimental and Theoretical Combined Study. Silicon 2019, 11 (1), 425–435. 10.1007/s12633-018-9837-9. [DOI] [Google Scholar]
- Mande P.; Mathew E.; Chitrambalam S.; Joe I. H.; Sekar N. NLO Properties of 1, 4-Naphthoquinone, Juglone and Lawsone by DFT and Z-Scan Technique – A Detailed Study. Opt. Mater. 2017, 72, 549–558. 10.1016/j.optmat.2017.06.058. [DOI] [Google Scholar]
- Ahsin A.; Ayub K. Remarkable Electronic and NLO Properties of Bimetallic Superalkali Clusters: A DFT Study. J. Nanostruct Chem. 2022, 12 (4), 529–545. 10.1007/s40097-021-00429-2. [DOI] [Google Scholar]
- Pandey N.; Mehata M. S.; Pant S.; Tewari N. Structural, Electronic and NLO Properties of 6-Aminoquinoline: A DFT/TD-DFT Study. J. Fluoresc 2021, 31 (6), 1719–1729. 10.1007/s10895-021-02788-z. [DOI] [PubMed] [Google Scholar]
- Asiri A. M.; Karabacak M.; Kurt M.; Alamry K. A. Synthesis, Molecular Conformation, Vibrational and Electronic Transition, Isometric Chemical Shift, Polarizability and Hyperpolarizability Analysis of 3-(4-Methoxy-Phenyl)-2-(4-Nitro-Phenyl)-Acrylonitrile: A Combined Experimental and Theoretical Analysis. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2011, 82 (1), 444–455. 10.1016/j.saa.2011.07.076. [DOI] [PubMed] [Google Scholar]
- Mandal U.; Beg H.; Misra A. Effect of Charge Transfer on the First Hyper-Polarizability of N,N-Dimethylaniline and Julolidine: A DFT Based Comparative Study. J. Mol. Model 2023, 29 (11), 351. 10.1007/s00894-023-05755-6. [DOI] [PubMed] [Google Scholar]
- Lokhande P. K. M.; Patil D. S.; Kadam M. M.; Sekar N. Theoretical Investigation of Optical and Nonlinear Optical (NLO) Properties of 3-Azabenzanthrone Analogues : DFT and TD-DFT Approach. ChemistrySelect 2019, 4 (34), 10033–10045. 10.1002/slct.201901681. [DOI] [Google Scholar]
- Asiri A. M.; Karabacak M.; Kurt M.; Alamry K. A. Synthesis, Molecular Conformation, Vibrational and Electronic Transition, Isometric Chemical Shift, Polarizability and Hyperpolarizability Analysis of 3-(4-Methoxy-Phenyl)-2-(4-Nitro-Phenyl)-Acrylonitrile: A Combined Experimental and Theoretical Analysis. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2011, 82 (1), 444–455. 10.1016/j.saa.2011.07.076. [DOI] [PubMed] [Google Scholar]
- Mandal U.; Beg H.; Misra A. Effect of Charge Transfer on the First Hyper-Polarizability of N,N-Dimethylaniline and Julolidine: A DFT Based Comparative Study. J. Mol. Model 2023, 29 (11), 351. 10.1007/s00894-023-05755-6. [DOI] [PubMed] [Google Scholar]
- Haroon M.; Akhtar T.; Khalid M.; Mehmood H.; Braga A. A. C.; Alhokbany N.; Ahmed S. Experimental and Quantum Chemical Studies of Hydrazone-Based Organic Chromophores: Synthesis, Spectroscopic and Nonlinear Optical Properties. ChemistrySelect 2023, 8 (28), e202301209 10.1002/slct.202301209. [DOI] [Google Scholar]
- El Behi S.; Ayachi S.; Znaidia S. Computational modeling for the design of new fluorescent organic compounds based on both diketopyrrolopyrrole and nitrobenzofurazan moieties. J. Mol. Liq. 2022, 360, 119550 10.1016/j.molliq.2022.119550. [DOI] [Google Scholar]
- Zahedi E.; Mozaffari M.; Karimi F.-S.; Nouri A. Density Functional Theory Study of Electric Field Effects on the Isomerization of a Photochromic Molecular Switch Based on 1,2-Dithienylethene. Can. J. Chem. 2014, 92 (4), 317–323. 10.1139/cjc-2013-0589. [DOI] [Google Scholar]
- Mostaanzadeh H.; Safari R.; Hadi H.; Javadi M. R. DFT Computational Study of a Candidate Field-Effect Molecular Wire. Russ. J. Phys. Chem. 2023, 97 (1), 202–211. 10.1134/S0036024423010120. [DOI] [Google Scholar]
- Sobrino N.; D’Agosta R.; Kurth S. Steady-State Density Functional Theory for Thermoelectric Effects. Phys. Rev. B 2019, 100 (19), 195142 10.1103/PhysRevB.100.195142. [DOI] [Google Scholar]
- Kumar P.; Rajput K.; Roy D. R. Structural, Electronic, Vibrational, Mechanical and Thermoelectric Properties of 2D and Bulk BaX (X = O, S, Se and Te) Series under DFT and BTE Framework. Physica E: Low-dimensional Systems and Nanostructures 2021, 127, 114523 10.1016/j.physe.2020.114523. [DOI] [Google Scholar]
- Rahmati E.; Bafekry A.; Faraji M.; Gogva D.; Nguyen C. V.; Ghergherehchi M. Thermoelectric Properties of Doped Graphene Nanoribbons: Density Functional Theory Calculations and Electrical Transport. RSC Adv. 2022, 12 (10), 6174–6180. 10.1039/D1RA08303A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safari R.; Sabzyan H. Local Energy Dissipation/Transition in Field Effect Molecular Nanoelectronic Systems: A Quantum Mechanical Methodology. Commun. Theor. Phys. 2019, 71 (4), 441. 10.1088/0253-6102/71/4/441. [DOI] [Google Scholar]
- Sabzyan H.; Safari R. Intramolecular Thermoelectric-like Effects in Field-Effect Molecular Nanoelectronic Devices. EPL 2012, 99 (6), 67005. 10.1209/0295-5075/99/67005. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data are included in the manuscript.