Abstract
Segmentation of multiple sclerosis (MS) lesions on brain MRI scans is crucial for diagnosis, disease and treatment monitoring but is a time-consuming task. Despite several automated algorithms have been proposed, there is still no consensus on the most effective method. Here, we applied a consensus-based framework to improve lesion segmentation on T1-weighted and FLAIR scans. The framework is designed to combine publicly available state-of-the-art deep learning models, by running multiple segmentation tasks before merging the outputs of each algorithm. To assess the effectiveness of the approach, we applied it to MRI datasets from two different centers, including a private and a public dataset, with 131 and 30 MS patients respectively, with manually segmented lesion masks available. No further training was performed for any of the included algorithms. Overlap and detection scores were improved, with Dice increasing by 4-8% and precision by 3-4% respectively for the private and public dataset. High agreement was obtained between estimated and true lesion load (ρ = 0.92 and ρ = 0.97) and count (ρ = 0.83 and ρ = 0.94). Overall, this framework ensures accurate and reliable results, exploiting complementary features and overcoming some of the limitations of individual algorithms.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-72649-9.
Keywords: Multiple sclerosis, Lesion segmentation, Consensus, MRI, Label fusion, Machine learning
Subject terms: Computational neuroscience, Diseases of the nervous system, Biomedical engineering
Introduction
Multiple sclerosis (MS) is a chronic and neurodegenerative disorder affecting millions of people worldwide1. The hallmark of MS is the formation of lesions in the white and gray matter of the central nervous system (CNS), which can lead to a wide range of neurological symptoms such as vision loss, muscle weakness and cognitive impairment2,3. MRI is highly sensitive in detecting the characteristic focal lesions in the brain and the spinal cord4 and therefore accurate and reliable segmentation of MS lesions on MRI scans is universally considered crucial for MS diagnosis and progression monitoring as well as for evaluating treatment response to assess the effectiveness of new therapies5. However, manual segmentation, the traditional (and still most accurate) method for identifying and quantifying MS lesions, is time-consuming, labor-intensive and prone to intra- and inter-expert variability6,7.
Over the past few decades, several automated MS lesion segmentation algorithms have been proposed, ranging from threshold-based methods to more sophisticated solutions based on deep learning (DL) models8–17. In particular, due to the increasing computational power available, convolutional neural networks (CNN) and their variants (such as U-Nets) have increasingly gained popularity in MS lesion segmentation, often gathering significantly better performances than non-DL approaches18. However, while each algorithm has its strengths and limitations, there is still no consensus on the best method for accurately and reliably segmenting MS lesions6. Indeed, the high variability in lesion size, shape and location are some of the major challenges in MS lesion segmentation19. These challenges can lead to inconsistencies in lesion detection across different algorithms and datasets, thus limiting the potential application of such automated tools in clinical practice20.
In this paper, we evaluate a consensus-based method for merging via majority voting the output of multiple open-source publicly available MS lesion segmentation algorithms to obtain better segmentation performances. Specifically, we aimed to address current problems and challenges in the field of MS lesion segmentation, such as the high variability of lesion characteristics and the lack of consensus on the best available algorithm. Albeit majority voting is a simple case of ensemble learning that has been already investigated in many other applications21–23, our proposal would potentially boost the application of this framework to the problem of MS lesion segmentation, as it entails with combining results from very different, as well as independently developed, trained and tested, lesion segmentation methods, for the first time. Rakić et al. also proposed a framework that combines two different approaches, a traditional unsupervised machine learning technique and a deep-learning attention-gate 3D U-net network, to improve the detection of infratentorial and juxtacortical lesions in a multi-center MS dataset24. However, in this study, the authors decided to take the logical OR of the only two lesion masks (with a rule-based approach) as resulting from the two pipelines without fully exploring the potential of a consensus approach. Two other works have proposed similar label fusion methods for MS lesion segmentation to expressly overcome the limitations of each individual method and thus obtain results closer to ground truth: Commowick et al. demonstrated that implementing a statistically robust consensus of the algorithms performed closer to human expertise on segmentation scores6; Carass et al. showed that by combining information from multiple algorithms, they could generate a segmentation that also gathered an improved performance in specificity of the selected lesions25. However, in both these two works, the authors built the consensus decision only from the algorithms submitted to a specific competition (MICCAI 2016 challenge and ISBI 2015 challenge, respectively), without considering other state-of-the-art methods developed more recently. In addition, in25, the authors constructed their consensus decision from algorithms that were trained and tested on images acquired on the same scanner, preventing to validate the robustness of the method across different vendors and/or sites. Thus, unavoidably, results obtained from these studies will necessarily exhibit a certain degree of bias due to the reference data used for developing the method26.
To address some of these limitations, we opted for a consensus approach that is based on five different algorithms and builds up the consensus decision by merging multiple more recent state-of-the-art algorithms, leveraging both unsupervised and supervised methods, including pre-trained deep learning models, and evaluated it on two independent unseen datasets. Critically, all algorithms used here had previously undergone an independent training on different datasets acquired with different MRI scanners and protocols and processed by different researchers on different machines. It is indeed widely recognized that especially machine and deep learning algorithms tend to work best when trained on data closely resembling the testing dataset, also in terms of acquisition and processing settings, but this does not fully address the generalizability of a model across other different settings or platforms. Thus, in this work, we essentially aimed to make all algorithms “data-blind” to ensure an impartial assessment of their marginal and combined performances, avoiding any form of bias deriving from specific training data. Overall, our proposed method provides several advantages over existing methods for MS lesion segmentation: first, it addresses the limitations of individual algorithms by combining the strengths of more than two algorithms; second, it is flexible and adaptable, allowing for the integration of new algorithms as soon as they become available. Finally, our proposed method is efficient, providing accurate and reliable segmentation results in a relatively short amount of time.
Methods
Datasets
All datasets were originally acquired in accordance with the relevant guidelines and regulations. In this study, we applied the automated lesion segmentation algorithms on two (unseen) independent datasets of 131 (Dataset I) and 30 (Dataset II) MS patients, respectively. Demographic/clinic information and lesion characteristics (volume and number) for both datasets are reported in Table 1.
Table 1.
Summary of the two datasets characteristics. Age is reported as mean ± standard deviation; EDSS, lesion load and number of lesions are reported as median (interquartile range).
| Dataset I | Dataset II | |
|---|---|---|
| Subjects | 131 | 30 |
| Age | 37.3 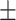 10.3 10.3 |
39.3 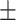 10.1 10.1 |
| Sex (F/M) | 89/42 | 23/7 |
| EDSS | 2 (1.5) | 2 (2.5) |
| Lesion load [ml] | 4.36 (7.23) | 14.2 (26.6) |
| Number of lesions | 57.0 (49.0) | 133 (120) |
Dataset I
Images for dataset I were acquired at the University of Campania Luigi Vanvitelli (Naples, Italy) from 131 subjects (89 female / 42 male, mean age 37.3 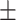 10.3). All subjects were patients diagnosed with MS according to the 2010 McDonald diagnostic criteria, i.e., all patients had confirmed MRI T2-weighted lesions. All experimental protocols were approved by the Ethical Committee of the University of Campania “Luigi Vanvitelli” and written informed consent was obtained from all participants at the time of data acquisition. Scanning was performed on a 3T GE MR scanner (Signa HDxt, GE Healthcare, Milwaukee, USA) equipped with an 8-channel head and neck coil. Each scan included a 3D T1-weighted sagittal image (IR-FSPGR, TR = 6.9 ms, TE = 2.8 ms, TI = 650 ms, FA = 8°, voxel size = 1 × 1 × 1.2 mm3, number of slices = 166, acquisition matrix = 256 × 256), a 2D T2-weighted axial image (dual-echo, TR = 3120 ms, TE = 24 ms, FA = 90°, voxel size = 0.5 × 0.5 × 3 mm3, number of slices = 44, acquisition matrix = 512 × 512) and a 2D flow attenuated inversion recovery (FLAIR) axial image (TR = 9000 ms, TE = 122 ms, TI = 2500 ms, FA = 90°, voxel size = 0.5 × 0.5 × 3 mm3, number of slices = 44, acquisition matrix = 512 × 512). Lesion masks were manually segmented on T2-weighted images by an experienced neuroradiologist and rigidly co-registered to the FLAIR space using FLIRT27,28.
10.3). All subjects were patients diagnosed with MS according to the 2010 McDonald diagnostic criteria, i.e., all patients had confirmed MRI T2-weighted lesions. All experimental protocols were approved by the Ethical Committee of the University of Campania “Luigi Vanvitelli” and written informed consent was obtained from all participants at the time of data acquisition. Scanning was performed on a 3T GE MR scanner (Signa HDxt, GE Healthcare, Milwaukee, USA) equipped with an 8-channel head and neck coil. Each scan included a 3D T1-weighted sagittal image (IR-FSPGR, TR = 6.9 ms, TE = 2.8 ms, TI = 650 ms, FA = 8°, voxel size = 1 × 1 × 1.2 mm3, number of slices = 166, acquisition matrix = 256 × 256), a 2D T2-weighted axial image (dual-echo, TR = 3120 ms, TE = 24 ms, FA = 90°, voxel size = 0.5 × 0.5 × 3 mm3, number of slices = 44, acquisition matrix = 512 × 512) and a 2D flow attenuated inversion recovery (FLAIR) axial image (TR = 9000 ms, TE = 122 ms, TI = 2500 ms, FA = 90°, voxel size = 0.5 × 0.5 × 3 mm3, number of slices = 44, acquisition matrix = 512 × 512). Lesion masks were manually segmented on T2-weighted images by an experienced neuroradiologist and rigidly co-registered to the FLAIR space using FLIRT27,28.
Dataset II
Images for dataset II from 30 subjects (23 female/7 male, mean age 39.3 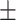 10.1) were retrieved from a public dataset29. Scanning was performed on a 3T Siemens MRI scanner (Magnetom Trio, Siemens Healthcare, Erlangen, Germany) at the University Medical Center Ljubljana (Slovenia). Each participant’s scan consisted in a 2D T1-weighted (turbo inversion recovery magnitude, TR = 2000 ms, TE = 20 ms, TI = 800 ms, FA = 120°, voxel size = 0.43 × 0.43 × 0.83 mm3), a 2D T2-weighted (turbo spin echo, TR = 6000 ms, TE = 120 ms, FA = 120°, voxel size = 0.57 × 0.57 × 0.83 mm3) and a 3D FLAIR image (TR = 5000 ms, TE = 392 ms, TI = 1800 ms, FA = 120°, voxel size = 0.47 × 0.47 × 0.80 mm3). Lesions were manually segmented on FLAIR images by three expert raters, which they then revised in several joint sessions to create a consensus-based gold standard segmentation. To reduce computational cost, we used the already available preprocessed data resampled to an isotropic 1 × 1 × 1 mm3 voxel size.
10.1) were retrieved from a public dataset29. Scanning was performed on a 3T Siemens MRI scanner (Magnetom Trio, Siemens Healthcare, Erlangen, Germany) at the University Medical Center Ljubljana (Slovenia). Each participant’s scan consisted in a 2D T1-weighted (turbo inversion recovery magnitude, TR = 2000 ms, TE = 20 ms, TI = 800 ms, FA = 120°, voxel size = 0.43 × 0.43 × 0.83 mm3), a 2D T2-weighted (turbo spin echo, TR = 6000 ms, TE = 120 ms, FA = 120°, voxel size = 0.57 × 0.57 × 0.83 mm3) and a 3D FLAIR image (TR = 5000 ms, TE = 392 ms, TI = 1800 ms, FA = 120°, voxel size = 0.47 × 0.47 × 0.80 mm3). Lesions were manually segmented on FLAIR images by three expert raters, which they then revised in several joint sessions to create a consensus-based gold standard segmentation. To reduce computational cost, we used the already available preprocessed data resampled to an isotropic 1 × 1 × 1 mm3 voxel size.
Methodology
To apply the consensus approach, we considered five publicly available and widely used algorithms for MS lesion segmentation:
SAMSEG9: this algorithm is used for the simultaneous segmentation of white matter lesions and normal-appearing neuroanatomical structures from multi-contrast brain MRI scans of MS patients. The method integrates an internal model for the spatial distribution of white matter lesions into a previously validated generative model for whole-brain segmentation30. The algorithm can adapt to data acquired with different scanners and imaging protocols without retraining by using separate models for the shape of anatomical structures and their appearance in MRI. SAMSEG only requires the initial co-registration of the T1-weighted scan to the FLAIR space without any further preprocessing step. The algorithm is publicly available as part of the open-source neuroimaging package FreeSurfer (https://surfer.nmr.mgh.harvard.edu/).
LST-lga13: this algorithm works by determining three tissue classes (gray matter, white matter and cerebrospinal fluid) from the T1-weighted image using SPM12 (https://www.fil.ion.ucl.ac.uk/spm/software/spm12/) and then analyzing the FLAIR intensity distribution of each tissue class to detect outliers, which are interpreted as lesion beliefs. These conservative lesion beliefs are expanded iteratively toward liberal lesion beliefs by analyzing neighboring voxels and assigning them to lesions under certain conditions, also depending on the likelihood of belonging to WM or GM versus belonging to lesions. Moreover, this method does not require any preprocessing step as it implements an internal fully automated preprocessing pipeline. We estimated the optimal threshold for each dataset by first letting the initial threshold range from 0.05 to 0.95 in intervals of 0.05 and then choosing the value returning the highest global Dice coefficient, as suggested by Schmidt et al.13.
nicMSlesions15,31: this algorithm uses a cascade of two 3D patch-wise CNNs. The first network is trained to identify possible candidate lesion voxels, while the second network reduces the number of misclassified voxels from the first network. Before running nicMSlesions, we bias-corrected the field for MR field inhomogeneity. This method is one of the few for which an implementation and a pre-trained model are publicly available (https://github.com/sergivalverde/nicMSlesions).
U-Net12: this algorithm is based on a 3D U-Net trained for the automated segmentation of both cortical and white matter lesions. The model was trained after rigid co-registering FLAIR scans to the corresponding T1-weighted image. A pre-trained model with this architecture is publicly available (https://github.com/FrancescoLR/MS-lesion-segmentation). As an alternative to the basic 3D U-Net, another algorithm (LST-AI), which is itself an ensemble of three 3D U-Nets, each inspired by the more advanced nnU-Net framework32, was considered as this algorithm similarly takes in input T1w and FLAIR images and generates three separate probability maps, from which the final binary lesion mask can be obtained via averaging and thresholding.
TrUE-Net33: this method combines predictions from three different planes using an ensemble triplanar network for accurate segmentation of white matter hyperintensities (WMHs). In addition, it incorporates anatomical information regarding WMH spatial distribution in the loss function. The network is publicly available online (https://git.fmrib.ox.ac.uk/vaanathi/truenet) with a pre-trained model.
Each one of these models was tested with a T1w and a FLAIR scan. We constructed a final consensus mask for each subject based on two different approaches: majority voting, meaning that a voxel is labelled as lesion if at least three algorithms (out of five) classify it as lesion, and the simultaneous truth and performance level estimation (STAPLE)34, which estimates a probabilistic mask of the true segmentation with an expectation-maximization algorithm. The final mask was fine-tuned by filling possible voids in detected lesions. Furthermore, only lesions with a minimum volume of 0.005 ml (i.e., at least 7 voxels for Dataset I and 5 voxels for Dataset II) were considered in the final mask, because lesions below that size are not well defined and are very likely to be false positive findings24,35–37.
Evaluation metrics
From the segmentation masks, we derived the total lesion load, an essential radiologic metric to evaluate the severity of the brain damage38,39. However, when it comes to monitoring disease progression and assessing treatment response, lesion count and the number of new lesions (irrespective of their sizes) assume a critical role40. Moreover, the lesion count is one of the components of MS diagnosis according to the McDonald criteria41. We have therefore counted the number of lesions detected from each algorithm and evaluated it against the true number of lesions identified from the ground truth masks. To assess the segmentation performance of the proposed method and to compare its accuracy with the other methods, we employed several evaluation metrics. These metrics included:
-
Dice coefficient score: measures the degree of overlap between two binary lesion maps and it is computed as:
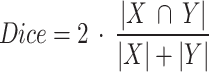
where X and Y denote the segmentation masks and |.| the sum of labelled voxels.
-
Precision and recall: the first measures the proportion of voxels correctly labelled as lesion with respect to the total number of voxels labelled as lesions, whereas the latter measures the proportion of voxels correctly labelled as lesion with respect to the total number of true lesion voxels. These measures are defined as:
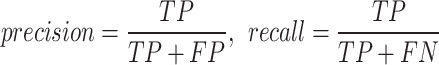
where TP, FP and FN count respectively the true positive, false positive and false negative voxels compared to manual segmentation.
Spearman correlation coefficient: to assess the relationship between lesion volume estimates and ground truth volumes and between the estimated number of lesions and the true number of lesions.
Mean absolute error (MAE): measures the average magnitude of errors between estimated lesion volumes and the corresponding true lesion volumes.
In addition, following similar previous works, we also compared lesion-wise metrics42,43. Namely, an individual lesion in the segmented map was considered a true positive lesion (TP) if there was an overlap by at least one voxel with a lesion in the ground truth map. Analogously, false positive (FP) and false negative (FN) lesions were defined. Thus, we could define the lesion true positive rate (LTPR) and the lesion false positive rate (LFPR), as lesion-wise metrics of sensitivity and precision, respectively, for the method. Wilcoxon rank-sum statistical tests were employed to assess if consensus methods led to statistically significant (p < 0.05) improvements or only marginal changes (p > 0.05) in the evaluation metrics compared to the best performing individual algorithm.
Ablation studies
We performed two ablation studies to test the robustness of the consensus approach with respect to the (variable) dataset size and (variable) number of combined algorithms. More specifically, we tested the importance of the dataset size by evaluating the combined approaches on different subsets of the private dataset. In more detail, we randomly subsampled by 40%, 60%, and 80% of the entire dataset, with each reduced subset sampled 10 times to eliminate data-dependency. In addition, we also evaluated the majority voting approach by iteratively excluding 2 algorithms from the consensus to test if (and how) the inclusion and/or exclusion of (which) algorithm affects the performances.
Experiments
All experiments and evaluations were carried out with custom-made python scripts (v. 3.10) on a Linux workstation equipped with a 10 core Intel Xeon Silver 4316 CPU @2.30 GHz and 36 GB RAM. For each subject, the total processing time was approximately 90 min.
Results
In Fig. 1, we present an example of a FLAIR image from an MS patient for each of the two datasets and their corresponding manual masks, along with the lesion mask as obtained from the five methods here considered and the consensus segmentation. We found that a threshold of 0.05 for the LST algorithm delivered the maximal Dice score for both datasets and therefore it was used for all further analyses. Mean Dice, precision and recall scores were computed to assess the voxel-wise performances, while LTPR and LFPR were computed to assess the lesion-wise performances of the different methods. The results obtained from the evaluation of the proposed method are presented in Table 2. In both datasets, the majority voting approach demonstrated higher Dice (0.42 ± 0.17, p < 0.05 for dataset I and 0.60 ± 0.18, p < 0.05 for dataset II), precision (0.51 ± 0.16, p > 0.05 for dataset I and 0.80 ± 0.18, p > 0.05 for dataset II), and lower LFPR (0.25 ± 0.19, p < 0.05 for dataset I and 0.11 ± 0.14, p < 0.05 for dataset II) scores, compared to the individual methods. The STAPLE approach achieved the highest Dice score for Dataset II (0.64 ± 0.17, p > 0.05) and, overall, higher recall (p < 0.05) and lower precision (p < 0.05) compared to majority voting. Table 3 presents the correlation coefficients between the estimated and true lesion load, as well as the number of lesions, along with the mean absolute error (MAE) measured in milliliters (ml). Majority voting demonstrated strong correlations with the true number of lesions, outperforming all other methods both in dataset I (ρ = 0.83) and in dataset II (ρ = 0.94). Additionally, it achieved a high correlation with the true lesion load both in dataset I (ρ = 0.92) and in dataset II (ρ = 0.97). In terms of MAE, for dataset I the majority voting method demonstrated the lowest score (2.59 ml), while for dataset II (5.99 ml) it was outperformed by LST (4.90 ml) and the STAPLE approach (2.05 ml). In Fig. 2, Dice coefficient scores are plotted against the lesion load as derived from manual segmentations, indicating decreasing Dice scores with decreasing lesion volume. To provide further insights, Table 4 presents the results for the subjects categorized into the first and last tertiles based on their lesion load. In the low lesion load tertile, the majority voting method demonstrated improved Dice (by 7% and 5% for dataset I and II, respectively) and precision (by 3% and 6% for dataset I and II) scores compared to the top-performing individual algorithm; in the high lesion load tertile, majority voting showed improved Dice score only in dataset I (by 2%) but decreased in dataset II (by 2%) and a slightly improved precision (by 2% and 1% for dataset I and II) compared to the top performing individual algorithm.
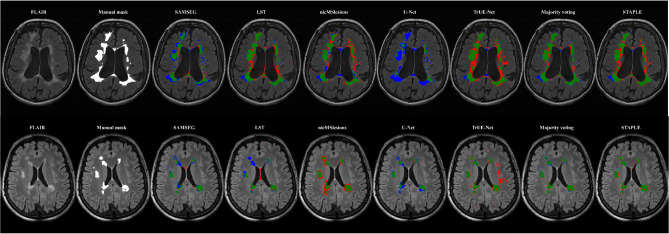
Fig. 1.
Examples of MS lesion segmentations: illustration of lesion segmentation masks on one representative subject from dataset I (Top) and dataset II (Bottom). Figures are color-coded for true positives (green), false positives (red), and false negatives (blue).
Table 2.
Results for each of the evaluated methods on the two MS datasets. Results are reported as mean (standard deviation). The best value for each metric is shown in bold. Last row shows results after excluding worst performing algorithm.
| Dice | Precision | Recall | LTPR | LFPR | |
|---|---|---|---|---|---|
| Dataset I | |||||
| SAMSEG | 0.38 (0.18) | 0.48 (0.19) | 0.36 (0.21) | 0.25 (0.15) | 0.56 (0.19) |
| LST | 0.35 (0.17) | 0.34 (0.17) | 0.41 (0.21) | 0.38 (0.15) | 0.71 (0.16) |
| nicMSlesions | 0.32 (0.14) | 0.26 (0.14) | 0.48 (0.19) | 0.50 (0.14) | 0.83 (0.10) |
| U-Net | 0.17 (0.13) | 0.27 (0.21) | 0.16 (0.11) | 0.24 (0.12) | 0.61 (0.20) |
| TrUE-Net | 0.35 (0.14) | 0.25 (0.13) | 0.68 (0.18) | 0.72 (0.15) | 0.83 (0.11) |
| Majority voting | 0.42 (0.14) | 0.51 (0.16) | 0.40 (0.20) | 0.33 (0.15) | 0.25 (0.19) |
| STAPLE | 0.42 (0.15) | 0.36 (0.14) | 0.56 (0.20) | 0.50 (0.15) | 0.37 (0.19) |
| Dataset II | |||||
| SAMSEG | 0.49 (0.24) | 0.76 (0.23) | 0.40 (0.22) | 0.18 (0.14) | 0.44 (0.21) |
| LST | 0.52 (0.24) | 0.64 (0.27) | 0.48 (0.22) | 0.30 (0.15) | 0.65 (0.26) |
| nicMSlesions | 0.51 (0.15) | 0.45 (0.16) | 0.63 (0.17) | 0.47 (0.11) | 0.75 (0.15) |
| U-Net | 0.30 (0.14) | 0.67 (0.31) | 0.24 (0.11) | 0.29 (0.10) | 0.30 (0.28) |
| TrUE-Net | 0.48 (0.25) | 0.42 (0.24) | 0.69 (0.15) | 0.61 (0.12) | 0.81 (0.16) |
| Majority voting | 0.60 (0.18) | 0.80 (0.18) | 0.49 (0.19) | 0.27 (0.11) | 0.11 (0.14) |
| STAPLE | 0.64 (0.17) | 0.62 (0.19) | 0.67 (0.16) | 0.41 (0.10) | 0.33 (0.26) |
Table 3.
Evaluation metrics based on estimated lesion volumes for the two MS datasets. The best value for each metric is shown in bold. Last row shows results after excluding worst performing algorithm.
| Correlation with true lesion volume | Correlation with number of lesions | MAE [ml] |
|
|---|---|---|---|
| Dataset I | |||
| SAMSEG | 0.91 | 0.67 | 2.81 |
| LST | 0.88 | 0.55 | 3.51 |
| nicMSlesions | 0.89 | 0.43 | 5.44 |
| U-Net | 0.51 | 0.64 | 5.46 |
| TrUE-Net | 0.92 | 0.28 | 9.5 |
| Majority voting | 0.92 | 0.83 | 2.59 |
| STAPLE | 0.93 | 0.80 | 4.08 |
| Dataset II | |||
| SAMSEG | 0.96 | 0.78 | 6.86 |
| LST | 0.95 | 0.24 | 4.90 |
| nicMSlesions | 0.93 | 0.75 | 7.57 |
| U-Net | 0.56 | 0.69 | 14.0 |
| TrUE-Net | 0.91 | -0.09 | 8.24 |
| Majority voting | 0.97 | 0.94 | 5.99 |
| STAPLE | 0.98 | 0.87 | 2.05 |
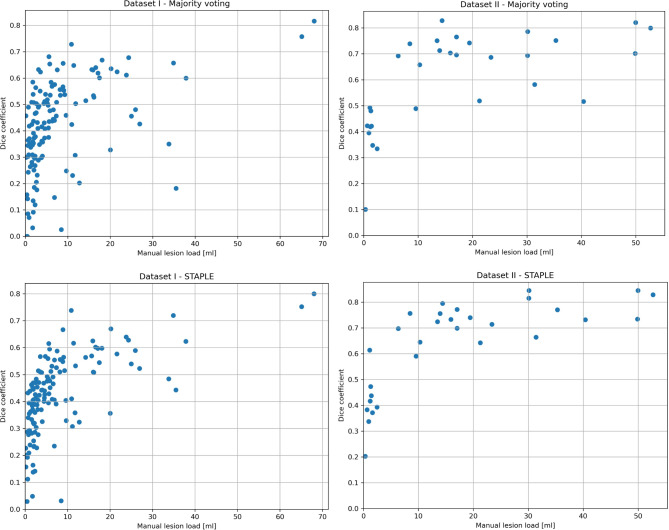
Fig. 2.
Scatter plots: Dice coefficients are plotted over lesion loads derived from manual segmentations for both datasets and both methods.
Table 4.
Evaluation metrics for subjects categorized in tertiles based on their lesion load. I tertile for dataset I (lesion load < = 2.33 ml); III tertile for dataset I (lesion load > = 6.88 ml); I tertile for dataset II (lesion load < = 7.75 ml); III tertile for dataset II (lesion load > = 20.0 ml).
| Dice | Precision | Recall | ||||
|---|---|---|---|---|---|---|
| I tertile | III tertile | I tertile | III tertile | I tertile | III tertile | |
| Dataset I | ||||||
| SAMSEG | 0.24 | 0.49 | 0.39 | 0.57 | 0.22 | 0.45 |
| LST | 0.21 | 0.48 | 0.19 | 0.46 | 0.28 | 0.55 |
| nicMSlesions | 0.18 | 0.42 | 0.12 | 0.39 | 0.40 | 0.51 |
| U-Net | 0.12 | 0.20 | 0.12 | 0.40 | 0.14 | 0.15 |
| TrUE-Net | 0.21 | 0.47 | 0.13 | 0.37 | 0.62 | 0.69 |
| Majority voting | 0.31 | 0.51 | 0.42 | 0.59 | 0.28 | 0.50 |
| STAPLE | 0.30 | 0.53 | 0.24 | 0.48 | 0.45 | 0.65 |
| Dataset II | ||||||
| SAMSEG | 0.23 | 0.62 | 0.60 | 0.87 | 0.17 | 0.49 |
| LST | 0.23 | 0.70 | 0.29 | 0.82 | 0.26 | 0.62 |
| nicMSlesions | 0.35 | 0.57 | 0.28 | 0.56 | 0.50 | 0.66 |
| U-Net | 0.23 | 0.21 | 0.26 | 0.90 | 0.27 | 0.12 |
| TrUE-Net | 0.26 | 0.69 | 0.10 | 0.66 | 0.56 | 0.74 |
| Majority voting | 0.40 | 0.68 | 0.66 | 0.91 | 0.31 | 0.56 |
| STAPLE | 0.43 | 0.76 | 0.40 | 0.77 | 0.50 | 0.75 |
Finally, we additionally considered LST-AI, a tool consisting in an ensemble of three 3D U-Nets, incorporating this tool in consensus, in place of the basic U-Net. The new results are summarized in Supplementary Table 1. With the inclusion of LST-AI, the majority voting approach still showed the highest Dice (0.45 ± 0.17, p > 0.05), precision (0.51 ± 0.15, p > 0.05), and lowest LFPR (0.22 ± 0.18, p < 0.05) for Dataset I, whereas for dataset II, while it still showed the highest precision (0.82 ± 0.08, p > 0.05) and the lowest LFPR (0.11 ± 0.11, p < 0.05), it was marginally outperformed by LST-AI in terms of Dice (0.71 ± 0.13, p > 0.05).
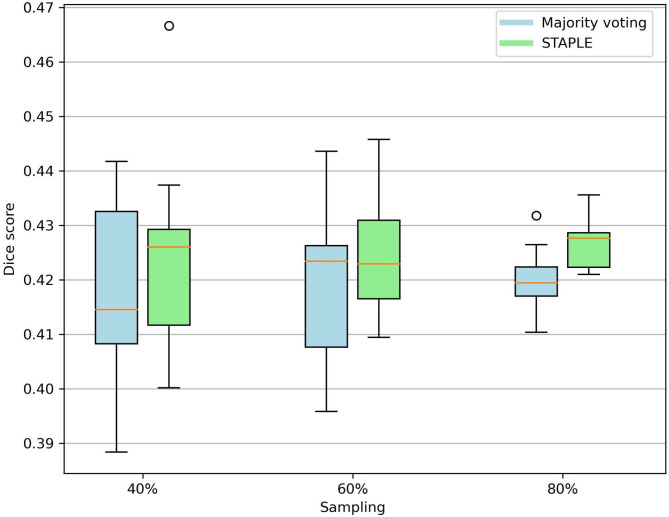
The results of the dataset size ablation study are shown in Fig. 3. No substantial differences in performance in terms of Dice score was observed between different sampling levels of the entire Dataset I. Results of the models-removing ablation study are summarized in Supplementary Table 2. When considering a maximum of three models (i.e., with two as threshold for the majority voting), the Dice scores ranged between 0.37 and 0.42, while precision (range between 0.38 and 0.57) and recall (range between 0.33 and 0.53) had greater variability.
Fig. 3.
Box plot for dataset size ablation study: evaluation of dataset size importance for model performance in terms of Dice score across different sampling levels.
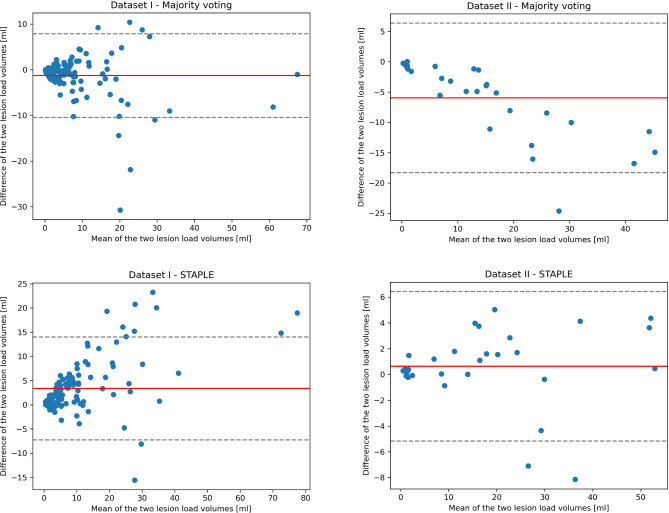
Figure 4 shows the Bland-Altman plots considering the volumetric differences between manual and automated segmentations. No particular bias was observed for both methods and datasets.
Fig. 4.
Bland-Altman plots of the manually and automatically segmented lesion volumes: The solid red line shows the mean difference, while the dotted gray lines the ± 1.96 SD limits of the mean difference.
Discussion
In this paper we have evaluated a consensus-based approach for the segmentation of focal lesions in MS from multi-contrast brain MRI scans. The primary objective of our study was to propose a general framework that could be useful to overcome some of the individual limitations and shortcomings of the state-of-the-art algorithms currently available. To validate the effectiveness of two consensus methods (i.e., majority voting and STAPLE) we conducted experiments using five different segmentation algorithms on two independent datasets that included ground truth lesion masks without further training. By leveraging these datasets, we were able to comprehensively evaluate and compare the performance of the consensus approaches against the existing methods. The results of our study demonstrated that the consensus with majority voting approach consistently outperformed the individual algorithms in terms of Dice coefficient and precision. The higher Dice coefficients (0.42 ± 0.17 and 0.60 ± 0.18 for dataset I and II, respectively) indicate a better overlap between the segmented lesions and the ground truth masks, suggesting improved accuracy of this approach compared to the other methods. Moreover, the higher precision (0.51 ± 0.16 and 0.80 ± 0.18 for dataset I and II, respectively) reflects a smaller ratio of false positives to true positives, further confirming the enhanced accuracy achieved by the consensus approach. Although the majority voting method exhibited lower recall and LTPR compared to some of the other methods (including STAPLE), i.e., generated a higher number of false negatives, it still demonstrated the ability to accurately detect a significant number of lesions, as indicated by the high precision and the significantly reduced LFPR. This suggests that this approach is effective in capturing a substantial portion of the overall lesion volume, despite the number of missed individual lesions. Overall, the majority voting method significantly improved some metrics (i.e., Dice score and LFPR), while having a more marginal effect on others (i.e., precision). Additionally, the majority voting method showed good agreement with lesions identified through manual segmentation, both in terms of volume (ρ = 0.92 and ρ = 0.97 for dataset I and II, respectively) and number of lesions (ρ = 0.83 and ρ = 0.94 for dataset I and II, respectively). This agreement indicates that estimated and ground truth masks share a good amount of their variability over the series of patient cases analyzed. Figure 2 clearly demonstrates a link between the total lesion load and the segmentation performance measured as Dice coefficient: the smaller the true total lesion load, the poorer the segmentation results. However, one important finding emerged from Table 4, which presents evaluation metrics for subjects categorized in tertiles, thus effectively distinguishing between patients with low lesion load and those with high lesion load. Majority voting demonstrates notable improvements in segmenting the subgroup of patients with low lesion load. Specifically, with the consensus method, Dice coefficient improved by 7% and 5% for the low lesion load tertile in dataset I and II, respectively, while for the high lesion load tertile the improvement was just 2% for dataset I and worsened by 2% for dataset II, compared to the individual top-performing algorithm. These results emphasize the efficacy of the method in accurately capturing and delineating lesions in cases where the lesion volume is relatively smaller. Similar results in terms of Dice scores were obtained with the STAPLE algorithm, although the trade-off between precision and recall is slightly in favor of the latter.
Ablations studies demonstrated that both majority voting and STAPLE approaches exhibited a good level of robustness across different dataset sizes. To further evaluate the majority voting method, we also iteratively removed two models and considered combinations of the remaining three algorithms. Results indicated that while performances in Dice scores remained relatively stable, precision and recall showed greater variability across different combinations in a complementary way, reflecting the expected performance trade-off.
Albeit the results presented may not yet be acceptable for clinical practice and still require manual correction by medical experts, we emphasize that these outcomes represent so far the best achievable results using pre-trained, publicly available algorithms on a generic (previously unseen) dataset. Undoubtedly, training a new model on an in-house dataset and testing it on a similar dataset (i.e. acquired on the same scanner with same acquisition parameters) would yield significantly improved results, potentially approaching human-level performance. Similarly, we may expect that fine-tuning the individual models on a subset of the data could potentially improve the performance of the consensus approach. However, this is beyond the scope of the work, which focuses exclusively on the use of pre-trained models without additional training. Moreover, it is crucial to acknowledge that developing, training, validating, and testing a new model can be unfeasible in many clinical settings, where lack of data remains a major challenge. Instead, open-source lesion segmentation algorithms offer a valuable and continuously expanding resource and our study demonstrates that by properly combining the results, the ultimate performances can be significantly improved even when local training is not feasible.
Notably, the individual performances of different models can vary significantly. Indeed, in our study we observed that one of the evaluated methods exhibited unsatisfactory performances in detecting MS lesions in both datasets. To test whether poorly performing algorithms negatively impact the overall performance of the consensus framework, we conducted a supplementary analysis with the inclusion of a more recently proposed model based on the more advanced nnU-Net architecture. Indeed, the U-Net model considered in this study is quite basic and this is reflected in its performance as the worst performing single algorithm on both datasets, whereas more recently, more advanced medical image segmentation models based on the nnU-Net framework44 have been proposed for various tasks, including MS lesion segmentation, with pre-trained models available online (see, e.g., https://zenodo.org/records/7626121, which was however trained with only FLAIR images and therefore not considered in this study for consistency with the inputs of the other models). Therefore, we additionally considered LST-AI, an algorithm consisting itself in an ensemble of three 3D U-Nets, each inspired by the nnU-Net framework32, as a viable alternative for our consensus as this algorithm (similarly to all other included algorithms) takes in input both T1w and FLAIR images. We therefore incorporated this tool in our consensus-based approach, in the place of the basic U-Net and results showed that the improvement given by a better model remains consistent with the majority voting approach, at least for Dataset I. Notably, the individual performance of the LST-AI model on Dataset II (which significantly outperformed all other individual algorithms) made any attempt of consensus between the segmented masks less effective. This suggests that, for a consensus-based approach to be successful, the individual methods should have comparable performance levels. One alternative approach for combining outputs from multiple segmentation algorithms is to assign different weights to each model. However, this would require evaluating each algorithm on a separate validation dataset, thereby introducing an additional source of variability or bias. To avoid this issue and to provide a straightforward proof of concept, we here adopted an agnostic approach, choosing to treat all models as equals, i.e., assuming that each model could contribute equally to the final consensus mask. Also, it is reasonable to hypothesize that including more algorithms would most likely enhance the robustness and accuracy of the framework, as it would contribute to the system’s ability to handle variations in lesion characteristics and detection techniques. In fact, by deploying a higher number of models, the framework has the possibility to include methods able to detect lesions that may have been missed by other methods, thereby improving the overall performance.
It is essential to acknowledge that not all the algorithms employed in this study were entirely blind to the datasets. Specifically, we estimated the optimal threshold for the LST algorithm as recommended in the original paper13. While the threshold value that maximized the Dice score was consistent across both datasets (i.e., 0.05), it may not necessarily be true for other datasets. However, we can hypothesize that opting for the lowest threshold (i.e., adopting a more conservative approach) could be a reasonable choice for the consensus implementation, irrespective of the dataset. This is because the algorithm might be able to detect more (small) lesions, while the increased number of false positive would be (at least partially) masked out in the final output.
MS lesions can exhibit significant variability in terms of size, shape and location19; this variability poses a serious challenge for the clinical application of automated tools designed for MS lesion segmentation, as existing methods often struggle to accurately capture the full extent of lesion burden due to the diverse manifestations of these lesions. The variability in size, shape and location of MS lesions calls for the development of segmentation methods that can adapt to these variations. In this context, one notable example is the SAMSEG algorithm developed by Cerri et al.9, which incorporates the capability to model the shape of lesions and their spatial distribution, making it one of the few approaches that explicitly addresses both these factors. Thus, it may not be surprising that lesion masks obtained from SAMSEG had the better concordance with the true lesion load and number among the individual algorithms.
Importantly, the performances of each method critically depend on the available ground truth masks. A limitation of the present study is that lesions on dataset I were annotated by only one neuroradiologist. Therefore, stronger conclusions might have been drawn from this study if multi-rater segmentations masks (e.g. from at least three raters) had been available for the private dataset. Furthermore, running 5 different algorithms, each with different requisites and software packages, might seem impractical and resource intensive; however, a possible solution to address this challenge would be to develop and distribute an online platform pre-equipped with the necessary packages required to run (possibly in parallel) the segmentation pipeline. Anyway, the detailed analytic assessment of the framework, as presented here, is a mandatory step before engaging into this kind of software design.
Automated consensus methods aim to tackle differently automated MS lesion segmentation by leveraging supervised and unsupervised methods, conventional threshold-based models and advanced neural network architectures, already validated and widely used. Overall, the results obtained from the study clearly illustrate the effectiveness of integrating lesion maps generated by multiple algorithms, leading to improved accuracy when compared to individual algorithms. It is important to highlight that the performance of the single algorithms varies across different datasets, as revealed by our results (e.g., in terms of Dice coefficient, SAMSEG was the top-performing method for dataset I, whereas LST returned the highest score for dataset II). Regarding this aspect, it is worth noting that employing a majority voting approach yielded more consistent and reproducible performances across different datasets. However, it is crucial to acknowledge that there are certain trade-offs associated with these consensus approaches. One notable drawback is the possibility of smaller lesions being undetected in the final consensus mask. Since these lesions might only be detected by one or two algorithms, they may not meet the consensus criteria (majority voting) and consequently be excluded from the final result, hence the lower recall emerged from our results. On the other hand, the STAPLE algorithm showed increased recall (yet lower precision) with similar Dice improvement, meaning that it includes more of the entire lesions albeit it also increases the risk of false positives. Nevertheless, the primary advantage of employing a consensus approach lies in the ability to leverage the strengths of various algorithms. Each algorithm possesses its own strengths and weaknesses, and by combining their outputs, the limitations of one algorithm can be compensated by the strengths of others. Consequently, this amalgamation of information increases the overall accuracy and performance of the system. Notably, from the work of Commowick et al. already emerged evidence that combining the results of the teams participating in the 2016 MICCAI challenge can lead to significantly better performances of each individual algorithm6. Our primary goal is to offer a more scalable and robust approach that addresses the pressing need to reduce manual labor in this complex task. Moreover, with the increasing number of (multi-center) MS studies with large sample size45–54, automating in an effective way the lesion segmentation task has become a crucial objective to standardize the preprocessing pipelines even in other applications (see, e.g., De Rosa et al.49). Our proposal aligns with this objective by providing a reliable and accurate solution that can be readily applied across diverse datasets and clinical settings. By improving the performance of other evaluated methods, the consensus-based approach significantly improves the detection accuracy of MS lesions. This, in turn, provides a more precise and refined framework for lesion segmentation, effectively minimizing inter- and intra-rater variability commonly associated with manual segmentation processes7. In conclusion, by avoiding the reliance on a single algorithm and incorporating a consensus approach, the majority voting method also aims at providing a more comprehensive and unbiased segmentation solution for MS lesion detection. This approach has the potential to enhance the practical utility of automated tools for MS lesion segmentation, enabling more accurate and reliable assessments of lesion burden in a variety of research and clinical settings.
Supplementary Information
Author contributions
A.P.D., R.T. and F.E. designed the methodology. A.P.D. and M.B. performed the image data analysis. F.B., F.E. and S.T. provided theoretical and computational resources. A.D., A.B. and A.G. provided the relevant information on patients, M.C. and F.E. retrieved the image data sets. A.P.D. and F.E. drafted the main manuscript text. All authors reviewed the manuscript.
Funding
Work supported by #NEXTGENERATIONEU (NGEU) and funded by the Ministry of University and Research (MUR), National Recovery and Resilience Plan (NRRP), project MNESYS (PE0000006) – A Multiscale integrated approach to the study of the nervous system in health and disease (DN. 1553 11.10.2022).
Data availability
Dataset I analyzed during the current study is not publicly available due to privacy issues but anonymized images from this dataset would be available from the corresponding author on reasonable request; Images from Dataset II analyzed during the current study was retrieved from a public repository (https://github.com/muschellij2/open_ms_data).
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Filippi, M. et al. Multiple sclerosis. Nat. Rev. Dis. Primers4, (2018). [DOI] [PubMed]
- 2.Lassmann, H. Multiple sclerosis pathology. Cold Spring Harb Perspect. Med.8, a028936 (2018). 10.1101/cshperspect.a028936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.McGinley, M. P., Goldschmidt, C. H. & Rae-Grant, A. D. Diagnosis and treatment of multiple sclerosis: A review. JAMA. 325, 765–779 (2021). 10.1001/jama.2020.26858 [DOI] [PubMed] [Google Scholar]
- 4.Rovira, À. et al. MAGNIMS consensus guidelines on the use of MRI in multiple sclerosis—clinical implementation in the diagnostic process. Nat. Rev. Neurol.11, 471–482 (2015). 10.1038/nrneurol.2015.106 [DOI] [PubMed] [Google Scholar]
- 5.Filippi, M. et al. Quantitative assessment of MRI lesion load in monitoring the evolution of multiple sclerosis. Brain. 118, 1601–1612 (1995). 10.1093/brain/118.6.1601 [DOI] [PubMed] [Google Scholar]
- 6.Commowick, O. et al. Objective evaluation of multiple sclerosis lesion segmentation using a data management and processing infrastructure. Sci. Rep.8, 13650 (2018). 10.1038/s41598-018-31911-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.García-Lorenzo, D., Francis, S., Narayanan, S., Arnold, D. L. & Collins, D. L. Review of automatic segmentation methods of multiple sclerosis white matter lesions on conventional magnetic resonance imaging. Med. Image. Anal.17, 1–18 (2013). 10.1016/j.media.2012.09.004 [DOI] [PubMed] [Google Scholar]
- 8.Aslani, S. et al. Multi-branch convolutional neural network for multiple sclerosis lesion segmentation. NeuroImage. 196, 1–15 (2019). 10.1016/j.neuroimage.2019.03.068 [DOI] [PubMed] [Google Scholar]
- 9.Cerri, S. et al. A contrast-adaptive method for simultaneous whole-brain and lesion segmentation in multiple sclerosis. NeuroImage. 225, 117471 (2021). 10.1016/j.neuroimage.2020.117471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Krishnan, A. P. et al. Multi-arm U-Net with dense input and skip connectivity for T2 lesion segmentation in clinical trials of multiple sclerosis. Sci. Rep.13, 4102 (2023). 10.1038/s41598-023-31207-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Krishnan, A. P. et al. Joint MRI T1 unenhancing and contrast-enhancing multiple sclerosis lesion segmentation with deep learning in OPERA trials. Radiology. 302, 662–673 (2022). 10.1148/radiol.211528 [DOI] [PubMed] [Google Scholar]
- 12.La Rosa, F. et al. Multiple sclerosis cortical and WM lesion segmentation at 3T MRI: A deep learning method based on FLAIR and MP2RAGE. NeuroImage Clin.27, 102335 (2020). 10.1016/j.nicl.2020.102335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schmidt, P. et al. An automated tool for detection of FLAIR-hyperintense white-matter lesions in multiple sclerosis. NeuroImage. 59, 3774–3783 (2012). 10.1016/j.neuroimage.2011.11.032 [DOI] [PubMed] [Google Scholar]
- 14.Shiee, N. et al. A topology-preserving approach to the segmentation of brain images with multiple sclerosis lesions. NeuroImage. 49, 1524–1535 (2010). 10.1016/j.neuroimage.2009.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Valverde, S. et al. improving automated multiple sclerosis lesion segmentation with a cascaded 3D convolutional neural network approach. NeuroImage. 155, 159–168 (2017). 10.1016/j.neuroimage.2017.04.034 [DOI] [PubMed] [Google Scholar]
- 16.Wu, Y. et al. Automated segmentation of multiple sclerosis lesion subtypes with multichannel MRI. NeuroImage. 32, 1205–1215 (2006). 10.1016/j.neuroimage.2006.04.211 [DOI] [PubMed] [Google Scholar]
- 17.Zhang, H. et al. ALL-Net: Anatomical information lesion-wise loss function integrated into neural network for multiple sclerosis lesion segmentation. NeuroImage Clin.32, 102854 (2021). 10.1016/j.nicl.2021.102854 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bonacchi, R., Filippi, M. & Rocca, M. A. Role of artificial intelligence in MS clinical practice. NeuroImage: Clin.35, 103065 (2022). 10.1016/j.nicl.2022.103065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nair, T., Precup, D., Arnold, D. L. & Arbel, T. Exploring uncertainty measures in deep networks for multiple sclerosis lesion detection and segmentation. Med. Image. Anal.59, 101557 (2020). 10.1016/j.media.2019.101557 [DOI] [PubMed] [Google Scholar]
- 20.Egger, C. et al. MRI FLAIR lesion segmentation in multiple sclerosis: Does automated segmentation hold up with manual annotation? NeuroImage Clin.13, 264–270 (2017). 10.1016/j.nicl.2016.11.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Artaechevarria, X., Munoz-Barrutia, A. & Ortiz-de-Solorzano, C. Combination strategies in multi-atlas image segmentation: Application to brain MR data. IEEE Trans. Med. Imaging. 28, 1266–1277 (2009). 10.1109/TMI.2009.2014372 [DOI] [PubMed] [Google Scholar]
- 22.Hsu, K. et al. Improving performance of deep learning models using 3.5D U-Net via majority voting for tooth segmentation on cone beam computed tomography. Sci. Rep.12, 19809 (2022). 10.1038/s41598-022-23901-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhao, J. et al. Automatic macaque brain segmentation based on 7T MRI. Magn. Reson. Imaging. 92, 232–242 (2022). 10.1016/j.mri.2022.07.001 [DOI] [PubMed] [Google Scholar]
- 24.Rakić, M. et al. Icobrain ms 5.1: Combining unsupervised and supervised approaches for improving the detection of multiple sclerosis lesions. NeuroImage: Clin.31, 102707 (2021). 10.1016/j.nicl.2021.102707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Carass, A. et al. Evaluating white matter lesion segmentations with refined Sørensen-Dice analysis. Sci. Rep.10, 8242 (2020). 10.1038/s41598-020-64803-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Paullada, A., Raji, I. D., Bender, E. M., Denton, E. & Hanna, A. Data and its (dis)contents: A survey of dataset development and use in machine learning research. Patterns. 2, 100336 (2021). 10.1016/j.patter.2021.100336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jenkinson, M., Bannister, P., Brady, M. & Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 17, 825–841 (2002). 10.1006/nimg.2002.1132 [DOI] [PubMed] [Google Scholar]
- 28.Jenkinson, M. & Smith, S. A global optimisation method for robust affine registration of brain images. Med. Image. Anal.5, 143–156 (2001). 10.1016/S1361-8415(01)00036-6 [DOI] [PubMed] [Google Scholar]
- 29.Lesjak, Ž. et al. A novel public MR image dataset of multiple sclerosis patients with lesion segmentations based on multi-rater consensus. Neuroinformatics. 16, 51–63 (2018). 10.1007/s12021-017-9348-7 [DOI] [PubMed] [Google Scholar]
- 30.Puonti, O., Iglesias, J. E. & Van Leemput, K. Fast and sequence-adaptive whole-brain segmentation using parametric Bayesian modeling. NeuroImage. 143, 235–249 (2016). 10.1016/j.neuroimage.2016.09.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Valverde, S. et al. One-shot domain adaptation in multiple sclerosis lesion segmentation using convolutional neural networks. NeuroImage Clin.21, 101638 (2019). 10.1016/j.nicl.2018.101638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wiltgen, T. et al. LST-AI: A deep learning ensemble for accurate MS lesion segmentation. NeuroImage Clin.42, 103611 (2024). 10.1016/j.nicl.2024.103611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sundaresan, V., Zamboni, G., Rothwell, P. M., Jenkinson, M. & Griffanti, L. Triplanar Ensemble U-Net model for white matter hyperintensities segmentation on MR images. Med. Image. Anal.73, 102184 (2021). 10.1016/j.media.2021.102184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Warfield, S. K., Zou, K. H. & Wells, W. M. Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation. IEEE Trans. Med. Imaging. 23, 903–921 (2004). 10.1109/TMI.2004.828354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fartaria, M. J., Kober, T., Granziera, C. & Bach Cuadra, M. Longitudinal analysis of white matter and cortical lesions in multiple sclerosis. NeuroImage: Clin.23, 101938 (2019). 10.1016/j.nicl.2019.101938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Guizard, N. et al. Rotation-invariant multi-contrast non-local means for MS lesion segmentation. NeuroImage Clin.8, 376–389 (2015). 10.1016/j.nicl.2015.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jain, S. et al. Two time point MS lesion segmentation in brain MRI: An expectation-maximization framework. Front. Neurosc.10, (2016). [DOI] [PMC free article] [PubMed]
- 38.Calabrese, M. et al. Cortical lesion load associates with progression of disability in multiple sclerosis. Brain. 135, 2952–2961 (2012). 10.1093/brain/aws246 [DOI] [PubMed] [Google Scholar]
- 39.Filippi, M. et al. Quantitative brain MRI lesion load predicts the course of clinically isolated syndromes suggestive of multiple sclerosis. Neurology. 44, 635–635 (1994). 10.1212/WNL.44.4.635 [DOI] [PubMed] [Google Scholar]
- 40.Bozsik, B. et al. Reproducibility of lesion count in various subregions on MRI scans in multiple sclerosis. Frontiers Neurology13, (2022). [DOI] [PMC free article] [PubMed]
- 41.Polman, C. H. et al. Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria. Ann. Neurol.69, 292–302 (2011). 10.1002/ana.22366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Carass, A. et al. Longitudinal multiple sclerosis lesion segmentation: Resource and challenge. NeuroImage. 148, 77–102 (2017). 10.1016/j.neuroimage.2016.12.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Krüger, J. et al. Infratentorial lesions in multiple sclerosis patients: Intra- and inter-rater variability in comparison to a fully automated segmentation using 3D convolutional neural networks. Eur. Radiol.32, 2798–2809 (2022). 10.1007/s00330-021-08329-3 [DOI] [PubMed] [Google Scholar]
- 44.Isensee, F., Jaeger, P. F., Kohl, S. A. A., Petersen, J. & Maier-Hein, K. H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods. 18, 203–211 (2021). 10.1038/s41592-020-01008-z [DOI] [PubMed] [Google Scholar]
- 45.Burggraaff, J. et al. Manual and automated tissue segmentation confirm the impact of thalamus atrophy on cognition in multiple sclerosis: A multicenter study. NeuroImage Clin.29, 102549 (2021). 10.1016/j.nicl.2020.102549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cagol, A. et al. Association of brain atrophy with disease progression independent of relapse activity in patients with relapsing multiple sclerosis. JAMA Neurol.79, 682–692 (2022). 10.1001/jamaneurol.2022.1025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Carotenuto, A. et al. Investigating functional network abnormalities and associations with disability in multiple sclerosis. Neurology. 99, e2517–e2530 (2022). 10.1212/WNL.0000000000201264 [DOI] [PubMed] [Google Scholar]
- 48.Cortese, R. et al. Clinical and MRI measures to identify non-acute MOG-antibody disease in adults. Brain. awac480 10.1093/brain/awac480 (2022). [DOI] [PubMed]
- 49.De Rosa, A. P. et al. Resting-state functional MRI in multicenter studies on multiple sclerosis: A report on raw data quality and functional connectivity features from the Italian neuroimaging network initiative. J. Neurol.270, 1047–1066 (2023). 10.1007/s00415-022-11479-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Moccia, M. et al. Longitudinal spinal cord atrophy in multiple sclerosis using the generalized boundary shift integral. Ann. Neurol.86, 704–713 (2019). 10.1002/ana.25571 [DOI] [PubMed] [Google Scholar]
- 51.Rocca, M. A. et al. Association of gray matter atrophy patterns with clinical phenotype and progression in multiple sclerosis. Neurology. 96, e1561–e1573 (2021). 10.1212/WNL.0000000000011494 [DOI] [PubMed] [Google Scholar]
- 52.Rocca, M. A. et al. Clinically relevant cranio-caudal patterns of cervical cord atrophy evolution in MS. Neurology. 93, e1852–e1866 (2019). 10.1212/WNL.0000000000008466 [DOI] [PubMed] [Google Scholar]
- 53.Sinnecker, T. et al. Evaluation of the central vein sign as a diagnostic imaging biomarker in multiple sclerosis. JAMA Neurol.76, 1446–1456 (2019). 10.1001/jamaneurol.2019.2478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Vrenken, H. et al. Opportunities for understanding MS mechanisms and progression with MRI using large-scale data sharing and artificial intelligence. Neurology. 97, 989–999 (2021). 10.1212/WNL.0000000000012884 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Dataset I analyzed during the current study is not publicly available due to privacy issues but anonymized images from this dataset would be available from the corresponding author on reasonable request; Images from Dataset II analyzed during the current study was retrieved from a public repository (https://github.com/muschellij2/open_ms_data).