Landau-phonon polaritons in Dirac heterostructures

Abstract

Polaritons are light-matter quasiparticles that govern the optical response of quantum materials at the nanoscale, enabling on-chip communication and local sensing. Here, we report Landau-phonon polaritons (LPPs) in magnetized charge-neutral graphene encapsulated in hexagonal boron nitride (hBN). These quasiparticles emerge from the interaction of Dirac magnetoexciton modes in graphene with the hyperbolic phonon polariton modes in hBN. Using infrared magneto-nanoscopy, we reveal the ability to completely halt the LPP propagation in real space at quantized magnetic fields, defying the conventional optical selection rules. The LPP-based nanoscopy also tells apart two fundamental many-body phenomena: the Fermi velocity renormalization and field-dependent magnetoexciton binding energies. Our results highlight the potential of magnetically tuned Dirac heterostructures for precise nanoscale control and sensing of light-matter interaction.

Magnetic control of phonon-polaritons is achieved via their strong coupling with Landau-level transitions.

INTRODUCTION

Polaritons are light-matter quasiparticles that play a fundamental role in the optical response of polarizable materials (1–18). Phonon polaritons were studied historically first (18), and they are examples of modes demonstrating strong light-matter coupling. In complex materials, polaritons can involve several distinct matter excitations, yielding a rich variety of collective phenomena (3, 19–21). If the optical properties of a material are tunable, polaritons inherit this tunability. For example, the dispersion of plasmon-polaritons in two-dimensional (2D) conductors can be controlled by changing their charge carrier concentration (13–15) or applying an electric current (16, 17). However, attaining strong mode coupling with conducting materials is difficult because of their high electronic losses. Graphene is one of the promising polaritonic platforms because of its low intrinsic electron scattering rate (22) and corresponding high quality factors (3, 8, 9).

Here, we report the discovery of the Landau-phonon polaritons (LPPs) in a 2D graphene-hexagonal boron nitride (hBN) heterostructure. The LPPs result from the hybridization (19–21) of phonon polaritons of the hBN encapsulating layers (8–10) with Dirac magnetoexcitons (6, 7) [or “Landau polaritons” (5)] of charge-neutral graphene (6, 7). LPPs belong under a broader umbrella of magneto-phonon resonance (MPR) effects, resulting from a near coincidence of the energy spacing between a pair of Landau levels (LLs) and the energy of an optical phonon. We comment on other MPR effects (23–28), such as magneto polarons (23–25), in the discussion. We also note that, in addition to graphene, Landau polaritons in semiconductor 2D electron gas systems have been demonstrated extensively at terahertz frequencies, which exhibit intriguing ultrastrong light-matter coupling phenomena in a solid-state cavity quantum electrodynamics system (29). Using the state-of-the-art magneto scanning near-field optical microscopy (m-SNOM) (6, 30–32), we have imaged real-space interference patterns created by the LPPs in a graphene-hBN heterostructure. We demonstrate that the LPP propagation can be switched on and off using magnetic fields. We have been able to detect as many as six different LPP branches. Several of them originate from optically dark transitions, suggesting that the usual selection rules (33–39) no longer apply in the extended momentum-frequency space accessible with the m-SNOM. Our high-precision mapping of the LPP dispersion has also enabled us to quantify many-body effects that yield the effective Fermi velocity in graphene (33–37, 40, 41).

Our experimental setup is depicted in Fig. 1A. The experiments involved focusing infrared radiation onto the tip of an atomic force microscope that acted as a scannable nanoscale antenna. Light scattered from the tip carried near-field information to a far-field detector. Another, stationary nanoantenna in the form of a metallic bar deposited on graphene played the dual role of an electrical contact and a polariton launcher. Both the sample and the m-SNOM resided in an optical cryostat allowing the control of temperature and magnetic field applied in the out-of-plane direction [see Materials and Methods and (6)]. We present and discuss the results of these measurements below after we have introduced the necessary theoretical background.

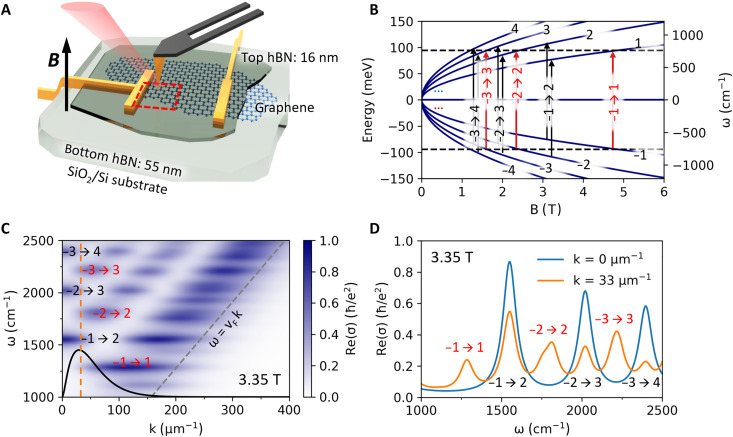
Fig. 1. High-momentum magneto-optics of graphene.

(A) Schematics of our sample and m-SNOM setup. Gold contacts enable transport measurements and gating of graphene and also serve as polariton launchers. (B) LL energy as a function of magnetic field B and LL index n = 0, ±1, …, ±4. Black (red) arrows mark −n → n ± 1 and −n → n inter-LL transitions (ILTs) for a photon energy of ℏω = 188 meV (1519 cm⁻¹). (C) Analytically calculated real part of the graphene conductivity (43) at B = 3.35 T as a function of frequency ω and in-plane momentum k calculated using Fermi velocity v_F = 1.19 × 10⁶ m/s and damping γ = 24.3 cm⁻¹. The relevant −n → n ± 1 (−n → n) ILTs are labeled in black (red). The black bell-shaped curve illustrates the momenta accessible via m-SNOM (14), which peak at around k = 1/r_tip = 33 μm⁻¹ as marked by the vertical dashed line. (D) The line cuts at momenta k = 0 and k = 33 μm⁻¹ extracted from (C).

RESULTS

High-momentum magneto-optics of graphene

In a transverse magnetic field, the density of states in graphene splits into LLs of energy $E_n=\text{sgn}\left(n\right)\sqrt{2\left|n\right|}\left(\hslash v_F/l_B\right)$, where n = 0, ±1, ±2, … is the LL index, v_F is the Fermi velocity, e is the elementary charge, $l_B=\sqrt{\hslash /e\mid B\mid }$ is the magnetic length, and B is the magnetic field (Fig. 1B). This characteristic square-root n- and B-dependence is a manifestation of the Dirac-like energy-momentum dispersion of graphene quasiparticles. In a charge-neutral graphene, the optical transitions can occur between LLs with indices of opposite sign, −n → n′, at frequencies $\mathrm{\omega }\propto \sqrt{\left|n\right|}+\sqrt{\mid n\prime \mid }$. The oscillator strength of each transition is a function of the in-plane momentum k. Conventional far-field infrared experiments excite graphene at very small k, with a nonnegligible oscillator strength only at |n| − $\mid n\prime \mid$ = ± 1. This selection rule at k → 0 is evident in the nonlocal optical conductivity σ(ω,k) of graphene shown in Fig. 1C (blue curve in Fig. 1D). Such peaks in the optical conductivity Re σ_xx have been observed in many magneto-optical absorption experiments (33, 35, 36, 38, 39, 42).

The theory also predicts that at finite momenta transitions between any pair of LLs become possible (43). Among these additional “forbidden” transitions, the first ones to become noticeable as k increases are the –n → n transitions; see Fig. 1C. Faint signatures of such forbidden modes have been seen in previous far-field experiments (33). They were attributed to mildly relaxed momentum conservation due to disorder scattering. As discussed below, our experiments have revealed much stronger evidence of the forbidden inter-LL transitions (ILTs), presumably because the requisite large in-plane momenta were created by scattering of light with the tip. The forbidden transitions become comparable in strength to the nearby allowed ones at momenta of the order of the inverse magnetic length, e.g., $l_B^{-1}=71 \mathrm{\mu }{\mathrm{m}}^{-1}$ at B = 3.35 T. The momentum range important in the m-SNOM is illustrated by the bell-shaped curve in Fig. 1C. For the estimated tip radius of r_tip = 30 nm, it is centered at k = 33 μm⁻¹ marked by the vertical dashed line (14). At such k, the forbidden transitions are only slightly weaker than the allowed ones; see the orange line in Fig. 1D. In addition, the allowed transitions at nonzero k are diminished with respect to the k = 0 case (the blue line in Fig. 1D) to fulfill the optical sum rule.

Modeling of polariton dispersion

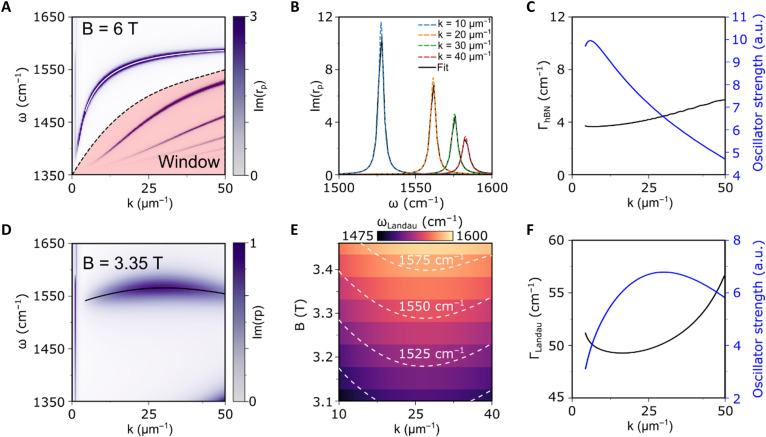
Each ILT gives rise to a collective excitation, which has been previously referred to as a Landau polariton (5) (the term we use here), Dirac magnetoexciton, or magnetoplasmon (6, 7). If the Landau polaritons are tuned in resonance with the hyperbolic phonon-polaritons in hBN by changing the applied magnetic field, the hybrid modes, which are the aforementioned LPPs, can form. We have carried out numerical simulations to model the LPP dispersion expected under our experimental conditions. As customary in near-field studies, we deduce the dispersion of the collective modes from the frequency- and momentum-dependent p-polarized reflection coefficient of the sample, r_p = r_p(k, ω). Figure 2 (A to C) demonstrates the imaginary part of r_P calculated for three representative values of the magnetic field. The multiple branches of phonon polaritons in the upper Reststrahlen band of hBN (~1360 to 1610 cm⁻¹) are evident in all three cases (8–10). Without the magnetic field (Fig. 2A), the charge-neutral graphene influences the response of the heterostructure only weakly via its “universal” optical conductivity σ = e²/4ℏ (33).

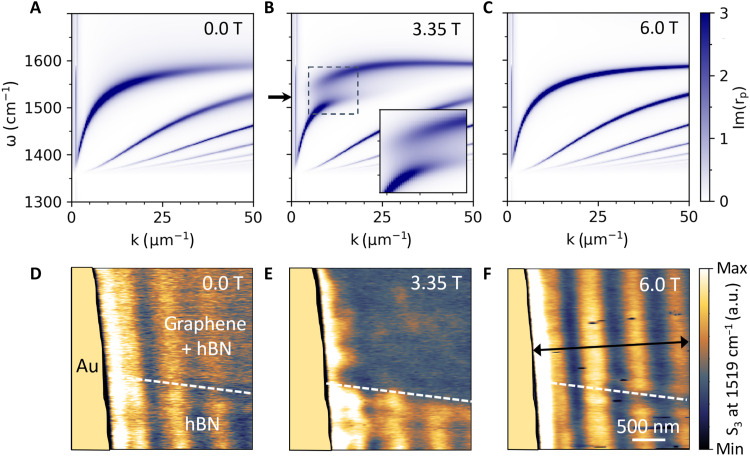
Fig. 2. Hybridization of hBN phonon polaritons with graphene Landau polaritons, resulting in LPPs.

(A to C) Calculated LPP dispersion at magnetic fields of 0.0, 3.35, and 6.0 T, respectively. The false color represents Im r_p(k, ω), the analytically calculated imaginary part of the reflection coefficient for p-polarized light. Graphene is assumed to be charge neutral with a constant LL broadening (33) γ = 24.3 cm⁻¹ and Fermi velocity v_F = 1.19 × 10⁶ m/s, the latter being the value extracted from Fig. 4C. Inset in (B): An enlarged view of the region exhibiting strong coupling and an avoided crossing between the Landau and the hBN phonon polaritons; the arrow marks ω = 1519 cm⁻¹ corresponding to the data in (D) to (F). (D to F) Nano-imaging data collected from the region marked by the red rectangle in Fig. 1A at T = 154 K and B = 0.0, 3.35, and 6.0 T, respectively. The near-field signal S₃ (demodulated at the third harmonic of the tip frequency; refer to Materials and Methods) shows relative differences between regions with and without graphene that strongly depend on the magnetic field. The enhanced signal-to-noise ratio in (E) and (F), compared to (D), is due to a slightly longer integration time. We also note that the mechanical stability of our system is slightly better at higher magnetic fields. The double-headed arrow in (F) marks the location of the line scan analyzed further in Fig. 3. a.u., arbitrary unit.

At 3.35 T (Fig. 2B), the frequency of the −1 → 2 ILT is inside the hBN upper Reststrahlen band, which generates avoided crossings in the polariton dispersion. These features manifest as a coupling and hybridization of the −1 → 2 inter-LL Landau polariton with the hBN phonon polaritons, i.e., the formation of the LPPs. Modeling the system as two coupled harmonic oscillators (44, 45) (see Materials and Methods), we extract the mode splitting Ω = 43.3 cm⁻¹ at the largest avoided crossing and mode linewidths of Γ_Landau = 50.6 cm⁻¹ and Γ_hBN = 4.0 cm⁻¹ for the uncoupled Landau polariton and hBN phonon polariton, respectively. Hence, the strong coupling criterion $C=\frac{2{\mathrm{\Omega }}^2}{{\mathrm{\Gamma }}_{\text{Landau}}^2+{\mathrm{\Gamma }}_{\text{hBN}}^2}=1.5>1.0$ is fulfilled at this magnetic field.

At 6.0 T (Fig. 2C), our calculations indicate no ILTs inside the Reststrahlen band, so the phonon-polariton dispersion is again largely unaffected by graphene. Notably, these calculations show that the polariton damping at 6.0 T should be lower than that at 0 T because the LL quantization makes graphene more optically transparent away from the discrete ILT frequencies (33).

Nano-imaging of LPP

We now turn to our experimental nano-imaging results that reveal field-tunable features of LPPs in real space. Figure 2 (D to F) shows m-SNOM images acquired at a temperature of 154 K and magnetic fields of B = 0.0, 3.35, and 6.0 T, matching Fig. 2 (A to C, respectively). The incident photon energy is 188 meV (wavenumber, ω = 1519 cm⁻¹). Note that our scan area contained three different regions: 1) a gold electrode on the left, which served as a polariton launcher; 2) hBN-encapsulated graphene on the top right, showing propagating LPP polaritons; 3) hBN without graphene in the bottom right, showing phonon-polariton modes only. At 0.0 T (Fig. 2D) and 6.0 T (Fig. 2F), we observed polariton fringes parallel to the gold electrode in both regions 2) and 3). At 0.0 T, the fringes in the region containing graphene exhibited a higher damping. At 6.0 T, the impact of graphene was minimal. These findings are consistent with our simulations (Fig. 2, A and C) and also previous work (33). On the other hand, at 3.35 T (Fig. 2E), there is a notable contrast between the regions with and without graphene. The polariton propagation in hBN-graphene ceases such that all but the first fringe is suppressed. This gives clear evidence for the existence of the hybridization gap in the LPP dispersion, i.e., the strong mode coupling, predicted by our theoretical calculations (Fig. 2B).

To study the magnetic-field dependence of the LPP dispersion in detail, we obtained a field-tip position map of the m-SNOM signal (Fig. 3A) by sweeping B from −6.0 to +6.0 T. The maps were acquired by performing repeated scans with the tip along lines perpendicular to the gold electrode, as marked by the black arrow in Fig. 2F. At our selected photon energy of 188 meV (ω = 1519 cm⁻¹) within the hBN Reststrahlen band, we observe the suppression of the fringes for certain distinct field values, e.g., for the discussed case of B = 3.35 T. When approaching such fields from a higher (lower) absolute magnetic field side, the polariton wavelength decreases (increases) along with an overall reduction in near-field signal and a decrease of the propagation length. Figure 3B shows line profiles that have been extracted at B=0.0, ±3.3, and ±5.8 T, respectively. While we observe oscillatory polariton fringes at 0.0 and ±5.8 T, at the −1 → 2 ILT at B = ±3.3 T, the fringes are strongly damped, consistent with the predicted observations in Fig. 2. These features are observed for both directions of the magnetic field, B > 0 and B < 0. We note that the ILTs can also be suppressed by doping graphene off charge neutrality [via the Pauli blocking (33, 35, 39)], which provides additional opportunities for controlling LPPs (see Materials and Methods).

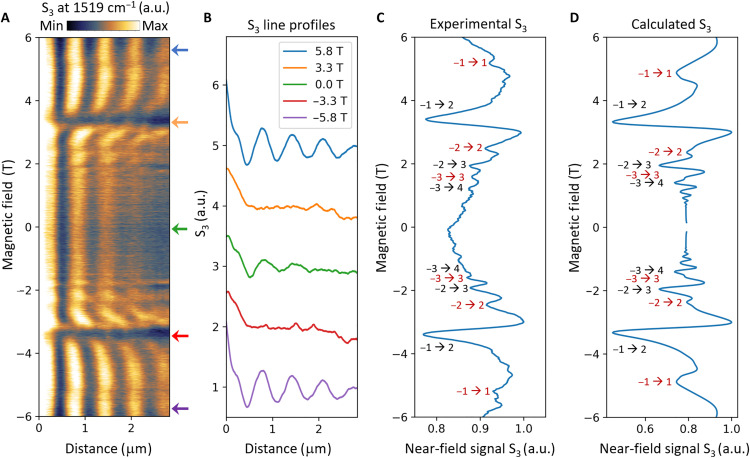
Fig. 3. Magnetic-field dependence of the polariton dispersion.

(A) Near-field signal S₃ acquired via a repeated line scan while sweeping the magnetic field from −6.0 to 6.0 T at a rate of 0.4 mT/s; measurement was taken at ω = 1519 cm⁻¹ and T = 154 K. The direction of this line scan was perpendicular to the gold contact to the left, which served as a polariton launcher; see Figs. 1A and 2F. (B) Line profiles extracted from (A) at magnetic fields B = 0.0, ±3.3, and ±5.8 T. (C) The near-field signal in (A) averaged over the distance. Minima of the averaged signal are assigned to the ILTs shown by the labels. The assignment is based on the calculation shown in (D). (D) Calculated near-field signal (Materials and Methods) as a function of magnetic field. Parameter values are chosen to be the same as in Figs. 1 (C and D) and 2 (A to C).

Averaging the data in Fig. 3A over the tip position removes the spatial oscillations, which allows us to focus on the B dependence of the signal (Fig. 3C). We can compare the trace in Fig. 3C with the theoretical simulations in Fig. 3D. For simplicity, in these simulations, we did not include a separate polariton launcher. Instead, we modeled a more common m-SNOM setup where the tip is the only nanoantenna interacting with the sample, which is uniform and infinite in size. It is fair to compare the predictions of this model with Fig. 3C since in both cases, the signal depends only on the magnetic field not the tip position. We see that Fig. 3 (C and D) are in good agreement. The dips in the theoretical curve come from distinct ILTs. Assuming that this is also the case in the data, we can label them accordingly. Furthermore, fitting the data to the theory allows us to determine the graphene Fermi velocity, which we discuss in detail below. Unassigned dips in the experimental spectrum are minor and might be attributed to the experimental conditions, such as mechanical vibrations.

We find that the dips corresponding to the −1 → 2 transitions are the strongest in our frequency window, testifying to a strong mode coupling regime (see also Materials and Methods). In addition, we observe clear signatures of several other transitions. They include allowed transitions −2 → 3 and −3 → 4, as well as transitions −1 → 1, −2 → 2, and −3 → 3 forbidden by the standard selection rules (33, 36, 38, 39). Any of these ILTs also induces a clear modification of the polariton wavelength as well as a reduction of the quality factor, which further supports our assignment and will be used for a quantitative analysis later. In total, we can resolve six different ILTs in our data. Notably, the forbidden transitions (26, 33, 46) show up much stronger compared to what was previously seen in far-field infrared spectroscopy (33). As hypothesized above, this massive breakdown of the selection rules originates from the greater role of high-momentum field components $\mathrm{k}\sim {\mathrm{l}}_{\mathrm{B}}^{-1}$ in our m-SNOM measurements (Fig. 1, C and D).

Tunability of LPPs

We have fitted the polaritonic fringes in Fig. 3 to exponentially decaying sine waves ∼e^ikx, where k = Re k + i Im k is the complex polariton momentum (Materials and Methods). From this fitting, we deduced the LPP wavelength λ_P = 2 π/ Re k (Fig. 4A) and the quality factor Q = Re k/ Im k (Fig. 4B). For example, at B = 0 T, we found λ_P = 647 nm and Q = 12. As B increases, the crossing of each ILT results in a deep minimum of the Q factor as well as a characteristic change in λ_p. Within the studied magnetic field range, we have observed a modulation depth of λ_max/λ_min ∼ 2 (Fig. 4A) and Q_max/Q_min ∼ 10 (Fig. 4B). The latter is much larger than the values Q_max/Q_min ∼ 2 reported for gate-tuning of doped graphene-hBN polaritons (19). In particular, near the −1 → 2 transition, altering the magnetic field by only 10% changes the Q factor by a factor of five. The great tunability of our system can be explained by the large optical conductivity associated with the LL transitions at infrared frequencies and the resultant externally controllable gap in the polariton dispersion (Fig. 2B). Therefore, the magnetic field provides a feasible path toward on/off switching of polariton propagation in 2D systems.

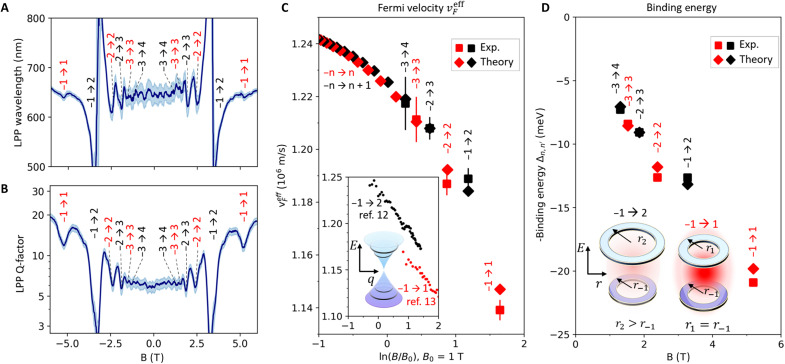
Fig. 4. Magnetic-field dependence of LPP properties and Fermi velocity renormalization.

(A) Polariton wavelength λ_P and (B) polariton quality factor Q = Re k/ Im k as a function of the magnetic field B. Solid lines show experimental values extracted from Fig. 2; shaded regions show the SD of the measurement. (C) Effective Fermi velocity ${\mathrm{v}}_{\mathrm{F}}^{\text{eff}}$ as a function of the logarithmic magnetic field ln(B) derived for different ILTs (see section Many-body effects): Squares show experimental values derived from (B). Diamonds represent calculated values of ${\mathrm{v}}_{\mathrm{F}}^{\text{eff}}$ (see Materials and Methods) (37). We observe a nonlogarithmic trend. Inset: The red (black) points show ${\mathrm{v}}_{\mathrm{F}}^{\text{eff}}$ for the −1 → 1 (−1 → 2) ILT measured via Raman spectroscopy (34) [far-field infrared spectroscopy (33)]. The tapering shape of the Dirac cone illustrates the Fermi velocity renormalization (33, 34, 40), resulting in a logarithmic B dependence of the far-field data (33, 34). (D) Squares and diamonds show the exciton binding energy ${\mathrm{\Delta }}_{\mathrm{n}\mathrm{n}\prime }$ of the Landau polaritons derived from the experiment and theory, respectively. The exciton binding energy is larger for the ILTs with $n\prime$ = −n compared to those with $n\prime$ = −(n ± 1) and generally increases with magnetic field. Inset: The dependence of the exciton binding energy on the magnetic field and type of the ILT can be explained within a semiclassical model where quantized electronic orbitals of the LLs are shaped as narrow rings of radius ${\mathrm{r}}_{\mathrm{j}}={\mathrm{l}}_{\mathrm{B}}\sqrt{2\left|j\right|}$, j = n, or $n\prime$. The magnetoexciton binding energy ${\mathrm{\Delta }}_{\mathrm{n}\mathrm{n}\prime }$ (see text) is given by the Coulomb attraction energy of these rings. For a fixed n, this binding energy is the largest when the ring radii are equal, at $n\prime$ = −n.

Many-body effects

Last, we discuss many-body effects manifested in deviations of the ILT frequencies from the $\sqrt{B}$ - law valid for free Dirac fermions. An alternative description of these deviations is the renormalization of the effective Fermi velocity $v_F^{\text{eff}}$ defined by Eq. 1 below. From the minima in the Q factor, we can read off the magnetic fields B associated with each ILT and obtain the corresponding field-dependent $v_F^{\text{eff}}$. We find that $v_F^{\text{eff}}$ decreases with B for all transition types following a non-logarithmic B dependence (squares in Fig. 4C). These values agree unexpectedly well with previous far-field infrared (33) and Raman (34) spectroscopy results. We extract $v_F^{\text{eff}}$ associated with both allowed and forbidden ILTs with the same measurement. In this regard, the m-SNOM provides a unified approach for LL spectroscopy that lifts many previous limitations.

Our theoretical calculations (Materials and Methods) of the effective Fermi velocity (diamonds in Fig. 4C) show a good agreement with the data using one adjustable parameter, the value of $v_F^{\text{eff}}$ at one specific ILT (here, −2 → 3 gives the best agreement). These calculations also corroborate our experimental observation that the effective Fermi velocity of the −n → n ILTs is consistently below the trend followed by the −n → n ± 1 ones.

Our explanation for the above observation of $v_F^{\text{eff}}$ is as follows: Despite its common usage, the term “effective” Fermi velocity is somewhat misleading in the present context. A more accurate statement is that the interaction corrections to the observed ILT energy ℏω, resulting in $v_F^{\text{eff}}$, include contributions from both the Fermi velocity renormalization (a polaronic effect) and excitonic effects. Namely, ℏω is given by the LL energy difference, |E_n| + $\mid E_{n\prime }\mid$, minus the magnetoexciton binding energy ${\mathrm{\Delta }}_{nn\prime }$

$$\mathrm{\hslash }\mathrm{\omega }\equiv \frac{\mathrm{\hslash }{v}_F^{\text{eff}}}{l_B}\left(\sqrt{2\left|n\right|}+\sqrt{2\left|n\prime \right|}\right)=\left(\left|E_n\right|+\left|E_{n\prime }\right|\right)-{\mathrm{\Delta }}_{\mathit{nn}\prime }$$ (1)

The LLs E_n in this expression obey the quantization rule |E_n| = E(q_n) where $E=\hslash v_F^{\text{ren}}q$ is the renormalized quasiparticle dispersion and $q_n=l_B^{-1}\sqrt{2\left|n\right|}$ is the quantized momentum of a Dirac fermion residing at the nth LL (inset Fig. 4C). The effective Fermi velocity $v_F^{\text{eff}}$ is (approximately) equal to the renormalized $v_F^{\text{ren}}$ only if the magnetoexciton binding energy ${\mathrm{\Delta }}_{nn\prime }$ is neglected. In that case, a logarithmic dependence of $v_F^{\text{eff}}$ on E (at fixed n and $n\prime$) follows from the perturbation theory formula $v_F\left(E\right)\approx v_F\left(\mathrm{\Lambda }\right)\left[1+\frac{1}{4}\mathrm{\alpha ln}\left|\mathrm{\Lambda }/E\right|+\dots \right]$ where α = e²/(κℏv_F) ≪ 1 is the Coulomb coupling constant, Λ is the high-energy cutoff, and κ is the effective dielectric constant of the graphene environment (36). This formula has been derived for graphene in zero magnetic field; however, it remains approximately correct at nonzero B (Materials and Methods), meaning that the renormalized Fermi velocity is first and foremost a function of energy, $v_F^{\text{ren}}=v_F^{\text{ren}}\left(E\right)$. Since E_n and $E_{n\prime }$ are B dependent (33, 34), $v_F^{\text{ren}}$ usually acquires a logarithmic B dependence for a given ILT, as found in previous far-field spectroscopy studies (inset in Fig. 4C) (31, 32, 34, 35, 38). On the other hand, here, we have studied ILTs at a fixed laser frequency so that the transition energy ℏω ≈ |E_n| + $\mid E_{n\prime }\mid$ remained the same, being split roughly equally between |E_n| and $\mid E_{n\prime }\mid$. Therefore, in our experiments, the renormalized Fermi velocity $v_F^{\text{ren}}\approx v_F^{\text{ren}}\left(\hslash \mathrm{\omega }/2\right)$ should have little B-field dependence and the observed variation of $v_F^{\text{eff}}$ (Fig. 4C) should mostly come from the change of magnetoexciton binding energy ${\mathrm{\Delta }}_{nn\prime }$, which follows nonlogarithmic trend with changing magnetic field. The data analysis in some of the previous works was oversimplified by emphasizing the logarithmic trend and not considering the additional field-dependent contribution due to the magnetoexciton binding energy.

Our theoretical calculation of the two competing terms, |E_n| + $\mid E_{n\prime }\mid$ and ${\mathrm{\Delta }}_{nn\prime }$, in Eq. 1 confirms that at fixed ℏω, the former gives a nearly constant contribution to $v_F^{\text{eff}}$ for all measured ILTs so that $v_F^{\text{eff}}$ variation comes from the latter, with characteristic dips occurring at $n\prime$ = − n points (Materials and Methods). This allows us to extract the binding energy ${\mathrm{\Delta }}_{nn\prime }$ (Fig. 4D) from $v_F^{\text{eff}}$. The absolute value of ${\mathrm{\Delta }}_{nn\prime }$ generally increases with magnetic field and is larger for the ILTs with $n\prime$ = − n compared to those with $n\prime$ = − (n ± 1). A simple way to think about the magnetoexciton binding energy ${\mathrm{\Delta }}_{nn\prime }$ is to imagine that it is equal to the Coulomb attraction energy of two LL orbitals shaped as concentric rings, one with charge +e, the other with charge −e (inset Fig. 4D). The ring radii are given by the formula $r_j=\mid E_j/e{v}_F^{\text{ren}}B\mid$, where j = n or $n\prime$, which is the semiclassical cyclotron radius of a Dirac particle with energy E_j. (Note additional relations $r_j=l_B\sqrt{2\left|j\right|}=l_B^2{q}_j$.) For a fixed n, this attraction energy is the largest when the ring radii are equal, i.e., at $n\prime$ = −n, yielding the lowest $v_F^{\text{eff}}$ at such ILTs.

DISCUSSION

Our study has shown that the physics of LPPs is very rich, and it involves simultaneously three types of effects: polaritonic, excitonic, and polaronic. These effects have distinct characteristics: 1) The polaritonic effects change collective mode properties in the heterostructure. Forbidden optical transitions are now accessible in the momentum space offered by m-SNOM. The mode coupling between Landau polaritons (magnetoexcitons) in graphene and phonon polaritons in hBN generates a tunable avoided crossing, which could potentially be further tailored by using other ILTs (e.g., 0 → 1 ILT) or multilayer engineering (e.g., adding additional layers of graphene). 2) The excitonic effects are manifestations of the electron-electron interactions. They lead to a finite binding energy, which also modifies the LPP dispersion. This binding energy can be further tuned via dielectric screening engineering. 3) The polaron effect is another term for the renormalization of the quasiparticle dispersion. Although above we emphasized the role of electron-electron interactions as the reason for the renormalization of the Fermi velocity $v_F^{\text{ren}}$, this interaction is screened by hBN. Hence, the interaction of electrons in graphene with phonons in hBN is included implicitly. In our case, $v_F^{\text{ren}}$ does not change much with magnetic field since we keep the incident photon energy the same throughout the experiments. In addition, in our calculation of the renormalized Fermi velocity, we approximated the hBN dielectric function by its dc (ω = 0) value. Goals for future work can be: i) incorporating more sophisticated theoretical approaches into our model to properly treat electron-phonon coupling and ii) experimentally studying in more detail the momentum dependence (e.g., via different m-SNOM tip radii) and frequency dependence of LPPs.

As mentioned in the introduction to this paper, LPPs are specific examples of MPR effects. Other known MPR effects include magneto-polarons (23–25), dc magneto-transport oscillations (27, 28, 47), and mode splitting in magneto-Raman spectroscopy (26). Most of them have been studied in bulk crystals or a single material system. It would be interesting to investigate whether these phenomena are affected by finite-momenta LPPs in a 2D heterostructure. Last, it would be desirable to explore a variety of other nano-magneto-optics phenomena using m-SNOM, including chiral edge magnetoplasmons (48–50), cavity magneto optics (51), magnon polaritons and magnon-phonon polaritons (5, 52), the polaritonic Hofstadter butterfly (53), magnetoexcitons of fractional quantum Hall states (54), and collective modes of stripe phases in partially filled LLs (55).

MATERIALS AND METHODS

Experimental setup: Magneto infrared nanoscopy

Details of our experimental setup have been described in references (6, 56). Infrared nano-imaging in magnetic fields up to 7 T is demonstrated using a home-built scattering-type scanning near-field optical microscope (57) that is placed within a closed-cycle cryostat (OptiCool, Quantum Design). The accessible sample temperature with our scanning probe system is ~10 to 350 K. For infrared near-field imaging, a tunable QCL laser (Hedgehog mid-IR laser by DRS Daylight Solutions) is focused onto an atomic force microscopy tip via a parabolic mirror. As the resulting light spot is diffraction limited, it is much larger than the atomic force microscopy tip. Hence, it also illuminates the gold electrode that here serves as a launcher for the polariton waves (refer to the sketch of the experimental setup in Fig. 1A). The light scattered from the tip contains information about both the sample material and its polaritonic excitation. We detect the scattered light with a mercury-cadmium-telluride detector via a self-homodyne detection scheme (11, 57, 58), which yields a stable scattering signal and a good signal contrast. To separate the near-field signal from far-field contributions to the detected optical signal, we use lock-in demodulation at higher harmonics nΩ_tip of the tip tapping frequency Ω_tip, with n = 3 for the data shown in the manuscript. We use an Akiyama-type scanning probe with a resonance frequency of about Ω_tip ≈ 65 kHz (56), and scanning stages and positioners from Attocube (ANSxyz100/LT/UHV and ANPxyz101/LT/UHV, respectively).

Fabrication of graphene-hBN heterostructure

The sample studied in this work is hBN-encapsulated monolayer graphene. We fabricated the hBN/graphene/hBN stack using the standard van der Waals dry transfer technique (59). Graphene and hBN flakes were exfoliated onto Si/SiO₂ (285 nm) substrates. The flakes were examined using an atomic force microscope and those with pristine surfaces and suitable thicknesses were selected. A polycarbonate (PC)/ polydimethylsiloxane (PDMS) was prepared and used to assemble the stack. We used the stamp to pick up the top hBN at ~120°C; then, monolayer graphene was picked up by the top hBN at ~100°C; and then, the bottom hBN was picked up by the graphene layer at ~120°C. The stack on the stamp was transferred onto a clean Si/SiO₂ (285 nm) substrate at 180°C, where the PC melted and detached from the PDMS. The finished stack was annealed in forming gas (95% N₂ and 5% H₂) at 450°C for 4 hours to minimize the polymer residue on the surface. Electrical contacts to the graphene channel were defined via standard electron beam lithography. The top hBN and graphene at the contact area were etched in CHF₃/O₂ (10:1) plasma (40 mTorr, 60 W), exposing the side of the graphene layer. Cr (5 nm)/Au (40 nm) was thermally evaporated to form side contacts to graphene (60).

Pauli-blocking and gate-switchable dispersion

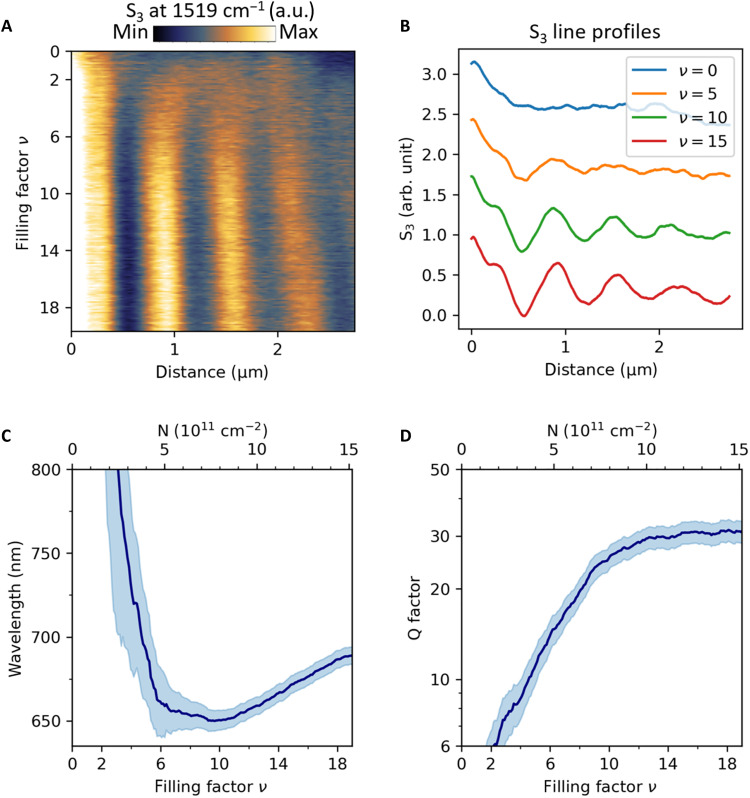
A transition n → $n\prime$ between two LLs can be suppressed (Pauli-blocked) by emptying the initial LL or filling the final LL via doping graphene off charge neutrality (33, 35, 39). Hence, Pauli-blocking is another clear signature of the ILTs. Here, we show that Pauli-blocking can be used to tune the LPP dispersion, requiring lower carrier doping than nonmagnetic tuning. This is in stark contrast to the tuning mechanism of plasmons in doped graphene that depends on modifying the plasma frequency via the charge carrier density (13, 15). Studying the same line as in Fig. 3A, Fig. 5A shows a measurement at constant magnetic field strength B = 3.3 T, with filling factor ν = 2πℏN/eB varied from 0 to 19 (N is the charge carrier concentration). Figure 5B shows corresponding line profiles at distinct filling factors ν = 0,5,10,15. At low ν, we find a strongly damped polariton, matching well to our magnetic-field dependent measurements of charge-neutral graphene above. When increasing the filling factor, due to the Pauli-blocking, we regain a propagating polariton mode with clear oscillatory behavior.

Fig. 5. Gate dependence of the −1➔ 2 graphene LPP at B = 3.3 T.

(A) Near-field signal acquired via a repeated scan of the same line as in Fig. 3A while sweeping the gate voltage and, thus, the filling factor from ν = 0 to 19; measurements were done at ω = 1519 cm⁻¹, and T = 154 K. (B) Line profiles extracted from (A) at four different filling factors of ν = 0, 5, 10, and 15, respectively. (C) Polariton wavelength λ_P and (D) polariton Q factor as a function of ν and charge carrier concentration N at 3.3 T; the shaded regions show the SD of the measurement.

A quantitative analysis of the line profiles yields the filling-factor dependence of the polariton wavelength λ_P (Fig. 5C) and quality factor Q (Fig. 5D). At a constant magnetic field of 3.3 T, for charge-neutral graphene with ν = 0, λ_P is larger than its value without a magnetic field due to the coupling with the −1 → 2 inter-LL resonance. However, the polaritons are strongly damped, preventing a meaningful estimate of λ_P at ν = 0. When increasing the filling factor to ν ≈ 10, λ_P decreases to a local minimum and approximately regains the wavelength observed at 0 T (compare to Fig. 3A). At the same time, the Q factor increases by more than a factor of 5. This is readily attributed to the expected Pauli-blocking of the −1 → 2 transition: One expects the second LL to be filled at a filling factor of ∣ν∣ = 4 $\mid n\prime \mid$ + 2 = 10 with $n\prime$ referring to the index of the highest LL contributing to the transition (33), i.e., here, $n\prime$ = 2. When increasing ν beyond 10, the Q factor remains almost constant while λ_P slowly increases again. This increase of λ_P is not directly related to the Pauli-blocking of the inter-LL excitation and can rather be assigned to the hybridization between hBN phonon polaritons and plasmon polariton modes in doped graphene (19). Overall, combining gate tuning with a constant magnetic field opens unique possibilities for polariton tunability in the low-voltage regime, with a charge carrier concentration difference of less than 10¹¹ cm⁻², resulting in a polariton wavelength change of several percent.

Additional insight into the coupling between graphene Landau polaritons and hBN phonon polaritons can be attained by studying the frequency dependence of the LPP dispersion along with its gate dependence. Like Fig. 5A, Fig. 6 shows near-field images that were acquired by repeatedly scanning the same line perpendicular to the gold electrode while sweeping the back gate voltage. The images have been acquired at six different photon frequencies; in Fig. 6 from left to right, these are: ω = 1498,1509,1519,1529,1537, and 1547 cm⁻¹. From top to bottom, the gate voltage was changed from 0 to −50 V for each scan (0 to −40 V for the scan at 1529 cm⁻¹). From the symmetry of the near-field images, one can see that the charge neutrality point (CNP) of graphene for these scans is found approximately in the middle of the scans, i.e., around −25 V. All the measurements shown so far (Figs. 2 to 5) have been taken in a single measurement run at 154 K. For the measurements shown in Fig. 6, the sample had been heated up to room temperature (to exchange the m-SNOM tip) and then cooled to 76 K. While both the thermal cycling (33) as well as the lower temperature may affect the measurement, the results in Fig. 6 appear consistent with the results discussed so far. As also observed in Fig. 5, Fig. 6 illustrates how the ILT gets Pauli-blocked when doping graphene away from charge neutrality. Well matching to the calculated dispersion in Fig. 2 (A to C) and literature results on the uncoupled hBN phonon polaritons (8), the LPP fringes show a clear positive dispersion, i.e., increasing polariton momentum (decreasing wavelength) with increasing frequency. Notably, Fig. 6 also directly illustrates how the gap in the LPP dispersion (Fig. 2B) opens and closes with frequency: While, around charge neutrality, the LPP propagation is gapped out at the central frequencies in Fig. 5 (e.g., at 1519 and 1529 cm⁻¹), one can see the width of the gap (along the voltage axis) decrease when moving to either lower or higher photon frequencies. For example, both at 1498 and 1547 cm⁻¹, the fringe suppression due to the coupling with the graphene ILT is less efficient, and some fringes can even be observed at charge neutrality. Again, this behavior agrees very well with the calculated dispersion shown in Fig. 2B.

Fig. 6. Frequency dependence of the gate dependence at B = 3.3 T.

Near-field signal acquired via a repeated scan of approximately the same line as in Fig. 3A while sweeping the back gate voltage from 0 to −50 V. The charge neutrality point (CNP) of graphene for these scans is found approximately in the middle of the scans, i.e., around −25 V. To investigate the dependence on the photon energy, the scans were performed at different frequencies, from left to right: ω = 1498,1509,1519,1529,1537,1547 cm⁻¹. The measurements were done at temperature T = 76 K. Scale bar, 1 μm.

Numerical calculation of graphene magneto-optical conductivity, polariton dispersion, and near-field signal: (Figs. 1, C and D, 2D, and 3D)

We calculate the longitudinal conductivity of graphene (plotted in Fig. 1, C and D of the main text) using the approximate Kubo formula

$${\mathrm{\sigma }}_{\mathit{xx}}\left(q,\mathrm{\omega }\right)=i{e}^2\mathrm{\omega }{\displaystyle \sum _{m=-\infty }^{\infty }}{\displaystyle \sum _{n=m+1}^{\infty }}\frac{\left(E_m-E_n\right)\left(f_m-f_n\right)}{{\left(E_m-E_n\right)}^2-{\mathrm{\hslash }}^2{\left(\mathrm{\omega }+i\mathrm{\gamma }\right)}^2} F_{\mathit{nm}}\left(q\right)$$ (2)

In this formula, the effect of disorder and electron interactions on LL broadening is expressed using a single phenomenological parameter γ. Equation 2 neglects contributions from intra-LL transitions, which are model dependent and difficult to compute. [For an example of such calculation, see (61).] These intra-LL contributions should be small at frequencies ω ≫ γ of interest and should be absent completely under the integer quantum Hall effect conditions, where each of the Fermi factors f_n is equal to either zero or unity (no partial LL filling occurs). In principle, the matrix elements F_nm(q) in Eq. 2 can be separated into two parts, $F_{\mathit{nm}}\left(q\right)=F_{\mathit{nm}}^0\left(q\right)+\mathrm{\delta }{F}_{\mathit{nm}}$, where the first one represents the response of an ideal system without electron scattering and the second one is a correction due to interactions and disorder. If γ and δF_nm originate from the same physical mechanism, such as the scattering of electrons by static disorder, then the matrix element δF_nm are expected to scale as γ²/(E_m − E_n)². In the aforementioned paper, for short-range disorder and in the absence of electron-electron interactions, the following result has been derived (61)

$$\begin{array}{c}\mathrm{\delta }{F}_{\mathit{nm}}=\frac{{\mathrm{\gamma }}^2}{4\mathrm{\pi }} \frac{\left(1+{\mathrm{\delta }}_{0,m}\right)\left(1+{\mathrm{\delta }}_{0,n}\right)}{{\left(E_m-E_n\right)}^2}\\ \left[ \frac{2\left|m\right|+2\left|n\right|+{\mathrm{\delta }}_{n,0}}{{\left(2\left|n\right|-2\left|m\right|+1\right)}^2}+\left(m\leftrightarrow n\right)\right]\end{array}$$ (3)

In our experiments, we typically have ${\mathrm{\gamma }}^2/{\mathrm{\omega }}_c^2\sim {10}^{-5}\dots {10}^{-4}$ so that δF_nm should be negligible. We do not consider such corrections below; however, the question of whether electron interaction can produce larger δF_nm for the same small γ is conceptually interesting and may warrant future theoretical study.

The formulas for F_nm(q) in the ideal system, which are well known, can be written as (43)

$$\begin{array}{c}{F}_{\mathit{nm}}\left(q\right)=\frac{2}{\mathrm{\pi }x} {\left|\text{sgn}\left(\mathit{mn}\right) A_{n_{<},n_{>}}\left(x\right)+A_{n_{<}-1,n_{>}-1}\left(x\right)\right|}^2,\\ n_{<}=\text{min}\left(\left|m\right|,\left|n\right|\right),n_{>}=\text{max}\left(\left|m\right|,\left|n\right|\right),x\equiv \frac{q^2{l}_B^2}{2},\\ A_{n_1,n_2}\left(x\right)={\left( \frac{1+{\mathrm{\delta }}_{0,n_1}}{2} \frac{1+{\mathrm{\delta }}_{0,n_2}}{2} \frac{n_1!}{n_2!} x^{n_2-n_1}\right)}^{1/2}{L}_{n_1}^{n_2-n_1}\left(x\right)e^{-x/2}\end{array}$$ (4)

where $L_n^{\mathrm{\alpha }}\left(x\right)$ is the associated Laguerre polynomial. At small momenta $q\ll l_B^{-1}$, function F_nm(q) scales as q^{2||m|−|n||−2} so that the conductivity σ_xx(q, ω) is dominated by the allowed transitions with |m|−|n| = ± 1, as discussed in the main text. Precisely at q = 0 (“far-field limit”), the conductivity is given by

$$\begin{array}{c}{\mathrm{\sigma }}_{\mathit{xx}}\left(0,\mathrm{\omega }\right)=i\frac{e^2}{2\mathrm{\pi }\mathrm{\hslash }} \overline{\mathrm{\omega }}\sum _{s=\pm 1}{\displaystyle \sum _{m=0}^{\infty }}\frac{N_{\mathit{ms}}}{{\left(\sqrt{m+1}-s\sqrt{m} \right)}^2-{\overline{\mathrm{\omega }}}^2} \frac{1}{\sqrt{\mathrm{m}+1}-s\sqrt{m}},\\ \overline{\mathrm{\omega }}\equiv \frac{\mathrm{\omega }+i\mathrm{\gamma }}{{\mathrm{\omega }}_c},N_{\mathit{ms}}=\left(f_{m+1}-f_{\mathit{sm}}\right)-\left(f_{-m-1}-f_{-\mathit{sm}}\right)\end{array}$$ (5)

Note that because of the factors 1 + δ_0,n in Eq. 4, the oscillator strength of the principal cyclotron transitions 0 → ± 1 is effectively doubled compared to other ILTs. In Eq. 5, this doubling is affected implicitly by summing over the band index s.

In the case of zero temperature, which we consider from now on, the numerators in the series of Eq. 5 can have only three possible values: N_ms = 0, −1, or −2. For example, at CNP, they are equal to N_m,−1 = − 2 if s = − 1 (inter-band transitions) and N_m,1 = 0 if s = 1 (intra-band transitions) for all m except m = 0, for which N_0,−1 = N_0,1 = − 2. The series for finite doping differs from that for the CNP only in a finite number of terms for which N_ms deviates from this rule. Hence, the far-field limit of the conductivity of a doped system can be easily computed from that for CNP by adding suitable corrections due to these terms.

Numerical evaluation of the series in Eq. 5 at CNP poses a problem, however, because of its slow convergence. To expedite the convergence, we transformed this series into an integral using standard techniques of complex analysis. The final expression for ${\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}$ is somewhat lengthy, so we split it into three parts

$${\mathrm{\sigma }}_{\mathrm{x}x}^{\text{CNP}}\left(0,\mathrm{\omega }\right)=\frac{e^2}{2\mathrm{\pi }\mathrm{\hslash }} \left(C_1+C_2+C_3\right)$$ (6a)

The first part C₁ is a partial sum of the original series (cf. Eq. 5),

$$C_1=-2i\overline{\mathrm{\omega }}{\displaystyle \sum _{m=0}^M}\frac{1}{{\left(\sqrt{m+1}+\sqrt{m}\right)}^2-{\overline{\mathrm{\omega }}}^2} \frac{1}{\sqrt{m+1}+\sqrt{m}}$$ (6b)

The upper limit of summation M is largely arbitrary, and the minimal choice (where M = 0 or 1) is given below. The second part C₂ is the integral

$$C_2=\overline{\mathrm{\omega }} {\displaystyle \underset{0}{\overset{\infty }{\int }}}\mathit{dz} \text{tanh}\mathrm{\pi }z\left[\frac{\sqrt{M+\frac{3}{2}+\mathit{iz}}-\sqrt{M+\frac{1}{2}+\mathit{iz}}}{{\left(\sqrt{M+\frac{3}{2}+\mathit{iz}}+\sqrt{M+\frac{1}{2}+\mathit{iz}} \right)}^2-{\overline{\mathrm{\omega }}}^2}-\left(z\to -z\right)\right]$$ (6c)

We ensure that this integral is free of singularities by taking M = 0 if Re m_ω > 1 where $m_{\mathrm{\omega }}=\frac{1}{4}{\left(\overline{\mathrm{\omega }}-\frac{1}{\overline{\mathrm{\omega }}}\right)}^2$and M = 1 otherwise. Parameter m_ω has the property that at m = m_ω, the summand in Eq. 6b has a pole in the complex plane of m. The final part of our formula comes from the residue of that pole

$$C_3=i\frac{{\overline{\mathrm{\omega }}}^4-1}{2{\overline{\mathrm{\omega }}}^4}\frac{\mathrm{\pi }}{\text{tan}\mathrm{\pi }{m}_{\mathrm{\omega }}}\mathrm{\Theta }\left(\left|\overline{\mathrm{\omega }}\right|-1\right)\mathrm{\Theta }\left(\text{Re} m_{\mathrm{\omega }}-M-\frac{1}{2}\right)$$ (6d)

where Θ(x) is a unit step function. Numerical evaluation Eq. 6a to d is very fast, yielding the numerically exact results for conductivity ${\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(0,\mathrm{\omega }\right)$ at CNP and thus σ_xx(0, ω) at any desired doping.

Next, we discuss our procedure for computing σ_xx(q, ω) at nonzero q. Here, both allowed and forbidden ILTs must be included. Once again, the problem is difficult because the terms in Eq. 2 decrease slowly with m and n. For simplicity, we focus on the CNP where only the inter-band transitions are possible. Applying the Wentzel-Kramers-Brillouin approximation to solve the differential equation for $L_{n_1}^{n_2-n_1}\left(x\right)$, we derived the following asymptotic formula, valid for m ≥ n ≫ 1

$$\begin{array}{c}{A}_{\mathit{nm}}-A_{n-1,m-1}\simeq \frac{\sqrt{2} {\left(-1\right)}^n}{\sqrt{\mathrm{\pi }\left(x_{+}-x_{-}\right)}}{\left( \frac{x-x_{-}}{x_{+}-x}\right)}^{1/4}\text{cos}\left(\mathrm{\psi }+\frac{\mathrm{\pi }}{4}\right),x_{-}<x<x_{+}\\ x_{\pm }={\left(\sqrt{m}\pm \sqrt{n} \right)}^2,\mathrm{\psi }\left(x\right)=-\frac{1}{2} {\displaystyle \underset{x}{\overset{x_{+}}{\int }}}\frac{\mathit{dy}}{y} \sqrt{\left(x_{+}-y\right)\left(y-x_{-}\right)}\end{array}$$ (7)

Substituting this formula into Eqs. 4 and 2, we see that the high-order terms in Eq. 2 scale as O(x^−1/2 n⁻²) if $n\gg \overline{\mathrm{\omega }}$ and that the dominant contribution comes from m’s that satisfy the double inequality $\sqrt{n}\le \sqrt{m}\le \sqrt{n}+\sqrt{x}$. Let us define the series residual $\mathrm{\Delta }{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}$ as the difference between ${\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}$ and the series of Eq. 2 truncated at some N_c so that

$$\begin{array}{c}{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(q,\mathrm{\omega }\right)=\frac{e^2}{\mathrm{\hslash }}i\overline{\mathrm{\omega }}{\displaystyle \sum _{n=0}^{N_c}}{\displaystyle \sum _{m=n}^{N_c}}\frac{\sqrt{m}+\sqrt{n}}{{\left(\sqrt{m}+\sqrt{n}\right)}^2-{\overline{\mathrm{\omega }}}^2}\\ F_{\mathit{nm}}\left(q\right)+\mathrm{\Delta }{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(q,\mathrm{\omega }\right)\end{array}$$ (8)

From the above reasoning, we expect that $\mathrm{\Delta }{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}$ scales as $N_c^{-1/2}$ if $N_c\gg \overline{\mathrm{\omega }}$. Hence, for strong enough magnetic fields where $\overline{\mathrm{\omega }}=\left(\mathrm{\omega }+i\mathrm{\gamma }\right)/{\mathrm{\omega }}_c$ is at most of the order of unity, we can achieve, say, 5% accuracy by simply summing over $N_c^2\sim {0.05}^{-4}\sim {10}^5$ terms. As the magnetic field decreases, $\overline{\mathrm{\omega }}$ increases, and this naïve strategy becomes unfeasible because of long computation times and, more importantly, the accumulation of roundoff errors in evaluating the Laguerre functions. As an alternative, we briefly experimented with various series acceleration methods (e.g., Levin’s method) but found them to be numerically unstable due to their own set of roundoff errors. Eventually, we settled on estimating the residual by using the asymptotic formula (Eq. 7) and replacing the summation with integration. After some manipulations, our result, in the absence of damping, can be presented as follows

$$\begin{array}{c}\mathrm{\Delta }{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(q,\mathrm{\omega }\right)=-\frac{e^2}{{\mathrm{\pi }}^2\mathrm{\hslash }{q}^2}\frac{i\mathrm{\omega }}{\sqrt{q^2{v}_F^2-{\mathrm{\omega }}^2}} {\displaystyle \underset{0}{\overset{q}{\int }}}d{k}_{-}\sqrt{q^2-k_{-}^2} \text{arccos}C\left(k_{-}\right),\\ C\left(k_{-}\right)=\frac{k_{+}^2{v}_F^2-2q^2{v}_F^2+{\mathrm{\omega }}^2}{k_{+}^2{v}_F^2-{\mathrm{\omega }}^2},\\ k_{+}=\text{max}\left(q,2q_c-k_{-}\right),q_c=\frac{\sqrt{2N_c}}{l_B}\end{array}$$ (9)

In weak magnetic fields where $x\equiv q^2{l}_B^2/2>4N_c$, Eq. 9 can be evaluated analytically. Here, we have k₊ = q, C(k₋) = − 1 so that

$$\mathrm{\Delta }{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(q,\mathrm{\omega }\right)=\frac{e^2}{4\mathrm{\hslash }}\frac{i\mathrm{\omega }}{\sqrt{q^2{v}^2-{\mathrm{\omega }}^2}}$$ (10)

which is a well-known expression for the conductivity of graphene at CNP in the absence of the magnetic field. Apparently, ${\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(q,\mathrm{\omega }\right)\simeq \mathrm{\Delta }{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(q,\mathrm{\omega }\right)$ in this regime. At stronger fields where <4N_c, Eq. 9 can be easily evaluated by a numerical quadrature. Last, to include a small LL broadening γ ≪ ω, we replaced ω by ω + iγ in these equations. Including $\mathrm{\Delta }{\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}$ in the calculation significantly improves the accuracy of the procedure so that reasonably accurate results can be obtained for modest N_c. We found that N_c = 70 is sufficient for the entire parameter space of momenta, frequencies, and magnetic fields we explored.

The parameters we used for calculating ${\mathrm{\sigma }}_{\mathit{xx}}^{\text{CNP}}\left(q,\mathrm{\omega }\right)$ according to Eqs. 4, and 8 to 10 were as follows. On the basis of our experimental results for the −1 → 2 transition (Fig. 4C), we choose a Fermi velocity v_F = 1.19 × 10⁶ m/s. Our choice of the LL broadening γ is based on (33), which suggests an energy-dependent LL broadening of the form γ = γ₀ + βE with γ₀ = 0.75 meV and β = 0.012. For our photon energy E = ℏω = 188 meV, it gives γ = 3.01 meV (24.27 cm⁻¹), which is the constant value that we used for our calculations.

Having calculated graphene conductivity, next, we compute the reflection coefficient r_p for the whole heterostructure using the transfer matrix formalism [see, e.g., (8, 13, 14)]. We assume that the sample has the following structure: hBN (16 nm), graphene, hBN (55 nm), SiO₂ (285 nm), and Si (semi-infinite); see Fig. 1D. Representative plots for Im r_p as a function of momentum, frequency, and magnetic field are shown in Fig. 2 (A to C) of the main text.

The near-field signal in Fig. 3D is calculated as described in (62), assuming the tip radius of r_tip = 30 nm, length of the long semi-axis of the spheroid of 160 nm, and tip tapping amplitude of A = 40 nm.

Momentum-range accessible via m-SNOM

As m-SNOM is based on scattering-type SNOM (s-SNOM), the accessible momentum range of both techniques can be described in the same manner, which originates in the simple point-dipole model (14, 57, 58, 63) of the tip-sample interaction. The bell-shaped curve in Fig. 1C represents the time-averaged function k²e^−2kz(t). Here, the time-dependent effective dipole position z(t) is (14): z(t) = b + A(1 − cos Ω_tipt), b is the shortest distance between the model dipole and the sample, A is the tip tapping amplitude, and Ω_tip is the tip tapping frequency. The analytical formula for this bell-shaped curve is therefore 〈k²e^−2kz〉_t = k²e^−2k(b+A)I₀(kA), where I₀(x) is the modified Bessel function of the first kind. We choose b = fr_tip with f = 0.79 based on s-SNOM modeling literature (64, 65), and we assume r_tip = 30 nm and A = 40 nm.

Extracting the coupling strength via the coupled harmonic oscillator model

Coupled harmonic oscillators model for hBN phonon polaritons and graphene Landau polaritons

We model the interaction between hBN hyperbolic phonon polaritons and graphene Landau polaritons as coupling of two harmonic oscillators (44, 45, 66, 67). The oscillator resonant frequencies and damping parameters are ω_i, and Γ_i, respectively, where i = {hBN, Landau}. The complex eigenfrequencies of this system are given by

$${\mathrm{\omega }}_{\pm }+i{\mathrm{\Gamma }}_{\pm }/2=\underset{\_}{\mathrm{\omega }}-i\underset{\_}{\mathrm{\Gamma }}/2\pm \sqrt{G^2+\frac{1}{4}{H}^2}$$ (11)

where the sign ± indicates the lower (−) and the upper (+) branch solution (42). Here, $\underset{\_}{\mathrm{\omega }}=\left({\mathrm{\omega }}_{\text{hBN}}+{\mathrm{\omega }}_{\text{Landau}}\right)/2$, $\underset{\_}{\mathrm{\Gamma }}=\left({\mathrm{\Gamma }}_{\text{hBN}}+{\mathrm{\Gamma }}_{\text{Landau}}\right)/2$, G is the coupling strength, and $H={\mathrm{\omega }}_{\text{hBN}}-{\mathrm{\omega }}_{\text{Landau}}-\frac{i}{2}\left({\mathrm{\Gamma }}_{\text{hBN}}-{\mathrm{\Gamma }}_{\text{Landau}}\right)$. The real parts of the eigenfrequencies are

$${\mathrm{\omega }}_{\pm }=\underset{\_}{\mathrm{\omega }}\pm \text{Re} \sqrt{G^2+\frac{1}{4}{H}^2}$$ (12)

By calculating ω_± and the parameters ω_i and Γ_i of the uncoupled oscillators, we can determine the coupling strength G from Eq. 12. Because of the dispersive nature of polaritons, each parameter depends on the momentum k. The following sections describe the procedure for extracting ω_i(k), Γ_i(k), and ω_±(k) from the simulated dispersions.

Extraction of the oscillator parameters for uncoupled modes

To calculate the parameters of the oscillators, we simulate the imaginary part of the reflection coefficient Im r_p that yields the dispersion for each uncoupled mode. For hBN phonon polaritons, we considered the Im r_p map at B = 6 T shown in Fig. 2C in the main text (and Fig. 7A). The reason we preferred to use B = 6 T instead of B = 0 T is that at zero field, the charge-neutral graphene influences the polaritonic response of the heterostructure via its universal optical conductivity σ = e²/4ℏ (33). We isolate the fundamental hyperbolic branch by applying a window mask to the dispersion map. The mask values are 1 in the interest region and 0 elsewhere (red area in Fig. 7A). Figure 7B shows line profiles from the map extracted for different momenta. The oscillator parameters were obtained by fitting these profiles to the function

$$\text{Im} r_p\propto \mathrm{\omega }{f}_i^2 \text{Im}\left(\frac{1}{-{\mathrm{\omega }}^2-i\mathrm{\omega }{\mathrm{\Gamma }}_i+{\mathrm{\omega }}_i^2}\right)$$ (13)

Fig. 7. Extraction of oscillator parameters from polariton dispersions.

(A) Im r_p at B = 6 T from the main text (Fig. 2C). The red-shaded region indicates the area excluded by the window function. The white solid line is the phonon polariton dispersion extracted from fitting. (B) Line profiles from (A) extracted for different momenta values (black lines). The fitted curve is represented as dashed lines. (C) hBN phonon polaritons damping and oscillator strength extracted from fitting. (D) Im r_p simulated for graphene on SiO₂ (thickness, 285 nm) at B = 3.35 T. The black solid line represents the dispersion extracted from fitting. (E) Extracted Landau polariton resonance as a function of magnetic field and momenta. The white dashed lines represent isofrequencies. (F) Landau polariton damping and oscillator strength from fitting.

The extracted dispersion ω_hBN(q) (white line in Fig. 7A) matches well with the dispersion in the Im r_p map. Figure 7C shows the extracted values for f_hBN and Γ_hBN.

To calculate the parameters for the Landau polaritons, we simulated Im r_p for graphene on top of SiO₂ (thickness, 285 nm). Figure 7D shows the map at B = 3.35 T. Using the same procedure described previously for hBN polaritons, we extracted the uncoupled oscillator parameters for the LLPs. Figure 7E shows the extracted ω_Landau(B, k). Figure 7D (black line) shows ω_Landau(k), and Fig. 7F shows Γ_Landau and f_Landau for B = 3.35 T.

Dispersion of branches and coupling strength extraction

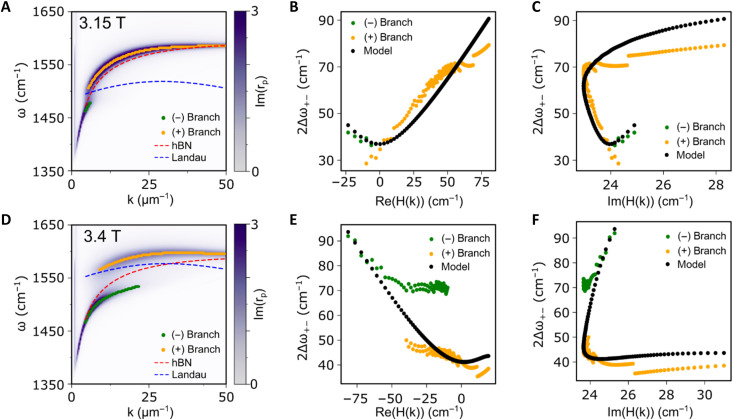
We extracted ω_±(k, B) from Im r_p by locating its maxima for every fixed k. The hBN phonon polariton dispersion was used as a reference to separate the ω₋ and ω₊ branches. The result of this extraction is illustrated in Fig. 8 (A and D), for B = 3.15 T and B = 3.4 T, respectively. Figure 8 (B, C, E, and F) shows the spectral gap $2\mathrm{\Delta }{\mathrm{\omega }}_{\pm }\left(k\right)=2\left({\mathrm{\omega }}_{\pm }-\underset{\_}{\mathrm{\omega }}\right)$ as a function of the complex parameter H(k). The coupling strength was obtained by fitting the spectral gap to Eq. 12.

Fig. 8. Determination of coupling strength from hybrid modes.

(A and D) Extracted dispersion of lower (green) and upper (yellow) branches for (A) B = 3.15 T and (D) B = 3.4 T. The simulated Im r_p and the dispersion of the uncoupled modes are shown for reference. Dependence of 2Δω_±(q) on (B and E) the real part and (C and F) the imaginary part of H(k) for B = 3.15 T and B = 3.4 T.

Coupling strength and criterium for strong coupling

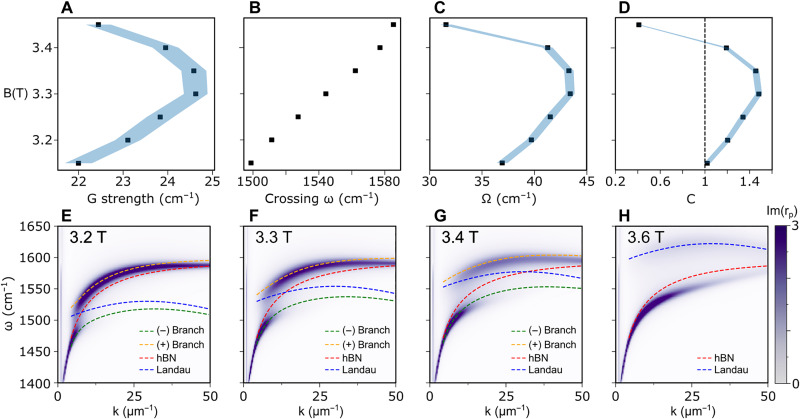
Figure 9A shows the calculated coupling strength G for different magnetic fields. We can observe that the coupling strength increases until it reaches a maximum at B = 3.3 T. The frequencies of hBN and Landau modes in which dispersion crossing occurs are shown in Fig. 9B. By calculating the branches splitting Ω_tip = ω₊ − ω₋ where crossing occurs (Fig. 9C), we calculated the criterion $C=2{\mathrm{\Omega }}^2/\left({\mathrm{\Gamma }}_{\text{hBN}}^2+{\mathrm{\Gamma }}_{\text{Landau}}^2\right)$ (Fig. 9D) (44). Strong coupling is achieved for 3.15 T < B < 3.4 T, where C > 1.

Fig. 9. Coupling strength analysis and model validation across varying magnetic fields.

(A) Coupling strength as a function of the magnetic field, extracted via fitting. (B) Extracted spectral position where the hBN phonon polariton and Landau polariton dispersion cross. (C) Branch separation Ω at the crossing point. (D) Criterion C for strong coupling. The blue-shaded areas represent the uncertainty of the presented variables, assuming straight connections between the data points as a guide to the eye. (E to H) Calculated branch dispersion based on the uncoupled modes and the extracted coupling strength for (E) B = 3.2 T, (F) B = 3.3 T, and (G) B = 3.4 T. For (H) B = 3.6 T, we only show the hBN phonon polariton and the Landau polariton dispersions. The Im(r_p) is presented on the background to show the expected dispersion from the simulation.

To verify the results, we show in Fig. 9 (E to H) the calculated frequency branches from Eq. 12, in which we used the parameters from the uncoupled hBN and Landau modes and the extracted coupling strength. Notice that we have calculated coupling values only in a narrow range of magnetic fields. This is because the coupled oscillator model is only well-defined at frequencies and momenta in which the dispersions of both modes overlap. Nevertheless, the hBN polariton dispersion is not fully recovered for B > 3.4 T (see Fig. 9H at B = 3.6 T), indicating that these polariton modes can still interact with each other.

Weak polariton fringes parallel to graphene boundary in fig. 2 (D to F)

Figure 2 (D to F) shows clear polariton fringes parallel to the gold electrode. The analysis of these fringes and their dispersion with magnetic field is a central part of this study. We note that weaker polariton fringes can be observed parallel to the graphene boundary marked by the dashed white line in Fig. 2 (D to F). This mode reflection is attributed to the polariton momentum mismatch between hBN regions with and without graphene. Therefore, the interference fringes parallel to the graphene boundary are most pronounced in pure hBN at 3.35 T where the momentum mismatch between the regions 2) and 3) is the largest. In our analysis, we do not focus on these weak polariton fringes.

Many-body effects: Fermi velocity and magnetoexciton binding energy

Figure 2 (D to F): The effective Fermi velocity was defined by Eq. 1, copied below for convenience (assuming n, n′ ≥ 0)

$$v_{F,-n\to n\prime }^{\text{eff}}\equiv \frac{l_B}{\mathrm{\hslash }}\frac{E_{-n\to n\prime }}{\sqrt{2n}+\sqrt{2n\prime }}$$ (14)

In the main text, we explained that the many-body correction $\mathrm{\Delta }{E}_{-n\to n\prime }$ to the energy $E_{-n\to n\prime }$ of a −n → $n\prime$ ILT (at zero momentum q = 0) has two parts: i) the correction due to the electron self-energies ΔE_m of m = −n, $n\prime$ LLs and ii) the magnetoexciton binding energy ${\mathrm{\Delta }}_{-n,n\prime }$

$${\mathrm{\Delta }E}_{-n\to n\prime }=\left(\mathrm{\Delta }{E}_{n\prime }-\mathrm{\Delta }{E}_{-n}\right)-{\mathrm{\Delta }}_{-n,n\prime }$$ (15)

We referred to the former as the Fermi velocity renormalization effect and to the latter as the excitonic effect. In this approach, the renormalized Fermi velocity of −n → $n\prime$ ILT is given by

$$v_{F,-n\to n\prime }\equiv v_F+\frac{l_B}{\mathrm{\hslash }}\frac{\mathrm{\Delta }{E}_{n\prime }-\mathrm{\Delta }{E}_{-n}}{\sqrt{2n}+\sqrt{2n\prime }}$$ (16)

where v_F is the bare Fermi velocity, so that $v_{F,-n\to n\prime }^{\text{eff}}$ and $v_{F,-n\to n\prime }$ are related by

$$v_{F,-n\to n^{\prime }}^{\text{eff}}=v_{F,-n\to n\prime }-\frac{l_B}{\mathrm{\hslash }}\frac{{\mathrm{\Delta }}_{-n,n\prime }}{\sqrt{2n}+\sqrt{2n\prime }}$$ (17)

Following previous work (37), we compute the quantities that enter these equations as follows

$$\begin{array}{c}\mathrm{\Delta }{E}_{n\prime }-\mathrm{\Delta }{E}_{-n}=-\int \frac{d^{2}q}{{\left(2\mathrm{\pi }\right)}^2}v\left(q\right)I_{-n,n\prime }\left(q\right),\\ I_{-n,n\prime }\left(q\right)=\sum _m{f}_m\left({\left|g_{m,n^{\prime }}\left(q\right)\right|}^2-{\left|g_{m,-n}\left(q\right)\right|}^2\right)\end{array}$$ (18)

$${\mathrm{\Delta }}_{-n,n\prime }=\int \frac{d^{2}q}{{\left(2\mathrm{\pi }\right)}^2}v\left(q\right)g_{-n,-n}\left(q\right)g_{n\prime n\prime }\left(q\right)$$ (19)

Here, f_m is again the Fermi occupation factor of mth LL [f_m = Θ(−m) if m ≠ 0 and f₀ = 1/2], g_mn(q) is the matrix element defined in Eq. 4, and $v\left(q\right)=\frac{2\mathrm{\pi }{e}^2}{\mathrm{ϵ}\left(q\right)q}$ is the screened Coulomb interaction. We neglect dynamical screening effects; however, we include static screening through the momentum-dependent dielectric function

$$\mathrm{ϵ}\left(q\right)=\mathrm{\kappa }\left(q\right)+{\mathrm{\kappa }}_g\left(q\right)$$ (20a)

$$\begin{array}{c}\mathrm{\kappa }\left(q\right)=\frac{{\mathrm{ϵ}}_{\text{hBN}}}{2}\\ \left( \frac{{\mathrm{ϵ}}_{\text{hBN}}\text{tanh}{\mathrm{\xi }}_{\text{hBN}}q{d}_1+{\mathrm{ϵ}}_0}{{\mathrm{ϵ}}_0\text{tanh}{\mathrm{\xi }}_{\text{hBN}}q{d}_1+{\mathrm{ϵ}}_{\text{hBN}}}+\frac{{\mathrm{ϵ}}_{\text{hBN}}\text{tanh}{\mathrm{\xi }}_{\text{hBN}}q{d}_2+{\mathrm{ϵ}}_{\text{SOS}}}{{\mathrm{ϵ}}_{\text{SOS}}\text{tanh}{\mathrm{\xi }}_{\text{hBN}}q{d}_2+{\mathrm{ϵ}}_{\text{hBN}}}\right)\\ {\mathrm{ϵ}}_{\text{SOS}}={\mathrm{ϵ}}_{\text{SiO}2}\frac{{\mathrm{ϵ}}_{\text{SiO}2}\text{tanh}q{d}_3+{\mathrm{ϵ}}_{\text{Si}}}{{\mathrm{ϵ}}_{\text{Si}}\text{tanh}q{d}_3+{\mathrm{ϵ}}_{\text{SiO}2}}\end{array}$$ (20b)

$${\mathrm{\kappa }}_g\left(q\right)=2\mathrm{\pi }\mathit{iq}\underset{\mathrm{\omega }\to 0}{\text{lim}} {\mathrm{\omega }}^{-1}{\mathrm{\sigma }}_{\mathit{xx}}\left(q,\mathrm{\omega }\right)$$ (20c)

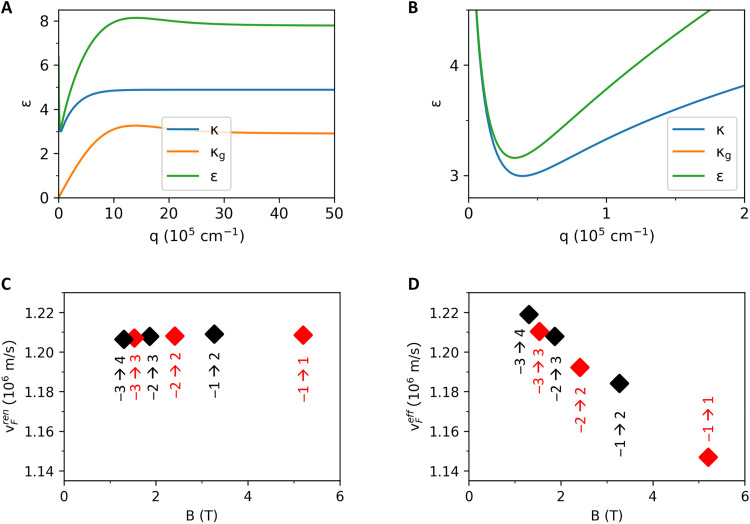
Function κ(q) has the meaning of the effective dielectric constant of graphene environment. Parameter ${\mathrm{ϵ}}_{\text{hBN}}\equiv {\left({\mathrm{ϵ}}_{\text{hBN}}^{\perp }{\mathrm{ϵ}}_{\text{hBN}}^{\parallel }\right)}^{1/2}=4.9$ is the dc (i.e., ω = 0) dielectric constant of hBN defined as the geometric average of its in-plane and out-of-plane dielectric constants, ${\mathrm{\xi }}_{\text{hBN}}\equiv {\left({\mathrm{ϵ}}_{\text{hBN}}^{\perp }/{\mathrm{ϵ}}_{\text{hBN}}^{\parallel }\right)}^{1/2}$ is the hBN anisotropy factor, ϵ_SiO2 = 3.9 is the dc dielectric constant of SiO₂, ϵ_Si = 11.7 is the dc dielectric constant of Si, and ϵ₀ = 1 is the dielectric constant of vacuum. Parameters d₁ = 16 nm and d₂ = 55 nm are thicknesses of the top and bottom hBN layers, respectively, and d₃ = 285 nm is the SiO₂ thickness. Function κ_g(q) specified by Eq. 19c accounts for the (static) screening of the Coulomb potential by electrons in graphene and σ_xx(q, ω) is the longitudinal conductivity of graphene in the presence of magnetic field computed as described in section Numerical calculation of graphene magneto-optical conductivity. Representative plots of functions κ(q), κ_g(q), and ϵ(q) are shown in Fig. 10 (A and B).

Fig. 10. Calculation of the Fermi velocities and many-body effects.

(A and B) Effective dielectric function for electrons in graphene. Functions κ(q), κ_g(q), and ϵ(q) defined by Eq. 19 (A to C) for B = 3.35 T. (B) shows a magnification of the small dip at low q that is observed for κ_g(q) and ϵ(q). (C) Renormalized Fermi velocities given by Eq. 26. (D) Effective Fermi velocities defined by Eq. 17 that include excitonic corrections.

As one can see from these graphs, κ(q) (the middle curve) is equal to (ϵ₀ + ϵ_Si)/2 at zero q, then has a small dip to approach (ϵ₀ + ϵ_SiO2)/2 within a narrow range of relatively low momenta $d_3^{-1}\lesssim q\lesssim d_2^{-1}$, and then rises and tends to ϵ_hBN at $q\gtrsim d_1^{-1}=6.7\times {10}^5 \mathrm{c}{\mathrm{m}}^{-1}$. The total dielectric function ϵ(q) (the top curve) shows the same small dip at low q, goes through a modest maximum, and then approaches the limiting value

$${\mathrm{ϵ}}_{\infty }={\mathrm{ϵ}}_{\text{hBN}}+\frac{\mathrm{\pi }\mathrm{\alpha }}{2},\mathrm{\alpha }=\frac{e^2}{\mathrm{\hslash }{v}_F^{\mathit{ren}}}\approx 2.2$$ (21)

at high momenta $q\gg l_B^{-1}$.

The calculation of the binding energies ${\mathrm{\Delta }}_{-n,n\prime }$ in Eq. 19 involves numerical evaluation of four integrals of the form

$$\int \frac{d^{2}q}{{\left(2\mathrm{\pi }\right)}^2}v\left(q\right)L_{n_1}\left(\frac{q^2{l}_B^2}{2}\right)L_{n_2}\left(\frac{q^2{l}_B^2}{2}\right)e^{-q^2{l}_B^2/2}$$ (22)

which are well behaved. On the other hand, the integral for the self-energy in Eq. 18 diverges at large momenta $q{l}_B\gg \sqrt{n},\sqrt{n\prime }$ because

$$I_{-n,n\prime }\left(q\right)\simeq \mathtt{-}\frac{\sqrt{2n}+\sqrt{2n\prime }}{4q{l}_B}$$ (23)

as can be deduced from Eqs. 4 and 18. We regularize this divergence by renormalization, i.e., subtraction of $v_{F,-n\to n\prime }$ evaluated at some reference field B₀. Let l₀ ≡ l_B(B₀) be the magnetic length at B₀. Since the high momenta enter through the product ql_B, we can rescale the integration variable in Eq. 18 by the ratio $R=l_B/l_0=\sqrt{B_0/B}$ to cancel the divergence. Performing the subtraction, we find

$$v_{F,-n\to n\prime }\left(B\right)=v_{F,-n\to n\prime }\left(B_0\right)-\frac{e^2}{8\mathrm{\hslash }{\mathrm{ϵ}}_{\infty }}\text{ln}\left(\frac{B}{B_0}\right)+{\mathrm{\Delta }v}_{F,-n\to n\prime }\left(B,B_0\right)$$ (24)

where

$${\mathrm{\Delta }v}_{F,-n\to n\prime }\left(B,B_0\right)=-\frac{l_B}{\mathrm{\hslash } \left(\sqrt{2n}+\sqrt{2n\prime }\right)}\int \frac{d^{2}q}{{\left(2\mathrm{\pi }\right)}^2}\left[v\left(q\right)-\mathit{Rv}\left(\mathit{Rq}\right)\right]I_{-n,n\prime }\left(q\right)$$ (25)

Note that if the dielectric function is replaced by a constant, e.g., ϵ_∞, then v(q) = 2πe²/(ϵ_∞q) and $\mathrm{\Delta }{v}_{F,-n\to n\prime }$(B, B₀) vanishes identically. In this case, the conventional logarithmic-in-B rule (37) for the Fermi velocity renormalization is recovered.

In our experiment, all the ILTs were measured at the same photon energy ℏω. Therefore, it is convenient to select a particular ILT, e.g., −2 → 3, as a reference, so that B₀ = B_−2→3, where B_−2→3 is the field at which this ILT occurs. Equation 24 entails

$$\begin{array}{c}{v}_{F,-n\to n\prime }=v_{F,-2\to 3}-\frac{e^2}{8\mathrm{\hslash }{\mathrm{ϵ}}_{\infty }}\text{ln}\left(\frac{B}{B_{-2\to 3}}\right)\hfill \\ -\frac{l_B}{\sqrt{2}\mathrm{\hslash } }\int \frac{d^{2}q}{{\left(2\mathrm{\pi }\right)}^2}\left[v\left(q\right)\frac{I_{-n,n\prime }\left(q\right)}{\sqrt{n}+\sqrt{n\prime }}-\mathit{Rv}\left(\mathit{Rq}\right)\frac{I_{-2,3}\left(q\right)}{\sqrt{2}+\sqrt{3}}\right]\hfill \end{array}$$ (26)

Our calculations using this formula show that $v_{F,-n\to n\prime }$ is almost the same for all the ILTs, as shown in Fig. 10C. On the other hand, $v_{F,-n\to n^{\prime }}^{\text{eff}}$, given by Eq. 17, exhibits characteristic dips at n = n′ because of relatively larger excitonic corrections ${\mathrm{\Delta }}_{-n,n\prime }$ at such ILTs; see Fig. 10D.

To obtain the experimental binding energies ${\mathrm{\Delta }}_{\text{exp},-n,n\prime }$, we use Eqs. 17 and 26 but set the effective Fermi velocities equal to their experimentally measured values $v_{F,\text{exp},m\to n}^{\text{eff}}$. Solving for ${\mathrm{\Delta }}_{-n,n\prime }$, we obtain

$$\begin{array}{c}{\mathrm{\Delta }}_{\text{exp},-n,n\prime }=\frac{\sqrt{2}\mathrm{\hslash }}{l_B}\left(\sqrt{n}+\sqrt{\mathrm{n}\prime }\right)\left\{v_{F,\text{exp},-2\to 3}^{\text{eff}}-\frac{e^2}{8\mathrm{\hslash }{\mathrm{ϵ}}_{\infty }}\text{ln}\left(\frac{B}{B_{-2\to 3}}\right)-v_{F,\text{exp},-n\to n\prime }^{\text{eff}}\right.\\ \left.-\frac{l_B}{\sqrt{2}\mathrm{\hslash }}\int \frac{d^{2}q}{{\left(2\mathrm{\pi }\right)}^2}\left[v\left(q\right)\frac{I_{-n,n\prime }\left(q\right)}{\sqrt{n}+\sqrt{n\prime }}-\mathit{Rv}\left(\mathit{Rq}\right)\frac{I_{-1,2}\left(q\right)}{\sqrt{2}+\sqrt{3}}\right]+\frac{l_B}{\sqrt{2}\mathrm{\hslash }}\frac{{\mathrm{\Delta }}_{-2,3}}{\sqrt{2}+\sqrt{3}}\right\}\#\end{array}$$ (27)

This gives ${\mathrm{\Delta }}_{\text{exp},-n,n^{\prime }}$ in terms of $v_{F,\text{exp},-n\to n^{\mathrm{\prime }}}^{\text{eff}}$ and $v_{F,\text{exp},-2\to 3}^{\text{eff}}$, the calculated electron self-energies, and the calculated binding energy Δ_−2,3 for the reference ILT.

Processing of experimental near-field data

The following section describes the processing of the experimental near-field data that are displayed in Figs. 2 (D to F), 3A, and 5A. We want to emphasize that we tried to keep data and image processing to a minimum. The data processing that we did apply is described below for each (sub-)figure showing experimental near-field data:

Figure 2 (D to F): The 2D scans at 0.0 T (Fig. 2D) and 3.35 T (Fig. 2E) show raw data. No filter was applied. The scan at 6.0 T (Fig. 2F) was corrected for horizontal strokes using the “correct horizontal scars (strokes)” function of gwyddion (program version 2.62).

Figure 3A: The near-field data were corrected for slow spatial drift during this linescan using the topography information recorded simultaneously with the near-field data. Each line was horizontally shifted such that the topography step of the gold electrode aligns for all lines (refer to Fig. 1D for a sketch of the sample). The topography information was also used to select the region without the gold electrode. Using this information derived from the topography data, the same procedure was then applied to the near-field data to obtain the drift-corrected version of the near-field response on hBN and hBN-graphene-hBN shown in Fig. 3A. In addition, we found that the average near-field signal of our measurement slowly decreased with time. This can be assigned to minor drift in the optical alignment over the long measurement time of >8 hours. Assuming a linear dependence on time, we estimated a drift of 1.01% signal reduction per hour of measurement time relative to the initial near-field signal. We multiplied the near-field signal of each line with a constant compensating for this slow linear drift.

Figure 5A: The near-field data were corrected for slow spatial drift during this line scan using the topography information recorded simultaneously to the near-field data; this procedure is identical to the one applied for the near-field data of Fig. 3A. We did not compensate for any potential temporal drift of the near-field signal, as we assume that it will be negligible because of the shorter measurement time compared to Fig. 3A.

Extracting the polariton wavelength and quality factor from near-field line profiles

Each horizontal line of the near-field data displayed in Figs. 3A and 5A represents a line profile such as the examples displayed in Figs. 3C and 5B. We analytically describe each line profile via an exponentially damped sine wave (20, 68–70) with linear background term

$$S\left(x\right)=S_0+S_{1}x+A{e}^{-x/L_p}\text{sin}\left(2\mathrm{\pi }\frac{x}{{\mathrm{\lambda }}_p}-{\mathrm{\phi }}_0\right)$$ (28)

The vertical offset S₀, the polariton wavelength λ_p, the polariton decay length L_p, and the phase offset φ₀ are optimized for each line using a least-square fitting procedure. For this fitting procedure, the left-most 10% of each line are neglected. The linear background slope S₁ and the amplitude A are constants that are optimized once for the whole dataset. However, S₁ and A are not part of the fitting procedure and, thus, have the same value for all line profiles within a dataset.

Applying this fitting procedure to the data displayed in Figs. 3A (Fig. 5A) directly yields the polariton wavelength λ_p displayed in Figs. 4A and 5C. The quality factor Q (Figs. 4B and 5D) is calculated as Q = 2πL_p/λ_p, i.e., it directly follows from the ratio of the fit parameters L_p and λ_p.

For our analytical description, we assume that our observed fringe pattern is dominated by polariton waves that are launched by the gold electrode (refer to Figs. 1D, and 2 D to F). This is opposed to polaritons launched by the tip and then reflected by the gold electrode.

Note that our analytical description above may be modified to reflect the geometrical spreading of the polariton waves, resulting in a function of the following form

$$S\left(x\right)=S_0+S_{1}x+A{x}^{-p} e^{-x/L_p}\text{sin}\left(2\mathrm{\pi }\frac{x}{{\mathrm{\lambda }}_p}-{\mathrm{\phi }}_0\right)$$ (29)

The additional factor x^−p reflects the amplitude reduction due to the geometrical spreading; the most common version of this factor uses a power p = 1/2, i.e., a factor x^−1/2 corresponding to circularly spreading waves in a plane (20, 68–70). If we apply this modified description to our data, we still obtain a good match to our data, but the resulting polariton quality factors are about three times larger compared to the values shown in the main text. However, while it is common to apply the geometrical spreading factor for polaritons launched by the tip or small antennas (20, 68–70), in our case, the edge of a gold contact (refer to Fig. 1A for the sample design) represents a linear launcher with extension larger than the analyzed polariton propagation length (70). This is why we chose not to add the factor x^−1/2 in our analysis. Nevertheless, this also suggests that the quality factors shown in Figs. 4B and 5D may be an underestimation.